Transformational Networks, Transpositional Combination, and Aggregate Partitions in Processional by George Crumb
Ciro G. Scotto
KEYWORDS: Crumb, transformations, transpositional combination, aggregate partition, networks, transpositionally invariant sets
ABSTRACT: George Crumb is popularly known as a composer who employs extended instrumental techniques. This characterization could divert attention away from investigating pitch structures in his compositions. Although some theoretical works have begun focusing attention on pitch, the scope of these investigations has been limited to the procedures associated with a limited number of symmetrical sets. Focusing solely on symmetrical sets could overshadow other methods of organizing pitch. Through an analysis of the solo piano work Processional (1983), I will demonstrate that Crumb’s procedures include techniques that link the compositional opportunities symmetrical sets offer to the procedures associated with aggregate-based atonal composition. The analysis will reveal that symmetrical and non-symmetrical set structures in Processional are part of a larger group of relations that include techniques such as aggregate partitions, transpositional combination, and transformational networks. My analysis will also demonstrate how these techniques and the techniques associated with symmetrical sets blend to create a larger compositional universe. Finally, I will suggest a more general model for the various networks that appear in Processional.
Copyright © 2002 Society for Music Theory
[1] The propensity of some composers to gravitate towards a select group of
set classes as the source of musical structure in their works has become a type
of equivalence relation in recent theoretical writings that tends to group some
composers into two large classes. Richard Bass has noted that this bifurcated
view of pitch structure essentially places Schoenberg and his followers on one
side of the divide and on the other side are composers, such as Bartok, Stravinsky,
and Messiaen, whose compositional procedures are inextricably linked to symmetrical
set classes.(1) Another factor contributing
to this bifurcated view is the tendency to raise the status of symmetrical set
classes to be on par with but independent of the diatonic collection. That is,
symmetrical set classes are seen as functionally equivalent to their diatonic
counterparts in their capacity to function as referential collections that generate
musical structure. They are emancipated from the diatonic, because the structures
and procedures they produce do not need to be legitimized as originating with
the diatonic. The simultaneous functional association of symmetrical set classes
with the diatonic and functional emancipation of symmetrical set classes from
the diatonic widens the gap between the classes of composers, since the compositional
procedures of Schoenberg and his followers tend not to be seen through the same
referential filter. A passage from the conclusion of Bass’s article implicitly
suggests that this might be the case:
The octatonic and whole-tone elements in “Music of Shadows,”. . . are distinctive in their emancipation from any enlarged diatonic context. At the same time, labels such as “chromatic” or “atonal” are too general to account for the pitch-structural orientation of the piece. The interpenetration of these referential collections is not without precedent, but Crumb’s specific approach is unique in its elevation of existing techniques to the level of independent procedures capable of generating motivically unified, complete musical structures. . . The ascendancy of aggregate-based atonal and serial methods during the mid-twentieth century may have temporarily relegated these symmetrical referential collections to a subordinate role, but recent works by a number of composers provide evidence that the compositional opportunities offered through interaction between octatonic, whole-tone, and related sonorities. . . were not exhausted in the early part of the century. Crumb in particular has developed clear and aurally accessible models for the integration of two, and sometimes more, non-diatonic reference sets that stand on a par with diatonic and chromatic writing within the broader spectrum of his eclectic harmonic language.(2)
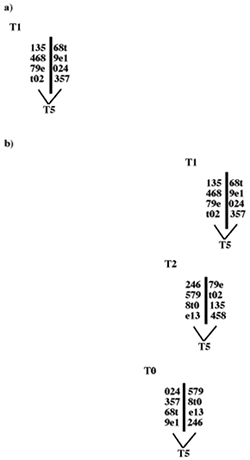
Example 1a. TINV Set Classes
(click to enlarge)
Example 1b. Generators of Set Class 4–25 by TC
(click to enlarge)
[2] Richard Cohn expounds a similar but more general view of symmetrical set
classes in his article “Properties and Generability of Transpositionally
Invariant Sets.”(3) As Cohn’s
article clearly states and Bass’ article implicitly states, the select
group of set classes that composers gravitate towards is the collection of transpositionally
invariant or transpositionally symmetrical set classes (see Example 1a). Cohn claims the gravitational pull of this collection of set classes
for a composer lies in their modes of generability. This means each member of
this select group is capable of being generated by a multitude of transformations
of its transpositionally related subsets, and conversely, each member of this
group can be disunited into a multitude of transpositionally related subsets.
Example 1b, adapted from Cohn’s
article, illustrates that members from each of the set classes 2-2, 2-4, 3-8,
and 4-25, which are all members of Cohn’s cyclic homomorphic equivalence
class [02] mod 6, generate a member of set class 4-25 under the operation of
transpositional combination with T6 as the operand. Conversely, members
of set class 4-25 can be disunited into T6 related members of the
generating set classes.
[3] Modes of generability is the fundamental transformational process that,
according to Cohn, reduces the power of diatonic interaction as an explanation
for the popularity of the TINV family of sets. One might suppose that if the
ability to interact with the diatonic generated the utility of TINV sets classes,
then both collections would share some essential structural features. For example,
besides transpositional invariance, TINV set classes are also inversionally invariant,
a property TINV set classes share with the diatonic hexachord 6-32 [024579].
Cohn notes, however, that TINV and diatonic collections rate below average on
any number of similarity scales. He goes on to say that dissimilarity is not,
of course, a prophylactic against TINV and diatonic interactions, nor is it
a preventative against raising those interactions to the level of forming a
compositional syntax, but the dissimilarity of the collections suggests that
a special relationship between the collections is not the source of their interaction.
Cohn cites historical/semantic reasons for why TINV collections might want to
legitimize themselves by associating with the more established member of the
diatonic, but “given a diatonic collection as a compositional premise,
it is not yet clear why TINV collections should be chosen as playmates.”(4)
[4] One aim of this study is to build a little more of one particular bridge
across the canyon separating the two views of pitch structure. Cohn laid this
bridge’s foundation by noting how modes of generability are related to
research in combinatoriality. The material for our bridge’s roadway will
come from the diatonic collection of sets. Consequently, another aim of this
paper is to explore syntactic connections that make the diatonic and TINV collections
good playmates. We will explore these issues by means of an analysis of Crumb’s
solo piano work Processional (1983). I will demonstrate that the work’s
compositional procedures include techniques that link the opportunities TINV
collections offer to procedures associated with aggregate-based composition.
The analysis will also reveal that TINV and non-TINV set structures in Processional
are part of a larger group of relations that include techniques such as aggregate
partitions, transpositional combination, inversional symmetry, generalized CUP
relations, K-nets, and other transformational networks.(5)
[5] Before we begin, however, we need to establish a rule of the game. “Aggregate-based composition” is a loaded expression that means many things to many people. One association I would like to avoid is that aggregate-based composition implies perceiving aggregate completion as a necessary foundation for comparing aggregates and their contents. I don’t want to avoid the sense of aggregate completion requiring the presence of all twelve tones, but I would like to avoid the implication of the aggregate as a perceptual unit that once perceived signals a change from one aggregate to another. This form of aggregate completion is most often associated with some forms of serial composition. In some serial contexts, we know we have moved from one row form to another or from one aggregate to another, because hearing the completion of an aggregate marks the boundary between aggregates. We can discover the transformational relationship between two row forms or compare the configuration of transformationally related subsets within each aggregate, once the aggregate boundary has been perceived. Most often, the non-immediate repetition of a pitch-class determines or can act as a signal that the aggregate boundary has been reached. Since Processional uses unordered or non-serially ordered collections, pitch-class repetition is an ineffective marker of aggregate boundaries, because the repetition of a pitch-class does not signify aggregate completion. Furthermore, any number of events can signal or be the impetus for the change from one aggregate to the next. Aggregates in the present discussion are, to use Robert Morris’ term, compositional spaces that are contained within the larger compositional space produced by the transformational networks that link aggregates. In Processional, the completion of one process and the initiation of a new process often determine the change from one aggregate to the next. In the former view, aggregate perception is necessary and it forms the basis of local comparison, while in the latter view local comparison does not depend on perceiving aggregates. I would also like to extend the concept of an aggregate compositional space to include transformations as well pitch classes. Object and process are inextricably intertwined in Processional, so aggregate transformational structures often mirror aggregate pitch-class structures. Furthermore, the concept of an aggregate transformational space is one source of the work’s coherence, since the space is closed with regard to the particular transformation. Partitioning the aggregate transformational space generates many of the work’s formal divisions. As I will demonstrate, these surface formations are the result of deeper or hidden processes.
[6] Processional, as a score and composition, has several features that
are worth noting. The score does not contain any barlines, except for double
bars that mark the work’s large divisions. In many ways, the absence of barlines
is a visual indicator that underscores viewing the piece as a single unfolding
process, such as the process that takes a fertilized egg from single cell to
a multi-celled functioning organism. The score also lacks any of the usual timbral
devices, such a plucking the strings inside the piano, which are associated
with Crumb’s music. The lack of extended timbral techniques focuses attention
on the work’s pitch-class structures. Crumb does include a one page appendix
containing six Ossia passages with, in the composer’s words, “a
few extended piano effects,” perhaps for players who may miss this aspect
of his music. Although the work lacks barlines and it is a single unfolding
process, it does divide up into several sub-processes (see Example 2). The work contains three large sections at the global level in the familiar
pattern A-B-A. The presence or absence of key signatures and the double bars
distinguish the A and B sections. The A sections each contain four sub-sections
that are distinguished by changing key signatures. Although the B section lacks
divisions marked by change of key, it also contains four sub-sections marked
by change of texture. Sections one and four are homophonic, section two is contrapuntal,
and section 3 is a hybrid homophonic/contrapuntal texture.
[7] Processional begins with a descending six-note motive that is a
member of the set-class 6-32[024579] commonly known as the diatonic hexachord
(Example 3a). Moving quickly to a
high level of generalization, however, bypasses many of the hexachord’s
more important features and implications generated by its pitch realization.
The three semitone or interval class (hereafter ic) 3 “gap” at the
hexachord’s center splits it into two trichordal subsets that are members
of set class 3-6[024]. Although many other pitch realizations, such as transposing
the lower trichord up an octave (Example 3b), produce similar results, the ic 3 gap at the hexachord’s center
perhaps emphasizes both the independence of the 3-6[024] trichords and their
role in generating the larger set. The “octave up” pitch realization,
for example, may at a higher level of abstraction contain the same information,
but it is not quite set into the same relief, since it perhaps emphasizes the
hexachord and de-emphasizes the trichords. While the pitch realization of the
motive emphasizes the generative role 3-6[024] trichords may play in producing
the hexachord, it does not say anything definitive about the chosen generative
path. Perhaps the simplest transformational route would be by means of transpositional
combination (hereafter referred to as TC) of the lower trichord at T7
(see Example 3c). However, the arrangement
of the pitches around the gap also strongly suggests inversional symmetry at
TeI or inversional symmetry around the pitch dyad B3/C4, or more
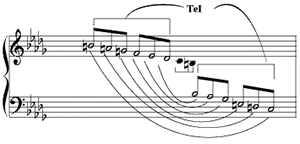
generally IC/B, as alternate transformational routes.(6)
Example 3b. Processional’s Motivic Cell (click to enlarge) | Example 3c. Processional’s Motivic Cell (click to enlarge) |
Example 4. Possible Diatonic Contexts for Processional’s Motivic Cell
(click to enlarge)
Example 5a. Possible Continuation of TC Generative Path
(click to enlarge)
Example 5b. Possible Continuation of TC Generative Path
(click to enlarge)
[8] The inversional dyadic center plays another important role with regard
to another ambiguity created by this motive’s pitch realization. The subset-superset
relation created by the trichord partitioning of the hexachord suggests inclusion
relations may play an important role in this work (Example 4). For example, including either member of the dual axis of symmetry around
which the 6-32 [024579] hexachord is constructed generates two different members
of the set class 7-35[013568t]. While the “key signature” of the piece
implies a 7-35[013568t] superset with a pitch class content of {
[9] The trichord partitioning of the hexachord also suggests hexachords may
be part of a larger partitioning scheme. Each of the outlined transformational
routes, for example, determines a different partitional path that the motive
may travel in its development (Example 5a). Continuing on the TC path produces a series of T7 related 3-6[024]
trichords. The T7 path that generates trichords is suggestive, because
T7 cycles of pitch classes generate the collections 6-32[024579],
7-35[013568t], and 8-23 [0123578t]. Of course, the new trichords maintain all
the structural features of the generating pair, but some of those features are
lost at the level of the hexachord. For example, unlike the trichords, the hexachords
do not maintain the non-intersecting pitch-class content feature of the trichords.
Continuing on the path of inversional symmetry, however, produces a new pair
of trichords that maintain the structural features of the generating pair, and
it produces a new hexachord that maintains the non-intersecting pitch-class
content feature of the trichords with the original hexachord (see Example 5b). The two diatonic hexachords, of course, produce the aggregate, since
their pitch-class content is non-intersecting or complementary with regard to
the total chromatic. If, however, the inversional center partitions the aggregate
rather than the diatonic hexachord, then the two hexachords generated by the
transformational schema are members of set class 6-35[02468T] or the whole tone
collection. As we shall see shortly, other combinations or partitions of this
aggregate’s components produce other hexachordal profiles. Therefore, perhaps
rather than viewing any particular hexachord as being fundamental, the 3-6[024]
trichord and its transformational stance should be thought of as fundamental,
in the same way that plate tectonics is responsible for the surface formations
of the earth. That is, surface formations are the result of deeper or hidden
processes.
[10] The question now, of course, is how does this transformational model play
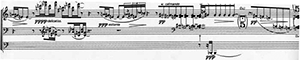
out in the music (see Example 6). While the
[11] Although the C4 completes the pitch-class aggregate in the third system
of Example 6,
the action within this aggregate compositional space continues, because the
process behind the procession in this section of Processional has not
reached its completion. Prior to this point, the ostinato hexachord has not
remained unaffected by the procession of notes around it. It constantly reinvents
its set-class profile by losing its own members, acquiring members from its
complement, or both losing and acquiring new members. Although the full implications
of how these changes contribute to the structure of the work are beyond the
scope of this paper, we can examine one or two key relationships. For example,
with the first appearance of B2 in the outer stream, the
[12] When the aggregate is finally completed with the entrance of the C4, the
process of hexachordal reinvention continues. For example, the C4 entrance produces
a 6-Z28 [013569] with four members of the opening 6-32 hexachord {
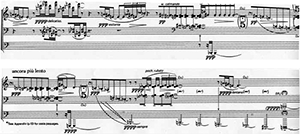
Example 8a. T(0167) [024] TC Networks
(click to enlarge)
Example 8b. T(0167) [024] TC Networks
(click to enlarge)
Example 9a. T(0369) [024] TC Networks
(click to enlarge)
Example 9b. T(0369) [024] TC Networks
(click to enlarge)
Example 10. Union of [0167] TC Networks
(click to enlarge)
Example 11. Section 2 of Processional
(click to enlarge)
Example 12. Unfolding of the T1 [0369] TC Networks in Different Streams
(click to enlarge)
Example 13. Joint Between Sections 1 and 2
(click to enlarge)
[13] Although the inversional transformational schema models the pitch realization
of the 3-6[024] trichords, a more general pitch-class transpositional network
based on TC relations produces another model of the four 3-6[024] trichords
that better explains their relationship to other structural features of the
composition. Taking the pc set {024} as the point of origin or T0,
the remaining trichords relate to it by T1, T6, and T7
(Example 8a). In this model, combinations
of interval cycle 6 or C6, following Perle and Cohn, generate the four trichords.(9)
An interesting consequence of this generative process is that it has two faces
that are revealed by exchanging object and process in the matrix. If the transformational
process, T0, T1, T6, T7 becomes
the pitch class set {0167}, and the pitch class set {024} becomes the transformational
process T0, T2, and T4, the new process generates
a differently partitioned aggregate from members of set class 4-9[0167]. Applying
the T(024) process to the original matrix produces an interesting
and related result. Example 8b illustrates,
that the three matrices produce all twelve transpositions of the 3-6[024] trichord,
which represents another level of saturation. The exchange of process and object
in this aggregate generating context creates a bond between two set classes
that do not rate very highly on any of the conventional similarity scales, and
it bonds a member of the TINV collection with a set class from outside its world.
[14] The T(0167) transformation is not the only cyclic generator
of the aggregate bonded to the 3-6[024] trichord. When the pitch C4 completed
the aggregate, it did so against a 6-Z28 [013569] hexachordal backdrop. This
hexachord weaves together the {
[15] The work’s second section, demarcated in the score by the change
of key signature from five flats to four sharps and demarcated in the processional
by another process, continues the homophonic texture from the end of the previous
section (see Example 11). Although the new section
continues the previous section’s texture, the processes generating musical
development begin all over again. The first chord of section two, E 6-32[024579],
repeats the generative role played by the
[16] The one exception is
[17] Sections one and two present several musical streams, the homophonic texture
of the middle register and the single note events that unfold around the center
form two streams.(10) Each stream
unfolds complementary related hexachords. Focusing on the center stream for
a moment reveals that its transpositional process is directly related to the
T1 T(0369) matrix of Example
10b, since the first two hexachords of the matrix are the hexachords unfolded
in the center stream. The outer registral stream simply follows a rotated version
of the matrix related to the original matrix by T6. These relationships
are more easily graphed by collapsing each hexachord into its first pitch class
and taking that pitch class as a representative of the hexachord and as a representative
of the member of the cycle generating the matrix (see Example 12). In the example, the number 1 represents the
[18] While each half of the T1 T(0369) matrix and each
half the graph contain complementary hexachords, adjacent hexachords in the
T1 T(0369) matrix and in the individual streams of the
graph share three common tones. Furthermore, the non-common tones are all adjacent
pitch classes. As the joint between sections one and two illustrates, these
pitch class properties translate into extremely smooth or parsimonious voice
leading in the pitch dimension (see Example 13). The pitches of the
[19] If the T1 T(0369) matrix model of hexachordal progression
is the model or process directing hexachordal motion in the work, then the next
hexachord to appear in the center stream should be G 6-32[024579], the hexachord
from section one’s outer stream. As the key signature change in score indicates
(see Example 14),
the G whole tone collection ending on
[20] Although the T1 T(0369) matrix model of hexachordal
progression predicts the next hexachordal change in the center stream (the hexachordal
stream that determines the key signature) should be a member of
[21] Two non-mutually exclusive explanations can account for this departure
from the T1 T(0369) matrix model of the process governing
hexachordal progression in Processional. First, since the previous section
saw the first return of a hexachordal collection and the crossing of hexachordal
streams, section three was the beginning of a modified return that sufficiently
represented the model, so there is no need to continue along its outlined path.
Consequently, the music is free to develop in other directions. Second, the
B 6-32[024579] hexachord really could be an interloper that just temporarily
halts the progression of the T1 T(0369) hexachordal progression.
In the latter case a new stream begins before the active stream finishes implying
that both streams, T1 T(0369) and T2 T(0369),
will continue to influence musical developments. The latter path is the one
we will follow.
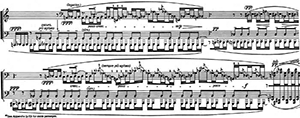
Example 15. Section 4
(click to enlarge)
Example 16. Four IS Models
(click to enlarge)
Example 17a. T(0369) [015] TC Networks
(click to enlarge)
Example 17b. T(0369) [015] TC Networks
(click to enlarge)
[22] Although the inversional transformational model underlies the pitch realization
of both hexachordal streams in section four, besides the key confirming pitch,
[23] Before the hexachordal progression through the T1 T(0369)
matrix was interrupted by the B 6-32[024579] hexachord, the expected hexachord
was
[24] Although inclusion relations and voice leading connections make a compelling
case for associating the {
[25] It should now be obvious that the other 4-20[0158] tetrachords accompanying
the
Example 17c. T(0369) [015] TC Networks
(click to enlarge)
Example 18. First Section of Section B
(click to enlarge)
Example 19. Alternation of 4-20 [0158] and 6-32 [024579] Complexes
(click to enlarge)
Example 20. Second Section of Section B
(click to enlarge)
Example 21. Completion of T(0369) 6-32 [024579] Complexes
(click to enlarge)
Example 24. Fourth Section of Section B
(click to enlarge)
Example 25. Return of the A Section
(click to enlarge)
Example 26a. Beginning of the Coda
(click to enlarge)
Example 26b. Beginning of the Coda
(click to enlarge)
Example 27. T(0167) Unfolding of the 6-32 [024579] Hexachords
(click to enlarge)
Example 28. 8-9[01236789] in the Coda
(click to enlarge)
Example 29a. Interweaving of T1 and T2 (0369) 6-32 [024579] Complexes in the Work’s Closing
(click to enlarge)
Example 29b. Interweaving of T1 and T2 (0369) 6-32 [024579] Complexes in the Work’s Closing
(click to enlarge)
Example 30. Transformational Networks Generating 6-35 [02468t] from 3-6 [024]
(click to enlarge)
[26] Example 12 demonstrated that
by collapsing each hexachord of the center stream to its first pitch class,
the cycle generating the hexachords, (147t), also represents the progression
of the hexachords. The same process applied to the pitch realizations of the
4-20[0158] tetrachords produces a reordering of the same cycle, <t471>,
which is a near retrograde of the generating cycle for the hexachords. Although
collapsing the pitch realizations of the 4-20[0158] tetrachords as “major
seventh chords” into their “roots” produces a generating cycle
of (147t), the cycle generating the pitch-class counterparts of 4-20[0158] tetrachords
in Example 17b is (0369). Consequently,
it always the second column of pitch-class matrices, such as the second column
of Example 17b, that links a pitch-class
complex of 4-20[0158] tetrachords to their hexachordal counterparts. Applying
the transformations T1 and T2 to the original 4-20[0158]
tetrachordal matrix generates two more matrices, which when combined with the
T0 matrix, produce all twelve transpositions of the 4-20[0158] set
class. (See Example 17c and again,
the interested reader may also wish to see Example
34 (below), which illustrates the transformational relationships more explicitly.)
The hexachordal counterpart of the T1 T(147t) tetrachordal
matrix is the T(258e) hexachordal matrix, and the hexachordal counterpart
of the T(258e) tetrachordal matrix is the T(0369) hexachordal matrix.
[27] The immediate appearance of hexachords
[28] The 6-32[024579] hexachords begin a similar progression and process in
between the 4-20[0158] complexes. In this section, the hyperaggregate of transformations
is not completed, but the implication that the interloping B 6-32[024579] hexachord’s
cycle will continue at some point is fulfilled (see Example
19). This is the only hexachordal cycle to be completed, in fact. A nice
compositional detail connecting the end of the A section with the T2
6-32[024579] matrix is the progression through the matrix’s hexachords.
The pitch realization of the final B 6-32[024579] hexachord is identical to
its counterpart at the end of section A (see Example
19). Although all the hexachords of the T2 6-32[024579] matrix
occur in the progression completing the cycle, the cycle is still incomplete
in another respect. The hexachords of the T2 6-32[024579] occupy
two different registral streams suggesting completion of the streams will occur
at a later point in the music. The next hexachord to appear in the upper stream
would be D 6-32[024579]. The D 6-35[02468t] whole tone hexachord that follows
the final incomplete 4-20[0158] complex substitutes for the outer stream D 6-32[024579].
Essentially, D 6-35[02468t] functions as a transitional collection leading to
the section that completes the 6-32[024579] hyperaggregate.
[29] The process of interpolation that began at the end of section A and characterized
the beginning of the developmental section B continues as the 6-32[024579] hexachords
complete their hyperaggregate (see Example 20). The T1 matrix
of 6-32[024579] hexachords, which was left incomplete in section A begins the
progression through the hyperaggregate (Example 21). It is significant that the progression begins with E 6-32[024579] and
moves directly to
[30] The new 3-4[015] interloper that separates the first two hexachordal complexes
is, of course, related to the 4-20[0158] complexes by inclusion, but its new
association with ic 6 foreshadows the translation of an earlier generative schema
into the pitch dimension. After the final 6-32 hexachordal complex completes
the hyperaggregate, the interpolated material moves to the foreground expanding
the 3-4[015] trichord and the 4-8[0156] tetrachord into 6-7[012678] hexachords
(see Example 22).
The first 6-7[012678] hexachord in the right hand part leads to a T6
re-mapping of itself that is immediately followed its complement at T9.
The 6-7[012678] hexachords travel along the same T6—T3—T6
or (3906) transformational path taken by the 4-20[0158] tetrachords and 6-32[024579]
hexachords. The left-hand parts are also T6—T3—T6
or (3906) related and complements of the right hand parts. The T(0167)
generative schema underlying the 3-4[024] trichords of the IS model from section
A translated into a member of set class 4-9[0167] is, of course, included in
set class 6-7[012678].
Example 22. Third Section of Section B (click to enlarge) | Example 23. Catalog of 8-9[01236789] Octachords (click to enlarge) |
[31] Set class 4-9[0167] emerges from the 6-7[012678] hexachordal cloud to
become a substantial entity in the following section where the super set generated
by T6 related 4-20[0158] tetrachords is regenerated by means of Cohn’s
concept of modes of generability. Each 4-20[0158] tetrachordal complex at the
opening of section B consist of two pairs of T6 related 4-20[0158]
tetrachords forming a member of set class 8-9[01236789], a member of the TINV
set classes (see Example 23). As
well as generating all the transpositions of set class 4-20[0158], the tetrachordal
complexes generate all the transpositions of set class 8-9[01236789]. In the
section following the 6-7[012678] hexachords (see Example 24a), two different tetrachordal
set classes, 4-9[0167] and 4-23[0257], generate the same collection of 8-9[01236789]
octachords that is essentially a rotated and retrograded version of the collection
of 8-9[01236789] octachords in Example
23 (see Example 24b).
[32] Although 4-9[0167] emerges as a pitch class event in the developmental
B section, it is the coda that makes explicit its dual nature and its generative
connection to the 3-4[024] trichords and the 6-32[024579] hexachords. After
another round of development progressing through the T0, T1,
and T2 T(0369) 6-32[024579] hexachordal matrices, G 6-32[024579],
the T6 complement of
[33] The progression of 6-32[024579] hexachords in the coda corresponding to
the progression of hexachords in the development that completed the hyperaggregate
reveals the dual nature of 4-9[0167] and its generative connection to the 3-4[024]
trichords and the 6-32[024579] hexachords. The succession of hexachords abandons
the (0369) transformational path to pursue the work’s other generative path,
(0167) (see Example 27). (The interested reader may
also wish to compare Example 27 with Example
31 (below), which illustrates how the same transformational path and the same trichordal
objects generate different hexachordal objects by changing the transformational
relationships relating hexachordal objects.) As if it is trying to bring a subconscious
thought into consciousness, the final reference to the 8-9[01236789] octachord
begins with a solo statement of 4-9[0167] (see Example 28). The work closes with the
T1 and T2 6-32[024579] hexachordal matrices following
intertwined (0369) transformational paths (see Examples 29a and b). While the T1 path
leads to and concludes on the
[34] The appearance of 6-35[02468t] as the goal of the of the intertwined T1
and T2 6-32 [024579] hexachordal matrices following the (0369) transformational
path gives rise to another view of the work’s final progression. Rather than
viewing the succession of 6-32 hexachords as following intertwined (0369) transformational
paths, we can also view the progression as a sequence of incomplete 7-35 septachords
whose collection defining pitch class is the bass note of the lower 3-6[024]
trichord.(11) The succession of
bass notes, A3, G3,
[35] Examples 30 through 35
and the discussion that follows summarize, in the abstract, the transformational
networks governing the exchange of object and process in Processional.
Reinterpreting the pitch-class matrices as transformational networks reveals
that the network of tritones generating the whole-tone collection and the replication
of transformations from one nodal level at higher or lower levels is a feature
shared by all the matrices and is a source of the work’s coherence. Each
of the T6 nodes in a column formed by the nodes of nodes in Example 30 generates 3-6[024] trichords whose union produces 6-35[02468t]. Applying
T1 to Example 30 produces
the T(0167) matrix of 3-6[024] trichords (see Example 31), and applying example 30’s supernode transformations to the new
supernodes produces the other matrices generating all twelve transpositions
of 3-6[024]. Simply changing the second level T1 transformation to
T3 produces all the T(0369) matrices of 3-6[024] trichords
(see Example 32). Example 33 illustrates that applying T5 to third level node of example
32 generates the hexachordal matrix, and applying T2 twice to this
new supernode generates all the hexachordal matrices. Example 34 illustrates the 4-20[0158] matrices keep the second level transformation
constant and change the third level transformations. Finally, Example 35 illustrates how successive T5 transformations of the T6
node produce two T6 related 4-23[0257] tetrachords whose union generates
8-9[01236789].
|
Example 31. Generating Larger Networks from the 6-35 [02468t]/3-6 [024] Networks (click to enlarge) |
Example 32. Transformation of the Larger Network by Substituting Operations (click to enlarge) | |
|
Example 33. Generating a 6-32 [024579] Network from a 6-35 [02468t] Network by Substituting Operations (click to enlarge) |
Example 34. Generating the 4-20 [0158] Network from the Same Set of Local Operations (click to enlarge) |
Example 35. T5 transformations of T6 nodes Generates Two T6 related 4-23[0257] tetrachords whose union generates 8-9[01236789]
(click to enlarge)
[36] The numerous generative transformational paths leading from subset to
superset is, as Cohn has noted, one of the most interesting features of the TINV
family of sets. It should not be surprising that the aggregate or 12-1 shares
this property, since it is a member of the TINV family. Translating TINV sets
into transformational networks that partition the aggregate, however, means
the TC property of 12-1 is non-trivial. The same cannot be said for a non-partitioned
aggregate. As well as bonding together members of TINV with sets from outside
the collection, TC aggregate partitioning can also be a bridge across different
means of generating larger sets from smaller ones. For example, the non-intersection
of generative components that is a hallmark of TC aggregate partitioning is
one of the defining features of Robert Morris’ complement union property
or CUP. In future work, I hope to demonstrate the general properties relating
TC TINV sets as a subset of generalized CUP relations. That is, we can view
the two methods of generating larger sets from smaller ones as concentric circles
with the smaller world of TINV contained within the larger CUP world with CUP
perhaps in a more general set of relations, such as K-nets.
[37] For example, in his generalization of CUP relations, Morris allows CUP
to expand in two directions by relaxing the constraint that the intersection
of the generating sets must be the null set and union of the members of the
generating sets classes must produce a single set class.(12)
The number of set classes generated by the generalized CUP relation is indicated
by a superscript added to CUP. CUP4, for instance signifies that the members
of the generating set classes produce four different set classes when the intersection
of the generating sets is the null set. Processional’s generative
3-6[024] trichord produces a CUP4 relation, when the generating sets are both
members of set class 3-6. The four hexachords produced by this CUP relation
are 6-1[012345], 6-35[02468t], 6-32[024579] and 6-8[023457]. Two of the resultant
hexachords, 6-1 and 6-35, are members of TINV, and the generation of these hexachords
from the smaller TINV collection 3-6 is a function of Cohn’s modes of generability.
The latter two hexachords, 6-32 and 6-8, are not members of TINV, however, but
the similar generative path from smaller to larger set demonstrates how the
smaller collection of TINV sets connects to the larger world of sets that are
not members of TINV. It also demonstrates another reason why, in the specific
case at hand, the diatonic makes a good playmate for TINV sets. The CUP4 relation
also demonstrates how the 7-23[0234579] from the work’s opening fits into the
larger framework of the piece, since the CUP4 hexachord 6-8[023457] is a subset
of the 7-23 hexachord. As was stated earlier, the 6-33[023579] hexachord from
the work’s opening is also a subset of 7-23, and the mutual inclusion of
6-8, 6-33, and 6-32 in 7-23 creates an indirect role for 6-8 as a unifying force
in Processional. K-nets, however, reveal that 6-33 hexachord is one path
through which the 3-6[024] trichord creates connections with other trichords.
[38] The pitch-class exchange of B2 for
[39] Expanding the analytical field of view to include the interconnection of object and process often reveals the camouflaged bridges connecting concentric circles. In this new worldview, compositional design would determine the utility of a circle’s structural properties, and it would determine movement between circles. Since there are bridges connecting circles, the circles themselves do not have to become equivalence classes. I hope my analysis Processional has demonstrated the importance of considering both objects and their interconnection with process in Processional and perhaps in Crumb’s work as a whole. The interconnection reveals his compositional procedures extend beyond the boundaries of any particular circle, such as exclusive use of symmetrical set classes. The study of object and process in a Crumb work also reveals that aggregate-based atonal methods and composing with symmetrical referential collections are concepts that can peacefully coexist and reinforce each other. In the spirit of Hegel, Processional is a synthesis of compositional procedures that often assume the roles of thesis and antithesis in the dialectic. Of course, the same observations hold with regard to the superset levels within the TINV family, so a well-partitioned aggregate is just as good a referential collection as any of the other supersets in the TINV family. That is, the properties that endow the whole tone and octatonic collections with special status within the TINV family are properties also possessed by a well-partitioned aggregate. Finally, I hope that I have shown the structural gap generating equivalence classes of composers may not be as large as it once appeared to be. Perhaps now it is just a similarity relation.
Ciro G. Scotto
Eastman School of Music
Department of Theory
26 Gibbs St.
Rochester, NY 14604
cscotto@theory.esm.rochester.edu
Footnotes
1. Richard Bass, “Models of Octatonic and Whole-Tone Interaction: George Crumb and His Predecessors,” Journal of Music Theory 38 (1994): 155–186.
Return to text
2. Bass, “Models of Octatonic and Whole-Tone Interaction,” 186.
Return to text
3. Richard Cohn, “Properties and Generability of Transpositionally Invariant Sets,” Journal of Music Theory 35 (1991): 1–32.
Return to text
4. Cohn, “Properties and Generability,” 4.
Return to text
5. CUP is Robert D. Morris’s term for the complement union property. He presented this work in the article “Pitch-Class Complementation and its Generalization,” Journal of Music Theory 34 (1990): 175–245. K-net is just a shorthand term for a Klumpenhouwer Network. The general properties of k-nets are presented by David Lewin in the article “Klumpenhouwer Networks and Some Isographies that Involve Them,” Music Theory Spectrum 12 (1990): 83–120.
Return to text
6. IC/B is Lewin’s label free method of notating inversional operations. See David Lewin, “A Label-Free Development for Twelve-Pitch-Class Systems.” Journal of Music Theory 21 (1977): 29–48.
Return to text
7. Hearing pitch events as occupying distinct registral steams affords each stream a degree of independence from the activities or processes unfolding in another stream. For example, pitches that are members of the same pitch class can have distinct functions determined by the registral stream they occupy. Therefore, the B2 and B4 of Example 6 are not merely octave duplications, they perform different functions determined by the process unfolding in their respective streams. This point will be reinforced in the above text and the text that follows.
Return to text
8. The significance of the 6-Z28 hexachord will be revealed later in the paper.
Return to text
9. This method of generating aggregates was introduced by Daniel Starr and Robert Morris in their two-part article “A General Theory of Combinatoriality and the Aggregate,” Perspectives of New Music 16/1 (1977): 3–35; Perspectives of New Music 16/2 (1978): 50–84.
Return to text
10. As indicated earlier, a third stream unfolds in the outer registers of the piano that is initiated by the pitch B2.
Return to text
11. The precedent for interpreting hexachords as incomplete members of the set class 7-35 was, of course, established at the work’s opening. Hearing the hexachords within a septachordal context allows us to hear the
Return to text
12. Robert Morris, “Pitch-Class Complementation and its Generalization,” 191–95.
Return to text
13. For a full explanation of the general properties of k-net isographies and the rules for generating network isomorphisms see Lewin, “Klumpenhouwer Networks and Some Isographies that Involve Them.”
Return to text
Copyright Statement
Copyright © 2002 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Timothy Koozin, Co-Editor and Tahirih Motazedian, Editorial Assistant