Review of David Kopp, Chromatic Transformations in Nineteenth-Century Music (Cambridge: Cambridge University Press, 2002)

[1] In light of the number of articles on transformational harmony appearing recently in scholarly journals, one might expect a book of this title to be a full-blown study in what has come to be called “neo-Riemannian” theory. Instead, however, it is a view of harmony based on a transformational system of the author’s own invention. And while he acknowledges some indebtedness to the work of other theorists, David Kopp’s specific goal is to account for and incorporate chromatic mediant relations within a functional system that is applicable to nineteenth-century harmonic practice. His notion of “functional” does not rely on traditional categories of tonic, dominant and subdominant chords and their syntactic roles within harmonic progressions; nor does he focus on diatonic scale degrees and the harmonies built on them, as in Roman-numeral analysis. Rather, Kopp defines functions as transformations between chords sharing one or more common tones. In these respects, his work is distinctive.

[2] In the book’s first chapter, which follows a thoughtful forward by Ian Bent, Kopp identifies the common-tone relationships that comprise his transformational system and examines in particular the role of chromatic mediants. Unlike definitions in other sources, which often include third-related triads that share no pitch classes (e.g., C major and E flat minor), Kopp appropriately limits his “chromatic mediant” designation to those with one common tone. The second chapter illustrates and discusses the use of chromatic mediants in three pieces by Schubert, and is the first of several such presentations that contribute to the book’s cogency by presenting the author’s views in relevant musical contexts.

[3] The next four chapters examine the treatment of third relations by theorists from Rameau through the twentieth century, with the heaviest emphasis on the work of Hugo Riemann. Although this material is impressive in scope as well as in attention to detail, it also seems a largely unnecessary and overly long digression from the author’s primary objective. This foray into the often-quirky quagmire of the history of theory makes up nearly forty percent of the book and forms a kind of barrier between the presentation of ideas in the opening chapters and their subsequent development. Here, most readers would likely prefer one or two chapters that focus more specifically on ways in which contemporary theoretical approaches (i.e., functional, Schenkerian, and neo-Riemannian) deal with chromatic mediants, and that point to the need for a more musically enlightened alternative.

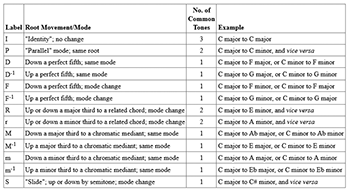
[4] In Chapter 7, Kopp returns to his own ideas of harmonic progression defined as triadic transformations, and presents a system based on the common-tone relationships identified in Chapter 1. Table 1 lists these thirteen transformations, which are characterized according to root movement and whether triad quality (i.e., major or minor mode) is retained or changed. Chapter 8 explores, through the use of brief examples from the nineteenth-century repertoire, occurrences of these transformations as harmonic mechanisms and examines their roles in various musical situations. This chapter uses score notation with transformations labeled, as well as network diagrams, to address in detail what Kopp sees as the “functional” nature of these progressions. The processes defined here serve the same general purpose as functional designations in traditional, diatonically oriented approaches to harmonic syntax in that they attempt to convey information about the relatedness of chords and the musical effect of different types of progressions. The final chapter presents five analyses that apply the transformational system and mechanisms explored in Chapters 7 and 8 to complete pieces. Because Chapters 7–9 carry the essential content of the study, I will consider them more carefully here.

[5] Readers familiar with transformational theory will recognize some important similarities and differences between Kopp’s transformations and those of other theorists inspired by Riemann’s prevenient efforts, notably David Lewin, Brian Hyer, and Richard Cohn. (Since the relevant studies are well documented by Kopp, I will omit specific citations here.) The P transformation is common to all these systems. S is from Lewin. The R transformation is the same as Riemann’s L (Leittonwechsel), which is retained by Cohn and other neo-Riemannian theorists, whereas Riemann’s R (Relative) becomes a lower-case r in Kopp’s system. D is a Riemannian function discussed also by Hyer, but eschewed by Cohn because it can be expressed as a compound of what he considers to be more basic functions, R plus L. These differences point up the most distinctive feature of Kopp’s system, which is its consistent expression of connections between chords sharing at least one common tone as unary transformations. Neo-Riemannian theory, by contrast, favors a smaller number of transformation types, and uses compound expressions more freely.

[6] The primacy of common-tone connections in Kopp’s system is tied to his ideas about chord functions, in particular with regard to the role of chromatic mediants (M and m). In the more traditional view of harmonic function, a direct chromatic-mediant juxtaposition is normally regarded as a non-functional, or tonally disruptive, event. In Schenkerian theory, such progressions must be absorbed into a larger harmonic motion, usually toward the dominant, and the chromatic mediant chord, instead of being understood as a harmony in its own right, is explained as an inflection of some diatonic harmony. And as important as chromatic mediant relationships are in neo-Riemannian theory, here too they lack independent standing in that they are interpreted, like D, as compound transformations (PL or RP for roots descending a major or minor third, respectively). The principal advantage of Kopp’s approach, then, is the treatment of these characteristic nineteenth-century harmonic events as completely intelligible and coherent tonal relationships that deserve to be on equal footing with other common-tone progressions, diatonic or chromatic, such as D, F, R and r. Many of the musical examples discussed in Chapter 8 make a strong and convincing case for this argument; thus for anyone sensitive to the special role of chromatic mediant progressions in this repertoire, Kopp’s ideas are likely to have considerable intuitive appeal.

[7] As successful as Kopp is in legitimizing chromatic mediants as tonally functional entities, his transformational system nevertheless fails to address a number of issues. If in fact he proposes that common-tone functions represent a more-or-less self-sufficient means for conducting meaningful harmonic analysis, there are some nagging questions that need answers. Foremost among the issues that confront all transformational harmonic theory is the choice of objects, or chord types, that make up the system. Kopp’s system is based on consonant (major and minor) triads. (This was also the case in neo-Riemannian theory at first, but more recent studies have begun to concentrate on seventh chords as well.) It cannot account for diminished or augmented triads, despite the larger role these sonorities assume in nineteenth-century music. Because Kopp treats sevenths as appendages to triads, seventh chords have no independent standing, and only those containing a consonant triad (especially the dominant seventh) are included. The system does not deal with diminished sevenths at all, and one is left to wonder whether, for example, a half-diminished seventh might be considered as a minor triad with a Rameau-esque “subposed” root. There are not compelling musical reasons why certain chords have a place in the system, whereas chords of similar construction or usage do not. The German augmented sixth, for instance, is in, because it has the same pitch-class content as a dominant seventh, but the French sixth is out. The dominant seventh with raised fifth is also out, even though its resolution is typically similar to that of the dominant seventh. Consider especially the relationship between the two situations given in Example 1, the so-called “common-tone augmented sixth” and “common-tone diminished seventh.” In terms of voice leading, they represent only slightly different versions of the same phenomenon; but again, only the former one has a place in Kopp’s chromatic system, and indeed figures prominently in his analysis of Wolf’s In der Frühe, as the progression that connects the two contrasting halves of the song.

[8] Another set of issues pertains to the application of the system in an analytic method that identifies transformations both in direct successions and in long-range harmonic relationships. Kopp’s analyses sometimes prioritize chord-to-chord movement, and at other times focus on larger-scale harmonic designs. In the latter case, his analysis of Chopin’s Mazurka, Op. 56 No. 1 (pages 235–40) is extraordinary in its revelation of an overall scheme in which a number of distantly-related tonalities are organized around the tonic as a symmetrical network of transformations. It is unlikely that any other approach could express this design more efficiently. At other times (e.g., the analysis of Liszt’s Consolation No. 3, pages 240–6), Kopp considers different views of harmonic structure based on different chord groupings. His multi-level thinking imparts analytical flexibility, but since there are no rules within the model itself that help to determine which relationships hold greater import or primacy, he is left to justify his choices somewhat informally, in terms of musical context.

[9] Kopp’s inherently musical perspective and intimate knowledge of the repertoire contribute as much to the success of the analyses as his transformational system, suggesting that the system is perhaps of greatest benefit when it can be incorporated into a multi-faceted view of musical structure. Wherever the analyses fall short, it is attributable to the fact that a hegemonistic harmonic orientation drives the analysis, consigning factors like melody and voice leading to a subsidiary role. As an illustration, consider Schubert’s Die junge Nonne, which is the final work examined in Chapter 9 (pages 254–63). The harmonic design of this song is remarkable in several respects, and Kopp’s claim that “notions of mediant function help to clarify the nature of harmony and musical meaning” (page 254) is correct as far as it goes. I propose, however, that in this work harmony and melody are equal partners in the musical structure and in the formation of relationships between music and text.

[10] Kopp divides the song into an introduction (mm. 1-8) and four stanzas (measures 9–34, 34–50, 51–61, and 62–92). Although he does not give an overview of the text (by Craigher), it would be helpful to the discussion. The young nun begins by describing a storm raging outside her window in the first stanza; then in stanza two she compares the storm to her life at an earlier time. In the third stanza she speaks of her recently acquired peace and spiritual freedom. The climax comes at the beginning of stanza four, where she calls for Christ to come and “take his bride.” The tension abates thereafter, and the song concludes with a serene “Alleluja” passage.

[11] In Schubert’s setting, the first two stanzas are similar, beginning and ending in F minor. The last two are in F major, reflecting the text’s change of mood. More striking harmonic relationships exist within the stanzas, especially in the tonal scheme. The first two stanzas move from F minor to F sharp minor before returning to the home key; the third stanza introduces some direct chromatic mediant progressions (C7 to A and A to F7), but the next strong tonicization is D flat major at the beginning of stanza four. Kopp’s analysis concentrates on the shift from R and D progressions in the first part of the song to chromatic third relations that emerge in the F major portion, culminating in a climactic M transformation from F to D flat (measure 63). His discussion includes correspondences between harmonic progressions and ideas in the text, and concludes by exploring how various melodic progressions in the vocal line directed toward high F operate within the harmonic structure.

[12] Example 2 offers what I believe is a useful expansion of Kopp’s view of this song. The first graph (Example 2a) shows the opening vocal line (measures 10–11) moving from F to its first melodic goal, D flat, that arrives with the first change of harmony. The voice’s next entrance is a sequential restatement (measures 18–19) in F sharp minor that pushes the D flat up to D natural before the tonality returns to F minor at the end of the stanza. The second graph (Example 2b) is the vocal phrase at the beginning of the fourth stanza, where Schubert sets the climactic words “take your bride” with an ascent to the melodic zenith of the song (G flat) that is the seventh of V7 and that resolves to F concomitantly with the authentic cadence on D flat. The example indicates conspicuous cross-references between melodic details and larger harmonic relationships that link the beginning of the song with its climax. The initial move from F to D flat in the voice is expressed also by the harmonic shift from F to D flat in measure 63 and the cadence in measure 65; also at this cadence-point, the pitch classes of the tonal scheme in the opening of the song appear as a melodic gesture emphasizing the high G flat. This exchange of melodic and harmonic events suggests that both carry equivalent weight as determinants of structure in the song, but Kopp’s harmonically-privileged approach cannot fully engage these important tonal processes. Another such melodic-harmonic process involves the conflict Schubert sets up between the two forms of the submediant, D flat and D natural. Both pitch classes occur in various contexts throughout the song (beginning with their functions in the keys of F minor and F sharp minor, as shown in Example 2a), but there is a large-scale conversion of D natural from the lowered submediant in F sharp to the diatonic submediant in F major within the “Alleluja” at the end, which parallels the progression of ideas in the text.

[13] The book is written in an intelligent and straightforward style, and the layout, including tables and illustrations, is clear and legible. The text is highly accurate, but there are problems with a few of the illustrations. Figure 1.6 (page 12) for instance, incorrectly identifies C major to B flat minor as a mediant relationship; Example 2.1b (page 19) is not the score excerpt to which the discussion refers; the clef and key signature for Figure 8.3 (page 197) are incorrect; and the climactic G flat in Die junge Nonne (measure 65) discussed above is shown as a G natural in Figure 9.12 (page 257).

[14] Kopp’s Chromatic Transformations is an ambitious study, particularly effective in its treatment of chromatic mediant relations. It successfully builds a new transformational system from Riemannian roots, yet offers an intriguing alternative to current neo-Riemannian theory. Despite certain limitations associated with the analytic method, Kopp’s system proves to be useful in elucidating aspects of harmonic structure. The book stands as an important contribution to the study of nineteenth-century harmony from a transformational perspective.

Richard Bass
Department of Music
Box U-12
University of Connecticut
Storrs, CT 06269
Richard.Bass@uconn.edu

Copyright Statement

Copyright © 2004 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.