Syntonic Tuning: Creating a Model for Accurate Electronic Playback
Roger Wibberley
KEYWORDS: Cents, Costeley, equal temperament, Finale, interval ratio, pitchbend, pitchwheel, Pythagorean, Syntonic comma
ABSTRACT: This essay is explicitly “educational” in the proper sense: although it has a technical focus this is intended to provide the means of re-examining and reassessing one’s own cognitive processes. It has often been argued that a proper understanding of early music is hindered by our own inability to “hear the music” in the way our ancestors did. Our “modern” ears have (it is often rightly said) become conditioned over time by the sound worlds of later systems of tuning and performance to the extent that our perception of the aesthetics applied to early styles can only be the result of educated guesswork. “We cannot know how a Pythagorean performance really sounded (can we?), and our understanding of the soundscape of Just Intonation (JI) is mainly intuitive, backed up perhaps by a complicated theoretical list of mathematical ratios (isn’t it?).” There is considerably more to a performance than accurate intonation (which is only the starting point) and this essay (along with the previous two) only seeks to explore the particular aspects of performance involving pitch. But the above sense of resignation and capitulation can at least be partly addressed by examining aspects of tuning, and the procedures discussed below will at least provide a means of capturing this single—albeit crucial—aspect of performance. Nothing will replace a group of well-equipped and trained singers, but it is my belief that such singers would need a highly specialized training before successfully achieving performances of the kind outlined. Even then, the nature of “live performance” (however accurate empirically) may still be the victim of only a subjective response from the listener (who is naturally more inclined to trust his or her own preconditioned cognitive responses than the results such singers might produce). This essay, therefore, provides a computer-generated means of evaluation, and the sounds provided are empirically correct in their intonation by all standards proclaimed in theoretical works of the time. The challenge, then, is to develop a self-critical approach in which—fully knowing that what is being heard is (intonationally) herein the same for us as it was for them—we can reappraise our own cognition. If any tunings that are created by the application of anything covered in the essay strike the listener as in any way “strange,” “out of tune” or “unusual,” this can be taken confidently as a direct invitation to the listener to reappraise his or her own cognition.
Copyright © 2004 Society for Music Theory
[1] In my previous two essays on Syntonic and Pythagorean tuning, numerous sound files were included together with graphic files showing in visual terms how the various notes in the scores were inflected upwards or downwards in order to fine-tune the harmonies according to the principles explained therein. The objective here is to show how Finale users can apply the same principles and achieve similar results from their own use of Finale.(1) What will be included is a downloadable Library file that can be imported into Finale and used as described. When this is applied to scores in the way specified, playback of files will be accurately tuned according to the user’s specification. In the case of those who simply wish to apply the file provided, much of the essay can be bypassed. But since an understanding of the principles will enable the application of other tuning systems (such as, for example, quarter-comma meantone), those who might wish to extend their use of tuning systems should follow the essay closely.(2)
[2] My own set-up is unremarkable: a Macintosh iMac running OS 9, together with a still-serviceable Roland D10 keyboard. All the principles and methods outlined in this essay equally apply to PC Windows or other Macintosh set-ups, and the downloadable files provided should work unhindered by any system using Finale from version 3.7.2 (Mac) onwards and equivalent PC Windows versions. Readers will find that a large screen is beneficial (though not essential) when working with scores, and when reading some of the graphic files contained in this essay. The files I have provided have deliberately been created in Finale 3.7.2 for the following reason: while users of later versions will find that their programs automatically apply the appropriate data transfer to these files, had I presented the items only in their newer formats users of early versions would be unable to apply the settings. For this reason I shall present numeric values first according to the system understood by “older versions” (e.g. 3.7.2), and then explain how these values are modified by “newer versions” (e.g. Finale 2000 and Finale 2003). Nobody using a newer version will, of course, ever have to work out the new values since the program itself does all the work. When the appropriate library in the downloaded file is Saved, all the changed values will be automatically applied by Finale when the file is loaded. Users of early versions also will be able to Save the library in its still unchanged format. They will find that if they then Load this library (or any music file containing it) into a newer version of Finale, the data transfer will be automatic.
[3] The keyboard that you are using will undoubtedly be configured to play in equal temperament.(3) The only way in which pitches that are different from the default pitches (set by the keyboard used) can be generated is by activating the pitchwheel. The pitchwheel will usually be set (by default) to raise or lower the pitch of a note by one octave.(4) Casual (and even seasoned) users of Finale may be unaware of the power it offers for playback. There is more than one method of asking Finale to alter the pitch of a note it plays from the score, but the method that is to be used here is the most accurate and uses the Staff Expression tool.(5)
[4] It will be helpful for you to know whether the Finale version you are using is what I shall henceforward call an “early version” as opposed to a “later version.” This knowledge will not affect your use of the files provided, but will help you to follow some of the explanations I shall shortly be offering for using the program. Generally an “early version” can be identified from the composition of the main tool palette. If it contains both Staff and Score Expression icons (the former indicated by the “mf” symbol and a white note, the latter by an “mf” symbol alone), this will be an “early version.” An example is illustrated in Figure 1, as used in Finale 3.7.2. If, however, your main tool palette contains only a single Expression Tool (indicated by an icon bearing only the “mf” symbol) you will be using a “later version.” Such palettes are shown in Figures 2 (Finale 2000) and 3 (Finale 2003).
|
Figure 1. Finale 3.7.2 main tool palette containing differing Expression Tools (click to enlarge) |
Figure 2. Finale 2000 main tool palette (click to enlarge) |
Figure 3. Finale 2003 main tool palette (click to enlarge) |
[5] The Expression tool (both “staff” and “score” in early versions) is normally used in order to insert dynamics into the score. It is important that when this method of tuning is used it is always applied to individual notes on a selected staff. This will mean that users of early versions will select the Staff Expression Tool, while users of later versions will prescribe this from the submenus that appear after selecting the common Expression Tool. This will ensure that the marking to be inserted only affects the actual note(s) to be changed. In order at this stage to understand what is going to be done using this tool to provide for pitch changes to individual notes, it will be helpful now to load a Finale file in order to explore the (Staff) Expression tool in the manner to be outlined next.
[6] USERS OF “LATER VERSIONS” SHOULD HERE SKIP TO [7] below. With a Finale file open, select the Staff Expression tool and click on any note in the score to open the Staff Expression box.(6) There will be all the current dynamic markings that are available, although these themselves are not going to be used. Select any of those available and then click the EDIT button. The next box that opens should also contain a section headed “Playback Options,” but if it does not simply click the button marked “Show Playback Options.” In the “Playback Options” window that is now visible there is a drop-down selection menu next to the word “Type” which allows the user to make various kinds of settings that affect playback. When the drop-down menu is opened the type to be selected is “Pitchwheel.” Having selected “Pitchwheel” there is also a “Set to” radio button that should be selected. A numeric value now needs to be inserted into the box alongside this “Set to” button. It is at this point that a value can be inserted into the box to specify exactly what the pitchbend value for the particular Staff Expression originally selected will be. This value will determine the pitch inflection of the note to be sounded.(7)
[7] USERS OF “OLDER VERSIONS” SHOULD SKIP TO [8] below. Later versions require the selection of the common Expression Tool (“mf”). When a note in the previously-opened score is selected the next window displays the current expression marks. Select one, and then click “note attached” or “note expression” (according to version). When the “Select” button is clicked, the next window will present the playback options, and from the “Type” submenu should be selected “pitchwheel.” A numeric value needs to be inserted into the adjoining box, and this value will determine the exact pitch inflection that Finale will apply on playback. Now click the various “Cancel” button to return to the score.
[8] The question is, of course, what should the pitchwheel “set to” values be? What is required is a completely new library of text expressions, each of which has a programmed pitchbend value that has been accurately created and inserted as described above. More specific understanding of the keyboard pitchwheel and the way Finale operates it is needed, first of all, and then an understanding of how the values to be inserted are calculated. In older versions of Finale the default pitchwheel value is 8192; when the pitchwheel is at its lowest pitch (having been pushed to the left) Finale’s pitchwheel value is 0; and when the pitchwheel is at its highest point (being pushed to the right) Finale’s value is 16384 (i.e. 8192 multiplied by 2). The range in older versions is therefore 0-8192 and 8192-16384 (the former giving the range of pitches below the default, and the latter those above). In later versions, however, these numbers have been changed, the default value now being set to 0 (zero), and the respective numeric ranges are therefore -8192-0 and 0-8192.(8) This means that Finale is capable of dividing the interval covered by the pitchwheel (pushed either upwards or downwards) into 8192 equal portions. Although this may seem generous for tuning purposes, it is actually insufficient for the purpose of accurate pitch changes as small as a Syntonic comma as long as the pitch bend set on the keyboard covers a whole octave.(9) What is needed is the facility of splitting the interval of a semitone (rather than an octave) into this number of divisions. This will provide the facility for generating pitches accurate to within 1 part in 8192 parts of one semitone.
[9] In order, therefore, to reduce the pitchbend range from an octave to a semitone, the bend setting needs changing on the keyboard itself. Editing the bend value is simple but the procedure depends upon the specification of the keyboard in use.(10) Whatever sounds (patches) are going to be used for playback from Finale need individually editing on the keyboard, and the bend value for each needs setting to “1.”(11) The accuracy that Finale will generate will therefore not be corrupted by incorrect bend settings within the keyboard itself.
[10] What now needs to be provided is a Finale Text Expression file that in effect significantly increases the number of separate pitches available for each octave. The object is to create a tool that enables vocal performance to be simulated, and this is something that was never available on keyboards of fixed pitches.(12) Since each of the twelve notes available on the keyboard now needs to be capable of delivering at least three different pitches separated by a Syntonic comma, the Text Expression library will need to provide for this. The default scale within which such pitch inflection occurs will, however, be purely Pythagorean since it is from these Pythagorean pitches that comma inflection upwards or downwards has to take place. So in addition to the pure Pythagorean intervals of the 4th, 5th and octave, pure 3rds and 6ths will be added to the system by the facility of modifying as necessary standard Pythagorean pitches by comma inflection. The first stage in constructing this new library of pitches is therefore to devise the values needed for the default Pythagorean scale.
PYTHAGOREAN TUNING
[11] I shall henceforward show numeric values for both “older” and “later” versions of Finale as follows: “later versions” will appear in square brackets following the values for “older” versions. It will always be noted that the values of the former are the same as those of the latter minus 8192.(13)
[12] In constructing the Pythagorean scale each existing note on the equally-tempered MIDI keyboard needs to be allotted an exact mathematical value such that when Finale plays a note with the value defined its pitch will be exactly the one required by the scale. In effect what this library will be doing is retuning the separate pitches of the scale so that they will all have a Pythagorean relationship instead of an equally-tempered one. What needs to be calculated is the exact amount by which each separate note has to be raised or lowered from its equally-tempered default when it is played by Finale. These defaults will all have a pitchwheel value of 8192 [0],(14) and the Pythagorean values will therefore be slightly more or less than this value depending upon the position of the note within the scale. A correct way of arriving at exact Pythagorean values is to take a starting note with the default value of 8192 [0], and then a) move upwards through a series of perfect fifths sharpwards, and b) move downwards through a corresponding chain of perfect fifths flatwards. Taking the note “C” as the starting point, the first deduction will move sharpwards through the fifths ending with A-sharp, while the second deduction will move from the same starting note flatwards through the fifths to end on C-flat. When this process has been completed all the “white notes” will have their correct pitches, and all the “black notes” will exist with two pitches separated by a Pythagorean comma. Sharps will thereby lie a major semitone higher than their parent naturals, and flats a major semitone lower than theirs. This will then provide for all the notes required by the combined use of musica recta and musica ficta. The octave will have been provided with 18 notes instead of the usual 12. As we shall see, however, 18 notes to the octave will be too few to permit Just Intonation which additionally requires the raising and lowering of these default Pythagorean notes by Syntonic commas. But this is nonetheless the starting point for arriving at the required scale.(15)
[13] To create precise Pythagorean pitches for the scale, it must be remembered that the notes are initially set on the keyboard to Equal Temperament. As such each note in the score will have a default Finale pitchwheel value of 8192 [0]. Only when this value is, for each separate note, raised or lowered by the exact value required will the Pythagorean scale come into being. And it is only when this new scale has been created that the addition or subtraction of comma values can be made with precision. When this scale, together with the comma values to be applied to it, has been constructed, it will then be possible to edit scores by adding the prescribed playback Text Expressions and achieve a playback in Just Intonation. The first task, therefore, is to construct an accurate Pythagorean scale.
[14] Because the task is to create audible pitches rather than to calculate relative string lengths, it is necessary to work in Cents rather than string length ratios.(16) Since construction of the Pythagorean scale is (as stated in [11] above) achieved by computing pure fifths in a chain upwards, and then downwards, it is therefore necessary to define the exact number of Cents required between successive notes that lie a fifth apart. Since we already know that by default each equally-tempered semitone contains 100 Cents, and therefore that the equally-tempered fifth contains 700 Cents, all we will need to do is to subtract 700 from the total number of Cents calculated for the interval overall to find the difference between the equally-tempered and the Pythagorean pitches of the note concerned. We shall also need to convert Cents value into pitchwheel value which is very simple: since the equally-tempered semitone (set on the keyboard) has a pitchwheel range of 8192 (being either 0-8192 [-8192-0] or 8192-16384 [0-8192]), it must follow that each Cent has a pitchwheel value of 81.92. When, therefore, the difference in Cents between an equally-tempered and a Pythagorean fifth is calculated, the Cents difference needs to be multiplied by 81.92, and the result added to (when moving upwards) or subtracted from (when moving downwards) the default pitchwheel value of 8192 [0]. This will yield the new pitchwheel value for the note that now lies a Pythagorean fifth above or below the note from which the calculation was made.
[15] All the new pitchwheel settings can easily be calculated when the formula for conversion from string-length ratio to Cents is applied. This formula is very simple: where the interval-ratio required is “i” and the Cents value sought is “c,” the conversion is achieved as follows:
c = log (i) * (1200/log (2))
By applying these principles to calculate the pitchwheel setting for “G,”(17) and taking “C” as the starting point with a normal pitchwheel setting of 8192 [0], the value for “G” will be arrived at as follows:
- the pitchwheel value of C (8192 [0]) is the starting point;
- the number of Cents required to arrive at G is log(3:2) X 1200/log 2;
- the difference between what G would have been (700 Cents greater than C) and what it now is as the result of b) above, is the total Cents value given in b) minus 700 (the number of Cents it would have been);
- this difference is multiplied by 81.92 (the pitchwheel value of each Cent);
- the result of d) above is added to 8192 [0] (which would have been the default value).
The complete formula for this calculation is therefore as follows:
FOR OLDER VERSIONS: 8192+(((log(3/2)) * ((1200/log(2))-700) * 81.92) = 8352.
FOR LATER VERSIONS: 0+(((log(3/2)) * ((1200/log(2))-700) * 81.92)=160
The pitchwheel setting for “G” is therefore 8352 (older versions) or 160 (later versions).(18)
[16] Having now determined the value of the first fifth in the chain sharpwards, the same formula is applied each time the next fifth in the chain is calculated. The only difference will be the starting value. When the G was calculated from the C, the starting value was that for the C (8192 [0]). The result for the G was 8352 [160], and this new result now becomes the starting point for calculating the value for D using otherwise the same formula:
OLDER VERSIONS: 8352+(((log(3/2)) * ((1200/log(2))-700) * 81.92) = 8512
LATER VERSIONS: 160+(((log(3/2)) * ((1200/log(2))-700) * 81.92) = 320
In then calculating the value for A, the starting point will next be the new value for D (8512 [320]). This process simply continues through the fifths sharpwards as far as D-sharp.
[17] The pitches that remain are those to be calculated in the chain of fifths flatwards from the C. The formula is almost identical, and only the first operand differs (since the movement is now flatwards). The calculation for F will take the value of C as the starting point, and the formula will now be:
OLDER VERSIONS: 8192-(((log(3/2)) * ((1200/log(2))-700) * 81.92) = 8032
LATER VERSIONS: 0-(((log(3/2)) * ((1200/log(2))-700) * 81.92) = -160
The old starting figure for C (8192 [0]) is now replaced with the new one for F (8032 [-160]) to find the value of B-flat. This process continues flatwards through the fifths until C-flat is reached. When this has been completed, the whole series of Pythagorean pitchwheel settings will have been determined. These are now given below (the figures appearing in square brackets being those that apply to later versions of Finale, and being equivalent in purpose and function to those given first for older versions):
C: 8192 [0]
D: 8512 [320]
E: 8832 [640]
F: 8032 [-160]
G: 8352 [160]
A: 8672 [480]
B: 8992 [800]
B-flat: 7872 [-320]
E-flat: 7712 [-480]
A-flat: 7552 [-640]
D-flat: 7392 [-800]
G-flat: 7232 [-960]
C-flat: 7072 [-1120]
F-sharp: 9152 [960]
C-sharp: 9312 [1120]
G-sharp: 9472 [1280]
D-sharp: 9632 [1440]
A-sharp: 9792 [1600]
Files created in early versions that are given the first values shown will, when loaded into later versions, have these values automatically changed to those appearing in square brackets. When creating new settings for early and late versions of Finale respectively, care must be taken to ensure that the correct data set is used: older versions using the pitchwheel range of 0-8192-16384, and later versions -8192-0-8192. There are consequently 18 different pitches in this system for each octave.
[18] To create an accurate playback of these values, and achieve true Pythagorean tuning, the procedures outlined in [5] to [7] above should now be followed. In the Expression window of Finale, it would be best to delete all existing expressions (unless you still to wish to use any of them, which is unlikely). For each Pythagorean pitch it is necessary to Create a new Text Expression entry in which is applied a) a convenient name tag, and b) a playback definition in which “Pitchwheel” is selected from the drop-down menu and the appropriate value (in the list above) typed into the box. The name tag is what will appear in your score when you apply the appropriate Text Expression to each of the notes in turn, and it should be kept clear and simple. The “white notes” can simply use the letter name (e.g. A, B, C etc.), and the flat notes can be supplied with a “b” after the letter (e.g. Bb, Gb etc.). The sharps should not however use the hash sign (#) because this is reserved in Finale.(19) In this essay, and the supporting files, I have replaced the hash sign with “$,” so F-sharp is tagged as “F$.”
[19] Once the new Text Expression library containing the Pythagorean playback values has been completed, each note in the score will need to be supplied with its appropriate Text Expression tag. Although this is labor intensive, it is a labor of love!(20) It is absolutely crucial, however, to make sure that each voice part is programmed by Finale to use a different channel for playback otherwise cross-contamination of playback values will occur.(21) The same actual sound (patch) can be used with no ill effect, but different lines must remain assigned to different playback channels.
[20] In order to illustrate the method of insertion to yield tuned playback,
here are provided some screen shots from three different versions of Finale. The
music file used (the same in each case) was created by version 3.7.2 (the
earliest of the examples) and has been loaded into each version to illustrate
the method of insertion. The first note in the highest staff is A, and the task
in each case is to insert an instruction to play the note back at its
Pythagorean pitch. The music file already has all the Pythagorean values in its
active Expression Library (this note is programmed to use a pitch bend value of
8672, as indicated in the list of figures in [17] above. Figure 4
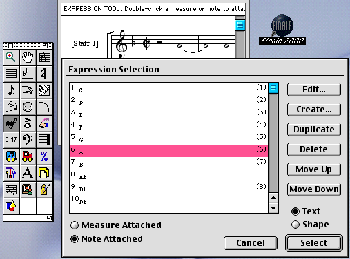
shows the initial window provided by Finale 3.7.2. This window appeared
because the Staff Expression icon in the left box was selected, and the first
note in the score was clicked. In this Selection window, the Staff Expression
“A” has now been selected. To discover what its current settings are (and even
to edit them) the “Edit
Figure 4. Staff Expression Selection window (version 3.7.2) (click to enlarge) | Figure 5. Text Expression Designer window (version 3.7.2) (click to enlarge) |
[21] In later versions, the methods are
similar, but the Pitchwheel value for “A” that appears after the same file is
loaded will now have been converted automatically to “480.”(23) Figures 6, 7 and
8 are screen shots from Finale 2000. Figure 6 shows the primary Expression
Selection window. The left box shows that the Expression Tool was selected (note
the absence now of the Staff Expression tool shown in Figure 4—choice
for insertion as “staff” or “score” expression appears in the next window), and
the Expression Selection box appeared because the first note in the score was
clicked. The expression “A” has now been selected, and when the “Select” button
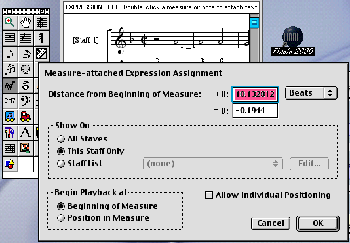
is clicked a new “Measure-attached Expression Assignment” window appears. This
is shown in Figure 7.
Here it is important to select “This Staff Only” (thereby making the expression
a “staff” one (as in version 3.7.2) rather than a “score” one. When the “OK”
button is clicked, the expression “A” is inserted above the note, and whatever
playback value (if any) was given will be activated upon playback. To check what
the current settings are (and even to edit them if desired) the “Edit
Figure 7. Measure-attached Expression Assignment window (Finale 2000) (click to enlarge) | Figure 8. Text Expression Designer window (Finale 2000) (click to enlarge) |
[22] Equivalent windows used in Finale 2003 are shown in Figures 9 and 10. The only obvious differences from Finale 2000 are what might be viewed as “window dressing” differences. For example “Note attached” (version 2000) has now become “Note Expression” (version 2003), although the functions are identical. The Text Expression Designer window is identical in function with its 2000 counterpart, and also shows—as expected—that the Pitchwheel value stands now at “480.”
Figure 9. Expression Selection window (Finale 2003) (click to enlarge) | Figure 10. Text Expression Designer (Finale 2003) (click to enlarge) |
[23] Below are two downloadable Finale files (Example 1 and Example 2).
Example 1: Josquin Desprez, Ave Maria (excerpt using equal temperament) [Ex1.zip (for PC users)] [Ex1.MUS.sit (for Mac users)]
Example 2: Josquin Desprez, Ave Maria (excerpt using Pythagorean tuning) [Ex2.zip (for PC users)] [Ex2.MUS.sit (for Mac users)]
The first is a straight file for playback using four separate channels, and the same patch number for each. You are advised to avoid using any “piano” sound because our ears are conditioned to assuming that anything sounding like a piano uses Equal Temperament. This might give the illusion that the piece is “out of tune” when it really is not. Select a melody instrument for playback through channels 1, 2, 3 and 4 (a Recorder sound is ideal). The file will not change your keyboard patch settings. This should give a normal playback using equal temperament. The second is an edited version of the first, but now attaches to each note its Pythagorean playback values. The correct Expression library (detailed above) is embedded within the file, so it should simply play the music correctly. But the following checklist should first be made before trying it:
CHECKLIST
- Have you reset your Pitchbend Range to a value of “1” on the keyboard? Test the bender manually to ensure that it inflects upwards and downwards by only a semitone for patches you will set for channels 1-4 (the setting used for Examples 1 and 2). If this has not been done, you will quickly find that comedy becomes tragedy! This setting must of course be applied to each and every patch you intend to use for playback.
- Before playing the file, open
the Instrument List window to ensure that your download has retained separate
channels for each staff. If not, you will have to assign these staves to
different channels using this window. You can, however, use the same patch
number for each channel (having, as in a) above, verified the pitch bend setting
as being “1”). Make sure that the “Send Patches before Play
. . . ” box is checked.
SYNTONIC TUNING
[24] As stated earlier, Syntonic tuning is only an inflection of the Pythagorean scale in which Syntonic comma adjustment is applied to particular notes of the tetrachords. Potentially any note of the scale can be adjusted upwards or downwards by a comma depending upon its tetrachordal location and context. For this reason, each note of the Pythagorean scale needs to be provided with complementary values reflecting upward and downward comma adjustment. Indeed this adjustment can sometimes be greater than a single comma over the course of a whole piece, so what needs to be provided for is two or three complementary values for each note sharpwards and flatwards. Where an unavoidable accumulation of commas causes a composition to undergo an audibly significant and irreversible rise or fall in base pitch, the assumption should be that Syntonic tuning is the wrong soundscape for that piece and that Pythagorean tuning was intended by the composer. It is still advisable, however, to provide for a certain number of comma shifts either way, if only to test the effect of Syntonic tuning in such cases and adjudge the impact of the pitch change.
[25] The Syntonic comma is a fixed though non-melodic interval whose ratio is 81:80.(24) As such it always gives the same quantifiable inflection when applied to an existing pitch. Whether the inflection is sharpwards or flatwards in no way changes its definition as a quantity. In order to calculate a pitchwheel value for the interval it must first be converted into Cents, and then multiplied by 81.92 (the pitchwheel value for each Cent). Conversion into Cents is via the normal formula for converting from an interval ratio (i):
LOG(i) * (1200/LOG(2)).
Pitchwheel value now requires this to be multiplied by 81.92, and the result is simultaneously added to or subtracted from the pitchwheel value of an already existing note. If, therefore, the pitchwheel value of “C minus a Syntonic comma” is computed, the formula (starting from 8192 for the C) will be:
8192-(LOG(81/80) * (1200/LOG(2)) * 81.92 = 6430
The result of 6430 will therefore be set for pitches where C is to be lowered by a Syntonic comma. Were it to be raised by a Syntonic comma, the first operand would be changed to a “+”:
8192+(LOG(81/80) * (1200/LOG(2)) * 81.92 = 9954.
This new value of 9954 will consequently be set for notes where C is raised by a Syntonic comma.(25)
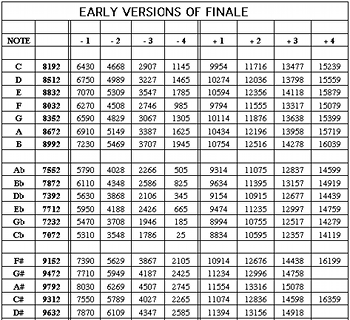
Figure 11. Pythagorean pitchwheel values with comma shifts (older versions)
(click to enlarge)
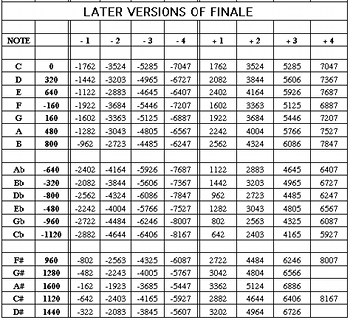
Figure 12. Pythagorean pitchwheel values with comma shifts (later versions)
(click to enlarge)
[26] Charts plotting all the pitchwheel values of the Pythagorean scale, together with comma shifts upwards and downwards, are most easily achieved by using a spreadsheet. Figures 11 and 12 show complete charts (Figure 11 for older versions, and Figure 12 for later) plotting up to four comma shifts upwards and downwards. It is unlikely that this number will be needed, let alone ever exceeded, although it can be extended if desired. The default value for C (8192 [0]) is the only simple numeric entry contained in these spreadsheets. Every other value has been automatically computed and generated by the insertion of formulae. What will be noted is that all the values in Figure 12 are less—by a value of 8192—than the corresponding values in Figure 11. In these the default Pythagorean pitchwheel value of each note is shown in column 2, and the remaining columns list the settings for the comma shifts as indicated at the head of each column. These are the values that need to be programmed into the new Expression library either from Figure 11 or Figure 12 as appropriate.
[27] In creating a complete library of Staff Expressions to give accurate playback, as outlined above, the name tags need to be simple and clear in order to indicate the exact inflections of each note. For this purpose, the library encoded in Example 2 above contained all the Pythagorean pitches and these are identified simply by the letter name of the note concerned. Where there is a flat this is indicated by the “b” suffix (e.g. Bb), but sharps are shown by the use of the suffix “$” (e.g. F$) for the reason stated in note 18 above. When this simple library is expanded so as to include all the upward and downward Syntonic comma inflections for every note, the tags need to indicate the base notes as well as the exact inflections. The simplest method of displaying these attributes is to use the letter name of the note, an operand indicating upward or downward inflection (“+” or “-”) and a numeral showing the number of comma values by which the note has been inflected. Thus the tag “C-1” will indicate C lowered by a comma, “F$+2” the note F-sharp raised by two commas, and “Bb+1” the note B-flat raised by one comma.(26)
[28] Example 3 below is a downloadable Finale file containing the complete active library of pitches displayed above in Figure 11.(27)
Example 3: Willaert, Sicut erat in principio from Vesper-Psalm 109 [Ex3.zip (for PC users)] [Ex3.MUS.sit (for Mac users)]
The score it displays has already been edited by the insertion of
appropriate Staff Expressions in which is encoded the exact pitchwheel values
for playback. If you are sure that your keyboard is set to the appropriate Pitch
Bend value, and you have verified that the bend is only a semitone upwards and
downwards when the pitchwheel is activated, you can play the file back and it
should be finely tuned to work in Just Intonation (for which soundscape it was
clearly designed and carefully controlled by the composer). Before playing it,
make sure that you have allotted appropriate patches to channels 1-4, and that
each patch to be used has a pitch bend setting (on the keyboard) of “1.” In
order to apply this library to other scores of your own, you should use the
“Save Library
[29] This essay has not primarily been offered in order to increase an interest in or awareness of technology, though hopefully those readers who use technology will have benefited from it in some way. The real purpose has rather been to demonstrate that not only is it possible to know that the pitches being created are indeed those understood and used by early musicians, but also that in hearing them with this certain knowledge we can extend our cognitive experience and thereby achieve a much better understanding of the soundscapes that for too long have remained obscure. Pitch, however, is only one part (even though an important one) of this soundscape. Furthermore an understanding of the ways in which these pitches can be recreated through simple technology does not in itself provide the musical understanding necessary to know where and how to apply the pitches that can be generated. Only by the development of a meticulous and clinical approach to comma analysis can the perceptions this yields be realized through the technology that has been created.
POSTSCRIPT: Guillaume Costeley: Seigneur dieu ta pitié
[30] This short postscript will offer a curiosity that demonstrates again Finale’s power to provide superfine tunings. While many readers will be familiar with Guillaume Costeley’s spiritual chanson Seigneur dieu ta pitié, very few will ever have heard it rendered, as the composer prescribed in his Preface to the 1570 print, in 19-tone equal temperament (19-tet). He there described the use of a keyboard upon which seven extra black keys were to be added.(28) The normal black keys were supplemented by a further seven, one lying alongside each existing one, and an extra one being added between B and C, and between E and F. In this system B-sharp was the same keyboard note as C-flat, and E-sharp the same as F-flat. This resulted in nineteen separate notes to each octave, and Costeley prescribed that the interval between each successive note should be one-third of a tone. Diatonic semitones are to be given the interval value of two-thirds of a tone.
[31] It is clear from this description that tones are smaller than standard.(29) It must also be the case that minor thirds (equaling five thirds of a tone) are larger than the Pythagorean minor thirds, and that major thirds (equaling four thirds of a tone) must be smaller than the Pythagorean ones. Thirds and sixths will therefore be nearer to the JI intervals, while the fourths and fifths will be slightly dissonant.(30)
[32] The programming of a playback for 19-tet is very easy in Finale, since only twenty-one different values have to be provided for (which is only three more than the Pythagorean scale required).(31) Since the octave (1200 Cents) divides into nineteen portions, each one-third step must be equal to 63.15789 Cents. When this scale is allotted Pitchwheel setting, the following values will be found to be correct (again values for the later versions of Finale appearing in square brackets):
C: 8192 [0]
C-sharp: 5174 [-3018]
D-flat 10348 [2156]
D: 7330 [-862]
D-sharp: 4312 [-3880]
E-flat: 9485 [1293]
E: 6467 [-1725]
E-sharp: 3449 [-4743]
F-flat: 11641 [3449]
F: 8623 [431]
F-sharp: 5605 [-2587]
G-flat: 10779 [2587]
G: 7761 [-431]
G-sharp: 4743 [-3449]
A-flat: 9917 [1725]
A: 6898 [-1294]
A-sharp: 3880 [-4312]
B-flat: 9054 [862]
B: 6036 [-2156]
B-sharp: 3018 [-5174]
C-flat: 11210 [3018]
When these values are created as playback data for the text expressions, a 19-note equally-tempered scale can be generated. Figure 13 shows such a scale together with the related text expressions that have been configured in this way for playback. When the audio file provided is played, the exact effect of the scale can be heard and each step lies exactly one-third of a tone from its neighbor.
[33] When these values are applied to the Costeley chanson, they provide a simple and striking opportunity to listen to the piece according to the rare soundscape of 19-tone equal temperament. Figure 14 provides a score of the chanson(32) while the attached audio file provides a 19-tone equally-tempered performance simulating an organ.
|
Figure 14. Guillaume Costeley’s spiritual chanson Signeur dieu ta pitié (click to enlarge and listen) |
Roger Wibberley
Goldsmiths University of London,
Department of Music,
New Cross,
London SE14 6NW
r.wibberley@gold.ac.uk
Footnotes
1. Of the many available music notation programs, my
preference for Finale here is only because it is particularly well suited to
combining visual analysis with superfine pitch control. But its method is
unique, and files converted into, say, Sibelius will not retain the MIDI
settings that have been applied. Although Finale has been upgraded regularly,
most of the changes have been designed only to enhance user friendliness and to
present better looking windows and scores. The window dressing aside, the
functionality of the program has remained fairly stable. But in the specific
area to be discussed below later versions of Finale have adopted a slightly
different (and perhaps more logical) method of data management. This will be
explained in due course.
Return to text
2. Readers might like to know that the writer does not
regard himself as a technological boffin, and they might perhaps be comforted
(or irritated if they expect boffin-style discourse) by the assurance that
explanations will be simple and comprehensible.
Return to text
3. If your keyboard provides other preset temperaments such
as “Pythagorean” or “Just,” you should make sure that it is only set to equal
temperament. All the settings that will be provided in this essay take the
equally-tempered keyboard as the default. None of the music to be generated will
actually use equal temperament of course, but the pitchwheel settings presume
this as being the default.
Return to text
4. You can verify this quite simply. Assuming your MIDI
keyboard is set up to generate sounds through your speakers, hold down any note
and move the pitchwheel fully to the right and then the left. The pitch of the
note should rise and fall by a full octave. If it is different this does not
matter, and it merely indicates that the default setting has been changed. The
setting will again be changed later to another value in any case.
Return to text
5. As will be shown, early versions of Finale provided both
Staff Expression and Score Expression tools, while later versions offer only a
common and single Expression Tool. In these later versions, setting of the
required entry for either “Staff” or “Score” is made via various sub menus. The
functionality of whatever entry is made remains identical however. A less useful
method of pitch control is to open the Midi Tool and edit the pitchbend values
of notes that are to be changed. This is far less accurate and anything that is
done remains invisible except to the inner workings of the program. The more
accurate method outlined here remains visible in the score, and can easily be
edited or changed.
Return to text
6. If the score is empty, perhaps because the file is newly
created, simply insert a note. Then select the Staff Expression tool icon and
click on the note.
Return to text
7. Now that the procedure for editing and inserting
pitchwheel values has been followed, the various “Cancel” buttons can be clicked
to close down the Staff Expression tool so as to avoid changing the note
originally selected. In order to rehearse the procedure again, the instructions
given in [6] above can be repeated.
Return to text
8. These are the new values that Finale automatically
converts to when a file created in what it recognizes as an “older version” is
loaded into the later version. In such a file, later versions will convert
original pitchwheel values of 8192 to 0, 0 to -8192, and 16384 to (+)8192. All
resulting values in the later versions will therefore be equivalent to all those
in the early version minus 8192.
Return to text
9. It is, however, much better than what is provided by the
MIDI tool which only splits the same pitchbend interval into 64 equal parts.
This is wholly inadequate for pitches of the accuracy required.
Return to text
10. The keyboard User Manual will give the information
needed for altering the bend value. On my Roland the bender range can be
accessed via the “Edit” and then the “Lower” buttons, and found by scrolling
through the list with the “Display” button. When “Bender Range” is displayed,
its value can be set to “1” with the “Value” button and the new setting saved
using the “Write” and “Enter” buttons. Other keyboards will have equivalent
methods of making changes to these settings.
Return to text
11. The Bend Range value increments by semitones so that
the default value of “12” yields a pitch bend of a full octave up and down. By
changing this setting to “1” the bend range will be reduced to only a semitone
up or down.
Return to text
12. Keyboards always adopted “compromise” tunings although
some experiments with split keys were designed to increase the number of pitches
available for each octave. This facilitated a differentiation between sharps and
flats so as to enable the consistent use of pure thirds on all degrees.
Unaccompanied vocal performance, however, did not need to compromise and comma
inflection was a normal part of a singer’s technique. This might require the
same note to vary in pitch (according to context) from its normal Pythagorean
position to a comma higher or lower. Frequently, but under tight compositional
control, this might be extended at times up to two commas higher or lower than
Pythagorean pitch. But such flexibility was completely out of the range of
normal keyboards whose tuning (in whatever compromise system was adopted) had to
remain entirely fixed for a particular performance.
Return to text
13. I should again stress that files created with older
versions are updated automatically when opened by later versions of Finale, but
when creating new
files in any version the user will need to know which set of values to
apply. If the list provided below for “older versions” is mistakenly used in
“later versions,” Finale—in blissful ignorance—will produce extremely bizarre
results.
Return to text
14. As stated in [11] above, “8192” here refers to the
default numeric value for “older versions” and the following “[0]” that for
“later.”
Return to text
15. It must be remembered that the Pythagorean scale is
the default scale for Just Intonation, and that the tuning of JI arises from the
addition/subtraction of the Syntonic comma (81:80) to/ from notes that are
modified for consonance purposes. The effect of this modification is to change
all the Pythagorean diatonic semitones from minor (256:243) to major (16:15), to
narrow all the major thirds and sixths, and to widen all the minor thirds and
sixths. But these changes all result from the single application each time of a
Syntonic comma adjustment (upwards or downwards) that changes the default
Pythagorean pitches concerned.
Return to text
16. Theorists who explain the Pythagorean scale do so in
terms of sounding length, and this leads to sounding length ratios. Thus, for
example, the pure fifth is 3:2, and the octave is 2:1. Although the same ratios
are inversely correct for the relative quantities defining the two pitches
involved, they do not define the pitches themselves (but only the relative
values between them). What is needed here is an unambiguous definition of the actual pitch
to be generated for each note defined. This can only be achieved by converting
the ratio values into Cents and then calculating the pitch of each note in terms
of the number of Cents that make it higher or lower than the default note from
which it is computed.
Return to text
17. This value for “G” will be the same for every “G” in
every octave, and all other respective values obtained for all other notes will
be the same for all octaves.
Return to text
18. Again the numeric value for later versions is less
than for older ones by a total of 8192. This, like all other pitchwheel values,
is calculated to the nearest 1 in 8192 parts of a semitone. Equally-tempered
fifths have been narrowed from their Pythagorean defaults. Since the pitchwheel
value of C is 8192 [0], the restoration of the G to its Pythagorean position
will necessarily increase its pitchwheel value. The new value of 8352 [160] has
raised the pitch by a pitchwheel value of 160. When this is divided by 81.92
(the pitchwheel value for each Cent as shown in [14] above), the difference is
found to be 1.953125 Cents
Return to text
19. If, for example, you indicated F-sharp with the tag
“F#,” Finale would show “9152” because it would assume that you had asked for
the numeric value assigned to be displayed in place of the tag itself.
Return to text
20. Experienced Finale users will know that the process of
inserting Text Expressions can be simplified and speeded up by the use of
metatools. Since most pieces using Pythagorean tuning only have a range of up to
nine different pitch classes in each octave, assigning each global pitch to a
metatool makes insertion very quick and easy. Other users will simply have to
make a separate insertion (via the Staff Expression window) for each and every
note in the score.
Return to text
21. In the Instrument List window it will be necessary to
assign a different instrument for each staff, and then a different channel. In
the “Prog.” column the same sound patch can be selected if wished.
Return to text
22. This number can, of course, be changed to whatever
value you like dependent upon the pitch needed relative to any tuning
requirement or system you wish to use. It will be set for the entire piece,
however, and the current value is the one needed for its Pythagorean pitch.
Return to text
23. The figure “480” indicates the same pitch inflection
within the 0-8192 numeric range (used by later versions) as does the figure
“8672” within the numeric range 8192-16384 (used by older versions),
representing simply an increase in pitch bend of 480 units.
Return to text
24. It is “non-melodic” since it was considered too small
to form a discrete interval in its own right. But when it was added to or
subtracted from a larger interval the overall result did yield a new melodic
interval. When added to a Pythagorean minor semitone, the result was a major
semitone (16:15) which was a distinct interval capable of being leant and
performed. Also when it was subtracted from a Pythagorean tone (9:8) the result
was the minor tone (10:9) which again was a discrete interval to be learnt and
sung. The addition or subtraction of this quantity is what gives rise to the new
intervals whose cognition and accurate delivery lies at the heart of the skills
required for the accurate performance of Just Intonation.
Return to text
25. Both these calculations are, of course, for the older
versions of Finale. For the newer versions (which will upgrade existing
old-version files automatically) the figure “8192” will be replaced with “0,”
and the results of the above calculations will be respectively “-1762” and
“1762.”
Return to text
26. In order to produce a clean and pure Syntonic
intonation, you are strongly advised to eliminate completely any default vibrato
that will undoubtedly be set on your MIDI keyboard. Since even the most gentle
vibrato is unlikely to create pitch fluctuation of less than a Syntonic comma,
it stands to reason that the presence of such vibrato will sabotage any attempt
to enter the true sound world of Syntonic tuning. On some keyboards, even the
“harpsichord” patch is infected by vibrato. Removing it is straightforward, but
reference should again be made to the User Manual or technical assistance
sought.
Return to text
27. If you load it into one of the later versions of
Finale, you will find that the values have automatically been updated to those
contained in Figure 12 above.
Return to text
28. The issues surrounding this composition are too
complex to be discussed here and will form the substance of a future article.
But his description of the keyboard upon which he stipulated the chanson could
be successfully performed, while remaining in tune throughout, shows it to have
been similar to the one discussed by other musicians of the time (notably
Vicentino).
Return to text
29. The tones must be smaller because if the octave equals
nineteen intervals of one-third of a tone each there must be at least six and
one-third tones in each octave. The Pythagorean octave contains only five tones
plus two minor semitones (which is less than six overall). The keyboard tones
described by Costeley must therefore be minor tones roughly equivalent to the
Syntonic (10:9) minor tones. In compensation for this, the diatonic semitones
are large (two-thirds the size of a tone in fact), and these, too, must
correspond roughly with the Syntonic diatonic semitones (16:15) although they
are marginally larger in size. The occasional use of non-diatonic semitones
(used either melodically or arising from close cross relations) provides,
according to Costeley’s assessment, movement equaling only one-third of a tone.
Return to text
30. In this temperament, the interval of a fifth is
perceptibly narrowed (much more so indeed than in 12-tone equal temperament),
and the fourths are correspondingly widened by a no less perceptible amount. The
overall effect of this temperament is radically different from that of 12-tone
equal temperament. In the latter, the effect (as we are used to) is one of
tolerably pure fourths and fifths together with pure octaves, upon which have
been superimposed distinctly out-of-tune thirds and sixths (to which our ears
have now become accustomed). In the former, however, the soundscape is one in
which the fourths and fifths are sufficiently out of phase to produce a wavy
timbre (similar to a gentle voix celeste organ sound), upon which has now
been superimposed strikingly pure thirds and sixths.
Return to text
31. There will need to be twenty-one separate values
because the B-sharp/C-flat and E-sharp/F-flat pairs will each need different
values for both notes (even though whichever is used will provide the same
actual pitch). Sometimes Finale will have to read F-flat, and sometimes E-sharp:
the first (= E in 12-tet) will have to be raised from its default pitch while
the second (= F in 12-tet) will need to be lowered. Whichever is used in the
version edited for keyboard will depend solely upon its diatonic context: if
G-flat descends by a diatonic semitone (= two-thirds of a tone) the following
pitch will be written as F-flat; but if a D-sharp rises by a diatonic semitone
the following note will appear as E-sharp. Finale therefore needs to have both
members of each pair provided for.
Return to text
32. The appearance of the score will sometimes look
strange, and somehow “between the cracks,” to those thinking in 12-tone equal
temperament. Frequently chords appear as though they need re-enharmonizing. In
reality, however, each note is completely pitch-specific and relates to a
particular key on the keyboard. Only the single black notes dividing the B/C and
E/F pairs have alternative means of notation.
Return to text
Copyright Statement
Copyright © 2004 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason, Managing Editor and Rebecca Flore and Tahirih Motazedian, Editorial Assistants