Interval-Classes and Psychological Space

[1] The concept of interval class (ic)—the grouping together of pairs of inversionally-related intervals, e.g., minor 2nd and major 7th, into single categories—is fundamental to theories of non-tonal music. Much journal space has been taken up with articles in which interval-classes are a basic structural construct, and many of the proposed functions for measuring the similarity of non-tonal sonorities rely on the concept by basing their calculations of similarity on the interval-class vectors (icvs) of the set-classes.⁽¹⁾ Such discussions have tended to treat interval-class purely as a structural idea, however, and not been concerned with whether the concept has any reality as a psychological construct. Neither does such discussion address the related question of what interrelationships the various interval-classes might have with each other, assuming that the concept has psychological validity in the first place.

[2] While most writers seem to believe that ics are the appropriate level of abstraction for discussing the function of intervals in atonal musical structures, a few have begun to consider alternatives. Marcus Castrén, for example, has suggested a partial separation of ic components, which he terms registrally-ordered intervals (ro-intervals); under this scheme, the two components of each interval-class are still paired but maintain separate identities by acknowledging differences in function in musical contexts, smaller intervals having more to do with melodic situations and larger intervals operating in a harmonic realm. Olli Väisälä has used the concept for an interesting analysis of Schoenberg’s op. 19, no. 2, allowing him to argue for a late-tonal interpretation of the piece.⁽²⁾ At least one author has brought up the question of the relationships between interval-classes: Eric Isaacson sounded a cautionary note in this journal in 1996, wondering, “[D]o we hear ic1 and ic2 as being equal in dissimilarity to, say, ic1 and ic5? Might their similarity be affected by factors such as relative consonance and dissonance?”⁽³⁾ In her dissertation of two years earlier, Diana Stammers had already found some empirical evidence that different ics were treated differently by listeners.⁽⁴⁾ Thus, there seems to be a strong need for more extensive empirical work to determine whether interval-class as defined by music theory has psychological validity.

[3] The number of empirical studies about non-tonal sonorities and the factors influencing the perceived similarities among them is still very small, despite the overwhelming importance of this issue in the music-theoretic community.⁽⁵⁾ This is a problem for those who believe that theories of the structure of music should have some connection to how music is actually perceived. These empirical studies by and large have been concerned with issues of similarity between non-tonal chords as holistic objects. This is a higher level of structure than interval-class itself, although a level that is certainly influenced by how interval-class might or might not operate in a psychological sense. To make any direct investigations about interval-class as a psychological construct requires empirical study at a more basic level, that of the similarity of intervals by themselves. Again, nearly no empirical studies have been taken on this subject, even though the issue of interval similarity has obvious pedagogical implications for aural skills curricula. (Similarity is strongly related to confusability, since similar items are more likely to be confused than dissimilar ones. Thus, better knowledge of interval similarity could help teachers optimize classroom drill time for interval identification skills.)

[4] Similarity data can be obtained in several direct or indirect ways. First, one can simply ask subjects to rate the similarity of two intervals on, say, a 5-point or 7-point scale. Second, one can present triples of intervals and ask subjects whether interval A sounds more like interval B or interval C—this is called “triadic comparison,” and has nothing to do with triads in functional tonality. Third, one can use confusion data, where the similarity of intervals A and B is a function of how often A is mistakenly identified as B.⁽⁶⁾ In all cases, however, a large matrix of data will be generated, and humans are ill-equipped for analyzing masses of numbers. Some form of numerical visualization technique is needed to help the researcher see patterns in the data, and such computational techniques have been developed over the last forty years.

[5] Multidimensional scaling (MDS) is the most important of these visualization techniques; it is a numerical method that solves the problem, given the inter-city distance matrix from a road atlas, derive the relative geometric locations of the cities.⁽⁷⁾ Similarity data is run through an MDS program, and the different dimensions of the resulting geometric configuration are then interpreted as factors determining the similarity of the objects involved. If interval-class has some existence as a psychological construct, then in any MDS solution of interval similarity data the minor 2nd and major 7th should situate near each other, in at least some of the dimensions, and likewise for other pairs of ic-components. We can also use MDS to directly compare empirical data to predictions of alternative theoretical models (for example, an interaction of interval-class and interval-size, something akin to Castrén’s ro-intervals) by generating similarity matrices for those models and comparing the resulting geometries to that produced by the actual data.

[6] Only a handful of articles on interval similarity have appeared. Some of the earlier works, by Ortmann and by Jeffries, present results in ways that preclude obtaining similarity matrices that could be used as input to an MDS program; a much earlier study by von Maltzew did provide quantitative data on interval identification but was concerned only with interval recognition at the uppermost extremes of human hearing (in the highest octave on the piano or above) and is thus not very relevant to typical musical experience.⁽⁸⁾ Two independent studies on interval similarity appeared in the 1970s, one by Reiner Plomp and colleagues and the other by Rosemary Killam and colleagues. Both generated usable matrices of confusion data, although neither group applied MDS analysis and only the paper by Killam et al. was concerned with the music-theoretic—and specifically pedagogical—implications of interval confusability. I shall return to discuss these later in this essay.⁽⁹⁾

[7] In the spring of 2002, I obtained confusion data on intervals from a sample of 27 undergraduate music majors at the Ithaca College School of Music, in a study to help improve aural skills pedagogy. The subjects all had had classroom training on the simple intervals (less than an octave); 18 had completed or exempted through third-term (chromatic tonal) or fourth-term (twentieth-century) aural skills. The subjects listened to sound files of the various simple intervals played on a computer using a pseudo-clarinet timbre, presented in three different presentation modes (harmonic, ascending melodic, and descending melodic), and at ten different transposition levels (top note of the interval in the range G♯4 to F5), for a total of 330 experimental trials per subject (11 intervals x 3 modes x 10 levels). Each harmonic interval sounded for .75 sec., while the components of the melodic intervals sounded for .5 sec. each with a .25 sec. gap between them. To forestall any systematic effects across trials, each subject was given the trials in a different random order, with several constraints between consecutive trials imposed on such orders: 1) no same interval; 2) no same presentation mode; and 3) no common tone between any interval members. After hearing a trial, the subjects clicked on one of 11 on-screen buttons to identify the interval type heard. They were told that while they should strive for correct identifications, they needed to make “snap judgments” and not try to analyze what they had just heard. They had 8.5 sec. within which to make a response, else a missing value was marked and the next trial commenced. Trials were presented in blocks of 20; while a subject could not stop during a block, they could take as long a break between blocks as they wished (and indeed were strongly encouraged to do so as often as needed, given the repetitiveness of the task!). Also, each experimental session was limited to 30 minutes, to further reduce any potential for cognitive fatigue.⁽¹⁰⁾

[8] The resulting confusion data were aggregated in a couple of ways (by transposition level, by presentation mode, and by both) and analyzed using several different techniques, including MDS. A number of interesting results with implications for aural skills pedagogy were obtained; these have been reported elsewhere⁽¹¹⁾ and are not germane to this discussion, so I shall not repeat them here. For present purposes, the implications of the MDS analysis for atonal theory are of interest.

[9] Based on goodness-of-fit analysis, three-dimensional solutions were obtained for the data aggregated across all presentation modes and transposition levels, as well as for the matrices for each individual presentation mode, again aggregated across all transposition levels. Other analysis indicated that transposition level of itself was not a factor in shaping error rates, so no discussion is given for the data as separated by pitch-level. Figure 1 shows the actual derived configuration for the aggregated data as a rotating .GIF file, allowing the reader to get a direct visceral sense of its geometry. Figure 2 shows a simplified and stationary schematic diagram of the configuration.

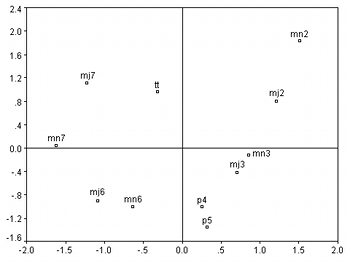
[10] The intervals group along three arcs, forming what can be termed an “octant right-triangle” on the surface of a sphere—think of a triangle on the globe with one vertex at the North Pole and the other two along the Equator at zero and ninety degrees longitude, respectively. Along one side of this triangle are the intervals less than a tritone, while along a second side are the intervals greater than a tritone; the tritone itself lies at about the midpoint of the remaining side. If we were to project this triangle onto a Euclidean plane, as in Figure 3, then one axis of that planar projection could be easily interpreted as “interval size in semitones.” Meanwhile, the various dissonances (the 2nds, tritone, and 7ths) all group along that third side of the triangle, with the perfect consonances clustered near the opposite vertex; the imperfect consonances occur at approximately the midpoints of the connecting sides.⁽¹²⁾ On the planar projection of Figure 3, the other axis could then be easily interpreted as “dissonance-class.” Since the different types of 2nds, 3rds, 6ths, and 7ths cluster strongly together, some effect of “diatonic interval type” appears to operate as well. Thus, the interpretation of the derived configuration is an interaction of interval-size, interval-type, and dissonance-class.

[11] Note that this interpretation has not led to three independent factors, each determining one of the Euclidean axes of the configuration. In fact, attempting to do so leads to awkward (at best) formulations for the two axes that do not involve the dissonance-classes. The interaction interpretation given above, by contrast, appears to be clear and readily accounts for the features of the configuration. Keep in mind that the projection operation of the previous paragraph was done only to aid in understanding the nature of the three-dimensional configuration. Such a projection is not a legitimate operation in the sense of trying to reduce the number of dimensions needed for the configuration, even though in essence the configuration “is” two dimensional if we were operating in spherical geometry rather than Euclidean geometry—all MDS algorithms involve a Euclidean space. If one wants to see what sort of two-dimensional configuration is produced by the algorithm, one must have the algorithm compute such a configuration ab initio. Doing so for this data yields a noticeably different topology, as shown in Figure 4.

[12] Three-dimensional configurations were also obtained for the matrices for the various presentation modes by themselves. These configurations have the same overall topology as the aggregate data, with a few variations occurring in the clustering of individual pairs of intervals (e.g., minor and Major 3rd; Major 3rd & Perfect 4th); the tritone is the most volatile in terms of moving around the various configurations, clustering closer to the 6ths when descending.

[13] Of particular interest, we can derive the “classical” set of interval-classes from this configuration by a particular Euclidean planar projection of the configuration, shown in Figure 5. On this projection, ic6 lies on an axis of symmetry; the members of the other ics can be read off directly with increasing distance from that axis. Because we can find such a projection, this study thus provides some empirical support for the idea of interval-class as operating in psychological space. Remember again, however, that as a projection this does not tell the whole story, for which we must refer back to the complete configuration.

[14] As a check against the predictions of various theoretical possibilities, MDS was applied to similarity matrices developed for models based on: interval-class only; interval-size only; acoustical dissonance only; and interval-class plus interval size. The topologies of all of the resulting configurations were obviously different than that for the actual data.

[15] As another comparison, the confusion matrices for the above-mentioned studies by Plomp et al. and Killam et al. were also analyzed by MDS. Both of those studies had included the octave as one of the intervals studied, unlike the current study; therefore, the data from those studies were analyzed in two ways—with the octave removed from consideration, and with it included. When the octave was omitted, the resulting topologies were fairly similar to that produced by the current data; when it was included, some non-trivial re-alignments took place. Figure 6 provides a stereoscopic view of the configuration for Killam et al.’s data with the octave removed, while Figure 7 gives a stereoscopic view of the configuration when the octave was included.⁽¹³⁾ It is not clear why such realignments occur in the configuration when the octave is included; one initial speculation would be, some sort of conflict took place between factors of acoustical dissonance and overall interval size, but this would be just a guess.

[16] The rule of thumb for MDS studies is that data from a minimum of about 30 subjects is needed in order to ensure a reliable solution. The current study falls just below that threshold, and thus begins to raise concerns about whether we should put any faith in the configuration obtained. Likewise, neither Killam et al.’s nor Plomp et al.’s studies meet this threshold.⁽¹⁴⁾ It is because all three configurations have the same overall topology (when the octave is excluded from consideration in the latter two) that it is possible to have any confidence in the current results; more thorough replications with larger subject samples are, of course, clearly needed. Also, it is critical that replications systematically include octaves and compound intervals: given that the configurations for the other studies change when the octave is included in the MDS analysis, we cannot assume that no new factors will appear when larger intervals are included.⁽¹⁵⁾ Furthermore, some means of including types of musical contexts will be necessary eventually, as opposed to testing similarity only in context-free situations as was done in all of the above studies: it would not be very surprising to learn that interval (and by extension, interval-class) similarity might change if a listener first heard several pieces dominated by whole-tone or octatonic textures rather than diatonic or chromatic tonal harmonies.⁽¹⁶⁾

[17] These MDS results have some mixed implications for atonal theory. Interval-class does appear to have some validity as a psychological construct, given that the pattern of “classical” interval-classes can be derived from the configuration. The very strong grouping of intervals by dissonance-class suggests that the different interval classes cannot be treated as being independent of each other for assessing chord similarity, however. Should the current results be supported by replications, then similarity functions that use the icv as the basis for their calculations will need revision in order to take these relationships into account. Of such functions, Scott and Isaacson’s ANGLE measure is the best pre-positioned for any upgrade, since they already discuss how to alter the calculation of the function to take correlations of ics into account.⁽¹⁷⁾

[18] The idea that interval-classes cluster into several groups should not be particularly onerous. Indeed, the observed clustering matches a well-established taxonomy in music theory, of perfect consonances, imperfect consonances, and dissonances, so any resulting modification of atonal theory will likely align it more closely to certain ideas for tonal theory. This may seem to fly in the face of a basic aesthetic stance in atonal theory, though, in that there seems to be an unwritten rule among most atonal theorists that “all intervals are created equal (but separate);” to group interval-classes in a way so explicitly associated with functional tonality would appear to undermine all the work that has gone into developing atonal theory as an analytical subdiscipline entirely separate from tonal theory. Any such fear is a red herring, however. As Fred Lerdahl has stated on more than one occasion, “One does not hear Elektra and Erwartung in entirely different ways. The historical development from tonality to atonality (and back) is richly continuous. Theories of tonal and atonal music should be comparably linked.”⁽¹⁸⁾ Further studies on the perceptual grouping of interval-class components, including how the octave and compound intervals fit into the overall picture, will help us develop such a linkage.

Art Samplaski
P. O. Box 4971
Ithaca, NY 14852

Footnotes

1. Literature reviews of many such functions can be found in Marcus Castrén, RECREL: A Similarity Measure for Set-Classes (Helsinki: Sibelius Academy, 1994), Eric J. Isaacson, “Similarity of Interval-Class Content between Pitch-Class Sets: The IcVSIM Relation,” Journal of Music Theory 34 (1990): 1–28, and Damon Scott and Eric J. Isaacson, “The Interval Angle: A Similarity Measure for Pitch-Class Sets,” Perspectives of New Music 36(2) (1998): 107–142.
Return to text

2. Marcus Castrén, “Joukkoluokitukseen perustuva sointuluokitus: perusperiaatteet ja esimerkkejä sovellusmahdollisuuksista” [Chord Classification Based on Set Classification: Basic Principles and Examples of Applicational Possibilities], Sävellys ja musiikinteoria 7 (1997): 6–25, and “Pairs of Chords as Objects Illuminating Set-Class Similarity: Some Viewpoints and a Computer-Assisted Procedure to Create Test Materials for Listener Experiments,” Electronic Journal of Music Theory and Analysis vol.1, no.2 (2000), www.musictheoryresources.com; Olli Väisälä, “Concepts of Harmony and Prolongation in Schoenberg’s Op. 19/2,” Music Theory Spectrum 21 (1999): 230–59.
Return to text

3. Eric J. Isaacson, “Issues in the Study of Similarity in Atonal Music,” Music Theory Online vol. 2.7, 1996, paragraph 11.
Return to text

4. Diana Stammers, “Set Theory in the Perception of Atonal Pitch Relations” (Ph.D. diss., Cambridge University, 1994). Major and minor 3rds were treated by her listeners as being closely related and confusable, whereas the two types of 2nds were considered distinct. She attributed this to prior learning from exposure to classical tonality, in which the two types of thirds have similar structural roles but the two types of seconds do not.
Return to text

5. Cheryl L. Bruner, “The Perception of Contemporary Pitch Structures,” Music Perception 2 (1984): 25–39; Don B. Gibson, “The Aural Perception of Non-Traditional Chords in Selected Theoretical Relationships: A Computer-Generated Experiment,” Journal of Research in Music Education 34 (1986): 5–23, “The Aural Perception of Similarity in Nontraditional Chords Related by Octave Equivalence,” Journal of Research in Music Education 36 (1988): 5–17, and “The Effects of Pitch and Pitch-Class Content on the Aural Perception of Dissimilarity in Complementary Hexachords,” Psychomusicology 12 (1993): 58–72; Tuire Kuusi, Set-Class and Chord: Examining Connection between Theoretical Resemblance and Perceived Closeness (Helsinki: Sibelius Academy, 2001), “Semantic Differential as a Method for Collecting Estimations of Chords,” in Proceedings of the 5th Triennial ESCOM Conference (2003), and “The Role of Set-Class Identity in the Estimation of Chords,” Music Theory Online vol. 9.3, 2003; Roger C. Lane, “A Multidimensional Scaling Study of Seven Theoretical Indices of Intervallic Similarity and Musicians’ Perceptions among Twenty-One Pitch-Class Sets with Implications for Music Teaching and Learning” (Ph.D. diss, University of North Carolina, Greensboro, 1997); Panayotis Mavromatis and Virginia Williamson, “Towards a Perceptual Model for Categorizing Atonal Sonorities” (paper presented at the Society of Music Theory meeting, Atlanta, GA, 1999); Jana K. Millar, “The Aural Perception of Pitch-Class Relations: A Computer-Assisted Investigation” (Ph.D. diss., North Texas State University, 1984); Art Samplaski, “The Perceived Similarity of Some Non-Tonal Tetrachords Compared to Predictions of Selected Twentieth-Century Chord Classification Systems,” presentation at the 2000 meeting of the Society for Music Perception and Cognition, Toronto, Ontario, and “The Relative Perceptual Salience of Tn and TnI,” Music Perception 21 (2004): 545–59; and Virginia Williamson and Panayotis Mavromatis, “Similarity in Atonal Music Theory: A Perceptual Study” (paper presented at the Society for Music Perception and Cognition meeting, Cambridge, MA, 1997), and “Categorizing Atonal Sonorities: Multidimensional Scaling, Tree-Fitting, and Clustering Compared” (paper presented at the Society for Music Perception and Cognition meeting, Evanston, IL, 1999).
Return to text

6. For other types of problems, other methods of data collection are also possible, e.g., consumer product preference ratings.
Return to text

7. There is an entire family of MDS models for different situations, with differing limitations and requirements; a related set of techniques called cluster analysis also provides for visualization of similarity by generating tree diagrams instead of geometric configurations. See Joseph B. Kruskal and Myron Wish, Multidimensional Scaling, Sage University Paper Series on Quantitative Applications in the Social Sciences, Series no. 07–011 (Newbury Park, CA and London: Sage Publications, 1978), for a basic introduction. Their short monograph discusses both the underlying mathematics as well as various important methodological issues that will not be discussed in this essay; such issues include determining the appropriate number of dimensions for the derived configurations (i.e., are three dimensions needed to adequately describe the relationships between the objects under investigation, or will two suffice?), and how to deal with any underlying asymmetries in the data (e.g., in a tonal context I→V will almost certainly be rated differently than V→I). I am currently finishing preparation on an article illustrating a different application of MDS for music-theoretic analysis that will include a detailed but non-technical tutorial about such issues.
Return to text

8. T. Jeffries, “The Effects of Order of Presentation and Knowledge of Results on the Aural Recognition of Melodic Intervals,” Journal of Research in Music Education 15 (1967): 179–90; Catrina von Maltzew, “Das Erkennen sukzessiv gebener musikalischer Intervalle in den äusseren Tonregionen,” Zeitschrift für Psychologie 64 (1913): 161–257; and Otto Ortmann, “Notes on Interval Discrimination,” Peabody Bulletin vol. 28, no. 2 (1932): 45–46. Ortmann provides only qualitative bar graphs of confusion data for two intervals (i.e., he gives no indication as to whether the vertical axes should be interpreted as percentage of times the played interval was identified as this, that, or the other answer—and if so, what percentage—or as numbers of times it was so identified). Jeffries was concerned with how the presence of particular intervals before and after a target interval in specific melodic contexts affected how the target was identified; he presents his results in a couple of ways, but they again are qualitative, not quantitative, tables and diagrams.
Return to text

9. Rosemary N. Killam, Paul V. Lorton, Jr., and Earl D. Schubert, “Interval Recognition: Identification of Harmonic and Melodic Intervals,” Journal of Music Theory 18 (1975): 213–234; R[einer] Plomp, W. Wagenaar, and A. M. Mimpen, “Musical Interval Recognition with Simultaneous Tones,” Acustica 29 (1973): 101–109. One slightly earlier study (W. J. M. Levelt, J. P. van der Geer, and R[einer] Plomp, “Triadic Comparisons of Musical Intervals,” British Journal of Mathematical and Statistical Psychology 19 [1966]: 163–179) actually carried out MDS analysis of data obtained by the triadic comparison method for intervals sounded as pure tones and as complex tones; that analysis appeared to show some support for the hypothesis of interval-class as a psychological construct. In my opinion, however, their paper contains significant methodological problems, which would be beyond the scope of the present article to critique in detail; the citation is given for those readers wishing to consult the work for themselves.
Return to text

10. Thirty additional duplicate trials were inserted into the generated random orders, subject to the same constraints between consecutive trials, as a check for subjects’ self-consistency. There were thus 360 trials (18 blocks of 20) in total. One additional subject was eliminated from consideration for failing this check.
Return to text

11. Art Samplaski, “Interval and Interval-Class Similarity: Results from a Confusion Study,” poster presentation at the 2003 meeting of the Society for Music Perception and Cognition, Las Vegas, NV; manuscript submitted for publication.
Return to text

12. The subsidiary arc drawn between the imperfect consonances on the schematic diagram in Figure 2 is to aid visualization. It is parallel to the arc along which the dissonances lie.
Return to text

13. The configurations derived from Plomp et al.’s data are not shown because of the minimal time for which their stimuli sounded—they did four experimental runs of stimuli with durations of 120, 60, 30, and 15(!) milliseconds respectively, only the longest of which is relevant to actual musical situations. Plomp et al. were concerned with how interval recognition degraded as stimulus duration was reduced, rather than any possible implications for theories of musical structure. It is thus all the more remarkable that the configuration for their data bears any resemblance at all to the other two.
Return to text

14. Killam et al. used a sample of 15 undergraduate music majors; they tested at two transposition levels rather than the ten used in the present study, using an organ timbre; the stimuli were presented in two durations, of 100 and 200 milliseconds. As in the present study, intervals were presented in all three presentation modes; while the authors provide some analysis separated by presentation mode, they only presented an aggregate confusion matrix. Plomp et al. used a sample of 15 music students; they used sine tones and sawtooth waves as timbres; the intervals were presented such that either the high or low notes of the intervals were always middle C or the C above, or else centered within that octave to the extent possible. The various intervals were thus presented different numbers of times (octaves could only be presented as C4 to C5 and major 7ths could only be presented with C as one component, while the other intervals were presented in three different forms); while they detail some efforts to reduce any bias caused by such lopsidedness, their paper remains problematic.
Return to text

15. Indeed, given that in a number of undergraduate aural skills programs music majors receive little or no training on the recognition of compound intervals, it is entirely possible that such MDS configurations could be chaotic jumbles if population samples of only undergraduates are used. This is a worst-case scenario, of course, but we have no way a priori to know what results might occur.
Return to text

16. Again, we cannot be certain that this would be the case, although it may seem like a perfectly plausible scenario. In making pronouncements about empirical situations, there is no substitute for collecting actual data. Because the number of factors that might influence the results, and their possible interactions, proliferate rapidly in imbedded-context situations, it is more difficult to develop well-designed studies of such types—context-free studies must first be carried out to provide a baseline for follow-up research.
Return to text

17. Scott and Isaacson, op. cit., pages 136–39.
Return to text

18. The most recent such statement is Tonal Pitch Space (New York: Oxford University Press, 2001), page 351.
Return to text

Copyright Statement

Copyright © 2004 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.