[1] I would like to elaborate upon several ideas brought up in Frank Samarotto’s thought-
provoking article on sharp that appeared in the last issue of MTO. The denial of sharp
’s tendency to lead to is a distinctive progression, the expressive qualities of which
were well addressed by Samarotto.
[2] Before turning to the article itself, I would like to applaud Samarotto’s desire to
heighten rather than downplay Schenker’s “energeticist” outlook. As he remarks, “the
added specificity of Schenker’s method . . . should render it more fine-grained,
concrete, and ultimately more defensible as a holistic analysis.” By emphasizing
the energetic dimension of Schenker’s thought, we are brought closer to a
consideration of a work’s expressive capabilities.
[3] Of all of Schenker’s works, it is his Harmonielehre that most strongly expresses the
dynamic aspect of music associated with “energetics.” Due to the many mystical
ruminations about tones and their biological life force, this book--his first theoretical
publication--is often regarded as more abstract than practical. One of the less speculative
parts of Harmonielehre, however, is the exhaustive listing of all the intervallic
relationships that exist between the scale degrees. The end result leads Schenker to the
conclusion that the intervals of the tritone (diminished fifth or augmented fourth) and the
diminished seventh (resulting from mixture of the major and minor modes) are
eindeutig, i.e. “open only to one interpretation.” In the major mode, for example, the tritone formed by the diatonic scale degrees and is unique, and thus defines the key
unequivocally. Schenker remarks that if a composer desires to “give us a sure perception
of the key, he will resort to a univalent [eindeutig] interval which, by its
very nature, will exclude any other key.”
Example 1a. Mozart, Piano Concerto in C, K. 467/I (bars 128–131)

(click to enlarge)
Example 1b. Chordal reduction of Mozart, Piano Concerto in C, K. 467/I (bars 128–131)

(click to enlarge)
Example 2. Beethoven, The Creatures of Prometheus, Op. 43, No. 16 (bars 1–16)

(click to enlarge)
[4] Paradoxical as it may seem, the static, eindeutig interval between and
embodies the notion of directed motion as warranted by “energetics.” When these scale
degrees appear in the dominant seventh chord their energetic tendencies become
heightened. Even greater than the urge of the leading tone () to resolve up to the tonic
scale degree, is that of to descend to . Due to its origin as a dissonant passing
motion from 5, the necessity of its resolving to is so vital that it will often be
realized despite appearances to the contrary.
[5] To illustrate this, let’s look at the second theme from the first
movement of Mozart’s Piano Concerto in C, K. 467 (Example 1a). The melody is made
up of descending arpeggio figures, and the opening four bars are subdivided into
a pair of two-bar groups. A parallelism in the top voice results: D to E and C
to D. However, this description of the top voice does not account for the true
voice leading. As shown in Example 1b, the top
voice C () in the third bar of the theme is the dissonant seventh of V7. It does not
return back up to D in the following bar, but resolves to B () in the bass. The
apparently straightforward symmetrical pattern of the melody belies the subtlety of the
voice leading. As is often the case in Mozart’s music, the apparent simplicity of its
outward appearance veils a more complicated tonal structure.
[6] A similar voice-leading occurs in the famous englische theme from the Finale of
the “Eroica” Symphony, as well as Beethoven’s ballet The Creatures of Prometheus
cited by Samarotto. Example 2
presents a voice-leading graph of the theme as it appears in the ballet. In bars
10–12, a♭2 () is prominently articulated as the seventh of the V7, and
this active tone resolves to G () in the bass of bar 13. As shown in my
analysis, I read a double harmonic progression in the bass, with as the
initial structural top voice tone. The melodic descent to occurs in the bass
voice before resurfacing in the melody with the structural descent of to
in bars 14–16.
[7] Superimposed over the structural melodic descent of to , is the chromatic motion
A♭ - A♮ - B♭, which serves as the focal point of Samarotto’s discussion of
this theme. He describes the deflection of the dissonant seventh A♭ to A♮
instead of G as “a manifestation of pure force.” Samarotto’s characterization of the
chromatic motion A♭ - A♮ - B♭ as expressing an “exuberant sense of heroic
resolve” is certainly appropriate. Nevertheless, I would argue that, despite the power of
this voice-leading aberration, the urgency of the dissonant seventh () must ultimately
be taken care of. In other words, there are two dimensions at play here: the surface
(foreground) melodic tension of going through sharp to , and the structural tonal
motion of resolving to . The effect of the passage is, in fact, heightened by the
conflict between the surface articulation and the larger tonal organization. The top voice
may appear to say, quoting Samarotto, “So there, I’ll do as I wish,” but the necessity of
the voice leading forces the tonal structure to find an alternative solution. Although in
the melody does not literally continue down to , its destiny is fulfilled in another voice.
Example 3a. Beethoven, The Creatures of Prometheus, Op. 43, No. 16 (bars 181–192)

(click to enlarge)
Example 3b. Chordal reduction of Beethoven, The Creatures of Prometheus, Op. 43, No. 16 (bars 181–192)

(click to enlarge)
Example 4. Beethoven, Piano Sonata No. 4 in E♭, Op. 7/II (bars 1–5)

(click to enlarge)
Example 5a. Mozart, Symphony No. 39 in E♭, K. 543/I (bars 22–25)

(click to enlarge)
Example 6a. The expansion of V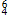 to I
to I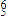

(click to enlarge)
Example 6b. Stölzel, (formerly attributed to J. S. Bach) “Bist du bei mir” (bars 1–9)

(click to enlarge)
[8] As Samarotto rightly points out, this chromatic motive is brought back in the elaboration of the final statement of the theme just before the coda. The a♮2, which results in an F-major 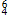 chord in bar 184, allows for an echo of the A♭ - A♮ - B♭ idea. Yet despite this chromatic inflection, the
chord in bar 184, allows for an echo of the A♭ - A♮ - B♭ idea. Yet despite this chromatic inflection, the 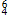 chord resolves, and the top voice a♮2 descends to g2. Example 3a offers an alternative interpretation to Samarotto’s of the voice leading of this unusual passage, showing how the harmonic progression from V7 to I♭7 is filled out by chromatic passing tones. The structural
melodic descent from remains in the top voice, and the recollection of the chromatic
motion A♭ - A♮ - B♭ hovers above the descent to . As shown in
Example 3b, Beethoven could have kept a♭2 in the top voice. In any case, the
alteration to a♮2 cannot prevent the top voice’s ultimate continuation down to g2,
but this chromatic inflection helps point to b♭2.
chord resolves, and the top voice a♮2 descends to g2. Example 3a offers an alternative interpretation to Samarotto’s of the voice leading of this unusual passage, showing how the harmonic progression from V7 to I♭7 is filled out by chromatic passing tones. The structural
melodic descent from remains in the top voice, and the recollection of the chromatic
motion A♭ - A♮ - B♭ hovers above the descent to . As shown in
Example 3b, Beethoven could have kept a♭2 in the top voice. In any case, the
alteration to a♮2 cannot prevent the top voice’s ultimate continuation down to g2,
but this chromatic inflection helps point to b♭2.
[9] The main focus of Samarotto’s article, however, explores the denial of sharp ’s
natural tendency to move to . He reminds us that sharp leading to is so
significant because “one of the most strongly directed motions in tonal music is
modulation to the dominant.” Since scale degree is, along with scale degree , one of
the two most important scale degrees in the tonal system, it’s not surprising that melodic
chromatic descents from are always written - sharp - ♮ instead of - ♭ - . Scale degree ’s status as a defining element of the tonal system precludes it from being
altered.
[10] In harmonic progressions the descending chromatic motion from sharp - ♮ usually results from a succession of two distinct chords with an elision of . A classic “textbook” example comes from the opening of the C-major slow movement of Beethoven’s Piano Sonata No. 4 in E-flat, Op. 7 (Example 4). In bar 4, F-sharp in the bass supporting a leading-tone chord is immediately followed by a V over F♮. Although our ear makes sense of the progression as resulting from an elision of G, the
deflection of our expectation gives this passage its expressive force.
over F♮. Although our ear makes sense of the progression as resulting from an elision of G, the
deflection of our expectation gives this passage its expressive force.
[11] A different situation occurs, however, when the deflection of sharp to ♮
occurs within the same chord. Without a change of harmony, the effect of neutralizing
sharp to ♮ is highlighted and the result becomes more powerful. One of the
most clear, yet breathtaking examples that I know occurs at the end of the introduction to
the first movement of the 39th Symphony by Mozart. Example 5a presents the last four
bars of the introduction. In bar 24, just before the dominant that ushers in the exposition,
Mozart presents an augmented sixth chord over C♭ on the third beat. What makes this
moment so striking is the way this augmented sixth chord is prepared. As shown in the
successive levels of Example 5b, it grows out of IV. Example 5c presents a
foreground reduction of this passage: the chromatic inflection from IV to the augmented
sixth chord is effected through a series of voice exchanges, culminating in the stark,
ominous canon in octaves between the outer voices. At the moment we finally achieve
the augmented sixth chord in bar 24, the tension is poignantly deflated by the unexpected
inflection down a chromatic semitone from A♮ to A♭. Despite the
intensification of ♮ to sharp , the motion towards is denied at the last
moment when sharp reverts back to ♮.
Example 5b. Successive reductions of bars 16–25 in Mozart, Symphony No. 39 in E♭, K. 543/I 
(click to enlarge) | | Example 5c. Mozart, Symphony No. 39 in E♭, K. 543/I (bars 16–26) 
(click to enlarge) |
[12] In his article, Samarotto presents several examples in which the potency of sharp
is neutralized back to ♮ over more elaborate prolongations. In the first of his
examples, the aria “Bist du bei mir,” Samarotto shows how sharp in the bass,
supporting a ♮-IV7 chord leads over bars 5–7 to ♮ as part of a IV6. Reflecting
upon the meaning of the words, he remarks that sharp “relinquish[es] its force, not
because it is denied, but because it is given up willingly.” While not disputing his
interpretation of the text, I would like to propose an alternative reading of the voice-
leading. In making a connection between the seventh chord over E♮ in bar 5 and
the E♭ 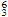 chord in bar 7, Samarotto reads bar 6 as a passing
chord in bar 7, Samarotto reads bar 6 as a passing 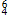 between them.
Although
between them.
Although 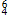 s often do function as passing chords, I read the harmony in this bar not as a
passing, but as a cadential
s often do function as passing chords, I read the harmony in this bar not as a
passing, but as a cadential 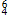 . The successive stages of Example 6a show how the
resolution of this cadential
. The successive stages of Example 6a show how the
resolution of this cadential 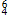 is expanded; instead of resolving directly to a
is expanded; instead of resolving directly to a 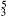 chord, it
goes to a V
chord, it
goes to a V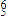 chord.
chord.
[13] Example 6b presents a voice-leading reduction of the first part of the aria. The modulation to the dominant at the end of the first part is achieved by reinterpreting the opening E♭ tonic as IV in B♭. In bar 5 this IV becomes chromatically inflected as ♮-IV7 with E♮ in the bass leading to the dominant F decorated by a 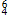 chord in bar
6. The E♭
chord in bar
6. The E♭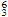 chord, which occurs at the beginning of bar 7, functions as a passing chord between the cadential
chord, which occurs at the beginning of bar 7, functions as a passing chord between the cadential 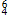 in bar 6 and its resolution to V
in bar 6 and its resolution to V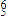 . Although the E♮ seventh chord in bar 5 and the E♭
. Although the E♮ seventh chord in bar 5 and the E♭ 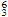 chord in bar 7 have the same root, the two chords function very differently. Thus, despite the close proximity of sharp and ♮, I would argue that there is not a direct transformation of one into the other as
Samarotto suggests.
chord in bar 7 have the same root, the two chords function very differently. Thus, despite the close proximity of sharp and ♮, I would argue that there is not a direct transformation of one into the other as
Samarotto suggests.
[14] Two other factors contribute further to this interpretation. The first concerns the skip in register from d2 down a seventh to e♭1 at the beginning of bar 7. The leap from d2 to e♭1 leaves a void, which is recovered at the appearance of c2 on the second beat. This gap in register connects the 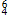 of bar 6 supporting d2 to the c2 over V6. The second
factor concerns the phrase rhythm. It is clear that bars 1–6 alternate in a succession of strong and weak bars. However, bar 7 is not heard as a strong bar, but as a weak one. With the arrival in bar 8 of B♭, bars 8–9 constitute another pairing of strong to weak bars. The succession of bars 6 and 7 as weak expands bars 5–7 as a three-bar hypermeasure. The cadential
of bar 6 supporting d2 to the c2 over V6. The second
factor concerns the phrase rhythm. It is clear that bars 1–6 alternate in a succession of strong and weak bars. However, bar 7 is not heard as a strong bar, but as a weak one. With the arrival in bar 8 of B♭, bars 8–9 constitute another pairing of strong to weak bars. The succession of bars 6 and 7 as weak expands bars 5–7 as a three-bar hypermeasure. The cadential 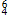 does not, therefore, fall on the second of a two-bar
hypermeasure, but the second of a three-bar one. This rhythmic extension, incidentally, accounts for the unusual nine-bar phrase length of the first part.
does not, therefore, fall on the second of a two-bar
hypermeasure, but the second of a three-bar one. This rhythmic extension, incidentally, accounts for the unusual nine-bar phrase length of the first part.
[15] In closing, I would like to offer an example which contains a similar voice-leading motion as in the aria, but one which does embody Samarotto’s idea of the sublimation of sharp to ♮. This occurs at the end of the recapitulation in the opening
movement of Beethoven’s “Eroica” Symphony with the statement of the final “second” theme (bars 512–547). The passage to be discussed includes one of the most dramatic moments in the movement: the six repeated statements of the A♮ diminished seventh chord in syncopation over bars 531–534.
Example 7. Beethoven, Symphony No. 3 in E♭, Op. 55 “Eroica”/I (bars 536–538 with hypothetical continuation)

(click to enlarge)
Example 8. Successive reductions of bars 512–547 in Beethoven, Symphony No. 3 in E♭, Op. 55 “Eroica”/I

(click to enlarge and see the rest)
Example 9. Beethoven, Symphony No. 3 in E♭, Op. 55 “Eroica”/I (bars 537–540 with enharmonic rewriting of bar 539)

(click to enlarge)
Example 10. Successive reductions of bars 539–542 in Beethoven, Symphony No. 3 in E♭, Op. 55 “Eroica”/I

(click to enlarge and see the rest)
[16] This diminished seventh chord represents an altered subdominant harmony,
chromatically inflected as ♮-IV♭7. The almost brutal insistence with which it is reiterated makes us expect a strong dominant to follow. Through a voice-exchange over bars 534–536, in which ♮-IV♭7 becomes ♮-IV6/♭5 (cf. Example 5b), Beethoven intensifies this expectation even further. The cadential 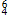 chord arrives with full force in bar 537, and in the following bar yet another statement of the ♮-IV6/♭5 chord
occurs, but now with C♮ instead of C♭ in the bass. Again, we expect
another statement of the dominant immediately to follow, and Example 7 presents
a hypothetical return of the cadential
chord arrives with full force in bar 537, and in the following bar yet another statement of the ♮-IV6/♭5 chord
occurs, but now with C♮ instead of C♭ in the bass. Again, we expect
another statement of the dominant immediately to follow, and Example 7 presents
a hypothetical return of the cadential 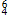 in bar 539. In the actual music, however, the a♮2 (sharp ) in the top voice of bar 538 does not resolve to b♭2 as it did previously; instead it leads to a♭2 (♮).
in bar 539. In the actual music, however, the a♮2 (sharp ) in the top voice of bar 538 does not resolve to b♭2 as it did previously; instead it leads to a♭2 (♮).
[17] The tonal meaning of this passage is presented through a series of voice-leading reductions presented in Example 8. Example 8a presents the basic structure of the double harmonic progression supporting a melodic descent from to . Example 8b shows how the first dominant is decorated by a cadential 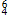 , which resolves to a V
, which resolves to a V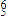 instead of V
instead of V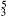 chord (cf. Example 6a). In Example 8c, we see how the ♮-IV♭7 is embellished by a voice exchange to ♮-IV♯6/♭5. The cadential
chord (cf. Example 6a). In Example 8c, we see how the ♮-IV♭7 is embellished by a voice exchange to ♮-IV♯6/♭5. The cadential 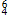 , which follows, now
leads through a passing chord to V
, which follows, now
leads through a passing chord to V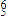 . The two ♮-6/♭5 chords, noted by asterisks, function differently. The ♮-6/♭5 chord over C♭ results from a voice exchange with the ♮-IV♭7, whereas the ♮-6/♭5 chord over C♮ is essentially a passing chord. The chromatic motion of A♮ to A♭ in the top voice results from an elision of B♭ (shown in parentheses). As in the Beethoven piano sonata extract quoted above (Example 4), sharp is deflected from its proper resolution through an elision.
. The two ♮-6/♭5 chords, noted by asterisks, function differently. The ♮-6/♭5 chord over C♭ results from a voice exchange with the ♮-IV♭7, whereas the ♮-6/♭5 chord over C♮ is essentially a passing chord. The chromatic motion of A♮ to A♭ in the top voice results from an elision of B♭ (shown in parentheses). As in the Beethoven piano sonata extract quoted above (Example 4), sharp is deflected from its proper resolution through an elision.
[18] Example 8d presents a foreground reduction of this passage. At this stage, the
chromatic motion A♮ to A♭ is no longer merely the result of an elision.
Beethoven goes one step further by altering the functional meaning of the top voice A♮. As shown in
Example 9, A♮ is enharmonically transformed into a B♭♭ in bar 539. This enharmonic transformation of A♮ to B♭♭ allows for a tonicization of a D♭ chord in bar 540. The top voice tone over this D♭
chord, a♭2, serves to prepare the dissonant seventh of the V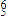 chord in the succeeding
bar. Not only does the neutralizing of sharp at this crucial moment create a most
expressive sigh of longing, but the enharmonic change of A♮ to B♭♭ is the
ultimate refutation of sharp .
chord in the succeeding
bar. Not only does the neutralizing of sharp at this crucial moment create a most
expressive sigh of longing, but the enharmonic change of A♮ to B♭♭ is the
ultimate refutation of sharp .
[19] Example 10 isolates bars 539–542, and shows how they can be understood as a
sequence. Example 10a presents the basic form of this sequence, and Example 10b
places A♭, the common tone of the first three bars, in the top voice. In
Example
10c, B♭♭ serves to decorate the top voice A♭ as its chromatic upper neighbor.
In the following bar, A♭ is shifted into an inner voice before resurfacing back in the
top voice. Example 10d shows how a descending third motion prolongs the top voice
A♭ . Furthermore, the 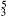 chords in bars 540 and 542 are decorated by suspensions and
chromatic lower neighbor notes. The resultant effect of these figurations is that each of
the
chords in bars 540 and 542 are decorated by suspensions and
chromatic lower neighbor notes. The resultant effect of these figurations is that each of
the 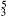 chords is heard initially as a minor instead of major triad (i.e. e♮ = f♭
over D♭ and f♯ = g♭ over E♭ ). This suggestion of a modal alteration in these
bars creates an uplifting quality to this passage. Following the denial of sharp ’s urge to
resolve to earlier in bars 538–539, darkness gives way to light, and there is a surge of
triumph leading to the final cadence. In bar 545, at the arrival of the dominant just before
the theme’s completion, b♭ 2 is regained; here it reasserts itself powerfully in the
register previously denied by the enharmonic change of a♮ 2 to b♭♭2 in
bar 539.
chords is heard initially as a minor instead of major triad (i.e. e♮ = f♭
over D♭ and f♯ = g♭ over E♭ ). This suggestion of a modal alteration in these
bars creates an uplifting quality to this passage. Following the denial of sharp ’s urge to
resolve to earlier in bars 538–539, darkness gives way to light, and there is a surge of
triumph leading to the final cadence. In bar 545, at the arrival of the dominant just before
the theme’s completion, b♭ 2 is regained; here it reasserts itself powerfully in the
register previously denied by the enharmonic change of a♮ 2 to b♭♭2 in
bar 539.
[20] It is clear that the motion from ♯ to ♮ has a special significance in
expressing unfulfillment and denial, or even, as Samarotto proposes, sublimation. As we
have seen, Samarotto and I have sometimes come to different conclusions about pieces
that exploit it. Occasionally our vantage points contradict each other, but hopefully they
can, more often, be complementary and help to illuminate the inner workings of
compositions where this motion occurs. As Samarotto concludes in his article, for
Schenkerians, “the inference of energetic forces can inform and even clarify one’s
understanding of structure, taking us back to the tones themselves, and their inner lives.”
Eric L. Wen
Curtis Institute of Music
Department of Musical Studies
1726 Locust Street
Philadelphia, PA 19103-6187
eric.wen@curtis.edu
1. Throughout the second half of the 20th century, there
has been a tendency to downplay this aspect of Schenker’s thought. Even among Schenkerians themselves, there was the
fear that this viewpoint would weaken their cause, especially in light of the exacting
objectivity in analyzing serial techniques throughout the late-20th century. The “toning
down” of Schenkerian rhetoric is well outlined in William Rothstein’s article “The
Americanization of Schenker” in Schenker Studies (Cambridge: Cambridge University
Press, 1990) pages 193–203. See also Rothstein’s update on the situation in his article
“Conservatory Schenker vs University Schenker” in the Tijdschrift voor Musiktheorie
VII/3, November 2002, pages 239–241.
Return to text
2. This passage (sections 66 and 67) is excised in the
standard English translation of Schenker’s Harmonielehre, published as Harmony,
ed. Oswald Jonas, trans.
Elisabeth Mann Borgese (Chicago: University of Chicago Press, 1954).
Return to text
3. The German words eindeutig, zweideutig, and mehrdeutig do not have exact
equivalents in the English language, but are usually translated as “unambiguous,”
“having a double meaning,” and “having many meanings,” respectively. Schenker uses
the words to specify the exact number of possibilities that different intervals have in
different keys, and expands his categories to include the words dreideutig, vierdeutig, etc. Borgese’s
translations of eindeutig as “univalent” and mehrdeutig
as “plurivalent” aim to capture the spirit of the original language, but are, unfortunately,
unidiomatic and somewhat clumsy (see William Mitchell’s review of the Borgese
translation in Musical Quarterly XLI/2, April 1955, pages 256–260).
Return to text
4. Schenker, op.cit. page 129. The original German text reads: “so bedient [der Künstler] sich der eindeutigen Intervalle, die eben durch ihre Eindeutigkeit naturgemäß alle
anderen Tonarten ausschalten.”
Return to text
5. Originally appearing as the seventh of Twelve Contradanses, WoO 14, this theme is
modeled after the “English,” as opposed to the “French” or “Italian,” country dances
popular at the turn of the 19th century. Thomas Sipe provides a succinct discussion of the
significance of this form of the country dance and its association with French
revolutionary ideals in his short monograph on the “Eroica” Symphony in the
Cambridge Music Handbooks series (Cambridge University Press: Cambridge, 1998)
pages 11–12.
Return to text
6. Mozart, in particular, seems to have had a penchant for
chromatically descending themes, and always writes them as - sharp - natural . See, for example, the opening themes of the first movement of the Piano Trio in E (K. 542), Minuet of the Symphony No. 41 in C (K. 551), and last movements of both the String Quartet in A (K. 464) and String Quintet in D (K. 593).
Return to text
7. Reasons of space do not allow me to include a discussion
of bars 512–531. An interpretation of the tonal structure of these bars can be
understood in light of Schenker’s analysis of the parallel passage from the
exposition in “Beethoven’s Third Symphony,” trans. Derrick Puffett and Alfred
Clayton, in The Masterwork in Music III (Cambridge: Cambridge University
Press, 1997) pages 21–23. Although several details of my own interpretation of
this passage differ from Schenker’s, we both essentially read the large-scale
harmonic progression harmonic progression as I leading to IV, becoming
chromatically inflected to natural-IV♭7 in bar 531 (see especially Schenker’s
Figure 16).
Return to text
Throughout the second half of the 20th century, there
has been a tendency to downplay this aspect of Schenker’s thought. Even among Schenkerians themselves, there was the
fear that this viewpoint would weaken their cause, especially in light of the exacting
objectivity in analyzing serial techniques throughout the late-20th century. The “toning
down” of Schenkerian rhetoric is well outlined in William Rothstein’s article “The
Americanization of Schenker” in Schenker Studies (Cambridge: Cambridge University
Press, 1990) pages 193–203. See also Rothstein’s update on the situation in his article
“Conservatory Schenker vs University Schenker” in the Tijdschrift voor Musiktheorie
VII/3, November 2002, pages 239–241.
This passage (sections 66 and 67) is excised in the
standard English translation of Schenker’s Harmonielehre, published as Harmony,
ed. Oswald Jonas, trans.
Elisabeth Mann Borgese (Chicago: University of Chicago Press, 1954).
The German words eindeutig, zweideutig, and mehrdeutig do not have exact
equivalents in the English language, but are usually translated as “unambiguous,”
“having a double meaning,” and “having many meanings,” respectively. Schenker uses
the words to specify the exact number of possibilities that different intervals have in
different keys, and expands his categories to include the words dreideutig, vierdeutig, etc. Borgese’s
translations of eindeutig as “univalent” and mehrdeutig
as “plurivalent” aim to capture the spirit of the original language, but are, unfortunately,
unidiomatic and somewhat clumsy (see William Mitchell’s review of the Borgese
translation in Musical Quarterly XLI/2, April 1955, pages 256–260).
Schenker, op.cit. page 129. The original German text reads: “so bedient [der Künstler] sich der eindeutigen Intervalle, die eben durch ihre Eindeutigkeit naturgemäß alle
anderen Tonarten ausschalten.”
Originally appearing as the seventh of Twelve Contradanses, WoO 14, this theme is
modeled after the “English,” as opposed to the “French” or “Italian,” country dances
popular at the turn of the 19th century. Thomas Sipe provides a succinct discussion of the
significance of this form of the country dance and its association with French
revolutionary ideals in his short monograph on the “Eroica” Symphony in the
Cambridge Music Handbooks series (Cambridge University Press: Cambridge, 1998)
pages 11–12.
Mozart, in particular, seems to have had a penchant for
chromatically descending themes, and always writes them as 5ˆ - sharp 4ˆ - natural 4ˆ. See, for example, the opening themes of the first movement of the Piano Trio in E (K. 542), Minuet of the Symphony No. 41 in C (K. 551), and last movements of both the String Quartet in A (K. 464) and String Quintet in D (K. 593).
Reasons of space do not allow me to include a discussion
of bars 512–531. An interpretation of the tonal structure of these bars can be
understood in light of Schenker’s analysis of the parallel passage from the
exposition in “Beethoven’s Third Symphony,” trans. Derrick Puffett and Alfred
Clayton, in The Masterwork in Music III (Cambridge: Cambridge University
Press, 1997) pages 21–23. Although several details of my own interpretation of
this passage differ from Schenker’s, we both essentially read the large-scale
harmonic progression harmonic progression as I leading to IV, becoming
chromatically inflected to natural-IV♭7 in bar 531 (see especially Schenker’s
Figure 16).
Copyright Statement
Copyright © 2004 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO)
are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of
scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance
notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are
to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written
permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee
is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society
for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research
purposes only.
Prepared by Brent Yorgason, Managing Editor and Rebecca Flore and Tahirih Motazedian, Editorial Assistants
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
















