Transformational Distance and Form in Berg’s “Schlafend trägt man mich”

Introduction

[1.1] Berg’s “Schlafend trägt man mich,” No. 2 of the Vier Lieder for voice and piano, Op. 2, was composed between the years 1908–1910 (Kett 1989, 69). Situated at the intersection of Berg’s tonal and free atonal periods (Simms 1992, 490; Straus 2005, 125), the work eschews functional tonality but does not yet incorporate the twelve-tone methods that characterize his later music. Op. 2 as a whole is considered by many to reflect this stylistic transition because the first song is in a tonal idiom, and each subsequent song progressively incorporates more atonal elements (Headlam 1996, 33–34). Thus “Schlafend trägt man mich” has been of particular interest to theorists; substantial analyses that informed the present analysis include writings by Ayrey (1982), Kett (1989), Simms (1992), Headlam (1996), Gauldin (1999), and most recently Straus (2005).

[1.2] This paper will extend beyond the scope of prior discussions by interpreting the song in terms of a music-transformational space designed specially to bring out its distinctive musical features and processes. Several key analytical points will be illustrated via animation, a medium that has the advantage of presenting an analysis temporally as a conjunction of aural and spatial sequences. Given the song’s textual emphasis on the ideas of distance and motion, this medium is especially appropriate, since it can manifest these metaphors visually. New perspectives on the work’s text/music relationships, chord progressions, harmonic rhythm, and voice leadings derive from a consideration of the divergences and convergences of transformational paths in the space.

Characteristics of the work

[2.1] Before invoking the theory, let us review the distinctive features of the work identified by prior analyses. Clearly, “much of the second song . . . is concerned with exploiting the structural and cyclic possibilities inherent in the French 6th chord” (Jarman 2001, 314). We will henceforth refer to it by its set-class name, 0268, rather than as a “French Sixth,” since the opening of the work conspicuously lacks the major or minor chords, traditional chord progressions, and normative resolutions of the French Sixths that could denote functional tonality. (As will become clear shortly, however, we do think it is significant that most instances of 0268 in this song preserve the major third above the bass that is characteristic of the French Sixth.)⁽¹⁾ The presence or absence of 0268 helps to define formal sections, creating an ABA' form (Headlam 1996, 41): measures 1–8 present the first progression featuring 0268, measures 9–12 present contrasting material alluding to other tonal chords, and measures 13–18 reprise the initial 0268 progression.

[2.2] Figure 1 shows the score of the A section and its transition to the B section, with colored boxes indicating instances of 0268. The A section divides into two subsections, the first corresponding to the opening vocal phrase (measures 1–4), and the second to the piano transition between this and the next line of text (measures 4–8). In the first vocal phrase, a series of 0268 tetrachords alternate between the two whole-tone collections, starting and ending on the same pc set, {B, D, E, A} (Straus 2005, 125–127). Also important are the voice leadings of the upper and lower parts: the bass moves by interval class (ic) 5, while motion by ic1 is prominent in the upper voices (Ayrey 1982, 190 and 197–199; Simms 1992, 494; Headlam 1996, 33–34; Gauldin 1999, 34–36.). The piano transition retrogrades the opening chord progression (Jarman 2001, 314) beginning in measure 4, concluding the opening ascending motion on a second instance of the initial pc set {B, D, E, A}. Ic1 and ic5 voice leadings continue in this subsection (Ayrey 1982, 192–193; Headlam 1996, 41), and the bass is now doubled at the major third above. The 0268 chords and their associated voice leading are abandoned at the end of the piano transition (measure 8).

[2.3] Figure 2 shows the A' section (beginning in measure 13), again indicating instances of 0268 (incomplete instances are enclosed by dashed boxes). In addition to the literal restatement of the opening chord progression with its characteristic voice leading (Kett 1989, 74; Headlam 1996, 41–42; Jarman 2001, 314), a melody similar to the opening vocal line, repeating the opening text, marks this passage as a reprise.

A suitable transformational space

[3.1] Let us consider how to construct a system of musical objects and transformations that will best reflect the musical features that these analysts have highlighted. Because 0268 is established by repetition from the very beginning of the work, it seems reasonable to consider the members of this set class as the characteristic objects for the analysis of the A and A' sections (it will turn out that this choice is also useful in analyzing the B section). We can also use the same criteria of repetition to determine which transformations are characteristic of the music. In the first phrase, the pitch-class intervals 5 and 1, which repeatedly connect members of these tetrachords in the bass and upper voices, respectively, can be represented transformationally as the transpositions T₅ and T₁₁, and accordingly, the retrograde progression of the second phrase presents the transpositions T₇ and T₁ in the voice leading. The transpositions featured in upper and lower voices are indicated above and below the slurs on Figure 3, a reduction of the A and A' sections (based on Gauldin 1999, 35).⁽²⁾

[3.2] However, in order to talk about voice leading, it is necessary to consider the 0268s as at least partially ordered. Let us therefore consider not the pc sets of set class 0268 as objects, but rather the 12 series of the form <<w, x>, {y, z}>, such that:

• w and x are referential pitch classes, where w represents the bass note, x represents a pitch class in one of the upper voices, and y and z represent the pitch classes of the other voices. The bass pitch class w is treated differently than the remaining pitch classes of each 0268 tetrachord because it is usually separated from them in register and because its voice-leading (by T₅/T₇) in the A and A’ sections differs from theirs (by T₁₁/T₁).
• the dyads <w, x> and {y, z} each belong to interval class 4, and x = T₄w (this will prove to be helpful in analyzing the B section, which features ic4 dyads, as well as the second subsection of A, which melodically elaborates parallel ic4s between the lowest two voices), and
• {w, x, y, z} belongs to transpositional set class 0268.⁽³⁾
  

These objects occupy the nodes of the space. Below, we refer to each by a string of pcs wxyz, indicating the bass pitch w first, its ic4 partner next, then the remaining two pcs.

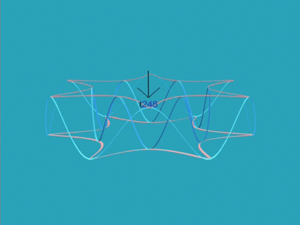
[3.3] The pathways between the nodes are determined by the structure of these objects under their characteristic transformations, T₅ and T₁₁ (and their inverses). The space surveyed from two sides in Figures 4a and 4b incorporates these objects and transformations (note that 7e15 on the right side of the front view is the same node as that on the left of the rear view, and vice-versa with 157e). Its 24 nodes represent a doubling of the 12 distinct partially ordered 0268 objects described in [3.2], an interpretive decision that will be rationalized below. Each node is located at the intersection of two axes, which represent the transpositions T₅/T₇ (red; counterclockwise and clockwise, respectively) and T₁₁/T₁ (blue; also counterclockwise and clockwise, respectively). From any node, one can move by T₅, T₇, T₁₁, and T₁. We will use color in the text when referring to these transformations to clarify their association with the colored paths in the figures. The toroidal shape of the space expresses the fact that (T₅)¹² = (T₁₁)¹² = T₀, cyclically generating all 12 partially ordered objects, and the multiple intersecting paths account for the fact that (T₅)² = (T₁₁)² = T₁₀ (the divergence of paths accounts for the fact that T₅ and T₁₁ produce different results when applied only once). Black and red arrows on the figures orient the viewer respectively to one particular node, labeled t248, and to another node, labeled with the T₆ transposition 48t2, that is also located on the top of the torus but in the rear, across its major axis. Because T₇T₁₁ = T₆, 48t2 also labels another node directly below t248 on the front view of the torus; indeed, every object in the family is represented twice in the space.

[3.4] This representation allows us to conceive any particular chord in the song in a variety of ways, considering the voice leading to it and from it in both immediate and larger-scale contexts. Sometimes the voice leading is uniform. Chord-changes in which all voices move by the same interval, such as at the end of the first system of Figure 3, measures 7–8, correspond to motion from one node to another along just one axis, in this case from t248 counterclockwise and downward along the blue axis to 9137. But other voice leadings are more complicated and so give rise to more complex representations of chords. For example, from the opening tetrachord t248, the bass voice changes by T₅, while the upper parts change by T₁₁. The resulting chord can therefore be conceived both as T₅ and as T₁₁ of t248, that is as both 3791 and 9137. Accordingly, we conceive of the second chord as represented by both nodes immediately counterclockwise (to the right in Figure 4a) from t248; the node 3791 is gained by following the red T₅ path, and the node 9137 is gained by following the blue T₁₁ path. The structure of our space, which includes moves by both T₅ and T₁₁ from every node, accommodates these two concurrent voice leadings.⁽⁴⁾

[3.5] The motion from the second chord to the third chord involves the same split voice leading. We might therefore conceive of the music analogously as proceeding counterclockwise along both T₅ and T₁₁ paths from both 3791 and 9137, to the two nodes labeled 8026 and 2680. Recall, however, that the two motions are representing different voices in the counterpoint. To be consistent, we should read the 9137 chord achieved by the bass voice leading as changing again by T₅, once more representing the bass motion. It does not change simultaneously by T₁₁. Similarly, we should read the 3791 chord achieved by the upper-part voice leading as changing again by T₁₁, once more representing the upper-part motion. It does not change simultaneously by T₅. These two paths (T₅ from 9137 and T₁₁ from 3719) converge on 2680, which we therefore adopt as the sole representative of the third chord. This convergence, which recurs every second chord, reinforces the agogic and metric accentuation on the first beat of each measure.

[3.6] Several aspects of this geometric conceptualization are musically suggestive. Chords can be understood as located with respect to one another, and thus, a sense of distance arises from the number of transformations necessary to get from one node to another. Each move has direction and speed, helping to identify reversals, rhythmically regular points of synchronization, and changes in harmonic rhythm. The circularity of the torus suggests a possible return to the beginning by completing a progression (of twelve moves in the same direction along each axis). Also, as Figure 5 shows, the six partially-ordered tetrachords that lie at the intersections of the outer blue and top red paths, {48t2, 6t04, 8026, t248, 046t, 2680}, all belong to the same whole-tone collection, {02468t}. Similarly, the six tetrachords at the intersections of the outer blue and bottom red axes belong to the other whole-tone collection. So any alternation of a chord on the top/outer path-pair with a chord on the bottom/outer path-pair also effects an alternation between the two whole-tone collections.

[3.7] It is possible to construct a smaller space containing only 12 nodes (one for each object), from each of which proceed both T₅/T₇ and T₁₁/T₁ paths. Such a space could be visualized as in Figure 6: the colored paths between the nodes represent the T₅/T₇ paths, and the dotted black paths represent the T₁₁/T₁ paths. Representing the chord progression of the first subsection, measures 1–4, would involve traveling six steps counterclockwise (six transpositions of the bass by T₅) along the colored path from t248 to 48t2. The second subsection, measures 4–7, would follow a dotted-black path from 48t2 to 59e3, then five steps clockwise (five transpositions of the bass by T₇) to the same 48t2 node, at which point all of the nodes would have been visited. This completion might be understood as bringing about closure to section A. However, we find this account lacking in some respects. By asserting completion so soon, it makes it difficult to explain what motivates the continuation of the song. Instead, we hear the repeated voice-leading in measures 1–4 to suggest the possibility of continuing the same pattern six more times back to its start, t248. And when that process is disrupted by the change of voice leading in measure 4, we hear the promise of completion—and thus the possibility of more music—still open. The presence of two 48t2 nodes in the 24-node space, one of which is visually distant from the opening t248, makes it possible to represent that openness vividly. Another feature of the music that the 12-node space obscures is audible association of chords that belong to the same whole-tone collection, through, for instance, the agogic and metrical emphasis mentioned above. It is difficult to see on the 12-node space how the opening progression alternates between the two whole-tone scales. In contrast, the 24-node space makes the whole-tone collections visually apparent; these whole-tone collections provide an orientation that we have found to be helpful for understanding some of the events in the piece.

[3.8] All the qualities and properties of the 24-node space are evident in Animation 1, which shows the chord changes during sections A and A' as moves from one node to another, synchronized with an audio recording. (During the B section, no changes are shown, but this lack will be addressed below.) As each new chord appears on the soundtrack, the corresponding label appears at the appropriate point on the space, and each chord change is animated as the chord label(s) moving toward the node(s) representing the next chord. Node labels persist, to show which parts of the space the music has visited.⁽⁵⁾ The following narration clarifies how the visual events in the animation express analytical insights about the song.

Distance and return in the outer sections

[4.1] The first vocal phrase establishes several important elements heard throughout the work: the simultaneous T₅ and T₁₁ transformations corresponding to motion in the bass and upper voices, respectively; the alternation of tetrachords between the two possible whole-tone collections; and a repeated half-plus-quarter rhythm corresponding to the harmonic rhythm, emphasizing this alternation (with the C whole-tone collection on the long note/strong beat and the D whole-tone collection on the short note/weak beat). The red and blue axes in Animation 1 respectively represent the T₅ and T₁₁ motion, the alternation between inner and outer pairs of path intersections represents the whole-tone exchange, and the time interval between node arrivals (that is, the speed at which the animation progresses) represents the harmonic rhythm. As the motion proceeds, it touches upon two versions of each chord from the odd-pc whole-tone collection, but only one version of each chord from the even-pc whole-tone collection, so it avoids the nodes on the inner/lower portion of the space.

[4.2] Associations between the text and music are established early on by spatial relationships in Animation 1. The first words, “Sleeping I am borne. . .”, are represented by a rocking motion that steadily pulls away from the starting node t248 (marked with a black arrow). But the text “. . .to my homeland” also suggests that the travel accomplishes a partial return of sorts, an idea that the animation signifies partly by its recurring return to the upper whole-tone circle. The vocal phrase ends (at 0:19 in the animation) when the chord progression reaches the point diametrically opposite to the starting node, a chord that thus signifies distance even though it contains the pitch classes of the initial chord. A red arrow appears in the animation at this moment of extremity and persists for future reference.

[4.3] When visualized in the space, the following transition takes on a particularly expressive character. During its first chord change in measure 4, the piano breaks the established pattern of T₅ motion in the bass, as the E2 slides up chromatically to F2 (this surprising T₁ motion is marked on Figure 3). With some rearrangement of register, the other voices can also be heard to change by T₁.⁽⁶⁾ Therefore, the animation of this progression shows the 48t2 chord progressing along only by T₁, downwards and clockwise to 59e3, with no simultaneous change by T₇. From 59e3 (starting at 0:22), the piano retrogrades the opening pc-set progression, arranging the chords in register and time such that we can again hear both ic 1 and ic 5 motion in the bass. So the animation resumes showing the chord changes along both axes, directed clockwise back towards the starting chord. Note, however, that it touches upon two versions of each chord from the even-pc whole-tone collection—exactly the opposite of how the original chord progression behaved, so that the nodes that were avoided in the first vocal phrase are now visited by the piano.⁽⁷⁾ It is as if these new chords make possible the undoing of the opening progression. Accordingly, when the opening 0268 collection is regained at the downbeat of measure 7 (at 0:30), its bass note is not the original B, but E, a long-range consequence of the disruptive T₁ shift in measure 4. The T₇ even pushes the piano’s progression one point beyond the starting chord, venturing into the half of the space not yet explored by the music.

[4.4] Perhaps motivated by this new environment, a new counterpoint begins on the second chord of measure 7 (0:31), where all voices move by pc interval 11. The paths in the animation change to reflect this: instead of converging every second move, there is only a single motion along the T₁₁ path. Then the 0268 harmonies effectively vanish until measure 13; accordingly, in Animation 1 during the B section, the space simply rotates towards the location where the next 0268 chord will appear.

[4.5] The D-grounded chord that reinstates 0268, in the middle of the final word of the contrasting B section (“Schlünde,” at 0:48), is one that was heard briefly in measure 2 as an odd-pc anacrusis to the even-pc chord in measure 3; it appears in the animation at 0:12 as part of the opening motion counterclockwise from the incipit t248. Here, however, it is treated quite differently, occurring twice with durational accent on the strong beat, and initiating a progression that leads entirely by semitone to measure 15, when the reprise of the opening progression begins. Therefore, its most appropriate representation in the space is not the node that represented it in measure 2, but the as-yet-untouched node on the opposite side of the space. Animation 1 shows how the succeeding T₁₁ motion connects this chord smoothly to the reprise in measure 15. The undulating movement in this space—a visual representation of the rapid alternation between tetrachords (and thus whole-tone collections) in the B section—together with the heightened melodic contour and increased tempo might be taken to allude to the wild geography mentioned in the text (peaks, ravines, and sea).

[4.6] The reprise of the opening vocal phrase (starting at “Heimatland”) reinforces the theme of return, and so does its visualization in Animation 1, starting at 1:04, which replays the dual-path counterclockwise motion from t248. But the reprise distorts the original in several important ways, accelerating the harmonic rhythm, leaving several tetrachords incomplete, and omitting the retrograde phrase. Most strikingly, it does not conclude at the anticipated terminus of the progression (<48t2>, the red arrow). Instead, it transgresses that limit, moving by T₅ and T₁₁ one further position counterclockwise to a 0268-chord with A and then E in the bass, represented by the dual nodes 9137 and 3791. The 157e that began the reprise in measure 13 is visible in the animation just to the right of this node—that is, this additional move nearly, but not quite, completes an entire circuit of the torus. Symbolically, we might understand this to mean that even though the singer has enacted a return of sorts, she has not quite completed her journey.

Dyadic transformations in the B section and in the vocal line

[5.1] The B section, measures 9–12 (Figure 7), apparently abandons the progression of 0268 tetrachords and their associated voice leadings; it contrasts with the surrounding atonal passages by featuring the “only clearly triadic bars in the song” (Headlam 1996, 41). Nevertheless, it does recall the common transformations, intervals, and melodic motives from measures 1–8. For example, in measures 9–10, the voice sings a melody which was first heard as the upper line of the accompaniment in measures 1–3, and immediately sequences it by T₁₁ (a characteristic transformation among 0268 tetrachords in the A section) during measures 11–12. This is indicated on Figure 7. The piano accompaniment of measures 8–12 echoes this melody in its inner voices, but also incorporates materials from the opening vocal phrase (Headlam 1996, 43). Two transpositions of this material are identified on Figure 7: the right hand of measure 9 is transposed by T₃ to produce the right hand of measure 11 (indicated in black), and the right hand of measure 10 is transposed by T₄ to produce the right hand of measure 12 (indicated in gray). Although these transformations are not those heard between tetrachords in Animation 1, T₄ does nonetheless occur prominently in several ways: it generates the left-hand melodic dyads in measures 4–6, and also the left-hand simultaneous dyads in measures 7–8, which continue in measures 8–12. Figure 8 shows that the piano right-hand in the latter passage presents a series of six 04 dyads, then begins to repeat it transposed by T₃.

[5.2] T₄ is integral to the objects of Animation 1, since each partially ordered instance of 0268 contains two 04 dyads, and since it is a characteristic transformation of the whole-tone collections, such as the one shown in Figure 5. This whole-tone emphasis is further supported by the whole-tone descent from D to A in the bass of measures 8–12, circled on Figure 7. The prominence of T₄ suggests constructing another transformational system in which the 12 ordered 04 dyads are the objects. Specifically, let us consider a space that is isomorphic to the one we used for tetrachords, such that every object has four pathways leading from it, one for each of the transpositions T₅, T₁₁, T₇, and T₁ that are characteristic of the chordal voice leading.

[5.3] Animation 2 presents such a space. The moving circle performs the succession of 04 dyads in Figure 8. It begins with two T₁₀ transformations that skip over nodes, since they are not explicit paths in the space, but then continues with three moves along the red and blue paths in the space. Thus, the B section reprises transformational motions that are characteristic of the A and A' sections, but applies them to different objects. By observing these transpositions in this particular space, we can also recognize allusions to the larger harmonic structures of the outer sections. For example, 48 and t2, which appear as the third and fifth dyads in the first progression of six, are aligned with each other laterally on the torus (that is, the 48 appears at the crest of a T₁₁ wave on the outside of the torus and t2 appears at the trough of the corresponding T₁₁ wave on the inside of the torus). The fourth and sixth dyads, 37 and 91, are similarly laterally aligned. Each such aligned pair forms a 0268 tetrachord—so the B section is not as contrasting as it appears on the surface.

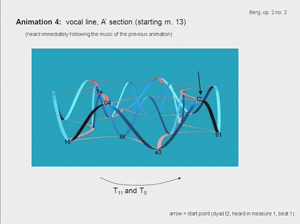
[5.4] Although the vocal line in the outer sections participates in the progression of 0268 tetrachords, the B section’s 04 structures (exposed by Animation 2) sensitize us particularly to its dyads. Figure 9 and Figure 10 show that the vocal part in sections A and A', respectively, can be reduced to a succession of 04s (some of the members of these dyads, indicated by open note heads on these figures, are provided by the accompaniment). Labeled arrows show that the progression of these dyads involves the characteristic transformations of the space, T₁₁ and T₇, much like the music of the B section. To elucidate the similarity, Animation 3 and Animation 4 perform the vocal line as a moving circle in the same space as Animation 2, retaining 04 dyads as objects, and T₁₁/T₁ and T₅/T₇ as the pathway transformations. These animations make plain the similarities of the vocal line and the piano dyads in section B. Both of them begin by alternating dyads that are laterally aligned on the torus, just like the alteration of the third through sixth dyads in section B, which form 0268s. This permits us to hear the B section as a development of the voice’s opening motive.

[5.5] While the paths traced in the tetrachord- and dyad-torus animations of the A and A' sections differ, they do coordinate in certain ways. Since the dyad attacks in the voice always synchronize with attacks of the 0268 tetrachords, their harmonic rhythms are related. Also—and unlike in the B section—only the characteristic T₁₁/T₁ and T₅/T₇ moves are executed in the A and A' dyad spaces. In this sense, we might understand the piano accompaniment to be the agent that is “bearing” the singer towards her homeland. At first, the dyad and tetrachord motions can be heard as consistent and identical at each moment. Later, however, this is not the case. For instance, at the beginning of the A' section, from beat 2 to beat 3 in measure 14, a tetrachord changes by T₁₁ into the next, but the voice’s dyad transforms by T₇ to the next. Perhaps this “departure” from synchronization indicates some resistance on the singer’s part. Thereafter, however, the song ends with a rhythmic and transformational synchronization of the two object types: in the final three measures (16–18), both the piano (featuring 0268 tetrachords) and the voice (featuring 04 dyads) are transposed by T₁₁, following a single blue path along the torus in each animation. This resynchronization enacts another kind of “return.”

Conclusion

[6.1] The animations accompanying this paper have a temporality and three-dimensionality, so different from the fixity and flatness of early transformational analyses, that bring many aspects of the music into the analysis: harmonic rhythm (which associates repeated visual patterns with regular time intervals), transformational similarities (as repeated motion paths within the analysis), and spatial concepts of distance and return suggested by the text. They distinguish within Berg’s song two types of characteristic objects, 0268 tetrachords and 04 dyads. Of course, the two object types are related, since 0268 can be understood as the union of two 04 dyads. But the contrast between them helps articulate the formal boundaries between the A and B sections, as dyads take over the musical surface. On the other hand, the animations show that the contrast is not stark. The whole-tone intervals in the tetrachord objects become the transformations between the dyad objects, and the dyads progress through the toroidal space in a way that alludes to 0268s, suggesting hidden connections between the two types of material.

[6.2] But the animations do more than focus on the set-class properties of this chord. Animation 1 treats the characteristic moves in the bass and upper voices in the outer sections as an integral part of the analysis. It clarifies the relation of process and form, to the extent that a change in path or direction indicates the start of a new phrase (such as in measure 4) or a return to previous material (measure 15). It also shows in what specific sense we might hear the progression, in the absence of tonality, to evoke “distance.” Animation 2 of the B section shows an interesting contrast in this respect. It begins with a somewhat static progression that alternates among a small number of nodes. This dramatizes the contradiction between distance and return embodied in the text: the A sections traverse a considerable distance within the space, but the B section returns to previously explored areas. The animations also show how Berg further dramatizes the contradiction, setting up goal-oriented processes and then subverting any attempts at completion.

Stephanie Lind
Queen’s University School of Music
Harrison-LeCaine Hall
39 Bader Lane
Kingston, ON
K7L 3N6 Canada
linds@queensu.ca

John Roeder
University of British Columbia School of Music
6361 Memorial Road
Vancouver, B.C.
V6T 1Z2 Canada
j.roeder@ubc.ca

Works Cited

Ayrey, Craig. 1982. “Berg’s ‘Scheideweg’: Analytical Issues in Op. 2/ii.” Music Analysis 1/2: 189–202.

Breivik, Magnar. 1998. “The Representation of Sleep and Death in Berg’s Piano Songs, Op. 2.” In Encrypted Messages in Alban Berg’s Music, edited by Siglind Bruhn, 112–21. New York: Garland.

Gauldin, Robert. 1999. “Reference and Association in the Vier Lieder, Op. 2, of Alban Berg.” Music Theory Spectrum 21/1: 32–42.

Headlam, Dave. 1996. The Music of Alban Berg. New Haven: Yale University Press.

Jarman, Douglas. 2001. “Alban Berg.” The New Grove Dictionary of Music and Musicians, 2nd ed., edited by Stanley Sadie and John Tyrell, 312–27. London: Oxford University Press.

Kett, Stephen W. 1989. “A Conservative Revolution: The Music of the Four Songs Op. 2.” In The Berg Companion, edited by Douglas Jarman, 67–89. Boston: Northeastern University.

O’Donnell, Shaugn J. 1997. “Transformational Voice Leading in Atonal Music.” Ph. D. diss., City University of New York.

—————. 1998. “Klumpenhouwer Networks, Isography, and the Molecular Metaphor.” Intégral 12: 53–80.

Simms, Bryan R. 1992. “Alban Berg’s Four Songs, Op. 2: A Tribute to Schoenberg.” In Musical Humanism and its Legacy: Essays in Honor of Claude V. Palisca, edited by Nancy Kovaleff Baker and Barbara Russano Hanning, 487–501. Stuyvesant: Pendragon Press.

Straus, Joseph N. 2005. Introduction to Post-Tonal Theory. 3d ed. Upper Saddle River, NJ: Pearson Prentice Hall.

Footnotes

1. Thanks to one of our anonymous readers for this observation.
Return to text

2. The reduction retains the original registers of most pitches, but alters the register of some to bring out recurring pc-voice leading more clearly (particularly the descending chromatic motion in the upper voices). Diamond-shaped note heads on the reduction (corresponding to the dashed boxes on Figure 1) show the implied voice leading in cases where these pitch classes do not occur in the music itself. For some chords, such as those on the last beats of measures 5 and 6, the bass moves by eighth-note between two members of the 0268 chord. The members we have chosen to represent the chordal bass in the reduction at these points bring out a repeated pattern of transposition.
Return to text

3. Because of the inversional invariance of the set, and the fact that inversions will not be considered as operations within the space, no concept of inversional set class is needed.
Return to text

4. The idea of multiple paths (and thus transformations) is reminiscent of Shaugn O’Donnell’s dual transpositions (O’Donnell 1997 and 1998), although our analysis does not incorporate the partitioning typical of O’Donnell’s K-net reconfigurations.
Return to text

5. The animations in this article were designed by Stephanie Lind and animated by Ali AbdulHussein (Animation 1) and Lind (Animations 2–4, based on the space created by AbdulHussein for Animation 1).
Return to text

6. The reduction of Figure 3 has altered the register of some pitches (especially in measures 4–7); while other reductions are certainly possible, this version keeps a significant number of pitches in their original registers while clearly demonstrating the chromatic motion in the upper voices and the fifth transposition in the bass.
Return to text

7. Recall (from [3.5]) that we heard certain nodes avoided in measures 1–4 because we maintained a distinction between the voice leading in the bass and in the upper parts. A similar distinction in this passage dictates our choice of nodes to represent the chords, and results in selecting different nodes.
Return to text

Copyright Statement

Copyright © 2009 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.

Prepared by Sean Atkinson, Cara Stroud, and Tahirih Motazedian, Editorial Assistants
Number of visits: