Cryptic Audiodiversity and the Dissonant Perfect Unison

– Albert Einstein

[1] For the past decade, scientists have been investigating a genetic phenomenon known as cryptic biodiversity (Beheregaray and Caccone 2007; García-París et al. 2000). Armed with the latest advances in DNA testing, researchers now know that two organisms sharing identical outward appearances may in fact be entirely different species—as genetically divergent as cats and dogs. The extent of cryptic biodiversity is just beginning to be appreciated, and studies have demonstrated its presence amongst amphibians, birds, mammals, reptiles, fungi, and plants. As the number of recognized species continues to grow, cryptic biodiversity will have a major impact on our perception of the endangered species list. Some scientists fear that the continual announcement of new species may diminish the desire to protect those already at risk of extinction.

[2] Although music theorists need not contend with such life-or-death matters, the concept of cryptic biodiversity resonates in musical analysis as well, where “seeing is believing” can be a hazardous modus operandi. Tonal music is a contextual art; the meaning of any pitch, harmony, or key depends on its surroundings—both immediate and long-range. The way something looks and the manner in which it operates do not necessarily correspond. Nor is the function of a musical entity limited to a single role based on its external façade. The remainder of this essay will illustrate examples of what I refer to as cryptic audiodiversity: musical objects that possess similar or identical surface visages, yet act in dissimilar ways. This preliminary study will culminate with a direct musical equivalent of cryptic biodiversity, a species of dissonant perfect unison that, to my knowledge, has not been addressed by music theorists.⁽¹⁾

[3] Consider the Trio from the third movement of Mozart’s Symphony no. 35 in D major, K. 385. Allen Cadwallader and David Gagné provide an illuminating account of this work in Analysis of Tonal Music (2007, 221–224, 381 n. 10) (see Example 1). What if one were to assert that measures 1–8 and 21–28, which are near carbon copies of one another, should be depicted with the same graphic symbols? One can counter this argument from two perspectives. From an analytical point of view, these passages represent different points in the overall structure of the composition. Motion of the Urlinie to scale-degree one represents more than melodic closure—it represents structural closure, and these two concepts are not synonymous. From a performance angle, measures 1–8 and 21–28 need not be played in exactly the same manner, even though they are virtual duplicates. They do not possess equal amounts of closure, nor must one apply the same amount of ritenuto and dynamic tapering to the ends of both passages.⁽²⁾

[4] Therefore, interpreting measures 1–8 and 21–28 depends not only on their own content, but, just as importantly on the presence or absence of subsequent events.⁽³⁾ (In this case the Trio can be viewed as an independent composition, and the return to the Menuetto can be considered a separate structure.) It is also true that what does or does not precede a repeated excerpt may strongly influence one’s hearing of it. At the onset of Schubert’s Moment Musical, D. 780 no. 6, the bass states the structural tonic immediately, initiating several measures of tonic prolongation (see Example 2a). When the same music returns after the Trio, it is no longer preceded by a blank slate. Instead, one hears it in relation to the subdominant key area of the Trio (see Example 2b). Not only does the D major Trio effect a large-scale key scheme that mimics the composition’s initial bass tones, it also transforms the meaning of the A major harmony that initiates the da capo statement of the Allegretto (see Example 2c). Now the upbeat tonic chord is enveloped by D sonorities that are stronger both metrically and agogically. The stable A major harmony that began the composition is transformed into a contrapuntal chord in the da capo, one that supports a passing tone, C, on its path toward B. From the last measure of the Trio to the second measure of the Allegretto, the tonic upbeat fulfills an ornamental role within a IV-(I)-II progression, an expression of the 5-6 technique that plays a central part in Schubert’s piece.⁽⁴⁾ Contrary to the initial statement of the Allegretto, partial harmonic solidity in the da capo is not achieved until I⁶ enters in measures 3–4.⁽⁵⁾

[5] Large quantities of intervening material are not required for similar-looking objects to portray dissimilar functions. In the opening movement of Mozart’s String Quartet in D minor, K. 421, several instances of “I⁶” appear within the close proximity of a four-measure span (see Example 3). Relatively stable first-inversion tonic harmonies occur twice in both measures 36 and 38. The latter harmony in each measure closely resembles its ensuing downbeat, with the only visual distinction being decorative suspensions of scale-degree six in the melody. Upon closer inspection, however, the “I⁶” chords in measures 37 and 39 have an altogether different function from their predecessors. These downbeats initiate functional voice-exchanges with the following beats in the outer voices, binding them together and suggesting that they share corresponding harmonic functions. The downbeats of measures 37 and 39, disguised as I⁶ harmonies, possess dominant function in the form of inver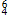ted cadential chords.⁽⁶⁾ Along with the voice exchanges, this reading is supported by harmonic syntax (predominant harmonies occur at the ends of measures 36 and 38), as well as the strong metric placement of the inverted cadential 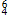chords. In many situations, composers use inverted cadential 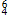chords to avoid problematic voice leading.⁽⁷⁾ In this instance, using traditional cadential 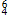chords with scale-degree five in the bass would produce empty fourths on the downbeats of measures 37 and 39.⁽⁸⁾

[6] Unlike the previous examples, Chopin’s Polonaise in A-flat major, op. 53, illustrates that intervening material is not a prerequisite in order to express cryptic audiodiversity. Adjacent entities can exhibit distinct functions even when they have congruent exteriors (see Example 4). An elementary change from tonic to dominant harmony is sufficient to transform the meaning of the pitches that constitute Chopin’s famous left hand ostinato. While the functions of C (passing tone) and B (chordal skip) remain constant, E alternates between a stable chord tone and a dissonant appoggiatura, and D begins as a passing tone and becomes a chord tone when dominant harmony arrives. Likewise, metrical placement and motivic factors distinguish the middleground function of upbeats from their ensuing downbeats in the first two measures of Brahms’s Waltz in E major, op. 39 no. 5. The anacruses express the primary harmonies at those moments, whereas the downbeats serve as dissonant suspensions with respect to the prevailing harmonies in measures 1 and 2 (see Example 5).

[7] Cryptic audiodiversity applies not only to closely resembling material recurring after varying amounts of time, but also to the dimension of structural hierarchy. Separated by the conceptual distance of structural levels, the same object can adopt contrasting characteristics according to its position relative to the surface and the Ursatz. In the ternary-form second movement of Mendelssohn’s Violin Concerto in E minor, op. 64, the tonality of the outer sections, C major, is unambiguous. Meanwhile, the key and mode of the middle section is, at least initially, less clear (see Example 6). The first harmonic sonority in measure 52 might suggest that the middle section is in A major, and the content of the entire measure might imply the key of D minor. In reality, A minor represents the tonal core of this section, but demonstrating this is not a straightforward task. For example, within the middle section’s twenty-seven measures, there are only two fleeting statements of root-position A minor triads (in measures 58 and 67). It may seem audacious to begin an A minor section with a triad in the parallel major, but at a deeper level the A major triad stands for a root-position A minor tonic harmony that has been contrapuntally embellished and contracted into a single gesture (see Example 7).⁽⁹⁾ Accordingly, the same object displays contrary characteristics at different structural levels: on the surface, the downbeat of measure 52 appears as a major triad that is rapidly transformed into a dominant seventh chord; at a deeper level, this sonority represents a stable A minor tonic triad.

[8] This interpretation is not mere idle speculation—one gains the impression that Mendelssohn composed the passage with similar thoughts in mind, as suggested by an earlier version of the Concerto, edited by R. Larry Todd and recently published by Bärenreiter (Mendelssohn-Bartholdy 2007). The 1844 draft features the very A minor harmony that constitutes the genesis for the A major chord used in the final product one year later (see Example 8). If both versions are sensible, the 1845 score more effectively accentuates common ground between distinct formal sections. First, the primary themes of the outer and inner sections feature motion from E to F, and the 1845 version allows both measures 9 and 52 to begin with major triads. Second, the A major and D minor sonorities in measure 52 recall similar progressions in measures 19–22. And third, by choosing an A major triad, the middle section begins with a familiar sonority. Starting with the A minor triad of the 1844 draft is somewhat jarring because this harmony has yet to appear in the second movement.

[9] What remains is to investigate more literal manifestations of cryptic audiodiversity, in which nearly identical objects occur simultaneously yet still demonstrate highly contrasting characteristics. Let us start with one of the most stable of all intervals, the perfect octave. A consistent thread in its description is the concept of equivalence. Thus Allen Forte (1974, 7) writes: “The notes which form the 8^ve always have the same letter name. One of the most fundamental axioms of tonal music is that notes which bear the same name are equivalent.... A note which stands at the interval of an 8^ve from another note and which has the same letter name is regarded as a duplication or 8^ve doubling of that note, not as an additional and different chordal element.” And, according to Rameau (1722, 11), the “...octave has only those properties communicated to it by the fundamental sound which generated it.... If one sound forms a perfect consonance with the fundamental sound, it will also form a perfect consonance with its octave; if another forms an imperfect consonance or a dissonance on the one hand, it will also form an imperfect consonance or a dissonance on the other....” Nevertheless, even this bedrock of musical stability can be transformed into a dissonant entity when situated in the proper context. Brahms features a dissonant perfect octave at the beginning of the Waltz in B major, op. 39 no. 1 (see Example 9). The bass voice reiterates a consonant tonic pedal until the last beat of measure 4, while the remaining upper parts unfold an ornamental tonic-predominant-dominant-tonic progression above the pedal. In measure 3, the melodic B-naturals reside within the sphere of decorative dominant harmony, not the underlying tonic pedal. The perfect octave between the two hands is dissonant: scale-degree one in the left hand articulates stable tonic harmony, and the same pitch classes in the right hand serve as dissonant accented passing tones.

[10] Cited at least as far back as the eighteenth century (Bach 1762, 297), the concept of a dissonant perfect octave is not a new discovery. What appears to be overlooked, however, is that similar events can undermine the seemingly fixed properties of the perfect unison. It is well understood that both tones in a perfect unison can be concordant with their surroundings, as demonstrated by the final measure of J. S. Bach’s Chaconne from the Violin Partita no. 2 in D minor, BWV 1004, or they can clash with their environs, as seen in the third measure of Bach’s Chorale no. 35 (“Gott des Himmels und der Erden”) (see Examples 10 and 11).⁽¹⁰⁾ In the words of Allen Forte, one might conclude that a fundamental axiom of tonal music is that the two tones of a perfect unison will have the same function respective to their context—either both are consonant or both are dissonant. This notion of unison equivalence is taken a step further by Zarlino (1558, 24), Mattheson (Harriss 1969, 216, 797), C. P. E. Bach (Bach 1762, 183–184), and Schoenberg (Schoenberg 1970, 1), all of whom assert that perfect unisons do not even qualify as an interval.

[11] Due to the overarching sentiment that perfect unisons “stand in the relation of absolute equality” (Fux 1725, 38), it makes sense that few, if any, have wondered if a perfect unison can be discordant with itself. It would seem that some musical properties must remain steadfast, no matter what the context. Even so, the question deserves to be asked: can one tone of a perfect unison be consonant while its twin, sounding the very same pitch, seeks resolution?⁽¹¹⁾ It turns out that it is indeed possible, and it is fitting that J. S. Bach would be the one to demonstrate this ingenious contrapuntal sleight-of-hand and marvelous example of cryptic audiodiversity. In the Preludio from the Solo Violin Partita no. 3 in E major, BWV 1006, Bach emphasizes an explicit tonic pedal at the onset of a bariolage passage in measure 13.⁽¹²⁾ Eight measures later, he initiates a series of 7-6 suspensions that encircles the tonic pedal (see Example 12). Although the pedal is situated in a middle voice, it functions as the bass and renders the entire passage a composing-out of tonic harmony. As the sequence of 7-6 suspensions nears its conclusion, something remarkable occurs in measure 27: E sounds in two voices (one voice emanates from the violin’s A-string and the other from its open E-string), and while the latter represents the consonant tonic pedal, the former is the seventh in a dissonant 7-6 suspension. This perfect unison is thus discordant with itself and requires descending stepwise resolution to a minor second; as such, it is a true instance of cryptic audiodiversity.⁽¹³⁾

[12] It is understandable if no one has previously noticed this odd form of unison. Due to its apparent simplicity, there should be no compelling reason to investigate aspects of the perfect unison—one would long think it a closed book. Furthermore, the dissonant perfect unison shown in Example 12 is based on a unique contrapuntal situation. Whether it can be generated within dissimilar contexts is still to be determined (at least, no such examples have crossed my mind). The dissonant perfect unison in J. S. Bach’s Preludio underscores the limitless flexibility of our tonal language and represents a veritable sonic depiction of cryptic biodiversity.⁽¹⁴⁾ Indeed, it is a continual source of inspiration to observe how seemingly crystallized musical elements can be rendered malleable and molded in an endless variety of ways when placed in the hands of a master composer.

Timothy Cutler
Cleveland Institute of Music
Cleveland, OH 44106
timothy.cutler@case.edu

Works Cited

Bach, C. P. E. 1762. Essay on the True Art of Playing Keyboard Instruments. Edited and translated by William J. Mitchell, 1949. New York: W. W. Norton.

Beach, David W. 1998. “Modal Mixture and Schubert’s Harmonic Practice.” Journal of Music Theory 42.1: 73–100.

Beheregaray, Luciano, and Adalgisa Caccone. 2007. “Cryptic Biodiversity in a Changing World.” Journal of Biology 6.4: 1–5.

Cadwallader, Allen, and David Gagné. 2007. Analysis of Tonal Music: A Schenkerian Approach. 2d ed. New York: Oxford University Press.

Cone, Edward T. 1968. Musical Form and Musical Performance. New York: W. W. Norton and Co.

—————. 1982. “Schubert’s Promissory Note: An Exercise in Musical Hermeneutics.” 19th-Century Music 5.3: 233–241.

Cutler, Timothy. 2008. “Inverted Cadential Six-Four Harmonies.” Paper read at the annual meeting of the American Musicology Society and the Society for Music Theory, Nashville, Tennessee.

Forte, Allen. 1974. Tonal Harmony in Concept and Practice. 2d ed. New York: Holt, Rinehart and Winston.

Fux, Johann Joseph. 1725. The Study of Counterpoint from Johann Joseph Fux’s ‘Gradus ad Parnassum.’ Edited and translated by Alfred Mann, 1975. New York: W. W. Norton.

García-París, Maria, David A. Good, Gabriela Parra-Olea, and David B. Wake. 2000. “Biodiversity of Costa Rican Salamanders: Implications of High Levels of Genetic Differentiation and Phylogeographic Structure for Species Formation.” Proceedings of the National Academy of Sciences 97.4: 1640–1647.

Harriss, Ernest C. 1969. Johann Mattheson’s Der vollkommene Capellmeister: A Translation and Commentary. Ph.D. diss., George Peabody College for Teachers.

Kivy, Peter. 1993. “The Fine Art of Repetition.” In The Fine Art of Repetition: Essays in the Philosophy of Music, 327–359. New York: Cambridge University Press.

Mendelssohn-Bartholdy, Felix. 2007. Concerto in E minor for Violin and Orchestra, op. 64 (1844/1845). Edited by R. Larry Todd. New York: Bärenreiter Kassel.

Meyer, Leonard B. 1973. Explaining Music. Los Angeles: University of California Press.

Pastille, William. 1990. “Music and Morphology: Goethe’s Influence on Schenker’s Thought.” In Schenker Studies, ed. Hedi Siegel, 29–44. New York: Cambridge University Press.

Rakowski, Andrzej. 1990. “Intonation Variants of Musical Intervals in Isolation and in Musical Contexts.” Psychology of Music 18.1: 60–72.

Rameau, Jean-Philippe. 1722. Treatise on Harmony. Edited and translated by Philip Gossett, 1971. New York: Dover Publications.

Rothstein, William. 2006. “Transformation of Cadential Formulae in the Music of Corelli and his Successors.” In Essays from the Third International Schenker Symposium, ed. Allen Cadwallader, 245–278. New York: Georg Olms.

Schachter, Carl. 1999. “Either/Or.” In Unfoldings: Essays in Schenkerian Theory and Analysis, ed. Joseph N. Strauss, 121–133. New York: Oxford University Press.

Schenker, Heinrich. 1906. Harmony. Edited by Oswald Jonas and translated by Elisabeth Mann Borgese, 1980. Chicago: University of Chicago Press.

—————. 1926. “Mozart’s Symphony in G minor, K. 550.” In The Masterwork in Music: A Yearbook, Vol. II (1926), ed. and trans. William Drabkin, 1996, 59–96. New York: Cambridge University Press.

Schmalfeldt, Janet. 1992. “Cadential Processes: The Evaded Cadence and the ‘One More Time Technique.’” The Journal of Musicological Research 12.1–2: 1–52.

Schoenberg, Arnold. 1970. Preliminary Exercises in Counterpoint. Edited by Leonard Stein. New York: St. Martin’s Press.

Solie, Ruth A. 1980. “The Living Work: Organicism and Musical Analysis.” 19th-Century Music 4.2: 147–156.

Zarlino, Gioseffo. 1558. The Art of Counterpoint: Part Three of ‘Le Istitutioni Harmoniche’ (1558). Translated by Guy A. Marco and Claude V. Palisca, 1968. New Haven: Yale University Press.

Zuckerkandl, Victor. 1956. Sound and Symbol: Music and the External World. Translated by Willard R. Trask. New York: Pantheon Books.

Footnotes

1. “We should get accustomed to seeing tones as creatures. We should learn to assume in them biological urges as they characterize living beings” (Schenker 1980, 6). Biological metaphors have maintained a long-standing role in the analysis of music and the arts in general. Schenker’s reliance on principles of organicism has been explicated by authors such as Solie (1980) and Pastille (1990). For a dissenting view on the validity of biological models see Kivy (1993).
Return to text

2. The single difference between measures 1–8 and 21–28 is not insignificant. Returning to a higher octave on second beat in measure 8, the bass creates a small degree of registral and rhythmic tension that is absent from the end of the Trio. By remaining in the lower register in measure 28, the bass counterbalances the ascending octave in the oboes and produces a greater sense of closure.
Return to text

3. In essence, I am putting forth the same argument as Edward T. Cone: “In general, there is no such thing as true redundancy in music” (Cone 1968, 46). Similar sentiments are expressed in Zuckerkandl (1956, 212) and Meyer (1973, 44–45). The latter uses the English folk tune “Lightly Row” to illustrate how identical musical passages can undertake contrasting structural functions due to their location in the composition.
Return to text

4. The changing nature of the opening sonority was pointed out to me by William Rothstein. Other insightful analyses of Schubert’s Moment Musical, D. 780 no. 6 have been written by Cone (1982) and Beach (1998).
Return to text

5. In his essay on Mozart’s Symphony no. 40, Schenker uses the term wandernde Melodien (“roving melodies”) to point out that musical entities with comparable semblances do not necessarily possess equivalent structures and function (Schenker 1996, 82). More recent investigations of this topic have been undertaken by Schmalfeldt (1992) and Schachter (1999).
Return to text

6. Discussions of inverted cadential chords appear infrequently in the literature. The most detailed investigations are found in Rothstein (2006) and Cutler (2008).
Return to text

7. Mozart employs an inverted cadential chord to avoid outer-voice parallel octaves in the first movement of K. 421, measures 93–94.
Return to text

8. Contrary to the warm confines of F major, Mozart does not avoid this hollow sonority within the gloominess of the D minor recapitulation (measure 107).
Return to text

9. The contrapuntal maneuver in measure 52 is not unique: Beethoven’s Symphony no. 1 in C major, op. 21 features an opening tonic harmony adorned with a passing seventh, and the initial tonic of Chopin’s Mazurka in E minor, op. 41 no. 1 contains both the elided chromatic passing tone and passing seventh shown in the final measure of Example 7.
Return to text

10. In the third measure of Example 11, the inner voices momentarily converge on a unison C that is dissonant with the prevailing supertonic harmony.
Return to text

11. While this discussion does not take into consideration microtonality and acoustic illusions created in science labs (examples of the latter can be found in the research of Diana Deutsch at http://deutsch.ucsd.edu), studies in music cognition, such as Rakowski (1990), have demonstrated that the presence or absence of musical context can greatly influence one’s perception of the intonation of musical intervals.
Return to text

12. Bach’s arrangements of the Preludio for Lute (BWV 1006a) and orchestra (BWV 29) feature explicit tonic pedals throughout measures 1–29. Additionally, the different registral placement of these pedals in measures 17–29 produces dissonant perfect octaves that are not present in the version for solo violin.
Return to text

13. The passage shown in Example 12 is transposed to A major later in the movement. Another example of a dissonant perfect unison occurs in the first movement of Bach’s Sonata for Violin and Basso Continuo in E minor, BWV 1023.
Return to text

14. The uniqueness of the dissonant perfect unison also is reminiscent of autoantonyms, rare cases when words have multiple meanings, two of which are the antithesis of each other.
Return to text

Discussions of inverted cadential chords appear infrequently in the literature. The most detailed investigations are found in Rothstein (2006) and Cutler (2008).

Mozart employs an inverted cadential chord to avoid outer-voice parallel octaves in the first movement of K. 421, measures 93–94.

In the third measure of Example 11, the inner voices momentarily converge on a unison C that is dissonant with the prevailing supertonic harmony.

Copyright Statement

Copyright © 2010 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.

Prepared by Sean Atkinson, Editorial Assistant
Number of visits: