Harmonic Progression in Magnus Lindberg’s Twine

Introduction

[1] In the 1980s and early 1990s, Finnish composer Magnus Lindberg (b. 1958) developed a distinct and sophisticated harmonic system for arranging dodecaphonic chords into recurring progressions centering on his inventive use of chaconne. While much has been written about the composer’s work on a surface level—including its dazzling orchestration, intricate patterns and figures, and sheer power—and several authors have mentioned the composer’s use of chaconne, this article will delve into the composer’s underlying harmonic system by analyzing an early work in which it is fully realized: Twine (1988) for solo piano.⁽¹⁾ I will discuss the construction of Lindberg’s dodecaphonic chords and illustrate how he applies his innovations to the chaconne technique to systematically arrange these harmonies into progressions. I will then demonstrate how the composer methodically deviates from his established harmonic framework in the second half of the piece and discuss the ramifications of this process on the work’s large-scale formal structure.

[2] The manner by which Lindberg arranges 12-tone aggregates into progressions is certainly a signature of his style. Two 12-tone aggregates are considered to be the same chord only if their lowest pitches and the vertical interval structures above those pitches are identical.⁽²⁾ The chord (i.e. the distinct vertical arrangement of the twelve tones) appearing in measures 1–2 of Twine, for example, returns at three structurally significant moments in the piece (measure 12, measure 86, and measure 158). Harmonic progression, then, is not the result of pitch-class changes from one moment to the next, but rather relies solely on the registral redistribution of the twelve tones.

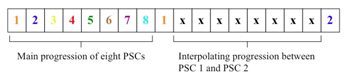
[3] Each of Lindberg’s compositions employing this unique harmonic system has a main progression of primary structural chords (PSCs) at its core.⁽³⁾ Twine opens with its main progression of eight PSCs (PSC 1–8) in measures 1–11 (shown in Examples 1 and 2). I will incorporate color into the musical examples and figures below to clearly differentiate each of the eight PSCs and highlight relationships between them and their derivative chords. The eight PSCs will be associated with the following colors: 1. orange, 2. blue, 3. yellow, 4. red, 5. green, 6. brown, 7. purple, and 8. light blue. A distinguishing characteristic of Lindberg’s PSCs is symmetry: each is built symmetrically with respect to its vertical arrangement of intervals around an “odd-numbered” axis (i.e. a minor second, a minor third, etc). Secondary harmonies (those that are not PSCs) may or may not exhibit this type of symmetry. Lindberg’s interest in 12-tone chords can certainly be traced back to his studies at the Sibelius Academy with Paavo Heininen, a dodecaphonic composer and his mentor. Their symmetrical quality, on the other hand, may be considered a continuing homage to another composer who incorporated symmetrical sonorities: Witold Lutoslawski. Lindberg’s admiration for the composer is clearly evident in the title of his large orchestral work Aura: In Memoriam Witold Lutoslawski, one of his few compositions to include such a dedication.

[4] Lindberg generates an array of interrelated secondary chord progressions—described by Julian Anderson as “large reservoirs of distinct but related harmonic fields” (Anderson 1992, 566)—from pitch-related characteristics of the main progression of PSCs by applying his innovations to the chaconne technique.⁽⁴⁾ Figure 1 describes each PSC using select pitch-related characteristics that I will refer to over the course of this discussion. PSC 1, for example, exhibits the following characteristics: it spans the middle of the piano’s range, its boundary pitches are D2 and F6, its axis is C4-G4⁽⁵⁾, and the hexachord on either side of its axis belongs to the set class (012346). As I will discuss in detail, the composer establishes harmonic connections throughout Twine by applying specific techniques to build secondary chord progressions exhibiting the main progression’s sequence of pitch-related properties. For example, the main progression’s sequence of set classes, (012346), (012367), (013469), etc., can be traced through some secondary progressions. Other secondary progressions share numerous common tones with the main progression. All of the secondary progressions, to some degree, exhibit the main progression’s register contour (as observed by each chord’s boundary pitches). In effect, each secondary chord progression may be considered a variation of the main progression of PSCs.

Innovations to the Chaconne Technique

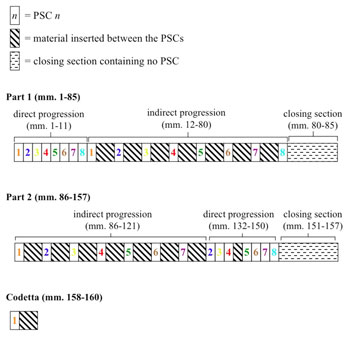
[5] Chaconne is the basic principle by which Lindberg organizes harmonies into progressions. When asked how he applies chaconne to his music, the composer replied: “I built a series of chords that comprised somehow the skeleton of the whole work. They are omnipresent, they give the work form and identity” (Eötvös 1994, 40). The traditional definition of the term accurately describes the succession of harmonies in Twine, but only to a point. At its core, the work is built on four successive instances of the main progression of eight PSCs (the “skeleton” of Twine) but the PSCs are not merely repeated as a harmonic ostinato. The composer’s innovations to the chaconne technique arise from the methods he implements to systematically insert new harmonies and progressions between the PSCs, thus greatly expanding the influence of the main progression.

[6] I use the terms direct progression and indirect progression to describe the composer’s innovations to the chaconne technique. A direct progression is one in which two PSCs appear adjacent to one another, while an indirect progression is one in which other material is inserted between two PSCs, resulting in secondary chord progressions. Twine is cast in an overall two-part form (measures 1–85 and measures 86–157), closing with a very brief codetta (measures 158–160). Part 1 opens with a direct progression through all eight PSCs, continues with an indirect progression through these chords, and ends with a short closing section containing no PSCs. Part 2, in contrast, opens with a predominantly indirect progression though the main chords, continues with a predominantly direct progression, and ends with a closing section containing no PSCs. Part 2, as illustrated in Figure 2, contains several deviations from the rigid harmonic framework established in part 1. These deviations, including the absence of an interpolation between PSC 4 and PSC 5 in the predominantly indirect progression and the addition of an interpolation between PSC 4 and PSC 5 in the predominantly direct progression, will be discussed in detail below.

[7] A close examination of Twine’s two indirect progressions reveals Lindberg’s innovations to the traditional chaconne technique. The expansion of the main progression of PSCs into each of the two indirect progressions is achieved through the employment of three distinct techniques. One technique involves applying the cyclic nature of the chaconne not to the actual PSCs themselves, but to pitch-related characteristics of those chords such as boundary pitches, set classes, or select pitches. This process results in a repeating sequence of chord properties from which Lindberg generates progressions of new harmonies resembling the work’s main progression and each other. A second technique is referred to by Julian Anderson as interpolation: the insertion of a new element between existing elements (Eötvös 1994, 16). When applied to his chaconne technique, interpolation refers to the insertion of a progression of new harmonies between two adjacent PSCs. The interpolating progression often functions as a gradual transformation between the two surrounding PSCs or a PSC and another harmonic entity. A third technique involves the juxtaposition of a work’s main progression of PSCs with a sustained or continuously reiterated chord from that progression. John Warnaby describes such a passage as exhibiting harmonic “counterpoint” (Warnaby 1992, 29). In my discussion with Lindberg, he simply, and quite evocatively, called this technique “freeze” (Lindberg 2005). These three techniques are illustrated below in Figures 3, 4, and 5.⁽⁶⁾

[8] Before discussing specific examples of each technique, one other term must be introduced. Position describes any chord’s relationship to the main progression of PSCs, and often describes relationships within secondary chord progressions as well (the exception being interpolating chord progressions that do not adhere to the pitch-related patterns of the main progression). A chord residing in position n is either the PSC n or a new chord sharing certain pitch-related properties with PSC n (which may include register, any number of common tones, boundary notes, and/or set class). For example, any chord occupying position 2 is either PSC 2 or exhibits properties of PSC 2. Additionally, PSC 2 will normally be preceded by a chord with properties of PSC 1 or PSC 1 itself, and will likely be followed by a chord resembling PSC 3 or PSC 3 itself. A chord in any given position may share one or several pitch-related characteristics with its corresponding PSC.

Sequence of Chord Properties

[9] Following the opening direct progression of PSCs (measures 1–11), part 1’s indirect progression (measures 12–80) contains eight secondary chord progressions, one for each PSC, and is built entirely on a sequence of chord properties in which the PSCs function on both a local and a global level. At the local level, each of the eight new secondary progressions constituting the indirect progression contain eight dodecaphonic chords occupying positions 1 through 8 respectively in that progression. Each of the eight PSCs appears in its corresponding position in each successive progression. On a global level, the PSC residing in each secondary progression influences pitch-related properties of all other chords in that progression. For example, each individual chord in measures 21–27, the second component progression of the indirect progression, is influenced by pitch-related properties of PSC 2. Figure 6 illustrates the harmonic framework of part 1’s direct and indirect progressions.

[10] A broad look at the indirect progression of part 1 reveals the composer’s cyclic application of the main progression’s register contour: the boundary pitches of the chord in each position are drawn toward those of the corresponding PSC. Figure 7 illustrates the register contour of the main progression of PSCs by showing each chord’s highest and lowest pitches. Figure 8 shows a register contour illustrating the average high and low pitches residing in each position of part 1’s indirect progression. A comparison of these two contours shows that the indirect progression’s component chord progressions share the main progression’s general register contour: each takes a similar route through the pitch space by climbing to its highest point in the fourth position and descending to its lowest point in the seventh. The similarities between these two contours reveal, on a large scale, the results of Lindberg’s generative process throughout part 1.

[11] A closer examination of the component progressions of part 1’s indirect progression reveals how the composer applies the chaconne technique to other pitch-related properties. The sequence of set classes associated with the main progression of PSCs (see Figure 1 above), for example, often dictates the manner in which the indirect progression’s 12-tone aggregates are partitioned. Lindberg applies this sequence by partitioning 12-tone aggregates into two groups of six pitches, each belonging to the set class associated with the corresponding PSC. The clearest example of this process occurs in measures 60–68, the sixth component progression of the indirect progression (Example 3). Notice PSC 6 resides in the sixth position. The chord occupying position 1 is divided into two gestures, each belonging to the set class associated with PSC 1: (012346). The chord in position 2 is divided into two overlapping gestures containing the PSC 2’s set class: (012367).⁽⁷⁾ With the exception of position 4, Lindberg carries this process through to the end of the progression. This set-class relationship, along with the register contour, creates a strong link between the main progression and measures 60–68.⁽⁸⁾

[12] Common tones also tie secondary harmonies to their corresponding PSCs. The fifth secondary progression (measures 50–59), shown in Example 4, offers a clear example. The chords in positions 1 and 2 share five pitches with PSCs 1 and 2; the chord in position 3 shares six pitches with PSC 3; the chord in position 4 only shares three pitches (the fewest of this progression) with PSC 4; PSC 5 occupies position 5; and the chords found in positions 6, 7, and 8 have six, four, and five tones in common with their corresponding PSCs respectively. These common tones contribute to the register similarities between the main progression and each secondary progression; notice that each chord’s lowest pitch, with the exception of the chord in position four, is identical to the lowest pitch of the corresponding PSC.

[13] As mentioned above, the relationship between the main progression of PSCs and part 1’s indirect progression exists not only on a local level within each secondary progression, but also on a global level unifying the entire indirect progression: the PSC residing in each of the eight secondary progressions functions as a “center of gravity,” drawing all pitches in that secondary progression toward the PSC. The global influence of the PSCs in part 1 can be observed by examining the overall register contour and common tones. If the indirect progression is taken as a whole, the overall tessitura occupied by the chain of secondary progressions exhibits the same register contour as the main progression of PSCs. In other words, the individual chords in each secondary progression, while still maintaining the contour of the main progression on a local level, are all drawn toward the PSC residing in that progression. Figure 9 shows a contour derived by taking the mean of the boundary pitches of all chords found in each of the eight secondary progressions. A comparison of this contour with that of the main progression (shown above in Figure 7) illustrates this relationship: the main progression of PSCs ascends to PSC 4 and descends to PSC 7 just as the indirect progression as a whole gradually ascends to the fourth progression and descends to the seventh. Additionally, further examination of the secondary progressions shows that common tones are often shared between each component chord and the PSC residing in that progression. An examination of the sixth secondary progression from this perspective, shown in Example 5, reveals that the entire progression is infused with tones from PSC 6, creating, along with its overall range, a global connection to that chord.

The Interpolation Technique

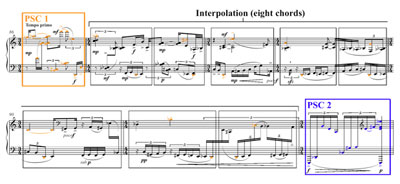
[14] Lindberg applies his interpolating and freeze techniques in the second half of Twine, which consists of a predominantly indirect progression (measures 86–121), a predominantly direct progression (measures 132–150), and a short closing section (measures 151–157). Part 2 opens with PSC 1 in measure 86, an interpolating progression of eight new dodecaphonic chords in measures 87–91, and PSC 2 in measure 92 (Example 6). As mentioned above, interpolating progressions often function as gradual transformations. In this case, PSC 1 is gradually transformed into the low, 12-tone cluster found in measure 91 beats 3–4 preceding PSC 2. The process by which PSC 1 is transformed, as illustrated in Example 7, is based on its component pitches: the lowest pitch of each chord in the interpolating progression remains D1 (PSC 1’s lowest pitch), while the highest pitch of each consecutive chord is the same as each successively lower pitch from PSC 1. The first interpolating chord’s highest pitch is the same as the next to highest pitch from PSC 1: A5. The second interpolating chord’s highest pitch is the same as the third to highest pitch of PSC 1: G5. Lindberg continues this process through the remaining six chords of the interpolating progression resulting in an extension of PSC 1’s influence up to the entrance of PSC 2 in measure 92.

The Freeze Technique

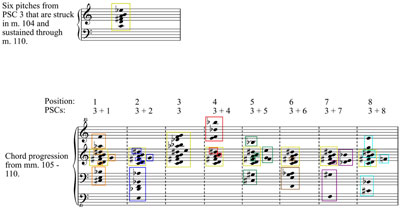
[15] The freeze technique can be observed in part 2’s second, third, fifth, and seventh progressions in which PSCs 2, 3, 5, and 7 respectively are juxtaposed with pitches foreign to those chords. It should be noted that Lindberg’s application of the freeze technique in Twine is more sophisticated than in later works: in Twine he does not simply juxtapose the main progression with a sustained PSC, but carefully combines the two progressions that create the new 12-tone chords. Part 2’s third secondary progression (measures 104–111, shown in Example 8) provides the clearest example of this technique. An instance of PSC 3 precedes this progression in measure 104 and beginning on beat 4 of that measure, six of PSC 3’s pitches (C4, D4, F4, A4, B4, and E5) are sustained through measure 110 with the sostenuto pedal. These six pitches are also frequently reiterated and consistently differentiated with staccatos. They are highlighted with yellow boxes in Example 8 and Example 9. The progression that follows (measures 105–111) consists of eight positions, each corresponding to one of the eight PSCs. Positions 1–2 and 4–8 contain seven new chords, each a summation of the six sustained pitches and some or all of the remaining notes required to complete the 12-tone aggregate. The sonority in each position is comprised of six pitches from PSC 3, which are always C4, D4, F4, A4, B4, and E5, and members of the complementary set C, E, F, G, A, and B (or their enharmonic equivalents), occupying the same register in which they appear in their corresponding PSC. For example, the first chord of this progression is an amalgamation of the sustained hexachord and its six complementary tones occupying the register in which they appear in PSC 1: C3, E3, F6, G4, A5, and B3. Lindberg’s application of the freeze technique results in a progression exhibiting properties of the main progression of PSCs on a local level and properties of PSC 3 on a global level, thus extending the influence of PSC 3 for eight measures.

Large-Scale Form

[16] Lindberg has stated that he is “a bit classical, in the sense that ... [he has] ... faith in equilibrium as a goal”(Cody 2000, 34). In another interview, he describes classicism as “certainly a taste for balance, for the drama in the balance of the form” (Eötvös 1994, 44). His innovative use of chaconne allows him to compose large formal structures that exhibit these traits by exploiting its cyclic nature to create expectation and formal balance on both a local and global level. The formal “drama” that he references is achieved when he ignores or alters the harmonic logic that he so carefully assembles, thus disrupting the overall structure with formal dissonances that may or may not be resolved later in the piece.

[17] A striking and significant difference between the first and second parts of Twine can be observed in the extent to which Lindberg alters the harmonic framework established by the opening direct progression of PSCs. The underlying harmonic skeleton of part 1 is very rigid. The direct progression proceeds through the eight PSCs without interruption, followed by an indirect progression that fits neatly into a structure composed of eight new progressions (containing PSCs 1 through 8, respectively) that each exhibit properties of the main progression. The short closing section that follows in measures 80–85 continues to adhere to the underlying harmonic structure. Compared to part 1, part 2 is notably less rigid: at several points, Lindberg adds or omits chords and entire progressions based on the strict harmonic scheme established in part 1. In my discussion with the composer, he compared part 2 of Twine to a classical development section, stating that these kinds of sections often do not develop material but just “mix it up” (Lindberg 2005). The harmonic structure of part 2, as illustrated in Figure 10, is certainly “mixed up” when compared to part 1, but this expression simply does not convey the careful and deliberate manner by which Lindberg reorders the material. The composer deviates from the rigid harmonic structure established in part 1 at four particular moments in part 2. By the work’s conclusion, however, he balances out these changes with four additional alterations. In effect, Lindberg devises a formal problem for himself and then composes a solution.

[18] The first digression from the rigid harmonic framework established in part 1 occurs at the onset of part 2 with the interpolating progression in measures 86–91. This progression, discussed above and shown in examples 16 and 17, does not resemble the main progression of PSCs and is the first to deviate from the sequence of chord properties that delineates the harmonic structure of part 1. The cyclic register contour of part 1 is replaced by a gradual transformation based only on the interval structure of PSC 1. This deviation immediately distinguishes the underlying harmonic structure of part 2 from that of part 1.

[19] The second deviation in part 2 is the absence of an interpolation centering on PSC 4. Lindberg deviates from the established harmonic framework by proceeding from a progression centering on PSC 3 in measures 105–110, to PSC 3 itself in measure 111, to PSC 4 in measure 112, to a progression built around PSC 5 beginning in measure 115. In effect, the composer momentarily inserts a direct progression between PSCs 3 and 4 into the predominantly indirect progression that opens part 2. Lindberg departs from his established harmonic framework a third time leading into measure 132 by omitting both PSC 8 and a secondary progression centering on PSC 8. The fourth and most significant digression is the absence of PSC 1 at the beginning of part 2’s direct progression, which begins with PSC 2. The omission of PSC 1 at this point in the piece is especially intriguing because the climax of the entire work occurs in measures 132–134. Lindberg creates a large-scale formal disruption at the loudest and most active moment of the work.

[20] These four digressions are answered by further alterations in the conclusion of the piece that restore the work’s formal balance in the context of part 1’s rigid harmonic framework. The first alteration is the insertion of an interpolating progression into part 2’s predominantly direct progression between PSCs 4 and 5 (measures 137–140). The nature of this interpolating progression is very similar to the interpolation between PSCs 1 and 2 at the beginning of part 2 (measures 87–91); in both cases, the interpolations are based on the register properties of the main chord that precedes them. The insertion of a brief interpolating progression based on the properties of PSC 4 in the midst of a predominantly direct progression is significant: it balances out the absence of a fourth secondary progression at measure 113 between PSC 3 and PSC 5.

[21] Following the conclusion of the direct progression, which adheres to the chaconne between PSCs 4–8 in measures 141–145, Lindberg inserts a brief interpolation followed by a second instance of PSC 8 in measure 150. The additional PSC 8 in measure 150 and the interpolation that precedes it in measures 146–149 remedies the omission of an eighth secondary progression from the indirect progression in measures 86–131.

[22] The second PSC 8 is followed by a short closing section in measures 151–157 that is very similar in both content and texture to that of part 1: both contain progressions of eight block chords that exhibit the register contour of the main progression. While the closing section from part 1 consists of only one progression, Lindberg expands the closing section in part 2 to include two progressions that gradually converge on the middle register of the piano. Part 2 closes with two additional cluster chords in measures 155–156, the latter of which is centered on middle C. While the expansion of the closing section cannot be linked to any specific deviation from the underlying structure in part 2, it may simply result from a general attempt by Lindberg to increase the length of part 2, balancing out the omission of material from the indirect progression.

[23] Twine closes with a very brief codetta, measures 158–159, consisting of PSC 1 followed by seven new 12-tone chords. The codetta compensates for two deviations in part 2: the interpolation between PSCs 1 and 2 in measures 87–91 and omission of PSC 1 at the climax of the work. Recall that the interpolation in measures 87–91 is one of the few moments that does not exhibit pitch-related properties of the main progression of PSCs. Lindberg balances out this discrepancy in the codetta by closing the work with a brief progression that opens with PSC 1 and that does adhere to the main sequence of chord properties. Lindberg’s treatment of the main progression of PSCs in Twine comes full circle: part 1 establishes formal stability by strictly adhering to the underlying harmonic framework; the beginning of part 2 deviates from this framework resulting in formal dissonance; and the conclusion of the work reestablishes its formal stability by reaffirming the harmonic framework. Lindberg’s comparison of part 2 to a development section is entirely appropriate: it highlights the section’s unstable nature caused by its carefully “mixed up” parts. The classical aspect of Twine's formal structure lies in the composer’s use of chaconne to build a formal skeleton that he can both depart from and return to, thus creating and resolving formal dissonances.

Conclusion

[24] Magnus Lindberg has developed a sophisticated system for the purpose of achieving harmonic unity. His use of chaconne enables him to create a cyclic harmonic foundation that he composes into, around, and through. Even a brief glance at the musical examples presented above, however, will give the reader a sense of the complex, information-packed surface level of Lindberg’s music (though the composer has consciously aimed for more clarity in recent years). While the bulk of this discussion has focused on the underlying harmonic system, we may still question the degree to which the listener is aware of the harmonic structure that underpins this (or any) work.

[25] Lindberg addresses this issue in a conversation with Tony Lundman in which the composer states, “... the actual structure of the work is not important to the process of listening” (Lundman 2002, 17). I am compelled to disagree with the composer on this point; while the listener would be amiss to concentrate solely on the underlying structure of a work, the structure is certainly integral to the process of listening. When untethered, Lindberg’s characteristically complex surface textures may be perceived as diffuse and lacking in focus. His systematically generated harmonic structures, however, ground these textures, giving them directed motion toward logical harmonic goals that are always present but never overt. Consequently, Lindberg has become quite skilled at managing very large formal schemes. While Twine is only eight minutes in length, the work begun in the solo piano piece led to such monumental compositions as the twenty-five minute Joy (1990), the thirty minute Concerto for Orchestra (2003), and his largest work to date, the forty-minute Aura: In Memoriam Witold Lutoslawski (1994).

[26] Regarding Aura, Anderson (Anderson 2004, 208) has thoughtfully described its final cadence as “unassertively inevitable.” In other words, to Anderson the listener, it feels just right. Moments such as this, spawned from the carefully crafted, long-range harmonic schemes developed in Twine, permeate Lindberg’s recent music. Ultimately, it is these moments that have allowed his music to attain a level of accessibility rarely encountered by such modern and innovative work, and they may help to explain his popularity with conductors and audiences alike.

Ed Martin
University of Wisconsin Oshkosh
Department of Music
800 Algoma Blvd.
Oshkosh, WI 54901
martine@uwosh.edu

Works Cited

Anderson, Julian. 1992. “The Spectral Sounds of Magnus Lindberg.” Musical Times 133: 565–7.

—————. 2004. “Sibelius and Contemporary Music.” In A Cambridge Companion to Sibelius, ed. Daniel M. Grimley. Cambridge: Cambridge University Press.

Anderson, Martin. 1998. “The Large Spans.” Nordic Sounds 2: 9–13.

Brabocz, Marta. 1993. “La Musique Contemporaine Finlandaise: Conception Gestuelle de la Macrostructure. Kaija Saariaho et Magnus Lindberg.” Les Cahiers du CIREM 26-27: 155–168.

Cody, Joshua and Kirk Noreen. 2000. “Magnus Lindberg in Conversation: Moving Between Extremes.” Musical Times 141: 33–37.

Eötvös, Péter. 1994. Magnus Lindberg. Ensemble Intercontemporain, CD program notes. Adès – Paris: IRCAM.

Häyrynen, Antti. 1998. “High Tide for Magnus Lindberg.” Finnish Music Quarterly 1:48–54.

Howell, Tim. 2006. After Sibelius: Studies in Finnish Music. Burlington and Aldershot: Ashgate.

Karttunen, Antero. 1996. “The Music of Our Time.” Finnish Music Quarterly 4 (1996): 31–63.

Korhonen, Kimmo. 1995. “Young Composers of the 1990's: Buffeted by the Winds of Change.” Finnish Music Quarterly 2: 16–18.

Lindberg, Magnus. 2005. Interview by Ed Martin. 6 October, Los Angeles.

Long, Stephen. 1999. “Magnus Lindberg’s Recent Orchestral Music.” Tempo 208: 2–8.

Lundman, Tony. 2002. “Music with Muscle.” Nordic Sounds 4: 14–19.

Martin, Edward. 2005. “Harmonic Progression in the Music of Magnus Lindberg.” DMA diss., University of Illinois at Urbana-Champaign.

Mäkelä, Tomi. 1992. “Magnus Lindberg: Changing Style.” Finnish Music Quarterly 3: 46–48.

Nieminen, Risto. 1996. Magnus Lindberg. Translated by Nick Le Quesne. Helsinki: Helsinki University Printing House, 1996.

Otonkoski, Lauri. 1991. “Marea: Beauty of Structure, Richness of Expression.” Finnish Music Quarterly 2: 20–24.

Warnaby, John. 1992. “The Music of Magnus Lindberg.” Tempo 181: 25–30.

Footnotes

1. A discussion of chaconne in Magnus Lindberg’s orchestral work Marea is found in Otonkoski 1991. Julian Anderson (1992) also mentions. John Warnaby (1992) discusses chaconne in Lindberg’s early works and cites its role in the orchestral work Kinetics. Stephen Long (1999) refers to the composer’s use of chaconne in the orchestral works Kinetics and Fresco. Tim Howell (2006) discusses balance in Lindberg’s Kinetics, Aura, and the Clarinet Concerto in his book. Howell mentions chaconne as one method by which the composer achieves formal balance, but does not go into detail. These sources do not offer an in-depth discussion of Lindberg’s innovations to the chaconne technique or its role in generating large-scale formal structures.
Return to text

2. In the author’s discussion with Lindberg and in other interviews, the composer describes his dodecaphonic pitch collections as “chords” or “harmonies” even though they are frequently partitioned into two or more vertical sonorities or melodic gestures. I have chosen to employ Lindberg’s terminology, rather than adopt other terms such as “harmonic fields” (used by Anderson 1992), because it highlights his conception of these pitch collections. The composer acknowledges that his harmonic system is steeped in the tradition of Western tonal music. His use of the terms “chord” and “harmony” is revealing; it suggests that he regards his dodecaphonic pitch collections as sonorities that can be strung together in progressions in the same manner as tertian harmonies are in common practice tonal music.
Return to text

3. Lindberg’s other compositions employing the harmonic system discussed in this article, variations on the system, or further innovations to the system include Kraft movement II (1985), Ur (1986), Kinetics (1989), Marea (1990), Joy (1990), Steam Boat Bill Junior (1990), Duo Concertante (1992), Aura: In Memoriam Witold Lutoslawski (1994), Fresco (1998), Parada (2001) and his Concerto for Orchestra (2003).
Return to text

4. The computer has played an important role in several aspects of Lindberg’s compositional process since the early 1980s, the most notable being its use in generating harmonies. He used the IRCAM computer software Patchwork (which has since evolved into Open Music) to generate large arrays of harmonies from which he composed Twine. The details of Lindberg’s use of this software lie outside the scope of this article: I will analyze the resulting chords and relationships between them, not the specific methods by which they were generated using Patchwork.
Return to text

5. C4 is middle C.
Return to text

6. See the author’s doctoral dissertation (Martin 2005) for an in-depth discussion of these three techniques in more recent works such as Kinetics for orchestra (1989), Marea for orchestra (1990), Steamboat Bill Jr. for clarinet and cello (1990), and Fresco for orchestra (1998).
Return to text

7. It is important to note that the chords in adjacent positions sometimes overlap with one another. For example, the A2 in measure 61 completes the 12-tone aggregate from measure 60 and the first half of beat 3 in measure 62 alternates between pitches from the harmonies in the positions two and three.
Return to text

8. Note, however, that in this particular progression, the chords in positions 3 and 5 contain higher notes than the chord in position 4. Local deviations from the underlying harmonic structure, such as this, do occur at certain points throughout the piece.
Return to text

Copyright Statement

Copyright © 2010 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.

Prepared by Sean Atkinson, Editorial Assistant
Number of visits: