Rhythmic Feel as Meter: Non-Isochronous Beat Subdivision in Jembe Music from Mali (1)
Rainer Polak
KEYWORDS: timing, rhythm, feel, pulse, meter, swing, Ingmar Bengtsson, Justin London, jembe (djembe), Bamako, Mali, West Africa
ABSTRACT: This article studies the empirical structures and theoretical status of rhythmic feels in jembe music, which is a popular style of drum ensemble music from West Africa. The focus is on systematic variations of durations (Bengtsson 1975)—that is, cyclic patterns of non-isochronous pulse streaming at the metric level of beat subdivision. Taking for example a standard piece of jembe repertoire that is set in a 4-beat/12-subpulse metric cycle (often notated as 12/8), I show that the ternary beat subdivision forms a repeated sequence of unequal (short, flexible, and long) subpulses. This stable rhythmic feel pattern, SFL, is unmistakable and non-interchangeable with a second ternary pattern, which is characterized by long, flexible, flexible subpulses (LFF) and occurs in other pieces of jembe music. As predicted in Justin London’s “hypothesis of many meters” (London 2004), these timing patterns distinguish individual meters. I further analyze how schemes of binary and ternary beat subdivisions can be synchronized to operate in parallel. Such metric nesting is based on the patterned non-isochrony of rhythmic feels. Cyclic variation of subpulse durations, I argue, is inherent in the repertoire and fundamental to the metric system of jembe music.
Copyright © 2010 Society for Music Theory
1. Rhythmic feel patterns in comparative perspective
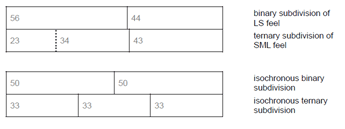
[1] In various styles of music with a regular metric beat, the fast pulse subdividing the beat is non-isochronous. Ingmar Bengtsson found that a consistent alternation of long and short subpulse durations (LS) is characteristic of the rhythmic feel of Swedish polska, a form of Nordic folk dance music. The subdivision of Vienna waltz is structured by the repeated sequence of short, long, and medium (SLM) subpulses. Bengtsson stressed that such cyclic variation of subpulse durations is essential to the feeling of rhythmic drive.(2)
[2] Non-isochronous beat subdivision is polymorphic and widespread in various musical traditions of the world. An SLL feel pattern (short, long, long) shapes the timing of insiraf, a rhythmic mode of classical Arab music from Algeria (Elsner 1990). An MSML pattern (medium, short, medium, long) underlies and identifies the subdivision of samba music from Bahia in northeastern Brazil. From the musician’s view, this pattern serves as a marker of their rhythmic dialect, which they address as suinge baiano (Bahian swing) and distinguish from the feels of other regional styles of samba (Gerischer 2003; 2006). Of course, the LS pattern is typical not only of Swedish polska. It marks the swing feel of jazz, the notes inégales of French Baroque music, and is also found in jembe music, a popular form of drum ensemble music from West Africa.(3)
[3] The present article analyzes the structures and music-theoretical status of non-isochronous beat subdivision in the standard repertoire of jembe music from Bamako, Mali. LS is only one among various timing patterns that appear in jembe music and I will describe three further patterns: two ternary and one quaternary. The approach is empirical and quantitative: I measure the timing of ensemble music performances. My theoretical aim is to show that rhythmic feel—the consistent characterization of subpulses by stable timing patterns—is inherent in the repertoire and fundamental to the metric system of jembe music. I think that music theorists, ethnomusicologists, and musicians of diverse backgrounds can learn from jembe music about what colloquially is referred to as swing. At the same time, I hope to promote the merging of perspectives from Africanist ethnomusicology and music theory.
[4] The layout of the article is as follows. Section 2 develops the theoretical argument and Section 3 reports on empirical methods and my personal background on the study. I investigate in detail the rhythmic feel of one particular piece of jembe music in Section 4. Section 5 roughly surveys the four most common feel patterns in the standard repertoire. In Section 6, I analyze the metric nesting of binary and ternary subdivisions in jembe music. Finally, in Section 7, I discuss the relation between rhythmic feel, meter, and expressive timing.
2. Metric type and rhythmic feel
[5] Analytical studies of African rhythm commonly assume a fast, single-track pulse of isochronous time spans to represent a time grid at the lowest (subdivision) level of meter: a basic time-unit or “orientation screen” (Kubik 1994, 42) that helps “performers maintain precise timing” (Locke 1982, 221) and “from which rhythmic patterns are composed” (Temperley 2000, 70). This concept was introduced in English under various terms such as “fastest pulse,” “equal-pulse base,” and “density referent,” in German as “Elementarpulsation,” and in French as “valeurs opérationelles minimales.”(4) Nobody has revealed its existence among the theories or experiences of African musicians or audiences (Merriam 1982).
[6] Some authors suggest the fastest pulse to constitute the sole or main level of metric reference.(5) The mainstream research on West African music, by contrast, assumes a metric system of three hierarchical levels, with the medium (tactus) level as regulative metric reference:(6)
- the fastest pulse at the level of beat subdivision
- the main beat at the medium level, which is subdivided by two, three, or four fast pulses
- the cycle, which is commonly divided by four beats (or multiples of four)
[7] In the following, I will often designate the “subpulse” (pulse at the metric level of beat subdivision, or “fastest pulse,” in Africanist theory terms) simply as “pulse.” The term “beat” will refer to the medium level of the metric hierarchy; “binary” (by twos), “ternary” (by threes), and “quaternary” (by fours) describe the number of pulses that subdivide a beat.(7) By “metric type,” I mean the hierarchically coordinated set of numerical relationships between metric levels of pulse, beat, and cycle (London 2004, 73–77).
[8] In jembe music, two metric types, one of ternary and one of quaternary beat subdivision, are prominent:
- a 4-beat/12-pulse cycle (often represented as 12/8 in staff notation)
- a 4-beat/16-pulse cycle (often represented as 4/4 in staff notation)
[9] Multiples of the 4-beat cycles are common as well; for instance, there are ternary 8-beat/24-pulse and quaternary 8-beat/32-pulse cycles.
[10] A topic of some controversy in Africanist music theory is metric ambiguity. Consistent off-beat phrasing and “two-in-the-span-of-three” cross-rhythm, two striking principles of polyphonic ensemble texture in West African music, amount to systematic displacement of rhythmic grouping and metric beat, and can allude to various alternative metric interpretations.(8) Africanist theory previously discussed these principles of polyphonic texture under the term of polymeter. The idea that one might simultaneously sense music through two or more distinct metric frameworks, which polymeter implies, has come under criticism.(9) Today, most authors agree that there is usually one particular cycle of regulative beats felt by encultured performers and listeners, which underlies the performance and listening even of those polyphonic textures that offer potential for metric ambiguity.(10) This cycle commonly counts four beats, as in the 4-beat/12-pulse and 4-beat/16-pulse metric types of jembe music, or counts a multiple of four.
[11] Analytical studies of West African drum ensemble music stress the role of so-called timeline patterns. Timeline patterns are asymmetrically grouped ostinatos, mostly of one 4-beat cycle in length, which are usually performed on instruments with timbres distinct from the rest of the ensemble, such as iron bells. All players of the ensemble relate their parts to the timeline pattern. Timeline patterns represent a framework of timing and phrasing reference that is complementary to meter.(11)
[12] Meter in African music is commonly assumed to rest on isochrony at the levels of both pulse and beat.(12) Deviations from isochrony at the pulse level have mostly been considered by-products of the inexactitude immanent in human motion. Acknowledging that “minimal” rhythmic imprecision can turn out to be greater than expected when empirically studied, Gerhard Kubik (Kubik 1972, 33) stated: “The listener’s and the player’s time perception ‘corrects’ this physical irregularity and unconsciously bends the beats into a regular series.” Kubik thought of cases of seemingly irregular timing as “non-linear off-beat-phrasing ... developed independently of the elementary pulsation (or regular division of the beat)” (Kubik 1999, 186; parenthesis in the original, italics mine). Cyclic variation of subpulse durations, or rhythmic feel, has not been a focus in studies of African music until now. Looking for concepts that consider both meter and rhythmic feel, I turn now to the works of non-Africanist music theorists.
[13] According to David Temperley,
a metrical structure consists of a framework of rows of beats, where beats are points in time, not necessarily events. The meter of a piece must be inferred from the events of the piece ... But once the meter is established, the events of the piece need not constantly reinforce it, and may even conflict with it to some extent. In this sense, a metrical structure is best regarded as something in the mind of the listener, rather than being present in the music in any direct way. (Temperley 2000, 66–67)
[14] From Temperley’s view, strong conflicts between rhythmic grouping and the underlying metric framework are typical in African music: “African listening requires a greater ability to maintain a steady beat despite conflicting accents” (Temperley 2000, 79). In general, however, he puts emphasis on the comparability of meter in African and non-African musical styles, rather than on difference.
[15] Justin London shares with Temperley the concept of meter as a feeling of pulsation that listeners gain from the rhythms they attend to: “Meter involves our initial perception as well as subsequent anticipation of a series of beats that we abstract from the rhythmic surface of the music as it unfolds in time” (London 2004, 4). London’s approach comes close to the Africanist concept of meter, in that it attaches great importance to the subpulse as “absolute value of the metric floor” (London 2004, 72) and “baseline for the level of rhythmic activity and energy in the music” (London 2004, 167). According to this notion of metric floor, establishing metric hierarchy is predicated on the categorical equivalence and nominal isochrony of subpulses, which “ensure that the overall metric pattern is ‘regular enough’ to permit a stable attending behavior” (London 2004, 72). In contrast to Africanist theory, however, London puts central value on integrating meter and timing patterns. He sees rhythmic feel patterns as a type of expressive variation.(13) This concept is meant to explain musical (not random) deviations from mechanically even timing. Its focus is on timing nuances demanded by the grouping structure of musical phrases.(14) London, however, ascribes a dual role, both metric and phrase-related, to expressive timing: “Although some expressive variations disambiguate metrical structure by indicating which note is on the downbeat, others define the affective or the motional quality of a particular figure” (London 2004, 28).
[16] There are (at least) two reasons why the concept of expressive timing takes mechanically even timing as reference. First, the question of how the performance of written music deviates from the nominal durations prescribed in notation has stimulated interest. Second, it is widely assumed that human listeners normalize instances of uneven timing to perceptual categories that consist of small whole number ratios of duration, such as 1:1, 1:2 and 1:3.(15) Music psychologist Eric Clarke has most explicitly formulated this assumption: “After the temporal information for rhythm has been perceptually categorized, any ‘remainder’ (i.e. any deviations from a perfect categorical fit) is considered to be expressive timing” (1987, 30; parenthesis in the original).
[17] A divide between structural (nominal-notational or categorical-perceptual) isochrony and performative expressivity is inherent in the concept of expressive timing. Analogously, Charles Keil’s (1995) notion of “participatory discrepancy” suggests a divide between syntactic structure on the one hand and groove on the other. However, the validity of this divide is questionable. Systematic interaction between structures at the macro (grouping) and micro (expressive) rhythmic levels has been shown by empirical studies, including analyses of off-beat phrasing in the soloing of samba percussionists (Gerischer 2006) and anacrusis in the backbeat of jazz grooves (Butterfield 2006).(16) Bengtsson advised “we should avoid calling [slightly differing durational values] ‘deviations’ ... without stating clearly that we just mean deviations from a mechanical norm that we use as a sort of temporal ruler” (Bengtsson 1987, 78; italics in the original). Going a step further, London questions the principle of the expressive-versus-structure divide: expressive “lengthenings and shortenings are not deviations from the norm—they are the norm” (London 2004, 150).(17) Similarly, Bruno Repp’s study argues that typical timing patterns in performance constitute norms or aesthetic standards and should be seen as an “integral part of the music, not as a ‘deviation’ from the mechanical timing suggested by the score. Rather, it is the timing of individual performances ... that should be regarded in terms of its deviations from the normative timing” (Repp 1997, 265).
[18] London suggests that humans internalize stable timing patterns which then shape their temporal expectations:
We are aware of differences in the ‘life’ or ‘swing’ of a performance ... precisely because we have internalized their characteristic timing patterns and other parametric differences. The fact that these differences exceed the limit of resolution of musical notation does not render them less structural ... What makes something a march and not a galop, for example, is in large part the characteristic metrical timing patterns of each genre—timing patterns that remain relatively fixed even though specific rhythmic figures vary from piece to piece within a given genre. And if we listen to marches and galops with any frequency, those characteristic timings will become part of our habitual entrainments to them (London 2004, 153–54).
[19] According to London’s “many meters hypothesis,” stable timing patterns can individuate numerical metric types into qualitatively distinct meters (2004, 142–60).(18) This conforms with Ingmar Bengtsson’s suggestion that cyclic variation of subpulse durations represents a property of metric structure (Bengtsson, Tove, and Thorsen 1972, 74). In support of this perspective, I hope to show that rhythmic feel is indeed inherent in, and characteristic of, the meters of jembe music pieces from Mali.
3. Objective and approach of the study
[20] The jembe is a goblet shaped hand drum of the Mande peoples of Western Africa, from the southern regions of Mali and the northeastern part of Guinea (Charry 2000, 193–241). Alternative spellings of the instrument’s name include djembé in French, jenbe in the Republic of Mali, and dyembe in the Republic of Guinea. Traditionally, jembe music has accompanied song and dance in the context of celebrating social occasions, such as life-cycle events (naming, circumcision, and wedding ceremonies), communal agricultural labor, harvest rites, and religious festivals. Since the 1960s, it has gone through processes of urbanization and commercialization in many parts of francophone West Africa. At the same time, it was institutionalized as national folklore in the form of state ballets.(19)
[21] Since the 1980s, jembe music from West Africa has traveled to Europe, North America, and more recently to Japan, Australia, Brazil, South Africa, and many other countries. The modern social contexts of jembe music outside West Africa include stage shows, music education (adult classes, school music), and social pedagogy (drum circles, team building). There is much interaction between traditional West African performance practice and the global contexts of jembe music (Polak 2000). Channels of mutual influence include the labor-migration of musicians, instrument exports from West Africa, cultural tourism to West Africa, and the mass-mediatization of jembe music in CDs, DVDs, teaching handbooks, and online resources.
3.1 Personal background
[22] This article was inspired by my personal experience of the musical style under study, as an anthropologist/ethnomusicologist, music teacher, and musician. Since 1991, I have done ethnographic research as well as studied, performed, and taught music with several of the musicians sampled for the chronometric project described below (Subsection 3.2). In 1997 and 1998, in the context of my dissertation project on the urbanization of jembe playing in the city of Bamako, I was an apprentice to the late Jaraba Jakite, regularly performing the second jembe in his ensemble on the occasion of life-cycle celebrations. I also performed with other ensemble leaders, such as Yamadu Dunbia, Jeli Madi Kuyate, and Drissa Kone, albeit less frequently. In 2000, 2006, and 2008, I toured Germany (my home country) giving concerts and workshops with artists from Bamako, including Jaraba Jakite, Madu Jakite, and Drissa Kone. Today, I make my living from both academic work and freelance teaching of jembe music.
[23] In my personal experience of jembe music, the cyclic variation of subpulse durations shapes the expectation for the timing of phrases; it distinguishes the rhythmic feels of different pieces and regional styles; and it disambiguates the beat. These opinions are the result of a long learning process. During my first stay in Bamako in 1991, when I was an amateur drummer and undergraduate student of Social Anthropology, African History, and African Languages at the University of Bayreuth, I experienced great difficulty in identifying and repeating the phrases my jembe teachers played for me. They played them fast and loud; phrases integrated in lengthy periods rather than in isolation; accompanied by other ensemble parts’ phrases, but without expressing the metric beat (clapping, tapping, or the like); and with strongly pronounced variations of pulse durations. After some weeks, I became aware of obviously uneven, yet repetitive timing patterns my teachers applied to almost every phrase. My inability to gain a stable subpulse from the phrases made it impossible to feel a stable beat, which again made me hear strangely shifting groupings instead of patterned phrases and themes: a painful experience. I then started to transcribe many patterns in two different schemes of subdivision (one quaternary, one ternary), and tried to learn them from both metric perspectives. In retrospect, this was not a bad idea, even if it did not resolve my difficulties for many years.
[24] In 1997, after two more study trips to Bamako in 1993 and 1994, I published my first academic paper on the structure of beat subdivision in jembe music. Based on analysis by ear, I modeled rhythmic feels as systematic inflections of isochronous subpulses.(20)
[25] As a teacher of jembe music in Germany, I discovered that the question of when to start introducing rhythmic feel patterns in the course of a jembe music student’s education is important. The pedagogy of jembe music in the German-speaking countries interprets most pieces with a domesticated, straightened beat subdivision. Sometimes, the idea behind this practice is didactic reduction—teachers reduce the music’s complexity to make it more accessible to beginners. In other cases, jembe teachers are themselves unable to perform the feel patterns that, as I will show in the present article, are inherent in the standard repertoire of jembe music.
[26] As a freelancer, I have specialized in coaching professional German jembe teachers. These teachers generally tend to relate the phrases and themes of jembe pieces to a metric cycle of beats and pulses, and to one another in their multi-part relationships. In their pedagogical work, they commonly use various forms of graph notation.(21) They have internalized and transformed the theory of meter in Africanist ethnomusicology (as outlined in Section 2) into analytical and pedagogical tools. What most of them find difficult, however, is to appropriate their African masters’ skills of rhythmic feel and expressive timing. My approach to the further training of jembe teachers accepts that first, we have to derive uneven feel patterns as deviations from isochronous pulsation. I then aim to undo the dependence on isochrony with the help of both demonstration, emulation, and focused exercises. It appears circuitous, however, to first suppress rhythmic feel in teaching beginners and then, later in the students’ education or vocational careers, to try to add it back in again. Indeed, many students find the readjustment problematic. This pedagogical problem highlights the insufficiency of accepted Africanist music theory for the understanding of jembe music.
3.2 Empirical method
[27] The present article is empirically based on a research project on the timing of traditional jembe music from the Republic of Mali. The project was dedicated to the chronometric measurement of ensemble music performances.
[28] In 2006 and 2007, I produced a body of about 180 multitrack recordings of more than 25 different jembe pieces in Bamako, Mali’s capital, and rural areas to its south.(22) The recordings feature nine lead jembe players in five ensembles. The focus of the recordings is on experienced representatives of the urban profession of jembe drumming that has developed in Bamako in the context of local dance drumming events—at wedding parties, for instance—since the 1960s. The recorded performer’s aesthetic ideals refer to the (now historical) performance practice of the 1970s and 80s.(23)
[29] The recordings usually took place in a private courtyard. There were no rehearsals or discussions of arrangements taking place during or before the sessions. At a traditional celebration, lead drummers shape musical form according to the needs of co-performing singers and dancers. During the recording sessions, dancers or singers were rarely present; thus, form depended on the players’ imaginations. However, the isolated studio situation did not seem to alter rhythmic feels and phrasing strategies. This was confirmed by spot check measurements of celebration dance music, and analysis of several situations where dancers spontaneously joined a recording session.
[30] The sessions usually lasted for one or two hours. Reflecting a practical, utilitarian orientation, professional jembe players in Bamako think of their music-making as labor and service, be it to the community at a local dance event, to the audience in a concert hall, or to a producer—or researcher, like myself—in a studio context.(24) The mood was mostly neither somber nor exalted.
Example 1. Open-air recording “studio” session
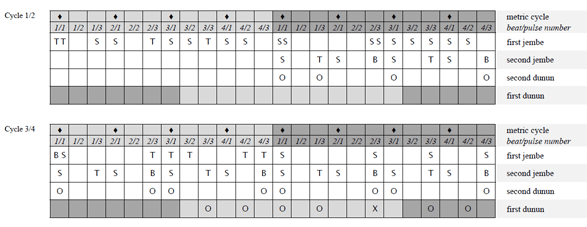
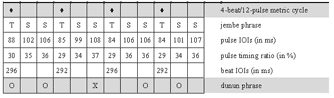
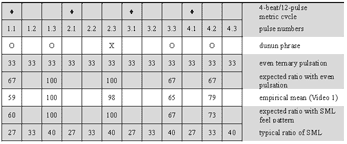
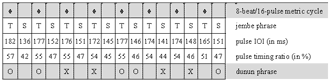
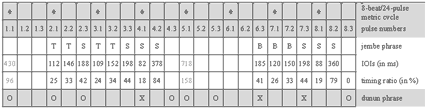
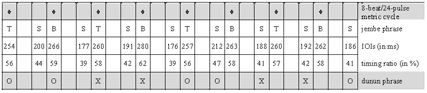
(click to enlarge)
Example 2. Visualization of inter-onset-intervals of a 4-beat/12-pulse cycle in video editing software
(click to enlarge)
Video 1. manjanin by the Drissa Kone Quartet
(click to view)
[31] I attached unidirectional clip-on microphones (AKG C419) directly onto the instruments (see Example 1) and recorded into a mobile four-track hard disk machine (Edirol R4). Recording sessions were located in open-air facilities. Thus, there was little acoustical crosstalk of instruments and reverberation from walls. The single tracks (representing individual ensemble parts) of the multitrack recordings were mostly clean enough for immediate measurement without the need for frequency filtering. I simultaneously videotaped the recording sessions. Monitoring the audio waveforms and corresponding films (see screenshot in Example 2) enabled me to study hand patterns, witness nonverbal communication among ensemble members, and corroborate soft attacks that do not always show up unambiguously in the waveform. I transferred the digital recordings to a computer workstation and archived, surveyed, and analyzed the data with Sony’s video editing software Vegas Pro, which includes a strong multitrack audio editor.
[32] The empirical approach was to measure the time spans between the attacks of drum strokes (inter-onset-intervals, or IOIs). Mostly, I jumped back and forth between close listening, inspection by eyesight and manually marking the onsets of particular phrases (see Example 2) that sounded either typical or special, and manually putting the data (intervals between markers) into calculation software for further processing. The gathering of quantitative data and qualitative analysis by ear was performed simultaneously and was closely related. This method was productive in the development, spot testing, and adjustment of hypotheses. It is premised on a high level of prior knowledge of the studied repertoire.
[33] A second approach is aimed at the mean values of continuous periods or whole pieces. I used this method mainly to test the significance of hypotheses. It implied measuring large amounts of IOIs; for instance, the second jembe’s accompaniment ostinato in the five-minute piece to be analyzed below (Section 4, Video 1) counts about 1,700 strokes. The facility of audio editing software to detect and mark onsets automatically was of much help in this procedure; the data of the markers was exported into text files and then imported into calculation software for further processing.(25)
[34] The objective of the chronometric project was to test the existence of rhythmic feel patterns, specify their structure and proportions, and analyze their stability and correlations with tempo, ensemble size, ensemble parts, rhythmic grouping structure, and personal styles. The approach was to calculate the intervals between strokes (IOIs), which are given in milliseconds (ms), as percentages of the normalized beat duration, or “(pulse) timing ratio.”(26) I give timing ratios as strings of relative values, such as A:B (binary subdivision), A:B:C (ternary subdivision), or A:B:C:D (quaternary subdivision).(27)
[35] This article is dedicated to the formal analysis of musical structure. Its approach can be criticized for abstracting jembe music from its functional, cultural, and social contexts. Players and audiences of traditional jembe music in Mali usually do not talk about drumming in terms of theoretical concepts, such as “melody,” “rhythm,” “pulse,” “beat,” and “cycle.” They rarely listen to recordings of pure jembe music; the common role of drumming is as live accompaniment for dance. This article does not generate knowledge of how Malians perceive and conceptualize jembe music. Its audio and video examples do not attempt to capture the dance, which might add important dimensions to the discussion of rhythmic feel. Further studies of jembe music should aim to redress these shortcomings.
[36] “Formalist” approaches to African music have been contested in the field of ethnomusicology, and this contesting met with criticism, in turn, from a postcolonial perspective.(28) In my view, the formal analysis of jembe music is complementary to historical and ethnographic approaches. Its validity and social relevance has increased with the recent spread and modernization—staging, formal teaching, and mediatization—of jembe music on all continents.
4. The rhythmic feel of manjanin
[37] This section analyzes the timing of one piece of jembe music. I start out with some remarks on the relation between repertoire and performance in jembe music (Subsection 4.1) and introduce the piece (4.2), before I go into analysis (4.3–4.8).
4.1 Repertoire and performance
[38] In the million-strong city of Bamako, there exists a standard repertoire of about 25–30 popular pieces of jembe music. There is no indigenous term, however, for the entity of repertoire, equivalent to, for instance, English terms like “piece,” “tune,” “groove,” or “rhythmic mode.”(29) The titles of some pieces contain attributes such as “-dòn” (dance of ... ) or “-fòli” ([instrumental music] playing of ... ). Not all the pieces bear a name, however, and calling the items of repertoire by name is not part of everyday language usage, even among drummers.
[39] The international jembe music scene usually addresses jembe pieces as “rhythms,” as is evident in CD liner notes, handbooks, online resources, stage performance announcements, and formal teaching practice. Working on this research project and article, I came to abandon that terminology for two reasons. First, I prefer to restrict the term rhythm to specific usage on analytical levels below that of the repertoire. I write of “rhythmic figure,” or “rhythmic grouping structure,” meaning the durational structure of note groups segmented by rests (non-sounding metric pulses); and I speak of “rhythmic feels,” addressing the cyclic patterns of unequal beat subdivision, which I suggest characterize the meters of jembe pieces. Second, I prefer terms such as “piece” or “composition” for items of repertoire, since they remind us that we do not deal with “just rhythm” (nor “essentially rhythm”)—a traditional European stereotype of African music, and West African drumming in particular, which unfortunately is still current.(30) The phrases of jembe music, for instance, do not only consist merely of rhythmic figures; their equally definite and characteristic timbre sequences also form melodies.(31)
[40] Performing traditional jembe music usually implies the improvisational interpretation of pre-composed materials and models, a process Meki Nzewi (Nzewi 1997, 68) terms “performance-composition” or “situational re-composition.” When I write of jembe music “compositions,” I mean those aspects of a piece that are usually stable across personal playing styles and specific performance situations. This refers mainly to the thematic materials, which consist of the individual parts’ basic phrases and their polyphonic relationships. Together, these make up the “ensemble thematic cycles” (Nzewi 1997, 45), which distinguish the identity of each piece in the standard repertoire.
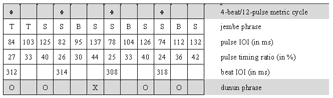
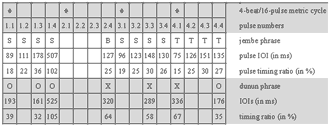
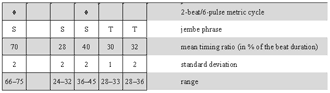
[41] Needless to argue, the situational re-composition of jembe music implies both tradition and change. For instance, youths began to demand televised pop music and dance to be transformed into jembe pieces in the 1990s. Competing drummers distinguished their personal styles as well as their repertoires to get jobs in urban and international market economies. Nonetheless, the compositions of the standard repertoire have remained recognizable as musical identities in the view of performers and audiences up to the present day. Though unwritten, the standard repertoire has endured. It is embodied in the skills and performance practice of drummers, dancers, singers, and listeners of jembe music.
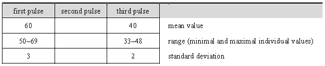
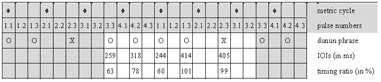
4.2 A piece of jembe music
[42] The composition studied in Section 4 is called manjanin (also menjani, mendiani, or bundiani). It is of the ternary 4-beat/12-pulse metric type. I base the analysis on a studio recording produced in 2006 (Video 1) and take some fifteen further recordings as reference for comparison.
[43] Manjanin is a jembe piece, a dance event, and a ritual institution, the focus of which is a spectacular dance performance by preadolescent girls. These girls are selected as the best dancers of their age-set and offered specific choreographic training. They get special costumes and insignia, and are initiated into specialized ritualistic knowledge. Manjanin was—and in some places still is—practiced all over the Manden region, roughly between Bamako in Mali and Kankan in Guinea, which is the heartland of jembe music. Throughout the 20th century, it has played a prominent part in representative cultural performances, for instance as a danse folklorique piece of Mali’s National Ballet in the 1960s. Manjanin has a place among the most culturally valued compositions in the repertoire of jembe music.(32)
[44] The recording studied here features a quartet consisting of two jembes and two dununs. The dunun is a cylindrical, double-headed drum beaten with a stick. In the classical style of jembe music from Bamako, duos (one jembe plus one dunun), trios (two jembes and one dunun), and quartets represent typical orchestras. Today, larger ensembles are also popular.
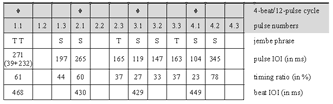
[45] The featured ensemble was well rehearsed, since the members have been regularly performing together at traditional celebrations since the 1980s. Lead jembe player Drissa Kone (born 1958) is versed in manjanin, which he knows both from his professional work in Bamako and from his native small town of Kourouba, some one hundred kilometers south of the Malian capital. He had already been learning jembe music as an apprentice for several years before he migrated to the city in 1974. In Bamako, he continued his apprenticeship in the urban style of celebration music as well as in stage performance of ballet companies. Since the late 1980s, he has been working as a lead player in Bamako and in Europe, where he performs and teaches regularly. Madu Jakite (born 1960) has been Kone’s expert dunun player since the mid-1980s. Second jembe player Sedu Balo (born 1960) has the musical skills of a lead player, yet works with Kone’s ensemble since he is not successful as an organizer and ensemble leader. Second dunun player Antoine Traore (born 1980) has been a trainee among the Kone ensemble’s wider pool of professionals since he was in his teens.
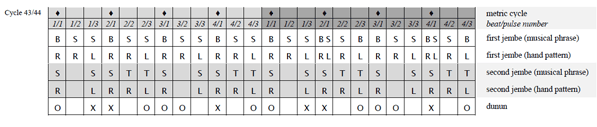
[46] Video 1 presents the studied recording, which is about five minutes in length and consists of 218 metric cycles. I list cycle numbers (001–218) in the lower left corner of the video image to help viewers find the excerpts analyzed in Subsections 4.3–4.7. The changeover of numbers is roughly synchronous with Beat 1 of each metric cycle; following the numbers can thus also improve metric orientation.
[47] The performance starts at a tempo of about 135 ternary beats per minute (bpm), equivalent to 405 pulses per minute (ppm); it is as fast as 205 bpm (615 ppm) at the end. The lead jembe achieves this acceleration largely by a nearly constant, gradual increase in tempo.
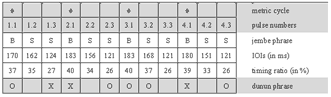
[48] Table 1 transcribes the audio component of Video 1. The first row in each line represents the 4-beat/12-pulse metric cycle that underlies the piece. The gray shading distinguishes the two cycles that fill a line. Boxes represent the pulses. I mark the beat by placing a diamond symbol in the boxes that represent on-beat pulses.(33)
[49] Following Locke (2010), I address each time point of the metric cycle with a distinctive two-place number. The first digit refers to the beat, the second to the pulse (“beat number.pulse number”). For instance, “Pulse 3.2” means the second pulse of the third beat, equivalent to the second eighth note in the third dotted quarter note beat in 12/8 staff notation. The score given in Table 1 shows pulse numbers only on Cycles 1–4; they will reappear below in some tables, the discussion of which refers to individual notes.
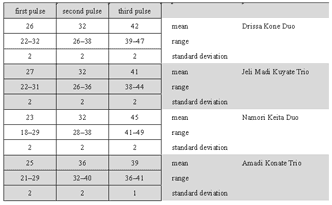
[50] The following letter symbols represent sonic events:
Jembe sounds S slap (sound of highest frequency spectrum) T open tone (sound of medium frequency spectrum) B bass tone (lowest sound; less loud and clear-cut than slap and tone) S/T/B muted slap/open/bass tones . ghost note (audible touch without specific sound) Dunun sounds O open dunun stroke X muted dunun stroke (higher in frequency spectrum, faster decay, and less loud than open dunun tone)
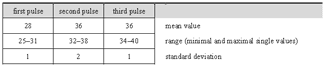
The first dunun
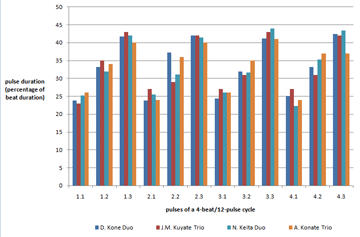
[51] In the classical style of Bamako jembe music, the first dunun’s basic phrase marks the identity of each composition and serves as a timeline and phrasing referent.(34) Dancers will often shout or sing it aloud, for instance to call up the piece at a celebration or in formal teaching situations, when it is important to unambiguously relate dance pattern and musical phrase. The lead jembe player continually relates to the dunun part.
[52] The bottom row of each line in Table 1 represents the first dunun and two cycles of the manjanin dunun phrase fill a line. The gray shading highlights the grouping structure. A note group of four open strokes, starting from Pulse 3.3 and ending on Pulse 1.3 of the next metric cycle, forms the core of the pattern. This grouping arches over the regulative time point of the metric cycle (Pulse 1.1). In other words, the dunun phrase and metric cycle are phase-shifted in manjanin. The first stroke of the note group (Pulse 3.3) is also commonly used as the point of entry (see Cycle 3).
[53] The basic dunun phrase appears identically in 164 of 218 cycles in Video 1. A standard variation, played about forty times, simply omits one stroke.(35) The omission is the open stroke on Pulse 1.1, which is the only on-beat stroke in the phrase. The variation thus intensifies the displacement and interplay (“conflict,” or “dissonance,” in music theoretical terms) between grouping structure and metric framework, which some of the lead jembe phrases further emphasize (see below).
The accompaniment parts
[54] The second dunun and second jembe invariably perform short ostinato accompaniment phrases of only two beats (six subpulses) length. They increase the rhythmic density of the polyphonic texture and strongly support the feeling of the ternary beat. The accompaniment parts join the ensemble during Cycles 2 and 3. From Cycle 5 onwards, I leave them out of the score.
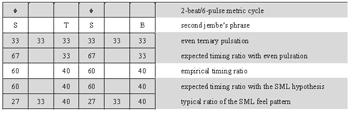
The first jembe
[55] The lead jembe contributes to the density of the ensemble’s polyphonic texture in various ways. Some of its phrases embellish the dunun’s grouping structure and, with the accompaniment parts, reinforce the dunun’s relation to the ternary 4-beat cycle. The rhythmic pattern of Cycles 68–71 and 73–76 serves both these functions. It shares most of its time points with the basic dunun phrase, with additional notes linking together the dunun strokes from Pulse 4.2 to 1.3. The lead jembe stroke on Pulse 3.1 marks Beat 3 and ties the combined lead jembe and dunun pattern to the metric beat.
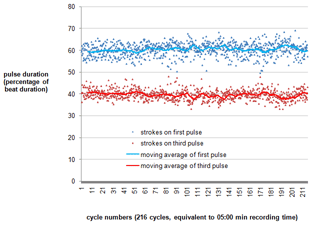
[56] In dance drumming, periods of so-called échauffement heat up individual dancers’ solo performances and push them towards a climax.(36) The lead jembe highlights the subpulse in échauffement phrases, which typically play out the fastest pulsation in a continuous series of strokes. Video 1 shows two échauffement periods. The first one occurs close to the end of the piece (Cycles 175–186). It repeats and varies a phrase that is typical of manjanin. The second échauffement period marks the finale of the piece (Cycles 206–217). Its simpler melodies, which do not use the soft timbre of the bass tone, further heighten the raw rhythmic power of the fast pulsation. The phrases of the final échauffement are not specific to the piece, but rather are generic to a whole cluster of structurally related compositions.
[57] Some lead jembe phrases contribute not only to the rhythmic density, but also to the polyphonic depth, or metric “multidimensionality” (Locke 2009), of the ensemble texture. These phrases exploit the principles of systematic cross-rhythm and off-beat phrasing, which create rhythmic tension and suspense (cf. Locke 2010). Passages of systematic off-beat playing, with slaps consistently falling on the third subpulse, or second and third subpulses, are frequent; see, for instance, Cycles 5–12, 17–24, and 170–172. For an example of cross-rhythm, see the ostensibly binary grouping of slap notes in Cycles 29–31, 45–46, and 166–167.
[58] Beyond contributing to the polyphonic ensemble texture, the lead jembe is responsible for creating musical form. An essential skill for lead players is to balance steady groove and thematic movement. Groove relies on the recycling—repetition and variation—of a few basic standard phrases.(37) Movement requires the alternation and sequencing of the groove cycles, and the insertion of linear (non-repetitive) phrases and passages.
[59] Some of the lead jembe’s standard phrases are of one metric cycle length (Cycles 32–34 and 67–71, among others), while others cover two cycles (Cycles 19–24 and 83–90, among others). Standard phrases are often expanded into longer passages by simple procedures of variation, as for instance in Cycles 32 through 42. The lead player first repeats a standard phrase three times in Cycles 32–34. In Cycle 35, he creates a variation by not cadencing on Beat 1, but instead extending the preceding melodic element (|STT| on Beat 4 of Cycle 34) over Beat 1 until Beat 2. From Cycle 36, the lead jembe returns to the basic form and then repeats the variation in Cycle 42.
[60] It is important for lead players to consider and decide how long to recycle one phrase before changing to another one. In our audio recording of manjanin, the lead jembe would sometimes recycle one phrase for just four metric cycles (see Cycles 7–10, or 61–64). Sometimes, however, a phrase is used six to ten times (see Cycles 17–24, or 83–90). The longest passage of one recycled phrase contains twelve metric cycles (Cycles 175–186).
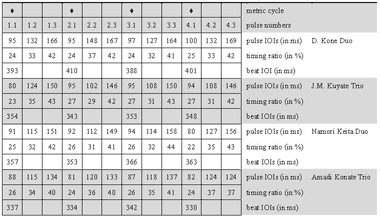
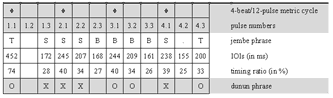
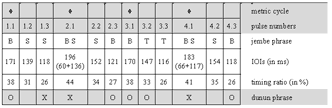
[61] Only a few standard phrases are non-repetitive. These appear as breaks or bridges between repetitive groove periods. A particular type of break phrase, called a blocage in the international jargon of francophone jembe players,(38) is prominent in jembe music. The grouping structure of such break patterns typically shows a specific placement in the metric cycle: they start with a flammed double note on Pulse 1.1 and end on or around Pulse 4.1. A characteristic example is the final break, which marks the end of the piece (Cycle 218). This phrase can occur in all compositions that structurally relate to manjanin (about a third of the whole repertoire). Another break, which is more specific to manjanin, appears with small melodic variations in Cycles 82, 94, 132, 137, 159, and 187.
[62] Breaks can have various functions. First, they finish échauffement periods. In traditional dance drumming, this means to cut off the finales of short solo dance performances. In modern contexts, such as ballet performances and formal teaching, lead jembe breaks also signal changes in pre-arranged choreographic or musical sequences. The use of a break as an initial call (Cycle 1) in Video 1 is an instance of such modern arrangement procedure.
[63] Lead player Drissa Kone refrains from showing off with original or spectacular phrases. His recycling and sequencing of standard phrases, which fills about 85% of the recording time, is rooted in traditional dance drumming. Kone generally accomplishes the sequencing through the use of immediate and fluid changes; he only occasionally inserts non-repetitive bridges. There are no sophisticated ensemble breaks or excursions from standard phrases. Experienced Bamako jembe players describe this valued lead playing style as calm and serene, or staid.(39) They contrast this ideal of staid playing with the more heated, ornate, and individualistic soloing, and with an alleged decline in style, of which they accuse the younger generation of jembe players.(40)
4.3 Rhythmic feel in non-segmented rhythm: the échauffement
[64] Jembe échauffement phrases mark out the fast pulsation as a regular series of strokes. They provide a quick and reliable guide to the feel of a jembe piece.
[65] In the first échauffement period of Video 1, which covers twelve cycles or fifteen seconds of time (Cycles 175–186), the lead jembe’s strokes show a repeated sequence of distinct durations. Of the three pulses that subdivide each beat, the first one is relatively short while the second is medium and the third is long (SML). The mean pulse-timing ratio is 27:33:40. This means that the first of the three subpulses takes on average 27% of the normalized beat duration, whereas the second takes 33%, and the third 40%. The standard deviation from this ratio is merely around 2% for each pulse and the SML feel pattern is stable. Unlike the unequal pulse, the beat is roughly isochronous. The standard deviation from the mean beat duration is between only 1% and 2%.
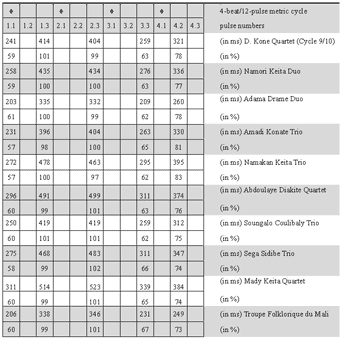
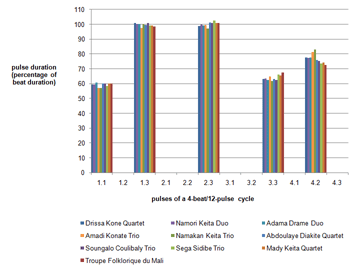
[66] To exemplify these statistical mean values with a typical phrase as actually performed, Table 2 lists the timing data of Cycle 178. First, the table measures the duration of each note, or “pulse IOI.” A pulse IOI gives the interval between the onset of a note (the one below which it is listed) and the following note. Second, the table lists the notes’ relative durations as percentages of the normalized beat duration, or “pulse-timing ratio.”(41) Third, the table specifies the intervals between notes falling on the beat (“beat IOI”).
[67] The pulse IOIs and timing ratio in Table 2 clearly show the cyclic SML feel pattern (short, medium, long, short, medium, long ...). The mean pulse-timing ratio over the 4-beat cycle is about 25:33:42. Despite the fast tempo of 192 bpm (575 ppm), the difference between the first and third pulse is pronounced; it amounts to 40–60 ms, which is striking in the context of a mean pulse duration of just above 100 ms. By contrast, the variation of beat duration is insignificant (below 10 ms).(42)
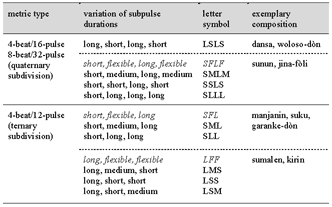
[68] I recommend relistening to Cycle 178, which is measured in Table 2, and trying to relate the pulse-timing ratio of the lead jembe (25:33:42) to the rhythmic drive it produces in the music. Audio 1a gives a looping of the one-cycle excerpt to allow for metric attunement. Audio 1b isolates the lead jembe track to make its timing nuances clearly audible.
|
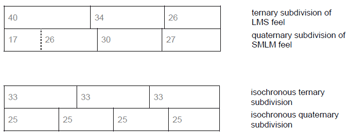
Audio 1a. manjanin échauffement |
Audio 1b. manjanin échauffement |
[69] In the following, I take Drissa Kone’s mean-timing ratio (27:33:40) as a working hypothesis for developing a descriptive model of rhythmic feel in manjanin performance. I do not develop a prescriptive model for the ideal timing of manjanin. Ingmar Bengtsson (1987) warned that we should not confuse isochronous exactitude with an ideal model for perfect musical performance. Analogously, it is important not to confuse the mean-timing ratios of rhythmic feels with non-isochronous perfection.
4.4 Rhythmic feel and rhythmic grouping: the call
Audio 2. manjanin opening call
(Cycles 1–4 from Video 1)
Table 3. Timing of the lead jembe in Cycle 1 from Video 1 (manjanin)
(click to enlarge)
[70] In this subsection, I address the relationship between rhythmic feel (cyclic variation of subpulse durations) and rhythmic figure (grouping structure) in the lead jembe part. I offer a close look at the opening call (Cycle 1 from Video 1; Audio 2), which displays one of the most distinctive phrases of the piece. As I will show, some details of the call’s timing relate to its rhythmic figure. At the same time, however, it is based on, and establishes for the listener, the composition’s hypothesized SML rhythmic feel.
[71] The call starts on Pulse 1.1 with a flammed double note of open tones, which represents one of the strongest timbral accents of jembe playing technique. The note on Pulse 1.3 has a duration of 44% of the normalized beat duration (see Table 3); this conforms with the long duration of the third pulse in the SML feel pattern. The two slaps on Pulses 1.3 and 2.1 form a comparatively broad pair of strokes.
[72] The group of six notes on Pulses 2.3 through 4.2 initially makes subtle use of the SML pattern, with durations only ranging between 27% and 37%. However, the last interval of the group is particularly short (Pulse 4.1=104 ms); it is audibly (15 ms) shorter than the note on the first subpulse of the preceding beat (Pulse 3.1=119 ms). The strong articulation of the shortness of Pulse 4.1 (23%) and the related length of the note on the following pulse (4.2=78%) mark the ending of the note group and of the phrase. In this example, the local strengthening of the recurring feel pattern contributes to the expressive timing of the phrase’s grouping structure.
[73] The relatively long durations of Beats 1 and 4 (compared with Beats 2 and 3) represent the only instance of expressive variation of the beat duration in Video 1. Variation of the beat tempo is not typical of jembe music.
4.5 Rhythmic feel and personal style
[74] The analysis of the rhythmic feel of manjanin has so far been based on a single recording of a single performer, Drissa Kone (Video 1). This subsection considers recordings of four lead jembe players. These will provide a basis for evaluating the role of individual playing styles.
Table 4. Mean timing ratios of échauffement periods (9–17 metric cycles in length) by four players (manjanin)
(click to enlarge)
[75] Table 4 measures échauffement periods by Jeli Madi Kuyate, Namori Keita, Amadi Konate, and, again, Drissa Kone. Kone, Kuyate, and Keita clearly conform to the SML hypothesis. Kone’s mean pulse-timing ratio is 26:32:42, thus nearly identical with the 27:33:40 rate of the first échauffement from Video 1 (see above, Subsection 4.3).(43) By contrast, the difference between medium and long (second and third) pulse is small in Amadi Konate’s timing. This hints at a possible SLL variation of the SML pattern, and future research might investigate the distinctiveness and overlapping of pulse classes in rhythmic feel patterns.
[76] All of the timing patterns are stable: the standard deviations from the mean relative duration amount to only 1–2% for each pulse class. The third subpulse is more than one and a half times as long as the first one for Kone, Kuyate, and Konate; in the recording of Keita, it is nearly twice as long. Beat subdivision in manjanin échauffements proves to be strikingly uneven.
[77] Table 5 lists the timing of randomly chosen single cycles from the échauffement periods compared in Table 4. A strongly pronounced SML feel pattern is characteristic of each of them. At tempi of between 150 and 180 ternary bpm (450–540 ppm), the third pulse is between 45 and 75 ms longer than the first. The only small variation is the change from SML to SLL in Beat 4 of the Amadi Konate Trio.
[78] Figure 1 translates the figures of Table 5 into a graphic pattern: the y axis shows the pulse duration as a percentage of the normalized beat duration; the x axis plots the twelve pulses of the measured 4-beat cycles. The variation of durations is consistent: the first subpulse of each ternary beat is relatively short; the second pulse is of medium duration; the third is long.
|
Table 5. Timing of jembe échauffement cycles of four lead jembe players (manjanin) (click to enlarge) |
Figure 1. SML rhythmic feel in manjanin échauffement cycles; data taken from Table 5 (manjanin) (click to enlarge) |
[79] I have considered four lead jembe players in this subsection. They differ slightly in the nuances and degree of pronouncedness with which they realize the uneven rhythmic feel of manjanin, but scarcely differ in the feel pattern’s structure. The hypothesized SML pattern of beat subdivision, with a possible SLL variation, is stable across personal playing styles. The analysis of the dunun part (Subsection 4.7) will further support this finding.(44)
4.6 Rhythmic feel, tempo, and the lower limit for meter
Table 6. Mean timing ratio of the lead jembe in the second échauffement period from Video 1 (Cycles 206–217) (manjanin)
(click to enlarge)
[80] The timing ratios of lead jembe player Drissa Kone in Video 1 mostly range from 25:33:42 to 27:33:40. This articulation of the rhythmic feel pattern is stable over a wide range of tempos, from 135 ternary bpm (405 ppm) at the beginning of the piece to beyond 190 bpm (576 ppm) in the first échauffement analyzed above (Section 4.3). The feel pattern changes only at the upper limit of tempos. In the second échauffement period at the end of the piece (Cycles 206–217), at a tempo of beyond 200 ternary bpm (600 ppm), the mean-timing ratio is 28:36:36 (see Table 6). Despite the extreme tempo, the relative shortness of the first pulse remains stable. The difference between second (medium) and third (long) pulse, however, blurs (SML→SLL). The SLL variation of pulse duration is repeated with standard deviations of only 1–2%. The duration of the first pulse, which is as short as 84 ms on average, has a standard deviation as small as 5 ms.(45) The distinction between pulse classes is pronounced: the longest of all durations of a stroke on a first pulse is still shorter than the shortest duration of strokes on second and third pulses.
Table 7. Timing of the lead jembe in Cycle 216 (manjanin)
Tempo: 204 ternary bpm (612 ppm)
(click to enlarge)
Audio 3. manjanin final échauffement (loop of Cycle 216)
Table 8. Mean timing ratio of the second jembe in Video 1 (Cycles 2–217) (manjanin)
(click to enlarge)
Table 9. Hypothetical and empirical timing ratios of the second jembe’s accompaniment phrase in Video 1
(click to enlarge)
Figure 2. Serial data curve of the timing ratio of the second jembe in Video 1 (manjanin)
(click to enlarge)
[81] Table 7 exemplifies the timing ratio of the final échauffement period; it lists the IOIs of the third to last cycle of the piece (Cycle 216). Here, the lead jembe performs with a timing ratio of 29:35:36. Despite the furious tempo, the timing pattern is remarkably stable: the durations of notes of the same pulse class (first, second, or third subpulse) vary by only 2–7 ms; the beat duration varies by only 4 ms. Meanwhile, the difference between strokes on first and third pulses still amounts to approximately 20 ms.
[82] Audio 3 provides a loop of Cycle 216 from Video 1. It seems impossible to make out the timing pattern in detail at this tempo. Nonetheless, one can feel the rhythmic drive that results from the short first pulse.
[83] I now analyze the second jembe’s part. The accompaniment player establishes an ostinato, |S.TS.B|, in Cycle 2 and invariantly repeats it until the end. The mean-timing ratio during the five-minute recording is 60:40 (Table 8).
[84] Assuming a straight ternary timing of that phrase, one would expect a timing ratio of (33+33≈)67:33. A ratio of 27:33:40, as performed by the lead jembe in the first échauffement of Video 1, would give (27+33=)60:40 in the accompaniment part. The empirical timing ratio of the second jembe thus meets the expectation of the SML feel pattern (Table 9).
[85] Figure 2 shows the development of the second jembe’s timing ratio during Video 1. The y-axis indicates the relative duration of strokes and the x-axis plots the course of Cycles 2–217. The blue markers show the relative duration of strokes on the first pulse while the blue curve displays the trend (moving average) of the single durations to remain stable around 60%. The red markers and red moving average curve show the strokes on the third pulse being stable around 40%. The tempo in the course of the five-minute piece is continually increasing from 135 bpm (405 ppm) to 205 bpm (615 ppm). The second jembe’s pulse-timing ratio thus turns out to be independent of tempo.
Discussion: rhythmic feel, tempo, and the lower limit for meter
[86] Rhythmic feel—the cyclic variation of subpulse durations—represents a variation of the beat subdivision. Its relation to the beat tempo is thus of obvious interest. Bengtsson and Gabrielsson speculated that “systematic variations of durations ... may appear most obviously in a ‘proper’ tempo region, while they may be less pronounced or ‘destroyed’ in too slow or too rapid tempi” (Bengtsson and Gabrielsson 1977, 32). Friberg and Sundström, in their study of prominent jazz drummers’ ride cymbal playing, have shown a linear correlation between increasing tempo and flattening timing ratios (Friberg and Sundström 2002, 337). Fernando Benadon, however, studied various equally prominent jazz instrumentalists and does not support this finding: “slower tempos do not necessarily yield higher swing ratios” (Benadon 2006, 83). Accordingly, Honing and Haas (Honing and Haas 2008, 475) “found no evidence for the swing ratio to scale linearly with tempo.” The same applies to the timing ratios in the jembe parts of manjanin. In recordings of this piece, I did not find a significant correlation of increasing tempo and flattening timing ratio. Instead, the pulse-timing ratio is broadly stable across a wide range of tempos. It changes only in situations marked by a combination of two critical factors: a very fast tempo (roughly beyond 570ppm) and note groups of three or more strokes on consecutive subpulses. Since the second jembe’s accompaniment phrase consists of note groups of only two strokes, it is playable, in contrast to many lead jembe phrases, with physical ease even at the most extreme tempos. The fact that the second jembe’s timing ratio is independent of tempo suggests that the overall musical intention is to keep the SML feel pattern stable for as long as possible.
[87] In all the manjanin recordings studied, jembe players perform the cyclic variation of subpulse duration with great resolve. Even in the context of long consecutive note groups at extremely fast tempos (beyond 200 ternary bpm, or 600ppm), the uneven rhythmic feel is never ironed out. The higher tempo limit of rhythm performance does not involve a linear flattening out towards isochrony; rather, it entails a feel pattern of reduced complexity (SLL), which is still strongly non-isochronous. The two feel patterns, SML and SLL, can be represented as varieties of a common model, SFL (short, flexible, long). The most characteristic denominator of both varieties is the first pulse being consistently short.
[88] A threshold of 100 ms is widely held to represent “the lower limit for meter, that is, the shortest interval that we can hear or perform as an element of rhythmic figure” (London 2004, 27). Jazz drummers, for instance, rarely play eighth notes on the ride cymbal shorter than 100 ms; this is assumed to represent a “practical limit on tone duration that may be due to perceptual factors” (Friberg and Sundström 2002, 333). Honing and Haas (Honing and Haas 2008) do not support that limit, however.
[89] The lower limit for meter in jembe music is below 100 ms. In the two échauffement periods of Video 1, for instance, the mean duration of the short pulse is respectively 86 ms and 84 ms.(46) The ability to perform such small durations while maintaining a stable timing pattern is not restricted to athletic instrumentalists; nor is it a question of exceptional timing skills. Every reasonably skilled drummer in Bamako plays this way. The low limit for meter in jembe music reflects, I suggest, a stylistic decision about how to deal musically with a perceptual threshold phenomenon. Jembe drummers prefer pronouncedly uneven feel patterns to remain stable even at tempos that make the short pulse turn out to be so short (75–90 ms) that a pair of strokes on the short and the following pulse may merge—or come close to merging—into a flam. A flam is a double note, the second attack of which follows the first one so closely that both are perceived as one rhythmic event.(47) Gerischer reports that 50 ms is a typical IOI between the two attacks of a flam in samba drumming (Gerischer 2003, 45–46). Iyer gives 30 ms as an example for a flam in jazz drumming (Iyer 2002, 400–401). In jembe music, the tightness of flams varies a lot. Some are as short as 15–30 ms, for instance those on Pulse 1.1 of Cycles 95–117 from Video 1. Others have intervals of 30–50 ms; for instance, the double note of the opening call has an interval of 39 ms (Pulse 1.1 of Cycle 1; see Subsection 4.4). Finally, there are also flams with IOIs between 50 and 85 ms.(48) In other words, there is no timing threshold to distinguish flammed double notes and tight pairs of metric pulses in jembe music; rather, there is an overlap of flam and pulse IOIs in the range of about 70 to 90 ms. I would speculate that the resulting ambiguity of rhythmic ornament and metric pulse is musically intended; and that other musical traditions of the world might tend to respect an approximately 100 ms threshold for metric pulsation because their performers and listeners prefer to avoid such ambiguity.
4.7 Rhythmic feel across instrumental parts: the dunun
Table 10. Mean timing ratio (given as percentages of the normalized beat duration) of basic dunun phrase over 150 cycles from Video 1 (manjanin)
(click to enlarge)
Table 11. Hypothetical and empirical mean timing ratios of the first dunun’s basic phrase (manjanin)
(click to enlarge)
Table 12. Timing of the dunun in Cycle 9/10 (manjanin)
Tempo: 146 ternary bpm (439 ppm)
(click to enlarge)
[90] The analysis so far has dealt only with jembe playing. In terms of motional pattern and grouping structure, dunun playing is different, since one plays the jembe with two bare hands and the dunun with only one stick. In this subsection I show that the timing of the first dunun in manjanin is, like the jembe, based on cyclic variation of subpulse durations according to the SML hypothesis. In Video 1, the average timing ratio of the dunun’s five strokes is about 59:100:98:65:79 (see Table 10).
[91] Table 11 compares two timing expectations, one derived from isochronous pulsation, the other from the SML hypothesis, with the empirical mean ratio. According to an even ternary pulsation, the dunun phrase would show a ratio of 67:100:100:67:67. Based on the pulse-timing ratio of 27:33:40, as taken from the first jembe échauffement, the SML pattern leads to an expectation of 60:100:100:67:73 for the dunun phrase. The empirical mean-timing thus turns out to be much closer to the expectation based on the SML hypothesis than to isochronous pulsation.
[92] Based on an isochronous pulsation, the open dunun strokes would form an undifferentiated group of four roughly equidistant notes, starting on Pulse 3.3 and ending on Pulse 1.3. However, the actual timing results in a phrase that audibly groups the four open dunun strokes into two pairs, the first one on Pulses 3.3 and 4.2, and the second one on Pulses 1.1 and 1.3. The relatively long note on Pulse 4.2 segments the pairs. The first pair (on Pulses 3.3+4.2) is slightly broader than the second one (on Pulses 1.1+1.3). However, this is a subtle nuance, in contrast to the distinct grouping of the four open strokes into two pairs.
[93] To exemplify the timing of the dunun, Table 12 lists the data for a randomly chosen cycle of the dunun phrase. As an exception, this excerpt does not isolate a metric cycle, since this would cut across two dunun cycles, but starts on Pulse 3.3 of Cycle 9 and extends to Pulse 3.2 of Cycle 10.
[94] Audio 4a and 4b loop the dunun phrase of Cycle 9/10. In both Audio 4a, which displays the full ensemble texture, and Audio 4b, which isolates the dunun track, the grouping of the four open strokes in two pairs is clearly audible.
|
Audio 4a. manjanin |
Audio 4b. manjanin |
[95] In Video 1, the dunun stroke on Pulse 4.2 is on average more than 60 ms longer than the stroke on Pulse 1.1. Its relative duration of 79% even surpasses the 73% predicted by the SML hypothesis. The grouping of the open dunun strokes into two pairs seems to be the dunun player’s musical (if unconscious) intention. He achieves the expressive timing of his phrase by the local rhythmic overstatement of a detail of the recurring feel pattern. In Section 4.4 above, I have shown the same for the lead jembe’s call.
[96] Table 13 and Figure 3 compare the timing of Cycle 9/10 of Video 1 (taken from Table 12) with a broad sample of a further nine dunun players of independent ensembles. All of them show the same cyclic variation of durations—medium duration of the stroke on Pulse 3.3, long duration of the stroke on Pulse 4.2, and short duration of the stroke on Pulse 1.1—based on the hypothesized SML feel pattern. The wide consistency of the dunun’s feel across personal and regional playing styles is obvious. Many of the players share the inclination towards segmenting the four open strokes into two pairs by a particularly long duration of the stroke on Pulse 4.2, exceeding the 73% expected from the SML hypothesis. With some, this variation of the feel pattern is expressive (Amadi Konate, 81%; Namakan Keita, 83%). Others largely conform to the SML expectation without expressive variation (S. Sidibe Trio, Mady Keita Quartet, Troupe Folklorique du Mali).
|
Table 13. Timing of randomly chosen single cycles of ten dunun players (manjanin) (click to enlarge) |
Figure 3. Timing ratios of the basic dunun phrase of ten different players; data taken from Table 13 (manjanin) (click to enlarge) |
4.8 Summary
[97] The analysis shows that a strongly non-isochronous subpulse, which subdivides an approximately isochronous beat, is essential to the timing of manjanin. The subpulse is consistently patterned according to an SFL model of ternary subdivision (short, flexible, long). The main pattern of this feel type is SML (short, medium, long) and a second variety is SLL (short, long, long). The feel is characteristic not only of specific phrases, particular grouping structures, single instrumental parts, or individual playing styles. Rather, it is inherent in the meter of the piece. Thus, I describe the meter of manjanin as 4-beat/SFL.
5 Four common rhythmic feel types: a rough survey
[98] Most standard compositions of Bamako jembe music display stable rhythmic feel patterns. I have found four common feel types (Table 14), which I will introduce in the subsections below. One of these is of specific, inflexible structure, while the others each have two or three varieties. In the latter cases I give (in italics) the type (structural model), which includes flexible pulses, and I also list the patterns (actual varieties), with all subpulses specified as either short, medium or long. Only one piece, maraka-dòn, often shows a “straight” feel based on roughly isochronous subdivision.
[99] David Temperley argues that in jazz music, “one effect of swing tempo is to provide a constant reminder to the listener of where the strong eighth-note beats are (since the strong eighth-note beats are longer than the weak ones)” (Temperley 2004, 324; parenthesis in the original). In jembe music, beat perception does not rely on long pulses marking the beat. While there are feel patterns that indeed have long pulses falling on the beat (LS and LFF), short pulses mark the beat in others (SFL and SFLF). From a comparative perspective, a hypothetical preference rule such as “place long subpulses on main beats” obviously cannot accommodate the empirical variety in the design of rhythmic feel patterns.
5.1 The LSLS (or LS) feel pattern
Example 3. Yamadu Dunbia
(click to enlarge)
Audio 5a. woloso-dòn (loop of a one cycle excerpt;
corresponds to Cycle 22 of Audio 5b). Jembe: Yamadu Dunbia. Dunun: Madu Jakite. Recording: R. Polak, Bamako 1995 (taken from Dunbia et al. 2006-disc)
Audio 5b. woloso-dòn (context of the excerpt in 5a)
(click to hear the audio)
Table 15. Timing of the jembe in Audio 5a (woloso-dón)
(click to enlarge)
Example 4. Jeli Madi Kuyate
(click to enlarge)
Table 16. Timing of the jembe in Audio 6a (sunun)
(click to enlarge)
[100] The quaternary LSLS feel pattern often occurs in 4-beat/16-pulse metric cycles. Provided the tempo is slow, one might alternatively hear binary 8-beat/16-pulse cycles. I choose to analyze the LSLS feel in its optional binary representation (LS). Its timing ratios are thus more directly comparable to the LS swing feel of jazz music. In addition, the binary representation better serves the need to explain how some compositions synchronize the LS(LS) feel with a ternary SML feel (see Subsection 6.1 below).
[101] I exemplify the LS feel pattern in jembe music with a recording of the composition woloso-dòn. Woloso-dòn means “serfs’ dance.” Yamadu Dunbia (1917–2002), who was among the pioneers of professional jembe playing in Bamako in the 1960s and 70s, belonged to this lowest stratum of formerly endogamous status groups in Mande society (see Example 3). He always performed the serfs’ dance—his own piece, in the sense that it is dedicated to his own status group—with particular empathy and verve.
[102] Audio 5a presents an 8-beat/16-pulse cycle as a loop. In this cycle, Dunbia performs a regular series of strokes working out the fast pulse. The mean-timing ratio is about 54:46 (see Table 15).
[103] Audio 5b is a two-minute passage of the piece from which the excerpt in 5a is taken. One can thus evaluate the degree to which the measured cycle is typical. The excerpt of Audio 5a corresponds to Cycle 22 of Audio 5b. While Audio 5b is an audio recording, I nevertheless provide it in video format, to list cycle numbers in the image.
[104] According to Benadon’s article on beat subdivision in jazz music, it is in the range of about 55:45 to 58:42 that “soloists aim to articulate a feeling of long-shortness at its ‘mildest’ possible state” (Benadon 2006, 88).(49) Dunbia’s LS timing ratios in woloso-dòn often are slightly milder; they typically range from 53:47 to 58:42.
5.2 The SFLF feel type
[105] The quaternary SFLF feel pattern, unlike LSLS, is not reducible to a binary form. Of the four pulses that subdivide each beat, the first is short (15–20%) and the third is long (30–35%). There is some flexibility to the second and fourth pulses. Usually, they are given medium durations. The main variety of the SFLF pattern is thus SMLM. SSLS and SLLL occur as well.
[106] I illustrate the SFLF type with a recording of the composition sunun. The performer, Jeli Madi Kuyate (see Example 4), was born in 1949 some 80 km south of Bamako. He started performing at the age of six, migrated to Bamako when he was twelve, and has been working as a professional jembe player ever since. He has been affiliated with the state-sponsored National Ballets of Mali since the late 1960s.
[107] In Audio 6a (Cycle 32 of Audio 6b), Kuyate performs a standard phrase that corresponds to a specific dance movement. Both his jembe part and the dunun, which plays the basic timeline phrase of sunun, show a strikingly uneven feel; in the jembe, the first pulse is consistently below 20%, and the third pulse is around or above 30% (Table 16). In Beat 4, the shortness of the first pulse is particularly pronounced (Pulse 4.1=15%). Its duration of only 75 ms allows it to merge, in the listener’s perception, with the stroke on Pulse 4.2, creating a flammed double note. In sunun, as well as in other compositions with the SFLF feel type, this merging of the first (short) and second pulse can occur regularly. Thus, the structure of beat subdivision can change to a ternary feel. I will analyze this synchronization, or transformation, of ternary and quaternary feels in Section 6.2.
|
Audio 6a. sunun (loop of a one-cycle excerpt; |
Audio 6b. sunun (context of the excerpt in 6a) (click to hear the audio) |
[108] There is frequent variation of timing patterns in Kuyate’s version of sunun (Audio 6b). For instance, the jembe performs various expressive timing patterns in the beginning of the piece and it does not establish the SFLF feel consistently until Cycle 24.(50)
[109] The dunun also suggests ambiguity of subdivision in sunun. Its main note group, heard from a quaternary perspective, consists of two pairs of open strokes (on Pulses 4.4+1.1 and 1.3+1.4). Mechanically even timing would give a 25% ratio between the two notes of a pair, and a 50% ratio between the pairs. In real performance, however, all the ratios of these open dunun strokes come closer to the 33% of an isochronous ternary feel; in Audio 6a (Table 16), these ratios are 35% (stroke on Pulse 4.4), 39% (on Pulse 1.1), and 32% (on Pulse 1.3).
5.3 The SFL feel type
[110] The SFL model of rhythmic feel (short, flexible, long) has already been analyzed in Section 4. Here I reconsider its representation in the example of another piece, called suku (also called soli). Associated with the social occasion of circumcision rituals, it ranks among the most widespread and culturally valued standard compositions of jembe music. The player is Jeli Madi Kuyate, who also performed the example of sunun above.
[111] In suku, just like in manjanin, SML is the most common variety of the SFL model. The duration of the second pulse is more flexible in suku than in manjanin, however. SLL is a second variety that appears frequently. In the liner notes to an ethnographic CD, Johannes Beer offered a rough description, based on analysis by ear, of rhythmic feels in the playing of Famoudou Konate, one of the most prominent representatives of jembe music from Guinea (Beer 1991, 12–13). He modeled the rhythmic feel of pieces such as manjanin and suku as SLM (short, long, medium). However, according to my spot check measurements of the CD, which Beer had annotated (Konate 1991), manjanin and suku mostly show SML or SLL feels as found in the styles from neighboring southern Mali.
|
Audio 7a. suku (loop of an excerpt; |
Audio 7b. suku (context of the excerpt in 7a) (click to hear the audio) |
[112] Audio 7a presents a looped excerpt taken from Jeli Madi Kuyate’s soloistic introduction to a duet performance of suku that I recorded in 1995. It corresponds to Cycle 2 in Audio 7b. The absence of the dunun part is a handicap to timing reference and metric orientation. In Audio 7a, I therefore add clicks (snare drum rim sound) to mark the beat during the first two loops of the 4-beat cycle. In the following loops, I put the click on Beat 1 alone and fade it out. In Audio 7b, I add clicks to the four on-beats of Cycle 1 (preceding the excerpt), and then to the starting and endpoints of the excerpt (Beat 1 of Cycles 2 and 3).
[113] The jembe in Audio 7a performs one of the most common groove phrases for suku; it follows the SML feel pattern with a pronouncedly strong timing ratio of, on average, 22:34:44 (see Table 17).
5.4 The LFF feel type
Example 5. Jaraba Jakite performing for a solo dancer at a wedding celebration
(click to enlarge)
Table 18. Timing of the jembe in Audio 8a (sumalen)
(click to enlarge)
[114] The relative length of the first pulse characterizes the LFF type of rhythmic feel and clearly distinguishes it from the SFL model. The LFF type is open to some variation in the relative duration of the second and third pulse. LMS, LSS, and LSM are all common manifestations of the model. Beer’s description of LSM in Guinean jembe music thus agrees with one of the three varieties I found in southern Mali (Beer 1991, 12–13).(51)
[115] I illustrate the LFF model with the example of the composition sumalen.(52) The recorded artist, Jaraba Jakite (1953–2005), originated from Kourouba, a small town some one hundred kilometers south of Bamako, which is also Drissa Kone’s hometown. Jakite moved to Bamako in 1984, after which he successfully specialized in performing at local family celebrations (see Example 5).
[116] In Audio 8a, Jakite performs a standard groove phrase, which he often used to accompany a solemn formation dance at the modest tempos typical of the beginning of a piece. The jembe shows an LMS feel during Beats 1, 2 and 3; on Beat 4, however, it shows an LSM pattern (Table 18). This variation of the regular LMS feel is related to rhythmic grouping structure—the jembe player applies it in all phrases that have a note group of two open tones on Pulses 4.4 and 1.1 (Cycles 1–6 and 10–12, for instance). Meanwhile, the long duration of the first pulse is stable at about 40% of the normalized beat duration. The excerpt measured in Table 18 (Audio 8a) is taken from Cycle 3 of Audio 8b.
|
Audio 8a. sumalen (loop of an excerpt; |
Audio 8b. sumalen (context of the excerpt in 8a) (click to hear the audio) |
5.5 Rhythmic feels and the “many meters hypothesis”
[117] The two ternary types of rhythmic feel in jembe music from Mali, SFL and LFF, are unmistakable and non-interchangeable. Specific patterns are sometimes interchangeable with other patterns of the same broader feel type (SML with SLL; LMS with LSS or LSM), but are non-interchangeable with patterns of a different feel type.
[118] Compositions such as manjanin, suku, and sumalen share the ternary 4-beat/12-pulse metric cycle. However, the meters of the respective jembe pieces are qualitatively different from each other; their distinct rhythmic feels produce different metric feelings. This is a case for Justin London’s (2004) “many meters hypothesis,” according to which stable timing patterns can distinguish individual meters from a common metric type.
[119] Staff notation commonly gives the 4-beat/12-pulse metric type in 12/8 time, or two measures of 6/8. In graphic notation, the metric cycle is sometimes specified by merely giving the quantity of subpulses, in this case 12.(53) Aiming at representing the difference between the two 4-beat/12-pulse meters of jembe music by specific time signatures, I suggest designating the meter of manjanin and suku as 4-beat/SFL (see Subsection 4.8), and the meter of sumalen as 4-beat/LFF.
[120] Pieces of the same feel and meter also share compositional macro-structures. For instance, they often share the same accompaniment phrases of the second jembe and dunun, and the lead jembe’s essential accent and melodic structures. Even wholesale phrases and periods, such as échauffements and breaks, are applied across individual compositions of the same feel. Conversely, pieces of different feels have relatively few characteristics in common. Rhythmic feel is one of several features that distinguish clusters of structurally related compositions.
[121] The situation is different with the binary and quaternary feel patterns (LS and SFLF). In some pieces, one of these two timing patterns rules (for example, LS in Audio 5b of woloso-dòn). However, there is frequent variation and change of feels in others, as in Audio 6b of the piece sunun. Some pieces in the Malian jembe repertoire systematically use both LS and SFLF feel types.(54) The binary and quaternary feels thus do not distinguish meters and clusters of compositions as clearly as is the case with the ternary metric type.
6 The metric nesting of rhythmic feels
[122] In this section, I show that beat subdivision in jembe music is often ambiguous. In many compositions, two feels (one ternary and one binary/quaternary) suggest themselves at the same time. How can different feels work simultaneously without producing permanent metric dissonance? The clue to the answer lies in their patterned variation of subpulse duration.
6.1 The nested LS/SFL feel system in woloso-dòn
Figure 4. Synchronization of LS and SFL feel types in contrast to isochronous binary and ternary pulses
(click to enlarge)
[123] A few pieces of the standard repertoire systematically synchronize the binary LS feel with the ternary SFL type.(55) LS can be transformed into SFL by regularly inserting an extra stroke early in the duration of the first (long) pulse of LS. Conversely, SFL can be transformed into LS by regularly not placing strokes on the second (medium) pulse of SFL. Figure 4 provides a model of the nesting, based on hypothetical timing ratios as taken from the analyses in Sections 5.1 and 5.3.
[124] The ambiguity of density referents in the nested LS/SFL feel system contributes to the hierarchic depth of meter. Due to the elegant structure of nested feel patterns, this does not disturb the metric system. It avoids metric dissonance by taking advantage of the nearly simultaneous onsets of the second pulse of the LS feel and the third pulse of the SFL feel. SFL triplets flow as smoothly in and out of the binary LS feel as double-time diminution does in roughly isochronous feels. By contrast, an isochronous binary pulsation in phase with an isochronous ternary one, when permanently applied, would result in permanent metric dissonance, because the second binary pulse would fall midway between the second and third ternary pulses (see Figure 4).
Video 2. woloso-dón
(click to view)
Table 19. Timing of the lead jembe in Cycle 8 from Video 2 (woloso-dón)
(click to enlarge)
[125] For an example of the nested LS/SFL feel system, I return to the composition woloso-dòn, which I have shown in Section 5.1 to be set in a binary 8-beat/LS meter.(56) However, only mature lead players, such as Yamadu Dunbia (Audio 5b), succeed in using this binary swing feel without more than sparse ornamental excursions. It has become popular in Bamako to set the lead jembe in a ternary feel. Most present-day players treat woloso-dòn as based on an 8-beat/SFL meter. They borrow accent structures, phrases, improvisational models, and ornamental techniques from 4-beat/SFL compositions, such as manjanin. Video 2 presents as an example a three-and-a-half-minute performance by the Drissa Kone Quartet.(57) The tempo starts at 106 ternary bpm (318 ppm) and reaches 185 bpm (555 ppm) by the end of the piece.
[126] The ternary feel SFL type is present almost throughout Video 2. In Cycle 8, for instance, the lead jembe performs a standard phrase with a pulse-timing ratio of about 25:33:42 (see Table 19).(58)
[127] The ternary timing ratio of 25:33:42 conforms to the proportions in unambiguously SFL compositions, such as manjanin and suku. A further similarity is the specific relation of rhythmic feel, rhythmic grouping, and expressive timing: the shortness of the first pulse is exceptionally pronounced in the strokes on Pulses 4.1 (18%) and 8.1 (19%).(59) As in the jembe call of manjanin (Subsection 4.4), this articulates the end of the respective note groups. Again, a selective local strengthening of the recurring feel pattern achieves expressive timing.
[128] Audio 9a loops Cycle 8 from Video 2, measured above in Table 19; Audio 9b isolates the lead jembe in that loop. In both examples, the SFL feel type, as well as its expressive variation at the end of note groups, are recognizable.
|
Audio 9a. Ternary version of woloso-dòn |
Audio 9b. Ternary version of woloso-dòn |
Audio 9c. Ensemble groove in ternary version of woloso-dòn
(loop of Cycle 8; accompaniment parts isolated)
Table 20. Timing of the second jembe in Cycle 8 (woloso-dón)
(click to enlarge)
[129] The lead jembe creates a ternary metric context that strongly invites the listener to hear the accompaniment parts also in a ternary feel. Audio 9c again loops Cycle 8 of Video 2. This time, the lead jembe track is muted, which isolates the accompaniment groove and in this context, a binary (swing) feel suggests itself.
[130] The second jembe in Cycle 8 (Audio 9a/c) has a timing ratio of 58:42 (Table 20). This is identical with the mean-timing ratio during the three and a half minutes of Video 2. The second jembe’s ratio is stable from the very beginning to the end of the piece with a standard deviation of only 2%. As was the case in Video 1 of manjanin, the feel of the accompaniment groove is independent of the drastic increase in tempo (106–185 bpm).
[131] In the ternary version of woloso-dòn (Video 2), the second jembe’s timing ratio (58:42) is only slightly softer than in the unambiguously ternary piece manjanin (60:40). On the other hand, it is only slightly stronger than in the binary version of woloso-dòn (54:56), as discussed in Section 5.1. In fact, it would not create metric dissonance in either feel.
[132] Many teaching methods and notations of jazz music conceive of the eighth-note swing feel (LS) as a triplet shuffle. Benadon argues against this approach (Benadon 2006, 90–91). His data display swing ratios with a preponderance in the range of roughly 55:45 to 58:42, thus seemingly far from a ternary subdivision (67:33, given the assumption of isochrony). In jembe music, however, the same timing ratios would not speak against a ternary interpretation. In a composition such as woloso-dòn, the reference for triplets is not isochronous ternary subdivision, but the SFL feel. Timing ratios of binary LS and ternary SFL, however, do overlap.
6.2 The nested LFF/SFLF feel system in sumalen
Figure 5. Synchronization of LFF and SFLF feel patterns in contrast to isochronous ternary and quaternary subpulses
(click to enlarge)
Video 3. sumalen
(click to view)
Table 21. Mean timing of second jembe in Video 3 (sumalen)
(click to enlarge)
Table 22. Timing of the lead jembe in Cycle 43 from Video 3 (sumalen)
(click to enlarge)
Table 23. Timing of the lead jembe in Cycle 46 from Video 3 (sumalen)
(click to enlarge)
Table 24. Timing of the jembe in Cycle 49 from Video 3 (sumalen)
(click to enlarge)
[133] In this subsection, I analyze the nesting of ternary (LFF) and quaternary (SFLF) subdivisions.(60) The principle here is the same as in the nested LS/SFL feel system. The resulting metric structure is different, however, and concerns a different family of structurally related compositions.
[134] Many LFF compositions synchronize their ternary feel with the quaternary SFLF type by regularly inserting an extra stroke early in the long (first) pulse.(61) For a schematic representation (Figure 5), I take timing ratios from the audio examples of Sections 5.2 and 5.4.
[135] The nesting of the non-isochronous LFF and SFLF beat subdivisions, just like the LS/SFL feel system, does not produce metric dissonance. The quaternary pulsation of the SFLF type meshes smoothly with the ternary LFF feel. Video 3 presents the example of a trio recording of sumalen, performed again by Drissa Kone and his ensemble. The one-and-a-half-minute piece starts at a tempo of 104 bpm and ends at 139 bpm.
[136] In Video 3, the dunun and second jembe both use an unambiguously ternary feel throughout. The second jembe’s timing, for instance, shows a stable LSS feel with a timing ratio of about 40:30:30 (see Table 21).
[137] The lead jembe often performs an LFF feel and thus supports the ternary pulse of the accompaniment groove. Extra strokes put into the long duration of the first pulse sometimes follow so closely after the regular on-beat stroke that the resulting impression is of a flammed double note. Equally often, however, the trend is towards a slightly smoother, more even distribution of the four strokes. Eventually one can hear the second stroke of the double note as a subpulse in its own right; a quaternary pulsation emerges.
[138] In the following, I analyze the lead jembe’s transformation of ternary into quaternary subdivision in the final section of Video 3. This section consists of a sequence of three periods: a pre-échauffement (Cycles 43–47); the main échauffement (Cycles 48–51), which brings the piece to its climax; and the final break (Cycle 52), which marks the end of the piece.
[139] The phrase for the pre-échauffement is of a ternary feel. In Cycle 43, it shows the LMS pattern (Table 22). In Beat 1, the durational difference between Pulses 1.1 and 1.2 is marginally small (8 ms); this hints at a possible LLS variety of the LFF type. In Beats 2–4, however, the LMS pattern is pronounced. For a quick listening reference, Audio 10a presents a loop of Cycle 43. Audio 10b mutes the accompaniment parts making the lead jembe’s timing more clearly comprehensible.
|
Audio 10a. sumalen (loop of Cycle 43 from Video 3) |
Audio 10b. sumalen (loop of Cycle 43; first jembe part isolated) |
[140] In Cycles 44–47, lead jembe player Drissa Kone inserts extra strokes closely after Beats 2 and 4 (Pulses 2.1 and 4.1). He thus systematically embellishes the basic phrase of Cycle 43. The IOIs between the on-beat and extra strokes range from 50 to 70 ms. The resulting impression is of flammed double notes, not of additional subpulses. The ternary feel (LFF) is thus stable. As an example, Table 23 lists the timing of Cycle 46, which can be heard by listening to Audio 11a/b below.
|
Audio 11a. sumalen (loop of Cycle 46 from Video 3) |
Audio 11b. sumalen (loop of Cycle 46; first jembe part isolated) |
[141] The main échauffement (Cycles 48 to 51) adds an extra stroke not only to Beats 2 and 4, but also to each on-beat (Pulses 1.1, 2.1, 3.1, and 4.1). The IOIs between the on-beat and extra stroke are slightly longer than in the pre-échauffement; they range from 78 to 94 ms. One can now hear the extra stroke as representing a distinct metric subpulse of its own right. The emerging quaternary subdivision shows the SFLF type, exactly as illustrated above (Section 5.2) in the example of sunun. The mean-timing ratio during the main échauffement period is 19:25:30:26. Cycle 49, for instance, shows a ratio of 20:25:30:25 (see Table 24; listen to Audio 12).
|
Audio 12a. Échauffement in sumalen |
Audio 12b. Échauffement in sumalen |
[142] Often, a particular arrangement of hand patterns, which is characteristic of the traditional jembe playing technique from Mali, underpins performances of the nested LFF/SFLF feel system. Some phrases of LFF compositions are usually performed with RRL hand patterns—right, right, left, right, right, left, and so forth, for right-handers playing out the subpulse.(62) The left hand is thus free to hit between the two subsequent right-hand strokes on the first and second pulses with much ease, turning RRL into R(L)RL. Moreover, this possibility of regularly inserting extra strokes into the first pulse’s duration facilitates the change to the quaternary SFLF feel type (Figure 6).
[143] Video 3 displays two examples of RRL hand patterns. First, the second jembe player, Sedu Balo, realizes the ostinato |S.SSTT| as |R.LRRL| throughout. Second, the lead player, Drissa Kone, uses the RRL/R(L)RL nested hand patterns in the final échauffement period analyzed above. He performs the pre-échauffement with the hand pattern RRL (Cycle 43), or R(L)RL (Cycles 44–47) (see Table 25). The seamless LFF→SFLF transformation of subdivision in the beginning of the main échauffement (from Cycle 48) is thus pre-figured; the quaternary feel is latently present already in the motional pattern of the ternary pre-échauffement.
[144] Video 4 provides the final period of Video 3 (Cycles 43–52) in slow motion (at 1/4 speed). One can thus more easily follow the jembe players’ hand patterns. For metric orientation and reference to the original, I audibly indicate the beat with clicks and count the numbers of cycles and beats in the image. During the pre-échauffement, the lead jembe consistently marks the beat with a right hand bass tone. The bass tones are recognizable as strokes in the middle of the drumhead rather than on the rim (Cycles 43–47).
[145] Hand patterns are more open to individual choice than feel patterns and some players make use of the RRL hand pattern more often than others. However, in SFL pieces such as suku or manjanin, nobody ever prefers RRL to the regular standard hand pattern for ternary meters, RLRLRL.(63) The advantage of RRL is the elegant option it offers for giving the first pulse a long duration, or subdividing it further. Yet, in SFL compositions, the lengthening or further subdivision of the first pulse does not make metric sense, because its duration is short. This is, I hold, why it is not used in this metric context. In other words, the nested RRL/R(L)RL hand pattern is designed to embody the nested LFF/SFLF feel system.
6.3 Summary
[146] Several jembe music compositions from Mali systematically make simultaneous use of two different but related beat subdivisions. Such nesting of feels adds to the meter’s hierarchic depth. It is organized as a densification, or thinning, respectively, of subdivisions:
- in the LS/SFL feel system
- binary can be synchronized with, or transformed into, ternary subdivision (2+1=3)
- ternary can be synchronized with, or transformed into, binary subdivision (3-1=2)
- in the LFF/SFLF feel system
- ternary can be synchronized with, or transformed into, quaternary subdivision (3+1=4)
- quaternary can be synchronized with, and transformed into, ternary subdivision (4-1=3)
[147] The extra strokes that achieve systematic densification, or thinning (by omitting strokes), are placed according to two essential timing strategies:
- the extra stroke cuts the long subpulse of a feel pattern; this applies to the LS and LFF patterns, which have the long subpulse as first pulse (on-beat)
- the extra stroke is placed relatively early in the duration of the first subpulse; this results in feel patterns with a short first pulse (SFL and SFLF); if the extra stroke is placed very early after the first subpulse, there can be ambiguity between metric densification of the fast pulsation and rhythmic embellishment (flam)
[148] The stable patterning of non-isochronous subpulse streams is a prerequisite condition of the synchronization and transformation of nested subdivisions in jembe music. Much music theory assumes nominal isochrony of metric beat subdivision. Some theories attribute primary significance to the number of nominally isochronous subpulses per cycle as an “elementary” (Kubik 1994) or “cardinal” (London 2004) property of meter. As I have demonstrated, jembe music from Mali is not subject to these assumptions.
7 Metric feel and expressive timing
[149] Expressive timing is usually defined as rhythmic, often phrase-oriented, variation of a durational norm. An essential qualifier of the concept is the definition of that norm. The common understanding of expressive timing as deviation from nominally (or categorically) isochronous pulsation is useful primarily in the context of musical styles that employ roughly isochronous meters. Analogously, the view of expressive timing as performative deviation from the nominal durational values of notation is relevant mainly for those musical traditions that rely on the writing and reading of music. From a culture-sensitive perspective, the common understandings of expressive timing emerge as limited. It is more universally valid, I suggest, to conceive of expressive timing as rhythmic variation of metric expectation (cf. Repp 1997). In jembe music from Mali, the characterization of metric types by cyclic variations of subpulse durations is inherent in the metric system. In such a context, what I have so far called rhythmic feel amounts to metric feel. Pulse-based metric feel, then, is not an instance of departure for expressive variation, but rather is the point of departure for expressive variation.
Rainer Polak
Bayreuth, Germany
Independent Scholar
rainer.polak@t-online.de
Works Cited
Agawu, Kofi. 2003. Representing African Music: Postcolonial Notes, Queries, Positions. New York: Routledge.
—————. 2006. “Structural Analysis or Cultural Analysis? Competing Perspectives on the ‘Standard Pattern’ of West African Rhythm.” Journal of the American Musicological Society 59, no. 1: 1–46.
Anku, Willi. 2000. “Circles and Time: A Theory of Structural Organization of Rhythm in African Music.” Music Theory Online 6.1.
Arom, Simha. 1984. “Structuration du Temps dans les Musiques d’Afrique Centrale.” Revue de Musicologie 70, no. 1: 5–36.
Beer, Johannes. 1991. “Trommelrhythmen der Malinke-Hamana/Guinea.” In Rhythmen der Malinke, ed. F. Konate (liner notes). Berlin: Museum für Völkerkunde.
Benadon, Fernando. 2006. “Slicing the Beat: Jazz Eighth-Notes as Expressive Microrhythm.” Ethnomusicology 50, no. 1: 73–98.
—————. 2007. “Commentary on Matthew W. Butterfield’'s ‘The Power of Anacrusis.’” Music Theory Online 13.1.
—————. 2009. “Time Warps in Early Jazz.” Music Theory Spectrum 31, no. 1: 1–25.
Bengtsson, Ingmar. 1975. “Empirische Rhythmusforschung in Uppsala.” Hamburger Jahrbuch für Musikwissenschaft 1: 195–219.
—————. 1987. “Notation, Motion and Perception: Some Aspects of Musical Rhythm.” In Action and Perception in Rhythm and Music, ed. A. Gabrielsson. Stockholm, Royal Swedish Academy of Music, 69–80.
Bengtsson, Ingmar, and Alf Gabrielsson. 1977. “Rhythm Research in Uppsala.” Music, Room, and Acoustics. Stockholm: Royal Swedish Academy of Music, 19–56.
Bengtsson, Ingmar, P.-A. Tove, and S.-M. Thorsén. 1972. “Sound Analysis Equipment and Rhythm Research Ideas at the Institute of Musicology in Uppsala.” In Bericht über die 3. Internationale Arbeitstagung der Study Group on Folk Musical Instruments des International Folk Music Council in Stockholm 1969 (Studia instrumentorum musicae popularis 2), ed. Erich Stockmann. Stockholm: Musikhistoriska Museet, 53–76.
Berliner, Paul. 1981. The Soul of Mbira. Berkeley: University of California Press.
Bilmes, Jeffrey A. 1993. “Timing is of the Essence: Perceptual and Computational Techniques for Representing, Learning, and Reproducing Expressive Timing in Percussive Rhythm.” Masters Thesis, Massachusetts Institute of Technology.
Butler, Mark J. 2001. “Turning the Beat Around: Reinterpretation, Metrical Dissonance, and Asymmetry in Electronic Dance Music.” Music Theory Online 7.6.
—————. 2006. Unlocking the Groove: Rhythm, Meter, and Musical Design in Electronic Dance Music. Bloomington and Indianapolis: Indiana University Press.
Butterfield, Matthew W. 2006. “The Power of Anacrusis: Engendered Feeling in Groove-Based Musics.” Music Theory Online 12.4.
—————. 2007. “Response to Fernando Benadon.” Music Theory Online 13.3.
—————. 2010. “Participatory Discrepancies and the Perception of Beats in Jazz.” Music Perception 27, no. 3: 157–175.
Carl, Florian. 2004. Was bedeutet uns Afrika? Zur Darstellung afrikanischer Musik im deutschsprachigen Diskurs des 19. und frühen 20. Jahrhunderts. Münster: Lit-Verlag.
Charry, Eric S. 2000. Mande Music: Traditional and Modern Music of the Maninka and Mandinka of Western Africa. Chicago and London: University of Chicago Press.
Chernoff, John M. 1979. African Rhythm and African Sensibility: Aesthetics and Social Action in African Musical Idioms. Chicago: University of Chicago Press.
Clarke, Eric F. 1987. “Categorical Rhythm Perception: An Ecological Perspective.” In Action and Perception in Rhythm and Music, ed. A. Gabrielsson. Stockholm: Royal Swedish Academy of Music, 19–34.
—————. 1999. “Rhythm and Timing in Music.” In The Psychology of Music, 2nd ed., ed. D. Deutsch. San Diego: Academic Press, 473–500.
Collier, Geoffrey L., and James L. Collier. 2002. “A Study of Timing in Two Louis Armstrong Solos.” Music Perception 19, no. 3: 463–83.
Doumbia, Abdoul, and Matthew Wirzbicki. 2005. Anke Djé Anke Bé: Djembe and Dounou Music from Mali, West Africa. Self-published.
Elsner, Jürgen. 1990. “Der Rhythmus Insiraf: Zum Problem quantitativer Rhythmik.” In Rhythmik und Metrik in traditionellen Musikkulturen, ed. Oskár Elschek. Bratislava: VEDA, 239–49.
Erlmann, Veit. 2004. “Resisting Sameness: À Propos Kofi Agawu’s Representing African Music.” Music Theory Spectrum 26, no. 2: 291–304.
Fraisse, Paul. 1982. “Rhythm and Tempo.” In The Psychology of Music, 1st ed., ed. D. Deutsch. San Diego: Academic Press, 149–80.
Friberg, Anders, and Andreas Sundström. 2002. “Swing Ratios and Ensemble Timing in Jazz Performance: Evidence for a Common Rhythmic Pattern.” Music Perception 19, no. 3: 333–49.
Gerischer, Christiane. 2003. O Suingue Baiano: Mikrorhythmische Phänomene in baianischer Perkussion. Frankfurt am Main: Peter Lang.
—————. 2006. “Suingue Baiano: Rhythmic Feeling and Microrhythmic Phenomena in Brazilian Percussion.” Ethnomusicology 50, no. 1: 99–119.
Honing, Henkjan and W. Bas de Haas. 2008. “Swing Once More: Relating Timing and Tempo in Expert Jazz Drumming.” Music Perception 25, no. 5: 471–476.
Huron, David. 1988. Review of Action and Perception in Rhythm and Music, edited by Alf Gabrielsson. Psychology of Music 16, no. 2: 156–62.
Iyer, Vijay. 2002. “Embodied Mind, Situated Cognition, and Expressive Microtiming in African-American Music.” Music Perception 19, no. 3: 387–414.
Kauffman, Robert. 1980. “African Rhythm: A Reassessment.” Ethnomusicology 24, no. 3: 393–415.
Keil, Charles. 1995. “The Theory of Participatory Discrepancies: A Progress Report.” Ethnomusicology 39, no. 1: 1–20.
Knight, Roderic C. 1973. “Mandinka Jaliya.” PhD diss., UCLA.
Koetting, James. 1970. “The Analysis and Notation of West African Drum Ensemble Music.” Selected Reports in Ethnomusicology 1, no. 3: 116–46.
Kroier, Hans. 1992. “Die Rumba in Matanzas (West Kuba).” Magistral Thesis, Freie Universität Berlin: Unpublished manuscript.
Kubik, Gerhard. 1972. “Transcription of African Music from Silent Film: Theory and Methods.” African Music 5, no. 2: 28–39.
—————. (1988). “Einige Grundbegriffe und -konzepte der afrikanischen Musikforschung.” In Zum Verstehen Afrikanischer Musik. Leipzig: Reclam, 52–113.
—————. 1994. Theory of African Music, Vol. 1. Wilhelmshaven: Florian Noetzel.
—————. 1999. Africa and the Blues. Jackson: University of Mississippi Press.
Locke, David. 1982. “Principles of Offbeat Timing and Cross-Rhythm in Southern Eve Dance Drumming.” Ethnomusicology 26, no. 2: 217–46.
—————. 1987. Drum Gahu: An Introduction to African Rhythm. Tempe, AZ: White Cliffs Media.
—————. 1992. Kpegisu: A War Drum of the Ewe. Tempe, AZ: White Cliffs Media.
—————. 2009. “Simultaneous Multidimensionality in African Music.” African Music 8, no. 3: 8–37.
—————. 2010. “Yewevu in the Metric Matrix.” Music Theory Online 16.4.
London, Justin. 2004. Hearing in Time: Psychological Aspects of Musical Meter. Oxford: Oxford University Press.
Moelants, Dirk. 1997. “A Framework for the Subsymbolic Description of Meter.” In Music, Gestalt, and Computing, ed. Marc Leman. Studies in Cognitive and Systematic Musicology. Berlin: Springer, 263–76.
—————. 2008. “‘Notes Inégales’ in Contemporary Performance Practice.” In The 10th International Conference on Music Perception and Cognition. Conference manuscript.
Merriam, Alan P. 1982. “African Musical Rhythm and Time Reckoning.” In African Music in Perspective. New York: Garland, 443–61.
Nzewi, Meki E. 1974. “Melorhythm Essence and Hot Rhythm in Nigerian Folk.” The Black Perspective in Music 2, no. 1: 23–28.
—————. 1997. African Music: Theoretical Content and Creative Continuum. The Culture-Exponent’s Definitions. Oldershausen: Institut für Didaktik populärer Musik.
Pantaleoni, Hewitt. 1972. “Three Principles of Timing in Anlo Drumming.” African Music 5, no. 2: 50–62.
Pfleiderer, Martin. 2003. “The Study of Rhythm in Popular Music: Approaches and Empirical Results.” In Proceedings of the 5th Triennal Conference of the European Society for the Cognitive Sciences of Music (ESCOM), ed. Reinhard Kopiez, Andreas C. Lehmann, Irving Wolther, and Christian Wolf, (CD-Rom). Hanover: 38–41.
—————. 2006. Rhythmus. Psychologische, theoretische und stilanalytische Aspekte populárer Musik. Bielefeld: Transcript.
Polak, Rainer. 1998. “Jembe Music in Bamako: Microtiming as Formal Model and Performance Practice.” Iwalewa-Forum 2: 24–46.
—————. 2000. “A Musical Instrument Travels Around the World: Jembe Playing in Bamako, in West Africa, and Beyond.” World of Music 42, no. 3: 7–46. Rpt. 2005 in Ethnomusicology: A Contemporary Reader, ed. J. Post. NY: Routledge Press, 161–85.
—————. 2004. Festmusik als Arbeit, Trommeln als Beruf. Jenbe-Spieler in einer westafrikanischen Großstadt. Berlin: Reimer.
—————. 2005. “Drumming for Money and Respect. The Commercialization of Traditional Celebration Music in Bamako.” In Wari Matters: Ethnographic Explorations of Money in the Mande World, ed. J. Jansen and S. Wooten. Münster: LIT, 135–61.
—————. 2006. The Jenbe Realbook, Vol. 1 (Transcription of CD Dunbia et al. 2006 disc). Nürnberg: Bibiafrica.
—————. 2007. “Performing Audience: On the Social Constitution of Focused Interaction at Celebrations in Mali.” Anthropos 102, no. 1: 3–18.
—————. 2008. The Jenbe Realbook, Vol. 2 (Transcription of CD Kone et al. 2008-disc). Nürnberg: Bibiafrica.
Prögler, J. A. 1995. “Searching for Swing: Participatory Discrepancies in the Jazz Rhythm Section.” Ethnomusicology 39, no. 1: 21–54.
Repp, Bruno H. 1997. “Expressive Timing in a Debussy Prelude: A Comparison of Student and Expert Pianists.” Musicae Scientiae 1, no. 2: 257–268.
—————. 1998a. “Musical Motion in Perception and Performance.” In Timing of Behavior: Neural, Psychological, and Computational Perspectives, ed. D. A. Rosenbaum and C. E. Collyer. Cambridge, MA: MIT Press, 125–44.
—————. 1998b. “Obligatory ‘Expectations’ of Expressive Timing Induced by Perception of Musical Structure.” Psychological Research 61, no. 1: 33–43.
Repp, Bruno H., Justin London, and Peter E. Keller. 2008. “Phase Correction in Sensorimotor Synchronization with Nonisochronous Sequences.” Music Perception 26, no. 2: 171–75.
Riemann, Hugo. 1884. Musikalische Dynamik und Agogik. Lehrbuch der musikalischen Phrasirung aufgrund einer Revision der Lehre von der musikalischen Metrik und Rhythmik. Leipzig: Kietner.
Serwadda, Moses, and Hewitt Pantaleoni. 1968. “A Possible Notation for African Dance Drumming.” African Music 4, no. 2: 47–52.
Stone, Ruth. 1985. “In Search of Time in African Music.” Music Theory Spectrum 7: 139–48.
Scherzinger, Martin. 2001. “Negotiating the Music-Theory/African-Music Nexus: A Political Critique of Ethnomusicological Anti-Formalism and a Strategic Analysis of the Harmonic Patterning of the Shona Mbira Song Nyamaropa.” Perspectives of New Music, 39, no. 1: 5–117.
Temperley, David. 2000. “Meter and Grouping in African Music: A View from Music Theory.” Ethnomusicology 44, no. 1: 65–96.
—————. 2004. “Communicative Pressure and the Evolution of Musical Styles.” Music Perception 21, no. 3: 313–37.
Todd, Neil P. 1985. “A Model of Expressive Timing in Music.” Music Perception 3, no.1: 33–58.
Waterman, Richard. 1952. “African Influence on the Music of the Americas.” In Acculturation in the Americas, ed. Sol Tax. Chicago: University of Chicago Press, 207–18.
Discography
Discography
Coulibaly, Soungalo. 1986. Na Yan. (Music cassette, no publisher listed.)
Diakite, Abdoulaye, and Mamadou Sidibe. 2001. JebeBara. Rootsy Records.
Drame, Adama. 1979. Rhythms of the Manding. Phillips 6586042 (UNESCO Collection). Re-edition 1984 Grem DSM 042.
Dunbia, Yamadu, Jaraba Jakite, and Jeli Madi Kuyate. 2006. The Art of Jembe Drumming: The Mali Tradition, Vol 1. Bibiafrica Records.
Jakite, Jaraba, Yamadu Dunbia, and Jeli Madi Kuyate. 1997. Dònkili—Call to Dance. Festival Music From Mali. Pan CD 2060.
Keita, Mady. 2005. Traditional Djembe Music from the Bamana and Manding Peoples. Kanaga System Krush.
Konate, Famoudou. 1991. Rhythmen der Malinke. Museum Collection Berlin CD 18, Museum für Völkerkunde Berlin.
Kone, Drissa, Jeli Madi Kuyate, and Jaraba Jakite. 2008. The Art of Jembe Drumming: The Mali Tradition, Vol 2. Bibiafrica Records.
Troupe Folklorique Malienne. (no date). African Rhythms and Instruments, Vol. 1. Lyrichord CD 7328.
Sidibe, Sega. 2003. Wasulun Fenkorow. Buda Musique.
Sidibe, Mamadou. 2000. Village Djembe Drumming. Rootsy Records.
Footnotes
1. I am grateful for various sorts of truly invaluable support that helped to produce and improve the present article. At its core is a chronometric study that was funded by the German Research Council (Deutsche Forschungsgemeinschaft, DFG) with a two-year research grant (2006–2007). Justin London, David Locke, Nicholas Hockin, Matthew Wirzbicki, Hans Sutton, and two anonymous reviewers offered thoughtful comments that provoked many revisions. Herbert Braun, Neil Dowling, Hockin, Wirzbicki, and above all Sutton proofread the paper at various stages of the draft. David Locke provided manuscripts of his latest works. Finally, I am greatly indebted to a group of professional drummers from Bamako (Mali), who have shared with me musical tradition, individual artistry, and personal friendship over a period of nearly two decades: Yamadu Dunbia (1917–2002), Jaraba Jakite (1953–2005), Jeli Madi Kuyate, Drissa Kone, Sedu Balo, and Madu Jakite.
Return to text
2. See Bengtsson, Tove, and Thorsen 1972; Bengtsson 1975; Bengtsson 1987; and Bengtsson and Gabrielsson 1977. Bengtsson’s concept of “systematic variation of durations” includes microdurational structuring at several (low) metric levels. Trying to be metrically specific—my focus is on the non-isochronous patterning of beat subdivision—I paraphrase Bengtsson’s term as “cyclic variation of subpulse durations.”
Return to text
3. On the swing feel of jazz, see Prögler 1995, Friberg and Sundström 2002, Collier and Collier 2002, Temperley 2004, and Benadon 2006. For a synopsis of research on rhythm in African-American popular music styles, see Pfleiderer 2003 and 2006. On the notes inégales, see Moelants 2008.
Return to text
4. See, among others, Koetting 1970, Kauffman 1980, Arom 1984, Stone 1985, Kubik 1988, and Kubik 1994.
Return to text
5. See Koetting 1970 and Pantaleoni 1972; compare Temperley’s skeptical and Agawu’s decided rejection of this approach (Temperley 2000 and Agawu 2006, 18–24).
Return to text
6. For a broad perspective on metric concepts in the study of what is commonly generalized as “African music,” see Nzewi 1997, 31–69; Kubik 1988, 71–99; and Kubik 1994, 37–46; one might also refer to Kubik’s entry on “Africa” in the New Grove Dictionary of Music and Musicians (2nd ed.), or the Grove Music Online (Oxford Music Online [accessed January 15, 2010]). For a view from music theory on meter in African music, and on the concept of meter in Africanist ethnomusicology, see Temperley 2000.
Return to text
7. Here, I follow David Locke’s stringent terminology for the analysis of rhythm and meter in West African music, as developed in his studies of drumming traditions from Ghana (Locke 1982, Locke 1987, Locke 1992, Locke 2009, and Locke 2010). Doing so, I deviate from using “pulse” synonymously with “beat;” compare Justin London’s entry on “pulse” in the New Grove Dictionary of Music and Musicians (2nd ed.), or the Grove Music Online (Oxford Music Online [accessed January 15, 2010]).
Return to text
8. Locke’s concept of regular “two-in-the-span-of-three cross-rhythm” (Locke 2009) corresponds to Nzewi’s “inter-rhythm” (Nzewi 1997) and Temperley’s “hemiola” (Temperley 2000). Compare Mark Butler’s extended argument for the relevance of metric ambiguity in electronic dance music (Butler 2001 and Butler 2006, part II). Electronic dance music bears much resemblance with West African percussion music with regard to the principles of systematic displacement of rhythmic grouping and metric beat, such as systematic cross-rhythm and consistent offbeat phrasing.
Return to text
9. See Nzewi 1997, 36–42 and Agawu 2003, 71–96; for views from music theory and music psychology that support that critique, see Temperley 2000, 80–81 and London 2004, 48–50.
Return to text
10. See, among others, Locke 1992, 104; Locke 2009; Locke 2010; Nzewi 1997, 42; Anku 2000; and Agawu 2006.
Return to text
11. See Serwadda and Pantaleoni 1968; Koetting 1970; Pantaleoni 1972; Locke 1982; Locke 1987; Locke 1992; Kubik 1988, 90–95; Nzewi 1997, 35–42; and Agawu 2006.
Return to text
12. Richard Waterman’s concept of an African “metronome sense” was seminal to this assumption (Waterman 1952).
Return to text
13. London defines “expressive variation” as timing patterns of “metric periodicities on each level” (London 2004, 28). From this perspective, “rhythmic feel,” which in my usage refers to timing patterns at only the beat subdivision level, would represent a subtype of London’s broader concept. The concept (“expressive variation,” or “expressive timing”) is common in music psychology and in the theory of European art music, with the rubato of Romantic music as a prominent example; see, among others, Todd 1985, Clarke 1987, Repp 1998a, and Repp 1998b. With some terminological variation (“expressive microtiming,” “expressive microrhythm”), it is also current in jazz music theory; see Iyer 2002, Benadon 2006, and Benadon 2009. The concept of “participatory discrepancy” (Keil 1995), which is widespread in studies of African-American music and in ethnomusicology, is similar in thrust: just like “expressive timing,” its core idea is to search for rhythmic quality in the deviation from mechanically even timing. The concept includes both the expressive timing of rhythmic patterns and phase shifting between ensemble parts (see Prögler 1995); compare Butterfield’s (Butterfield 2010) argument against the importance of drummers and bassists being “out of phase” in the creation of swing in jazz.
Return to text
14. Hugo Riemann’s term “agogic” (Agogik, in German) (Riemann 1884) might be seen as a conceptual precursor of “expressive timing.” “Agogic” refers to the working-out of musical phrases (Phrasierung, in German) by accentuating their grouping structure, particularly through the expressive (lively, non-isochronous) timing of durations.
Return to text
15. Recent psychological research shows that we do not need simple integer ratios to produce stable rhythms (Repp, London, and Keller 2008). I am grateful to Justin London for directing my attention to this in a personal communication. However, the assumption that we do has been prominent in music psychology (cf. Fraisse 1982, Clarke 1999), and has so far underlain most theories of rhythm and meter.
Return to text
16. See Repp 1998a for the interpretation of expressive timing as a function of rhythmic grouping in European art music.
Return to text
17. See also David Huron’s review of Clarke 1987 (Huron 1998).
Return to text
18. London speaks of “metrical timing pattern” (London 2004, 153); see also Moelants 1997, suggesting the term “metric microstructure.”
Return to text
19. On the ethnography and social history of jembe playing in Mali, see Polak 2004, Polak 2005, Polak 2007, and Polak, in press.
Return to text
20. See Polak 1998 for an English language version of that paper.
Return to text
21. Graph notation, which represents the metric time grid of the fastest pulse by either equidistant vertical lines or boxes (see Serwadda and Pantaleoni 1968, Koetting 1970), is standard in formalized jembe music pedagogy. Compare David Locke’s work, by contrast, for examples of staff notation of Ghanaian forms of West African drum ensemble music.
Return to text
22. The recorded pieces include: bara, bamana-fòli (tisanba), bònjalan, burun, dansa, fula-fòli, garanke-dòn, jina-fòli, kirin (wasulunka), kòfili, kòmò, madan, maraka-dòn (denba-fòli), manjanin, numu-dòn, nyagwan, sanja (lamban), sogoninkun, suku (soli), sumalen, sunun, tansole, woloso-dòn.
Return to text
23. Five of the recorded musicians (Jeli Madi Kuyate, Drissa Kone, Sedu Balo, Kasim Kuyate, and Madu Jakite) grew up as village drummers in different rural areas to the south or west of Bamako, and became urban professional drummers in the 1960s or 70s as apprentices to the late Yamadu Dunbia (approx. 1917–2002). Thus, the musicians whose playing represents the core reference of the present article came from the same stable. For the sake of comparison, I also recorded two older players, Sega Cisse and Baji Jara, who represented different schools of professional jembe playing in Bamako, and one from an urban satellite: Isa Kulibali from Kati. Beyond that, I included in the sample two semi-professional drummers, Amadi Konate and Tanba Dunbia, from Kourouba, a small town about one hundred kilometers south of Bamako. The study makes use of older recordings of my private archive as well as some published recordings. Among the featured musicians are my former masters, Yamadu Dunbia and Jaraba Jakite (approx. 1953–2004), plus further Bamako drummers of excellent repute, Sega Sidibe, Abdoul Doumbia, and Mady Keita; Namori Keita (approx. 1925–2000) from Kati; Namakan Keita from Sagele; Adama Drame and Soungalo Coulibaly (1955–2004) from Bouaké, Ivory Coast; and Mamady Sidibe and Abdoulaye Diakite from Tambacounda, Senegal. The published recordings are listed in the discography. Audio and video examples provided with this article are all of my own recordings.
Return to text
24. See Polak 2004, 187–278 on the ethnography and concept of jembe playing as work in Mande society.
Return to text
25. I used both Steinberg’s Wavelab and Sony’s Soundforge. Wavelab turned out to be quite reliable in the automatic detection of drum strokes, yet only marks IOIs of over 100 ms. This is a disadvantage, since jembe music can feature pulse durations as short as 80 ms (see Section 4.6 on the lower level for meter). Soundforge does not have this limitation, but is less good at detecting the first peaks of onsets and thus requires considerable manual reworking of flawed marker positions.
Return to text
26. I normalized the beat duration as the average over the metric cycle, usually a 4 beat cycle, equated with 400%. Compare Butterfield’s argument for the measure as reference for the timing analysis of jazz grooves (Butterfield 2007, par. 4–10).
Return to text
27. Timing studies often represent relative durations as a quotient; for instance, a 60:40 ratio of swing eighth notes or notes inégales (LS) can be given as 1.5, whereas 50:50 (isochronous binary subdivision) would equal 1.0. This representational format is disadvantageous from a comparative perspective, because calculating a quotient makes sense for binary subdivision, but does not work well for metric types of higher subdivision. For example, timing ratios such as 25:35:40 or 40:30:30 in case of ternary subdivision cannot be calculated into quotients.
Return to text
28. On the contestation of “formalist” approaches, see Chernoff 1979 and Berliner 1981, both classics of Africanist ethnomusicology. On the criticism of “anti-formalist” approaches to African music, see Scherzinger 2001; Agawu 2003, chap. 8; and Agawu 2006. On ethnomusicological concerns about turning the study of African music over to (a unified) music theory, see Erlmann’s review of Agawu 2003 (Erlmann 2004).
Return to text
29. The vernacular language of Bamako and lingua franca of Mali is Bamanankan (also: Bambara), which belongs to the Mande branch of Niger-Congo languages. Closely related are Maninkakan (Malinké) and Wasulunkakan (Wassoulou).
Return to text
30. On the deconstruction of “African rhythm,” see Agawu 2003, 55–70 and Carl 2004.
Return to text
31. On the melodic aspect of West African drumming patterns, compare, among others, Serwadda and Pantaleoni 1968, Koetting 1970, Pantaleoni 1972, Nzewi 1974, and Locke 2010.
Return to text
32. The oldest identifiable audio recording of manjanin (to my knowledge) is of the National Ballet of the Republic of Mali from the Premier Festival Panafricaine, Algiers, 1969 (Troupe Folklorique Malienne, no date, tracks 4 and 5). For further historical and iconographic references, see Polak 2004, 58–59.
Return to text
33. The concepts of fastest pulse (density referent, elementary pulsation) and graph notation may run the risk of over-emphasizing the metric relevance of the fastest pulsation as against the beat (Agawu 2006, p. 21, n. 42; Agawu 2003, 48–53, 64–68). Jembe pedagogy is sensitive to this issue and usually represents both pulse and beat in its notations (see Doumbia and Wirzbicki 2005, Polak 2006, and Polak 2008.
Return to text
34. Since the 1990s, there has been a tendency towards more variative and expressive dunun playing in the urban and international contexts of jembe music from Mali. This tendency is not featured in Video 1, or generally in the sample of audio and video materials presented in this article.
Return to text
35. See Cycles 18–20, 33–37, 39, 60, 62, 64, 69–72, 74–77, 84, 104–110, 118–124, 128, 149–154, 166, 195, and 197.
Return to text
36. The French term échauffement means “warming up,” “heating,” or “excitement.” When talking of échauffements in Mande languages such as Bamanankan of Bamako, the usual term is the verb goloba (“to rush,” “to accelerate,” “to activate”).
Return to text
37. On the concept of recycling (repetition plus variation) as different from redundantly repetitive re-circling, see Nzewi 1997, 59–67.
Return to text
38. The French term blocage means “stop;” in Bamako, they use the Bamanankan verb tigè (“to cut/cut off something”). I will refer to blocage as “break,” which is common usage in the anglophone parts of the international jembe music scene. In contrast to breaks of other musical styles (including modern—stage and classroom—jembe music), the blocage of traditional jembe dance music does not imply an interruption in the accompaniment, and, thus, does not provide room for spectacular soloistic passages or ensemble arrangements.
Return to text
39. In Bamanankan, they say basigilen, the past participle form of the verb basigi, which means “being serious,” “being calm,” or “being well equipped.” See Chernoff 1979, 100–101 on taking time and fluidity of change in the lead part of drum ensemble music from northern Ghana; also see his discussion of restrained lead playing as “respectful” and “cool” (106–113 and 149–151).
Return to text
40. On the dialectics of musical change and culturally conservative discourse in the context of urban market economy and professionalization process, see Polak 2004, 287–310.
Return to text
41. As already stated, I calculate pulse timing ratios with reference to the normalized beat duration, which is the beat duration averaged across the 4 beat cycle. The total for the percentages listed in any cycle is thus 400%. The sum of values for any single beat, by contrast, does not necessarily amount to 100%. Minor deviations from the total 400% (mostly between 399 and 401%) can result from the rounding of decimal places.
Return to text
42. Expressive or systematic variation of durations requires a certain minimum of absolute timing difference in order to be discernible from random variation. In jazz research, this discrepancy threshold often is assumed to lie between 10 to 20 ms; see Prögler 1995, note 11; Benadon 2007, par. 13–15; and Butterfield 2007, par. 12–15.
Return to text
43. The recording of Kone listed in Table 4 is published on CD in Kone, Kuyate, and Jakite 2008, track 14; the measured period corresponds to Cycles 19–35 (00:32–00:58 min).
Return to text
44. The differences between individual musicians in performing rhythmic feel patterns appear to be more striking in other styles of music; for instance, compare Prögler 1995, Friberg and Sundström 2002, and Benadon 2006 on jazz; and Moelants 2008 on Baroque music.
Return to text
45. The durations of the forty-four first (short) pulses of Cycles 206–216 are as follows (in ms): 85, 87, 80, 86, 86, 76, 76, 83, 79, 83, 83, 82, 92, 80, 84, 82, 86, 76, 91, 87, 87, 85, 78, 80, 92, 82, 74, 86, 88, 87, 80, 91, 83, 84, 81, 78, 84, 90, 79, 88, 88, 85, 84, and 84 (mean=84; sd=5).
Return to text
46. Gerischer reports on similar values (below 90 ms) for Brazilian samba music (Gerischer 2003, 55).
Return to text
47. In jazz drum rudiments, the flam usually consists of a principal note preceded by a grace note. In jembe music, the two notes of a flam can be of equal dynamic stress and nominal importance.
Return to text
48. Listen to the double notes on Pulse 1.1 of Cycles 81 (57 ms), 159 (67 ms), 161 (72 ms), 187 (50 ms); I tend to hear those double notes as flams. Further listen to the double notes in Cycles 193 (74 ms), 195 (76 ms), 197 (80 ms), 199 (77 ms), 203 (84 ms), 204 (85 ms), and 205 (83 ms); I can here these both as flams and as metric pulses.
Return to text
49. Here I have translated Benadon’s quotients of 1.2 and 1.4 into percentages of beat duration (see Benadon 2006, 88–90.
Return to text
50. Analysis of changes of feel patterns within pieces is not included here, because it would exceed the framework of this section, the aim of which is but a rough survey of the most common feel patterns.
Return to text
51. According to my spot-check measurements, LSM applies to pieces such as gidamba and soko as performed by Famoudou Konate (Konate 1991, tracks 1 and 11).
Return to text
52. The composition has become popular under the name of sumalen in the context of youths’ entertainment dances in Bamako in the 1980s. The same composition is addressed as jòn-dòn by Doumbia and Wirzbicki 2005.
Return to text
53. See Kubik 1988, 1994, and 1999; Kubik’s term for this alternative form of time signature is “cycle number,” or “form number” (Formzahl, in German).
Return to text
54. These compositions include sogoninkun, komo, tansole, and madan; listen, for instance, to the respective pieces in Dunbia, Jakite, and Kuyate 2006 and Kone, Kuyate, and Jakite 2008.
Return to text
55. See Knight 1973, 270–271 on metric ambiguity between binary and ternary feels in Mande kora (harp) playing and song in The Gambia.
Return to text
56. Pieces from Mali that use the LS/SFL feel system inlude bolon and sandia (lamban); yankadi is a Guinean piece discussed in the European and American jembe music scenes for its ambiguity of binary and ternary (LS/SFL, I suggest) subdivision.
Return to text
57. See also the ternary notation, and listen to the pronounced SML feel, of woloso-dòn in Doumbia and Wirzbicki 2005, pp. 121–129; corresponding to CD 2, tracks 18–23.
Return to text
58. In Table 19, the values for Pulses 1.1 and 5.1, which are not sounded by the lead jembe, have been derived from the accompaniment parts.
Return to text
59. Listen to the identical articulation of both the cyclic feel pattern and its expressive variation in Doumbia and Wirzbicki 2005, CD 2, track 20, 00:39–01:00 min; corresponds to Cycles 5–14 of p. 21.
Return to text
60. See Kroier 1992, 48–58 on the ambiguity and synchronization of ternary and quaternary feels in Afro-Cuban rumba drum ensemble music.
Return to text
61. LFF/SFLF pieces from Mali include kirin (wasulunka), sogoninkun, fula-fòli, sunun, jina-fòli, and sumalen.
Return to text
62. RRL/RLRL hand patterns are used in all LFF/SFLF pieces (see footnote 61).
Return to text
63. I base this statement on the chronometric project’s video footage and on my long-term participant observation of Malian jembe players (see Section 3).
Return to text
Copyright Statement
Copyright © 2010 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by John Reef, Editorial Assistant
Number of visits: