Grouping Hierarchy and Trajectories of Pacing in Performances of Chopin’s Mazurkas
Mitchell S. Ohriner
KEYWORDS: Expressive timing, grouping structure, performance and analysis, Chopin
ABSTRACT: Theories of expressive timing in the performance of tonal music emphasize the role of grouping structure, whereby performers are understood to communicate the ends of groups through group-final lengthening (GFL). But this approach depends on a one-way mapping from a single grouping-structural analysis onto performed durations, denying a role for interpretive difference on the part of performers and analysts. Drawing on contour theory, this article reverses this mapping by presenting a method for recovering the hierarchical grouping structure of a performed phrase that is sensitive to the constraints of temporal perception. Groups whose durational contour segments reduce to a contour adjacency series of <+> or <–,+> are understood to be GFL-reflective. By observing which levels of time-span organization are GFL-reflective among different performances of the same phrase, unique construals of grouping structure can be attributed to different renditions.
The article employs this method in order to examine different approaches to pacing in performances of two of Chopin’s mazurkas. The pieces in question present eight-measure themes in which the salience of different levels of grouping structure contrast. Through duration decisions, performers can accentuate, amend, or bypass these suggestions of contrast in pacing. By presenting an analytical method that recognizes the creative power of performance to interact with a grouping structure implied by a score, I hope to reshape the relationship between performers and analysts as a dialog about the possible structural descriptions a piece can support.
Copyright © 2012 Society for Music Theory
[1] The last three decades have seen a growing interest in the slight beat-to-beat changes in duration that pervade performances of tonal music. Many current approaches originating in the work of music psychologists interpret durational variability as the means by which performers convey both segment boundaries and hierarchical relationships between segments. But these approaches depend on a one-way mapping from a single grouping-structural analysis onto performed durations, a mapping at odds with the possibilities for interpretive difference that are increasingly acknowledged in music analysis (Cook 1999).
[2] In this article, after expositing how performers can suggest novel descriptions of grouping structure by lengthening group-final events (Sections I and II), I will introduce a method grounded in contour theory for determining the relative salience of hierarchically nested groups in a particular recorded performance (Section III). I will then argue that shifts in the level of grouping structure presented as most salient affect the perceived pacing of a piece (Section IV). In later analyses, I will show how performers can address contrasts in pacing, or trajectories in pacing, latent in two of Chopin’s mazurkas (Section V). By introducing an analytical method that begins with the particularities of a phrase as it is performed, I hope to demonstrate one way in which performance can affirm, nuance, or even circumvent a grouping structure implied by a score.
I. Introduction: Performance, Segmentation, and Musical Flow
[3] Since the 1980s, music psychologists have explained durational variability in performances of tonal music largely through a phenomenon termed “phrase-final lengthening,” a means of conveying grouping structure by decelerating at the ends of groups (Bengtsson and Gabrielsson 1980; Todd 1985; Palmer 1989). Because the word “phrase” in this usage refers to a linguistic rather than musical unit, I’ll refer to this practice as “group-final lengthening,” hereafter GFL. Scholars also recognize that not all lengthenings are responses to grouping structure: meter, melodic contour, and ornamentation also affect beat durations (Gabrielsson and Bengtsson 1983; Friberg, Bresin, and Sundberg 2006; Desain and Honing 1994). Since performance timing is inherently multivariate, earlier work (especially Todd 1985) tends to construe timing decisions in individual performances as a “signal” of grouping structure conveyed through the “noise” of local effects such as meter or melodic contour. Furthermore, performers may use multiple strategies to convey the same grouping-structural interpretation. One might emphasize an event by lengthening it or by lengthening the preceding event that anticipates it (Clarke 1988, 15). Therefore models of performance timing that take a single determination of grouping structure and return an expected timing profile can be deemed robust even if timing profiles in actual performances vary considerably.(1)
[4] The grouping structure thought to be conveyed through performance timing amounts to a segmentation of a piece. Yet this idea that tempo variation in performance primarily communicates grouping structure disregards two key aspects of musical segmentation. First, as Dora Hanninen (2001, 351) points out, music presents a variety of potentially conflicting criteria relevant to segmentation, and thus multiple segmentations are always possible depending on differences in the predilections and aims of performers and analysts. Second, because grouping structure in music can be represented as hierarchical, both the locations of group endings and their hierarchical relationships are subject to interpretation. In the extant models of performance timing, the relationship between timing, the interpretability of grouping structure, and grouping-structural hierarchy has not been adequately addressed.
Example 1a. Frédéric Chopin, Mazurka in C major, op. 24, no. 2, measures 21–28, score excerpt
(click to enlarge)
[5] An eight-measure phrase by Frédéric Chopin (see Example 1a), segmented variously through the apparatus of Fred Lerdahl and Ray Jackendoff’s 1983 A Generative Theory of Tonal Music, illustrates the multiplicities of hierarchical grouping structure that might be expressed by performance. Examples 1b and 1c show two grouping-structural analyses using arches familiar to readers of Lerdahl and Jackendoff. The analyses invoke different grouping preference rules (GPRs) to address the F4 at end of measure 24, construing it as an anacrusis to the group that includes the following measure (Example 1b) and as a group ending (Example 1c; Lerdahl and Jackendoff 1983, 345). Example 1b invokes GPR 2b, which associates F4 with the following measure because the time interval between A4 and F4 is longer than the interval between either the previous G4–A4 or the subsequent F4–C4. A different pair of preference rules associates F4 with the group that includes the previous downbeat (see Example 1c). First, because measure 25 parallels measure 21, both should be understood as group beginnings according to GPR 6. Once that determination is made, the GPR that discourages one-note groups (GPR 1) would likewise assign F4 to the previous group.(2)
|
Example 1b. Frédéric Chopin, Mazurka in C major, op. 24, no. 2, measures 21–28, segmentation wrought by Lerdahl and Jackendoff’s Grouping Preference Rule (GPR) 2b, which addresses attack-point proximity (click to enlarge) |
Example 1c. Frédéric Chopin, Mazurka in C major, op. 24, no. 2, measures 21–28, segmentation wrought by a combination of GPRs 6 and 1 (click to enlarge) |
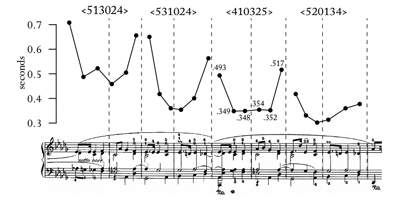
[6] These readings cannot be evaluated against each other because the two criteria that generate them—duration and parallelism—cannot be directly compared. In Hanninen’s approach to segmentation, either reading is viable provided the analyst explicates his or her weighting of various criteria. But at least two phenomena constrain the analyst’s process of segmentation. First, pertaining to the salience of the parallelism—what Hanninen (2001, 350) calls a “contextual criterion”—Elizabeth Margulis (2011) has shown that the ability to detect repetition depends on the repetition’s position within the hierarchical grouping structure: repetitions below the tactus level of metric structure are not easily detected, nor are those separated by substantial intervening material. Familiarity with an excerpt also affects the detection of repetitions, but not in a strictly linear fashion. In Margulis’s study, repeated exposures improved the detection of the repetition of larger groups but hindered the detection of the repetition of smaller units. Margulis’s research suggests that listeners may lean more towards the analysis of Example 1c with repeated exposures.
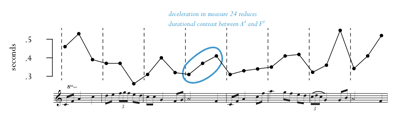
Example 2. Durational contours of Chopin, Mazurka in C major, op. 24, no. 2, measures 21–28, in recorded performances
(click to enlarge, see the rest, and listen)
Example 3. Durational contours of Chiu (light blue line) and Ashkenazy (gray line)
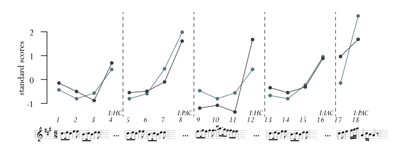
(click to enlarge)
Example 4. Temporal segmentation of op. 24, no. 2, measures 21–28 in the renditions of Ashkenazy (top) and Chiu (bottom)
(click to enlarge)
[7] A second constraint on segmentation recognized but not highlighted by Hanninen is the role of performance. Performance affects both the placement of group endings and their hierarchical relationships and may constrain whether one hears Example 1b or 1c.(3) Example 2 shows what I call “durational contours” of the Chopin phrase in two recorded performances of the phrase, those of Frederic Chiu (2a) and Vladimir Ashkenazy (2b).(4) Points in the contours represent onset-to-onset durations of events “on the beat,” measured in seconds (i.e., higher points are longer beats and thus indicate slower tempo).(5) Among other differences in the contours, Chiu decelerates through measure 24 while Ashkenazy accelerates. In effect, Ashkenazy’s rendition accentuates the grouping preference rule that generates the analysis of Example 1b, possibly affording a listener to construe F4 as the beginning of a group despite the imminent parallelism.(6)
[8] At higher levels of time-span organization, performed durations also affect the salience of different levels of grouping structure.(7) Example 3 shows durational contours of the two performers in which each point represents the duration of a measure rather than a beat. The contours are broken between the two four-measure groups to emphasize their relations. Both performers lengthen the first measure to show the beginning of the new eight-measure group, play the second measure much faster, and then begin to decelerate. Whereas Ashkenazy gradually decelerates through the remainder of the phrase, Chiu interrupts his deceleration in the fifth measure, bisecting the temporal experience of the phrase to a greater extent than Ashkenazy. Those who hear these two performances may therefore have a different sense of the phrase’s rate of salient group endings. Perhaps Ashkenazy and Chiu both convey the same hierarchical grouping structure in higher levels of the excerpt, but the salience of these levels may be distinct because of the GFL observable in Chiu’s treatment of measures 21–24. Example 4 represents the differences in temporal segmentation between the two renditions in terms of both group-final placement and hierarchical salience.
[9] If performance can alter perceptions of grouping structure and its hierarchy, then it can also alter whatever analytical conclusions can be drawn from grouping structure. In the sections that follow, after reviewing the origins of GFL in speech and movement, I will formalize a method for recovering the hierarchical grouping structure suggested by a performance and explore the impact of divergent understandings of grouping structure hierarchy in contrasting performances of the same work. By engaging grouping structure in a comparative analysis of divergent performances, I hope to draw attention to the ways performances respond to a piece’s implied grouping structure rather than neutrally convey something determinate.
II. Curved Durational Contours as an Expression of Grouping Structure
[10] Group-final lengthening is evident in the earliest studies of performed durations (Seashore 1936). Neil Todd (1985, 34) connects this phenomenon to speech, where lengthening not only indicates phrase boundaries but also imparts syntactical information at levels of organization below the phrase, especially in the communication of potentially ambiguous sentences like “Pat or Antonia and Dave will help” (Scott 1982).(8) Furthermore, and particularly relevant to the previous discussion of the relative salience of different levels of hierarchical grouping structure, there is some evidence that the extent of phrase-final lengthening in speech imparts information regarding the hierarchical significance of the unit (O’Malley et al. 1973).
Example 5. Structural communication through phrase final lengthening
(click to enlarge and see the rest)
Example 6. Actually and perceptually constant velocities
(click to enlarge)
Example 7. Todd’s model of timing (by measure) in the theme of the first movement of Mozart’s Sonata in A major, K. 331
(click to enlarge)
Example 8a. “Timing patterns of six instances of the same melodic gesture in “Träumerei”
(click to enlarge)
Example 8b. Instances of the five-note melodic gesture in Schumann’s “Träumerei”
(click to enlarge and see the rest)
[11] The evidence from linguistics suggests that musical group finals will be lengthened as in the hypothetical durational contour of Example 5a. But in music performance, lengthened group finals affect the durations of many surrounding events, resulting in the more common parabolic durational contour of Example 5b, sometimes called a tempo curve (Desain and Honing 1993, 129). Parabolic changes in rates of motion have been observed in a variety of human movements. The velocity of both our shoulders and elbows are parabolic during point-to-point movements in order to minimize abrupt changes in the forces acting on ourselves or the objects we carry; perhaps curved durational contours lend an analogous smoothness to implied musical movements as well (Flash and Hogan 1985; Shove and Repp 2005). Parabolic velocity is also related to intentionally constant movement; objects moving along an elliptical path with a parabolic velocity are more easily tracked with the fingers than those with constant velocity (Viviana and Stucchi 1989). Finally, parabolic velocities are important to visual perception. When an object moves at a constant velocity in front of us, we attribute a much greater speed to the first part of the motion. Conversely, in order for the velocity of an object to be perceived as constant, it must begin with a constant acceleration before attaining a constant velocity (Runeson 1974, 12; see Example 6). Our ability to reproduce a timing pattern similarly improves if it has a parabolic durational contour that matches the grouping structure of the music (Clarke and Baker-Short 1987).
III. Curved Durational Contours as an Assessment of Hierarchical Grouping Structure
[12] While studies of human movement and speech production may explain why performers “curve” durational contours within a phrase, they do not address how performers decide which spans of music constitute “phrases.” The earlier studies of expressive timing that demonstrate the prominence of tempo curves in performed music often address rather different levels of a piece’s structural hierarchy. Neil Todd (1985), for example, predicted that every four measures of the theme of the first movement of Mozart’s Sonata in A major, K. 331 would present a parabolic durational contour. Furthermore, his model increases the duration of a group’s final measure proportional to its significance in the grouping hierarchy. Todd’s model correlates with an averaged durational contour derived from twenty-three recordings strongly and significantly (i.e., r = .78,
[13] Nevertheless, another series of studies conducted by Bruno Repp (1992a, 1992b, 1995, 1996), informed by an examination of a large collection of recordings rather than a speculative model of timing, detected GFL-reflective curves (i.e., groups performed with GFL) at a much lower level of time-span organization. Studying timing in twenty-eight performances of Robert Schumann’s “Träumerei” from Kinderszenen op. 15, no. 7, Repp determined that a five-note ascending gesture, heard six times in the piece at the beginnings of phrases with varying pitch content, tended to be presented with a GFL-reflective contour (see Example 8a and 8b). Furthermore, higher levels of time-span organization in the performances of “Träumerei” (such as the four-measure level) do not exhibit GFL-reflective contours because the second measure of each four-measure group is frequently lengthened, especially in the second phrase.(9) How, then, might one ascertain which level of time-span organization hosts groups with GFL-reflective durational contours in a given segment of music? And furthermore, what might be the analytical significance of such a finding when comparing different phrases of the same piece or different performances of the same phrase?
[14] I propose that the salience of different levels in a grouping-structural hierarchy in a performance can be deduced through recent music-theoretical approaches in contour theory. A segment at a certain level of time-span organization is for my purposes GFL-reflective if its durational contour, interpreted as a contour segment (or cseg) has an uninterrupted acceleration towards its durational minimum and an uninterrupted deceleration towards its group-final maximum. Put more formally, in order for a durational contour at some level of time-span organization to be GFL-reflective, it should have a contour adjacency series (hereafter CAS, see Friedmann 1985, 226) of, essentially, <–,+>. Because many examples of GFL can be observed without an initial acceleration, I also consider the CAS <+> to be GFL-reflective. Example 9 illustrates these criteria on all the csegs of cardinality three and returns three csegs (<012>, <102>, <201>) that are GFL-reflective (Example 9c).
Example 9. Contour segments
(click to enlarge and see the rest)
Table 1. Contour segments of cardinalities two through eight that reduce to csegs with adjacency series of <+> or <–,+>:
(click to enlarge and listen)
Example 10. Durational contour of Stanislav Bunin’s rendition of the Mazurka in C-sharp minor, op. 63, no. 3, measures 33–40
(click to enlarge and listen)
[15] Many durational contours relevant to performed music have a cardinality greater than three, and therefore any durational contour segment that can be reduced to a cseg with a CAS of either <+> or <–,+> is also GFL-reflective. By “reduce” I refer to an application of Morris’s contour reduction algorithm (1993, 212). Morris’s method scans durational contours with a moving window of three elements and marks for deletion elements that are neither a minimum nor a maximum with respect to their immediate neighbors. For example, the contour <3102> would be initially reduced to <302>, since the second element is neither a local minimum nor maximum. <302> would then be reduced to <201> so that all elements of the cseg are consecutive integers.(10) Table 1 lists the number of csegs of cardinalities two through eight that present group-final lengthening as described above.
[16] The higher cardinalities are not musically relevant given the paucity of, say, seven-measure phrases or seven-beat measures. Nevertheless, contours of cardinality six are especially relevant in a study of Chopin’s music as two-measure groups in triple meter. At this level of time-span organization, contours whose adjacency series reduce to <+> or <–,+> are less likely to appear because such contours form a very small percentage of possible contours. Roughly curvilinear contours such as <431205> [
Example 11. A method for determining whether a performed phrase is GFL-reflective at some level of time-span organization
(click to enlarge)
[17] This tiny difference of timing, measured in thousandths of a second, is probably not discernable. Indeed, this is a difference of only one or two frames of audio in the spectrogram from which onsets were identified, and the measurements may not be that precise. Estimating the just-noticeable difference of changing tempo in a rich aural environment like the one presented by Bunin is difficult, but scholars have suggested a range of values for the just-noticeable difference between five and nine percent.(12) Of these studies, I believe the Madison and Merker (2002) finding of 8.6% represents the most ecologically valid. When reducing durational contours with Morris’s contour-reduction algorithm, elements that differ by less than five percent should first be pruned in order to reflect this limitation of our perception. This pruning should also be done iteratively such that, for example, in a durational contour of <1.00, 1.04, 1.08, 1.12, 1.20>, 1.04 and 1.08 will be removed in turn, but 1.12 will not be removed since it represents a deceleration from 1.00 that is perceptible. Example 11 demonstrates the complete process by which I determine if a performed phrase is or is not GFL-reflective.
[18] Before proceeding to analytical examples that rely on this method for detecting GFL-reflective durational contours at various levels of time-span organization, a few other comments on working with performed durations are necessary. First, the durational contours presented here were mostly generated by manually marking note onsets on a spectrogram with the aid of the software application Sonic Visualiser (Cook and Leech-Wilkinson 2010). When the onsets of events are not obscured by soft volume and pedaling, repeated annotations of the same rendition suggest an error in measurement of around three milliseconds. The error rate for inconspicuous onsets is surely higher, but even at very fast tempos, the 8.6% just-noticeable difference employed here more than encompasses the potential measurement error.(13)
[19] At times, beat onsets are obscure not because they are difficult to hear but because many notes nominally sharing a beat are attacked asynchronously. The phenomenon of arpeggiated or “spread” chords, especially in the music of Chopin, can be problematic because listeners may have a propensity toward attending to one part of the musical texture. In addition, listeners seem to prefer smoother durational contours and may place the beat with onsets that enable smoother tempo changes (Dixon, Goebl, and Cambouropoulos 2006). It is beyond the scope of this article to propose a consistent method for determining where the beat is placed for all listeners in all musical contexts. Rather, I take the average of the first and last onsets nominally sharing a beat, with the understanding that different listeners might place the beat slightly earlier or later in the case of spread chords. Much of this variation will also be absorbed by the just-noticeable difference threshold.
[20] Finally, as Henri Bergson (1946) and others have pointed out, the durations presented may not be the durations perceived. The factors that contribute to the accuracy of time estimation include the amount of information presented in the interval (Poynter 1983) and the amount of attention directed at the stimulus being estimated (Zakay and Block 1997). As these factors vary in listening, so too will the accuracy of estimation. Consider one possible example: a listener very familiar with the timing profile of a certain performance (perhaps his or her own) encounters an unexpected durational choice in a new performance, and must momentarily increase attention in order to maintain tracking the performance, thereby potentially distorting the timing estimation. Because the perception of durations in performance involves both the performer’s choice of durations and the listener’s varyingly successful estimations of those durations, a study such as this addresses temporal segmentation in a slightly idealized context, one in which full attention is paid to the task of measuring time.
IV. Difference in Presentations of Hierarchical Grouping Structure
Example 12. Selected eight-measure phrases from Chopin’s output. Evidence for segmentation at various levels of time-span reduction given below
(click to enlarge and see the rest)
Example 13. GFL-reflectivity in performances of the three excerpts given in Example 12
(click to enlarge and see the rest)
[21] As an entree into the relationship between the apparent grouping structure of a notated phrase and its hierarchical temporal segmentation in performance, Example 12
shows three phrases from Chopin’s output, two excerpted from mazurkas and one from a nocturne.(14) Each of these excerpts is eight measures in length, and, as the evidence below each excerpt documents, each phrase can be segmented into four two-measure groups, two four-measure groups, or an undivided eight-measure group depending on the relative salience of tonal, rhythmic, thematic, and dynamic criteria. For example, foregrounding thematic repetition would suggest more salient group boundaries every two measures in the op. 30, no. 2 excerpt, every four measures in the op. 24, no. 2 excerpt, and every eight measures in the op. 9, no. 1 excerpt (whose theme does not repeat). Tonal criteria affirm these segmentations: the op. 30, no. 2 excerpt pairs harmonies whose basses are related by descending fourth every two measures, the op. 24, no. 2 excerpt repeats the phrase-model I–![]()
[22] Although analysts may often be drawn to tonal and thematic criteria in segmenting music, are these the criteria to which performers respond in choosing durations? Example 13 shows GFL-reflectivity at various levels of time-span organization for 20–32 performances of each of these phrases. The lowest level of each grid (in green) looks for GFL-reflectivity among the durations of six quarter notes in successive two-measure groups, the middle level (in teal) does the same for the durations of four dotted quarter notes in successive four-measure groups, and the highest level (in blue) does so for the durations of the four dotted whole notes in the eight-measure phrase. There are some strong correspondences between the notational features of grouping structure given in Example 12 and the performed GFL-reflectivity shown in Example 13. Nearly every performance of the three excerpts is GFL-reflective at the eight-measure level. Additionally, there is broad agreement on the relative salience of different levels of time-span organization in the two mazurkas: most performers highlight two-measure groups in op. 30, no. 2 whereas very few do so in op. 24, no. 2. In contrast, GFL-reflectivity permeates performances of op. 24, no. 2 at the four-measure level but is present at that level to a lesser extent in renditions of op. 30, no. 2. From these tendencies it seems performers do emphasize thematic and tonal criteria in segmentation. In contrast, segmentation criteria such as the two-measure crescendo/decrescendo pairing in op. 24, no. 2, or the four-measure segments created by melodic contour in op. 9, no. 1, do not seem salient in performers’ choices of temporal segmentation.
[23] Yet two features of Example 13 undercut this apparent mapping between thematic or tonal layout and presented temporal segmentation. First, even when many performances suggest an intersubjective agreement regarding the relative salience of various levels of grouping structure (as in the two-measure segments in op. 30, no. 2 or the four-measure segments in op. 24, no. 2) individual performers can still suggest quite different segmentations (see, for example, the op. 30, no. 2 renditions of Biret and Brailowsky or the op. 24, no. 2 renditions of Brailowsky and Cortot). Second, at some levels of organization, there is no such agreement regarding a level’s salience, and performers are roughly evenly divided between those who emphasize the two- and four-measure groupings of op. 9, no. 1 and those who do not. Both the presence of outliers as well as the occasional lack of agreement on relative salience suggests that the hierarchical grouping structure presented in a performance is both a complex response to a variety of segmentation criteria and an expressive prerogative.
[24] The differences among the individual performances listed in Example 13 pertain to the experience of musical flow in those renditions because salient grouping boundaries are a primary means by which music’s temporality is articulated. In each of these phrases one can construe similar hierarchies of grouping structure, with groups of approximately two, four, and eight measures. But in most performances of the eight-measure phrase of the Nocturne, attention is drawn across the entirety of the phrase by a single acceleration/deceleration gesture, thereby minimizing the salience of the smaller groups. In contrast, the opening of op. 30, no. 2 is more quickly paced in most renditions since several two-measure temporal segments are presented. By highlighting the salience of different levels of grouping structure according to those that present GFL-reflective durational contours, I do not mean to imply that alternative analyses are unviable, only that they do not have the same psychological reality in that particular listening experience. In the next section, I will explore how these differences in presented grouping structure can create unique experiences of pacing within performances of complete works.
V. Trajectories of Temporal Experience
[25] Questions of pacing—the relative frequency of salient grouping boundaries—are especially pertinent to the stylized dances of Chopin. Unlike his larger forms (e.g., ballades, sonatas, and concertos), the stylized dances often present concatenations of diverse themes rather than the repeated deployment of related themes or motive forms that underlie Schoenberg’s notion of “intelligibility” in much of the music of the eighteenth, nineteenth, and twentieth centuries (Dahlhaus 1987, 77). Rose Rosengard Subotnik has stressed this internal heterogeneity in Chopin’s style:
What Chopin demonstrates rather explicitly is that structure need not be autonomous in the sense of internally generated in order to be perceptibly coherent. . . .Stated another way, it is aesthetically acceptable if a piece by Chopin is internally fragmentary (1991, 193).(15)
[26] Subotnik is not arguing that all of Chopin’s pieces are fragmentary in this way, or that certain features do not generate internal coherence in his music: most (but not all) of Chopin’s shorter pieces begin and end in the same key and many have thematic recurrences familiar from the work of other composers (e.g., ternary forms). But they are also rife with eight-measure themes terminating in cadences that in other contexts could end works. Without movement-spanning thematic processes to motivate the connection of one section to the next, questions of pacing come to the foreground. In his stylized dances, two trajectories of pacing are particularly common. First, Chopin will often pair two unrelated melodies of contrasting pacing, perhaps an eight-measure phrase that emphasizes two-measure groups followed by one of more continuous presentation, and a listener who hears this contrast may wonder which pacing will be more evident later in the piece. In other pieces, Chopin will set in motion a trajectory toward continuously faster pacing. In each of these schemes, performers have a unique role to play in shaping these trajectories by modulating the continuity or fragmentation of thematic presentations through the use of GFL-reflective durational contours at different levels of time-span organization. Below I will explore how performers negotiate each of these schemes in two of Chopin’s mazurkas.
Oppositions in Pacing in Op. 30, No. 2
Example 14. Mazurka in B minor, op. 30, no. 2, abbreviated score
(click to enlarge and see the rest)
[27] The B-minor Mazurka op. 30, no. 2, is an exemplar of Chopin’s mode of contrasting pacing (see the abbreviated score of Example 14, which also offers evidence for segmentation at various levels of time-span organization). Theme A, eight measures in length and subsequently repeated, establishes the two-measure span as the focus of attention, as shown in the grids of GFL-reflectivity discussed in connection with Example 13 above. Theme B, also eight measures and repeated, generally contrasts the fragmentation of Theme A with an unbroken ascent in the right hand, rhythmic saturation, and rising third sequences.(16) The pacing of Theme C is poised equidistant between that of Themes A and B, with several criteria supporting both the two- and eight-measure pacing. The rhythmic surface, thematic repetition, and shorter slurs highlight the two-measure pacing predominant in Theme A. At the same time, the consistent piano marking, short pedaling duration, and continuous tonal motion toward A major suggest the eight-measure continuity predominates in Theme B. Theme C, therefore, does not resolve the opposition in pacing presented in the first thirty-two measures. At measure 48, the end of the repetition of Theme C, it is still uncertain what kind of pacing this mazurka aspires to. Chopin offers one opinion by ending the piece with a reprise of the more continuous Theme B and not the more fragmentary Theme A, a choice all the more remarkable because it prevents the Mazurka from ending in the original tonic key, B minor.
Example 15. Durational contours of the Mazurka in B minor, op. 30, no. 2, with GFL-reflective groups in black
(click to enlarge, see the rest, and listen)
[28] Depending on the treatment of Theme C in performance, a number of trajectories of pacing in the piece are possible. Example 15a shows the durational contour of the recorded performance of Frederic Chiu (1999) at three levels of time-span organization and highlights the GFL-reflective segments. In his rendition of Theme A and its repetition, Chiu creates several GFL-reflective contour segments at the beat level, but these contours are not always modulated in relation to each other such that the higher levels are also GFL-reflective. In contrast, Chiu resists temporally segmenting Theme B below the eight-measure level by presenting more even durations at the beat level and a continuous acceleration at the beginning of the theme. Chiu’s presentation of Theme C combines features of the pacing of the two previous phrases, creating GFL-reflective contours at the beat level (as in the presentation of Theme A), but also shaping those contours into GFL-reflective ones at higher levels of time-span organization. In each theme, Chiu’s pacing highlights the levels with the greatest number of supporting criteria: the two-measure level in Theme A, the eight-measure level in Theme B, and a more balanced approach in Theme C.
[29] A different experience of pacing in the piece is possible if Theme C is presented not as a compromise between the faster pacing of Theme A and the slower pacing of Theme B but rather as an affirmation of one or the other. In the rendition of Ts’ong Fou (2005), like that of Chiu, GFL-reflective contours dominate the lowest level of Theme A and are less pronounced at that level of Theme B (see Example 15b). Unlike Chiu, Fou seemingly attends to the continuous tonal motion toward A major in Theme C, avoiding GFL-reflective contours below the eight-measure level. This treatment strongly aligns the pacing of Theme C with the pacing of Theme B, evident in the outsized acceleration/deceleration pairings at the highest levels of both themes. Thus, in Fou’s rendition, Theme B’s continuity, suggested by a variety of criteria, corrects Theme A’s tendency towards disjuncture and that sense of slower pacing continues through the remainder of the piece.
[30] By attending to different criteria, György Ferenczy (1956) crafts an experience of frequent oscillation between continuous and discontinuous styles of presentation (see Example 15c). The durational contour of Theme A is temporally segmented, with decelerations on beat two of every measure, more so on even-numbered measures.(17) A rarity in performances of Chopin’s eight-measure phrases, Ferenczy’s repetition of Theme A is not even GFL-reflective at the eight-measure level. Theme B continues the extreme beat-to-beat variability, but also presents GFL-reflective contours at the eight-measure level. Yet Ferenczy sharply departs from the approach of Chiu and Fou in his presentation of Theme C: curves do emerge at the eight-measure level, but they do not diminish the strong sense of segmentation at the two-measure level. In Fou’s rendition, reiterations of the F-sharp mordent flow smoothly into one another, relating it to Theme B in its continuity of presentation. Ferenczy nearly comes to a halt in even-numbered measures of Theme C, relating it to the fragmented Theme A. The effect of Ferenczy’s treatment of Theme C is to accentuate the smoothness of Theme B upon its return in measure 49.
[31] In Fou’s rendition of the piece, the jarring transition from a span with frequent temporal disjunctures to one with continuous presentation only occurs once, in the transition from A2 to B1. Thereafter, GFL-reflective contours are found primarily at the eight-measure level. Ferenczy inserts two other such transitions, from B2 to C1 and from C2 to B3, thereby highlighting Theme B’s continuity in comparison to Theme C, material that one familiar with other renditions of the piece (such as Fou’s) would expect to be presented more smoothly. In Ferenczy’s rendition, Theme B returns not out of tonal obligations, nor because it is necessary to the internal coherence of the piece, but to correct the abandonment of its mode of presentation. The impact of Ferenczy’s durational decisions, to my mind, is a reconstrual of the unfolding of pacing in the piece at the highest hierarchical levels. Whereas Chopin implies (and many performers present) a contrast in styles of pacing followed by their synthesis, Ferenczy refuses to ameliorate that initial contrast. In his rendition Ferenczy goes beyond conveying “the” grouping structure of the Mazurka. Rather, by choosing inconsistently from among diverse criteria—attending to tonal continuity in Theme B but not in Theme C, attending to dynamic contrast in Theme A but bypassing the salience of dynamic continuity in Theme C—Ferenczy creates an experience of frequent and arresting changes in pacing not explicit in Chopin’s notation.
Trajectories of Continuity in Op. 63, No. 3
Example 16. Mazurka in C-sharp minor, op. 63, no. 3, abbreviated score and evidence for segmentation at various levels of time-span organization
(click to enlarge)
Example 17. Mazurka in C-sharp minor, op. 63, no. 3, formal diagram
(click to enlarge and see the rest)
Example 18. Durational contour of Ignacy Paderewski (1930), op. 63, no.3
(click to enlarge)
Example 19. Durational contour of Roberto Poli (2003), op. 63, no. 3
(click to enlarge)
[32] The Mazurka in C-sharp minor, op. 63, no. 3, displays a different plan of pacing than the two-measure/eight-measure contrast of op. 30, no. 2. Like the B-minor Mazurka discussed above, op. 63, no. 3 also has three themes, though these progress toward ever more frequent salient group endings (see the abbreviated score of Example 16 and the formal diagram of Example 17). Theme A, which modulates to the mediant in its repetition, comprises a sentence and thereby resists segmentation in the fourth measure more so than a period construction would due to its lack of a cadence. Theme B, by repeating its first two measures as its fifth and sixth measures, suggests four-measure segments more strongly. Finally, Theme C features contrapuntal cadences every four measures.
[33] Although the process toward shorter segments does not continue beyond Theme C, the fragmentation of that theme seems to pervade the return of Theme A as the concluding section of the piece. One familiar with Chopin’s mazurkas could imagine measure 49 beginning another statement and repetition of Theme A, slightly adjusted to close in C-sharp minor rather than E major.(18) Instead, the recurrence of Theme A is saturated with harmonic reversals, two arresting fermatas in measures 62 and 74, and an unusual fusion of the ending material of Theme B with recurrences of Theme A. These alterations to Theme A in its return amount to a greater sense of temporal disjuncture, perhaps a reaction to the fragmentation of Theme C.
[34] This trajectory towards fragmentation in the first forty-eight measures of the piece is reflected in the 1930 rendition of Ignacy Jan Paderewski (see Example 18). Paderewski presents Theme A and its repetition with GFL-reflective contours at the four- and eight-measure levels. The sense of a <–,+> contour is not evident at the eight-measure level of Theme B; although the ends of those phrases are lengthened, Paderewski also decelerates on the augmented sixth in the third measure of the phrase, amplifying the salience of the following measure and thereby drawing attention to the four-measure groups. Theme C presents four-measure GFL-reflective contours very clearly and consequently contains no implication of eight-measure groups.
[35] Insofar as Paderewski emphasizes more frequent salient group boundaries by shifting the location of GFL-reflective contours “downwards” from the eight-measure to the four-measure level in the first forty-eight measures, he affirms the trajectory implicit in the score. Yet performers are not obligated to emphasize this trajectory; Roberto Poli’s 2003 rendition presents another approach to the piece, one that synthesizes the tendency toward more frequent grouping boundaries with an accruing continuity of presentation (see Example 19). Unlike Paderewski, Poli conveys very clear four-measure groups during Theme A and its repetition. GFL-reflective contours at the eight-measure level do not emerge until the repetition of Theme B. Poli’s trend continues into Theme C where the evident four-measure grouping wrought by the cadences is undermined by Poli’s tendency to hold the second measure longer than the first. More significantly, the durations of two-measure groups (i.e., the points in the highest contour in the example) themselves plot a GFL-reflective contour at the sixteen-measure level, suggesting a continuity of presentation across the entirety of Theme C and its repetition.(19)
[36] Poli’s trajectory toward ever longer projected segments in the first forty-eight measures carries over into the recurrence of the main theme. Whereas the initial presentation of that theme featured clear four-measure GFL-reflective contours without such contours at higher levels, the recurrence of the theme shapes the durations of four-measure groups into a larger GFL-reflective contour in measures 49–64 reminiscent of the sixteen-measure curved contour of Theme C and its repetition. As with Ferenczy’s performance of the B-minor Mazurka, Poli’s durational decisions create a trajectory in the pacing of successive eight-measure statements that is not immediately apparent from the score. These decisions are designed not to communicate what the grouping structure of the C-sharp minor Mazurka is, but rather to enlarge the scope of what the grouping structure can be when realized in performance.
Performance: Reflection or Assessment?
[37] Music-psychological studies of timing in performance have made a valuable contribution by demonstrating a relationship between lengthening and grouping structure. Demonstrations of this relationship are particularly effective when performers are in broad agreement on questions of grouping. For example, the phrase from op. 24, no. 2 discussed in connection with Example 13 is almost always presented with GFL-reflectivity at the four-measure level and only very rarely at the two-measure level. In cases such as this, the idea that performance timing conveys an aspect of grouping structure explicitly rooted in the score is unproblematic. But just as often there is far less agreement among performers. In Theme A of op. 63, no. 3 (Examples 16–19), for example, most analysts would think the four-measure grouping is prominent even though only ten of twenty-four performers I have surveyed project that level through group-final lengthening.
[38] An approach that construes this kind of difference as approximations of structure immanent in the score—like that encountered in the writings of Todd, Clarke, Chew, and others—misinterprets the role of timing in performance but also the role of performance in the creation of musical meaning. Performers do not passively transmit structure in a one-to-one mapping, but neither do they “interpret” structure, layering inessential details over something determinate and fixed. Performers create structure much the same way as readers create poems (Fish 1980, 332). An analytical method that recognizes the creative power of performance—the power to reshape trajectories of pacing or to bypass seemingly clear aspects of grouping structure in scores—might help to likewise reshape the relationship between performers and analysts by encouraging a dialog about the possible structural descriptions a piece can support.
Mitchell S. Ohriner
Shenandoah Conservatory
Shenandoah University
1460 University Dr.
Winchester, VA 22601
mohriner@gmail.com
Works Cited
Bengtsson, Ian, and Alf Gabrielsson. 1980. “Methods for Analyzing Performance of Musical Rhythm.” Scandinavian Journal of Psychology 21: 257–68.
Bergson, Henri. 1946. The Creative Mind. Translated by Mabelle Louise Cunningham Andison. New York: Philosophical Library.
Bor, Mustafa. 2009. “Contour Reduction Algorithms: A Theory of Pitch and Duration Hierarchies for Post-Tonal Music.” Ph.D. dissertation, University of British Columbia.
Caplin, William. 2000. Classical Form: A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven. New York: Oxford University Press.
Cheng, Eric, and Elaine Chew. 2008. “Quantitative Analysis of Phrasing Strategies in Expressive Performance: Computational Methods and Analysis of Performances of Unaccompanied Bach for Solo Violin.” Journal of New Music Research 37, no. 4: 325–38.
Clarke, Eric F. 1988. “Generative Principles in Music Performance.” In Generative Processes in Music, ed. John Sloboda. 1–26. Oxford: Clarendon Press.
Clarke, Eric and Cathy Baker-Short. 1987. “The Imitation of Perceived Rubato: A Preliminary Study.” Psychology of Music 15: 58–75.
Cook, Nicholas. 1999. “Analyzing Performance and Performing Analysis.” In Rethinking Music, ed. Nicholas Cook and Mark Everist. Oxford: Oxford University Press.
—————. 2009. “Squaring the Circle.” Musica Humana 1, no. 1: 5–28.
Cook, Nicholas and Daniel Leech-Wilkinson. 2010. “A Musicologist’s Guide to Sonic Visualiser,” Centre for the History and Analysis of Recorded Music, accessed November 12, 2010, http://www.charm.rhul.ac.uk/analysing/p9_1.html.
Dahlhaus, Carl. 1987. Schoenberg and the New Music. New York: Cambridge University Press.
Desain, Peter and Henkjan Honing. 1993. “Tempo Curves Considered Harmful.” Contemporary Music Review 7: 123–38.
—————. 1994. “Does Expressive Timing in Music Performance Scale Proportionally with Tempo?” Psychological Research 56: 285–92.
Dixon, Simon, Werner Goebl, and Emilios Cambouropoulos. 2006. “Perceptual Smoothness of Tempo in Expressively Performed Music.” Music Perception 23, no. 3: 195–214.
Dodson, Alan. 2008. “Performance, Grouping, and Schenkerian Alternative Readings in Some Passages from Beethoven’s ‘Lebewohl’ Sonata.” Music Analysis 27, no. 1: 107–34.
Fish, Stanley. 1980. Is There a Text in This Class? The Authority of Interpretive Communities. Cambridge, MA: Harvard University Press.
Flash, Tamar and Neville Hogan. 1985. “The Coordination of Arm Movements: An Experimentally Confirmed Mathematical Model.” Journal of Neuroscience 5, no. 7: 1688–1703.
Friberg, Anders and Johan Sundberg. 1995. “Time Discrimination in a Monotonic, Isochronous Sequence.” Journal of the Acoustical Society of America 98, no. 5: 2524–31.
Friberg, Anders, Lars Frydén, Lars-Gunnar Bodin, and Johan Sundberg. 1991. “Performance Rules for Computer-Controlled Contemporary Keyboard Music.” Computer Music Journal 15, no. 2: 49–55.
Friberg, Anders, Roberto Bresin, and Johan Sundberg. 2006. “Overview of the KTH Rule System for Musical Performance.” Advances in Cognitive Psychology 2, nos. 2–3: 145–61.
Friedmann, Michael L. 1985. “A Methodology for the Discussion of Contour: Its Application to Schoenberg’s Music.” Journal of Music Theory 29, no. 2: 223–48.
Gabrielsson, Alf, and Ian Bengtsson. 1983. “Performance of Musical Rhythm in 3/4 and 6/8 Meter.” Scandinavian Journal of Psychology 24: 193–213.
Hallé, Charles. 1896. The Life and Letters of Sir Charles Hallé. London: Smith Elder.
Hanninen, Dora. 2001. “Orientations, Criteria, Segments: A General Theory of Segmentation for Music Analysis.” Journal of Music Theory 45, no. 2: 345–433.
Kallberg, Jeffrey. 1998. “The Rhetoric of Genre.” In Chopin at the Boundaries: Sex, History, and Musical Genre. 3–29. Cambridge, MA: Harvard University Press.
Leong, Daphne. 2002–2003. “Kaleidoscopic Symmetries: Time and Pitch Relations in Cordon Nancarrow’s Tango?” Intégral 16–17: 187–224.
Lerdahl, Fred and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. Cambridge, MA: MIT Press.
London, Justin. 2004. Hearing in Time: Psychological Aspects of Musical Meter. New York: Oxford University Press.
Madison, Guy. 2004. “Detection of Linear Temporal Drift in Sound Sequences: Empirical Data and Modeling Principles.” Acta Psychologica 117, no. 1: 95–118.
Madison, Guy and Björn Merker. 2002. “On the Limits of Anisochrony in Pulse Attribution.” Psychological Research 66: 201–7.
Margulis, Elizabeth Hellmuth. 2011. “Repetition Detection across Multiple Exposures.” In Proceedings of the Eleventh International Conference on Music Perception and Cognition (ICMPC11), Seattle, WA, ed. Steven M. Demorest, Steven J. Morrison, and Patricia S. Campbell. 325. Seattle, WA: University of Washington Press.
Michon, John. 1978. “The Making of the Present: a Tutorial Review.” In Attention and Performance VII, ed. Jean Requin. 89–111. Hillsdale, NJ: Erlbaum.
Morris, Robert. 1993. “New Directions in the Theory and Analysis of Musical Contour.” Music Theory Spectrum 15, no. 2: 205–28.
O’Malley, Michael H., Dean R. Kloker, and Benay Dara-Abrams. 1973. “Recovering Parentheses from Spoken Algebraic Expressions.” IEEE Transactions on Audio and Electroacoustics 21, no. 2: 217–20.
Palmer, Caroline. 1989. “Mapping Musical Thought to Musical Performance.” Journal of Experimental Psychology: Human Perception and Performance 15, no. 2: 331–46.
Poynter, W. Douglas. 1983. “Duration Judgment and the Segmentation of Experience.” Memory and Cognition 11, 77–82.
Repp, Bruno. 1992a. “A Constraint on the Expressive Timing of a Melodic Gesture: Evidence from Performance and Aesthetic Judgment.” Music Perception 10, no. 2: 221–41.
—————. 1992b. “Diversity and Commonality in Music Performance: An Analysis of Timing Microstructure in Schumann’s ‘Träumerei.’” Journal of the Acoustical Society of America 92, no. 5: 2546–68.
—————. 1995. “Expressive Timing in ‘Träumerei’: An Analysis of Performances by Graduate Student Pianists.” Journal of the Acoustical Society of America 98, no. 5: 2413–27.
—————. 1996. “The Dynamics of Expressive Piano Performance: Schumann’s ‘Träumerei’ Revisited.” Journal of the Acoustical Society of America 100, no. 1: 641–650.
Rink, John, Neta Spiro, and Nicolas Gold. 2011. “Motive, Gesture, and the Analysis of Performance.” In New Perspectives on Music and Gesture, ed. Anthony Gritten and Elaine King. 267–92. Burlington, VT: Ashgate Publishing Company.
Rothstein, William. 1989. Phrase Rhythm in Tonal Music. New York: Schirmer Books.
Runeson, Sverker. 1974. “Constant Velocity—Not Perceived as Such.” Psychological Research 37, no. 1: 3–23.
Sapp, Craig. 2007. “Comparative Analysis of Multiple Musical Performances.” In Proceedings of the Eighth International Conference on Music Information Retrieval. September 23rd–27th, 2007, Vienna, Austria.
—————. 2008. “Hybrid Numeric/Rank Similarity Metrics for Music Performance Studies.” In Proceedings of the Ninth International Conference on Music Information Retrieval. September 14th–18th, 2008, Drexel University, Philadelphia, PA.
Schultz, Rob. 2008. “Melodic Contour and Nonretrogradable Structure in the Birdsong of Olivier Messiaen.” Music Theory Spectrum 30, no. 1: 89–137.
Scott, Donia. 1982. “Duration as a Cue to the Perception of a Phrase Boundary.” Journal of the Acoustical Society of America 71, no. 4: 996–1007.
Seashore, Carl. 1936. Objective Analysis of Musical Performance. Iowa City, IA: University of Iowa Press.
Shove, Patrick and Bruno H. Repp. 2005. “Music Motion and Performance: Theoretical and Empirical Perspectives.” In The Practice of Performance, ed. John Rink. 55–83. New York: Cambridge University Press.
Stern, Daniel. 2004. The Present Moment in Psychotherapy and Everyday Life. New York: W. W. Norton and Company.
Subotnik, Rose Rosengard. 1991. Developing Variations: Style and Ideology in Western Music. Minneapolis: University of Minnesota Press.
Thomas, Kim. 2007. “Just Noticeable Difference and Tempo Change.” Journal of Scientific Psychology 2: 14–20.
Todd, Neil. 1985. “A Model of Expressive Timing in Tonal Music.” Music Perception 33, no. 1: 33–57.
Tufte, Edward. 1983. The Visual Display of Quantitative Information. Cheshire, CT: Graphics Press.
Viviani, Paolo and Natale Stucchi. 1989. “The Effect of Movement Velocity on Form Perception: Geometric Illusions in Dynamic Displays.” Perception and Psychophysics 46, no. 3: 266–74.
West-Marvin, Elizabeth. 1991. “The Perception of Rhythm in Non-Tonal Music: Rhythmic Contours in the Music of Edgard Varèse.” Music Theory Spectrum 13, no. 1: 61–78.
Zakay, Dan and Richard A. Block. 1997. “Temporal Cognition.” Current Directions in Psychological Science 6, no. 1: 12–16.
Recordings Cited
Ashkenazy, Vladimir. 1977 [1987]. Mazurkas. London 417 584-2.
Bunin, Stanislav. 1988. Four Impromptus, Four Waltzes, Five Mazurkas, Three Ecossaises, Two Etudes, Nocturne. Deutsche Grammaphon 431 585-2 G CE.
Chiu, Frederic. 1999 [2000]. Complete Mazurkas. Harmonia Mundi HMU 907247.48.
Ferenczy, György. 1956 [2002]. Great Hungarian Musicians: György Ferenczy. Hungaraton Records HCD 32121.
Paderewski, Ignacy. 1930 [1999]. Great Pianists of the Twentieth Century: Ignacy Jan Paderewski. Philips Classics 456919-2.
Poli, Roberto. 2003. Chopin: Complete Piano Works Volume One. OnClassical OC27R–27.
Ts’ong, Fou. 2005. Mazurki. The Fryderyk Chopin Institute NIFCCD 001.
Footnotes
1. More recently, Cheng and Chew (2008, 335) have attempted to quantify the extent to which local effects impact GFL through their measurement of “phrase typicality,” the proportion of performances within a corpus that place a local maximum in duration on a proposed group ending. The phrase typicality of group endings in a corpus of recordings of the Andante movement of J. S. Bach’s Second Violin Sonata, for example, shows a wide range, from .25 to nearly 1. This range suggests a diversity in performance practice at odds with existing models of timing derived from grouping-structural descriptions.
Return to text
2. One might suppose that Chopin’s slur, drawn from measure 3 through the end of measure 4 in the first German, French, and English editions, adequately addresses the question (see Chopin First Editions Online, accessed April 21, 2011, http://www.cfeo.org.uk/). William Rothstein (1989, 220) observes, however, that for every phrase boundary explicated by Chopin’s slurring, another is obfuscated.
Return to text
3. In arguing that analysis is constrained by performances heard, I must emphasize that for most analysts, the performance most often heard is the informal and perhaps inaudible one undertaken in the processes of becoming familiar with a piece. Thus the boundary between the performer and the analyst cannot be understated.
Return to text
4. Others would term Example 2 a plot of “expressive timing” in performance. I avoid this term because of the vagueness of what is being “expressed.” In the music-psychological literature, “expressive timing” refers to the expression of a score’s immanent content (usually grouping structure) and, as I and others have argued, such a construal of the role of performance minimizes the performer’s role in the creation of musical meaning (Cook 1999, 242).
Return to text
5. In making plots, Edward Tufte has cautioned against using graphical elements that only present information already available through other elements. The lines in Example 2 may be such an element, though they are a hallmark of the expressive timing literature. The danger of connecting measured durations with lines can be illustrated at the beginning of Example 2a. Although a line ascends between beat one and beat two, this does not mean that the eighth notes that bisect beat one decelerate. Lines are necessary in subsequent examples to distinguish, within a single plot, different performances (e.g., Example 3), contiguous groups (e.g., Example 7), and different hierarchical levels (e.g., Example 15). I use them in Example 2 only to introduce a consistent graphical style. A number of methodological issues involving the measurements plotted in Example 2 are discussed below (see ¶18–20).
Return to text
6. Another means of highlighting this difference is through the measurement of the “durational contrast” between the two melodic events in measure 4 of the example (Friberg, et. al. 1991, 51). In a “metronomic” rendition, the durational contrast (i.e., the ratio of the duration of the half note compared to the duration of the quarter note) would be 2 (2 ÷ 1 = 1). Because Ashkenazy accelerates through the measure, his durational contrast is .78s ÷ .37s = 2.11, whereas Chiu’s durational contrast is .67s ÷ .42s = 1.59.
Return to text
7. I mean “time-span organization” in the sense of Lerdahl and Jackendoff (1983, 124–44).
Return to text
8. The sentence “Pat and Antonia or Dave will help” is ambiguous in that it can be parsed as “[Both] Pat and Antonia or [only] Dave will help” or “Pat and [either] Antonia or Dave will help.” Alan Dodson (2008) takes a similar approach, exploring the effect of performance on ambiguous grouping situations in performances of Beethoven’s “Lebewohl” sonata.
Return to text
9. Though Repp did not discuss curved durational contours at higher levels of time-span organization in his articles on “Träumerei,” the occasional absence of curved contours at higher levels has been confirmed by the author using data supplied by Repp.
Return to text
10. The application of contour-theoretical approaches to durations is not new; see especially West-Marvin (1991), Leong (2002–03), and Bor (2009). The difference between these authors’ approach and my own is that they begin with whole-number multiples of some notational constant and I begin with real-number measurements of performed durations.
Return to text
11. Other algorithms might reduce these csegs further. Schultz (2008), for example, modifies Morris’s algorithm to address these sorts of “saw-toothed” contours by eliminating minima and maxima within 3-element windows that are not minima or maxima within the entire contour unless they occupy the first or last position of the contour. This algorithm would remove the central element of <41203> and <40213>; both contours would then reduce to <201> with a CAS of <–,+>. Schultz is clearly more concerned with csegs that refer to pitches rather than durations, and I would argue that if the local maxima in durations can be perceived they should not be reduced out. Bor (2009) has recently presented another algorithm that prunes csegs based on a 5-element window rather than a 3-element window, though he has also cautioned against using contour reduction algorithms when addressing durations rather than pitches.
Return to text
12. Estimates for the just-noticeable difference (jnd) in tempo change range from 2.5% of durations with a threshold of 6ms at fast tempos (Friberg and Sundberg 1995; Madison 2004) to above 8% of durations at moderate tempos (Thomas 2007, Madison and Merker 2002). Whether the jnd for tempo change scales with tempo (i.e, whether Weber’s Law applies) is controversial, as is whether the jnd is the same for increments and decrements of tempo—Thomas reports inconclusive evidence casting doubt on both—but I’ll assume these statements to be true.
Return to text
13. For example, even at 220 beats per minute, changes in duration less that 14 milliseconds are not deemed perceptually significant in this study.
Return to text
14. The B-flat minor Nocturne is notated in 6/4. I have re-barred it to 3/4, reflecting the rate of what Caplin (2000, 35) distinguishes as “real measures” rather and “notated measures,” a decision warranted by the tempo and harmonic rhythm. Data for op. 30, no. 2 and op. 24, no. 2 was collected through the The Mazurka Project at the AHRC Research Centre for the History and Analysis of Recorded Music (Sapp 2007). Using a hybrid data collection method that combines human-generated tapping data with automated onset detection techniques, the Project has published onset data for as many as 80 performances of many of the mazurkas. The Project has already produced several publications on issues of timing in Chopin performance (Sapp 2008; Cook 2009; Rink, Spiro, and Gold 2011).
Return to text
15. Jeffrey Kallberg (1998) makes a similar point in a discussion of the G-minor Nocturne op. 15, no. 3, a piece that mixes diverse thematic material, topical content, and tonal areas without any eventual integration.
Return to text
16. Though as the evidence cited in Example 14 demonstrates, other criteria might lend greater saliance to other levels, such as the repetition of the two-measure linear intervallic pattern in Theme B.
Return to text
17. Ferenczy accentuates the two-measure grouping of Theme A by lengthening the second beats of even-numbered measures. Yet these groupings are not GFL-reflective because the second beats of odd-numbered measures are also lengthened, though not to the same extent. Ferenczy’s consistent lengthening of beat two is a response not only to grouping structure but also to meter, and these components of timing are always entangled. Averaged over the whole performance, the durational contour of Ferenczy’s triple meter is <.28,.40,.32>, not the isochronous <.33,.33,.33>. A consistently lengthened second beat is a tendency found in many performances of the mazurkas, perhaps deriving from Chopin’s own playing (Hallé 1896, 34), and Ferenczy reflects this tendency more than any other rendition presented here. Justin London argues (through a concept he calls the “Many Meters Hypothesis”) that consistent alterations of even beat durations constitute a meter in their own right, one that experienced listeners will draw upon when attending to performances (London 2004, 155, 160). Thus durational responses to grouping structure are heard through the patterned adjustments that respond to meter. The relevant question for temporal segmentation is not how each beat relates to adjacent beats, but how each beat’s relationship to the overall <.28, .40, .32> metric type compares with adjacent beats’ relationships to that type. This can be modeled by dividing the durations of each measure by <.28, .40, .32>, making the second beats slightly shorter in relation to the first and third beats. Such a transformation can be understood as removing the meter-specific component of Ferenczy’s durational contour. If this is an accurate model of how listeners detect lengthening, then most of Ferenczy’s two-measure groups are GFL-reflective as I’ve described.
Return to text
18. Twelve of Chopin’s forty-one published mazurkas, nearly a third, end this way. See mazurkas in F-sharp minor (op. 6, no. 1), C-sharp minor (op. 6, no. 2), G minor (op. 24, no. 1), C minor (op. 30, no. 1), B minor (op. 30, no. 2), D-flat major (op. 30, no. 3), G-sharp minor (op. 33, no. 1), C major (op. 33, no. 3), F minor (op. 63, no. 2), G major (op. 67, no. 1), G minor (op. 67, no. 2), and F major (op. 68, no. 3).
Return to text
19. At Poli’s tempo, Theme C and its repetition last around twenty seconds. By noting the GFL-reflective contour of the entire group, I am suggesting that attention in listening (i.e., the “perceptual present”) can occupy this entire span. Estimations of the perceptual present usually extend from 2–12 seconds, but I would argue that the accruing length of projected groups in Poli’s rendition might enable this longer span to be taken in as a whole. For assessments of the duration of the perceptual present, see Stern (2004, 23–41) and Michon (1978).
Return to text
Copyright Statement
Copyright © 2012 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Editorial Assistant
Number of visits: