Musical Forces and Agential Energies: An Expansion of Steve Larson’s Model

[1] From the time Steve Larson and I were friends at Michigan nearly thirty years ago, I have appreciated Steve’s native intelligence and sensitive musicianship, and admired its flowering into some of the most original and thought-provoking work in the interdisciplinary reaches of music theory. Whether adapting Schenkerian analysis to explain jazz improvisation, drawing on music cognitive findings to explain prolongation and improve aural skills pedagogy, or collaborating with a renowned philosopher to explain how we interpret movement in music, Steve’s creative energies knew no bounds.⁽¹⁾

[2] Steve’s metaphorical application of physical forces to explain continuities in melodic and rhythmic patterning is one of his signature contributions to the field of music theory. As he gathered converging evidence for his theory of musical forces, I was honored to help shepherd his book, Musical Forces: Motion, Metaphor, and Meaning in Music, to publication in January 2012.⁽²⁾ As early as 2003, during his residency in Bloomington, I had shared with him some of my own conjectural expansions to his theory, from the perspective of my work on gestural agency and its energies. In my book on musical gesture I cited his evidence for musical forces as part of a virtual physical environment with reference to which listeners can experience, or infer, embodied agency. I also briefly introduced agentially motivated motion, considered momentum as a supplement to the concept of inertia, and suggested the possibility of virtual musical friction (Hatten 2004, 115–16).⁽³⁾ Here, in honor of Steve and inspired by his own quest for analogues and metaphors of motion in music, I will expand on those initial speculations.⁽⁴⁾

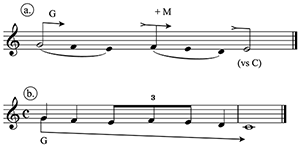
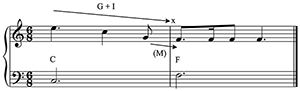
[3] First, let’s review how we hear music when we infer Larson’s musical forces of gravity, magnetism, and inertia. A melody, as he puts it, “gives in” to these musical forces, and throughout the book he offers compelling examples of the typicality of such motion. Gravity, by analogy to our human experience of it on earth, is the tendency to descend to a stable platform (stability here determined by tonal context). Magnetism is the tendency to move in either direction to the closest stable pitch in a given collection’s alphabet, or scale. And inertia is the tendency of a given state, process, or patterning to continue. These forces can be mutually supportive, or they can counteract each other. In Example 1 a stepwise descent from scale-degree $\hat{4}$ to $\hat{3}$ in C major is impelled by both gravity (descent to a stable platform) and magnetism (moving toward the closest stable pitch—here, a half step away). Continuing by step to tonic will exemplify inertia (in tandem with gravity in this example) but contradict magnetism, since E moves to D a whole step away, instead of back by half step to F.⁽⁵⁾ Continuing stepwise motion past the tonic C to B further exemplifies inertia, in that the downward motion tends to continue, here with enough force to push past a stable platform. But in this example, the magnetism of B to resolve to C may then be understood as counteracting both inertia and gravity: overcoming inertia by changing direction, and overcoming (earthbound) gravity by changing that direction from down to up. This brief example illustrates only the most basic application of the theory.

[4] Larson also annexes Schenker’s prolongational levels; when a pattern of pitches moves as a unit (e.g., in the case of a sequence), both the pattern and its structural pitches will be constrained by Larson’s three forces. Example 2 demonstrates how different patternings of the same six pitches will imply movement to a different seventh pitch, based on the distinct structural pitches that emerge. This hierarchical conception also means that the listener will shift among relevant gravitational platforms as the relevant harmonic context affects interpretation of the melodic pitches. For example, if an implied harmonic root shifts from C to F, the gravitational platform will shift accordingly. In Example 3 a melody descends by arpeggiation, and we would expect a continuation of the tonic arpeggiation would lead next to E, but the shift of harmonic underpinning produces an alternative goal, F, which displaces the inertial continuation of the original pattern. This shift is not as disruptive because the melody is still giving in to the locally relevant gravitational platform. Voice-leading in a Schenkerian sense is thus clearly affected by the harmonic orientation of Larson’s forces, which constitute the diatonic tonal system’s means of creating what I have termed a virtual environment in which movement can flow to a point of repose (Hatten 2004, 115). For Schenker, the patterns by which melodic lines move inexorably to closure are the Ur-forms that contribute to the coherence of tonality, which may be understood as a hierarchy of resolutions—or, in Leonard B. Meyer’s memorable phrase, a “hierarchy of closures” (1973, 89).

[5] But constraints are not the whole story. Melodies exhibit at least some degree of freedom, which listeners can infer when a melody simply does not give in to one of the three forces that Larson has theorized. Consider Example 4. What might a listener infer when hearing an upward leap in a tonal melody, a move that immediately counters both gravity and magnetism? And what if this happens at the very beginning of a melody, thereby counteracting the inertia of stasis as well? If, as I have suggested, we imagine a virtual environment in which Larson’s three forces constitute environmental constraints, then such a leap would require additional energy, and the requisite energy cannot be provided by the three musical forces if it contradicts each of them. Instead, we are invited to infer an agent—not only embodied but able-bodied, and capable of generating what might be called initiatory energy—the hitherto-unaccounted force necessary to overcome the inertial stasis of the first pitch, the gravitational pull that would press the pitch downward, and the magnetism that would exert it to move instead by step (not by leap) in whichever direction was closest or most stable. This brief example suggests that the tendency to hear musical motion as embodied depends on our hearing a succession of pitches as motivated by an energetic agency that can counteract as well as give in to the virtual environmental forces of gravity, magnetism, and inertia.

[6] Let us examine inertia more closely. Is it really a force, or is it rather the result of the momentum achieved by an independent agent? Consider another basic example, that of a melody which ascends by step. In its embodied interpretation, as “climbing upward by step,” we understand that climb to have required energy. Magnetism may provide an assist along the way, tipping the balance whenever the option is a half step up instead of a whole step down. However, starting from tonic, this will occur only between $\hat{3}$ and $\hat{4}$, and $\hat{7}$ and $\hat{8}$. Once a stepwise process begins to emerge perceptually (by the time we hear the third pitch), an interpretation of climbing implies an injection of agential energy sufficient to achieve momentum, which may be defined more generally as “strength or continuity derived from an initial effort” (Brown 1993). What the concept of musical momentum implies is that there must be some source of energy capable of overcoming inertial stasis, and that energy clearly cannot be provided by Larson’s three forces in many cases of upward melodic motion, including upward leaps. It is only after having achieved momentum that an unimpeded continuation of consistent motion (by step or by arpeggiation) can reflect an analogue to the physical law of inertia, which is simply the tendency of a given state (whether moving or stationary) to persist. Inertia, as in the physical world, does not contribute any energy of its own. Instead, the energy creating momentum must be inferred as having its source in a presumed agent (whether human or not).

[7] Leonard B. Meyer hints at a notion of momentum in Explaining Music when he introduces the concept of a reversal as a kind of deflection that “change[s] the implications generated by the initial, primary patternings” (1973, 119). As he continues: Particularly when they tend toward uniformity, so that no decisive points of structural stability are established, patterns develop a strong internal momentum. In such cases, a marked, unequivocal break in process is needed if closure is to be effective and convincing. Since as a rule such uniform patterns take the form of linear sequences, reversals generally involve a skip followed by a change in the direction of the motion—from descending to ascending, or vice versa (119). This “break in process” as a means of countering the non-closural momentum created by patterning reflects a principle Meyer learned from Barbara Herrnstein Smith’s Poetic Closure (1969).⁽⁶⁾ With the locution “patterns develop a strong internal momentum,” Meyer clearly suggests that momentum arises from the implicative force of a pattern. What is missing in Meyer’s account is an agent, as opposed to a disembodied pattern, as source of that energy—and ultimately of the decision to move in a new direction, in the case of a break in process (reversal).

[8] What Meyer suggests by momentum is actually pattern implication, and thus similar to Larson’s inertia at the level of the pattern and its structural pitches. Meyer draws his concept of pattern implication from the Gestalt law of good continuation, as does Larson. And both go further, emphasizing not only continuation but completion. As Larson phrases it,

Experienced listeners of tonal music expect melodic completions in which the musical forces of gravity, magnetism, and inertia control operations on alphabets in hierarchies of elaboration whose stepwise displacements of auralized traces create simple closed shapes (Larson 2012, 110).

Larson goes further than Meyer in elaborating rules (which are then formulated as algorithms) that will predict listener expectations for melodic continuation and completion in various tonal contexts.

[9] But it is my concept of musical momentum, with its implied injection of energy by an agent, that is missing from both Meyer’s and Larson’s accounts. And such agential energy must build up to a level sufficient to overcome the inertia of an object at rest, as well as any virtual environmental forces such as gravity, in order to achieve continuity of motion (an isolated upward leap, as in Example 4, clearly loses its initial momentum if it does not produce another leap in the same direction). The inertia of an object in motion, then, may be understood as the result (not the cause) of sufficient energy having been invested earlier by an agent such that the object could have initially achieved the very motion that can then be continued. The law of inertia with respect to motion merely recognizes this prior achievement and predicts the continuation of achieved momentum in the absence of any impedance. Although we can incorporate the implication of pattern continuation into an enlarged concept (which I will call implicative momentum), the embodied formulation of such patterned processes still requires an investment of energy sufficient to reach a state of motion that can then be continued.

[10] Does musical motion, once it achieves momentum, continue unimpeded through a neutral environment? Or does it require a continual investment of energy to be sustained? A sense of winding down when sustaining energy begins to decline can be heard as attenuating any sense of momentum achieved. The third movement of Beethoven’s String Quartet in B-flat major, op. 130 (Example 5) offers clear examples of such “winding down” effects, as I have argued elsewhere (Hatten 2004, 35–52). In the third measure of Example 5 a chromatically side-slipping sequence suggests, already for Leonard Ratner (1980, 391–92), the winding down of a clockwork mechanism. I interpret this passage slightly differently, as embodying a breakdown of willed energy on the part of a virtual agent.

[11] In the physical world, friction is the effect of an environmental medium (for example, air) that acts as a drag and slows down inertial motion; hence, a constant infusion of agential energy is required to counteract environmental friction, in order to maintain a given motion. Might we infer a virtual musical effect akin to friction, functioning as an environmental constraint alongside Larson’s musical forces? A melody climbing up from tonic may require initiatory energy and implicative momentum to override gravity, but the tonic left behind will not typically be heard as offering friction to further constrain the effort to rise. However, if the tonic continues to sound as a stationary pedal point, its ongoing stasis might be interpreted as creating a drag-anchor effect on the rising melodic line, which must invest extra agential energy in order not only to climb, but now to struggle upward. Oblique motion between two voices beginning on the same pitch or pitch class will generate dissonance with the first diverging step, and this dissonance between gradually expanding lines may further suggest the frictional effect of an environmental element that impedes the motion of an agent. The extra expenditure of energy required of an agent to overcome friction as well as gravity may well be reflected musically by increased dynamics in the score.

[12] But the pedal may in turn be heard as an agent in its own right, with its own “pull,” so to speak.⁽⁷⁾ The drag-anchor analogy need not assume that the pedal is part of a neutral environment of physical forces. Such a pedal point under an obliquely rising line may at times be interpretable as an opposing agential force that has been introduced into the virtual environment. As an example, consider the opening of Brahms’s First Symphony (Example 6), in which the pedal may be interpreted as an external agency akin to Fate, against which the ascending voices are struggling to emerge and free themselves. Further agential friction is generated by contrary motion in this example. However, once we infer agential energy, we have left the analogue of a physical environment and moved to the more complex realm of a contextual situation. Instead of friction, then, we might simply interpret agential conflict as the more appropriate analogy.⁽⁸⁾

[13] Now let us consider the implications of Larson’s analogy involving magnetism. The degree of closeness of pitches in a given alphabetized collection determines their degree of attraction. But attraction is not only attributable to closeness—it also is attributable to the degree of stability of one of the two pitches (compare gravity, where a more stable pitch is interpreted as the platform). Thus, in C major, a chromatic F♯ is pulled magnetically to G, not to F-natural, even though scale-degrees $\hat{4}$ and $\hat{5}$ are equidistant (in equal-tempered tuning) to the chromatic pitch ♯$\hat{4}$. Imagine the weight of a structural scale degree as analogous to physical mass. Larson’s force of magnetic attraction, possessed by centers of stability in the style, might in that case have been subsumed under the more global force of gravity. But as Larson points out (Larson 2012, 22–23), the physical environment for our bodies is not that of outer space, where mass determines degree of gravitational attraction (ignoring for purposes of the analogy Einstein’s more accurate theory). Since we do not experience in our bodies the local gravitational mass of smaller bodies or objects, Larson (2012, 95) metaphorically captures this musical force by analogy with our experience of magnetism (and by further analogy with common metaphors of magnetism as forms of attraction, whether charismatic or sexual).

[14] Physically, the closer metal comes to a magnet, the greater the attraction, and analogously, the closer a pitch approaches a center of relative stability (e.g., by half step instead of whole step), the greater the pull toward that center (leading to a resolution into that center).⁽⁹⁾ The center need not actually be sounded—it exerts its force within the virtual environmental field established by tonality.⁽¹⁰⁾ But one might note that when hearing C♯ as a chromatic passing tone moving between two scale degrees, C and D, the C drags on C♯ even while the D pulls on it. C and D have equivalent half-step attractiveness to C♯. But C would be more stable than D in the key of C major; thus the drag would be greater than the pull. And conversely, D would be more stable than C in the key of G; thus in that key the pull would be greater than the drag.⁽¹¹⁾

[15] The opposite of attraction is repulsion, which Larson touches upon briefly in his discussion of magnetism: “Magnets (if you reverse the poles) can also repel each other” (2012, 95). But if we require two magnets to illustrate this phenomenon, an analogue of repulsion in music presupposes two agents possessing a reciprocal magnetic power. Thus, Example 7 introduces two independent voices in the right hand. The analogy resembles the one just presented involving friction; in this case, an agential reaction against a sounding center of relative stability (which may also imply an opposing agent) produces a dissonance that repels the other pitch and forces it to move in an opposite direction from the initial agent. The prototype for this kind of agential repulsion is the 2–3 suspension.⁽¹²⁾ In measure 2 of Example 7, F moves closer to the opposing agent E, but instead of magnetism drawing E into F (the more stable local pitch), a dissonant repulsion forces the E to move in the opposite direction, toward D. If the dissonance first produced is a minor second, as here, the force of repulsion will be felt as correspondingly greater than in the case of a major-second dissonance, which further supports the analogy with magnetism.

[16] Interestingly, effects akin to repulsion do not depend entirely on closeness. Consider the suspension illustrated so expressively by Mozart in his “Confutatis” movement from the Requiem (Example 8). Here, the “salve me” features a major third moving to a perfect fourth, which in triadic tonality is heard as a dissonance. The originally stable C is repulsed by the F, and C gives way to B. Remarkably, the acoustically greater dissonance of a diminished fifth that this produces is an acceptable resolution of the non-triadic dissonance of a perfect fourth, since the diminished fifth represents two chord tones in the dominant-seventh chord. Of course, as a tritone the diminished fifth must also resolve, and here Larson’s magnetism nicely captures the forces drawing B to C and F to E. I would simply add that the diminished-fifth interval itself (a higher-level pattern) is also drawn into the more stable major-third interval, C–E, providing further evidence that stability and not solely proximity is crucial for the effect of magnetism. In effect, $\hat{1}$ and $\hat{3}$ are magnetized by their tonal stability in the style.

[17] Figure 1 summarizes the various forces or effects I have discussed thus far, interpretable either (1) as reflecting a virtual environment, (2) as contextually created by an opposing virtual agent, or (3) as arising from a central virtual agent with sufficient energy to counteract environmental or other agential forces.

[18] We can now consider further interactions of these forces. Gravity requires a (lower) stable platform, like the earth beneath our feet, to which pitches are drawn. The inertia of a descending motion (i.e., sustained agential momentum without any braking or acceleration) will result in an impact. Is it possible for the platform to be pliable, enabling it to absorb the shock of a gravitational impact? Consider the various kinds of impacts upon a platform (such as the tonic) in cases of uninflected (unbraked) inertial contact, as shown in Example 9. These impacts may serve to indicate the platform’s relative rigidity, as well as the force of the inertial descent (which may be greater than presumed gravity would warrant, depending on the degree of already-achieved agential momentum). A hardened platform (9a) will result in either a hard “bounce” or, as here, a “splat”; a soft platform (9b) may be inferred from a gentle “rebound” or “reverberation”;⁽¹³⁾ and a more permeable platform (9c) will allow a descent just past the platform, before recapture by magnetism (imagine the game of Red Rover, in which the defenders’ linked arms absorb the weight of the attacking body as it bulges the line, which flexes but holds, before bringing the body to a halt).

[19] But the descent may also be modified by agential intervention—for example, by some kind of willed braking, as shown in Example 10. Composers have several means of implying the braking of momentum, ranging from decrescendo (10a), reflecting a decline in dynamic energy required to sustain momentum against friction, to ritardando (10b), indicating a decline in momentum as implied by slowing down. Other braking devices include durational expansions (10c), motivic liquidations (10d), ornaments (especially the anticipation in 10e), hemiola, and so forth. With sufficient braking, any inertial tendency to bulge beyond the platform can be neutralized.

[20] I have demonstrated ways in which the counteraction of musical forces can provide a strong trace of a willful agency—allowing for a sense of agential “free will” while moving within the constraints of a virtual environment’s field of forces. I now consider the possibility that these forces, as inferred from the fluctuations through tonal space of a common-practice melody, can themselves reflect a kind of agency—perhaps even willfulness on the part of that agent. This claim would be provocative in its extreme form: once we began to hear music as agential, all actions could be interpreted as continuous reflections of willed or received energies by the subjective agent. But how might such a presupposition affect interpretation? An implied agent would be able to “own” or even “will” (as opposed to merely “give way to” ) environmental forces by adding agential energy to the very movements implied by those forces. In Example 11a, a crescendo on a leading tone might imply willful resolution to the subsequent tonic, suggesting the power of an agent and supplementing the force of magnetism. In Example 11b an accelerated descent might supplement the effect of gravity, implying a forceful action by the agent to ground an arrival. An agent cannot “enhance” inertia, however, since inertia is not a source of energy but rather the lack of impedance by the environment to either an object’s continued motion or stasis. But an agent may easily increase momentum by any of the musical means familiar to us—especially by the directness of an accelerando.

[21] Rhythm and meter also respond to and/or reflect musical forces. Larson devotes a lengthy chapter to this phenomenon (2012, 136–79), but here I will simply mention the effect of the virtual environment created by meter (Hatten 2004, 117), in which we can experience an embodied sense of up vs. down. Meter accomplishes this over and over, which might suggest that all metric music “flows,” in the trivial sense of alternating downs and ups, and thus already emulates motion. But meter’s establishment of a stable virtual environment can perhaps be defended by analogy with the constant perceptual refreshing accomplished in vision by the “saccades,” or ever-adjusting eye movements, that occur even when we think we are focusing on a particular spot. The bar-by-bar refreshing of a virtual environment enables us to experience gravity not only tonally but metrically, as a continuous field re-instantiated by each downbeat. Once again, we can venture agential action from the energy implied by rhythms that do not conform to the metric environment. A compelling example (Hatten 2004, 117) is the opening theme from the third movement of Brahms’s Third Symphony. Example 12a shows the melody as rhythmically “normalized” in ${}_4^3$ and Example 12b as Brahms actually composed it. In Brahms’s version there is a rhythmic/metric contradiction between the anacrusis to the first bar and its downbeat placement in the second bar. The stretching of the previous pattern that engenders the contradiction is clearly expressively motivated (even if we cannot describe the effect adequately in words). The feeling of going over a wave may describe the loss of grounding created by the metric displacement of the motive in its second occurrence, along with the expansion that extends its first statement. The expansion suggests gestural yearning, and yearning in turn implies agential energy—perhaps wanting to hold on too long? How might we then interpret the contradiction between agential yearning (the suspended motive) and environmental inexorability (the downbeat)? A given performance might add enough “willful” dynamic energy to the second anacrusis such that we hear the virtual agent insisting on the environmental inexorability of the downbeat—perhaps enhancing the effect of yearning with that very insistence, while still experiencing the effect of a kind of stomach-wrenching loss of gravity. And these decidedly mixed physical sensations might be further interpreted as creating a sense of existential uncertainty. But even if we cannot decide whether this or another performance interpretation best conforms to our reconstruction of the movement’s energetic forces, we nonetheless have a better means of explaining the effects of each interpretation, and perhaps explaining our preference for one over the other. And the possibility that each may be compelling in its own way further enriches the interpretive potency and freshness of this movement.

[22] Thus far I have confined my discussion to tonal music. Larson extends the same principles to the interpretation of musical forces in tonal jazz (2012, 233–37). Could the theory be further extended to atonal music? Consider one of the landmarks of emerging atonality, the first of Schoenberg’s Drei Klavierstücke, op. 11 (Example 13). The absence of scale-degree information provided by common practice tonality means we do not have built-in environmental forces such as those hypothesized for a tonal hierarchy. Thus, any implications of forces leading to expected pitch outcomes must be earned by the work itself. Indeed, each of Larson’s musical forces can be locally activated. Gravity pulling down to a platform pitch need not imply a traditional tonal center but simply a locally asserted pitch. Magnetism as a kind of attraction between pitches will be more heavily dependent on proximity, since the magnetic power of stability within a tonal hierarchy is absent. The effect of stability may be approximated in an atonal context by gestures that recall appoggiaturas or suspension formations. For example, the melodic movement from F to E in measures 2–3 suggests a rearticulated suspension, but the presumed “resolution” is unusual in that E is actually more dissonant with respect to the accompanying chord than the suspended F. The familiar gestural pattern allows us to hear E as an implicative goal tone, despite lack of consonant resolution. Finally, inertia, as the tendency of events or patterns to continue, is relevant for any linear movement (understood as a “vector” combining direction and force), as well as for any (roughly) sequential patterning (for example, the descending third plus second pattern that is sequenced irregularly—by developing variation—in the top voice in measures 1–3).

[23] I return to tonality for a final example, of my own composition, the beginning of which I hinted earlier in Example 3 and Example 7. In the opening measures of Example 14, one may hear a virtual agent giving in to virtual environmental forces, but by the second system, the agent begins to express itself in opposition to that lulling environment. At any rate, I hear (and compositionally intended) a sense of comfort and well-being in the first four measures, which is correlated with the melody’s unproblematic “giving in” to environmental forces. The suspensions may suggest a hint of conflict (the “repulsion” discussed earlier), but their immediate resolution in an overwhelmingly consonant tonal context contributes to a sense of being enfolded. The lullaby-like, siciliana-based metric setting helps support this interpretation. In the subsequent measures the melody appears willfully to counteract the easy concession to environmental constraints and instead begins to project energetically, as implied by the large leaps in the melody. If we hear the willfulness of an agent as motivating this change in melodic contour, we may experience a corresponding expressive shift from well-being to emotional urgency. I interpret this willful projection as a kind of restless yearning, made poignant by the more plangent dissonances. The short piece then returns to “acceptant” giving in to environmental forces, leading to a gentle close.

[24] It is not hard to extrapolate from this example to countless tonal works in which agency is inferred from such flexing of melodic muscle, interpretable as increased emotional expressiveness. Such marked moments are the heart of romanticism, whether found in Bach, Mozart, Chopin, or Mahler.⁽¹⁴⁾ Understanding musical forces and their interaction with agential energies is one key to unlocking the mysteries of musical meaning, a project that was close to Steve Larson’s heart. “Wordless Carol” is dedicated to his memory.

Robert S. Hatten
Butler School of Music
University of Texas at Austin
Austin, TX 78712-1555
rohatten@austin.utexas.edu

Works Cited

BaileyShea, Matthew L. 2012. “Musical Forces and Interpretation: Some Thoughts on a Measure in Mahler.” Music Theory Online 18, no. 3.

Bharucha, Jamshed J. 1984. “Event Hierarchies, Tonal Hierarchies, and Assimilation” Journal of Experimental Psychology 113, no. 3: 421–425.

Brown, Lesley, ed. 1993. New Shorter Oxford English Dictionary. Oxford: Clarendon Press.

Hatten, Robert. 2004. Interpreting Musical Gestures, Topics, and Tropes: Mozart, Beethoven, Schubert. Bloomington and Indianapolis: Indiana University Press.

—————. 2010. “Aesthetically Warranted Emotion and Composed Expressive Trajectories in Music” Music Analysis 29 nos. 1–3: 83–101.

Larson, Steve. 2012. “Musical Forces and Melodic Patterns.” Theory and Practice 22/23: 55–71.

Meyer, Leonard B. 1973. Explaining Music: Essays and Explorations. Berkeley: University of California Press.

Pierce, Alexandra. 2007. Deepening Musical Performance through Movement: The Theory and Practice of Embodied Interpretation. Bloomington: Indiana University Press.

Ratner, Leonard. 1980. Classic Music: Expression, Form, and Style. New York: Schirmer Books.

Smith, Barbara H. 1969. Smith, Barbara H. 1969. Poetic Closure: Or Why Poems End. Chicago: University of Chicago Press.

Footnotes

1. My thanks to Jack Boss, Tim Pack, Steve Rodgers, and Caitlin Snyder of the University of Oregon for the opportunity to deliver this keynote address to a community of scholars united in their deep respect and gratitude for the life of Steve Larson. Our hearts go out to Steve’s family and friends, with whom we grieve.
Return to text

2. In my book series, “Musical Meaning and Interpretation,” with Indiana University Press.
Return to text

3. Steve graciously credited some of these ideas in two concluding sections of his book. In “Forces and Intention” (2012, 315) he mentions my characterization of his musical forces as environmental, as well as the relationship between those forces and “a perceived or implied source of gestural [agential] energy” (2004, 115–16). In “Other Forces” (2012, 320) he notes my suggested addition of musical friction to his set of musical forces (2004, 116).
Return to text

4. For an additional extension of Larson’s theory of musical forces, see Matt BaileyShea’s article in this issue (2012).
Return to text

5. However, if we take harmony into account and assume that D and F are locally stable as members of a V⁷ chord, then D would be more stable than F (the 7^th), and hence D’s greater stability might make it magnetically more attractive despite its slightly greater distance from E.
Return to text

6. As Meyer acknowledges in a footnote on p. 81, “the vital importance of closure in the articulation of forms and processes was made clear to me by Barbara H. Smith’s book, Poetic Closure: Or Why Poems End (Chicago: University of Chicago Press, 1969).”
Return to text

7. Compare Matthew BaileyShea’s use of the term “pull” in his essay in this issue (2012).
Return to text

8. Or, in BaileyShea’s terminology, we might interpret the pedal as a non-sentient “elemental force” (BaileyShea 2012, 12).
Return to text

9. Larson clearly defines magnetism “so that it describes the attraction of any unstable pitch to the closest stable pitch” (2012, 92), as discussed above (see also note 4).
Return to text

10. Larson (2012, 55) cites Jamshed J. Bharucha’s (1984) distinction between tonal hierarchies (independent of pieces in which they occur) and event hierarchies (ordered with respect to the time of a piece within which they occur). My “virtual environmental field established by tonality” would be an example of a tonal hierarchy.
Return to text

11. Our interpretation of dragging vs. pulling may thus be useful as a refinement of the experience of magnetism as it interacts with gravity.
Return to text

12. As Larson notes, “the analogy to a string of 2–3 suspensions, in which two voices seem to push each other away each time they are a step apart, might be a good example of this phenomenon” (2012, 95).
Return to text

13. Alexandra Pierce (2007, 120–35) has theorized a nuancing of timing in performance that allows for reverberation in the finishing envelope of arrival gestures; reverberation then becomes the first stage in the juncture required for elegantly embodied transitions between phrases.
Return to text

14. See, for example, my interpretation of marked expressive moments in the slow movement of Mozart’s Piano Sonata in F major, K. 533, in (2010).
Return to text

Copyright Statement

Copyright © 2012 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.

Prepared by Carmel Raz, Editorial Assistant
Number of visits: