Applying Schenkerian Theory to Mainstream Jazz: A Justification for an Orthodox Approach
David J. Heyer
KEYWORDS: jazz analysis, jazz theory, Schenkerian theory, tonic added sixth chords, V13 chords, modified Urlinien, Steve Larson, Henry Martin
ABSTRACT: This paper examines several recent modified Schenkerian analyses in order to compare the strengths and weaknesses of a modified approach with those of an orthodox approach to analyzing jazz. The comparative analyses will reveal that while the application of orthodox Schenkerian theory may be unnecessary to produce meaningful analyses, its abandonment is also unnecessary. In fact, applying an orthodox Schenkerian approach reveals transformations on structural levels that may go otherwise unnoticed, and these transformations often illuminate important relationships between jazz and common-practice music.
Copyright © 2012 Society for Music Theory
The fundamental structure represents the totality. It is the mark of unity and, since it is the only vantage point from which to view that unity, prevents all false and distorted conceptions. In it resides the comprehensive perception, the resolution of all diversity into ultimate wholeness.—Heinrich Schenker ([1935] (1979, 5) my emphasis)[1.1] Skepticism has always surrounded, and likely always will surround, the theories of Heinrich Schenker. Central to what became his best-known theory is the idea that all musical surfaces result from the composing-out of a fundamental structure, or Ursatz.
[1.2] An Ursatz, as defined by Schenker, includes one of only three possible fundamental lines, or Urlinien: ––, ––––, and –––––––. To account for other deeper-level structures, several theorists have advocated modifications to this aspect of Schenker’s theory. This has caused a rift among music theorists. Those who maintain that such modifications are essential, particularly when applied to more modern styles, argue that an analytical method must evolve along with the music to which it is being applied.(1) Other theorists contend that such modifications are unnecessary if the work in question is tonal.
[1.3] While a thorough account of these viewpoints is beyond the scope of this paper, one particular discourse relating to modified Schenkerian Urlinien seems particularly relevant. In his article “The 3-part Ursatz,” David Neumeyer (1987a) advocates a new kind of background structure (one with three voices).(2) In his published response to this essay, Steve Larson (1987a) is not convinced that Neumeyer’s new category of Ursätze is necessary, and instead advocates an orthodox two-voice reading of each of the pieces that Neumeyer analyzes. Neumeyer’s subsequent response criticizes Larson for taking what he calls a “conservative” Schenkerian stance. He writes,
The conservative Schenkerian is a fundamentalist: He or she takes Schenker’s work as a given and contributes mainly commentary or exegesis. . . The “liberal” Schenkerian, on the other hand, is more like a typical university scholar in the humanities: He or she refuses to believe that any theory is complete, any methodology perfect. The conservative Schenkerian considers “extensions” to mean filling in the details in the master’s grand design; the liberal finds the design itself a historical idea, to be given no more reverence than its due. To the conservative Schenkerian, any real change is radical, to be resisted with whatever means are at hand; to the liberal, change is a part of the natural—and necessary—growth of a discipline (Neumeyer 1987b, 36).[1.4] Neumeyer’s response implies that the theorists whom he calls “conservative” Schenkerians are unwilling to accept any modifications to Schenkerian theory even if such modifications are necessary and convincing, a characterization that hardly seems fair. Why should “conservative” Schenkerians not approach modified analyses with the same level of skepticism that “liberal” Schenkerians apply to the theory itself? After all, some of these modifications result in eliminating Schenker’s central claim—the fascinating theory that all tonal works share one of only three possible backgrounds.
[1.5] Perhaps it is not surprising that this debate is relevant to the applicability of orthodox Schenkerian theory to mainstream jazz, which contains harmonic features never addressed by Schenker. When chordal extensions appear in the melody in either the penultimate or final measure of a tune, they can have important implications for the Urlinie. Some scholars (most notably Henry Martin) have concluded that such chord tones resist a reductive explanation and should therefore be considered members of modified Urlinien. In his dissertation and subsequent book Analyzing Jazz—A Schenkerian Approach (2009), Steve Larson takes the opposing view. He writes,
So-called ninths, elevenths, and thirteenths occur in both repertories. And in either case, a complete explanation of the functions of these ‘chord extensions’ seems to require an account of their melodic relationship with more stable notes at more basic structural levels (Larson 2009, 5).[1.6] This article examines several recent modified Schenkerian analyses in order to compare the strengths and weaknesses of a modified approach with those of an orthodox approach to analyzing jazz. The comparative analyses will reveal that while the application of orthodox Schenkerian theory may be unnecessary to produce meaningful analyses, its abandonment is also unnecessary. In fact, applying an orthodox Schenkerian approach reveals transformations on structural levels that may otherwise go unnoticed, and these transformations often illuminate important relationships between jazz and common-practice music.
The Tonic Added Sixth Chord
[2.1] In his unpublished article “From Classical Dissonance to Jazz Consonance: The Added Sixth Chord,” Henry Martin examines the origins and development of the tonic added sixth chord (Iadd6), concluding that a supported by the tonic serves one of three functions (progressing from the most decorative to the most structural): (1) a dependent non-chord tone (a surface-level embellishment of ), (2) an independent chord tone (reducible only at deeper levels of structure), and (3) an inclusive chord tone (consonant and therefore left unreduced).(3)
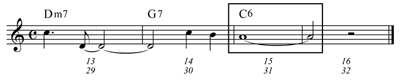
Example 1. “Mack the Knife” (Kurt Weill), measures 13–16 (also measures 29–32)
(click to enlarge)
Example 2. Henry Martin’s Example 25
(click to enlarge)
[2.2] Martin’s system of categorization places (appearing in a Iadd6 chord) on a spectrum of stability, and he provides clear and compelling examples to support his first two categories. His third category, however, places him squarely at odds with Larson’s orthodox Schenkerian view, as an orthodox approach requires to ultimately derive its meaning from a more stable pitch at a deeper level of structure—a level of structure consistent with common-practice harmony. In either approach, it can be assumed that the tonic added sixth chord sets jazz and common-practice harmony apart on the surface because, unlike common-practice pieces, countless jazz tunes, such as “Mack the Knife” (Example 1), end on a tonic added sixth chord. But Martin’s modified approach retains such a in the background, while an orthodox approach ultimately reduces it out.(4)
[2.3] Example 2 reproduces Martin’s Example 25, a voice-leading analysis of “Mack the Knife.”(5) Each measure of his graph accounts for two measures of the tune, and because the second half of “Mack the Knife” repeats the first without alteration, his graph accounts for all 32 measures of the ABAB form.
[2.4] The soprano voice at level C displays the most prominent notes of the melody in a 1:1 contrapuntal structure. Level B displays the resolution of each that appears within a Iadd6 chord to . Level A retains only the notes of resolution. The objective of his analysis is to show that if one treats as a note that resolves to, and is replaced by, at a deeper level, the voice-leading analysis becomes problematic. In measures 1–2, level B shows resolving to over the I chord; thus replaces completely at level A. He writes, “In this case, neither level A nor level B seems to help clarify the function of ” (36).
[2.5] Referring to the parallel fifths between the outer voices in measures 2–3, he writes, “The parallel chords
. . . do not seem to underlie level C” (36). Likewise, in measures 15–16 at level B, he shows resolving to , which again replaces at level A. He writes, “At the final cadence, viewing the as underlying the requires us to posit an awkward scale degree resolution of to ” (37).[2.6] Martin finds that a modified approach is needed to adequately address these problems. He notes, hypothetically, that “if Example 25C were to be reduced to a background level, that level would consist of the tonic added sixth chord with A4 as the soprano note” (36, my emphasis). The following comparative analysis, by contrast, attempts to address these problems through Steve Larson’s orthodox approach.
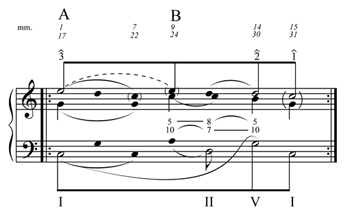
Example 3. A reduction of “Mack the Knife,” measures 1–8 (also measures 17–24)
(click to enlarge)
[2.7] Example 3 displays my analysis of measures 1–8 (also measures 17–24). The reduction adheres to Steve Larson’s strict-use method of analytic notation (Larson 1996).(6) There are several important discrepancies between Example 2 (Martin’s Example 25) and Example 3. Perhaps most importantly, level b of Example 3 includes a less prominent voice-leading path shown with downward stems not shown in Martin’s analysis.(7) This voice begins on the pickup note E, remains on E as the third of the C6 chord in measure 2, moves to the D that forms the root of the Dm7 chord in measure 4 (although the D “belongs” with the change of harmony in measure 3), and remains on D as the fifth of the G7 chord in measure 6.
[2.8] The other voice, shown with upward stems at level b, offers an interpretation in which each resolves to . While Martin concedes the resolution to an implied G in measure 6, he avoids an analysis in which the Gs in measures 2 and 8 appear at a deeper level of structure. But an orthodox viewpoint is certainly reasonable here, as in both cases the note G, an arpeggiated chord tone in the melody, literally sounds on the surface. The structural role of both Gs is of course obscured by both the length of each A that precedes them (both As occupy six beats), and by each G’s metrical placement (the G in measure 2 appears on the “and” of beat 4, while the G in measure 8 appears as part of the pickup figure to the next phrase). Although this may lessen the prominence of each G, it seems unnecessary to claim that it also alters each G’s deeper-level structural function. Instead, one can claim that the As spanning measures 1–2 and measures 7–8 function as upper neighbors, as shown at level b.
[2.9] The prominent A that spans measures 1–2 does of course obscure the parallel fifths that span measures 2–3. While a modified approach eliminates this intervallic succession, an orthodox approach shows it at both the foreground and middleground levels (levels b and a). As Schenker explains, “The middleground frequently displays forbidden successions; it is then the task of the foreground to eliminate them” (Schenker ([1935] (1979, 56). Here, the orthodox analysis highlights a key difference between common-practice music and jazz: Brahms would have eliminated these parallel fifths from the surface altogether; Kurt Weill only obscures them.
[2.10] Example 3 displays the voice shown with downward stems at level b as a structural soprano at level a. Only an implied resolution to C in measure 7 is required to complete an orthodox Schenkerian prototype. Likewise, the voice shown with upward stems at level b (G–A–G) is shown as an alto voice at level a.
[2.11] The A in measures 3–5, while consonant with the ii (Dm7) chord, functions on a deeper level as an upper neighbor to the G in measure 1 that appears over the tonic and the implied G in measure 6 that appears over the dominant. This reading draws attention to an essential orthodox Schenkerian principle that “prominent” and “structural” are not synonymous terms. Often prominent voice leading that appears on the top of a melody can function as an inner voice on a deeper level, while less prominent voice leading that appears beneath the melody can function as the structural soprano. The A is certainly prominently featured throughout the melody. But the note functions on a deeper level as an upper neighbor to G, a cover tone that appears above the structural soprano on the surface.
[2.12] Schenker gives three examples in Free Composition in which a cover tone “carries with it a neighboring note of its own” (Schenker [1935] (1979, 107). And, like the A in “Mack the Knife,” the neighbor note in each of Schenker’s examples is a that functions as an upper neighbor to .
Example 4. A reduction of “Mack the Knife,” measures 9–16 (also measures 25–32)
(click to enlarge)
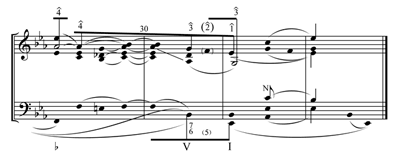
[2.13] Example 4 displays a reduction of measures 9–16, which are also measures 25–32. Like the first section, this section also contains two clear voice-leading paths, as shown at level a. As indicated at level b, the A on the downbeat of measure 15 functions, on a deeper level, as a passing tone to the G that sounds in measure 16 and is implied at the song’s conclusion in measure 32.
[2.14] In his discussion of his Example 25 (Example 2 above), Martin describes the resulting deeper-level motion from the B in measure 14 to the G in measure 15 as an “awkward” scale degree resolution. It is true that traditionally one would expect the melody note B (the leading tone) to resolve to C. But assigning this motion to a deeper-level alto voice decreases this awkwardness if we think of it as a frustrated leading tone. And while a frustrated leading tone rarely includes a passing tone, such passages can be found in earlier music, as shown by the circled notes in Example 5.
Example 5. Grieg, “En Svane,” op. 25, II, measures 29–31
(click to enlarge)
Example 6. A Schenkerian graph of “Mack the Knife”
(click to enlarge)
[2.15] Example 6 displays a Schenkerian graph of “Mack the Knife” that contains only the notes from level a of each strict-use reduction (Examples 3 and 4). The tune is unique in that the second half of its form (measures 17–32) contains no alteration of its first half (measures 1–16).(8) And while a true orthodox Schenkerian graph would likely place greater weight on the concluding cadence in measure 31, the graph nevertheless reveals the orthodox Urlinie as a 3-line that extends from the E in measure 1 to the implied C in measure 31.
[2.16] The most controversial aspect of this graph is likely the implied tone C that concludes the Urlinie—an analytical feature that a modified Schenkerian theorist would likely find troubling, as the written melody concludes on such a prominent A. Yet most jazz performers, such as Louis Armstrong (1957), conclude this tune on C in their actual performances, and this common alteration supports an orthodox reading (listen to Audio Example 1).
Audio Example 1. “Mack the Knife”
[2.17] The purpose of this orthodox Schenkerian graph is not to minimize the A’s prominence or its stylistic importance. Instead, the graph attempts to reveal other voice-leading features, at the same time explaining the prominent A, not as an irreducible chord tone (thus highlighting only the way in which it deviates from common-practice harmony), but rather as a chord tone that deviates from common-practice harmony while also functioning as an embellishment of a traditional background.
The “V13” Chord and the –– “Urlinie”
Example 7. “I Love You,” measures 28–32.
(click to enlarge)
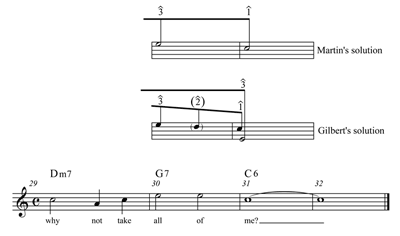
[3.1] Even more common than tunes that conclude on are tunes such as “I Love You,” the final five measures of which appear in Example 7, that conclude with a – melodic motion in which appears over the dominant chord and resolves directly to over the tonic. A that appears over the dominant (creating a chordal thirteenth) in the penultimate measure has important implications, as seems to replace , a member of an orthodox Schenkerian Urlinie.
[3.2] In his book Charlie Parker and Thematic Improvisation (1996), Henry Martin advocates modifying Schenker’s possible Ursätze to include a set of Urlinien that conclude with –, as shown in Example 8a. In his book The Music of Gershwin (1995), Gilbert addresses this topic in his analysis of “’S Wonderful.” He writes, “The so-called dominant thirteenth
. . . is so idiomatic. . . in its unresolved state that one can rightly argue against changing it” (22). Gilbert’s solution is to show as a note that is sustained over the final tonic, as shown in Example 8b (a reproduction of the second half of Gilbert’s Example 11). An orthodox Schenkerian view, on the other hand, must view a in such penultimate V13 chords as a note that ultimately has a deeper-level dependency on . This particular deeper-level dependency is so firmly rooted in common-practice music that this discussion requires an overview of the musical features that led to V13 chords in jazz.
Example 8a. Martin’s Example 2–13a
(click to enlarge)
Example 8b. Gilbert’s Example 11b (second half), the refrain of “’S Wonderful”
(click to enlarge)
[3.3] Escape tones, such as the one circled in Example 9a, are one of the clearest origins of V13 chords. While appears over the dominant chord, and is the note that immediately precedes the arrival on the tonic, the note is clearly an embellishment of, and thus dependent on, the preceding .
Example 9a. Dussek, op. 20, no. 2, measures 15–16
(click to enlarge)
Example 9b. “It Could Happen to You,” measures 29–32
(click to enlarge)
Example 10a. Chopin, Prelude in F-sharp major, op. 28, no. 13, measures 19–20
(click to enlarge)
Example 10b. “They Didn’t Believe Me,” measures 27–32
(click to enlarge)
Example 11a. Haydn, Symphony no. 101, IV, measures 7–8
(click to enlarge)
[3.4] Example 9b displays the concluding cadence of the jazz standard “It Could Happen to You,” a tune that concludes with a similar escape tone. Despite the note’s longer durational value, it is clearly an embellishment of .
[3.5] Common-practice composers often elongated such escape tones, creating a stronger harmonic effect, as shown in Example 10a.(9)
[3.6] Example 10b offers an analogous escape tone that appears in the concluding cadence of the jazz standard “They Didn’t Believe Me.” As in the Chopin example, the escape tone’s metrical weight and its durational value contribute to its increasing harmonic implication.
[3.7] In the excerpt appearing in Example 11a, the escape tone occupies the entire sounding dominant, while appears only in the predominant harmony.(10) From a Schenkerian point of view, however, the in the predominant belongs with the dominant on a deeper level; thus can still be considered an escape tone.
[3.8] Example 11b displays an analogous passage in the concluding measures of the jazz standard “There Will Never Be Another You.” Like the Haydn example, appears only in the predominant chord, while its escape tone occupies the entire sounding dominant.
[3.9] In addition to being the result of an elongated escape tone, a V13 chord can also be heard as an unresolved implied cadential
. Example 12a displays measures 6–7 of “Georgia on My Mind.” Here, the melody fulfills the resolution of to over the C7 chord, thus resulting in an implied cadential = , as indicated by the Roman numeral analysis. Example 12b displays the conclusion of the tune. Here, because the melody remains on in measure 30 instead of resolving as it did earlier, the cadential resolution comes into question, and can only be inferred.
Example 11b. “There Will Never Be Another You,” measures 29–32
(click to enlarge)
Example 12. “Georgia on My Mind,” measures 6–7 and measures 30–31
(click to enlarge)
Example 13. Schenker, Free Composition, Fig. 46, Ex. 2
(click to enlarge)
[3.10] That is not literally present in the melody of such penultimate measures is central to the skepticism of its implied presence. The most typical common-practice comparison occurs when appears within a cadential
but does not move to with the resolution, as shown in Example 13 (a reproduction of Schenker’s Fig. 46, Ex. 2 in Free Composition). Despite no literal sounding of the structural in the melody, the expected = resolution nevertheless implies its presence, and Schenker shows the note in parentheses. [3.11] Usually, such an implied is the result of a melodic motion from to in which functions on a deeper level as a member of an inner voice. This occurs frequently in both common-practice music and jazz. Examples 14a and b display reductions of measures 32–33 and measures 36–37 of Schubert’s “Mein!” from Die schöne Müllerin.(11)
Example 14a. A reduction of “Mein!,” measures 32–33
(click to enlarge)
Example 14b. A reduction of “Mein!,” measures 36–37
(click to enlarge)
[3.12] In the music of Example 14a, no sounds in the melody, but it appears as an implied tone in the reduction in measure 32. In the music of Example 14b, a leap to immediately precedes the arrival on the tonic, seemingly confirming the implied of the earlier passage.
[3.13] Two passages from Chet Baker’s improvisation on “There is No Greater Love” (1982) offer a jazz version of the Schubert examples. In the music of Example 15a, Baker’s motion from to creates an implied over the dominant, much like the music of Example 14a. Baker even includes a similar embellishing leap to . While in this case a ii chord, not a cadential
, supports on the surface, the implied resolution to over the dominant is equally compelling.
Example 15a. Baker’s solo on “There Is No Greater Love,” measures 14–15, first chorus
(click to enlarge)
Example 15b. Baker’s solo on “There Is No Greater Love,” measures 14–15, second chorus
(click to enlarge)
[3.14] The music of Example 15b shows a reduction of Baker’s improvisation over these same two measures on his second improvised chorus. Here Baker, like Schubert, seems to confirm the implied of the earlier passage by articulating immediately before arriving on the tonic, which, in this case, is anticipated.
[3.15] The preceding examples displayed instances in which receives substantial harmonic support from the dominant (as an escape tone) and instances in which does not literally sound (being an implied resolution of a cadential
). Yet from an orthodox Schenkerian perspective, in each case is dependent on a deeper-level , regardless of style. And a proponent of a modified Schenkerian approach would likely agree with this claim in most cases. Where the disagreement between approaches most clearly surfaces is in instances like the end of “Georgia on My Mind” and “I Love You,” where no appears before (thus calling into question its escape tone function) and proceeds directly to the tonic (thus calling into question its implied = resolution). Example 16. “All of Me,” measures 29–32
(click to enlarge)
Example 17. “All of Me,” measures 29–32
(click to enlarge)
[3.16] Example 16 displays another such example—the concluding measures of the jazz standard “All of Me.” Modified Schenkerian theorists would likely describe the that immediately precedes the resolution to as an irreducible member of the Urlinie, thus assigning “All of Me” a modified background, such as the two indicated in the example. But because s that appear over dominant chords have historically depended on , it seems reasonable to view them as being dependent on at some level. Schenker writes, “Origin, development, and present I call background, middleground, and foreground” (Schenker [1935] (1979, 3). While Schenker meant this in a metaphorical sense, in this particular case it has literal meaning if we think of the process of displacement ( replacing a deeper-level ) as a history of the harmonic development that led to V13 chords.
[3.17] Example 17 displays four ways in which one with common-practice ears would likely hear this substitution occurring: a) as an implied cadential
that resolves to an implied , b) as an implied over the dominant that moves to a surface-level escape tone, c) as an implied over the predominant that moves to an escape tone over the duration of the dominant, or d) as an implied over the predominant that returns to an implied over the dominant. Any of these readings will ultimately produce an implied over the dominant, as shown by Example 17e.(12) [3.18] While any of the readings in Example 17 may be implemented depending on the context, it seems reasonable, in cases such as “All of Me,” for an orthodox Schenkerian analysis to avoid committing to any one particular solution by simply replacing with at a deeper level (Example 17e). Such a substitution is hardly outside of the realm of Schenkerian normality because structural soprano notes are often implied anyway.(13) When addressing this topic in his review of Henry Martin’s and Steven Gilbert’s books, Steve Larson writes, “The fact that one tone of the fundamental line is implied rather than literally present does not distinguish Gershwin or Parker from Bach” (Larson 1999, 115). In other words, the actual notes that occur over the final cadence are not critical for an orthodox Schenkerian Urlinie in either style.(14) In fact, in his section on first-level substitutions in Free Composition, Schenker writes, “Even at the first level, a tone which is not part of the fundamental line can substitute for a fundamental-line tone
. . . Most frequently the substitution applies to the ” (Schenker ([1935] (1979, 51).Other Modified “Urlinien”
[4.1] The call for modified Urlinien is a central objective for those who advocate modified Schenkerian theory, and the debate has not been limited to post common-practice music, as can be seen in the analyses of David Neumeyer. But Henry Martin’s article “Schenker and the Tonal Jazz Repertory” (2011) is the first article intended solely to present this argument for jazz. Martin advocates viewing certain deeper-level melodic structures, such as ––– or –, as Urlinien, which he claims can produce “superior readings” (Martin 2011, 1).
[4.2] A discussion of every tune that Martin analyzes would be impractical here. Instead, the following comparative analysis uses Martin’s first example of a modified Urlinie (his –– Urlinie in “Moten Swing”) in an effort to show the benefits and drawbacks of Martin’s modified approach in one illustrative example. This analysis attempts to demonstrate that while an orthodox Schenkerian approach might not result in the same reading as Martin’s, it nevertheless provides an equally compelling and illuminating analysis of “Moten Swing.” (15)
Example 18. Martin’s reading of “Sentimental Journey,” measures 1–8
(click to enlarge)
Example 19. Martin’s Example 3
(click to enlarge and see the rest)
[4.3] Martin begins his article with a reduction of the melody “Sentimental Journey,” which produces an orthodox Schenkerian –" –– interruption structure, as shown by Example 18. His reading seems clear and indisputable—there are no implied tones, and every member of the deeper-level structure appears in a prominent and expected location in each phrase.
[4.4] Martin then turns to “Moten Swing” as an example of a melody that, unlike “Sentimental Journey,” appears to lack a clearly orthodox Schenkerian deeper-level prototype. Example 19 displays a reproduction of Martin’s Example 3, a reduction of the first eight measures of “Moten Swing.” His reading diverges from orthodox Schenkerian theory in two ways. First, Martin labels the deeper-level structure that he shows spanning the A section only as an Urlinie. An orthodox Schenkerian definition, by contrast, requires an Urlinie to span an entire piece, not just a single formal section.(16) Second, Martin’s –– Urlinie is not one of the three possible Urlinien permitted by Schenker. This divergence highlights his essential claim—that an unorthodox –– structure provides a superior reading to one that would result from an orthodox approach.
[4.5] Martin’s reading certainly has one clear benefit. It reveals a motivic connection to the melody’s opening, as the first three notes,
A♭ –B♭ –A♭ , predict Martin’s –– Urlinie. Interestingly, Martin does not comment on this connection. In what seems like an attempt to reinforce this connection, the melody repeatsA♭ –B♭ –A♭ three more times in measures 1–2. Exposing this particular hidden repetition is certainly a possible advantage to Martin’s analysis, but an orthodox approach also reveals important deeper-level relationships.Example 20. A reduction of “Moten Swing,” measures 1–7
(click to enlarge)
Audio Example 2. “Moten Swing,” first A section of the head, performed by Count Basie (1959)
[4.6] Example 20 displays a strict-use reduction of the first A section of “Moten Swing” (measures 1–7) that adheres to orthodox principles (listen to Audio Example 2). Level c displays a different interpretation of many of the surface-level embellishments that Martin shows in his Example 3, level b. While Martin’s slurring suggests that the
B♭ on beat 3 of measure 2 is an anticipation of theB♭ of measure 3 (with the intermittingA♭ andB♮ functioning perhaps as double neighbors), Example 20 labels bothB♭ s in measure 2 as upper neighbors toA♭ (the root of theA♭ 6 chord), and theB♮ in measure 3 as an appoggiatura.(17) Additionally, Martin’s slurring in his Example 3 (Example 19 above), measures 3–6, suggests that theA♭ s on beat 4 of measure 4 and the “and” of beat 4 in measure 5 are lower neighbors toB♭ . Example 20, by contrast, considers these notes chord tones that produce voice leading that requires a deeper-level explanation. Lastly, Martin’s analysis indicates that the leap to F on beat 4 of measure 6 is an embellishing leap that occurs within an anticipatedA♭ 6 chord, a reading that certainly seems reasonable. In fact, Example 15b in the preceding analysis contained an analogous passage that I interpreted similarly. Example 20, however, suggests that theA♭ in measure 6 can also be heard as a suspension of theA♭ s in measures 4–5 (as shown at level b), and the F can also be heard resolving down by step to an impliedE♭ in measure 7 (as shown at level c).[4.7] The voice leading that spans measures 1–4 seems clear. As shown at level b, the melody note
A♭ in measures 1–2 accompanies the tonic, while theB♭ in measures 3–4 accompanies the dominant. While our reductive processes may have differed, this reading essentially matches Martin’s Example 3, level a. But the deeper-level readings differ profoundly in measures 5–7. Martin’s analysis indicates only a – deeper-level structure in these measures. Example 20, by contrast, shows that two upper voices span measures 5–7. One voice, shown as an alto at level b, begins on anA♭ (the chordal seventh of theB♭ 7 chord in measure 5) and resolves to an implied G in measure 6 before returning toA♭ at the cadence in measure 7. The other voice, shown as a soprano, remains onB♭ in measure 5, ascends to an enharmonically re-spelledC♭ in measure 6, and returns to theB♭ on beat 2 before joining the alto voice on the concluding tonic. TheC♭ in measure 6, in conjunction with the alto’sA♭ , forms a modally borrowed cadentialover the phrase’s structural dominant.(18) [4.8] Level a shows how this interpretation results in an orthodox Schenkerian reading of the phrase. The
A♭ in measures 1–2 and theB♭ in measures 3–4 form an initial ascent to the primary tone C, , in measure 6, which then descends to the tonic, forming a standard 3-line. This reading may strike some as atypical. As Henry Martin notes, “Such a primary tone does not work here because [it] receives no tonic support” (Martin 2011, 6). Furthermore, appears at level b as, a chromatic alteration of the primary tone. ♭ [4.9] It is true that the analyses in Free Composition happen to contain no cases in which the primary tone makes its initial appearance over a cadential
. Nevertheless, several of Schenker's analyses contain within a fundamental line (a 5- or 8-line) in that context (see, for example, Schenker’s Fig. 83.2 and 104.3). And while Schenker insisted on there being only three possible Urlinien, he made no requirement that the primary tone receive tonic support on the surface. [4.10] Schenker also specifically addresses the issue of modally borrowed members of the fundamental line, even singling out as a member that can be treated to mixture at remote levels of structure. He writes,
In the fundamental structure, the fundamental line remains strictly diatonic. At the first level, however, it can contain a mixture of the major and minor third. In this regard, it makes no difference whether the fundamental line begins with , , or (1979, 40–41, my emphasis).In Example 20, level b represents what Schenker calls the first level.
[4.11] Some aspects of the reading shown by Example 20 may seem anomalous at first. But a closer examination of the relevant analyses in Free Composition shows that it adheres to orthodox Schenkerian theory quite well, and this reading illuminates several deeper-level features that relate to common-practice music. But to provide a truly orthodox reading of the Urlinie in “Moten Swing,” one must examine the entire tune.
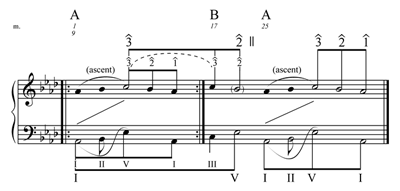
[4.12] The form of “Moten Swing” can best be described as a 32-measure AABA form. Typically, the bridge of such forms concludes with a half cadence that allows for a return of the final A section. If the reading suggested by Example 20 holds true, then one might expect this form to support a – " –– interrupted structure.
Example 21. “Moten Swing,” measures 17–24
(click to enlarge)
Example 22. A Schenkerian graph of “Moten Swing”
(click to enlarge)
[4.13] Example 21 displays the bridge of “Moten Swing,” measures 17–24. As though attempting to confirm the primary tone that was obscured by both its non-tonic harmonic support and chromatic alteration in the previous phrase, the melody here features an unaltered throughout the entire bridge. Not only does this receive strong harmonic support (as the root of the local tonic) and metrical emphasis (appearing on the downbeat of the first measure of each phrase), it also appears frequently in its lower octave. With the direct modulation (
B♭ m7–E♭ 7) in the final measure, moves to an implied , setting up the return to the final A section, which repeats the first two A sections without alteration.[4.14] To show the way in which these formal sections combine to produce an orthodox background, Example 22 provides a Schenkerian graph that includes only the notes from level a of Example 20, and the stemmed notes of Example 21. As one might expect in an AABA form, the – " –– interruption appears as a deeper-level structure true to Schenker’s concept of the Urlinie.
[4.15] Martin’s modified analysis produces a –– Urlinie, a structure outside of Schenker’s three allowable prototypes. As the comparative analysis revealed, an orthodox approach is equally compelling and illuminating. It reveals that a typical –– structure does in fact span the A section, although surface and middleground features may obscure the clarity of its presentation. The orthodox analysis also reveals the role that this structure plays in the tune’s overall melodic design—it predicts the tune’s orthodox Urlinie.
[4.16] The preference for a –– or –– reading of the A section ultimately rests in the ears of readers, who must ask themselves: which deeper-level structure does one more clearly hear spanning the A section? Or perhaps just as importantly, which deeper-level structure better explains the way in which the tune is constructed? Of course, even if one prefers Martin’s –– reading, it still does not require his use of terminology, as one could convey the same analysis as effectively by describing –– simply as a deeper-level motive or unorthodox middleground structure, thus avoiding the term Urlinie altogether.
Conclusion
[5.1] The preceding three case studies demonstrated the ways in which modified and orthodox Schenkerian analysis differ in approach. While the first portion of this paper addressed only the tonic added sixth and V13 chords, the differing approaches applied to other chord tones (such as major sevenths or major ninths) would likely lead to an analogous debate; orthodox Schenkerian theorists insist that such chord tones should always be placed on a spectrum of stability in which they ultimately derive their meaning from more stable pitches at deeper structural levels, while modified Schenkerian theorists insist that since some chordal extensions do not resolve, they should therefore be described as stable, irreducible, or consonant.
[5.2] The comparative analysis of “Moten Swing” demonstrated that the modified approach might be useful in showing a desirable deeper-level motive. But even in such cases, it seems unnecessary to describe such motives as “Urlinien,” and unfair to describe such readings as “superior,” as an orthodox reading can be equally compelling.
[5.3] Modified Schenkerian theorists may conclude that orthodox Schenkerian theorists are refusing to let go of an outdated system. But because that system was originally used for a style of music that has shaped the way we hear, abandonment should occur only when the music to which it is being applied can no longer relate to common-practice music in any meaningful way. And because mainstream jazz is tonal, its relationship to common-practice music is meaningful.
[5.4] An orthodox approach can offer readings that are as compelling and insightful as those produced by modified approaches. Therefore, we need not abandon it. Doing so would result in the loss of a valid point of view—a point of view that addresses the ways in which jazz departs from common-practice music by highlighting firmly rooted similarities in deeper-level voice leading.
David J. Heyer
University of Oregon
School of Music
1225 University of Oregon
Eugene, OR 97403
davidheyer@gmail.com
Works Cited
Aldwell, Edward, Carl Schachter, and Allen Cadwallader. [1978] 2011. Harmony and Voice Leading. 4th ed. Boston: Schirmer books.Aldwell, Edward, Carl Schachter, and Allen Cadwallader. [1978] 2011. Harmony and Voice Leading. 4th ed. Boston: Schirmer books.
Gilbert, Steven E. 1995. The Music of George Gershwin. New Haven: Yale University Press.Gilbert, Steven E. 1995. The Music of George Gershwin. New Haven: Yale University Press.
Hood, Alison. 2012. “Ambiguity of Tonal Meaning in Chopin’s Prelude op. 28, no. 22.” Music Theory Online 18, no. 3.Hood, Alison. 2012. “Ambiguity of Tonal Meaning in Chopin’s Prelude op. 28, no. 22.” Music Theory Online 18, no. 3.
Kalib, Sylvan. 1973. “Thirteen Essays from the Three Yearbooks ‘Das Meisterwerk in der Musik.’” PhD diss., Northwestern University.Kalib, Sylvan. 1973. “Thirteen Essays from the Three Yearbooks ‘Das Meisterwerk in der Musik.’” PhD diss., Northwestern University.
Kostka, Stefan, and Dorothy Payne. 2009. Tonal Harmony. 6th ed. New York: McGraw-Hill.Kostka, Stefan, and Dorothy Payne. 2009. Tonal Harmony. 6th ed. New York: McGraw-Hill.
Larson, Steve. 1987a. “Schenkerian Analysis of Modern Jazz.” PhD diss., University of Michigan.Larson, Steve. 1987a. “Schenkerian Analysis of Modern Jazz.” PhD diss., University of Michigan.
Larson, Steve. 1987b. “Questions about the Ursatz: A Response to Neumeyer.” In Theory Only 10, no. 4: 11–31.—————. 1987b. “Questions about the Ursatz: A Response to Neumeyer.” In Theory Only 10, no. 4: 11–31.
Larson, Steve. 1996. “A Strict Use of Analytic Notation.” Journal of Music Theory Pedagogy 10: 37–77.—————. 1996. “A Strict Use of Analytic Notation.” Journal of Music Theory Pedagogy 10: 37–77.
Larson, Steve. 1999. “Review: Alan Forte’s book ‘The American Popular Ballad of the Golden Era, 1924–1950,’ S.E. Gilbert’s book ‘The Music of Gershwin,’ H. Martin’s book ‘Charlie Parker and Thematic Improvisation.’” Music Theory Spectrum 21: 110–21.—————. 1999. “Review: Alan Forte’s book ‘The American Popular Ballad of the Golden Era, 1924–1950,’ S.E. Gilbert’s book ‘The Music of Gershwin,’ H. Martin’s book ‘Charlie Parker and Thematic Improvisation.’” Music Theory Spectrum 21: 110–21.
Larson, Steve. 2009. Analyzing Jazz—A Schenkerian Approach. Hillsdale, N.Y.: Pendragon Press.—————. 2009. Analyzing Jazz—A Schenkerian Approach. Hillsdale, N.Y.: Pendragon Press.
Larson, Steve. 2012. “Expressive Meaning and Musical Structure” (Chapter 1 from the unpublished textbook Schenkerian Analysis: Pattern, Form, and Expressive Meaning). Music Theory Online 18, no. 3.—————. 2012. “Expressive Meaning and Musical Structure” (Chapter 1 from the unpublished textbook Schenkerian Analysis: Pattern, Form, and Expressive Meaning). Music Theory Online 18, no. 3.
Martin, Henry. 1996. Charlie Parker and Thematic Improvisation. Lanham, Md.: Scarecrow Press.Martin, Henry. 1996. Charlie Parker and Thematic Improvisation. Lanham, Md.: Scarecrow Press.
Martin, Henry. 2003. “Early Dissonance Into Jazz Consonance: The Added Sixth Chord.” Paper presented at the Society for Music Theory annual meeting at the University of Wisconsin-Madison (November, 2003).—————. 2003. “Early Dissonance Into Jazz Consonance: The Added Sixth Chord.” Paper presented at the Society for Music Theory annual meeting at the University of Wisconsin-Madison (November, 2003).
Martin, Henry. 2011. “Schenker and the Tonal Jazz Repertory.” Dutch Journal of Music Theory 16, no. 1: 1–20.—————. 2011. “Schenker and the Tonal Jazz Repertory.” Dutch Journal of Music Theory 16, no. 1: 1–20.
Martin, Henry. n.d. “From Classical Dissonance to Jazz Consonance: The Added Sixth Chord”. Unpublished manuscript.—————. n.d. “From Classical Dissonance to Jazz Consonance: The Added Sixth Chord”. Unpublished manuscript.
McGowan, James. 2008. “‘Consonance’ in Tonal Jazz: A Critical Survey of Its Semantic History.” Jazz Perspectives 2, no. 1: 69–102.McGowan, James. 2008. “‘Consonance’ in Tonal Jazz: A Critical Survey of Its Semantic History.” Jazz Perspectives 2, no. 1: 69–102.
Neumeyer, David. 1987a. “The Three-Part Ursatz.” In Theory Only 10, no. 1: 3–29.Neumeyer, David. 1987a. “The Three-Part Ursatz.” In Theory Only 10, no. 1: 3–29.
Neumeyer, David. 1987b. “Forum: Reply to Larson” In Theory Only 10, no. 1: 33–37.—————. 1987b. “Forum: Reply to Larson” In Theory Only 10, no. 1: 33–37.
Neumeyer, David. 1987c. “The Ascending Urlinie” Journal of Music Theory 31, no. 2: 275–303.—————. 1987c. “The Ascending Urlinie” Journal of Music Theory 31, no. 2: 275–303.
Rothstein, William. 1991. “On Implied Tones.” Music Analysis 10, no. 3: 289–328.Rothstein, William. 1991. “On Implied Tones.” Music Analysis 10, no. 3: 289–328.
Salzer, Felix. 1952/1962. Structural Hearing: Tonal Coherence in Music. New York: Charles Boni (1952). Reprinted, New York: Dover Publications (1962).Salzer, Felix. 1952/1962. Structural Hearing: Tonal Coherence in Music. New York: Charles Boni (1952). Reprinted, New York: Dover Publications (1962).
Schenker, Heinrich. [1906] 1954. Harmonielehre. Translated by Elisabeth Mann Borgese. Chicago and London: University of Chicago Press.Schenker, Heinrich. [1906] 1954. Harmonielehre. Translated by Elisabeth Mann Borgese. Chicago and London: University of Chicago Press.
Schenker, Heinrich. [1935] 1979. Free Composition. Translated and edited by Ernst Oster. New York: Longman Inc.—————. [1935] 1979. Free Composition. Translated and edited by Ernst Oster. New York: Longman Inc.
Discography
Discography
Armstrong, Louis. 1957. Louis Armstrong in Concert. Wally Heider Collection (Library of Congress).Armstrong, Louis. 1957. Louis Armstrong in Concert. Wally Heider Collection (Library of Congress).
Baker, Chet. 1982. Out of Nowhere. New York: Milestone Records. LP.Baker, Chet. 1982. Out of Nowhere. New York: Milestone Records. LP.
Basie, Count. 1959. Chairmen of the Board. New York: Roulette Records. LP.Basie, Count. 1959. Chairmen of the Board. New York: Roulette Records. LP.
Footnotes
1. Modified Schenkerian theory dates back to the work of Felix Salzer, who includes structural dissonances in some graphs in his book Structural Hearing (1952/1962).
Return to text2. In his subsequent article “The Ascending Urlinie,” Neumeyer (1987c) advocates a ––– Urlinie, also a background structure explicitly excluded by Schenker.
Return to text3. This article is an expanded version of Martin’s earlier paper, “Early Dissonance Into Jazz Consonance: The Added Sixth Chord” (2003), presented at the 2003 Society for Music Theory annual meeting.
Return to text4. James McGowan (2008) dismisses the application of orthodox Schenkerian theory to jazz by claiming that “when a section or piece is over, and the voice leading and harmonic progression of the performance ends on a sonority with four or more different notes, harmonic extensions need not be explained away” (93). In his view, a melody like “Mack the Knife,” which concludes prominently on an extension, resists a reductive explanation. McGowan argues that “the added 6th sounds in addition to the 5th, and it functions independently of the 5th in voice leading” (ibid.).
Return to text5. The measure numbers and Roman numeral analysis at the bottom of this example were added to Martin’s example to facilitate comparative analysis.
Return to text6. For more on strict use see Alison Hood’s essay in this volume (Hood 2012) and chapter 1 of Larson’s textbook, Schenkerian Analysis: Pattern, Form, and Expressive Meaning. Larson’s textbook is currently unpublished, but chapter 1 is included with this volume (Larson 2012).
Return to text7. Martin does include inner voices in his analysis, but he shows the E in measures 1–2 as an alto voice that moves to F in measures 3–4, a motion that follows the guide-tone path instead of the voice leading articulated by the melody, which includes a D in measure 4, beat 3.
Return to text8. Similar jazz forms often appear as either ABAC (such as “All of Me” and “I Can’t Give You Anything But Love”) or ABAB' (such as “There Will Never Be Another You” and “Out of Nowhere”). In either case, the B section typically ends with a half cadence. Less common are ABAB forms like “Mack the Knife” in which each B section ends with a cadence of seemingly equal strength.
Return to text9. Schenker would have most likely considered such an escape tone as an anticipation of the tonic harmony. See Schenker’s Harmony ([1906] 1954, 302, Example 270). That interpretation likely inspired Gilbert’s analysis of “’S Wonderful.”
Return to text10. Some texts distinguish between a that appears over a V chord (a Classical-period characteristic) and one that appears over a V7 chord (a Romantic-period characteristic), calling the former a Vadd6 chord. See, for example, Stefan Kostka and Dorothy Payne’s Tonal Harmony (2009, 445). In either case, the contrapuntal function of and the preceding remains the same.
Return to text11. Both Sylvan Kalib (1973, 83) and William Rothstein (1991, 291) have used this example to demonstrate this point as well.
Return to text12. In the section of their textbook titled “dominant eleventh and thirteenth chords,” Aldwell and Schachter suggest a preference for the reading of Example 17a, writing that “4ths and 6ths can appear over V7 as suspensions or incomplete neighbors; they will normally resolve to 3rds and 5ths. Sometimes, especially in nineteenth-century music, such dissonances are left unresolved, the resolutions being supplied mentally by the listener” (Aldwell, Schachter and Cadwallader 2011, 449.
Return to text13. The allowance of implied tones, or substitutions, is a critical aspect to an orthodox Schenkerian approach. In the conclusion of his article “On Implied Tones,” William Rothstein writes, “Schenker’s theory would collapse without the implied tone,” adding that “the interaction of the literal and the imagined is central to the Schenkerian way of hearing” (Rothstein 1991, 323, his emphasis).
Return to text14. William Rothstein comments specifically on the desirability of an orthodox fundamental line even if is implied. While his argument refers to cases in common-practice music where replaces , his words certainly apply here. He writes, “The substitution for the is so common, why, one might ask, should it be considered a deviation from the norm rather than as a norm itself? Why not allow alternative forms of the fundamental line
. . . ? To answer [this] question is to illustrate the Gestalt nature of Schenkerian thinking. Three principles are involved. First there is Schenker’s concept of melodic fluency. . . which always gives precedence to stepwise motion. . . Second, there is the Gestalt principle of ‘good continuation,’ according to which a perceiver seeks to connect new stimuli with old ones in the simplest and most predictable way possible. . . The third principle was the imaginary continuo. When these three principles are conjoined, the restriction to a stepwise fundamental line becomes easier to understand” (1991, 305–06) .
Return to text15. In this particular case, an orthodox approach will result in the omission of Martin’s deeper-level (––) structure, an omission that Martin would likely consider unfortunate. It should be noted, however, that often an orthodox approach produces a traditional background while still including such deeper-level structures as either first-level middleground structures or inner voices.
Return to text16. In our email correspondence, Professor Martin explained that he considers his reading of the A section’s deeper-level structure a shorthand for the tune’s overall melodic design, which he also considers a –– structure.
Return to text17. Schenker would have likely described this
B♮ as a neighbor note. The term appoggiatura, however, is a more descriptive term, as theB♮ is a special kind of neighbor note—an incomplete upper neighbor approached by leap (in this case a “leap” of an augmented second) and resolved by step in the opposite direction.
Return to text18. Some may find this reading inconsistent, as it treats the
B♮ in measure 3 differently than theB♮ in measure 6, despite both notes appearing over the same chord (E♭ 7). There are two justifications for this discrepancy. First, theB♮ in measure 6 is repeated, giving the note additional emphasis. Second, and more importantly, theE♭ 7 chord in measure 6 appears over the phrase’s penultimate measure (at the cadence), giving the chord more structural weight than theE♭ 7 chord in measure 3, and allowing one to hear theB♮ in measure 6 as a chord tone in a modally-borrowed cadential.
Return to textModified Schenkerian theory dates back to the work of Felix Salzer, who includes structural dissonances in some graphs in his book Structural Hearing (1952/1962).In his subsequent article “The Ascending Urlinie,” Neumeyer (1987c) advocates a 5ˆ–6ˆ–7ˆ–8ˆ Urlinie, also a background structure explicitly excluded by Schenker.This article is an expanded version of Martin’s earlier paper, “Early Dissonance Into Jazz Consonance: The Added Sixth Chord” (2003), presented at the 2003 Society for Music Theory annual meeting.James McGowan (2008) dismisses the application of orthodox Schenkerian theory to jazz by claiming that “when a section or piece is over, and the voice leading and harmonic progression of the performance ends on a sonority with four or more different notes, harmonic extensions need not be explained away” (93). In his view, a melody like “Mack the Knife,” which concludes prominently on an extension, resists a reductive explanation. McGowan argues that “the added 6th sounds in addition to the 5th, and it functions independently of the 5th in voice leading” (ibid.).The measure numbers and Roman numeral analysis at the bottom of this example were added to Martin’s example to facilitate comparative analysis.For more on strict use see Alison Hood’s essay in this volume (Hood 2012) and chapter 1 of Larson’s textbook, Schenkerian Analysis: Pattern, Form, and Expressive Meaning. Larson’s textbook is currently unpublished, but chapter 1 is included with this volume (Larson 2012).Martin does include inner voices in his analysis, but he shows the E in measures 1–2 as an alto voice that moves to F in measures 3–4, a motion that follows the guide-tone path instead of the voice leading articulated by the melody, which includes a D in measure 4, beat 3.Similar jazz forms often appear as either ABAC (such as “All of Me” and “I Can’t Give You Anything But Love”) or ABAB' (such as “There Will Never Be Another You” and “Out of Nowhere”). In either case, the B section typically ends with a half cadence. Less common are ABAB forms like “Mack the Knife” in which each B section ends with a cadence of seemingly equal strength.Schenker would have most likely considered such an escape tone as an anticipation of the tonic harmony. See Schenker’s Harmony ([1906] 1954, 302, Example 270). That interpretation likely inspired Gilbert’s analysis of “’S Wonderful.”Some texts distinguish between a 3̂ that appears over a V chord (a Classical-period characteristic) and one that appears over a V7 chord (a Romantic-period characteristic), calling the former a Vadd6 chord. See, for example, Stefan Kostka and Dorothy Payne’s Tonal Harmony (2009, 445). In either case, the contrapuntal function of 3̂ and the preceding 2ˆ remains the same.Both Sylvan Kalib (1973, 83) and William Rothstein (1991, 291) have used this example to demonstrate this point as well.In the section of their textbook titled “dominant eleventh and thirteenth chords,” Aldwell and Schachter suggest a preference for the reading of Example 17a, writing that “4ths and 6ths can appear over V7 as suspensions or incomplete neighbors; they will normally resolve to 3rds and 5ths. Sometimes, especially in nineteenth-century music, such dissonances are left unresolved, the resolutions being supplied mentally by the listener” (Aldwell, Schachter and Cadwallader 2011, 449.The allowance of implied tones, or substitutions, is a critical aspect to an orthodox Schenkerian approach. In the conclusion of his article “On Implied Tones,” William Rothstein writes, “Schenker’s theory would collapse without the implied tone,” adding that “the interaction of the literal and the imagined is central to the Schenkerian way of hearing” (Rothstein 1991, 323, his emphasis).William Rothstein comments specifically on the desirability of an orthodox fundamental line even if 2ˆ is implied. While his argument refers to cases in common-practice music where 7ˆ replaces 2ˆ, his words certainly apply here. He writes, “The substitution for the 2ˆ is so common, why, one might ask, should it be considered a deviation from the norm rather than as a norm itself? Why not allow alternative forms of the fundamental line . . .? To answer [this] question is to illustrate the Gestalt nature of Schenkerian thinking. Three principles are involved. First there is Schenker’s concept of melodic fluency . . . which always gives precedence to stepwise motion . . . Second, there is the Gestalt principle of ‘good continuation,’ according to which a perceiver seeks to connect new stimuli with old ones in the simplest and most predictable way possible . . . The third principle was the imaginary continuo. When these three principles are conjoined, the restriction to a stepwise fundamental line becomes easier to understand” (1991, 305–06) .In this particular case, an orthodox approach will result in the omission of Martin’s deeper-level (1ˆ–2ˆ–1ˆ) structure, an omission that Martin would likely consider unfortunate. It should be noted, however, that often an orthodox approach produces a traditional background while still including such deeper-level structures as either first-level middleground structures or inner voices.In our email correspondence, Professor Martin explained that he considers his reading of the A section’s deeper-level structure a shorthand for the tune’s overall melodic design, which he also considers a 1ˆˆˆ structure.Schenker would have likely described this B♮ as a neighbor note. The term appoggiatura, however, is a more descriptive term, as the B♮ is a special kind of neighbor note—an incomplete upper neighbor approached by leap (in this case a “leap” of an augmented second) and resolved by step in the opposite direction.Some may find this reading inconsistent, as it treats the B♮ in measure 3 differently than the B♮ in measure 6, despite both notes appearing over the same chord (E♭7). There are two justifications for this discrepancy. First, the B♮ in measure 6 is repeated, giving the note additional emphasis. Second, and more importantly, the E♭7 chord in measure 6 appears over the phrase’s penultimate measure (at the cadence), giving the chord more structural weight than the E♭7 chord in measure 3, and allowing one to hear the B♮ in measure 6 as a chord tone in a modally-borrowed cadential .
Copyright Statement
Copyright © 2012 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Carmel Raz, Editorial Assistant
Number of visits: