Rethinking Octatonicism: Views from Stravinsky’s Homeland
Philip A. Ewell
KEYWORDS: octatonicism, modal theory, modality, Russian music, theory of modal rhythm, neotonality, Rimsky-Korsakov, modernist music, Stravinsky, Yavorsky, Protopopov, Kholopov, Berger
ABSTRACT: Recent and long-standing debates about the role of octatonicism in works by Stravinsky and other late-chromatic and early-modernist composers have taken place with little mention of how octatonicsim is viewed in Russia—the country of Stravinsky’s birth and formative years as a composer. In this article, the author seeks to put music that is often considered octatonic in North America into a Russian framework. He does this by examining the work of three Russian music theorists: Boleslav Yavorsky, Sergei Protopopov, and Yuri Kholopov. The author seeks not to invalidate American views on octatonicism but, rather, to enrich the current discussion with Russian perspectives.
Copyright © 2012 Society for Music Theory
[1] Introduction
[1.1] The debate on octatonicism in North America is far from over.(1) As proof, one need look no further than the Symposium in the recent issue of Music Theory Spectrum (Volume 33, No. 2, Fall 2011). In his “Catching Up with Rimsky-Korsakov,” Richard Taruskin (2011) throws down the gauntlet before the entire field of Music Theory. Though he certainly discusses Rimsky-Korsakov, the chief subject of the article is octatonicism, and the role it plays in music by Rimsky-Korsakov and Stravinsky. Nothing is more central to the octatonic debate than “Problems of Pitch Organization in Stravinsky” (1963), by Arthur Berger. In numerous publications, both Taruskin and Pieter van den Toorn, using Berger’s article as a fountainhead, have sought to prove that a significant and characteristic part of Stravinsky’s music is octatonic.(2)
[1.2] This, significantly, is not how Stravinsky is viewed in Russia. There he is considered to be a modal composer in the spirit of the system of Boleslav Yavorsky (1877–1942)—American octatonicism accounts for but one of Yavorsky’s many modes.(3) His theory of modal rhythm (Russian teoriia ladovogo ritma) is an elaborate and compelling method for analyzing not only Stravinsky’s music but also much of the problematic tertian music of the late-ninteenth and early-twentieth centuries.(4) With respect to Stravinsky, I believe that Yavorsky’s theory—whose impact on twentieth-century Russian Music Theory cannot be overstated—could have significant ramifications on how we view Stravinsky’s music in the United States. In Russia, music theorists have been practicing octatonic analysis—steeped in Yavorsky’s theories—for over eighty years, so it seems plausible that they would have much to offer.
[1.3] In this article I will offer Russian views on music that theorists often consider to be octatonic in the United States. In some cases I will suggest new ways of interpreting this music, beyond the octatonic. In a broader sense then, I will discuss general Russian methods for analyzing the pitch structure of music from the late-nineteenth and early-twentieth centuries. I will focus primarily on the work of three Russian authors: Yavorsky, his disciple Sergei Protopopov (1893–1954), and Yuri Kholopov (1932–2003). It is not my goal, in this article, to invalidate American ideas on octatonicism. Rather, in offering these Russian views, I aim to provide new interpretations of music that is often considered octatonic and to enrich the general understanding of Stravinsky and other late-romantic and modernist composers.
[1.4] In the second section of my article, “Yavorsky’s Modes,” I will explain Yavorsky’s system for understanding late nineteenth- and early twentieth-century music and the reasons behind his quest for this system. In the third, “Kholopov’s Neotonality,” I will explain Kholopov’s version of a new functionality. In the fourth, “Berger’s Octatonicism,” I will consider Berger’s article, stressing those elements that are often overlooked in the debate on octatonicism. In the fifth, “Analytical Examples,” I will offer analyses—two from Russia and one of my own—that show how Russian ideas differ from, and offer advantages over, those found here in North America. In the Conclusion, I reflect on these Russian perspectives on Stravinsky’s music while suggesting what further research along these lines may be fruitful for Stravinsky scholarship.
[2] Yavorsky’s Modes
Yavorsky’s Theory of Modal Rhythm(5)
[2.1] Though I will address only Yavorsky’s ideas on pitch structure below, it is worth noting that his elaborate theory also addresses concepts of form, time, melody, and harmony. He first published his work in 1908 under the title Stroenie muzykal’noĭ rechi (The Structure of Musical Speech). Three additional works followed: Uprazhneniia v golosovedenii (Exercises in Voice Leading) (1913); Uprazhneniia v obrazovanii ladovogo ritma (Exercises in the Formulation of Modal Rhythm) (1915); and Struktura melodii (Structure of Melody) (1929).(6) In addition to his theoretical work, Yavorsky was active as a pedagogue in Kiev and Moscow, teaching theory, piano, and composition. And he enjoyed fame as a composer as well: his opera Vyshka oktiabria (The Turret of October), for example, was performed at the Bolshoi Theater in Mosocow in 1930.
[2.2] In Russia the concept of “mode” (lad) has a far broader meaning than the normal view of the term in the United States. About this most important term in Russian theory, Ellon Carpenter says, “In Russian Music Theory, the concept of mode forms one of the major and most important tenets upon which that theory is based. In its broadest interpretation, the Russian concept of mode has no exact equivalent in western music theory” (Carpenter 1995, 76–77). She quotes Kholopov on “mode,” from his article by the same name in the Soviet Muzykal’naia Entsiklopediia (Music Encyclopedia):
As a whole, mode is revealed in the completeness of the structure enveloping the entire complex making it up—from the sound material through the logical regulating of the separate elements to the crystallisation of the specifically aesthetic systemic relationships of measure, of proportion, of interconformity (in a wide sense—symmetry). Always important also is the individual concretisation of a definite mode in a given work, revealing the richness of its possibilities and regularly expanding into a vast modal construction. (Translated by and cited in Carpenter 1995, 77)
[2.3] The reason that the concept of mode is complicated in Russia is that, in addition to Church, Byzantine, Russian, or other historical modes, Yavorsky’s modes are also prevalent.
The Semitonal Basis for Yavorsky’s System
[2.4] Gordon McQuere argues that the paramount element in Yavorsky’s system is the tritone and the motion that is required to resolve it (2009, 113). Though this is certainly important, it is not at the foundation of the system. The reason that the tritone became so important to Yavorsky was because the functional tonal system had, by the late nineteenth century, been weakened, and he felt that something other than the T–S–D–T formula was necessary to account for structure in music. It was clear to Yavorsky that the seven-step system of functional tonality had been replaced by a twelve-step system. This notion he learned from his teacher at the Moscow Concervatory, Sergei Taneev (1856–1915). In his Vospominaniia o Taneeve (Remembrances of Taneev), Yavorsky recounted how Taneev taught his private students:
With his private students Taneev conducted a “course of harmony,” using Tchaikovsky’s harmony textbook and Arensky’s collection of 1000 exercises.
The main principles of harmonic devices were:
- The existence of a twelve-note chromatic row (the chromatic scale);
- In order to use this scale, it was necessary to organize it and transform it into a tonality [so that it could be used in the same sense as a tonality based on a septatonic scale];
- Any tone of this twelve-note scale could be primary for the organization of such a tonality; this tone was declared “scale degree 1,” which was assigned as primary tone (the tonic or, more accurately, the melodic tonic). Consequently, a tonality could be formed from a chromatic scale twelve times (twelve tonalities). (Yavorsky 2008, 215)(7)
Example 1. Yavorsky, Number of Semitones Expressed as Traditional Intervals (From Yavorsky 1908)
(click to enlarge)
[2.5] Yavorsky took up the mantle of explaining this new system with his theory. Already in 1904, in a letter to his friend, the music theorist Nadezhda Briusova, Yavorsky explained the uselessness of multiple names for notes and intervals: “You ought to write a Music-Theory Fundamentals textbook that is void of everything that results from the confusion of naming one note with three names (e.g.,
[2.6] However, Yavorsky had different ideas of where to go with this new information. The many modes that he heard in folksongs and the function of the tritone in the new twelve-tone system most interested Yavorsky, who believed that with the death of functional tonality came the death of voice leading. Instead, pitch leading and pitch gravitations became the norm. This type of motion focused on local pitch movement, which was dependent on the tritone and not on the conduct of separate voices or on the logical progression of harmonies. He was particularly influenced in this regard by his teacher Sergei Taneev. In remarks attached to a letter to Soviet People’s Commissar Anatoliĭ Lunacharskiĭ from late 1927, Yavorsky explained the impact of Taneev’s books on counterpoint ([1909] 1959) and canon, and the dawning of a new musical era.
[Taneev’s] books witness that the principles of contrapuntal thought and voice leading by intervals are finished, since the absurdity of these principles is amply shown in these books. A new epoch of pitch-leading consciousness, of pitch gravitation, the epoch of modal rhythm, has begun. (Rabinovich, ed. 1972, vol. 1, 377; emphasis original)
The Single and Double Symmetrical Systems
Example 2. Yavorsky, Single and Double Symmetrical Systems
(click to enlarge)
[2.7] As early as April of 1906, in a letter to Taneev, Yavorsky spelled out his basic premise: “From my studies of folk music I have come to the conclusion that the basic cell in musical language is the tritone and its resolution.” Yavorsky continues to say that such resolution, whether the two sounding pitches occur simultaneously, successively, or at a distance, must occur by “contrary motion by semitone” (Yavorsky 2008, 5; emphases original). Motion by semitone was paramount in Yavorsky’s system, as is evidenced in Example 2, which shows the two basic cells in his modal system, the single and double symmetrical systems (these appeared in the letter to Taneev from 1906, as well as in his main work from 1908).(9) Note how the double symmetrical system contains two interlocking tritones (connected with diagonal lines in the example). Further, Yavorsky uses open and closed noteheads to represent stable and unstable notes, respectively, and both systems have two forms, converging and diverging. Any two (single symmetrical system) or three (double symmetrical system) linear notes are termed a “conjunction” (sopriazhenie), which sometimes happens alone, without the other conjunction that creates the system, and which represents a melodic unit of the modal system. Yavorsky indicated that the unstable notes of the single system represent the dominant (“D”) harmony, while the stable notes represent the tonic (“T”) harmony. In the double system, the unstable notes represent the subdominant harmony (“S”), while the stable notes represent the “subtonic” harmony (“t”). Neither Yavorsky nor his trusted student, Sergei Protopopov, who famously elaborated on Yavorsky’s ideas in a later work (Protopopov 1930), does a good job explaining the harmonic functions of the system.(10) Protopopov comes closest when he explains that “the instabilities in the double system, as the value derived from two dominants, is called the subdominant and is labeled with an uppercase ‘S’” and “the stability of the double system, as a value derived from two tonics, is called the subtonic and labeled with a lowercase ‘t’” (Protopopov 1930, vol. 1, 80). Perhaps it is the two dominants (the dominant of the dominant?) that allow him to call the double-system instabilities the subdominant. Or perhaps it is because, in any major mode (shown below in Example 4), three of the four notes that comprise these instabilities—,
Example 3. Yavorsky, Formation of the Double Symmetrical System (from Yavorsky 2008, 5; also shown in Protopopov, vol. 1, 80)
(click to enlarge)
[2.8] Yavorsky’s derivation of the double symmetrical system with its interlocking tritones is also problematic. Realizing that a great many current compositions were tertian in nature but not traditionally tonal, he wanted a system that could encompass all of this highly chromatic new music. In light of this new twelve-step system and knowing that this tertian music featured not only major but also minor thirds, Yavorsky faced a challenge: since tritone movement by semitone was paramount, how could he devise a system that resolved to not only a major third by semitone (which was unproblematic) but also to a minor third, with both voices moving by semitone. His solution was the double symmetrical system. Example 3 shows how Yavorsky formed the double symmetrical system; this first appeared in Yavorsky’s letter to Taneev in 1906 (Yavorsky 2008, 5). It also appeared in Protopopov’s Elementy (vol. 1, 80). Protopopov explains the interlocking tritones of the double system in the following fashion. The first unstable D of the first system resolves to a stable
The Four “Triadic” Modes
Example 4a. The Major and Minor Modes
(click to enlarge)
Example 4b. The Augmented and Diminished Modes
(click to enlarge)
Example 5. Diminished Mode, Tonic and Connecting Moment from Ex. 4b
(click to enlarge)
[2.9] The combination of two or more systems results in a mode.(11) Further, the combination of the stable tones in the mode represent the tonic (T) of the mode, and the combination of the unstable tones in the mode represent the “connecting moment” (soedinennyĭ moment), which could contain dominants, subdominants, or a combination thereof. With this, Yavorsky began building major and minor modes—for instance, all the stable notes (i.e., those with open noteheads) in Example 2 would form the major mode on the pitch C (if the main pitch were specified, Yavorsky would call the mode a “modal-tonality” [lado-tonal’nost’]). Yavorsky built four modes to form the four basic triads of functional tonality, as shown in Examples 4a and 4b. The first three—the major, minor, and augmented (uvelichennyĭ) modes—Yavorsky called “stable consonant” modes, while the diminished (umenshennyĭ) mode was the first example of the “stable dissonant” mode, with a dissonant tonic. He recognized that the tonic of the diminished mode contained a tritone, and he wrote that in and of itself that tonic is unstable. But within the system and with respect to the tritone gravitations, the diminished triad gained relative stability. Notably, while the diminished mode has the diminished triad as stable tonic, the unstable tones represent the octatonic scale. As mentioned above, Yavorsky called the unstable tones of any mode, collectively, the “connecting moment.” This is shown in Example 5.
[2.10] At this point it is worth mentioning an important distinction with respect to the Russian understanding of “mode.” In Russian theory, a “mode” may refer to a collection of pitch classes—as in North American pitch class set theory. The American term “mode,” on the other hand, typically references melodic and scalar conceptions. Of course the term is complex in both English and Russian, and the scalar conception is also relevant in the Russian context. American theories of octatonicism, in turn, treat the octatonic scale both as a scale and as a collection of pitch classes.
Chain Modes
Example 6. The Chain Mode
(click to enlarge)
Example 7c. The Z Chain Mode
(click to enlarge)
[2.11] By overlapping major with major or major with minor triads, Yavorsky came up with four chain modes, the most basic of which formed the common major/minor triad, or (0347) tetrachord. At first he called this the “major/minor” mode, but then simply the chain (tsepnoĭ) mode (see Example 6).(12) In point of fact, the chain mode is much like van den Toorn’s (0 3/4 7) “Minor-Major Third” partitionings of the octatonic (see van den Toorn 1983, chapter 10).
[2.12] Aside from the generic chain mode, Yavorsky identified three other chain modes, the X, Y, and Z chain modes, shown in Examples 7a–7c. They combine either different major thirds or a major third with a minor third.
|
Example 7a. The X Chain Mode (click to enlarge) |
Example 7b. The Y Chain Mode (click to enlarge) |
Duplex Systems and Duplex Modes
[2.13] Since each tritone has two possible resolutions, Yavorsky expanded his system to include what he called “duplex” (dvazhdy) modes, which were the unification of two or more duplex systems. A duplex system is simply a tritone, written both possible ways, with converging resolutions, either in a single or a double system. Examples 8a and 8b show these two possibilities. Notice that in both cases the roots of the two tonics are a tritone apart. The lowercase “d” before the chord signifies the duplex element of the system. In the duplex double system one must look diagonally to find the repeating tritones. That is, in the lower system in Example 8b, the D–
|
Example 8a. Duplex Single System (click to enlarge) Example 9a. The Duplex-Chain Mode (click to enlarge) |
Example 8b. Duplex Double System (click to enlarge) Example 9b. The Duplex-Diminished Mode (click to enlarge) |
Example 10. The Duplex-Major Mode
(click to enlarge)
Example 11. Modal Gravitations for the C-Duplex-Major Mode
(click to enlarge)
[2.14] The duplex-chain mode is the combination of two duplex single systems that combine to form two chain modes. This is precisely the mode that best corresponds to American octatonicism. In this mode the duplex tonic is none other than the octatonic scale, and the connecting moment (which in this case represents the dominant) is the fully diminished seventh chord that is not contained in that particular octatonic. Notably, Protopopov acknowledged the limitation of three transpositions with this mode, which is a cornerstone of American octatonic analysis: “It is possible to form only three duplex-chain modes in twelve-tone temperament, since when forming a duplex-chain mode a minor third higher than the given mode there will be a transposition of the very same duplex-chain mode” (Protopopov 1930, vol. 2, 95). While the duplex-chain mode represented a stable octatonic and an unstable diminished-seventh chord, just the opposite is true with the duplex-diminished mode, shown in Example 9b. This is an important mode in the history of octatonic analysis, since the stability in octatonic pieces is, in fact, often the diminished-seventh chord and not the octatonic scale. This mode combines two duplex double systems (not duplex single systems) and forms two diminished modes (not chain modes).
Example 10 shows an important mode for Stravinsky studies, the duplex major mode, in this case with the tonic C. It is made up of two duplex systems, one single and one double. The duplex single system in the example yields two major thirds located a tritone apart and the duplex double system yields two minor thirds located a tritone apart. The resulting tonic for the entire mode is the six-note entity, the C-major and
Problems with Yavorsky’s System
[2.15] Yavorsky’s theory fails in two crucial areas, the first of which concerns the interlocking tritones of the double system.(14) That Yavorsky conceived of two revolutionary ideas in music—the non-hierarchical twelve-tone basis of the system coupled with the dissonant stability—cannot be in question. That any minor third, harmonic or melodic, is the result of two simultaneously resolving tritones is suspect, however. In other words, I believe it is hard to hear a minor third as the result of this dual-tritone motion. Realizing the primacy of the semitone in the system, it is clear why he sought to prove that the minor third is the result of dual tritone motion. The system is logical, but not very musical; the perceptual and compositional relevance is unclear. (I note here that the duplex-chain mode contains only single systems, that is, no interlocking tritones, so its unassailability remains intact.)
[2.16] The second failing of Yavorsky’s theory lies not in the theory itself, but in its application to tonal works. Yavorsky would often use his system to analyze works by Beethoven or Chopin, for example, claiming that his modal ideas encompassed their works (and, by extension, all functional-tonal works) as well. What he is essentially saying is that these tonal works are modal, which is incorrect. Kholopov sums this up nicely: “Yavorsky’s mistake occurs from the expansion of old methods of thinking to new material: he wants to see his new modes as being just as universal as major and minor, and he wants to construct all new modes by one and the same concrete models” (Kholopov et al. 2006, 381; emphases original). Or to put it another way, witnessing the end of functional tonality, Yavorsky was wrong to turn around and say his new system accounted for this defunct tonality.
[3] Kholopov’s Neotonality(15)
Kholopov’s Neotonal SystemIf we bear in mind the substitution of the
system’s elements, then it is possible to
capture the entire evolution of Stravinsky’s
harmony with the sole concept of neotonality
(Kholopov 1997, 33).
[3.1] A stalwart defender of twentieth-century music, Yuri Kholopov sought to gain a deeper understanding of new music throughout most of his career as a music-theory professor at the Moscow Conservatory. Kholopov defines neotonality thus:
Twentieth-century neotonality is a qualitatively different phenomenon in comparison with classical tonality, since neotonality relies mainly on dissonance (a dissonant chord, that is, any group of notes expediently collected by the composer) and on a 12-tonestructure . . . based on a scalar foundation, and does not have a directly sensed gravitation to a central complex at every moment. Neotonality is structurally diverse and individualized. At the same time, as with classical tonality, it represents a logical, well-formed, hierarchically ordered system of functional pitch connections—in other words, a mode. The pitch situation of motives and chords in neotonality is esthetically regulated (and not “atonally” indifferent) (Kholopov 1991b).
Significantly, Kholopov equates neotonality with the concept of mode, which sheds light on the concept of mode in Russia: it is that group of notes to which all others from twelve-note pitch-class space are subordinate.
[3.2] Kholopov’s early views on neotonality and, significantly, octatonicism, can be found in his “Klassicheskie struktury v sovremennoĭ garmonii” (Classical Structures in Contemporary Harmony) (1967b). After explaining how dissonant sonorities can function as stabilities in the new music of the early twentieth century, he lays out his argument for the neutralization of tonal hierarchies and the foundation of a twelve-tone neotonal system:
The abrupt leap forward in the sphere of harmonic thinking (in approximately 1910), which found artistic embodiment in the works of Scriabin, Stravinsky, Prokofiev, Bartók, and other composers, expressed itself, in particular, in the rise of still more new forms of tonality. Particularly unusual were those that manifested, with greater clarity, an understanding of dissonance as an independent harmonic element and an understanding of tonality as a 12-tonesystem. . .
The independence of dissonance allows it to become the tonic (in a more general sense, the central element of a harmonic structure) and, what is more, a different element of harmony that is subordinate to the tonic. The twelve-tone essence of contemporary tonality allows for practically any chordal or melodic formation to be subject to the influence of the tonic; on the other hand, it allows (or even necessitates) the rise of new additional factors of tonal organization, factors that are conditioned on the globalism of twelve-tone tonality. (1967b, 96; emphasis mine)
From this quotation we can sense Yavorsky’s influence. Further, the hierarchy of scale degrees inherent in the tonal system is gone, while the idea of one supreme tonic is still active. This would become a hallmark of Kholopov’s neotonal system, namely, the idea of a “central element” (tsentral’nyĭ element) (“CE”) to which all other elements would be subordinate. At the same time, he is mindful of the fact that, with the new tonic, new elements of tonal organization would now determine how this music is held together in this new global “twelve-tone tonality.”
Example 12. Scriabin, Ninth Sonata, measures 1–23
(click to enlarge and see the rest)
Example 13. Fundamental Chord from Ninth Sonata (From Kholopov 1967b, 97)
(click to enlarge)
[3.3] Example 12 shows the first twenty-three bars of Scriabin’s Piano Sonata no. 9 (1912–13), which Kholopov uses to demonstrate this new music. Kholopov bases many of his late-Scriabin analyses on a single fundamental chord from which structure—at first harmonic and from there formal—emanates; the mystic chord is but one manifestation of this type of chord. For Kholopov, any of Scriabin’s late harmonies that feature a root and a major third and minor seventh above that root fit the description of the fundamental chord. Example 13 shows such a chord, the fundamental chord for the Ninth Sonata, about which Kholopov says:
In essence this chord is the tonic, in the sense that we understand tonic to imply the central element of a tonal system. In this fashion, the establishment of the “fundamental chord” as the foundation in the harmony of late Scriabin is the establishment of a new tonic. . .
The specific properties of the tonic of the Ninth Sonata are conditioned on the “dominant” basis of the chord: at its basis lies the stable major-minor seventh chord. The most important thing here is the stable tritone. This situation starkly contradicts the usual role of the tritone; from here there are concrete specific differences in the properties of harmonic material. (1967b, 98; emphases original)
Kholopov is speaking of the relativism of tonal function in music in this quotation. Whatever the CE of the system is, it should be labeled and thought of as the tonic, irrespective of what that harmony may have meant in the past. This CE, of course, has special significance with the music of Scriabin, insofar as his late harmonies clearly evolved from earlier dominant harmonies.(16)
[3.4] After a discussion of how root motion by tritone represents maximally removed motion in traditional tonal harmony, Kholopov speaks of tritone transposition (since much root motion in Scriabin’s late music is by tritone), and how roots related by tritone can be part of the same tonality:
For the tonic [in Scriabin’s music], the tritone is so important as a constituent element that the sonority whose root is a tritone away from the tonic root is not only not far removed from the tonic, but it can actually be a different form of the same chord, or even a simple displacement (inversion) of the notes of one and the same chord, not yielding one newnote. . . . If the interval of a tritone transposed at the tritone yields the same notes, then between all other intervallic transpositions sharp dissonances arise, more or less, with the exception of transposition at the minor third, during which no seconds or sevenths are formed [with the original tritone]. (1967b, 98; emphasis original)
Example 14a. Abstract Monofunctional Sphere for Scriabin’s Ninth Sonata
(click to enlarge)
Example 14b. Altered Monofunctional Sphere for Scriabin’s Ninth Sonata, measures 5–7
(click to enlarge)
Example 14c. Skeletal Framework Derived from Example 14b
(click to enlarge)
By putting these ideas together, Kholopov came up with the concept for what he called a “monofunctional sphere” (monofunktsional’naiia sfera). Example 14a shows a monofunctional sphere in which a fully diminished seventh chord is sustained in the treble clef and a different fully diminished seventh chord is arpeggiated in the bass. (This is Kholopov’s abstract design for the Ninth Sonata.) Notice how each of the four chords of the sphere contains the minimum of Scriabin’s late harmony, a root, major third, and minor seventh. Most important, all four of these chords represent the same tonality in Kholopov’s neotonal system. The aggregate of notes in Example 14a is an octatonic collection, but Kholopov makes no mention of this fact.
[3.5] Example 14b shows Kholopov’s altered sphere for the beginning of the Ninth Sonata (compare with the chords enclosed in boxes in Example 12, measures 5–7). Kholopov calls each of these chords a variant of the basic dominant-sounding chord shown in Example 13. When dealing with these variants, he says:
Since the chord may have variants even within the limits of one composition, and since the combination of one and the same “basis” (incomplete major-minor seventh chord) with altered layers is the essence of each of them, then it is possible to consider only the “basis” of the chord. (1967b, 99)
Taking the root, third, and seventh of each of the chords shown in Example 14b yields the skeletal framework shown in Example 14c (also from Kholopov 1967b), closely approximating the original monofunctional sphere from Example 14a. The slurs in the bass in Examples 14b and 14c show the tritone root connections.
[3.6] Kholopov is clear that the monofunctional sphere should be likened not to a chord from classical tonality, but rather to the “sphere of the main tonality.” He claims (1) that the chord that governs the other three chords within the sphere is the new tonic, (2) that the chord whose root is a tritone away is the “second form of the tonic,” and (3) that all four chords of the tonic sphere together represent the “main tonality” (1967b, 100). The other two chords also function as tonic substitutes, though they are not as closely related as the tritone-related tonic.
Example 15. Modulation up a Semitone in the Ninth Sonata (From Kholopov, 1967b, 102)
(click to enlarge)
[3.7] Modulation from one monofunctional sphere to another is accomplished by the repetition of material at an interval other than a tritone or minor third, as in measures 16–19 (see the boxes in Example 12). Example 15, from Kholopov, shows the root motion up by a semitone in these measures.
[3.8] The secondary key area of the exposition explores two additional monofunctional spheres (one in passing), and the exposition as a whole thus exploits all three possible monofunctional spheres. Kholopov writes, “In all Scriabin has, in essence, three tonal spheres (though each can have four different tonic chords). And all of these spheres are already used in the exposition” (1967b, 104). Kholopov also likens this motion among the monofunctional spheres in the Ninth Sonata to motion among tonic, dominant, and subdominant keys. He states, “In precise correspondence with the fundamental laws of sonata form the exposition has two tonal
[3.9] In his posthumously published textbook Garmoniia: Prakticheskiĭ kurs (Harmony: A Practical Course) (2003), Kholopov speaks of the motion among the three monofunctional spheres in relation to harmonic function: “Movement of the four-bases system a semitone higher, that is to the scale degree of the dominant double, yields a ‘motion to the dominant’ or ‘modulation to the dominant,’ depending on the function of this transposition in the compositional structure. Transposition a semitone lower, that is to the scale degree of the subdominant double, yields, correspondingly, a general motion to the subdominant” (2003, vol. 2, 176). Thus we see again the likening of the three monofunctional spheres to the three basic harmonic functions of tonal harmony. Still, the notion of “modulation to the dominant” is strong here, inasmuch as the dominant double does represent the actual dominant as a tritone substitution.
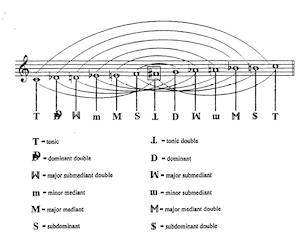
Example 16. Kholopov’s Neotonality, C Tonic Center
(click to enlarge)
Example 17a. Duplex-Chain Mode,
(click to enlarge)
Example 17b. Analysis of Scriabin’s Ninth Sonata, measures 1–7
(click to enlarge and see the rest)
[3.10] The terms “subdominant double” and “dominant double” are part of Kholopov’s neotonal system, shown in Example 16.(17) The slurs on top connect notes symmetrical around the tritone and the slurs on the bottom connect notes a tritone apart. Kholopov begins this system with the traditional Riemannian designations for tonic, subdominant, and dominant.(18) The main harmonies in Scriabin’s Ninth Sonata would be the tonic, the tonic double, the minor mediant, and the minor submediant. Of course any of Kholopov’s twelve harmonies could be in effect within one monofunctional sphere but, more likely, if there is a strong motion to and prolongation of a dominant double chord, for example, it will likely be the new tonic of a new monofunctional sphere.
[3.11] In Example 17 I have done a neotonal analysis, based on Kholopov’s ideas, of measures 1–7 of Scriabin’s Ninth Sonata.
Example 17a shows the relevant mode, the duplex-chain (caten) mode with an
[3.12] Notably, octatonic analysis as practiced in America would fall short in dealing with this passage, for the simple reason that the main chord is five of six notes of a whole-tone scale. Many have noted that, aside from the octatonic, the whole-tone scale is prominent in Scriabin’s work. Indeed, it is often said that Scriabin’s Mystic chord is five-notes of a whole-tone scale with a semitone at one end of the five-note scale. In this capacity it is often referred to as a member of set class 6–34, whose prime form is (013579). The whole-tone element of this set class is immediately apparent from its prime form, and this is often elaborated in the literature. In other words there is confusion with respect to the whole-tone aspect of the Mystic chord. What one must understand with respect to Scriabin’s music is that the Mystic chord evolved from the dominant harmony.(19) Because of this, it makes sense to take only the root, third, and seventh of any Mystic chord—or the chord shown in Example 13—as structural. Then, in Example 17b, I have shown the logical modal gravitations that are part of the duplex-chain mode shown in Example 17a. Notably, the whole-tone scale is not fundamental here.
Example 18. Kholopov’s Neotonality in Cyclic Representation, Tonic of “C”
(click to enlarge)
[3.13] Example 18 shows Kholopov’s neotonal system in a cyclic representation. I have changed some of the designators to reflect the tritone double aspect of the main harmonies. (Kholopov sometimes writes the four changed harmonies—the dominant double, the major submediant double, the major mediant double, and the subdominant double—as I have here.) For example, “MM” represents the tritone double of the major mediant “M.” The shaded areas represent the four tonics of the diminished mode within the neotonal system. The arrows on the inside of the circle show the tritone relation between a harmony and its tritone double, and the direction of the arrow shows the dependence of the “double” harmony on the main harmony from the key.
Problems with Kholopov’s System
[3.14] Kholopov’s neotonality, though extremely efficacious with a composer like Scriabin, is not as useful with other modernist composers. Where it succeeds, it does so by naming a central tone or complex of tones that others gravitate toward. In conjunction with Yavorsky’s neomodal ideas, neotonality offers a useful system with which to frame troublesome passages of tertian music, by Stravinsky or others. It is most useful in analyzing passages that feature common symmetrical modes—such as the whole-tone, hexatonic, or octatonic modes—and the root motion by major or minor third that is common in these passages. Further, it is useful in identifying tritone root relations. But to suggest that there lies an overriding functionality in all neotonal music is a bridge too far, it seems to me. Kholopov fails to explain what the rules of functionality are in his neotonal system. That is, he never sets forth how chord functions work with each other or how a logical progression is formed. (I do not think that such an overriding functionality exists within Kholopov’s neotonality.) Ultimately, with all the work that has been done in twentieth-century music, it is clear that there will never be anything like functional tonality that governed the procedures that composers used in the twentieth century. Still, the search for such a functional system for this music has merit in that there are many late-nineteenth and early-twentieth century composers whose links to tonal procedures were strong, yet their music, not entirely tonal. It therefore stands to reason that such composers conceived of a certain functionality as they composed. Kholopov’s work goes far to answer the call to find such a functionality.(20)
[4] Berger’s Octatonicism
The validity of these [potentially tonal]
interpretations, their relation to tonal functionality or,
conceivably, their relevance to a functionality of a
new order—these are problems that ought to be
seriously explored, preferably in a concerted effort.
(Berger 1963, 42; emphasis mine)
“Problems of Pitch Organization in Stravinsky”
[4.1] Berger’s highly influential article “Problems of Pitch Organization in Stravinsky” (1963) established the American method for dealing with octatonic music. Berger assiduously avoids the language of tonal harmony in hopes of establishing new terms for the analysis of Stravinsky’s music. In a larger sense then, Berger helped give voice to a new language of post-tonal analysis that is now commonplace: the eight-note scale became the “octatonic” (Berger’s own contribution), tonic pitches became “priorities,” chords became “simultaneities,” diminished chords became octatonic “subsets,” and pitch classes were referred to by the integers 0–11. With respect to Berger’s call for a “functionality of a new order,” this is clearly what Kholopov strove for with his version of neotonality. So, in this sense Kholopov answered Berger’s call.
[4.2] That the octatonic scale (1) can begin with a whole step or half step, (2) can be expressed in one of three transpositions, (3) can contain any tonal triad or seventh chord except for the augmented triad (or any seventh chord that contains an augmented triad), and (4) is symmetrical at the (0369) “nodes” or “partitionings” of twelve-note pitch-class space, is so well known that it does not even warrant a musical example. The scale is rich in triadic and seventh-chord material, which should explain why composers such as Chopin, Liszt, Rimsky-Korsakov, Scriabin, and Stravinsky began using it. Still, although it was an extremely important link between functional diatonic tonality and non-functional post-tonality (or “neomodality” or “neotonality”), the octatonic remains but one of many pitch collections, but one of many scales of use in chromatic and modernist music, from the fin through the debut de siècle. To say it represents more than that would be off the mark, in my opinion. Berger implicitly acknowledges this in his article, as I will show below.
[4.3] Those who have used Berger’s article as an inspiration, most notably Taruskin and van den Toorn, have downplayed Berger’s warnings to not read too much into his octatonic interpretations. In perhaps the most-cited passage of Berger’s article, he sets out to establish what he will do with the music of Stravinsky: “A worthwhile objective is certainly an approach that would no longer use tonality as a crutch, a new branch of theory, as it were, starting from what this music itself is, rather than dwelling upon its deviation from what music was previously” (Berger 1963, 11). What is almost never cited is what follows immediately afterward, parenthetically: “(Granted we might still be ultimately obliged to come to terms with traditional schemata, since it is untenable to claim for the music in question anything like the degree of cleavage with tonality that characterized twelve-tone composition)” (1963, 11). What Berger means when he says “traditional schemata” is functional tonal harmony, or functionality in general, which he felt Stravinsky’s music lacked (he speaks about that functionality at different points in the article). Regrettably, no one has yet focused on this traditional side of Berger’s argument. While the great majority of his work focuses on his new octatonic methodology, at several points he steps back and admonishes the reader that it would be a mistake to sever ties with tonality and, more important, with functionality, in any analysis that grapples with a composer like Stravinsky.
[4.4] In setting the stage for his article, Berger speaks of twentieth-century music that is centric, but not tonally functional, stating that there are essentially no theoretical writings yet available that can adequately deal with it. He adds:
There are, to be sure, a number of labels in circulation for referring to this music: pantonality, pandiatonicism, antitonality, modality, tonicality—even “atonality” has been stretched to embrace it. But their function is largely identification, and where any one of them presumes to represent a theory, this is more likely to be descriptive of surface detail than in the nature of an interpretation of internal relations or structural significance. (1963, 11)
In painstaking detail Berger explains his new approach and the neologisms he will be using. He is also clear in distinguishing between two referential categories of pitch classes: a “collection” or an “ordering of intervals” (1963, 14). He splits his article on Stravinsky’s music into four sections: “I) diatonic writing in which ‘tone center’ is not functional ‘tonic’; II) a symmetrical [octatonic] scale used in such a way as to emphasize tritone relation; III) the same scale with minor-third emphasis; IV) interaction between diatonic elements of I and the symmetrical scale of II and III” (1963, 12). It was this system (with a special emphasis on the fourth section) that became the impetus for a large swath of theoretical writings – first on Stravinsky and later on Scriabin and Bartók, among other modernist composers – in the United States in the late twentieth century.
Example 19. Stravinsky, Les Noces (from Berger 1963, 18)
(click to enlarge)
Example 20. Circular Representation of Berger’s Octatonic
(click to enlarge)
[4.5] The first octatonic example from Stravinsky’s music that Berger gives is from Les Noces, shown here in Example 19. It is categorically eight-note music, and a prime example of Stravinsky’s octatonic sound. With such an excerpt, one of the main tasks is to establish pitch-class priority. Berger quickly establishes “A” as the priority for this section and writes an octatonic scale “a–
Within any given octatoniccollection . . . the first element of any of the partitions of the octave at 0, 3, 6, and 9 has the potentiality of being the pitch class of priority in an identical ordering referable to the same given octatonic collection, and this also holds true, analogously, for 1, 4, 7, and10 . . . Therefore, in the interval ordering of the scale as represented above, there are, loosely speaking, four potential “tone centers’ of equal weight and independence. (1963, 21)
Thus, in Example 20, the two main axes link 0, 3, 6, and 9 and the secondary dotted axes link 1, 4, 7, and 10. The main octatonic scale from Les Noces is represented with lines drawn inside the circle linking the scale, 0-1-3-4-6-7-9-10. Lastly, the 0-3-6-9 tetrachord is shaded gray to emphasize its priority.
[4.6] Berger is keenly aware of the tonal tradition from which Stravinsky came. He concedes that Stravinsky’s music is nothing like that of the twelve-tone composers, and that dealing with tonal aspects in the music will be necessary. Further, in Section I of his essay, when addressing seven-note music that exhibits non-tonal procedures, as is the case with Stravinsky, he says, “it would therefore seem to follow from this that what to some may appear to be unjustifiable tonal bias is not only legitimate but necessary for dealing rationally with this music” (1963, 14). Lastly, in the conclusion of the essay, after having discussed several aspects of tonality in Stravinsky’s music and the need to deal with such tonal relationships, Berger argues:
If an adequate theory is to be developed to deal with such relationships as have just been discussed, what attitude should be adopted toward them? Are they actually tonal functional relations or are they “semblances,” and if the latter, in what sense? Surely it is illuminating to approach Stravinsky’s music from the angle of the octatonic scale and the basic cell. But Stravinsky, for all his genuine independence and original musical outlook, was born into a generation that had, in a manner of speaking, a “congenital” orientation toward those concepts of “traditional harmony” that are now being questioned.
Consequently, even though an attempt was made here to avoid tonal theory as a norm from which to depart, we found ourselves eventually obliged to confront it as a result of certain potentially tonal interpretations which arose out of what I believe to be the essential nature and significance of the music. (1963, 42)
It is worth repeating Berger: “the essential nature and significance of the music [of Stravinsky]” can be found in “potentially tonal interpretations.” So, it would seem that Kholopov’s neotonality, based on Yavorsky’s modes, could be useful in analyzing Stravinsky’s music.
Example 21. Kholopov’s Neotonality with Berger’s Octatonicism
(click to enlarge)
[4.7] Example 21 shows the two cyclic representations of the octatonic, one from Kholopov and the other from Berger. Underneath I have shown a Venn diagram displaying the convergence of these two concepts, which I consider to be crucial in order to understand music that is often deemed octatonic in America. Within this overlap I have mentioned several composers whose octatonic work could be thought of in neotonal terms. With this diagram I do not wish to suggest, however, that all eight-note music of these composers exhibits aspects of both Kholopov’s and Berger’s methods. I rather wish to emphasize that the decoupling of these two realms that has occurred over the past few decades is unfortunate. For to turn one’s back on the tonal underpinnings of the music of Bartók, Scriabin, and Stravinsky is to miss a large part of the picture indeed. The work of these composers, and others, would be better understood through the combination of post-tonal methods based on Berger’s ideas and the neotonal ideas of Kholopov: a merging of neotonality and octatonicism. Though this would certainly be a fruitful area of further study, it is beyond the scope of the present article.
[4.8] It seems as though Berger knew of the pitfalls inherent in an analysis of music by a composer such as Stravinsky that completely neglected his tonal underpinnings:
The [octatonic-diatonic] synthesis produces a curious alchemy that brings tonal functionality in its wake. Yet this conclusion does not, I trust, invalidate the initial intention [to look at music in a new way—from outside of tonality]; since it is better for tonal functionality to insinuate itself gradually, than for it to confine all discussion at the outset to the level of established theory. (Berger 1963, 12)
Yet I believe that Berger would add that, with certain modernist composers (and surely with Stravinsky), this insinuation was not only beneficial but also necessary in order to better understand this music. Again, this is an aspect of Berger’s original work that is often overlooked in the octatonic analyses that have cropped up since he wrote his seminal article.
Berger’s Regrets
[4.9] In his Reflections of an American Composer, Berger says, “I was not elated at the thought that what most readers got out of my article was a new locution [octatonic] and a new scale formation. My concern was the significance of tone center in nontonal music and how it was established” (Berger 2002, 187). Yet it was this new locution that most picked up on. (And, with the case of van den Toorn, it was a locution that would provide the basis for an entire analytical method—see van den Toorn 1983 and 1987.) However, it was the following quotation about which Berger expressed the most regret. It is worth quoting in its entirety:
It is tempting to speculate on whether Stravinsky’s choice of “polarity,” a word which cannot accurately be applied (as he applies it) to one thing without its opposite, either had implications that escaped the intermediary who transcribed his thoughts, or—which seems more likely—reflected an awareness, if only on a subverbal level where it was difficult to articulate, of the special properties of the tritone which make it possible for pitches at 0 and 6 (capable of graphic representation as “poles” in a circle offifths . . . ), by virtue of similitude or equal and thus independent weight, to remain in equilibrium or—to the end that a tone center is asserted by neither—to stand in a certain opposition. This speculation might easily take flight in a direction which would establish, as a necessary condition of “polarity,” the denial of priority to a single pitch class precisely for the purpose of not deflecting from the priority of a whole complex of tones. And from here, it would be a simple step to the conclusion that short of twelve-tone and so-called “atonal” procedures, nothing provides this condition better than the octatonic scale. (Berger 1963, 25–26)
About this quote in particular, Berger later said, “I do
[4.10] Berger’s regrets are understandable. He wanted to write an article about tone centers in the music of Stravinsky, but when interpreting Stravinsky’s famous usage of the term “poles,” Berger, recognizing the preponderance of tritones in Stravinsky’s music, took the 0–6 tritone partition as a possible representation of those poles.(22) Further, if in fact no one tone center could be established above all others, he speculated that octatonic music could provide an ideal framework for the denial of pitch-class priority, as with the atonality of the Second Viennese School. In so doing however, Berger opened the door for analyses that completely ignored the “traditional schemata” (which emphasize tone center) that he talked about. I believe that this is one reason for his misgivings.
[5] Analytical Examples
[5.1] In a letter to the composer Ivan Kryzhanovskiĭ from 1909, Yavorsky identifies his modes in the works of Liszt, Rimsky, Chopin, Beethoven, Grieg, and Scriabin. Further, with respect to Rimsky, Yavorsky identifies the augmented mode in The Tale of Tsar Saltan, Kashcheĭ the Immortal, Sadko, and The Golden Cockerel, while he identifies the diminished mode in Sadko (Yavorsky 2008, 10). Though Yavorsky was not a fan of Stravinsky’s music, he seemed to think it was suitable for modal analysis. In the letter to Anatoliĭ Lunacharskiĭ from the end of 1927, mentioned above, Yavorsky writes: “Stravinsky makes a mockery of his listeners (in terms of content but not according to the principles of the formation of his music)” (Rabinovich, ed. 1972, vol. 1, 374). So we see that Yavorsky, though unimpressed with Stravinsky’s sound, still thought that Stravinsky’s music was well formed. This was likely because Yavorsky felt that his modes were present in Stravinsky’s music.
[5.2] For his part, Kholopov identifies the use of Yavorksy’s modes in Stravinsky’s music in his “Simmetrichnye lady v russkoĭ muzyke” (Symmetrical Modes in Russian Music) (2008).(23) Kholopov says:
In his early period Igor Stravinsky directly continued the path of his teacher, Rimsky-Korsakov. He also further developed the principles of the usage of symmetrical modes. In particular, there are many symmetrical modes in Firebird, whose plot, in fact, is directly connected with Rimsky’s Kashcheĭ the Immortal. Stravinsky’s sympathies toward symmetrical modes turned out to be rather steadfast. He returned to the minor-third system in his neoclassical period (with his Symphony in Three Movements, forexample). . . .
One sees all types of symmetrical modes in Stravinsky’smusic. . . .
As with Rimsky-Korsakov, Stravinsky particularly preferred the minor-third system (Fireworks, Scherzo fantastique, The Rite of Spring, The Nightingale, Symphony in Three Movements), striving for distinctness in the chordal development of a given complex of notes. (2008, 133–34)(24)
So, Russian theorists have also long known about Stravinsky’s predilection for the octatonic. But they acknowledge much more than this in his music.
Protopopov on Scriabin’s Prelude, Op. 74, No. 3 (1914)
Example 22. Protopopov’s Analysis of Scriabin’s Op. 74, No. 3, measures 1–4 (from Protopopov 1930, vol. 2, 141–146)
(click to enlarge)
[5.3] One of the earliest examples of octatonic analysis in Russia is Sergei Protopopov’s analysis of Scriabin’s op. 74, no. 3 (Protopopov 1930, vol. 2, 141–46). The piece is unremittingly octatonic. Of the many hundreds of notes in the short prelude, only ten lie outside of the one main octatonic collection, what van den Toorn calls Collection III.(25) Protopopov’s analysis focuses on the “duplex-chain” mode, which he writes at the top of his analysis and which is shown in Example 22. Notice the four single symmetrical systems, labeled I–IV, each of which contains a tritone and its resolution to a major third. (In his own compositions Protopopov would often list the mode that he composed the piece in, in the same fashion that he lists the mode in this analysis of Scriabin’s prelude.) I have included only the first four measures from Protopopov’s analysis in the example, though he did analyze the entire piece. There are two notes outside of the tonic in the example, enclosed in boxes. He shows these non-tonic notes and their resolutions into the stabilities of the system (in other words, the conjunctions), which I have shown with a dotted slur, and he also writes the roman numeral of the system from which the conjunction came. The remaining such conjunctions are:
- The octatonic scale represents the stability of the mode and the remaining diminished-seventh chord represents the instability;
- The active mode is the duplex chain, and not the duplex diminished;
- The centric pitch is
F♯ ; - There are only ten notes outside of the mode, and each is only an eighth note in duration; and
- “Consequently, the entire prelude is written in the
F♯ duplex-chain mode which, with an eight-note tonic, has four unstable tones that occur in descending conjunctions of the four single systems of the mode.” (Protopopov 1930, vol. 2, 144–46)
I include this analysis here not to show that Scriabin composed diminished-mode music—many have made similar observations about his pieces. Rather, I include it to show how, only fifteen years after Scriabin died, Yavorksy’s method of modal analysis could accurately encapsulate music that was not traditionally tonal.
Kholopov on Stravinsky’s Firebird
Example 23a. Stravinsky, Firebird, measures 1–2
(click to enlarge)
Example 23b. The Z Chain Mode Relevant to Firebird, measures 1–2
(click to enlarge)
[5.4] This brief analysis of the opening of Firebird offers a glimpse into how Stravinsky might be viewed through Yavorsky’s modes. Notably, van den Toorn considers this opening to be octatonic (van den Toorn 1983, 11–17). I have shown the first two bars, which occur in the cellos and basses of Stravinsky’s work, in Example 23a. The key of
[5.5] Kholopov mentions an interesting connection between Yavorsky and Rimsky at the end of his brief analysis of Stravinsky’s Firebird:
It is probable that the coinciding with Yavorsky’s “tables” is not entirely by chance. Stravinsky was obviously oriented toward his teacher’s opera Kashcheĭ the Immortal (in which there are similar structures), but Yavorsky could also take Rimsky’s Kashcheĭ into account, since it had been performed not long before the publication of The Structure of Musical Speech; and later, Stravinsky’s Firebird itself could turn out to be in Yavorsky’s field of view under the design of the Z-mode. (Kholopov et al. 2006, 384)
In a discussion of this passage, Tatiana Kiuregian, Professor of Music Theory at the Moscow Conservatory, adds:
When creating his theory, Yavorsky was focused on the music of Rimsky-Korsakov (among others), that is, he was searching for the key to its structure. Yavorsky knewKashcheĭ. . . . Rimsky-Korsakov’s music is one of the sources of Yavorsky’s theory, that is, Rimsky-Korsakov’s creative practice suggested this theory toYavorsky. . . . Consequently, it is possible to say that Rimsky-Korsakov is a prototype of a) Stravinsky’s early music, and b) Yavorsky’s theory. Therefore, Yavorsky’s theory also explains Stravinsky’s music so well.(26) (Kiuregian 2011)
Indeed it does. Without Rimsky there would have been no theory of modal rhythm. (Of course, without Rimsky there probably would have been no Stravinsky either.) It is no surprise then that Yavorsky’s method is primary in Russia when dealing with Stravinsky’s music.
Stravinsky’s Petrushka
Example 24. Kholopov’s Analysis of Sadko, Scene 2, measures 1–10 (excerpted)
(click to enlarge and see the rest)
[5.6] Both van den Toorn (1983, 35–36) and Taruskin (1996, vol. 1, 273–76ff) view the Second Scene from Rimsky’s Sadko as an important precursor to Stravinsky’s Petrushka and the Petrushka chord. Indeed, such a chord occurs right at the opening of this scene. Notably, they analyze this opening as octatonic. Meanwhile, Kholopov (2003, 228–31) views the opening as having two active modes, duplex major and diminished. (See Examples 10 and 11 above for Yavorsky’s derivation of the duplex major mode and its gravitations.) Part of his analysis is shown in Example 24. In his system of analysis, Kholopov can distinguish between different modes if they are active in the piece. Notice also that he writes out the active scale of the mode. So, what van den Toorn and Taruskin must view as octatonic, Kholopov can label as duplex major (measures 1–7) and diminished (measures 8–10). This is significant in that it provides for more variety in the analysis, further refining the realm of the octatonic. Also, the modal gravitations gain new meaning if the music is considered to be in more than one governing mode. Taruskin and Kholopov analyze slightly more than these first ten bars in their work. (Kholopov does mention that the duplex-major mode can be thought of as a subset of the given octatonic collection.) This is, of course, a small difference, but significant.
[5.7] With respect to the Petrushka chord, Berger states:
However, since the entire configuration [of the Petrushka chord] may now be subsumed under a single [octatonic] collection with a single referential order, i.e. the octatonic scale, the dubious concept of “polytonality” need no longer be invoked; nor does such an interpretation make it impossible to acknowledge a certain compound nature of the configuration, since this can be done entirely within the referential collection of the octatonic scale, by means of the partitions. (1963, 22–23)
While van den Toorn says:
It becomes more accurate to speak of the “compound nature of the configuration [the Petrushka chord]”—or of the “opposition” or “polarity” that this “compound nature” projects—in terms of the oscillating or superimposed (0,6) tritone-related (0 4 7) triads of the octatonic collection. (1983, 64)
And Taruskin’s view, though octatonic, is more nuanced, and involves the possibility of bitonal readings. When speaking of the possibility of “two keys” embedded in the Petrushka chord, Taruskin writes that it is possible to take into account these two keys,
so long as it is borne in mind that the keys in question were chosen not simply ad libitum but from among the circumscribed and historically sanctioned wares of the octatonic complex. (1996, vol. 1, 749)
Example 25. Modal Analysis of Petrushka, Rehearsal 49
(click to enlarge and see the rest)
Example 26. Gravitational Analysis of Non-Modal Notes, Petrushka, R. 49
(click to enlarge)
[5.8] With the addition of Yavorsky’s duplex-major mode to the mix, we no longer have to use an eight-note collection to name a six-note entity. Also significant are the modal gravitations of the duplex major mode. Now, there is no need to speak of how the two non-octatonic notes that any Petrushka chord excludes work within the context of the six-note sonority; rather, the six notes outside of the mode gravitate inward to the six-note Petrushka chord. The following analysis of Rehearsal 49 from Petrushka (in Example 25) will demonstrate some of the concepts I have raised thus far. The
[5.9] This “neomodal” interpretation of the Second Tableau of Petrushka differs from a typical octatonic reading in six ways. First, it treats the Petrushka chord as the six-note entity that it is, rather than viewing it as an octatonic subset. Second, it shows the modal gravitations inherent in the mode. Third, it seeks to establish one centric pitch over all others. Fourth, the duplex-major reading places the six non-tonic notes (the connecting moment) on equal footing, treating them as instabilities that require resolution in the tritone systems. In other words, the
[6] Conclusion
[6.1] One reason American octatonic collectional analyses have gained so much currency over the past few decades, in my opinion, is because they are relatively easy. Consequently, the waters have been muddied with countless analyses and articles that, taken together, overstate the case for octatonicism in late-Romantic and modernist music.(28) True, there is much octatonic music out there, but too often it seems that the late twentieth-century American analyst uses octatonicism as a crutch. In other words, it is easier to find some octatonic music in a certain composer’s works and then “discover” that this was the main method of composition for that composer than it is to accept the fact that this was, to a large extent, not true (or at least not fundamental). When we take his various statements on the issue into account, it seems Berger understood this concerning Stravinsky’s music. Unfortunately, this side of Berger’s work is neglected. Instead, Taruskin and van den Toorn have held up Berger’s article as the first source that revealed the true essence of Stravinsky’s music. However, their argument for octatonicism in his music oversimplifies Stravinsky’s pitch organization, in my opinion, and the Russian views outlined here provide valuable added nuance.
[6.2] Kholopov’s neotonality goes a long way in answering Berger’s call for the “functionality of a new order.” The CE (Central Element) is an intriguing concept for understanding pitch gravitations in new music: in many ways it is similar to the “set complex” from American pitch-class set analysis. But by assigning chord functions, Kholopov distinguishes himself. Notably, he only felt that these functions were active in tertian music. (With a composer like Webern, for instance, he felt another system was active, which he called “Hemitonicism” [Gemitonika].) And when dealing with root motion by major or minor third, this system was particularly apt in describing neotonal music, as in the passage from Scriabin’s Ninth Sonata considered above. Later in his career, the monofunctional sphere gave way to the diminished mode in Kholopov’s writings, though their functions were quite similar. The sphere emphasized root motion by third, which Yavorsky did not stress in his system.
[6.3] In the United States, very little work has been done with Yavorsky’s writings. In his two-volume work on Stravinsky, Taruskin mentions Yavorsky, but he conflates Yavorsky’s theory with his own ideas about octatonicism, thus detracting from the true beauty of Yavorsky’s system. Taruskin writes: “The concept of a stable, consonant, and harmonically static diminished fifth is recognized in Russian music theory by Boleslav Yavorsky’s formulation of the ‘diminished
[6.4] Yavorsky’s system is compelling if one accepts the tenets upon which it is founded: 1) An equal twelve-step chromatic system, 2) The absence of tonal-functional harmony, 3) Enharmonic equivalence of notes, 4) Enharmonic equivalence of semitonally expressed intervals, and 5) The tritone as the basis for motion. The historical connections among Yavorsky, Taneev, Arensky, and Rimsky (and specifically the link between Yavorsky and his teacher, Taneev or, possibly, the link between Yavorsky and Rimsky) serve to solidify the compelling nature of Yavorsky’s work. Perhaps most compelling is how easily his ideas can be applied to much if not all of the nonfunctional tertian music of the late-nineteenth and early twentieth centuries, music that consistently poses problems for analysts to this day. (One could easily envisage how his theory could be applied to the music of Bartók, for instance.) More specifically, Yavorsky’s system works well with Stravinsky’s music: certain of his works that are sometimes interpreted as octatonic in America get new meaning via Yavorsky’s modes.
[6.5] In rethinking octatonicism, it is my hope that the Russian concepts I discussed in this paper will enrich the current dialogue surrounding Stravinsky’s music and its relation to octatonicism. Though I did not strive to invalidate the important contributions made in the United States regarding the eight-note scale, I do believe that American octatonic analysis has shortcomings, especially with respect to Stravinsky’s music. In using Yavorsky’s theory to analyze this music, some of those shortcomings are redressed.
[6.6] In light of the rich offerings of Yavorsky’s theory of modal rhythm, I think more analyses of Stravinsky’s music using this system would be extremely beneficial. The debate over the role of octatonicism in Stravinsky’s music is really part of a larger debate over how post-tonal composers organized pitches in their music. One particularly useful area of further research would be in the area of modal gravitations, and how they relate to the idea of voice leading as understood in American music theory. Clearly, the idea of a tritone from a dominant harmony resolving into a tonic harmony is relevant to both, but what of the gravitational and voice-leading considerations in a post-tonal context? Another area of interest would be in exploring the possibility of long-term symmetrical systems in the analysis of larger works. Did Yavorsky (or Protopopov) conceive of their modal system only in purely local terms, or did they acknowledge a deeper structural component? It is my hope that this article might move the general conversation in American music theory, if only in some small way, toward these Russian theoretical topics, which offer a treasure trove of inspired writings and provocative concepts.
Philip A. Ewell
Hunter College and CUNY Graduate Center
Department of Music
695 Park Ave.
New York, NY 10065
pewell@hunter.cuny.edu
Works Cited
Berger, Arthur. 1963. “Problems of Pitch Organization in Stravinsky.” Perspectives of New Music 2, no. 1: 11–42.
—————. 2002. Reflections of an American Composer. Berkeley: University of California Press.
Carpenter, Ellon. 1995. “Russian Theorists on Modality in Shostakovich’s Music.” In Shostakovich Studies, ed. David Fanning, 76–112. Cambridge: Cambridge University Press.
Ewell, Philip. 2001. “Analytical Approaches to Large-Scale Structure in the Music of Alexander Scriabin.” PhD diss., Yale University.
—————. 2006. “Scriabin’s Dominant: The Evolution of a Harmonic Style.” The Journal of Schenkerian Studies 1 (2006): 118–48.
Gjerdingen, Robert O. 2011. “Gebrauchs-Formulas.” Music Theory Spectrum 33, no. 2 (Fall): 191–99.
Honti, Rita. 2007. Principles of Pitch Organization in Bartók’s “Duke Bluebeard’s Castle.” 2nd Edition. Helsinki: Faculty of Arts, Dept. of Musicology, University of Helsinki.
Kholopov, Yuri. 1967a. “Diatonicheskie lady i tertsovie khromaticheskie sistemy v muzike Prokof’eva.” In Ot Liulli do nashikh dneĭ, 256–79. Moscow: Muzyka.
—————. 1967b. “Klassicheskie struktury v sovremennoĭ garmonii.” In Problemy sovremennoĭ muzyki, first edition, 91–128. Moscow: Muzyka.
—————. 1971. “Simmetrichnye lady v teoreticheskikh sistemakh Iavorskogo i Messiana.” In Muzyka i sovremennost’. Installment 7, 247–93. Moscow: Muzyka.
—————. 1991a. “Ladovyĭ ritm” (Modal Rhythm). In Muzykal’nyĭ entsiklopedicheskiĭ slovar’. Moscow: Sovetskaia Entsiklopediia.
—————. 1991b. “Tonal’nost’” (Tonality). In Muzykal’nyĭ entsiklopedicheskiĭ slovar’. Moscow: Sovetskaia Entsiklopediia.
—————. 1997. “O sisteme garmonii Stravinskogo.” In I. F. Stravinsky: Sbornik Stateĭ. Moscow: Moskovskaia Konservatoriia.
—————. [(1988)] 2003. Garmoniia: Teoreticheskiĭ kurs. Moscow: Muzyka. Reprint, Moscow: Lan’.
—————. 2003. Garmoniia: Prakticheskiĭ kurs. Moscow: Kompozitor.
—————. [1975] 2008. “Symmetrische Leitern in der Russischen Musik.” Die Musikforschung 28, 379–407. Kassel. Reprinted as “Simmetrichnye lady v russkoĭ muzyke” in Idei Iu. N. Kholopova v XXI veke, 114–45. Moscow: Muzizdat.
—————. [1981] 2008. “Problema novoĭ tonal’nosti v russkom i sovietskom teoreticheskom muzykoznanii.” In Voprosy metodologii sovietskogo muzykoznaniia. Moscow: Moscow State Conservatory, 100–126. Reprinted in Idei Iu. N. Kholopova v XXI veke, 199–219. Moscow: Muzizdat. Citation is to the 2008 edition.
Kholopov, Yuri, L. Kirillina, T. Kiuregian, G. Lyzhov, R. Pospelova, and V. Tsenova. 2006. Muzykal’no-teoreticheskie sistemy. Moscow: Kompozitor.
Kiuregian, Tatiana. 2011. Email correspondence with author. December 11.
Lendvai, Ernő. 1955. Bartók stílusa. Budapest: Zeneműkiadó.
—————. 1971. Béla Bartók: An Analysis of His Music. London: Kahn and Averill.
—————. 1983. The Workshop of Bartók and Kodály. Budapest: Editio Musica.
McQuere, Gordon D. [1983] 2009. “The Theories of Boleslav Yavorsky.” In Russian Theoretical Thought in Music, ed. Gordon D. McQuere. Ann Arbor: UMI Research Press. Reprint, Rochester: University of Rochester Press.
Protopopov, Sergei Vladimirovich. 1930. Elementy stroeniia muzykal’noĭ rechi. 2 vols. Moscow.
—————. 1978. Elementy stroeniia muzykal’noĭ rechi. Translated as The Elements of the Structure of Musical Speech by Gordon Daniel McQuere. Ph.D. diss., The University of Iowa.
Rabinovich, I. S., ed. 1964. B. Iavorskiĭ: vospominaniia, stat’i i pis’ma. 2 vols. Moscow: Muzyka.
—————, ed. 1972. B. Iavorskiĭ: stat’i, vospominaniia, perepiska. 2 vols. Moscow: Kompozitor.
Savenko, Svetlana. 2001. Mir Stravinskogo. Moscow: Kompozitor.
Stravinsky, Igor. [1947] 1959. Poetics of Music. Trans. Knodel and Dahl. Cambridge: Harvard University Press. Reprinted with Preface by Darius Milhaud. New York: Vintage Books. Citation is to the 1959 edition.
Taruskin, Richard. 1996. Stravinsky and the Russian Traditions: A Biography of the Works through “Mavra”. Berkeley: University of California Press.
—————. 2011. “Catching Up with Rimsky-Korsakov.” Music Theory Spectrum 33, no. 2 (Fall): 169–85.
Van den Toorn, Pieter. 1983. The Music of Igor Stravinsky. New Haven: Yale University Press.
—————. 1987. Stravinsky and “The Rite of Spring.” Berkeley: University of California Press.
Wason, Robert. 1988. “Progressive Harmonic Theory in the Mid-Nineteenth Century.” Journal of Musicological Research 8: 55–90.
Wilson, Paul. 1992. The Music of Béla Bartók. New Haven: Yale University Press.
Yavorsky, Boleslav. 1908. Stroenie muzykal’noĭ rechi. Moscow.
—————. 1913. Uprazhneniia v golosovedenii. Moscow: Iurgenson.
—————. 1915. Uprazhneniia v obrazovanii ladovogo ritma. Moscow: Iurgenson.
—————. 1929. Struktura melodii. Moscow.
—————. 2008. Izbrannoe: pis’ma, vospominaniia. Moscow: Kompozitor.
Footnotes
1. Parts of this article were first presented at the annual meeting of the Music Theory Society of New York State, April 2005, at Baruch College in New York City. I would like to thank Kofi Agawu, Olga (Ellen) Bakulina, Ellon Carpenter, Sylvia Kahan, Tatiana Kiuregian, Gordon McQuere, Andrew Pau, Svetlana Savenko, and Joseph Straus, all of whom helped in one way or another in preparing this paper. I also thank the two anonymous reviewers of this journal for their thorough reading and helpful suggestions. Lastly, I would like to acknowledge a grant from the Faculty Fellowship Publication Program of the City University of New York, which provided funding for a course release to aid in preparation of this article.
Return to text
2. See Taruskin 1996 and 2011 and van den Toorn 1983 and 1987, among other publications.
Return to text
3. For example, Svetlana Savenko, professor of musicology at the Moscow State Conservatory, writes, “At the foundation of pitch organization in Stravinsky’s music lies the principle of modality” (2001, 127).
Return to text
4. All translations from Russian to English are my own unless otherwise noted. I have used the transliteration system of the Library of Congress in this work, which can be found in the Chicago Manual of Style (16th ed.), on page 568 as Table 11.3. (Though typical anglicized names—Prokofiev, Stravinsky, Tchaikovsky, and Yavorsky, or Moscow and St. Petersburg, for example—appear throughout.)
Return to text
5. In Russia this theory is also called the “theory of auditory gravitation,” or the “theory of musical thought” (see Kholopov 1991a). For an excellent summary of Yavorsky’s ideas in English, see McQuere [1983] 2009, 109–64. The best summary in Russian, arguably, is by Kholopov (Kholopov et al. 2006, 375–94).
Return to text
6. His book on voice leading is really a book of counterpoint exercises in two, three, and four voices, in strict and free styles. His book on the formulation of modal rhythm is also an exercise book on forming the modes of his system. And his book on melody is an important work summarizing some of his developing views on his system.
Return to text
7. Arensky’s exercise book featured prominently in the recent Spectrum Symposium (see, in particular, Robert Gjerdingen’s response to Taruskin, 2011, 191–99). The connections from Rimsky through Arensky to Taneev are certainly worth exploring. Though it appears in this publication from 2008, Yavorsky’s Vospominaniia is undated: it was likely written not long after Taneev died in 1915. There are four more points to this list, which I have not included here.
Return to text
8. What is shown in Example 1 would later become, of course, the ordered pitch-class interval in American pitch-class set analysis. Yavorsky gives no method for calculating such intervals using modulo-12 arithmetic. For an even earlier instance of ordered pitch-class intervals and modulo-12 arithmetic, see Wason 1988. In his article Wason cites a work by H. J. Vincent from 1894, in which Vincent argues for a 12-note system using mod-12 arithmetic. It is highly unlikely that Yavorsky was aware of Vincent’s work as he devised his own system.
Return to text
9. In his letter from 1906 the symmetrical system (simmetrichnaia sistema) was as yet unnamed, and in his book from 1908 Yavorsky called it the “tritone system” (tritonnaia sistema). The earliest evidence of Yavorsky’s formulation of this system is from 1899, in which he spoke of a “collision” (kolliziia) and its resolution (Rabinovich, ed. 1964, vol. 1, 613). It is important to note that in Example 2 and further examples, Yavorsky is showing one of twelve possibilities of his system. That is, a tritone of a single symmetrical system could resolve to twelve different major thirds, not only to C–E as shown in the example. (That is, in addition to C–E, the tritones could resolve to
Return to text
10. Protopopov’s book (1930) was under the general editorship of Yavorsky. For an English translation, see Protopopov 1978.
Return to text
11. That is, so long as the tritones of the two systems are not a semitone apart—if they were they would constitute a double symmetrical system. This is why it was not possible for Yavorsky to form a hexatonic mode in his system, a shortcoming, to be sure. Kholopov would later call the hexatonic an augmented mode with a “1.3” or “3.1” scale pattern.
Return to text
12. Protopopov, with Yavorsky’s approval, took to using Latin terms for the diminished, augmented, and chain modes. Further, with the solfège syllables that are used as note names in Russia, they would use the Russian terms, but with letter names they would use the Latin terms. So, the diminished, augmented, and chain modes on the note
Return to text
13. Kholopov calls the duplex-major mode the “Petrushka Mode” (2003, 227).
Return to text
14. Kholopov calls these interlocking tritones a “cunning trick” (2008, 203n).
Return to text
15. The Russian for “neotonality” is novaia tonal’nost’, a direct translation of which would be “new tonality.” I have chosen to use the Greek prefix and conflate the Russian into the one-word “neotonality.” It would be possible, in Russian, to use one word as well, novotonal’nost’.
Return to text
16. Notably, Kholopov began to use the term “sonority” over “triad,” “chord,” or “harmony” when discussing this music. (Sozvuchie and not trezvuchie, akkord, or garmoniia. Sozvuchie can also be translated as “simultaneity.”)
Return to text
17. Alternate versions of this example are given in Kholopov [1988] 2003, 446, and Kholopov 2003, vol. 2, 20. Kholopov made the version shown in Example 18, the most recent version, available to me in person in 2000.
Return to text
18. Riemann’s impact on Music Theory in Russia is hard to overstate. When he was only 22, Yavorsky translated Riemann’s Systematische Modulationslehre als Grundlage der musikalischen Formenlehre (Hamburg 1887) into Russian, for example. Further, Chapter 11 from Kholopov’s treatise on harmony ([1988] 2003), “A Theory of Functions,” which accounts for over a third of the book, draws heavily on Riemann. His impact on Russian Music Theory is a field of study that, sadly, remains largely unexamined.
Return to text
19. For a discussion of this evolution see Ewell 2006.
Return to text
20. Another author who tried to envision octatonic music in a neotonal framework was Ernő Lendvai. Lendvai’s system, like Kholopov’s, seeks to assign a significance and harmonic function to each of the twelve steps of the chromatic scale, thereby expanding the range of tonal functions from three scale degrees to all twelve. Lendvai’s system, which he called the “axis system,” is far more conservative than Kholopov’s, with all twelve scale degrees representing only tonic, dominant, or subdominant functions. Lendvai applied this system almost exclusively to the music of Bartók. The system is explicated in Lendvai 1955, 1971, and 1983. For two takes on the axis system see Wilson 1992, 6–8 and 203–8, and Honti 2007, 53–60.
Return to text
21. Berger says that “a, c,
Return to text
22. For Stravinsky’s discussion of “poles” in his music, see Stravinsky [1947] 1959, 37–38.
Return to text
23. Kholopov wrote this article in 1973, however, it was published for the first time in Russia in 2008. It was published in German in 1975. Many of Yavorsky’s modes—such as the whole tone, diminished, and augmented—fall under the rubric of “symmetrical modes” in Kholopov’s understanding. See Kholopov 1971 for more on this.
Return to text
24. Kholopov uses “minor-third system” synonymously with “diminished mode.”
Return to text
25. For a discussion of these collectional definitions see van den Toorn 1983, 48–51.
Return to text
26. Here is the original Russian for this passage: “Яворский, создаваЯ свою теорию, ориентировался (среди прочего) на музыку Римского-Корсакова, т.е. искал разгадку ее строения. Яворский знал
Return to text
27. Yavorsky allowed for five forms of the mode when the double-symmetrical system was involved: complete (all of the modes I discussed in Section 3 were complete), natural, harmonic, fourth, and fifth. The natural mode omitted the chromatic passing tone of the double system, thereby allowing linear motion by whole tone, which I suggest above with the motion of
Return to text
28. I myself am guilty of overstating this case. In my dissertation, “Analytical Approaches to Large-Scale Structure in the Music of Alexander Scriabin,” I argued for the case of “non-tonal octatonicism” in Scriabin’s music, saying that this was “the most perspicacious
Return to text
Copyright Statement
Copyright © 2012 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by John Reef, Editorial Assistant
Number of visits: