The Interruption-Fill and Corollary Procedures *
Yosef Goldenberg
KEYWORDS: Schenker, interruption, form, caesura-fill, Bach, Haydn, Mozart, Beethoven, Chopin, Schubert, Liszt, Wagner, Grieg, Widor, Kalinnikov
ABSTRACT: Occasionally a link is inserted between the two branches of paradigmatic interruption structure. The chief type is based on chromatic ascent from pre-interruption to the regained primary tone. This is a stock figure in classical themes, especially in slow movements, but also serves as the basis for special artistic devices. The interruption-fill poses some theoretical difficulties.
Copyright © 2012 Society for Music Theory
[1] Many artistic devices in classical and romantic music aim at “blurring the frontiers between different sections.”(1) Examples include the lack of synchronization between the beginning of the recapitulatory rotation and the regaining of a structural tonic,(2) or the “linkage technique,” where “a new phrase takes as its initial idea the end of the immediately preceding one” (Jonas 1982 [1934/1972], 7).(3)
[2] In certain cases, the blurring effect creates phrase overlaps, and thus challenges the existence of separate sections. This is common at the local level, as with parallel periods where the pre-interruption V only arrives at the beginning of the consequent (usually in parallel with a non-tonic opening of the antecedent).(4) On a large scale, the complete absence of a true tonic at the beginning of a sonata-form recapitulation might cancel the interruption in favor of an undivided Ursatz (Suurpää 2005).
[3] Sometimes, however, the borders between the musical units remain clear, but there is nevertheless some link between them. The paradigmatic situation for such links is the interruption-fill, i.e., motion that connects the two branches of an interruption structure. This may appear as a connection from the end of the antecedent to the beginning of the consequent in a parallel period, but also in larger forms based on interruption (such as sonata form and many cases of rounded binary).(5)
[4] I shall examine a simple instance of an interruption-fill before dwelling on the theoretical problems that emerge from it. The study will proceed with a discussion of the various ramifications of the interruption-fill before primary tone or , special artistic devices based on the ordinary interruption-fill, other formal contexts for the chromatic lead-in, other interruption-fill configurations in the upper voice and interruption-fill in the bass, and finally analogous cases of “illegal” passing motion.
The Basic Upper-Voice Interruption-Fill with Primary Tone
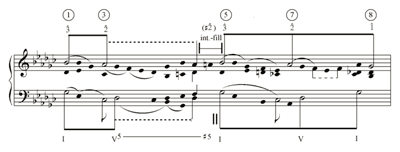
Example 1. Basic upper-voice interruption-fill before : Schubert, Impromptu op. 90 no. 3 (D. 899), measures 1–8. Voice-leading graph
(click to enlarge)
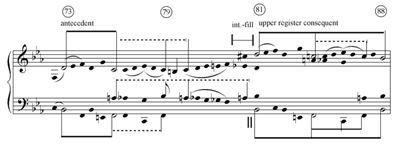
[5] Example 1, from Schubert’s Impromptu op. 90 no. 3, shows a paradigmatic simple instance of the most basic form of interruption-fill. The interruption-fill connects the pre-interruption with the regained primary tone . The punctuation between antecedent and consequent is preserved in the bass, and only the upper voice moves between the phrases via a chromatic passing tone (
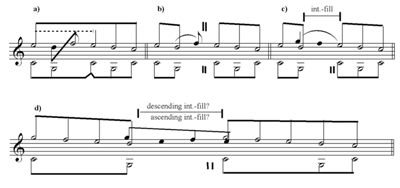
[6] Normative interruption occurs at a specific point in time, as is evident in the symbol of the two vertical strokes that is placed in a single location. When the pre-interruption V is prolonged, Schenker’s normative practice correctly locates the interruption symbol after that prolongation is over (for example Schenker 1979 [1935/1956], Figs. 34b, 35,1 and 35,2). Exceptions do occur, where the prolongation of the pre-interruption V continues after the interruption symbol (Schenker 1979 [1935/1956] Fig. 26b; in Fig. 39,2 the interruption symbol is confusingly located at the middle of the V prolongation). When there is an interruption-fill, i.e., passing motion between the pre-interruption V and the following regained primary tone, Schenker locates the interruption symbol immediately after the consonant V, and before the passing motion (addition of a seventh in Figs. 32,7 and 47,1; more substantial passing motion in Figs. 22a and 22b). This way of presenting the interruption-fill indicates that for Schenker the interruption proper precedes the interruption-fill. My own graphic presentation of the interruption-fill shows it as an interpolation between the two vertical strokes of the interruption symbol, meaning that the interruption proper continues throughout the process of the interruption-fill and, unlike normative interruption, occupies a span of time.
Example 2. Continuous motion across interruption without interruption-fill: Haydn, Symphony no. 92 (Oxford), fourth movement, measures 1–9. Annotated reduction
(click to enlarge)
[7] From a Schenkerian point of view, the interruption-fill is arguably problematic. The problem is not the mere lack of rhythmic or textural articulation at the point of interruption.(8) For example, the opening period of the finale of Haydn’s Symphony no. 92 (Oxford) (Example 2) has a normative interruption despite the perpetual motion in the upper voice.(9) That period is normative since the basic voice-leading before the interruption is based on a circular prolongation (in this case, motion into an inner voice) within the pre-interruption V, ending on tones that belong to the V.(10) Since the bass does pause at the end of the antecedent, the motion in the upper voice does “fill a gap in sound,” and it thus forms a caesura-fill in the terms of Hepokoski and Darcy (2006, 34). However, in Schenkerian terms, based on tonal procedures, the descent into an inner voice precedes the caesura and does not fill it.
[8] It should go without saying that normative prolongation of pre-interruption V does not challenge Schenkerian norms. After all, interruption proper most often occurs long after the arrival of the structural pre-interruption V. For example, in paradigmatic sonata form in major, the interruption proper takes place just before the recapitulation, after the V has been prolonged throughout the entire second group and development. This also conforms with Schenker’s notation practice discussed above (paragraph 6).
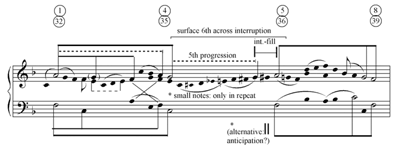
[9] The true source of the problematic nature of the interruption-fill is that the chromatic motion passes paradoxically through a “dead” space between unrelated tones, a space that ought not to exist, after the pre-interruption V (and not within a prolongation thereof).(11) In Schenker’s normative view, “The first [in an interruption structure] is not a neighboring note” [as one might think in the case of primary tone ], but rather a passing tone toward the that will only arrive at the end of the consequent (Schenker 1979 [1935/1956], 37, §91). The rule that “the first is a passing tone toward the that will only arrive at the end” should also apply to interruption structures from , where the alternative does not give rise to a neighboring note. Since they are unrelated, the pre-interruption and the regained primary tone should not be conceived as boundary tones of a normative space capable of being filled-in. Nevertheless, in interruption-fills within genuine interruption structures the pre-interruption V and the regained primary tone perform precisely this function: true boundaries of passing motion in the course of the interruption-fill. The passing motion in that space must count as “illegal.” It should be emphasized that the paradox emerges precisely because the interruption is not cancelled; if the true interruption is overridden in the first place (as in cases described in paragraph 2), no true interruption-fill can take place either.
[10] To further explain why the interruption-fill is problematic, one must understand how it differs from normative passing motion. Normative passing motion takes place within linear progressions. Usually, linear progressions fill in boundary tones that are conceptually simultaneous at a deeper level (Rothstein 1981, 87–91; Schenker 1979 [1935/1956], §115). Exceptions do occur where connective linear progressions move between different chords, as Schenker (1996 [1926], 3) notes: “linear progressions in the treble that descend signify motion to an inner voice of the original chord or the ensuing one” (my emphasis). For example, in fifth progressions from over a subdominant harmony to V, when the goal tone arrives, the initial tone changes into an implied (Goldenberg 2008, vol. 1, 11). The latter situation is always tricky, but in the case of interruption the immediate structural chord after the pre-interruption V is not at all the truly ensuing chord.
[11] Indeed, even without the interruption-fill, passing motion may take place within the space of a boundary second that does not represent a conceptually simultaneous interval. This happens in chromatic passing tones toward or from a neighbor (whole) tone. As Proctor (1978, 79–82) observes, even that situation poses a paradox, as it violates the distinction between steps and leaps.(12) In interruption-fills, when the primary tone is in the same register as the preceding , the only possible fill is a single chromatic passing tone in major (in minor, the mere semitone between and simply leaves no space to be filled in). The chromatic motion from at the end of the antecedent to at the beginning of the consequent flies in the face of both the unrelatedness of these tones (this is also true of motion to ) and the step-leap distinction.
[12] The configuration of the interruption-fill cannot be reconciled with normative Schenkerian ideas. Although Schenker arrived late at the concept of interruption, and left it underdeveloped and at times inconsistent (Marston 1999), such inconsistencies in Schenker’s view of interruption hardly affect the study of the interruption-fill; Schenker acknowledged certain “free forms of interruption” (discussed in Samarotto 2004), but interruption-fills normally take place between the branches of strict interruption; Schenker was undecided with regard to the deeper hierarchy among the elements of interruption (Smith 1994, esp. 79–84), but the interruption-fill occurs at the surface.(13) One theoretical issue where Schenker’s inconsistencies are indeed relevant is the status of an added seventh to the pre-interruption V. This configuration will be dealt with at a later point, in relation to motion toward a regained .
[13] Some theorists nevertheless regard the lead-in as a normative element of the surface level. Schachter (2006, 286), for example, seems unbothered by the lead-in when he argues that in “a parallel period generated by an interruption V . . . any connection from that V to the I that begins the next phrase is clearly a foreground device.” The rest of this study does not collapse if one denies the problematic nature of the interruption-fill; rather, those inclined to regard the interruption-fill as a normative phenomenon might still find my exploration of the variety of manifestations of the interruption-fill and corollary procedures useful.
More Upper-Voice Interruption-Fills with Primary Tone
Example 3. Larger chromatic motion starting from the chromatic lead-in: Haydn, Piano Variations in F minor, Hob. XVII:6, measures 30–34. Voice-leading graph
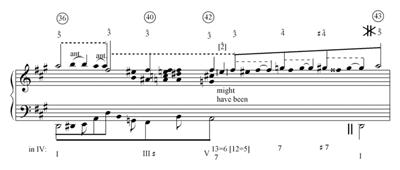
(click to enlarge)
Example 4. Expansion of the consequent based on the interruption-fill: Haydn, Symphony no. 104, second movement, measures 16–25. Annotated reduction
(click to enlarge)
Example 5. Interruption-fill continues motion from an inner voice: Beethoven, Piano Sonata op. 2 no. 1, second movement, measures 1–8 and 32–39. Voice-leading graph
(click to enlarge)
[14] Even the basic passing chromatic lead-in might be emphasized by means of hypermetric expansion, as in the retransition in the Trio from Mozart’s Symphony no. 35, K. 385 (Haffner), iii (not given here). Whereas in Schubert’s Impromptu the
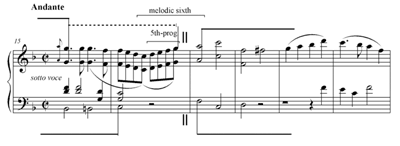
[15] The chromatic lead-in may combine with chromatic motion within the phrases to create chromatic continuity. Example 3 presents a case in point from the second theme (in major, of course) of Haydn’s F minor Piano Variations, Hob. XVII:6.
[16] In this theme, both antecedent and consequent start with chromatic ascents from the primary tone toward the upper , which serves in this passage as a conceptual inner voice. The chromatic lead-in combines with the ensuing third-progression into a chromatically filled melodic fourth that runs across the interruption, thus achieving smooth continuity. To appreciate this smooth moment, one must of course acknowledge the chromaticism rather than explain it away according to a strictly structuralist approach, but it is also important to acknowledge the structural point of division, without which the chromatic smoothness at that specific point loses its particular effect.(15)
[17] In other cases, the lead-in seems to generate an insertion of chromatic motion in the consequent with no counterpart in the antecedent. This is perhaps the case with the
[18] The chromatic succession might obscure the precise point of interruption, especially if the ascent begins earlier as motion from an inner voice.(17) Consider the theme of the second movement of Beethoven’s Piano Sonata op. 2 no. 1 (Example 5).
[19] In the lead-in to the consequent, the range of a sixth is chromatically filled-in. In the repeat (measures 35–36), the chromaticism becomes even more complete (condensed in triplets). Hearing this lead-in as a sixth-progression underlines its parallelism with the opening interval of the movement, the sixth from the upbeat to the antecedent. This is the interpretation endorsed by Salzer (1952/1962, Fig. 442), and in greater detail by Cadwallader and Gagné (1998/2007, Ex. 7.11).(18) Strictly speaking, however, the change of harmony and the division into phrases do not support a true sixth-progression, but rather a fifth-progression followed by an interruption-fill. Unlike the normative chromatic notes that are inserted into the motion from an inner voice, the last chromatic note (
Example 6. A diatonic melodic sixth based on a fifth-progression plus a step: Priestermarsch. From Mozart, Die Zauberflöte, K. 620, Act 2. Measures 15–20. Annotated reduction
(click to enlarge)
Example 7. Ascent across interruption without filling-in, combining motion from an inner voice with initial ascent: Mozart, Serenade K. 320, fourth movement, measures 1–16. Voice-leading graph
(click to enlarge)
[20] The basic problem of telling a sixth-progression from a combination of a fifth-progression and an additional step in the same direction can also arise in a diatonic context, as in Example 6 from the priests’s march in Mozart’s Die Zauberflöte.(21)
[21] In this case no interruption-fill occurs and, despite the melodic continuity, a precise point of interruption may be detected. This case is analogous to the more familiar descending melodic sixth from I, which embeds a fifth-progression (motion into an inner voice) from the ensuing V.(22) Even a chromatic context may include upper-voice melodic continuity across an interruption point that is nevertheless clear and unfilled. This requires a semitone between the upper-voice tones on both banks of the interruption, which is possible with an ascent to in minor, and also when the consequent (usually in parallel with the antecedent) starts with an intial ascent from . Consider Example 7, from the main theme of Mozart’s Serenade K. 320 (Posthorn), iv (“Rondo”). In this theme, the melodic sixth that ascends across the interruption is divided differently from those encountered in the previous examples: it includes a third-progression from an inner voice (in fact, from one inner voice to another), a step with harmonic shift at the point of interruption, and another third-progression that forms the initial ascent of the consequent. The theme is saturated with chromatic embellishments (not all of them shown), especially in the antecedent. The scoring of this theme also supports both the division of the opening period into phrases and the continuity across that division: the soloist changes at the start of the consequent (oboe replaces flute), but the flute does play the first note of the consequent, overlapping with the oboe.
Example 8. Magnified ascent to the lead-in: Widor, Valse-Impromptu op. 15 no. 6, measures 39–47. Annotated score
(click to enlarge)
[22] The sense of continuous ascent across the interruption may be intensified if the pre-interruption chromaticism occupies more than mere motion from an inner voice. It is magnified indeed in Example 8, from Valse-Impromptu op. 15 no. 6 by Widor. This is a free and unaccompanied retransition in an otherwise fairly square piece. The ascent begins in the bass and encompasses more than three octaves; in its final portion every chromatic step is itself embellished. Theoretically, however, the final half-tone before the regaining of the tonic is the only one to occupy the non-normative position of interruption-fill. Some local embellishments of the chromatic passing tones are also unclear.(23)
Example 11. Lack of simultaneous V before interruption-fill: Chopin, Nocturne op. 9 no. 1, measures 36–40. Annotated score
(click to enlarge)
Example 12. Basic upper-voice interruption-fill before : Beethoven, Theme for Piano Variations op. 34, measures 1–6. Annotated score
(click to enlarge)
Example 13. The seventh at the middle of an interruption-structure from : a) the seventh as a true upper neighbor to cancels the interruption; b) the seventh as an offshoot from V left unexplained; c) the seventh as a descending interruption-fill from a cover tone before ; d) the seventh as a descending interruption-fill from a cover tone before , paradoxically combined with the ascending interruption-fill
(click to enlarge)
[23] Further ramifications of the interruption-fill before occur when the consequent takes place an octave above the antecedent. The shift of register emphasizes the division between the phrases, and the chromatic lead-in that usually compensates for that division must choose between the register of the antecedent and that of the consequent (unless it encompasses a ninth, see Example 24 below). Examples 9–10 show both possibilities from two Chopin pieces. In Example 9, from the Poco più lento middle section of Nocturne op. 48 no. 1, the lead-in occurs before the shift of register, and leads to the lower doubling of the regained .(24) By contrast, in Mazurka op. 56 no. 3 (Example 10), the
|
Example 9. Lead-in in the original register before an octave shift: Chopin, Nocturne op. 48 no. 1, measures 25–30. Annotated score (click to enlarge) |
Example 10. Lead-in grouped with the consequent: Chopin, Mazurka op. 56 no. 3, measures 73–88. Voice-leading graph (click to enlarge) |
[24] In our last example with primary tone (Example 11), again from a Chopin Nocturne, the peculiar aspect relates to the lack of synchronization between outer voices at the location of the interruption proper. Over a tonic pedal point, the bass of the pre-interruption V only arrives at the moment of the interruption-fill chromatic motion. Thus, the normative pre-interruption V and never sound simultaneously.
Upper-Voice Interruption-Fills with Primary Tone
[25] Example 12 shows the basic formula of an upper-voice interruption-fill before reestablishment of , as realized in the theme of Beethoven’s Piano Variations op. 34. In my experience, this is the most common kind of interruption-fill, and has become a true cliché.(26) It is interesting to follow the treatment of the interruption-fill in the Variations. Variations nos. 2 and 5 omit it, no. 4 replaces it with a diatonic anticipation of , and no. 6 preserves it with an 8–7 counterpoint in the bass, whereas nos. 1 and 3 intensify it by means of parallel tenths. The following voice arrives at –
[26] The – interruption-fill has room for more passing motion than that whose goal is . The passing motion moves via , which creates theoretical problems as a lead-in, even in its diatonic form: as the seventh of V, it must resolve downwards, but such a resolution would contradict the sense of interruption. In Free Composition, Schenker (1979 [1935/1956]) demonstrates this situation in both Fig. 23 and Fig. 32,7. Unfortunately, however, both graphs combine contradicting interpretations. My Example 13 attempts to separate them.
[27] If the seventh is a true upper neighbor (Example 13a), the interruption is cancelled altogether. By contrast, if the interruption structure prevails (Example 13b), the pre-interruption seventh is disconnected from its resolution. A better explanation (Example 13c, after Fig. 23 in Free Composition) regards the seventh as a passing tone from a cover tone that accompanies the pre-interruption . This reading involves a descending interruption-fill.(27)
[28] The resolution of the seventh of V at the interruption-fill into makes it more apt with the regained primary tone . With primary tone , a paradox emerges (Example 13d): the seventh might be said to resolve into in an inner voice, yet the drive of the melodic ascent during the V– interruption-fill goes upwards. In any case, an unequivocal ascending interruption-fill toward arises when the lead-in continues to ascend past via
Example 14. Emphasized
(click to enlarge)
[29] Unlike , is a member of the V too. This creates new theoretical ramifications. First, the goal may appear before the return of the tonic. In that case, the
Example 15.
(click to enlarge)
[30] A related procedure occurs when the ascending line that contains
Example 16. Ascent to the regained based on anticipation without interruption-fill: Mozart, Violin Concerto no. 5, K. 219, third movement, measures 1–16. Voice-leading graph
(click to enlarge)
[31] Since an ascent toward also moves via , a potential alternative division exists, according to which the ascent includes an anticipation of the tonic. If
Special Artistic Devices Related to the Interruption-fill
[32] As noted above, simple interruption-fills are commonplace. Occasionally, however, one encounters special artistic devices that exploit interruption-fills in an unusual way and do not remain within the constraints of the stock figure. In such cases, the interruption-fill should also be noted in general analytical examinations of pieces where it takes place.
Example 17. Deformation of interruption-fill: Haydn, Symphony no. 101, second movement, (1) measures 1–10 (normative); (2) measures 25–34. Annotated score
(click to enlarge)
Example 18. Combination of anticipation from an augmented triad and interruption in the bass: Grieg, Poetische Bilder op. 3, no. 3: Con moto, measures 1–15. Annotated score
(click to enlarge)
Example 19a. Kalinnikov, Nocturne in F-sharp minor, measures 40–43. Annotated score
(click to enlarge)
Example 19b. Kalinnikov, Nocturne in F-sharp minor, measures 36–43. Voice-leading graph
(click to enlarge)
[33] In the clock theme from Haydn’s Symphony no. 101, ii (Example 17), the opening period includes a normative interruption-fill to I, but when the phrase returns in an inner recapitulation within the theme, a deformation of the interruption-fill leads instead to , still harmonized with V. The interruption is thus cancelled, and the phrases are fused. Technically, the deformation is based on inserting the two chromatic tones that have been omitted in the normative interruption-fill. The goal is now one whole tone below the original goal ( rather than ), while complete rhythmic parallelism is preserved (expansion does occur in the theme later on).(32)
[34] We move now to late Romantic examples that explore possibilities that seem to lie beyond the limits of the classical style, where the interruption-fill emerged and was used most extensively. Notice that although some nineteenth-century chromatic techniques are not placed within a diatonic framework (Proctor 1978), the present examples explore new paths of chromatic interpolation into a well-established diatonic structure.
[35] The following two examples display special ramifications of the ambiguity between interruption-fill and lead-in based on the initial ascent from discussed above. An unusual anticipation of the consequent takes place in Example 18, from the third of Grieg’s Poetische Bilder op. 3 (1863). The on the upbeat definitely serves as anticipation: the rhythmic pattern, where serves as a passing tone within a triplet from , makes this the only acceptable reading. It is further reinforced by the parallelism with the upbeat to sub-phrases and the antecedent in measure 9 (notice the a tempo indication is located at the point of anticipation). Indeed, the upbeat ascending triplet becomes a main motivic idea in this theme. The , however, not only occurs within the time-span of V, but even takes place over the other members of V ( in the bass and in the inner voice). The result is the literal augmented III, described by Skoumal (1994) as an androgynous harmony that functions simultaneously as both I and V.(33) The ascent, however, does not function as both anticipation and interruption-fill, but rather as anticipation alone.(34) Moving from V to I via III might blur functional harmony, but, in this example, the division of the period remains clear.
[36] This passage includes additional complications. At the upbeat to measure 3 (repetition of the basic idea), the same ascent above in the literal bass at that moment functions within the tonic (after the assertion of the lower tonic bass).(35) Also, the lead-in forms “motion from an inner voice” in a most literal sense, as it starts on below a cover tone, and ends on the upper above an inner-voice . It is even questionable whether the pre-interruption is approached by descent from the upper (the descent toward the end of the consequent is more normative).(36) After the V has arrived, at the only moment the literal is heard, the seventh is added in the bass to form ![]()
[37] Example 19, from the middle section in D major of an 1894 Nocturne in
Example 20. Tonicization of the lead-in
(click to enlarge)
[38] Finally, Example 20 includes a brief tonicization of the lead-in
Other Formal Contexts for the Chromatic Lead-in
[39] The chromatic lead-in might occasionally appear in non-interruption contexts. For example, if the second phrase turns out to end on a half-cadence and thus repeat the antecedent, the different context does not essentially alter the problem of the lead-in.(41) The lead-in is also fairly common at the middle of modulating periods, where the consequent tonicizes another key (usually the dominant).(42)
Example 21. Chromatic Lead-in in an Open Chromatic Context Wagner, Tristan und Isolde, Act 2, scene 2 (excerpt). Reduction by Hans von Bülow
(click to enlarge)
[40] Less often, the chromatic lead-in approaches phrases that start at a different tonal level than the preceding material. Example 21 from Wagner’s Tristan und Isolde shows a lead-in that connects two phrases (based on the leitmotif known as “love’s peace”) that are in V–I relations, without a complete diatonic framework.
that[41] In an infrequent but important procedure, the chromatic lead-in occurs before the secondary group in sonata form.(43) In terms of Hepokoski and Darcy’s sonata theory, this fill occurs at the medial caesura. As already noted, Hepokoski and Darcy (2006, 34 and 40–45) discuss certain paradigmatic links as caesura-fills, and indeed focus on filled medial caesuras, mostly based on melodic descent (see paragraph 51 below). The chromatic ascent, however, is absent from their discussion.
[42] A peculiar use of the
|
Example 22a. Liszt, Piano Sonata in B minor, measures 145–152 (click to enlarge) |
Example 22b. Liszt, Piano Sonata in B minor, measures 612–617. Annotated score (click to enlarge) |
[43] The details are different each time. The latter occurrence is especially innovative, as it makes the tonal shift more directly. The chromatic tone (D=C![]() ) is first harmonized as a consonance (somewhat reminiscent of the tonicization of the passing tone in Example 20 above [Grieg]). In real-time listening, the chromatic chord sounds first as its enharmonic equivalent, V13/7 of B minor (although that chord, too, requires enharmonic interpretation of the
) is first harmonized as a consonance (somewhat reminiscent of the tonicization of the passing tone in Example 20 above [Grieg]). In real-time listening, the chromatic chord sounds first as its enharmonic equivalent, V13/7 of B minor (although that chord, too, requires enharmonic interpretation of the
Other Forms of the Upper-Voice Interruption-Fill.
Example 23. Descending upper-voice interruption-fill to : Haydn, Symphony no. 77, second movement, measures 1–16. Annotated score
(click to enlarge)
Example 24. Division of a ninth into two fifths replaces ordinary lead-in: Chopin, Mazurka op. 63 no. 1, measures 1–8. Annotated score
(click to enlarge)
[44] Whereas the previous examples have shown special treatment of the basic interruption-fill formulas, some different configurations are also possible. Interruption-fills usually connect with or (the regained primary tone), but they may also arrive at via
[45] Registral manipulations offer further possibilities. Approaching the regained from above would make it possible to move via (arriving from or after a longer span); descending to would involve the familiar problem of V8–7 (see Example 13 above). As for cases with register shift between the antecedent and consequent, along with the ordinary solution that adds the chromatic lead-in to either antecedent or consequent (see Examples 9–10 above), Chopin’s Mazurka op. 63 no. 1 replaces the chromatic passing tone at the division point of the opening modulating period (measure 8) with a non-harmonic ninth above the bass (), whose melodic function is to divide the ascending ninth (from to the upper ) into two equal leaps in an exceptional type of lead-in (Example 24).(48)
[46] Finally, descents from to occasionally appear in upper-voice interruption-fill. This is a procedure that essentially belongs to the bass, and will be dealt with in that context.
Interruption-Fill in the Bass
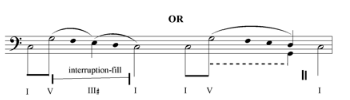
[47] In his basic presentation of the concept of interruption, Schenker discusses (in a polemic and rather non-didactic manner) the idea of continuity across interruption: “The interruption has such a strong effect that no connective linear progressions or similar features can obscure it.” (Schenker 1979 [1935/1956], 36, §88 and Fig. 22). This seems to be an analytical point concerning the specific examples that attracted Schenker’s attention, however, rather than a general unbreakable law. The two associated examples (Figs. 22a and b in Free Composition) show the relatively uncommon motion in the bass from the pre-interruption V to the first tonic after the interruption (Fig. 22a in ascent and 22b in descent).
Example 25. Ascending interruption-fill in the bass: “Ich bin‘s, Ich sollte büssen.” From Bach, St. Matthew Passion, no. 16. Voice-leading graph (after Schenker)
(click to enlarge)
[48] Fig. 22a in Free Composition, from Bach’s chorale “Ich bin’s, ich sollte büssen” (no. 16 in St. Matthew Passion = Nun ruhen alle Wälder, Riemenschneider no. 117), based on the complete analysis in Five Graphic Analyses (Schenker 1969 [1933]), shows an ascending fourth-progression from the pre-interruption V. The relevant portion is reproduced and annotated in Example 25. This example is exceptional in that the interruption-fill takes place within the time-span of the consequent, and indeed re-harmonizes the repeated beginning. Notice that the borders of this fourth-progression are not determined by the melodic chromatic ascent that arises from the bass pre-interruption . The melodic ascent encompasses no less than a thirteenth, and aims at the tenor: a fifth within the antecedent, chromatic motion to , and a complete octave within VI (ending as a major chord, perhaps V/ii). The continuous ascent is reminiscent of similar ascents in upper-voice interruption-fills (as in Example 3 above), and might count as a case of “contra-structural melodic impulse” (a term derived from Samarotto 2009). The completion of the fourth-progression is not the immediate ascent but rather a delayed one after the VI prolongation. The arrival at the regained tonic is not clearly articulated. This might be regarded as a weakness of the analysis, although it is difficult to suggest a convincing alternative. Usually, an immediate ascending fourth from to in the bass serves as a third-progression from the root to the third of V before a harmonic change over a further melodic step in the same direction across the moment of the unfilled interruption proper (Cf. examples 6–7 above). However, the particular realization in the chorale does not support such a clear point of division, and the reading of a fourth-progression interruption-fill in the bass is preferable.(49)
[49] Fig. 22b in Free Composition, an analysis of Schumann’s “Aus meinen Tränen spriessen” (no. 2 in
Dichterliebe, op. 48), shows the V–I motion as based on bass arpeggiation via
Example 26. Alternative interpretations of the descending bass from V to I
(click to enlarge)
Example 27. The – caesura-fill as a fourth-progression plus a step: Mozart, Symphony no. 39, K. 543, first movement, measures 87–97. Annotated melodic line
(click to enlarge)
[50] Both Beach (1983) and Willner (1988) discuss the V–
[51] The V–I descending fill is also the main type of caesura-fill within the medial caesura discussed by Hepokoski and Darcy (2006, 34 and 40–45), usually in an entirely diatonic form. Sometimes the fill might be said to delay the point of caesura proper by means of post-cadential standing on the dominant (V of the secondary key in the case of expositional medial caesuras).(52) The cleanest way, theoretically speaking, to understand the filling in of the – descent is as a – fourth-progression above the V, before a further descent of one more step at the moment of regaining the I. This explanation works well, for example, in the filled medial caesura in Mozart’s Symphony no. 39, i (Example 27). In this passage, each step in the descent except the final replicates the pre-cadential motive, and although no general pause takes place, the strings reach an actual stop before the . The only element that prevents a clear-cut caesura in this example is the addition of the seventh to the V; theoretically, had the been harmonized as a simple triad, the preservation of a clear if delayed moment of punctuation might have been possible.(53)
Example 28. A descending — caesura-fill that defies clear division: Haydn, Piano Sonata XVI:40, second movement, measures 1–5. Annotated score
(click to enlarge)
[52] Some other cases of the descending – caesura-fill defy punctuation after the . For example, in the opening modulating period of Haydn’s Piano Sonata Hob. XVI:40, ii (Example 28), each tone in the caesura-fill is preceded by an incomplete upper neighbor, the inserted between the and the anticipates the ensuing tonic, and at the same time continues the former melodic sequence at the diminution level. A caesura proper cannot be located at any precise moment, but a feeling of caesura is clear nevertheless, reinforced (as often happens) by the reduced texture: the descending line from to takes place in the upper register above a silent bass.(54)
Motion in Other “Dead” Spaces
[53] Occasionally, passing motion occurs within other “dead” spaces between tones that are said to be unrelated, analogous to passing motion within interruption. Such situations enable a generalization of the problem: passing motion is “illegal” when it connects true boundary events, of which either the source or the goal belong to a lower level. This assumes that the lower-level event does not prolong the other boundary event (as would be the case, for example, with normative motion from the tonic into a lower-level back-relating dominant) but rather a third event; the following examples will illustrate.
Example 29. “Illegal” passing tones after a back-relating dominant: “Der hölle Rache kocht in meinem Herzen.” From Mozart, Die Zauberflöte, K. 620, Act 2. Voice-leading graph (bass only)
(click to enlarge)
[54] A lower-level source for “illegal” passing motion occurs after a back-relating dominant. The more substantial progression moves from the tonic to which this dominant is related, directly to a later scale degree. For example, the great aria of the Queen of the Night from Mozart’s Die Zauberflöte (Example 29) is based on the progression I (back-relating V) III IV V I. The melodic link from the back-relating V to the ensuing III is “illegal.” Certain passages may lend themselves to a different interpretation, where the V after the opening tonic is not back-relating, but rather a strong opening of a dominant prolongation—a reading in which the motion from V to III would present no theoretical problems. It would be unmusical, however, to decide on the structural weight of such a V according to the the local passing motion that follows it.(55)
[55] Lower-level goals for the lead-in emerge on several occasions. In a sequence that includes secondary dominants, e.g., V–I, V/II–II, the structural progression merely includes the goals of these dominants. Nevertheless, in some instances one may find passing motion from the I to the ensuing secondary dominant, e.g.: G–C [passing
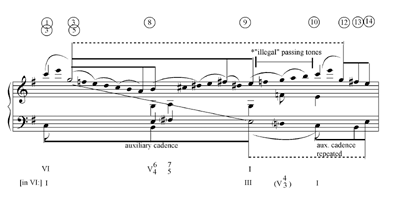
Example 30. “Illegal” passing tones between two occurrences of an auxiliary cadence: Beethoven, String Quartet op. 59 no. 2, fourth movement, measures 1–18. Voice-leading graph
(click to enlarge)
[56] A further ramification of the latter situation occurs when the melodic goal of the lead-in opens an auxiliary cadence. Consider Example 30, from the finale of Beethoven’s String Quartet op. 59 no. 2, in E minor. This movement opens with an auxiliary cadence that initially sounds stable in C major. This auxiliary cadence is then repeated after a short link that connects the tonic goal of the initial statement to the beginning of the repeat. As in ordinary interruption-fills, this link is not salient to the ear, yet it creates theoretical problems, since the initiation point of the repeated auxiliary cadence is said to point forward only, to the repeated goal. The same passing motion might have been a normative link from III to I in C major, but not in E minor, the true retrospective key.(57)
Example 31. “Illegal” passing tones from a cover tone: Mozart, Piano Sonata K. 576, first movement, measure 48. Voice-leading graph
(click to enlarge)
[57] Cover tones create a more subtle opportunity for “illegal” passing tones. Example 31, from Mozart’s Piano Sonata K. 576, presents a case in point. The basic progression includes a neighbor chord with upper neighbor tones in both outer voices (the soprano has –– of the chord). However, in the upper voice, a larger descent starts from the cover tone. This is not a fourth-progression at the diminution level, due to the local change of harmony. But the passing tones from the cover tone to the upper neighbor of the main voice have no theoretical justification. They are, again, “illegal.”(58)
Conclusion
[58] The interruption-fill is an arguably problematic phenomenon from a theoretical point of view. In its basic manifestations, it lacks perceptual salience. The insights to be gleaned from the study of multiple occurrences of these basic patterns are, by and large, historical rather than theoretical. It is evident that the phenomenon first emerges in the classical era. It is very common in Mozart, Haydn, Beethoven, and perhaps even more in Chopin, with particular ubiquity in main themes of slow movements. The interruption-fill also appears in the works of other Romantic composers, and special variants may be found in the late nineteenth century, after the decline of the formulaic pattern. Further examples appear in early popular music, as in Scott Joplin’s The Entertainer. A more systematic examination of the frequency and variety of the interruption-fill and its derivatives (perhaps after the model of Gjerdingen 1988) must await further research.
[59] To return to theoretical matters, pointing out “illegal” passing tones not only draws attention to potential pitfalls of an overly dogmatic theoretical apparatus, but also indicates a true problem. Whenever intervallic spaces emerge, they turn out to be open to filling in, regardless of their theoretical status. The lead-in deserves deep analytical (as distinct from theoretical) attention in those few works that use the pattern in special ways; awareness of the basic formulas is also necessary in order to serve as a normative theoretical framework for understanding these exceptional instances.
Yosef Goldenberg
The Hebrew University of Jerusalem and the Jerusalem Academy of Music and Dance
Giv’at Ram Campus 91904 Jerusalem
Israel
yosefg@jamd.ac.il
Works Cited
Agmon, Eytan. 1996. “Conventional Harmonic Wisdom and the Scope of Schenkerian Theory: A Reply to John Rothgeb.” Music Theory Online 2, no. 3. http://www.mtosmt.org/issues/mto.96.2.3/mto.96.2.3.agmon.html
Beach, David. 1983. “A Recurring Pattern in Mozart’s Music.” Journal of Music Theory 27, no. 1: 1–29.
Burstein, Poundie L. 1998. “Surprising Returns: the
Cadwallader, Allen and David Gagné. 1998/2007. Analysis of Tonal Music: A Schenkerian Approach. Oxford: Oxford University Press. 2nd ed.
Caplin, William E. 1998. Classical Form: A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart and Beethoven. Oxford: Oxford University Press.
—————. 2004. “The Classical Cadence: Conceptions and Misconceptions.” Journal of the American Musicological Society 57, no. 1: 51–117.
Ellis, Mark. 2010. A Chord in Time: The Evolution of the Augmented Sixth from Monteverdi to Mahler. Farnham and Burlington: Ashgate.
Feofanov, Dmitry, ed. 1984. Rare Masterpieces of Russian Piano Music. New York: Dover.
Forte, Allen, and Steven Gilbert. 1982. Instructor’s Manual for Introduction to Schenkerian Analysis. Norton: New York.
Gjerdingen, Robert O. 1988. A Classic Turn of Phrase: Music and the Psychology of Convention. Philadelphia: University of Pennsylvania Press.
Goldenberg, Yosef. 2008. Prolongation of Seventh Chords in Tonal Music. Lewiston: Edwin Mellen Press.
Hepokoski, James and Warren Darcy. 2006. Elements of Sonata Theory: Norms, Types and Deformations in Late Eighteenth-Century Sonata. Oxford: Oxford University Press.
Jackson, Timothy. 1999. “Diachronic Transformation in a Schenkerian Context: Brahms’s Haydn Variations.” In Schenker Studies 2, ed. Carl Schachter and Hedi Siegel, 239–75. Cambridge: Cambridge University Press.
Jonas, Oswald. 1982 [1934/1972]. Introduction to the Theory of Heinrich Schenker. Revised edition. Trans. and ed. John Rothgeb. New York: Longman.
Kamien, Roger. 2001. Review of The Masterwork in Music [part of: “A Schenker Symposium, part 1”]. Journal of Music Theory 45, no. 1: 162–69
—————. 2005. “Quasi-Auxiliary Cadences Beginning on a Root-Position Tonic Chord: Some Preliminary Observations.” Journal of Schenkerian Studies 1: 32–43.
Kopp, David. 2002. Chromatic Transformation in Nineteenth-Century Music. Cambridge: Cambridge University Press.
Laufer, Edward. 1988. “On the Fantasy.” Intégral 2: 99–133.
—————. 1991. “Voice-Leading Procedures in Development Sections.” Studies in Music from the University of Western Ontario 15: 69–120.
Marston, Nicholas. 1999. “Schenker and Interruption: Don’t Hear Everything You Believe.” Paper presented at the Third International Schenker Symposium, New York.
McKee, Eric. 2004. “Extended Anacruses in Mozart’s Instrumental Music.” Theory and Practice 29: 1–37.
Mitchell, William J. 1962. “The Study of Chromaticism.” Journal of Music Theory 6, no. 1: 2–31.
Mooney, Kevin. 2000. “Hugo Riemann’s Debut as a Music Theorist.” Journal of Music Theory 44, no. 1: 81–99.
Proctor, Gregory. 1978. “Technical Bases of Nineteenth-Century Chromatic Tonality: A Study in Tonality.” PhD diss., Princeton University.
Rapoport, Erez. 2004. “The Smoothing-Over of Formal Junctures as a Style Element in Mendelssohn’s Instrumental Music.” PhD diss., City University of New York.
Rosen, Charles. 1995. The Romantic Generation. Cambridge, Mass.: Harvard University Press.
Rothgeb, John. 1990. “Schenkerian Theory and Manuscript Studies: Modes of Interaction.” In Schenker Studies, ed. Hedi Siegel, 4–14. Cambridge: Cambridge University Press.
http://www.mtosmt.org/issues/mto.96.2.1/mto.96.2.1.rothgeb.tlk.html
—————. 1996. “Eytan Agmon on Functional Theory.” Music Theory Online 2, no. 1.
http://www.mtosmt.org/issues/mto.96.2.1/mto.96.2.1.rothgeb.tlk.html
Rothstein, William. 1981. “Rhythm and the Theory of Structural Levels.” PhD diss., Yale University.
—————. 1989. Phrase Rhythm in Tonal Music. New York: Schirmer.
—————. 1990. “Rhythmic Displacement and Rhythmic Normalization.” In Trends in Schenkerian Research, ed. Allen Cadwallader, 87–113. New York: Schirmer.
Salzer, Felix. 1952/1962. Structural Hearing: Tonal Coherence in Music. New York: Dover. New corrected edition.
Samarotto, Frank. 2004. “Schenker’s ‘Free Forms of Interruption,’ and the Strict: Toward a General Theory of Interruption.” Paper presented at the annual meeting of the Society for Music Theory, Cambridge, Mass.
—————. 2009. “‘Plays of Opposing Motion’: Contra-Structural Melodic Impulses in Voice-Leading Analysis”. Music Theory Online 15, no. 2. http://www.mtosmt.org/issues/mto.09.15.2/mto.09.15.2.samarotto.html
Schachter, Carl. 1999 [1980]. “Rhythm and Linear Analysis: Durational Reduction.” In Music Forum 5; reprinted in Unfoldings, ed. Joseph Straus, 54–78. New York: Oxford Univesity Press.
—————. 1999 [1981]. “A Commentary on Schenker’s Free Composition.” Journal of Music Theory 25, no. 1: 115–42, reprinted in Unfoldings, ed. Joseph Straus, 184–208. New York: Oxford University Press.
—————. 2006. “Che Inganno! The Analysis of Deceptive Cadences.” In Essays from the Third International Schenker Symposium, ed. Allen Cadwallader, 279–98. Hildesheim: Georg Olms.
Schenker, Heinrich. 1954 [1906]. Harmony, ed. Oswald Jonas, trans. Elizabeth Mann Borgese. Chicago: University of Chicago. Abridged translation.
—————. 1987 [1910]. Counterpoint, vol. 1, trans. John Rothgeb and Jürgen Thym, ed. John Rothgeb. New York: Schirmer.
—————. 2004 [1921]. “Beethoven’s Sonata in F Minor, Op. 2, No. 1,” trans. Joseph Dubiel. In Der Tonwille, ed. William Drabkin, vol. 1: issues 1–5 [originally in issue 2], 72–95. Oxford: Oxford University Press.
—————. 2005 [1924]. “Schubert’s Impromptu D. 899 (Op. 90), No. 3,” trans. Joseph Dubiel. In Der Tonwille, ed. William Drabkin, vol. 2: issues 6–10 [originally in issue 10], 137–42. Oxford: Oxford University Press.
—————. 1996 [1926]. “Further Consideration of the Urlinie II,” trans. John Rothgeb. In The Masterwork in Music, vol. 2, ed. William Drabkin, 1–22. Cambridge: Cambridge University Press.
—————. 1969 [1933]. Five Graphic Music Analyses, republished with a new introduction and glossary by Felix Salzer. New York: Dover.
—————. 1979 [1935/1956]. Free Composition, rev. and ed. Oswald Jonas, trans. and ed. Ernst Oster. New York: Longman.
Skoumal, Zdenek. 1994. “Liszt’s Androgynous Harmony.” Music Analysis 13, no. 1: 51–72.
Smith, Peter H. 1994. “Brahms and Schenker: A Mutual Response to Sonata Form.” Music Theory Spectrum 16, no. 1: 77–103.
Straus, Joseph. 1987. “The Problem of Prolongation in Post-Tonal Music.” Journal of Music Theory 31, no.1: 1–21.
Suurpää, Lauri. 1996. “Schumann, Heine, and Romantic Irony: Music and Poems in the First Five Songs of Dichterliebe.” Intégral 10: 93–123.
—————. 2005. “The Undivided Ursatz and the Omission of the Tonic Stufe at the Beginning of the Recapitulation.” Journal of Schenkerian Studies 1: 66–91.
Wagner, Naphtali. 1986. “The Apparent Tonic in the Western Music of the Eighteenth and Nineteenth Centuries.” PhD diss., Hebrew University, Jerusalem.
Wen, Eric. 1999. “Bass Line Articulations of the Urlinie.” In Schenker Studies 2, ed. Carl E. Schachter and Hedi Siegel, 276–97. Cambridge: Cambridge University Press.
Willner, Chanan. 1988. “Chromaticism and the Mediant in Four Late Haydn Works.” Theory and Practice 13: 79–114.
Yellin, Victor Fell. 1998. The Omnibus Idea. Warren, Michigan: Harmonie Park Press.
Footnotes
* An earlier version was read at the Fourth International Schenker Symposium (Mannes School of Music, New York, 2006).
Return to text
1. Rosen (1995, 453) describes the art of Chopin in these words, and Rapoport (2004) finds similar features to be a Mendelssohnian style element. I believe this is a general characteristic of the Western classical-romantic tradition.
Return to text
2. See for example the re-harmonization of the opening with iiø7 in Brahms’s Symphony no. 2, i, measures 298–301; the transformation of the opening motto into part of a ![]()
Return to text
3. The original German term is Knüpftechnik. See for example the beginning of the development in Beethoven’s Piano Sonata op. 10 no. 2, i. This is an extreme case of what Hepokoski and Darcy (2006, 215) call “C-based openings of the developmental space.” Later in their book (page 527), Hepokoski and Darcy identify linkage technique between modules of the concerto solo exposition. An example from a later repertoire may be found in the pentatonic segment in Sibelius’s Symphony no. 3. i, measures 16–18.
Return to text
4. See the theme of Chopin’s Mazurka op. 6 no. 1, as analyzed by Rothstein (1989, 46–48). A similar device is accompanied with asymmetric phrase rhythm and a truncated antecedent in “To Life” from Jerry Bock’s Fiddler on the Roof. Jackson (1999) suggests a different kind of fusion in “diachronic readings” as an alternative to Schenker’s normative readings for Brahms’s Variations on a Theme by Haydn, nos. 5, 6, and 8.
Return to text
5. Rounded binary and small ternary forms are usually one and the same. See Caplin 1998, 71–86. Certain pure ternary forms (ABA with complete recapitulation of the opening section) are also based on interruption, provided that the contrasting section is in the dominant. I shall restrict the terms antecedent and consequent to the phrases of parallel periods. The neutral terms pre-interruption and post-interruption better serve to indicate the sections of the interruption structure when larger forms are involved.
Return to text
6. Kamien (2001, 164 and 169) cites this analysis by Schenker as a hint of the technique of interruption that predates the full development of that concept. Cadwallader and Gagné (1998/2007, 128–29) analyze the antecedent alone and omit the lead-in.
Return to text
7. Other examples of the basic –
Return to text
8. My point is congruent with Caplin’s discussion of “stop” versus “end.” See Caplin 1998, 51.
Return to text
9. For a stricter perpetual motion in the entire texture of a (modified) interruption-fill, see Schumann, Toccata op. 7, measures 10–11.
Return to text
10. In example 2, the precise location of the interruption in the upper voice is tricky. Harmonically, it occurs simultaneously with the bass; the grouping structure based on parallelism with the beginning of the antecedent would put it one eighth-note earlier; yet, the articulation makes it possible to hear a two-eighths anacrusis to the consequent and place the interruption one more eighth earlier. The articulation revealed in the 2010 Henle Urtext edition differs considerably from that in most editions. Many editions also present the melody doubled in thirds, but the Urtext edition has such a doubling only in the repeat at measure 17.
Return to text
11. The phrase “ought not to exist” derives from Schachter (1999b [1981], 193), who discusses Peter Westergaard’s theoretical objection to the Urlinie from .
Return to text
12. Straus (1987, 5) presents this distinction as the “harmony/voice leading condition,” one of four conditions for the existence of prolongation. The space between the root and the seventh of seventh chords with a minor seventh (including V7) raises similar issues, but there it is questionable whether the second is not conceptually simultaneous. See Goldenberg 2008, vol. 1, 35–37. Chromatic passing tones within linear progressions are free of that problem.
Return to text
13. Oster, in footnote 7 of Schenker 1979 [1935/1956], 37, attempts to explain Schenker’s inconsistent view of the deeper hierarchy of the interruption structure as deriving from practical, graphical considerations.
Return to text
14. Schachter (1999a [1980], 63–64) offers a meticulous analysis of this expansion. Another lead-in from Mozart symphonies that has received a close reading is the retransition in Symphony no. 36 (Linz), i, measure 162. The chromatic passing tone arrives after an ascent from an inner voice, with a following voice a third below. The distribution of the diatonic tones differs in each of the voices that move in parallel major thirds. See Schenker 1987 [1910], 148–49, Examples 200–201.
Surface syncopation may highlight the
Return to text
15. The Schenker-oriented discussion of chromaticism by Mitchell (1962) gives a good basis for the evaluation of chromaticism in clearly diatonic contexts.
Return to text
16. Corollary interesting examples: Beethoven, Violin Sonata op. 30 no. 2, ii—in the rounded binary theme, the
Return to text
17. A shorter device that achieves the goal of chromatic continuity across interruption appears in the theme of Haydn’s String Quartet op. 64 no. 5, ii (measure 8, in a modulating period), where the chromatic link includes both a lower incomplete neighbor (
Return to text
18. Schenker’s own reading of the movement in Der Tonwille 2 (Schenker 2004 [1921], 78) does not go into great detail on this point and omits the lead-in altogether.
Return to text
19. Gagné himself proposed this observation in response to an earlier presentation of the present paper.
Return to text
20. Even though we are dealing here with the surface itself, the hierarchical approach is nevertheless evident. Compare Hugo Riemann’s designation of a harmonic degree on every sixteenth note in this lead-in (reproduced in Mooney 2000, 88).
The same configuration achieves a quite different, dramatized, effect in the retransition of Verdi’s “Giorni poveri vivera” from Il Trovatore, measures 69–74. The difference results not only from the larger formal context but also from a general pause between the
Return to text
21. As in Haydn’s Symphony no. 104, ii (Example 4 above), the interruption in Example 6 arrives after a contrasting middle section that prolongs the dominant.
Return to text
22. Forte and Gilbert (1982, 75) rightly observe that “A seeming elementary error . . . is to treat [a case in point from the theme of Mozart’s Piano Variations K. 500] as a prolongation of [] through the interval of the sixth. Doing so ignores the harmonic shift to the dominant.”
Return to text
23. See also the two-octave chromatic lead-in in Mozart’s Rondo K. 485, measures 123–24.
Return to text
24. In this piece, as in Chopin’s Waltz op. posth. 70 no. 1 mentioned in footnote 7, the passing sonority includes the seventh. In a related device, the –
Return to text
25. In Harmony, Schenker (1954 [1906], 285) draws attention to this lead-in
Return to text
26. Other examples of the basic – interruption-fill: Mozart, Serenade K. 320 (Posthorn), i, measure 53 (before an expanded consequent), and several slow-movement main themes: Haydn, String Quartet op. 64 no. 3, ii (modulating period); Haydn, String Quartet op. 74 no. 2, ii (modulating period); Mozart, Horn Concerto K. 447, ii; Mozart, Piano Sonata K 457, ii; Mozart, Piano Sonata K. 570, ii, with a registral manipulation similar to our Example 9. In the retransition of K. 570, ii (measure 27), the context is slightly altered since it arrives from within
Return to text
27. See further discussion in Goldenberg 2008, vol. 1, 95–96 and vol. 2, Ex. 4.15. Naphtali Wagner (1986, 47–49) discusses the analogous case of the incomplete neighbor ––()–, ––()––, and convincingly concludes that “only when [] is strongly recognized as the seventh of the V that requires resolution, should one take into account the possibility of avoiding interruption” (my translation). For another case of dilemma, consider the theme of Chopin, Nocturne op. 62 no. 2: the half-cadence at measure 8 is clear, but is extremely de-emphasized in favor of a – unfolding—could it indeed override division? It is not an interruption, since the consequent modulates.
The model presented here is logically consistent but the actual arrival of the seventh might be realized by an ascent from the fifth of V, as in Chopin’s Etude op. 10 no. 12 (a good example suggested by an anonymous reviewer). Laufer (1991, 72) even presents the linear ascent toward the seventh of V as the paradigmatic skeleton of developments. However, in most of the movements he discusses, the seventh in fact arrives at the last moment, after the consonant V has been regained—sometimes in his own readings. See further discussion in Goldenberg 2008, vol. 1, 126. This topic might require further research.
Return to text
28. In the V–––I progression, the may also serve as an incomplete neighbor to the V7. This is the preferred reading in the transition from the slow introduction of Beethoven’s Piano Sonata op. 81a, i. After an emphasized before V arrival (IV6, measure 16, end of slow introduction), the short on an unaccented beat (measure 20) is too weak to sound as a goal.
Return to text
29. For special emphasis on
Return to text
30. The passage from K. 465, ii forms the entire retransition between the exposition and the recapitulation of a “sonata without development.” Hepokoski and Darcy (2006) call this a “type 1 sonata,” and show the specific movement to be a deformation of that type due to expansion in its second rotation (349). Other examples of large ascending lead-ins that approach I via
Return to text
31. Whereas the actual shift of harmony occurs at the moment of anticipation, the normalized shift of harmony takes place, of course, on the next strong beat. For the principles of normalization, see Rothstein 1990; for the specific normalization of anticipations, see Rothstein 1981, 26–28.
In some cases it might be ambiguous whether –
Return to text
32. The that serves as the goal of the interruption-fill deformation resolves to in the bass, after the has been stated in the bass too. On that procedure, see Wen 1999. For a case with V resolving into the I6 with in the bass, see Wen’s Example 9, from the opening of Brahms’s Clarinet Sonata op. 120 no. 2, i. In our example, an alternative reading of the opening period itself might consider the that opens measure 4 to continue until the structural V and sound as its seventh (after a diminished-fifth descent to and ascent from an inner voice). In that case, its resolution must be to in the bass at the opening of the consequent. According to that interpretation, a mild fusion of the phrases is already present at the opening period, but is more strongly realized at the repeat.
Return to text
33. Rothgeb (1996) and Agmon (1996) debated the status of such an anticipatory “III.” They discuss only examples in major, where “III” is consonant (as Agmon 1996, §6, points out). While Rothgeb (1996, §9) stresses that “III” means V (in Schumann’s Am Kamin [no. 8 in Kinderscenen op. 15], measure 31) and that it “may equally well mean I,” he does not take into account the simultaneous function as both I and V.
Return to text
34. In turn, taking into account the configurations of the lead-in offers interesting ramifications of Skoumal’s ideas. In particular, the lead-in pattern diverges from the smoother abstract configurations presented by Skoumal (1994, 59).
Return to text
35. The theme of Grieg’s op. 3 no. 3 is a sixteen-measure period, where each phrase is constructed as a sentence. Such periods lack a contrasting idea typical of eight-measure periods (Caplin 1998, 65). Whereas the harmony of this piece includes many idiosyncrasies, its form is quite square.
Return to text
36. This model has been proposed by Ernst Oster (footnote to Schenker 1979 [1935/1956], 139): “a sonata movement [i.e., an interruption structure, here on the small scale] that starts on , the upper voice does not descend via , , at the interruption point . . . [as] in Fig. 152,4. . . the . . . . . . comes here from the chordal third of the tonic harmony, and must be considered an inner-voice tone. . . . In the meantime the is extended . . . it only descends to . . . as late as the end of [the recapitulation, here, the consequent].”
Return to text
37. The precise progression under is not functional. It includes only one functional segment (
Return to text
38. The procedure of a voice-leading graph that includes unrealized expected routes derives from Laufer 1988; see, for example, the graph of Mozart’s Fantasy K. 394 on page 117, with the indication “not this.”
Return to text
39. A corollary case to Burstein’s examples is the tonicization of
Return to text
40. One more late-Romantic exception: in Wolf’s Verborgenheit (Mörike song no. 12, composed 1888), the vocal line uses the lead-in form –
Return to text
41. See Schumann, Album für die Jügend, no. 14 (Kleine Studie), measure 16.
Return to text
42. Lead-ins in modulating periods have been noted in footnote 17 and 26, and 27. See also Examples 24 and 28 below as well as Schumann, Album für die Jügend, no. 15 (Frühlingsgesang), measure 4.
Return to text
43. See Beethoven’s Cello Sonata op. 5 no. 2, i, measure 105 (measure 61 of the Allegro).
Return to text
44. The exposition includes a large interpolation between the secondary group and the closing section (measures 120–52) that is omitted in the recapitulation. This discussion relates to a single-movement form, and ignores the (inconsistent) common view that this sonata also functions as a multi-movement work.
Return to text
45. In the terminology suggested by Kopp (2002, 8–13), these are upper sharp mediant relations.
Return to text
46. The ![]()
![]()
![]()
Return to text
47. Another example: Chopin, Etude op. 10 no. 2, measures 1–8, interruption-fill at the end of measure 4. There is unceasing chromatic movement in equal sixteenth notes, but melodic parallelism nonetheless makes the division into phrases absolutely clear. The identity of the primary tone is ambiguous, especially in the antecedent, but the arrival at is clear.
Return to text
48. In another Chopin Mazurka op. 59 no. 2, the ninth V at the last beat before the interruption in the opening period (measure 8) probably functions as an upper neighbor to a cover tone above a more essential primary tone.
Return to text
49. A related ascending filling-in of the V–I path occurs in Schubert, “Gesänge des Harfners II,” op. 12 no. 2, D. 480, measures 12–17. However, in that case no melodic parallelism occurs in the upper voice. Again, I thank an anonymous reviewer of this paper for drawing my attention to this example.
Return to text
50. In particular, Suurpää (1996, 105) reads a continuous structure without interruption in this song. The V that Schenker reads as a pre-interruption divider is a lower-level event for Suurpää, and the V7/IV, which is an altered form of a regained tonic for Schenker, becomes a mere local secondary dominant into a middleground passing chord in Suurpää’s reading.
Return to text
51. Modified interruption structures whose phrases open with I6 (and might count as auxiliary half- and authentic cadences respectively) enable descent in the bass from the pre-interruption to the regained . See, for example, the theme of Schubert, Symphony no. 5, iv.
Return to text
52. This explanation generally conforms to that given by Caplin (2004, esp. 97–100). Caplin refutes the idea that a post-cadential filling-in obscures the very existence of a cadence.
Return to text
53. Another device that underlines the fourth-progression – within the – caesura-fill is the literal return of after . See Schubert, “Auf dem Flusse” (no. 7 in Die Winterreise, D. 911), measures 38–40, bass.
Return to text
54. See also Chopin, Impromptu no. 2, op. 36, measures 18–19. Fifth-descents from the other members of V to other members of I sound odd. The descent from to might be perceived as an unfolding of – before its resolution; the descent from to creates parallel fifths with the bass. See, however, both of these fifths filled in Mahler, Symphony no. 4, iii, measure 24.
Return to text
55. Other examples of motion from a back-relating V to the ensuing (not back-relating) chord: before III—Beethoven, Piano Sonata op. 28, ii, measure 4; before V/VI—Beethoven, String Quartet op. 135, iii, measure 6.
Return to text
56. Examples of motion into a secondary dominant of the next structural chord seem to be a fingerprint of Chopin. See motion to V/II[
Return to text
57. Another example: Schubert’s Wandrers Nachtlied op. 4 no. 3, D. 224. Schenker (1979 [1935/1956], Fig. 37a) reads the configuration () —a configuration that can also constitute interruption—but in the song, due to phrase structure and proportions, the latter branch is minimized into a quasi-auxiliary cadence (as elucidated in Kamien 2005; see especially his Example 5). Omitted from Schenker’s graph is a passing
For a passing tone in a presumably “dead” space between a modulating phrase and its repeat, see Chopin, Mazurka op. 41 no. 4, end of measure 24.
Return to text
58. Another example of “illegal” motion from a cover tone: Chopin, Ballade no. 3, measures 214–15. This is an ornamented repeat of the main theme, whose upper voice is based on a relatively structural upper neighbor , preceded by motion of the primary tone to the cover tone . An alternative analysis based on passing motion –– is possible, but the strong metric emphases make the –– much more straightforward. In the repeat, however, a passing
Return to text
Surface syncopation may highlight the ♯2ˆ even without changes in meter or hypermeter. See the main theme of Spohr, Violin Concerto no. 11, iii.
The same configuration achieves a quite different, dramatized, effect in the retransition of Verdi’s “Giorni poveri vivera” from Il Trovatore, measures 69–74. The difference results not only from the larger formal context but also from a general pause between the ♯2ˆ and the 3̂. This general pause underlines the point of division so strongly that any continuity across the interruption is hardly felt.
The model presented here is logically consistent but the actual arrival of the seventh might be realized by an ascent from the fifth of V, as in Chopin’s Etude op. 10 no. 12 (a good example suggested by an anonymous reviewer). Laufer (1991, 72) even presents the linear ascent toward the seventh of V as the paradigmatic skeleton of developments. However, in most of the movements he discusses, the seventh in fact arrives at the last moment, after the consonant V has been regained—sometimes in his own readings. See further discussion in Goldenberg 2008, vol. 1, 126. This topic might require further research.
In some cases it might be ambiguous whether 4ˆ–♯4ˆ serves within interruption-fill or passes within an initial ascent to the consequent. For example, in the second theme of Mozart’s Piano Sonata K. 311, i (measures 17–25), the features of the lead-in itself suggest that it is a normative interruption-fill, mainly because the embedded 3̂ occurs on an unaccented eighth note. Nevertheless, since the antecedent starts with an anticipatory initial ascent, it is reasonable to hear a similar if modified initial ascent in the consequent as well. Another artistic device that helps to smooth the phrases in that period is the accented passing ♯2ˆ on the first strong beat of both antecedent and consequent. See also Daniel Barenboim’s Eingang for the returning rondo theme in measure 178 in Mozart, Piano Concerto K. 467 (McKee 2004, 26). While the harmony of measure 178 supports the tonic, the bass enters a measure later and measure 178 completes a hypermeasure expressing V. I thank an anonymous reviewer of this paper for drawing my attention to this example.
For a passing tone in a presumably “dead” space between a modulating phrase and its repeat, see Chopin, Mazurka op. 41 no. 4, end of measure 24.
Copyright Statement
Copyright © 2012 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Editorial Assistant
Number of visits: