Historical Hypermetrical Hearing: Cycles and Schemas in the String-Quartet Minuet
Stefan Caris Love
KEYWORDS: hypermeter, perception
ABSTRACT: This paper proposes a cyclic model to represent how hypermeter in the minuet was perceived by the typical late eighteenth-century listener: a first-time listener intimately familiar with the local style. The listener seeks to match the music to a quadruple hypermetrical cycle whenever possible. Disruptions to the cycle include interruption, where a cyclic hyperdownbeat arrives unexpectedly early; deferral, where an expected cyclic hyperdownbeat is delayed; and irregular hypermetrical schemas. The fluctuation between easy hypermetrical regularity and tense disruption animates the music for the listener.
Copyright © 2015 Society for Music Theory
[1.1] Vienna, late eighteenth century: Elise, the young adult daughter of a wealthy family, attends a string-quartet performance. She hears such a work not at a formal concert, but rather at the home of an aristocrat, in a gathering as much social as musical (Klorman 2013, 1–15, 59–60). The performers are likely sight-reading (Klorman 2013, 73). Elise might never hear this particular quartet again, nor will she have the opportunity (nor likely the inclination) to ever study a score (Klorman 2013, 2; Parker 2002, 45). What is “hypermeter” to Elise?
[1.2] As a regular guest at these gatherings, and an amateur musician herself, Elise is well acquainted with the local style. But she has not studied the latest compositional treatises, nor does she pay any special attention to meter. Subtle metrical effects intended for the most knowledgable listeners (Kenner) may be lost on her.(1) Instead, her hearing unconsciously draws on her past musical experiences: these govern what she expects and how she reacts to the unexpected.(2) She is not necessarily able to articulate the substance of these expectations and reactions, but they determine how easily she follows a piece and which of its moments stand out.
[1.3] Throughout this paper, the character of Elise will stand for a community of historical listeners. Their perception of hypermeter likely differed from our own, in ways elaborated below. To describe their understanding of hypermeter, I propose a cyclic model of hypermetrical perception. The model depicts listeners’ moment-to-moment impressions of hypermeter, manifested as sensations of metrical accent, expectation, surprise, confusion, tension, and relief. For greater specificity, I focus exclusively on the minuet and trio in the string quartet. However, the model should be adaptable to all other late eighteenth-century genres.
* * *
[2.1] Two traits distinguish Elise’s listening context from our own. First, she is usually hearing a piece for the first time. Our depiction of her hearing should not be overly subtle, and it should make ample allowance for states of hypermetrical uncertainty. Second, unlike ourselves, Elise is narrowly and deeply immersed in her local musical culture, while modern listeners hear an extraordinary variety of styles and genres, but explore few in any depth. These traits are complementary: because Elise only hears a piece once or twice, she relies on her familiarity with the style to make sense of unfamiliar pieces.
[2.2] Eighteenth-century metrical theory is one possible guide to Elise’s hearing (cf. Mirka 2009; Rothstein 1989, 2008). But the main goal of eighteenth-century theorists like Kirnberger and Koch was not to model perception, but rather “to teach a beginning composer how to correctly notate music” (Mirka 2009, x; my emphasis). Their conceptions of meter must be understood in this light. At best, they provide circumstantial evidence of historical perception; at worst, their ideas can be downright misleading, since they were pursuing other goals.
[2.3] Instead, Elise’s perception depends first and foremost on the music she hears (and plays) (Byros 2012, 2013; Gjerdingen 1988, 2007). Through exposure to the style, Elise unconsciously internalizes its small- and large-scale conventions—its statistical tendencies (Huron 2006). She comes to make unconscious predictions as she listens, and she experiences unfamiliar pieces in light of these predictions’ success or failure.
[2.4] Elise has heard hundreds of minuets, both in chamber performance and while dancing. This experience establishes a norm of duple and quadruple hypermeter. Musicologist Tilden A. Russell has surveyed “almost 100 eighteenth-century recueils [anthologies]” of published minuets for amateur performance, concentrated in the period from 1760–1820 (Russell 1999, 399). While unusual phrase structures and formal plans crop up, Russell concludes that “about one in four” anthologies “contains only minuets in which the number of measures in every reprise is divisible by four” (Russell 1999, 399; my emphasis).(3) Minuets intended for listening rather than dancing also tended to conform to this norm. The 1752 composition manual of Joseph Riepel offers further corroboration: Riepel recommends clear two- and four-bar units, especially at a minuet’s beginning, and encourages the beginner to follow an 8+8 metrical plan (Eckert 2000). The two-measure minuet dance step further reinforces the duple norm.(4) While we cannot be certain of this norm’s psychological reality, as a hypothesis, it is supported by several kinds of evidence. Very likely, Elise unconsciously expects two- and four-bar hypermeter from the moment a minuet begins; this expectation remains in her perceptual background for the entire minuet.
[2.5] Of course, minuets depart from this norm on occasion, with passages of triple hypermeter, a four-measure phrase expanded to five, and so on. When such a device is widespread, it can become a hypermetrical schema, outlined further below: Elise will recognize it once it begins or just after it concludes; she will understand a particular instance of the schema in light of previous instances.(5) This entails a kind of prediction: once a schema begins, Elise recognizes it and predicts its continuation. But the quadruple norm operates at a deeper level: because of its ubiquity, it is the perceptual default, from which the music sometimes departs and to which it strongly tends to return.
* * *
[3.1] What are the psychological consequences of the quadruple norm? Metrical perception involves two processes: finding the cycle and maintaining it.(6) In some cases, finding meter involves a complex series of unconscious deductions from the musical surface (Mirka 2009). But the quadruple norm simplifies the task of finding hypermeter: Elise seeks a four-bar hyperdownbeat from among a stream of downbeats.(7) The most common signals for a four-bar hyperdownbeat are a new phrase or group, and a significant harmonic change.(8) Signficantly, these cues can only be recognized after they have occurred, in retrospect: while Elise expects four-bar hypermeter in general, she does not know exactly when it will begin. This is a case of “reactive attending,” that is, checking what was just heard against expectations (Jones et al. 2002: 313).
[3.2] Once Elise has identified a four-bar hyperdownbeat, the duple and quadruple norm induces a set of expectations for the future: “anticipatory attending,” or actively expecting the precise onsets of certain future events (Jones et al. 2002, 313). She anticipates a strong hyperdownbeat four measures later. She also divides the four-bar hypermeasure in two, and anticipates a two-bar hyperdownbeat at the midpoint. Then she checks whether musical events corroborate these expectations—she “maintains” the hypermeter. Cognitively, these expectations result from cycles of attention, their peaks aligned with expected hyperdownbeats: in colloquial terms, Elise pays more attention near these moments.(9) The attentional peaks reach Elise’s consciousness in the form of “metrical accents”; their approach feels like mounting “tension” (Huron 2006, 307). When the peaks of multiple cycles overlap, the perceived result is an even stronger beat (Large and Palmer 2002; Snyder and Large 2005, 123–24).
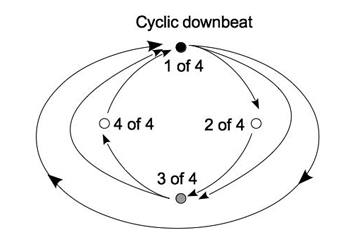
Example 1. The hypermetrical cycle
(click to enlarge)
[3.3] The quadruple hypermetrical norm implies three cycles of attention: the downbeat level and two upper levels, “tuned” to ratios of 1:2 and 1:4 with the downbeat level. Example 1 depicts these as three nested cycles. Together, these form the “hypermetrical cycle,” the core of the cyclic model. The notation of Example 1, adapted from London 2012, incorporates the following elements:
- Three kinds of downbeat: four-bar hyperdownbeat, or “cyclic downbeat” (black dot), two-bar hyperdownbeat (gray dot), and regular downbeat (white dot);
- Realized “projections”: solid arrows, representing the expectation for a future beat generated by a present beat, and its subsequent realization, once the future beat arrives;
- Notation indicating where a particular downbeat is perceived to fall within the cycle as a whole (e.g., “3 of 4” for the third downbeat of four).(10)
The use of three kinds of downbeat-dot emphasizes that Elise builds the hypermeter up from the downbeat level: hypermeter feels like downbeats of varying strength, rather than three separate metrical levels.(11) The projective arrows (as in Hasty 1997 and Mirka 2009) show that a particular metrical event was expected in advance, and subsequently occurred as expected. Each downbeat’s label stands in for the set of realizations and expectations characteristic of that downbeat. For instance, downbeat “2 of 4” is associated with the realization of a downbeat-level expectation, two as-yet-unrealized expectations leading to the next downbeat (“3 of 4”), and a more distant expectation for the next cyclic downbeat (“1 of 4”).(12)
[3.4] What are the limits of metrical perception? (By “metrical perception,” I refer only to the spontaneous sensation of metrical accent; conscious effort increases what can be heard.) Though the evidence is equivocal, two points seem fairly certain. First, there is some limit on the maximum perceptible metrical span, likely ten seconds or less; this limit relates to the “psychological present,” the several-second window of sensory information directly bearing on perception, its leading edge at the true present (Fraisse 1984, 9–29; Iyer 1998, chapter 5; London 2004, 27–28; Repp and Doggett 2007). And second, the perception of hypermetrical levels likely draws on lower metrical levels for reinforcement (Brower 1993, 27–28; Jones 1990; London 2012, 16–17). For a minuet at a tempo of 100 quarter notes per minute, a four-bar hypermeasure lasts 9.6 seconds; at 150 quarter notes per minute, 6.4 seconds. As this falls within the plausible limit of hearing, spontaneous perception of four-bar hypermeter in the minuet seems probable.
* * *
Example 2. A cyclic analysis of a regular passage (Haydn, op. 33, no. 4, mvt. 2, mm. 1–8)
(click to enlarge and listen)
[4.1] Hypermetrical perception consists of fitting a minuet’s events to the hypermetrical cycle. In Example 2, Elise hears the beginning of an unfamiliar, hypermetrically regular minuet, the second movement of Haydn’s String Quartet op. 33, no. 4. Level 1 shows the hypermeter just after the excerpt begins; each lower level advances time forward by one measure. P indicates the leading edge of Elise’s psychological present. A dotted arrow depicts a projection that has not yet been realized. (Downbeat-level projections are not shown in most subsequent examples, since the downbeat remains constant.) Each level shows only the events and projections salient to Elise at that moment.
[4.2] To enter the hypermetrical cycle, Elise locates a candidate cyclic downbeat. The downbeat of m. 1 fits the bill: it initiates a new phrase. Level 1 shows the projections that emerge from this downbeat.(13) Though a projective arrow leads to the next cyclic downbeat, in m. 5, this downbeat’s dot is not yet visible in the notation. It is too far in the future to be particularly salient—it is just over the perceptual horizon. In practical terms, this means that the events of mm. 2–3 could still evaporate this expectation before it had grown very strong. In level 2, Elise checks the downbeat of m. 2 against that of m. 1, and as expected, finds it weaker: tonic harmony persists in a weaker first inversion. The projection from m. 1 to m. 3 is corroborated. (If the downbeat of m. 2 had received more emphasis, the projection to m. 3 might have been denied.) The expected strong downbeat to m. 5 grows more salient: it is now visible in the notation.
[4.3] In level 3, Elise checks the downbeat of m. 3 against that of mm. 1 and 2. As expected, the m. 3 downbeat is stronger than that of m. 2 because the harmony has changed and because the lower two voices re-enter. The arrow from m. 1 to m. 3 solidifies. As expected, the downbeat of m. 3 is weaker than that of m. 1: mm. 1 and 3 form a parallel pair; the second member of such a pair is normally weaker than the first.(14) This corroborates the four-bar projection. (Again, if the downbeat of m. 3 had been unexpectedly strong, it might have denied the four-bar projection from m. 1 to m. 5.) The two-bar level now joins the four-bar in foretelling the strong downbeat of m. 5: notice the new arrow from m. 3 to m. 5, as anticipation mounts. The downbeat dot of m. 2 has disappeared, representing its dwindling salience.
[4.4] In level 4, the downbeat of m. 4 is weak, as expected, corroborating both of the projections to m. 5. The details of m. 1 fade behind the horizon. In level 5, the downbeat of m. 5 is strong, as expected: tonic harmony returns, and the texture and melody change. At this point, the cycle resets itself. All the downbeat-dots of the first hypermeasure disappear, since the metrical details of these measures need no longer be retained in working memory. The next hypermeasure proceeds in the same way as the first (level 6).(15)
[4.5] These events reach Elise’s consciousness as metrical accents of varying strength, a sense of growing anticipation leading into hyperdownbeats, and a generally pleasant predictability.(16) Across mm. 1–5, anticipation for m. 5 grows and the awareness of m. 1 dissipates. After m. 5, a new set of expectations looks forward to m. 9. Elise is crossing an archipelago of cyclic downbeats, just beyond the horizon from one another: she sets off in the direction of a downbeat, with a sense of its distance (level 1); in between, she is aware of the cyclic downbeats before her and behind her (levels 2 and 3); as the next downbeat approaches, the first fades from awareness (levels 4 and 5).(17)
* * *
[5.1] Examples 1 and 2 represent what happens when the music proceeds according to expectation, and expected hyperdownbeats are confirmed by commensurate musical events, with no significant conflicts. But intermittent hypermetrical irregularities are a hallmark of late eighteenth-century Viennese style. While inertia can sustain the hypermetrical cycle through a vague or ambiguous passage, it cannot overcome genuine conflict. No listener would perceive four-bar hypermeter through an unambiguous five-bar phrase: the perceived hypermetrical downbeat would subsequently be offset from all surface evidence, an unsustainable condition. Therefore, a single, strongly contradicted expectation—for example, one expected weak downbeat that turns out to be strong—can throw Elise out of the cycle. She seeks to re-establish the cycle as soon as possible.
[5.2] Before proceeding with irregular examples, I offer a caveat: the analyses here represent one possible hearing of each passage (sometimes two). In hypermetrically complex passages, different hearings are usually possible, especially with conscious intervention. The cyclic model does not determine a single correct analysis; it only limits analyses to a cognitively-informed framework and provides a common analytical vocabulary.(18) (As you work through the examples, I recommend that you listen to the recordings, without conducting, rather than auralizing or playing them. This lessens the possibility of top-down bias.)
Example 3. Interruption, then deferral (Haydn, op. 64, no. 1, 2nd mvt., mm. 45–60)
(click to enlarge and listen)
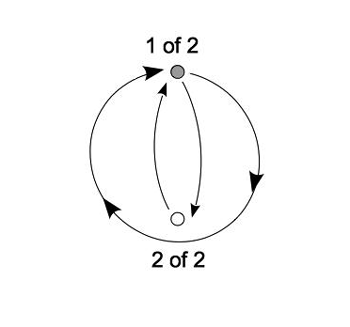
Example 4. The two-bar hypermetrical cycle
(click to enlarge)
Example 5. A longer deferral (Haydn, op. 64, no. 3, 3rd mvt., mm. 1–14)
(click to enlarge and listen)
[5.3] Elise now hears the Trio of op. 64, no. 1, followed by a series of other minuets by Haydn that reflect his penchant for hypermetrical play. Example 3, the first section of the Trio, begins with a four-bar hypermeasure, establishing the cycle. As shown in level 1, the downbeat of m. 49 maintains the cycle with a four-bar hyperdownbeat. The consequent phrase (seems to) begin, and Elise expects a two-bar hyperdownbeat in m. 51. But the surprise re-appearance of the consequent, this time in the first violin with tutti support, produces another four-bar hyperdownbeat (level 2). The cycle that started in m. 49 is interrupted: forcibly restarted by an unexpected cyclic downbeat. For Elise, the effect is surprise and an abrupt reorientation within the cycle.(19)
[5.4] In the second half of the passage, building on the cyclic downbeat of m. 51 (level 3), Elise expects a weak cadence in m. 54 and a subsequent cyclic downbeat in m. 55. In mm. 51–53, she may recognize the beginning of the “Prinner” schema, adding to her anticipation (Gjerdingen 2007, 45–60). But in an “overridden caesura,” Haydn evades the potential m. 54 cadence: the music presses forward into a more decisive cadence in m. 56 (Mirka 2011, 250). The expected cyclic downbeat is denied, and the quadruple cycle has been deferred. The deferred expectation increases Elise’s feeling of tension as she seeks possible cyclic downbeats (Huron 2006, 314–18).
[5.5] Elise will likely hear mm. 54–58 in one of two ways, shown in levels 4A–5A and 4B–5B. First, Elise might hear the downbeat of m. 55 as a two-bar hyperdownbeat, but not a four-bar (4A). In other words, the quadruple cycle is broken, but m. 55 retains some hypermetrical accent, perhaps because of the cadential ![]()
[5.6] The deferral of mm. 55–56 is brief. Example 5, the beginning of the minuet from Haydn’s op. 64, no. 3, includes a longer deferral, with concomitantly greater tension. Elise has no trouble tracking the cycle in mm. 1–6. In mm. 5–6, Elise perceives the beginning of a four-bar cadential module, I6–ii6–V–I, and anticipates the next cyclic downbeat in m. 9 (level 1). However, in m. 7, the persistence of ii6 harmony and the sparse texture deny the two-bar hyperdownbeat, bringing about a deferral (levels 2 and 3). (If inertia carries the hypermeter through mm. 7–8, then m. 9 will be unexpectedly weak.) Elise awaits for the return of the cycle.
[5.7] The remainder of the passage may be heard in one of two ways. In hearing A, the cadential ![]()
![]()
[5.8] Hypermetric deferral is especially common at the conclusion of a minuet or trio’s B section, to prepare the A’ section: the return of the theme thus coincides with the restoration of the cycle, evoking relief.(20) The twin devices of interruption and deferral encompass the vast majority of disruptions to the quadruple cycle. In paragraphs 7.5–7.8 below, I introduce a third device, the irregular schema.
* * *
[6.1] In the examples presented so far, Elise’s first interpretation of a downbeat has held fast through subsequent events. But in the right context, Elise can retrospectively reinterpret a downbeat in light of subsequent events. Retrospective reinterpretation is only possible while the event remains in the psychological present; older downbeats are closed to such reinterpretation, since their strength or weakness is no longer perceptually meaningful.(21)
[6.2] Since a strong beat is a peak of attention, weak-to-strong reinterpretation entails directing extra attention to an event in the immediate past. While this sounds very abstract, Elise experiences a related phenomenon in everyday conversation: initially, she mishears something just said; a moment later, she suddenly (re-)comprehends.(22) The utterance remained within the psychological present, and she directed further attention backwards in time to decode it. On the other hand, since weak downbeats are characterized only by a relative lack of attention, a psychological account of strong-to-weak reinterpretation is harder to offer; this phenomenon is not addressed here.
Example 6. Retrospective reinterpretation (Haydn, op. 74, no. 1, mvt. 3, mm. 61–74)
(click to enlarge and listen)
[6.3] Elise’s hearing of Example 6, the first section of the Trio from the third movement of Haydn’s op. 64, no. 1, involves retrospective reinterpretation. In m. 67, Elise finds herself towards the end of an apparent 4+4 phrase structure spanning mm. 61 to 68. She expects the next cyclic downbeat to arrive in m. 69 (level 1). But once she reaches m. 69 (level 2), two factors lead her to reinterpret m. 67 as a cyclic downbeat, and downgrade m. 69 to the two-bar level. First, mm. 67–68 and 69–70 are parallel; the first member of a parallel pair is normatively strong, the second, weak. Naturally, she can only recognize this parallelism in retrospect. Second, by m. 70, Elise might perceive the beginning of a modified “Prinner” spanning mm. 67–74, leading to the key of the dominant. This schema usually begins on a strong beat, further strengthening m. 67. Since the downbeat of m. 67 is unexpectedly retroactively strong, this is an instance of hypermetrical interruption—but an interruption in which the unexpected strong beat is in the past! As with all interruptions, the effect will be surprise and a sudden reorientation within the cycle.
[6.4] A new four-bar projection emerges (retroactively) from m. 67: Elise now expects a cyclic downbeat in m. 71. Changes in rhythm and texture confirm this, and the excerpt concludes (level 3). Elise assesses the accentuation of each downbeat twice: first in comparison with previous downbeats, and again, retrospectively, in comparison with later beats. It is inadequate to say that the downbeat of m. 67 is either weak or strong; rather, it is first weak, then strong.
* * *
Example 7. A general pause defers the hypermetrical cycle (Dittersdorf, String Quartet no. 6 in A major, 2nd mvt., mm. 13–22)
(click to enlarge and listen)
[7.1] Now Elise hears three minuets by Haydn’s friend and contemporary Carl Ditters von Dittersdorf, illustrating a few other late eighteenth-century hypermetrical techniques. First, she listens to the second movement of Dittersdorf’s String Quartet no. 6 in A major. After an entirely regular A section and first portion of the B section, Elise comes to the passage in Example 7. Partway through the B section, m. 17 begins with a cyclic downbeat (level 1). But in m. 19, instead of the expected two-bar hyperdownbeat, all four instruments rest, cutting off two- and four-bar projection (level 2): a general pause.(23) The hypermeter is deferred, sparking Elise’s attention for the next cyclic downbeat. Measure 20 restarts the downbeat level, but the texture and harmony make its downbeat weak (level 3). The hypermetrical cycle only begins anew with the cadential arrival in m. 21. General pauses usually have the effect of deferral. The hypermeter may restart immediately after the pause, or after one or two weak measures (as here).
[7.2] In some performances, it is possible to perceive regular hypermeter through the general pause in m. 19: the hyperdownbeat in m. 21 is exactly four measures after that in m. 17, so in a numerical sense, the hypermeter is “regular.” Conducting the hypermeter, a common perceptual tactic today, would make this easy. But numerical regularity does not imply perceptual regularity. Elise does not know the piece, has no score, and is not consciously focusing on hypermeter. And as a perceptual strategy for this style, it would not make sense for Elise to assume that hypermeter remains consistent through general pauses: general pauses vary in duration, and are not always numerically regular. Instead, this general pause suspends the hypermeter and builds tension, such that the restart in m. 21 elicits relief.
Example 8. A minuet ends in a state of deferral (Dittersdorf, String Quartet no. 3 in G major, 2nd mvt., mm. 24–36)
(click to enlarge and listen)
Example 9. Triple-hypermeter schema (Dittersdorf, String Quartet no. 5 in E-flat major, 2nd mvt., mm. 13–27)
(click to enlarge and listen)
[7.3] Next, Elise hears the second movement of Dittersdorf’s String Quartet no. 3 in G major. The minuet’s middle section ends with a long deferral, such that the return of the main theme in m. 25 restores the cycle (Example 8, level 1). The first six measures of the A’ section (mm. 25–31) are identical to those of the A section, which was a perfectly regular eight measures. Therefore, “dynamic expectations” stemming from the A section lead Elise to hear mm. 25–31 as regular (level 2 and 3), and she expects a regular continuation in m. 32 (Huron 2006, 227–31). These dynamic expectations overcome the local factors that accent the downbeat of m. 31.
[7.4] Trouble begins in mm. 32–33, when A’ begins to diverge from A. The A section reached a cadence in its eighth measure, but in m. 32, the A’ section continues. Whereas Elise expected a cyclic downbeat in m. 33, parallelism with m. 31 downgrades this downbeat to the two-bar level (level 4). Elise reverts to the two-bar cycle and awaits the next four-bar hyperdownbeat. m. 35 continues the pattern, sustaining the two-bar cycle but further deferring the four-bar (level 5)—indefinitely, as it turns out: the minuet ends on a note of uncertainty, as the four-bar cycle never returns.(24)
[7.5] Finally, Elise hears the second movement from Dittersdorf’s String Quartet no. 5 in
[7.6] Two possible hearings follow. If Elise is especially cycle-bound, she begins another four-bar cycle in m. 20 (level 3A), only to have it interrupted again by the resolution to dominant harmony in m. 23 (4A). However, if her hearing is more flexible, she slips into triple hypermeter, as shown in hearing B. As in hearing A, in m. 20, the change in texture and harmony interrupts the four-bar cycle (level 3B): she did not expect the first three-measure group. But from the vantage of m. 20, Elise relates mm. 17–20 to similar passages she has heard before; drawing on that experience, she expects that one three-measure group will be followed by another.(25) In the analysis of Example 9, the dashed time-span between the downbeats of mm. 17–20, projected from mm. 20–23, represents the retrospective recognition of the just-past three-measure group and the projection of its expected three-measure partner.(26) At the next moment (level 4B), in mm. 20–22, Elise recognizes another familiar device: the “le–sol–fi–sol” schema, a conventional dominant preparation (Byros 2012, 284–305). This leads her to anticipate the dominant arrival in m. 23. Such an arrival tends to coincide with a resetting of the quadruple cycle, so she is not surprised by the return to a four-bar cycle in m. 23. Ultimately, hearing B incorporates a broad range of Elise’s prior experience, and seems more convincing.
[7.7] Hearing B also illustrates how to integrate the quadruple cycle with less common, but familiar, hypermetrical schemas. Elise does not predict the precise occurrence of these devices in advance, since no individual device is more common than the quadruple norm. But she can recognize a device once it begins and quickly adjust her subsequent expectations.
[7.8] Interruption and deferral are not hypermetrical schemas. Schemas allow Elise to make sense of the hypermeter: to understand each downbeat as part of a pre-learned framework. The triple-hypermeasure schema, for example, fits each downbeat into a three-measure template. Instead, interruption and deferral are simply two ways of disrupting the quadruple cycle; they are too broadly defined to serve as schemas. However, interruption or deferral may be found within a well-defined schema. For instance, in sonata-form first movements, the transition section often begins with an interruption on the fourth downbeat of a cycle. On hearing this event, Elise can process it in relation to similar events, fitting what she just heard into a pre-learned framework. Its specific context and implementation allows this pattern to serve as a schema in a way that “interruption” more broadly cannot.
* * *
[8.1] In the analyses so far, Elise has been in the dark about the musical future. But given the repetition scheme of the minuet and trio, she actually hears each section of a minuet three times and each section of a trio twice. How does this affect her experience?
[8.2] A surprising metrical event grows less surprising on repetition. The attentional component of metrical accent explains this effect. Attention, including metrical attention, responds to top-down intervention (Iversen, Repp, and Patel 2009). Knowing that a surprising downbeat is coming, Elise can adjust her attention in advance; the long lag between hypermetrical beats, compared to lower metrical levels, allows more time to redirect attentional resources.(27) This adjustment does not need to be intentional. Elise’s acquisition of the quadruple cycle and irregular schemas relies on unconscious learning. Similarly, having just heard a surprising passage, Elise retains an impression of its surprising events, and her attentional cycles can anticipate these and adjust to them without conscious mediation.
Example 10. Elise hears the repeat of Example 3 (Haydn, op. 64, no. 1, 2nd mvt., mm. 45–60)
(click to enlarge and listen)
[8.3] Consider Elise as she listens to the repeat of Haydn’s duplicitous trio from op. 64, no. 1 (Example 10). Now she knows about the surprising re-entry of the consequent in m. 51 and the overridden caesura in m. 54. She will still hear the downbeat of m. 49 as a four-bar hyperdownbeat—the cycle in mm. 45–48 and the four-bar parallelism dictate this—but this time, the four-bar projection from m. 49 to m. 53 dissipates, rather than being forcibly cut off (level 1). At some level, Elise knows that m. 51 will begin a new phrase, so her four-bar attentional cycle is prepared to reset (level 2). Similarly, in anticipation of the overridden caesura and extension in mm. 54–56, her expectation of a four-bar downbeat in m. 55 dissipates gradually, rather than being unexpectedly frustrated (levels 2 and 3). The deferral of the quadruple cycle still evokes tension; but this time, in mm. 55–56, Elise forms a definite expectation for when it will return (levels 4 and 5). Overall, she experiences cyclic downbeats in mm. 49, 51, and 57—as though these downbeats had occurred within regular cycles—and the surprise of m. 51 and tension of mm. 54–56 are attenuated.
[8.4] Example 10 provides a segue to some broader questions. First, how does Elise’s perception compare to that of historical musical experts? Experts face the same circumstantial limitations as Elise: no access to a score, and little opportunity to hear any particular piece more than once. Experts’ advantages include acquaintance with more pieces and a better musical memory. Having heard more pieces, they have a larger and better-learned vocabulary of hypermetrical schemas. When a reprise is repeated, their better memory allows them to accommodate irregularities more easily the second time around. But their perception of hypermeter does not differ fundamentally from Elise’s: the quadruple cycle remains the foundation of hearing; they cannot predict the future, so they remain susceptible to interruptions and deferrals.
[8.5] Conversely, consider listeners less knowledgeable than Elise. The comparative simplicity of late eighteenth-century symphonic music speaks to the relative broadness of its intended audience, compared to the chamber music analyzed here. This audience knows fewer pieces and has a worse memory than Elise. Nevertheless, they too rely on the quadruple norm and a (small) vocabulary of irregular schemas to parse the hypermeter.(28) They lose track of the quadruple cycle more easily than Elise; to compensate, composers need to make their hypermetrical cues more obvious. But in outline, the model posited here remains applicable.
Example 11. An analysis of Example 10, in the style of Rothstein 1989
(click to enlarge)
[8.6] To conclude, let us consider the relationship between the cyclic model and the view of hypermeter first articulated by Carl Schachter and William Rothstein. This view is inspired by Schenkerian analysis and, like the cyclic model, refers to perception.(29) William Rothstein articulates one of this approach’s tenets as follows: “Metrical irregularities can often, though not always, be traced to more regular models,” most often, the four-measure phrase (1989: 12). These “regular models” relate to the musical surface through transformations like the “durational expansion, which extends a four-measure group [at a hypothetical higher level] to five measures” (Schachter 1999: 57). Example 11 shows a hypermetrical analysis of Example 10 in the style of Rothstein 1989. The false consequent in mm. 49–50 is a “parenthesis” (Rothstein 1989, 87–92). The phrase in mm. 51–56 expands a four-bar prototype.
[8.7] This approach remains tied to perception: it “begins and ends with direct musical experience, with hearing”—specifically, such an analysis begins with the listener’s perceptual intuition, and ends with “hearing that is incomparably clearer and more comprehensive than it had been before” (Schachter 1999: 35). But the situation and aims of this kind of listener—call her Clara—differ radically from those of Elise. Clara has studied the score and recordings, and she has dissected the piece’s harmony and voice leading in pursuit of pre-defined analytical goals. The analysis in Example 11 integrates metrical accent with these other features: it depicts phrase rhythm, not merely hypermeter. Guided by this analysis, Clara aims to direct her attention to all the right downbeats. In order to make her hearing “clearer and more comprehensive,” she actively coordinates her perception of metrical accent with other aspects of the music’s structure. In contrast, Elise has not heard the piece before, does not have a score, and has no special interest in hypermeter. The cyclic analyses depict her real-time, fleeting impressions.
[8.8] These two approaches also differ over hypermeter’s broader significance. Clara aims to hear beyond her initial uncertainty to the certainty of the music’s deeper structure. She understands irregularities as composers’ subtle variations on the regular, quadruple norm. Of course, the quadruple norm also governs Elise’s hearing: it is active before a piece begins, and she seeks to return to it from states of uncertainty. But uncertainty and surprise remain at the core of her perception: she experiences hypermeter as a fluctuation between regularity and irregularity, stability and tension. Her perceptual vocabulary consists of the duple and quadruple cycles and a handful of irregular schemas, which she can only recognize in retrospect. Any passage that does not fit one of these patterns is irreducibly irregular.
[8.9] Finally, these approaches reflect deeper analytical dichotomies: real-time hearing versus final or “best” hearing; “descriptive” versus “suggestive” analysis (Temperley 2001b); and analysis of the listener versus analysis of the piece. Both approaches have something to offer. But if we are interested in historical perception, Clara’s analysis seems alienated from Elise’s experience. Late eighteenth-century composers wrote for listeners like Elise, who were intimately familiar with the style, but had only a fleeting experience of any particular piece. Composers anticipated and manipulated these listeners’ moment-to-moment reactions (Bonds 2008, 37–40). The fluctuation between easy hypermetrical regularity and tense disruption animates this music, and was a vital part of these reactions. The cyclic model of hypermeter provides a way into this experience.
Stefan Caris Love
University of Massachusetts Amherst
Department of Music and Dance
151 Presidents Dr., Ofc. 1
Fine Arts Center—273 East
Amherst, MA 01003–9330
sclove@music.umass.edu
Works Cited
Bonds, Mark Evans. 2008. “Listening to Listeners.” In Communication in Eighteenth-Century Music, ed. Danuta Mirka and Kofi Agawu, 34–52. Cambridge University Press.
Brochard, Renaud, Donna Abecasis, Doug Potter, Richard Ragot, and Carolyn Drake. 2003. “The ‘Ticktock’ of Our Internal Clock: Direct Brain Evidence of Subjective Accents in Isochronous Sequences.” Psychological Science 14 (4): 362–66.
Brower, Candace. 1993. “Memory and the Perception of Rhythm.” Music Theory Spectrum 15 (1), 19–35.
Byros, Vasili. 2013. “Trazom’s Wit: Communicative Strategies in a ‘Popular’ Yet ‘Difficult’ Sonata.” Eighteenth-Century Music 10 (2): 213–52.
—————. 2012. “Meyer’s Anvil: Revisiting the Schema Concept.” Music Analysis 31 (3): 273–346.
Cone, Edward T. 1968. Musical Form and Musical Performance. Norton.
Eckert, Stefan. 2000. “Ars Combinatoria, Dialogue Structure, and Musical Practice in Joseph Riepel’s Anfangsgründe zur musicalischen Setzkunst.” PhD Thesis, SUNY Stony Brook.
Ferreira, Fernanda, Karl G. D. Bailey, and Vittoria Ferraro. 2002. “Good-Enough Representations in Language Comprehension.” Current Directions in Psychological Science 11 (1): 11–15.
Fodor, Janet Dean. 1998. “Unambiguous Triggers.” Linguistic Inquiry 29 (1): 1–36.
Fraisse, Paul. 1984. “Perception and Estimation of Time.” Annual Review of Psychology 35 (1): 1–36.
Gjerdingen, Robert O. 2007. Music in the Galant Style. Oxford University Press.
—————. (1988). A Classic Turn of Phrase: Music and the Psychology of Convention. University of Pennsylvania Press.
Hasty, Christopher. 1997. Meter as Rhythm. Oxford University Press.
Huron, David. 2006. Sweet Anticipation: Music and the Psychology of Expectation. MIT Press.
Ito, John Paul. 2013. “Hypermetrical Schemas, Metrical Orientation, and Cognitive-Linguistic Paradigms.” Journal of Music Theory 57 (1): 47–85.
Iversen, John R., Bruno H. Repp, and Aniruddh D. Patel. 2009. “Top-Down Control of Rhythm Perception Modulates Early Auditory Responses.” Annals of the New York Academy of Sciences 1169 (1): 58–73.
http://archive.cnmat.berkeley.edu/People/Vijay/%20THESIS.html.
Iyer, Vijay S. 1998. “Microstructures of Feel, Macrostructures of Sound: Embodied Cognition in West African and African-American Musics.” PhD dissertation, University of California, Berkeley. Available at
http://archive.cnmat.berkeley.edu/People/Vijay/%20THESIS.html.
Jackendoff, Ray. 1991. “Musical Parsing and Musical Affect.” Music Perception: An Interdisciplinary Journal 9 (2): 199–229.
Jones, Mari Riess, Heather Moynihan, Noah MacKenzie, and Jennifer Puente. 2002. “Temporal Aspects of Stimulus-Driven Attending in Dynamic Arrays.” Psychological Science 13 (4): 1313–19.
Jones, Mari Riess. 1990. “Learning and the Development of Expectancies: An Interactionist Approach.” Psychomusicology: A Journal of Research in Music Cognition, Music Expectancy, 9 (2): 193–228.
Klorman, Edward. 2013. “Multiple Agency in Mozart’s Music.” PhD dissertation, City University of New York.
Krebs, Harald. 2005. “Hypermeter and Hypermetric Irregularity in the Songs of Josephine Lang.” In Engaging Music: Essays in Music Analysis, edited by Deborah Stein, 13–29. Oxford University Press.
Large, Edward W., and Caroline Palmer. 2002. “Perceiving Temporal Regularity in Music.” Cognitive Science 26 (1): 1–37.
Large, Edward W., and Joel S. Snyder. 2009. “Pulse and Meter as Neural Resonance.” Annals of the New York Academy of Sciences 1169 (1): 46–57.
Lerdahl, Fred, and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. MIT Press.
Little, Meredith Ellis. n.d. “Minuet.” Oxford Music Online, www.oxfordmusiconline.com.
London, Justin. 2012. Hearing in Time: Psychological Aspects of Musical Meter. 2nd ed. Oxford University Press.
—————. 2004. Hearing in Time: Psychological Aspects of Musical Meter. Oxford University Press.
Maurer Zenck, Claudia. 2008. “‘Mannichfaltige Abweichungen von der Gewöhnlichen Sonaten-Form’: Beethoven’s ‘Piano Solo’ Op. 31 No. 1 and the Challenge of Communication.” In Communication in Eighteenth-Century Music, 53–79, ed. Danuta Mirka and Kofi Agawu. Cambridge University Press.
McClelland, Ryan. 2006. “Extended Upbeats in the Classical Minuet: Interactions with Hypermeter and Phrase Structure.” Music Theory Spectrum 28 (1): 23–56.
Mirka, D. 2011. “Punctuation and Sense in Late-Eighteenth-Century Music.” Journal of Music Theory 54 (2): 235–82.
Mirka, Danuta. 2009. Metric Manipulations in Haydn and Mozart: Chamber Music for Strings, 1787–1791. Oxford University Press.
Mirka, Danuta, and Kofi Agawu, eds. 2008. Communication in Eighteenth-Century Music. Cambridge University Press.
Ng, Samuel. 2012. “Phrase Rhythm as Form in Classical Instrumental Music.” Music Theory Spectrum 34 (1): 51–77.
Parker, Mara. 2002. The String Quartet, 1750-1797: Four Types of Musical Conversation. Ashgate.
Pritchett, Bradley L. 1988. “Garden Path Phenomena and the Grammatical Basis of Language Processing.” Language 64 (3): 539–76.
Repp, Bruno H., and Rebecca Doggett. 2007. “Tapping to a Very Slow Beat: A Comparison of Musicians and Nonmusicians.” Music Perception 24 (4): 367–76.
Rothstein, William. 2008. “National Metrical Types in Music of the Eighteenth and Early Nineteenth Centuries.” In Communication in Eighteenth-Century Music, ed. Danuta Mirka and Kofi Agawu, 112–59. Cambridge University Press.
—————. 1995. “Beethoven with and without Kunstgesprang: Metrical Ambiguity Reconsidered.” Beethoven Forum 4: 165–93.
—————. 1989. Phrase Rhythm in Tonal Music. Schirmer Books.
Russell, Tilden A. 1999. “Minuet Form and Phraseology in Recueils and Manuscript Tunebooks.” Journal of Musicology 17 (3): 386–419.
Schachter, Carl. 1999. Unfoldings: Essays in Schenkerian Theory and Analysis. Oxford University Press.
Smyth, David H. 1992. “Patterning beyond Hypermeter.” College Music Symposium 32 (January): 79–98.
Snyder, Joel S., and Edward W. Large. 2005. “Gamma-Band Activity Reflects the Metric Structure of Rhythmic Tone Sequences.” Cognitive Brain Research 24 (1): 117–26.
Temperley, David. 2009. Review of Metric Manipulations in Haydn and Mozart: Chamber Music for Strings, 1787–1791. Journal of Music Theory 53 (2): 305–28.
—————. 2008. “Hypermetrical Transitions.” Music Theory Spectrum 30 (2): 305–25.
—————. 2001a. The Cognition of Basic Musical Structures. MIT Press.
—————. 2001b. “The Question of Purpose in Music Theory: Description, Suggestion, and Explanation.” Current Musicology 66: 66–85.
Temperley, David, and Christopher Bartlette. 2002. “Parallelism as a Factor in Metrical Analysis.” Music Perception 20 (2): 117–49.
Wick, Norman L. 1991. “Transformations of Middleground Hypermeasures in Selected Mozart Keyboard Sonatas.” Theory and Practice 16: 79–102.
Wheelock, Gretchen A. 1992. Haydn’s Ingenious Jesting with Art: Contexts of Musical Wit and Humor. Schirmer Books.
Zuckerkandl, Victor. 1969. Sound and Symbol. Princeton University Press.
Footnotes
1. Bonds 2008 explores how composers appealed variously to Kenner and Liebhaber not only at the level of the piece, but also within individual pieces. Maurer Zenck 2008 and Mirka 2009 discuss some subtle metrical effects intended for Kenner.
Return to text
2. This view of historical hearing, in which past experience governs future expectations, proceeds in the spirit of Byros (2012, 2013) and Gjerdingen (1988, 2007). Iyer discusses cultural influence on metrical perception more generally (1998, chapter 5).
Return to text
3. Some of these reprises might still be irregular; e.g., an eight-measure reprise might divide into a five-measure and a three-measure phrase. Nevertheless, it seems safe to assume that most of these are regular quadruple phrases.
Return to text
4. The basic step of the minuet is a six-beat pattern divided into three two-beat gestures, implying a hemiola against two measures of
Return to text
5. Contrapuntal schemas are discussed in Byros 2012, 2013; and Gjerdingen 1988, 2007. Ito 2013 discusses hypermetrical schemas, though in different terms than I do here.
Return to text
6. This complete process is more generally called “entrainment.” See Jones 1990; Jones et al. 2002; London 2012; Mirka 2009. For a critique, see Temperley 2009, 310–11.
Return to text
7. Compare London’s “template matching” (2012, 67–68) and Ito’s schematic metrical hearing (2013). I take the downbeat level for granted; though not inviolable, the downbeat level is always more reliable than hypermetrical levels. Metrical dissonance that obscures the downbeat disrupts the hypermeter as well.
Return to text
8. Lerdahl and Jackendoff (1983) note the importance of grouping to hypermeter; Rothstein emphasizes the importance of harmony and grouping for hypermeter (1995, 173); Temperley grants harmony “decisive importance” to determining hypermeter (2008, 310); Mirka calls harmony the “most important” metrical cue, aside from “phenomenal accent” (2009, 50).
Return to text
9. See Brochard et al. 2003, Jones et al. 2002, Huron 2006 (175–85), Large and Palmer 2002, Large and Snyder 2009, London 2012 (83, 91), and Snyder and Large 2005. For a discussion of competing views, see Iversen, Repp, and Patel 2009: 69–72. Neurologically, the peaks slightly anticipate the beats themselves, illustrating that metrical accent is anticipatory, not reactive (Jones et al. 2002; Snyder and Large 2005, especially 123–24).
Return to text
10. Example 1 does not literally depict anything in Elise’s brain or mind, and many of its features are arbitrary: the placement and notation of the downbeat dots, the overall round shape, and so on. The example is intended to model the cyclic nature of metrical attention as described in neurological research, and connect it to familiar ideas of measure and hypermeasure.
Return to text
11. This notation thus collapses into a single level what would be represented as three levels in Lerdahl and Jackendoff 1983.
Return to text
12. This notation is inspired by the fractional notation in Ito 2013, where “
Return to text
13. The rapid formation of these expectations, made possible by the quadruple norm, distinguishes the cyclic model from Mirka’s model of lower metrical levels (2009, 17–30): Mirka’s listener has few prior assumptions about meter, and metrical expectations emerge only gradually, in several steps.
Return to text
14. Temperley describes the role of parallelism, a component of grouping (2001a, 51; Temperley and Bartlette 2002); Mirka also cites the importance of parallelism (2009, 137–39).
Return to text
15. Note that the next expected hyperdownbeat, of m. 9, comes just after the tonic cadence in m. 8: the cadential downbeat is hypermetrically weak. Metrically strong phrase beginnings and weak cadences are standard for Haydn minuets and the Germanic style which they typify. See Rothstein 2008.
Return to text
16. David Huron discusses the “positive valence” of hypermetrical downbeats (2006: 175–85).
Return to text
17. Elise’s island-hopping evokes two famous musical metaphors, Victor Zuckerkandl’s “waves” of meter (1969, 168–85) and Edward Cone’s analogy between the phrase and a thrown and caught ball (1968: 26–27).
Return to text
18. The possibility of multiple interpretations is typical of “preference rule”-based analytical methods, as in Lerdahl and Jackendoff 1983. See Lerdahl and Jackendoff 1983, 53–55 and Temperley 2008, 314 for further discussion.
Return to text
19. For more on the “surprise” of an early arrival, see Huron 2006, 307. William Rothstein calls this device a metrical “reinterpretation” (1989, 52–56).
Return to text
20. Some contemporaneous minuets whose B sections end with deferral of the four-bar cycle: Dittersdorf, String Quartet no. 3, movement 2; Haydn, op. 55, no. 2, movement 3, and no. 3, movement 3; op. 64, no. 4, movement 2, and no. 5, movement 3; Mozart K. 428, movement 2, K. 563, movement 3.
Return to text
21. This differs from the description of retrospective reinterpretation in Temperley 2008, 312–14.
Return to text
22. Metrical retrospective reinterpretation is also comparable to the linguistic phenomenon of the “garden path sentence,” a sentence whose ending forces a surprising reinterpretation of its first portion; a canonical example is “The horse raced past the barn fell.” (See Ferreira, Bailey, and Ferraro 2002, Fodor 1998, or Pritchett 1988 for a sample of the linguistic literature.) This analogy is inexact, however: since language must convey semantic meaning, listeners or readers must arrive at some “final” interpretation, whereas Elise can experience a downbeat as first weak, then strong, without needing to understand the former interpretation as incorrect, the latter as correct.
Return to text
23. Danuta Mirka discusses the general pause at length; she notes its attention-getting effect, and she distinguishes four categories, based on phrasing function (2009, 101–16).
Return to text
24. Other minuets ending in a state of deferral may be found in Haydn’s op. 50, no. 3, 3rd movement; op. 64, no. 5, 3rd movement; and op. 76, no. 6, 3rd movement.
Return to text
25. Other passages that include paired three-measure groups may be found in Haydn, op. 50, no. 4, 1st movement, mm. 56–62; op. 54, no. 3, 3rd movement, mm. 20–26 and 47–52; op. 76, no. 4, 3rd movement, mm. 40–50; and Mozart, K. 516, 2nd movement, mm. 37–43 and 57–63.
Return to text
26. The model of metrical perception in hearing B more closely resembles Mirka 2009, 17–30. However, in Mirka’s model, a time-span still has to recur twice before it elicits projections; here, Elise recognizes the triple-hypermeter schema after a single instance; its familiarity allows her to immediately project the next three-bar group.
Return to text
27. For another view, see Huron 2006, 269–70; Jackendoff 1991, 227; and Temperley 2008, 314–15. All three argue that some measure of surprise remains even for a well-learned “surprising” example, but none invokes the attentional theory of metrical accent.
Return to text
28. For discussion of the four-bar phrase and hypermeasure as prototypical across late eighteenth-century genres, see Cone 1968, 74–75. Ito 2013, Rothstein 1989, and Schachter 1999 (54–78) also assume this norm.
Return to text
29. Rothstein and Schachter’s view of hypermeter has influenced much subsequent work: for example, see Krebs 2005, McClelland 2006, Ng 2012, and Wick 1991. For a critique, see Smyth 1992.
Return to text
Copyright Statement
Copyright © 2015 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Rebecca Flore, Editorial Assistant
Number of visits:
13262