Measuring a Measure: Absolute Time as a Factor for Determining Bar Lengths and Meter in Pop/Rock Music
Trevor de Clercq
KEYWORDS: Rhythm, meter, form, drum feels, popular music, rock music
ABSTRACT: The prevailing approach to bar lengths in pop/rock music uses the standard rock drum beat as a model, whereby the kick is assigned to beats 1 and 3 and the snare to beats 2 and 4 in a bar of
Copyright © 2016 Society for Music Theory
Introduction
Example 1. Three readings of meter and bar lengths for “Norwegian Wood” (The Beatles, 1965)
(click to enlarge and listen)
Example 2. Kick and snare configuration for a standard rock drum beat
(click to enlarge)
[1.1] When analyzing a pop/rock song, how much music constitutes a measure? For example, the Beatles song “Norwegian Wood” has been analyzed by Beatles experts as being in
[1.2] The prevailing approach to meter in pop/rock music, generally speaking, has been to base bar lengths on the standard rock drum beat, whenever possible. This is the general rule suggested by Moore, and Stephenson espouses a similar methodology.(1) The standard rock drum beat, as shown in Example 2, delineates a bar of
[1.3] Inherently, an approach based on the standard drum beat does not offer much guidance in dealing with songs that are not in
[1.4] Part of the issue may be that, although a number of landmark works on rhythm and meter have been published in the past few decades, most take bar lengths and time signatures for granted. In Western classical music, we have an expert listener—the composer—who has already determined how much music should constitute a measure and in what meter it should be conceived; traditional theories of rhythm and meter are thus not forced to tackle these sorts of concerns. For example, one finds no index entries in Lester 1986, Rothstein 1989, Hasty 1997, or Krebs 1999 for the terms “measure” or “bar,” and none of these works give detailed guidelines on how to determine measure lengths or time signatures in the absence of a score. (Cohn 2015 highlights many of these lacunae in music pedagogy, more broadly.) Perhaps the most systematic approach to meter, and thus measure lengths, can be found in Temperley 2001, but his preference-rule system does not offer any advice on how to select between a variety of well-formed, hierarchically-congruent meters, such as those we find in the various published analyses of “Norwegian Wood.”
[1.5] Some readers may feel that the choice of how much music constitutes a measure hardly matters.(4) The choice of time signature, one might argue, serves only to facilitate the communication of rhythmic organization, which can be represented in a variety of equally valid ways. I strongly disagree with this mindset. In popular music, formal prototypes are often predicated on specific bar lengths. The 12-bar and 16-bar blues, for example, are standard units of form, as is the 32-bar AABA. Additionally, some authors have built theories of form around specific bar lengths. Summach, for example, predicates the difference between a full-fledged prechorus and a nascent prechorus on the difference between 8-bar and 4-bar units, respectively (2011, [22]). Bar lengths may not matter, admittedly, if a song is considered in complete isolation, but if we hope to compare a song to other songs and draw conclusions from those comparisons, bar lengths are an important benchmark.
[1.6] In other words, bar lengths are a central component for theories of form—a point of view that is echoed in William Caplin’s work on Classical-era music. In his 1998 book, Caplin distinguishes between a real, experiential measure (i.e., what a listener perceives as one full measure) and a notated measure (i.e., what is given in the score), stating that the real measure “is the only valid measure for an analysis of form based on our musical experience” (35). According to Caplin, form in Classical music is strongly predicated on phrase models of specific bar lengths, which are best understood in terms of real measures. Unfortunately, Caplin does not specify exactly how much musical content comprises a real measure, except to say that bar lengths generally do not change during the course of a movement, and formal conventions can guide our decisions. That said, Caplin does briefly hint at one other possible factor. He states that in an adagio movement, for example, we may perceive a single real measure to be only one half of the notated measure, whereas in a faster movement such as a scherzo, a real measure may constitute two notated measures. While Caplin presumably means for these examples to be purely hypothetical, these two cases imply that absolute time—i.e., the passage of time as quantified by a clock in minutes and seconds—may play a role in determining a real measure, in that a listener’s perceptual window for a real measure may apparently accommodate more beats at a faster tempo and fewer beats at a slower tempo.
[1.7] In this article, I show that the forms of many pop/rock songs share strong similarities within the domain of absolute time. As a result, a song’s drum pattern should not be considered a reliable or consistently appropriate indicator of measure lengths. I argue that we should also consider absolute time as a factor. Specifically, I speculate that the two-second measure acts as an ideal for the experiential (or “real”) measure, and thus—all other factors being equal—we may often be best served by partitioning a song into measure lengths that most closely approximate this two-second window. As I detail below, my approach derives from research on tempo perception, corpus analysis, and my own analyses of popular music. To be clear, I am not advocating for an automatic approach to measure lengths based on absolute time, only that absolute time is one important perceptual marker among many. At the end of the article, I consider meter in pop/rock music somewhat more broadly and offer a few counterexamples, so as to highlight other factors that possibly participate in our sense of bar lengths in this style.
Background Research
[2.1] At a basic level, choosing a time signature involves identifying how many beats are in a bar. Meter perception is thus closely tied to beat perception. In “Norwegian Wood,” for example, do we hear the beat at the
[2.2] Work in the field of cognitive science has implied that a somewhat higher tempo may be more optimal for beat perception. As discussed in London (2012), for example, Fraisse (1982) reports that preferred tempo—i.e., the speed that is neither too fast nor too slow—tends to be around 100 BPM. Parncutt (1994) found a similar result: through a series of tapping experiments, he reported that pulse salience was highest around 100 BPM. Later experiments by Semjen, Vorberg, and Schulze (1998) confirm this rate as a mean tempo for self-paced tapping.
[2.3] In more recent research incorporating popular music, ideal tempo seems to lie higher still. In a meta-analysis of existing experimental studies involving beat perception, Moelants (2002) found that a rate of 120–125 BPM appears to be most preferred. Later in the same article, he confirms this finding via a survey of tempos across a variety of popular music styles. Following up on this work, Moelants and McKinney (2004) report that listeners perceive the most unambiguous tempo ratings for popular music to be around 120 BPM. Specifically, listeners tend to least often tap at different metrical levels when listening to music rated at 120 BPM. Levy (2011), in a study on speed perception, also found that popular music with a tempo of around 115–120 BPM is most often perceived to be neither fast nor slow.
[2.4] The relatively wide range of speeds that has been reported for ideal tempo—almost a rhythmic octave from 70 BPM to 125 BPM—seems somewhat confounding. One explanation for these differences derives from the dissimilar ways that listeners embody tempo. Iyer, for example, describes three separate components of the sensory-motor image associated with rhythm perception: 1) a body-sway, breathing component, 2) a foot-tap, head-bob component, and 3) a finger-tap, speech component (2002, 396). Each component involves different musical correlates and ideal rates. For instance, Iyer reports that body-sway and breathing correspond to the musical phrase, with an ideal rate in the range of 30–60 BPM; foot-tap and head-bob motion correspond to the musical pulse, with an ideal rate in the range of 60–180 BPM; and hand gestures correspond to divisions of the pulse, somewhere in the range of 180–600 BPM (2002, 393).
[2.5] Differences in ideal tempo may also relate to differences in musical style. In his discussion of African-American popular music, Sykes categorizes moderate tempos as those from 93 to 138 BPM (1992, 116). Somewhat similarly, Zeiner-Henriksen reports the normal tempo for club-oriented dance music (i.e., EDM) to be around 120–135 BPM (2010, 12). For listeners more accustomed to Western classical music, these values for moderate or average tempo may seem somewhat high. For example, Willi Apel, in the 1950 printing of the Harvard Dictionary of Music, writes that the “practical limits for the duration of the beat” are between 50–120 BPM, with 60–80 BPM representing “normal” tempo (736). This edition of the Harvard Dictionary of Music pre-dates the birth of rock ‘n’ roll, typically taken to be somewhere around 1955 (Covach 2009), and thus it may be that classical musicians have a different way of conceptualizing or embodying the beat than do rock musicians.
[2.6] For the purposes of this paper, since I deal exclusively with meter and bar lengths in pop/rock music, I take 120 BPM to be the best available approximation of ideal tempo, given a time signature of
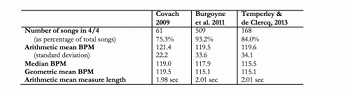
Table 1. Average tempos (measured in beats-per-minute [BPM]) for all songs in which 4/4 was determined to be the main meter, as found in three recent corpora of popular music
(click to enlarge)
[2.7] Recent corpora of popular music also provide evidence for a rate of 120 BPM as the midpoint for tempo in a
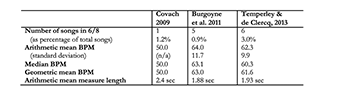
Table 2. Average tempos (measured in beats-per-minute [BPM]) for all songs in which 6/8 was determined to be the main meter, as found in three recent corpora of pop/rock music
(click to enlarge)
[2.8] Interestingly, other time signatures found in these corpora do not show the same average tempo. Table 2, for example, shows that the average tempo for songs in
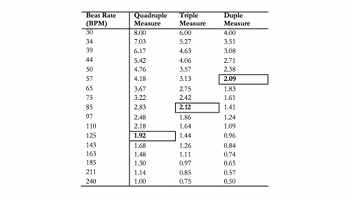
Table 3. Durations in seconds of measures across the usable tempo scale (adapted from London 2012, 46 [Table 2.5])
(click to enlarge)
[2.9] As further evidence of this interplay between absolute time and our perception of measure lengths, consider the data shown in Table 3. The left-hand column of this table shows the range of accepted tempos at which humans can viably feel a beat, spanning from about 30–240 BPM (London 2012, 30). (These BPM values are distributed here on a logarithmic scale, so as to reflect our perception that one tempo will be twice or half the speed of another.) The three right-most columns show the resultant measure lengths for quadruple, triple, and duple meters, given each of these BPM values. Note that a two-second measure lies at the exact geometric midpoint between the longest and shortest possible durations for a measure, given these meter and tempo possibilities. (Eight seconds is exactly four times as long as two seconds, while 0.5 seconds is exactly one fourth as long as two seconds.) Similarly, the calculated durations closest to two seconds—boxed and in bold for each meter—can be seen to optimize the possible values for measure lengths across these three meter types. In other words, while a two-second measure lies somewhat on the shorter side of all possible quadruple measures, it lies somewhat on the longer side of all possible duple measures, and at the midpoint of all possible triple measures. We can also see that at a very fast tempo, a bar of duple meter spans only a very small window of time, probably too small to be a useful cognitive chunk; at a very slow tempo, conversely, a bar of quadruple meter probably spans too much absolute time to be a manageable cognitive chunk.(8) The perception of whether a song is in a duple or quadruple meter, therefore, may shift depending on tempo—all other factors being equal—so as to best partition the music into more normative measure lengths, with the two-second measure appearing to be the most normative partition.
Drum Feels
Example 3a. Kick and snare configuration for a standard rock drum beat
(click to enlarge)
Example 3b. Double-time kick and snare pattern
(click to enlarge)
Example 3c. Half-time kick and snare pattern
(click to enlarge)
[3.1] In order to allow for absolute time to be a factor in measure lengths, we need to uncouple our conception of bar lengths in pop/rock music from the drum beat. One important concept in this paper, accordingly, is that the number of kick and snare instances in a measure may often differ from a standard
Example 4a. “Should I Stay or Should I Go” (The Clash, 1982), verse material
(click to enlarge and listen)
Example 4b. “Should I Stay or Should I Go” (The Clash, 1982), chorus material
(click to enlarge and listen)
[3.2] Some illustrations of these different drum feels should help clarify this concept. Consider, for example, the song “Should I Stay or Should I Go” by The Clash (1982). The verse material of the song (Example 4a) is based on a standard 12-bar blues, embellished via neighbor chords, and the chorus material of the song (Example 4b) retains the same harmonic structure, as well as most of the melodic structure of the verse. Because the harmonic and melodic content is almost identical, it makes sense from the perspective of musical form to retain the same bar lengths in both sections. In the chorus, however, the drum pattern changes such that the kick and snare occur twice as often as in the verse.
[3.3] We could frame the change in the drum pattern in a relative way: the chorus doubles the rate of kick and snare in the verse, and thus the chorus evinces a double-time pattern. But the chorus could also be considered double-time in an absolute way. The tempo of the verse—about 112 BPM—lies just under the ideal tempo mark of 120 BPM for a quadruple meter. This generates measure lengths of about 2.14 seconds, very close to the average time for a bar. From the perspective of absolute time, therefore, it seems sensible to retain these bar lengths in the chorus. In doing so, the 12-bar blues basis of the chorus remains clear, despite the increased activity of the kick and snare.
Example 5a. “Five Minutes to Midnight” (Boys Like Girls, 2006), chorus material
(click to enlarge and listen)
Example 5b. “Five Minutes to Midnight” (Boys Like Girls, 2006), final chorus
(click to enlarge and listen)
Example 6a. “Teardrops on My Guitar” (Taylor Swift, 2008), “pop” version, chorus
(click to enlarge and listen)
Example 6b. “Teardrops on My Guitar” (Taylor Swift, 2006), original version, chorus
(click to enlarge and listen)
[3.4] In other songs, the drum pattern changes to a half-time feel. Consider, for example, the song “Five Minutes to Midnight” by Boys Like Girls (2006). The chorus (Example 5a) employs a standard drum beat, with a tempo of approximately 164 BPM and bar lengths around 1.46 seconds. At the end of the song, the drum pattern changes dramatically (Example 5b), even though the rest of the music (e.g., harmony and melody) stays generally the same. Because the harmony and melody do not change significantly, it seems sensible from the perspective of form (as in “Should I Stay or Should I Go”) to retain the same bar lengths in this final chorus as in the other chorus sections. If we retain the same time signature, which seems appropriate to maintain the same notational look-and-feel as the original chorus, the snare drum in the final chorus no longer occurs on beats 2 and 4 (the normal backbeats) but rather with any regularity only on beat 3: i.e., a half-time pattern. We could also maintain the same bar lengths by notating the final chorus in
[3.5] Double-time and half-time relationships are fairly clear when they occur within a single song, because we are compelled to compare the drum pattern from one passage to the original or prevailing drum pattern in the same song. Some readers may be under the assumption, consequently, that “double-time” and “half-time” are terms that only describe relationships between drum patterns within a song. In the next set of examples, I show that these drum feels can exist between songs, such that no part of one song exhibits a normal-time drum feel. The song “Teardrops on My Guitar” by Taylor Swift (2006), for instance, was released in multiple versions, all of which have the same harmony and melody but different instrumentations. The “pop” version (Example 6a), released as a bonus track on the 2008 reissue of the album Taylor Swift, conveys a normal
[3.6] The rate of kick and snare alternations in the original version (track 3 on the 2006 release of the same album) is noticeably slower. In Example 6b, I have notated the original version as a half-time feel. This seems like the most sensible choice, because it retains the same harmonic and melodic content per bar as the pop version. It is also the most sensible solution based on absolute time: had I based measure lengths on the standard rock drum beat, bar lengths would have bloomed to 4.8 seconds each. It would have been possible to notate the original version as a normal feel, with the pop version as a double-time feel; this approach would derive from using drum feels in a relative way, since the original version could be considered the main version, against which other versions would be compared. Had we done so, however, the chorus would be only four bars long, which seems far too short for a full-fledged chorus. Listening to the entire song, it seems clear that the music in Examples 6a and 6b comprises the full chorus section. The original version, therefore, makes more sense as a half-time feel in an absolute way, even if we had never heard the pop version as a normal-time reference.
Example 7a. “Wrecking Ball” (Miley Cyrus, 2013), chorus material
(click to enlarge and listen)
Example 7b. “Wrecking Ball” (The Gregory Brothers, 2014), chorus material
(click to enlarge and listen)
Example 7c. “Wrecking Ball” (Daja, 2014), standard feel
[3.7] The opportunity to compare different drum feels in different versions of the same song by the same artist is somewhat rare, since artists do not often release multiple versions of the same song. Different artists, however, often release different versions of the same song, i.e., a cover version. In a cover song, one aspect that might change is the drum feel. This is the case with the song “Wrecking Ball,” originally recorded by Miley Cyrus (2013) and covered a year later by The Gregory Brothers in a country version (2014). The Miley Cyrus version (Example 7a) presents a clear example of a half-time feel, in my opinion, with kick-snare alternations occurring at 60 BPM. (As a result, some listeners may find themselves tapping at a rate of 120 BPM.) In transcribing the cover version by the Gregory Brothers (Example 7b), it seems logical to retain the same harmonic and melodic material per bar as the original, as I have done. The Gregory Brothers version lacks a traditional kick-snare alternation, but the bass guitar seems to take on the role of the kick while the accents in the brushed snare part suggest the backbeat. Using this approach, the Gregory Brothers version conveys a double-time feel. A standard-feel version of the song can be heard in the version recorded by Daja (Example 7c).
[3.8] These examples may not fully convince the reader that half-time and double-time feels necessarily operate in absolute ways. When comparing two songs, we can always frame the relationship in a relative way. That said, I hope to have demonstrated at least one important idea: that it is often useful to view the drum pattern of a song as non-congruent with a standard (or normal) feel. Further evidence for considering drum feels in an absolute way will be provided in the following section.
Using Absolute Time in Analysis
[4.1] The pairs of examples discussed above were obviously related, so we did not necessarily need the concept of absolute time to show similarities. When songs are less obviously related, however, the consideration of absolute time can be especially helpful to expose connections that would be otherwise hidden or obscured. In the paragraphs that follow, I illustrate the types of structural relationships that can be gleaned via a number of song comparisons.
Example 8a. “When the Levee Breaks” (Led Zeppelin, 1971), opening drum beat
Example 8b. “When the Levee Breaks” (Led Zeppelin, 1971), 6-bar reading of opening vocal passage
(click to enlarge and listen)
[4.2] A good starting example is the song “When the Levee Breaks,” since it involves versions that we know to be at least somewhat related. The original recording is a 1920s-era blues song by Kansas Joe McCoy and Memphis Minnie, although most readers are probably more familiar with Led Zeppelin’s 1971 recording. I urge the reader here to listen to the opening of the Led Zeppelin version (Example 8a) and decide when and how often bar lines occur. How many bars long, for instance, is the opening drum beat, before the guitars and blues harp enter?
[4.3] Following the traditional approach to meter in pop/rock music, in which the backbeat aligns with beats 2 and 4 in a bar of
[4.4] If we acknowledge that the drum beat may not necessarily be a standard feel, however, we potentially arrive at a different metric analysis of the Led Zeppelin version. In particular, the tempo implied by the kick and snare alternations—around 72 BPM—lies well below the ideal tempo for a quadruple meter. The rubric of absolute time thus implies that the main drum beat for the Led Zeppelin version might better be considered a duple or half-time feel. As with most half-time feels, listeners may find themselves conflicted when listening to Led Zeppelin’s version as to whether to synchronize body movements with the hi-hat or the kick/snare alternation.
Example 8c. “When the Levee Breaks” 12-bar blues reading of original song (Kansas City Joe and Memphis Minnie, 1929) mashed-up with Led Zeppelin drum beat
(click to enlarge and listen)
[4.5] Reading the drum beat of the Led Zeppelin version as a half-time feel has important ramifications for our analysis of the song, in that it engenders a 12-bar length for the main vocal material. A standard 12-bar blues pattern is still not fully clear, since the Led Zeppelin version has no chord changes during the verse. But it is not too difficult to imagine a re-harmonization of Led Zeppelin’s version that re-establishes the harmonic scheme of a standard 12-bar blues. To illustrate this, I have mashed-up the original version of the song with the Led Zeppelin drum beat in Example 8c.(12) In this mash-up, the vocal phrase lengths in the Led Zeppelin version—assuming we want to retain a correspondence in form with the original song—should each span about two bars, ending on the downbeat of the third bar in each four-bar hypermetric unit. This is a standard vocal phrase structure for 12-bar blues songs, as described in Stoia 2013. Thus while it is undeniable that Led Zeppelin have radically altered the original song, in my interpretation they have not entirely abandoned the strophic 12-bar blues format. They have, however, significantly changed the “feel” of the song.
Example 9a. “Heartbreak Hotel” (Elvis Presley, 1956), main material
(click to enlarge and listen)
[4.6] As this last comparison shows, our method for determining measure lengths affects how we view the relationship between a song and its formal prototype. To further elucidate this point, let us compare two songs by Elvis Presley, “Heartbreak Hotel” (1956) and “That’s All Right” (1954), both of which can be considered blues-based songs. The meter of “Heartbreak Hotel” is relatively clear. Covach (2009, 102), for example, views the main material as an 8-bar passage in
[4.7] Covach notes that “That’s All Right” is also derived from the blues (2009, 104). Perhaps because this song has a fast backbeat, Covach posits a duple meter (
Example 9b. “That’s All Right (Elvis Presley, 1954), main material
(click to enlarge and listen)
[4.8] If we reassess the bar lengths of “That’s All Right” based on absolute time, however, we uncover a different relationship between this song and the blues. As shown in Example 9b, the main material of “That’s All Right” can be understood instead as a 9-bar span, in which the fast backbeat conveys a double-time feel, with measure lengths around 2.3 seconds. The reader should compare “Heartbreak Hotel” (Example 9a) to this new reading of “That’s All Right.” Despite significant differences in surface rhythms, the two songs disburse highly similar formal structures over the course of absolute time. In terms of harmony, for example, both songs have four bars of tonic, followed by two bars of subdominant, then a move to the dominant—which is expanded in “That’s All Right” by a bar—and a single final bar of tonic. In terms of melodic structure, both songs exhibit a
Example 10a. “Down to the River” (Buck Owens, 1962), verse
(click to enlarge and listen)
Example 10b. “Cryin’ Time” (Buck Owens, 1964), verse
(click to enlarge and listen)
Example 10c. Shared voice-leading scheme for verse sections of “Down to the River” and “Cryin’ Time” (Buck Owens)
(click to enlarge)
[4.9] In addition to relating songs to established prototypes such as the blues, absolute time can also help uncover new prototypical organizational schemes in pop/rock music. Two songs by Buck Owens are pertinent in this regard. Consider the verse material from the song “Down to the River” (1962). As transcribed in Example 10a, the verse can be viewed in a quadruple meter. The kick and snare alternations occur at a rate of about 148 BPM; measure lengths, given four beats in the bar, are thus about 1.62 seconds, which is the closest reading to the two-second ideal. The song has a swing feel, so
[4.10] I have transcribed the verse material from the other Buck Owens song, “Cryin’ Time” (1964), in Example 10b. “Cryin’ Time” has the same swing feel as “Down to the River,” but at a much slower tempo. Based on the kick and snare alterations, the tempo is somewhere around 76 BPM. If we assume a quadruple meter, i.e., a slow
[4.11] Note that while “Down to the River” and “Cryin’ Time” have very different rhythmic feels, both songs disburse highly similar harmonic and melodic content at roughly the same pace. Each melodic phrase, for example, spans from the first bar of one four-bar phrase to about the downbeat of the third. Moreover, we can abstract a generic voice-leading scheme that the two songs share, as shown in Example 10c. The first eight bars consist of a double-neighbor figure: in the melody over a tonic harmony falls to over a dominant in the third bar; the melody rises to the chordal seventh of the dominant in bar 5 and then resolves back to in bar 7. In the third hypermeasure, the melody rises to over tonic, which begins a descent through over the subdominant in bar 11, followed by cadential motion in bars 13 and 14, which resolves via a perfect authentic cadence on the downbeat of bar 15. This sequence is a highly determined musical skeleton, not only in terms of the harmonic and melodic content, but also the rate at which this content plays out over absolute time, despite the different metric settings.
Example 11a. “Honey (I Miss You)” (Bobby Goldsboro, 1968), verse material
(click to enlarge and listen)
Example 11b. “Gentle on My Mind” (Glen Campbell, 1967), verse material
(click to enlarge and listen)
[4.12] The 8-bar double-neighbor figure that begins the verses of both “Down to the River” and “Cryin’ Time” is a relatively common melodic-harmonic structure in the songs of Buck Owens.(13) Similar 8-bar melodic-harmonic schemes can be found in other country songs as well, such as “Honey (I Miss You)” by Bobby Goldsboro (1968). Deducing bar lengths in “Honey (I Miss You)” is relatively straightforward, as shown in Example 11a. There is no clearly-audible kick drum, but accents on the snare convey a backbeat on beats 2 and 4 at a tempo of about 92 BPM, which implies bar lengths in a quadruple meter of about 2.6 seconds. The pitch and phrase structure of the melody here should remind the reader of the first eight bars in the two previous Buck Owens examples. The harmonic content is somewhat different, admittedly, but only in that the dominant chord is embellished via a toggling between ii and V.
[4.13] This particular variant of the 8-bar double-neighbor figure can be found in many popular songs.(14) Of these, “Gentle on My Mind” (Glen Campbell, 1967) is an especially relevant example, since its relationship to this variant is predicated on viewing its metric structure through the lens of absolute time. As can be heard in the audio portion of Example 11b, the rhythmic feel of “Gentle on My Mind” is both similar to and different from “Honey (I Miss You)”: both songs have a persistent brushed snare drum part, but the brushed snares in “Gentle On My Mind” chug along at a fast pace, in contrast to the slowly brushed snares in “Honey (I Miss You).” We can thus posit that “Gentle on My Mind” evinces a double-time feel, such that the snare accents occur not on beats 2 and 4 but rather on the “ands” of each beat, as shown in Example 11b. Reading “Gentle on My Mind” as a double-time feel, its main material spans 8 bars and can be seen to share much in common with the 8-bar double-neighbor figure variant of “Honey (I Miss You),” including the same melodic phrase lengths. The exact pitch content is slightly different; “Gentle on My Mind” sits on the supertonic for an extended period of time before progressing to the cadential dominant. But the essential melodic-harmonic framework of the double-neighbor figure should be clear.
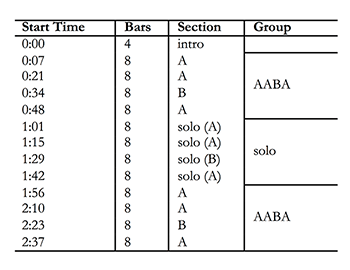
Table 4. Form of “Hey, Good Lookin’” (Hank Williams, 1951)
(click to enlarge)
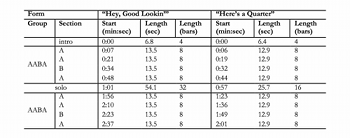
[4.14] As these last examples show, absolute time helps uncover structural similarities between songs that many not have the exact same rhythmic framework. To extend this point one step further, let us compare the rhythmic and large-scale organization of two songs: “Hey, Good Lookin’” by Hank Williams (1951) and “Here’s a Quarter (Call Someone Who Cares)” by Travis Tritt (1991). As shown in Table 4, “Hey, Good Lookin’” evinces a prototypical 32-bar AABA form commonly found in songs from the early years of rock music.(15) Transcriptions and audio files of the AA and BA portions of the form can be found in Examples 12a and 12b, respectively. The drums in this early 1950s-era recording are somewhat hard to hear, but there is a clear and strong backbeat that conveys a bouncing tempo of about 140 BPM. The best time signature for “Hey, Good Lookin’” would perhaps be
|
Example 12a. “Hey, Good Lookin’” (Hank Williams, 1951), AA sections (click to enlarge and listen) |
Example 12b. “Hey, Good Lookin’” (Hank Williams, 1951), BA sections (click to enlarge and listen) |
[4.15] With “Hey, Good Lookin’” in mind, the reader should listen to the opening vocal passage—before the drums come in—of “Here’s a Quarter (Call Someone Who Cares),” as provided in Example 13a. I hear this passage in a triple meter with swing, so I have transcribed it in
|
Example 13a. “Here’s a Quarter (Call Someone Who Cares)” (Travis Tritt, 1991), part 1 (click to enlarge and listen) |
Example 13b. “Here’s a Quarter (Call Someone Who Cares)” (Travis Tritt, 1991), part 2 (click to enlarge and listen) |
Table 5. Comparison of section lengths between “Hey, Good Lookin’” (Hank Williams, 1951) and “Here’s a Quarter (Call Someone Who Cares)” (Travis Tritt, 1991)
(click to enlarge)
[4.16] Based on a hearing of “Here’s a Quarter” as a half-time
Other Factors in Determining Bar Lengths and Meter (Counterexamples)
[5.1] As I hope I have shown, it is useful to consider the speed or “feel” of the drums as a separate aspect of a song from the rate of change in harmonic and melodic content, i.e., form. Of these two aspects—drum feel and harmonic/melodic content—I believe bar lengths should represent the latter rather than the former. The reader should not misconstrue my argument thus far, however, as implying that the rate of change in harmonic and melodic content is necessarily determined by absolute time, but rather that it often occurs at a more moderate pace than the rate implied by the drum pattern. That said, some songs are indeed slow, both in terms of drum pattern and harmonic/melodic content, just as other songs are indeed fast. Unfortunately, I cannot offer a comprehensive method on how to distinguish between a song with a slow pacing of harmonic-melodic content versus a song with a medium pacing of harmonic-melodic content and a slow drum pattern. Nonetheless, I will touch on a few factors here, other than absolute time, that could affect how we view bar lengths and meter in pop/rock music.
Example 14. “He Stopped Loving Her Today” (George Jones, 1980)
(click to enlarge and listen)
[5.2] In the song examples above, taking absolute time into account revealed similar rates of harmonic rhythm despite differences in the drum pattern. Harmonic rhythm may therefore also be an important factor in determining measure lengths. Moore, for example, states that rock songs tend to change chords every bar (2001, 42), and so we might optimize measure lengths to obtain a moderate rate of chord change. Consider, for instance, the song “He Stopped Loving Her Today” by George Jones (1980), as provided in Example 14. The song has an undeniably slow feel, and my impression of its tempo is that it lies around 72 BPM. This is the same BPM value that engendered a half-time reading of Led Zeppelin’s version of “When the Levee Breaks.” My hearing of “He Stopped Loving Her Today,” however, is not as a half-time song, but instead as just a slow song. While it is difficult to fully justify this differentiation, I believe that harmonic rhythm is one important factor. Had I heard “He Stopped Loving Her Today” as a half-time
Example 15. “You Shook Me” (Led Zeppelin, 1969)
[5.3] In previous examples, considering absolute time revealed similar forms between songs with dissimilar drum patterns. Form is thus another factor that may influence determinations of bar lengths. “You Shook Me” (Led Zeppelin, 1969) is a good example in this regard. The main material of the song (Example 15) is a slow shuffle feel, with kick and snare alternations that convey a tempo of about 55 BPM. Taking absolute time as the only factor, I would assign the song to a duple meter, i.e.,
Example 16a. “Sitting on Top of the World” (Grateful Dead, 1967)
(click to enlarge and listen)
Example 16b. “Sittin’ on Top of the World” (Cream, 1968)
(click to enlarge and listen)
[5.4] As a final counterexample, I will discuss two versions of the song “Sitting on Top of the World.” In his survey of tempos across 570 rock songs, Walter Everett notes that the Grateful Dead version (1967) is one of the fastest songs at 252 BPM, whereas the Cream version (1968) is one of the slowest at 44 BPM (Everett 2009, 322). This wide disparity in tempos for different versions of the same song is intriguing, and it is worth more closely investigating how this disparity arises. The Grateful Dead version (Example 16a) has a quick alternation between kick and snare, which—as noted by Everett—conveys a tempo of about 252 BPM. It is doubtful, however, that most listeners foot-tap or head-bob along at this rate, since it is too fast to be comfortable for any extended period of time. As a result, I posit that the Grateful Dead version is a typical double-time feel, with the primary tactus closer to 126 BPM and measure lengths as shown in Example 16a. The Cream version (Example 16b) is undoubtedly much slower. The rate of the kick and snare alternation is indeed somewhere around 44 BPM, as Everett notes. But while this tempo might imply a duple meter via the rubric of absolute time, I have transcribed Example 16b as a quadruple meter in order to align the pacing of its harmonic and melodic content with the Grateful Dead version in Example 16a. (The lyrics of the two versions are rather different, so I could not choose an exactly corresponding passage.) I have thus, in my transcription of the Cream version, invoked factors other than absolute time to determine measure lengths: harmony, form, and melodic structure.
[5.5] Overall, we have two conflicting gauges of tempo in the two versions of “Sitting on Top of the World.” By the rubric of the drum pattern alone, the Grateful Dead version is about six times as fast as the Cream version (252 BPM versus 44 BPM). But by the rubric of measure lengths, i.e., the passage of harmonic and melodic content over time, the Grateful Dead version is only about three times as fast as the Cream version (1.90-second measures versus 5.45-second measures). We thus find evidence here again that the speed of the kick and snare alternations should be considered as distinct from the rate of change in harmonic and melodic content.
[5.6] In summary, I do not claim that we must always tether measure lengths to a two-second ideal. I do assert, however, that we should have good reasons—apart from the drum pattern—for not doing so. Examining how other factors play into our perception and conception of bar lengths and meter in popular music is a topic well worth exploring in future work.
Conclusion
[6.1] Historically speaking, absolute time is well known to have influenced the overall length of pop/rock songs. During the early years of rock, individual songs (“singles”) were released on vinyl records, typically 7-inch, 45-RPM discs, which—due to sound quality issues—could not generally exceed more than about five minutes (Everett 2009, 326). Despite the fact that singles are now no longer tied to any physical medium, the lengths of popular songs have not dramatically changed. (Songs may be somewhat longer now than in the 1950s, but 10-minute pop songs are still extremely rare.) Given that absolute time affects not only overall song length but also our perception of beats, as discussed above, it seems reasonable to assume that absolute time also shapes in some way our perception of intermediate levels in the metric hierarchy.
[6.2] My goal in this essay was to convince the reader of three main points: 1) that the drum pattern is not a reliable or consistently appropriate guide by which to determine measure lengths; 2) that absolute time is worth considering as a factor when determining measure lengths; and 3) that the two-second measure length may be the ideal perceptual reference point by which measure lengths in popular music can be assessed on this basis. I admit that factors other than absolute time, such as harmonic rhythm and formal prototypes, are central to our conception of measure lengths. Nonetheless, pop/rock music—perhaps because it is primarily a vocal medium, and speech declamation rates are somewhat limited given the confines of intelligibility—often exhibits a consistent and moderate pacing of harmonic and melodic content, i.e. form, that is relatively stable in terms of absolute time, despite the rhythmic framework implied by the drum pattern or other percussion.
Example 17a. “The Shortest Straw” (Metallica, 1988), heavy metal double-time feel
Example 17b. “I Don’t Wanna Hear It” (Minor Threat, 1984), punk double-time feel
Example 17c. “My All” (Mariah Carey, 1997), R&B half-time feel
Example 17d. “About the Money” (T.I., 2014), southern rap half-time feel
[6.3] One concept that helps unlink the drum pattern from measure lengths is the notion of different “feels,” such as half-time and double-time. Many of the examples I presented above were drawn from the early years of pop/rock music, especially blues and country. I used examples from these styles primarily because they most clearly support my argument. The reader should not assume, however, that the ideas in this paper apply only to this limited range of styles. In fact, many styles appear to utilize drum feels in consistent and characteristic ways. Double-time feels, for example, are relatively common in heavy metal (Example 17a) and punk (Example 17b), while half-time feels are relatively common in R&B (Example 17c) and southern rap (Example 17d).
[6.4] I began this essay with a question about the best meter for “Norwegian Wood” (Example 1), but the question was never resolved. Of the possible readings—
Trevor de Clercq
Middle Tennessee State University
Department of Recording Industry
1301 East Main Street, Box 21
Murfreesboro, TN 37132
trevor.declercq@mtsu.edu
Works Cited
Apel, Willi. 1950. The Harvard Dictionary of Music. Harvard University Press.
Biamonte, Nicole. 2014. “Formal Functions of Metric Dissonance in Rock Music.” Music Theory Online 20 (2).
Burgoyne, John, Jonathan Wild, and Ichiro Fujinaga. 2011. “An Expert Ground-Truth Set for Audio Chord Recognition and Music Analysis.” 12th International Society for Music Information Retrieval Conference (ISMIR).
Butler, Mark J. 2001. “Turning the Beat Around: Reinterpretation, Metrical Dissonance, and Asymmetry in Electronic Dance Music.” Music Theory Online 7 (6).
Caplin, William. 1998. Classical Form: A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven. Oxford University Press.
Cohn, Richard. 2015. “Why We Don’t Teach Meter, and Why We Should.” Keynote presentation at the Music Theory Midwest Conference, Rochester, MI.
Covach, John. 2006. “From ‘Craft’ to ‘Art’: Formal Structure in the Music of the Beatles.” In Reading the Beatles: Cultural Studies, Literary Criticism, and the Fab Four, ed. Kenneth Womack and Todd Davis, 37–53. SUNY Albany Press.
—————. 2009. What’s That Sound? An Introduction to Rock and Its History. 2nd ed. W. W. Norton.
Danielsen, Anne. 2006. Presence and Pleasure: The Funk Grooves of James Brown and Parliament. Wesleyan University Press.
—————. 2010a. “Introduction: Rhythm in the Age of Digital Reproduction.” In Musical Rhythm in the Age of Digital Reproduction, ed. Anne Danielsen, 1–16. Ashgate Publishing.
—————. 2010b. “Here, There and Everywhere: Three Accounts of Pulse in D’Angelo’s ‘Left and Right’.” In Musical Rhythm in the Age of Digital Reproduction, ed. Anne Danielsen, 19–35. Ashgate Publishing.
—————. 2015. “Metrical Ambiguity or Microrhythmic Flexibility? Analysing Groove in ‘Nasty Girl’ by Destiny’s Child.” In Song Interpretation in 21st-Century Pop Music, ed. Ralf von Appen, André Doehring, Dietrich Helms, and Allan F. Moore, 53–71. Ashgate Publishing.
Everett, Walter. 2001. The Beatles as Musicians: The Quarry Men through Rubber Soul. Oxford University Press.
—————. 2009. The Foundations of Rock: From “Blue Suede Shoes” to “Suite: Judy Blue Eyes.” Oxford University Press.
Fraisse, Paul. 1982. “Rhythm and Tempo.” In The Psychology of Music, ed. Diana Deutsch, 149–80. Academic Press.
Hasty, Christopher. 1997. Meter as Rhythm. Oxford University Press.
Headlam, Dave. 1995. “Does the Song Remain the Same? Questions of Authorship and Identification in the Music of Led Zeppelin.” In Concert Music, Rock, and Jazz Since 1945: Essays and Analytical Studies, ed. Elizabeth W. Marvin and Richard Hermann, 313–63. University of Rochester Press.
Iyer, Vijay. 2002. “Embodied Mind, Situated Cognition, and Expressive Microtiming in African-American Music.” Music Perception 19(3): 387–414.
Krebs, Harald. 1999. Fantasy Pieces: Metrical Dissonance in the Music of Robert Schumann. Oxford University Press.
Lerdahl, Fred and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. MIT Press.
Lester, Joel. 1986. The Rhythms of Tonal Music. Pendragon Press.
Levy, Mark. 2011. “Improving Perceptual Tempo Estimation with Crowd-Sourced Annotations.” 12th International Society for Music Information Retrieval Conference (ISMIR), 317–22.
London, Justin. 2012. Hearing in Time: Psychological Aspects of Musical Meter. 2nd ed. Oxford University Press.
Mattingly, Rick. 2006. All About Drums: A Fun and Simple Guide to Playing Drums. Hal Leonard Corporation.
McCandless, Gregory. 2013. “Metal as a Gradual Process: Additive Rhythmic Features in the Music of Dream Theater.” Music Theory Online 19 (2).
Miller, Clement. 1968. “Gaffurius’s ‘Practica Musicae’: Origin and Contents. Musica Disciplina 22: 105–28.
Moelants, Dirk. 2002. “Preferred Tempo Reconsidered.” 7th International Conference on Music Perception and Cognition, 580–83.
Moelants, Dirk and Martin McKinney. 2004. “Tempo Perception and Musical Content: What Makes a Piece Fast, Slow, or Temporally Ambiguous?” 8th International Conference on Music Perception and Cognition, 558–62.
Moore, Allan. 2001. Rock: The Primary Text: Developing a Musicology of Rock. 2nd ed. Ashgate.
Osborn, Brad. 2010. “Beats that Commute: Algebraic and Kinesthetic Models for Math-Rock Grooves.” Gamut 3 (1): 43–68.
—————. 2014. “Kid Algebra: Radiohead’s Euclidian and Maximally Even Rhythms.” Perspectives of New Music 52: 1–25.
Parncutt, Richard. 1994. “A Perceptual Model of Pulse Salience and Metrical Accents in Musical Rhythms.” Music Perception 11 (4): 409–64.
Pieslak, Jonathan. 2007. “Re-casting Metal: Rhythm and Meter in the Music of Meshuggah.” Music Theory Spectrum 29 (2): 219–45.
Pollack, Alan. 1993-1999. “Notes on... Series.” Available at http://www.recmusicbeatles.com/public/files/awp/awp.html
Rosenberg, Nancy. 2011. “Popular Music in the College Music Theory Class: Rhythm and Meter.” In Pop-culture Pedagogy in the Music Classroom, ed. Nicole Biamonte, 47–71. Scarecrow Press.
Rothstein, William. [1989] 2007. Phrase Rhythm in Tonal Music. Musicalia Press.
Semjen, Andras, Dirk Vorberg, and Hans-Henning Schulze. 1998. “Getting synchronized with the metronome: Comparisons between phase and period correction.” Psychological Research 61 (1): 44–55.
Snyder, Bob. 2000. Music and Memory: An Introduction. MIT Press.
Stephenson, Ken. 2002. What to Listen for in Rock: A Stylistic Analysis. Yale University Press.
Stoia, Nicholas. 2013. “The Common Stock of Schemes in Early Blues and Country Music.” Music Theory Spectrum 35 (2): 194–234.
Summach, Jay. 2011. “The Structure, Function, and Genesis of the Prechorus.” Music Theory Online 17 (3).
Sykes, Charles. 1992. “A Conceptual Model for Analyzing Rhythmic Structure in African-American Popular Music.” Ed.D. dissertation, Indiana University.
Tamlyn, Garry. 1998. “The Big Beat: Origins and Development of Snare Backbeat and Other Accompanimental Rhythms in Rock ‘n’ Roll.” Ph.D. dissertation, University of Liverpool.
Temperley, David. 2001. The Cognition of Basic Musical Structures. MIT Press.
Temperley, David and Trevor de Clercq. 2013. “Statistical Analysis of Harmony and Melody in Rock Music.” Journal of New Music Research 42 (3): 187–204.
Zeiner-Henriksen, Hans. 2010. “The ‘PoumTchak’ Pattern: Correspondences Between Rhythm, Sound, and Movement in Electronic Dance Music.” Ph.D. dissertation, University of Oslo.
Footnotes
1. Moore writes, “the consistent appearance of a snare drum on the second and fourth beats of a bar allows this length [the bar] to be standardized” (2001, 42). Stephenson writes that “in rock, steady backbeats (beats 2 and 4) on the snare drum usually help make the length of a measure clear” (2002, 2).
Return to text
2. Drum beats in this paper are represented in the conventional manner, with the kick on the lowest space of a 5-line staff, the snare on the second-highest space, and the hi-hat above the top line.
Return to text
3. See Tamlyn 1998, which not only surveys the origins of backbeat patterns in rock music from jazz and swing-era drumming, but also discusses the variations in snare patterns around the backbeat framework.
Return to text
4. Moore, for example, writes: “In a music that is not notated, how long is a ‘bar’ (or, for that matter, any other transferable unit)? Ultimately, of course, it hardly matters, except to enable communication about rhythm to take place” (2001, 42).
Return to text
5. The only exception I have found is Image-Line Fruity Loops, which has a default session tempo of 140 BPM.
Return to text
6. The corpora for Burgoyne, Wild, and Fujinaga (2011) and Temperley and de Clercq (2013) are freely available online, at http://ddmal.music.mcgill.ca/billboard and http://rockcorpus.midside.com, respectively. The corpus for Covach was compiled by hand from the analyses in his 2009 textbook.
Return to text
7. Covach is the only analyst to use a
Return to text
8. Evidence that absolute time plays into our perceptual chunking of music—in terms of event fusion, melodic and rhythmic grouping, and form—is reviewed in Snyder 2000.
Return to text
9. Following Danielsen (2006, 2010a, 2010b, 2015), the pulse layer implied by the time signature and various rhythmic events thus acts as a reference structure, which the kick and snare play against in a half-time or double-time feel.
Return to text
10. The notion that two levels in the metric hierarchy may vie for the designation of tactus is not new. Lerdahl and Jackendoff, for example, appear to concede that a listener might hear the tactus on two metric levels. They write, “the listener tends to focus primarily on one (or two) intermediate level(s) in which the beats pass by at a moderate rate.... we call such a level the tactus” (1983, 21).
Return to text
11. For the purposes of this analysis, I am ignoring the short instrumental tag or link that separates each verse.
Return to text
12. Some tempo and pitch modifications were necessary to align the two songs, of course.
Return to text
13. Other Buck Owens songs with verses that feature the 8-bar double-neighbor pattern (allowing for some variation) include “Nobody’s Fool But Yours” (1962), “Fool Me Again” (1962), “My Heart Skips a Beat” (1964), and “If You Fall Out of Love With Me” (1965).
Return to text
14. Other songs with passages that evince this prototypical structure include “Little Green Apples” by Roger Miller (1968), “A Better Man” by Clint Black (1989), “I May Hate Myself in the Morning” by Lee Ann Womack (2005), and “Just Got Started Lovin’ You” by James Otto (2008).
Return to text
15. Covach (2009, 42) analyzes this song as a prototypical AABA form. Other AABA exemplars from 1957 alone include “Butterfly” by Andy Williams, “Everyday” by Buddy Holly, “Great Balls of Fire” by Jerry Lee Lewis, “You Don’t Owe Me a Thing” by Johnnie Ray, and “Come Go with Me” by The Del-Vikings.
Return to text
Copyright Statement
Copyright © 2016 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
16531