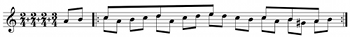Cohn’s Platonic Model and the Regular Irregularities of Recent Popular Multimedia
Scott Murphy
REFERENCE: http://mtosmt.org/issues/mto.16.22.2/mto.16.22.2.cohn.html
KEYWORDS: asymmetrical meter, syncopation, film music, television music, popular music
ABSTRACT: Richard Cohn’s Platonic model of funky rhythms can be converted into a property that closely matches the asymmetrical temporal successions that most frequently occur in recent popular English-language multimedia. In the case of quintuple and septuple meters, this property also closely matches successions that most frequently occur in other forms of popular music as well. The movies from which the evidence for this claim comes range from The Magnificent Seven of 1960 to Kung Fu Panda 3 of 2016. Some short but close analyses of filmic scenes demonstrate this property's effectiveness as a hermeneutical tool. A related property of “near realization” recruits Christopher Hasty’s projective model to explain this stylistic bias, and connects these asymmetrical successions with another seemingly dissimilar class of syncopated rhythms favored in popular music.
Copyright © 2016 Society for Music Theory
I. A Stylistic Generalization
[1.1] Cohn’s recent article (2016) explores the phenomenon whereby a series of triple durations—like a succession of dotted quarter notes, or an iterated pattern of three eighth notes—unfolds over, and then reconciles with, a pure duple meter—like 2/4 or 4/4. He analogizes this phenomenon to a succession of pure 3:2 fifths that, courtesy of 2:1 octave equivalence, can almost, but inescapably never exactly, return to its starting point. On one end of Western music’s timeline, he finds this analogy among others in ideas attributed to Plato, including the notion that 3-generated successions exhibit a centrifugal aspect and 2-generated successions exhibit a centripetal aspect. On the timeline’s other end and on the other side of the earth, he finds examples—and cites scholars who have found examples—of these “funky rhythms” in a wide variety of primarily American popular musical styles from ragtime to twenty-first-century pop.(1)
[1.2] At the least, this article adds another American popular musical style to this list: recent popular English-language multimedia, or “RPELM” for convenience. (By “recent,” I mean since 1960, but especially since 1990. By “English-language,” I mean mostly North American, and mostly from Hollywood. By “multimedia,” I mean mostly dramatic film and some television.) But, moreover, as Cohn’s model can subsume examples from another style, a generalized approach to time’s divisions can subsume Cohn’s model. More precisely, this article investigates RPELM’s use of what could be called asymmetrical meters or syncopated rhythms. It recognizes that a property that inheres in the funky rhythms that Cohn models also inheres in a kind of asymmetrical meter or syncopated rhythm that occurs more frequently in RPELM than other kinds. Importantly, this property more closely matches this stylistic bias—to which the word “regular” of my title refers—more than other previously proposed properties of temporal organization.
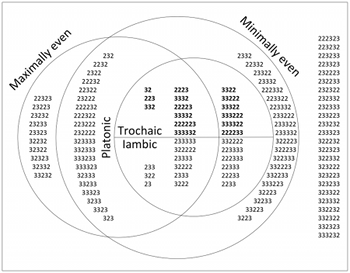
Figure 1. An Euler diagram showing successions of two to six durations of 2s or 3s and some of the features they possess
(click to enlarge)
[1.3] Figure 1 helps to show this. Each one of the 104 series of numbers in Figure 1 is a temporally ordered succession of contiguous durations.(2) I use the term “durations” rather than “time spans” or “inter-onset intervals” because, while they generally match onsets on a musical surface, they do not necessarily match all such onsets, nor do the surface’s onsets necessarily match all of the succession’s durations, as I will suggest later. Each duration is either two (2) or three (3) times the length of a durational unit. Figure 1 displays only successions with no fewer than two durations and no more than six durations, but this limitation is mostly pragmatic. Furthermore, Figure 1 displays no succession that is rotationally invariant, although it may be a subset or superset of a succession that is rotationally invariant. In other words, Figure 1 excludes successions entirely generated by one or more repetitions of a smaller succession, such as 22 (2×2), 333 (3×3), 332332 (332×2), 323232 (32×3), and so forth. The purpose of this exclusion is to focus on divisions of time that lack this rotational invariance among their 2s and 3s—the “irregularities” of my title, and the “asymmetries” described above and below.(3)
[1.4] I use the expression “succession of durations” to leave its series of quantities open to an interpretation either as a layer in a meter or as a rhythm. On the one hand, with a limitation to durations of 2 and 3, each of these duration successions conforms to a well-formedness rule for a metrical layer.(4) The metrical hierarchy that includes this asymmetrical layer has at least two other layers. There is a faster “unit” layer, assumed to be either overt or clearly implied, that divides time evenly into unit durations. There is also a slower “measure” layer that divides time evenly, such that the onset of the first duration of the asymmetrical layer is on a downbeat.(5) Depending upon the number of unit durations in the measure, there may also be additional metrical layers in between the asymmetrical layer and the measure layer. Some scholarship on asymmetrical meter has paid attention to this “subcycle” region of the metric hierarchy, but, in generalizing about RPELM’s asymmetrical meters, I find such attention to be largely unprofitable, as I will demonstrate later. The group of examples that follow tolerate a tempo range for this metric hierarchy that is fairly wide, although not indiscriminately so: the unit duration stretches from 120 to 500 ms, and the measure duration extends from 2000 to 4600 ms.
[1.5] On the other hand, these duration successions could also be interpreted as rhythms, especially when concurrent with a clear metrical grid, such as the pure duple meters of the examples from Cohn’s article. A focus on successions with durations only of 2 or 3 units has an additional benefit of providing a set of rhythmic prototypes, which may or may not also be understood metrically. An analogy using pitch structures can demonstrate this benefit. Dmitri Tymoczko’s (2004) seven “Pressing scales” are the only scales in 12-note equal temperament that meet two criteria: 1. each has no consecutive semitones, and 2. each is not a subset of a scale that has no consecutive semitones. In musical analysis, these prototypical scales often serve as a means of categorically interpreting the pitch content of portions of musical works. For instance, a passage may still be interpreted as octatonic if its pitch classes form either a distinctive subset of an octatonic collection, or a superset weighted toward—or readily delineating—an octatonic collection. A commitment to some manageable group of prototypical categories—pc-set genera, formal types, harmonic-syntactic functions, and so forth—can enable significant stylistic insights, although choosing one group of categories over another can be difficult or contentious or, at the least, a work in progress. But struggles to identify distinctive features and categories seem to be worthwhile when one is interested in generalizing about temporal curiosities: the unqualified descriptor “syncopation” offers only the most basic of judgments, as Cohn explores in his article (2016, 8.2–8.4).
Figure 2. Alan Silvestri, Back to the Future Part III, 38:48, melody
(click to enlarge)
[1.6] Like the Pressing scales, all of the successions in Figure 1 are the only successions of their respective cardinalities that meet two criteria: 1) each has no consecutive duration onsets, and 2) each is not a subset of a succession that has no consecutive duration onsets.(6) Here, “consecutive” refers to durations of the unit layer; therefore, the first criterion excludes 1 as a duration. The second criterion excludes durations of 4 or larger, as they may be subdivided into successions of 2s, 3s, or a mix of both. For example, the succession 3234 invites a 32322 interpretation, as the 4 can be divided into 22; in fact, 32322 is the only element of Figure 1 of which 3234 is a subset. For another example, the music of Figure 2 uses an inter-onset interval succession of 12212. This is a superset of exactly two successions from Figure 1: 323 and 332. Nonetheless, the general preference for longer durations on beats, as well as the fourth note’s subordinate role as neither a local maximum nor local minimum in terms of pitch height, suggests 332 as the preferred categorical interpretation for this measure. As I will discuss, this interpretation also connects this music to other 332 successions in Western-themed film and television music.
[1.7] Figure 1 groups the 104 successions by certain features they do or do not possess into a Euler diagram, which is a Venn diagram minus the constraint that a space is allocated to every possible combination of features. Such a Venn diagram would be excessive, as these features are not all independent from one another. The four features of Figure 1, defined only for successions of 2s and 3s, are described below:
- Maximally even. For a succession in Figure 1 to be maximally even, like durations are distributed as far from one another as possible. This treats the last duration in a succession as adjacent to the first, as in an immediate repetition of the succession. For example, both 232 and 322 are maximally even, because, with an immediate repetition of the succession, the 2s are just as far from each other in 322 as they are in 232, and the 2s can get no farther apart in a succession with one 3 and two 2s. A more customary definition of a maximally even duration succession (Clough and Douthett 1991) focuses on timepoints rather than timespans: a succession whose durational beginnings are as far from one another as possible. However, when limited to groups of 2s and 3s, these two definitions are equivalent, and privileging durations over timepoints will serve an upcoming argument. In Figure 1, the 48 maximally even successions are grouped into four columns within the leftmost circle.
- Minimally even. A minimally even succession such as 2233 lumps its like durations together.(7) My use of this descriptor is distinct from its application in other contexts. For example, 1117 would be a least even distribution of four onsets that conforms to a ten-unit measure, and much less even than 2233. However, my context restricts durations to 2s and 3s. In this context, the four beginnings of the durations in the succession 2233 cannot get any closer together without abandoning the restriction. Of course, as with maximal evenness, minimal evenness is independent of a succession’s rotation, so within a measure, a minimally even meter could begin and end with the same duration, such as 2332. In Figure 1, the 70 minimally even meters are grouped into the five middle columns within the largest circle.
- Platonic. Motivated by Cohn 2016, I call a succession Platonic when it is a minimally even succession that begins and ends with different durations. Within the restriction to 2s and 3s, a Platonic succession either begins with a series of one or more 3s and ends with a series of one or more 2s, or vice versa. Following Royer and Garner 1966, as cited in Gotham 2015, I will call the beginning string the “run,” and following Cohn 2016, I will call the ending string the “comma.” In Figure 1, the 30 Platonic successions are grouped into the three middle columns within the smallest circle.
- Platonic-trochaic. Adopting a durational understanding of the trochaic metric foot as long-short, the feature I call Platonic-trochaic applies to Platonic successions in which the sum of the durations in the run (the “long” of the generalized trochee) exceeds the sum of the durations in the comma (the “short” of the generalized trochee). For example, a succession such as 33322 is Platonic-trochaic because 3+3+3 > 2+2. A succession in which these two sums are equivalent is Platonic-trochaic only if the run’s constituent duration is longer than the comma’s constituent duration. For successions limited to 3s and 2s, a Platonic-trochaic succession with equivalent run and comma will start with 3s, as in 33222. In Figure 1, the 15 Platonic-trochaic successions are above the horizontal midline, whereas the 15 successions that are Platonic but not trochaic—what I will call Platonic-iambic—are below the horizontal midline. All of the funky rhythms in Cohn 2016 can be categorized as Platonic-trochaic. Given his analogy with pitch collections, this makes sense, as a pitch-based comma is typically a relatively small span. Although most of his article focuses on Platonic-trochaic successions whose runs comprise 3s, he entertains other types, including 2223, and comments “that there is an arbitrary aspect to the particular affiliations” (2016, 8.8) between the 3-series and the run, and between the 2-series and the comma. My definition of Platonic embraces this arbitrariness. In fact, I will conclude by generalizing Cohn’s model even further to other pairs of durations.
[1.8] I could label additional enclosures in Figure 1 to show other features. For example, the successions within the intersection of the maximally even and minimally even sets in Figure 1 belong to Brad Osborn’s (2014) fourth type of Euclidean rhythm. Or I could bring to bear the many different features discussed in Godfried Toussaint’s book (2013). However, Figure 1 is designed to show only those concepts that are most salient to my argument.
[1.9] To get straight to the point: the kinds of asymmetrical rhythms and meters that I experience categorically—that is, only with 2s and 3s—when listening for decades to RPELM music tend to be distinctively Platonic-trochaic more than they distinctively conform to some other extant feature. The 15 Platonic-trochaic successions in Figure 1 are in boldface; there are other Platonic-trochaic successions of greater length not shown. While a number of these asymmetrical duration successions are also maximally even, there are other maximally even duration successions that do not occur nearly as often in this repertoire. In Figure 1, examples of these “false positives” are in the maximally even circle but are not in boldface. Moreover, quite a few durational successions that are common in this repertoire are not maximally even. In Figure 1, examples of these “false negatives” are in boldface but not in the maximally even circle. The feature of minimal evenness, when applied to durations consisting of 2s and 3s, comes closer to matching the patterns common in RPELM practice in that it eliminates false negatives (no boldface succession is outside of the minimally even circle), but there remain many false positives (the non-boldface successions that are inside the minimally even circle).
[1.10] An artifact of limiting the purview to durations of 2s and 3s is that, with successions of three durations or fewer, the features of maximal and minimal evenness are both present, apparently canceling out one another. For example, within this purview, 332 and its rotations are both maximally and minimally even. Metric layers of four or five durations must be maximally even, minimally even, or both, which takes some of the (metaphorical) wind out of these two features’ superlative sails. This is why the successions that lie outside of all circles in Figure 1 have no fewer than six durations, and would be joined by some successions of more than six durations if the figure were expanded.
[1.11] However, another more widely recognized deficit of using maximal and minimal evenness as criteria is that they do not account for rotation: for example, these features cannot distinguish 332 from 323 or 233. The Platonic feature, along with the trochaic subfeature, accounts for rotation, which puts it in company with features like Justin London’s WFC (Well-Formedness Constraint) 4.2.2 (2012, 129). This constraint specifically addresses the asymmetrical layer, which he calls it a non-isochronous (NI) beat layer. The constraint requires that either 1) this layer be maximally even, or 2) the layer immediately above (that is, slower than) the asymmetrical layer but below the measure layer be maximally even. Therefore, of 323233 and 333322, neither of which is maximally even, only 323233 meets this constraint, because its durations can be grouped into 88 (323|233), which is maximally even (London 2012, 164), whereas 333322 cannot. But among such features, the Platonic-trochaic feature better correlates with the more common successions in music for RPELM, and, in some ways, may do the same for a broader assortment of musical styles, as I argue later.
II. Evidence and Analysis
[2.1] I will survey Platonic-trochaic successions in three batches: the tresillo family, particularly 332 and 333322, where the succession’s durations sum to a power of two (Biamonte 2014); shorter non-tresillo successions of 32, 223, 3322, and 2223; and longer non-tresillo successions, including some successions longer than six durations that are not included in Figure 1. Several videos that compile a sample of representative excerpts from RPELM provide illustrative examples.(8) In general, each video is annotated in time with the succession that I interpret as categorically representing the music. For the first instance of the succession, the annotations mark the beginning of each duration, and then the appearance of the word “continued . . .” coincides with the beginning of the next instance. Some videos are annotated in ways that are tailored to the clip. In some cases where the succession is difficult to hear because of its soft volume or because dialogue and sound effects dominate the soundtrack, I hope the annotations will help the listener to identify the succession. In some cases, the annotations are prospective or retrospective, in that they reflect a clearer perception of a duration succession that has not yet occurred or has already transpired.
[2.2] Because the location of the beginnings of each measure and each duration crucially distinguish the categories I have decided upon, it behooves me to spell out my criteria for making such interpretations, although I believe these criteria to be commonly accepted. Beginnings of measures are often articulated by the beginnings of the cues themselves; the frequent musical silences in a movie’s soundtrack afford good opportunities for the music that enters to easily assert a downbeat. Beginnings of measures are also articulated by the beginnings of fairly stable and often terraced textural blocks, which are distinguished from one another by secondary parameters such as instrumentation, number of lines, volume, and register. Sometimes, beginnings of measures are synchronized with a visual “hit” or a cut to another filmic shot. Both the beginnings of measures and the beginnings of durations in the asymmetrical succession are often articulated through change of pitch, either harmonic or melodic, and recurrence of some pattern. Beginnings of durations in the succession, if not implied through the process of categorization, tend to be accented through contour, duration, dynamics, and so forth, if the onset itself is not sufficient.
[2.3] The occasionally distorted relationship between an original soundtrack recording and the film’s soundtrack can complicate matters. Sometimes an edit late in post-production, even if it involves only fractions of a second, can significantly perturb the temporality of prerecorded music that has already been fit to an earlier cut of the film. These edits arguably perturb asymmetrical successions even more, given their more precarious structure. For example, this appears to be the case in the excerpt I provide from Soldier, where the 223 is uninterrupted in the original soundtrack recording but not in the movie. While the generalizations I suggest here could be made of “the film music itself” outside of its union with image and narrative, and perhaps even more strongly, I am invested in how these successions relate to these other cinematic components.
a. The Tresillo Family
Video 1. Examples of 332 and 333322 in music for Westerns from 1960 and later
(click to watch)
Figure 3. a. Elmer Bernstein, The Magnificent Seven, beginning of theme; b. Jerome Moross, The Big Country, ostinato from “The Flight” and “The Stalking”; c. A metric interpretation of 3b
(click to enlarge)
[2.4] Countless examples from the tresillo family can be found throughout RPELM. However, in my estimation, one instance of film music that is especially important precisely because of its inclusion of these temporal elements is Elmer Bernstein’s main theme for The Magnificent Seven from 1960. The accompaniment to the rather unsyncopated melody uses both 332 and 333322; both can be heard in Video 1, and the latter can be seen in Figure 3a. As Biamonte 2014 and Cohn 2016 both point out, the six durations of the double tresillo 333322 can group into the three durations of 664, a doubling of the durations of the (single) tresillo 332. Against these three durations of 664, Bernstein cleverly pits a twice-sounding harmonic-melodic pattern, constituting a skewed but effective “double-tresillo hemiola,” which Figure 3 illustrates.
[2.5] Starting around 1960, 332 and 333322 become especially associated with the archetypal Western, and Bernstein’s theme undoubtedly contributed to this change, although it was certainly not its only agent. A sample of main themes of pre-1960 Western television programs (Maverick, The Rebel, Bat Masterson, Gunsmoke, Wyatt Earp, Cheyenne, Have Gun Will Travel, The Rifleman, Bonanza, Bronco) and scores for pre-1960 Western movies (including The Tin Star and Saddle the Wind, Bernstein’s two Westerns before The Magnificent Seven) might use the Scotch snap—a short-long rhythm at the beginning of a metrical span—or other asymmetrical successions as a rhythmic sonic signifier for the Wild West, but none conspicuously uses successions from the tresillo family as plainly as those from Bernstein’s Magnificent Seven theme.(9) However, after 1960, tresillo rhythms become more commonplace in the main themes for television westerns and in the scores for many Western films, including the music by Bernstein for Westerns of the ’60s and ’70s starring John Wayne.(10) As an arranger for Glenn Miller’s Army Air Force Band during his World War II service, Bernstein would certainly have been familiar with 333322-infused songs such as “In the Mood” and “String of Pearls.” By straightening the swung funky rhythms of jazz and big-band music and amalgamating them with the harmony and orchestration of “Americana” art music, Bernstein helped to fashion another quintessentially American sound. Video 1 is a compilation of some scenes representative of this sound.
Figure 4. Jerome Moross, The Big Country, 0:50, melody and bass line
(click to enlarge)
[2.6] Along with Bernstein’s score, film musicologists often single out Jerome Moross’s main theme for the 1958 movie The Big Country as a landmark that contains a number of important Wild-Western musical topoi, such as what Frank Lehman (2013) calls the “subtonic half cadence.” Figure 4 provides the melody and bass line of the first eight measures of Moross’s theme after the opening fanfare; I will use the eighth note as the unit. While it is certainly possible to hear 332s in this theme, especially when guided by a cognition that is retrospectively situated post-1960 and appropriate to the genre, it is also possible to hear 323s: the harmonic rhythm’s recurring 35 is a subset of both, and the melody’s onset pattern of 122111 in odd-numbered measures is a superset of both. Moreover, occasional long durations on beat-class 5 (the “and”-of-3) in both melody and accompaniment (not shown) push for a 323 interpretation and push back against a 332 default.
Video 2. The Big Country, 2:42:34-2:43:57
(click to watch)
[2.7] Clearer tresillo rhythms can be found later in the score, such as in the “Ambush in Blanco Canyon” cue (Whitmer 2012, 166). For the movie’s two duel scenes, Moross also composed a double-tresillo ostinato, as shown in Figure 3b, which employs the same “double-tresillo hemiola” effect that Bernstein would use two years later. Video 2 shows the second duel, with purposefully equivocal annotations. With its sparse materials strewn over a five-second succession and its complete lack of a continuous unit pulse or clear duple meter at any entrainable level, this ostinato initially resists being heard as a double tresillo at all: the opening 333 of the 333322 succession sounds completely metrical and completely unsyncopated. In fact, when I first heard this music, I interpreted the “x” of the video’s annotation as an “augmented 3” rather than a concluding 4, categorically 22. Figure 3c notates this 15/8 interpretation of the ostinato. More than any other double tresillo that I know, this ostinato insinuates the mistunings, wolf intervals, and other more visceral incongruities that Cohn’s evocation of a metaphorical comma entails.(11) Furthermore, this disturbing comma resonates well with the scene and with the film’s pacifist message that such duels are futile: both duelists are killed. Although this music can certainly be heard as a double tresillo, to hear it as that classic Western signifier seems as much a musical contrivance as a duel is a political contrivance.
Video 3. Examples of 332 and 333322 in music for RPELM from the 1980s to the present
(click to watch)
[2.8] As sociologist and film historian Will Wright (1975) both observed and anticipated, the Hollywood action film became the successor to the Hollywood western. Video 3 provides a compilation of a few of the countless 332 and 333322 successions in RPELM. The three excerpts from the 1980s that begin the video offer a snapshot of the transition from a brass-led Wild-West-evoking use of the tresillo family to music that conforms more to pop-rock idioms. Just as the 332 and 333322 successions frequent popular music from the 70s to the present, so these successions also frequent RPELM from roughly the same time period.(12) They occur particularly often in the action, adventure, and suspense genres, and particularly for scenes of tension, excitement, industry, and harnessed energy, although they do not necessarily accompany conflict. The incorporation of popular songs using tresillos into RPELM’s soundtracks certainly contributes to this bias, as in the use of AC/DC’s 333322-featuring “Shoot to Thrill” in an early scene from Iron Man 2. But just as significant is the influence of pop-rock music on original cinematic scores. Predictably, the timbres of rock and pop tend to accompany tresillo music in the movies more often than other asymmetrical successions, as can be heard in my examples from Twister, Foolproof, Erased, Kingsman: The Secret Service, and Draft Day. The music accompanying the end titles for Brian de Palma’s Mission: Impossible succinctly and transparently demonstrates post-1970-rock’s influence, as composer Danny Elfman—who came into movie music from pop-rock—extends the 3322 of Lalo Shifrin’s original theme of 1967 to a 333322 bass line below Shifrin’s tune.(13)
[2.9] Equally important to the frequency of 332s and 333322s in this musical genre is the relative infrequency of the other rotations and permutations of these successions, especially as periodic asymmetrical meters—at least in the sample of RPELM to which I have been exposed. Therefore, the Platonic-trochaic feature correlates with the bias against other rotations, which I have observed and extrapolated to the style, better than other features such as maximal or minimal evenness.
b. Shorter Asymmetrical Successions
[2.10] The degree of bias toward the family of tresillo successions in scholarship on pop-rock music corresponds well with the degree of bias toward this same family in RPELM. However, this correspondence decreases somewhat in my second batch of excerpts, consisting of music that employs relatively short successions whose durations sum to 5, 7, 9, or 10. (Successions that sum to 4 and 6 cannot be asymmetrical with 2s and 3s, and the already discussed tresillo rhythm sums to 8.) Regarding rock music, Nicole Biamonte has written that asymmetrical meters “are typically perceived, and are often explicitly marked in the musical texture, as combinations of duple and triple groupings: 5 is 3+2 or 2+3; 7 is 3+2+2, 2+2+3, or less commonly, 2+3+2” (2014, 2.3) The observations of Mark Gotham, in an article concerned with art music, agree with Biamonte’s regarding septuple meter, recognizing a “preference for 223 and 322 rotations” over the 232 rotation (2015, 6.12). In discussing the six permutations of two 2s and two 3s, he further claims that “2233 and 3322 orderings are comparatively rare meters, though perhaps no rarer than the maximally even 2332” (2015, 6.13) Here, Gotham’s designation of 2332 as maximally even is in reference to its maximally even subset of 55, and to features like London’s aforementioned WFC 4.2.2.
[2.11] In my experience listening to RPELM, the stylistic inclinations toward one succession over one of its permutations in this second group appear to be considerably steeper than these statements suggest for any tendencies in rock and art music’s asymmetries, respectively. To summarize my contention: in RPELM, an asymmetrical Platonic-trochaic succession occurs more often than an asymmetrical permutation of this succession when the durations sum to 5, 7, or 10. This means that 32 is more common than 23; 223 is more common than 322 or 232; and 3322 is more common than 2233, 2332, and 3223. These more frequent successions—32, 223, and 3322—are all Platonic-trochaic, and none of the permutations of these successions are. I know of no other feature that better corresponds with this stylistic bias.
Video 4. Examples of 32 and 3322 in music for RPELM
(click to watch)
Video 5. Examples of 223 in music for RPELM
(click to watch)
[2.12] Video 4 provides a representative sample of 32 and 3322 successions in RPELM. In this style, 32 (expanded to 64) tends to occur simultaneously with 3322 (33)(22), in a manner analogous to the relationship between the single tresillo 332 (expanded to 664) and the double tresillo 333322 (33)(33)(22). Shifrin’s Mission: Impossible theme is an important precedent for 3322’s significance, providing an obvious model for similar genres, like Michael Giacchino’s music for undercover superheroes in The Incredibles. However, other excerpts show how 3322 has grown well past the precise semiotic confines of espionage, especially in Ben Newhouse’s use of it for Disney’s DVD logo.(14)
[2.13] Video 5 provides a compilation of some 223 moments in RPELM. The excerpts from Soldier and Minions deserve some brief comments, as they make more of 2212 than the other excerpts do. All other aspects aside, 2212 would conform to 232 (2)(21)(2) better than 223 (2)(2)(12), as this interpretation would pair up the beginning of each longer inter-onset interval with the beginning of each duration of the categorical succession. However, I freely concede that my interpretation of both excerpts is guided by a strong stylistic bias away from 232 and toward the 223 succession that many other examples display. Removing these and other excerpts with 2212 from the sample to avoid a circularity of argument does not unseat 223 from its position as the most frequent among the three rotations. Moreover, the 2212 in Minions succeeds both a 13-second block of music that is more clearly grouped as 223 and an immediately preceding 2221, forming a 2221|2212 intoned by a comically grand chorus. These intraopus contexts strengthen the extraopus bias toward a 223 reading. (Readers who disagree with assigning 22212212 to the 223 category at all may appreciate another analysis of this rhythm toward the end of this article.)
[2.14] In recent publications, Juan Chattah (2015a, 2015b) recognizes that a listener’s challenge in embodying asymmetrical temporal divisions—relative to the ease of entraining to more symmetrical divisions—elicits somatic discomfort and struggle, which can signify tension and conflict. This is often the case with 32, 223, and 3322, as Videos 4 and 5 illustrate in part, and these successions accompany these narrative elements even more intensely and more often than 332 or 333322, probably because the latter is typically grounded in a more familiar and complaisant pure duple environment. The skydiving scene from Kingsman: The Secret Service provides a good example of this difference of intensity. One scene shows six young candidates for a top-secret intelligence agency in the middle of a skydiving test, accompanied by occasional 332s. Video 3 contains the moment when the candidates are told that one of them has no parachute and the longer 333322 begins. The movie’s protagonist has a plan for the six to pair up, but then another chickens out and pulls his chute, which opens. As the protagonist exclaims “Shit, we’re an odd number now!” the meter changes to 223, as shown in the excerpt from Kingsman included in Video 5. On the one hand, this is the first time the scene has used a succession whose durations sum to an odd number, amplifying the tension with tongue in cheek. On the other hand, 223 is a more common rotation of septuple meter, reflecting blockbuster conformance.
[2.15] However, as with successions in the tresillo family, the successions in this second batch can accompany relatively positive moments as well, reflecting a balanced kineticism in line with Cohn’s centrifugal-centripetal model, and finding a place for this balance in the film’s story. For example, in the movie Hoosiers, each time the Hickory high school basketball team wins an important game, except the final state championship game, Jerry Goldsmith switches the meter into a celebratory 223. In Apollo 13, composer James Horner opts for the 3322 succession as both ship and ground crew get down to business after takeoff. What follows soon thereafter is presented in Video 7 (below), as the succession 33222, with its even sub-cycles of 66, accompanies a technical problem: a center engine cutoff. If dramatic tension is supposed to correlate perfectly with the degree to which a succession is uneven, I would think these two successions should instead be swapped. Rather, considering them in the same category of Platonic-trochaic ultimately links these two moments together in a single narrative arc. James Newton Howard’s use of 223 for the conclusion of Concussion strikes a happy medium between the afterglow of the hero’s triumph—the dramatic norm matches the Platonic-trochaic norm—and a depiction showing that American football remains a popular and dangerous sport among newer generations of players.
[2.16] I would like to further suggest that this bias I have noticed in RPELM may be in line with a more diverse range of musical genres and practices. Appendices A and B list examples of quintuple and septuple meter, respectively, from a wide array of popular musical styles (various genres of rock and pop, musical theater and operetta, jazz, lighter classical, video game music, and examples of RPELM with which I was initially unfamiliar) taken from two sources: the Wikipedia sites on these two meters, and a book chapter by Nancy Rosenberg (2010). Presumably, these examples congregated simply because they were in five or seven, and not also because they were some particular version of five or seven. I considered every single example from these sources if they met two conditions: I could find them to hear them, and the prevailing quintuple or septuple successions clearly centered upon one of the possible asymmetrical divisions for some, if not all, of the work: 2+3 or 3+2 for quintuple, and 2+2+3 or 2+3+2 or 3+2+2 for septuple.(15) In my corpus of 38 quintuple examples, 31 (82%) of them use the division 3+2 and 7 (18%) use the division 2+3. Of the 31 3+2 examples, 21 (68%) further subdivide the 3+2 into 3+3+2+2 with a unit duration of half the length. In my corpus of 70 septuple examples, 51 (73%) of them use the division 2+2+3, 16 (23%) use the division 3+2+2, and 3 (4%) use the division 2+3+2. This comports with, but also refines, Biamonte’s claim cited earlier. Other listeners may disagree with some of my interpretations, but, even after overturning any debatable 32 or 223 successions, I suspect that these Platonic-trochaic successions will still have the majority among their rotations.
Video 6. Examples of 2223 and 3222 in music for RPELM
(click to watch)
Figure 5. Michael Giacchino, Inside Out, 1:04:13, reduction of melody
(click to enlarge)
[2.17] The one group of rotationally equivalent successions in this second batch that is much less represented in RPELM is the group of successions with one 3 and three 2s. The lone succession in this group that is Platonic-trochaic is 2223, which is the division used in Dave Brubeck’s “Blue Rondo à la Turk,” the oft-cited locus classicus for this succession. Video 6 offers two examples from this group, one each for the two Platonic successions of 2223 (trochaic) and 3222 (iambic). The example from Inside Out, with its smooth wave-like line, punctuates the asymmetrical durations much less than Brubeck’s leaps do. However, as shown in Figure 5, its 3-lines on two different middleground levels articulate 2223 better than any other rotation.
[2.18] The Battlestar Galactica excerpt shows a Cylon antagonist, in the form of a tall blonde female human, initially behaving in a favorable, nurturing manner, but her violent and unfeeling nature manifests itself later in the scene. I offer two interpretations. My first interpretation applies foreknowledge of 3222 as the thematic succession for the Cylon character and applies it inflexibly. The second recognizes that the music’s fade-in entrance favors 2223 over 3222, and that the occasional changes of harmony initially obscure the location of the downbeat. My Platonic-trochaic generalization suggests that the 3222 rotation is not as common as 2223. Only at the end of the scene, when the antagonist breaks the baby’s neck—in fact, perhaps right at that moment—does the change of harmony clearly promotes 3222 over 2223, cutting against the Platonic-trochaic stylistic grain. These themes, one rhythmic and one dispositional, follow this character throughout this television series.
c. Longer Asymmetrical Successions
Video 7. Examples of successions of eleven units or longer in music for RPELM
(click to watch)
[2.19] For each measure length that is ten unit durations or less, there is at most one Platonic-trochaic succession, all of which have been surveyed above: 5 (32), 7 (223), 8 (332), 9 (2223), and 10 (3322). However, for each measure length that is longer than ten unit durations, there can be more than one Platonic-trochaic succession.(16) For example, two Platonic-trochaic successions have length 11: 3332 and 22223. In RPELM, successions in this third batch—Platonic-trochaic successions of length 11 or more, outside of any in the tresillo family—unsurprisingly occur less often than those in the first two batches. However, with so many more possible permutations of each of these successions, each occurrence of a Platonic-trochaic succession helps to reinforce this feature as one of RPELM’s distinctive characteristics. Each occurrence also achieves a salutary compromise between stylistic convention and temporal novelty, in that it complies with the Platonic-trochaic feature while also finding a more original way to express it. Video 7 provides some examples of these, primarily ordered by the number of units in each succession and secondarily by chronology.
[2.20] More consistently than successions from the first two batches, these longer non-tresillo successions accompany dire or anxiety-invoking situations, although the 33332 for Mychael Danna’s “Lullaby” that opens Life of Pi, with its relatively slow tempo and gentle atmosphere, appears to employ the succession instead to invoke a geographic and cultural Other. Exceptions like this aside, there appears to be a rough correspondence between how divisible the unit length of a long succession is and the degree to which the succession is associated with something negative. Brad Fiedel’s music for the first two Terminator movies delivers a fine case in point. In the first movie, the thematic rhythm fits the 33322 category—curiously, it fits this category in either of the two readily heard rotations of 21212122 and 12121222, where the 2 is the duration begun with an accented onset—and Arnold Schwarzenegger’s character is the primary villain. In the second movie, Fiedel favors a 12-unit rhythm of 1221222—an abundant number of units—that is almost identical to the 13-unit rhythm of 12121222—a prime number of units.(17) Much to the heroine’s initial horror, Schwarzenegger returns looking like the same character from the first movie, but now has become a hero.
[2.21] 1221222 is a superset of only the Platonic-trochaic succession 33222, a succession known as the guajira rhythm (Toussaint 2013, 271–72) or as a “horizontalized hemiola” (Manuel 2006, 102); it is the primary succession for “America” from Leonard Bernstein’s West Side Story. The fact that 22233 has earned the marked phrase “reverse hemiola” (Malin 2010, 63, for example) reveals one way in which scholars of art music understand 33222 as the more normative of the two successions unfolding within a metric (or, quite often, hypermetric) span. The experiments with hemiola by Hans Zimmer and many other film composers like Klaus Badelt who have passed through Zimmer’s company Remote Control Productions have become a signature part of their sound, as in scores like Gladiator and Pirates of the Caribbean. A bias toward the 33222 succession emerges occasionally from these experiments. Although Brian Tyler is not among these composers, his action scores often resemble the “Zimmer sound” and use 33222 more overtly. Moreover, his fanfare for the Marvel logo has adopted 33222 as a rhythmic brand for the studio.
[2.22] In the excerpt from the denouement of Kung Fu Panda 3, Zimmer appears to take advantage of the distinction between 33222 and 22233 to subtly underline a narrative progression. However, unlike the Battlestar Galactica scene, which I argue moves from a more common succession to a less common succession in order to parallel the narrative, this scene does so by moving in the opposite direction. 22233 enters as the title character has emerged victorious in the final battle in the spirit world, and is promoted to Grandmaster. This succession is Platonic, and lends the moment ample buoyancy and gratification. But it is still iambic, rather than the more common trochaic, underscoring how the hero is still apparently trapped in the spirit world. But as the hero learns that he can return to his beloved family in the mortal world, Zimmer inconspicuously transfers the downbeat so that 22233 becomes 33322, which accompanies the hero’s passage home.
III. Perception and Hermeneutics
[3.1] Needless to say, many examples of successions that are not Platonic-trochaic can be found in the music for RPELM. Jerry Goldsmith’s music has a fair share, even among his main themes: a metric 2332 for The Man from U.N.C.L.E., a metric 22232 for Capricorn One, and intermittent rhythmic 323s for Total Recall. However, I contend that, as a whole, they are the exception to the Platonic-trochaic rule. Furthermore, as I have argued elsewhere regarding the stylistic biases of chromatic harmony in film music (Murphy 2014), an exposure to the stylistic biases in RPELM’s use of asymmetrical successions can both affect one’s cognition of these exceptional successions and inform interpretations of expression, affect, and meaning. I have already offered two examples of this in my analyses of music from Battlestar Galactica and Kung Fu Panda 3; what follows are two more, where the more frequent Platonic-trochaic successions are kept at arm’s length.
Video 8. The Dark Knight Rises, 1:16-2:09 and 4:01-4:16
(click to watch)
[3.2] Hans Zimmer’s theme for the mercenary antagonist Bane in The Dark Knight Rises, which is introduced in the second scene of the movie, provides a good example of this, as shown in Video 8. An incessantly repeating, minimally even succession of two 2s and two 3s fades in under the dialogue at the end of the first scene, as we see the CIA take custody of a Russian scientist-informant and three hooded prisoners who are supposedly all Bane’s henchmen. Sound effects and dialogue partially mask the succession, making it difficult to attend to closely, but the 2s and 3s are clear enough.
[3.3] Less clear, however, is where the downbeat of the measure is. The cut to the second scene coincides with a single sub-bass onset that orients the succession to the customary 3322. However, the later entrance of a soft chromatic ostinato, along with a bass line that moves every ten unit durations, rotate this succession around to the less customary 2233. As the scene progresses, the terraced entrances of new musical aspects—increase in volume, addition of new instruments, and resumption of the ostinato after a pause—intermittently reinforce the 2233. Yet remaining in between these intermittent aspects are plenty of opportunities for a listener to rotate the succession back around to the Mission: Impossible stylistic default of 3322.(18) Therefore, knowledge of this default invokes a palpable tension between what should be or appears to be, and what is, a tension befitting an exciting action scene. Moreover, these musical turnabouts accord with the narrative’s duplicities: one of the hooded henchmen is actually Bane, who had planned the capture all along so that he could fake the Russian scientist’s death and take him into custody himself.
Video 9. Mad Max: Fury Road, 35:27-38:05
(click to watch)
[3.4] A similar musical tension (and, coincidentally, involving the same primary actor, who is once again masked) unfolds during a fight scene in Mad Max: Fury Road, provided in part in Video 9. Following silence, composer Tom Holkenborg (aka Junkie XL) brings in two loud, drum-led statements of 332222 when the melee begins. Repetitions of this same succession continue to alternate with dramatic pauses in the skirmish. For me, this succession resonates with the volatility of the scene not only because it is asymmetrical, but also because it is the less customary Platonic-iambic and not the more customary Platonic-trochaic. With each 2 after the first, I hear the music denying one conventional Platonic-trochaic succession after another—the 332 tresillo, the 3322 of Mission: Impossible, and the 33222 “horizontal hemiola”—until it becomes a Platonic-iambic succession. I suspect that any one of these three Platonic-trochaic successions used in place of Holkenborg’s 332222 to accompany this scene would be less unsettling.
IV. Theory
[4.1] I am glad that Cohn’s article came along. Before it, I felt discouraged from attempting to reconcile the asymmetrical successions I was hearing repeatedly in the relatively narrow niche that RPELM occupies with the features that scholars had identified as best characterizing centuries of the world’s music, particularly the feature of maximal evenness. I was resigned to thinking that either the successions I was hearing over and over again were not “good” or “well formed” (such as 3322, which is not maximally even on any level lower than the measure level), or they were no “better” or no more “well formed” that other successions that I heard far less often in this type of music (such as 223, which is just as maximally even on all levels as 322 and 232). I have appreciated how some scholars have found ways to accommodate non-maximally-even successions within theoretical frameworks regulated by the maximal evenness criterion, such as Justin London’s (2012, 158–60) accounting for 33222 by citing Richard Plotkin’s (2010) applications of filtered point-symmetry. But accommodations like this do not weed out the false positives.
[4.2] Nonetheless, there remains a powerful two-part psychological argument for maximal evenness (London 2012, 131–32): these successions 1) allow listeners to maximize the potential for our fluctuating attention to notice a musical event, and 2) they tap into the sensorimotor preference—both productive and perceptual—for periodic motions. For a completely even division of time like 2222, these two priorities are both present; indeed, they are mutually implicative. But, the longer and more rotationally invariant a succession is, the more that these two priorities are mutually exclusive: optimizing one prohibits an optimization of the other. For example, given two 3s and three 2s, 23232 optimizes evenness but not periodicity, while 33222 optimizes periodicity, as I will assert below, but not (quite) evenness. But, at least with regards to these two priorities, both are better than, say, 53211.
[4.3] This suggests another way to define a “well-formed” or “good” asymmetric succession. Some current scholarship bases the definitions of these concepts simply on the presence of a feature or set of features in a succession, or the maximal/minimal degree of this presence if the feature can be gradated, like evenness. Other scholarship that relies on these gradated features defines these concepts through a “Goldilocks” principle. Using this principle, the succession has not too much, but not too little, of a feature, compared either to what is possible or to how much the feature is present in other related successions.(19) Using this principle, features appear to no longer wholly correspond to desiderata; otherwise, why settle for less? I am suggesting a third way that hybridizes these two approaches and, in addition, offers one answer to this “why” question. In this third way, a succession is “well formed” or “good” because it is one of potentially multiple optimizations—none of which is necessarily better than the other—of a set of priorities that are not mutually possible or compatible.(20) In an asymmetrical succession, evenness and periodicity are two such priorities. This third approach accommodates any psychological and somatic aspects shared by humans of different cultures, which might give rise to some core set of priorities, as well as stylistic variety among these cultures, which originates with some incompatibility among these priorities that diversifies the set of their optimal solutions.
[4.4] My argument for the Platonic-trochaic succession type as one of these solutions is inspired by Hasty’s (1997) concept of “projection.”(21) An immediately past event’s duration projects onto a presently unfolding event the potential that the present event will span the same duration as the previous. The present event may or may not realize this potential. While rhythm comprises any succession of durations, a particular succession that realizes the projective potential of its durations to some extent engages Hasty’s processive notion of meter to that extent; hence, meter is a kind of rhythm. If one imagines a perfectly even succession set in a loop, such as
[4.5] Of course, a minimally even distribution of attentional energy is not as ideal as a maximally even distribution of such, but with durations limited to 2s and 3s, the succession’s distribution is still quite close to a maximally even distribution: one is likely to be on guard when some event worthy of notice takes place. It seems that minimally even successions compensate for this modest cost, because near realization offers near-optimal benefits of periodicity—in most cases, one’s body and mind can entrain to much of the succession. The only minimally even distributions with no realizations are 32 and 23, because they contain only two durations. This fact supports one hypothesis for why a 32 subdivided as 3322 at half the unit duration is more frequent (and more often associated with positive aspects) in music for RPELM (and perhaps also a wider array of popular musical styles) than a 32 without this subdivision.
[4.6] Only at two moments per loop through a minimally even succession will the performer and listener need to shift gears. In Cohn’s (2016) model, these moments are the shift from the centrifugal motion of the “run” to the balancing centripetal motion of the “comma,” and then, if the pattern repeats, vice versa. These gearshifting moments are more rhythmic than metric; moreover, they are analogous to onsets in a rhythm, because they are moments of (probable) change, like the change in pitch in a melody or harmonic progression. As a study by David Huron and Ann Ommen shows (2006), within a metric span like a measure (from a downbeat up to but not including the next downbeat), the most likely place for an onset is the very beginning of the span: it is at this point that the listener is most prepared for change. To expand the aforementioned analogy, this would predict that one of the two durations in a minimally even succession that does not realize the projective potential of the preceding duration would come first in the succession, to put it in the proximity of the succession’s downbeat. Thus one of the two gearshifts coincides with a moment where change is most expected anyway. A minimally even succession that is Platonic would provide this coincident moment. For example, rotating
[4.7] Within a metric span, the next most likely place for an onset is halfway through the span, but this is only true for meters with spans that are divided into halves. More generally, the next most likely place for an onset is during the second half of the span. The long-short trochaic duration succession, rather than the short-long iambic durational succession, is more likely to start at the beginning of a metric span. Thus, the other gearshift of the Platonic succession—the one whose beginning is not on the downbeat—occurs during a time where change is more expected. A Platonic-trochaic succession would provide this. For example, rotating
V. Conclusion
[5.1] This model replaces the feature of maximal evenness with another feature, prompted by Cohn’s Platonic model, which more closely corresponds with the kinds of asymmetrical successions that tend to occur more frequently in RPELM than other kinds of asymmetrical successions. I further submit that the notion of near realization, generalized for successions of other pairs of short durations besides 2s and 3s, especially 3s and 4s, and 1s and 2s, has the potential to continue this kind of close categorical correspondence for RPELM as well as other types of popular music.
[5.2] For example, a restriction to durations of 3 and 4 results in the following Platonic-trochaic successions with lengths of sixteen units or less: 43, 334, 443, 3334, 4443, 4433, and 33334. By necessity, all of these are subsets of exactly one Platonic-trochaic succession with 2s and 3s. The example that has garnered the most press is 33334, which is a subset of 333322. But what is not obligatory is that these seven successions all have representation in my survey. The parallel set of successions with 2s and 3s—that is, with a length of sixteen units or less—cannot boast this: Video 5 does not have examples of 3332 or 333222 (or the 17-unit 333332, for that matter, to round out the 15 boldfaced successions in Figure 1) because I do not know of any of these in RPELM. So, as others have done before me, I see benefit in using a succession like 33334 to categorize a rather frequent articulation of time in certain popular styles, but because it is Platonic-trochaic and not because it is maximally even.
[5.3] A restriction to durations of 1s and 2s also has the potential to provide stylistic insights into RPELM’s customary rhythms, and maybe other popular styles as well. A minimally even succession with these durations could only have a single 1, assuming it adheres to a prohibition of consecutive 1s analogous to the same prohibition adhered to by the Pressing scales. Furthermore, those that are Platonic-trochaic beyond the familiar 21—221, 2221, and so on—carve out but a small niche of RPELM’s common rhythmic practices concerning successions with an odd number of units. However, a generalization of a Platonic-trochaic succession to a succession with exactly two gearshifts gets us much farther along. In the special case of the set of successions with 1s and 2s, I postulate that each gearshift is not a progression of two unequal durations as established earlier, such as 2 to 1, or 1 to 2. If it were, then, for every 1 in a succession of 1s and 2s, there would be two gearshifts: one into each, and one out of each. For example, 21212 would have four gearshifts: two 1s in the succession times two gearshifts each. However, although 1s disrupt duple projection, their own projections are incapable of being disrupted, because, by definition, a unit duration is compatible with any series of categorical durations that could follow it. Therefore, it makes sense that, for a succession with 1s and 2s in particular, the gearshifts are the 1s themselves. Therefore, to be nearly realized, a succession from this set will contain exactly two non-adjacent 1s. The rhythm from Back to the Future Part III notated in Figure 2—12212—and the aforementioned rhythm from Minions in Video 5—22212212—are two instances of this kind of succession.
[5.4] From this perspective, ostensibly unlike categorical successions such as 333322 and 222122212—which are both well represented in music for RPELM as well as other forms of popular music—now have something structurally in common besides the fact that their durations sum to 16.(23) While 333322 could be understood to invoke grouping dissonance (Butler 2006, 157–60) and 222122212 could be understood to invoke displacement (Temperley 1999), both are nearly realized.
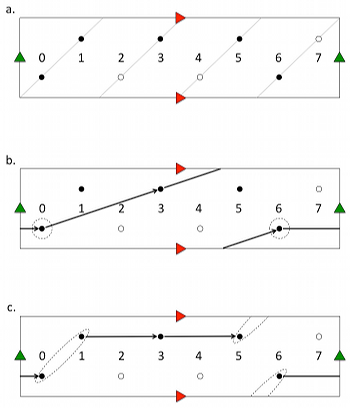
Figure 6. a. A toroidal view of eight timepoints b. An interpretation of Figure 2’s rhythm as 332 c. An interpretation of Figure 2’s rhythm as 12212
(click to enlarge)
[5.5] Furthermore, some music can be categorized as nearly realized both with 2s and 3s and with 1s and 2s, like the music in Figure 2. Its onsets use a 12212 succession, while the longer inter-onset intervals well suit the 332 category, as argued above. Figure 6 visualizes these two interpretations on a geometric backdrop prompted by Cohn’s (2016) Figure 2, and further demonstrates the similarities between near realizations using two different successions of durations. The small circles represent timepoints labeled 0 through 7, where 0 is the downbeat, and the solid circles show the onsets from Figure 2. Figure 6a situates the timeline (number line) that connects these timepoints on a torus: parallel sides with same-colored triangles pointing in the same direction should be considered as “glued” together. In other words, the left and right sides correspond like those of a flat map of a sphere; however, unlike such a map, the top and bottom sides correspond in the same fashion. In this torus, not only is the timeline’s circular or “necklace” shape familiar from metric/rhythmic scholarship now a straight line, but also every single succession of equal durations is a straight line—a fully realized projection—in this space. I have oriented the torus so that any succession of 2s is flat as in Cohn’s Figure 2, and the four even-numbered timepoints are on the bottom, presenting this line as a baseline from which either 1s or 3s can deviate. In Figures 6b and 6c, the dashed enclosures are the gearshifts: points in the case of 3s and 2s (Figure 6b), and durations connecting points in the case of 1s and 2s (Figure 6c). Each interpretation uses exactly two gearshifts; therefore, both are nearly realized.
[5.6] I propose that the feature of near realization—for successions with 1s and 2s, freed from the rotational specificity of the Platonic restriction—rather than the feature of maximal evenness is a better fit for categorical interpretations of common rhythms in RPELM, and perhaps in other popular styles as well.(24) This feature of near realization has the potential to lead to a more general theory of temporal articulation that unites outwardly dissimilar rhythms and meters that nonetheless intermingle and interchange in many forms of popular music.
Scott Murphy
University of Kansas
School of Music
1530 Naismith Dr Rm 220
Lawrence, KS 66045-3102
smurphy@ku.edu
Works Cited
Biamonte, Nicole. 2014. “Formal Functions of Metric Dissonance in Rock Music.” Music Theory Online 20 (2).
Butler, Mark J. 2006. Unlocking the Groove: Rhythm, Meter, and Musical Design in Electronic Dance Music. Indiana University Press.
Caplin, William E. 1981. “Theories of Harmonic-Metric Relationships from Rameau to Riemann.” PhD diss., University of Chicago.
—————. 1998. Classical Form: A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven. Oxford University Press.
Carr, Philip. 2013. English Phonetics and Phonology: An Introduction, Second Edition. Wiley-Blackwell.
Chattah, Juan. 2015a. The Conversation: A Film Score Guide. Rowman and Littlefield.
—————. 2015b. “Film Music as Embodiment.” In Embodied Cognition and Cinema, ed. Maarten Coëgnarts and Peter Kravanja, 81–112. Leuven University Press.
Clampitt, David. 1997. “Pairwise Well-Formed Scales: Structural and Transformational Properties.” PhD diss., State University of New York at Buffalo.
Clough, John, and Jack Douthett. 1991. “Maximally Even Sets.” Journal of Music Theory 35: 93–173.
Cohn, Richard. 2016. “A Platonic Model of Funky Rhythms.” Music Theory Online 22 (2).
Gotham, Mark. 2015. “Meter Metrics: Characterizing Relationships Among (Mixed) Metrical Structures.” Music Theory Online 21 (2).
Hasty, Christopher. 1997. Meter as Rhythm. Oxford University Press.
Hesselink, Nathan D. 2013. “Radiohead’s ‘Pyramid Song’: Ambiguity, Rhythm, and Participation.” Music Theory Online 19 (1).
Huron, David. 2006. Sweet Anticipation: Music and the Psychology of Expectation. MIT Press.
Huron, David, and Ann Ommen. 2006. “An Empirical Study of Syncopation in American Popular Music, 1890–1939.” Music Theory Spectrum 28 (2): 211–31.
Lehman, Frank. 2013. “Hollywood Cadences: Music and the Structure of Cinematic Expectation.” Music Theory Online 19 (4).
Lerdahl, Fred, and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. MIT Press.
London, Justin. 2012. Hearing in Time: Psychological Aspects of Musical Meter. 2nd ed. Oxford University Press.
Malin, Yonatan. 2010. Songs in Motion: Rhythm and Meter in the German Lied. Oxford University Press.
Manuel, Peter. 2006. “Flamenco in Focus: An Analysis of a Performance of Soleares.” In Analytical Studies in World Music, ed. Michael Tenzer, 92–119. Oxford University Press, 2006.
Murphy, Scott. 2014. “Transformational Theory and the Analysis of Film Music.” In The Oxford Handbook of Film Music Studies, ed. David Neumeyer, 471–99. Oxford University Press.
Osborn, Brad. 2014. “Kid Algebra: Radiohead’s Euclidian and Maximally Even Rhythms.” Perspectives of New Music 52: 1–25.
Plotkin, Richard J. 2010. “Transforming Transformational Analysis: Applications of Filtered Point-Symmetry.” PhD diss., The University of Chicago.
Richards, Mark. 2013. “Musical Themes in the Dark Knight Trilogy, Part 5 of 6: The Dark Knight Rises.” Website at http://www.filmmusicnotes.com/.
Rosenberg, Nancy. 2010. “Popular Music in the College Music Theory Class: Rhythm and Meter.” In Pop-Culture Pedagogy in the Music Classroom, ed. Nicole Biamonte, 47–71. Scarecrow Press.
Royer, Fred, and Wendell Garner. 1966. “Response Uncertainty and Perceptual Difficulty of Auditory Temporal Patterns.” Perception and Psychophysics 1: 41–47.
Temperley, David. 1999. “Syncopation in Rock: A Perceptual Perspective.” Popular Music 18: 19–40.
—————. 2001. The Cognition of Basic Musical Structures. MIT Press.
Toussaint, Godfried. 2013. The Geometry of Musical Rhythm: What Makes a “Good” Rhythm Good? CRC Press, Taylor & Francis Group.
Tymoczko, Dmitri. 2004. “Scale Networks and Debussy.” Journal of Music Theory 48 (2): 215–92.
—————. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. Oxford University Press.
Whitmer, Mariana. 2012. Jerome Moross’s The Big Country: A Film Score Guide. Scarecrow Press.
Wright, Will. 1975. Sixguns and Society: A Structural Study of the Western. University of California Press.
Footnotes
1. A complement of Cohn’s approach suggests a way to distinguish pre-1890 European and post-1890 American compositional resolutions of the irreconcilability between a series of triple durations and a pure duple meter. In Cohn’s model, if either of these series acquiesces to the other, it is the triple series that gives way to the pure duple meter, and this model befits a lot of post-1890 American music. However, the pure duple meter can also acquiesce to the triple durations by introducing a three- or six-measure hypermeasure that allows duple and triple divisions to realign. Examples of this resolution that I know of occur in eighteenth- and nineteenth-century European music, including mm. 22–24 of the last movement of Haydn’s String Quartet op. 76/4, mm. 25–36 of the last movement of Schumann’s Faschingsschwank aus Wien, and mm. 16–18 of the first movement of Brahms’s Concerto for Violin and Cello op. 102. Remarkably, a work that cuts across this geographic/structural mapping is Dvorak’s Symphony No. 9 “From the New World” of 1893, particularly during moments in the last movement.
Return to text
2. To save space, no separator is used in the presentation of these successions; for example, 223 is short for 2+2+3, 2-2-3, or
Return to text
3. This qualification is, in part, a response to Butler (2006, 85), who rightly notes that there are many different types of asymmetries.
Return to text
4. Fred Lerdahl and Ray Jackendoff’s MWFR (Metric Well-Formedness Rule) 4 states “[a]t each metrical level, strong beats are spaced two or three beats apart” (1983, 69). David Temperley’s MWFR (Metric Well-Formedness Rule) 2 is essentially the same, requiring that “[e]xactly one or two beats at a given level must elapse between each pair of beats at the next level up” (2001, 37). Hasty (1997, 131–32) writes “[p]resented with a series of ‘objectively’ homogenous pulses (at a moderate tempo), we will spontaneously create groups of two or three (or multiples of two or three) and not groups of five or seven. And if we are given a group of five (at a moderate tempo) we will hear this as a composite of duple and triple groups.”
Return to text
5. Somewhat like William Caplin’s (1981, 1998) distinction between a real or expressed measure and a notated measure, the music may be written so that what I am calling a “measure” layer spans multiple notated measures or a portion of a notated measure.
Return to text
6. London’s WFC 4.2.2 (2012, 129) requires that “[e]ach subcycle must connect nonadjacent time points on the next lowest cycle.” This criterion also resembles what has been called the “Stress Clash Avoidance Principle” in phonology: “one should try to avoid having two adjacent stressed syllables” (Carr 2013, 75).
Return to text
7. Minimally even has also been called “maximally lumpy” (Clampitt 1997, 42).
Return to text
8. The examples from Angels and Demons and Breaking Bad were drawn from
http://tvtropes.org/pmwiki/pmwiki.php/Main/UncommonTime.
Return to text
9. The Scotch snap is completely agnostic regarding the prototypical successions of Figure 1, because, for example, 17 is not a subset of any of these successions. However, the short-long rhythm can initiate a series of short-long rhythms that support a succession of 3s through their parallel structure, even though they contradict the preference for longer durations on beats. This phenomenon supports Cohn’s tresillo reading in his Figure 9, a 3322 interpretation of the accompaniment figure from Paul Desmond’s “Take Five,” as well as my interpretations of 3322 in an excerpt from True Grit and 33322 in an excerpt from The Terminator.
Return to text
10. One reason that I have argued for a distinctive association between 332 and 333322 and the Hollywood Western from 1960 forward is that the rotations of these successions are used far less often in this genre. One possible exception to this for 333322 might be its two rotations of the five that satisfy London’s WFC 4.2.2: 332233 and 233332. The former conspicuously participates in the main themes for The Sons of Katie Elder (Elmer Bernstein) and Quigley Down Under (Basil Poledouris), and the latter does the same for the 1999 big-screen adaptation of Wild Wild West (Elmer Bernstein’s last Western score). Another feature that equally sets these two rotations apart from the other five is that these are the only two rotations that either begin or end with 332, the other distinctively Western succession. In the case of Bernstein in particular, I hear a composer varying the signature 333322 succession in such a way as to maintain its connection to the genre while still avoiding overt musical recycling.
233332 plays an role in some popular songs; in many cases, its use reifies it as a rotation of 333322 by vacating 233332’s downbeat and instead beginning a line of text or an instrumental motive with the first 3. Examples include Journey’s “Faithfully,” Van Halen’s “Love Walks In,” Aerosmith’s “Rag Doll,” Carly Simon’s “Comin’ Around Again,” Bon Jovi’s “Lay Your Hands on Me,” Phish’s “Tweezer,” and The Rembrandts’ “I’ll Be There for You.”
Return to text
11. The metric underdetermination of this scenario is somewhat like the first verse of Radiohead’s “Pyramid Song,” as discussed by Nathan Hesselink (2013) and Brad Osborn (2014, 6–7). However, in The Big Country’s ostinato, not only is a pure duple grid absent, but a compound triple feel is present, further suppressing a duple hearing. One might even say that pure triple is present to some extent, as the double-tresillo hemiola initially projects a 333, and the cue even begins with an anacrustic 333 that precedes the full 3333x statements of the ostinato.
Return to text
12. Biamonte 2014, 3.3: “The double-tresillo rhythm is common in jazz from the mid-twentieth century onwards and in rock and related genres from the 1970s onwards.” Butler (2006, 82–83) cites 332, 333322, and 332332 as the most common asymmetrical divisions in electronic dance music. Osborn (2014, 16) hears 33334 and 43333 with equal frequency in modern rock music.
Return to text
13. Joe Kraemer’s music for the opening of Mission: Impossible—Rogue Nation offers a challenging and rewarding exercise for interpreting successions with durations of 4 units or more using my proposed succession categories. His thematized 6433 succession (assigned to the same four pitches/chords as the 3322 succession of Lalo Shifrin’s original 5/4 theme) allows two categorical interpretations: 332233, which embeds Shifrin’s original 3322 and is a superset of the 3+13, 3+3+10, and 10+6 successions that precede it in Kraemer’s score; and 2222233, which is the more customary Platonic-trochaic succession and the only other one of 16 units that Elfman did not use in the first Mission: Impossible film (333322). Although the score reuses 6433, it never subdivides it, leaving it open to interpretation.
Return to text
14. The Disney DVD animated logo included in Video 4 is the first instance of this logo, which was used from 2001 to 2007. Here, the downbeats of Newhouse’s quintuple-meter music are tightly synchronized with Tinkerbell’s presentations of each of the letters D-V-D. After 2007, Disney continued to use the same music for the logo, but the updated animation’s synchrony with Newhouse’s downbeats became much more subtle and diffuse. In a personal communication (August 22, 2016), Newhouse shared how, in the later logos, “the primary role of the initial 5/4 meter is to give the music a playful energy that imitates Tinkerbell's character.”
Return to text
15. The music may more clearly project another asymmetrical succession outside of this categorization, however. For example, Motion City Soundtrack’s “Box Elder” blatantly sounds 33332 with a unit of half the duration; however, the snare drum articulates duple at the start of each measure, leaning the music toward the 223 category.
Return to text
16. With a succession of 20 or more unit durations, there can be more than two Platonic-trochaic successions, and so forth.
Return to text
17. An abundant number is one whose divisors (other than itself) sum to a value that is greater than the number itself. 12 is an abundant number because 1+2+3+6 > 12.
Return to text
18. A recent exchange about Bane’s theme on filmmusicnotes.com, a website run by music theorist Mark Richards (2013), substantiates my claim. A commenter was having “a hard time finding the beginning of the 5/4 ostinato [of Bane’s theme] when it is playing in the score,” and asked Richards for tips for finding the downbeat. “As for finding the downbeat,” Richards replied, “the quicker 2+2 beats tend to sound like pickups to me, so the first 3-eighth beat [Richards’s notated unit duration] sounds like a downbeat to me. But I’m sure there are others who will hear the downbeat on the first 2-eighth beat instead.”
Return to text
19. Toussaint (2013, 279–91) uses this approach to single out the clave son rhythm from five other “distinguished” rhythms. For ten gradated features—evenness, off-beatness, and so forth—the son rhythm is centrally positioned. Only with regards to rhythmic oddity is the son rhythm an outlier.
Return to text
20. In classical microeconomics, a solution where it is impossible to come closer to achieving one goal while maintaining the degree to which all other goals are met is called Pareto optimal. In most multiple-goal scenarios of interest to economists, there are typically multiple Pareto-optimal solutions.
Return to text
21. Butler (2006, 100–6) scrutinizes 332 and 333322 in particular from a Hastian perspective.
Return to text
22. This is intended as a parallel construction to the descriptor “nearly even” for pitch-class sets, as defined in Tymoczko 2011.
Return to text
23. An exemplar of 222122212 in RPELM is Klaus Badelt’s music at 58:55-59:09 in Pirates of the Caribbean: The Curse of the Black Pearl. In terms of popular song, the 222122212 succession category—if allowing for a “swing” proportion between 1 and 2 in some cases— well designates passages in the Beatles’ “Day Tripper” (opening guitar hook), Beach Boys’ “Wouldn’t It Be Nice” (“wouldn’t it be | nice if we were older, then we wouldn’t | have. . .”), Elton John’s “I’m Still Standing” (| I’m still standin’, better than I | ev-. . .), and George Harrison’s “I’ve Got My Mind Set on You” (“I got my mind |set on you. . .”). (The | comes before the beginning of the succession.) One possible approach to investigating rhythm in popular musical styles is to track the frequency of rhythms that conform to certain categorical successions of 1s and 2s, of which there are 6 with 8 units (12122, 12212, 12221, 21212, 21221, and 22121), 28 with 16 units, and 120 with 32 units.
Return to text
24. This approach could harmonize nicely with Temperley’s (1999) study of syncopation in rock, in that it provides a theory for both the preference for backwards displacement (provided by the 1 of the first gearshift) and the trend that displaced onsets tend to cluster together (provided by the presence of only two 1s over a relatively long metric span, like a succession of 16 units).
Return to text
http://tvtropes.org/pmwiki/pmwiki.php/Main/UncommonTime.
233332 plays an role in some popular songs; in many cases, its use reifies it as a rotation of 333322 by vacating 233332’s downbeat and instead beginning a line of text or an instrumental motive with the first 3. Examples include Journey’s “Faithfully,” Van Halen’s “Love Walks In,” Aerosmith’s “Rag Doll,” Carly Simon’s “Comin’ Around Again,” Bon Jovi’s “Lay Your Hands on Me,” Phish’s “Tweezer,” and The Rembrandts’ “I’ll Be There for You.”
Appendix A. A list of popular works in quintuple meter.
| Artist/Composer | Work | Succession | Unit tempo | Subdivided? |
| Akeboshi | “Kamisama no Shitauchi” | 32 | 152 | |
| Akeboshi | “Wind” | 32 | 176 | |
| Andrew Lloyd Webber | Jesus Christ Superstar, “Everything’s Alright” | 32 | 138 | ✓ |
| Don Ellis | “5/4 Rock” | 32 | 146 | ✓ |
| Don Ellis | “Indian Lady” | 32 | 270 | |
| Dream Theater | “Erotomania” | 23 | 180 | ✓ |
| Emerson, Lake, and Palmer | “Tarkus/Eruption” | 23 | 215 | ✓ |
| Ginger Baker | “Do What You Like” | 32 | 160 | ✓ |
| Gorillaz | “5/4” | 23 | 187 | |
| GZR | “Cycle of Sixty” | 32 | 137 | |
| Jethro Tull | “Living in the Past” | 32 | 154 | ✓ |
| John Rutter | “Donkey Carol" | 32 | 195 | |
| Lalo Shifrin | Cool Hand Luke, “Tar Sequence” | 32 | 148 | ✓ |
| Led Zeppelin | “Four Sticks” | 32 | 211 | ✓ |
| Leonard Bernstein | Candide, “Ballad of Eldorado” | 32 | 122 | |
| Muse | “Animals” | 32 | 172 | ✓ |
| Nick Drake | “River Man” | 32 | 113 | ✓ |
| Paul Desmond | “Take Five” | 32 | 196 | ✓ |
| Queens of the Stone Age | “Hangin’ Tree” | 32 | 214 | ✓ |
| Radiohead | “15 Step” | 32 | 190 | ✓ |
| Radiohead | “Morning Bell” | 32 | 144 | ✓ |
| Rush | “Kid Gloves” | 32 | 182 | ✓ |
| Siouxsie and the Banshees | “Overground” | 32 | 116 | ✓ |
| Sky | “Dance of the Little Fairies” | 32 | 139 | |
| Soundgarden | “My Wave” | 23 | 127 | ✓ |
| Stephen Sondheim | Sweeney Todd, “Ladies in Their Sensitivities” | 32 | 250 | |
| Sting | “Seven Days” | 32 | 189 | ✓ |
| Sufjan Stevens | “A Good Man is Hard to Find” | 32 | 180 | ✓ |
| Sufjan Stevens | “All Good Naysayers” | 32 | 180 | ✓ |
| Sufjan Stevens | “The Tallest Man, the Broadest Shoulders Part I: The Great Frontier” | 32 | 280 | ✓ |
| The Turtles | “Grim Reaper of Love” | 23 | 175 | |
| Tool | “Rosetta Stoned” | 23 | 235 | |
| Tool | “The Grudge” | 32 | 360 | |
| Tool | “Vicarious” | 32 | 114 | ✓ |
| Vanessa Hudgens | “Last Night” | 32 | 183 | ✓ |
| Venetian Snares | “Hiszékeny” | 32 | 160 | |
| XTC | “English Roundabout” | 32 | 175 | ✓ |
| Totals: | 32: 31/38 23: 7/38 |
3322: 21/31 2233: 3/7 |
||
Appendix B. A list of popular works in septuple meter.
| Artist/Composer | Work | Succession | Unit tempo | Subdivided? |
| Alice in Chains | “Them Bones” | 223 | 165 | ✓ |
| Anathallo | “The River” | 223 | 208 | ✓ |
| Andrew Lloyd Webber | Evita, “And the Money Kept Rolling In (and Out)" | 223 | 302 | |
| Andrew Lloyd Webber | Jesus Christ Superstar, “Heaven on Their Minds” | 223 | 263 | |
| Animal Collective | “What Would I Want? Sky” | 322 | 177 | |
| Anthrax | “Time” | 223 | 386 | |
| Between the Buried and Me | “Selkies: The Endless Obsession” | 223 | 340 | |
| Blondie | “Heart of Glass” | 223 | 120 | |
| Broken Social Scene | “7/4 (Shoreline)” | 223 | 158 | |
| Cat Stevens | “Rubylove” | 322 | 288 | |
| Chris Squire | “Lucky Seven” | 223 | 160 | |
| Dave Brubeck | “Unsquare Dance” | 223 | 225 | |
| Dave Matthews Band | “Seven” | 223 | 94 | ✓ |
| David Bowie | “Soul Love” | 223 | 76 | |
| Dethklok | “I Tamper with the Evidence at the Murder Site of Odin” | 223 | 420 | |
| Don Ellis | “Beat Me, Daddy, Seven to the Bar” | 322 | 350 | |
| Don Ellis | “Pussy Wiggle Stomp” | 223 | 230 | ✓ |
| EL VY | “Sad Case” | 223 | 251 | |
| Frank Zappa | “Don’t Eat the Yellow Snow” | 223 | 275 | |
| Fu Manchu | “Pick Up Summer” | 232 | 82 | |
| Genesis | “The Battle of Epping Forest” | 223 | 103 | |
| Grateful Dead | “Estimated Prophet” | 232 | 134 | |
| Grateful Dead | “Lazy Lightning” | 322 | 152 | |
| Grateful Dead | “Supplication” | 322 | 152 | |
| IQ | “State of Mine” | 322 | 300 | |
| Iron Maiden | “Brighter than a Thousand Suns” | 223 | 127 | |
| Jack Wall | Mass Effect 2, “Suicide Mission” | 223 | 235 | |
| Jeff Wayne | “Thunderchild” | 223 | 134 | |
| José Neto, Flora Purim, and Diana Moreira | “Tombo in 7/4” | 223 | 258 | |
| Leonard Bernstein | Candide, “Oh, Happy We” | 223 | 129 | |
| Leonard Bernstein | Candide, “Words, Words, Words” | 223 | 167 | |
| Midnight Oil | “No Time for Games” | 223 | 131 | ✓ |
| moe | “Wind It Up” | 223 | 370 | |
| Motion City Soundtrack | “Box Elder” | 223 | 144 | |
| Murray Gold | Doctor Who, Fifth Series, “I Am the Doctor” | 223 | 330 | |
| Nickel Creek | “In the House of Tom Bombadil” | 223 | 290 | ✓ |
| Nobuo Uematsu | Final Fantasy VI, “Another World of Beasts” | 322 | 183 | |
| Nomad Soul | “Murmuration” | 223 | 340 | |
| Ozzy Osbourne | “Diary of a Madman” | 232 | 87 | |
| Peter Gabriel | “Solsbury Hill” | 322 | 102 | |
| Philip Glass | Concerto Fantasy for Two Timpanists and Orchestra | 322 | 340 | |
| Police | “Mother” | 322 | 200 | |
| Porcupine Tree | “Dark Mother” | 223 | 254 | |
| Porcupine Tree | “So Called Friend” | 322 | 140 | |
| Radiohead | “2+2=5” | 223 | 300 | |
| Radiohead | “Paranoid Android” | 223 | 310 | |
| Red Hot Chili Peppers | “Ethiopia” | 223 | 200 | ✓ |
| Rush | “La Villa Strangiato” | 223 | 280 | |
| Rush | “Tom Sawyer” | 223 | 352 | |
| Sam Bush | “Laps in Seven” | 223 | 311 | |
| Slint | “Breadcrumb Trail” | 223 | 105 | ✓ |
| Soda Stereo | “(En) El Séptimo Día” | 223 | 215 | |
| Soundgarden | “Outshined” | 223 | 94 | |
| Stephen Stills | “Cherokee” | 223 | 140 | |
| Steve Vai | “Die To Live” | 223 | 134 | |
| Sting | “Like a Beautiful Smile” | 223 | 339 | |
| Sting | “Love is Stronger than Justice” | 223 | 320 | |
| Sting | “St. Augustine In Hell” | 223 | 180 | |
| Sting | “Straight to My Heart” | 322 | 310 | |
| Sum 4 | “Nothing on My Back” | 322 | 170 | |
| The Beatles | “All You Need is Love” | 223 | 100 | |
| The National | “Demons” | 223 | 300 | |
| Tool | “Ticks and Leeches” | 223 | 300 | |
| Tori Kelly and Ed Sheeran | “I Was Made For Loving You” | 322 | 68 | |
| Traci Lords | “Good-n-Evil” | 223 | 244 | ✓ |
| UK | “In the Dead of Night” | 223 | 290 | |
| Weather Report | “Mysterious Traveler” | 322 | 88 | |
| XTC | “The Man Who Sailed Around His Soul” | 223 | 174 | ✓ |
| Yanni | “Marching Season” | 322 | 330 | |
| Yanni | “Waltz in 7/8” | 223 | 315 | |
| Totals: | 223: 51/70 322: 16/70 232: 3/70 |
222233: 10/51 | ||
Copyright Statement
Copyright © 2016 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
16443