Instruments of Music Theory *
Alexander Rehding
KEYWORDS: history of music theory, critical organology, sound studies, acoustics, epistemic thing, Pythagoras, Gaffurius, Vicentino, Cowell, monochord, archicembalo, siren, rhythmicon.
ABSTRACT: This article explores musical instruments as a source for the historical study of music theory. The figure of Pythagoras, and his alleged penchant for the monochord, offers a way into this exploration of the theory-bearing dimensions of instruments. Musicians tend to think of instruments primarily in terms of music-making, but in other contexts instruments are, more broadly, tools. In the context of scientific experimentation, specifically, instruments help researchers come to terms with “epistemic things”—objects under scrutiny that carry specific (but as yet unknown) sources of knowledge within them. Aspects of this experimental practice can productively be transferred to the study of music theory and are explored in two test cases from different periods of musical theorizing (and instrument building): Nicola Vicentino’s archicembalo from mid-sixteenth century Italy, and Henry Cowell’s rhythmicon from early twentieth-century America.
Copyright © 2016 Society for Music Theory
1. Pythagoras musicus
[1.1] With his emblematic monochord Pythagoras ruled music and the cosmos. As its name suggests, the monochord (monos = single, chordê = string) is a very simple instrument, consisting of little more than a string stretched out from one side of a wooden plank to the other so it can freely vibrate. The length of the string can be divided by means of a moveable bridge to effect changes in pitch. In the collective imagination, Pythagoras of Samos—the mythical philosopher, mathematician, and founder of a religious cult, who may (or may not) have walked the earth from ca. 570–ca. 495 BCE—had long been associated with this instrument and was often hailed as its inventor.(1) This connection between the philosopher and his monochord only grew stronger over time, so much so that the late Roman statesman, philosopher, and musical thinker Cassiodorus (ca. 485–ca. 585 CE) awarded the Greek philosopher the honorific “Pythagoras musicus.”(2) Despite his undeniably strong affinities with arithmetic, Pythagoras was particularly associated with music throughout the Middle Ages and into the early modern period, in ways that parallel the astronomer Ptolemy with his emblematic planetary rulers, or the geometer Euclid with his compass.
Figure 1. Mythical acoustic experiments on a variety of instruments, from Franchinus Gaffurius, Theorica musicae (1492, Bk. 1, Ch. 8)
(click to enlarge)
[1.2] Thus it is not too surprising to see a detailed four-panel woodcut giving pride of place to a music-making Pythagoras in Figure 1. This image appears in the Theorica musicae (1492) by the North Italian humanist Franchinus Gaffurius (1451–1522), one of the first music theory books to appear in print. What we see, however, takes some time to decode. If we did not know that Pythagoras’s emblem was the monochord, it would be hard to recognize the musical instrument in the bottom left panel. The six-string instrument, which Pythagoras plays with two sticks, resembles more a zither-type instrument, such as a psaltery or a hammered dulcimer, than the traditional ancient instrument. Is this really still a monochord?(3) At a more detailed level, the Pythagorean implications of the image, however, are clear beyond any doubt: the weights hanging down on the left side of the instrument follow a series of numbers that can be recognized as Pythagorean without problem: 4–6–8–9–12–16. It seems the six-string monochord represents the technological and logical extension of the principle that Pythagoras discovered in ancient times, according to legend.
[1.3] The legend in question—a primal scene of music—originated with the Greek philosopher Nicomachus of Gerasa (ca. 60–ca. 120 CE), and has Pythagoras lift the secret of sound serendipitously, as he walks past a smithy and hears the harmonious clanging of four hammers on anvils, weighing 6, 8, 9, and 12 units of weight (Barker 1989, 256–58). This story, which determines the ratios of the consonant intervals of the octave, fifth, and fourth at 2:1 (= 12:6), 3:2 (= 12:8 and 9:6), and 4:3 (= 12:9 and 8:6), was transmitted throughout the Middle Ages and well into the mid-sixteenth century, primarily in Boethius’s influential variant, and need not be further rehearsed here.(4) For all the numerical beauty of the Pythagorean ratios, we know that the account is apocryphal, as the underlying physics is problematic: the relationship between the weight of a hammer and the pitch it produces suggested by the illustration does not hold. It is now well known, too, that the story in the smithy never happened in this way. It is very unlikely that Pythagoras—or anyone in the ancient world—ever cared to carry out this experiment. Nor is there any real reason to assume they should have done: Pythagoreanism is best understood as a religion, not as an empirical science.(5) In fact, it would take until the sixteenth century for someone to “fact-check” this story and to correct the physical basis of the claim: Vincenzo Galilei (1520–1591), father of Galileo, first conducted acoustical experiments to test the Pythagorean claims that had been perpetuated, unchallenged, for more than a millennium. For instigating this groundbreaking change in scientific thought and paving the way for a turn to empiricism, Galilei senior, not junior, has been hailed by some scholars as the first modern experimental scientist.(6)
[1.4] Pythagoreans’ primary interest, as far as we can ascertain from the historical record, was not in music as such, but in that which lies beyond the sounding phenomena. Aristotle wrote, derisively, that the Pythagoreans understood even the heavens in terms of musical scales [harmoniai] and numbers (Metaphysics, 1.986a). But this is no mere empty, dismissive hyperbole: Pythagoreans were primarily interested in music insofar as it was an expression of the numerical relations that held the cosmos together. Music was for them inextricably connected to astronomy, via arithmetic and geometry—the subjects that were to be joined in the medieval quadrivium. The sounds and the experience of music, as later ancient commentators such as Ptolemy never got tired of complaining, were secondary to Pythagoreans; sounding music only got in the way of the perfection and beauty of ratios.(7) The attribution of the monochord to Pythagoras, as its inventor, did not come to the fore until the much later accounts by Diogenes Laertius (3rd century CE), Gaudentius (prob. 4th century CE) and Boethius (480–524/5 CE) (see Creese 2011, 90). By the time Gaffurius picks up the topic, in the context of fifteenth-century humanism, he can make an elegant pun:
In this way, Pythagoras discovered the monochord rule [regula], which gets its name “rule” from the object not because a rule is made of wood or brass and we measure sounds and magnitudes with it but because a rule is a certain fixed and stable observation that leaves the judgment in no doubt. It is so named from “ruling” [regendo], as if it ruled us in such a way that we cannot fall into error.(8)
The monochord is also known as kanôn or regula (which means rule or ruler in Greek and Latin); Gaffurius’s statement “regulam invenit” can mean either: he “found the rule” or he “invented the monochord.” Both versions would be equally true.
[1.5] Returning to the initial image, what kind of instrument is Pythagoras’s six-string monochord? While the presence of multiple strings would not in itself have been as striking at the time, we are now in a position to dig a little deeper with regard to the number six. What appears unusual in Gaffurius’s version is the expanded number of strings on which Pythagoras plays. But in going beyond the four of the original legend, Gaffurius weaves an interesting new twist into the story. By adding the outer strings, labeled 4 and 16, he expands the range of the instrument to 2 octaves (8:4, 16:8), and considerably expands the possibilities of Pythagorean intervals between pairs of strings, which are laid out in the table below. (The ratios in square brackets mark compound variants of the simple intervals.)
| Octave | 8:4 | 12:6 | 16:8 | [16:4] |
| Fifth | 6:4 | 9:6 | 12:8 | [12:4] |
| Fourth | 8:6 | 12:9 | 16:12 | [16:6] |
| Whole tone(9) | 9:8 | [16:9] | [9:4] |
[1.6] On what authority did Gaffurius make these changes? Gaffurius offers a disarmingly simple explanation in the text of his treatise for why he believed that Pythagoras had extended the range of his monochord to six strings. To understand this better, we have to go back to Boethius’s powerful retelling of the story, on which Gaffurius based his own theorizing. In Boethius’s variant of the smithy myth, Pythagoras encounters not four, but five hammers. This fifth hammer is dissonant, Boethius explains, in ways that cannot be reconciled with Pythagorean principles, and Pythagoras quickly discards it. In this way, by adding a new hammer to the story and immediately discarding it again, Boethius further underlines the necessity for perfect numbers and for eliminating any element that might disturb their harmony. Boethius’s rhetorical flourish seems to highlight, above all, that exactly four hammers are needed, not more or less. But Gaffurius turns this rhetorical maneuver against itself by making explicit reference to the “fifth” hammer.(10) On the basis of Boethius’ influential variant, Gaffurius concludes:
We may suppose that Pythagoras himself entirely changed the inconsonant fifth hammer into another and added a sixth above the fifth, which has been established in the number 4, which would surpass all others in smallness of weight and also a sixth hammer, which would exceed all the others, that is, in the number 16.(11)
To paraphrase Gaffurius: if, as Boethius relates, Pythagoras temporarily exceeded the number four, even on a trial basis, he must surely have realized that adding two more hammers would greatly increase the number of possible intervals. Gaffurius blithely overlooks any new complications that his additions introduce; he seems mainly excited about the extended range of intervals that a fifth and sixth hammer would allow.
[1.7] No longer does the fifth hammer function as a marker of an outer boundary that cannot be exceeded, as it did for Boethius, but rather it becomes the basis of further experimentation. What is more, Gaffurius manages to give this old story its new twist without ever so much as questioning Boethius’s supreme authority, but rather building on it. “In this manner,” Gaffurius sums up his excursion and expansion of the Pythagoras myth, “he found out that when these different weights were laid out, all the musical consonances were contained solely in the multiple and in the superparticular ratios; and the heavier hammers sounded against the higher in a certain mutually corresponding order, so that both returned to the sense of hearing with an established dimension by presenting out of the different blows a single consonant sound.”(12) In Gaffurius’s hands, Pythagoras represents nothing so much as the spirit of perfectibility in the realm of numbers. Gaffurius’s Pythagoras, in a word, offers an improved and perfected version of the cosmos.
[1.8] Gaffurius emphasizes the wide applicability of this universal Pythagorean principle. In the remaining panels of Figure 1 he shows the Greek philosopher in a number of different musical situations, which all closely reflect Boethius’s retelling of the myth. In the bottom right corner Pythagoras is joined by his disciple, the philosopher and mathematician Philolaus, in playing a number of pipes. Even given the scant reliable biographical information we have about these two figures, it seems very unlikely that Philolaus (ca. 470–ca. 395 BCE) would have overlapped with Pythagoras, but in this context we probably do not need to lose much sleep over such details. The lengths of the pipes are in the same proportions as his sixfold monochord. The images are very explicit about the ratios: all units carry numbers. In the top right corner of the woodcut two Pythagorean figures can be seen striking bells and tapping glasses of water, according to the same proportions. Claude Palisca has pointed out that these images, despite the display of mathematical rigor, are mostly physically false: in fact, the intervals formed by the bottles and bells are not governed by the ratios of their dimensions in the simple way suggested by the numbers in the woodcut, just as the weight of the hammers was eventually found to be unrelated to the resulting pitches. Only the pipes actually correspond to acoustical reality (Palisca 1985, 229).
[1.9] The most striking panel of the woodcut is the top left image. This is probably the first panel viewers look at; it therefore carries particular rhetorical weight. We see the famous scene in the blacksmith’s workshop; the hammers carry the same numbers. But the person listening to the anvils being struck is not the ancient Greek figure of Pythagoras, but the biblical figure of Jubal, the “ancestor of all who play the harp and flute,”(13) and who is often regarded as the inventor of music in biblical chronology.
[1.10] This displacement might seem surprising, particularly since the accompanying text, Book I of Theorica musicae, is primarily concerned with Pythagoras, and only brings in Jubal fleetingly at the very end of this discussion, almost as an afterthought. It is not until much later in the treatise, in Book V, that Gaffurius clarifies Jubal’s foundational role in his text.(14) To be sure, no precedent is found in the ever-authoritative Boethius. But it is possible to reconstruct the reasons for this choice. The question of primi inventores, or prôtoi heuretaí as they were called in Greek, the “first inventors” of the ancient world, came to the fore again during the humanist revival during the fifteenth century as a central concern. Ancient cultural techniques—such as fire-making, agriculture, ship-building, bronze-casting, and music-making—had to be explained by creating a firm association with a mythical, divine, or heroic figure who could count as its first inventor.(15) In the context of humanism, however, such questions of primacy became a contested space between ancient sources on the one hand—that is to say, pagan myths—and biblical authority on the other. By opting for Jubal as the ultimate inventor of music, Gaffurius managed to pass the crown to biblical authority, even though nothing in the text prepares the reader for this maneuver.(16)
[1.11] But this displacement also gives rise to another possible conclusion, which is possibly more troubling. The woodcut in Gaffurius’s Theorica musicae visually separates the primal scene in the noticeably disorderly smithy from the other scenes. Jubal is looking on, quite literally overseeing the six blacksmiths as they hammer away. Meanwhile, the multiple Pythagorases in Figure 1 are seen to explore the more strictly musical implications of the discovery of the mathematical secrets of sound. Pythagoras is actively engaged, playing the bells, a kind of glass harmonica, the flutes, and the six-string monochord. Where Jubal examines noise, Pythagoras performs music.
[1.12] We know that Gaffurius followed Boethius’ lead in valuing the musicus, the scholarly musician, over the cantor, who merely performs music by singing or playing without reflecting on it.(17) In drawing such a clear visual distinction between Jubal and Pythagoras, and between the science of sound on the one hand and the practice of music on the other, the image from Gaffurius’s Theorica musicae actually presents us with a problem: the music-making Pythagorases of Figure 1 appear more as cantores—that is, they seem to fall on the wrong side of the scholar/performer divide. From this perspective, the zither-like six-string monochord with which we started, and which is rather more versatile than the traditional one-stringed version, serves to underline this impression. This technologically improved instrument seems to allow Pythagoras to perform music, and he seems to relish his task as a musical virtuoso. Has Pythagoras musicus really become Pythagoras cantor? Has he been degraded to a mere performer? Or is this all a mistake?
2. The Monochord as Instrument and System
[2.1] How far can we take this idea of Pythagoras as a practicing musician, against any Boethian admonitions? We know the monochord was used as a measuring device in ancient Greece, but was it in fact used as a musical instrument? The question, strange as it may seem, is not without precedent. An early-twentieth-century student of classical philology, Sigfrid Wantzloeben, advanced the thesis in his German doctoral dissertation, Das Monochord als Instrument und als System (1911), that Pythagoras was actually a performer of the monochord, which he regarded as a musical instrument.(18)
[2.2] Wantzloeben’s Exhibit A is precisely the passage from Nicomachus that began the Pythagorean myth: Pythagoras rushes home from the smithy to test his newly found knowledge about music on a number of devices: “cymbals [krousin(19)], flutes [aulous], pan pipes [syringas], monochords, triangular harps [trigona], and others like them.”(20) Wantzloeben notes that Nicomachus mentions the monochord among a list of other instruments that could be used in musical performance, and concludes that the monochord must itself have been an instrument on which music was performed (1911, 2). (Like many other commentators, Wantzloeben is relatively indifferent to the complicating factor that Nicomachus wrote this some six centuries after Pythagoras’s time.) Other pieces of evidence Wantzloeben offers are highly questionable; his interpretations often hinge on distinctly dubious translations.(21)
[2.3] Perhaps the best evidence that Wantzloeben could have marshaled from ancient Greek texts in support of his bold hypothesis are a few negative comments from later commentators, such as Ptolemy, who argues that the monochord makes a rather lousy musical instrument. The fact that Ptolemy felt moved to include this passage suggests that there were indeed some efforts to use the monochord as a makeshift musical instrument (see Barker 1989, 341 and 497n14). There is no reason, however, to assume that this had anything to do with Pythagoras at all.
[2.4] For all its obvious problems, however, there is a kernel of a good idea in Wantzloeben’s hypothesis, which is the same thesis that we just read out of Gaffurius’s illustration: music theorists do well to take musical instruments seriously. They are embodiments of theoretical ideas about music. All musical instruments carry theoretical properties, and it can be instructive to consider them in terms of what they can tell us about music on a more abstract level. From this angle, Wantzloeben gets one thing exactly right: “the monochord as an instrument and as a system,” as the title of his thesis runs in English. The specific question of Pythagoras’s role as a performer is something of a red herring (as even Wantzloeben seems to come close to admitting occasionally) that in fact distracts from a more important point. The main interest is in the double function of the instrument itself.
[2.5] The idea that I want to pursue here is nothing other than the literal meaning of “instrument”—or, for that matter, organon, as the Greek has it. At the heart of our concept of the instrument is the Latin verb instruere, to construct or equip, just as ergon, or work, is the cognate of the Greek organon.(22) That is to say, an instrument is a device that allows us to accomplish something, to work; it is an implement or a tool.(23) In our case, musical instruments can be, quite literally, instrumental in shaping thoughts and ideas about music.
[2.6] In a musical context, this leads us to a double meaning of the term “instrument.” On the one hand, we have the tool, or indeed the “measuring rod” (Barker 1989, 256) that Pythagoras sought in Nicomachus’ story: in a word, a device that can tell us something about how music as a system works. In this case, the device tells us about how some of the most fundamental musical intervals can be derived and quantified. On the other hand, we have the musical instrument on which compositions or improvisations can be performed. In the case of the monochord, this performative function is at best rudimentary (and at worst fanciful)—which is exactly why the early modern representations of Pythagoras in Gaffurius’s work piqued our interest initially—but the principle of performance, of engaging in musical activities, is clearly a chief aspect of musical instruments. Instruments are the site of performance as well as of theorizing.
[2.7] To return to the Boethian distinction with which we ended the previous section: we can put aside our worries about the musicus/cantor division, we don’t need to decide—it is not an either/or. As Wantzloeben correctly pointed out, the monochord serves as both instrument and musical system. And, as Gaffurius knew, regula or kanôn means simultaneously the rule that governs music and the instrument from which it is derived. Our investigation of instruments will cheerfully explore both aspects, and the interactions between both sides, which can be at times intricate.
3. Music-Theoretical Instruments
[3.1] Musicology has recently rediscovered its interest in musical instruments. John Tresch and Emily Dolan revived the venerable discipline of organology, the study of musical instruments, by calling for a “New Organology” (Tresch and Dolan 2013). As the moniker “new” underlines, the main interest is not classificatory or taxonomic, which was one of the chief tasks of the “old” organology, but rather exploratory and interpretive. What exactly is an instrument? Following Bruno Latour’s clarion call to rethink the sociology of science, Tresch and Dolan, a team consisting of a historian of science and a musicologist, propose that in both music and science, instruments are not passive or transparent, but possess agency, taking an active part in social networks. My ambition here is a little less wide-ranging than theirs, though it shares some of their central concerns. I am specifically interested in exploring what instruments can tell us about the musical system in which they operate: in other words, the epistemic aspects of instruments. What can instruments tell us about musical knowledge? How can we “read” an instrument? How do instruments help us understand what music is? Without offering specific answers for now, instruments are useful objects for this kind of inquiry because they can work on two epistemic levels, which we could variously contrast using any of the following pairs: hearing and counting, sensing and cogitating, empiricism and logic—or, to return to our earlier distinction: cantor and musicus.
[3.2] Since the “musical” aspect (in the modern experiential sense) of the instrument is more likely to be self-evident, it is perhaps useful to take a closer look at the “scientific” sense in which I am thinking of instruments here. Several influential figures from the study of science provide important impulses. Historian of science Simon Schaffer and sociologist Steven Shapin both fundamentally re-examined the creation and communication of knowledge during the scientific revolution, highlighting the specific role of the instrument within scientific experimentation during that period.
[3.3] In several groundbreaking studies focusing on such central figures from the Scientific Revolution as Isaac Newton (1642–1727) and Robert Boyle (1627–1691)—in other words, areas that seemed to be exhaustively known—Schaffer and Shapin drew attention not so much to the results of the scientists’ work, but the ways in which they got their results (see Shapin and Schaffer 1985 and Schaffer 1989). Following a famous pronouncement by the French philosopher of science Gaston Bachelard (1884–1962) that instruments are nothing but “materialized theories”(24) (théorêmes réifiées), they stressed that the experimental set-up, sometimes down to the precise make of the instruments, played a major role for the generation of scientific knowledge. They showed how in the work of Boyle and Newton the fundamental status of the experiment changed, from a demonstration that merely illustrates a scientific phenomenon but is of no further relevance to scientific knowledge, to an integral part in the process of discovery and theory-making.
[3.4] In the case of Newton’s Opticks, the experimentum crucis, the critical experiment upon which the authority of the scientific claim hinged, was entirely dependent on the make of the prism. This was more complicated than we imagine, since prisms were widely available, the stuff of fairground attractions, but even small flaws in the glass would ruin the experimental outcome. Newton himself relied on high-quality prisms imported from the Netherlands, but it is not surprising that other researchers trying to replicate Newton’s experimentum crucis failed in their efforts. Understandably, they were quick to find fault with Newton’s hypothesis. Schaffer shows how much work and effort Newton put into convincing his correspondents that the experiment must be replicated precisely and that the physical properties of the prism are decisive for the success of the experiment and hence the scientific theory. These studies helped usher in a new disciplinary paradigm for the history of science, a field that had traditionally been particularly interested in a history of discoveries, progressively unfolding, as scientific understanding marches on through time. By contrast, it had been much less interested in the process of experimentation leading up to these discoveries, and in the material conditions that made them possible in the first place.
[3.5] How do we adapt this idea for our purposes? Of course, Schaffer and Shapin were talking about a very specific moment—indeed, a turning point in the history of science, the Scientific Revolution in the seventeenth century—and it is hardly an accident that their interest focuses on Newton and Boyle, figures who occupy a central position in the canon of the history of science. It is important to bear in mind that the experimental method of the Scientific Revolution is specific to this period—in fact, this is what makes the Scientific Revolution—and it would be wrong to generalize broadly, outside of this specific context. That said, we fare better if we turn this thought on its head: we remember that the Pythagoreans showed no interest in experimental proof of the numerical hypothesis. And as we saw earlier, the fabled story of Pythagoras in the smithy—and with it, the entire physical basis on which the Pythagorean arithmetic paradigm rested—was questioned by Vincenzo Galilei, precisely during the first stirrings of the Scientific Revolution in Italy.
[3.6] Galilei’s new critical angle suggests that the significance of the monochord changed. It would be foolhardy to argue that for a millennium and a half, Pythagoreans from Nicomachus to Zarlino had used or thought about the monochord illegitimately, and that Vincenzo Galilei finally put an end to this faulty usage. Rather, what it suggests is a fundamental reconfiguration of the two questions of what the monochord is purported to show and what status is assigned to its demonstrative power. It is perhaps useful to think of this shift as a change from an arithmetic way of thinking to a physical one, from an abstract, numerical approach to an empirical one. This is an important difference. It was the Pythagorean worldview—with its faith in universal correspondences and its liberal associations—that assigned music its place beside astronomy, geometry, and arithmetic, which ushered in the medieval quadrivium. And from a strictly arithmetical point of view, the mechanics of the instrument are irrelevant; the sound that the monochord produces, the experiential dimension of its effects, is at best incidental. The mathematical distinction between epideixis (demonstration) and apodeixis (proof) springs to mind here.(25) For Pythagoreans, the monochord was simply a device whose existence was enough to underline the universal validity of the mathematical ratios that they believed to underlie all worldly phenomena, from the smallest to the largest scale. In fact, even in the ancient world Pythagoreans were regularly taken to task for the chasm that opened up between their painstaking calculations and the scant relevance these precise proportions bore with respect to musical practice (see Creese 2012).
[3.7] Only in Galilei’s hands did the monochord become part of an experimental design in a context that can be understood from the perspective of modern science. Of course, this did not change overnight the way in which the monochord was used. Cosmological models, such as Robert Fludd’s famous celestial monochord from Utriusque cosmi historia (1617–24), which outlined the traditional Great Chain of Being, from divine beings and angels via stars and planets all the way to humans and animals, continued to feature it, sometimes prominently so. But the idea of correspondences or resemblances that determined so much of Pythagorean thinking all the way to the Renaissance and that proceeded on the basis of analogical or symbolic thinking, was on the way out. As it became harder and harder to bring together musical intervals and divine celestial order, new constellations between numerical ratios and sound as an empirical phenomenon—that is, as a perceptually verifiable object—emerged as powerful and convincing arguments. From this perspective, Johannes Kepler’s foundational astronomical treatise Harmonices mundi (1619), in which the third law of planetary motion is proposed, with explicit reference to the Music of the Spheres, is perhaps best understood as a final grandiose gasp of the Pythagorean worldview that succeeded in holding the quadrivium together for the best part of a millennium.
4. What Kind of “Thing” Is A Music-Theoretical Instrument?
[4.1] What does it mean to consider instruments from the perspective of scientific inquiry—or perhaps better, knowledge acquisition—as well as from their musical qualities? As Pythagoras puts on his white lab coat, metaphorically speaking, and starts experimenting with his monochord, it makes sense to draw on another model borrowed from the history of science. Hans-Jörg Rheinberger (1997) developed a concept of the “epistemic thing” to describe an important aspect of the process of scientific experimentation. Rheinberger emphasizes “the power of material objects—in contrast to ideas or concepts—as driving forces in the process of knowledge acquisition” (2005, 406). The epistemic thing is a material object, phenomenon, or process that arouses our curiosity and that, within an experimental system, holds a certain knowledge that can be uncovered by the scientist. The “epistemic thing” is neither identical with the mere phenomenon or material object, nor with the scientific instrumentarium used to examine it; the epistemic thing only emerges as the conjunction of both. What makes Rheinberger’s concept so productive is that these epistemic things possess a certain fundamental “fuzziness” or “blurriness” (Verschwommenheit). There is no a priori epistemological content that the researcher extracts from the thing under scrutiny; the thing itself does not exude knowledge.(26) Keenly avoiding the problem of determinism, Rheinberger argues that the epistemological value of the epistemic thing is only constituted by its place and interaction within the experimental system; it is contextually and historically determined.(27)
[4.2] There is a steadily growing body of reflections on the epistemology of the “thing,” not least nurtured by a resurgent interest in a materialistic perspective. Sometimes “thing” and “object” are used interchangeably (see, for instance, Chang 2011). The art historian W. J. T. Mitchell, however, cautions: “objects are the way things appear to a subject—that is, with a name, an identity, a gestalt or stereotypical template. . . . Things, on the other hand, [signal] the moment when the object becomes the Other, when the sardine can look back, when the mute idol speaks, when the subject experiences the object as uncanny and feels the need for what Foucault calls ‘a metaphysics of the object, or, more exactly, a metaphysics of that never objectifiable depth from which objects rise up toward our superficial knowledge” (quoted in Bennett 2010, 2). Objects, it is generally agreed, are characterized by a certain passivity, in that they require a contemplating subject, whereas Things are characterized by an irreducibility to objects, in that they have an existence in their own right, which may imbue them with agency, as Bruno Latour underlined (1993). And Bill Brown reminds us, in a more poetic vein, that things are “encountered” and never quite apprehended (2001). The epistemologies underlying these various approaches to “thingness” fall along a continuum between idealism and materialism, with Bachelard’s “reified theorems” reaching over into the material world from a firmly held position at the idealist end of the spectrum, and Rheinberger’s “epistemic things” erecting their superstructure from a materialistic base.(28)
[4.3] And in the musical realm? We can see how certain aspects of this epistemology can easily be adapted to musical purposes. Just as certain scientific phenomena, especially those existing below the level of perception, must be brought to our attention, examined, and understood with the aid of scientific instruments, so certain musical phenomena can only be subjected to theoretical scrutiny when they manifest themselves as sounds, produced by musical instruments. Anyone who has taught an introductory music theory class knows about the importance of the piano in explicating music-theoretical concepts. Or, for a somewhat more specialized example, Anna Gawboy (2009) has traced the rise of the Wheatstone Concertina accordion as the instrument of choice among the acoustically inclined members of the Royal Society in Victorian Britain—making it surely the most ennobled music-theoretical instrument. We should be careful not to construct a simple cause-and-effect schema. The difficulty in deciding between apodeixis and epideixis in the realm of music is symptomatic here: does sounding music “prove” or “demonstrate” a music-theoretical proposition? As we will see, different scenarios require different epistemological regimes. Perhaps the best way out of this dilemma, for now, is to think of the instrument as functioning as a filter that allows certain propositions to be made in sound, while inhibiting certain others.
[4.4] Whereas the piano clearly plays a supreme music-theoretical role, it is often less common instruments that are theoretically most interesting.(29) The monochord is a representative example here—leaving aside the dogged question of whether it should count as a musical instrument or not. But there is no doubt that it gives us valuable insights about how music works. The monochord contains, and makes readable, some of the fundamental systemic aspects on which music draws. In producing sounds, it also produces knowledge about music. This is the essential function of a music-theoretical instrument.
[4.4] In this model, in other words, we can imagine musicians becoming veritable scientists experimenting with instruments to uncover musical knowledge and to demonstrate its principles in sounds. We will examine two short examples of musical experimentalists from different historical periods: the first is Nicola Vicentino (1511–1575 or 76) and his archicembalo, which was constructed in the 1530s, and the second is the rhythmicon, an instrument that was devised in the 1930s by the American experimentalist composer Henry Cowell (1897–1965) and his collaborator, the Russian inventor Leon Theremin (1896–1993). The point here is not to construct a coherent history of music theory or an organological survey, but to show the diversity of possibilities. It goes without saying that, in principle, every musical instrument is also a music-theoretical instrument. But it is not the case that every musical instrument carries very useful insights about the musical system in which it operates. (A rattle or a triangle, for instance, will hold limited music-theoretical information of interest.) The more interesting examples, at least for our exploratory purposes, tend to be the more experimental ones: they are often those that go beyond a conventional notion of what music is or can be, precisely because in testing the limits they show us most clearly what is at stake.
5. The Archicembalo
[5.1] Our story about the archicembalo centers on a strange bet.(30) At a private concert in Rome given by the influential banker Bernardo Acciaiuoli-Rucellai, at his palace on the Tiber in May of 1551, a polyphonic Regina coeli was performed. In the wake of this concert, two musicians in the audience started an argument: Nicola Vicentino, household musician in the service of Cardinal Ippolito ii d’Este (1509–1572), Cardinal of Ferrara, and the papal singer Vicente Lusitano (d. after 1561). These two were engaged in a discussion about whether the Regina coeli belonged to the diatonic genus or not. It is possible that Lusitano was the composer, in which case he would have had a personal stake in this debate, but we do not know this with any certainty.(31) As the discussion quickly got heated, it was decided that a formal debate between the two musicians should settle this question once and for all. The agreed wager was two gold scudi, a handsome amount of money at the time. Three judges were appointed to adjudicate the debate. In the event, one of the judges, the Netherlandish musician Ghiselin Danckerts (1510–1567), was called out of town and had to miss the actual debate. In response to a request by Danckerts, Vicentino sent him a short written statement immediately, whereas Lusitano apparently took more time to write a much longer letter outlining his position. This discrepancy struck Vicentino as unfair—especially after Lusitano was declared the winner of the debate. The affair turned bitter soon. Both Vicentino and judge Danckerts continued to hold a grudge for several years and published their respective versions of the heady events of 1551, even in multiple versions.(32) One of the sticking points seemed to have been a definitional issue. As Maria Rika Maniates observes, Vicentino’s written and notarized account insisted on specifying the diatonic genus as “purely diatonic music” or musica diatonica semplice, a term that was not included in the original documents signed by the judges and four witnesses.(33) (Vicentino’s document was also signed by four witnesses, three of which were the same as the official document.) Danckerts noticed the discrepancy and took great exception to Vicentino’s tampering with the documents. Why would Vicentino make this apparently petty distinction, and why would it matter so much?
[5.2] Vicentino took a rather complicated position on the question of diatonicism: he argued that the chromatic and enharmonic genera of the ancients were never abandoned by musicians, but that they had instead been fully internalized and were being used unconsciously.(34) Every time a singer sang the interval of the minor third, or the “incomposite trihemitone,”(35) Vicentino argued, they would unwittingly employ the chromatic genus, and when they sang a major third, or the “incomposite ditone,” they were in the enharmonic genus. In itself this is a strange claim that seems hard to defend, since these intervals can easily be constructed within the diatonic genus. From this perspective it should come as no surprise that Vicentino was widely held to have lost the debate. But this is not to say that Vicentino’s argument was completely baseless. However complicated it may be, it is possible to reconstruct his case—around his music-theoretical instrument, the archicembalo.
Figure 2. Examples of tetrachords in Vicentino’s three genera, from L’antica musica, 3.45. Other configurations are possible.
(click to enlarge)
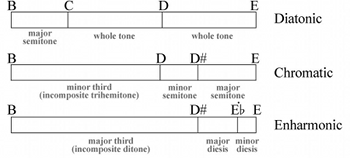
[5.3] We can approach Vicentino’s claim by considering his perspective on ancient genera and the way in which he imagined tetrachords, the basic unit of ancient Greek music. Jonathan Wild (2014) has recently provided a lucid account of Vicentino’s complex theory, which I will use as a basis here. Figure 2 shows diagrams of tetrachords in the three genera and the relations between them. The diatonic genus is quite straightforward, consisting of one semitone and two whole tones. The chromatic tetrachord is composed of a minor third and two semitones. The enharmonic tetrachord consists of a major third and two dieses (two microtonal intervals, which together make up a diatonic semitone). To mark these microtones, Vicentino had to invent a new notational convention: he added a dot over the note, indicating that it is raised by one minor diesis. While these genera may look familiar from Greek music theory, the detail of Vicentino’s ideas puts an interesting, indeed revolutionary, twist on these concepts.
[5.4] One major difference from ancient conceptions is that Vicentino’s genera can smoothly be converted from one into another.(36) Vicentino is quite specific about how these transformations work: the semitone of the diatonic genus is transformed into the minor third of the chromatic or the major third of the enharmonic genus. This may appear counterintuitive, if we expect these transformations to be parsimonious—similarity of interval size or short voice-leading distances do not seem to matter here. Instead, Vicentino’s rule of thumb is to put “the big step in the location of the small diatonic one, and the small steps in place of the big diatonic ones.”(37)
[5.5] Given this transformative potential, it is useful to approach Vicentino’s tetrachords from the perspective of their smallest constituents, the minor diesis. It is this lowest common denominator that allows Vicentino to move between genera smoothly and effortlessly.(38) During the Renaissance the diesis commonly describes the minute interval that separates one tone from its enharmonic neighbor.(39) Vicentino specifically defines the diesis as “exactly one-half of the minor semitone”(40)—or, expressed in modern mathematical terms, √(18:17). This innocent definition is more explosive than it may at first appear: the Pythagorean tradition held that irrational numbers—which at that time could not be expressed arithmetically, only derived geometrically—were inadmissible as musical intervals.(41) Even two decades later, after the dust of the Rome debate had long settled, the Spanish music theorist Francisco de Salinas (1513–1590) would condemn Vicentino particularly for straying from the path of rational numbers.(42)
Figure 3. Vicentino divides each whole tone into five microtones
(click to enlarge)
Audio Example 1
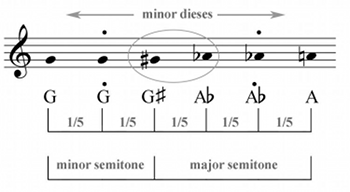
[5.6] But despite offending orthodox Pythagoreans, this definition certainly had practical advantages. As Figure 3 shows, Vicentino used the convenient fact that this diesis corresponds almost perfectly to a fifth of a whole tone, and systematized it by dividing up the whole tone into five equal microtones (Audio Example 1 provides a demonstration). On the basis of this rigorous subdivision of the whole tone, it is possible to conceptualize the three tetrachords from the ground up, starting with the smallest unit, the minor diesis. Each tetrachord consists of thirteen such dieses, which are differently distributed across the sounding intervals. Going back to Figure 2, we can recapture the diatonic tetrachord as 3 + 5 + 5 minor dieses, the chromatic as 8 + 2 + 3, and the enharmonic as 10 + 2 + 1. The whole octave is subdivided in this system into 31 minor dieses (5 whole tones and 2 diatonic semitones, that is, 5 × 5 + 2 × 3 = 31). Vicentino’s transformational conception of genera has some important consequences: if the basic building block of all three tetrachords is the minor diesis, and we can move freely between them, then we can only distinguish between the genera by means of the characteristic intervals that they employ.
[5.7] These background considerations put Vicentino’s bet against Lusitano in a somewhat different light. It turns out that Vicentino phrased his claims very carefully: every time we employ a melodic major third, we are in Vicentino’s enharmonic genus, and every time we employ a minor third, we are in his chromatic genus. Or, put more sharply: we know by sounding these characteristic intervals that we cannot but be in the respective genus. It is also interesting that Vicentino keeps quiet in this public debate about the other intervals of the chromatic and enharmonic genera. The minor chromatic semitone (2 dieses) is mathematically identical to the major enharmonic diesis; the two intervals only derive their different meanings from the genera in which they are employed; they cannot therefore define the genus. This interval can only shed its ambiguity when it is paired with the respective other small interval from each genus: the major semitone of the chromatic genus, or the minor diesis of the enharmonic genus. The major semitone is similarly ambiguous, as it is shared between the diatonic and chromatic genera. The only remaining unique interval is the minor diesis, the controversial “irrational ratio” on which Vicentino’s system is founded. Needless to say, he does not highlight the diesis in his bet—though, in any case, it probably helps that the diesis is not employed as a melodic interval in conventional sixteenth-century music.
[5.8] But this hedging gets us to the heart of the argument: Vicentino’s conception of what music is, or should be, was fundamentally different from the music that existed. (One can hardly blame the sixteenth-century Romans in attendance at the debate between Lusitano and Vicentino for being mystified by these ideas.) As Wild observes, it offers a “tantalizing glimpse of an alternative pathway for musical development,” drawing on a greatly extended microtonal pitch collection (2014, [1]). Vicentino’s scale, with its 31-fold division of the octave, not only covers the three genera (albeit in Vicentino’s idiosyncratic understanding) but it also presents a closed system, spanning the entire enharmonic system over 31 fifths. In his own assessment, his system had the advantage of offering “a greater abundance of steps, consonances and harmony.”(43) He was convinced that he had made a major discovery—no less than the perfect division of music.
[5.9] In his subsequent reflection on the debate, Danckerts commented on the extreme secrecy under which Vicentino operated.(44) Despite the likely bias of this testimony from a hostile juror, this observation sounds fairly plausible: the careful framing of Vicentino’s bet suggests that he was convinced that his claims must reflect some fundamental truth about music, and that he was unwilling to reveal the principle—the 31-fold division of the octave—on which this insight was based. It seems that this secrecy was a major contributing factor to losing the bet: Lusitano and the opposing side had no insight into the very specific, idiosyncratic meaning of his terms. From a conventional music-theoretical perspective, Vicentino’s claims simply do not stand up to scrutiny and seem close to nonsensical.
[5.10] Meanwhile, Vicentino was hard at work developing polyphonic music that would make use of its full microtonal potential. As Wild points out, his compositions go a long way toward clarifying Vicentino’s understanding of the three genera: adherence to one specific order of the tetrachord, that is to say, to one fixed pitch collection, was not important. Instead, it was the intervals employed in each voice that mattered: any minor third and semitonal movement, major or minor, across the 31-tone gamut constituted the chromatic genus, and major third and movement by either of the dieses constituted the enharmonic genus (Wild 2014, [32]).
[5.11] It is the 31-tone division that is at the heart of Vicentino’s ideas about music, which gave him the confidence—the ludicrous overconfidence, one might say—that made him engage in the fateful bet with Lusitano. The material manifestation of this idea was the archicembalo, a microtonal harpsichord that Vicentino probably first developed in the 1530s, several years before the public debate and the publication of his theories in L’antica musica ridotta alla moderna prattica (1555).(45) This was his experimentum crucis.
Figure 4. Vicentino celebrates his accomplishments with a medal. The recto shows his profile, the verso shows his two instruments, the archicembalo and the arciorgano. The medal marks him as the “inventor of the perfect division of music.” (From Morton & Eden, Auction Catalog 59, November 13–14, 2012.)
(click to enlarge)
[5.12] As the fifth and final book of his treatise details, the archicembalo is a harpsichord with two manuals. Each manual has three orders of keys, including several divided ones: the lower manual has 19 and the upper 17 keys to the octave. (There are some complicating factors with the keyboard layout, notably the confusing fact that Vicentino adds five more keys than necessary for his tonal system, so that his keyboard has thirty-six keys to the octave. The remaining keys are not part of the tonal system, but allow for purer harmonies, and they need not concern us here.) In 1561 Vicentino also presented a similar organ, which he called the arciorgano; the machinations behind both instruments are comparable (Kaufmann 1961). Keyboard instruments with divided keys that distinguished enharmonically between sharps and flats had been around for some time, but the lengths to which Vicentino went with his instruments were all but unprecedented (Barbieri 2008). His two instruments must have seemed like the philosopher’s stone to Vicentino. In fact, he was so proud of his accomplishment that he had a coin forged, reproduced in Figure 4, showing his profile on one side and his instruments on the other. His instruments instantiated his ideas about music, making it possible to perform polyphonic music in any of the three genera—and to switch freely between them.(46) What is more, given that the backbone of his musical system was the irrational diesis, there was no way for him to explain his principles by arithmetic means—at least not according to the Pythagorean principles at the time.(47) The validity of his musical system, with its transgressive √(18:17), could be demonstrated in sounds, but not by numerical proof.(48) The only way to understand Vicentino’s music, and its underlying principles, was to hear it—and for that, the archicembalo was crucial.
[5.13] One major obstacle that Vicentino had to tackle in order to put his complex microtonal system into practice was that singers are not very good at picking out the exact interval of one-fifth of a tone. Vicentino, whose surviving compositions are vocal, conceived his music very much along instrumental lines. He complained: “O how immeasurably excellent would music be if singers . . . could intone and sing a composition as accurately as the organ!”(49) Vicentino was working intensively with a group of singers to train them to intone his microtonal intervals precisely. He had sworn the singers to secrecy, under threat of steep fines, lest they give away his revolutionary ideas. To be sure, this extreme precaution raised several eyebrows among Vicentino’s detractors (Palisca 1994a, 276).
[5.14] He insisted that all music, vocal and instrumental, should be based on his principles. But given the technical complexities of this musical system, and the difficulty singers had in intoning his fifth tones correctly, this instrument was clearly the backbone, the embodiment, of Vicentino’s ideas.(50) Vincenzo Galilei, a voluble critic of Vicentino, recalls the trouble the singers had with this enharmonic music:
If by misfortune one of the singers lost his way while singing, it was impossible to put him back onto the right spot. . . . Thus this kind of music necessarily required an instrument to guide the voices of the singers through unknown paths, not to say through precipitate cliffs. (Galilei 1980, 166)
Apart from the disparaging tone, Vicentino might even have agreed: he also recommended that vocal music be always accompanied by instruments.(51)
[5.15] The archicembalo was in every sense instrumental to Vicentino’s theory.(52) It alone could produce the required intervals that made the theory a musical reality.(53) His instrument was very much a “materialized theory,” in Bachelard’s sense as we encountered it above. Where musical experience was in conflict with established scholarly authority, it was clear which way Vicentino would turn. He admitted—in something of an understatement—that certain theoretical positions were not in accordance with Boethius, the foremost musical authority of Vicentino’s age, but they were certainly in agreement with his instrument.(54) But this was all that mattered: the archicembalo, which allowed listeners to experience his idea of music, functioned as the ultimate epistemological authority in his musical universe.
[5.16] The sixteenth-century debate swirling around Vicentino got stuck on the question of whether or not human voices could be trained to sing intervals as small as fifth tones (Maniates 1992, 91). That historical discussion is not quite the same point we are raising here; the issue is less about the capacity of the human voice and more about what such training should be based on—it is a question of “turtles all the way down”: the demonstration, the epideixis, of the feasibility of polyphonic music within a 31-tone system is ultimately dependent on the existence of an instrument that can produce those tones precisely and unambiguously to train those voices. Vicentino wore his epistemological heart on his sleeve when he speculated on the origin of musical intervals: “It is probable that the first person to discover the way to sing the distance of the steps of the whole tone and semitone . . . could not have done so without the expedient of an instrument.”(55) The same is true for the archicembalo and Vicentino’s challenging music. A better invocation of the epistemic thing is hard to imagine.
[5.17] To return to Vicentino’s musical bet in Rome in 1551, all things considered, it is probably understandable that the judges were not convinced by Vicentino’s radical ideas. These were experimental ideas in every sense, and they clearly contradicted Boethius’ weighty authority. It is also understandable why Vicentino would insist on the “purely diatonic genus,” and why this fastidious distinction was lost on everybody else. He had very particular ideas about how music worked or should work, ideas that took several decades to be seriously considered, and another two centuries to become worked out in their music-theoretical implications.(56) Even though he felt it was too early to lift the shroud of mystery to the public that surrounded his “perfect division of music,” Vicentino was convinced all along that he was right. For him, the proof was in the pudding, or rather in his archicembalo.
6. The Rhythmicon
[6.1] The second case study, Henry Cowell’s rhythmicon, takes us to Berkeley, California, ca. 1915, where Cowell, then a young composition student, was working with the ethnomusicologist Charles Seeger (1886–1979). Seeger introduced him to polyrhythms, but Cowell became increasingly disillusioned by the inability of human musicians to execute these complex rhythms precisely. He wrote:
It is highly probable that an instrument could be devised which would mechanically produce a rhythmic ratio, but which would be controlled by hand and would therefore not be over-mechanical. For example, suppose we could have a keyboard on which, when C was struck, a rhythm of eight would be sounded; when D was struck, a rhythm of nine; when E was struck, a rhythm of ten. (Cowell [1930] 1996, 65–66)
Cowell’s opening tag “it is highly probable” should be read as tongue-in-cheek, since he knew quite well that the underlying mechanism had long existed. After all, earlier in the same text, Cowell had explained, enigmatically but perfectly accurately:
There is a well-known acoustical instrument which produces a sound broken by silences. When the silences between the sound occur not too rapidly, the result is a rhythm. When the breaks between the sound are speeded, however, they produce a new pitch in themselves, which is regulated by the rapidity of the successive silences between the sounds. (Cowell [1930] 1996, 51)
The well-known acoustical instrument he was thinking of was the mechanical siren, which had been around for a hundred years.
[6.2] Let us briefly rewind from twentieth-century American experimentalism to nineteenth-century French engineering. In 1819 Charles Cagniard de la Tour (1777–1859) presented his latest invention, which he called the sirène (Cagniard de la Tour 1819). It was originally not the warning signal of modern life that we all know today, but rather an experiment to test the theory of sound generation. At the time, following Ernst Chladni and Thomas Young’s important work on acoustics, it was agreed that all musical sounds had to follow the model of wind or string instruments, which set up a standing wave of regular oscillations of pressure changes in positive and negative directions around a neutral zero point (which can be represented graphically by sinusoids of varying degrees of complexity).(57) The siren, by contrast, produced sound in a radically different way, which can best, if anachronistically, be described as “digital”: the siren created a series of alternating on and off impulses, just as Cowell described.
Figure 5. A popular introduction to the mechanism of the siren, from Harper’s New Monthly Magazine (1872).
(click to enlarge)
Video 1. Demonstration of Caignard’s siren, from the National Museum of American History, Smithsonian Institution, Washington DC.
(click to watch)
Figure 6. The ratio 3:2 corresponds to the interval of the fifth. Opelt’s multiphonic siren shows how the compound rhythms, translated into spatial sequences of dots, as shown on the right, produce two (or more) sounds. (The circular diagram included in Figure 7 shows this pattern in its second ring from the center.)
(click to enlarge)
Video 2. A demonstration of Opelt’s siren, from Florence Science and Technology Foundation (FirST, Firenze Scienzia e Technica)
(click to watch)
Figure 7. Even chords can be captured as compound rhythms. The ratio 4:5:6:8, first marked by arrows along the harmonic series, then translated into a sequence of holes, corresponding to the compound rhythm of our complex ratio, and finally projected onto a schematized siren disc.
(click to enlarge)
Figure 8. Henry Cowell’s friend Joseph Schillinger behind the rhythmicon (1932). Photo now held at Stanford University.
(click to enlarge)
Audio Example 2
Figure 9a. The opening of Henry Cowell’s Quartet Romantic (1915) codifies a major harmony in four voices in the pulsating rhythms of each part
(click to enlarge)
Figure 9b. In his own analysis of Quartet Romantic, Cowell decodes the rhythmic structure of his music into higher-order harmonies
(click to enlarge)
[6.3] Figure 5, taken from a popular science article in Harper’s New Monthly Magazine, shows how the siren works (Anonymous 1874). As the cross-section shows, air is blown through a bellows at the bottom of the device. The air passes through a metal disc with diagonal holes, which sets another metal disc on top in rotation. This rotating disc also has holes at regular intervals. Every time the air passes through the holes an air puff will be released. (Two counters at the top keep track of the number of rotations.) When the air pulses are slow, we hear them as a series of regular pulsations, a steady rhythm. But when the rotation speed passes 20 impulses per second, in other words: 20 Hz, our ear converts these fast rhythms into a pitch, which rises as the frequency increases. (Cagniard’s siren in action can be heard in Video 1.) That’s the familiar noise of the siren. The principle was nothing short of revolutionary: the siren demonstrated that the two musical parameters, rhythm and pitch, are in fact not separate dimensions at all, but exist on a continuum.
[6.4] The scientific world was aghast when Cagniard’s siren began to wail and scream, but he had made his point (Hilgers 2003). The siren was the perceptual proof that pitched sounds could be created out of rhythmic pulsations, depending on whether the patterns that created them were presented above or below the auditory threshold around 20Hz. For Caignard, this phenomenon was a mere side effect, which he did not pursue any further. But the idea of a rhythm-pitch continuum genuinely excited musicians.
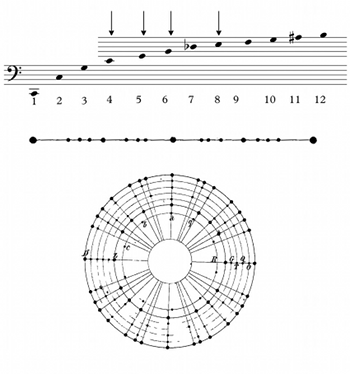
[6.5] It was left to other thinkers, scientific and musical, to explore the implications for music, of which the Ohm-Seebeck debate is the best-known scientific dispute (see Turner 1977). But in the musical world it is worth drawing attention to the little-known figure of Friedrich Wilhelm Opelt (1794–1863), a state official, astronomer, and hobby music theorist. Opelt erected a whole conception of how music works on the basis of the mechanism of the siren, which caused all-too-brief excitement in the 1830s.(58) Opelt made the startling claim that the siren provided the mechanism to explain all aspects of music, by which he meant rhythm, pitch, and harmony. Building on the knowledge that multiple frequencies could be sounded simultaneously on one disc, Opelt experimented with multiphonic sirens and explored the effects of merging two separate frequencies into one. Take the simple hemiolic rhythm two-against-three, as shown in Figure 6. We know from Pythagoras that this ratio corresponds to the interval of the fifth. This compound rhythm can be imprinted on a siren disc. When rotating at sufficient speed, the 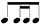 rhythm will turn into the interval of the fifth. It makes no difference whether the frequencies are kept separate on the disc or combined.
rhythm will turn into the interval of the fifth. It makes no difference whether the frequencies are kept separate on the disc or combined.
[6.6] The same is obviously true for other ratios as well. Opelt produced a disc with multiple different frequencies happening at the same time. This multiphonic siren can be heard in Video 2. The circular illustration included in Figure 7 shows Opelt’s diagram for bores in the ratio 4:5:6:8. The four circles marked G, T, Q, O (for Grundton, Terz, Quinte, Oktave) describe the separate regular frequencies, and the outermost circle outlines the irregular compound rhythm of all four put together. We also see this compound rhythm, translated into spatial distances and laid out on a straight line, in the middle portion of Figure 7. As the siren demonstrates, this complex rhythm 4:5:6:8 is the same as a major triad in close position with its octave doubled.(59)
[6.7] Fast-forwarding back to early-twentieth-century California, all these ideas stood behind Cowell’s call for a new musical instrument that would couple specific rhythmic pulsations with specific pitches. Around 1930 Cowell found a congenial collaborator for this project in the inventor and Russian émigré Leon Theremin, who had made a name for himself with his eponymous electrical instrument, and who created the rhythmicon on the basis of Cowell’s ideas. Depicted in Figure 8, apparently the rhythmicon was originally conceived as little more than a “highly sophisticated metronome” (Lichtenwanger 1986, 132), and it is now sometimes hailed as the first-ever beat machine—but both these characterizations miss some of the central features of the instrument, especially as regards pairing rhythms with pitches. Early reviews, it is true, suggest that the original instrument, demonstrated at the New School in New York City on January 19, 1932, had very little to offer in the way of pitch or timbre, and various commentators were particularly concerned about improving the pitch dimension.(60) But its conception was clearly as a musical instrument: Cowell and his friend Nicolas Slonimsky (1894–1995) composed a number of pieces for it, including Cowell’s own Concerto for Rhythmicon and Orchestra.(61) A historic recording of the rhythmicon, from the holdings of his friend Joseph Schillinger (1895–1943) that now survives in the Smithsonian Institution, is presented as Audio Example 2.
[6.8] Like the siren, the mechanism of the rhythmicon is based on two metal discs with varying numbers of holes arranged in regular intervals. (62) As Slonimsky describes, by “manipulating a rheostat with a rudimentary crank, the performer automatically produced precise synchronization of the harmonic series, the number of beats per time unit being equal to the position in the series. . . . The result was an arithmetically accurate synchrony score of 32 different time pulses” (Slonimsky 1971, 1495).
[6.9] We can see how Cowell’s rhythmicon pursues effectively the same phenomenon as Opelt’s musical siren a hundred years previously, with one important difference: the rhythmicon had a keyboard attached to the mechanism, which made it playable as a musical instrument, with fixed pitches and rhythms. Charles Ives (1874–1954), who financed the development of the rhythmicon, expressed relief that the device was “nearer to an instrument than a machine.”(63) The presence of the keyboard no doubt had a lot do with its status as a musical instrument.(64) The keyboard suggested visually and haptically that the sounds would qualify as musical.
[6.10] As a composer, Cowell was clearly excited by this correlation between his musical intervals and rhythmic pulsations. He used this principle as the basis of youthful Quartet Romantic (1915–17).(65) This composition, for two flutes and two violins, works on two levels at the same time: the four instruments play freely atonal melodies at fixed rhythms, but the rhythms themselves contain encoded pitch information, so that the proportions between these rhythmic pulsations outline an underlying tonal structure. To give just one example, in Figure 9a, the first measure juxtaposes 6, 5, 4, and 2 pulsations, ratios that correspond to a major triad over a root in the bass. These rhythms actually encrypt a fully tonal Bach-style chorale in four parts, a secret meta-composition that remains unheard by human ears, along the lines indicated in Figure 9b. It is true that this piece does not sound remotely like a Bach chorale. But we could imagine etching the compound rhythms onto an Opelt siren and speeding them up. Played at a sufficiently fast tempo, the proportions of this secret music would become audible as (admittedly, extremely short-lived) harmonies.
Conclusions
[7.1] Turning to the bigger questions, what does the examination of musical instruments as deeply engaged in the process of musical theorizing do for us? What good is this “material” turn within theory? Let’s take a wider look at the cultural history of music theory. One of the key issues that the field has battled with for some time is its relationship with specific musical repertoires. Attempts to relate theorists from the past to the composers of their own time, to map historical theories onto contemporaneous composers, tend to be relatively frustrating, quite simply because our interests do not necessarily align: the questions that we, in the twenty-first century, ask of music are not necessarily the same ones that the figures from the past were interested in (see Judd 2000/01). A historically more sympathetic and musically more sensitive approach is a fundamental necessity.
[7.2] By incorporating music-theoretical instruments into our investigations, as I suggested earlier, we turn the theorist’s study into something like a scientist’s laboratory—or perhaps, depending on the period we are discussing, something akin to natural philosophers and Wunderkammern. In operating with sounds, with the materials that make up what we usually mean by music, these music-theoretical instruments are located somewhere between compositional practice, theoretical speculation, and experiential listening. It is no coincidence that the two examples discussed here, from the mid-sixteenth and the early twentieth centuries, are taken from periods of intense experimentation. But this is not to say that other, less intellectually fluid periods, would not be open to this kind of inquiry. Any number of other possible scenarios suggest themselves—and they are not restricted to the West: the Chinese 12 lü 十二律 or the Arabic oud عود are prime examples of music-theoretical instruments in other cultures.
[7.3] Ultimately, the issue of how a music-theoretical instrument works is always a matter of the specific questions we ask of the music and of the theory. A precise answer changes from historical period to historical period—or, if you will, from one Foucauldian episteme to the next—and also from instrument to instrument. Certain recurring factors and issues, however, are noticeable. First of all, instruments tend to come to the fore whenever human performers reach their limit—pitch accuracy in Vicentino’s case or rhythmic accuracy in Cowell’s case. The instrument, as an object located outside the human sphere, can make greater claims to objectivity (in every sense conceivable) and is therefore a preferred argumentative strategy (see Gallison and Daston 1992). At times, this necessity to hold human intervention at bay, or remove it altogether, is counterbalanced by a concern at the other end of the spectrum: if no human input is required, is it still music that we hear? This concern is voiced from time to time, and the specter of the dehumanized machine, fed by essential humanistic anxieties, invariably looms large behind those concerns. This suggests that the desired epistemic objectivity of music-theoretical instruments operates in a force field that is determined by a carefully calibrated balance between human agency on the one hand, which expresses itself in (soulful) music-making, and the dehumanized, soulless machine on the other.
[7.4] Second, all these music-theoretical instruments rely in some sense on a scientific—or, more broadly, numerical—conception of sound. This seems fundamentally alien to much of the work that we are familiar with in contemporary musicological and music-theoretical thought. The figure of Pythagoras is more than emblematic here: the numerical way of thinking about sound, which plays such a small part in today’s musical discourse, is fundamental to virtually all music-theoretical instruments. Since this fundamental conception feels so unfamiliar to us, we would do well to learn to appreciate the subtleties between different conceptions. Not all number-based approaches to sound are Pythagorean, and as we saw above, there are important distinctions between an abstract mathematical way of conceptualizing sound and physical-acoustical ones—even though from our modern perspective, the similarities between them seem by far to outweigh the differences.
[7.5] And third, we would do well to reconsider the relationship between music-theoretical instruments and the music theory they occasion. Our starting point, Pythagoras playing the monochord, provides a good example here. Classicist David Creese, after carefully reviewing the ancient sources mentioning Pythagoras and the monochord, concluded that there was no contemporaneous evidence that Pythagoras actually used the monochord. He noted that the first document to make the connection between the two was the very passage from Nicomachus we encountered initially. Nicomachus, it should be remembered, lived some six centuries after Pythagoras, so his testimony was at best based on hearsay passed down the generations. Nicomachus’ claim has been repeated uncritically throughout the centuries, and over time Pythagoras even morphed into the inventor of the instrument. Tempting as it is, we should not assume that the monochord was around when the math at the basis of musical relations was first worked out. It became an object of scientific experimentation much later than the mathematical relations it proved. Creese concludes forcefully: “[D]oing mathematical harmonics without the monochord was not only possible, but. . .there is no credible ancient evidence to suggest that there was any other way to study the subject before the late fourth century.(66) He points out that the “mirage” that Pythagoras operated with, or even invented, the monochord has been consistently fed by the assumption that the discovery of harmonic ratios and the invention of the monochord must have been concurrent. The monochord seems to serve no other purpose than to measure and demonstrate the ratios of musical intervals, which encouraged authors from late antiquity to the most recent past to assume a concurrency or even causal relation.
[7.6] In a word, Pythagoras did not play the monochord. We can put this myth to rest once and for all. Loosening the firm ties between Pythagoras and his monochord, between theorist and instrument, will also allow us to revisit two parts of our earlier methodological observations: we defined the music-theoretical instrument, on the one hand, in terms of Bachelard’s “materialized theory,” and on the other, in terms of Rheinberger’s “epistemic thing.” In fact, the two models are at opposite ends of the spectrum of possibilities: while Bachelard considers the instrument to be the reified embodiment of a theory, Rheinberger conceptualizes the instrument as a material object that allows certain theoretical propositions to issue forth. Put differently, Rheinberger is Marx to Bachelard’s Hegel. Yet, this does not mean in this exploration of music-theoretical instruments that we must make a firm commitment to one position or the other. It is not necessary that the machine gives rise to or emerges from a theory, but rather that it can embody or exemplify it. In the two examples at play we saw two different ways in which the instrument was featured: in the case of Vicentino and the archicembalo, the instrument was the linchpin that held musical theories and practice together in a situation where the paradigm of unassisted vocal music necessarily failed. In the case of Henry Cowell and the rhythmicon, by contrast, we saw how the instrument explicitly piggy-backed on mechanical devices that had been around for a century and transformed some preexisting theories of music into a practical application that could then be used in composition. All of these instruments are linked by the fact that they put to the test a specific idea about how musical sound works—how it can or should work. In this way, theorizing, composing, and hearing come together, in often surprising ways. Other cases are possible in which musical instruments fulfill the function of “epistemic things” and provide us with musical knowledge—if we only know how to make use of them: either by performing experiments on them, or music, or both.
Alexander Rehding
Harvard University
Department of Music
3 Oxford Street
Cambridge, MA 02138
arehding@fas.harvard.edu
Works Cited
Adkins, Cecil D. 1963. “The Theory and Practice of the Monochord.” Ph.D. Thesis, State University of Iowa.
Anon. 1874. “The Siren of Science; Or the Mode of Numbering Sonorous Vibrations.” Harper’s New Monthly Magazine 270: 844–49.
Bachelard, Gaston. 1984. The New Scientific Spirit, tr. Arthur Goldhammer. Beacon Press.
Barbera, André. 1984. “The Consonant Eleventh and the Expansion of the Musical Tetractys: A Study of Ancient Pythagoreanism.” Journal of Music Theory 28: 191–223.
Barbieri, Patrizio. 2008. Enharmonic Instruments and Music 1470–1900. Levante.
Barker, Andrew. 1989. Greek Musical Writings, Volume 2: Harmonic and Acoustic Theory. Cambridge University Press.
Bennett, Jane. 2010. Vibrant Matters. Duke University Press.
Berger, Karol. 1980. Theories of Chromatic and Enharmonic Music in Late 16th Century Italy. UMI Research Press.
Beyer, Robert. 1999. 200 Years of Acoustics. Springer.
Blackburn, Bonnie, and Edward Lowinsky, eds. 1991. A Correspondence of Renaissance Musicians. Clarendon.
Blankenburg, Quirinius van. 1739. Elementa musica of niew Licht. Laurens Berkoske.
Boethius, 1989. De Institutione Musica. Tr. as Fundamentals of Music by Calvin Bower. Yale University Press
Brown, Bill. 2001. “Thing Theory.” Critical Inquiry 28: 1–22.
Cagniard de la Tour, Charles. 1819. “Sur la Sirène, nouvelle machine d’acoustique destinée à mesurer les vibrations de l’air qui constituent le son.” Annales de chimie et de physique 12: 167–71.
Cassiodorus. 537. Variae epistolae.
Chang, Hasok. 2011. “The Persistence of Epistemic Objects Through Scientific Change.” Erkenntnis 75: 413–29.
Chladni, Ernst F. 1802. Die Akustik. Breitkopf und Härtel.
Cohen, H. Floris. 1984. Quantifying Music: The Science of Music as the First Stage of the Scientific Revolution 1580–1650. Reidel.
Cordes, Manfred. 2007. Vicentinos Enharmonik: Musik mit 31 Tönen. Akademische Druck- und Verlagsanstalt.
Cowell, Henry. [1930] 1996. New Musical Resources, ed. David Nicholls. Cambridge University Press.
Creese, David. 2011. The Monochord in Ancient Greek Harmonic Science. Cambridge University Press.
—————. 2012.“Instruments and Empiricism in Aristoxenus’ Elementa harmonica.” In Aristoxenus of Tarentum, ed. C. F. Huffman, 29–63. Transaction.
Danckerts, Ghiselin. n.d. [ca. 1551]. Sopra una differentia musicale. Bibliotheca Vallicelliana, Ms R 56A.
Drake, Stillman. 1970. “Renaissance Music and Experimental Science.” Journal of the History of Ideas 31: 483–500.
Feest, Uljana. 2011. “Remembering (Short-term) Memory: Oscillations of an Epistemic Thing.” Erkenntnis 75: 391–411.
Fludd, Robert. 1617–24. Utriusque cosmi historia. 4 vols. Oppenheim: Johann Theodor de Bry.
Gaffurius, Franchinus. 1492. Theorica musicae. Milan: Filippo Mantegazza for G. P. da Lomazzo. Tr. Walter Kurt Kreyszig as The Theory of Music. Yale University Press, 1993.
Galilei, Vincenzo. [1591] 1980. Discorso intorno all’uso dell’enharmonio. Tr. in Frieder Rempp, Die Kompositionstraktate des Vincenzo Galilei. Arno Volk.
Gallison, Peter, and Lorraine Daston. 1992. “The Image of Objectivity.” Representations 40: 81–128.
Gawboy, Anna. 2009. “The Wheatstone Concertina and Symmetrical Arrangements of Tonal Space.” Journal of Music Theory 53/2: 163–90.
Gotham, Mark, and Iain Gunn. 2016. “Pitch Properties of the Pedal Harp.” Music Theory Online 22.4.
Heller-Roazen, Daniel. 2011. The Fifth Hammer: Pythagoras and the Disharmony of the World. MIT Press.
Hilgers, Philip von. 2003. “Sirenen: Lösungen des Klanges vom Körper.” Philosophia Scientiae 7/1: 85–114.
Humpert, Hans Ulrich, and Herbert Eimert. 1973. Lexikon der elektronischen Musik. Gustav Bosse.
Judd, Cristle Collins. 2000/01. “The Dialogue of Past and Present: Approaches to Historical Music Theory.” Intégral 14/15: 56–63.
Kaufmann, Henry W. 1961. “Vicentino’s Arciorgano: An Annotated Translation.” Journal of Music Theory 5: 32–53.
Kepler, Johannes. 1619. Harmonices mundi. Linz: Gottfried Tampach.
Kleingünther, Adolf. 1933. Πρῶτος Εὑρετής: Untersuchungen zur Geschichte einer Fragestellung. Dieterich’sche Verlagsbuchhandlung.
Kreysig, Walter Kurt, trans. 1993. The Theory of Music by Franchinus Gaffurius. Yale University Press.
Latour, Bruno. 1993. We Have Never Been Modern. Harvard University Press.
Lichtenwanger, William. 1986. The Music of Henry Cowell. Institute for Studies in American Music.
Maniates, Maria Rika. 1992. “Bottrigari versus Sigonio: On Vicentino and his Ancient Music Adapted to Modern Practice.” In Musical Humanism and Its Legacy, ed. Nancy Kovaleff Baker and Barbara Russano Hanning, 79–107. Pendragon Press.
Maniates, Maria Rika, trans. 1996. Ancient Music Adapted to Modern Practice by Nicola Vicentino, ed. Claude Palisca. Yale University Press.
Mastrocola, Giordano. 2013. “Vicente Lusitano entre histoire et historiographie: nouvelles perspectives.” In Chanter sur le livre de la Renaissance, ed. Philippe Canguilhem, 58–78. Brepols.
McKinnon, James. 1978. “Jubal vel Pythagoras: Quid sit inventor musicae?” Musical Quarterly 64/1: 1–23.
Mead, Rita. 1978. Henry Cowell’s New Music 1925–1936. UMI Research Press.
Macrobius. n.d. Commentarii in Somnium Scipionis.
Münxelhaus, Barbara. 1976. Pythagoras musicus. Verlag für systematische Musikwissenschaft.
Netz, Reviel. 2003. The Shaping of Deduction in Greek Mathematics. Cambridge University Press.
Nicholls, Roger. 1990. American Experimental Music 1890-1940. Cambridge University Press.
Opelt, Friedrich W. 1834. Ueber die Natur der Musik. Leipzig: Hermann und Langbein.
Palisca, Claude. 1985. Humanism in Italian Renaissance Musical Thought. Yale University Press.
—————. 1994a. “A Clarification of Musica reservata in Jean Taisnier’s Astrologiae, 1559.” In Studies in the History of Italian Music and Music Theory, 239–280. Clarendon.
—————. 1994b. “Scientific Empiricism in Musical Thought.” In Studies in the History of Italian Music and Music Theory, 200–235. Clarendon.
Pesic, Peter. 2010. “Hearing the Irrational: Music and the Modern Conception of Number.” Isis 101/3: 501–30.
Pinch, Trevor, and Frank Trocco. 2004. Analog Days: The Invention and Impact of the Moog Synthesizer. Harvard University Press.
Quintilianus, Aristides. n.d. De musica.
Rehding, Alexander. 2016. “Three Music Theory Lessons.” Journal of the Royal Musical Association 141/2: 251–82.
Rheinberger, Hans-Jörg. 1997. Towards a History of Epistemic Things. Stanford University Press.
—————. 2005. “A reply to David Bloor: ‘Toward a Sociology of Epistemic Things’.” Perspectives on Science 13: 406–10.
Rippe, Volker. 1981. “Nicola Vicentino und seine Instrumente: Versuch einer Erklärung.” Die Musiktheorie 34/4: 393–413.
Robel, Ernst. 1891–1900. Die Sirenen. Berlin: Gaertner.
Sachs, Joel. 2012. Henry Cowell: A Man Made of Music. Oxford University Press.
Salinas, Francisco. 1577. De musica libri septem. Salamanca: Mathias Gastius.
Schaffer, Simon. 1989. “Glass Works: Newton’s Prisms and the Uses of Experiment.” In The Uses of Experiment: Studies in the Natural Sciences, ed. David Gooding, Trevor Pinch, and Simon Schaffer, 67–104. Cambridge University Press.
Shapin, Steven, and Simon Schaffer. 1985. Leviathan and the Air Pump: Hobbes, Boyle, and the Experimental Life. Princeton University Press.
Slonimsky, Nicholas. 1971. Music Since 1900, 4th ed. Scribner’s.
—————. (1988). Perfect Pitch. Oxford University Press.
Smith, Leland. 1973. “Henry Cowell’s Rhythmicana.” Anuario Interamericano de Investigaciones 9: 134–47.
Tresch, John, and Emily I. Dolan. 2013. “Toward a New Organology: Instruments of Music and Science.” Osiris 28: 278–98.
Turner, Stephen. 1977. “The Ohm-Seebeck Dispute, Hermann von Helmholtz, and the Origins of Physiological Acoustics.” British Journal for the History of Science 10: 1–24.
Vicentino, Nicola. 1555. L’antica musica ridotta alla moderna prattica. Rome: Antonio Barre. Trans. Maria Rika Maniates, Ancient Music Adapted to Modern Practice. Yale University Press.
Walden, Daniel. 2016. “Daniele Barbaro, Nicola Vicentino, and Vitruvian Music Theory in Sixteenth-Century Italy.” In Daniele Barbaro: Vénitien, patricien, humaniste. Brepols, (in press).
Walker, Daniel Pickering. 1978. Studies in Musical Science in the Late Renaissance. Brill.
Warren, Ambrose. 1725. The Tonometer. J. Cluer and Alex Campbell.
Wantzloeben, Sigfrid. 1911. Das Monochord als Instrument und als System. Halle an der Saale: Ehrhardt Karras.
Wild, Jonathan. 2014. “Genus, Species and Mode in Vicentino’s 31-tone Compositional Theory.” Music Theory Online 20/2.
Winthrop-Young, Geoffrey. 2013. “Cultural Techniques: Preliminary Remarks.” Theory, Culture & Society 30/6: 3–19.
Young, Thomas. 1800. “Theory of Sound and Light.” Philosophical Transaction of the Royal Society 90: 106–28.
Footnotes
* An earlier version of this article was presented as the Peter LeHuray lecture at the 50th RMA conference in Leeds on September 4, 2014. Special thanks go to Joseph Auner, Bevil Conway, Evan McCarthy, Alexander Nikolaev, Steven Rings, Daniel Walden, and the anonymous reviewers whose careful reading of this article has given me the opportunity to sharpen and clarify my points.
Return to text
1. The iconography surrounding Pythagoras and the monochord is explored in Münxelhaus (1976).
Return to text
2. Cassiodorus, Variae epistolae, 1.45.4.
Return to text
3. By the Renaissance, a wide variety of instruments could be called “monochord,” irrespective of the actual number of strings, including even keyboards. See the letters collected in Blackburn and Lowinsky (1991).
Return to text
4. See Boethius 1989, 17–19 (Bk. 1.10-11). Daniel Heller-Roazen (2011) has recently taken up the medieval Pythagoras myth. Gaffurius’s understanding of ancient theory was clearly channeled by Boethius, not earlier sources. He includes a paraphrase of Boethius in Bk 1.8: 4–16, including the additional hammer (Kreyszig 1993, 46).
Return to text
5. As André Barbera suggests, Pythagoras’s standing was such that the ratios not working in practice may even have heightened the mystique surrounding him: “After all, the experiments did work when he performed them” (Barbera 1984, 200).
Return to text
6. There is a sizeable body of literature surrounding the question of whether Vincenzo Galilei should count as an experimental scientist or not. See Drake (1970), Walker (1978, 14–33), Cohen (1984), and Palisca (1994b).
Return to text
7. See Ptolemy, Harmonics Bk. 1, Ch. 5, discussed in Barker (1989, 284–6). To be sure, this should be taken with a grain of salt. As with everything in this discussion, many of the positions rely on later testimonies that were projected backwards.
Return to text
8. Gaffurius, Theorica musicae, Bk. 1, Ch. 8: 34–35, trans. in Kreyszig (1993, 48)
Return to text
9. 16:9 is an outlier, as it describes not the whole tone but the minor seventh, which I have included here for the sake of completeness. Gaffurius does not comment on this scenario.
Return to text
10. To be sure, Gaffurius adds additional late Roman sources, notably Calcidius’s Commentary on Plato’s Timaeus (ca. 321 CE) and Macrobius’s Dream of Scipio (early 5th century). Both these authors allow for more than the orthodox Pythagorean ratios, though neither offers a direct model for Gaffurius’s expansion.
Return to text
11. Gaffurius, Theorica musicae, Bk. 1, Ch. 8: 20, trans. in Kreyszig (1993, 47).
Return to text
12. Gaffurius, Theorica musicae, Bk. 1, Ch. 8: 26, trans. in Kreyszig (1993, 47).
Return to text
13. Genesis 4: 21. The connection to Pythagoras in the smithy is not so far away as it might seem: Jubal’s half-brother Tubal-Cain is “the forger of all instruments of bronze and iron.” See McKinnon 1978.
Return to text
14. See Gaffurius, Theorica musicae, Bk. 5, Ch. 1: 4, trans. in Kreyszig (1993, 144). Note that Gaffurius’s text of Bk 1, Ch. 8: 4 (Kreyszig 1993, 46), confusingly, assigns the smithy story to Pythagoras, even though the picture does not.
Return to text
15. See Kleingünther 1933 and Creese 2011, 85. The concept of “cultural techniques” has recently been foregrounded by German media theorists surrounding Sybille Krämer and Bernhard Siegert; see Winthrop-Young 2013.
Return to text
16. Gaffurius is not the first to make this connection to Jubal. This tradition can be traced back to the Roman historian Josephus. See Palisca (1985, 227), and Münxelhaus (1976, 47–50).
Return to text
17. Boethius, De institutione musica, Bk. 1, Ch. 34, trans. in Bower (1989, 50–51).
Return to text
18. Wantzloeben 1911. He later all but admitted that his documentary evidence was rather thin.
Return to text
19. It is unclear what exactly this word should mean in this context. In their authoritative dictionary, Liddell and Scott translate krousis as “the tapping of earthen vessels, to see whether they ring sound.” Barker renders this, somewhat cautiously, as “beaten pots,” whereas Wantzloeben—who tends to throw interpretive caution to the wind—suggests cymbals. Given this context, I follow those who use a slightly bolder translation that foregrounds the musical aspects, though room for doubt remains.
Return to text
20. Barker (1989, 258); translation modified.
Return to text
21. Exhibit b is a famous passage from Aristides Quintilianus, De musica (Περὶ Μουσικῆς), Bk. 3, Ch. 1: 97.4, trans. in Barker (1989, 497): “At the end of his life, it is said, Pythagoras admonished his friends to play the monochord.” Wantzloeben’s German translation renders the unspecific verb “μονοχορδίζειν” (literally “to monochordize”) tendentiously as “to play the monochord,” no doubt to underline his hypothesis of Pythagoras as a musical performer. The broader translation, “use the monochord,” or “work at the monochord,” which could also include measurements of intervals, would be much closer to the flavor of the original. (This mistranslation has often been accepted uncritically in the literature, see Adkins 1963 and Münxelhaus 1976.) Other such tendentious interpretations can be found throughout Wantzloeben’s thesis.
Return to text
22. For readers interested in etymology: the archaic form of ergon began with a digamma, *werg-, which is unmistakably related to the Germanic Werk and the English work.
Return to text
23. Gaffurius seems very conscious of this etymology: in Bk. 1, Ch. 4: 7 (Kreyszig 1993, 39) he goes so far as to call lung, throat, palate, tongue, lips, and teeth “instruments”—where “organs” (even the Latinized organa) seems a more obvious choice.
Return to text
24. Bachelard 1984, 13. This line, in a more literal translation, functions as an epigraph in Schaffer’s article “Glass Works.”
Return to text
25. For a wider discussion of the epistemological status of proofs in Euclidian science see Netz 2003.
Return to text
26. See especially Feest 2011. Feest’s own reading attributes “blurriness” to concepts, not objects.
Return to text
27. Hasok Chang (2011, 413) highlights this aspect.
Return to text
28. For a further exploration of the epistemic thing in musical contexts, see Rehding 2016.
Return to text
29. For a reconsideration of the piano, see Rehding 2016; for a consideration of the pedal harp, see Gotham and Gunn 2016.
Return to text
30. This story has been immaculately reconstructed by Maria Rika Maniates, in her edition of Vicentino’s Ancient Music Adapted to Modern Practice (1996, xi–lxiii).
Return to text
31. For a detailed and sensitive reconsideration of these documents, see Mastrocola 2013.
Return to text
32. Vicentino’s side of the events is included in his treatise L’antica musica ridotta alla moderna prattica (1555, Bk. 4, Ch.43); see Maniates (1996, 302–14). Danckert’s side exists in three versions, bearing the title Sopra una differentia musicale (Rome: Bibliotheca Vallicelliana, Ms R 56A), nos. 15a, 15b, and 33. See Maniates (1996, xiv–xv).
Return to text
33. Maniates argues that Vicentino did not tamper with the document, and suspects that Ghiselin Danckerts likely fabricated this aspect of the story. It seems more plausible to me that the witnesses did not notice this small difference or did not consider it significant in any way, whereas for Vicentino it made all the difference.
Return to text
34. Vicentino reiterates his claims that most people misunderstand genera and mode in L’antica musica (1555, Bk. 3, Chs. 15 and 48; see Maniates 1996, 150 and 203–4.)
Return to text
35. The terms of Vicentino’s position are outlined in L’antica musica (1555, Bk. 4, Ch. 43; Maniates 1996, 305).
Return to text
36. Karol Berger’s (1980) reading of Vicentino stresses the transformational properties of Vicentino’s theories. In L’antica musica (1555, Bk. 3, Ch. 52; Maniates 1996, 211), Vicentino underlines the transformational nature of genera with the (startling) suggestion that the music examples in his treatise, which are often fully fledged madrigals or motets, be played through multiple times: first without any accidentals, in the diatonic genus, then by adding the chromatic accidentals, and finally by also observing the dots that mark the enharmonic intervals. This point has occasionally caused confusion, since it seems to contradict much of what Vicentino argues elsewhere. From a performer’s perspective, however, this recommendation is probably less paradoxical than it may first appear. The recent collaboration between Peter Schubert and Jon Wild in which they recorded Vicentino’s microtonal music operated along similar lines. See Wild (2014, n51) on the recording and post-production process.
Return to text
37. Vicentino (1555, Bk. 3, Ch. 45; Maniates 1996, 198).
Return to text
38. Vicentino (1555, Bk. 3, Ch. 52; Maniates 1996, 210–11). This is perhaps the biggest departure from ancient theories, which tend to propose separate ratios for each genus, thus foreclosing the option of genera converting smoothly into one another.
Return to text
39. Vicentino’s contemporary Francisco de Salinas, for one, insists that a diesis corresponds to the ratio 128:125. He derives this ratio from the difference between major (16:15) and minor (25:24) semitones. See Salinas (1577, Bk. 2, Ch. 21).
Return to text
40. Vicentino (1555, Bk. 0, Ch. 15; Maniates 1996, 18).
Return to text
41. Vicentino carefully outlines the consequences of this “irrational ratio” for the enharmonic genus (1555, Bk. 3, Ch. 50; Maniates 1996, 207). Pesic 2010 explores the connections between musical intervals such as Vicentino’s diesis and the formulation of irrational numbers in sixteenth-century mathematics.
Return to text
42. For a Pythagorean, imagining the world in cosmic analogies on the basis of perfect proportions, the existence of irrational intervals meant that the cosmos was somehow out of order. (According to Pythagorean lore, Hippasus discovered irrational numbers and was punished by the gods by drowning.) Salinas dedicates a whole chapter of De musica (1577, Bk. 3, Ch. 27) to an excoriation of Vicentino and his archicembalo. Their different interpretation of the diesis is at the heart of this matter.
Return to text
43. Vicentino (1555, Bk. 1, Ch. 8; Maniates 1996, 49).
Return to text
44. Danckerts speculated that Vicentino was hoping for a papal appointment. See Palisca 1994a, 276.
Return to text
45. Salinas (1577, Bk. 3, Ch. 27) indicates that Vicentino’s experiments with the archicembalo occurred “in the last forty years.”
Return to text
46. The tuning of Vicentino’s instrument is often interpreted as 31-tone equal temperament; see for instance, Barbieri 2008, 308–24. Vicentino discusses at least two different tuning systems; see also Rippe 1981, Cordes 2007, and Wild 2014 ([4–9] and n16).
Return to text
47. Maniates notes Vicentino’s reluctance to give a definition of the diesis, which caused much confusion among his detractors and supporters (1992, 99). This coyness is only too understandable, given that his diesis wreaks havoc with Pythagorean certainties.
Return to text
48. Vicentino was aware that he was effectively reviving the age-old discussion between the empiricist Aristoxenus and the mathematical Pythagoreans, as his opening statements on sense versus reason make clear (1555, Bk. 0, Ch. 1; Maniates 1996, 6).
Return to text
49. Vicentino (1555, Bk. 3, Ch. 52; Maniates 1996, 302).
Return to text
50. The recent recording of Vicentino’s music by Manfred Cordes is telling: all the parts except the soprano are performed instrumentally. The lone soprano makes a valiant effort to intone the microtones precisely; the struggle of the voice with the music is an impressive part of the performance. Contrast this with the exquisite rendition under Peter Schubert, which relies on the technology of autotune to produce a performance that exceeds Vicentino’s wildest dreams. (Excerpts can be heard in the sound examples included in Wild 2014.)
Return to text
51. Vicentino (1555, Bk. 4, Ch. 42; Maniates 1996, 300).
Return to text
52. Daniel Walden (2016) particularly explores the connections of Vicentino’s theoretical ideas to the visual arts, and suggests that the archicembalo may be modeled on the perspectival apparatus of Dürer and his contemporaries.
Return to text
53. Salinas’ outrage at the archicembalo, which he called “prava” (crooked or perverse), suggests that he was all too aware that it brought irrational ratios into the world. See Salinas (1577, Bk. 3, Ch. 27).
Return to text
54. Vicentino (1555, Bk. 1, Ch. 15; Maniates 1996, 59).
Return to text
55. Vicentino (Vicentino 1555, Bk. 1, Ch. 12; Maniates 1996, 55).
Return to text
56. Barbieri (2008, 346–47) discusses two circles of fifths based on the 31-tone scale, by Ambrose Warren, The Tonometer (1725) and Quirinius van Blankenburg, Elementa musica of niew Licht (1739).
Return to text
57. See especially Young 1800 and Chladni 1802; see also Beyer 1999.
Return to text
58. Opelt’s theory, Ueber die Natur der Musik (1834) is all but forgotten nowadays. Robel (1891–1900, 5–12) considers Opelt to be foundational, and discusses his contribution in depth. Humpert and Eimert acknowledge Opelt at various points in their Lexikon der elektronischen Musik (1973).
Return to text
59. Technically, all the holes of 4 coincide with those of 8, so the lower octave is not sounded separately, as Opelt recognized in his text. It seems, though, that he did not realize this complication until after he produced the disc.
Return to text
60. See Mead (1978, 188–90) and Nicholls (1990, 140–41).
Return to text
61. A reconstruction of Cowell’s Rhythmicana was premiered in 1971 at Stanford University; see Smith 1973.
Return to text
62. A small number of rhythmicons were built. One instrument, at Stanford, was discarded (to be sure, with Cowell’s permission). Slonimsky sold his instrument to Joseph Schillinger, which ended up at the Smithsonian. A further instrument has surfaced in Moscow—doubtless built by Theremin after his return to the Soviet Union. It can be heard on https://www.youtube.com/watch?v=HkodVcuPVAo. It is possible that this is the same rhythmicon that Joel Sachs located in Budapest, see Sachs (2012, 539n110). The sound quality is notably improved from the earlier instrument of the Schillinger recording.
Return to text
63. See Slonimsky 1988, 151. Similarly, Mead (1978, 190) cites letters in which Cowell tells Ives that the rhythmicon has been accepted as a “real artistic instrument,” “with almost wild acclaim,” “as opening up a field for both music and investigation.”
Return to text
64. Trevor Pinch and Frank Trocco convincingly argue that the presence of a keyboard—clearly signifying “musical instrument”—gave the Moog the edge over other kinds of synthesizer. See Pinch and Trocco 2004.
Return to text
65. The quartet was written around the same time as New Musical Resources, though not published until much later. A detailed analysis is found in Nicholls 1990, 140–48.
Return to text
66. Creese 2011, 92. On the basis of the available evidence, Creese traces the monochord to the Euclidian treatise Sectio canonis (Κατατομὴ κανόνος) dating from the 3rd century bce. Pythagoras is not associated with this instrument in this treatise.
Return to text
Copyright Statement
Copyright © 2016 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
32994