Transformations in Tonal Jazz: ii–V Space*
Michael McClimon
KEYWORDS: jazz, harmony, transformational theory, ii–V–I progression, tritone substitution, “Ceora,” “Blues for Alice”
ABSTRACT: This article presents a transformational model of jazz harmony based on the ii–V–I progression. This progression is fundamental to jazz harmony, and to its improvised performance. It serves as the foundation for a more rigorous transformational approach, developed in the first two sections here. This approach is easily extensible; the final section suggests a few such extensions.
Copyright © 2017 Society for Music Theory
Figure 1a. The bridge of “All the Things You Are” (Jerome Kern/Oscar Hammerstein)
(click to enlarge)
Figure 1b. A four-voice realization of the chord symbols
(click to enlarge)
Figure 1c. Guide-tone lines highlighting efficient voice-leading. (Common tones are indicated by ties)
(click to enlarge)
Figure 1d. Broken into smaller units, highlighting ii–V–I progressions
(click to enlarge)
[0.1] Consider the set of chord changes in Figure 1a: the bridge of Jerome Kern and Oscar Hammerstein’s “All the Things You Are.” If we imagine ourselves for the moment to be jazz improvisers, we might consider approaching this passage in a number of different ways. One approach might be to realize the chord changes as simply as possible (Figure 1b), and then to play a melody highlighting these chord tones. Another might notice the efficient voice-leading implicit in the harmonic structure (Figure 1c), and highlight this in our improvisation. A third might instead divide the music into smaller units, each in a single key (Figure 1d), and use these units as the basis for an improvised melody. These three techniques for understanding the changes are all valid, and an experienced musician might move fluidly among them (and countless others not enumerated here) in the course of an improvisation. This article, though, uses the last of these approaches as a point of departure: many jazz compositions can be described in terms of their constituent ii–V–I progressions, and it seems natural to use this progression as the basis for developing a more general model of jazz harmony.
[0.2] Before getting underway, it will be useful to limit the terms of this study somewhat. The term in this article’s title, “tonal jazz,” combines two potentially confusing elements. As Steven Rings reminds us, “‘tonality’ is at once one of the most familiar and most elusive terms in music-theoretical discourse” (2011, 2), and the word “jazz”—which has been used at various times to describe artists as diverse as McKinney’s Cotton Pickers, Benny Goodman, Sun Ra, John Zorn, Tito Puente, and Brad Mehldau—is not much clearer. Nevertheless, the expression “tonal jazz” seems to come closest to describing the music in which under consideration here: jazz in which traditionally functional harmonic progressions are still the norm. Tonal jazz includes much of the music that most people think of when they hear the word “jazz,” including big-band swing (Count Basie, much of Duke Ellington’s music), bebop (Charlie Parker, Dizzy Gillespie, Thelonious Monk), and the mainstream jazz that followed it (John Coltrane’s early work, Sonny Rollins, Bill Evans, and many others).(1) This definition is admittedly quite broad, but does exclude music like modal jazz (in which harmonic progression is of secondary importance), free jazz (in which sometimes there is no identifiable harmonic progression at all), and various jazz fusion styles (in which the harmonies sometimes do not function in the same way as mainstream tonal jazz).
[0.3] Why, then, should we turn to transformations to analyze tonal jazz? Schenkerian analysis has proven to be a vital tool for analyzing tonal music in general, and Steve Larson’s pioneering work in applying its methods to jazz has led to many productive insights into a wide variety of music.(2) Transformational theory, by contrast, often focuses on music that is perceived to be somehow less tonal. As Rings has it:
Neo-Riemannian analysis—with its focus on local, chromatically striking passages—has led to a view that some works are divvied up into some music that is tonal (for example, because it is well analyzed by Schenkerian methods) and some that is transformational (because it is well analyzed by neo-Riemannian methods). But this is to misconstrue the word transformational, treating it as a predicate for a certain kind of music, rather than as a predicate for a certain style of analytical and theoretical thought. (Rings 2011, 2)
As he is right to point out, there is nothing about transformational theory that necessitates its restriction to this locally chromatic music; his book uses the theory to explain more traditionally tonal music. It is this use of “transformational” that I wish to bring to bear on tonal jazz in the present article.
[0.4] Other transformational approaches to jazz exist, but, as with many transformational approaches for non-jazz repertories, they aim to “model chromatic progressions whose tonal status is somehow in doubt” (Rings 2011, 2). These approaches often focus on artists whose music is less clearly tonal, like Chick Corea (Strunk 2016, Waters 2016), Herbie Hancock (Waters 2005), or Wayne Shorter (Strunk 2003, Waters and Williams 2010); as Rings points out, to use transformational theory to illuminate “specifically tonal aspects of tonal music” (2011, 2) is to go a step further.(3)
[0.5] Likewise, much of the existing neo-Riemannian literature is not very applicable here either: many of those analytical models focus only on triads, and nearly all chords in jazz are (at least) seventh chords.(4) Still, though, it will be useful here to explore those theories that deal in some way with non-triadic music. This work falls into two basic categories: theories that deal exclusively with a single type of chord, and those that deal with musical objects of different types.
[0.6] Most of the studies dealing with a single chord type are concerned with members of set class (0258), the half-diminished and dominant seventh chords. Childs 1998 develops a model for these chord types that is closely related to standard neo-Riemannian transformations on triads; Gollin 1998 (in the same issue of the Journal of Music Theory) explores three-dimensional Tonnetze more broadly, with special focus on the dominant and half-diminished seventh chords. In general, neo-Riemannian-type operations on the (0258) tetrachords turn out to be somewhat less useful than their triadic counterpoints, owing to the inherent symmetry of set class (0258).(5) Any one tetrachordal Tonnetz can only show a subset of all of the (0258) tetrachords, while the familiar triadic Tonnetz of course shows all 24 major and minor triads. Recognizing this limitation, Douthett and Steinbach 1998 presents a model that also includes minor sevenths and fully diminished seventh chords, using a digram they refer to as the “Power Towers” (255–56). While their description accounts for two of the three main types of seventh chords commonly used in jazz (it is missing the crucial major seventh), all of these neo-Riemannian models focus on parsimonious voice leading. While this focus is valuable, it proves to be impractical for the functional harmony that is the focus of this study.
[0.7] The other group of transformational models consists of what Julian Hook (2007a) has termed “cross-type transformations”: he extends David Lewin’s definition of a transformation network to allow for transformations between objects of different types. This category of transformations contains the inclusion transformations (discussed in both Hook 2002 and Capuzzo 2004), which map a triad into the unique dominant or half-diminished seventh chord that contains it and vice versa. Also included here are more general approaches for relating set classes of different cardinalities, including Joseph Straus’s formulation of atonal voice leading (2003) and Clifton Callender’s split and fuse operations (1998). Finally, Dmitri Tymoczko’s continuous tetrachordal space (2011, 93–112) can accommodate all four-note chords, but as Hook (2011, [13–14]) notes, Tymoczko downplays (and sometimes ignores) the transformational aspects of his geometric models.
[0.8] One methodological issue does arise when trying to analyze jazz harmony, using transformations or otherwise: it is often difficult to determine what exactly one should be analyzing. Lead sheets as circulated in fake books can be highly inaccurate, and often cannot be relied upon as a single source for any particular jazz performance, since it is rare that performers play directly from a lead sheet with no modifications.(6) In the case of standards that may have originated outside of jazz (in movies or musical theater, for example), we might wonder whether we should rely on the original sheet music instead. In many cases, however, the version usually played by jazz musicians may be significantly different from the original version, reflecting a history of adaptation by generations of jazz musicians.(7) To make matters worse for the hopeful analyst, this knowledge is often hidden, not written down and learned only from more experienced musicians.
[0.9] Many published jazz analyses rely on transcriptions of particular performances, which can help to mitigate some of these difficulties of the nature of harmony in jazz. Indeed, if one’s goal is to analyze a single performance, a transcription of that performance is often a necessary first step. In this more general study of jazz harmony, though, transcriptions can confuse matters somewhat. The kinds of questions I am interested in answering here are of the type “What can we say about harmony in the piece ‘Autumn Leaves?’” and not of the type “What can we say about Bill Evans’s use of harmony in the recording of ‘Autumn Leaves’ from Portrait in Jazz?” Furthermore, even transcriptions are not definitive when it comes to harmony: the pianist and guitarist might not be playing the same chord; the soloist might have a different harmony in mind than the rhythm section; or the bassist might play a bass line in a way that affects our perception of the chordal root.
[0.10] This is a problem without one clear solution, but for this article, using chord symbols will serve us well. The chord symbol is a basic unit of harmonic understanding for most jazz musicians, even when they are not playing from sheet music. Because of their ubiquity and relative simplicity, chord symbols are able to act as metonyms for the process of harmonic elaboration and reinterpretation that occurs in the course of jazz performance. The chord symbol
1. A Descending-Fifths Arrangement
[1.1] The most common harmonic progression in jazz is undoubtedly the ii7–V7–IM7 progression (hereafter, simply ii–V–I, or often just ii–V). It is the first progression taught in most jazz method books, and is one of the only small-scale harmonic progressions to have an entire Aebersold play-along volume dedicated to it.(9) As noted in the introduction, the progression is so prevalent that many jazz musicians describe tunes in terms of their constituent ii–Vs; a musician might describe the bridge of “All the Things You Are” as being “ii–V to G, ii–V to E, then V–I in F” (recall Figure 1d).
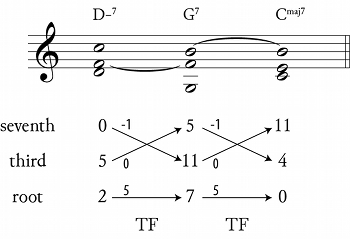
Figure 2. A transformation network for a ii–V–I in C major: Dm7–G7–CM7
(click to enlarge)
[1.2] Figure 2 shows a transformation network for a single ii–V–I progression; I will begin by developing the formal apparatus for this progression, after which we can begin to combine ii–V–I progressions to form a larger musical space.(10) This figure, with its combination of general Roman numerals and specific key centers, is designed to reflect how many jazz musicians tend to talk about harmony; we might read this network as “a ii–V–I in C.” (In this figure, the arrow labeled “TF” stands for the “two–five” transformation, which is explained in detail below.) The combination of Roman numerals and key areas bears some similarity to Fred Lerdahl’s chordal-regional space (2004, 96–97), but Figure 2 is a transformation network, while chordal-regional space is strictly a spatial metaphor.
[1.3] Transformation networks are a major part of Lewin’s project in Generalized Musical Intervals and Transformations (GMIT), and have been thoroughly covered in the literature, so the formalism needs to be considered only briefly here.(11) A transformation network consists of objects of some kind (here, they are chords) represented as vertices in a graph, along with some relations (transformations) between them, represented as arrows. In Lewin’s definition, all of the objects in a transformation network must be members of a single set \(S\), and the transformations must be functions from \(S\) into \(S\) itself (Lewin [1987] 2007, Definitions 9.3.1 and 1.3.1).
[1.4] The transformation TF in Figure 2 is in fact a cross-type transformation, as defined in Hook 2007a. Hook expands Lewin’s definition of a transformation network to include objects of different types, necessary to define transformations in the ii–V–I progression. This progression contains musical objects consisting of three types of diatonic seventh chords: minor, dominant, and major sevenths. Using Hook’s less restrictive definition, we are free to define transformations from any set of objects to any other; to understand the figure above, we need to define the transformation TF such that it maps ii7 chords to V7 chords and V7 chords to I7 chords.
Figure 3. The underlying transformation graph for a single ii–V–I progression
(click to enlarge)
[1.5] Before defining the transformations, however, we need first to define the sets themselves. To help with this, Figure 3 shows the underlying transformation graph of the transformation network in Figure 2. Throughout GMIT, Lewin is careful to distinguish transformation graphs from transformation networks: a graph is an abstract structure, showing only relations between unspecified set members, while a network realizes a graph, specifying the actual musical objects under consideration.(12) Because cross-type transformation graphs contain objects of different types, a node in a cross-type transformation graph must be labeled with the set from which the node contents may be drawn (Hook 2007a, 7). In Figure 3, the nodes are labeled simply \(S\)min, \(S\)dom, and \(S\)maj, which we can understand as the sets of minor, dominant, and major seventh chords, respectively.
[1.6] While at its core the ii–V–I progression contains three types of seventh chords, in reality a jazz musician might add any number of extensions or alterations to this basic structure. Given this practice, defining the archetypal progression as being composed of four-note set classes (seventh chords) seems unnecessarily restrictive. In order to allow for some freedom in the chord qualities, we will consider only chordal roots, thirds, and sevenths; these pitches are sufficient to distinguish the three chord qualities in a ii–V–I.(13)
[1.7] We will represent a chord with an ordered triple \(X = (x_r, x_t, x_s)\), where \(x_r\) is the root of the chord, \(x_t\) the third, and \(x_s\) the seventh. The definitions of the three sets are as follows:(14)
The definitions are intuitive and have clear musical relevance: ii7 chords have a minor third (interval 3) and minor seventh (interval 10), V7 chords have a major third and minor seventh (intervals 4 and 10), and I7 chords have a major third and major seventh (intervals 4 and 11). Defining the chords this way rather than as four-note set classes offers the great advantage of flexibility. Using the ordered-triple representation, the progressions Dm7–G7–CM7 and Dm9(
[1.8] With the space of the nodes defined, we can now formulate the transformation representing a ii–V–I, which we will call simply “TF”:
Figure 4. Voice leading in the ii–V–I progression
(click to enlarge)
| If \(X = (x_r, x_t, x_s) \in \Smin\), | then | \(\mathrm{TF}(X\,) = Y = (\,y_r, y_t, y_s) = (x_r + 5, x_s - 1, x_t) \in \Sdom\) |
| If \(Y = (y_r, y_t, y_s) \in \Sdom\), | then | \(\mathrm{TF}(Y\,) = Z = (\,z_r, z_t, z_s) = (y_r + 5, y_s - 1, y_t) \in \Smaj\) |
Again, these definitions are designed to be musically relevant; the voice-leading diagram in Figure 4 illustrates this more clearly.(15) The root of the second chord is a fifth below (or fourth above) the root of the first (\(y_r = x_r + 5\)), the third of the second chord is a semitone below the seventh of the first (\(y_t = x_s - 1\)), and the seventh of the second chord is a common tone with the third of the first (\(y_s = x_t\)). (We may also write ii7 \(\TFarrow\) V7, rather than TF(ii7) = V7.) Note that the transformation TF is also valid between V7 and I7—the second equation above, involving sets \(\Sdom\) and \(\Smaj\). The fact that the same transformation describes both ii7 \(\to\) V7 and V7 \(\to\) I7 reflects the similarity of the two harmonic motions. In Lewin’s transformational language, if a jazz musician is “at a ii7 chord” and wishes to “get to a V7 chord,” (or at a V7 chord and wishing to get to a I7 chord) the transformation that will do the best job is the same in both cases: TF, that transformation which moves the root down a fifth and the seventh down a semitone to become the new third. TF is both one-to-one and onto for sets of ordered triples; it maps each ii7 to a unique V7, and each V7 to a unique I7. As such, its inverse (\(\mathrm{TF}^{-1}\)) is well defined, and allows motion backwards along the arrows shown in the transformation graph in Figure 3.
[1.9] It is worth mentioning here that TF and TFT (which is defined in the next section) are well-defined operations for any ordered triple of members of the integers mod 12 (i.e., a member of the set \(\mathbb{Z}_{12} \times \mathbb{Z}_{12} \times \mathbb{Z}_{12}\)). There is nothing mathematically incorrect about the statement \((0, 1, 2) \TFarrow (5, 1, 1) \TFarrow (10, 0, 1)\), for example, but this succession has little musical relevance for the applications under consideration here. Because Hook does not formally define what he means by a “type,” the formulation allows for situations like this one, in which the three types are all members of a single larger set.(16) The advantage for defining TF as a cross-type transformation is that the content of a single node in the transformation graph is restricted to members of a 12-element set of specific ordered-triple configurations.
Figure 5. A transformation graph (left) and transformation network (right) for a small portion of ii–V space
(click to enlarge)
Figure 6. The complete ii–V space, arranged around the circle of fifths
(click to enlarge)
Figure 7. Changes for the A section of “Ceora” (Lee Morgan)
(click to enlarge)
Video 1. The A section of “Ceora” in ii–V space. Recording from Morgan [1965] 1988
(click to watch)
Figure 8. Changes for the B section of “Ceora” (Lee Morgan)
(click to enlarge)
[1.10] With this understanding of the transformations involved in a single ii–V–I progression, we can see how we might connect multiple progressions in order to form a larger ii–V space. Because root motion by descending fifth is extremely common in jazz, we might consider connecting ii–V–I progressions by descending fifth; Figure 5 illustrates this arrangement both as a transformation graph and a transformation network. This descending-fifths arrangement means that all of the chords sharing a root are aligned vertically (directly below GM7 is G7, which is itself above Gm7), and allows us to define two more transformations, which we will call simply 7th and 3rd:
| If \(L = (l_r, l_t, l_s) \in \Smaj\), | then | 7th\((L) = M=(m_r, m_t, m_s)=(l_r, l_t, l_s-1) \in \Sdom\) |
| If \(M = (m_r, m_t, m_s) \in \Sdom\), | then | 3rd\((M) = N=(n_r, n_t, n_s)=(m_r, m_t-1, m_s) \in \Smin\) |
Like the TF transformation, the 7th and 3rd transformations have clear musical relevance: each lowers the given note by a semitone. Although adjacent progressions are connected by descending fifth, the \(T_5\) labels connecting adjacent ii7 chords and IM7 chords are shown in gray in the graph (and omitted in the network, and in later examples), since these chords are not often directly connected in jazz.
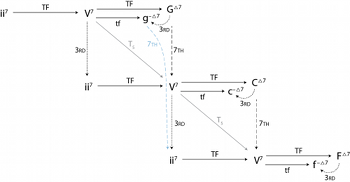
[1.11] By extending the network of Figure 5, we arrive at the entirety of ii–V space, as shown in Figure 6. Because ii–V space includes cross-type transformations, it does not easily form a Lewinian gis.(17) More generally, though, it is easy to see that by considering a single ii–V–I progression as a unit, ii–V space maps cleanly onto ordinary pitch-class space. As Figure 6 makes clear, we can consider the ii–V–I in C as being three perfect fifths above the ii–V–I in
Lee Morgan, “Ceora”
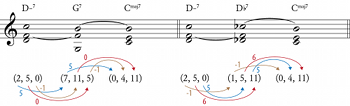
[1.12] Though we will return to formalism below, enough of ii–V space has been defined at this point to see how it might be useful in analysis. To do so, we will examine Lee Morgan’s composition “Ceora,” first recorded on the 1965 album Cornbread. The changes for the A section are given in Figure 7, and an animation in ii–V space is shown in Video 1.(19) “Ceora” is in the key of
[1.13] At this point, we might expect the ii–Vs to continue in descending fifths, but the potential ii7 chord in
[1.14] A similar progression in
[1.15] The B section of “Ceora” (the changes to which are shown in Figure 8) is nearly identical to the A section until the last four bars; the only differences are the addition of the
[1.16] At this point, we have successfully mapped all of the chords in “Ceora” to their associated locations in ii–V space; it is reasonable to ask, though, what good this mapping of chords to space locations has done. After all, ii–V space contains each minor, dominant, and major seventh chord exactly once, so we did not even need to make any decisions as to where in the space a particular chord should go. Have we, in fact, learned anything about “Ceora” from this initial exploration of ii–V space?
[1.17] To be sure, the foregoing discussion has not produced a complete picture of “Ceora”: nothing at all has been said about the melody, any of its inherent middleground voice-leading, the way in which pianist Herbie Hancock expresses any of the harmonies, how this harmonic structure is elaborated in the ensuing improvisations, and so on. Just as applying Roman numerals to a passage of tonal music does not constitute a complete analysis, so too is the representation of “Ceora” in ii–V space a first step. Because ii–V space is designed to show paradigmatic harmonic motion in jazz, the visual representation allows us to focus on those passages which are distinctive: the representation in ii–V space highlights that the first five bars of the tune are relatively unremarkable, while the unresolving, upward-moving ii–Vs in mm. 9–14 draw our attention.
[1.18] That this analytical interlude has not produced a synthetic analysis of “Ceora” is emblematic of what Rings sees as a feature of transformational theory and analysis in general. Drawing on Lewin’s initial description of his transformational enterprise (2007, 16), Rings writes that “to the extent that such [transformational] analyses reveal ‘structures’ at all, they are esthesic structures rather than immanent ones” (2011, 37, emphasis original). A transformational analysis can rarely purport to describe “the structure of a piece”; rather, a transformational approach can offer multiple perspectives (or “apperceptions”) of a single aural phenomenon. To be fair, this discussion of “Ceora” has offered only one such perspective; to embrace others, it will be useful to continue filling out the details of ii–V space.
2. Tritone Substitutions
[2.1] There is an important aspect of jazz harmony that has not yet been considered in our discussion of ii–V space. Crucial to harmony beginning in the bebop era is the tritone substitution: substituting a dominant seventh chord for the dominant seventh whose root is a tritone away.(21) Because tritone-substituted dominants are functionally equivalent, both the progressions Dm7–G7–CM7 and Dm7–
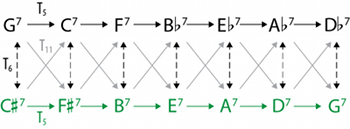
Figure 9. The complete ii–V space, showing tritone substitutions
(click to enlarge)
Figure 10. The Möbius strip at the center of ii–V space
(click to enlarge)
Figure 11. Voice leading in the TF (left) and TFT (right) transformations, compared
(click to enlarge)
Figure 12. A transformation network for a small portion of ii–V space, with tritone substitutions shown in green
(click to enlarge)
Figure 13. The SLIDE7 transformation from
(click to enlarge)
Figure 14. Changes for “Blues for Alice” (Charlie Parker)
(click to enlarge)
Video 2. An analysis of “Blues for Alice” in ii–V space. Recording from Kirk [1961] 1991
(click to watch)
[2.2] This functional equivalence means that a tritone-substituted dominant can act as a shortcut to an otherwise distant portion of ii–V space. In the circle-of-fifths arrangement of Figure 6, keys related by tritone are maximally far apart (diametrically opposed on the circle), but in jazz practice, G7 and
[2.3] This arrangement of key centers is topologically equivalent to a Möbius strip, which is somewhat easier to see by focusing only on the dominant seventh chords, as shown in Figure 10.(22) By wrapping this figure into a circle and gluing the left and right edges together with a half-twist (so that the two G7 chords and
[2.4] While it is possible to navigate this space using only the transformations TF and \(T_6\), it is convenient to define another transformation to describe a common progression like Dm7–
| If \(X = (x_r, x_t, x_s) \in \Smin\), | then | TFT\((X\,) = Y = (\,y_r, y_t, y_s) = (x_r -1, x_s + 5, x_t + 6) \in \Sdom\) |
| If \(Y = (y_r, y_t, y_s) \in \Sdom\), | then | TFT\((Y\,) = Z = (\,z_r, z_t, z_s) = (y_r -1, y_s + 5, y_t + 6) \in \Smaj\) |
The TFT transformation represents a tritone substitution, but it transforms bass motion by fifth into bass motion by semitone (not bass motion by tritone); Figure 11 highlights the relationship with the ordinary TF. Because TF and \(T_6\) commute, TFT can be considered as either TF followed by \(T_6\), or vice versa. With this new transformation, we can understand the progression
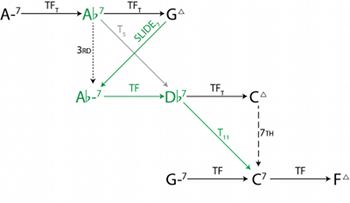
[2.5] The introduction of tritone substitutes complicates the space somewhat; Figure 12 shows a transformation network of the same portion of the space as in Figure 5, but with some chords replaced with their tritone substitutes (shown in green).(23) The relationship between a substituted dominant in G major (
[2.6] Perhaps most interesting in this tritone-substituted space is the new relationship between a major seventh chord and the substituted ii7 in the progression a fifth below (in this figure, between GM7 and
| If \(X = (x_r, x_t, x_s) \in \Smaj\), | then | slide7\((X\,) = Y = (\,y_r, y_t, y_s) = (x_r +1, x_t, x_s) \in \Smin\) |
In jazz this progression occurs frequently when moving between key centers related by half step, though it is uncommon in classical music.(26) We have encountered this transformation once already: the motion from
Charlie Parker, “Blues for Alice”
[2.7] Equipped with these new tritone-substitution transformations, we can now analyze somewhat more chromatic music; Charlie Parker’s “Blues for Alice” will serve as a useful example (the changes are given in Figure 14).(27) The essential structure of the blues is present: the tune arrives on a subdominant in m. 5, and on a home-key ii–V in m. 9 of the twelve-bar form.
[2.8] Parker elaborates this basic structure with a series of stepwise descending ii–V progressions (see Video 2). The first of these is a diatonic descent: m. 2 jumps from the tonic F major to a ii–V in D, which resolves (via the 7th and 3rd transformations) to a Dm7 chord as the ii7 of C major. We first saw this progression in “Ceora” (mm. 6–7), where I noted that it is a very common way of maintaining harmonic motion; instead of a ii–V resolving to its tonic, it resolves to the minor seventh chord with the same root.(28) Because this progression is so common, it is convenient to define it as its own transformation, which we will call EC (for “evaded cadence” or “elided cadence”).(29) Unlike TF, EC is practical only as a transformation from V7 chords to ii7 chords:
| If \(X = (x_r, x_t, x_s) \in \Sdom\), | then | EC\((X\,) = Y = (\,y_r, y_t, y_s) = (x_r+5, x_s-2, x_t-1) \in \Smin\) |
EC is of course equivalent to TF • 7th • 3rd, but only when the starting chord is a V7 chord (a member of \(\Sdom\)).(30) In ii–V space, EC can be represented by starting on a dominant, then following one arrow to the right and two arrows downward (since two descending fifths combine to produce a descending whole step). The structure of the space immediately shows that EC is impossible beginning on a ii7 chord; we can follow a single arrow to the right, but there is only one downward arrow from a V7 chord.(31)
[2.9] This pattern of stepwise descending ii–Vs continues until arriving at the subdominant
Em7(
[2.10] After this
(Here, ECC is the chromatic variant of EC, equivalent to TF • slideS, applied to a dominant seventh chord.) Once this sequence arrives on Gm7 as the ii chord of the tonic F, there is a ii–V–I progression in the home key. After the resolution in m. 11, the progression moves backwards through fifths space to begin a VI–ii–V turnaround to F major to begin the next chorus.(33) As with “Ceora,” there is still much to be said about “Blues for Alice”; we will return to this piece below.
3. A Few Extensions
Minor Tonic Chords
[3.1] As it has been developed thus far, ii–V space has a glaring omission: it requires that all tonic chords be major sevenths. Certainly there are jazz tunes in minor keys, and thus there is a need to account for the minor tonic. We have already seen ii–V progressions that resolve to minor chords—recall the transformation EC in the previous section—but the only minor chords in the space are ii7 chords, not tonics. One of the advantages of ii–V space is that it is easily extended to account for harmonic features specific to particular situations; this section presents one such extension that allows for stable minor tonic chords.
[3.2] The minor ii–V–i progression is usually played as ii7(
Figure 15. Transformations involving minor tonic chords
(click to enlarge)
Figure 16. A small portion of ii–V space, including minor tonic chords
(click to enlarge)
Figure 17. Changes for “Solar” (Miles Davis)
(click to enlarge)
Video 3. An analysis of “Solar” in ii–V space, with C minor tonic. Recording from Davis [1957] 1991
(click to watch)
Figure 18. A generic version of ii–V space, with unspecified tonic chords
(click to enlarge)
Figure 19. Voice leading in the TFblues transformation
(click to enlarge)
Figure 20.
(click to enlarge)
Figure 21. A small portion of “blues ii–V space.”
(click to enlarge)
Figure 22. A pivot fifth between
(click to enlarge)
[3.3] With this definition in place, we can explore how this set interacts with the three sets we have already encountered. These transformations are shown summarily in Figure 15; the formalism underlying them is straightforward, and has been omitted here. The 3rd and 7th transformations both work intuitively, and transform a chord’s quality without changing its root (shown in the left side of the figure). It will also be useful to define versions of the TF and TFT transformations that transform a dominant seventh into a minor tonic, equivalent to TF • 3rd or TFT • 3rd. We will call them simply “tf” and “tfT” (the lowercase here is meant to parallel the use of lowercase letters to indicate minor triads). Note that unlike the standard TF and TFT transformations, tf and tfT only transform V7 chords to ImM7 chords; the same transformations do not hold for ii7 to V7.
[3.4] Figure 16 shows a small portion of ii–V space that includes minor tonic chords, illustrating the transformations described in the previous paragraph.(36) Because most jazz tunes do not contain exclusively minor chords, this figure gives both major and minor tonic chords in every key. Though we will not do so here, determining how to fill in the figure with tritone substitutions, or to arrange it around the circle of fifths in the manner of Figure 6, is easy enough to imagine (if not to draw, given the added complexity of the minor-major sevenths).
[3.5] By way of a brief example, Figure 17 gives the changes for Miles Davis’s “Solar.” This tune is in C minor, though that is not immediately apparent from the changes themselves; in the canonical recording of this piece (from Davis’s own Walkin’), the C minor chords are played as minor-major sevenths, and the piece ends on a CmM7 chord, clarifying its status as the tonic. The fact that the only tonic chord appears in the opening bar of the form gives performances of this tune even more of a cyclical quality than is usual in jazz. By not arriving on a tonic at the end of the short 12-bar form, Davis achieves a formal elision at every chorus: the opening tonic serves simultaneously as the harmonic resolution of the previous chorus and the formal beginning of the next.
[3.6] The visualization in ii–V space, shown in Video 3, is mostly unremarkable. Note that the usual CM7 at the top of the space has been replaced in this video with a minor tonic, CmM7, and as such there is no arrow between the C-minor tonic and V7/F. This analysis, though, is not possible in the ii–V space of the previous section, since the C-minor harmony of the first bar is decidedly not a ii7 chord (it would be ii of
Other Kinds of Tonic Chords
[3.7] The problem of tonic chords that happen to be minor-major seventh chords has now been solved, but in fact the problem is more general: it would be nice to have some way of allowing for any kind of tonic chord we might find in actual practice. James McGowan (2005, 76–79) has argued for what he calls three “dialects of consonance” in jazz (extended tones we might consider consonant): the added sixth, the minor seventh, and the major seventh. So far, this article has focused only on the major-seventh dialect, when it appears atop both major and minor triads. Many Tin Pan Alley tunes end with tonic add-6 chords (which appear nowhere in ii–V space), and as we noted in our discussion of “Blues for Alice,” it is very common for a blues tonic to be a major-minor seventh chord (a type that appears only as V7 chords in the space).
[3.8] The solution to this shortcoming of the space is to introduce some general transformation (which we might call “ResI”, for “resolve to I”) that could be redefined as needed for each style.(37) The generic space would then appear as it does in Figure 18. This space is still arranged in perfect fifths, and the basic shape of the ii–V–I progressions is still present, but the quality of the tonic chords is unspecified. Before using this space in analysis, of course, we must actually define what we mean by a “tonic chord” in a given situation. Because ii–V space contains cross-type transformations, both the set of tonic chords and the transformation ResI, from \(\Sdom\) to the set of tonics, need to be defined.(38) (By defining ResI to be equivalent to TF and defining tonic chords to be members of \(\Smaj\), for example, the generic space here becomes the specific layout of ii–V space first presented in Figure 9.)
[3.9] Again, it will be easiest to demonstrate exactly how this generic space might be realized by means of an example. In the analysis of “Blues for Alice” above, we noted that the
[3.10] The generic ResI transformation offers a better solution, in that we can define a “blues TF,” which resolves a V7 to a tonic major-minor seventh:
| \(S_{\mathrm{IMm7}} = \{ (x_r, x_t, x_s)\ |\ x_t - x_r = 4; x_s - x_r = 10 \}\) | |||
| If \(X = (x_r, x_t, x_s) \in \Sdom\), | then | \(\mathrm{TF}_\mathrm{blues}(X\,)\) | \(= Y = (\,y_r, y_t, y_s)\) |
| \(= (x_r + 5, x_s - 1, x_t - 1) \in S_{\mathrm{IMm7}}\) | |||
Note that TFblues is equivalent to \(T_5\), but is defined in a way to demonstrate its similarity to TF (see the voice leading in Figure 19; TFblues is undefined on ii7 chords). We have also defined the set \(S\)IMm7, the set of tonic major-minor seventh chords; this seems intuitive, but is somewhat complicated. \(S\)IMm7 is exactly equivalent to \(\Sdom\)—in the language of mathematical set theory, they are the same set. The difference between them is not structural, but interpretive: \(S\)IMm7 is the set of tonic major-minor seventh chords, while \(\Sdom\) is the set of dominant major-minor sevenths. This distinction allows us to capture the difference between
[3.11] This sort of interpretive analysis lies at the heart of Rings’s work in Tonality and Transformation; the gises he develops there are designed to capture the intuitions that collections of pitches can be heard (or experienced) differently in different contexts. We can adapt this work slightly to capture the intuition that tonic major-minor sevenths are experienced differently than dominant major-minor sevenths; this formalism is necessary if we are to understand \(\Sdom\) and \(S\)IMm7 to be different sets (which we must, since tonic major-minor sevenths cannot stand in for true dominant sevenths in ii–V space, or vice versa). The tonal gis Rings develops in his second chapter consists of ordered pairs of the form (scale degree, acoustic signal); as he has it, “the notation (, x) . . . represents the apperception: ‘scale degree seven inheres in acoustic signal x’” (2011, 44). Rings goes on to describe sets of these ordered pairs, which we will use to capture our intuitions about the varying roles of the
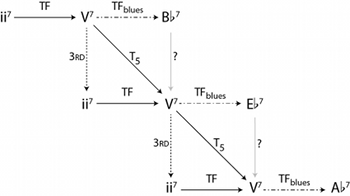
[3.12] With the distinction between tonic and dominant major-minor sevenths worked out, we can now specify the generic space of Figure 18 to create what we might call a “blues ii–V space”; a small portion of this space is shown in Figure 21. This space, though, presents another complication: the top arrow marked with a question mark represents a transformation from
[3.13] Because this transformation is one of quale, Rings’s tonal gis again provides an explanation. Intervals in this gis are measured with ordered pairs, like the elements themselves: the first element is a scale-degree interval (measured upward), and the second is a pitch-class interval (Rings 2011, 46–48). “Pivot intervals” are those intervals where the second element of the pair is 0. In the situation here, we have what Rings would call a “pivot fifth” between the two
. . . Cm7 \(\TFarrow\) F7 \(\xrightarrow{\mathrm{TF}_{\mathrm{blues}}\ }\)
Interaction with Diatonic Spaces
[3.14] The preceding consideration of other kinds of tonic chords has taken us relatively far afield from the starting point of this article, and indeed these extensions are not necessary to understand most tonal jazz. For many purposes, the conventional space developed in Sections 1 and 2 will be sufficient. What is missing in this treatment so far, though, is the concept of a global tonic. As noted above, this article focuses on tonal jazz, and most of this music is in a key (certainly all of the examples considered here are). To this point, we have acknowledged this fact only by mentioning the key of a particular tune in our analytical commentary, or circling the tonic chord in a representation of the space. Defining ii–V space as a fully chromatic space has many advantages: it is rare that every chord in a tune can be understood in a single key, and it is convenient not to have to switch continually between diatonic collections.(41) Moreover, chromatic spaces are much more regular than their diatonic counterparts: chromatic step size is consistent, while diatonic step size varies between one and two half steps.
Figure 23. A portion of ii–V space, conformed to the white-key diatonic circle of fifths
(click to enlarge)
Figure 24. An
(click to enlarge)
Figure 25. An analysis of “Ceora” in diatonic ii–V space
(click to enlarge)
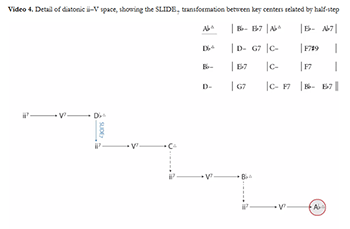
Video 4. Detail of diatonic ii–V space, showing the SLIDE7 transformation between key centers related by half-step
(click to watch)
[3.15] Still, given that all the examples here do have a global tonic, it seems wise to consider what a diatonic ii–V space might look like. The space was first made chromatic by arranging individual ii–V–I progressions in descending fifths (recall Figure 6). We could instead arrange the space according to the diatonic circle of fifths, as shown in Figure 23. This space looks much like the chromatic space, with the exception of the diminished fifth between and , where the regular transformational structure of the chromatic space breaks down. The change of the descending perfect fifth (\(T_5\)) to a diminished fifth (\(T_6\)) means that all of the transformations linking these two key areas must all be combined with \(T_1\): C7 \(\xrightarrow{3\text{rd}\ \bullet\ T_1}\)
[3.16] Unlike chromatic space (which can only be generated by half-steps and perfect fifths), diatonic space can be generated by any of its members.(42) Diatonic ii–V space, then, offers the interesting possibility of departing from the fifths-based space used so far, in favor of some other organization of the space (since any interval we might choose will generate the entire space). To see how such an organization might allow us to capture different kinds of analytical insights, I will return to briefly to Morgan’s “Ceora.”
[3.17] In the analysis of “Ceora” above, it was apparent that the whole tune takes place in four key areas:
[3.18] This figure is structurally a bit different than the other spaces explored thus far, so it will be helpful to examine it in some detail before returning to “Ceora.” The arrangement into descending steps means that we can no longer align all of the seventh chords sharing a root.(43) The GM7 and Gm7 (as ii7/F) chords are close to one another, for example, but G7 (V7/C) is farther removed. The key areas in this figure are not connected by \(T_5\), but instead by the diatonic transposition operator \(t_6\): all of the roots of the major seventh chords (reading down the right side of the figure) are members of the 4-flat diatonic collection.(44) Though the diatonic distance between key areas is consistent, the chromatic distance varies: there are two points in the space in which the connection between key areas is a half step rather than whole step (compare, for example, FM7 \(\xrightarrow{\;t_6\;}\)
[3.19] As noted above, the tritone appearing in diatonic space alters the transformational structure somewhat: transformations spanning this tritone must must be combined with \(T_1\). Here, the relationship between most IM7 and ii7 chords is the transformation 7th • 3rd, but between the keys of
[3.20] All of “Ceora” takes place in a relatively small portion of diatonic ii–V space; Video 4 gives an analysis of the A section in this space.(45) The analysis of course looks very similar to the analysis above, but the stepwise arrangement of the space helps us to show different analytical insights. Moves in the space that are relatively close in the chromatic fifths arrangement in Video 1 appear much larger in this arrangement (for example, the move from
[3.21] It is worth noting at this point that although the space has been adapted to show aspects of diatonicism, the space itself is still chromatic. The transformations are still defined on ordered triples of mod-12 (not mod-7) integers, and nothing in the ii–V–I progressions themselves has changed. The guiding influence of a diatonic collection is used only to choose the key centers that are shown in any particular representation of the space. This use reflects the nature of jazz harmony itself; tunes are often globally diatonic (in a key), while locally chromatic, using ii–V–I progressions to tonicize other key areas to a much greater extent than is usually seen in classical music. The reason for this may be largely practical. The head–solos–head form of most jazz means that we hear the same progression repeated many times (Morgan’s recording of “Ceora” runs about 6½ minutes, for example), and using only pitches from the
[3.22] The arrangement of ii–V space in Figure 24, combining chromatic and diatonic operations, is mathematically complicated. As Rings observes, transformation networks involving both chromatic and diatonic operations violate Lewin’s formal definition of a transformation network, since they act on different sets (Rings 2011, 98–99). The underlying transformation graph is not path-consistent, since the transformation slide7 • TF • TF is in general not equal to the transformation \(t_6\).(46) Put another way, putting GM7 in the top row of Figure 24 while leaving the transformational labels unchanged does not work: obeying the \(t_6\) arrow requires FM7 to occupy the row below, but following the other path would yield
4. Conclusions
[4.1] Before drawing to a close, I will return once more to “Blues for Alice.” This tune has been discussed twice already: the first simply to illustrate how tritone substitutions fit into ii–V space, and the second to formalize our intuitions about the stable
Figure 26. The diatonic seventh chords in F major, arranged around the diatonic circle of fifths
(click to enlarge)
Figure 27. A possible derivation of “Blues for Alice,” mm. 1–5, from a diatonic model
(click to enlarge)
Video 5. A diatonic analysis of “Blues for Alice”
(click to watch)
[4.2] But on the other hand, FM7 and Em7(
[4.3] Figure 27 illustrates how one might hear the opening bars of “Blues for Alice” as derived from this diatonic background. Figure 27a gives the progression as it would appear diatonically in F major; the notation DC2 indicates two successive applications of DC, here describing a motion from IM7 to viiø7.(49) In 27b, the chords rooted on A and G have been transformed from minor sevenths into dominant sevenths via the inverse-3rd operation. This has the effect of turning the chain of DC transformations into the TF and EC transformations observed in Section 2 above. In 27c, the diatonic progression C7–FM7–
[4.4] The resulting progression in Figure 27d is Parker’s original, and captures the intuition that the motion from FM7 to Em7(
[4.5] Rings has described the transformational apparatus as prismatic, an approach “in which multiple phenomenologically rich local passages are refracted and explored from multiple perspectives” (2011, 38); the three discussions of “Blues for Alice” in this article demonstrate the utility of this approach. As listeners and analysts, we need not decide which hearing of the opening five bars represents the structure of the piece. Rather, we can use the transformational approach developed in this article to explore these intuitions in a more formal manner. In some situations, we might wish to hear the motion from FM7 to Em7(
[4.6] As Hook notes in his review of GMIT, “transformation theory is a large and varied toolbox: there are only some minimal instructions for using the tools, and no designs at all for what can build with them” (2007b, 166). This article, as it were, has used the toolbox to build another tool: the spaces developed here offer a foundation for applying a prismatic transformational approach to tonal jazz. One might use transformations to explore intuitions about how players express harmony over the course of a recorded performance (or several different performances), or how a listener’s understanding of a harmonic progression changes over time. Though the examples here have focused on small-group jazz, the transformational approach would also bring valuable insight to music in which the harmony is more tightly controlled, such as big-band arrangements and compositions. Perhaps more practically, visualizing tunes in ii–V space may help musicians already familiar with jazz to learn or memorize tunes, by grouping similar harmonic progressions together. (This has been an unexpected benefit of ii–V space in my own playing!)
[4.7] My transformational approach to tonal jazz may also intersect fruitfully with the existing transformational literature. Although my aim here (following Rings) has been to view traditionally tonal harmonic progressions through a transformational lens, this approach could be combined with existing transformational methods for analyzing the music of composers like Chick Corea, Herbie Hancock, or Wayne Shorter (cited in the introduction), where functional tonality is less obviously present but usually not forsaken entirely. The flexibility of the ordered-triple representation in particular may prove productive in this regard, since it allows for transformation definitions that are still valid when the actual realization of a chord might differ greatly from instance to instance. The syntax of jazz harmony as globally diatonic, yet locally chromatic, is shared with much 19th-century chromatic music, and some of the ideas here might be imported there, where other kinds of transformational analysis have already been shown to be useful.(50)
[4.8] It hardly needs to be said that examining ii–V–I progressions does not constitute a complete theory of jazz harmony, but thinking transformationally about tonal jazz allows for a deeper understanding of this music. To be sure, there are circumstances in which other methodologies may lead to more productive insights than transformational ones, but the opposite seems to be equally true. Jazz, in particular, admits a multitude of approaches for making music—it seems natural to embrace analytical pluralism as well.
Michael McClimon
Furman University
Music Department
3300 Poinsett Highway
Greenville, SC 29613
michael@mcclimon.org
Works Cited
Aebersold, Jamey. 1974. The II–V7–I Progression. Jamey Aebersold Play-A-Long Series, vol. 3. Jamey Aebersold Jazz.
Aebersold, Jamey, ed. 1978. Charlie Parker Omnibook. Atlantic Music Corp.
—————, ed. 1979. Turnarounds, Cycles, and II/V7s. Jamey Aebersold Play-A-Long Series, vol. 16. Jamey Aebersold Jazz.
—————, ed. 1999. Dominant Seventh Workout. Jamey Aebersold Play-A-Long Series, vol. 84. Jamey Aebersold Jazz.
Biamonte, Nicole. 2008. “Augmented-Sixth Chords vs. Tritone Substitutes.” Music Theory Online 14 (2).
Callender, Clifton. 1998. “Voice-Leading Parsimony in the Music of Alexander Scriabin.” Journal of Music Theory 42 (2): 219–33.
Capuzzo, Guy. 2004. “Neo-Riemannian Theory and the Analysis of Pop-Rock Music.” Music Theory Spectrum 26 (2): 177–99.
Childs, Adrian P. 1998. “Moving Beyond Neo-Riemannian Triads: Exploring a Transformational Model for Seventh Chords.” Journal of Music Theory 42 (2): 181–93.
Cohn, Richard. 2012. Audacious Euphony: Chromatic Harmony and the Triad’s Second Nature. Oxford University Press.
DeVeaux, Scott. 1997. The Birth of Bebop: A Social and Musical History. University of California Press.
Douthett, Jack, and Peter Steinbach. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition.” Journal of Music Theory 42 (2): 241–63.
Gollin, Edward. 1998. “Some Aspects of Three-Dimensional Tonnetze.” Journal of Music Theory 42 (2): 195–206.
Harrison, Daniel. 1994. Harmonic Function in Chromatic Music: A Renewed Dualist Theory and an Account of Its Precedents. University of Chicago Press.
Hook, Julian. 2002. “Uniform Triadic Transformations.” Journal of Music Theory 46 (1/2): 57–126.
—————. 2007a. “Cross-Type Transformations and the Path Consistency Condition.” Music Theory Spectrum 29 (1): 1–40.
—————. 2007b. “David Lewin and the Complexity of the Beautiful.” Intégral 21: 155–90.
—————. 2008. “Signature Transformations.” In Music Theory and Mathematics: Chords, Collections, and Transformations, edited by Jack Douthett, Martha M. Hyde, and Charles J. Smith, 137–60. University of Rochester Press.
—————. 2011. Review of Dmitri Tymoczko, A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice (Oxford University Press, 2011). Music Theory Online 17 (3).
—————. 2013. “Contemporary Methods in Mathematical Music Theory: A Comparative Case Study.” Journal of Mathematics and Music 7 (2): 89–102.
Kernfeld, Barry. 2006. The Story of Fake Books: Bootlegging Songs to Musicians. Scarecrow Press.
Larson, Steve. 1998. “Schenkerian Analysis of Modern Jazz: Questions about Method.” Music Theory Spectrum 20 (2): 209–41.
—————. 2005. “Composition versus Improvisation?” Journal of Music Theory 49 (2): 241–75.
Lerdahl, Fred. 2004. Tonal Pitch Space. Oxford University Press.
Levine, Mark. 1989. The Jazz Piano Book. Sher Music.
—————. 1995. The Jazz Theory Book. Sher Music.
Lewin, David. [1987] 2007. Generalized Musical Intervals and Transformations. Oxford University Press.
Love, Stefan. 2013. “Subliminal Dissonance or ‘Consonance’: Two Views of Jazz Meter.” Music Theory Spectrum 35 (1): 48–61.
Martin, Henry. 1988. “Jazz Harmony: A Syntactic Background.” Annual Review of Jazz Studies 4: 9–30.
—————. 1996. Charlie Parker and Thematic Improvisation. Scarecrow Press.
—————. 2011. “Schenker and the Tonal Jazz Repertory.” Dutch Journal of Music Theory 16 (1): 1–20.
McClimon, Michael. 2016. “A Transformational Approach to Jazz Harmony.” PhD diss., Indiana University.
McFarland, Mark. 2012. “Schenker and the Tonal Jazz Repertory: A Response to Martin.” Music Theory Online 18 (3).
McGowan, James. 2005. “Dynamic Consonance in Selected Piano Performances of Tonal Jazz.” PhD diss., Eastman School of Music.
—————. 2011. “Psychoacoustic Foundations of Contextual Harmonic Stability in Jazz Piano Voicings.” Journal of Jazz Studies 7 (2): 156–91.
Mulholland, Joe, and Tom Hojnacki. 2013. The Berklee Book of Jazz Harmony. Berklee Press.
Owens, Thomas. 1995. Bebop: The Music and its Players. Oxford University Press.
Pöhlert, Werner. 1989. Basic Harmony. Trans. Jürgen Krohn and Norman Bowie. Werner Pöhlert Publications.
The Real Book. n.d. 6th ed. Hal Leonard.
Rings, Steven. 2011. Tonality and Transformation. Oxford University Press.
Straus, Joseph. 2003. “Uniformity, Balance, and Smoothness in Atonal Voice Leading.” Music Theory Spectrum 25 (2): 305–52.
Strunk, Steve. 1996. “Linear Intervallic Patterns in Jazz Repertory.” Annual Review of Jazz Studies 8: 63–115.
—————. 2003. “Wayne Shorter’s Yes and No: An Analysis.” Dutch Journal of Music Theory 8 (1): 40–56.
—————. 2016. “Tonal and Transformational Approaches to Chick Corea’s Compositions of the 1960s.” Music Theory Spectrum 38 (1): 16–36.
Terefenko, Dariusz. 2014. Jazz Theory: From Basic to Advanced Study. Routledge.
Tymoczko, Dmitri. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. Oxford University Press.
Waters, Keith. 2005. “Modes, Scales, Functional Harmony, and Nonfunctional Harmony in the Compositions of Herbie Hancock.” Journal of Music Theory 49 (2): 333–57.
—————. 2016. “Chick Corea and Postbop Harmony.” Music Theory Spectrum 38 (1): 37–57.
Waters, Keith, and J. Kent Williams. 2010. “Modeling Diatonic, Acoustic, Hexatonic, and Octatonic Harmonies and Progressions in Two- and Three-Dimensional Pitch Spaces; or Jazz Harmony after 1960.” Music Theory Online 16 (3).
Discography
Discography
Davis, Miles [Miles Davis All Stars]. [1957] 1991. Walkin’. Prestige PRLP 7076. Reissued, Original Jazz Classics OJCCD 213, CD.
Kirk, [Rahsaan] Roland. [1961] 1991. We Free Kings. Mercury 20679. Reissued, Mercury 826455-2, CD.
Morgan, Lee. [1965] 1988. Cornbread. Blue Note BLP 4222. Reissued, Blue Note BNZ 109, CD.
Footnotes
* This article is based on chapter 2 of my dissertation; earlier versions were presented at the annual meetings of the Music Theory Society of the Mid-Atlantic (Philadelphia, 2013) and the Society for Music Theory (Milwaukee, 2014). I am grateful for many helpful comments along the way, and especially for those from the anonymous MTO reviewers.
Return to text
1. Bebop and its descendants constitute a style which has been referred to as the lingua franca of jazz (see Owens 1995, 5; Love 2013, 48); as Scott DeVeaux puts it, bebop is “both the source of the present . . . and the prism through which we absorb the past” (1997, 3).
Return to text
2. Schenkerian analysis of jazz is now commonplace: for an introduction, see Larson 1998. Other important sources include Larson 2005, Martin 2011, and Strunk 1996, to name but a few.
Return to text
3. Incidentally, the edited title of Strunk 2016 (published after his untimely death in 2012) makes the same separation between “tonal” and “transformational” that Rings observes. Strunk’s original title was “Analytical Approaches to Chick Corea’s Compositions of the 1960s.” Like much of Strunk’s work, this article combines Schenkerian and transformational techniques.
Return to text
4. This point is worth underscoring briefly: although the chord symbol Dm7 might be taken to mean the four-note set D–F–A–C, it might also imply, for example, the entire D dorian collection. Indeed, it is relatively rare for chordal instruments in jazz to play these simple four-voice seventh chords, though they are often used for pedagogical purposes and for structuring single-line improvisations (as suggested above). Understanding harmony in jazz involves more than understanding the voice-leading among four-voice seventh chords.
Return to text
5. Because (0258) contains a tritone, two different inversions can map a single dominant seventh to a single half-diminished seventh chord, which is not the case with triads. Gollin refers to the differences between the two-dimensional triadic Tonnetz and his three-dimensional tetrachordal version as “degeneracies” (1998, 200, see also 205n9). Child’s cubic representation only shows 8 of the possible 24 (0258) tetrachords: those related by parsimonious voice leading to a single diminished seventh chord (1998, 188).
Return to text
6. Fake books are collections of lead sheets that traditionally were compiled anonymously and sold illegally, in order to avoid paying the copyright owners of the compositions they contained. The name “fake book” comes from the fact that with the melody and chord changes, jazz musicians can easily “fake” a tune they do not know. The most famous jazz fake book is ironically titled The Real Book, and was compiled in Boston in the early 1970s. In recent years, fake books have become mainstream, and most of them have now obtained proper copyright permissions. Hal Leonard now publishes the 6th edition of The Real Book (a nod to the five illegal editions); many of the notorious errors in the earlier editions have been corrected and it is now available for purchase legally. Further references to The Real Book here refer to this version unless otherwise noted. For a history of fake books, see Kernfeld 2006.
Return to text
7. For example, the tune “Alice in Wonderland” is known to jazz musicians as a jazz waltz with one chord per bar (as played, for instance, by Bill Evans on the album Portrait in Jazz). The main title music in the 1951 film from which it was taken, however, is in
Return to text
8. Namely, that the chord should be a dominant seventh with
Return to text
9. Aebersold 1974. The Aebersold play-along series is a staple of jazz pedagogues; most volumes contain a selection of tunes, along with a CD providing rhythm-section accompaniment so that students can practice with a recording. The ii–V volume is number three of well over 100, and includes the phrase “the most important musical sequence in jazz!” on the cover. Other Aebersold play-alongs dedicated to small-scale harmonic progressions include Aebersold 1979 (focusing on turnarounds) and 1999 (focusing on the V7 chord); both of these volumes also make extensive use of the ii–V progression.
Return to text
10. The triangle on the C chord in this figure indicates a major seventh. The triangle (instead of “maj7” or “M7”) saves space and reduces clutter in the graphical representations.
Return to text
11. The original definition of a transformation network is in Lewin [1987] 2007, 196. For a relatively concise summary, see Rings 2011, 110–16.
Return to text
12. Lewin [1987] 2007, 195–96. See also Hook 2007a, 6–8.
Return to text
13. In fact, many jazz piano texts begin with “three-note” or “shell” voicings, consisting only of chordal roots, thirds, and sevenths; see, for example Levine 1989, 17–22; and Mulholland and Hojnacki 2013, 211–12. The half-diminished seventh chord (which is indistinguishable from a minor seventh chord in the three-note representation used here) does appear frequently in jazz as the ii chord in minor-key ii–V–I progressions; we will return to this point in section 3 below. McGowan 2005, 156, following Harrison 1994, refers to chord roots as “bases,” thirds as “modal agents,” and sevenths (and sixths) as “defining agents,” while fifths are merely “triadic associates”; his terms also capture the more important role of the chord members used here.
Return to text
14. Here and throughout, pitch classes are represented as mod-12 integers, with C = 0; all calculations are performed mod 12.
Return to text
15. This figure represents what Straus 2003 calls “transformational voice leadings.”
Return to text
16. Hook himself makes this clear, noting that for any two sets S and T it is possible to define a single-type transformation in the union set S \(\cup\) T, though it is not always clear how a function defined on one set should be extended to cover both. He also notes that even when a single-type transformation is possible, “the cross-type approach is often simpler and more natural,” which certainly seems to be the case here (Hook 2007a, 5n8).
Return to text
17. It would be possible to form a GIS by considering all ordered triples as the group, as suggested above. While this is possible, defining an interval function in this group is much more difficult: such a function would need to account for the 36 ordered triples in ii–V space (ii7, V7, and I7 chords) as well as the many more (1,692) that are not included in the space. Such a function is conceivable, but would not in any case reflect the musical realities ii–V space is designed to portray.
Return to text
18. ii–V space is a directed graph, so in circumstances where the pitch-class distance metric is somehow not sufficient, we can instead rely on the standard way of measuring distance in a directed graph: by counting the number of edges in the shortest path between two chords. The distance from ii7 of C to V7 of
Return to text
19. These changes are taken from The Real Book, and reflect what is played on the Cornbread recording. The following discussion also uses the formal labels given in The Real Book, which describes “Ceora” as an AB form, although it may also be heard as a 32-bar ABAC form. In this video (and those below), the shaded circle indicates the overall tonic. Because “Ceora” uses only a part of the space, the circle of Figure 6 has been squared off here so that the labels are easier to read.
Return to text
20. The concept of tritone substitutes is covered in detail in the next section.
Return to text
21. The tritone substitution has been treated extensively in the literature, so it will not be discussed at any length here. See, for example, Biamonte 2008, Martin 1988, 11, McFarland 2012, 43–48, and Tymoczko 2011, 360–65. In addition to these music-theoretical sources, nearly every introductory jazz harmony textbook contains an explanation of tritone substitution; see Levine 1995, 260–71, Mulholland and Hojnacki 2013, 63–79, or Terefenko 2014, 152–54, among many others.
Return to text
22. A similar diagram can be found in Pöhlert 1989, 5, and can be seen implicitly in Figure 1-1 of Martin 1988.
Return to text
23. This figure also uses actual chord names instead of the ii7 and V7 symbols in each key so that the highlighted relationships can be seen more easily.
Return to text
24. Though chords are defined as ordered triples here, I have included the fifth in this description to highlight the relationship to the triadic slide, which maintains the root and fifth of a triad while changing the quality of the third. If the fifths are omitted, the voice-leading distance between GM7 and Dm7 is much larger—7 semitone displacements—while GM7–
Return to text
25. The SLIDE transformation was introduced by David Lewin (2007, 178), but has since become a part of of the standard set of Neo-Riemannian transformations. SLIDE7 is defined here only as a transformation from I7 chords to ii7 chords, but of course the triadic SLIDE is an involution (two successive applications of SLIDE to any triad will result in the same triad).
Return to text
26. The SLIDE7 transformation can be found in a chromatic sequence in the second movement of Gabriel Fauré’s string quartet, mm. 36–39. Hook 2013 analyzes this passage from a number of different mathematical perspectives.
Return to text
27. This progression is often known as the “Bird Blues,” though Mark Levine (1995, 228) calls it the “descending blues.” Like many sets of Parker changes, several different versions exist; the changes here represent a mediation among these sources. The Real Book gives Am7 (a vi chord) instead of FM7 in m. 11; Levine 1989 gives
Return to text
28. As ii–V space makes clear, this minor seventh chord is understood as a ii7 chord, and not as a minor tonic chord, which are not commonly shown as minor seventh chords. We will return to minor tonic chords in the next section.
Return to text
29. There are of course many ways to evade a cadence, in jazz and in other styles of music. Because transformations are designed to model intuitions, calling this “EC” here seems reasonable: the label captures the intuition that the V chord was going to resolve, but instead moved to a minor chord. In other situations—if a musical passage evaded cadence in several different ways—“EC” would probably not be sufficient, and we might wish to rename this transformation something more descriptive; the “minor continuation” evasion shown here might appear alongside, say, a “3rd-transformation” evasion (as in mm. 4–5 of Billy Strayhorn’s “Take the A Train,” for example).
Return to text
30. The bullet here indicates left-to-right function composition: TF • 7th means the transformation TF followed by the transformation 7th. Note that the example transformation TF • 7th is a single transformation, defined to be equal to TF followed by 7th. This function composition is familiar from pitch-class set theory: we say that the operation \(T_7I\) applied to a C major triad yields a C minor triad. Although the operation involves two functions (invert, then transpose upward by seven semitones), there is no sense in which an intermediate F minor triad exists. Just as there is an alternate notation for \(T_7I\), namely \(I_7\), we could easily define an alternate notation for the composition TF • 7th.
Return to text
31. EC is impossible beginning on a ii7 chord only if we want to stay within the three sets under consideration here. Like the other transformations defined here, EC is an admissible transformation on the set of all mod-12 ordered triples: if we begin with a Dm7 chord, \((2, 5, 0)\), EC gives us the triple \((7, 10, 4)\), which of course is not a major, minor, or dominant seventh chord.
Return to text
32. The major-minor seventh chord as a stable chord is characteristic of the blues; see, for example, McGowan 2011, 158–59 and throughout. This fact is somewhat obscured in ii–V space, since major-minor sevenths appear in the space only as V7 chords; we will return to this limitation below.
Return to text
33. A “turnaround” is what jazz musicians call a short progression that leads from a chord (often a tonic chord) back to itself. They appear most commonly at the ends of forms, and provide harmonic interest during solos, when a player might play several choruses in a row. The ii–V appears frequently in this formal location, as do many progressions based on it: vi–ii–V; iii–VI–ii–V (which can be understood as two ii–Vs separated by a whole step, as in “Ceora” above); iii–
Return to text
34. The extensions used for the dominant chord in a minor ii– are quite flexible: Aebersold 1974 gives the quality as 7(
Return to text
35. It is worth underscoring here that the use of cross-type transformations to define ii–V space allows us to consider the IIm7(
Return to text
36. The 7th transformation from a minor-major seventh to a minor seventh, shown in light blue in this figure, clutters the representation somewhat. An identical arrow would also connect CmM7 with Cm7 (as ii7/
Return to text
37. The name of the transformation ResI is inspired by the transformation “ResC” in Rings 2011, 25–27.
Return to text
38. In practice, ResI will usually be a transformation that moves the root of a V7 down either by perfect fifth or semitone. In theory, however, there is no limitation on the definition of ResI. One might, for example, construct a space where tritone substitutes are normative by defining ResI to be equal to TFT; in this case, the gray arrows in Figure 18 would represent the transformation 7th • \(T_6\).
Return to text
39. In fact, similar statements could be made for all of the sets developed in this article: \(\Smin\) would then become (speaking loosely) “the set of minor-minor seventh chords acting as , , and in some key.” In most cases, however, this level of precision is unnecessary, since in ordinary ii–V space, presented in sections I and II, the quality of the chord uniquely identifies its function as either ii, V, or I.
Return to text
40. Recall that the composition “pivot fifth” • 3rd is a single operation: in no sense does an intermediate
Return to text
41. To say that ii–V space is chromatic is not to say it is atonal. The study of harmony is often broken down by type: “tonal harmony” plays a different role than does “chromatic harmony” in both theoretical research and pedagogy: studies that focus specifically on chromatic harmony often differentiate themselves from other tonal theoretical traditions.
Return to text
42. In general, a cyclic group (like the diatonic or chromatic groups) can be generated by a member only if the generator and the size of the group are relatively prime. The chromatic group, for example, can be generated only by 1, 5, 7, or 11 (because 2, 3, 4, and 6 and their mod-12 complements divide evenly into 12). Put another way, only the chromatic scale and circle of fifths/fourths cycle through all 12 pitches in the chromatic octave before returning to the starting point. Since the diatonic group has 7 elements, any of its members will generate the entire collection. (Or another way, the diatonic scale can be generated by any generic interval size: 2nds, 3rds, 4ths, or their complements.)
Return to text
43. This figure has been skewed somewhat to conserve horizontal space. If it were drawn in a manner parallel with standard ii–V space, the ii7 chords would be directly below the IM7 chords. As is the case throughout, the particular visual representation chosen for a given space does not affect the abstract structure of the space itself.
Return to text
44. The diatonic transposition operator \(t_k\) is defined in Hook 2008, 139.
Return to text
45. “Ceora” is perhaps even more diatonic than this space implies, since CM7 and
Return to text
46. Path consistency is described in Hook 2007a, 25–28.
Return to text
47. My thanks to the anonymous MTO reviewer for this suggestion.
Return to text
48. The formalism has been omitted here, but is easy enough to supply for the interested reader. Unlike ii–V space, this cycle forms a gis, isomorphic to ordinary diatonic pitch-class space.
Return to text
49. This diatonic progression is not unheard of in jazz: Joseph Kosma’s “Autumn Leaves” and Bart Howard’s “Fly Me to the Moon,” among others, both make use of completely diatonic progressions.
Return to text
50. Tymoczko (2011, 389) argues that jazz is a “modernist synthesis,” and that jazz musicians “act as custodians of a tradition of advanced tonal thinking.”
Return to text
Copyright Statement
Copyright © 2017 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
29984