North Indian Classical Music and Lerdahl and Jackendoff’s Generative Theory – a Mutual Regard
David Clarke
KEYWORDS: Lerdahl and Jackendoff, generative theory, syntax, musical universals, Indian music, khyāl, rāg, ālāp, improvisation, diachronic modeling of music
ABSTRACT: This article applies aspects of A Generative Theory of Tonal Music by Fred Lerdahl and Ray Jackendoff to the analysis of Hindustani (North Indian) classical music, with a double-edged purpose. On the one hand, the GTTM methodology is used to illuminate the workings of an ālāp (as performed by Vijay Rajput, a vocalist in the khyāl style). On the other hand, the analysis acts as a case study to assess the viability of this methodology for the analysis of Indian classical music, and in particular, to test out Lerdahl and Jackendoff’s claim that GTTM presents a universal musical grammar, transcending specific cultures.
This pilot study considers what modifications would be necessary to GTTM’s preference rules to make a viable generative theory for Hindustani classical music—or at least for its melodic aspects, governed as these are by the principles of rāg. With such modifications, it is possible to formally represent levels of musical knowledge involved in the production and perception of this music, and to verify the generative principles whereby a performer is able to improvise a potentially infinite number of musical utterances from a finite set of rules.
The investigation also fosters a critique of Lerdahl and Jackendoff’s theories. Among the questions addressed is that of the diachronic modeling of improvised musical performance—which, unlike the score-based studies of GTTM, cannot be analyzed entirely outside the flow of time. Consistent with this critical position is the conclusion that, rather than the pursuit of universals per se, it is an openness to the tension between universals and particulars that may lead to the most valuable knowledge.
Copyright © 2017 Society for Music Theory
[1] Introduction: background and rationale
[1.1] For all that Fred Lerdahl and Ray Jackendoff’s A Generative Theory of Tonal Music (1983) was hailed as a seminal, if problematic, contribution to music theory at the time of its publication, one of its most audacious claims seems never to have been seriously tested.(1) This is the authors’ contention that their account formally describes a set of “universals of musical grammar” (1983, 282). Following on from Noam Chomsky, whose generative theories of linguistic grammar inform their own work, Lerdahl and Jackendoff argue that the principles of tonal syntax expounded in GTTM “reflect cognitive similarities among all human beings—innate aspects of mind that transcend particular cultures or historical periods” (282; see also 278–81). Perhaps unsurprisingly, this claim—in one sense ancillary to the general thrust of their exegesis, but also one of their most striking inferences from its cognitive principles—was dismissed as questionable or ethnocentric by early reviewers (E. Clarke 1986, 15; Hantz 1985, 202; Peel and Slawson 1984, 275–6, 291–2). And because subsequent users of, or commentators on, ideas from GTTM have tended, like its authors, to write from the perspective of Western classical music, little progress has been made in seriously investigating the theory’s supposed relevance to other musical cultures. Moreover, there has been little reverse traffic: few analysts of non-Western music have availed themselves of its methodological resources.
[1.2] In this lacuna, then, lies a task for ethnomusicologically minded analysts or analytically inclined ethnomusicologists. Possessing something like these amphibian tendencies,(2) I here develop an application of Lerdahl and Jackendoff’s generative theory to Hindustani (North Indian) classical music.(3) My investigation represents a pilot study (or feasibility study) rather than a fully fledged exegesis. I focus on a single musical ‘movement’, an ālāp in the khyāl vocal style, whose essence is melodic, and which I analyze giving particular attention to Lerdahl and Jackendoff’s concept of time-span reduction. While relatively brief, this extract from a larger rāg performance is a strong exemplar of its musical idiom;(4) the ālāp studied here embodies principles of melodic improvisation that are pervasive in Hindustani classical music. Hence this case study should enable significant judgments in principle about the potential wider viability of GTTM’s methodology beyond Western classical music. From this starting point, further developments could be envisaged beyond the scope of the present article that also consider the metrical dimensions of Hindustani music (the cyclic principles of tāl), as well as wider comparative study between further exemplars of khyāl and other kinds of Indian classical performance.
[1.3] The ālāp that I will analyze forms the first part of a recorded performance of Rāg Yaman by Vijay Rajput. Born in India and now established in the UK as a performer on the national and international stage, Rajput (b. 1971) is a śiṣya (disciple) of the late great Pandit Bhimsen Joshi (1922–2011), who was one of India’s most renowned exponents of the khyāl vocal style. In this capacity, Rajput numbers among those artists who continue the heritage of the Kirana gharānā.(5) I undertake the following account both as a theorist versed in Western analytical traditions and as student of Rajput, having studied khyāl with him since 2004. This anchors me in the space of the Indian guru–śiṣya paramparā (master-disciple tradition), which has its own, informal theoretical and pedagogical precepts; and it provides an emic (i.e. culturally internal) perspective from which to judge the etic (i.e. putatively externally verifiable and empirically testable) principles developed by Lerdahl and Jackendoff.
[1.4] My stance towards GTTM is somewhat agnostic. I do not seek to advocate it as a paradigm-shifting model for the analysis of Indian classical music, since much effective work has already been done in this field using more idiomatic methodologies derived from the specifics of Indian styles (e.g. Magriel 1997, Pearson 2016, Widdess 2011, Zadeh 2012). Moreover, no less fruitful mileage may be gained in applying and adapting concepts from Schenkerian theory, such as structural levels, reduction, prolongation and voice-leading, though these in any case also overlap to some extent with ideas in GTTM.(6) Yet there are features in GTTM bound up with its aspirations to cross-cultural significance that suggest it merits serious consideration in relation to such highly codified practices as Indian classical music. These include the theory’s close (but carefully qualified) relationship to linguistics, and with this the idea of generativity: the notion that an infinite series of well-formed verbal or musical utterances can be brought forth from a finite set of syntactic constraints, and that these are an innate part of the human cognitive apparatus (GTTM, 231–3). These, then, are avenues of potentially major significance that would show Indian classical music as implicated not only in a much wider cultural field, but also in a human capacity, in which music and language coalesce in certain important respects.
[1.5] While the stylistic features considered below are sufficiently different from the Western classical canon to enable us to evaluate the cross-cultural applicability of GTTM, we should be wary of construing this as evidence for wholesale universalism (Hindustani classical music, like that of the West, is clearly just one further example of the world’s musics). Nevertheless, as Lerdahl and Jackendoff point out, “A musical universal need not be readily apparent in all musical idioms
[1.6] Occasional references to Indian classical music in GTTM (18, 106, 294, 295) suggest it as a background presence in Lerdahl and Jackendoff’s thinking, and perhaps as providing unconscious support for their universalizing claims. Martin Clayton briefly evaluates the metrical elements of GTTM in his own account of meter in Indian tāl structures (2000, 29, 31–3, 39, 41). Otherwise, as far as I know, the current detailed application is the first of its kind. I offer it as a contribution to a growing body of analytical, theoretical and stylistic research into South Asian music.(7) In turn, this corpus makes a significant contribution to the analytical study of world music, which—as journals like Analytical Approaches to World Music make plain—is no longer a fledgling sub-discipline.
[1.7] Seeking to address a wider analytical and music-theoretic community as well as those with interests in Indian music brings its own challenge, since neither interest group is likely to be equally familiar with all the prerequisite bodies of theory. Hence the first stages of this article involve various preliminaries, some of which—depending on readers’ particular fields of expertise—may need less close attention than others. I initially outline some of the essential tenets of GTTM, following which I present some of the basics of the Hindustani rāg principles. I then consider some issues around the transcription of the passage being analyzed—a necessary further preliminary, given the essentially non-notated nature of the musical material, and itself a kind of proto-analysis—before turning to the application of GTTM proper. The main body of the investigation will entail the formulation of new preference rules peculiar to the Indian idiom being investigated; and it will also bring to light some of the problematics of GTTM itself, including its suppression of the diachronic (the real-time nature of musical performance) and its questionable need for two types of reductive, tree-diagram representation. However, before we get too far ahead of ourselves, let us now turn to the promised outline of some of the key principles of GTTM.
[2] Preliminaries 1: essentials of GTTM
[2.1] Lerdahl and Jackendoff’s expressed primary objective is “a formal description of the musical intuitions of a listener who is experienced in a musical idiom” (GTTM, 1). In other words, the tenor of their work is the theoretical formalization of what is already understood intuitively, just as Chomsky seeks to make explicit the principles of language he holds to be innately acquired. Yet while Lerdahl and Jackendoff undertake this process ostensibly in relation to musical listening, the operation of these principles in the act of musical creation is no less significant (in fact all the case studies in GTTM draw from repertories whose conventions are mutually understood by listener and composer). This point is particularly germane to my application of their principles to Hindustani classical music, given its focus on the improvising performer who creates material from an internalized (and in certain respects intuitively acquired) set of conventions. The creative process is generative partly in a literal sense: of producing something in the moment—not out of nothing, but out of creative engagement with a set of rules and constraints.(8) And this shades over into the strong sense in which Lerdahl and Jackendoff intend the term “generative”: “the mathematical sense
Example 1. J.S. Bach “O Haupt voll Blut und Wunden,” BWV 244, as analyzed in GTTM (144; Example 6.25)
(click to enlarge and see the rest)
[2.2] Example 1 illustrates what a formalized representation of intuitive musical knowledge looks like under such generative principles. This is Lerdahl and Jackendoff’s analysis of J. S. Bach’s chorale “O Haupt voll Blut und Wunden” from the St Matthew Passion, BWV 244 (GTTM, 144, Example 6.25). Within the graphology, it is the tree structure above the musical notation (showing the time-span reduction) that most closely resembles the parsings of sentence structure in generative linguistics. But, as the authors stress, the syntax graphed here is based on structural principles that are specifically musical, rather than being a naive translation of linguistic categories (GTTM, 5–6, 112–13).(10) For all that, the structures can be classed as syntactic—especially if, rather than construing musical syntax a posteriori as a mere analogy for linguistic syntax, one argues for syntax as an innate cognitive faculty that manifests differently in musical and linguistic forms. As Aniruddh Patel puts it:
Syntax may be defined as a set of principles governing the combination of discrete structural elements (such as words or musical tones) into sequences. Linguistic and musical sequences are not created by the haphazard juxtaposition of basic elements. Instead, combinatorial principles operate at multiple levels, such as in the formation of words, phrases and sentences in language, and of chords, chord progressions and keys in music. (2013, 674)
While Patel’s terms of reference are, again, Western tonal ones, his point about avoiding the haphazard is apposite to an improvised form like Hindustani classical music, since it is incumbent on the performer to make satisfying—or well-formed—musical utterances that go beyond mere noodling: the operation of “combinatorial principles” on “multiple levels” is of the syntactic essence.
[2.3] And multiple levels are exactly what we get in Example 1: in the tree diagram above the principal staff system (where lower-level events branch off from higher-level ones); in the corresponding nested slurs below; and in the similarly corresponding levels of harmonic reduction below that. The second of these features, the array of reticulated slurs, represents the music’s grouping structure, which is related to, but distinguished from, its metrical structure shown by the arrays of dots immediately below the stave. On the one hand, the metrical hierarchy organizes rhythm according to the relative strength of beats (represented by the number of dots), which combine into units we know as measures and, in faster tempi, as hypermeasures. On the other hand, the temporal flow of the music is articulated into groups, shown by the braces, whose beginning and end points are conditioned by melodic, harmonic and tonal factors (e.g. cadence points, phrase endings and beginnings), although their length is conditioned by the metrical structure—e.g., determined at the two-, four-, and eight-measure levels, and so on. Thus the grouping structure relates to the metrical structure but is not always coterminous with it; indeed GTTM’s positing of the interaction of these two aspects as crucial to a theory of rhythm has been acknowledged by reviewers as of seminal importance (E. Clarke 1986, 7–8; Hantz 1985, 193; Peel and Slawson 1984, 275).
[2.4] While the grouping structure of Example 1 broadly corresponds to an intuitive analysis of the music’s phrase structure, what Lerdahl and Jackendoff also deliver is an explicit formal description of the factors that condition such intuitions. They express these, drawing on Gestalt psychology, as well-formedness rules (WFRs), which are supplemented by preference rules (PRs) that arbitrate between different possible readings of the WFRs. For example, Grouping Well-Formedness Rule 1 (GWFR 1) reads: “Any contiguous sequence of pitch events, drum beats, or the like can constitute a group, and only contiguous sequences can constitute a group” (37). This rule clearly has a potentially universal application, including to Indian music. Extensive sets of well-formedness and preference rules are derived for each of the structural domains that Lerdahl and Jackendoff see as essential to their account: metrical and grouping structure, as discussed here; and time-span and prolongational reductions, to be discussed presently.
[2.5] Perhaps the most significant formal principle of all is what Lerdahl and Jackendoff call the Strong Reduction Hypothesis, under which
The listener attempts to organize all the pitch-events of a piece into a single coherent structure, such that they are heard in a hierarchy of relative importance.. . . Structurally less important events are not heard simply as insertions but in a specified relationship to more important events. (GTTM, 106)
Hence, every single musical event is heard—and must be analytically represented—as hierarchically subordinate and/or superordinate to some other event. At each level of the analysis, a structural pitch-event or “head” for each time-span within the grouping structure must be determined, the remaining feature(s) from that group or time-span being heard as its elaboration. Successive heads are evaluated in turn for their relative superordinacy or subordinacy to one another, thus determining the heads at the next level, and so on recursively. This generates the corresponding tree-structure analysis, where at each level the head is designated by a relatively longer branch, and its elaboration by a shorter one branching from it. This, then, constitutes the process of time-span reduction, based on the reduction of successive levels to fewer and fewer heads governing ever larger musical time-spans. Below the staff, a secondary notation shows the specific pitch content of the heads for each of the levels labeled a–f, mirroring the tree structure. The hierarchic principles here are broadly analogous to the organic conception of Schenker’s voice-leading analyses, except that Lerdahl and Jackendoff claim to have developed—in contradistinction to what they term Schenker’s “artistic” approach—a theory whose precepts are explicit throughout and are in principle empirically testable (GTTM, 111–12). These precepts take the form of Time-span Reduction Well-Formedness Rules and Time-span Reduction Preference Rules (TSRWFRs and TSRPRs).
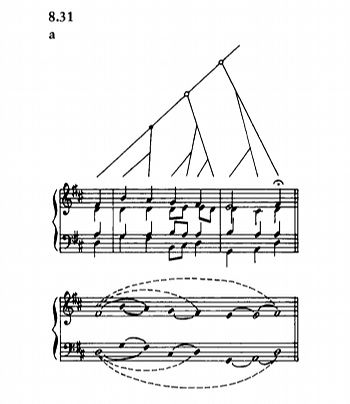
Example 2. Prolongational reduction of opening of “O Haupt voll Blut und Wunden” (GTTM, 202; Example 8.31)
(click to enlarge)
[2.6] In addition to time-span reduction, Lerdahl and Jackendoff argue the need for a further form of analytical tree structure known as prolongational reduction, the fourth component of their methodology. This is intended to map patterns of tension and relaxation in the music, and hence to capture the dynamism of tonal structures. The authors do not provide a complete prolongational reduction of “O Haupt voll Blut und Wunden”, but do include a treatment of the chorale’s opening phrase within their discussion of PR methodology, as shown in Example 2 (GTTM, 202; Example 8.31), whose tree structure subtly differs from its counterpart in Example 1. As Eric Clarke also points out (1986, 11–12), the need for such a supplementary graphing is debatable, being both presentationally unwieldy and theoretically less than parsimonious; I will return to this matter later.
[2.7] Notwithstanding GTTM’s claims to musical universality, its preferred repertory is unquestionably the Western classical canon, and its habitus a certain brand of Western music theory. On the face of it, then, any application to Indian classical music might look like the incongruous—or even hegemonic—imposition of a foreign model. Yet the historical long view suggests a more nuanced picture. For while GTTM is informed by present-day (or at least twentieth-century) linguistics, that discipline itself has its deepest roots in no less a figure than the Indian grammarian Pāṇini, active in the fourth century BCE. Pāṇini’s Aṣṭādhyāyī (c. 350 BCE) is an exhaustive grammar of Sanskrit, and as Paul Kiparsky writes, “Western grammatical theory has been influenced by it at every stage of its development for the last two centuries
[2.8] It is also clear that any analysis of Indian classical music along generative lines needs to take account of its culturally specific principles of musical organization, in this case those of rāg. Further, as Example 1 strongly implies, it would be difficult to conduct such an analysis without some notated record of the performance. Since Indian classical music is practiced within an oral culture, a formal analysis of its music will need to rely on some prior act of musical transcription. These two features—an account of rāg, and a consideration of transcription—are considered in the next two sections.
Audio Example 1. Vijay Rajput, Ālāp in Rāg Yaman (from CD, Twilight Raags from North India), Track 4
[2.9] But prior to all this, to ensure that what follows is experienced in more than abstract terms, readers are first encouraged to familiarize themselves with the musical passage I will consider, which can be heard in Audio Example 1. This comes from a recorded performance of Rāg Yaman from the CD Twilight Raags from North India (2006). As mentioned above, the CD’s principal artist is vocalist Vijay Rajput, accompanied by Shahbaz Hussain on tablā (drums), Fida Hussain on harmonium, and Praveena Srikantan on tānpūrā (a kind of lute, which provides the background drone throughout the performance). The recording was made at Newcastle University in the UK, with John Ayers as sound engineer and myself as producer. Yaman is an evening rāg, usually performed just after sunset, and Rajput’s rendition amply captures the calm, romantic mood often associated with it. As with most classical Indian performances, Rajput establishes the rāg by means of an ālāp—an unmetered prelude—and it is this section (track 4 of the CD) to which the analysis below is devoted. While ālāps may be considerably extended, especially in instrumental performances and in the dhrupad vocal style, this one is quite short (lasting only three minutes). This is typical of khyāl performances that include a baṛā khyāl (or vilambit khyāl) immediately after the ālāp; in the first stages of the stately baṛā khyāl the vocalist continues the unmetered feel of the ālāp, notwithstanding the presence of the tāl (rhythmic cycle) now provided by the tablā. In the ālāp itself, however, the tablā player is silent, leaving the vocalist to extemporize freely against the tānpūrā drone, discreetly shadowed by the harmonium. It is worth noting that the term khyāl, which designates the particular vocal style represented by this performance, is a borrowed Arabic word meaning “imagination”—a reminder of the performer’s need to draw from the creative faculties of his or her mind.
[3] Preliminaries 2: Principles of rāg
[3.1] Listening to this ālāp should confirm that pitch organization in Indian classical music is conceived principally in melodic terms: there is no concept of harmony. Hence, anticipating our application of GTTM, we can prognosticate that all well-formedness and preference rules based on harmonic considerations can be “switched off”; the key parameters will be melody and duration. As indicated above, the precepts of melodic organization in Indian classical music are those of rāg. Rāg is as much an aesthetic principle as a grammatical one: each rāg embodies its own mood and state of feeling,(13) whose performance style—often involving extreme subtleties of melodic inflection and ornament—can ultimately only be learned orally through a sustained personal bond between master and disciple (guru and śiṣya). Nonetheless, key structural precepts of rāg organization can be more explicitly articulated in terms of scale forms and scale degrees, which constitutes part of what a teacher communicates to a student, in what is essentially a kind of informal theorizing. Teachers may also reference terms and concepts from Indian theorists such as Vishnu Narayan Bhatkhande (1860–1936), including his classification of rāgs into parent scale groups, or ṭhāṭs (“frameworks”), notwithstanding anomalies in this system recognized even by Bhatkhande himself (see Bor et al. 1999, 3–4).
Example 3. Scale degrees with Sanskrit note names and abbreviations
(click to enlarge)
[3.2] To enumerate some basics:(14) Every rāg is rooted on a tonic or final, known as Sa—which, as we hear in the audio example, is present as an unchanging drone played by the tānpūrā throughout a performance; there is no concept of modulation. Every rāg is also based on a scale form, with scale degrees being described using so-called sargam notation (equivalent to Western solfège): Sa, Re, Ga, Ma, Pa, Dha, Ni. These are shown, with Western transnotation, in Example 3, which also gives the Sanskrit names in full. The staff-notated counterparts do not signify absolute pitches, since Sa may be set at whichever pitch is comfortable for the performer; rather, here and subsequently, noteheads in effect signify scale degrees. Modal in nature, rāgs are differentiated by, among other things, being based on differently inflected scales. While Sa and Pa ( and ) are “immovable notes” (acal svar), the remaining five scale degrees are movable (vikrit): Re (), Ga (), Dha () and Ni () can all take flattened (komal) form; and Ma
Example 4. Rāg Yaman scale—ascending (āroh) and descending (avroh)
(click to enlarge)
[3.3] The latter property applies to Rāg Yaman, whose ascending and descending scales are shown in Example 4. It belongs to the Kalyāṇ ṭhāṭ, whose scale is inflected by a sharpened fourth—broadly analogous to the Western Lydian scale. However, while Yaman describes the complete scale in its descending melodic figurations (avroh), it typically circumscribes the tonic and fifth degrees in ascent (āroh). A further way in which rāgs are differentiated from one another (and hence articulate their own place within a differential rāg system) is through the prominence of particular scale degrees. Bhatkhande terms these salient tones (normally one in each tetrachord of the scale, and placed a fourth or a fifth apart) vādī and saṃvādī—sometimes translated as “sonant” and “consonant”. In Yaman, these tones are the third and seventh degrees respectively, and their salience is evident in Audio Example 1. But actually, the grammar of a rāg is more complicated than this: learning it involves the student in understanding the relative importance and behavioral characteristics of every note in relation to the others. For example, in Yaman (unlike many other rāgs) the performer may sustain all pitches to a greater or lesser extent; it is just a question of how. Pa () may be prominent—often as a psychological resting point—while Sa () is perhaps more significant as a structural final than for any commensurable statistical prominence. Re () and Dha (), while usually perceived as being en route to one or another adjacent tones, have a status (and a related beauty) stronger than that of mere passing notes (in Western terms).
[3.4] Describing the behavior of tones (svar) in Rāg Yaman in this way is to informally outline what I will henceforth term its rāg grammar. A generative approach could be developed to describe this more formally, and indeed Cooper (1977) has undertaken this for the North Indian rāg system as a whole. But my concern here is less to model rāg grammar in the abstract (supratemporally) and more to map its implementation in an actual performance, using a version of GTTM’s time-span reduction rules.
[4] Preliminaries 3: transcription as proto-analysis
[4.1] Musical writing is a tacit condition for Lerdahl and Jackendoff’s generative methodology. For all its ostensible orientation towards the innate cognitive capacities of the listener, it is predicated on the affordances of the musical score, which can be contemplated outside the real time of performance. Related to this, it is also clearly founded on the work concept.(15) By contrast, in Indian classical music, which is largely an oral tradition, there is neither work concept nor score. An application of GTTM methodology to this idiom, then, requires not only musical transcription but also a degree of reflexivity about how this is undertaken.
[4.2] This is not to say that notation is entirely absent from Indian musical praxis—in fact it has a long history. Widdess (1980) identifies some of the earliest written evidence of sargam notation as that found in the musical inscription at Kuḍumiyāmalai in Tamil Nadu, dating from the seventh or eighth century. And sargam is regularly used (at least as much in oral as written form) in the quotidian interactions of musicians in the present day, especially between teacher and student. More formal notation systems were developed in the later nineteenth and early twentieth centuries, particularly in the latter period as Indian classical music entered the sphere of middle-class Hindu life and pedagogy became centered in music schools and academies—especially under the aegis of Vishnu Digambar Paluskar.(16) Perhaps the most common notation system in use today is that devised by Bhatkhande, which he employed throughout his Kramik pustak mālikā (1937), the extensive collection of song compositions (bandiś) that he elicited from hereditary Muslim and Hindu performers. While the transmission of compositions between musicians continues to have a strong oral emphasis, notated song collections such as Bhatkhande’s remain important points of reference.
Example 5a. Transcription of ālāp from Vijay Rajput’s performance of Rāg Yaman (Twilight Raags from North India, track 4) using sargam notation
(click to enlarge and see the rest)
Example 5b. Transnotation using Western staff notation
(click to enlarge and see the rest)
[4.3] Notation and transcription in these contexts, however, tend to have a prescriptive rather than descriptive function, to apply Charles Seeger’s (1958) dichotomy. Typically, notation is used as an aide-mémoire for the execution of songs and other materials, though what is actually performed in that process may depart significantly from the written trace that facilitated it. By contrast, transcription for ethnomusicological and analytical purposes may need to capture levels of detail that might stimie a performer if read prescriptively. A case in point would be the extreme refinement of the system for notating vocal ornamentation developed by Nicolas Magriel in his and Lalita du Perron’s monumental study of khyāl (Magriel and du Perron 2013, 70–82). Magriel’s meticulous descriptive transcriptions of specific song performances is motivated by his “conviction
[4.4] This double transcription, then, creates a fixed object of analysis out of the fluidity of an improvised performance—a necessary reification in order to construct a GTTM-type analysis of the passage; but one whose implications we shall need to bear in mind when we reach that analytical stage. The transcription methodology in Example 5 is loosely modeled after Bor et al. (1999, vii–viii.), albeit that in their case sargam and staff notations are superposed rather than separated. Their transcription style is valuable because it deploys a form of proportional notation that foregrounds the relative length of each pitch (svar)—a feature that will become germane when we consider concepts of prolongation below. For related reasons, the distinction Bor et al. make between sustained notes and their many embellishments is also pertinent, though the distinction between decorative and “structural” notes in my transcription is sometimes more relative than absolute. Decorations are superscripted in the sargam notation (where, additionally, the carat symbol indicates a “mordent” and the sawtooth symbol a double shake), and are shown as ornaments in the staff transnotation.
[4.5] Some further aspects of the notation need explanation. In Example 5(a), letters are abbreviations of sargam scale degrees (see Example 3); hence S = Sa (), R = Re (), etc. The wedge above M indicates tīvra Ma (
[4.6] Example 5 represents an important step towards analysis not only in providing notated material for that purpose, but also because the transcription itself reflects and makes possible certain analytical judgments. For example, it presents a segmentation of the material into phrases and, towards the end of the passage, subphrases. In the same proto-analytical spirit, the proportional notation of both versions of the transcription reveals how each phrase tends to be focused around a single prolonged tone. Such tones are highlighted in the transnotation by adding the sargam abbreviation of the prolonged tone in question below the staff. On the one hand, “prolonged” here commonsensically means “sustained for some time”: the prolongations reflect a standard practice of improvising an ālāp in the khyāl style, in which phrases are built by extemporizing around a sustained svar (pitch/note/tone). But equally, “prolonged” can also be applied in the more formal sense of generative theory, in which a prolonged tone is accorded structural status—which may or may not be a function of its empirical duration alone. This, then, is one way in which an informally theorized practice and a formal theorization of structure start to converge.
[5] Applying GTTM: some essential preference rules
[5.1] These last observations lead me finally to a formal analysis of Rajput’s ālāp in Rāg Yaman on generative lines. What those comments point toward, and the transcription itself illuminates, is the operation of Lerdahl and Jackendoff’s strong reduction hypothesis, under which “structurally less important events are not heard simply as insertions but in a specified relationship to more important events” (GTTM, 106). This hypothesis is elaborated through the time-span reduction procedures of GTTM, and in order to apply these to our ālāp I will start from the following working assumptions, with the intent of subsequently formalizing them into something closer to rules:
1. (a) that each phrase of the transcription in Example 5 constitutes a group or time-span, and (b) that each such group belongs to the same hierarchic level.
2. that the empirically identified prolonged tone in each phrase represents that group’s head; and that all remaining materials in each phrase/group are therefore in some way subsidiary to that head.
3. that successive heads themselves determine larger groups, which in turn contain a higher-level head; and that this process may be applied recursively to reveal a nested hierarchic structure for the entire utterance.
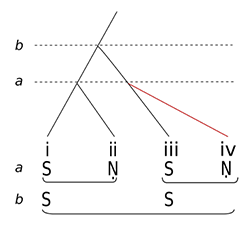
[5.2] Regarding assumption 1(a): The prior cognitive act of identifying a phrase is itself dependent on the perception of a boundary between that phrase and its successor. The strongest cue for this is, among other things, the gap the performer places at the end of each phrase (I will later consider other factors such as quasi-cadential figurations). This is formally described under GTTMs Grouping Preference Rule 2a (proximity) (see GTTM, 45).
[5.3] Regarding assumption 1(b): In a metrical piece, the time-spans associated with groups—and hence the hierarchic level to which they belong—would (unsurprisingly) be calibrated metrically; thus groups might be articulated at the two-measure, four-measure, eight-measure levels, etc. But in unmetered music such as an ālāp, time-spans are necessarily more elastic. For example, while phrases i–vi differ in length somewhat, they are perceived as occupying equivalent time-spans because each phrase has an equivalent morphology: a clearly identifiable prolonged tone (or head) which the rest of the material is understood to elaborate (cf. assumption 2).(17)
[5.4] Assumption 2 can be readily reformulated as a Time-span Reduction Preference Rule (TSPR) that will be fundamental to the unmetered conditions of an ālāp. This is one of several idiom-specific preference rules that I here term Ālāp Preference Rules (APRs),(18) which supplant the TSRPRs from GTTM that are no longer relevant in the ametrical, monophonic context of an ālāp. For the record, these redundant rules are TSRPR 1 (metrical position), TSRPR 2 (local harmony), TSRPR 3b (bass registral extreme), TSRPR 5 (metrical stability), and TSRPR 6b (harmonic progression). The new preference rules, then, will need to be based solely on the parameters of melody (pitch) and duration. APR 1, based on assumption 2 above, formalizes the role of duration:
APR 1 (pitch duration) In selecting a head of a time-span, prefer the tone sustained for perceptibly the longest duration.
This is to reaffirm the point made at the end of the last section: that if a tone is prolonged empirically, it is prolonged structurally. For the moment, the qualifier “perceptibly” needs no further comment, since at the surface level currently under scrutiny, and in phrases i–vi especially, the prolonged tones sing out loud and clear—as the sargam annotations below the staff in Example 5(b) make plain. These are, in order: Sa (phrase i), .Ni (phrase ii), Sa (phrase iii), .Ni (phrase iv), .Ni (phase v), and Sa (phrase vi).(19) In this context, then, the principle and application of APR 1 seem disarmingly simple. Can this really be the case?
[5.5] A few glosses are called for. First, if the structural heads are easy to identify, this is because the performer has generated things that way. In other words s/he has executed the kinds of conventions that artists in this tradition internalize as part of their training. I would hazard that such conventions reflect well-formedness rules, which could be formalized as follows: (1) ensure that in each phrase there is a principal sustained svar (note/tone); (2) ensure that sustained tones and any ancillary sustained notes are those permitted to be sustained under the grammar of the rāg.
[5.6] Secondly, any loss of subtlety or depth that might attach to the direct identification of a sustained note and structural head is amply compensated for by the fact that a “note” (svar) in Indian music has an acknowledged life beyond mere pitch and duration. This is a life lived in microcosm—for example in the way Rajput plays with the vowel formants of the sustained Ga in phrases vii and x of the ālāp (at 1:16–1:22 and 2:05–2:17 of the recording), and also in the near-ubiquitous tiny ornaments (alankār) that decorate the sustained svar, and further decorate the decorations. The analytical implications of this suggest a possible culture clash, since Lerdahl and Jackendoff incline against systematic analysis of musical minutiae and tend to focus on higher levels—a point to which I shall return in the final section.
[5.7] Thirdly, this seemingly straightforward conflation of empirical and theoretical salience does not obtain at every level. At the micro-level just mentioned, and at meso- and macro-levels still to be discussed, further complexities in the identification and grouping of structural heads arise, which will presuppose additional preference rules.
Example 6. Time-span reduction analysis of phrases i–ii of ālāp: (a) surface level (b) including next hierarchic level
(click to enlarge)
[5.8] With this last point in mind, let us now consider assumption 3, regarding the higher-level groupings of successive heads. If correctly founded, this assumption would show the operation of syntactic principles well beyond the musical surface that could be understood as ultimately generating it. As an initial step in building a time-span reduction, Example 6 graphs the relationship between phrases i and ii.(20) Example 6(a) shows Sa () and .Ni (.) as the heads of their respective phrases (their status is readily discerned from the transcriptions in Example 5). These two heads in turn form a group in which, as the right-branching tree structure indicates, the .Ni of phrase ii is heard as an elaboration of—and hence subordinate to—the Sa of phrase i. In other words, and as Example 6(b) indicates, Sa functions as the head of this analytical level (a), and maintains a presence in the next level (b) of the TSR, while .Ni is reduced out.
[5.9] In the first instance, such judgments are made intuitively; but under what kind of preference rule could they be formally corroborated? APR 1, which served well in identifying heads at the surface level, will not suffice here, since Sa and Ni are not of perceptibly different lengths and hence cannot be discriminated on grounds of duration. (This is where the qualifier “perceptibly” comes into play, for while these tones may be of objectively different lengths, they are similar enough to be perceived in context as being of equivalent length and hence also functionally equivalent.)(21) Accordingly, a further preference rule is warranted. The rationale for Sa as the head in Example 6 is largely self-evident: Sa is the tonic, and, like the tonic in Western common-practice tonality, Sa determines the ultimate presiding level: sooner or later, all departures from it, at whatever level, will return there.(22) As in Western music, then, the function as well as the duration of a pitch is significant in determining its hierarchic status. Hence:
APR 2 (tonic function) Where there are rival candidates for a head of a time span and one of them is Sa, prefer Sa.(23)
[5.10] While this rule resolves the current matter of the choice between Sa and Ni, it is not difficult to foresee situations where neither rival candidate for a head is Sa. What then? Such cases would still need to refer to pitch function, but in terms of the grammar specific to the rāg. This itself comprises a hierarchy, with (in Bhatkhande’s language) the vādī and saṃvādī tones being of the greatest importance, and, after this, other tones having relative prominence (for example, Pa () in Rāg Yaman). From this we can posit the following further preference rule:
APR 3 (pitch function in rāg grammar) Where there are rival candidates for a head and neither of them is Sa, prefer the svar (pitch) that has relatively greater importance in the rāg grammar (typically vādī or saṃvādī).(24)
The stability of a rāg may be underwritten by a convergence of these rules in performance. In this opening period of our Yaman ālāp, for example, .Ni is particularly salient and stable against Sa, being prolonged in a number of the opening phrases (APR 1) and functioning as the saṃvādī tone of Yaman (APR 3).
[6] Phrases i–vi: meso-level analysis and the question of the diachronic
Example 7. Time-span reduction of phrases i–iii (alternative analyses)
(click to enlarge)
Example 8. Time-span reduction of phrases i–iv
(click to enlarge)
Example 9. Time-span reduction of phrases i–vi
(click to enlarge)
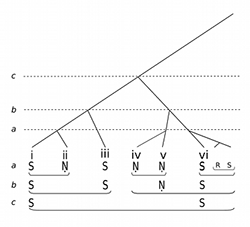
[6.1] We now have enough basic axioms to complete a time-span reduction of the opening period of the performance, phrases i–vi. At this stage in the analysis I want to raise a further issue that forms part of this essay’s critique of GTTM. This concerns a matter that is somewhat repressed in GTTM but that cannot be so readily avoided in relation to improvised performances such as Hindustani classical music: their generation in real time. As mentioned above, one of the working assumptions of GTTM is that the score of a work is always available in its entirety for consultation. GTTM’s analyses are synchronic: any given detail can always be considered in the light of the larger whole at whatever level is necessary; as Lerdahl and Jackendoff put it, “we will be concerned only with the final state of [the listener’s] understanding” (GTTM, 3–4). But the essence of an improvised performance is that it is diachronic: at any given moment, the rest of the performance—and with this, its structure—does not exist in any finalized form; future content that might be used to make judgments on what we are actually hearing, or have just heard, is not yet available. Meanings often remain ambiguous and open, not least to the performer. Hence the following time-span reduction of Rajput’s ālāp attempts to map the performance as it is delivered and conceived: as an accumulation of phrases whose future content is not fully known.
[6.2] So let us resume our TSR analysis where we left off, with the determination of .Ni in phrase ii as an elaboration of Sa from phrase i (Example 6). At the actual time of its sounding, .Ni displaces Sa, yet is heard as subordinate to it. This creates a tension that implies resolution by a future return to Sa, an implication realized in phrase iii. As shown at level b in Example 7(a), the new phrase confirms Sa as the presiding head for the overall timespan i–iii. However, as the analysis also shows, this moment introduces an ambiguity around the status of .Ni from the prior phrase, ii, now heard in the past tense as it were. On the one hand, we might continue to consider .Ni as an elaboration of the initial Sa, tensing away from it (Example 7a). On the other hand, we might hear it as having anticipated the Sa at iii, relaxing into it (Example 7b). Our options here are either to seek to resolve the ambiguity by devising or invoking a preference rule, or to live with it as an inherent aspect of the performance, and allow both representations to co-exist (which would also reflect the prominent agency of Ni in Rāg Yaman). I am inclined to entertain the latter option, and extend this principle to the rest of the analysis.
[6.3] Successive phrases in any case continue to rewrite the hierarchic order of things. As Example 8 demonstrates, phrase iv (highlighted), another prolongation of .Ni, causes the status of the .Ni in phrase ii to be reviewed again, because the entire time-span, i–iv, now manifests a parallelism (Sa–.Ni / Sa–.Ni) that invokes GPR 6 and TSRPR 4 from GTTM (51, 164). Making a jump-cut to phrase vi (Example 9), we can see a further reconceiving of this structure, in which .Ni from phrase iv (again highlighted) is heard to have anticipated its further prolongation at v, finally to resolve back to Sa at phrase vi. This point clinches an overarching prolongation of Sa for the time-span i–vi, and with it an additional level, c, in the time-span reduction structure.(25) This moment retrospectively overwrites the symmetrical 2+2 structure that obtained at the end of phrase iv, with a no less symmetrical (but different) 3+3 structure at the end of phrase vi.
[6.4] The deeper point revealed by this modeling of the diachronic structure in successive snapshots is this: that the different versions of the structure we experience, while not assimilable to one another, are all true; only they are true at different times. Engaging with an improvised structure such as this ālāp is what it takes to force an explicit engagement with the diachronic—a matter inadequately treated in GTTM—out into the open. True, Lerdahl and Jackendoff do posit prolongational reduction as an additional stage of analysis to model the flow of tension and release in a piece across time. But one of the many problems with this supplementary process of syntactic parsing is that it is executed top-down, only after the TSR has been undertaken,(26) and thus it assumes, once again, that all information about an entire piece—or improvised performance—is simultaneously available. Hence it remains an essentially synchronic standpoint.
[6.5] As if in response to this lacuna, Jackendoff made his own attempt to address the diachronic in his article “Musical Parsing and Musical Affect” (1991). And while he models the diachronic a little differently from the successive-snapshots approach taken here, he similarly finds it necessary to offer multiple analytical renderings of the music being considered as it moves along its course. This is consistent, Jackendoff argues, with Daniel Dennett’s multiple-drafts model of consciousness (Dennett 1991), in which cognition entails several parallel analyses of what the subject is attending to, most of which remain unconscious. As a piece or performance proceeds, a previously unconscious positing of an element’s structural function might become activated into consciousness, overwriting an earlier construal, as more information gradually becomes available—much as we have seen in the successive re-writings of our ālāp analysis up to this point.
[7] Excursus: the cadenced group in Hindustani classical music
[7.1] What is clear from the above analysis is that we feel intuitively how phrase vi imparts closure not only to its local time-span but also to this entire period of the ālāp so far. This raises the question of how we might formally define structural cadences in Hindustani classical music and how this construct compares to its Western counterpart. As these matters are foundational for much of the ensuing analysis, I will now consider them in some detail.
[7.2] Hindustani classical music does have certain formulae akin to cadences in Western terms, such as tihāī, a figure repeated three times, the end of whose final iteration usually coincides with sam, the beginning/end of a rhythmic cycle; and also mukhṛā, an anacrustic melodic phrase (usually associated with a baṛā khyāl) similarly culminating on sam. But these are always heard in the metrical context of a tāl, and since that condition does not obtain in an ālāp, this points to other, less semiotically overt forms of melodic figuration that can function cadentially (and are not confined to ālāps either). In fact, while Indian classical music does not have an explicit term that is analogous to “cadence”, it nonetheless avails itself of similar or equivalent structural gestures, which I will outline below. This, then, suggests a universal or cross-cultural aspect of musical syntax, for all that the structure is named in one culture but not in the other.
[7.3] The TSR of phrases i–vi (Example 9, level c) exemplifies what Lerdahl and Jackendoff term a cadenced group: an overarching structure defined by a structural beginning at one end and a structural ending at the other (GTTM, 168–70). The concept of a structural ending—more commonly known as a cadence—is familiar enough. But as the authors put it, “a cadence must be a cadence of something”; hence it will have a higher-level connection back to some structural beginning (although TSRPR 8 of GTTM leaves the definition of this open). The notion of a structural beginning is far from alien to Indian music. The opening of a rāg performance (such as phrase i) amply meets the criterion: one way or another, with whatever variation, this is where the performer usually intones—“tunes into”—Sa: a focused transition from the prevailing ambience of the tānpūrā (whose role is to provide a drone on this note) into the start of the performance proper. It is in every sense a beginning, in every sense structural. Hence in Example 9 the branch from phrase i projects beyond phrase vi itself, across the entire analysis.
[7.4] What then of structural ending? How are we to define cadence in the Hindustani classical context? We can begin by adapting TSRPR 7 from GTTM (170), positing that a figure can be classified as a cadence if it meets all of the following criteria:
1. it contains a sequence of two (or possibly more) events that conform to a cadential progression.
2. the last event is at the end of its time-span or is prolonged to the end of that time-span.
3. there is a larger group for which the progression can (also) function as a structural ending.
As regards criterion 1, a cadential progression in Indian classical music will clearly be defined in melodic rather than harmonic terms, most plausibly as a progression to the final of the rāg (Sa) from above or below. Assuming that the Gestalt principles that partly inform GTTM are universal, this is likely to be a stepwise motion or involve a relatively small interval, since this induces greatest stability, and stability is a key criterion for a cadence. This is also likely to be further inflected by the grammar of the rāg. Hence in Rāg Yaman, when Sa is approached from above, this may well be as part of the conjunct motion Ga–Re–Sa (––), as found at the end of phrases x and xiii (2:15–2:21 and 3:09–3:14); shown as motif z in Example 5(b)).(27) But when Sa is approached from below in a Yaman context, this is less likely to be directly from .Ni, and more elliptically via the motion .Ni–.Dha–Sa
[7.5] This latter motion is found at several places in phrases i–vi (which occupy the lower octave of the rāg), and is identified in Example 5(b) as motif x. The paradox is that we nearly always hear this figure at the beginnings of phrases, which would seem to debar it from being considered as a structural ending, as is apparent in phrase i. But this is only true at the surface level, a. As the music unfolds, x can also be heard to function in the context of an emerging hierarchic structure, articulating closure at higher levels even as it continues to appear locally at the beginning of phrases. Hence in phrase iii, motif x connects back to its counterpart at the opening of phrase i: the two elements function respectively as structural ending and beginning for the time span extending across the opening three phrases, shown as a single overarching group at level b of Example 9. Hence x in this context fulfills all three criteria for a structural ending: its constituent melodic events leading to Sa are recognized as a closural melodic formula (criterion 1); locally it is prolonged to the end of its phrase (criterion 2); and it forms a structural ending for the larger group shown at level b of Example 9 (criterion 3).
[7.6] In phrase vi the cadential function of x is felt even more deeply, albeit that the situation is more complex. The figure again appears at the beginning of the phrase, but there is now plenty of preceding material on which it can act closurally. Most immediately, it resolves the prolongation of .Ni across phrases iv and v, creating another cadenced group at level b of Example 9. Furthermore, as pointed out above, it also connects back across the entire ālāp so far, to articulate a cadenced group at level c. Again, then, all three cadential criteria are satisfied. As Example 5(b) further shows, motif x in phrase vi is followed by a short suffix (from 1:02) based on motif y, which temporarily foregrounds Re () before returning to Sa, voicing another tiny version of x as it does so. This is a moment of delightful and carefully calculated ambiguity (shown at the end of Example 9 as a subgroup of level a). On the one hand, the suffix prolongs the closural Sa of x to the end of phrase vi (criterion 2); on the other hand, the motion to Re—a new feature—adumbrates its own prolongation in the subsequent phase of the ālāp. Hence this point of maximal closure thus far is also left subtly open.(28)
[7.7] While Lerdahl and Jackendoff are coy about taxonomizing levels, declining to adopt Schenker’s foreground–middleground–background schema, they do entertain a loose hierarchy that construes cadenced groups as a higher level of organization than uncadenced groups, and the latter as superordinate to subgroups, granting that each type may obtain at several levels (GTTM, 317, 319). As we have seen in Example 9, the cadenced group structure so far obtains at both levels b and c of Rajput’s ālāp, spanning phrases i–iii and i–vi respectively. It will be helpful (for the rest of this analysis at least) to confirm the nomenclature of time-spans determined by cadenced groups on the latter level as periods. Phrases i-vi, then, comprise period 1 of the ālāp.
[7.8] Another question regarding this first period is significant for the rest of the analysis: namely, whether we should regard its structural beginning or structural ending (cadence) as its head. Lerdahl and Jackendoff do not seem to explicitly indicate which way one might incline as a general principle. On the one hand, their preliminary formulation of TSRPR 7 (GTTM, 167) seems to favor the cadential element: “Of the possible choices for the head of a time-span T, strongly prefer an event
[8] Phrase vii onwards: priorities of analytical representation
[8.1] While my discussion could continue with representing the diachronic structure of this ālāp as an iterative series of self-revising drafts, I will take that point as having been made, and will focus instead on a different matter that similarly invites critical questions of GTTM (and again relates to the real-time dynamics of performance). This concerns our analytical priorities as we progress through the ālāp and get closer to the full picture. Specifically, how are we to evaluate the larger-scale dynamics of goal direction against the stabilizing tendencies of larger-scale cadenced groups? Or to put it another way, what is more significant: teleology or morphological integrity? But before proceeding I need to set the scene by outlining three key features of the remaining part of Rajput’s ālāp rendition, phrases vii–xiii, accounting for about two thirds of the overall length.
[8.2] First, the material becomes generally more complex, in accordance with what one might term the performance grammar of Indian classical music, in which each phase of the performance is structured by an overall pattern of intensification. This can be effected by some combination of increasing rhythmic movement, which in metrical sections might also mean an increase in tempo (lay), a general pattern of registral ascent, and increasing complexity of invention and other resources for musical development (see Clayton 2000, 106–11; Magriel 1997). Here, still in the early stages of the performance, Rajput applies these options judiciously; but that they subtly obtain is evident from the transcription in Example 5, which shows how phrases gradually admit more ornamentation and generally get longer. As we will soon see, they get structurally more complex too, with each phrase tending to comprise more than one time-span at the equivalent level of their counterparts in period 1.
[8.3] Second, the phrases of this latter part of the ālāp also group into higher-level periods, articulating two further time spans of equivalent length to period 1:
period 2 comprises phrases vii–x; period 3, phrases xi–xiii. Third, these are organized around Ga
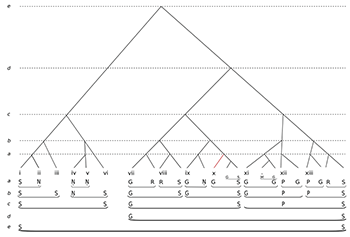
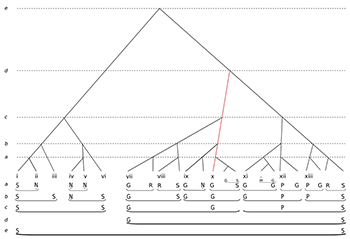
Example 10. Time-span reduction of entire ālāp, prioritizing cadenced groups
(click to enlarge)
[8.4] All of these elements—the more elaborate phrase structure, the aggregation into periods, and the goal-directed structural ascent through Ga and Pa—need to be reflected analytically. Example 10 presents one possible TSR of the complete ālāp. At level a we can trace one corollary of increasing morphological complexity. As indicated above, whereas in period 1 each of phrases i–vi at this level was coterminous with a single head note, the longer phrases of periods 2 and 3 usually involve a progression across two head notes (and hence time-spans) at the same structural level (e.g. Ga–Re in phrase vii, Re–Sa in phrase viii). Extending further, phrase xiii executes the descent from the overall goal tone Pa to the structural ending Sa across four equivalent heads, grouped as 2+2 (P–G, R–S).(29)
[8.5] Level c of Example 10 transparently maps the period structure, which is articulated as three cadenced groups. The representation of the first period (Sa–Sa) is carried over from Example 9; now added to it are the second and third periods: Ga–Sa, and Pa–Sa. Thus the cadenced-group construction remains formative, reflecting the middleground of the performance. However, while the analysis elegantly renders the morphological equivalence between periods, in certain key respects it obscures the teleological significance of Ga and Pa in periods 2 and 3 respectively. And this brings us to the dichotomy to which I alluded at the outset of this section: the question of what to prioritize in an analytical representation. Matters are least problematic in period 3, where Pa in phrase xii is represented as a head at level c and is subordinate (left-branching) only to the structural final Sa at the end of phrase xiii. For all that Pa is teleologically dominant, it would have been undesirable to reverse the branching and so demote the Sa that is the structural ending for the entire ālāp, since this would undermine the top-level connection (level e) between this Sa and the Sa of the structural beginning (phrase i). Here, then, the representation appropriately prefers morphological integrity over teleological salience without downgrading the latter.
Example 11. Alternative analysis of ālāp, prioritizing final Sa of phrase x
(click to enlarge)
[8.6] However, in period 2 matters are more ambiguous. In Example 10 the general salience of Ga across phrases vii–x is reflected in the right-branching structure at level c. This shows the structural ending on Sa at the end of phrase x as subordinate to the structural beginning on Ga at the start of phrase vii. For the record, an alternative graphing of this period would be possible, as shown in Example 11. This reverses the preferences and shows the structural ending on Sa of phrase 10 (highlighted) as superordinate—now a left-branching structure. However, I prefer Example 10 as a plausible reading that respects the teleological importance of Ga, and hence (at level c) shows the period as non-closed. In this version, the eventual resolution of Ga to Sa takes place instead at level d, taking the final Sa of phrase 13 as a structural ending, and so articulating periods 2 and 3 as a single overarching cadenced group at this higher level. This representation seems appropriate given the sheer salience of the prolongation of Ga at the ālāp’s apex.
[8.7] So far, so good. Except that Ga’s most salient expression of all comes in phrase x, which Example 10 seemingly perversely shows as having relatively low status: a left-branching elaboration at level a (highlighted). Indeed this contradiction is endemic: as the three structural Ga-s, in phrases vii, ix and x, increase in empirical salience (manifesting successively longer and more decisive prolongations in Rajput’s performance), they are shown as having diminishing structural importance: as left-branching elaborations of Sa at levels d, b and a respectively.
[8.8] How can we reconcile these conflicting claims of representation: between morphological integrity on the one hand and teleological salience on the other? We know what Lerdahl and Jackendoff might suggest: that in addition to a time-span reduction (TSR) to model patterns of elaboration we develop a prolongational reduction (PR) to show patterns of tension and relaxation (which would require its own rulebook—see GTTM, chapters 8 and 9). However, as already indicated, Lerdahl and Jackendoff’s dualistic methodology is problematic. The difference between an “arc of tonal motion” from structural beginning to structural ending (in TSR) and a progression from “tensing” to “relaxing” prolongations (in PR) is arguably a matter of semantic nuance over the same set of structural relations (GTTM, 189 and Ex. 8.13); it is not necessarily the pretext for an entire complementary graphing system. Lerdahl and Jackendoff’s requirement that the PR analysis of a piece be modeled not on the actual musical surface but on its TSR analysis (in effect as a re-reading of the latter) effectively points to the intimate mediation of the two processes,(30) with the unaddressed epistemological implication that they ought to be brought into unity (GTTM, 187–8, and 220–1 (PRPR1)).(31) If the dilemma around the structural function of Ga in the present discussion forces us to consider graphical variants, this need not mean a comprehensive reformulation of the entire analysis.
Example 12. Further alternative analysis of ālāp, prioritizing teleology
(click to enlarge)
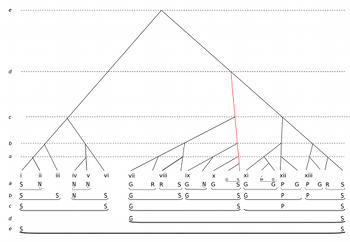
[8.9] For instance, Example 12 makes just one small but decisive adjustment to Example 10, which is to assign the highest structural status to the most empirically prominent head tone in period 2, the Ga of phrase x. This is now shown (again highlighted) as a left-branching prolongation at level d from the structurally closural Sa of phrase xiii. This modification upstages the Ga in phrase vii from its former superordinate place, and further downgrades the cadential Sa at the end of phrase x, but in all other respects the relative structural weightings of Example 10 are preserved.
[8.10] So, if Example 10 inclines more towards morphological propriety and Example 12 towards teleology, and if, pace Lerdahl and Jackendoff, we wish to refute the need for a dualistic analysis, which of these versions should we privilege? And what kind of preference rules would provide a formal description of our musical intuitions?
[9] Preferring teleology?
[9.1] Favoring Example 10 would require no significant emendation to the existing TSRPRs. This would identify the cadenced pair as the primary structural principle in both performing and listening: the arc of motion from whichever tone was the head at the structural beginning to the closing Sa at that same level. However, teleology could only be registered in a somewhat unspecific way. As noted, in Example 10, level c of period 2 shows Ga to be prominent within a larger scale group, but the actual moment of peak prominence, in phrase x, goes unrepresented as such. If this seems contrary to the aesthetics of performance and listening, then we would need a preference rule that permits us to override the priority of the cadenced group—to downgrade Sa as a structural ending in these kinds of contexts. In the case of phrase x in Example 12, such a rule would demote Sa from its status as a structural ending at levels a, b, and c in Example 10 to being significant only at level a. How can such a significant suppression be formally justified? This would be a marked departure from GTTM, which continues to accord priority to the cadenced group in its account of prolongational reduction, re-casting it as part of the “basic form” (GTTM, 188–9) that helps ensure that PR remains founded on the prior TSR reading (PRPR1).
[9.2] The upshot of this is to hypothesize that in Hindustani classical music (in ālāps at least) there is another principle that may under certain circumstances be understood to have greater importance than that of the cadenced group. What is this principle, and what are those circumstances?
[9.3] Let us call the principle structural strong prolongation. The term is adapted from Lerdahl and Jackendoff (GTTM, 182), who define strong prolongation as obtaining between two identical pitch events—in their case, identical as regards roots, bass notes and melodic tones; whereas from our standpoint only the melodic tone is relevant. The epithet “structural” in my proposed nomenclature implies that the prolongation obtains at a level some distance beyond the surface—as is seen in the prolongation Ga–Ga in period 2 at level c of Example 12, which extends across phrases vii–x (period 2 in its entirety). Like cadenced groups, structural strong prolongations have both a structural beginning and a structural ending, but if the beginning is not on Sa, then neither is the ending, and this form may trump any rival cadenced pair, such as the motion Ga–Sa at the same level across the same period in Example 10.
[9.4] This is possible in principle because Sa in Indian classical music has a different status from the tonic of Western classical tonality. Like the latter, it is of course structurally foundational; but at the same time, because it literally sounds all the time (in the tānpūrā drone) it is never really displaced or othered in the way it is under a structural modulation in Western tonality. Structural departures from Sa in Indian classical music do not engender a dialectic in the same way that prolongations of a non-tonic degree or triad would in Western classical music. Analogously, returning to Sa, while necessary to bring a period to closure, does not evince the same dialectical movement either. Hence a temporary “downgrading” of analytical representations of Sa at points where they might be shown as structural endings of a cadenced group need not be seen as a violation.
[9.5] So what are the conditions that would cause a strong structural prolongation to be preferred over a cadenced group? I advance the following preference rule:
SSP preference rule Let the two svar (tones) of a structural strong prolongation (SSP) be called a prolongational pair (PP). Where there are rival claims between a cadenced group and a structural strong prolongation (SPP), prefer the latter, if: (a) the SPP is articulated at least as a high a level as the rival cadenced group; and if: (b) the PP incorporates another PP based on the same svar in a shorter time span.
Condition (a) ensures that the SSP is of equivalent structural status to the rival cadenced group, while condition (b) helps tip the balance by requiring that the prolonged tone has a significant empirical presence at more than one level. Under these rules, we would prefer the analytical representation in Example 12 to that of Example 10. As to whether the structural beginning or ending of the SPP is taken as the head, APR 1 suggests itself (“prefer the tone sustained for perceptibly the longest duration”), again supporting the representation of Example 12.
[9.6] To reiterate: this is in principle a different process from supplying a supplementary analytical representation in the form of GTTM’s prolongation reduction graphs. It involves weighing up the alternatives and putting one’s cards on the table as to which constitutes the most appropriate version. Example 12 should not be read, then, as a supplementary prolongational reduction analysis, but as simply the most appropriate analysis, showing the balance of formal propriety and teleological salience (or, in Lerdahl and Jackendoff’s parlance, combining TSR and PR principles) that most faithfully represents what we hear going on in the performance, and that we also impute to the performer’s intent.
[10] Discussion and conclusions
[10.1] The preceding analysis represents a first foray into the application of GTTM to Hindustani classical music, based on a relatively brief example of one formal type (ālāp) from that repertory. I have endeavored to make this account sufficiently robust to afford a preliminary general evaluation both of the viability of the method for the analysis of this area of the world’s music, and of Lerdahl and Jackendoff’s claims for the universal applicability of their generative theory. Further, this non-Western application has interrogated some of the weaknesses of GTTM (as applied to Western music or any other)—principally regarding shortfalls in the treatment of real-time performance, and the problematic bifurcation of time-span and prolongational reduction—and has made some suggestions as to how these might begin to be resolved.
[10.2] The above account furnishes evidence that, with suitable adjustment to preference rules, GTTM’s methodology can effectively model at least certain features of Hindustani classical music. We have seen how Indian classical music, like its Western counterpart, depends on syntactic principles as a necessary, if not sufficient, condition for both creation and listener comprehension. A further important point that I want to develop here, which reinstates Schenkerian constructs that Lerdahl and Jackendoff suspend, is that these principles can be understood to obtain at background, middleground and foreground levels, with each level displaying a distinct character. The background level is coterminous with a ubiquitous tonic (ṣaḍj) that, unlike its counterpart in Western classical music, functions non-dialectically; the middleground is determined by features such as the cadenced group and structural strong prolongation; and the foreground is characterized by high levels of ornamental detail ostensibly cognized under the same syntactic principles (more on this presently). Further consideration of these levels in their specifically Indian determinations will inform the ensuing evaluation of GTTM in relation to this non-Western idiom.
[10.3] As already observed, the background functions non-dialectically: Indian classical music has no equivalent of a Schenkerian Bassbrechung—no structural motion to and from the dominant (or other-than-tonic); there is simply, and eternally, Sa.(32) This brings us back to the question of whether Sa should be shown as left- or right-branching at the highest level of tree-diagrams—that is, whether the highest-level structural beginning or structural ending should be shown as the ultimate head. In Examples 10 and 12, I have resolved this question by showing neither as super- or subordinate: the two principal branches bifurcate quasi-symmetrically from a single apex. This seems consistent with the notion of the status of Sa as an unchanging presence that ultimately embraces every feature of the performance. (Empirically speaking, this is reflected in the experience of the accompanying tānpūrā player, who provides the background drone by plucking the instrument at a nominally unchanging tempo and volume throughout, regardless of the intensifying trajectory of the soloist.)(33) Epistemologically, and in psychological terms, we can conjecture that Sa might be a permanently open Gestalt—or possibly even that it deconstructs the dualism of open and closed Gestalts: ultimately it is perhaps outside the agenda of structural beginnings and endings (just as a tānpūrā player is both inside and outside a performance). Pragmatically, the representation in Examples 10 and 12 is the most congenial accommodation to this fact.
Example 13. Ascending “fundamental line” for Rāg Yaman
(click to enlarge)
[10.4] Interestingly, Hindustani rāg performance is guided by an approximate equivalent of the Schenkerian fundamental line (Urlinie). However, in contradistinction to Schenker’s descending structure, this takes the form of a progression through the principal tones of the ascending (āroh) form of the scale of the rāg, congruently with the overall intensification across the course of a performance. Example 13 provides the archetype of this structure for Rāg Yaman (cf. the ascending scale form shown in Example 4). This should be read in conjunction with Example 12, which shows, in levels b–d of the secondary notation beneath the tree diagram, how structural tones other than Sa are introduced in ascending order: lower Ni (phrases iv and v), then Ga (phrases vii, ix, x and xi), then Pa (phrases xii and xiii). Less salient but still significant tones in the rāg grammar—namely Re and tīvra Ma (shown with filled-in noteheads in Example 13)—appear, appropriately, at the less structural level a, and between their respective adjacent structural tones.(34) While the Schenkerian representation of Example 13 shows this as an uninterrupted octave line, the distribution of the variably significant scale degrees across several levels of the TSR in Example 12 reflects the rāg grammar, showing how the different scale elements emerge at the right time and with the right degrees of prominence. In effect then, this teleological progress is not a background structure in quite the same way as its Schenkerian counterpart; rather, it is manifested across various middleground levels, the background proper being reserved for Sa itself. This captures a subtle but important difference between Western and Indian classical tonal systems.
[10.5] Graphical representations of these middleground levels, such as those of Examples 10 and 12, show how the abstract, supratemporal rāg grammar is rendered by a performer in real time. Significantly, these formal representations evidence knowledge about such real-time execution that practitioners themselves would normally convey informally, or simply absorb intuitively. A teacher might explicitly explain to a student which notes in a rāg should be included, omitted, sustained, touched on, or approached in this way or that; but answers to the question of how to produce a well-shaped delivery of a rāg normally remain implicit. The question may nonetheless be raised. After I once gave a somewhat shapeless rendition of an ālāp in a lesson with Vijay Ji, he asked me pointedly, “What is your plan?”—presupposing that accomplished performers do indeed have one.(35) This would be communicated to a student through general guidelines, such as (in the case of Yaman), “First sustain lower Ni, then Ga, then Pa,” and so on. But it takes representations such as the ones developed in this analysis to show just how artful and subtle a plan a skilled performer is able to formulate and reformulate in the moment of improvisation. Such representations of normally unrepresented knowledge arguably constitute one of the most significant potential contributions of this form of analysis.
[10.6] In other respects the adaptation of GTTM has its shortcomings, or at least would need further iterations. Most trenchant is the question of whether and how to model nuances of foreground detail. Lerdahl and Jackendoff themselves do not routinely orient their analyses around the minutiae of the musical surface;(36) so my own relative neglect of this level in the current treatment perhaps intuitively mirrors this tendency. But this is a greater sin of omission in the Hindustani context precisely because microscopic foreground ornamentation is so much of the essence (in khyāl, certainly; and even more so in the case of the light classical genre ṭhumrī). As noted above, its capture is the driving imperative in Magriel and du Perron’s study of khyāl (2013), in which transcription is the principal proto-analytical technique. It ought to be possible also to apply the GTTM methodology to the ornamentation of the extreme foreground of a khyāl performance, since this largely follows the same syntactic principles. However, one problem is that to pursue this extensively and systematically would lead to graphical demands of near-impracticable complexity. Even so, this would in principle be possible, even if applied only to selective examples.(37) A case in point is the grouping structure implicit in the transcription of the muṛkī, an ornamental anticipatory flourish that begins phrase xiii of Example 5. It would not be inconceivable to apply TSR principles to such figures, though given that they comprise notes of equal (and extremely brief) duration, this application may need some adaptation of preference rules specific to this level, which would be a task for future research.
[10.7] There are challenges at the other extreme too. One possible reason why much of the ālāp considered here comfortably fits a modified GTTM rulebook is that it is of relatively short duration. But what of a more extended ālāp—particularly, say, one in the dhrupad style which might go on for an hour or more? Would an extended time axis really generate diagrams that extended vertically too, into ever more remote reaches of reticulation? Arguably to structure or hear a performance modeled on dozens of nested hierarchic levels would go beyond what is cognitively and empirically possible (a point relevant to extended Western pieces too, for that matter). It is more likely, then, that beyond a certain level and beyond a certain time-span measure we experience a concatenation or accumulation of periods, rather than ever-recursive groupings of groupings. Indeed one radical modification to GTTM’s methodology would be to find a way to model forgetting. This would arguably be a more authentic representation of cognitive processing and the phenomenology of listening to extended stretches of improvised music, in which there is no recourse to the prosthesis of writing (and in particular to a notated score) to help record or formalize musical structures that are ever-further temporally receding.(38) This points again to a tension between the implicitly synchronic tendencies of the GTTM methodology (based on the concept of the written musical work) and the strongly diachronic nature of an improvised Indian music performance (based on orally transmitted principles), and points to a further avenue for future research.
Audio Example 2. Vijay Rajput, Drut khyāl in Rāg Yaman (from CD, Twilight Raags from North India), Track 6
[10.8] There is another essential difference between Hindustani classical music and the Western tonal staples analyzed in GTTM, which points to yet further territory for research. The works chosen by Lerdahl and Jackendoff are methodologically tractable because they embody forms of recursive antecedent–consequent phrase structure that marry up well with the bi-nodal tree structures of their approach. The Western archetype here is the articulated phrase of the Classical era, whose juxtaposition of mutually balancing periods (time-spans) is the projection of divisive metrical principles—to use Curt Sachs’s terminology (1953, 24–6)—onto a larger temporal canvas. By contrast, Indian classical music shows a much looser attachment to such constructions. Certainly, the compositions of many a fast (drut) khyāl are comprised of clearly articulated, balanced, interdependent, hierarchically arranged phrases. (This can be heard, for example, at the start of the drut khyāl that concludes Rajput’s Yaman performance, given in Audio Example 2.) But these are always rhythmically embedded in a tāl cycle whose principles are cyclic and (in the longer term) cumulative. As regards Sachs’s divisive/additive binarism, Hindustani classical music probably represents a hybrid of both types, the one working in complementation with the other at various levels.(39) Hence the potential appropriateness of the notions of large-scale background structure discussed in the preceding paragraph, where larger-scale additive or cumulative principles curtail the indefinite recursion of divisive pairs. We would also expect to find some form of interaction between these principles going on at foreground levels, such as in the formation of tāns (improvised virtuosic runs) in which minute additive motivic expansions and contractions might countervail emerging symmetrical patterns, and resist binaristic groupings.
[10.9] The preceding qualifications inject several notes of ambivalence into this mutual regard between GTTM and Indian classical music. That these ambivalences register at quite a deep level is probably as it should be. On the one hand, the cross-cultural adaptability of GTTM is by no means a trivial finding: it confirms the operation of musical syntax across cultures, and shows in detail how this is plays out in a significantly different cultural idiom; and to that end it also provides an additional resource in the world-music analyst’s toolbox. On the other hand, the previous countervailing observations point to ways in which local musical grammars may need to be developed in complementation with the supposedly universal one; and we cannot discount the possibility that ultimately this may require such different premises and modes of representation as to transcend their starting point in GTTM.(40) And then there are those aspects of performance that perhaps elude syntax altogether: the traces of a seemingly ineffable subjectivity found in the qualities of a voice, the seamless passage from one tone (svar) to the next, and microscopic judgments of timing and nuance (but then, this is also true for Western music). All this sets an agenda for further study in which potential points of resistance to an application of GTTM should not necessarily be seen as undermining the process, but rather as part of an iterative journey towards a modeling of syntax that is ever more authentic to the style itself, but that does not lose sight of possible cross-cultural principles. This would entail an anthropologically sensitive disposition that seeks to grasp what is specific to a culture but that is not oblivious, either, to what connects us.
David Clarke
University of Newcastle upon Tyne, UK
International Centre for Music Studies
Armstrong Building, Queen Victoria Rd,
Newcastle upon Tyne, NE1 7RU
d.i.clarke@newcastle.ac.uk
Works Cited
Battacharya, Krishna. 2013. “Linguistic Approach to Music: The Case of Bangla Lyrical Songs.” Ninād: Journal of ITC Sangeet Research Academy 26/27: 12–29.
Bhatkhande, Vishnu Narayan. 1937. Kramik pustak mālikā. 6 vols. Hathras: Sangeet Press.
Bor Joep, Suvarnalata Rao, Wim van der Meer, and Jane Harvey. 1999. The Raga Guide: A Survey of 74 Hindustani Ragas. Nimbus Records.
Chakraborty, Soubhik, Rayalla Ranganayakulu, Shivee Chauhan, Sandeep Singh Solanki, and Kartik Mahto. 2009. “A Statistical Analysis of Raga Ahir Bhairav.” The Journal of Music and Meaning 8 (section 4). At http://www.musicandmeaning.net/issues/showArticle.php?artID=8.4.
Clarke, David. 2011. “Music, Phenomenology, Time Consciousness.” In Music and Consciousness: Philosophical, Psychological, and Cultural Perspectives, ed. David Clarke and Eric Clarke, 1–28. Oxford University Press.
Clarke, Eric. 1986. “Theory, Analysis and the Psychology of Music: A Critical Evaluation of Lerdahl F. and Jackendoff. R., A Generative Theory of Tonal Music.” Psychology of Music 14 (1): 3–16.
Chomsky, Noam. 1964. Current Issues in Linguistic Theory. Mouton.
—————. 1965. Aspects of the Theory of Syntax. MIT Press.
Clayton, Martin. 2000. Time in Indian Music: Rhythm, Metre, and Form in North Indian Rāg Performance. Oxford University Press.
—————. 2007. “Time, Gesture and Attention in a Khyāl Performance.” Asian Music 38 (2): 71–96.
—————. 2008. “Toward an Ethnomusicology of Sound Experience.” In The New (Ethno)musicologies, ed. Henry Stobart, 135–69. Scarecrow Press.
Cooper, Robin. 1977. “Abstract Structure and the Indian Rāga System.” Ethnomusicology 21 (1): 1–32.
Dennett, Daniel. 1991. Consciousness Explained. Penguin.
Deshpande, Vamanrao H. 1987. Indian Musical Traditions: An Aesthetic Study of the Gharanas in Hindustani Music. Popular Prakashan.
Fink, Robert. 1998. “Elvis Everywhere: Musicology and Popular Music Studies at the Twilight of the Musical Canon.” American Music 16 (2): 135–79.
Gasparov, Boris. 2013. Beyond Pure Reason: Ferdinand de Saussure’s Philosophy of Language and its Early Romantic Antecedents. Columbia University Press.
Hantz, Edwin. 1985. Review of A Generative Theory of Tonal Music by Fred Lerdahl and Ray Jackendoff. Music Theory Spectrum 7: 190–202.
Jackendoff, Ray. “Musical Parsing and Musical Affect.” 1991. Music Perception 9 (2). 199–230.
Jairazbhoy, N. A. 1971. The Rāgs of North Indian Music: Their Structure and Evolution. Wesleyan University Press.
Katz, Jonah, and David Pesetsky. 2011. “The Identity Thesis for Language and Music.” Lingbuzz/000959. http://ling.auf.net/lingbuzz/000959.
Kiparsky, Paul. 1993. “Pāṇinian Linguistics.” In The Encyclopedia of Languages and Linguistics, ed. R.E. Asher, 2918–23. Pergamon Press.
Leante, Laura. 2009. “The Lotus and the King: Imagery, Gesture and Meaning in a Hindustani Rāg.” Ethnomusicology Forum 18 (2): 185–206.
Lerdahl, Fred. 2001. Tonal Pitch Space. Oxford University Press.
Lerdahl, Fred, and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. MIT Press.
Magriel, Nicolas. 1997. “The Barhat Tree.” Asian Music 28 (2): 109–33.
Magriel, Nicolas, with Lalita du Perron. 2013. The Songs of Khyāl. 2 vols. Manohar.
Music in Motion: The Automated Transcription for Indian Music (AUTRIM) Project by NCPA and UvA. https://autrimncpa.wordpress.com/.
Patel, Anniruddh, D. 2013. “Language, Music, Syntax, and the Brain.” Nature Neuroscience 6 (7): 674–81.
Pearson, Lara. 2016. “Coarticulation and Gesture: An Analysis of Melodic Movement in South Indian Raga Performance.” Music Analysis 35 (3): 280–313.
Peel, John, and Wayne Slawson. 1984. Review of A Generative Theory of Tonal Music by Fred Lerdahl and Ray Jackendoff. Journal of Music Theory 28 (2): 271–94.
Qureshi, Regula Burckhardt. 1995. Sufi Music of India and Pakistan: Sound, Context and Meaning in Qawwali, 2nd ed. University of Chicago Press.
Rohrmeier, Martin, and Richard Widdess. 2014. “Recursion in Indian Music: Towards a Grammar of Ālāp.” Unpublished paper presented at the Third International Conference on Analytical Approaches to World Music. SOAS, University of London.
Sachs, Curt. 1953. Rhythm and Tempo: A Study in Music History. Norton.
Saussure, Ferdinand de. 1959. Course in General Linguistics, ed. Charles Bally and Albert Sechehaye, trans. Wade Baskin. Philosophical Library.
Schachter, Michael. 2015. “Structural Levels in South Indian Music.” Music Theory Online 21 (4). http://www.mtosmt.org/issues/mto.15.21.4/mto.15.21.4.schachter.html.
Seeger, Charles. 1958. “Prescriptive and Descriptive Music Writing.” The Musical Quarterly 44 (2): 184–95.
Sengupta, Ranjan, Asoke Kumar Datta, and Nityananda Dey. “Objective Analysis of Consonance (Vaditya) in Indian Classical Music.” 2010. Eunomios. http://www.eunomios.org/.
Wade, Bonnie. 1997. Khyāl: Creativity within North India’s Classical Music Tradition. Munshiram Manoharlal.
—————. 2004. Music in India: The Classical Traditions, rev. ed. Manohar.
Widdess, Richard. 1980. “The Kuḍumiyāmalai Inscription: A Source of Early Indian Music in Notation.” Musica Asiatica 2: 115–50.
—————. 2011. “Dynamics of Melodic Discourse in Indian Music: Budhaditya Mukherjee’s Ālāp in Rāg Pụriyā-Kalyān.” In Analytical and Cross-Cultural Studies in World Music, ed. Michael Tenzer and John Roeder, 187–224. Oxford University Press.
—————. 2013. “Schemas and Improvisation in Indian Music.” In Language, Music and Interaction, ed. Ruth Kempson, Christine Howes, and Martin Orwin, 197–209. College Publications.
Widdess, Richard, and Ritwik Sanyal 2004. Dhrupad: Tradition and Performance in Indian Music. Ashgate.
Zadeh, Chloe. 2012. “Formulas and the Building Blocks of Ṭhumrī Style: A Study in ‘Improvised’ Music.” Analytical Approaches to World Music 2 (1): 1–48.
—————. 2013. Analysing Ṭhumrī. PhD diss. SOAS, University of London.
Discography
Discography
Chimmalgi, Sanjeev. 2003. Quest. CD. Navras. NRCD 0142.
Joshi, Bhimsen. 2001. Vocal Classical Selection. CD. Sagarika. S-300-11-2.
Rajput, Vijay. 2006. Twilight Raags from North India. CD. Newcastle University. CETL U4NE-1.
Sahasrabuddhe, Veena. 2008. Khayal: Classical Vocal. CD. Saregama. CDNF 1 50866.
Footnotes
1. Earlier versions of the content in this article were presented at several conferences and seminars, including the Perspectives on Musical Improvisation Conference (Oxford, 2012), the South Asian Music and Dance Forum (London, 2014), and as part the seminar series South Asia and Musical Cognition (All Souls Oxford, 2016). I am grateful to participants at those events for various helpful points of feedback.
Return to text
2. I have stolen this conceit from Robert Fink (1998), albeit that he uses it in a different context and with a different intent.
Return to text
3. A note on terminology: in this article I use the term “Hindustani classical music” to refer principally to the North Indian style of classical music; “Indian classical music” when observations might equally pertain its Karnatak (South Indian) counterpart; “Indian music” when observations might extend to other styles, such as light classical, which might, for example, also deploy principles such as rāg; and “South Asian music” when the styles in question (e.g. ghazal, qawwālī) may be at least as prominent in countries such as Pakistan (which in fact also goes for Hindustani classical music). The term “South Asia”, while often preferred by scholars, is seldom used by people of actual South Asian heritage. As one might surmise, these categories are fluid and not necessarily mutually exclusive.
Return to text
4. Ālāp is an extremely elastic phenomenon in Indian classical music. An ālāp may comprise just a few phrases totaling 20–30 seconds leading to a bandiś (composition), in which guise it is also known as aucar. At the other extreme, it may take much more extended form, dividing into discrete subsections and lasting 30–40 minutes or longer, as in many instrumental performances or in vocal performances in the dhrupad style. The ca. three-minute version here is long enough, and complete enough, to be considered an ālāp in its own right, and is typical of a form of shorter vocal ālāp that prefaces a much longer baṛā khyāl (a section which itself continues to deploy ālāp principles). Ālāps in this vein may segue into their subsequent baṛā khyāl, or first attain closure, as in the recording considered here. For some further khyāl examples, see the discography attached to this article, or consult the many recordings (plus their automated transcriptions) on the website Music in Motion (https://autrimncpa.wordpress.com/), compiled by Suvarnalata Rao and Wim van der Meer.
Return to text
5. Gharānās are lineages of musicians that have been historically important in the transmission of idiomatic performance styles. The stylistic peculiarities of the Kirana gharānā are discussed by Bonnie Wade (1997, 184–226) and Vamanrao Deshpande (1987, 41–5). Kirana is located in what is now the state of Uttar Pradesh.
Return to text
6. Among the most significant recent applications of Schenkerian concepts to Indian music is Michael Schachter’s detailed and impressive study, “Structural Levels in South Indian Music” (2015), which considers the classical tradition of Karnatak music. As regards both methodology and repertory, then, my article (developed independently) might be seen to complement Schachter’s, though his addresses a much broader range of musical examples while mine has a stronger epistemological focus. The question of structural levels, explicit in Schachter’s essay, is also a running concern in mine. While I pervasively address this in terms of Lerdahl and Jackendoff’s time-span reduction concept, I also consider Schenkerian notions of background, middleground and foreground in the closing section, though my formulation differs subtly from Schachter’s.
Return to text
7. This literature includes (in addition to works cited above) Chakraborty et al. 2009, Clayton 2007, Cooper 1977, Leante 2009, Magriel and du Perron 2013, Qureshi 1995, Sengupta et al. 2010, Widdess 2013, Widdess and Sanyal 2004, and Zadeh 2013.
Return to text
8. The matter of improvisation (including a reference to rāg) is in fact touched on by Lerdahl and Jackendoff—see GTTM, 106).
Return to text
9. In Chomsky’s words: “a generative grammar must be a system of rules that can iterate to generate an indefinitely large number of structures” (1965, 15–16); “[generative] grammar, then, is a device that (in particular) specifies the infinite set of well-formed sentences and assigns to each of these one or more structural descriptions” (1964, 9).
Return to text
10. Even so, Jonah Katz and David Pesetsky argue against claims by Lerdahl and Jackendoff and by others that “the fine structure of music and the fine structure of language are distinct and largely unrelated” (2011, 2), favoring instead a stronger “identity thesis” of the two domains. If nothing else, such debates confirm the continuing currency of GTTM in theoretical research.
Return to text
11. Among those who may have been influenced by Pāṇini is Ferdinand de Saussure, not only the founder of twentieth-century structural linguistics, but also—in his other avatar—Professor of Sanskrit at the University of Geneva (see Gasparov 2013, 88–9).
Return to text
12. Notwithstanding the legacy of Pāṇini, there seem to be few explicit adaptations of linguistic theories to Indian music by South Asian scholars. One such is Krishna Battacharya’s (2013) discussion of Bangla lyrical songs by Tagore, which mentions GTTM but deploys other methodologies. The website of the ITC Sangeet Research Academy provides a good window onto current Indian musicological scholarship (see http://www.itcsra.org/ITC-SRA-Publication). More recent works of music theory by some South Asian authors reflect a global research culture and a predilection for the application of science—see, for example, the rāg analysis by Soubhik Chakraborty et al. (2009) based on statistical principles and influenced by Western scholars such as David Temperley.
Return to text
13. Rāgs are said by some to number in the thousands, though in practice a much smaller corpus is performed with any regularity. For an excellent concise introduction to the issues of rāg, see The Raga Guide by Joep Bor et al. (1999, 1–7), and for a more detailed account see N.A. Jairazbhoy’s classic The Rāgs of North Indian Music (1971).
Return to text
14. For a more detailed account see Jairazbhoy 1971, chapter 2.
Return to text
15. Eric Clarke is critical of the supratemporal assumptions of GTTM, writing that “If pieces of music are mental constructs derived from a physical signal, then presumably that signal is usually acoustical, and unfolds over time, rather than being entirely co-present as it is in a score. The sorts of generative rule that could perform such derivations must operate over (and in) time, and cannot be the kind of abstract timeless statement that characterises the rules proposed by Lerdahl and Jackendoff” (1986, 16).
Return to text
16. For a discussion of notation systems see Magriel and du Perron 2013, 47–70; also Wade 2004, 24–48.
Return to text
17. As will be discussed below, from phrase vii onwards this situation mutates (already partly anticipated in phrase vi), in that two tones now becomes salient in each phrase, and phrases thus contain two heads and two time-spans rather than being coterminous with a single time-span as before. This, then, will be an eventual qualifier to assumption 1(b); but, for the time being, the simpler conditions of phrases i–vi provide a heuristically useful starting point.
Return to text
18. Technically the term should be Ālāp Time-Span Reduction Preference Rule (ATSRPR), but this would allow the acronyms to get out of hand. It is possible that the preference rules outlined below could also be applicable to other forms of unmetered monodic music, but these issues lie outside the concerns of the present article.
Return to text
19. Here and elsewhere, the dot in front of “Ni” signifies the lower octave.
Return to text
20. Here and in the following graphics, roman numerals signify the phrases of the transcription in Example 5 (thus acting as a cipher for quoted musical material as found in the TSR analyses of GTTM); braces indicate time-spans/groups, as in GTTM; and Roman letters indicate, in sargam abbreviations, the pitch head of each phrase. This last is equivalent to the secondary notation for TSRs in GTTM (as shown below the staff in Example 1).
Return to text
21. In linguistics such a difference would regarded as phonetic but not phonemic, i.e. different in objective terms but not commuting any change of meaning. The equivalence between such tones is most probably dependent on their relative durational difference from notes that ornament them—a point echoing the structural linguist Saussure’s point that “in language there are only differences without positive terms” (Saussure 1959, 120).
Return to text
22. However, in some rāgs alternative scale degrees may put up an extraordinary tension against Sa—for example Dha () and komal Re (
Return to text
23. At middleground or ‘meso’ levels, a significant part of the rationale for preferring Sa over other tones is provided by the concept of the cadenced group, discussed below. Notwithstanding this, there may be occasions, which I term structural strong prolongations, where Sa at higher structural levels can itself be superseded by a different tone, as discussed below under the heading “preferring teleology?”.
Return to text
24. This could be seen as a version of TSRPR 2b: “Of the possible choices for head of time-span T, prefer a choice that is
Return to text
25. Eagle-eyed readers will by now have spotted that my labeling of levels proceeds along the opposite vector to that of GTTM (cf. Example 1). While Lerdahl and Jackendoff use the label a to denote the very highest level of the piece, and then apply b, c, d etc. to successively lower ones (in a top–down approach), I use a to denote the lowest level, and apply successive labels to higher ones (proceeding from the bottom up). This is consistent with the switch from synchronic to diachronic modeling: as I do not yet know how the entire performance will unfold, it is not possible to determine an ultimate presiding level of the piece and its corresponding head; and if we cannot determine where to locate levela, we cannot label any other level in relation to it either. Hence a is best applied to the lowest level under scrutiny, and subsequent levels can be added in relation to it as the performance unfolds.
Return to text
26. “[T]he prolongational reduction derives not from the musical surface but from its associated time-span reduction” (GTTM, 187).
Return to text
27. Another idiosyncratic closural formula in Yaman, Pa–Re–Sa (––), does not manifest in this ālāp.
Return to text
28. This improvisatory procedure of hinting at what is to come as a performer nears the end of a period is quite a common device, and one communicated to me in my lessons with Rajput.
Return to text
29. It remains moot whether this sequence might not comprise more than one phrase, but this does not decisively change the analysis. The segmentation and grouping remain the same whether regarded as discrete phrases or subphrases of a single larger phrase (labeled A, B and C in the transcription). I interpret this ambiguity, together with the need to indicate momentary additional subsidiary levels in phrases x and xi, as an index of further subtle increments of complexity.
Return to text
30. Cf. Lerdahl and Jackendoff’s Prolongational Hypothesis 2: “The choice of events that define prolongational regions is strongly influenced by the relative importance of events in the time-span reduction” (GTTM, 213).
Return to text
31. Lerdahl goes some way to resolving this dichotomy in his more recent Tonal Pitch Space (2001), by representing TSRs with only the secondary staff notation (as shown below the staff of Example 1, above) and then using this as the basis for the corresponding PR which is represented only by tree structures. This more parsimonious approach is certainly more elegant, and suggests a partial synthesis of these two dimensions that treats TSR as a staging post to a final PR.
Return to text
32. For this reason I do not quite agree that the Schenkerian background can be so unproblematically translated into a “basic structure” for Indian classical music as Schachter seems to imply (2015, [4–5] and Examples 2 and 3). I explain an alterative rendition in relation to an ascending quasi-Urlinie below.
Return to text
33. In practice, tānpūrā players may in some instances unconsciously entrain to the activity of the soloist (see Clayton 2008, 156–61); but the principle remains to provide a uniform sonic ambience around Sa.
Return to text
34. Had this ālāp been longer, the ascent would most likely have continued to middle Ni (via Dha), followed by upper Sa, as shown in the complete structure of Example 13, but this full progress is deferred to the next section, the baṛā khyāl.
Return to text
35. A related point is made by Schachter 2015, [59].
Return to text
36. See their comments on PRPR 6 in GTTM, 248, including “time-span reduction itself represents a considerable degree of abstraction from the musical surface.”
Return to text
37. Valuable toward this end is software such as Transcribe! (used in the production of Example 5), which permits extreme slowing down of a recording. This allows one to inhabit the micro-world in ways that can be both surreal and insightful—surreal because this can lead one to question the reality of what one hears (was this really the artist’s intent, or is it just an acoustic artefact? This point is also made in Magriel and du Perron 2013, 83); insightful because it can support judgments about tiny details that may indeed be authentic and lead to further research questions.
Return to text
38. I make a related point in connection with Husserl’s phenomenology of internal time consciousness in David Clarke 2011, 14–16.
Return to text
39. Sachs’s account of additive and divisive rhythm is discussed in relation to Indian music by Clayton (2000, 37–41) in a critique that also highlights the problematics of Lerdahl and Jackendoff’s theory of rhythm and meter as a possible model for tāl structures.
Return to text
40. Chloe Zadeh (2012) for example considers the manipulation of musical formulae as an alternative creative principle – though this would not necessarily preclude considerations of syntax in an analysis: the syntax might be seen, for example, as pre-loaded into the formulae, underwriting their well formedness, and also understood to inform the grammaticality of their combination.
Return to text
Copyright Statement
Copyright © 2017 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Tahirih Motazedian, Editorial Assistant
Number of visits:
13195