Canons as Hypermetrical Transitions in Mozart *
Ellen Bakulina
KEYWORDS: hypermeter, Schenkerian analysis, Mozart, chamber music
ABSTRACT: This article explores gradual hypermetrical shifts, or hypermetrical transitions, in imitative contexts. The concept of hypermetrical transition, introduced by David Temperley, presupposes metrical conflict in the course of the transition. My principal goal is to place imitative metrical conflicts in the context of Schenkerian theory and to propose that each imitative part may suggest its own middleground structure, based on this part’s individual metrical pattern. The relative validity of the two resulting voice-leading graphs, based on harmonic and other musical cues, is then viewed as a tool for “measuring” the smoothness of the shift. The article includes analyses of several imitative passages from Mozart’s chamber works and culminates in a discussion of a lengthy canon from the String Quartet K. 499, movement 1, an exemplary case of a smooth hypermetrical transition.
Copyright © 2017 Society for Music Theory
Introduction
[1.1] In a Music Theory Spectrum article from 2008, David Temperley introduced the concept of hypermetrical transitions, gradual shifts of duple hypermeter from odd-strong to even-strong pattern, or vice versa.(1) A hypermetrically transitional passage is, by definition, characterized by conflicting metrical cues. “As with tonal transition,” he writes, “passages of hypermetrical transition tend to be at least somewhat compatible with both duple phases, though they may slightly favor one or the other” (Temperley 2008, 310).(2) He then investigates just how gradual, as opposed to a sudden, hypermetrical changes are executed in common-practice works.
[1.2] Temperley’s work is a significant contribution to the study of metrical conlficts; he explores in detail at least one type of situation in which two different meters may coexist, at least conceptually. It is a theoretical problem that has been explored by many (see a brief literature overview below). While he presents some convincing examples, he never considers a certain kind of hypermetrical transition: imitations, where two conflicting hypermeters are represented by individual, though melodically identical, lines. And yet, imitations are among the most powerful vehicles for achieving individuality of textural layers, producing individuality of simultaneous rhythmic and metric structures. Imitations are an ideal vehicle for the study of metrical conflicts precisely thanks to the equivalence of the melodic lines they produce. For the same reason, these conflicts, and the metrical shifts they may produce, are also among the most readily perceptible. Moreover, as a legacy of older music—Baroque and even Renaissance polyphony—imitative textures offer an alternative to the periodicity of the later, homophony-based structures.
Example 1. Mozart. String Quintet K. 614, movement 1, Imitation in mm. 26–31
(click to enlarge)
[1.3] Example 1 illustrates the way imitations can produce a hypermetrical shift. The passage from Mozart’s Quintet in
[1.4] The present article seeks to explore examples of this kind in selected chamber works of Mozart. My goal is threefold: to show canonic passages that produce shifts from even-strong to odd-strong hypermeter, or vice versa; to relate conflicting hypermeters to middleground voice-leading analysis; and to use this relationship for determining just how smooth the hypermetrical transition is. This work is, therefore, similar to Temperley’s, which is also centrally concerned with smoothness; in this article, I suggest a more precise tool for assessing this smoothness.
[1.5] The issue of metrical conflicts has been extensively studied. Virtually any important study of meter and/or rhythm includes some mention of the possibility that meter can be expressed differently in different musical dimensions (instrumental lines, registral layers, and so on).(3) Most of these studies of metrical and hypermetrical conflicts have an important feature in common: they engage the issue of texture in one way or another. This is only natural. If one and the same passage of music is to project more than one strand of strong beats, the simplest way for a composer to produce this situation (and for an analyst to explain it) is to fall back upon individual strands of the musical fabric.(4)
[1.6] Given this obvious and much-studied interaction between texture and meter (in conjunction with rhythm), it is surprising how little analytical attention imitative techniques have attracted from a metrical perspective. Schenker, in Chapter 4 of Free Composition, touches upon meter in imitative contexts (see his explanation of Fig. 149-8), and his brief discussion nearly amounts to a refusal to discuss meter in fugal and/or canonic texture.(5) One of the most significant studies of meter to date, Lerdahl and Jackendoff’s, explicitly refuses to engage polyphonic structures (Lerdahl and Jackendoff 1983, 37). They rightly assume that their system of metrical and grouping preference rules has to be established for a single musical stream (and therefore a homophonic texture), before it can be applied to the more complex contexts. Other writings also ignore this topic for the most part. A representative example is found in Kamien (1993, 314–17, Example 3a), which examines a notable hypermetrical conflict between the accompaniment (piano) and melody (clarinet) in a Beethoven quintet, but leaves the imitation between the clarinet and the bassoon without comment.(6)
[1.7] The present article attempts to fill this gap in the study of imitations, and more specifically canons. I examine the topic from the perspective of hypermetrical transition. That is, I am concerned with the canons that fill the space between and an odd-numbered and an even-numbered strong downbeat (hyperdownbeat), or vice versa.(7) My central argument is that, in certain cases, individual imitative parts suggest alternate prolongational analyses, based on the idea that metrical strength (in each individual imitative part) is associated with the onset of a new harmony at a middleground level. Such canons present what may be called a prolongational transition, a situation of prolongational ambiguity that enables—in fact, even encourages—multiple metrical interpretations, from which the listener may choose. I then explore how prolongational ambiguity interacts with other musical cues, and how (and why) this interaction strengthens or weakens the hypermetrical transition.
[1.8] Celebrating the metrical power of individual parts is generally similar to Klorman’s (2016) “decentered view” of meter, where each performer in a chamber ensemble may hear and “enact” meter differently from the other participants. (Of course, the concept is also applicable to genres other than chamber music.) But my approach differs in that I explore the relationship between the multiple “agents” on the surface and the structural harmonic events at deeper levels.(8) Finally, it should be noted that, in the discussion of specific metrical concepts and events, I use Lerdahl and Jackendoff’s (1983) system of Metrical Preference Rules (MPRs), and when necessary, also Temperley’s (2001) MPRs, which differ from Lerdahl and Jackendoff’s in both content and numbering. Form terminology relies on Caplin (1998).
Theoretical Context: Hypermetrical Shifts and the Schenkerian Middleground
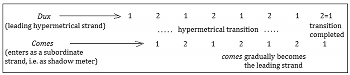
Example 2. Scheme of a hypermetrical transition in imitative contexts. Numbers 1 and 2 denote strong and weak hyperbeats
(click to enlarge)
[2.1] The basic principle of a hypermetrical transition effected by a canon, or more generally an imitation, is presented in Example 2. The example shows an initial hypermeter, in this case duple and odd-strong, established presumably before the passage begins (that is, beyond the left edge of the scheme) and maintained by one of the imitative voices, most often the dux (the leading part). This hypermeter is then challenged by the entrance of the comes—the part that enters second—which introduces a series of hyperdownbeats on even measures, by virtue of being melodically equivalent to the dux.(9) At first, this strand serves as a shadow (hyper)-meter, which here may be called an imitative shadow.(10) Later, however, a general shift to even-strong hypermeter suggests a retrospective reinterpretation of the shadow meter as the primary, not secondary (“shadow”) strand. The shift, therefore, can be understood, not as sudden, but gradual, this gradualness manifested by the two canonic voices that give conflicting metrical cues during the transitional passage.
[2.2] At this point, the issue of perception needs to be raised. For Temperley, the term “hypermetrical transition” refers to the arrangement of musical cues, rather than to the listener’s experience: a hypermetrical transition occurs when the metrical cues shift gradually, as opposed to suddenly, from one structure to another. This does not mean the shift in meter is perceived to be gradual. I will depart from Temperley’s usage by using the terms “gradual” and “sudden” to refer to the listener’s perception, at least, sometimes. From this perspective, every hypermetrical transition can, in principle, be perceived as either a sudden or gradual shift. With regard to canonic passages such as Example 2, a sudden shift can occur either at the entrance of the comes or at the end of the canon (or, sometimes, soon after the end); either case can be viewed as a metrical deletion in Lerdahl and Jackendoff’s terms.(11) In the former case (earliest deletion point), a radical metrical hearing is adopted—the shift is accepted as early as it is first suggested. The comes is immediately understood as the primary metrical strand, and the dux as an imitative shadow. In the latter case (latest deletion point), a conservative reading is chosen, interpreting the dux’s meter as dominating until it is no longer tenable.(12) In this scheme, the time interval of imitation (one measure) is half of the unit of repetition in each individual part (two measures); to use Krebs’s (1999) expression, a metrical dissonance D 2+1 occurs, where 1 equals a measure.(13)
[2.3] I claim that the conflicted passage, where the two imitative parts metrically rival each other, may suggest alternative prolongational readings. This claim rests on the idea that harmonic change is coordinated with a strong beat; this is Lerdahl and Jackendoff’s MPR 5f (Temperley’s MPR 6), which Rothstein (1995) calls the “rule of harmonic rhythm,” specifically at the hypermetrical level. Since the melodic strong beats do not coincide in the imitative parts, each part projects its own pattern of harmonic change, thereby providing two different harmonic structures at the middleground level. The rule of harmonic rhythm is thus understood in a somewhat abstract way. A time span taken up by a certain chord composed-out at this level represents a prolongational span, whose onset is aligned with a hypermetrical accent.(14) The resulting simultaneous structures produce a kind of “prolongational transition,” permitting for a maximal ambiguity of hypermeter.(15)
[2.4] Another question about perception arises here: Is it possible to hear two simultaneous conflicting meters? Both Temperley (2001, 2008) and Justin London (2012) argue against this possibility. Temperley (2008) writes that, in hypermetrical transitions, the listener perceives the initial hypermeter until a certain moment, when the new pattern begins to be experienced as having been in place for some time. To this, I wish to add two ideas. First, if the perception of multiple meters is imaginable at all, or if we wish to train ourselves to hear simultaneous meters, imitative contexts are an ideal vehicle for such training. In a way, imitations are the purest, the “elementary” expression of metrical conflict, simplified thanks to the melodic equivalence of the participating voices.
[2.5] Second, I propose that situations of prolongational conflict allow for a greater flexibility for individual listeners to switch at a subjectively preferred moment; however, they do not necessarily determine that moment. The actual choice—and how strongly this choice is preferred by individual listeners—also depends on a second subjective element: which specific cues bear greater significance in determining the subjective shift. In other words, the musical “validity” of each prolongational reading ultimately depends on the entirety of musical material, including larger melodic shape, formal considerations, instrumentation, etc. The analyses below are ordered with regard to the two principles described above. First, I present examples where, in my view, the moment of shift is relatively more pronounced, for harmonic and other reasons—these represent the less gradual transitions.. Then come instances with the least clearly determined shift—the smoothest transitions. The degree of “smoothness” is directly correlated with several factors: (1) textural uniformity (the musical cues give the least information about where the shift might be experienced), (2) surface harmonic rhythm (the faster it is, the more prolongational possibilities it presents), and (3) the structural level of the events affected by conflicting analyses.(16)
[2.6] To be sure, there remain some factors independent of the canon, such as binary regularity (MPR 10) established before the canon, as well as the first-statement-strong rule—MPR 9 in Temperley (2001) and MPR 11 in Klorman (2016). Both rules suggest that the previously established hypermetrical phase remain in force as long as possible (that is, they suggest a conservative metrical hearing), and both underplay the independence of the comes. If one consciously focuses, in analysis as well as performance, on conflicts produced by imitations, these two rules play a relatively minor role.
[2.7] One other perception-related question needs to be addressed: once the rule of harmonic rhythm is understood in the sense of the Schenkerian middleground, how does this affect our perception of metrical strength? Although this question may be nearly unanswerable, at least in the confines of this article, the answer will certainly involve the nature of prolongation itself. That prolongation can and should be heard is a stance upheld by many Schenkerians, most enthusiastically by Felix Salzer in Structural Hearing. In the analyses below, all prolongational spans in alternative readings begin with the harmony that is being prolonged, i.e., with a structural, rather than embellishing, harmony. While issues of perception are clearly important to such analyses, I will avoid delving into matters of phenomenology in the interest of producing internally consistent, cogent readings of musical structure.
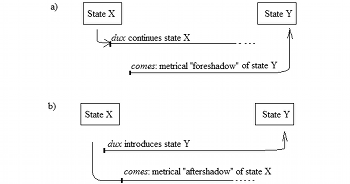
Example 3. Relationship between individual parts in an imitative hypermetrical transition
(click to enlarge)
[2.8] The location of hypermetric downbeats, whether strongly or weakly suggested by the musical cues, is necessarily related to the metrical profile of the imitated motives. To put the problem very generally, the possible disagreement lies in the placement of hypermetrical accent at the beginning or end of a motive.(17) To facilitate the navigation of such disagreements, Example 3 visualizes the relationship between an abstract hypermetrical transition and a dux/comes combination. The two opposite metrical states, odd-accented and even-accented, are designated X and Y; the dux either maintains the initial state X or introduces the future state Y, depending on how the motivic material is interpreted. The comes, therefore, also either foreshadows the future state—hence the word fore-shadow in the example, as a noun—or continues the old one. The latter case could perhaps be called an “after-shadow.” The reader is encouraged to use this scheme when their metrical reading of motives differs from mine: the metrical assignment of the parts will be flipped, as well as their order. The overall harmonic and hypermetric process will remain intact, as well as the parallelism between the parts. As Temperley states, “parallelism in itself says nothing about phase, that is, where in the pattern the strong beats should occur.” (2001, 50)
[2.9] The methodology of my analyses involves several steps. First, I extract the two imitative parts from the texture and add an imaginary continuo, the harmonic progression either implied or literally stated by the rest of the voices. I then discuss the possibility of two alternative readings of this progression. (Sometimes, one of these analyses is too strained for a meaningful voice-leading graph.).(18)
Analysis of Imitative Hypermetrical Transitions
Example 4a. Piano sonata, K. 533, movement 1. Canon in the transition section, mm. 33–37
(click to enlarge)
[3.1] My first example is not, in fact, a hypermetrical transition. Example 4a presents an excerpt from the Piano Sonata in F Major, K. 533. The first movement, with some insignificant fluctuations, establishes odd-strong hypermeter from the beginning. In the transition section, the dux (right hand) of a nearly exact canon continues this pattern throughout the passage presented here. The left hand adds a hypermetrical shadow on even-numbered measures. But by the end of the canon, m. 37, the previously established pattern is re-articulated (notice the new texture and new bass line beginning at 37), continued after the medial caesura and into the next theme (mm. 43ff., not shown in the example).
Example 4b. Recomposition of the canon in K. 533: an additional measure effects a hypermetrical transition from odd-strong to even-strong pattern
(click to enlarge)
[3.2] What Mozart could have done in order to create a hypermetrical shift is shown in a recomposition, Example 4b. Here, an extra measure has been inserted, which continues the imitative activity: the right hand imitates the left hand’s C-minor version of the descending motive. What was the strong m. 39 in the original is now m. 40, and thus an even-strong pattern takes control from this moment on. The example shows a gradual shift to the even-strong pattern, a shift expressed in the conflicting accents in the dux and comes, with an earliest deletion point at the comes’s entry (m. 34) and the latest at the (inserted) m. 38. The imitative passage in the actual sonata is, therefore, an opportunity for a gradual shift; however, the composer does not avail himself of this possibility.
Example 5a. Piano Sonata, K. 576, movement 1. Canon in the development, mm. 63–68: score and an imaginary continuo. Hypermetrical transition at the two-measure level
(click to enlarge)
Example 5b. Canon in K. 576: combination of the alternative versions in Example 3b, with the hypermetrical conflict removed
(click to enlarge)
Example 5c. Canon in K. 576. Alternative prolongational readings based on (1) the right hand’s odd-strong hypermeter and (2) the left hand’s even-strong hypermeter
(click to enlarge)
[3.3] My goal in showing this passage is to introduce the idea of an imitative hypermetrical transition through a counter-example and to demonstrate at least one compositional strategy needed to achieve a real shift. This preliminary demonstration will hopefully illuminate my next example, a true hypermetrical transition, although not the most gradual one. It comes from another piano sonata, Mozart’s last one, the Sonata in D major, K. 576; see Example 5. The first movement is replete with polyphonic activity—fully fledged canons, as well as imitations of a more modest scope. This is one of those works where polyphonic elaboration of the initial melodic idea, the “testing” of its contrapuntal potential, seems to be the compositional rationale behind the music.(19) From a purely melodic viewpoint, the principal motive, the main theme’s basic idea, allows for both a beginning-accented and an end-accented hearing. I choose a beginning-accent (first-downbeat-stronger; MPR 2), which means that the hypermeasure is congruent with the two-measure motive, resulting in what Rothstein (2008) has called “German (hyper-)meter.”
[3.4] The most metrically adventurous imitations of this motive arrive during the development’s core section beginning in m. 63.(20) After a four-bar odd-strong introduction, a canon enters with a one-bar time interval. The dux (right hand) continues the established odd-accented pattern; the comes (left hand) introduces an even-strong shadow, confirmed as the true hypermeter by m. 70—the opening of a new canon and a new prolongational span.(21) The canon, therefore, produces a hypermetrical shift. Example 5 offers an analysis of the passage in three stages. Example 5a presents the canonic parts and an imaginary continuo, inferred from the two-voice combination. In harmonic terms, the most noticeable event is the three measures of the dominant harmony (in
[3.5] Since the harmonic rhythm is rather slow, and the time span taken up by most chords equals the length of the imitated motive (two measures), potential alternative readings have to do with surface, rather than middleground harmony. For this reason, a voice-leading analysis will essentially preserve the harmonic rhythm of the imaginary continuo. Such an analysis is presented in Example 5b. The two hypothetic alternatives that do, in fact, offer different points of harmonic change are presented in Example 5c. The difference between them concerns the arrival of
[3.6] From my present viewpoint, therefore, this hypermetrical shift is rather sudden because no prolongational ambiguity takes place. Listeners who favor harmony as a meter-defining factor, such as myself, will experience a definitive shift in m. 68; the imitative conflict will be, for them, downplayed to a mere textural detail. On the other hand, listeners who are more willing to assign metrical independence to individual parts regardless of harmony are more likely to hear a gradual shift in the course of the canon, and they may or may not read an implied change of harmony (with a “ghost”
Example 6a. String Quintet, K. 614, movement 1. Canon in the transition section, mm. 26–31. Hypermetrical transition at the two-measure level (but each imitative strand exhibits four-bar hypermeasures)
(click to enlarge)
Example 6b. Canon in K. 614. Alternative prolongational readings based on (1) second violin’s even-strong pattern and (2) first violin’s odd-strong pattern
(click to enlarge)
[3.7] The potential for prolongational ambiguity increases dramatically when surface harmonic rhythm is faster—that is, when each imitative entry receives at least one new harmony. One such example is found in the String Quintet in
[3.8] The passage leads up to the goal HC in
[3.9] A comparison of the two graphs shows why the second reading is rather forced. Harmonically, both readings are well-formed, since MPR 5f is applicable to both occurrences of the F chord, mm. 27 and 31. And yet, a variety of other musical cues demonstrate why harmony alone cannot decide the issue. The location of the half cadence can hardly generate questions: it comes at m. 31, with the arrival of the long F in the cello and new, non-imitative texture (MPRs 5a, 5d, and 6), followed by two four-bar units sustaining the F harmony (standing on the dominant, in Caplin’s terms). Moreover, the longer passage mm. 22–31 forms a sentential structure where the imitative passage serves as a continuation (see Example 5a). For all these reasons, hearing a HC in m. 27 would obviously ignore important musical dimensions. The shift in m. 31 is rather sudden (for reasons other than harmony), and the first violin’s meter is indeed only a shadow, at least for the duration of the canon.
Example 7a. String Quartet, K. 421, movement 1. Development section, mm. 50–69
(click to enlarge)
Example 7b. String quartet, K. 421. Canon in the development, mm. 58–67 (first and second violin) and an imaginary continuo
(click to enlarge)
Example 8a. String Quartet, K. 428, movement 1. Imitation in the development, mm. 69–75: hypermetrical transition at the four-measure level
(click to enlarge)
Example 8b. Canon in K. 428, mm. 69–75, and an imaginary continuo
(click to enlarge)
Example 8c. Imitation in K. 428. Alternative prolongational readings, based on (1) the two violins’ hypermeter and (2) cello’s and viola’s hypermeter. Note especially the difference in mm. 71–73
(click to enlarge)
[3.10] Another case of potential ambiguity that concerns a half-cadential arrival is found in the D minor String Quartet, K. 421, first movement (Example 7a). As in the preceding example, textural and formal cues override a certain degree of prolongational ambiguity; the imitative dux leads strongly enough to create a relatively sudden shift. Polyphonically, the exposition here is comparatively simple; this is perhaps why it has been perceived as a vocal piece, as early as Momigny (1806).(24) The meter, relatively un-capricious, shifts in broad strokes, rather than the kaleidoscopic changes of the quintet. In the development, a brief but astonishing modulation by tritone (
[3.11] In hypermetrical terms, this core opens with three-bar hypermeasures, articulated by the pattern of imitative entries, a minor second and an augmented second (see Example 7a). This is followed by a spinning-out passage in the form of a canonic sequence involving the two violins. The canon leads from the strong m. 59 to the strong m. 66, the development’s goal cadence—a HC in D minor.(25) Example 7b presents the canon and an imaginary continuo.
[3.12] The principal kinship between this example and the quintet concerns the relationship of the voices: the comes (second violin) never gains enough strength to truly compete with the other strand, until a decisive later shift. This subordinate role of the second part is conditioned by several factors. First, it is the briefness of the canon (it dissolves after two entries in each part). Second, mm. 59–66 form a quasi-sentential structure and we are thus conditioned to hear them as a unit. Finally, harmonic events also strongly favor the latest possible shift, m. 66, mainly due to the strength of the cadential arrival there. Given the second violin’s even-strong pattern, the first occurrence of the expected V harmony would be m. 64—in Caplin’s terms, a premature dominant arrival, rather than a true cadence. But the metrical influence of root-position dominant at m. 66 (MPRs 6 and 9), intensified by the preceding augmented chord and the metrical stability of the four-cycle that follows, overrides the inverted chord at 64.(26) A sense of arrival in the three lower voices (see the quarter note at m. 66) supports this reading. In short, the majority of the musical cues, including surface harmony, support a cadential interpretation and a shift to an even-strong pattern in m. 66; until then, the meter of the second violin remains a shadow. Listening with a focus on the second violin’s part, and the middleground harmonic changes that it suggests, will reveal why the dominant at m. 64 is too weak to function as an arrival.
[3.13] Few imitations in this repertoire exceed the time interval of one measure; nonetheless, a two-measure interval occasionally occurs, thus destabilizing the four-bar level of hypermeter. One such example is found the String Quartet K. 428, movement 1, which has some intricate contrapuntal work in the exposition, including triple invertible counterpoint in the closing section. Of interest to us is a short canon in the pre-core section of the development (Example 8a). The canon, resembling a fugal stretto, is a four-measure phrase, stated in unison by the upper and lower pairs of instruments that overlap only for two measures. The following core section moves in regular groups of four, and the six measures of the pre-core lead into this regularity through a shift in the course of the imitation.
[3.14] Example 8a shows that the hypermetrical conflict resides within the time span of the comes’s imitative entry, mm. 71–74. The upper voice enters in m. 69, the next projected hyperdownbeat being at m. 73.(27) The lower voice contradicts this four-cycle by “breaking” it in the middle and accentuating m. 71. The strong m. 75 completes the shift.(28) Example 8b presents the outer parts of the texture and the chord progression. Given the minimal degree of melodic or other contrast within this passage, imitative cues alone determine the deeper-level (slower) changes of harmony underneath the accelerating harmonic surface. The resulting alternative readings in Example 8c show that the imitative conflict maps onto strikingly different, but equally well-formed, middleground structures. The dux asserts a
[3.15] The reason why none of the two readings overrides the other is mainly due to the uniformity of texture. Except for the surface-rhythmic change in m. 73, which adds emphasis to the dux’s hyperdownbeat in that measure, no other cues support or contradict any of the two interpretations. Both readings are thus fully plausible here, and the hypermetrical transition is the smoothest of all I have examined so far.
[3.16] My last and principal example, the String Quartet in D major, K. 499, exhibits a transition just as gradual as that in K. 428, but in a much longer canon. This is another monothematic movement, like the Piano Sonata K. 576, and also rich in imitations, though somewhat less tonally adventurous. The canon I wish to discuss is located in the subordinate theme, mm. 40–53.
Example 9a. String Quartet K. 499, movement 1. Opening motive and its subsequent hypermetrical treatment
(click to enlarge)
Example 9b. String Quartet K. 499. Transition and subordinate theme (beginning), mm. 38–60
(click to enlarge)
Example 9c. String Quartet, K. 499. Canon in the subordinate theme, mm. 41–52
(click to enlarge)
Example 9d. Vanon in K. 499. Prolongational readings based on (1) the cello’s even-strong hypermeter and (2) the violin’s odd-strong hypermeter
(click to enlarge)
[3.17] To better understand the hypermeter of the passage, we need to explore the opening motive (Example 9a), which creates ambiguities from the start. These ambiguities result partly from the lack of accompaniment: one is forced to deduce the metrical accent from the unison line alone—a strong foreshadowing of the melody’s future role in metrical conflicts. The two downbeats make a roughly equal claim to accent. A beginning-accent is suggested by the sheer force of the opening (MPR 2) and from the (implied) two-bar length of the opening tonic harmony. The longer note A, on the other hand, suggests an end-accent (m. 2 is strong). Mozart’s subsequent harmonizations, summarized in Example 9a, take advantage of both possibilities. The beginning-accented version comes at the outset of the recapitulation and in a long canon in the development, where the harmonies change on the motive’s first downbeat. The end-accented version is at its clearest towards the end of the subordinate theme (mm. 63 and 65), where long bass notes, the cadential \(\substack{6\\4}\), and the final tonic all arrive on the motive’s last note. This metrical variety has implications for the canon to be discussed shortly, the one in the subordinate theme. I will consider each metrical version of the motive in turn.
[3.18] Example 9b includes a large portion of the exposition that established a solid even-strong pattern, arriving at m. 40 (opening of the subordinate theme).(30) From here, the canon leads to the strong m. 53, thus serving as a shift to an odd-strong pattern. Example 9c shows the canon (first violin and cello). An imaginary continuo inferred mostly from the second violin’s figuration shows unusual harmonic stasis—nine measures of the E major harmony (V of A). The two prolongational readings in Example 9d differ with respect to the moment when this long-sustained harmony ends.(31) According to the beginning-accented view of the motive, the odd-strong violin (the second graph in the example) accentuates m. 49, the first tonic chord—I6 in the new key of A. At the middleground, this harmony is followed by what Caplin calls an expanded cadential progression (ECP), I6–IV–V, with a deceptive gesture in m. 52. (A few more failed attempts at an authentic cadence follow, until it is finally reached in 73— Hepokoski and Darcy’s essential expositional closure.) For the even-strong cello (the first version in the example), m. 49 continues the dominant harmony, which resolves to a root-position tonic only at m. 50, and there is no ECP. At m. 53, both readings converge on a pre-dominant chord, with another deceptive cadence in 57.(32)
[3.19] The two versions are equal in well-formedness to a remarkable degree. The perceptual reality of the two prolongational alternatives can be verified by listening to the passage twice, while playing an A major chord first at m. 49, and then at m. 50. This equality is partly conditioned by a relatively low structural level that the difference involves: the conflicting arrival of the A chord in m. 49 and m. 50 is only a local event in the theme, which neither begins nor ends at this moment. Also, like in K. 428, the uniformity of texture creates a kind of neutral environment, where the imitative voices and harmony are the only meter-producing forces. As a result, the passage creates an ideal situation for a subjectively chosen moment for the shift—and thus a truly smooth hypermetrical transition. To experience the smoothness, one can also conduct both conflicting hypermeters with two hands several times in a row, mentally switching to the odd-strong phase at different moments.
[3.20] Some readers may argue, perhaps, that the analysis just presented is somewhat strained because the comes (cello), not the dux (violin), continues the established hypermeter (review Example 9c again). To address this issue, let us turn to the alternative, end-accented version of the motive. Thanks to the strong m. 40, the next projected strong downbeat occurs at m. 42 (MPR 10—binary regularity, which corresponds to Temperley’s MPR 5). If one maintains this pattern, then the motive is end-accented in the dux, and by parallelism in the comes as well. The metrical relationship of the parts, embodied in the prolongational readings, will be reversed, yielding an even-strong first violin and an odd-strong cello. Example 3 reveals the logic of such a reversal. The overall gradual motion from an even- to an odd-strong pattern, however, remains in force.
Conclusion
[4.1] I wish to finish this article by suggesting a connection between hypermetrical shifts and form. At the end of his 2008 article, Temperley addresses the issue of form, expressing skepticism towards analytical connections between form and hypermetrical changes. His skepticism is based on the idea that odd-strong and even-strong hypermeter as such can hardly have the same structural meaning as thematic material and other musical dimensions. He writes: “I would be wary of constructing large-scale hypermetrical narratives involving odd-strong and even-strong hypermetrical states” (2008, 323). And later: “The very idea of hearing a passage in one metrical state X, while experiencing this state as being dissonant against state Y, seems very doubtful to me” (323n16).
[4.2] I agree that hearing meter in this way does not seem very appealing. But I believe that the issue of form can be addressed from a different angle. Metrical changes can be related to large-scale form, but not by identifying specific metrical states with some other dimensions (for example, various emotional states). Rather, the fact that there is a metrical change, especially a gradual change, should be related to formal structures. A metrical shift, like a tonal shift (modulation), creates instability, and as such, may be included in the category of destabilizing techniques, which Caplin calls “loosening techniques.” In K. 499, for example, the first movement displays three hypermetrical transitions, one per large-scale section (exposition, development, and recapitulation). All three transitions involve an odd number of measures in a phrase, and all occur at formal areas of heightened instability—Caplin’s looser regions: the subordinate theme and the developmental core. All participate in a motion towards a cadence—in form-functional terms, the continuational area.
[4.3] To be sure, a single movement cannot be taken as a norm. But one can cite more examples of a coordination between hypermetrical change and formal function. The developments in the first movements of K. 421, examined above, the C minor Piano Sonata K. 457, and Beethoven’s Fifth Symphony (analyzed in Imbrie 1973 and Temperley 2008) belong to this category. They all show that the process of intensification, most often leading to up to what Cone 1968 dubbed a structural downbeat, may be accompanied by a hypermetrical transition. That this process is also typically accompanied by imitations, especially in developments, is common knowledge.
[4.4] In conclusion, I would like to re-assert the idea I proposed at the beginning of this article—that it is prolongational ambiguity that allows one to propose multiple hypermetrical analyses of imitations. To be sure, harmonic structure alone cannot guarantee such analyses; one has to take into account other musical cues, as I have done here, to make sure that both readings are musically meaningful. But a harmonic foundation for prolongational alternatives—the possibility to interpret the voice leading and chord progression in two convincing ways—serves as a basis for understanding such ambiguity. It is this possibility that helps one to experience each imitative line (not necessarily at the same time) as having a hypermetrical structure of its own. Whether this logic is perceptually necessary—or at least analytically desirable—for hypermetrical ambiguity in contexts other than imitations is possibly the subject of future research.
Ellen Bakulina
University of North Texas
College of Music
415 Avenue C
Denton, TX 76201
Ellen.Bakulina@unt.edu
Works Cited
Bakulina, Olga (Ellen). 2012. “The Loosening Role of Polyphony: Texture and Formal Functions in Mozart’s ‘Haydn’ Quartets.” Intersections 32 (1–2): 7–42.
Benjamin, William. 1982. “Models of Underlying Tonal Structure: How Can They Be Abstract, and How Should They Be Abstract?” Music Theory Spectrum 4: 28–50.
Berry, Wallace. 1976. Structural Functions in Music. Prentice Hall.
Caplin, William. 1998. Classical Form: a Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven. Oxford University Press.
—————. 2009. “What Are Formal Functions?” In Musical Form, Forms, and Formenlehre, ed. Pieter Bergé, 21–41. Leuven University Press.
Cohn, Richard. 1992a. “Dramatization of Hypermetric Conflicts in the Scherzo of Beethoven’s Ninth Symphony.” Nineteenth-Century Music, 15 (1): 22–40.
—————. 1992b. “Metric and Hypermetric Dissonance in the Menuetto of Mozart’s Symphony in G Minor, K. 550.” Integrál 6: 1–33.
Cone, Edward T. 1968. Musical Form and Musical Performance. Norton.
Duane, Ben. 2012. Texture in Eighteenth- and Early Nineteenth-Century String-Quartet Expositions. PhD diss.: Northwestern University.
Fraenov, Viktor. 2000. Uchebnik polifonii. [A Textbook on Polyphony.] Moscow: Muzyka.
Grave, Floyd. 1985. “Metrical Displacement and the Compound Measure in Eighteenth- Century Theory and Practice.” Theoria 1: 25–60.
Hasty, Christopher. 1997. Meter as Rhythm. Oxford University Press.
Hepokoski, James, and Warren Darcy. 2006. Elements of Sonata Theory. Oxford University Press.
Imbrie, Andrew. 1973. “Extra Measures and Metrical Ambiguity in Beethoven.” In Beethoven Studies, ed. Alan Tyson. Norton: 45–66.
Jackendoff, Ray. 1991. “Musical Parsing and Musical Affect.” Music Perception 2 (9): 199–230.
Kamien, Roger. 1993. “Conflicting Metrical Patterns in Accompaniment and Melody in Selected Works by Mozart and Beethoven.” Journal of Music Theory 37: 311–50.
Kirkendale, Warren. 1979. Fugue and Fugato in Rococo and Classical Chamber Music, trans. by Margaret Bent and Warren Kirkendale. Duke University Press.
Klorman, Edward. 2016. Mozart’s Music of Friends: Social Interplay in the Chamber Works. Cambridge University Press.
Koch, Heinrich Christoph. 1983 [1789–93]. Introductory Essay on Composition: The Mechanical Rules of Melody, sections 3 and 4, translated by Nancy Kovaleff Bake. Yale University Press.
Krebs, Harald. 1997. “Some Early Examples of Tonal Pairing: Schubert’s ‘Meeres Stille’ and ‘Der Wanderer’.” In The Second Practice of Nineteenth-Century Tonality, edited by William Kinderman and Harald Krebs. University of Nebraska Press: 17–33.
—————. 1999. Fantasy Pieces: Metrical Dissonance in the Music of Robert Schumann. Oxford University Press.
Küster, Konrad. 1996. Mozart: A Musical Biography, trans. Mary Whittal. Clarendon Press.
Lerdahl, Fred, and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. MIT Press.
Levy, Janet M. 1982. “Texture as Sign in Classical and Romantic Music.” Journal of the American Musicological Society 35 (3): 482-531.
Lewin, David. 1986. “Music Theory, Phenomenology, and Modes of Perception.” Music Perception 3: 327–392.
London, Justin. 2012. Hearing in Time: Psychological Aspects of Musical Meter, 2nd edition. Oxford University Press.
Love, Stephan Caris. 2015. “Historical Hypermetrical Hearing: Cycles and Schemas in the String-Quartet Minuet.” Music Theory Online 21 (3). http://www.mtosmt.org/issues/mto.15.21.3/mto.15.21.3.love.html
Mirka, Danuta. 2009. Metric Manipulations in Haydn and Mozart. Oxford University Press.
Momigny, Jerôme-Joseph. 1806. Cours Complet d’Harmonie et de Composition. Paris.
Ng, Samuel. 2012. “Phrase Rhythm as Form in Classical Instrumental Music.” Music Theory Spectrum 31 (4): 51–77.
Parker, Mara. 2002. The String Quartet, 1750-1797: Four Types of Musical Conversation. Ashgate.
Rothstein, William. 1995. “Beethoven with and without Kunstgepräng’: Metrical Ambiguity Reconsidered.” In Beethoven Forum 4, ed. Lewis Lockwood and James Webster
—————. 2003. “Clash of The Titans: What to do When Tovey and Schnabel disagree about hypermeter in Beethoven’s piano sonatas?” Keynote Address to MTSNYS/NECMT, New Haven.
—————. 2007 (1989). Phrase Rhythm in Tonal Music, 2nd edition. Musicalia Press.
—————. 2008. “National Metrical Types in Music of the Eighteenth and Early Nineteenth Centuries.” In Communication in Eighteenth-Century Music, ed. Danuta Mirka and Kofi Agawu, 112–59. Cambridge University Press.
—————. 2011. “Metrical Theory and Verdi’s Midcentury Operas.” Dutch Journal of Music Theory 16/2: 93–111.
Samarotto, Frank. 1999. “Strange Dimensions: Regularity and Irregularity in Deep Levels of Harmonic Reduction.” In Schenker Studies 2, ed. Carl Schachter and Hedi Siegel, 222–38. Cambridge University Press.
Sadie, Stanley. 1964. “Mozart, Bach and Counterpoint.” The Musical Times 105: 23–24.
Salzer, Felix. 1962. Structural Hearing. Dover.
Schachter, Carl. 1999. “Rhythm and Linear Analysis: Aspects of Meter.” In Unfoldings, edited by Joseph Straus. Oxford University Press. 79–117.
Schenker, Heinrich. [1935] 1979. Free Composition. Trans. and ed. Ernst Oster. Longman.
Sutcliffe, Dean. 2003. “Haydn, Mozart, and Their Contemporaries.” In The Cambridge Companion to the String Quartet, ed. Robin Stowell, 185-209. Cambridge University Press.
Temperley, David. 2001. The Cognition of Basic Musical Structures.
—————. 2008. “Hypermetrical Transitions.” Music Theory Spectrum 30 (2): 305–325.
Tetzel, Eugen. 1920-21. “Der Grosse Takt.” Zeitschrift für Musikwissenschaft 3: 605–15.
Trimmer, Maud Alice. 1981. Texture and Sonata Form in the Late String Chamber Music of Haydn and Mozart. PhD diss., City University of New York.
Footnotes
* I extend heartfelt thanks to William Rothstein, who saw this article through many stages of revision. I also thank David Temperley and two anonymous reviewers for their valuable comments.
Return to text
1. Temperley writes: “In common-practice music. . . hypermeter is almost invariably duple, involving an alternation of strong and weak measures; extended passages of triple hypermeter are extremely rare. Thus most hypermetrical shifts involve a shift from an odd-strong pattern to an even strong one, or vice versa” (2008, 305–6).
Return to text
2. Significantly, hypermetrically conflicted passages that do not lead to a new phase are not considered transitional.
Return to text
3. Carl Schachter (1999) includes a discussion of conflicting metrical cues in Mendelssohn and Schumann. William Rothstein (2007) discusses Mendelssohn’s technique of conflicting downbeats between the melody and accompaniment; Roger Kamien (1993) explores similar examples, using the term conflicting metrical patterns. Other important terms include Frank Samarotto’s (1999) shadow meter, used for hypermeter as well (Rothstein 1995, for instance) and Harold Krebs’s (1999) metrical dissonance. Significant contributions to the topic are found in the work of Andrew Imbrie (1973), Richard Cohn (1992a and 1992b), Danuta Mirka (2009), and Justin London (2012). Mostly recently, Edward Klorman (2016) has viewed the issue from the perspective of agency.
Return to text
4. On texture in general, and texture in the Classical chamber music, see Maud Alice Trimmer (1981) Janet Levy (1982), Mara Parker (2002), Dean Sutcliffe (2003), and Ben Duane (2012). See also Warren Kirkendale (1979) on the role of fugal writing in the instrumental music of the time.
Return to text
5. What Schenker does not mention is that multiple imitative parts can, in fact, produce conflicting metrical accents—that a newly entered imitative voice does not necessarily cancel the established (hyper-)meter. This is precisely the subject of the present paper.
Return to text
6. Some exceptions to the general tendency to ignore imitations include Mirka (2009) and Klorman (2016).
Return to text
7. Exceptions to this principle include cases where the time interval of imitation is more than one measure.
Return to text
8. My approach is also more strongly oriented towards an end-state analysis, even when choosing a single preferred version seems to be impossible or undesirable (see, for instance, my analysis of the quartet K. 499).
Return to text
9. There is also a grouping conflict based on the non-coinciding beginnings and resting points (Koch’s term Ruhepunkt des Geistes).
Return to text
10. The term shadow meter originated in Frank Samarotto (1999); imitative shadow was first introduced by Ellen Bakulina (2012, 15). Klorman discusses the same phenomenon as “conflicting metrical signals expressed by the ongoing violation of parallelism (MPR 1)” (2016, 199); see his Figure 6.1 for a (modified) list of MPRs.
Return to text
11. Metrical deletion occurs when a metrical shift is effected by deleting one of the beats in a previously established pattern. For example, in duple meter (or hypermeter), a beat expected as weak may, for contextual reasons, arrive as strong (weak beat is deleted), or vice versa (strong beat is deleted) (Lerdahl and Jackendoff 1983, 103–4). Another relevant term is metrical reinterpretation (it is used in Free Composition, pp. 125–26). A recent contribution to the study of hypermeter, Love 2015, calls an early, unexpected hyperdownbeat an interruption of a hypermetrical cycle; the opposite of interruption is deferral.
Return to text
12. The terms radical and conservative metrical hearing originates with Andrew Imbrie (1973).
Return to text
13. In Krebs’s system (1999), the notation D 2+1 means that the unit affected by a displacement dissonance is twice longer than time interval between the conflicting metrical cues. At the level of a single measure, this would be a canon per arsin et thesin, in the parlance of the eighteenth century. The term “per arsin et thesin,” as an eighteenth-century adaptation of Greek terms, refers to displaced accents of a canonic or fugal subject. The concept of displaced metrical accents brings up a historical aspect of meter: eighteenth-century notions of duple and quadruple measure; see Floyd Grave (1985).
Return to text
14. This idea is somewhat related to (not is not the same as) MPR9, which has to do with harmonic stability, as well as PRPR 1 (prolongational reduction preference rule)—time span important for prolongational reduction.
Return to text
15. The idea of multiple (alternative) harmonic interpretations has appeared in various theoretical studies to serve different purposes—metric, tonal, and other. Examples include William Benjamin (1982), Krebs (1999), and David Lewin (1986).
Return to text
16. Where imitative passages represent phrase expansions, hypermetrical conflicts do not affect deeper-level harmonic structure and phrase rhythm in Rothstein’s sense; when they do (such as the case in the Quintet K. 614), one of the parts—and the metrical pattern associated with it—strongly outweighs the other, making the large-scale tonal arrival ultimately unambiguous. For more on phrase rhythm, see also Samuel Ng (2012).
Return to text
17. This choice is connected to what Rothstein (2008) calls German (beginning-accented) and Italian (end-accented) meter. I read most melodic material as beginning accented; this correspond to Lerdahl and Jackendoff’s MPR 2 (accent early in the group). Given that, by mid-1780s, Mozart had been strongly influenced stylistically by both Italian and German music, decisions on one or the other as the “right” way hardly seems useful. In addition, I wish to suggest that imitative contexts stimulate a beginning-accented hearing due to the spirit of “rivalry” inherent in imitations: a motive’s beginning is naturally the moment of “assertion.”
Return to text
18. On the flowering of Mozart’s polyphonic writing in the early 1780s, see Stanley Sadie (1964), Kirkendale (1979), Konrad Küster (1996), Bakulina (2012), and Klorman (2016).
Return to text
19. The Russian theorist Viktor Fraenov, in his polyphony textbook (2000), offers a brief, but profound observation on polyphony’s compositional role in Mozart. “While studying [Mozart’s] art, one is fascinated by many things, but especially by his striving towards most complex techniques, those at the limits of the human capabilities. Of course, it would be wrong to suppose that Mozart set himself the goal of necessarily writing a quintuple fugato or a triple canon. Rather, he heard the desired form in the material itself, and a quintuple fugato was ‘simply’ an optimal way to reveal a theme’s potential” (Fraenov 2000, 190, translation mine). Some of the works explored in the present paper illustrate this idea.
Return to text
20. “Core section” is Caplin’s (1998) term for the (usually) central portion of the development that introduces one or more sequential passages.
Return to text
21. This is one of the cases where the motive may be heard as both beginning-accented and end-accented; that is, both German and Italian meter are viable at the two-bar level. I have chosen a beginning-accented view; those who prefer the opposite view may use Example 3 to reverse the relationship between the voices. This reversal will bear no influence on the prolongational reading of the passage.
Return to text
22. This is the kind of shift that Grave (1985) explores in compound meters (the compound
Return to text
23. Although the shift involves the two-bar level, each part exhibits four-bar hypermeasures within the canon.
Return to text
24. Klorman’s (2016) web resources include a recording of Momigny’s operatic setting of the Quartet K. 421, first movement.
Return to text
25. This metrical reading depends on the hearing of the imitated motive as beginning-accented. This interpretation goes against MPR3—the requirement to have an “event” (an attack) on an accented beat—since the motive begins with a quarter rest. Given the full quartet texture, however, attacks come on all the beats. Measure 59, in fact, gets a rather salient “event” in the cello—the local lowest point Bb, and receives an accent as a potential beginning of a new triple hypermeasure (MPR 1). MPR 5a (new articulation pattern) also supports odd-strong hypermeter. Finally, the two-bar hypermeasure beginning at m. 59 are congruent with respect to two-bar segments of the first violin’s sentential structure that cadences at m. 66. The term “cycle” is by Rothstein (2011) and means a group of four beats or hyperbeats at any level—metrical or hypermetrical. The cycle can take one, two, or four notated measures.
Return to text
26. This four-cycle, however, is somewhat challenged by the three-bar group in mm. 67–69, which reproduces the minor-and-augmented second imitative pattern from earlier in the development.
Return to text
27. “Projection” is Christopher Hasty’s (1997) term.
Return to text
28. Measure 75 is strong thanks to a new harmony, a new bass (sustained for eight measures; MPR 5f), new texture and dynamic, and new material (MPRs 8, 5d, and 5b).
Return to text
29. In this reading, the G harmony, as an upper fifth of C, is on a shallower level.
Return to text
30. MPR 5d is also at work: m. 40 begins a new module of patterned activity.
Return to text
31. In form-functional terms, this long-sustained E major chord is somewhat ambiguous: it would have been the transition’s standing on the dominant, if the passage didn’t also serve as the opening of the subordinate theme.
Return to text
32. Both of these versions require a special remark on the status of the
Return to text
Copyright Statement
Copyright © 2017 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
13371