Scriabin’s Atonal Problem
Inessa Bazayev
KEYWORDS: Scriabin, atonal problem, Schoenberg, Disability Studies, orthography, Russian music theory, Yavorsky, voice leading
ABSTRACT: An integral feature in many of Scriabin’s late musical narratives is the presence of an atonal problem—a musical event that threatens a harmony which the piece is based on. I offer a new interpretation of Scriabin’s late music, in which the idea of an atonal problem becomes a defining feature of his style (after op. 58). This atonal problem is defined as a non-chord tone, which disrupts the balance of the collection (octatonic, whole-tone, or Mystic) which the work is based on. Drawing from Schoenberg’s concept of a tonal problem and from Straus’s expansion of this concept in Disability Studies in music, I use Scriabin’s piano miniatures to show that, within each work, a single pitch class always stands out registrally, dynamically, and/or rhythmically, and becomes an important staple of Scriabin’s late style. Thus, the accommodation of this “wrong” note no longer represents that pitch class as a disruptive note, but rather it adds to the unique aspect of that work.
Copyright © 2018 Society for Music Theory
I. Introduction
[1.1] The concept of a tonal problem has been widely theorized, most notably in Schoenberg’s organicist view of a musical work, in which a tonal problem is a single note that threatens to destabilize the prevailing tonality by imbalance and unrest: “Every succession of tones produces unrest, conflict, problems. . . . Every musical form can be considered as an attempt to treat this unrest either by halting or limiting it, or by solving the problem” (Schoenberg 1967, 102). Most recently, the narrative of a tonal problem (or a problem note) has been reexamined by Joseph N. Straus (2006 and 2011) through the analytical lens of Disability Studies.(1) Straus discusses tonal problems in two ways: musical narratives of disability overcome and musical narratives of disability accommodated.(2) A tonal problem is introduced early in the piece and fails to be incorporated into the so-called “normal” body of the work, ultimately creating imbalance and unrest. This type of tonal problem marks the musical body in a visible and audible way, leaving the performer and the listener to grapple with its hermeneutical possibilities.
[1.2] I argue that some of Scriabin’s non-tonal works (i.e., those after op. 58) feature a single pitch class that threatens to destabilize the prevalent collection (octatonic, whole-tone, or Mystic [sc(013579)]) of the piece.(3) I introduce the concept of an atonal problem: a single non-collection tone—often emphasized by register, dynamics, and/or rhythm—that does not belong to the main referential collection of the work. All of the works that I discuss follow a very clear pattern of introducing and not resolving an atonal problem, one in which the unresolved non-collection tone leaves a permanent mark on the musical body.(4)
[1.3] In order to understand Scriabin’s use of the atonal problem, we need to address some Russian analytical approaches. I will first summarize Boleslav Yavorsky’s symmetrical system in order to establish the importance of pitch orthography in Russian theoretical thought. Then, I will introduce and define an atonal problem and show a unique case study in “Etrangeté,” op. 63, no. 2, the only example in which an atonal problem reaches its true resolution at the end of the work. For the remainder of the essay, I discuss an atonal problem’s most common function—its unflinching struggle to hold its own ground and avoid resolution. The last section of my essay provides a synthesis and considers the significance of an atonal problem in Scriabin’s late oeuvre.
II. Yavorsky’s Symmetrical System in Scriabin’s Late Works
[2.1] In Russian music theory, non-tonal music has been traditionally viewed in light of the circle of fifths.(5) Beliaev (1923), Roslavets (1927), Ogolevets (1941), and Dërnova (1968) describe Russian contemporary music with absent key signatures (including the late music of Scriabin, Prokofiev, and Shostakovich, among others) from a tonal perspective.(6) This circle of fifths helped shape another important concept—tiagotenie, or gravitation among the pitches (Yavorsky 1908; Ogolevets 1941, 343–45). Within this system, the spelling or orthography of pitches dictates their function: a sharped note resolves upward, and a flatted note resolves downward.(7) This approach creates a kind of continuity from tonal to non-tonal music. The present article expands on this notion of continuity and applies it to Scriabin’s late music. Although Scriabin’s late music is not rooted in the circle of fifths, I argue that it still continues and develops from the tonal tradition, further validating Scriabin’s late compositional style within Soviet theoretical thought.(8)
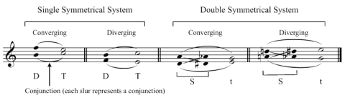
Example 1. Yavorsky’s single and double symmetrical systems (2008, 5), reproduced from Ewell 2012, example 2
(click to enlarge)
[2.2] Boleslav Yavorsky’s (1908) symmetrical systems help us understand some of the significant concepts in Russian tonal and non-tonal music. One of the central concepts in Yavorsky’s theory of symmetrical systems is the tritone and its resolution (2008, 5).(9) Example 1 reproduces Yavorsky’s single and double symmetrical systems, with open noteheads denoting stable notes and closed noteheads denoting unstable notes (i.e., the notes that constitute a tritone).(10) The orthography of the unstable notes is significant to Yavorsky’s system, especially in the double symmetrical system.(11) Yavorsky’s systems can be extended to imply clear pitch function of non-chord tones in Scriabin’s late works, including those based on special referential collections.(12)
[2.3] My method generalizes Yavorsky’s approach and examines pitch function in a new way. In all the works analyzed below, an atonal problem’s orthography is crucial to understanding Scriabin’s late compositional style. In each of the pieces discussed below, Scriabin uses a systematic method of singling out an atonal-problem note. An atonal-problem note appears in the following ways: (1) it does not belong to the prevalent referential collection of the work; (2) it is highlighted in the work’s first phrase, registrally, rhythmically, and/or dynamically; and (3) its spelling dictates the expected resolution.
III. An Atonal Problem with an Unconventional Resolution: Op. 63, No. 2
Example 2a. Scriabin’s “Etrangeté,” op. 63, no. 2, with pc D as its atonal problem; the excerpt is based on OCT0,1; mm. 1–7
(click to enlarge and listen)
[3.1] Examples 2a–c show excerpts from “Etrangeté,” op. 63, no. 2, a work that features transpositions of the octatonic collection and an “atonal problem” of pitch class (pc) D. Let us first trace its initial journey in the opening sections of the piece. Example 2a shows the A section of the work (mm. 1–7), which uses OCT0,1 as its main collection. Pc D in m. 3 and in mm. 6–7 is a “problem” because it does not belong to the prevailing collection. In this section, pc D is presented in two contexts: it is part of an ascending passage in m. 3, and it is heard as a part of a chord in mm. 6–7. While Reise 1983 also examines the same passage as octatonic, his non-chord tones always resolve by different kinds of half steps, regardless of their spelling.(13) These “half-step” resolutions may involve an interval of an augmented prime, a diminished prime, or a minor second. Thus, the orthography of the non-chord tones and their resolutions has been overlooked. An examination through a Russian theoretical lens—a Yavorskian lens—produces different analytical results. In the generalized Yavorskian system that I have described in the previous section, the spelling of notes dictates their function, even in non-tonal works. Thus, as we re-examine op. 63, no. 2, the actual local resolution of D5 (and D6) occurs only in mm. 6–7, where D5 resolves downward to
[3.2] The use of the non-collection tone D in mm. 6–7 is crucial in tracing its journey throughout the work. In mm. 6–7, pc D is demarcated in four significant ways: (1) it clearly does not belong to the prevalent OCT0,1 collection; (2) it is rhythmically syncopated (i.e., in mm. 6 and 7, the projections of pc D occur on accented weak beats in the latter part of each measure); (3) pc D is further stressed, due to its registral placement—as the highest note in the left hand (D5), as well as in the right hand (D6), and its repetition in m. 7 further emphasizes its importance; and (4) because of these features, the executed dynamic tends to be louder than the indicated piano.(14) Thus, these gestures highlight pc D as an atonal problem of the work, visually on the musical score, as well as aurally.
Example 2b. The B section of “Etrangeté,” with pc D (shown in dashed ovals) as a chord member, mm. 8–19
(click to enlarge, see the rest, and listen)
[3.3] Pitch-class D takes on a more vital registral role in the middle section of the work. Example 2b shows the B section, where pc D returns as part of the octatonic collection. This section is based on OCT1,2 and OCT2,3, consecutively, collections that both include D, of course. There are two interesting features worth noting: the D5 occurring at the very beginning of the B section (m. 8), and D6 and D7 occurring at the climax of the B section (mm. 13–17). First, let’s examine the rhythmic and registral placement of the first chord-tone D in the B section (m. 8). Pitch class D occurs immediately after the non-chord tone Ds in mm. 6–7 (from the A section). The
Example 2c. The final section of “Etrangeté,” (OCT0,1), with an atonal problem (D) resolving upward to
(click to enlarge and listen)
[3.4] At this point of the piece, the analyst has been convinced that an atonal problem was prematurely resolved in mm. 6–7 (see again Example 2a) and that the return of the high-register Ds in the middle section has confirmed its transformed status from an atonal problem to a chord tone. However, this is not true. At the return of the last section (mm. 18–31), OCT0,1 collection also brings back the atonal-problem note. Example 2c shows this last section, and pc D is finally normalized by resolving upward to an
IV. Atonal Problem Unresolved
Example 3a. The A section of “Guirlandes” from Two Dances, op. 73, no. 1, with pc B as its atonal problem, mm. 1–12
(click to enlarge and listen)
Example 3b. The return of the AB’ section of “Guirlandes,” with pc B unresolved in m. 63
(click to enlarge, see the rest, and listen)
[4.1] The pieces discussed in this section firmly establish the prevalent unresolved function of an atonal problem. In each of the pieces, an atonal problem is presented and unresolved in a similar way. Example 3a shows the opening section of “Guirlandes” from Two Dances, op. 73, no. 1 (mm. 1–12), which is based on two octatonic collections—OCT0,1 followed by OCT2,3.(17) This work’s atonal problem is introduced right away in m. 1 as pc B, which does not belong to the prevailing OCT0,1. At its first appearance, this pitch is not very noticeable. It is the second note in the right hand’s ascending arpeggiation, the dynamics are piano, and the descending contrary motion in the left hand further masks its presence. (The B4 returns in a similar way in m. 5.) As we listen onwards, however, pc B returns an octave higher in m. 3. It is demarcated in two ways: it is the highest note of the passage thus far and it is approached by a leap. The recurrence of this atonal problem is further intensified by the
Example 4a. The opening section of “Poème,” op. 69, no. 1, with pc
(click to enlarge and listen)
Example 4b. The second half of “Poème,” op. 69, no. 1, with pc
(click to enlarge, see the rest, and listen)
[4.2] In the last section, pc B remains unresolved.(18) Example 3b shows the second half of the piece, which brings back the A section (mm. 31–42) and the B section, now expanded (B’) (mm. 43–65). It is the B’ section where pc B is confirmed as an atonal problem or a permanent foreigner.(19) Especially noteworthy of this final section is the orthographical shift in OCT2,3. At the beginning of the piece (see again Example 3a), OCT0,1 was associated mainly with sharp spellings and OCT2,3 with flat spellings.(20) By the end of the piece, however, the pcs of OCT2,3 become enharmonically spelled with sharp signs, in an effort to push pc B into its non-chordal function as an atonal problem. Even as a respelled collection, OCT2,3 tries to absorb pc B as a chord tone, but OCT0,1 does not allow for this change. This visual orthographic push proves to be useless. After rotating through all three octatonic collections, the music finally returns to its initial OCT0,1 (mm. 56–65). This final passage is crucial to the piece, because pc B (m. 63) no longer resolves to pc C but rather remains unresolved, having been permanently sewn into the musical fabric of OCT0,1 collection as its ninth pc.
[4.3] Another piece that uses an atonal problem is “Poème,” op. 69, no. 1. This work is based on different transpositions of the Mystic collection, or set class (sc) (013579), as well as the whole-tone collection, sc (02468T).(21) Example 4a shows the opening section (mm. 1–8), with pc
Example 5. “Masque,” op. 63, no. 1, with pc
(click to enlarge and listen)
[4.4] Scriabin also uses atonal problems in a strictly motivic sense. An atonal problem is presented at the opening of a piece and becomes associated with a very specific gesture. Every time it reappears later in the piece, it is heard the same way—registrally, dynamically, and rhythmically. Example 5 shows “Masque,” op. 63, no. 1, with
Example 6a. The opening section of Vers la Flamme, op. 72, with pc
(click to enlarge, see the rest, and listen)
Example 6b. Build up to the climax of Vers la Flamme, with its atonal problem
(click to enlarge and listen)
[4.5] My last example focuses on one of the most pianistically challenging pieces in Scriabin’s oeuvre—Vers la Flamme, op. 72—which features pc
Example 6c. The last section of Vers la Flamme with its atonal problem (which remains unresolved) prominently highlighted in various registers, but remains unresolved; the passage is based on OCT1,2, mm. 95–137
(click to enlarge, see the rest, and listen)
[4.6] The unsettling sojourns of an atonal problem within the different registers reach their climax at the last section of the work, where the texture, dynamics, and rhythm of the section add to the tumultuous whirl of the piece. Example 6c shows the concluding section (mm. 95–137), with all recurrences of its atonal problem. Atonal problem
V. Conclusion
[5.1] As I have shown in this essay, the atonal problem is an integral part of Scriabin’s late compositional oeuvre. Generalizing Yavorsky’s symmetrical systems allows for a broader understanding of orthography in Scriabin’s late works. Furthermore, my analyses demonstrate the determined path of these unique non-chord tones as they emerge from the musical surface. An atonal problem is clearly highlighted in the opening measures of a work (registrally, dynamically, and/or rhythmically) and leaves a permanent mark on the surface of the prevailing collection of the work. Thus, in Scriabin’s late compositions, an atonal problem is a significant pc that lives among a homogeneous land of a Mystic, octatonic, or whole-tone collection. This outsider makes itself known right away (both aurally and visually) and continues to relentlessly stand out against the normative body of the prevailing referential collection. The aim of an atonal problem’s journey is not to yield, but rather to add a new color or distinct mark on the main structure or body of the work. This unresolving nature of an atonal problem is crucial to understanding Scriabin’s late style because it defines a significant compositional practice: an atonal problem is a desirable, unique type of a non-chord tone, which adds to Scriabin’s innovative approach to his late music.
Inessa Bazayev
Louisiana State University
College of Music & Dramatic Arts
102 School of Music
Baton Rouge, LA 70803
ibazayev@lsu.edu
Works Cited
Bazayev, Inessa. 2013a. “Triple Sharps, Qnt Relations, and Symmetries: Orthography in the Music of Nicolaĭ Roslavets.” Music Theory Spectrum 35 (1): 111–31.
—————. 2013b. “The Circle of Fifths in Russian Non-Tonal Music: A Case Study of Selected Works by Roslavets and Stravinsky.” Dutch Journal of Music Theory 18 (2): 51–68.
—————. 2014. “The Expansion of the Concept of Mode in Twentieth-Century Russian Music Theory.” Music Theory Online 20 (3).
Beliaev, Viktor. 1923. “Mekhanika ili Logika?” [Mechanism or Logic?] K Novym Beregam 3: 21–30.
Callender, Clifton. 1998. “Voice-Leading Parsimony in the Music of Alexander Scriabin.” Journal of Music Theory 42 (2): 219–33.
Carpenter, Patricia. 1988. “A Problem in Organic Form: Schoenberg's Tonal Body.” Theory and Practice 13: 31-64.
Cheong, Wai-Ling. 1993. “Orthography in Scriabin's Late Works.” Music Analysis 12 (1): 47–69.
Cone, Edward T. 1982. “Schubert’s Promissory Note: An Exercise in Musical Hermeneutics.” 19th-Century Music 5(3): 233–41.
Dërnova, Varvara. 1968. Garmoniia Skryabina [Scriabin’s Harmony]. Muzgiz.
Ewell, Philip. 2012. “Rethinking Octatonicism: Views from Stravinsky’s Homeland.” Music Theory Online 18 (4).
Guenther, Roy J. 1979. “Varvara Dernova’s Garmoniia Skriabina: A Translation and Critical Commentary.” Ph.D. diss., Catholic University of America.
—————. 1983. “Varvara Dernova’s System of Analysis of the Music of Skryabin.” In Russian Theoretical Thought in Music. Edited by Gordon McQuere, 165-216. University of Rochester Press.
McQuere, Gordon, 1983. “The Theories of Boleslav Yavorsky.” In Russian Theoretical Thought in Music. Edited by Gordon McQuere, 217-52. University of Rochester Press.
Ogolevets, Alekseĭ. 1941. Osnovy Garmonicheskogo Iazyka [The Fundamentals of Harmonic Language]. Gosudarstvennoe muzykal’noe izdatel’stvo.
Reise, Jay. 1983. “Late Skriabin: Some Principles Behind the Style.” 19th-Century Music 6 (3): 220–31.
Roslavets, Nicolaĭ. 1927. “Novaia sistema organizatsii zvuka i novye metody prepodavaniia teorii kompozitsii: Tezisy doklada” [The New System of Tone Organization and New Methods of Teaching the Theory of Composition: Theses of Lectures]. Lecture given at the Stravinsky Musico-Vocal courses, Moscow.
Saslaw, Janna. 1997–98. “Life Forces: Conceptual Structures in Schenker's Free Composition and Schoenberg's The Musical Idea.” Theory and Practice 22–23: 17–33.
Schoenberg, Arnold. [1946] 1984. “New Music, Outmoded Music.” In Style and Idea: Selected Writings of Arnold Schoenberg. Translated by Leo Black and edited by Leonard Stein, 113–23. Faber & Faber.
—————. 1967. Fundamentals of Musical Composition. Edited by Gerald Strang and Leonard Stein. Faber & Faber.
—————. 1995. The Musical Idea and the Logic, Technique, and Art of Its Presentation. Translated and edited by Patricia Carpenter and Severine Neff. Columbia University Press.
Straus, Joseph N. 2006. “Normalizing the Abnormal: Disability in Music and Music Theory.” Journal of the American Musicological Society 59(1): 113–184.
—————. 2011. Extraordinary Measures: Disability in Music. Oxford University Press.
—————. 2014. “Harmony and Voice Leading in the Music of Stravinsky.” Music Theory Spectrum 36 (1): 1–33.
Yavorsky, Boleslav. 1908. Stroenie muzykal’noĭ rechi [The Structure of Musical Speech]. Gosudarstvennoe muzykal’noe izdatel’stvo.
—————. 2008. Izbrannoe: pis’ma, vospominaniia [Selected Letters, Reminisces]. Kompozitor.
Selected Discography
Selected Discography
Vladimir Ashkenazy, pianist. 2015 [1998]. Scriabin: The Complete Works. Decca KTC 002280502, box set, 18 compact discs.
Vladimir Feltsman, pianist. 2012. A Tribute to Scriabin. Nimbus Alliance KTC 6198 1CD 710357619823, compact disc.
Roger Woodwood, pianist. 2004. Alexander Skryabin: Late Piano Works. Et’cetera KTC 1126 1CD 8711525112605, compact disc.
Footnotes
1. In bridging Schoenberg’s theory with his own, Straus explains: “The normative and desirable bodily state (balance and rest) is understood in relation to a non-normative and undesirable state (imbalance and unrest)” (Straus 2011, 49). For further reading on the idea of a tonal problem, see Cone 1982; Carpenter 1988; Schoenberg 1995; Saslaw 1997–98; Straus 2006 and 2011.
Return to text
2. Straus gives numerous examples from Beethoven’s “heroic” period, in which a tonal problem is presented as “disability overcome.” Some of these works, for instance the finale of Symphony no. 8, introduce the tonal problem (in this case, the
Return to text
3. The Mystic chord has been traditionally associated with a harmony, that is a verticality. Instead, I treat the chord as a collection, because it also appears melodically.
Return to text
4. This concept resonates with Straus’s “disability accommodated.” Straus describes such musical works in terms of struggle: the tonal problem can be only “won through suffering” (Straus 2011, 64).
Return to text
5. The Russian/Soviet analytical approach greatly differs from those of its Western counterparts. Tonal elements that usually include the prevalence of the circle of fifths on both harmonic and melodic levels in both tonal and non-tonal works (e.g., the music of Nicolai Roslavets) are viewed as progressive because they continue the traditions set forth by tonal principles; see Bazayev 2013a. This continuity can also be traced throughout Stravinsky’s entire compositional oeuvre. For more on the significance of perfect fifth (bi-quintal) structures in Stravinsky’s music, see Straus 2014.
Return to text
6. For further reading on the role of the circle of fifths in non-tonal works of Roslavets and Stravinsky, see Bazayev 2013b.
Return to text
7. This concept is crucial to Ogolevets’s system of tiagotenie, as well as to my own analytical approach. For more on pitch function in non-tonal Russian works, see Bazayev 2014.
Return to text
8. This concept is also noted in Dërnova 1968.
Return to text
9. See also McQuere 1983. For a thorough discussion of the system, see Ewell 2012.
Return to text
10. Yavorsky explains that the unstable notes making up the single symmetrical system represent the dominant harmony, and the unstable notes making up the double symmetrical system represent the subdominant harmony (2008, 5–6).
Return to text
11. Although Yavorsky does not always take orthography as an essential component of motion among different pitches, semitonal resolutions are crucial to understanding his system. Further, Ogolevets modifies this system and takes orthography as a prominent element that drives music forward (from a dissonant note to a consonant note), so that orthography becomes central to understanding resolutions of dissonant tones: a raised note would resolve upward and a lowered note would resolve downward (1941, 343–45).
Return to text
12. In Russian music theory, the orthographic function of pitches within non-tonal Russian works plays a significant role in understanding the music of twentieth-century Russian composers, including Shostakovich and Prokofiev. For a survey of some significant writings on the topic, see Bazayev 2014.
Return to text
13. For more on intervallic dissonance in non-tonal works of early twentieth-century Russian composers, especially on the augmented prime, see Ogolevets 1941, 133–35 and 340–43.
Return to text
14. In all notable recordings of the pieces, especially those by Vladimir Ashkenazy (2015), Roger Woodward (2004), and Vladimir Feltsman (2012), the D in mm. 6–7 always stands out regardless of the piano dynamic indication.
Return to text
15. Upon return of the A section (mm. 18–31), the initial octatonic collection returns (OCT0,1). Pitch class D appears only once as a chromatic passing tone (m. 20). Further, it is part of a large-scale chromatic motion in the soprano line, and it quickly resolves to
Return to text
16. In Disability Studies, the resolution of the problem note can be also described as “disability overcome.”
Return to text
17. Reise 1983 also analyzes this work. As noted earlier, Reise’s approach is not concerned with orthography. He determines that all non-chord tones resolve by half step, without any consideration for their spelling. For instance, the B4 in m. 1 resolves to the
Return to text
18. The B section is based on the OCT2,3 collection, and all the pcs in that section belong to that collection, even our atonal problem.
Return to text
19. Reise 1983 explains this non-chord tone differently, taking the
Return to text
20. OCT0,1 [C,
Return to text
21. The interchangeable use of Mystic and whole-tone collections is prevalent in Scriabin’s late works, since the modulations between them only require a deletion or an addition of a single pitch, creating smooth voice leading among the collections.
Return to text
22. Once again, Reise explains this non-chord tone first as a neighbor note to the
Return to text
23. Following Reise’s system of non-chordal resolutions,
Return to text
24. The final chord of the piece does contain pc C in the bass (in octaves). However, because of its extremely low registral placement, coupled with the triple piano dynamic indication, pc C is not to be taken as a resolution. Given the consistent lack of resolution of atonal problem notes within Scriabin’s late works, the final pc C in “Poème,” op. 69, no. 1, is a humorous gesture or joke, on the composer’s part.
Return to text
25. Pitch class
Return to text
26. The piece can be loosely divided into four sections: mm. 1–40; mm. 41–76; mm. 77–106; mm. 107–125. There are only two main themes in the piece—theme A, which is established in mm. 1–6, and theme B, which is characterized by a half-step melodic descent in mm. 27–34. These themes return either fully, partially, or in altered form in each section of the work.
Return to text
27. Throughout the work, the atonal problem note is prominently associated with OCT1,2.
Return to text
28. There are other false resolutions within the work. See the beginning of the second section (mm. 40–44). The very slow-moving melodic line (nine eighth-notes long) features false resolutions of the atonal problem to an
Return to text
Copyright Statement
Copyright © 2018 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
13152