Prokofiev’s Symphony no. 2, Yuri Kholopov, and the Theory of Twelve-Tone Chords

Introduction

[1] This paper bases a history and theory of twelve-tone chords around an unlikely starting point: Sergei Prokofiev, whose Symphony no. 2 (1924) features a chord with all twelve pitch classes.⁽¹⁾ Scholars have developed sophisticated models for various aspects of twelve-tone technique—such as tone-row structure, invariance, hexachordal combinatoriality, and rotation—but with isolated exceptions have not to date examined the phenomenon of twelve-tone verticals. Prokofiev, of course, is not widely associated with twelve-tone technique, and twelve-tone composition has not been a major area of Prokofiev studies. In contextualizing Prokofiev’s twelve-tone chord, this article will investigate the history of twelve-tone chords, the theorists who have described them, and the composers in whose works they have appeared. I draw on the work of Yuri Kholopov (1932–2003)—longtime professor at the Moscow Conservatory, and the foremost Soviet and post-Soviet theorist of his era—whose writings connect Prokofiev to twelve-tone technique in two ways.⁽²⁾ First, Kholopov viewed Prokofiev’s “twelve-step” chromatic system, with independent harmonic functions on all degrees of the chromatic scale, as the true innovation of twentieth-century aggregate-based composition.⁽³⁾ Second, Kholopov argued more generally in several writings for a broad conception of twelve-tone technique that included not only serial dodecaphony (his term for Schoenberg’s practice) but also a variety of other techniques, including twelve-tone chords (dodekakkordï), the topic of this article.⁽⁴⁾ Kholopov’s (1983a) chronology of Schoenbergian precursors and parallels includes the twelve-tone chord from Prokofiev’s symphony. In this article, I survey the issues involved in analyzing twelve-tone chords and assemble a theory of twelve-tone chords. I return to Kholopov’s more detailed analysis of Prokofiev’s twelve-tone chord, in order to decipher its contradictions and propose an alternative. Finally, I argue that twelve-tone technique is a construction, rather than a fixed concept, that can be used in various ways by various authors.

[2] In considering twelve-tone chords as an independent topic, my paper engages not only with Kholopov, but also with other composers and theorists who have written on twelve-tone chords. Several authors of compositional treatises—namely Alois Hába (1927), Vincent Persichetti (1961), Ctirad Kohoutek (1976), and Eugen Suchoň (1979)—outlined possible forms and uses of twelve-tone chords. Among theorists, Martina Homma (1999, 2001) has most thoroughly investigated the issue, having traced the history of twelve-tone chords and their theoretical explication. Homma has advanced two arguments that will be taken up in the course of this article: first that twelve-tone chords constitute an independent and continuous compositional practice, and second that twelve-tone chords are a vertical analogue to the horizontal technique of twelve-tone rows. In general prior writers have addressed the problem of differentiating twelve-tone chords from one another, given that they all contain the same notes, as well as a variety of additional issues (explored below). As they demonstrate, there is more to consider regarding twelve-tone chords than simply how many notes they contain.

[3] The theoretical formulation proposed here draws on a catalogue of twelve-tone chords found in the repertoire. In describing twelve-tone chords as a compositional practice, several writers have referred to specific examples in the repertoire. This study collates all such examples for the purpose of drawing larger conclusions. Although there are exceptions, twelve-tone chords tend to feature the following properties: they avoid doubled pitch classes, they have a range of about 3 to 5.5 octaves, and their internal intervallic structure follows some sort of pattern. These features support the concept of a twelve-tone chord as an intentional compositional object, deliberately structured in such a way as to reinforce its identity as a twelve-tone chord. For this reason, chords containing only 10 or 11 distinct pitch classes are excluded from the study. Twelve-tone chords are special cases of highly chromatic sonorities, as through their purposeful exhaustion of the aggregate they forge a connection to twelve-tone technique more broadly, reinforcing the historically emergent conceit of composing with all twelve pitch classes.

[4] Kholopov (2009) offers Prokofiev’s Symphony no. 2 as a case study for analyzing twelve-tone chords, and I address both his analysis and an alternative analysis in this essay. Whereas early sections of the article will focus on ways in which twelve-tone chords can be differentiated from each other, the Prokofiev symphony offers a testing ground to consider how a twelve-tone chord can be analyzed in the context of an individual work, particularly a work that does not otherwise consist of twelve-tone chords. A twelve-tone chord appears in the symphony’s second movement. Kholopov’s attempts to relate the intervallic content of Prokofiev’s twelve-tone chord to other motives in the same movement leads to conflicting interpretations of the same chord. As a twelve-tone chord contains every pitch class, so can it be parsed to contain a variety of motives and intervals.

[5] Finally, I’ll propose a perspective of twelve-tone technique as a construction, with a shifting, negotiable definition. What “counts” as twelve-tone technique can change over time and from author to author, and the issue is worth considering from a historiographic standpoint. Specifically, a gambit such as Kholopov’s that broadens the conception of twelve-tone technique beyond serial dodecaphony allows connections to be drawn between the Schoenbergian approach and other aggregate-based practices of the early twentieth century. This perspective is thus historical as well as theoretical.

Background

[6] Yuri Kholopov, with the title to an article, poses the question: “Who Invented Twelve-Tone Technique?” (1983a).⁽⁵⁾ The answer, he assures us at the outset, is Arnold Schoenberg, if by “twelve-tone technique” we mean serial dodecaphony, the technique of composing with transformationally manipulated twelve-tone rows. But he nonetheless outlines a chronology of precursor techniques to Schoenberg’s compositional method, most created independently of Schoenberg and therefore not casting a direct influence on the later method. Composers in the early twentieth century experimented with a number of ideas that seemed to coalesce in the music of Schoenberg and his followers. Kholopov notes early instances of several techniques, including the following: “microserial” technique (a three-note cell in Webern’s String Quartet [1905], a four-note cell in Stravinsky’s Firebird), isolated melodic statements of the aggregate (twelve-tone rows in early Berg and Webern), referential non-twelve-tone vertical sonorities used also for horizontal content (Scriabin’s Mystic Chord, Roslavets’s synthetic chords), and twelve-tone fields in which all twelve pitch classes freely circulate (Nikolai Obukhov, Yefim Golïshev). He also includes the well-known tropes of Josef Matthias Hauer. Through Kholopov’s article, Schoenberg’s technique appears to emerge from a swirling cloud of ideas in the air at the time. Far from presenting Schoenberg as a visionary genius who invented an important method on his own—although Schoenberg, it must be said, is given due credit for the depth of his contribution—Kholopov historicizes Schoenberg, accounting for the way in which he solved problems that composers had been grappling with for decades.

[7] In this chronology that leads up to (and slightly past) Schoenberg’s first serial works of 1921–24, we read the following entry: “In the Finale of the Symphony no. 2 (1924) Prokofiev wrote a contrapuntal layer of sonoristic twelve-tone chords” (Kholopov 1983a, 56).⁽⁶⁾ (The chords, as will be shown below in Example 1, consist of a single twelve-tone chord transposed via parallel planing.) This is striking, not only because Prokofiev is not typically associated with twelve-tone technique (nor, for that matter, with the sonorism of the later Polish avant-garde), but also because Kholopov himself used Prokofiev as a foil for twelve-tone practices in earlier writings. Kholopov had argued that Prokofiev extended tonal harmony to allow for independent harmonic functions on all twelve degrees of the chromatic scale—what Kholopov called dvenadtsatistupennost’, or the “twelve-step” or “tonal chromatic” system. Thus Prokofiev, with his twentieth-century tonality, had been considered the true innovator of aggregate-based composition.⁽⁷⁾ Now Prokofiev is marshaled into service not as an alternative to twelve-tone composition, but rather as a progenitor.

[8] In subsequent writings, Kholopov develops his chronology of twelve-tone techniques into twelve categories of “twelve-toneness,” one of which is twelve-tone chords.⁽⁸⁾ Later textbooks and analysis manuals introduce each twelve-tone technique separately.⁽⁹⁾ The adumbration of twelve-tone chords in Garmonicheskiy analiz [Harmonic Analysis] (2009) is particularly notable in the present context, for it uses Prokofiev’s Symphony no. 2 as its primary example. In this chapter, as in every chapter, Kholopov presents a brief theoretical overview of the topic at hand (that for twelve-tone chords is very short, just a few paragraphs) and then applies his comments to the musical excerpt (again, in the present case, very briefly), before inviting the student-reader to complete the analysis.⁽¹⁰⁾ Example 1 shows the Prokofiev excerpt under discussion, from the second variation (in A major) of the second movement.⁽¹¹⁾ In the commentary, Kholopov remarks how the variation’s main melodic motive (see the top violin line) is harmonized in parallel with twelve-tone chords, played by twelve-part divisi strings, with each part playing a different transposition of the melody.⁽¹²⁾ On every sixteenth note, the divisi strings project the aggregate, each pitch class appearing once among the twelve parts. The right side of Example 1 shows the pitches of the twelve-tone chord as it sounds on the second sixteenth note of the measure; this chord is transposed to form the remaining chords.

[9] Of what does Kholopov’s brief theoretical overview consist? He writes that there are many ways one could organize a twelve-tone chord, bottom to top. One could arrange it with common subsets (e.g., superimposed diatonic or whole-tone subsets, diminished seventh chords, or augmented triads, or as a verticalized interval cycle) or with diverse subsets (e.g., different triad types, sonoristic sound blocks, combinations of the above subsets). The emphasis on subsets suggests that there tends to be—or perhaps, is supposed to be—some logical principle underlying the construction of twelve-tone chords. For some construction types, a specific work or composer is identified (although vaguely, as with an overtone series chord attributed only to Karamanov), but mostly Kholopov lists compositional possibilities, whether realized in known works or not. The possibility of writing a twelve-tone chord not based on a logical principle is not explicitly excluded, but neither is it clearly stated as an option. Prokofiev’s chord is parsed as involving several quartal subsets, although this interpretation will be addressed further below.

[10] In focusing on possibilities (in interval and subset construction) rather than actualities (in chords drawn from the repertoire, though a couple are cited), Kholopov is drawn into the orbit of several earlier compositional or practical theorists, in whose treatises the possibilities of writing twelve-tone chords of various sorts were laid out. Kholopov does not cite any of these authors; they each formulated theories of twelve-tone chords independently of the others. Alois Hába (1927, 89–92) extensively lists twelve-tone chords based on 3rds (of various qualities), 4ths, 5ths, 6ths, and 7ths.⁽¹³⁾ The compositional opportunities are not dwelt upon, although in the introduction to the same volume, Hába does point out a (quintal) twelve-tone chord from one of his own early orchestral compositions dated 1913 (so, according to the New Grove, probably Mládí), in a bid to be credited as the first composer ever to think of such a thing (but, as shown below, he wasn’t).

[11] Other treatises go beyond cataloguing the possible interval types. Vincent Persichetti (1961, 87–90) provides a thoughtful exposition on twelve-tone chords, explaining for composers-in-training their potential use (harmonic punctuation, quiet and sustained tension, contrasts with unison or two-part writing) and construction (equal-interval, heterogeneous, mirror-symmetrical, polychordal). His musical examples are self-composed excerpts, and he appends a list of several examples from the repertoire, which are considered in the discussion below.

[12] In more recent scholarship, Martina Homma (1999, 2001) has addressed the problem of twelve-tone chords most directly and comprehensively. Her important work undertakes a recovery of early theoretical descriptions of twelve-tone chords, beginning with the accordo dodecafonico of Domenico Alaleona, an Italian theorist who first formulated the conception in an article published in 1911. Homma identifies several compositions that incorporate early twelve-tone chords, including those by composers in possible contact with Alaleona, leading to an argument that twelve-tone chords form their own tradition in compositional history. Much of Homma’s theoretical discussion involves differentiating twelve-tone chords on the basis of their interval content.

Issues

[13] A twelve-tone chord is, to provide a working definition, a simultaneity that contains all twelve pitch classes. Various authors have discussed the issues involved in treating twelve-tone chords theoretically.⁽¹⁴⁾ These extend to concerns regarding their internal structure, perceptibility, function, and their relationship to twelve-tone technique more broadly (including to serial dodecaphony). The present section summarizes the issues involved in analyzing twelve-tone chords; the following section discusses twelve-tone chords from the repertoire.

[14] Differentiation. Every twelve-tone chord contains the same twelve pitch classes. If a twelve-tone chord is defined by its pitch-class content, then there can be only one twelve-tone chord; it cannot be transposed.⁽¹⁵⁾ But, conversely, as a variety of twelve-tone chords exists in the repertoire, then they must be differentiable according to their internal interval structure. Homma (2001, 102) summarizes the issue best, explaining that somewhere between the “only one” perspective and the “infinitely many” perspective lies the theory of twelve-tone chords, which must account for how the same set of pitch classes can be organized in perceptibly different ways.

[15] Interval structure. To the extent that twelve-tone chords can be compared on the basis of internal characteristics, their intervallic profile (or subset content), ordered vertically from bottom to top, offers a basis. Although there is technically no need for any twelve-tone chord to follow a predetermined pattern in its intervallic construction, it turns out that many such chords in the literature do so, exactly as predicted by Kholopov’s short synopsis. Some chords are based on a single interval size (e.g., 3rds, 4ths, 5ths). Others are based on patterns in the intervals (e.g., all-interval chords that contain every interval from 1 to 11 semitones, or symmetrical patterns of pitches based around an axis). Of course it is entirely possible for a twelve-tone chord to emerge as a compositional accident, if a large number of polyphonic layers happen to sound each of the twelve pitch classes, all at the same moment. But perhaps the reason for such commonly encountered intervallic patterns is that composers’ decisions to write twelve-tone chords are deliberate, and thus when they do not appear by chance, they may very well be organized in some logical manner—logical, that is, from the standpoint of the theory able to describe them (and not necessarily from the standpoint of the scoreless listener).

[16] Doubling. In Alaleona’s description of twelve-tone chords, doubling was expressly forbidden (Homma 2001).⁽¹⁶⁾ And in most twelve-tone chords in the repertoire, doublings do not exist. The reason seems similar to that proposed above, namely that writing a twelve-tone chord is a deliberate act, and likely composers treat the issue as one of arranging each of the twelve pitch classes vertically into an intervallic pattern. Avoiding doublings draws attention to the fact that the chord is a twelve-tone chord. To admit doublings would be tantamount to allowing repetitions in a twelve-tone row—that is, repetitions not in the presentation of the row, but within the row itself. The prohibition on doublings helps determine the intentionality of a twelve-tone chord. In those cases where exactly twelve tones are used, the chord may seem an intentional twelve-tone chord, whereas in cases where more than twelve notes sound simultaneously, the question is raised of whether the twelve-tone chord is merely incidental.

[17] Perceptibility. The fact that a given chord contains twelve pitch classes, as opposed to ten or eleven, may not be particularly perceptible to listeners, and its patterned intervallic structure may be likewise aurally obscure. For this reason, Mikhail Tarakanov (1968, 108) and Kholopov (1979, 107; 2009, 14) characterize Prokofiev’s twelve-tone chord, with its sixteenth-note planing, as producing a swirling sound mass, relating the technique to avant-garde sonorism. Although the specific intervals within a twelve-tone chord may not be perceived by ear, their arrangement and distribution affects the sound character of the overall chord.⁽¹⁷⁾

[18] Function. The earliest descriptions of twelve-tone chords discuss the possibilities of hearing them as conveying harmonic function. Example 2 shows two progressions from the theoretical literature in which twelve-tone chords “resolve” to tertian sonorities. As shown in the first progression, Alaleona organized twelve-tone chords as dominant sevenths with a full spectrum of extensions, and then resolved the upper notes as appoggiaturas (Homma 2001, 101–2). The twelve-tone chord was thus considered not a stable entity, but rather an embellishing one. In an analysis of the second progression (from an unpublished composition by Jean Huré), which begins with a quartal twelve-tone chord and arrives eventually (beyond the excerpt shown) on a first-inversion D major added-sixth harmony, René Lenormand (1940, 127) writes that the progression “defies analysis.” By contrast, Taruskin (2010, 225–26, 283–84), rather than describing twelve-tone chords in terms of harmonic function, relates them to a significatory function, by which they are understood to contain anything and everything, their identities remaining stable as their parts move around. Thus for Scriabin (in the unrealized Acte préalable) and Ives (in the unrealized “Universe” Symphony), the twelve-tone chord was to signify the all-encompassing One.

[19] Relationship to twelve-tone practice. Kholopov attempts to subsume twelve-tone chords under a larger category of twelve-tone practices. The deliberate or systematic use of the aggregate of twelve pitch classes was a constant concern among early twentieth-century composers, and both twelve-tone chords and twelve-tone rows, he seems to argue, are reflective of that. Martina Homma advances a more directed argument toward associating twelve-tone chords with twelve-tone rows, viewing the former as the verticalization of the latter. This argument will be addressed in further detail below.

[20] We might point out that any twelve-tone row can produce a twelve-tone chord if its pitches are sustained, so that the culminating sonority is the full chromatic. We may want to consider whether such resultant chords are twelve-tone chords in the sense under discussion here, or whether the blurred-together notes of a twelve-tone row should be considered a distinct category. There is an irony here, however. When a twelve-tone chord is presented as a chord (that is, a block chord), it may not be perceptually clear that it contains twelve tones. When, on the other hand, a twelve-tone chord is presented as a series of twelve tones—that is, sustained tones introduced one at a time, in a perceptually salient manner—it may not be clear that the resultant conglomeration is meant to be understood as a chord. Britten’s The Turn of the Screw (1954) features such a sustained-series chord (Example 3). The row’s presentation highlights its ic5 pairs—every discrete dyad is a perfect 4th or 5th, and every discrete tetrachord forms a four-note quartal harmony (i.e., prime form [0257]). But its identity as a twelve-tone chord may be less clear.

[21] Positional twelve-tone chords. Beginning in the 1960s, several composers—such as Lutosławski and Carter—began to use twelve-tone chords as “background” structures to be arpeggiated in the following sense. Each pitch class was assigned to a fixed register, and every instance of that pitch class would sound in that register, but there was no requirement that all twelve pitches be sounded simultaneously in the manner of a chord. Although twelve-tone chords rarely appear in a given positional span, the general practice has been related to the earlier twelve-tone chords under discussion. Homma (1999) refers to this background-structure technique as “pitch-positioning,” as it fixes the registral position of each note. I adopt her terminology and refer to the resultant structures as “positional” twelve-tone chords. Example 4 shows positional twelve-tone chords from the works of various composers, although given the extent to which they employed them—Stucky (1981, 116–17) catalogues dozens of Lutosławski’s twelve-tone chords based on the interval classes they emphasize—this example should be taken as a representative sample only.⁽¹⁸⁾ Carter has a predilection for all-interval twelve-tone chords spanning five-and-a-half octaves from bottom to top.⁽¹⁹⁾ Magnus Lindberg also uses positional twelve-tone chords, having stated a preference for both all-interval chords and overtone chords modeled on the natural harmonic series; the example demonstrates the latter.⁽²⁰⁾ Alfred Schnittke’s Variations on a Chord uses an all-interval positional chord as the titular “chord.” (See Example 4; here and in similar examples later in the paper, accidentals affect only the pitches to which they apply, and natural signs are omitted for ease of reading.)

[22] Several authors have associated positional chords with twelve-tone chords more generally. Homma in particular has argued that pitch positioning forms a crucial link between twelve-tone chords and twelve-tone rows—the former is the vertical analogue of the latter. Because positional twelve-tone chords control the pitch content of extended passages of music, but do not necessarily sound as simultaneities, they have a different function, sound, and conceptual basis than the other twelve-tone chords considered in this study. The question as to whether a positional twelve-tone background structure is truly a chord may be debatable.

[23] Problem cases. Some twelve-tone chords identified as such in the literature raise particular problems. Above, with reference to Britten’s Turn of the Screw, I discussed the issue of considering a blurred-together twelve-tone row as a twelve-tone chord. Along similar lines, Suchoň (1979, 162–63) identifies a twelve-tone chord in Boulez’s Sonatina for Flute and Piano that not only contains doubled pitch classes—a red flag in twelve-tone chord analysis—but (more to the point) results from four measures of music pedaled together. The “chord” is never articulated as such (when Chopin’s pedaling indications invite a blurring together of harmonies, do we refer to polychords?), and perhaps Kholopov’s twelve-tone field would be a better characterization of the passage.⁽²¹⁾

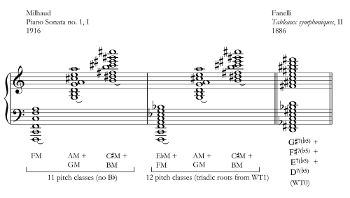
[24] Persichetti (1961, 90) identifies a twelve-tone chord in Milhaud’s Piano Sonata no. 1 that warrants close analytical scrutiny (Example 5). The pianist pedals together three polychords on successive beats. At first, eleven of twelve possible pitch classes are engaged—only eleven, even as the pianist articulates 22 different notes! Finally the pianist changes the first polychord and the twelfth pitch class enters the fray. But the logic seems not to be that of the twelve-tone chord, despite the aggregate completion. Rather the pianist appears to complete the whole-tone scale, which provides the root of every constituent triad within the polychords. The aggregate is a by-product of the fifth of a major triad belonging to a different whole-tone collection than its root, and therefore when the roots spell out one complete whole-tone collection, the fifths spell out the other one. One could imagine a similar technique with different constituent harmonies failing to produce an aggregate—for instance, the sixteen-note (but six-pitch-class) chord in Ernest Fanelli’s unpublished Tableaux symphoniques (Lenormand 1940, 130–31), of which the constituent chord type is the dominant seventh ♭5, all notes of which belong to a single whole-tone collection. This chord of the 31st contains only those pitch classes belonging to WT₀ (see again Example 5).

[25] To summarize this section, what emerges from prior theoretical considerations of twelve-tone chords is a recognition that if such chords are to be differentiated, it must be so on grounds of internal interval content, and the more clearly the twelve pitch classes are presented distinctly, the less chord-like the resultant simultaneity will be perceived to be. The criteria developed above are useful for providing a yardstick for determining whether a twelve-tone chord is intentional or incidental, to the extent that such a distinction matters. They also show how Kholopov’s discussion mirrors that of other twelve-tone chord theorists, who describe the variety of ways that twelve-tone chords can be constructed.

Features

[26] Although potentially there are infinitely many possible twelve-tone chords, the actual twelve-tone chords identifiable in the literature share several features in common. In other words, for Kholopov to lay out the possible ways of writing twelve-tone chords is congruent with other approaches to the topic. In what follows, I survey twelve-tone chords drawn from the repertoire, many from works by composers not previously associated with twelve-tone technique. I focus in particular on non-positional twelve-tone chords, and thus twelve-tone chords articulated as chords, not as background structures. In this way I avoid the multitudes of positional chords—such as those used by Lutosławski and Carter—which have their own properties that have been discussed by other theorists (as mentioned above).

[27] The theory of twelve-tone chords begins with the three properties they tend to share: no doublings, a range of about 3–5.5 octaves, and a deliberate interval pattern. There are exceptions to these properties—they are not absolute rules, neither in theory nor in practice—and the exceptions will be discussed in due course. But an examination of the repertoire verifies that twelve-tone chords tend to share these features.

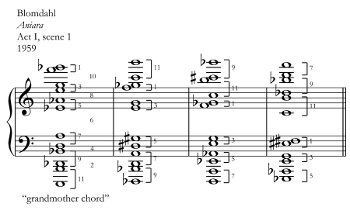
[28] 1. No doublings. Nearly all twelve-tone chords surveyed here avoid doublings—that is, they contain exactly one instance of each pitch class. For purposes of illustration, Example 6 presents a variety of twelve-tone chords from the repertoire that avoid doublings, but that also avoid the types of interval patterns discussed below. One chord (the first of two by Everett Helm) has a bass note reinforced at the octave, but no other doublings of any sort appear. The proscription against doubling was discussed above as a primary concern in the prior theoretical literature, extending backward in time all the way to Alaleona’s first description of the twelve-tone chord. The reason is that the presence of a doubled pitch class would lend undue influence to that particular note, tipping the balance away from an equal distribution of all pitch classes and toward an emphasized tone that may be construed as a root. The equivalent justification has been offered in twelve-tone row theory, expressed as a prohibition against note repetition (although this prohibition has been debunked convincingly by Joseph Straus [2009]). A more pragmatic compositional reason may be that when a composer intends to deliberately write a twelve-tone chord, that composer will conceive of the chord as a vertical ordering of the twelve pitch classes, and not merely as a large chord that happens to contain at least one of every pitch class. As a consequence, each pitch class will be represented exactly once. The compositional challenge becomes one of ordering the pitch classes more than anything else—exactly the same principle employed in twelve-tone row construction. Although it has not been previously argued as such, this may be the way that twelve-tone chord composition most clearly mirrors twelve-tone row composition.

[29] Exceptions. The repertoire contains a few exceptions—that is, recognizable twelve-tone chords that incorporate pitch-class doubling—that fall into two (related) categories: those that emphasize a tonic pitch class, and those structured to resemble the overtone series. The first case is represented by the final chord of Persichetti’s Symphony (no. 6) for Band, which contains three doubled pitch classes in an otherwise orthodox twelve-tone chord (Example 7). Two of the doubled pitch classes are B♭ and F, the two lowest notes of the chord, and also the most hierarchically stable (the other doubled pitch class is A). The work is in B♭ major, and this chord is understood as the final, culminating tonic. (The B♭ and F are further reinforced by a timpani roll.) Thus the doublings reinforce Schoenberg’s warning that an emphasized pitch class might sound like a root. Here the emphasis has a functional basis.

[30] Another subset of twelve-tone chords with doublings involves those attempting to mirror the interval structure of the overtone series. At a minimum, these overtone-based chords have a doubled bass note (at the octave) and perhaps additional doubled roots and fifths. In a twelve-tone chord from Karamanov’s Symphony no. 18 (see again Example 7), the reinforced root and fifth provide an overtone-structured grounding, even though the overtone pattern is not strictly maintained with the upper notes.⁽²²⁾ As noted above, Lindberg has also used positional overtone-series chords in his works (Martin 2005).

[31] 2. Range. Most twelve-tone chords surveyed have a range of between 3 and 5.5 octaves from bottom to top. A twelve-tone chord stacked strictly in thirds is about three octaves tall, whereas an all-interval twelve-tone chord reaches exactly 66 semitones (five-and-a-half octaves). In some cases twelve-tone chords exceed this upper limit, as when the internal intervals are all very large, or when a large gap exists in the middle of a chord. The range may depend on the limitations of the instruments called upon to perform the chord.

[32] The minimum range of three octaves is likely necessary to avoid clusters. If the range is smaller than three octaves, a twelve-tone chord will have to use adjacent pitches, calling into question the distinction between a twelve-tone chord and a cluster. In fact Alaleona’s basic form of the twelve-tone chord was essentially a twelve-tone cluster, with all notes within a single octave (Homma 2001), but this theoretical basic form seems analogous to a set-class prime form (0123456789TE) and does not reflect any individual chord’s registral disposition or voicing, not even in an idealized fashion. (In Alaleona’s subsequent examples, the twelve-tone chords were not presented as clusters.) Of course a one-octave twelve-tone cluster does, technically speaking, fulfill the implied requirements of the term “twelve-tone chord,” in a trivial way. But this is akin to characterizing a chromatic scale as a twelve-tone row.⁽²³⁾

[33] 3. Interval patterns. The majority of twelve-tone chords surveyed exhibit a distinctive internal interval pattern. Again, this speaks to the sense in which writing a twelve-tone chord is a deliberate act. It additionally speaks to the difficulty of distinguishing twelve-tone chords from one another. Because every twelve-tone chord contains the same twelve pitch classes, they cannot technically be distinguished by chord quality. Instead, the internal intervallic makeup is the only way that twelve-tone chords can be structured, and presumably made to sound, as distinct chords. Twelve-tone chords thus admit several distinct sound possibilities, not by their quality or absolute pitch-class content, but rather by their intervallic profile.

[34] Several types of patterns exist in the repertoire. The most commonly encountered are patterns by consistency of interval, patterns by superimposition of discrete subsets, patterns based on intervallic variety, and patterns based on rearrangable subsets.⁽²⁴⁾ The patterns encountered overall attest to a conception of the twelve-tone chord as a theoretical problem as much as a sound object. Composers play, deliberately, with the twelve pitch classes, arranging them into patterns.⁽²⁵⁾

[35] Pattern by consistency of interval. In compositional treatises by Alaleona, Hába, Schoenberg, Kohoutek, and Suchoň, twelve-tone chords are introduced in terms of consistent intervals. Outside the context of specific works, the authors produce possible chords based on the stacking of single intervals, from 2nds to 7ths—the last, says Hába (1927, 90), requiring too great a range to be of any practical use. Nicolas Slonimsky (1947) and Persichetti (1961) display further types of twelve-tone chords, including all-interval chords, again outside the context of the existing repertoire.

[36] Triadic patterns (twelve-tone chords based on 3rds). Several twelve-tone chords in the repertoire are based primarily on stacked-3rd harmonies, including some shown in previous examples (e.g., Alaleona, Persichetti, Karamanov). Example 8 presents further twelve-tone chords that incorporate 3rds as their primary interval of construction. In the chord by Sergei Slonimsky, the 3rds have been used to the greatest possible extent (a residual perfect 4th appears on top), with accidentals carefully chosen to ensure that the pattern can continue without duplication of pitch class.⁽²⁶⁾ The Bernstein example presents a chord that emphasizes (in its lowest pitches) a root, third, seventh, and ninth. This chord is clearly meant to be heard as a seventh chord (or ninth chord) with a full complement of dissonant extensions.

[37] Along the lines of Bernstein’s seventh chord with extensions, there is a particular group of triadic twelve-tone chords organized as dominant seventh chords with aggregate-completing extensions. Recall the theoretical example offered by Alaleona, shown above in Example 2, where the chord’s upper extensions are non-functional appoggiaturas that resolve by step, without a change of harmonic function, to the nearest members of the basic sonority, a dominant ninth. In the musical example from Liebermann (see again Example 8), a third-stream work that incorporates aspects of jazz technique, the opening chord, sustained in the strings and subsequently arpeggiated (positionally) in the solo piano, is best understood as an extended E7 harmony.

[38] Quartal and quintal patterns (twelve-tone chords based on 4ths and 5ths). Several composers, presumably independently, came up with the idea to extend quartal harmony (based on perfect 4ths) or quintal harmony (based on perfect 5ths) until the full chromatic was exhausted (Example 9). As mentioned above, Hába’s own twelve-tone quintal chord appeared as early as 1913. But a twelve-tone quartal chord appears in an unpublished work by Jean Huré written in 1910–12, transmitted through the theoretical writings of Lenormand and Koechlin (and only thus after 1913).⁽²⁷⁾ I’ll address the problem of locating the “earliest” twelve-tone chord below. For now, observe the conspicuous feature that marks these exhaustive quartal and quintal chords specifically as twelve-tone chords: each contains twelve notes and no more. There are no doublings, as the chords do not extend beyond their twelfth pitch. Any of them could have kept going, reaching higher into the registral stratosphere—for that matter, widely spaced quartal and quintal chords could have stopped prior to reaching the twelfth pitch, as with a ten-note quintal harmony from Ligeti’s Melodien (1971)—but they extend only as far as the final note of the aggregate. These are twelve-tone chords—intended, conceived, and theorized as such.

[39] Pattern by superimposition. Kholopov describes an approach to constructing twelve-tone chords based on superimposing discrete subset chords. One can make a twelve-tone chord by layering on top of one another, for instance, four augmented triads, or three diminished seventh chords, or a variety of triad types. This represents a second approach to patterning in a twelve-tone chord. Its logic consists of finding the right chords that “fit together” to produce the full chromatic. Nicolas Slonimsky’s Thesaurus (1947) addresses the same issue from a different perspective, outlining various combinations of four triads—all drawn from the traditional quality types of major, minor, diminished, and augmented—that exhaust the aggregate when juxtaposed (horizontally instead of vertically, in his examples). (In his memoirs Perfect Pitch [1988], he exuberantly congratulates himself for having figured this out.) With Slonimsky’s book in hand, one could pile the triads on top of another to produce a twelve-tone chord with triadic subsets.

[40] Superimposed triads. Several twelve-tone chords can be parsed as consisting of triadic subsets, even if they are not emphasized as such through orchestration (Example 10). Webern’s culminating twelve-tone chord in the Orchestral Piece op. 6, no. 5—a chord from 1909, a date preceding the “earliest” chords identified by other authors—results from juxtaposing a seven-note sustained chord in the strings, a four-note chord that emerges from an oscillating ostinato pattern, and a final melodic note in the trumpet. From bottom to top, however, the chord can also be viewed as a collection of contiguous triad types: minor, major, and two augmented. Similarly, Schoenberg’s twelve-tone chord in Die glückliche Hand op. 18, can be understood as a combination of major and minor triads. A later twelve-tone chord by John Weinzweig is analyzed by Catherine Nolan (2011) as involving three minor triads, plus a leftover trichord of prime form (015).⁽²⁸⁾ This last chord perhaps helps explain Slonimsky’s self-congratulatory air: it is a particular mathematical problem to find three non-overlapping triads, the complementary notes of which also form a standard triad type. Much more easily encountered is a set of three non-overlapping triads, with three leftover notes not forming anything triadic.

[41] Superimposed diminished seventh chords. A polychord of three different diminished seventh chords produces a twelve-tone chord.⁽²⁹⁾ Berg’s Wozzeck contains such a triple diminished seventh chord, with constituent chords separated by four semitones (Example 11). The three diminished sevenths enter the texture one at a time, following each other quickly to produce a full twelve-tone amalgam. Berg’s triple diminished seventh chord takes to a new extreme a harmony associated with terror and distress in eighteenth-century opera. In the dissonant twentieth century, perhaps only a maximal superimposition of diminished seventh chords can approach the equivalent effect.

[42] Superimposed quartal subsets. Several twelve-tone chords surveyed contain quartal subsets—trichords of prime form (027), or tetrachords of prime form (0257). This is a variation on the extended quartal and quintal chords seen earlier. Twelve-tone chords with quartal subsets have local, contiguous segments drawn from the circle of 5ths, but the overall chord rearranges those segments to avoid a strict quartal pattern from bottom to top. Works by Berg and Milhaud feature this type of twelve-tone chord (Example 12). The “chord of death” from Berg’s Lulu (Headlam 1996) exhibits this structure. Milhaud, while composing the Orestie d’Eschyle cycle, had a predilection for this type of twelve-tone chord: it appears in both Les choéphores and Les euménides (Homma 1999, 2001; Pearsall 2012). As discussed further below, the twelve-tone chord from Prokofiev’s Symphony no. 2, the primary object that this study seeks to contextualize, is analyzed by Kholopov as containing quartal subsets. This conception of the chord is based on its instrumentation: each group of divided first violins, second violins, and violas plays a three-note quartal segment.

[43] Other superimpositions. Scriabin’s unrealized—or, for Morrison (2002) and Taruskin (2010), unrealizable—sketches for the Acte préalable contain a twelve-tone chord consisting of discrete four-note subsets (Example 13). Taruskin analyzes the chord as two superimposed “French” augmented sixth chords (that is, two dominant seventh ♭5 chords) and one diminished seventh chord. Each augmented sixth draws its pitches from a single whole-tone collection, but the two augmented sixths belong to different collections, so that they do not overlap in terms of pitch-class content. This distinguishes Scriabin’s chord from the Fanelli chord invoked earlier, which consisted of a superimposition of four such chords, all however drawn from the same whole-tone collection.

[44] Pattern by maximal diversity of interval. The all-interval twelve-tone chord has captured the theoretical and compositional imagination since the early 1920s. The chord consists of a particular arrangement of pitch classes such that every interval size (from 1 to 11 semitones) is represented, and all twelve pitch classes appear. The combination of the two criteria limits the range of solutions, as a chord consisting of the eleven vertical intervals will not necessarily contain twelve different pitch classes. A further restriction, often encountered, is induced by the all-interval twelve-tone chord that is inversionally symmetrical—so that an interval of one semitone on the bottom will be balanced by an interval of eleven semitones, its complement, on the top, and so forth.

[45] Fritz Klein’s so-called “mother chord” exhibits this property. Its nickname was apparently suggested by Alban Berg, who used the chord in his Chamber Concerto (1923–25) and the song, “Schliesse mir die Augen beide” (1925) (Homma 1999, 112–13). Not to be outdone, Nicolas Slonimsky—apparently out of feelings of competitive jealousy, having heard Ernst Krenek refer to the chord as “unique”—created the “grandmother chord,” which, like Klein’s chord, is all-interval, twelve-tone, and inversionally symmetrical, but also exhibits an incremental pattern with regard to interval class wedging—outermost intervals are ic1 complements, second-to-outermost intervals are ic2 complements, and so forth (Slonimsky 1988, 176–77). Excited about his finding, Slonimsky included the chord in his Thesaurus (1947) and shared the idea with several composers, including Karl-Birger Blomdahl (see below).⁽³⁰⁾

[46] Pattern based on rearrangable subsets. The problem of theorizing twelve-tone chords leads to the related problem of writing a succession of twelve-tone chords. Since every chord contains every note of the chromatic scale, what would (or should) a succession of such chords entail? Does one string together differently structured chords or similarly structured chords (on the basis of internal interval content)? Surprisingly, this has not received attention in the theoretical literature, perhaps because theorists and composers assumed these chords would be used sparingly or in isolation from other such chords.

[47] Occasionally, however, composers have used multiple twelve-tone chords in succession. One strategy by which consecutive twelve-tone chords have been related is through the use of rearrangable subsets. The subsets, such as those identified in the discussion above, are kept intact internally as they are rearranged as a group. Thus in the case of a twelve-tone chord comprised of four discrete triads, the triads would be reordered, bottom to top, even as the same four triads were retained. In this way, the compositional logic might go, consecutive chords have a connection to one another based on internal content (in this way mirroring the logic of pitch-class set theory, which associates chords and other groups of pitch classes based on internal interval-class content), while also providing some degree of variety.

[48] Blomdahl’s “space opera” Aniara (1959) features this technique in conjunction with Slonimsky’s grandmother chord (Example 14). The opera begins with the chord being arpeggiated up and down, alternately by strings and winds. In Blomdahl’s introduction, the chord is taken apart and reassembled, measure after measure, but always in a way that preserves its spiral symmetry. The rearrangable subsets are the six discrete dyads, each conforming to an interval size with an odd number of semitones. The dyads are arranged in various configurations, so that the space between consecutive dyads always amounts to an even number of semitones, satisfying Slonimsky’s grandmotherly concern of inversional symmetry and all-interval construction.

[49] Milhaud’s Choéphores also features the rearranging technique (Example 15). The twelve-tone chords from this work consist of quartal subsets. Milhaud creates a succession over a period of several measures by redistributing, and at the same time reorchestrating, the same four quartal subsets. In this way, the sound of Milhaud’s twelve-tone chords—its heavy emphasis on quartal components—is retained as the chords themselves shift. This is analogous to the technique of intervallic consistency in twelve-tone row practice. If a row emphasizes certain intervals, then the sounds of those intervals, the compositional argument suggests, will control the sound of the row over all. Likewise, the discrete intervals and subsets will control the sound of a twelve-tone chord.

[50] To summarize, although there are clearly many ways to arrange the twelve pitch classes into a vertical chord, the repertoire presents a certain number of consistencies, which can largely be explained through an understanding of twelve-tone chord writing as a deliberate compositional act. Twelve-tone chords tend to avoid doubling, to have a range of between three and five-and-a-half octaves, and to involve intervallic patterns. These observations reinforce the approach commonly taken in the literature, and taken by Kholopov in particular, to describing twelve-tone chords theoretically—that is, outlining the options for arranging the twelve pitch classes into a chord, and identifying selected examples from the repertoire.

Analysis

[51] Much of the above commentary centers on distinguishing twelve-tone chords from one another, primarily on the basis of internal characteristics. Given that Kholopov introduces twelve-tone chords in the context of an analytical example from Prokofiev’s Symphony no. 2, and given that he invites the reader to complete the analysis of the variation, one might ask how one is to analyze a twelve-tone chord in the context of a specific work. This section explores how a twelve-tone chord can be understood as a culmination of motivic processes in a work or movement—and the ways in which this understanding may be problematic or contradictory. My goal is to contextualize Kholopov’s analytical approach by exploring the difficulties in appealing to unity in understanding twelve-tone chords.

[52] Kholopov’s (2009, 14) brief discussion of twelve-tone chords does not explicitly explain how to analyze them in any given context, but he does relate Prokofiev’s use of them to another technique encountered in other works. He relates Prokofiev’s twelve-tone chords to the final chord of the second movement of Bartók’s Concerto for Orchestra, which acts as a “synthesis” of the intervallic identities offered to each wind instrument. He further specifies Bach’s Well-Tempered Clavier as an additional antecedent, as the final fugue is based on a twelve-tone theme, summarizing the exploration of the full chromatic spectrum that the entire collection undergoes. The idea here is one of culmination. Some musical events can be understood to combine motives or other pitch ideas developed throughout the preceding work. In this sense the Prokofiev twelve-tone chord grows out of earlier motivic and intervallic concerns, as will be discussed below.

[53] Of course the final Bartók chord is not twelve-tone, and the reference to the twelve-tone attribute of Bach’s fugue subject seems a red herring, as the point is not that Bach’s composition relates to twentieth-century twelve-tone technique in any meaningful way, but rather that it involves another illustration of the idea of culmination. It is this very idea of culmination, mentioned in passing in Kholopov’s brief (one-page) chapter and thus not highlighted as a primary concern of the theoretical exposition, that emerges as the hidden theme in Kholopov’s discussion. Each chapter of Garmonicheskiy analiz contains suggestions for “further reading” and “further analysis.” The list of further analytical examples is telling. Kholopov suggests three excerpts for the student who has finished the Prokofiev analysis. The first is Webern’s Orchestral Piece op. 6, no. 5 (1909), mentioned above as containing one of the earliest twelve-tone chords identified (earlier, at least, than the earliest twelve-tone chords identified by Homma, Hába, and Lenormand). This twelve-tone chord appears as a structural culmination, synthesizing three contrapuntal layers, all of which coalesce in the movement’s final measure. Kholopov’s other two excerpts do not even contain twelve-tone chords. The sixth of Roman Ledenyov’s Ten Sketches op. 17 (1967) is a twelve-tone work, based on three partitions of a twelve-tone field. But the twelve pitch classes never sound simultaneously, whether incidentally or as a twelve-tone chord. Rather, the short movement summarizes its layered ostinato materials in a showcase occurring in the final measures, where each ostinato of two to four pitch classes is verticalized into a single chord—in other words, a culminating event.⁽³¹⁾ Kholopov’s third excerpt is given simply as: “S. Slonimsky, Ikar, excerpt,” without specifying where the “excerpt” appears in the ballet. But the first number features a culminating event, when successive pitches a perfect 4th apart enter the texture one at a time, ultimately resulting in a nine-tone quartal harmony. Again the emphasis is on the process of culmination, not the presence of a twelve-tone chord.

[54] So the real point is that Prokofiev’s twelve-tone chord can be understood in its context as a culmination—but a culmination of what? Kholopov parses the chord into four subsets, as mentioned above: three quartal subsets, plus an augmented triad (Example 16). Each subset, so parsed, is performed by a different divisi string group. The emphasis on quartal subsets is reinforced by the winds, which play another six-note chord in approximate contrary motion with the strings, the contrary motion (and alternative slurring) ensuring that they are heard as forming a separate polyphonic layer, and thus not doublings of the twelve-tone chord’s pitches. The winds’ six-note chord is a quartal-subset harmony, consisting of two contiguous segments of strictly stacked perfect 4ths. The overarching emphasis on perfect 4ths, we are told, relates to the motivic perfect 4th in the basses, which oscillates, in the A-major context of the variation, between the pitches A (heard on strong beats) and E (heard as eighth-note pickups).

[55] Kholopov thus highlights the motivic use of certain salient intervals. We might offer a few additional details to adumbrate this interpretation. The A–E perfect 4ths in the bass clearly derive from the bass line of the original theme, which begins with an ascending perfect 4th in the bass line, D–G, using the same rhythm (at a considerably slower tempo). But the second variation opens with a variant of this figure, involving a major 3rd, A–F, that dips down to the flat submediant degree, rather than the dominant. On the other hand, perhaps this major 3rd reinforces the cello subset within the twelve-tone culminating chord, that is, the lowermost augmented triad, made up of major 3rds. Considered in Kholopov’s light, the twelve-tone chord is a sort of psychic projection of the variation’s bass line. Its major 3rds and perfect 4ths pile on top of one another, exhausting the complete pitch-class spectrum.

[56] But Kholopov’s quartal parsing is facilitated by the orchestration. Each instrumental part plays a quartal subset or augmented triad, although no single player within the divisi performs the complete trichord. Heard as a single unit, the twelve-tone chord might be parsed into discrete registral subsets, rather than instrumental-part subsets.⁽³²⁾ The subsets, that is, overlap one another in register. Prokofiev’s chord, read in three-note groupings from bottom to top, consists of four triads: augmented, minor, diminished, major (Example 17).⁽³³⁾ This alternative parsing does not admit explanation by way of a bassline emphasis on perfect 4ths.

[57] The movement is a theme and variations, and an alternative analysis can be advanced by comparing the variation with the original theme on which it is based. This is not the approach in Garmonichesiy analiz, as Kholopov does not provide the score for the theme, but it does offer an alternative understanding. The theme is constructed as a pair of phrases in D minor (or A minor, depending on whom you ask),⁽³⁴⁾ structured as an antecedent–consequent pair (although because the consequent ends on an A-based harmony, the same as the antecedent, it may be best considered a “failed” consequent), itself followed by a short cadential tag that reaffirms D minor through the tonic resolution of a dissonant harmony. The dissonant harmony that begins the tag, shown in Example 18, is the most striking chord in the theme, which is otherwise triadic and locally diatonic. This dissonance contains six different pitch classes, and although its function may be initially obscure, I invite readers to hear the D♭ as an enharmonic C♯ leading tone and imagine an implied A bass for this chord, suggesting its dominant quality. Upper tones move first by step to extended chord members (like Alaleona’s extensions), and then the harmony resolves to D minor.

[58] The second variation reimagines the thematic material quite comprehensively. Now in A major, the variation contains some notable changes, particularly in the realm of phrase structure. The (former) antecedent and consequent have been rent apart, with a new contrasting middle interpolated, so that the variation is now in small ternary form. The cadential tag is subsumed into a coda that begins with a transitional introduction, building swirling momentum that will culminate in, and release onto, the twelve-tone chords under discussion. The tag itself follows a gradually softening peroration as the twelve-tone chords fade out of the texture. It is clear that the twelve-tone chords substitute for the dissonant six-tone chord of the theme. Everything else in this variation is enlarged or intensified: languorous rhythms transformed into bustling sixteenths, period structure torn apart by an interpolated middle. Its climactic dissonance likewise explodes into a hyperdissonance, saturating the chord chromatically with all twelve pitch classes.

[59] This alternative interpretation, of course, does not quite explain why the chord contains twelve pitch classes (instead of ten or eleven), why the twelve-tone layer contains no doublings, or why the contrapuntal six-tone layer exists at all. This is the drawback of an intervallic-motivic approach. Just as the twelve-tone chord contains every note, and thus every combination of notes, so can one relate its contents to other events in the work. But it does suggest ways that we, as listeners, might be primed to interpret the function of the chord, when it arrives.

[60] In sum, although much prior theoretical discussion concerns comparing twelve-tone chords to other possible twelve-tone chords, relatively little discussion centers on interpreting twelve-tone chords within the works in which they appear. Alternative partitionings of these chords might suggest relationships that can be forged with other elements of the work. None of these interpretations necessarily “validates” the chord within that work; rather, it simply suggests how it might be heard. This may be what underlies Kholopov’s association of Prokofiev’s twelve-tone chord with the implicit concept of culmination. The chord results from ongoing processes, and thus its intervallic structure, not only its rhetorical manner of presentation, establish it as the variation’s climactic event.

Twelve-Tone Chords as Twelve-Tone Technique

[61] Kholopov argues that the phenomenon of twelve-tone technique should include more than simply serial dodecaphony. Twelve-tone chords constitute one branch of a diverse array of techniques, all of which involve ordering and manipulating the twelve pitch classes in a deliberate manner. Throughout this essay I have made passing comparisons between twelve-tone chords and twelve-tone rows, mentioning how both involve an ordering of exactly twelve pitch classes without duplications, and how the specific interval content of each (whether horizontal or vertical) controls the resultant sound of the complex. In the final section of this essay, I would like to share some further thoughts regarding the position of twelve-tone chords within twelve-tone theory and composition more generally. Specifically I will argue that twelve-tone technique is a construction that can vary from theorist to theorist (or within the works of a single theorist), and what matters more than what “counts” as twelve-tone technique is to whom a given technique might “count” as twelve-tone.

[62] Martina Homma has advanced two arguments in favor of considering twelve-tone chords an aspect of twelve-tone technique. Her two arguments are worth relaying in turn. First, she argues that the technique of twelve-tone chords ought to stand as a distinct category because it was treated as such historically (Homma 2001). Her research on the earliest theorists and composers to make use of twelve-tone chords attempts to connect them all together into a single causal chain. Her goal is to trace everything back to the “first” theorist to identify twelve-tone chords, Domenico Alaleona.⁽³⁵⁾ Homma attempts to trace the chains of influence, pointing out that Casella and Alaleona taught at the same university in Rome, and that Milhaud and Obukhov were both active in Paris around 1920. She remarks on the particular influence of Klein’s “mother chord,” which Berg used, and Slonimsky’s “grandmother chord,” shared with several composers, including Krenek, Hindemith—and even Prokofiev!

[63] Prokofiev is not mentioned in this connection as a composer who used the twelve-tone chord. According to Slonimsky (1988, 177), Prokofiev is reported to have scrawled in Slonimsky’s visitors’ book, “To the devil with grandmothers! Let us write music!” If Slonimsky’s story is true, it is surely startling, first because (unknown both to Slonimsky, who reported the tale, and to Homma, who transmits it) Prokofiev had indeed written a twelve-tone chord in 1924, fourteen years before Slonimsky’s “discovery” of the grandmother chord (Slonimsky came up with the idea in February 1938, during Prokofiev’s final American tour, the only such tour following his Soviet return), and second because it is a surprisingly worded comment to have come from the composer of Tales of the Old Grandmother (op. 31).

[64] But what is missing from the earliest-known-ancestor approach is the acknowledgment that writing a twelve-tone chord is a really obvious thing to do! One does not need a theorist to show the way. It does not strain credulity to suppose that multiple composers independently wrote chords that included all twelve pitch classes, especially at a time in compositional history when the full aggregate was being deployed in increasingly creative (and self-conscious) ways, and there was increasing pressure on composers to develop new techniques and ideas.⁽³⁶⁾ None of this denies twelve-tone chords from occupying a position within twelve-tone history. The technique need not have been organized or institutionalized in order to be treated as a viable compositional concept.

[65] Homma’s second argument asserts that the twelve-tone chord is the vertical analogue to the horizontal technique of twelve-tone rows (Homma 1999). She ties this explicitly to the positional twelve-tone chords that emerged in the second half of the twentieth century, which she considers a culmination of the incipient twelve-tone-chord technique developed in the first half. The argument proceeds as follows. Twelve-tone rows position the twelve pitch classes in time (that is, in relative temporal order) but not in register. By contrast, twelve-tone chords position the twelve pitch classes in register, but not in time. Each is the counterpart of the other, and they should be considered two complementary aspects of the same conceit.

[66] This argument is convincing, and it explains well how the twelve-tone technique of Lutosławski, Carter, and Lindberg both relates to and departs from traditional Schoenbergian dodecaphony. But positional twelve-tone chords are not the same as the earlier non-positional twelve-tone chords, such as those discussed in this essay. Positional twelve-tone chords, as background structures, need not be stated as chords (that is, with all twelve notes sounding simultaneously), and they do not even require that all twelve pitches appear at any point during their span. Whatever the relationship between positional chords and twelve-tone rows, the argument does not extend to other types of twelve-tone chords.

[67] Kholopov’s approach is different. Rather than associate twelve-tone chords with the twelve-tone rows of serial dodecaphony in particular, he argues that there are several different types of twelve-tone technique, not all of which need be traced back to Schoenberg. In this way, he avoids the necessity to claim the technique of twelve-tone chords, or any other type of twelve-tone technique, as some version of Schoenbergian rows. The Schoenbergian rows, too, are simply one technique of many.

[68] Why did Kholopov take such a broad view of twelve-tone technique? His chronology of Schoenbergian antecedents contains many Russian names—is that the reason? He makes a place in twelve-tone history for a variety of Russian composers, by tracking early developments in referential sonorities (Scriabin) and synthetic chords (Roslavets) that can be transposed to any pitch level, microserial techniques involving transformations of short cells (Stravinsky’s Firebird),⁽³⁷⁾ twelve-tone fields (Golïshev), and early twelve-tone chords (Obukhov, before Prokofiev). I wouldn’t suggest, on this basis, that Kholopov is acting on specifically nationalist impulses (as some may be inclined to argue), but rather it seems likely that, arising as a result of his access to and interest in Russian composition, Kholopov’s exposure to the diverse array of Russian repertoire—in addition to the Western European composers who figure in his chronology, such as Webern, Berg, Klein, Hauer, and several others—would have necessitated a broader historical view of twelve-tone technique beyond the one commonly promulgated in English-language discourse.

[69] During the 1960s, Kholopov was instrumental in elevating Prokofiev’s compositional status to that of a twentieth-century innovator. In several publications, as summarized incisively by Peter Schmelz (2008), Kholopov argued that Prokofiev’s assignment of individual functions to all twelve degrees of the chromatic scale—an explosion beyond the tonic, dominant, and subdominant of nineteenth-century functional harmony—meant that Prokofiev, not Schoenberg, was the true chromatic firebrand of the modernist period.⁽³⁸⁾ Understandable as this kind of advocacy was, a historical narrative that radicalizes as “twelve-tone technique” the many experiments with chromatic musics during the first half of the twentieth century obviously does an injustice to the variety of creative solutions one can find in music of that era. What the treatment of twelve-tone chords can tell us is that the desire to consciously deploy the twelve pitch classes in a systematic manner manifested itself in several types of compositional strategy. Viewing twelve-tone rows, twelve-tone chords, and twelve-step functions as solutions to the same problem of comprehensively organizing the aggregate reveals the underlying concern that not only links Schoenbergian serialism to other compositional techniques, but also contextualizes it as part of a larger enterprise.

[70] The very notion of “twelve-tone technique” is a construction, subject to negotiation by individual authors. From this standpoint, the answer to Kholopov’s question—“Who Invented Twelve-Tone Technique?”—is none other than Kholopov himself, as he “invented” the particular construction that subsumes twelve-tone chords, rows, fields, tropes, and so forth, under a single umbrella. Other writers may construct the term in other ways, but Kholopov defines it in such a way as to diversify the range of meanings twelve-tone composition can have. Prokofiev, like Schoenberg, is one of a large number of composers interested, to varying degrees of systematization, in controlling the twelve pitch classes of the aggregate in a deliberate compositional manner.

Christopher Segall
University of Cincinnati
College-Conservatory of Music
PO Box 210003
Cincinnati OH 45221
segallcr@ucmail.uc.edu

Works Cited

Auner, Joseph H. 1996. “In Schoenberg’s Workshop: Aggregates and Referential Collections in Die glückliche Hand.” Music Theory Spectrum 18 (1): 77–105.

Brown, Stephen C. 2015. “Twelve-Tone Rows and Aggregate Melodies in the Music of Shostakovich.” Journal of Music Theory 59 (2): 191–234.

Cairns, Zachary A. 2012. “Svetlana Kurbatskaya on Serial Music: Twelve Categories of ‘Twelve-Toneness.’” Gamut 5: 99–132.

—————. 2014. “A Glimpse at Iuriĭ Kholopov’s Garmonicheskiĭ analiz.” Music Theory Online 20 (3).

Callender, Clifton. 2007. “Continuous Harmonic Spaces.” Journal of Music Theory 51 (2): 277–332.

Carter, Elliott. 2002. Harmony Book. Edited by Nicholas Hopkins and John F. Link. Carl Fischer.

Hába, Alois. 1927. Neue Harmonielehre des diatonischen, chromatischen Viertel-, Drittel-, Sechstel- und Zwölftel-Tonsystems. Kistner und Siegel.

Headlam, Dave. 1996. The Music of Alban Berg. Yale University Press.

Homma, Martina. 1999. “The Twelve-Tone Chord: Towards a New Definition of Twelve-Tone Music? Considering Early 12-Tone-Chords (Since 1911) and Discussing Theoretical Implications of 12-Tone-Chord-Music by Darius Milhaud, Nicolaj Obuchov and Witold Lutosławski.” In Witold Lutosławski: Człowiek i dzieło w perspektywie kultury muzycznej XX wieku, edited by Jan Astriab, Maciej Jabłoński, and Jan Stęszewski, 109–27. Wydawnictwo Poznańskiego Towarzystwa Przyjaciół Nauk.

—————. 2001. “Domenico Alaleonas accordo dodecafonico (1911) und (s)ein ungelöstes Problem: Musiktheoretische Überlegungen über frühe Zwölftonakkorde.” In Aspetti musicali: Musikhistorische Dimensionen Italiens 1600 bis 2000: Festschrift für Dietrich Kämper zum 65. Geburtstag, edited by Norbert Bolin, Christoph von Blumröder, and Imke Misch, 101–10. Christoph Dohr.

Kholopov, Yuriy. 1962. “O sovremennïkh chertakh garmonii S. Prokof’yeva.” In Chertï stilya S. Prokof’yeva: Sbornik teoreticheskikh statey, edited by L. Berger, 253–311. Sovetskiy kompozitor.

—————. 1967. Sovremennïye chertï garmonii Prokof’yeva. Muzïka.

—————. 1972. “Tvorchestvo Prokof’yeva v sovetskom teoreticheskom muzïkoznanii.” In S. S. Prokof’yev: Stat’i i issledovaniya, edited by Vladimir Blok, 299–332. Muzïka.

—————. 1974. “Ob obshchikh logicheskikh printsipakh sovremennoy garmonii.” In Muzïka i sovremennost’, vol. 8, edited by Dmitriy Frishman, 229–77. Muzïka.

—————. 1979. “Poliakkordika v garmonii S. Prokof’yeva.” In Studia musicologica: Aesthetica, theoretica, historica, edited by Elżbieta Dziębowska, Zofia Helman, Danuta Idaszak, and Adam Neuer, 95–108. Polskie Wydawnictwo Muzyczne.

—————. 1983a. “Kto izobryol 12-tonuvuyu tekhniku?” In Problemï istorii avstro-nemetskoy muzïki: Pervaya tret’ XX veka, 34–58. Gosudarstvennïy muzïkal’no-pedagogicheskiy institut imeni Gnesinïkh.

—————. 1983b. Zadaniya po garmonii. Muzïka.

—————. 1997. “Alemdar Karamanov: An Outsider in Soviet Music.” In Underground Music from the Former USSR, edited by Valeria Tsenova, translated by Romela Kohanovskaya, 110–27. Harwood Academic.

—————. 2005. Garmoniya: Prakticheskiy kurs, vol. 2. 2nd ed. Kompozitor.

—————. 2009. Garmonicheskiy analiz, vol. 3. Moskovskaya konservatoriya.

—————. 2013. “On the System of Stravinsky’s Harmony.” Translated by Philip A. Ewell. Music Theory Online 19 (2).

Klein, Michael L. 1995. “A Theoretical Study of the Late Music of Witold Lutosławski: New Interactions of Pitch, Rhythm, and Form.” PhD diss., State University of New York at Buffalo.

Klochkova, Yelena. 2010. Bibleyskiye simfonii Alemdara Karamanova. Klassika-XXI.

Kohoutek, Ctirad. 1976. Tekhnika kompozitsii v muzïke XX veka. Translated by K. N. Ivanov. Muzïka.

Koivisto, Tiina. 2004. “Syntactical Space and Registral Spacing in Elliott Carter’s Remembrance.” Perspectives of New Music 42 (2): 158–89.

Kurbatskaya, Svetlana. 1996. Seriynaya muzïka: Voprosï istorii, teorii, estetiki. Sfera.

Lenormand, René. 1940. A Study of Twentieth-Century Harmony: A Treatise and Guide for the Student-Composer of To-Day. New ed. Translated by Herbert Autcliffe. B. F. Wood.

Link, John F. 2002. “The Combinatorial Art of Elliott Carter’s Harmony Book.” In Harmony Book, by Elliott Carter, edited by Nicholas Hopkins and John F. Link, 7–22. Carl Fischer.

Martin, Edward Paul. 2005. “Harmonic Progression in the Music of Magnus Lindberg.” DMA diss., University of Illinois at Urbana-Champaign.

Morrison, Simon. 2002. Russian Opera and the Symbolist Movement. University of California Press.

Nice, David. 2003. Prokofiev: From Russia to the West, 1891–1935. Yale University Press.

Nolan, Catherine. 2011. “The First Canadian Serialist.” In Weinzweig: Essays on His Life and Music, edited by John Beckwith and Brian Cherney, 131–50. Wilfrid Laurier University Press.

Pearsall, Edward. 2012. Twentieth-Century Music Theory and Practice. Routledge.

Persichetti, Vincent. 1961. Twentieth-Century Harmony: Creative Aspects and Practice. Norton.

Prokofiev, Sergey. 1998. Selected Letters of Sergei Prokofiev. Translated and edited by Harlow Robinson. Northeastern University Press.

Sallmen, Mark. 2007. “Listening to the Music Itself: Breaking Through the Shell of Elliott Carter’s ‘In Genesis.’” Music Theory Online 13 (3).

Schmelz, Peter J. 2008. “After Prokofiev.” In Sergey Prokofiev and His World, edited by Simon Morrison, 493–529. Princeton University Press.

Slonimsky, Nicolas. 1947. Thesaurus of Scales and Melodic Patterns. Charles Scribner’s Sons.

—————. (1988). Perfect Pitch: A Life Story. Oxford University Press.

Sokolov, Aleksandr. 2007. Muzïkal’naya kompozitsiya XX veka: Dialektika tvorchestva. Kompozitor.

Straus, Joseph N. 2009. Twelve-Tone Music in America. Cambridge University Press.

Stucky, Steven. 1981. Lutosławski and His Music. Cambridge University Press.

Suchoň, Eugen. 1979. Akordika: Od trojzvuku po dvanástzvuk. Opus.

Tarakanov, Mikhail. 1968. Stil’ simfoniy Prokof’yeva. Muzïka.

Taruskin, Richard. 1993. Musorgsky: Eight Essays and an Epilogue. Princeton University Press.

—————. 2010. Music in the Early Twentieth Century. Oxford University Press.

Footnotes

1. This article uses the Russian-to-English transliteration system developed by Gerald Abraham for the New Grove and modified by Richard Taruskin (1993, xix–xx). Exceptions (in the main text) include names familiar to readers in their Anglicized form (Prokofiev, Scriabin, Sergei, Yuri). The list of works cited does not contain these exceptions.
Return to text

2. For a more detailed overview of Yuri Kholopov and his importance to Russian music theory, see Philip Ewell’s commentary (Kholopov 2013, [1.1]).
Return to text

3. Schmelz (2008) summarizes in detail the relevant writings by Kholopov (1962, 1967, 1972), which promote the twelve-step system as a tonal alternative to atonality and dodecaphony.
Return to text

4. In an earlier work, Kholopov (1967, 28) referred to twelve-tone chords as “universal” chords. In English-language scholarship, twelve-tone chords have sometimes been called aggregate harmonies or vertical aggregates.
Return to text

5. This paragraph summarizes several ideas from Kholopov 1983a.
Return to text

6. Prokofiev’s Symphony no. 2 in D minor consists of two movements, a sonata-form first movement followed by a theme and variations. It was Prokofiev himself, in a May 1925 letter to Boris Asafiev, who likened the structure to that of Beethoven’s Piano Sonata in C minor, op. 111 (Prokofiev 1998, 98–99).
Return to text

7. Kholopov argued for Prokofiev’s twelve-step harmonic innovations, contrasting them specifically with Schoenbergian twelve-tone technique, in a series of books and articles published during the 1960s and ‘70s (Kholopov 1962, 1967, 1972). Peter Schmelz (2008) richly contextualizes Kholopov’s writings within the broader context of Soviet theoretical inquiry into contemporary musical technique (in general) and the raising of Prokofiev’s profile as a twentieth-century innovator (in particular).
Return to text

8. Kholopov’s twelve categories are: free atonality, Klangzentrum (“chord center,” after Hermann Erpf, here in reference to Scriabin’s mystic chord), synthetic chords (as in Roslavets), twelve-tone chords, twelve-tone rows (as isolated statements, in the sense of Stephen Brown’s [2015] “aggregate melodies”), twelve-tone fields, tropes (after Hauer), serial technique (not necessarily throughout an entire work), dodecaphony (use of a 12-pitch-class series), microserialism (use of a series of fewer than 12 pitch classes), total serialism, serialism (in the sense of controlling all pitch aspects of a single work). See Cairns (2012) for additional commentary. Cairns discusses Kholopov’s categories of “twelve-toneness” in the context of their presentation in an early chapter of a monograph on serial music by Svetlana Kurbatskaya (1996). Kurbatskaya’s own chronology of twelve-tone developments, which extends up to the present (i.e., the 1990s), excludes Prokofiev’s symphony, and in a brief, perfunctory discussion of twelve-tone chords, she cites only Berg’s Altenberg-Lied op. 4, no. 3, and Webern’s Orchestral Piece op. 6, no. 5, as examples. Although Kurbatskaya recites Kholopov’s twelve categories in an introductory chapter, as a means of acknowledging this previous scholarly work, it should be noted that her book is not otherwise concerned with them. Twelve-tone chords thus do not appear elsewhere in the volume.
Return to text

9. Chapters and sections on twelve-tone chords can be found in three of Kholopov’s books (Kholopov 1983b, 206; 2005, 410–11; 2009, 14–18).
Return to text

10. For a further discussion of Garmonicheskiy analiz—particularly as concerns its aims, its structure, and the range of repertoire covered—see Cairns (2014).
Return to text

11. Kholopov’s excerpt extends beyond mine, to the end of the variation (i.e., another nine measures). My example shows only the string parts; the winds, which play a sixteenth-note figure in counterpoint with the strings, will be addressed further below.
Return to text

12. As Kholopov (1979, 108) points out elsewhere, in every eighth chord—that is, the chords that fall directly on beat 3 and, when the pattern repeats, beat 1—the lowest two cello lines deviate from an otherwise strict transposition of the melody, playing A♭ and C instead of B♭ and D. This, of course, means that every eighth chord is not a twelve-tone chord.
Return to text

13. Treatises by Ctirad Kohoutek (1976) and Eugen Suchoň (1979) likewise outline twelve-tone chords built on various intervals, although they do not explore as many possibilities as Hába.
Return to text

14. As mentioned above, the primary authors to deal with twelve-tone chords are Alaleona (Homma 2001), Hába (1927), Persichetti (1961), Kohoutek (1976), and Suchoň (1979), in addition to Kholopov (1983b, 2005, 2009). Homma (1999, 2001) offers an overview of historical approaches to twelve-tone chords.
Return to text

15. Alaleona was the first to make this point (Homma 2001); see also Taruskin (2010, 225).
Return to text

16. Arnold Schoenberg, in Harmonielehre (1911), also recommends avoiding octave doubling within twelve-tone chords, so as not to make one pitch class sound like a root (Auner 1996, 99).
Return to text

17. Clifton Callender (2007, 318–20) develops equations for measuring a chord’s distinctiveness, or concentrated use of intervals, and thereby qualifies how Carter’s twelve-tone chords sound different from Lutosławski’s.
Return to text

18. Lutosławski’s positional twelve-tone chords are also discussed by Klein (1995, 26–78), Homma (1999), and Callender (2007).
Return to text

19. Carter’s use of positional twelve-tone chords has been written about extensively. Notable studies include Link (2002), Koivisto (2004), Callender (2007), Sallmen (2007), and Straus (2009, 52–54). Carter’s own Harmony Book (2002, 54–76, 358–61) provides a catalogue.
Return to text

20. Lindberg has acknowledged Lutosławski as an influence on his own positional twelve-tone chords (Martin 2005).
Return to text

21. In a twelve-tone field (pole), the twelve pitch classes circulate freely, both vertically and horizontally. Although all twelve pitch classes are available, it is not necessary that they all be present within a given field. A twelve-tone field can thus be incomplete (Kholopov 1983b, 216–18; 2005, 411).
Return to text

22. Both Kholopov (1997, 121) and Klochkova (2010, 141) describe the chord from Karamanov’s Symphony no. 18 as reflecting the series of natural harmonics. In Garmonicheskiy analiz, Kholopov (2009, 14) refers to a twelve-tone chord by Karamanov that has the same structure as that from the Symphony no. 18, but starting on F instead of F♯. No work is cited as the source for this chord.
Return to text

23. Kholopov (2005, 410–11) presents a twelve-tone chord with an exceptional range of less than two octaves, from the fifth of Dmitriy Smirnov’s Six Poems of William Blake (1981), consisting of two six-note whole-tone clusters, the lowest note of the upper cluster one semitone above the highest note of the lower cluster, sustained by a crescendoing organ to represent the roar of the “Tyger.”
Return to text

24. Patterns based on inversional symmetry in pitch space, common in the positional twelve-tone chords of Carter and Lindberg, will not be discussed here.
Return to text

25. It should be mentioned that Lutosławski’s positional twelve-tone chords involve various sorts of patterns—chords based predominantly on 3rds, 4ths, tritones, etc.—as well documented by Stucky (1981).
Return to text

26. Slonimsky’s twelve-tone chord is the result of an accumulative pitch process (Kholopov 1974, 243).
Return to text

27. See Taruskin’s (2010, 195–96) sardonic commentary on the nationalist impulse to identify the “first” twelve-tone chord in the repertoire.
Return to text

28. Weinzweig used additional twelve-tone chords in works throughout his career, including the Piano Concerto (1966) and the Divertimento no. 6 (1972) (Nolan 2011).
Return to text

29. Kohoutek (1976, 49) describes a triple diminished seventh chord, with constituent diminished sevenths separated by two semitones, as a “Bartók chord,” following Ernő Lendvai, who derived from it a particular dissonant harmony, a diminished triad with diminished 8ve (e.g., C♯, E, G, C), as a subset. The full twelve-tone chord, it seems, does not itself appear in Bartók’s music.
Return to text

30. The positional use of all-interval twelve-tone chords is a hallmark of Elliott Carter’s music (Carter 2002, Link 2002, Straus 2009). The “chord” from Schnittke’s Variations on a Chord, it should be mentioned, is also an all-interval positional twelve-tone chord.
Return to text

31. Sokolov (2007, 90–93) provides similar commentary on the work, and verifies, based on a review of the composer’s sketches, that the twelve-tone materials were not conceived as a row.
Return to text

32. A similar situation arises in the second movement of Schnittke’s String Quartet no. 3. In the twelve-tone chord of measures 114–17, each instrument plays a trichord with prime form (016) or (024), and the trichords overlap registrally as with the Prokofiev chord. The difference in Schnittke, however, is that the individual performers play all three notes of each trichord, whereas in Prokofiev, individual performers play only one note within the complete texture.
Return to text

33. Nicolas Slonimsky’s Thesaurus (1947, 178) verifies this specific “solution” of four triads of different quality exhausting the chromatic.
Return to text

34. The symphony as a whole is in D minor. The second movement’s theme uses no key signature, emphasizes A melodically, and does not use a D minor triad until the final measure. Tarakanov (1968, 100–102) hears the theme in D minor, Nice (2003, 213–14) in A minor.
Return to text

35. As pointed out above, Webern’s 1909 twelve-tone chord predates Alaleona’s 1911 article, published in the journal Rivista musicale italiana. (On Alaleona, see Homma 2001.)
Return to text

36. Taruskin (2010, 193–96) ridicules the entire enterprise as “rush-to-the-patent-office modernism.” His derision is aimed not at the musical technique itself, but rather at the historiographical attitude of equating novelty with ingenuity, and the attempt to give primary credit to the earliest known instigator. Even so, in Taruskin’s reading, twelve-tone chords are sometimes put to excessively obvious expressive ends.
Return to text

37. See Kholopov (2013), and the attendant commentary by Philip Ewell, for a more in-depth exploration of “microserialism” in the context of The Firebird.
Return to text

38. Kholopov (1983b, 216) also offered Prokofiev’s “The Rain and the Rainbow,” from Music for Children, op. 65 (1935), as an illustration of the technique of twelve-tone fields, which (as mentioned above) distribute the twelve pitch classes, unordered, vertically and horizontally. The piano piece, in C major with chromatic cluster “raindrops,” uses the black keys only as sound effects, and hardly represents an engagement with twelve-tone technique.
Return to text

Copyright Statement

Copyright © 2018 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.