Sequences: Between Affirmation and Destruction of Tonality
Jan Philipp Sprick
KEYWORDS: sequences, tonality, Riemann, Fétis, Capellen, Weigl, Gjerdingen, schema theory, Funktionstheorie, Satzmodell
ABSTRACT: In the history of music theory, we encounter the paradox that harmonic sequences are simultaneously seen as fundamental, affirmative examples for tonality (Rameau, Sechter, et al.) and as structures that threaten or even destroy cadence-oriented understandings of tonality (Fétis, Riemann, Grabner, et al.). Sprick (2012) has argued that the discussion of sequences around 1900 functioned as a kind of “testing ground” for individual conceptions of tonality. This article goes further in relating historical discourses on the sequence with a contemporary perspective, a study that reveals striking similarities suggesting the sequence remains an important and challenging structural device within the theoretical discourses of tonality.
DOI: 10.30535/mto.24.4.14
Copyright © 2018 Society for Music Theory
[1] The sequence is frequently described as one of the most distinct phenomena of tonal music. In this article, I will examine how thinking about sequences as represented in historical documents of music theory still influences contemporary understandings of the phenomenon. To achieve that goal, I will proceed in a kind of zigzag movement back and forth between historical and contemporary writings. Due to the fact that the sequence is such a self-evident device of tonal harmony, we find theoretical treatments of it in almost every Harmonielehre or music theory textbook. Against this background, however, it is surprising that not many explicit theories of the sequence as an important structural device exist in contemporary music theory.
[2] I will present a selective overview of the relation of historical and contemporary theory on the sequence. The former is represented particularly by Fétis, who conceived of the sequence as a means of suspending tonality and whose theoretical treatment is the first in the history of music theory that discusses the sequence explicitly in combination with the relatively new concept of tonalité. The contemporary theory I will survey includes the few models for the sequence that exist in the theoretical literature, along with writings on schema theory and German Modelltheorie, both of which rely heavily on sequential structures. Both also deal mostly with seventeenth- and eighteenth-century repertoires and therefore with music that was composed long before the theoretical concept of tonalité was developed in the nineteenth century. And both understand themselves as alternatives to traditional theories of tonality, namely Schenkerian theory in the United States and Funktionstheorie in Germanophone countries. Finally, I will discuss some interesting overlaps with respect to the understanding of tonality between schema theory, Modelltheorie, and neo-Riemannian theory.
[3] Substantive commentary on the sequence in contemporary German theory starts with Carl Dahlhaus’ Studies on the Origin of Harmonic Tonality (1990). This seminal publication forms the cornerstone for research on historical sequential models, or Satzmodelle, and their integration into theory and harmony teaching as well as into musical analysis.(1) Dahlhaus’s central argument was that Klangfortschreitungs-Modelle have relatively stable meanings across historical periods and that they are structurally based on a combination of contrapuntal and harmonic principles, a fact that calls root-oriented theories of harmonic tonality into question. This model-oriented approach to tonal harmony was further developed by Dahlhaus’s students and led to a general criticism, following from Hermann Grabner and Wilhelm Mahler, of influential approaches of functional harmony. Within this context of historical music theory, we can observe a variety of didactic approaches for many different music theoretical disciplines such as improvisation, analysis, and ear training.(2) In all these approaches, the sequence plays a crucial role.
[4] Whereas in earlier music theory the individual work was confronted by a “grand theory,” such as Funktionstheorie, Stufentheorie, or Schenkerian analysis, the influence of standard intervallic progressions on tonal works of the whole repertoire now seems to be understood more broadly (Menke 2009, 87). With this understanding, we can see a change that involves departing from a work-oriented perspective of “grand theories” to an approach that focuses on models and conventions. A unifying feature of these approaches is their critique of analytical paradigms such as Funktionstheorie or Stufentheorie for an inability to adequately represent the horizontal-melodic structure of sequences.
[5] Some general and often quoted observations, however, do not seem to support a high status for sequences. Many theorists consider sequences to be a “minor method of construction,” to quote Arnold Schoenberg, who is speaking here as both composer and theorist (1976, 126). This opinion follows from his pejorative view of repetition in comparison to the highly esteemed ideal of motivic-thematic development. A similarly negative image is projected by much earlier writers, as well. Already in 1812, Christian Friedrich Daniel Schubart described the sequence in as an example of “poverty of the mind” in his widely-read text “Von den Rosalien,” which also coined the term “Rosalia” for certain types of sequences.(3) Schubart’s text was the starting point for the nineteenth-century’s generally negative reception of the sequence.
[6] An aesthetic evaluation of sequential repetition, however, is secondary to the role of the sequence within the tonality of the piece. Both can be related, but do not have to be related to each other. Sequences can be and sometimes are used mechanically, and in those cases the disapprobation of Schoenberg and others may be warranted. But sequences can also serve as integral aspects of the harmonic, motivic, and formal content of a piece. In fact, the extremely important structural role of sequences in traditional tonal music can hardly be overestimated. In the second half of the nineteenth century, sequences became even more important because they not only appear in developmental passages but they also start to influence large parts of exposition sections due to their growing importance within the thematic material. Dahlhaus argues that “it would be wrong to dismiss the change in the function of modulatory sequence from a developmental technique to an expositional technique as an event of merely peripheral significance.” He goes so far as to compare the impact of this process with the “chromatization of harmony” (1980, 47).
[7] In recent writings on the sequence, we can readily observe a kind of “rhetoric” of neglect. Richard Bass, for example, states that there is “neither a consistent, established terminology adequate for in-depth analyses of sequential passages nor general agreement as to classification of sequence types, or even about what constitutes a proper sequence” (Bass 1996, 265). In terms of the latter—that is, what constitutes a sequence—Bass is correct in that there is no consistency in the theoretical literature, specifically to the question of whether only one repetition of the sequence unit is sufficient, or whether one needs at least two repetitions. Adam Ricci asserts that it is striking that “so vital a musical device still lacks a suitable and consistent theoretical apparatus” (Ricci 2004, 1). In her recent treatment of the sequence in the Oxford Handbook of Musical Concepts, Naomi Waltham-Smith gives a solid account of the role of the sequence in the history of music theory, especially its role as a testing ground for the individual concepts of tonality, but she also broadens the discussion into the philosophical realm. Influenced by the philosophy of Gilles Deleuze, she advances a notion of the sequence as a “bipolar machine for transforming identity into difference and difference into identity” (Waltham-Smith 2017).
[8] When we return from the heights of poststructural theorizing to the pragmatic discourse of current functional harmony, in Germanophone countries the sequence is largely understood to remain at a place outside harmonic functionality. In his Lexikon der Harmonielehre, for example, Reinhard Amon claims that “the cadence sets a clear caesura, whereas the sequence drives forward. These forces, that are not easy to define, as well as the difficulties that sequences oppose a harmonic analysis, may have led to the fact that they have not obtained the place in music theory that they deserve” (Amon 2005, 230; translation mine). From this, Amon concludes that cadences represent Funktionalität and sequences represent Nichtfunktionalität.
[9] In his Harmonielehre from 1925, the Czech music theorist Bruno Weigl presents a concise summary of a number of important statements about the sequence from about 1850 to the year of the publication of his book. These statements reveal the multifaceted discussion of sequences in the nineteenth and early twentieth century. Sequences can, according to Weigl, highlight certain musical moments and can therefore help one to remember difficult harmonic progressions (Weigl 1925, 79). Following Halm, Kurth, and others, Weigl also mentions the music of Bruckner as an example of the use of “magnificent harmonic” sequences. In this context, he nevertheless cites negative views on the mechanism of sequential repetition. The most important moment in his summary of properties of harmonic sequences, however, is his reference to Fétis’s often cited explanation of tonality within sequential progressions. Fétis’s definition of tonality attempts to clarify vertical and horizontal relationships in tonal music from the seventeenth to the nineteenth centuries. Due to the fact that root position chords in a diatonic sequence appear on every scale step, the constitutive hierarchies for his definition of tonalité are questioned fundamentally by sequential progressions.(4) He therefore explains the role of tonality within a sequential progression as a “halt of the proper harmonic progression” and emphasizes the importance of the melodic progression of the sequence. Still, we have to keep in mind that Fétis differentiates between modulating and non-modulating sequences: a “suspension of tonality” only occurs within non-modulating sequences, because in modulating sequences, every chord could become a new tonic.
[10] Fétis’s explanation, especially his description of the sequence as a melodic phenomenon, is repeated frequently in the course of the twentieth century, long after Weigl’s Harmonielehre. A prominent implicit point of reference for this return is Allen Forte and Steven Gilbert’s notion of the linear intervallic pattern from their 1982 Introduction to Schenkerian Analysis. It is clear that the concept of tonality is completely different in this context, but Fétis’s understanding of the sequence as a melodic—rather than harmonic—event is reflected in it. A Schenkerian understanding of tonality certainly integrates a linear intervallic pattern within tonality and not as something “extratonal.” The sequence in this context is an important device in the process of Auskomponierung: the two pillar chords that frame a sequence can be integrated into the overall tonal structure of the piece. That is to say, they are always in “the service of some musical element of larger scale” (Forte and Gilbert 1982, 84). Sequences or linear intervallic patterns therefore could figure as a “connector of harmonies”: “harmonic importance (if any) resides in where the pattern begins and where it ends.” Another feature reminds us of Fétis’s explanation: a linear intervallic pattern represents a “directed tonal motion with complete precision and without ambiguity
[11] To conceptualize a linear intervallic pattern as a “connector” of structurally more important harmonies resonates surprisingly with some ideas of Hugo Riemann. Riemann deals with sequences in very interesting ways on many occasions in his large theoretical oeuvre. A recurrent element in Riemann’s diverse discussions of the sequence is again Fétis’s definition of the sequence as a primarily melodic phenomenon. Riemann states that the sequence has disturbed theorists for a long time until “Fétis discovered the true character of the sequence as a ‘melodic’ rather than a ‘harmonic’ structure.” (Riemann 1887, 25) What Riemann clearly borrows from Fétis is the notion that in hearing sequences the mind becomes totally absorbed in the contemplation of musical repetition. So absorbed, in fact, that functions, were they perceptible, would be irrelevant.
[12] In his Vereinfachte Harmonielehre Riemann explains sequences in a way somewhat similar to the notion of the sequence as a “connector of harmonies.” Despite his claim that tonal functions “regain their importance” when the sequence ends, he analyzes some sequences completely with functional symbols. Through the course of the chapter, however, Riemann formulates his opinion that it makes no sense to label every tonal function within a sequence. He then offers a compromise: “As the tonal functions are suspended during the imitations of the sequence motive, there can be no object in indicating them; we therefore only give indications for the harmonies of the motive, and just indicate at the first imitation, whether the sequence rises or falls; but for the rest, abbreviate the indications by means of brackets.” (Riemann 1893, 138). This designation reflects the fact that in Riemann’s understanding the functional progression gets suspended within the sequence. Against this background, even Amon’s claim that the functionality within a sequence gets suspended can be connected to Riemann.
[13] From this perspective it is particularly striking that the discussion of sequences in his Vereinfachte Harmonielehre is reduced to the minimum necessary. Riemann certainly shows an awareness of the problems of a functional analysis of sequences. Nevertheless, he seems to have trouble admitting it, because to do so would threaten the systematic coherence of his harmonic system in a fundamental way. The sequence thus becomes an extra-territorial device that threatens his system with some destructive power.
Example 1. Pergolesi, Stabat Meter, beginning, from Riemann’s Große Kompositionslehre
(click to enlarge)
[14] Riemann’s Große Kompositionslehre from 1902/1903 differs significantly in its conceptual design from his systematic treatises. In the ninth chapter of the second volume, “Der polyphone Satz,” under the title “Kontrapunktische Manieren,” he extensively discusses “Ligaturenketten” or “suspension chains” that are—in his words—the foundation of every homophonic conception of music (Riemann 1903, 32). In the preface to that volume, Riemann tries to explain why there was no space for melodic-contrapuntal sequence-models in his purely theoretical works. He states that in his Kompositionslehre he wants to reconcile “thinking musicians” with his earlier treatises (Riemann 1903, VIII). For him, these contrapuntal-sequential models are mainly compositional techniques and therefore not a subject of theoretical exploration. The fact that he incorporates such a variety of sequential models in his composition treatise certainly shows his awareness of them. One particularly prominent example is the beginning of Pergolesi’s Stabat Mater (see Example 1).
[15] In this example, he stresses the free bass line that contradicts the “rigid manner of the model” (38). It seems as if Riemann the “composer” was always well aware of the crucial role of sequential patterns or other kinds of schemata, whereas Riemann the “theorist” faced major problems integrating the sequence into his system of harmonic functions.
[16] If we now take a look at recent publications on schema theory, namely Robert Gjerdingen’s Music in the Galant Style (2007a) and several articles by Vasili Byros (2009; 2012 et al.), we see—in a paradoxical way—resemblances to Riemann’s account of the sequential schemata or Satzmodelle in his Große Kompositionslehre. This is surprising, given that the orientation of Riemann’s theory towards concepts of tonality is fundamentally different from those of Modelltheorie and schema theory. The intersecting point is the fact that Riemann accounts for Satzmodelle or schemata in a context where he does not talk about systematic theory but rather about compositional technique. When it comes to the teaching of composition—which was in Riemann’s case not necessarily contemporary composition—he seems to follow a kind of script-like, or filo-principle.(5) These principles form the basis of an understanding of tonality within schema theory, as well, and within approaches of historically informed music theory in general. They resonate also with Byros’s assertion that “eighteenth-century harmonic schemata functioned as cognitive maps that regulated the cognition and communication of key” (2012, 120). The same is true for the German Satzmodell-discourse, in whose context Ludwig Holtmeier claims that the “rule of the octave is a theory of ‘harmonic functionality’” (2009, 11). With this claim, he raises the status of the figured bass tradition through association with “harmonic functionality,” quite different from Riemann’s dismissal of figured bass as a purely compositional technique without theoretical dignity. It is not easy to pin down the main differences between the concepts of Satzmodell and schema, but it seems reasonable to suggest that Satzmodelle are tonally and semantically indifferent and, in principle, are open to far-reaching transformation and combination, as well as being amenable to various contextualizations and functional ascriptions. A schema, on the other hand, appears to be a tonally-determined network of distinct structural components that constitute a field of flexible relations.(6)
Example 2. Edvard Grieg, Elegie op. 38, no. 6, mm. 15–18
(click to enlarge)
[17] If we move back in history again and consult the theoretical writings of German theorist Georg Capellen—a Riemann contemporary—we encounter a music theorist who offers some radically idiosyncratic views on the sequence. In his book Die Freiheit oder Unfreiheit der Töne und Intervalle (1904), he states his position explicitly when he discusses a simple circle of fifths sequence in a piano piece by Edward Grieg—see Example 2.
[18] Capellen comments on this example as follows:
We have here an example of a tonal sequence, whose nature it is that the absence of a complete equality of the harmonic and melodic development . . . is hidden, due to the persistence of tonality [Tonität] by means of the imitation of the model on the different scale steps. Therefore, one feels a complete symmetry of the progression of sounds and tones, although this is normally only true for strict, which means modulating, sequences. The perception of tonal sequences therefore relies on an acoustic delusion. (Capellen 1904, 52)
[19] This opinion has its origins in Capellen’s overall rejection of the diatonic harmonic system. Proceeding from views guided by a negative reaction to harmonic dualism, he regards major chords as representing the normal chord type and minor chords as structurally less important. Against this background, real sequences represent the normal type of progression because of the sequential repetition of the same major chords. Since this is not the case within the tonal sequence, where different chord types follow one another, Capellen sees the sequence as corroborating his overall view on harmony and harmonic systems. Regardless of whether we are convinced by his argument of the “acoustic delusion” within tonal sequences, his discussion brings to the fore the important antagonism between tonal and real sequences in music of the nineteenth century, especially in the music of Wagner and Bruckner (certainly also in earlier music by Schubert, Schumann, and Chopin). But there is yet another aspect to Capellen’s theory, one that connects it with later developments: a “tonic-free” understanding of Verwandtschaft forms the basis for his symmetrical understanding of sequences, and it is against this background that real sequences figure as the “normal” progression. Capellen’s thinking thus connects with some general aspects of neo-Riemannian theory and serves to bring our own discussion back to contemporary music-theoretical thinking.
[20] It is quite striking that Richard Cohn takes Fétis’s explanation of sequences and his understanding of sequential progression as suspension of tonality as a point of reference in the first chapter of his book Audacious Euphony. Whether Cohn is quoting Fétis just for historical reference, or whether he takes Fétis’s thinking as a true starting point for his own understanding of tonality, is not quite clear. “It is evident,” Cohn writes, that “Fétis conceives of classical tonality (‘transitonality’) as a category whose constituent elements are not integral ‘pieces’—compositions or complete movements—but rather musical moments” (Cohn 2012, 10). In Fétis’s view, Cohn continues to explain, “the faculty of (transi)tonal listening is capable of spontaneous suspension and reengagement without notice of fuss, like a carpenter exchanging a screwdriver for a hammer.” Also in a purely diatonic environment, when a sequence arises midphrase, “the ‘law of tonality’ is placed in abeyance, as our cognition is submitted to a ‘law of uniformity’.” Finally, Cohn quotes Fétis and seems to agree with him: “The mind, absorbed in the contemplation of the progressive series, momentarily loses the feeling of tonality, and regains it only at the final cadence, where the normal order is reestablished” (Cohn 2012, 10).(7) This approach has to do with the understanding of tonality in neo-Riemannian theory. Tonality does not function in the sense that every chord is measured in its relation to an existing tonic, as in Funktionstheorie. It is rather the case that neo-Riemannian theory primarily models chord progressions based on Riemann’s system of Schritte and Wechsel and not necessarily in relation to a tonic. It is clear that the boundaries between Funktionstheorie and neo-Riemannian theory are fluid, but it is also clear that the fundamental differences between these two theoretical approaches lie especially in their different understanding of tonality. Whereas the sequence figures as a challenge for a tonic-oriented understanding of tonality, it can be very well integrated into the graphic representation and the analytical procedures of neo-Riemannian theory.
[21] Cohn further mentions Ernst Kurth’s discussion of sequences in Romantische Harmonik und ihre Krise in Wagners ‘Tristan’ (1920), where Kurth “discovered an agent of tonal disruption in chromatic sequences, which, like Fétis’s’s diatonic ones, are governed by the logic of repetition” (quoted in Cohn 2012, 10). Cohn describes these kinds of progressions as “extratonal” in the sense that their relation to the tonal pillars that bound them on either side “is not tonally determined” (2012, 10). In this respect, Fétis’s understanding of suspension is turned upside down, because in Fétis’ theory, it was the diatonic sequence that was responsible for the “suspension of tonality.”
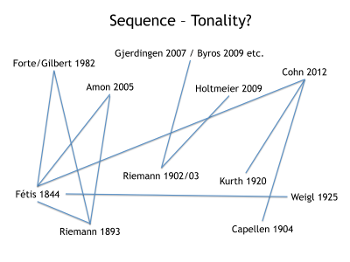
Example 3. Network of Discourses
(click to enlarge)
[22] As a result of these case studies we can construct a preliminary network of discourses around the question of sequences and tonality (see Example 3). This network could well be enlarged to include a number of other authors and theoretical aspects, but it illustrates concisely the general connections among the several authors and their arguments.
[23] On a broader methodological level, the kind of discourse analysis employed in this article can be valuable in order to retrace the way certain concepts—in this case Fétis’s problematic or at least insufficient explanation of tonality within sequential progressions—can persist and sometimes tacitly influence thinking over a long period. Let me summarize some aspects:
[23.1] We find an expanded notion of sequences in schema theory and within the German Satzmodell-discourse. In these theoretical approaches we normally encounter an understanding of tonality that is—like Gjerdingen’s filo-concept—not oriented towards functional coherence but rather is based on the succession of single events. A similar approach can be found in Riemann’s Große Kompositionslehre, where the use of contrapuntal Satzmodelle or schemata was not brought under the umbrella of a systematic theory, but rather treated as a means of learning to compose.
[23.2] Neo-Riemannian theory takes Fétis’s notion of the suspension of tonality in sequential progressions as a general point of departure, in order to theoretically explain and to visually represent what happens within a certain sequential or non-sequential progressions. This connects the neo-Riemannian understanding of sequences in a paradoxical way to notions of functional harmony, where it is still claimed—as the example by Amon showed—that within sequential progressions, functional logic is abrogated. This example shows again that the reference to Fétis’s thesis of the “suspension of tonality” is very typical.
[23.3] In hierarchical approaches, such as Schenkerian theory, sequences or linear intervallic patterns are viewed as structural features that are located on a foreground or middleground level, but could also govern larger structural portions of a piece. In this context, sequences can even function as affirmative devices of tonality, since they are responsible for the linear connection of two chords that are part of the overall tonal structure. Especially from a Schenkerian perspective on tonality, frequent reference in the literature to Fétis’s explanation of tonality would seem to miss the point.
[24] This by no means complete overview shows that the sequence is still an important aspect of actual discourses on tonality, although it is often thematized in an implicit way. But it is striking how many similarities we can find in comparing the discourses of the nineteenth and early twentieth century, even if the individual solutions are quite different. With respect to current music theoretical thinking, sequences play an important role in very different theoretical approaches such as schema theory or Modelltheorie and neo-Riemannian theory, but it is also very clear that these theoretical approaches do not put forward an emphatic understanding of tonality whose main aspect is to model and understand the relation of every chord to an underlying tonic; rather, they represent an understanding of tonality whose main focus is to model and understand chord progressions. Tonal coherence can therefore also be achieved by sequential repetition. In this respect, the sequence remains a musical device whose explanation can show in nuce the specific understanding of tonality in different theories.
Jan Philipp Sprick
Hochschule für Musik und Theater Hamburg
jan.sprick@hfmt-hamburg.de
Works Cited
Aerts, Hans. 2007. “‘Modell’ und ‘Topos’ in der deutschsprachigen Musiktheorie seit Riemann.” Zeitschrift der Gesellschaft für Musiktheorie 4 (1–2): 143–58.
Amon, Reinhard. 2005. Lexikon der Harmonielehre. Doblinger.
Bass, Richard. 1996. “From Gretchen to Tristan: The Changing Role of Harmonic Sequences in the Nineteenth Century.” 19th-Century Music 19 (3): 263–85.
Byros, Vasili. 2009. “Towards an ‘Archaeology’ of Hearing: Schemata and Eighteenth-Century Consciousness.” Musica Humana 1 (2): 235–306.
—————. 2012. “Unearthing the Past: Theory and Archeology in Robert Gjerdingen’s Music in the Galant Style.” Music Analysis 31 (1): 112–24.
Capellen, Georg. 1904. Die Freiheit oder Unfreiheit der Töne und Intervalle. Kahnt.
Cohn, Richard. 2012. Audacious Euphony: Chromaticism and the Triad’s Second Nature. Oxford University Press.
Dahlhaus, Carl. 1980. Between Romanticism and Modernism. Four Studies in the Music of the Later Nineteenth Century. Trans. by Mary Whittall. University of California Press.
Dahlhaus, Carl. 1990. Studies on the Origin of Harmonic Tonality. Trans. by Robert O. Gjerdingen. Princeton University Press.
Fétis, François-Joseph. 2008. Complete Treatise on the Theory and Practice of Harmony. Trans. Peter Landey. Pendragon Press.
Fladt, Hartmut. 2005a. “Modell und Topos im musiktheoretischen Diskurs. Systematiken/Anregungen.” Musiktheorie 20 (4): 343–69.
—————. 2005b. “Satztechnische Topoi.” Zeitschrift der Gesellschaft für Musiktheorie 2 (2–3): 189–96.
Forte, Allen, and Steven E. Gilbert. 1982. Introduction to Schenkerian Analysis. W. W. Norton.
Gjerdingen, Robert O. 2007a. Music in the Galant Style. Oxford University Press.
—————. 2007b. “Partimento, que me veux-tu?” Journal of Music Theory 51 (1): 85–135.
—————. 2011. “Gebrauchs-Formulas.” Music Theory Spectrum 33 (2): 191–99.
Holtmeier, Ludwig. 2009. “Zum Tonalitätsbegriff der Oktavregel.” In Systeme der Musiktheorie, ed. by Clemens Kühn and John Leigh, 7–19. Sandstein.
Jeßulat, Ariane. 2001. Die Frage als musikalischer Topos. Studien zur Motivbildung in der Musik des 19. Jahrhunderts. Studio-Verlag.
Kaiser, Ulrich. 1998. Gehörbildung: Satzlehre—Improvisation—Höranalyse. Bärenreiter.
—————. 2007a. Die Notenbücher der Mozarts als Grundlage der Analyse von W. A. Mozarts Kompositionen 1761–1767. Bärenreiter.
—————. 2007b. “Was ist ein musikalisches Modell?” Zeitschrift der Gesellschaft für Musiktheorie 4 (3): 275–89.
Kurth, Ernst. 1920. Romantische Harmonik und ihre Krise in Wagners ‘Tristan.’ P. Haupt.
Menke, Johannes. 2009. “Historisch-systematische Überlegungen zur Sequenz seit 1600.” In Passagen. Theorien des Übergangs in Musik und anderen Kunstformen, ed. by Christian Utz and Martin Zenck (musik.theorien der gegenwart 3), 87–111. Pfau Verlag.
Möllers, Christian. 1989. “Analyse durch Improvisation. Chaconnebässe der Barockzeit als Improvisationsmodelle.” Üben und Musizieren 6: 73–86.
Moreno, Jairo. 2000. “Challenging Views of Sequential Repetition: From ‘Satzlehre’ to ‘Melodielehre.’” Journal of Music Theory 44: 127–69.
Preuss, Volkhardt. 1991. “Die Anwendung der Clausellehre des 17. Jahrhunderts im Theorieunterricht.” Unpublished manuscript.
Ricci, Adam. 2004. “A Theory of the Harmonic Sequence.” PhD dissertation, University of Rochester.
Riemann, Hugo. 1887. Systematische Modulationslehre als Grundlage der Musikalischen Formenlehre. No publisher.
—————. 1893. Vereinfachte Harmonielehre oder die Lehre von den tonalen Funktionen der Akkorde. English translation published as Harmony Simplified, 1895. Augener.
—————. 1903. Große Kompositionslehre, II. Band: Der polyphone Satz. Berlin/Stuttgart.
Schoenberg, Arnold. 1976. “Kriterien für die Bewertung von Musik.” In Stil und Gedanke: Aufsätze zur Musik, ed. by Ivan Vojtech. Fischer, 123–33. S. Fischer Verlage.
Schubart, Christian Friedrich Daniel. 1812. “Von der Rosalien.” In Vermischte Schriften I, Zürich, 220–27. Nabu Press.
Schwab-Felisch, Oliver. 2007. “Umriss eines allgemeinen Begriffs des musikalischen Satzmodells.” Zeitschrift der Gesellschaft für Musiktheorie 4 (3): 291–304.
Sprick, Jan Philipp. 2012. Die Sequenz in der deutschen Musiktheorie um 1900. Olms.
—————. 2014. “Schema, Satzmodell and Topos: Reflections on Terminology.” Music Theory & Analysis 1 (1 & 2): 102–107.
Waltham-Smith, Naomi. 2017. “Sequence.” In The Oxford Handbook of Critical Concepts in Music Theory, ed. by Alexander Rehding and Steven Rings. Oxford University Press. Online publication, 2015.
Weigl, Bruno. 1925. Harmonielehre. Schott.
Footnotes
1. As exemplars, see Kaiser 1998; 2007a; 2007b; Schwab-Felisch 2007. For a detailed description of this development, see Aerts 2007. In the United States, where research in the history of theory did not have as much influence on theory teaching as in Europe, there nevertheless exist historically oriented approaches, the most important being Robert O. Gjerdingen’s work on “schema” theory (Gjerdingen 2007a; 2007b; 2011).
Return to text
2. On improvisation, see Möllers 1989 and Preuss 1991. On Satzmodelle, see Kaiser 1998. Hartmut Fladt (2005a; 2005b) and Ariane Jeßulat (2001) broaden this primarily structurally oriented understanding of models with their integration of the concept of Topos and therefore a semantic level.
Return to text
3. Schubart 1812, 223. For more information on Schubart, see Sprick 2012; Moreno 2000, 133ff.
Return to text
4. Fétis 1844, 253: “Il y a de ces progressions qui modulent à chaque mouvement: il en est d’autres qui ne modulent pas. Dans ces dernières, l’esprit suspend toute idée de tonalité et de conclusion jusqu’à la cadence finale, en sorte que les degrés de la gamme perdent leur caractère tonal, l’oreille n’étant préoccupée que de l’analogie du mouvement.”
Return to text
5. For Gjerdingen’s understanding of the filo-principle, see Gjerdingen 2007a, 369.
Return to text
6. Sprick 2014 provides a more detailed discussion of the differences between schema theory and Modelltheorie.
Return to text
7. Cohn quotes Fétis’s Traité from the translation by Peter Landey (2008, 27).
Return to text
Copyright Statement
Copyright © 2018 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Sam Reenan, Editorial Assistant
Number of visits:
8209