Guide-Tone Space: Navigating Voice-Leading Syntax in Tonal Jazz
Sean R. Smither
KEYWORDS: jazz, harmony, transformational theory, Neo-Riemannian theory, guide tones, double syntax, voice leading
ABSTRACT: This article develops a transformational space based on the concept of guide tones. In jazz pedagogy, guide tones are the chordal third and seventh and are often used to connect consecutive chords through efficient voice leading. Transformational representations of guide-tone syntax illustrate how guide tones provide a pathway for listeners and improvisers to seamlessly traverse the tonally complex harmonic progressions often found in jazz compositions.
DOI: 10.30535/mto.25.2.4
Copyright © 2019 Society for Music Theory
Example 1. Lead sheet showing the chord changes and melody to “Tune Up” (Miles Davis)
(click to enlarge)
Example 2. Smooth guide-tone voice leading in “Tune Up”; ties indicate common tones
(click to enlarge)
[0.1] Consider the chord changes of Miles Davis’s “Tune Up,” (Example 1(1)) a 16-measure tune(2) that contains several ii–V–I progressions in various keys. Efficient voice leading between chordal thirds and sevenths connects nearly every chord in the progression (see Example 2); the notes involved in this voice leading are familiar to many jazz musicians as guide tones.(3) The concept of guide tones originates in jazz pedagogy, where such tones form melodic skeletons called guide-tone lines; guide-tone lines may be used by improvisers to smoothly navigate from one chord to the next.(4)
[0.2] In this article, I examine guide-tone voice leading using tools from Lewinian and neo-Riemannian transformational theories, beginning with an overview of the concept of guide tones as they appear in jazz pedagogy, followed by exploration of some affinities between the voice-leading properties of guide-tone dyads and consonant triads. From these affinities, neo-Riemannian theory suggests a methodology for engaging guide-tone voice leading as a kind of syntax. The term “syntax” is adopted from Cohn (2012) and means the “ordering of events as they sequentially unfold in time” (13). An informal use of the concept here offers a way to discuss the relationships between sequentially-related pitches and pitch sets. In order to more closely examine guide-tone syntax, I develop a transformational space based on various voice-leading transformations between guide-tone dyads, demonstrate that space’s utility in modeling jazz chord changes, and propose a few ways guide-tone syntax interacts with tonal syntax in order to achieve a sense of seamlessness amidst tonal complexity.
[0.3] Before we begin, it will be useful to unpack the notion of “tonal jazz,” the repertoire with which I am principally concerned in this essay. For Henry Martin (1980), the tonal jazz repertoire includes “the New Orleans and Chicago styles, swing, bop, hard bop, gospel jazz, and blues” and is defined at least in part by the frequent use of the seventh chord as a basic sonority (9). James McGowan (2005) divides tonal jazz into two eras, “Traditional and Modern, with the advent of the latter heralded by the birth of the Bebop style in the 1940s” (4). These broad definitions speak to the prevalence of tonal jazz within the jazz repertoire generally and suggest that the term might be better understood in contrast to what is not typically included. Both McGowan (2005) and McClimon (2017) note that modal and free jazz do not fall under the category, while Waters (2016) and Martin (1980) stress the tonal ambiguity presented by many postbop compositions. It should be noted that the use of the term “tonal” here may be misleading, since many types of so-called modal jazz and postbop both frequently feature some kind of centricity (albeit sometimes ambiguously.)(5) The present study focuses primarily on compositions associated with bebop and hard bop styles, with the prevalence of seventh chords (with or without tertian extensions) constituting an important prerequisite. Since the technologies developed below model relations between chordal thirds and sevenths, any repertoire that takes the seventh chord as its basic sonority may be examined through this lens.
[0.4] Despite the increasing number of transformational approaches to jazz harmony in recent years, theorists have struggled to determine what the primary harmonic object, and therefore the transformational object family, of jazz ought to be. In his article “Wayne Shorter’s Yes and No: An Analysis,” Steven Strunk articulated the difficulty of selecting a paradigmatic chord type for a neo-Riemannian approach to jazz harmony, writing that
in jazz, the degree to which a chord is extended is variable and is determined on an ad hoc basis by the pianist (or whoever is playing the chords). Thus, for example, a major ninth chord, a major seventh chord, and a major triad (all on the same root) are normally functionally interchangeable in a jazz context (Strunk 2003, 48).
Strunk argues that the seventh chord is a practical compromise since triads are seldom found in jazz and ninth chords are awkward to display on a Tonnetz. He also notes that such a choice corroborates the practice of many jazz lead sheets, which represent most chords as seventh chords. Strunk models these seventh chords as parallelograms on the familiar neo-Riemannian Tonnetz.(6) Keith Waters and J. Kent Williams (2010) expand on Strunk’s approach by situating both seventh and ninth chords in diatonic, acoustic, hexatonic, and octatonic collections, eventually arriving at a three-dimensional Tonnetz able to model the syntactic innovations of many post-1960 jazz compositions. Conversely, Michael McClimon argues that, because of the common omission or alteration of the chordal fifth, a trichord consisting of root, third, and seventh is sufficient for modeling much of jazz harmony, arriving at a transformational space defined by transformations between these trichords.(7) When focusing primarily on smooth voice leading, however, the chordal root becomes less important. While chordal thirds and sevenths are seldom substituted and are indeed the tones most frequently involved in voice leading, the voice in which the chordal root sounds progresses smoothly to the next chordal root only some of the time. For these and other reasons discussed below, jazz pedagogy often places emphasis on guide tones as the principal tones of voice leading. Taking guide tones as a basis, I argue for a transformational approach to jazz where the primary harmonic object is the guide-tone dyad. This change of focus affords many insights not otherwise possible.
1. Guide-Tone Theory in Jazz Pedagogy
[1.1] Most jazz theory textbooks contain some explanation of guide tones.(8) Because only minor discrepancies arise between authors, I refer to the body of ideas in this literature as “guide-tone theory.” Barrie Nettles’s textbooks for Berklee College of Music’s harmony courses contain some of the earliest references to guide tones. According to Nettles, guide tones are “essential chord tones” that form guide-tone lines, “single lines which are developed by the voice leading of the essential chord tones and guide the listener through the chord progression” (Nettles 1987, 26). Two notable features can be gleaned from Nettles’s description: (1) Guide tones are the most essential chord tones, and (2) they allow for smooth voice leading between chords.
[1.2] The term “essential” in Nettles’s description may require some explanation. In jazz, harmonies are typically represented by chord symbols that specify a particular seventh chord, possibly with added tensions.(9) When chords are played by an accompaniment instrument such as the piano or guitar, tensions are usually considered variable: for instance, a chordal ninth may be raised, lowered, or omitted. Chordal fifths are likewise flexible and, except in the case of a half-diminished chord, do not distinguish chord qualities from one another (see Martin 1980, 9). For this reason, only the root, third, and seventh are considered essential: they may not be substituted because any alterations would fundamentally change the identity of the chord.(10)
Example 3a. Voice leading between thirds and sevenths in a fifths progression
(click to enlarge)
Example 3b. Voice leading when tritone substitutes replace chords in the progression from Example 3a
(click to enlarge)
[1.3] While the root, third, and seventh are all essential, only the third and seventh typically participate in smooth voice leading.(11) Mark Levine, for instance, notes that, in a ii–V–I progression, “the 7th of each chord resolves down a half step and becomes the 3rd of the next chord” (Levine 1995, 22).(12) This voice leading phenomenon is found not only in ii–V–I progressions but in all diatonic progressions involving falling-fifth root motion (see Example 3a). A common variant of this root motion is the tritone substitute, whereby a given chord is replaced by the dominant seventh chord a tritone away.(13) Tritone substitutes usually share some or all of the same guide tones as the chords they replace, preserving the smooth voice leading through the progression.(14) Example 3b shows guide-tone voice leading through a circle-of-fifths progression where a tritone substitute,
[1.4] The presence of guide-tone theory in so many pedagogical works attests to its intuitiveness to jazz musicians and pedagogues. Likewise, its proliferation as a pedagogical tool has facilitated its reception both intellectually and in musical practice: students who are trained to think of guide tones as essential and practice playing and/or hearing guide-tone lines develop an understanding of jazz harmony and voice leading undergirded by guide-tone theory.
[1.5] In many descriptions, the two principal features of guide tones, chord identity and voice-leading frugality, symbiotically reinforce one another. For instance, Nettles and Graf (1997) define guide tones in their glossary as “[t]he essence of a chord progression distilled from the voice-leading of each chord’s basic sound” (178). Likewise, Sarath (2010) claims that guide tones “are the essential tones defining harmonic movement” (334). In these descriptions, the essential status of guide tones is imparted partially through the fact they participate in smooth voice leading. As we will see, the relationship between these two principal features helps guide-tone dyads to establish a kind of syntax.
[1.6] In this study I work not with single guide tones but instead with guide-tone dyads, which are comprised of both the third and seventh of any given chord. Guide-tone dyads may span either a perfect fifth/fourth (ic5) or a tritone (ic6). When taken as harmonic objects, the set-theoretical properties of guide-tone dyads, set classes [05] and [06], have many affinities with the consonant triad, set class [037]. [05] and [037] are both minimal perturbations of maximally even sets in mod 12 chromatic space and are themselves maximally even in mod 7 diatonic space, while [06] is maximally even in both chromatic and diatonic spaces. These properties allow parsimonious voice leading to generate one member of [037] from another (that is, a stepwise motion in one voice of a consonant triad can generate a different consonant triad). Despite the fact that the two kinds of guide-tone dyads belong to two different set classes, a similar property exists: smooth voice leading from [05] can generate other members of [05], as well as members of [06]. In this sense, [05] and [06] function similarly to the two modes of the consonant triad: just as certain neo-Riemannian operations preserve or reverse mode, certain transformations preserve or reverse dyad type. As Cohn (2012) argues, this property allows the consonant triad to establish a “pan-triadic” syntax, which, unlike diatonic syntax, is based on voice leading rather than on relation to a tonal center (xiv). Similar claims can be made for the syntax of guide-tone dyads, which produce their own syntactic norms through the routine use of a handful of smooth voice-leading transformations. The relationship of guide-tone syntax to diatonic syntax, however, is often rather ambiguous due to the types of transformations that relate dyads as well as their harmonic status as subsets of complete chords. A more thorough examination of the parallels between guide-tone and pan-triadic syntax is undertaken in section 4.
[1.7] In many tunes, guide-tone lines support an impression of seamlessness as they provide a means of traversing tonal space through efficient voice leading. Depicting guide-tone voice leading as a transformational space allows us to visualize more clearly these voice-leading relationships and the melodic paths that they afford listeners and improvisers. One of the benefits of transformational spaces is their comprehensive nature, as one can easily visualize the entire gamut of transformations afforded by the space. By taking guide-tone dyads as our transformational object-family and formalizing a transformation-family to relate those objects, we can investigate the possibilities afforded by guide-tone voice-leading syntax in jazz.(15) In the section that follows, I formalize this transformational space.
2. Guide-Tone (GT) Space: Definitions and Preliminaries
Example 4. Guide tone dyads in various seventh chord qualities
(click to enlarge)
[2.1] A guide tone (gt) is a pitch class (pc), either the third or seventh of a given seventh chord. Guide-tone dyads (gt dyads) comprise both the third and seventh of a given seventh chord.(16) Gt dyads may be of two types, a perfect fourth/fifth (ic5) or a tritone (ic6). Ic5 gt dyads, which I will call “5-dyads,” are found in major seventh (∆7), minor seventh (-7), half-diminished (-7
[2.2] Gt dyads are presented as an ordered pair X = (x1, x2), where x1 is the third of a chord and x2 is the seventh of the same chord.(18) All calculations are performed mod 12. The following sets are used in subsequent formalizations of transformations:
S1 (5-dyads) = collection of all ordered pairs of pcs \((x_1, x_2)\) such that \(x_2 - x_1 = 5\) or 7
S2 (6-dyads) = collection of all ordered pairs of pcs \((x_1, x_2)\) such that \(x_2 - x_1 = 6\)
Throughout, this article is concerned with idealized voice leading between gt dyads.(19) The probability that idealized voice leading between gt dyads may be experientially salient can be determined by the extent to which voice leading is smooth. According to Joseph Straus (2003) voice-leading smoothness between two sets, X and Y, may be measured by determining “the total displacement, the sum of the intervals traversed by each note from its origin in X to its destination in Y” (320, emphasis in original). Throughout this article, gt voice leading is defined as smooth if the distance each gt travels in pc space individually does not exceed 2 semitones (a diatonic step) and the total voice-leading displacement in pc space between two gt dyads does not exceed 4 semitones. Transformations that feature lower total displacement values are considered to be smoother than those with higher ones, requiring less voice-leading work to be enacted.
Example 5. An excerpt of the ic1/ic5 gt Tonnetz, the grid underlying gt space
(click to enlarge)
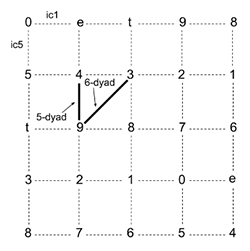
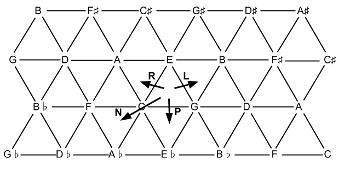
[2.3] Voice leading between gt dyads may be understood as transformations between objects in gt space. The grid of relationships that defines this space is an ic1/ic5 Tonnetz (shown in Example 5), generated by an ic1 x-axis and an ic5 y-axis.(20) It is worth briefly dwelling on the kind of space the gt Tonnetz depicts. While gts function as chord members in harmonies that participate in tonal hierarchies, their voice leading is not limited to diatonic space. It is my contention that gts function in two distinct roles in jazz (an argument which is taken up in more detail in section 4). On the one hand, they are chordal thirds and sevenths and may therefore serve as unstable tendency tones. On the other hand, any given gt dyad is able to progress smoothly to a large number of other gt dyads in mod 12 chromatic pitch-class space. Gt voice leading is therefore useful in providing a sense of fluid movement between key areas, or a sense of directed motion when traveling in diatonic space. This dual role of gts influences the visual orientation of the gt Tonnetz. As Brown (2003) argues, the orientation of a dual-interval space ought to reflect how we might visually conceptualize the music, especially with regard to our associations with Western musical notation of “the y-axis with the ‘vertical’ or harmonic dimension in music, and the x-axis with the ‘horizontal’ or melodic dimension” (37).(21) In this case, I have represented descending gt motion on the ic1 x-axis from left to right. This is because gt voice leading most frequently occurs in descending fifths progressions, which feature descending gt voice-leading motion (see Example 3). Because Western notation associates progression through time with rightward movement on the x-axis, the Tonnetz is constructed so that descending guide-tone motion through time involves rightward movement across the space.(22) Additionally, I have opted to represent 5-dyads as a perfect fifth rather than as the smaller, five-semitone perfect fourth because the interval between the third and seventh, when written in root position (as in Example 4) appears as a vertical perfect fifth. When mod 12 is applied to the Tonnetz, it wraps around itself and forms a three-dimensional Tonnetz in the shape of a torus. The three-dimensional form of this Tonnetz is usually not of any analytical relevance, but certain points of overlap that may facilitate a more succinct representation of a given gt space may be utilized when analytically appropriate.
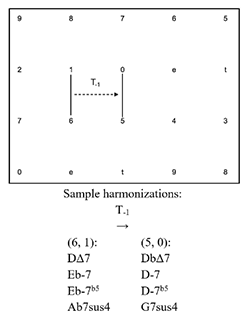
[2.4] 5-dyads are represented as vertical line segments between two adjacent pc vertices on the Tonnetz. 6-dyads are represented as diagonal line segments extending from southwest to northeast between two diagonally adjacent pc vertices in the Tonnetz. Musical transformations between gt dyads may be visualized as geometrical transformations on the two-dimensional Tonnetz grid.(23) The most familiar of these is the transposition operation, Tn, formalized below.(24) The Tonnetz representation of the Tn operation is shown in Examples 6a and 6b, where gt dyads are translated left or right along the x-axis. Sample harmonizations of each dyad involved in the transformation are shown beneath each of the examples. It is worth emphasizing that, in each case, any chord in the left column may progress to any chord in the right column (or vice versa) and preserve the smooth guide-tone voice leading illustrated in the example. Following the constraints developed above (gt motion may not exceed ic2, total displacement may not exceed 4), only four values are used for n of Tn throughout this article: 2, 1, -1, and -2.(25)
If \(X = (x_1, x_2) \in S1\), then \(T_n(X) = Y\), where \(Y = (y_1, y_2) = (x_1 + n, x_2 + n) \in S1\)
If \(X = (x_1, x_2) \in S2\), then \(T_n(X) = Y\), where \(Y = (y_1, y_2) = (x_1 + n, x_2 + n) \in S2\)
Example 6a. Tn operation on 5-dyads, where n = -1 (click to enlarge) | Example 6b. Tn operation on 6-dyads, where n = -1 (click to enlarge) |
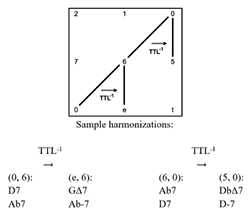
Example 7. TTR and TTL operations and their inverses modeled on the gt Tonnetz
(click to enlarge)
Example 8. 6-dyads (0, 6) and (6, 0) may lead to different 5-dyads using the same (TTL-1) operation
(click to enlarge)
Example 9. Rt transformation along the ic6 axis of the gt Tonnetz
(click to enlarge)
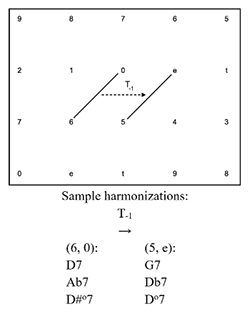
[2.5] Similar to the Tn operation are a group of cross-type transformations that convert 5-dyads into 6-dyads and vice versa, each visually represented by a translation of a single gt along the x-axis.(26) These operations are formalized below. “TTR” stands for “tritone right”, while “TTL” stands for “tritone left.” Although the inverses of each operation are implicit in the operations themselves, they are of great use analytically and are presented below.(27) The Tonnetz representations of these operations are shown in Example 7. Geometrically, the TTR operation rotates the vertical line of the 5-dyad clockwise about its lower vertex, resulting in the diagonal line of the 6-dyad. TTR-1, the inverse of the TTR operation, rotates the diagonal line of the 6-dyad counterclockwise about its lower vertex, resulting in the vertical line of the 5-dyad. The TTL operation rotates the vertical line of the 5-dyad clockwise about its upper vertex, resulting in the diagonal line of the 6-dyad. TTL-1, the inverse of the TTL operation, rotates the diagonal line of the 6-dyad counterclockwise about its upper vertex, resulting in the vertical line of the 5-dyad. Sample harmonizations for each dyad are shown beneath Example 7.
If \(X = (x_1, x_2) \in S1\), then \(TTR(X) = Y\), where \(Y = (y_1, y_2) = (x_1, x_2-1) \in S2\)
If \(X = (x_1, x_2) \in S2\), then \(TTR^{-1}(X) = Y\), where \(Y = (y_1, y_2) = (x_1, x_2+1) \in S1\)
If \(X = (x_1, x_2) \in S1\), then \(TTL(X) = Y\), where \(Y = (y_1, y_2) = (x_1+1, x_2) \in S2\)
If \(X = (x_1, x_2) \in S2\), then \(TTL^{-1}(X) = Y\), where \(Y = (y_1, y_2) = (x_1-1, x_2) \in S1\)
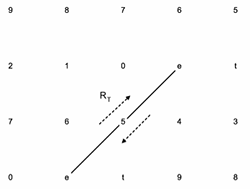
[2.6] When considering these cross-type transformations, the enharmonic equivalence of dyads that span ic6 poses a technological problem. Because guide-tone dyads are ordered (that is, because one of them is the third of the chord and the other is the seventh), two ordered 6-dyads containing the same pair of pitch classes in a different order are aurally equivalent but are technically distinct guide-tone dyads and are represented as such in the Tonnetz. This distinction affects the output of all operations whose input is a 6-dyad. For instance, when applied to dyad (0, 6), TTL-1 yields dyad (e, 6). When applied to dyad (6, 0), however, TTL-1 yields dyad (5, 0). This comparison is shown in Example 8. Sample harmonizations are shown beneath the example. In order to reflect the fact that two 6-dyads are enharmonically equivalent (and function in much the same way, as for instance when a tritone substitute replaces a dominant chord), an operation is needed to convert one ordered 6-dyad into its enharmonic equivalent. This operation, Rt (tritone reflection), is shown in Example 9 and does not occur over a span of time but rather serves solely as a technological apparatus for navigating guide-tone space efficiently. The Rt transformation reflects a 6-dyad about either of its vertices. In order to spatially convey smoothness on the gt Tonnetz, 6-dyads may be displayed as flipped (that is, with the third at the top and the seventh at the bottom), with the Rt operation serving to illustrate the toroidal quality of the space.
If \(X = (x_1, x_2) \in S2\), then \(R_t(X) = I^{x2}_{x1}(X) = Y\), where \(Y = (y_1, y_2) = (x_2, x_1) \in S1\)
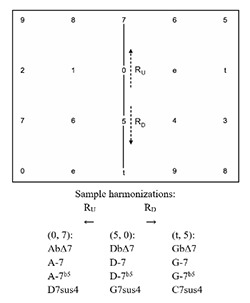
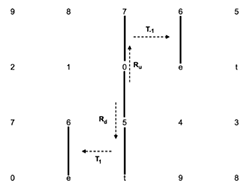
[2.7] Reflections of the 5-dyad are also of analytical use as they model parsimonious voice leading where the moving voice moves by a whole step. These operations, Ru and Rd (reflection up and reflection down, respectively) are formalized below. Their Tonnetz representations are shown in Example 10. The Ru operation reflects a 5-dyad across the x-axis of its upper vertex while the Rd operation reflects a 5-dyad across the x-axis of its lower vertex. Sample harmonizations for each dyad are shown below Example 10.
If \(X = (x_1, x_2) \in S1\), then \(R_u(X) = I^{x2}_{x2}(X) = Y\), where \(Y = (y_1, y_2) = (x_2, x_1+2) \in S1\) If \(X = (x_1, x_2) \in S1\), then \(R_d(X) = I^{x1}_{x1}(X) = Y\), where \(Y = (y_1, y_2) = (x_2-2, x_1) \in S1\)
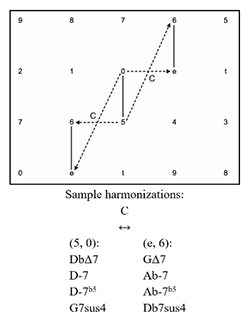
Example 10. Ru and Rd operations modeled on the gt Tonnetz (click to enlarge) | Example 11. C transformation modeled on the gt Tonnetz (click to enlarge) |
Example 12. C is equivalent to RuT-1 or RdT1, but neither of these capture semitonal contrary motion and both require more voice-leading work
(click to enlarge)
[2.8] When both guide tones of a 5-dyad move by semitone in contrary motion and form another 5-dyad, this is represented by the C (contrary motion) transformation. The C transformation is best visualized as a translation along the southwest/northeast axis, shown in Example 11. Sample harmonizations for each dyad are listed beneath Example 11. Note that a translation northeast results in the same dyad as a translation southwest due to the redundancy of the ic6 axis. This motion may also be understood as either RuT-1 or RdT1 (shown in Example 12). However, neither of these combinations captures the semitonal voice leading involved in the C transformation, and both require more voice-leading work. For this reason, I prefer the visualization found in Example 11.(28)
If \(X = (x_1, x_2) \in S1\), then \(C(X) = I^{x1}_{x2}(X) = Y\), where \(Y = (y_1, y_2) = (x_2-1, x_1+1) \in S1\)
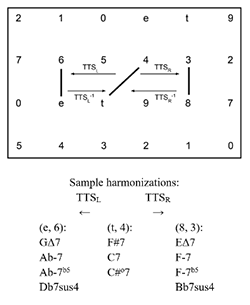
Example 13. TTS operations modeled on the gt Tonnetz
(click to enlarge)
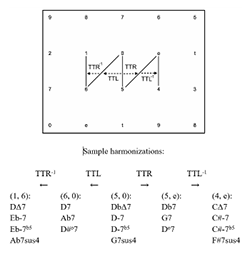
[2.9] There is one final family of cross-type transformations worth discussing, termed TTS (for tritone shift). Similar to the TTL and TTR operations, which move either tone of a 5-dyad by semitone to produce a 6-dyad, TTS maps 5- and 6-dyads onto one another by shifting them right or left on the gt Tonnetz (see Example 13). A rightward shift is termed TTSR, and a leftward shift is termed TTSL. As with the TTL and TTR operations, the inverses of both TTS transformations are frequently useful and as such are presented inclusively in Example 13. The voice leading involved in the TTS family is less parsimonious than many of the transformations explored above. In each case, one gt moves by ic1, while another gt moves by ic2, making the total voice-leading displacement 3 semitones. Because of this higher displacement, the voice leading may be more easily obscured in the musical texture and possibly more difficult to hear. This is reflected in its visual representation on the gt Tonnetz in Example 13, where all three dyads are substantially separated. Sample harmonizations for each dyad are shown below Example 13. While a few characteristic harmonic progressions (e.g. V→i and I→V/V) warrant the use of the transformation, it should be employed cautiously in analysis due to the greater voice-leading work involved.
If \(X = (x_1, x_2) \in S2\), then \(TTS_L(X) = Y\), where \(Y = (y_1, y_2) = (x_1+1, x_2+2) \in S1\)
If \(X = (x_1, x_2) \in S1\), then \(TTS_L{}^{-1}(X) = Y\), where \(Y = (y_1, y_2) = (x_1-1, x_2-2) \in S2\)
If \(X = (x_1, x_2) \in S2\), then \(TTS_R(X) = Y\), where \(Y = (y_1, y_2) = (x_1-2, x_2-1) \in S1\)
If \(X = (x_1, x_2) \in S1\), then \(TTS_R{}^{-1}(X) = Y\), where \(Y = (y_1, y_2) = (x_1+2, x_2+1) \in S2\)
[2.10] Transformations where each gt moves by greater than ic2 may be diagrammed on the gt Tonnetz, but are less likely to be heard because the tones are moving by more than a step. Because this article is chiefly concerned with smooth voice leading, I have left all such transformations in the space unformalized.
[2.11] As with many, if not most, geometric and graph depictions of voice-leading relationships, following transformations on the gt Tonnetz can feel more alien than simply following the same transformations on a musical staff. It is worth emphasizing that the purpose of using the gt Tonnetz is not that the space is easier to follow, but that it more accurately represents the ways in which the gts in harmonies progress from one to another without direct reference to the contexts to which they belong. In some ways, this is similar to the Neo-Riemannian Tonnetz: while it may not be easier to think in terms of moves on a Tonnetz, it is an alternative means of notation that clarifies its syntax. Indeed, both the Neo-Riemannian and gt Tonnetze are useful in part because they defamiliarize otherwise familiar music-theoretical objects. This opens new avenues for interpreting their relationships. Unlike the Neo-Riemannian Tonnetz, however, gt space also helps to separate the relationships between gt dyads from their surrounding context. This separation has two uses: First, it allows us to see the various transpositional and inversional relationships that are established between particular gt dyads; second, it suggests that even when tonal coherence is not found through other harmonic-analytical ventures, coherence may be established through gt transformations. Thus, the gt Tonnetz helps to visualize a significant alternative space, where coherence is established solely through the voice-leading properties of guide tones.
Example 14. Chord changes, gt dyads, and, voice-leading transformations in “Nefertiti” (Wayne Shorter)
(click to enlarge)
[2.12] In order to demonstrate the utility of the technologies developed above, let us examine Wayne Shorter’s 1967 composition “Nefertiti.” The tune uses an unusually wide variety of gt transformations. Example 14(29) shows the chord changes for “Nefertiti” and their corresponding gt dyads; an ordered pair of pitch classes below each chord identifies the gt dyad in integer notation, while transformations in gt space are displayed between each chord. Notably, only one transformation, which maps (6, 1) onto (t, 5), is not smooth; for this reason it is listed as N/A in Example 14.
Example 15. Guide-tone voice leading for “Nefertiti” (Wayne Shorter), plotted on the gt Tonnetz
(click to enlarge and see the rest)
[2.13] Examples 15a–d plot the gt voice leading of Nefertiti on the gt Tonnetz and show the corresponding chord changes beneath. To make it easier to see the correspondence between transformations and dyads, four versions of the Tonnetz are shown (Examples 15a–d), each presenting a different section of the chord changes. In each case, corresponding gt dyads and chord changes are highlighted in the same color. Dotted lines represent points of overlap in mod 12, three-dimensional space. “Nefertiti” is notable for the density of its gt voice leading, which reflects its tonally adventurous harmonic relationships. Waters (2011) notes that, although the chord progression “relies significantly on traditional bass motions, progressing primarily through descending fifth and chromatic motion characteristic of functional harmonic progressions,” the piece “remains strikingly elusive and enigmatic” (219). These unusual connections between functional progressions are made possible in part through gt voice leading. Indeed, despite featuring nearly continuous smooth voice leading, the tune winds unpredictably through gt space, sometimes revisiting gt dyads that were sounded earlier in the progression before departing from them in different ways. Because of the relationships afforded by smooth gt voice leading, gt space allows Shorter to explore some unusual harmonic relationships while retaining a sense of tonal coherence. The exploratory nature of “Nefertiti” is visually apparent in Example 15, where transformational arrows criss-cross and compete for space as gt dyads wind about the Tonnetz.
[2.14] Keith Waters and Steven Strunk have drawn attention to the ways that the melodic structure, motivic processes, and unusual phrasing of “Nefertiti” work together to create a sense of overlap and circularity.(30) The continuity provided by smooth gt voice leading contributes to this circular effect by helping to obscure a sense of tonal centricity and weaken what might otherwise appear to be a strong dominant-tonic resolution from
3. Gt Space, ii–Vs, and the Tonal Jazz Repertory
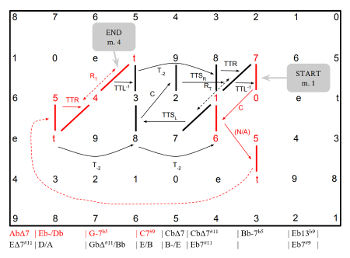
[3.1] While “Nefertiti” uses smooth voice leading as a coherent backdrop for harmonic experimentation, gt space is also useful in elucidating how more conventional tonal frameworks may be embellished. Let us examine Charlie Parker’s “Blues for Alice,” an elaborately ornamented twelve-bar blues featuring smooth gt voice leading. Example 16 displays the chord changes, gt dyads, and transformations for “Blues for Alice,” while Examples 17a–c plot the voice leading from m. 1 through the first chord of m. 11 on the gt Tonnetz and display the corresponding chord changes below. Note that the dyads consistently lead to the right (that is, downwards in pitch space) until they wrap around to the beginning due to the toroidal quality of the space, represented by the dotted line connecting both (9, 4) dyads. The continuously smooth voice leading helps to provide seamless motion but also to propel the tune forward. This sense of directed motion is captured by the many rightward arrows that guide the dyad motion in Example 17. Note that the initial motion from the tonic in m. 1 to the subdominant in m. 5 involves transformations requiring more voice-leading work, such as T-2 and TTSR, whereas the chain of three ii–V progressions connecting
Example 16. Chord changes, gt dyads, and voice-leading transformations in “Blues for Alice” (Charlie Parker) (click to enlarge) | Example 17. Guide-tone voice leading for “Blues for Alice” (Charlie Parker) mm. 1–11, plotted on the gt tonnetz (click to enlarge and see the rest) |
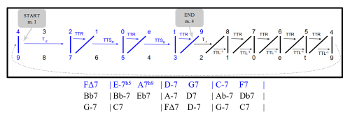
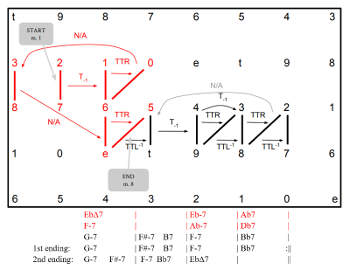
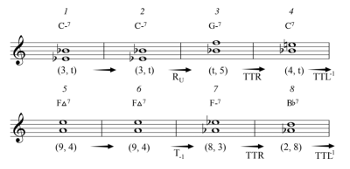
[3.2] Miles Davis’s “Four” is in some ways even more economical than “Blues for Alice” in its use of gt space. Example 18 displays the chord changes, gt dyads, and transformations, while Examples 19a–d plot these on the gt Tonnetz. While the A section (Example 19a) makes use of the northwestern region of the space, the B section (Examples 19b–d), with its two endings, makes several passes through the southeastern region. Notably, several harmonic progressions do not feature smooth gt voice leading; these progressions are marked “N/A” in Examples 18 and 19. Two of these progressions are deceptive resolutions of V chords (
Example 18. Chord changes, gt dyads, and voice-leading transformations in “Four” (Miles Davis) (click to enlarge) | Example 19. Guide-tone voice leading for “Four” (Miles Davis), plotted on the gt Tonnetz (click to enlarge and see the rest) |
Example 20. McClimon’s ii-V space. Reprinted by permission from McClimon 2017
(click to enlarge)
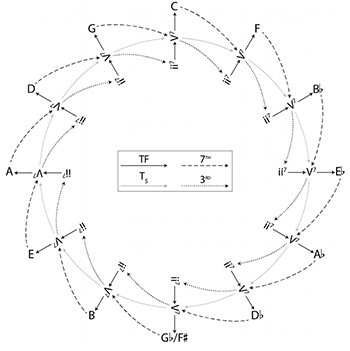
[3.3] Both “Blues for Alice” and “Four” are characterized by their reliance on ii–V progressions. Indeed, the most common string of gt transformations, TTR followed by TTL-1, is found primarily in ii–V–I progressions and their variants. It is worth exploring the overlap between guide-tone space and the transformational model of ii–V progressions developed in McClimon (2017). McClimon’s harmonic object-family consists of trichords comprising root, third, and seventh; in other words, guide-tones plus root. A single transformation, TF (short for two–five), serves to transform the ii7 chord in any given key to a V7 chord, and the V7 chord into a I7 chord. A handful of other transformations connect ii–V–I progressions in different keys and account for other variants, resulting in a larger network McClimon calls ii–V space, shown in Example 20.
[3.4] Despite some superficial similarities, the conceptualizations of jazz harmony that gt space and ii–V space entail are very different. Each node in ii–V space constitutes a unique harmony, leading to a one-to-one relationship between a ii–V space trichord and a chord symbol on a lead sheet.(32) In gt space, the relationship between nodes and chord symbols is not one-to-one; a single gt dyad may represent a number of chords. This is both a weakness and a strength: while the structure of gt space models less intuitively the way chords are typically represented in jazz, its abstraction allows us to visualize parsimonious voice leading more clearly. In other words, whereas ii–V space simply involves voice leading, gt space is properly a voice-leading space. Transformations in gt space are limited to those that model salient voice leading; gt space therefore provides a visual representation of the voice leading of essential tones in a composition.
Example 21. An example of a ii-V-I region: The gt voice leading of a ii-V-I progression modeled on the gt Tonnetz
(click to enlarge)
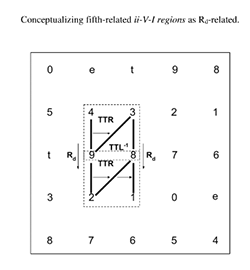
[3.5] Nonetheless, there is a clear overlap between gt space and ii–V space because two of the pcs in each trichord of ii–V space constitute a gt dyad. In order to represent ii–V–I progressions in gt space, we may draw a box around the three dyads on the gt Tonnetz that are involved in the ii–V–I progression (as shown in Example 21). I call any three such dyads in this configuration on the gt Tonnetz a ii–V–I region. Notably, the dominant and the tritone substitute share the same gt dyad, so gt voice leading may represent either progression.
Example 22. Transformational relationships between ii-V-I regions
(click to enlarge and see the rest)
[3.6] Gt voice leading not only occurs within ii–V–I progressions but also frequently serves to connect ii–V–I progressions to each other. Transformations in gt space may be used to clarify how the gt dyads between ii–V–I progressions are related. In many cases, multiple transformations may be used to describe the relationship. For example, two fifth-related regions may be connected by either the Rd or the C transformation; these relationships are shown in Example 22. Other relations between regions may be derived by charting ii–V–I regions on the gt Tonnetz and determining the transformations between the constituent gt dyads of each region.
Example 23. Transformations of gt dyads in mm. 1–12 of “Tune Up” on a gt Tonnetz
(click to enlarge)
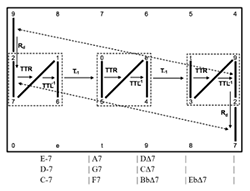
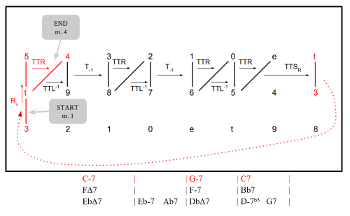
[3.7] One particularly common transformation between ii–V–I regions is T-1, typically resulting in the I chord of a ii–V–I progression becoming the ii of the next. A paradigmatic example of this relation is found in Miles Davis’s “Tune Up.” The gt voice leading for mm. 1–12 is shown in Example 23. Each ii–V–I region is connected by a T-1 transformation. An Rd transformation connects the final 5-dyad of the rightmost ii–V–I region to the first 5-dyad of the leftmost ii–V–I region.
4. Neo-Riemannian Parallels, Double Syntax, and the Transformational Attitude
[4.1] In the previous sections, we formalized a transformational space that visualizes the voice-leading syntax established by guide tones and explored some of the ways in which the space may be used to model various kinds of harmonic structures. It will now be useful to consider how guide-tone syntax relates to tonal, diatonic syntax. To do this, let us more closely examine the parallels between neo-Riemannian theory and gt space.
[4.2] In his book Audacious Euphony, Richard Cohn describes what he calls the “overdetermined” nature of the consonant triad: On the one hand, the consonant triad is acoustically resonant, and on the other it is an ideal voice-leading object, because when minimal voice-leading effort is exerted, it is able to generate other members of the same set class (Cohn 2012, 40). The latter feature is made possible by virtue of [037] being nearly even (a minimal perturbation of a perfectly even set); this feature differentiates it from other possible trichords.(33) Cohn’s studies of the voice-leading parsimony of consonant triads give rise to a number of tools that show how such voice leading connects triads in a coherent and cyclic manner. He uses the term “pan-triadic syntax” to refer to the harmonic and voice-leading syntax these tools help describe. In pan-triadic syntax, triads relate to one another without reference to the diatonic collection within which they are so often situated (Cohn 2012, xiv).(34) Cohn is thus able to identify instances of what he calls “double syntax,” where pan-triadic and tonal/diatonic syntaxes overlap and interact. This provides a more rigorous method to tease out the interplay of chromatic and diatonic systems and show how such interplay might affect the perception of tonal ambiguity.
[4.3] Though differences exist, guide-tone dyads and consonant triads share a few notable properties. Like consonant triads, gt dyads can be generated from one another using parsimonious voice leading. These smooth voice-leading procedures form a syntax by being constrained in particular ways (following the transformations codified above): no single gt may move by more than ic2 and the total voice-leading displacement may not exceed 4.
[4.4] Yet gt dyads establish a much more complicated relationship with their musical surroundings. Unlike consonant triads, which may often faithfully represent the entirety of pitch material over a given span of time, gt dyads are always situated within a larger harmonic context as chord members, and the harmonies to which they belong are often at least somewhat indeterminate due to the improvisational circumstances of jazz performance. Indeed, although an isolated 5-dyad would be acoustically resonant, such resonance is mostly irrelevant when the dyad is placed in its larger context as the third and seventh of a given harmony. This makes establishing relationships with parent collections problematic as well. In pan-triadic syntax, the handful of distinct triads generated by chains of L and P operations may be considered subsets of a parent hexatonic collection, the symmetric properties of which avoid establishing tonal hierarchies found in the diatonic collection. The voice-leading syntax of gt dyads is more varied and is always in dialogue with these tonal hierarchies, within which gt dyads are subsumed.
Example 24. The neo-Riemannian Tonnetz
(click to enlarge)
[4.5] A comparison between the neo-Riemannian Tonnetz (Example 24(35)) and the gt Tonnetz sheds light on the complications involved in describing the nature of gt syntax. Whereas the neo-Riemannian Tonnetz only deals with a single transformational object, the consonant triad, gt space features two types of objects, 5- and 6-dyads. Because of this, the kinds of transformations that map objects onto one another are more numerous in gt space than on the neo-Riemannian Tonnetz. Only four operations (L, P, R, and N) are used to connect triads on the neo-Riemannian Tonnetz, whereas five transformations (Tn, TTR, TTL, R, and, TTS) connect 5- and 6-dyads to surrounding dyads.(36) On the neo-Riemannian Tonnetz, any transformation can be performed on any object in the space. In gt space, however, the R and T operations only connect objects of the same type, while the TTR, TTL, and TTS transformations are cross-type transformations. Indeed, the output of all transformations depends on what kind of object the input is. On the neo-Riemannian Tonnetz, triads may be one of two modes (major or minor), with operations preserving or changing mode; on the gt Tonnetz, dyads may be either 5- or 6-dyads, with operations preserving or changing dyad type.(37)
[4.6] Let us consider a more specific example. If we begin with a C minor triad on the neo-Riemannian Tonnetz—the triangle at the bottom center of Example 24—three available operations allow us to move to adjacent triangles: P moves up to C major; R moves right to
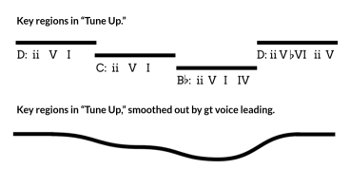
Example 25. Visualization of the dialectic between key regions and gt voice leading in “Tune Up.”
(click to enlarge)
[4.7] Let us return to Miles Davis’s “Tune Up.” Some simple tonal analysis would reveal ii–V–I progressions in three different key centers (D, C, and
[4.8] The seamlessness provided by gt voice leading may be reinforced by David Lewin’s transformational attitude and the interpretive flexibility it affords.(42) In Generalized Musical Intervals and Transformations, Lewin writes:
Given locations s and t in our space, [the transformational attitude] does not ask for some observed measure of extension between reified “points;” rather it asks: “If I am at s and wish to get to t, what characteristic gesture
. . . should I perform in order to arrive there?” (Lewin 1987, 159)
The resulting change in perspective situates the analyst inside the music, rather than acting as an observer.(43) Harrison (2011), in his discussion of the transformational attitude, notes that “it is easy to change the gloss from speculating about what has to be done in order to move from s to t to speculating about what has to be done to move s itself to t” (549). In this sense, he observes, we are able to conceive of “s being transformed ‘into’ t in the sense that it ‘becomes’ t” (ibid.). Such an interpretive gloss recasts transformation not as a series of related musical objects but as a process whereby a single musical object repeatedly undergoes transformation. Under this interpretation, we may imagine that gt dyads are not separate objects that lead to one another but instead represent a singular object undergoing transformation, providing a sense of continuation between harmonies.
[4.9] It is worth commenting on the term “changes” here as it is used in jazz parlance. While McClimon (2014) notes that the term accords well with the dynamic conception of relations found in Lewin’s transformational attitude, I wish to note that the term may also emphasize the differences (and thus ontological distinctions) between each harmony in a jazz composition. The coherence offered by gt voice leading helps listeners and improvisers to navigate through these changes by providing a pathway from one chord to the next.
Example 26. Chord changes, gt dyads, and voice-leading transformations in “All the Things You Are” (Jerome Kern)
(click to enlarge)
Example 27. Guide-tone voice leading for “All the Things You Are” (Jerome Kern), plotted on the gt Tonnetz
(click to enlarge and see the rest)
[4.10] Two analytic vignettes will demonstrate how we might use this interpretive lens to examine the double syntax of gts. Example 26(44) provides the chord changes, gt dyads, and transformations of Jerome Kern’s “All the Things You Are,” and Examples 27a–d plot them on the gt Tonnetz. The A section (Example 27a) begins with the vi chord of
Example 28. Visualization of key regions connected by gt transformation
(click to enlarge)
[4.11] Among the most salient and characteristic aspects of Kern’s composition is the mediant tonicization in the midst of a descending fifths sequence, first seen in the A section as a motion from
[4.12] Example 29 shows the chord changes, gt dyads, and transformations in Miles Davis’s(45) “Solar.” Examples 30a–c show the corresponding gt space. The composition features smooth, consistently descending gt motion that enables improvisers to efficiently thread through a series of brief tonicizations. The tune begins with the tonic C minor, then uses Ru to move from C-7 to G-7, initiating a ii–V–I in F major. The remainder of the tune consists of a series of ii–V–I regions connected to one another by T-1. Notably, the 5-dyad (5, 0) is shared between
Example 29. Chord changes, gt dyads, and voice-leading transformations in “Solar” (Miles Davis) (click to enlarge) | Example 30. Guide-tone voice leading for “Solar” (Miles Davis), plotted on the gt Tonnetz (click to enlarge and see the rest) |
Example 31. Comparison between chord changes of “Solar” and minor twelve-bar blues
(click to enlarge)
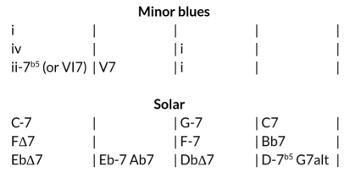
[4.13] The form and harmonic layout of “Solar” are similar to that of the twelve-bar blues (see Example 31). Although there is debate as to whether the composition may be considered a blues,(46) the twelve-bar form of “Solar” at least places the piece in dialogue with the minor variant of the twelve-bar blues, inviting comparisons of similarity and dissimilarity. The most obvious similarities are the root relationship of a fourth between the starting tonic chord (C-7) and the chord in m. 5 (FΔ7) and the increase in harmonic rhythm starting in m. 9. Unlike a standard minor blues, however, the modes of the subdominant and tonic chords in mm. 5 and 1, respectively, do not match. And although the root motion down a whole tone from
[4.14] Indeed, the changes of “Solar” may be understood as the result of a negotiation between smooth voice leading and the paradigmatic minor blues chord progression. At least two compositional decisions evince this: (1) When a ii–V is used to approach the subdominant in m. 5, the smoother TTL-1 transformation is favored over the TTSR transformation, resulting in a subdominant chord the mode of which does not match the global tonic; (2) The tonicizations of
5. Concluding Thoughts
[5.1] Much scholarly and pedagogical work has sought to elucidate aspects of tonal syntax in jazz.(47) In this article, I have argued that gt voice leading, a concept borrowed from jazz pedagogy, may be modeled using tools derived from Lewinian and neo-Riemannian transformational theories and that the resulting transformational space, the gt Tonnetz, may be used to depict the unique syntactic properties established by gts.(48) By taking seriously how jazz musicians and pedagogues conceptualize voice-leading structure, gt space allows us to formalize aspects of jazz practice that are seldom examined and to consider how those aspects fit into the larger mosaic of jazz syntax.
[5.2] Throughout this article, I have argued that the voice-leading parsimony of gt dyads constitutes a syntax that helps to shape the idiosyncratic tonal trajectories of many jazz tunes. This argument has many ramifications for jazz analysis. In some situations, gt space can be used as a lens through which to examine stylistic characteristics. Because only a handful of transformations smoothly connect gt dyads, many compositions and improvisations share the same transformations and transformation patterns. This small but shared set of patterns allows us to probe the unique ways that voice-leading preferences constrain and influence harmonic practice in jazz, especially as the harmonic language of bebop gives way to that of postbop. Just as Cohn (2012) argues that the voice-leading capabilities of the consonant triad help to loosen the norms of tonal music and open avenues for increasing uses of chromaticism (205–207), the dual-syntactic role of gts may be understood to serve a similar evolutionary function in jazz. This evolutionary perspective, in which composers and improvisers, over time, became increasingly aware of the harmonic possibilities afforded by smooth gt voice leading and began to use them in more unusual ways, may be supported by the adventurousness of “Nefertiti’s” dense, knotty use of gt space in Example 15 as compared with the other, more tonal examples provided throughout this essay.(49) Although gt voice leading may have emerged as a byproduct of other tonal processes, composers were able to exploit the properties that facilitated more tonally ambiguous harmonic frameworks. By providing an intuitive way of modeling the intersections between essential harmonic tones and smooth voice leading, gt space suggests new ways of thinking about the relationships between jazz harmony and compositional possibility.
Sean R. Smither
Rutgers University
Mason Gross School of the Arts
33 Livingston Ave.
New Brunswick, NJ 08901
sean.smither@rutgers.edu
Works Cited
Attas, Robin. 2009. “Metaphors in Motion: Agents and Representation in Transformational Analysis.” Music Theory Online 15 (1). http://www.mtosmt.org/issues/mto.09.15.1/mto.09.15.1.attas.html
Berliner, Paul. 1994. Thinking in Jazz: The Infinite Art of Improvisation. University of Chicago Press.
Biamonte, Nicole. 2008. “Augmented-Sixth Chords vs. Tritone Substitutes.” Music Theory Online 14 (2). http://www.mtosmt.org/issues/mto.08.14.2/mto.08.14.2.biamonte.html
Brown, Stephen C. 2003. “Dual Interval Space in Twentieth-Century Music.” Music Theory Spectrum 25 (1): 33–57.
Buchler, Michael. 2017. “Are There Any Bad (or Good) Transformational Analyses?” Intégral 30: 41–51.
Clough, John, and Jack Douthett. 1991. “Maximally Even Sets.” Journal of Music Theory 35 (1): 93–173.
Cohn, Richard. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions.” Music Analysis 15 (1): 9–40.
—————. 1997. “Neo-Riemannian Operations, Parsimonious Trichords, and Their ‘Tonnetz’ Representations.” Journal of Music Theory 41 (1): 1–66.
—————. 1998. “Introduction to Neo-Riemannian Theory: A Survey and a Historical Perspective.” Journal of Music Theory 42 (2): 167–80.
—————. 2000. “Weitzmann’s Regions, My Cycles, and Douthett’s Dancing Cubes.” Music Theory Spectrum 22 (1): 89–103.
—————. 2012. Audacious Euphony: Chromatic Harmony and the Triad’s Second Nature. Oxford University Press.
Gioia, Ted. 2012. The Jazz Standards: A Guide to the Repertoire. Oxford University Press.
Harrison, Daniel. 2011. “Three Short Essays on Neo-Riemannian Theory.” In The Oxford Handbook of Neo-Riemannian Music Theories, edited by Edward Gollin and Alexander Rehding, 548–77. Oxford University Press.
Heetderks, David J. 2011. “A Tonal Revolution in Fifths and Semitones: Aaron Copland’s Quiet City.” Music Theory Online 17 (2). http://www.mtosmt.org/issues/mto.11.17.2/mto.11.17.2.heetderks.html
Hook, Julian. 2007 “Cross-type Transformations and the Path-Consistency Condition.” Music Theory Spectrum 29 (1): 1–40.
Kernfeld, Barry. 2006. The Story of Fakebooks: Bootlegging Songs to Musicians. Lanham, MD: Scarecrow Press.
Klumpenhouwer, Henry. 2006. “Essay: In Order to Stay Asleep as Observers: The Nature and Origins of Anti-Cartesianism in Lewin’s Generalized Musical Intervals and Transformations.” Music Theory Spectrum 28 (2): 277–89.
Larson, Steve. 2012. Musical Forces: Motion, Metaphor, and Meaning in Music. Indiana University Press.
Lerdahl, Fred, and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. MIT Press.
Levine, Mark. 1995. The Jazz Theory Book. Sher Music Co.
Lewin, David. 1987. Generalized Musical Intervals and Transformations. Oxford University Press.
Martin, Henry. 1980. “Jazz Harmony.” PhD diss., Princeton University.
—————. (1988) “Jazz Harmony: A Syntactic Background.” Annual Review of Jazz Studies 4: 9–30.
—————. 2018. “Prolongation and Its Limits: The Compositions of Wayne Shorter.” Music Theory Spectrum 40/1: 84–105.
McClimon, Michael. 2014. “Jazz Harmony, Transformations, and ii–V Space.” Paper presented at the annual meeting of the Society for Music Theory, Milwaukee, WI.
—————. 2017. “Transformations in Tonal Jazz: ii–V Space.” Music Theory Online 23 (1). http://mtosmt.org/issues/mto.17.23.1/mto.17.23.1.mcclimon.html
McGowan, James. 2005. “Dynamic Consonance in Selected Piano Performances of Tonal Jazz.” PhD diss., Eastman School of Music.
Morris, Robert. 1995. “Compositional Spaces and Other Territories.” Perspectives of New Music 33 (1/2): 328–58.
Mulholland, Joe, and Tom Hojnacki. 2013. The Berklee Book of Jazz Harmony. Berklee Press.
Nettles, Barrie. 1987. Harmony 2 Workbook. Berklee Press.
Nettles, Barrie, and Richard Graf. 1997. The Chord Scale Theory & Jazz Harmony. Advance Music.
Pachet, François. 2000. “Computer Analysis of Jazz Chord Sequences: Is Solar a Blues?” In Readings in Music and Artificial Intelligence, edited by Eduardo Reck Miranda, 85–114. Routledge.
Park, Joon. 2016. “Reflections On (and In) Strunk’s Tonnetz.” Journal of Jazz Studies 11 (1): 40–64.
Rawlins, Robert, and Nor Eddine Bahha. 2005. Jazzology: The Encyclopedia of Jazz Theory for All Musicians. Hal Leonard.
The Real Book. n.d. 5th ed. Underground publication; no publisher information available.
The Real Book. n.d. 6th ed. Hal Leonard.
Rings, Steven. 2011. Tonality and Transformation. Oxford University Press.
Roeder, John. 2009. “Constructing Transformational Signification: Gesture and Agency in Bartók’s Scherzo, Op. 14, No. 2, measures 1–32.” Music Theory Online 15 (1). http://www.mtosmt.org/issues/mto.09.15.1/mto.09.15.1.roeder_signification.html
Rusch, René, Keith Salley, and Chris Stover. 2016. “Capturing the Ineffable: Three Transcriptions of a Jazz Solo by Sonny Rollins.” Music Theory Online 22 (3). http://mtosmt.org/issues/mto.16.22.3/mto.16.22.3.rusch.html
Santa, Matthew. 2003. “Nonatonic Progressions in the Analysis of John Coltrane’s Music.” Annual Review of Jazz Studies 13: 13–25.
Sarath, Edward. 2010. Music Theory Through Improvisation: A New Approach to Musicianship Training. Routledge.
Salley, Keith. 2012. “Ordered Step Motives in Jazz Standards.” Journal of Jazz Studies 8 (2): 114–36.
Stover, Chris. 2012. Review of Keith Waters, The Studio Recordings of the Miles Davis Quintet: 1965–68 (Oxford University Press, 2011), Music Theory Online 18 (1). http://mtosmt.org/issues/mto.12.18.1/mto.12.18.1.stover.html
—————. 2013. “Analysis as Multiplicity.” Journal of Music Theory Pedagogy 27: 111–42.
—————. 2014. “Jazz Harmony: A Progress Report.” Journal of Jazz Studies 10 (2): 157–97.
Straus, Joseph N. 1997. “Voice Leading in Atonal Music.” In Music Theory in Concept and Practice, edited by David W. Beach, James M. Baker, and Jonathan W. Bernard, 237–74. University of Rochester Press.
—————. 2003. “Uniformity, Balance, and Smoothness in Atonal Voice-leading.” Music Theory Spectrum 25 (2): 305–52.
—————. 2011. “Contextual-Inversion Spaces.” Journal of Music Theory 55 (1): 43–88.
Strunk, Steven. 1985. “Bebop Melodic Lines: Tonal Characteristics.” Annual Review of Jazz Studies 3: 97–120.
—————. 2003. “Wayne Shorter’s Yes and No: An Analysis,” Tijdschrift voor musiektheorie 8 (1): 40–56.
—————. 2005. “Notes on Harmony in Wayne Shorter’s Compositions, 1964–67,” Journal of Music Theory 49 (2): 301–32.
Terefenko, Dariusz. 2009. “Jazz Transformations of the ii7–V7–I Progression.” Current Research in Jazz 1.
—————. 2014. Jazz Theory: From Basic to Advanced Study. Routledge.
Tymoczko, Dmitri. 2008. “Lewin, Intervals, and Transformations: A Comment on Hook.” Music Theory Spectrum 30 (1): 164–68.
Waters, Keith. 2011. The Studio Recordings of the Miles Davis Quintet, 1965–68. Oxford University Press.
—————. 2016. “Chick Corea and Postbop Harmony.” Music Theory Spectrum 38 (1): 37–57.
Waters, Keith, and J. Kent Williams. 2010. “Modeling Diatonic, Acoustic, Hexatonic, and Octatonic Harmonies and Progressions in Two- and Three-Dimensional Pitch Spaces; or Jazz Harmony after 1960.” Music Theory Online 16 (3). http://www.mtosmt.org/issues/mto.10.16.3/mto.10.16.3.waters_williams.html
Waters, Keith, Henry Martin, Steve Larson, and Steven Strunk. 2016. “Circular Thinking: A Roundtable on ‘Blue in Green’ and ‘Nefertiti’.” Journal of Jazz Studies 11 (1): 105–20.
Footnotes
1. Melody and chord changes adapted from the lead sheet in The Real Book (Vol. 1, fifth edition). The lead sheet found in the sixth edition of The Real Book features two endings, with the latter ending featuring a ii–V–I progression. For the sake of simplicity, I have opted to use the lead sheet found in the fifth edition of The Real Book. Throughout, I use Δ to refer to major chords and - to refer to minor chords. The harmony in the fourteenth measure of “Tune Up” is frequently performed as F7 instead of A7. Both options produce efficient voice leading.
Return to text
2. In jazz, the term “tune” refers to the compositions on which improvisations are based. This term is rich with meaning, yet at times ambiguous. The chord changes of tunes are frequently flexible and can vary widely between performances. Most of the chord changes throughout this article are drawn from The Real Book (Vol. 1, sixth edition), an authorized and legal alternative to the popular, underground fakebook known as The Real Book (Vol. 1, fifth edition). While both the legal and illegal editions of The Real Book feature many inaccuracies, they also represent a useful compromise given that many jazz musicians rely on the chord changes provided by them. Well-known alternatives to the chord changes given here are discussed as necessary. For more on The Real Book and other fakebooks, see Kernfeld (2006). For more on the flexibility of tunes, see Berliner (1994, 63–88).
Return to text
3. It should be noted that not all writers restrict the definition of guide tones to chordal thirds and sevenths. Dariusz Terefenko (2014) notes that guide tones may provide opportunities for chord substitution in improvisation, with “individual tones of the guide-tone line hav[ing] the potential of being reinterpreted as chord tones or as extensions of other harmonic formations” (66).
Return to text
4. Voice-leading smoothness refers to the closeness of pitches when voices lead from one note to another. As Straus (2003) notes, synonymous terms used in the literature include “parsimoniousness, efficiency, nearness, closeness, and proximity” (320). Constraints on smoothness in guide-tone voice leading are discussed in more detail in section 2 of this article.
Return to text
5. The precise definition of “modal jazz” is much contested. Waters (2011) offers a list of possible attributes (46), but as Stover (2012) notes, these do not necessarily constitute a clear set of criteria for determining whether something should be identified as modal. Stover questions whether the term is appropriate since in most cases it is simply used to describe slow harmonic rhythm.
Return to text
6. Strunk’s approach also involves a transfer of transformational properties from algebraic group theory to geometry. For more on the implications of this methodological maneuver, see Park (2016).
Return to text
7. McClimon finds corroboration for this in the pedagogical concept of shell voicings and in James McGowan’s characterization of the function of chord members in jazz, where chordal fifths are simply “triadic associates.” (See McClimon 2017 and McGowan 2005.)
Return to text
8. Discussions of guide tones appear in Nettles (1987), Levine (1995), Rawlins and Bahha (2005), Sarath (2010), Mulholland and Hojnacki (2013), Terefenko (2014), and Nettles and Graf (1997).
Return to text
9. In jazz theory and pedagogy, the terms “extension” and “tension” are usually used interchangeably. Tensions include chordal 9ths, 11ths, and 13ths. For more on tensions, see Strunk (1985).
Return to text
10. For more on the essential nature of guide tones, see Mulholland and Hojnacki (2013, 212), Sarath (2010, 143), and Terefenko (2014, 65). In an earlier article, Terefenko also notes that guide tones “have the potential of being reinterpreted as chord tones or chordal extensions of various substitute formations” (Terefenko 2009).
Return to text
11. Chordal thirds and sevenths are frequently sounded together as a basic accompaniment chord called a “shell” voicing, which may be elaborated with other chord tones and tensions. For more on shell voicings, see Rawlins and Bahha (2005, 140).
Return to text
12. Of course, it is common for chordal sevenths to resolve down by a whole step (rather than half step) in the minor mode.
Return to text
13. For more on tritone substitutions, see Biamonte (2008). McClimon (2017) undertakes a similar transformational approach to tritone substitutes; the differences between my approach and McClimon’s are discussed in section 3.
Return to text
14. A tritone substitution preserves both guide tones when it replaces a dominant seventh chord; one guide tone when it replaces a major seventh, minor seventh, or half-diminished chord; and no guide tones when it replaces a fully-diminished seventh chord.
Return to text
15. Here I follow the recommendation in Roeder (2009) for a clear and rigorous transformational methodology. Such clarity has become especially desirable in the wake of skepticism toward the sometimes uncritical evaluation of transformational analyses, as in Buchler (2017).
Return to text
16. The exception to this is the 7sus4 chord. Because the third of the chord is withheld, the pc acting as the suspension (the fourth above the root) stands in for the chordal third and is considered a guide tone.
Return to text
17. In jazz, chord symbols in the form of X/Y, where X is a harmony and Y is a bass note, are often called “slash chords.” Slash chords where X = Y-2 (e.g. G/A) are sometimes considered interchangeable with 7sus4 chords.
Return to text
18. In the case of 7sus4 chords, the fourth substitutes for the third and therefore provides the value for x1.
Return to text
19. That is, the actual register in which a pitch may occur is not significant. Likewise, no distinction is made between enharmonically equivalent tones.
Return to text
20. For more on the special properties of ic1/ic5 Tonnetze, see Brown (2003) and Heetderks (2011).
Return to text
21. There are also strong parallels between the space developed here and the more generalized contextual-inversion spaces formalized in Straus (2011).
Return to text
22. One consequence of this orientation is that rightward progressions through the space are more common than leftward ones. An example of the latter may be found in mm. 11–12 of Wayne Shorter’s “Speak No Evil,” where A7 (1, 7) moves to
Return to text
23. As Tymoczko (2008) notes, geometrical and group-theoretical transformations are not necessarily isomorphic. Geometrical representations of group-theoretical transformations are nonetheless common in transformational writings, especially in neo-Riemannian theory, and are used here as a convenient way to represent transformational relationships.
Return to text
24. According to Rings (2011), “an operation is a transformation that is one-to-one and onto” (26). That is, each unique input has one unique output.
Return to text
25. It is worth noting that, here and throughout this article, T-1 and T-2 are used in favor of T11 and T10, respectively, to emphasize the short distance in gt space these transformations represent. When calculating total displacement, direction is not taken into account; the total displacement of T-1 is therefore 2, while the total displacement of T-2 is 4.
Return to text
26. Cross-type transformations are those transformations that map an object of one type onto an object of another type. In this case, 5- and 6-dyads are of different types because their set classes ([05] and [06], respectively) are different. For more on cross-type transformations, see Hook (2007).
Return to text
27. Throughout, inverses are identified with the superscript -1 (e.g. TTL-1). All other transformations use only subscripts.
Return to text
28. On the gt Tonnetz, a C transformation necessarily involves one voice leaping northeast or southwest through the space despite both voices moving only by a semitone. This uneven representation of voice-leading distance is due to the nature of the Tonnetz, specifically its diagonal ic6 axis. Because of this, the C transformation appears to “twist” the gt dyad through gt space.
Return to text
29. The chord changes here are adapted from Waters (2011, 218). Note that, in the case of inverted triads (e.g. D/A, E/B), the chordal seventh is presumed to be a major seventh. It is possible to conceive of these chords as simply not having sevenths, in which case smooth voice-leading connects only the chordal thirds.
Return to text
30. See discussions in Waters (2011) and Waters et al. (2016). Salley (2012, 131–32) corroborates this claim by uncovering linear motives, which he calls Ordered Step Motives (OSMs), that operate at both local and deeper levels, arguing that “connections between surface-level motives and those that lie beneath them can influence our perception of continuity in a composition with a circular form” (131). Many of the tones that comprise Salley’s OSMs are in fact guide tones and therefore also participate in the gt space of “Nefertiti.”
Return to text
31. This is not to say that tonal ambiguity alone is responsible for the sense of circularity in “Nefertiti.” Indeed, Waters (2011) identifies the melodic phrasing as the “decisive factor in creating ‘Nefertiti’s’ circularity” (219). Nonetheless, as Waters points out, tonal ambiguity does help to undermine the dominant-tonic resolution, providing an opening of which the melodic phrasing may take advantage.
Return to text
32. McClimon does represent enharmonically equivalent chords using the same trichord; in this sense, the relationship is not strictly one-to-one. Gt space, however, involves more abstraction: two chords that are otherwise not at all equivalent (e.g., E-7 and
Return to text
33. Cohn (1997) demonstrates this using set class [015] as an example. For more on evenness, see Clough and Douthett (1991) and Cohn (2012, 33–37).
Return to text
34. These technologies include hexatonic cycles and Weitzmann regions, developed in Cohn (1996) and (2000), respectively. Cohn adopts the term “pan-triadic” from Evan Copley.
Return to text
35. Adapted from Cohn (1998, 172).
Return to text
36. For explanations of L, P, N, and R operations and how they operate in hexatonic cycles and Weitzmann regions, see Cohn (1996) and (1998).
Return to text
37. It is important here to distinguish between the two modes of the consonant triad, which are represented by a single transformational object (set class 037) on the neo-Riemannian Tonnetz, and the two different transformational objects (5- and 6-dyads) that make up gt dyads. The difference in type means that cross-type transformations (see Hook 2007) are necessary to explain relations between objects on the gt Tonnetz, whereas no such extensions are necessary on the neo-Riemannian Tonnetz. The mode-inverting LPR operations do not change depending on their input; the same actions are performed on the triad, whether the input is a major triad or a minor triad; in every case, the opposite mode is the output. This may be contrasted with, for instance, the RD operation, which requires a 5-dyad as its input.
Return to text
38. If we consider T+/-2 , TTSL-1 and TTSR-1, all of which are less parsimonious, to be permissible transformations, this number rises to ten.
Return to text
39. There are five options available when beginning with a 6-dyad as opposed to a 5-dyad, because there is only one reflection transformation (RT) for 6-dyads as opposed to two (RU and RD) for 5-dyads. As before, if we consider T+/-2, TTSL and TTSR permissible transformations, this number of possibilities rises from five to nine.
Return to text
40. The pattern of tonicizations used in “Tune Up” (I,
Return to text
41. It is worth noting here that tendency tones may be understood to arise in part due to the voice leading relationships they establish within a tonal context (e.g., the third of a V chord is a tendency tone primarily because it is the leading tone and voice-leads smoothly to the tonic). Yet it is important not to confuse this kind of voice leading with the voice-leading syntax of gt space: the voice-leading relationship gts establish within their key is, I argue, often separate from the parsimonious voice-leading transformations that comprise gt space because the latter is limited only by the proximity of individual pcs to one another in mod 12 space, not by diatonic tonality.
Return to text
42. Lewin’s transformational attitude has been discussed in great detail in the literature. His original discussion can be found in Lewin (1987, 158). Commentary and reflections on the attitude may be found in Klumpenhouwer (2006), Harrison (2011), Attas (2009), and Roeder (2009).
Return to text
43. Lewin characterizes the observational quality of analysis as Cartesian. For a closer examination of this conceptualization see Klumpenhouwer (2006).
Return to text
44. Chord changes adapted from The Real Book (Vol. 1, fifth edition).
Return to text
45. There is controversy over whether “Solar” was indeed written by Davis. Although the copyright is in Davis’s name, the composition bears a great deal of resemblance to Chuck Wayne’s earlier piece entitled “Sonny.” Gioia (2012) notes that Davis’s alterations, which include the minor tonic chord that begins the composition, as well as an ascending scalar melodic line at the turnaround, have become some of the better known characteristics of the tune. For more on the authorship of “Solar,” see Gioia (2012, 377–78).
Return to text
46. Pachet (2000) uses computer analysis to investigate whether “Solar” is in fact a blues. He finds that the tune does not qualify as a blues, despite the reportedly commonly held perception that it is. Gioia (2012) attributes the tune’s popularity in part to the fact that it “adopts the 12-bar form of the blues, but with chord changes that are more boppish than bluesy” (377). Gioia likewise considers the tune to suggest the changes of a minor blues, only to thwart that expectation in the fifth measure.
Return to text
47. For an overview of recent scholarly and pedagogical work on jazz harmony, see Stover (2014).
Return to text
48. There are additional uses for gt space that I have not explored here. Rather than focusing only on gt dyads, single gt lines may be modeled on the gt Tonnetz in order to show how efficient voice leading connects chords where only one gt moves smoothly. Similarly, gt space may shed light on how soloists navigate chord changes by plotting structurally significant gts in improvised solos. The gt Tonnetz may also be used compositionally to plot a series of gt voice-leading transformations that can be fleshed out harmonically or improvisationally to help improvisers conceive of chord substitutions through shared gt voice leading. In this sense, gt space functions similarly to what Robert Morris (1995) calls a “compositional space.”
Return to text
49. Similar uses of gt voice leading in postbop may be found in Shorter’s “E.S.P.,” as well as in Herbie Hancock’s compositions “Dolphin Dance,” “Speak Like a Child,” and “One Finger Snap.”
Return to text
Copyright Statement
Copyright © 2019 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Sam Reenan, Editorial Assistant
Number of visits:
13863