Uniform Information Density in Music
David Temperley
KEYWORDS: information, probability, counterpoint, performance expression
ABSTRACT: The theory of Uniform Information Density states that communication is optimal when information is presented at a moderate and uniform rate. Three predictions follow for music: (1) low-probability events should be longer in duration than high-probability events; (2) low-probability events should be juxtaposed with high-probability events; (3) an event that is low in probability in one dimension should be high in probability in other dimensions. I present evidence supporting all three of these predictions from three diverse areas of musical practice: Renaissance counterpoint, expressive performance, and common-practice themes.
DOI: 10.30535/mto.25.2.5
Copyright © 2019 Society for Music Theory
1. Introduction
[1.1] Describing the music of Palestrina eighty years ago, Knud Jeppesen offered this general characterization:
It avoids strong, unduly sharp accents and extreme contrasts of every kind and expresses itself always in a characteristically smooth and pleasing manner.
. . . (1939, 83)(1)
Much more recently, William Rothstein made the following suggestions for the performance of a passage from a Chopin Prelude:
The heightened chromaticism and dissonance, along with the faster harmonic rhythm, offer resistance to the uniform acceleration that might be appropriate to a simpler or more diatonic sequence.
. . . [T]he frequent chord changes require a little more time than repeated chords would have done. (2005, [25])(2)
These two quotes—the first about a Renaissance composer, the second about expressive piano performance—might seem to have little in common. I will suggest, however, that they both reflect a fundamental principle of communication: the principle of Uniform Information Density (UID). In this article I will argue that UID has great explanatory value with regard to music. I begin with an overview of the mathematical foundation of UID and consider some of its general predictions for music. I then consider a variety of musical phenomena that are illuminated by the principle of UID, drawing from three quite different musical domains: Renaissance counterpoint, expressive piano performance, and motivic repetition in common-practice music. In the final section of the article, I consider some possible objections to the current argument, alternative explanations for the findings, and possible directions for further research.
2. Information and UID
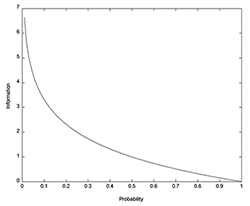
Example 1. The relationship between probability and information
(click to enlarge)
[2.1] Information, in the mathematical sense, is the negative log (base 2) of probability (see Example 1). As probability goes up, information goes down. Information is typically measured in “bits”: outputs of a binary variable (i.e. a variable that can be either 0 or 1).(3) If an event has a probability of 1/2, it conveys 1 bit of information, since –log(0.5) = 1. (Base 2 is assumed in all logarithmic expressions that follow.) If its probability is 1/4, it conveys 2 bits; if its probability is 1/8, it conveys 3 bits. If an event has a probability of 1—we were certain that it would happen, and it did—it conveys no information, which seems intuitively right. If it has a probability of zero, it conveys infinite information (somewhat less intuitive, perhaps), since –log(0) is infinity. The information conveyed by a single event A, which we will notate as I(A), is sometimes known as its surprisal.
[2.2] Probability is clearly subjective—what is expected for one listener may be surprising for another—and therefore information is subjective too. In order to generalize about probability and information in music, one must make assumptions about the shared expectations of a population of listeners. It is natural to suppose that a listener’s expectations and perceptual inferences are shaped by the music that they hear, and there is in fact considerable evidence for this (Krumhansl 1990; Saffran et al. 1999; Hannon and Trehub 2005). Expectations are thus (to some degree anyway) style-specific, dependent on the listener’s experience.(4) Probabilistic methods provide a powerful way of modeling such learned expectations.
[2.3] The value of probabilistic modeling has been proven in a variety of areas of cognitive science, including vision (Kersten 1999), language (Bod et al. 2003), and reasoning (Tenenbaum et al. 2006). In music research, probabilistic modeling has a considerable history, going back to the 1950s. Early studies in this area drew inspiration from the field of information theory (Meyer 1957; Youngblood 1958; Cohen 1962); more recent work has explored other probabilistic approaches (Huron 2006; Pearce and Wiggins 2006; Temperley 2007; Mavromatis 2005; White 2014).(5) Particularly noteworthy in the current context is the work of Duane (2012, 2016, 2017), who has used information content to quantify the textural prominence and “agency” of musical lines, and to distinguish thematic from non-thematic textures. The current study complements this work, introducing a further musical application of probabilistic modeling that has not been much explored.
[2.4] In a sequence of multiple events A, B, C,
(1) P(A, B, C
. . . ) = P(A) × P(B) × P(C) ×. . .
Crucially, the “probability of an event” here refers to its conditional probability, taking into account everything that is used to judge its probability. In music, this could include the previous event or events, structural factors such as the key and meter, and more general stylistic context. Given equation (1), it follows that the total information conveyed by a sequence, I(A, B, C
(2) I(A, B, C,
. . . ) = –log(P(A, B, C,. . . )) = –log(P(A) × P(B) × P(C) ×. . . ) = – (log P(A) + log P(B) + log P(C) +. . . ) = I(A) + I(B) + I(C) +. . .
It is useful also to think of the information of the sequence per unit time, representing the information flow or information density of the sequence; this can be calculated for the entire sequence, or for smaller segments or individual events.(6)
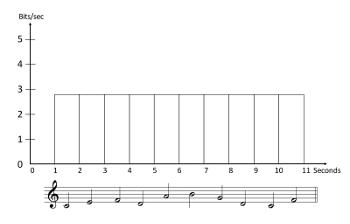
Example 2. A 10-note melody, showing the information density (bits per second) of each note, assuming that the seven notes of the C major scale in the octave above middle C each have a probability of 1/7
(click to enlarge)
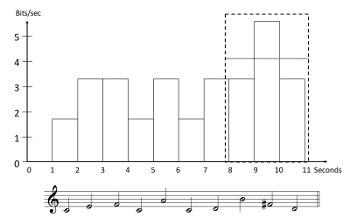
[2.5] Consider a very simple example. Suppose we have a musical style constructed entirely from the seven degrees of the C major scale, in just one octave, C4 to B4; each note is one second long (see Example 2). If all seven pitches are equal in probability, each one will have a surprisal of –log(1/7) = 2.8 bits, and the information density will be 2.8 bits per second. (For the probabilities to be well-defined, the probabilities of all possible events must sum to 1: in this case, 7 × 1/7 = 1.) If the speed were doubled, the surprisal of each note would stay the same, but the information density would double, to 5.6 bits per second.
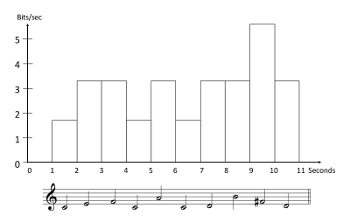
Example 3. A 10-note melody, showing the information density of each note, assuming P(C) = .3, P(D) = P(E) = P(F) = P(G) = P(A) = P(B) = .1, and P(
(click to enlarge)
[2.6] Let us consider a slightly more complex musical language. Now all twelve degrees of the chromatic scale are allowed, still in the octave above middle C. C has a probability of 0.3 (1.7 bits); the other six degrees of the C major scale have probabilities of 0.1 each (3.3 bits); the five chromatic degrees have probabilities of 0.02 each (5.6 bits). A rather typical melody generated from this language is shown in Example 3. Again, we assume each note is one second long; thus the height of each rectangle in the example represents both the surprisal of the corresponding note, and its information density (bits per second).
[2.7] An infinitely long melody generated with the probabilities defined above would have an average information density of 3.1 bits per second.(7) From moment to moment, however, the information density is highly variable. The frequent C’s have a density of 1.7 bits per second; at the other extreme, the occasional chromatic notes have a much higher density of 5.6 bits per second. This brings us to the concept of Uniform Information Density (Fenk-Oczlon 1989; Levy and Jaeger 2007). The idea of UID is that communication is most efficient if information is presented at a moderate and fairly uniform rate: high enough to take full advantage of the listener’s information-processing capacity, but not so high as to overwhelm it. Research in psycholinguistics has shown that this principle affects language production in a variety of ways. For example, unexpected words tend to be pronounced more slowly than expected words; this tends to smooth out the information density, since the high information of an unexpected word is spread out over a longer time interval (Bell et al. 2003; Aylett and Turk 2004). (Other examples of UID from psycholinguistics will be presented below.) The central thesis of the current study is that this principle is operative in music as well.
[2.8] How could the information density of the melody in Example 3 be made more uniform? (For now, we simply calculate the density of each note individually, though this is not the only way to do it, as explained below.) One way would be to change the actual pitch content of the melody—for example, making it consist entirely of C’s—but that would change the distribution of events, and therefore their probabilities, if it were done consistently throughout the style. Let us consider other ways of adjusting the information density of the melody that maintain the overall event distribution.
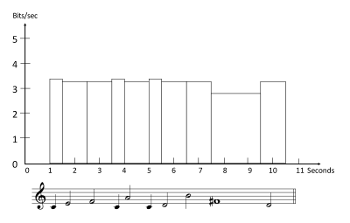
Example 4. The melody in Example 3, with the durations of notes adjusted to create a more uniform information density
(click to enlarge)
[2.9] One way to make the information density of Example 3 more uniform would be to lengthen the less probable notes and shorten the more probable ones. (This is exactly analogous to the phenomenon of lengthening unexpected words, mentioned above.) Example 4 provides a graphic representation of this. As before, the height of each rectangle represents the information density of the note; now, however, the surprisal of each note, its information content, is represented by the area of the rectangle, not its height. If the surprisal of a note is constant, then increasing the duration of the note (the width of the rectangle) will reduce the information per unit time (information density—the height of the rectangle) by a corresponding amount. In Example 4, the C’s have been halved in length, doubling their density, and the
UID Strategy 1 (Stretching): Lengthen low-probability events and shorten high-probability events.
[2.10] It should be noted that rhythm itself carries information: we form expectations not only for what will occur but also when it will occur (Hasty 1997; Jones et al. 2002). The examples presented in this section make sense only if we assume that the rhythm and timing of the melody is known beforehand (thus conveying no information). I retain this implausible assumption for now, but address it more critically later in the article.
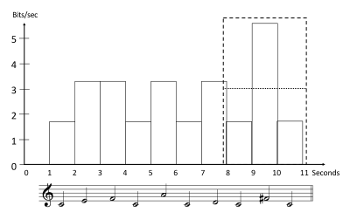
[2.11] Up to now, we have assumed that density is calculated for each event individually. Suppose we assume, instead, that density at each point is calculated over the last several events—say, three. In terms of our graphic representation, the information density at a point in the melody is now calculated as the average height of the preceding three rectangles (weighting each rectangle by its width). In Example 5, the melody from Example 3 is shown, along with the density calculation for the final three notes, yielding a value of 4.1 bits per second. The idea of calculating density over multiple events seems cognitively plausible. The processing of an event, whatever that entails (categorizing it, interpreting it, and so on), might well continue as the following events are being presented, so that multiple notes are being processed at once. If a very unexpected note occurs, the possible information overload due to this could be mitigated by surrounding it with events that are low in information. In the case of our artificial musical language, information density could be made more uniform by juxtaposing very low-probability events (such as chromatic notes) with high-probability events (such as C’s), as shown in Example 6. For the three-note window around the
UID Strategy 2 (Juxtaposing): Place low-probability events in close proximity to high-probability events.
Example 5. The dashed rectangle shows a window of three events within which information density is calculated; the dotted line shows the resulting value (the melody is the same as in Example 3) (click to enlarge) | Example 6. The melody is the same as in Examples 3 and 5, except the 8th and 10th notes are altered, reducing the information density of the last three notes; the dotted line shows the resulting value (click to enlarge) |
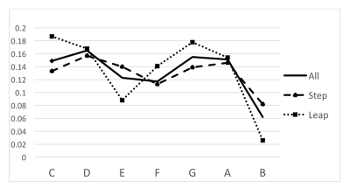
Example 7. The melody is the same as in Example 6, but now the probability of each note is calculated as the average of its scale-degree probability, SDP (calculated as before), and its interval probability, IntP, where P(step) = .2 and P(leap or repetition) = .025. Calculations are shown in the table above the graph
(click to enlarge)
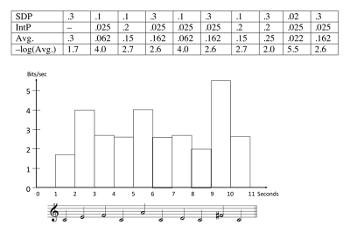
[2.12] A third strategy for smoothing out information flow is illustrated in Example 7. Suppose now that the probability of each note is determined not only by its scale degree, but by a second factor as well: the pitch interval to the previous note. We define the probabilities of intervals in a very simple way: each of the four stepwise motions (+m2, +M2, –m2, –M2) has a probability of 0.2; the remaining 0.2 is divided equally among the other eight pitches, giving each one a probability of .025.(8) (This includes seven “leaps” as well as the unison interval, i.e. a repetition. Intervals that go outside the one-octave range wrap around to the other side: from C4, –m2 goes to B4.) At each note in the melody, the “interval” probability of the note must be combined with its “scale-degree” probability to yield a single probability for that pitch, given its prior context. This can be done in various ways; one simple method is to take the average of the two probabilities.(9) The pitches that are most probable overall will then be ones that are probable under both measures: probable as scale-degrees (tonic or diatonic), and approached by step. Consider the information density that results from this for the melody in Example 7. (Once again, we calculate information density on a note-by-note basis; since all notes are one second long, surprisal and density are equivalent.) It can be seen that the density is highly variable: the
UID Strategy 3 (Softening). If the probability of an event is determined by multiple factors or dimensions, events that are low in probability in one dimension should be high in probability in other dimensions.(10)
In the remainder of the article, I examine a variety of phenomena in music composition and performance that can be explained by the three UID strategies presented above.
[2.13] The most straightforward prediction of UID is that the rate of information flow will be uniform across all music. This is not a prediction that can be tested now or in the foreseeable future. Even quantifying the overall flow of information in a single musical style is a daunting prospect. Every aspect of music conveys information—this includes timbre, dynamics, articulation, and so on; quantifying the information content of all of these dimensions would be a monumental task. Comparing the flow of information across styles would be even more difficult.(11) A more manageable goal is to examine the flow of information within certain dimensions of a single style, to determine whether it seems to reflect the strategies of UID articulated above. This is my approach in the discussions that follow.
[2.14] Information is often associated with the concept of complexity: something containing more information tends to be perceived as more complex. From this viewpoint, UID connects with the ideas of the psychologist Daniel Berlyne (1960, 1971). Berlyne hypothesized that a moderate level of complexity is aesthetically optimal, applying this idea to music as well as to other arts. A number of experimental studies have tested Berlyne’s theory with regard to music, finding qualified support for it (Vitz 1964; Heyduk 1975; North and Hargreaves 1995; Witek et al. 2014). Intuitively, Berlyne’s hypothesis rings true: many of us have had the experience of finding a piece either so complex as to be incomprehensible, or so simple as to be boring—suggesting both that complexity is a factor in aesthetic experience, and that an intermediate level of complexity is optimal. In theory, information offers a rigorous, precise way of quantifying complexity—though the subjective nature of information itself, and of its aesthetic value, must be borne in mind.(12) Berlyne himself recognized the connection between complexity and information (see especially Berlyne 1971), but did not explore its musical implications in depth, as the current study does.
[2.15] Any theory of musical experience and behavior that relies heavily on expectation faces the problem that listening to music can be rewarding even when the music is very familiar; in that case we presumably know what is going to happen, so little or no information is being conveyed. This problem has long been recognized, and various solutions have been proposed (Meyer 1961, Bharucha 1987, Jackendoff 1991); one possibility is that our musical expectations are to some extent “modular,” unaffected by our knowledge of what will actually occur. In any case, the idea that expectation plays an important role in musical experience—even with familiar music—seems widely accepted (Lewin 1986, Hasty 1997, Narmour 1990, Larson 2004, Margulis 2005, Huron 2006), so I see no need to defend it here.
3. UID in Renaissance Counterpoint
[3.1] Renaissance counterpoint involves a number of rules that tend to be quite strictly and consistently applied. Treatises on counterpoint rarely attempt to explain why the rules are as they are. An exception is the work of Huron (2001, 2016), who shows that many contrapuntal rules can be attributed to the fundamental goal of maintaining the perceptual cohesion and independence of the voices; this explains, for example, the preference for small intervals and the avoidance of parallel perfect consonances. In this section, I will show that the principle of UID complements Huron’s theory, explaining a number of rules that are not covered by his account.
[3.2] Modern treatises on Renaissance counterpoint tend to take Palestrina as the primary model—perhaps because his style is the most “rule-governed”—and I will do so here as well. I rely mainly on the codification of the rules presented in Gauldin (1985), though other texts offer quite similar presentations (Benjamin 1979; Schubert 1999; Green and Jones 2011). Where possible, I verify the rules using statistical corpus data. Here I employ a corpus of 717 Palestrina mass movements; I will refer to this as the “Palestrina corpus.”(13)
Example 8. From Gauldin 1985, 38
(click to enlarge)
Table 1. Pre-Leap and Post-Leap Lengthening in Palestrina
(click to enlarge)
[3.3] One set of rules concerns the intervallic treatment of notes of different rhythmic values. According to Gauldin (1985, 39), eighth notes in Renaissance counterpoint must be approached and left by step. Regarding quarter notes, the situation is complex. For multiple quarter notes in sequence, “downward leaps generally take place from the beat to the offbeat, while upward leaps take place from the offbeat to the beat” (1985, 38). (The “beat” in Palestrina’s style is the half note. One of Gauldin’s examples of characteristic quarter-note usage is shown in Example 8.) In other words, downward leaps to metrically strong quarter notes and upward leaps to weak quarter notes are generally avoided. The use of quarter notes adjacent to longer notes is restricted also: leaps to quarter notes from whole notes are prohibited, as are ascending leaps to quarter notes after dotted half notes (1985, 38). Regarding longer notes (half notes, whole notes, and breves), there are no constraints on intervallic treatment, beyond the global constraints on melodic intervals (nothing larger than a perfect fourth except perfect fifths, octaves, and ascending minor sixths) and those relating to adjacent shorter notes. Altogether, then, the constraints on leaps to and from notes increase as the notes get shorter: for half notes (and longer), leaps are unrestricted; for quarter notes, they are somewhat restricted; and for eighth notes, they are prohibited. This is borne out by a statistical analysis of the Palestrina corpus, as shown in Table 1: the proportion of leaps to and from notes increases as the notes get longer. We might say, then, that Renaissance music exhibits both “pre-leap lengthening” and “post-leap lengthening.”
[3.4] To explain this phenomenon from a UID perspective, we must consider the surprisal (information content) of different intervals. Counterpoint treatises on Renaissance counterpoint generally emphasize that conjunct (stepwise) motion is the norm, with occasional leaps and repetitions. In Gauldin’s words, the style “features basically stepwise movement” (1985, 17). The Palestrina corpus reflects this as well: 68.0% of all melodic intervals are stepwise, 21.0% are leaps, and 11.0% are repetitions. Thus, a given note is most likely to be followed by another note a step away. Moreover, a leap could be to one of a number of different notes, whereas a step could only be to one of two. (Palestrina’s music stays almost entirely within the “white-note” scale, with the exception of leading tones at cadences; one other important exception is discussed below.) Thus the two stepwise possibilities are far more likely than any other. Combining this with the statistics on post-leap lengthening shown in Table 1, we can say that the shorter the note, the more probable it tends to be in terms of pitch, and thus, the less information it tends to convey. Eighth notes, always approached by step, convey very little pitch information; whole notes, often approached by leap, are relatively high in information. Viewed in this way, post-leap lengthening would seem to be a clear-cut case of the “Stretching” strategy proposed above (UID Strategy 1): notes high in information are generally longer, thus evening out the overall information flow.
[3.5] This reasoning accounts nicely for post-leap lengthening; but there is also strong evidence for pre-leap lengthening (see Table 1). Why would the note before a leap tend to be long? One could possibly attribute this to the “Juxtaposing” strategy: A long note before a leap, being low in information density due to its length, gives the listener a chance to “clear the decks,” as it were, and finish up the processing of the pre-leap note and preceding notes (processing that might normally spill over into the post-leap note), freeing up cognitive resources for the post-leap note. But I find this explanation rather unconvincing. We would expect the tendency for pre-leap lengthening to be weaker than that for post-leap lengthening, since the pressure of UID applies more directly in the latter case; adding time after an unexpected event is presumably more helpful to the listener than adding time before it. But in fact, Table 1 suggests that the two tendencies are about equally strong. There may be another factor at work here, suggested by Huron (2001, 28–30): large intervals tend to follow long notes because a large jump in pitch requires more time to plan and execute.(14) However, this reasoning does not convincingly explain why the note after a leap would tend to be lengthened; in that case, UID offers a better explanation. If I am correct, then, pre-leap lengthening and post-leap lengthening may arise for quite different reasons.
Example 9. Pitch classes approached by step and leap in Palestrina masses
(click to enlarge)
[3.6] Another constraint on the use of leaps is also of interest. Gauldin states: “Although leaps may occur to any pitch class, the note
[3.7] Why would leaps to B be avoided? Let us assume, as suggested earlier, that the subjective probability of a note—its expectedness in the mind of an experienced listener—depends, inter alia, on the pitch class of the note and the interval from the preceding note. The two probabilities must be combined in some way to produce a single probability—perhaps by averaging or multiplying them, as proposed in Section 2. Since (as already established) leaps are relatively low in probability, leaping to a pitch class that is low in overall probability will produce a note that is low in probability in both respects, creating a marked “spike” of information. Favoring a stepwise approach to B avoids such spikes. The dispreference for leaps to B, then, could be attributed to the “Softening” strategy proposed above; its effect is that a pitch class that is low in probability in one respect tends to be high in probability in another respect. (Why the rule should apply especially to ascending leaps is not obvious. It may be because B has an especially strong tendency to move up by step, so that approaching it by ascending leap would result in the undesirable pattern of a leap followed by a step in the same direction. But this is does not entirely explain the rarity of leaps to B, since—as noted earlier—it is evident in descending leaps as well.)
[3.8] Other rules relate to the setting of text. In general, a quarter note or eighth note may not carry a syllable of text; such notes must be part of a melisma spanning multiple notes.(15) There are constraints on melismas as well: A melisma “normally” begins with a “relatively long duration” (22), and it must end with something longer than a quarter note (39). All three of these rules can be attributed to the UID “Stretching” strategy. The beginning and ending of a syllable both convey information: in phonological terms, the beginning carries the onset (the initial consonant, if any) and vowel, while the end carries the coda (the final consonant, if any). Thus, the boundary between two syllables is high in information, conveying both the end of one syllable and the beginning of the next. Elongating the notes on either side of this boundary stretches out the pitch information around this point (and perhaps the linguistic information as well—increasing the distance to other syllable boundaries), reducing the overall density of information. This explains the lengthening of the first and last notes of a melisma, which carry the beginning and ending of a syllable, respectively, as well as “syllabic” notes which carry both the beginning and ending of a syllable and thus have a boundary on either side.
Example 10. From Gauldin 1985, 39
(click to enlarge)
[3.9] There is one curious exception to the prohibition of syllabic short notes. When a word has three or more syllables and the second-to-last syllable is unstressed, it may be attached to a quarter note, as shown in Example 10 (Gauldin 1985, 39). Here too, UID offers an explanation. A non-initial syllable of a polysyllabic word is highly predictable, given the previous syllable(s); therefore, its information content is low, making the usual “stretching” of syllables unnecessary.
[3.10] One might question my assumptions about the information content of texts in this style. Many texts were used repeatedly—especially the text of the mass; thus, the words were presumably very familiar and thus predictable to listeners. Once we hear “Kyrie” at the beginning of a mass, the following word “eleison” is not a surprise! (The same point may be made about syllables and their sub-parts.) But in some pieces, such as motets, the texts were not so familiar; a general strategy of smoothing out the flow of text information may have done some good in those cases, and little harm the rest of the time.
[3.11] In this section, I have considered a number of rules of Renaissance counterpoint that can be explained by strategies of UID, pertaining to three different aspects of the style: the intervallic treatment of notes of different duration, the intervallic approach to B, and the setting of text. The current perspective complements Huron’s idea that many rules of counterpoint are explicable as strategies to maintain the perceptual independence of voices; a number of the remaining rules seem to be attributable to UID. The style of Palestrina appears to be particularly strongly influenced by information flow, perhaps more than any other musical style. It may be this that gave rise to Jeppesen’s intuition, reflected in the quote at the beginning of this article, that Palestrina’s music “avoids strong, unduly sharp accents” (perhaps a “sharp accent” is a spike in information?) and “expresses itself always in a characteristically smooth [my italics] and pleasing manner.”
4. UID in Expressive Performance
[4.1] A successful performance of a classical piece must be not only technically correct, but also aesthetically compelling and satisfying—in a word, “expressive.” The factors contributing to expressive performance have long been a topic of study in music psychology. Of particular interest in this regard, researchers at the KTH Royal Institute of Technology in Stockholm (Sundberg 1988, Friberg et al. 2006) have explored a variety of expressive strategies and their effects on judgments of performance quality. On the basis of this work, they propose a series of prescriptions for good expressive performance, relating structural musical features to interpretive dimensions such as timing, dynamics, and articulation. Some of these prescriptions are well-known maxims of applied music teaching: for example, a decrease in tempo is recommended at the end of a phrase. Others are less obvious, or at least less frequently articulated, such as the “Harmonic Charge Rule,” which prescribes an “emphasis on chords remote from [the] current key,” by means of dynamics (increased loudness) and tempo (slowing down). “Remoteness from the current key” would seem to imply chromatic chords, or perhaps chords that initiate a modulation to a distant key. The KTH team actually quantify the remoteness of a chord as the average circle-of-fifths distance of its notes from the current tonic, which roughly enforces the “chromatic versus diatonic” distinction, though not precisely.
Example 11. Chopin, Prelude op. 28, no. 17, mm. 21–28 (with my harmonic analysis)
(click to enlarge)
[4.2] Why would one slow down on chromatic chords? Presumably chromatic chords are less common than diatonic chords, at least in music before the late 19th century. (Corpus studies provide evidence —if any is needed—that tonal pieces predominantly use pitches from the scale of the current key [Krumhansl 1990; Temperley 2007].) Thus, chromatic chords are generally unexpected, as are chords that initiate modulations to distant keys (which also tend to go outside the current scale). The UID “Stretching” principle predicts that one would typically slow down on these unexpected events. Note that this is an application of UID rather different from those discussed previously: It is not only surface elements (notes) that convey information in music, but also the structural elements that they convey, such as harmonies; thus, it is natural that less expected harmonies would be lengthened.(16) (Exactly that situation is illustrated in Examples 3 and 4, though now we are taking the rectangles to represent harmonies, not notes.) And this aligns with Rothstein’s advice about the Chopin Prelude, quoted at the beginning of this article; his comments concern the passage shown in Example 11, specifically mm. 24–6. Since this is a passage of “heightened chromaticism and dissonance,” Rothstein argues, one should take more time on it, avoiding “the uniform acceleration that might be appropriate to a simpler or more diatonic sequence.”(17) (The idea that one would normally accelerate on a sequence is interesting too, and I will return to it below.)
Example 12. A pair of excerpts used in Bartlette’s (2007) experiment
(click to enlarge)
[4.3] The KTH team’s tests of their performance rules were rather informal: they played performances artificially generated with different combinations of rules, and had listeners judge their quality. Is there any more definitive evidence that expert performers slow down on chromatic harmonies? Bartlette (2007) examined this question in an experimental study. Expert pianists (graduate-level piano students) played short tonal excerpts like those shown in Example 12; the excerpts were in pairs that only differed in one “target” chord (marked with a box in the example), which was diatonic in one case and chromatic in the other. The timing, dynamics, and articulation were then examined. The performers were given as much time as they desired to practice the excerpts before performing them, so as to eliminate any factor of performance difficulty. Consistent with the predictions of UID, Bartlette found that the chromatic target chords were indeed lengthened slightly in relation to the diatonic ones; the difference was small (about 2%) but statistically significant (2007, 82). When the statistical analysis was confined to excerpts in a “lyrical” style (like Example 12)—as opposed to “march-like” or “moto perpetuo” ones—a somewhat greater lengthening of chromatic chords was found, about 5% (2007, 83).(18)
[4.4] An additional feature of Rothstein’s quote deserves comment: it is not just the chromaticism of the harmony in Example 11, but also the “frequent” chord changes that exert pressure for a decrease in tempo. Here too, we can find an explanation in UID, applying the principle once again to the underlying harmonies rather than the notes themselves. In general, a faster harmonic rhythm will have a higher information density than a slower one. In the case of the Chopin Prelude, the harmony shifts from a one-measure rhythm, as has prevailed through most of the piece up to that point, to a half-measure rhythm (or arguably even faster) in m. 24.(19) So by the “Stretching” rule, a relaxation of the tempo would be quite appropriate, regardless of what the harmonies are.(20)
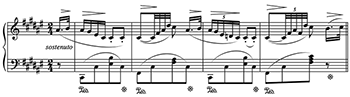
Example 13. Brahms, Intermezzo op. 116, no. 6, mm. 1–8
(click to enlarge)
[4.5] If we expect expert composers to facilitate UID, it seems natural to expect expert performers to do so as well. With regard to performance expression, UID predicts a decrease in tempo on remote harmonies (whether they are chromatic or modulatory), and on passages of rapid harmonic change. There is experimental evidence for the first prediction; for the second, I have presented no evidence beyond Rothstein’s quote. Another source of evidence for both predictions, anecdotal but in my view rather compelling, comes from expressive tempo markings in scores. In many cases, indications of tempo deceleration—ritardandi, rallentandi, and the like—seem to coincide with moments of chromatic or modulatory harmony or rapid harmonic rhythm, and do not seem explicable in any other way. (Such tempo indications reflect the thinking of composers rather than performers, though presumably they influence performers’ behavior.) Romantic piano music offers abundant examples of this; one is shown in Example 13. Why does Brahms mark mm. 6–8 with a sostenuto (implying a slowing of tempo) and a fermata? One might normally slow down a bit at the end of any eight-measure phrase, but composers do not usually indicate this explicitly.(21) I suggest that Brahms’s expressive markings here are due to the somewhat increased harmonic rhythm—mm. 6–8 feature chord changes on six quarter-note beats in a row, which has not occurred previously—as well as the remoteness of the harmonies in relation to the previous harmonies and to one another: we first move to D dominant seventh on the last beat of m. 6, far in the flat direction given the previous tonicization of
5. UID in Common-Practice Motivic Patterns
[5.1] A fundamental feature of common-practice music is the immediate repetition of intervallic patterns, sometimes at the original pitch level but often shifted along the diatonic scale; such shifting preserves the diatonic intervals within the pattern, but not usually the chromatic ones. The shifting of the four-note motive down by a step at the beginning of Beethoven’s Fifth Symphony is one famous example; the repetition of the four-measure melodic phrase at the opening of Mozart’s Symphony no. 40, also down by a step, is another. The term “sequence” is often used to describe such patterns, though not always (the two themes just mentioned would not normally be described as sequential). From the point of view of information, such patterns raise an important general point: Given that we expect repetition (in most styles anyway), the second instance of a pattern (and any subsequent instances) will generally be lower in information than the first. Given the first four measures of the Mozart theme, for example, the repetition of the pattern in the next four measures surely becomes more predictable, especially after it starts and one realizes that a repetition is underway. To model the information content of such passages in a rigorous way is quite challenging. One way is to assume that each note has a schematic probability, reflecting general considerations such as its scale-degree and intervallic context, as well as a contextual probability, reflecting whether it takes part in a repetition of a preceding intervallic pattern; notes that do are contextually more probable than those that do not.(22) These probabilities must then be combined in some way. I have proposed such a model in another recent study (Temperley 2014); I present just a brief summary of the study here.
[5.2] The widespread use of repeated intervallic patterns in music is, in itself, something of a counterexample to the UID theory, since it generally causes an unevenness in information density: the first pattern instance tends to be much lower in contextual probability (and therefore overall probability) than subsequent instances. It is notable that Palestrina’s style generally avoids sequential patterns (Gauldin 1985, 23)—another reflection, perhaps, of its unusually strong preference for uniform information flow.(23) In common-practice music, where sequential repetition is common, UID predicts that composers and performers might take steps to increase the information density of non-initial pattern instances. One way to do this, from a performer’s viewpoint, would be to accelerate on non-initial pattern instances; I know of no evidence of this, though interestingly, Rothstein seems to advocate it in the passage quoted above (“uniform acceleration” would be “appropriate” for a diatonic sequence). Another possibility is that composers might seek to lower the schematic probability of non-initial pattern instances, so as to counterbalance their high contextual probability.
Example 14. (A) Mozart, “Non so piu” from Le nozze di Figaro, mm. 1–5; (B) Mozart, Piano Trio K. 548, II, mm. 1–2
(click to enlarge)
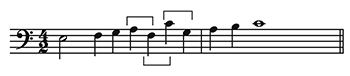
[5.3] If a composer wished to lower the schematic probability of a non-initial instance of a repeated pattern, how might this be done? One way would be to change its intervallic content. Suppose just a single interval was changed in the second instance of the pattern (I will call this an “altered repetition”). The other intervals of the pattern would remain high in contextual probability (since they repeat the intervals of the first pattern instance); to counteract this, it would be desirable for the altered note to change to one whose schematic probability was relatively low. This could be done by altering a small interval to a larger one. Example 14a shows a case in point: a single interval is increased in size (from a sixth in the second measure to an octave in the fourth measure).(24) The schematic probability of the second pattern instance could also be lowered by changing a diatonic note to a chromatic one, as in Example 14b.
[5.4] I tested the general validity of these predictions using a corpus of about 10,000 common-practice melodies, Barlow and Morgenstern’s Dictionary of Musical Themes.(25) In cases where a single interval in a sequential repetition is changed, the interval is increased in size in a majority of cases (57.8%). And alterations from a diatonic note to a chromatic note in sequential repetitions are significantly more common than alterations from a chromatic note to a diatonic one: 74 themes show the former pattern, versus 48 showing the latter pattern. (See Temperley 2014 for further details of the study.) Both of these phenomena are representative of the “Juxtaposing” UID strategy described in Section 2 (though they also involve the mixture of contextual and schematic probabilities for each note, and thus have elements of the “Softening” strategy). The overall low information density of a non-initial motivic segment can be mitigated by mixing in a note that is low in both contextual probability (by breaking the repetition) and schematic probability (by being chromatic or approached by a large interval). Interestingly, there is a parallel with language here. In coordinate constructions, where two noun phrases are joined together with a conjunction like “and” (e.g. “he wore a black suit and a magenta cummerbund”), there is a strong tendency for the second noun phrase to match the first in syntactic structure, making the second phrase high in contextual probability; but the second phrase also tends to use less frequent words, making it lower in schematic probability (Fenk-Oczlon 1989; Dubey et al. 2008; Temperley and Gildea 2015).
Example 15. Chopin, Nocturne op. 15, no. 2, mm. 1–4
(click to enlarge)
[5.5] Another way that one might lower the schematic probability of the non-initial instances of a pattern is by adding notes, thus increasing the rhythmic density of the pattern (and hence its information density). And indeed, this strategy is very frequent. A striking source of evidence is the piano music of Chopin, which is full of repeated patterns that are varied and elaborated; usually the pattern is presented first in a relatively simple, sparse form, and notes are then added in subsequent instances. Example 15 shows one case of this. That this is the general norm in such situations—the simple version of the pattern is presented first, then the elaborated one—seems so obvious as to require no proof. (Imagine how odd it would sound if Chopin had started with mm. 3–4 of Example 15, followed by mm. 1–2!) Again, we should bear in mind that rhythm itself carries information; but even if a denser rhythmic pattern is more probable than a sparser one, the denser pattern involves more choices in terms of pitch content, and thus is likely to be less probable overall.(26)
Example 16. Rare types of non-chord tone used motivically
(click to enlarge)
[5.6] UID may affect motivic repetition in another way as well. In his book on Baroque counterpoint, Gauldin discusses various types of non-chord tones: common types such as passing and neighboring notes, and less common types such as leaping tones (approached by leap, left by step), escape tones (approached by step, left by leap), and anticipations (left by repetition). Gauldin notes that the latter three types of non-chord tones are rare, but “can be exploited motivically” (1995, 62). Similarly, Schubert and Neidhöfer write that when an anticipation in Baroque counterpoint “is used in the course of a line, it is best used as a recurring motive” (2006, 42). Example 16 shows this phenomenon in two of Bach’s most famous themes. Why would leaping tones, escape tones, and anticipations be especially associated with motivic usage? Since these types of non-chord tones are rare, they are low in schematic probability; but as with any melodic pattern, an immediate repetition of the pattern will have increased contextual probability. So again, the “Softening” strategy seems to be at work here: the pattern’s increased contextual probability compensates for its low schematic probability. UID explains why it is the rarest types of non-chord tones that are particularly conducive to motivic repetition. Admittedly, this explanation only applies to non-initial instances of the pattern; the first instance creates an information spike that is not softened. Possibly the “Juxtaposing” strategy is applicable here: the low information of the second pattern instance somewhat mitigates the high information of the preceding first instance. Here again, there is an analogy in language: rare syntactic structures show an especially strong tendency to be repeated (Reitter et al. 2011; Temperley and Gildea 2015).
6. Discussion
[6.1] In three very different musical domains—rules of Renaissance counterpoint, patterns of performance expression, and the construction of common-practice themes—we have seen evidence that composers and performers have pursued strategies to enhance the uniformity of information density. In most of the phenomena discussed here, our focus has been on strategies that avoid very high information density. (This is reflected in my names for two of the UID strategies: “Stretching” and “Softening.”) This applies, for example, to ritardandi at points of rapid harmonic change or remote harmony. But UID also predicts the avoidance of very low information density, and that pressure is also often in evidence: for example, the intervallic rules of Renaissance counterpoint serve to avoid both very high density (by restricting the intervallic approach to short notes) and very low density (by imposing fewer restrictions on the approach to longer notes). In the case of altered motivic repetitions, it seems most plausible that composers first considered a literal repetition of the pattern and then altered it so as to raise the information density to a more satisfactory level.
[6.2] Why is UID desirable? In the case of language, there are obvious practical—indeed, evolutionary—advantages to conveying information in a way that is both comprehensible and succinct. (Consider a sentence like “There is a lion behind you.”) In the case of music, those practical advantages are less obvious. But, as discussed earlier, there is an aesthetic motivation for the principle—connecting with Berlyne’s idea of an optimal level of complexity—which is intuitively plausible, supported by some experimental evidence, and consistent with findings in other domains such as visual patterns (Berlyne et al. 1968). Very low information density may leave us bored and unchallenged; very high density may make us feel overwhelmed, unable to process and interpret the events we hear, or even to identify them. The escape-tone motive in Wachet Auf (Example 16a) is so odd that, after its first presentation, we are inclined to wonder if we misheard it; when the pattern is repeated, we realize that, yes, we heard it correctly!(27) Again, research in language offers a parallel: a very unexpected sequence of words can cause us to misidentify the words themselves (Levy et al. 2009).
[6.3] The predictions of UID are to some extent convergent with another important compositional goal, which might be called clarification of structure, or simply “clarity” (Temperley 2007). Consider the case of chromatic notes (in a tonal context): since such notes are high in information, UID predicts that a high concentration of them would result in an overload of information. But a high concentration of chromatic notes might be undesirable from another viewpoint as well: it would create tonal ambiguity—uncertainty about the key—since identification of the key depends at least in part on the distribution of pitch classes (Krumhansl 1990; Temperley 2007). A similar point could be made about highly syncopated rhythms, which are high in information (in common-practice music anyway) and also obscure the meter. While the goals of UID and clarification of structure converge in these cases, they do not always do so. A diatonic hexachord such as C-D-E-F-G-A is tonally ambiguous, as it belongs to the major scales of two keys and contains the tonic triads of both; but since it is fully diatonic in both keys, it is relatively low in information.(28) The goal of structural clarification also offers no reason why very low information density should be avoided; only the UID theory makes this prediction. Thus, the two goals, while often convergent, are in principle distinct.
[6.4] The current theory is open to a number of possible objections. Below I present three of them, with responses. All three of the objections have validity, and I do not claim to decisively refute any of them, but I do think some points can be made in the theory’s defense.
[6.5] Objection 1. The current theory assumes that perception is a fixed system and that composition evolves in response to it. But doesn’t perception, in turn, evolve in response to composition (especially under the “statistical” view of perception assumed here)? If Renaissance composers avoided leaps to B in response to listeners’ expectations of B, wouldn’t that compositional shift change listeners’ expectations?
[6.6] It is certainly true that the causal relationships assumed in the current study are oversimplified. Compositional practice adjusts in response to listeners’ expectations (if the UID theory is correct), but (as discussed in section 2) listeners’ expectations are also shaped by the music they hear. Thus, perception and composition co-evolve in a complex interactive process. However, I do not believe that this fundamentally invalidates the current argument. Consider the case of leaps to B in the style of Palestrina. Perhaps there was an earlier stage in the evolution of Renaissance counterpoint in which leaps to B were not specifically avoided, but B was still less common than other white-note pitches, and leaps were relatively rare, making leaps to B especially rare and thus high in information. In response to this situation, composers might have made a further effort to avoid leaps to B. Perhaps this did affect listeners’ expectations, making leaps to B even less expected before; this would not invalidate (and indeed might even intensify) the motivation for avoiding leaps to B. However, this account posits a certain historical pattern which may or may not be correct; the interactive relationship between composition and perception makes it very difficult to model such historical processes in a rigorous way.
[6.7] Objection 2. The evidence cited in the current study is highly selective: certain rules of Renaissance counterpoint, certain phenomena of expressive performance, and so on. But given the number of musical styles that could potentially be considered, and phenomena within those styles, we would expect a certain number of phenomena to match the predictions of UID just by chance. Didn’t you simply “cherry-pick” phenomena that fit the theory?
[6.8] This objection can be broken down into two parts—one concerning styles, the other concerning phenomena within a style—and I address them separately. Regarding styles: It is true that I focused on certain styles that seemed to offer evidence for UID; other styles may do so much less, if at all. Much twentieth-century art music, abandoning previous conventions with regard to both pitch and rhythmic organization, would seem to be extremely high in information: Meyer (1957, 420) suggested that this might explain many listeners’ “difficulties” with such music. Even if one style of music has a much higher average rate of information flow than another, it might still be the case that each style reflects UID in relation to the average information flow for that style.(29) Or perhaps UID only has validity for certain musical styles; but even in that case, it may offer a useful theory with regard to those styles, in that it provides a parsimonious, principled explanation for a variety of previously unexplained phenomena.
[6.9] With regard to my selectivity of features within a style, I think the validity of this objection depends on the style in question. In the case of Palestrina’s style, a number of diverse phenomena seem to reflect UID, including some very basic features of the style, such as the relationship between interval and duration. Other features of the style may not be explicable in terms of UID, but I have not claimed that UID is the only factor in the evolution of the style; indeed, I have acknowledged that other goals—especially maintaining the perceptual independence of the voices—are at work. In this case, then, the “cherry-picking” objection seems to have little merit. In the case of common-practice music, I have admittedly been much more selective, and it is possible that the reflections of UID that I have observed are merely coincidental; more work would be needed to determine whether UID really plays a role here. And this brings me to the third objection.
[6.10] Objection 3. The current theory suggests that there should be “trade-offs” between musical dimensions with regard to information flow: when a segment of music is high in information in one dimension, it should be low in information in others. But conventional wisdom suggests that the opposite may sometimes occur: there may be situations in which the composer seeks to maximize information flow across many or all dimensions. For example, Meyer (1957, 422) writes that “the development section of a sonata-form movement involves much more deviation—much more use of the less probable—than do the exposition and recapitulation”; this very general claim is not confined to one particular musical dimension.(30) Similarly, Rosen (1980, 106) asserts that development sections are higher in “tension” than expositions and recapitulations, and that this tension “is sustained harmonically, thematically and texturally: the harmony can move rapidly through dominant and subdominant key areas, establishing none of them for very long; the themes may be fragmented and combined in new ways and with new motifs; and the rhythm of the development section is in general more agitated, the periods less regular, the change of harmony more rapid and more frequent.” Is this not a striking counterexample to UID?
[6.11] This seems to me both the most worrying and the most interesting objection to the UID theory. Don’t common-practice pieces often seem to revel in the non-uniformity of information flow—in the contrast between very low-information passages and very high-information ones? Indeed, isn’t this an important aspect of the style as a whole? And if we allow that information flow in common-practice music is sometimes purposefully uniform and sometimes purposefully non-uniform, we would seem to lose any possibility of falsifying, thus testing, the theory. In that case, what justification do we have for arguing that information flow plays any role in musical evolution or compositional thinking?
Example 17. Mozart, Sonata K. 332, I, mm. 109–23
(click to enlarge)
[6.12] My first response to this objection is that Meyer’s and Rosen’s assertion about development sections may not actually be true. Certainly, development sections are more modulatory than other sections (this hardly needs to be proven); no doubt this raises information flow (because it makes the specific pitches less expected and also because key changes themselves are unexpected), and the sense of tension and complexity resulting from this may make us think of development sections as being complex in general. But are they? As I look through the development sections of sonata-form movements in Mozart’s and Beethoven’s piano sonatas, I find simple, repetitive textures (often of a melody-and-accompaniment sort, though the melody may be passed between two voices) and sequential, repetitive harmonic patterns (albeit often modulatory); the harmonic rhythm does not appear to be especially fast, and the rhythm does not seem especially complex; the phrase structure tends to be rather seamless, less clearly demarcated than in expositions, but it is not clear that this increases complexity to any significant degree. Example 17 shows an excerpt that I think is characteristic of classical development sections in general (at least in piano sonatas); while this passage is modulatory, it seems relatively simple and predictable—more so than most of the exposition—in almost every other respect. (The dynamic shifts add an element of drama, but even these quickly become predictable!) Examples such as this suggest that the high information in development sections due to frequent modulations may actually be counteracted by low information and predictability in other domains such as texture, motive, and harmonic motion.(31)
[6.13] Development sections aside, I will admit that the general idea that composers often seek contrasts—trajectories—of information flow is intuitively appealing. Other examples could also be cited. Drum patterns in Indian classical music often feature passages of great complexity, density, and metric ambiguity, followed by a return to a simple repetitive pattern aligned with the metrical cycle (Nelson 1999, 153–4; Clayton 2000, 3). In my own work, I have pointed to contrasts of information flow in both common-practice music (2007) and rock music (2018); in rock, the prechorus (between the verse and chorus) often reflects a peak of complexity in such domains as harmony, phrase structure, and melodic density. These claims of systematic non-uniformity of information flow have not yet been rigorously tested; but if they are borne out, they will present a serious problem for the UID theory. The challenge will then be to explain why music favors UID in some respects and avoids it in others. While I have some tentative ideas along these lines, I will stop here, with the hope that others will find enough merit in these thoughts and investigations to pursue them further.
David Temperley
Department of Music Theory
Eastman School of Music
26 Gibbs St.
Rochester, NY 14604
dtemperley@esm.rochester.edu
Works Cited
Aylett, Matthew, and Alice Turk. 2004. “The Smooth Signal Redundancy Hypothesis: A Functional Explanation for Relationships between Redundancy, Prosodic Prominence, and Duration in Spontaneous Speech.” Language & Speech 47 (1): 31–56.
Barlow, Harold, and Sam Morgenstern. 1948. A Dictionary of Musical Themes. Crown.
Bartlette, Christopher. 2007. “A Study of Harmonic Distance and its Role in Musical Performance.” PhD diss., Eastman School of Music.
Bell, Alan, Daniel Jurafsky, Eric Fosler-Lussier, Cynthia Girand, Michelle Gregory, and Daniel Gildea. 2003. “Effects of Disfluencies, Predictability, and Utterance Position on Word Form Variation in English Conversation.” Journal of the Acoustical Society of America 113 (2): 1001–24.
Benjamin, Thomas. 1979. The Craft of Modal Counterpoint. Schirmer.
Berlyne, Daniel. 1960. Conflict, Arousal, and Curiosity. McGraw-Hill.
—————. 1971. Aesthetics and Psychobiology. Appleton-Century-Crofts.
Berlyne, Daniel E., J. C. Ogilvie, and L. C. Parham. 1968. “The Dimensionality of Visual Complexity, Interestingness, and Pleasingness.” Canadian Journal of Psychology 22 (5): 376–87.
Bharucha, Jamshed. 1987. “Music Cognition and Perceptual Facilitation: A Connectionist Framework.” Music Perception 5 (1): 1–30.
Bod, Rens, Jennifer Hay, and Stefanie Jannedy, eds. 2003. Probabilistic Linguistics. MIT Press.
Clarke, Eric. 1988. “Generative Principles in Music Performance.” In Generative Processes in Music, ed. John Sloboda, 1–26. Clarendon Press.
Clayton, Martin. 2000. Time in Indian Music: Rhythm, Metre, and Form in North Indian Rag Performance. Oxford University Press.
Cohen, Joel. 1962. “Information Theory and Music.” Behavioral Science 7 (2): 137–63.
Cuthbert, Michael, and Christopher Ariza. 2010. “music21: A Toolkit for Computer-aided Musicology and Symbolic Music Data.” In 11th International Society for Music Information Retrieval Conference (ISMIR 2010), ed. J. Stephen Downie and Remco C. Veltkamp, 637–42. https://dspace.mit.edu/handle/1721.1/84963.
Duane, Ben. 2012. “Agency and Information Content in Eighteenth- and Early Nineteenth-Century String-Quartet Expositions.” Journal of Music Theory 56 (1): 87–120.
—————. 2016. “Repetition and Prominence: The Probabilistic Structure of Melodic and Non-Melodic Lines.” Music Perception 34 (2): 152–66.
—————. 2017. “Thematic and Non-Thematic Textures in Schubert’s Three-Key Expositions.” Music Theory Spectrum 39 (1): 36–65.
Dubey, Amit, Frank Keller, and Patrick Sturt. 2008. “A Probabilistic Corpus-Based Model of Syntactic Parallelism.” Cognition 109 (3): 326–44.
Fenk-Oczlon, Gertraud. 1989. “Word Order and Frequency in Freezes.” Linguistics 27 (3): 517–56.
Friberg, Anders, Roberto Bresin, and Johan Sundberg. 2006. “Overview of the KTH Rule System for Musical Performance.” Advances in Cognitive Psychology 2 (2–3): 145–61.
Gauldin, Robert. 1985. A Practical Approach to Sixteenth-Century Counterpoint. Waveland Press.
—————. 1995. A Practical Approach to Eighteenth-Century Counterpoint. Waveland Press.
Genzel, Dmitriy, and Eugene Charniak. 2002. “Entropy Rate Constancy in Text.” In Proceedings of the 40th Annual Meeting of the Association for Computational Linguistics, 199–206. Association for Computational Linguistics.
Green, Douglas, and Evan Jones. 2011. The Principles and Practice of Modal Counterpoint. Routledge.
Hannon, Erin, and Sandra Trehub. 2005. “Metrical Categories in Infancy and Adulthood.” Psychological Science 16 (1): 48–55.
Hasty, Christopher. 1997. Meter as Rhythm. Oxford University Press.
Heyduk, Ronald. 1975. “Rated Preference for Musical Compositions as it Relates to Complexity and Exposure Frequency.” Perception & Psychophysics 17 (1): 84–90.
Huron, David. 2001. “Tone and Voice: A Derivation of the Rules of Voice-Leading from Perceptual Principles.” Music Perception 19 (1): 1–64.
—————. 2006. Sweet Anticipation. MIT Press.
—————. 2016. Voice Leading: The Science Behind a Musical Art. MIT Press.
Jackendoff, Ray. 1991. “Musical Parsing and Musical Affect.” Music Perception 9 (2): 199–229.
Jeppesen, Knud. 1939. Counterpoint: The Polyphonic Vocal Style of the Sixteenth Century. Trans. by Glen Haydon. Prentice-Hall.
Jones, Mari Riess, Heather Moynihan, Noah MacKenzie, and Jennifer Puente. 2002. “Temporal Aspects of Stimulus-Driven Attending in Dynamic Arrays.” Psychological Science 13 (4): 313–19.
Kersten, Daniel. 1999. “High-Level Vision as Statistical Inference.” In The New Cognitive Neurosciences, ed. Michael Gazzaniga, 353–63. MIT Press.
Krumhansl, Carol. 1990. Cognitive Foundations of Musical Pitch. Oxford University Press.
Larson, Steve. 2004. “Musical Forces and Melodic Expectations: Comparing Computer Models and Experimental Results.” Music Perception 21 (4): 457–98.
Levy, Roger, Klinton Bicknell, Tim Slattery, and Keith Rayner. 2009. “Eye Movement Evidence That Readers Maintain and Act on Uncertainty about Past Linguistic Input.” Proceedings of the National Academy of Sciences 106 (50): 21086–90.
Levy, Roger, and Florian Jaeger. 2007. “Speakers Optimize Information Density through Syntactic Reduction.” In Advances in Neural Information Processing Systems, ed. Bernard Schölhopf, John Platt, and Thomas Hofmann, 849–56. MIT Press.
Lewin, David. 1986. “Music Theory, Phenomenology, and Modes of Perception.” Music Perception 3 (4): 327–92.
Margulis, Elizabeth. 2005. “A Model of Melodic Expectation.” Music Perception 22(4): 663–714.
Mavromatis, Panayotis. 2005. “A Hidden Markov Model of Melody Production in Greek Church Chant.” Computing in Musicology 14: 93–112.
Meyer, Leonard. 1957. “Meaning in Music and Information Theory.” The Journal of Aesthetics and Art Criticism 15 (4): 412–24.
—————. 1961. “On Rehearing Music.” Journal of the American Musicological Society 14(2): 257–67.
—————. 1989. Style and Music. University of Pennsylvania Press.
Narmour, Eugene. 1990. The Analysis and Cognition of Basic Melodic Structures: The Implication-Realization Model. University of Chicago Press.
Nelson, David. 1999. “Karnatak Tala.” In Garland Encyclopedia of World Music, vol. 5: South Asia: The Indian Subcontinent, ed. Alison Arnold, 138–61. Routledge.
North, Adrian, and David Hargreaves. 1995. “Subjective Complexity, Familiarity, and Liking for Popular Music.” Psychomusicology 14 (1–2): 77–93.
Pearce, Marcus, and Geraint Wiggins. 2006. “Expectation in Melody: The Influence of Context and Learning.” Music Perception 23 (5): 377–405.
Reitter, David, Frank Keller, and Johanna Moore. 2011. “A Computational Cognitive Model of Syntactic Priming.” Cognitive Science 35 (4): 587–637.
Rosen, Charles. 1980. Sonata Forms. W. W. Norton.
Rothstein, William. 2005. “Like Falling off a Log: Rubato in Chopin's Prelude in A-flat Major (op. 28, no. 17).” Music Theory Online 11 (1).
Saffran, Jenny, Elizabeth Johnson, Richard Aslin, and Elissa Newport. 1999. “Statistical Learning of Tone Sequences by Human Infants and Adults.” Cognition 70 (1): 27–52.
Schubert, Peter. 1999. Modal Counterpoint, Renaissance Style. Oxford University Press.
Schubert, Peter, and Christoph Neidhöfer. 2006. Baroque Counterpoint. Prentice Hall.
Shannon, Claude. 1948. “A Mathematical Theory of Communication.” Bell System Technical Journal 27: 379–423.
Sundberg, Johan. 1988. “Computer Synthesis of Music Performance.” In Generative Processes in Music, ed. John Sloboda, 52–69. Clarendon Press.
Temperley, David. 2007. Music and Probability. MIT Press.
—————. 2014. “Information Flow and Repetition in Music.” Journal of Music Theory 58 (2): 155–78.
—————. 2018. The Musical Language of Rock. Oxford University Press.
Temperley, David, and Daniel Gildea. 2015. “Information Density and Syntactic Repetition.” Cognitive Science 39 (8): 1802–23.
Tenenbaum, Joshua, Thomas Griffiths, and Charles Kemp. 2006. “Theory-Based Bayesian Models of Inductive Learning and Reasoning.” Trends in Cognitive Sciences 10 (7): 309–18.
Vitz, Paul. 1964. “Preferences for Rates of Information Presented by Sequences of Tones.” Journal of Experimental Psychology 68(2): 176–83.
White, Christopher. 2014. “Changing Styles, Changing Corpora, Changing Tonal Models.” Music Perception 31 (3): 244–53.
Witek, Maria, Eric Clarke, Mikkel Wallentin, Morten Kringelbach, and Peter Vuust. 2014. “Syncopation, Body-Movement and Pleasure in Groove Music.” PloS One 9(4).
Youngblood, James. 1958. “Style as Information.” Journal of Music Theory 2 (1): 24–35.
Footnotes
1. Quoted in Gauldin 1985, p. 15.
Return to text
2. The passage is shown in Example 11 and will be discussed further below.
Return to text
3. The idea of representing information in bits comes from the field of information theory (Shannon 1948). The information of an element corresponds to the number of bits needed to represent it in the most efficient possible encoding of the entire language.
Return to text
4. It is possible that some aspects of expectation are innate or universal, as proposed by Narmour (1990). Even these expectations might be modeled probabilistically, though of course they would not be learned.
Return to text
5. Early information-theoretic studies of music (Youngblood 1958 and others) have a connection to the current study, in that they attempted to quantify information content. However, these studies all used the concept of entropy, which is essentially the mean surprisal of all the events of a piece, where probabilities are defined by the distribution of events in the piece. It seems likely that listeners’ expectations are based on knowledge beyond the current piece; thus it seems appropriate to model them using a larger corpus. This is the approach used here.
Return to text
6. Both “information flow” and “information density” are used in the psycholinguistic literature, with more or less equivalent meanings (Fenk-Oczlon 1989; Levy and Jaeger 2007). “Information density” is more precise, but “information flow” resonates more with my experience; I use both terms here.
Return to text
7. This can be calculated as the average of the densities of the seven pitches, weighting each one by its probability: —
Return to text
8. This can be viewwed as a very simple implementation of the principle of “pitch proximity”—the preference for small melodic intervals. Most musical styles exhibit this preference very strongly, as corpus studies have shown (e.g. Huron 2006); most models of melodic expectation incorporate it as well (e.g. Narmour 1990). It is also reflected in the data presented below on steps and leaps in Palestrina’s music (see [3.4]).
Return to text
9. While this is the simplest method, it is not necessarily the most effective. Elsehwere I have proposed multiplying the scale-degree and interval probabilities of a note to get its overall probability (Temperley 2007, 2014). In effect, this gives each factor a kind of “veto power” over the other; if either of the two probabilities is very low, the overall probability will be as well. This method gives intuitively better results, in my opinion, but it is mathematically more complex; the resulting overall probabilities have to be normalized so that they sum to 1.
Return to text
10. An analogous finding in language is that sentences occurring later in a discourse tend to contain less frequent words and word combinations (Genzel and Charniak 2002). From a UID perspective, earlier sentences in a discourse make later ones more predictable (lower in information), which allows them to have higher information content in other respects.
Return to text
11. The subjective nature of probabilities complicates this task still further. Presumably the information content of each musical style would need to be defined in relation to the expectations of listeners representing the music’s intended audience—or at least, listeners with similar musical knowledge.
Return to text
12. Elsewhere I have explored the connection between information and complexity in greater depth (Temperley 2007, Temperley 2018 ). My focus there is on information flow from the listener’s perspective, which I relate to the experience of tension; and my emphasis is on the non-uniformity of information flow rather than its uniformity. I return to this apparent contradiction later in the article.
Return to text
13. The corpus is encoded in kern notation, and is part of the music21 corpus (Cuthbert and Ariza 2010); I included all of the Palestrina mass movements available in that corpus.
Return to text
14. Huron mentions a corpus study showing that notes before and after leaps are lengthened but provides no details.
Return to text
15. Gauldin does not state this rule directly, but it follows from more specific rules. There may not be a change of syllable within a series of quarter notes (1985, 39), and a longer note following a quarter note may not begin a syllable (Gauldin 1985, 39); it follows from these rules that a quarter note may not carry the end of a syllable. Clearly, then, attaching an entire syllable to a quarter note, so that it begins and ends the syllable, is prohibited (except for the special case about to be discussed). Eighth notes may never carry the beginning or end of a syllable (Gauldin 1985, 40).
Return to text
16. My assumption here is that listeners form expectations for harmonies and then predict notes given those harmonies. Alternatively, it is possible that listeners simply predict notes directly; but even in that case, chromatic notes are less common than diatonic ones, so chromatic harmonies (which contain chromatic notes) should generally be less expected than diatonic ones (which do not).
Return to text
17. The claim that mm. 24–6 contain “heightened chromaticism” seems unobjectionable; the passage contains rapid modulations as well as chromatic chords (augmented sixths) in relation to the tonicized keys. I am less sure what Rothstein means by “dissonance,” or what the predictions of the UID theory would be in this regard. I will say more about the harmony of mm. 24–6 in note 19.
Return to text
18. Interestingly, Bartlette found that when the chromatic chord initiated an actual modulation, no slowing down on the chord was observed. From the performers’ point of view, perhaps the fact that the chord belonged to the key of the subsequent passage made it seem less chromatic and thus less deserving of durational “stretching,” though this would not lessen its unexpectedness from the listener’s point of view.
Return to text
19. The harmonic rhythm of mm. 24–6 is somewhat ambiguous; my preferred analysis is shown under the staff. One could posit a faster harmonic rhythm at some points: for example, a German sixth on the second eighth of m. 25. Faster harmonic changes could be posited elsewhere too, e.g. in m. 22. To my mind, the bass notes play an important role in establishing the underlying harmonic rhythm; my analysis aligns with them.
Return to text
20. It should be noted that harmonic rhythm itself conveys information. There might be cases where the continuation of the current harmony is more surprising than a change of harmony; for example, if a persistent one-measure harmonic rhythm is followed by a lack of change on a downbeat. But a change of harmony conveys the additional information of what the new harmony is (the probability of a change in harmony must be divided among a number of possible harmonies); so that even in that case, the unchanging harmony might be the most likely single continuation.
Return to text
21. The fact that performers tend to slow down at the ends of phrases and other formal units seems to run counter to the predictions of UID, since the cadential harmonies at such points are often very predictable. As suggested by Clarke (1988), slowing down at phrase boundaries probably serves a different communicative function: helping to convey structural boundaries to the listener. It seems that this imperative often outweighs the pressure of UID.
Return to text
22. This distinction is similar to Narmour’s (1990) distinction between “intra-opus” and “extra-opus” norms and to Huron’s (2006) distinction between “dynamic” and “schematic” expectations.
Return to text
23. There is repetition of motives—due to the imitative texture—but in a way that is somewhat irregular and unpredictable. In addition, the decrease in information due to the motivic repetitions is counterbalanced by the thickening of texture as each new voice is added.
Return to text
24. An anonymous reviewer pointed out a connection with the concept of “stretching,” as proposed by Meyer: “an increase in degree relative to some nonsyntactic standard or precedent.” (1989, 259). (This is distinct from my use of the term “stretching,” which implies stretching in time.) Several of Meyer’s examples of stretching involve exactly the pattern discussed here: a repeated motive in which a single interval is enlarged.
Return to text
25. Thanks to David Huron for making available the encoding of the themes in kern notation.
Return to text
26. The details of this would require some working out. In Example 15, the notes of the first instance of the pattern are all present in the second instance (though they do not all occur at the same metrical positions), so one could argue that they are expected, and convey low information when they occur, counterbalancing the high information of the new notes. By contrast, if the elaborated version of the pattern were presented first, all of the notes in the first instance would be high in contextual information. And of course, the accompaniment repeats in the second pattern instance, as do structural elements such as the harmony, further reducing its overall information load.
Return to text
27. The same point could be made about chromatic chords. This may account for the fact that the KTH team found it desirable to play such chords louder, as well as more slowly: playing them louder makes it easier to identify them. There is a convergence here, also, with Huron’s work on voice leading, since perceiving independent voices requires correctly identifying the notes of those voices. Some rules of counterpoint facilitate that goal in ways that are unrelated to UID; an example is the prohibition of parallel perfect consonances, which lessens the risk that simultaneous notes will fuse into one.
Return to text
28. Indeed, one might say that the ambiguity of the scale collection increases its probability, since it has high joint probability with two different keys. (See Temperley 2007, 116–20, for further discussion of this point.) Conversely, a large pitch interval is low in probability but would seem to have little effect on the perception of tonality—though one might say that it potentially obscures another kind of underlying structure, namely, the structure of lines or voices; a large leap can create ambiguity as to whether the two notes belong to the same voice or not.
Return to text
29. I find this a suggestive possibility with regard to twentieth-century music, though it would be very difficult to test, given the incredible diversity of that repertory.
Return to text
30. Elsewhere in the same essay, interestingly, Meyer (1957, 419) offers thoughts that seem tantalizingly close to the idea of UID. In discussing the interplay between “systemic uncertainty” (resulting from expectations generated by the style as a whole) and “designed uncertainty” (resulting from expectations generated by the specific piece), Meyer suggests that designed uncertainty should be high when systemic uncertainty is low. There is a trace of UID thinking here, but considerable theoretical work would be needed to establish the connection in a rigorous way.
Return to text
31. A recent study by Duane (2017) deserves mention here. Duane argues that information content may be used to distinguish thematic from non-thematic passages in common-practice music, and further suggests that development sections are often non-thematic in character. However, Duane’s claim is not that non-thematic sections are higher in information overall, but rather that in thematic sections, unlike non-thematic ones, the information tends to be concentrated in a single strand of the texture.
Return to text
Copyright Statement
Copyright © 2019 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Andrew Eason, Editorial Assistant
Number of visits:
11584