Volume 14, Number 1, March 2008
Copyright � 2008 Society for Music Theory
KEYWORDS: Klumpenhouwer Networks, analysis, Lacan
REFERENCE: Michael Buchler, “Reconsidering Klumpenhouwer Networks,” Music Theory Online 13.2, and the commentaries thereto in Music Theory Online 13.3.
ABSTRACT: The recent debate in Music Theory Online over the nature and efficacy of Klumpenhouwer Networks in the analysis of post-tonal music is representative of and, indeed, instructive in its engagement with methodological anxiety. In four short meditations, this commentary engages implicit ideological frameworks articulated by various positions in the K-net debate, problematizes their assumptions and proposes ways in which future work on K-nets might proceed.
Received January 2008
[1] Just a little bit of theory can create a good deal of anxiety. Throughout its modern disciplinary history, American music theory has maintained a predilection for meta-theoretical critique, often shrouded in any number of assorted anxieties. Unity, prolongation, organicism, and symmetry have each garnered their share of attention in music-theoretical meta-discourse, even as these very concepts continue to make up the heart of analytical methods still employed (sometimes uncritically) in contemporary scholarship. The recent debate in Music Theory Online over the nature and efficacy of Klumpenhouwer Networks (hereafter, K-nets) in the analysis of post-tonal music is representative of and, indeed, instructive in its engagement with methodological anxiety.(1)
[2] In four short meditations, I will engage implicit ideological frameworks articulated by various positions in the K-net debate, problematizing their assumptions and qualifying their proposals for further research. The recent dialogue on K-nets has left some properties of the analytical system unexplored and some aspects of the analytical process undertheorized. It is my contention that both sides in the K-net debate make recourse to a “musical surface” that has received insufficient critical attention. Directly engaging this concept, I will suggest ways in which future work on K-nets might proceed.
I. On Promiscuity
[3] Michael Buchler’s recent Music Theory Online article, “Reconsidering Klumpenhouwer Networks,” challenges the analytical technique developed by Henry Klumpenhower and David Lewin on two basic counts. Buchler asserts that K-nets have the potential to “open a Pandora’s Box of relational permissiveness;”(2) this aspect of Buchler’s K-net critique is concerned with the ability of K-nets to act as a cipher, particularly for trichords. This first aspect is related to a second, which sees the K-net model’s design as an affordance for its relational permissivity. Both critiques, however, are to be understood as a corrective to the theory’s purported abstractness. Buchler is most concerned with “try[ing] to have our networks reflect the musical surface to the greatest degree possible.”(3)
[4] Bucher claims that of the 78 possible pairs of trichords, 78.8% can form isographic K-nets with one another. Two lines of inquiry follow from Buchler’s assertion: 1) the truth content and nature of Buchler’s claim itself and 2) the implications for a “promiscuous” or flexible analytical relationship. In his response to Buchler, Shaugn O’Donnell notes that it is only the three-note set classes that relate to one another 78.8% of the time. Three-note pitch-class sets, by contrast, relate to one another only 10.5% of the time, even with the use of O’Donnell’s double emploi.(4) Yet the facts surrounding the relational permissivity of trichordal K-nets seem less than important to the other participants in the debate, who fail to comment on this potential error on Buchler’s part and focus instead on the issue of analytical relationships in general. This may be because there is a fair amount of anxiety concerning the claims of the analytical method at hand, or any analytical method at all. If it is true that K-nets are able show relationships (almost) wherever we would like them to, then analysts must decide if this is to the method’s credit or detriment.
[5] Phil Stoecker and Gretchen Foley address idiosyncratic scenarios in order to provide a foil for Buchler’s broadly written critique. Stoecker, in a dialectical turn, explores the unique properties of moments in which it is not possible to show a trichordal K-net relationship. Foley importantly points out particular situations in Perlean theory where K-nets show relationships that other analytical tools miss.
[6] O’Donnell, having already demonstrated that K-nets do in fact show significant relationships, nonetheless “embraces” their relational promiscuity, asserting that “music analysis is like storytelling,” and that “the relational abundance generated by K-nets further emphasizes that musicality, whatever that means in a given context, is in the hands and ears of the analyst rather than the theoretical apparatus itself.”(5) It is important to note here that in embracing the (potential) relational abundance of trichordal K-nets, O’Donnell has shifted the burden of proof from what he calls the “theoretical apparatus” to “musicality, whatever that means in a given context.” O’Donnell therefore implicitly asserts that theory is distinct from musicality.
[7] Klumpenhouwer clarifies the nature of Buchler’s complaint, pointing out that it is the top-down hierarchy—generated by the search for multiple levels of K-net relationships—that most bothers Buchler. Klumpenhouwer then proceeds to relate K-net analysis to Schachter’s theory of Schenkerian levels, claiming that both systems operate dialectically:
The various levels of structure are to be conceived heuristically as a single system, so that levels emerge simultaneously, rather than one and then the other.(6)
Importantly, Klumpenhouwer notes that Buchler’s aversion to the top-down “theory-driven” approach in favor of a hypothetical bottom-up approach seems to reference a misguided interaction with empiricism, which seems to have “strayed into the picture.”(7) Indeed, elsewhere Klumpenhouwer has written rigorously against such analytical ideologies.(8) However, his own defense of K-net analysis as a dialectical procedure seems to skirt the real issue, which recurs in every author’s critique or defense: the musical surface. The advocacy of a dialectical approach still leaves the “bottom” undertheorized, especially considering the attention it has received in the commentary. Even through O’Donnell’s, Stoecker’s, and Foley’s defenses of K-net analysis there remains an urgent concern for “a true reflection of the musical surface.”(9)
II. On Hierarchies and Graph Theories
[8] The nature of the K-net itself and its relationship to networks of K-nets, or recursive network structures, is another significant aspect of Buchler’s critique. Buchler attempts to show that the structure of the K-net is both arbitrary (it can be re-drawn in a number of ways) and unnecessarily complicated. In addition, Buchler criticizes recursive network structures for their abstract quality: rather than expressing relationships about pitch-class sets, they instead express relationships about relationships (K-nets). As a possible solution to the arbitrariness and complexity of K-nets, Buchler proposes doing the analytical work of K-nets with O’Donnell’s dual transformations. However, Buchler does not propose an alternative way of conceptualizing the recursive network structures—in his criticism these are perhaps the most objectionable aspect of K-net analyses.
[9] In their responses to Buchler, Klumpenhouwer and Nolan both demonstrate the ontological difference between the K-net and the dual transformation. Dual transformations are not substitutable for K-nets, nor are they a simplification, since they show fundamentally different relational structures. However, the insightful responses of Klumpenhouwer and Nolan fail to address Buchler on his own terms. If Buchler claims ontological equivalence between the dual transformation and the K-net, it is only implicitly and in the service of using the dual transformation to do the work heretofore done by the K-net. In this regard, O’Donnell’s response to Buchler is the most appropriate. O’Donnell shows that the internal In arrows of the K-net are not necessary to recognize isography or calculate hyper transformations, but “are still necessary for the unity of the musical sonorities participating in these transformations.”(10) Following O’Donnell, then, dual transformations cannot do the work of K-nets, as Buchler would suggest. However, a separate question arises concerning the very unity of the musical sonorities participating in the transformations. O’Donnell assumes that we do, in fact, hear the unity of such sonorities, but quickly amends:
Even when we hear the independent paths of two subsets in a dual transformation, we very often hear the supersets as single, unified musical “objects,” particularly in homorhythmic contexts. A good example would be Catherine Nolan’s analysis of Webern’s Das Augenlicht that Buchler champions as a successful use of K-nets.(11)
Two aspects of O’Donnell’s astute answer to Buchler (on the latter’s own terms) slightly weaken its impact. Firstly, although O’Donnell asserts that we indeed do hear the supersets modeled by K-nets as unified objects, he scare-quotes the term “objects.” Secondly, he scales the extent of his claim back to “particularly in homorhythmic contexts.”
[10] It is significant that Catherine Nolan’s analysis of the chorale passage from Webern’s Das Augenlicht has received so much positive attention in the K-net debate.(12) This analysis has served as a paragon for a successful modeling of the musical surface using K-nets. Praised almost unanimously for its reflection of register and rhythm, Nolan’s analysis appears to be very much the exception rather than the rule. But why is it that Nolan’s application of K-nets seems more “musical” than others? I argue that it is only by making recourse to the organization of other parameters (apart from pitch-class) that Nolan’s analysis is able to quell musical-surface anxieties. Since the progression of the non-hierarchical K-nets in her analysis follows a normative parametric organization that we have already been trained to hear (after all, it is an analysis of a chorale passage), it does not incur the abstraction citation.
[11] The anxiety surrounding abstraction on all sides of the debate is at its paramount in Buchler’s dismissal of recursive network structures. Catherine Losada’s commentary adds support to Buchler’s argument, asserting that relationships between inversional subscripts in network recursion are “completely spurious.”(13) Scott Murphy’s response complicates the critiques, however, showing that Buchler’s various complaints regarding recursion are not universally applicable to all types of network recursion.(14) But Buchler’s criticism of levels is only one portion of his critique of recursive network structures, the core of which was originally articulated by Joe Straus:
[Recursive network structures are] a problem when our desire for [them] leads us to emphasize musical features that might otherwise be of relatively little interest.(15)
Once again, the core of analytical anxiety rests with the problem of modeling musicality (perhaps even locating the “context” in O’Donnell’s phrase “whatever that means in a given context”), and always returns to the musical surface.
III. The Musical Surface?
[12] We might generally understand that references to the musical surface for those involved in the K-net debate point to some natural, pre-theoretical approach to the score that is sensitive to the concerns of the musician. The process in which theory is undercut by reference to musicality is part of a general anxiety surrounding the theoretical apparatus. Both critics and defenders of the K-net theory are quick to assure their readers that their real concerns lie with music and musicianship. The problem with this position is that it assumes a vantage point somehow outside of any theoretical lens; it assumes that notions of musicality are themselves untouched by theoretical discourse, pedagogy, or enculturation. This position seems to eschew theory for something more “real” which is found only a step away in musicality.
[13] In his book on the future of Theory, Jean-Michel Rabaté explains the relationship between Theory and Lacan’s notion of the hysteric. Both Theory and hysteria are “never satisfied with a neat answer, [they] always ask for more in the name of a certain notion of truth.”(16) Rabaté brings Theory together with hysteria in order to show that detractors of Theory deploy a hysterical mode of discourse that is similar to the very practice of Theory itself. In this way, the critique of Theory returns itself back to Theory:
The discourse of the Hysteric will want to put the subject in the first place, but in order to insist upon subjective division in the quest for the master-signifier. Often one single signifier... will orient the quest and be taken for the whole truth, perhaps in the hope of proving that all theoreticians are essentially wrong or lacking somewhere ...
If Theory reproduces this pattern, it is because it has anticipated it, by what could be described either as a hermeneutical circle or a hysterical ellipsis. Theory will indeed aim at questioning all types of knowledge and discourses ... In doing so, it will generate some kind of knowledge and will aim, no doubt, at a truth.(17)
[14] As Rabaté points out, a “single signifier” often guides the mission to prove Theory inadequate. In the case of the K-net debate, musicality and the musical surface seem to have assumed this role. Nonetheless, these notions return themselves to theory in Rabaté’s “hermeneutical circle or hysterical ellipsis,” as they themselves are also constructed through a theoretical lens of some kind.(18)
[15] Hysterical or not, I assert that the cry for musicality on both sides of the K-net debate is truly a cry for more theory rather than less. If K-nets cast too broadly, drawing relationships where they will, then perhaps what they want is the company of other theories. If rhythm and register frame a passage readily for K-net analysis—as is the case in Catherine Nolan’s analysis of Das Augenlicht—then perhaps what we need are theories of rhythm and register to accompany K-nets in the analytical endeavor. Attempting to clarify what is meant by the various references to the musical surface or musicality in the K-net debate, I wish to explore the potential for K-nets to work in tandem with other theories.
IV. More Theory
[16] The recent outpouring of meta-literature on K-nets points up several of their interesting relational properties. However, as we might imagine, there are additional properties of K-nets yet unexplored. In this meditation, I will examine a particular property of the negative isography relationship, showing its invariant connection to a particular dodecaphonic configuration. Rather than employing this observation in a critique of K-nets as a cipher for the “musical surface,” we might imagine situations where this property of K-nets becomes more interesting in the company of additional theory.
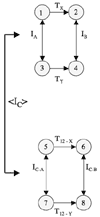
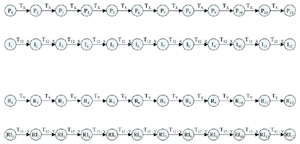
[17] Figure 1 shows the negative isography relationship between two box-style four-node K-nets. The negative isography relationship allows us to see inverse relationships between the T-transforms in these K-nets. Because its analytical insight centers on inverse relationships, negative isography is a relative of the inversional pairings between Prime (P) and Inversional (I) row-form pairs in dodecaphonic organization. This also holds for the inversional pairings between Retrograde (R) and Retrograde-Inversional (RI) row-form pairs. Both sets of relationships—negative isography and P&I/R&RI row-form pairs—show inverse relationships between transforms of successive PCs: in the box-style four-node K-nets of Figure 1, this inverse relationship occurs between the pairs of transformations on either side of the two K-net boxes. In row-form pairs, the inverse relationship occurs between any set of successive PCs in prime or retrograde row forms, as related to their corresponding set of successive PCs in inversion or retrograde-inversion row-forms respectively. Figure 2 shows this relationship between row-form pairs. |
Figure 1.
Negative isography between two
(click to enlarge) |
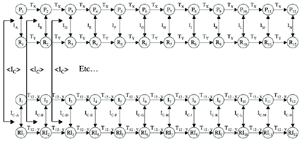
[18] Figure 3 below shows how their shared tie to the inverse relationship affords an invariant interaction between K-nets and a particular row-form configuration. It follows from the observations above that a negatively isographic K-net will model any relationship between successive PCs from a P/R row-form pair to an I/RI row-form pair, as pictured in Figure 3. The inversional relationships between the P and I, R and RI row forms themselves is responsible for the invariant ability to draw this relationship.
|
Figure 2. Inversional pairings between P&I, R&RI row-form pairs(19)
(click to enlarge) |
Figure 3. An
invariant, negative isography relationship holds between
(click to enlarge) |
[19] It would seem, then, that we might add this particular interaction between negatively isographic K-nets and row forms to the litany of K-net relational permissivities. After all, any row-form pairing like that shown in Figure 3 will render negatively isographic K-net relationships wherever one might wish to show them, fully allowing for an analysis that would “emphasize musical features that might otherwise be of relatively little interest.”(20) I will argue again, however, that such relationally permissive associations become interesting in the company of more theory. In order to illustrate this point, I will turn to an example from Webern’s Das Augenlicht. Apart from its fame in the K-net debate, Das Augenlicht is particularly pertinent in the present context because of Webern’s negotiation of row forms through the piece.
[20] The voice parts in Webern’s Das Augenlicht enter in a pair of duets, beginning with the soprano and tenor voices in measure 8, as shown in Example 1. While the soprano line in measures 6–11 comprises the P8 row-form, its partner the tenor line comprises the R8 row form in those same measures. The lower voices answer with their own duet in the measures that follow; the alto line completes the I8 row-form in measures 14–19, while the bass line completes the RI8 row-form in measures 14–18. Hence, a P/R row-form pair in measures 6–11 is answered by an I/RI row-form pair in measures 14–19. [21] A number of interesting relationships hold between these paired duets. The melodic unfolding is somewhat similar in all voices, as are the harmonic relationships between the two duets. In order to examine the correspondences closely, a theory of melody will relate the diachronic unfolding of each row form, while K-nets show relationships between melodic segments. |
Example 1. Paired duets in Webern, Das Augenlicht,
(click to enlarge) |
[22] Example 2 shows melodic relationships between the paired duets. I chose Eugene Narmour’s Implication-Realization model for melody to relate the different melodic characters of the four row-forms in this excerpt. Narmour’s I-R theory not only gives us a lexicon to relate melodic qualities (outside of a tonal context), but also offers a theory of segmentation rooted in the basic gestalt notions of similarity and difference. Like Christopher Hasty’s approach in his 1981 “Segmentation and Process in Post-Tonal Music,” (also quite celebrated in post-tonal analytical literature), Narmour’s I-R theory is sensitive to degree of change and degree of consistency. Narmour’s theory also allows for modification based on style (intra-opus as well as extra-opus), and can be applied and related to other parameters such as duration or even harmony.(21) |
Example 2. I-R analysis of the paired duets in Webern,
(click to enlarge and see the rest) |
[23] The I-R model is grounded on two basic theoretical propositions: (1) similarity engenders the expectation of more similarity, or A + A implies A; and (2) differentiation engenders the expectation of more differentiation, or A + B implies C. These theoretical propositions correspond to the two primary archetypes that govern Narmour’s model: Process (P) and Reversal (R). Where registral direction is constant over the course of two successive intervals (three pitches), the analytical symbol applied is P, where registral direction changes, R. Additional symbols +, –, ~, and º reflect degree of intervallic change, ranging from exact intervallic repetition (º), basic similarity (~), a great decrease in intervallic size (–), to a great increase in intervallic size (+). Sufficient parametric difference (in duration, accentuation, register, or harmony in a tonal context) renders a break in grouping structure. If a group consists of two pitches, the symbol applied simply shows the interval size between them.
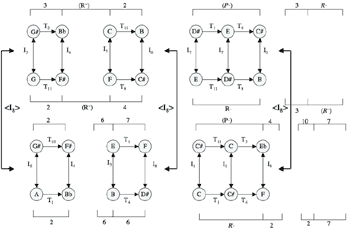
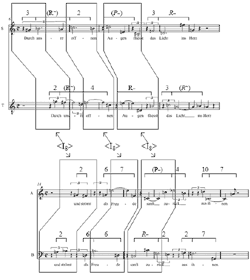
[24] As Example 2 illustrates, several melodic grouping structures are common to voices in the same duet, while some melodic structures echo across between the two duets. The I-R grouping structures point out the rhythmic canon in each duet, and the labels for these grouping structures also allow us to see which melodic segments in the duets are the most closely related. Both duets open with a dyad in each voice: the soprano line in measure 6 and bass line in measure 14 rise while the alto line in measure 6 and tenor line in measure 14 fall. While Narmour’s theory accounts for the functional similarity of these openings in terms of the grouping structure for their respective melodies, a K-net describes how they relate to one another harmonically. The box-style 4-node K-net pictured in Example 3 is in keeping with both register and Narmour’s grouping structure for the melodic unfolding of these sonorities. The harmonic relationship between the opening of the first and second duets can be described through the use of the negative isography label <I8>, as shown in Example 4.
|
Example 3. K-nets show harmonic relationships between
(click to enlarge) |
Example 4. <I8> describes the harmonic relationships between
(click to enlarge) |
[25] While the melodies in the first duet continue directly to retrospective reversals after the opening dyad, the melodies of the second duet have a more fragmented opening. The next correspondence in grouping structure between the two duets is the sonority formed by the fourth and fifth pitches of each line. Again, a box-style 4-note K-net models the harmonic relationship between the two melodic dyads, which consistently is described by the negative isography label <I8>.
[26] A melodic grouping structure consisting of the sixth through eighth pitches in each line proves the most melodically consistent between the two duets. The soprano and alto voices both contain two large intervallic leaps in one registral direction: melodic retrospective P– structures. The tenor and bass, in their respective duets, also exhibit large intervallic leaps, but in alternating registral directions: melodic R– structures. The <I8>, box-style 6-note K-net models the harmonic relationship between these corresponding melodic segments.
[27] As explicated above, any string of corresponding successive pitches will form the negative isography <I8> between the two duets. For this reason, the melodic grouping structures towards the end of the duets are less interesting. Neither grouping nor melodic symbology correspond, and so the K-net relationships that are possible to draw here would model melodic correlates that are non-correspondent in Narmour’s model.
[28] Rather than make recourse to a hazily defined “musical surface,” or argue that these correspondences are “otherwise of relatively little interest,” K-nets can keep company with more theory in order to show multifaceted relationships. Not only does the K-net theory benefit from the melodic integration with Narmour’s I-R, but I-R can also gain post-tonal harmonic insight in this cooperative effort. In tandem, both theories make reference outside their own systems, but they do so with reference to very specific parameters. As individuals with predilections for precision, I imagine that this aspect of theory-coupling may appeal to those interested in refining K-net theory.
Roger Mathew Grant
University of Pennsylvania
Departmental of Music
201 S. 34th Street
Philadelphia, PA 19104
Roger2@sas.upenn.edu
References
* I am grateful to Shaugn O’Donnell, Gavin Steingo,
and an anonymous reader, for their assistance in the preparation of this
commentary.
1.
The K-net debate properly began at the 2006 meeting of the SMT in Los Angeles,
where Michael Buchler gave the paper that later appeared in Music Theory Online
13.2. See Michael Buchler, “Reconsidering Klumpenhouwer Networks,”
Music Theory
Online 13.2 (2007);
and the responses in the next volume: Scott Murphy, “Considering Network
Recursion and Bartók’s ‘Fourths,’” Music Theory Online 13.3
(2007);
Gretchen Foley, “The Efficacy of K-Nets in Perlean Theory,�
Music Theory Online 13.3 (2007);
Henry Klumpenhouwer, “Reconsidering Klumpenhouwer Networks: a Response,�
Music Theory Online 13.3 (2007);
Catherine Losada, “K-nets and Hierarchical Structural Recursion: Further
Considerations,” Music Theory Online 13.3 (2007);
Catherine Nolan, “Thoughts on Klumpenhouwer Networks and Mathematical Models:
The Synergy of Sets and Graphs,” Music Theory Online 13.3
(2007); Shaugn O’Donnell, “Embracing Relational Abundance,”
Music Theory Online 13.3 (2007);
Philip Stoecker, “Without a Saftey (k)-Net,”
Music Theory Online 13.3 (2007); Dmitri Tymoczko, “Recasting K-nets,”
Music Theory Online 13.3 (2007).
Return to text
2. Buchler, “Reconsidering Klumpenhouwer Networks,” [abstract]. 3. Buchler, “Reconsidering Klumpenhouwer Networks,” [60]. 4. O’Donnell, “Embracing Relational Abundance,” [3]; See also Shaugn
O’Donnell, “Klumpenhouwer Networks, Isography, and the Molecular Metaphor,”
Intégral 12 (1998), 53–80. 5. O’Donnell, “Embracing Relational Abundance,” [2, 1]. 6. Klumpenhouwer, “Reconsidering Klumpenhouwer Networks: A
Response,” [12].
See also Eugene Narmour’s classic critique of a true levels vs. systems view:
Eugene Narmour, “Some Major Theoretical Problems Concerning the Concept of
Hierarchy in the Analysis of Tonal Music,” Music Perception 1.2 (1984): 129–99. 7. Klumpenhouwer, “Reconsidering Klumpenhouwer Networks: A
Response,” [10]. 8. Henry Klumpenhouwer, “Commentary: Poststructuralism and Issues of Music Theory,”
in Music/Ideology: Resisting the Aesthetic, ed. Adam Krims, (Amsterdam: Overseas
Publishers Association, 1998), 289–310. 9. Foley, “The Efficacy of K-nets in Perlean Theory,” [12]. 10. O’Donnell, “Embracing Relational Abundance,” [5]. 11. Ibid., [5]. 12. The analysis cited by these authors is Catherine Nolan’s “More Than Meets The
Eye: Text, Texture and Transformation in Webern’s Das Augenlicht, Op. 26.” Paper
presented at the Dublin International Conference on Musical Analysis, Dublin,
Ireland, 2005. 13.
Losada, [17]. 14. Murphy, “Considering Network Recursion and Bartók’s ‘Fourths.’” 15. Joseph N. Straus, “Three Problems in Transformational Theory,”
talk delivered at the
closing plenary session of the Mannes Institute on Transformational Theory, New
York City, NY, 2003; as cited in Buchler, “Reconsidering Klumpenhouwer Networks,” [4]. 16. Jean-Michel Rabaté with Gregg Lambert, “Conversation on the Future of Theory,”
Symploke 11:1/2 (2003): 47. 17. Jean-Michel Rabaté, The Future of Theory (Oxford: Blackwell Publishing, 2002),
16. 18. I am grateful to an anonymous reader for reminding me of Michael Polanyi’s
“tacit” forms of knowledge, which, one might argue, aptly characterize
musicality. If it is true that for many of us musicality is knowledge of the
“tacit” sort, it is also true that we acquire this knowledge in a particular
tradition of pedagogy, one that is not entirely non-discursive or, as Polanyi
has it, “ineffable.” In any case, this tension (or aura?) surrounding the
pedagogical tradition of musicality is quite interesting in its own right and
certainly merits the space of a separate theoretical study. See Michael Polanyi,
Personal Knowledge (London: Routledge, 1958), particularly pp. 87–97. 19. For notational convenience, this figure and those following represent the
different successive transformations in row forms simply as X (for the P form)
and Y (for the R form). 20. Straus, �Three Problems in Transformational Theory,� as cited in Buchler, “Reconsidering Klumpenhouwer
Networks,” [4]. 21. The application of Narmour’s I-R theory in this context may rightly give some
readers pause. The claims of Narmour’s system are explicitly cognitive, while
the relationship of K-net theory to hearing is, as the recent debate
demonstrates, at least suspect. Narmour’s claims notwithstanding, his I-R theory
carries its own merit as an analytical tool. It is useful to me here in carving
basic melodic structures and relationships through the use of his parametric
scales, which—even if one might challenge their claims to cognitive innateness—serve to differentiate types of musical relationships from one another in a
systematic way. See Eugene Narmour, The Analysis and Cognition of Basic Melodic
Structures (Chicago: University of Chicago Press, 1990), and idem., The Analysis
and Cognition of Melodic Complexity (Chicago: University of Chicago Press,
1992).
Return to text
Return to text
Return to text
Return to text
Return to text
Return to text
Return to text
Return to text
Return to text
Return to text
Return to text
Return to text
Return to text
Return to text
Return to text
Return to text
Return to text
Return to text
Return to text
Return to text
Copyright Statement
Copyright � 2008 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason, Managing Editor
Updated
22 March 2008
Number of visits: