Turning the Beat Around: Reinterpretation, Metrical Dissonance, and Asymmetry in Electronic Dance Music
Mark J. Butler
KEYWORDS: rhythm, meter, reinterpretation, metrical dissonance, layering, asymmetry, electronic dance music, African music, Harald Krebs, Jay Rahn, Stephen Handel, Christopher Hasty
ABSTRACT: This paper considers some of the issues involved in the analysis of rhythm and meter in electronic dance music. It begins by considering metrical dissonance and ambiguity within the context of a layered approach to musical meter; it also highlights some of the distinctive ways in which these phenomena are manifested in this repertory. The second half of the paper focuses on the use of asymmetrical patterns in electronic dance music and considers some broader questions of rhythmic and metrical theory. Throughout, the paper draws upon a number of different music-theoretical sources, including work by Harald Krebs, Jay Rahn, and Christopher Hasty, as well as scholarship in ethnomusicology and cognitive science.
Copyright © 2001 Society for Music Theory
[1] Within the past decade, music-theoretical analysis of popular music has become increasingly common. Nonetheless, until quite recently the purview of such research has been relatively limited, focusing mainly on classic and art rock from the 1960s and 70s. While these repertoires have provided fertile ground for analytical exploration, several more recent genres and styles raise interesting structural, semiotic, and aesthetic questions that also merit study.
[2] One of the most distinctive types of contemporary popular music is electronic dance music, a broad category that includes styles such as techno, house, drum-n-bass, and trance.(1) Electronic dance music differs from both rock and art music in a number of ways, all of which suggest avenues for productive theoretical investigation. While many genres of popular music are distinguished from each other on the basis of “surface” differences such as instrumentation or lyrical content, electronic dance music presents a distinctive overall formal structure in addition to its characteristic instrumentation. It also differs from most other types of Western music in its rejection of harmony as a primary musical parameter. Its use of pitch is typically restricted, with the majority of musical development taking place instead in the realms of rhythm, meter, texture, and timbre. Consequently, these areas should be principal concerns for the analyst wishing to pursue a close examination of musical sound in this repertoire.
[3] Rhythm provides an ideal starting point, as it seems to be the element to which listeners and fans of EDM relate most directly. This connection is most immediately apparent on the dance floor, where audiences physically enact the rhythms of the music. Written discussions of electronic dance music also tend to highlight its rhythmic qualities—references to its “unrelenting rhythm,” “pulsing dance rhythms,” and “irresistible tribal rhythm” are common(2)—and fans often refer to the music simply as “beats” (as in, “let’s go to the club and hear some beats”). Yet EDM poses a challenge to the analyst, for it differs in many ways from the repertoires that current music-theoretical models of rhythm and meter were developed to address. Transcription can give the impression that it is less complex rhythmically than these other bodies of music: although it typically consists of many different textural layers, each of which has a different rhythmic pattern, these patterns can appear quite simple when considered individually, and they repeat for long periods of time without changing. Nonetheless, the experience of listening to electronic dance music is neither simple nor monotonous, for it engages one’s perception of rhythm and meter in a number of interesting ways. In this paper I will examine some of the issues involved in the analysis of rhythm and meter in this repertoire. In the first half of my paper, I will consider metrical dissonance and ambiguity within the context of a layered approach to musical meter. The discussion, which will be centered upon several short musical examples, will also highlight some of the distinctive ways in which these phenomena are manifested in EDM. The second half of my paper will focus on the use of asymmetrical patterns in EDM. Though this section will begin with two musical examples, it will develop into a more general discussion focusing on broader questions of rhythmic and metrical theory. Throughout the paper I will draw upon scholarly work in a number of different fields, including music theory, ethnomusicology, and cognitive science.
[4] Let us first consider a brief musical example, an excerpt from the song “Piku” by The Chemical Brothers. At the beginning of this example, two distinct textural layers, defined by timbre and by rhythmic patterns, are audible; they are not aligned, however (Example 1a). Accents are created by register in the synthesizer pattern and by attack-point spacing in the percussion part, thus suggesting two different streams of quarter-note pulses. This state of nonalignment continues for about thirty seconds. Although the balance between the two parts changes as the example unfolds, neither beat pattern stands out clearly as the dominant one. Thus one can easily shift attention from one pattern to another, so that the figure/ground relationship between the two patterns reverses.(3) In fact, the reader is encouraged to do so while listening to the example.
[5] This pattern forms what Harald Krebs would describe as
a displacement dissonance, a type of metrical dissonance in which two or more layers
of the same length are nonaligned.(4)
The term metrical dissonance is derived from Maury Yeston’s discussion of
rhythmic consonance and dissonance.(5)
Like Yeston, Krebs believes that meter is formed by the interaction of several different
layers of motion. Usually at least three layers are present: the pulse layer, which
is the fastest regular layer of motion, and two or more slower-moving interpretive
layers, which group the pulse layer into larger units. In
[6] A displacement dissonance occurs when an interpretive layer sounds like it is displaced from a metrical layer; the conflicting layer is called the antimetrical layer. Since electronic sound production facilitates this sort of nonalignment, it is not surprising that it is a frequent source of metrical dissonance in EDM. In Example 1a, a sixteenth-note pulse layer is grouped by two different patterns moving in quarter notes. This excerpt differs from most of Krebs’ examples, however, because it is in a certain sense prior to meter; there is no larger layer grouping the quarter notes into measures. This heightens the ambiguity of the example: it is unclear which layer is metrical and which is antimetrical.(7) If we decide to focus on the synthesizer pattern, then we hear the snare drum being displaced by three sixteenth notes, a dissonance that Krebs would describe as D4+3.(8) On the other hand, if we attend to the snare drum pattern, then we hear the synthesizer as displaced by a single sixteenth-note, or D4+1. Both of these possibilities are summarized at the bottom of Example 1a. According to Krebs, the closer a dissonance is to a state of alignment, the greater the intensity of its dissonance. In this example, then, either possibility creates a rather strong dissonance. If the layers were displaced by two sixteenth notes, however, the dissonance would be less intense; furthermore, there would be less opportunity for reinterpretation.
Example 1b. The Chemical Brothers, “Piku”
(click to enlarge and listen)
Example 1c. The Chemical Brothers, “Piku,” transcribed so the synthesizer is less syncopated
(click to enlarge)
Example 2. Underworld, “Cups”
(click to enlarge, see the rest, and listen)
[7] Example 1b, another excerpt from “Piku,” begins in the same place as the previous example but continues further into the song. I suggest listening to the example apart from the transcription at first; as before, try to experiment with different figure/ground relationships, and note the nonalignment of the layers.
[8] Near the end of the example, a bass drum with a regular half-note pulse enters
(see Example 1b). This new layer
seems to solve the problem of nonalignment. The snare drum part of
Example 1a drops out, and the
new synthesizer pattern seems like a union of the previously nonaligned layers,
combining the two-eighths pattern on B and
[9] In this example, the entrance of a new layer resolves a metrical dissonance.
In other cases, such an entrance may actually create a metrical dissonance.
For example, at the beginning of the song “Cups” from Underworld’s 1998 album
Beaucoup Fish, the synthesizer pattern clearly begins on the downbeat of a
[10] Electronic dance music is not the only type of popular
music in which displacement dissonances occur, of course. Other scholars have pointed
out related phenomena in repertoires such as rock, jazz, and blues. For instance,
Dave Headlam has discussed the use of metrical conflict and “metric shift” in “Rollin’
and Tumblin’,” a work that began as a blues song and was subsequently recorded by
the rock band Cream. Headlam’s analysis centers on a motive that appears in several
versions of the song. In recordings by blues musicians such as Muddy Waters, the
motive is syncopated, emphasizing beats 2 and 4 of each
[11] Another example of metrical dissonance in rock is provided by John Covach, who discusses the presentation, development, and eventual resolution of a metrical dissonance across the course of Yes’s song “Close to the Edge.”(12) Examples of metrical dissonance are also easily found in jazz.(13) For the purposes of the present discussion, then, the significance of these metrical phenomena lies not in the mere fact of their occurrence in electronic dance music, but rather in the distinctive ways in which they are used. For instance, consider how the metrical dissonances described above are situated within the larger works of which they are a part. In the EDM examples, metrical dissonance almost always occurs as part of a process unfolding continuously in real time. In comparison, in the examples discussed by Headlam and Covach, related metrical dissonances are generally separated from each other temporally, sometimes by rather considerable distances (for instance, the time interval between the second and third appearance of the dissonance in “Close to the Edge” is approximately 9 minutes). After their initial presentations, their implications and inherent tensions are developed in various ways, as might occur with a motive in a Classical work.(14) The exploration of motivic possibilities is also a well-known feature of jazz improvisation, and Cynthia Folio’s examples can be understood in these terms.(15) In electronic dance music, on the other hand, the emphasis is not so much on the long-range exploration of a motive’s possibilities as it is on producing an immediate and striking effect—either to create a point of formal articulation (as in Example 1b, in which the resolution of the opening metrical dissonance coincides with the beginning of the work’s first groove), or to introduce an element of surprise (as in Example 2, in which an otherwise straightforward textural buildup is complicated by the introduction of a displacement dissonance).
[12] Furthermore, while the types of metrical dissonance
discussed by Krebs can occur in many different repertoires, they are particularly
relevant to electronic dance music for a number of reasons. As discussed above (paragraph
5), the Yeston/Krebs model conceptualizes meter as the union of several layers
of motion. As in the music of Robert Schumann (the composer upon whom Krebs has
focused most extensively), these layers are particularly clear in electronic dance
music. They often appear as discrete elements of the texture, individuated by timbre,
register, and pattern repetition. For instance, in a
[13] The situation just described might not seem all that unusual in and of itself. In electronic dance music, however, this layered approach to metrical construction is further emphasized by the relative equality of its textural layers. No single voice dominates the texture: in contrast to the vast majority of commercial popular music produced in America and Europe since the advent of rock-n-roll, EDM is not vocal music; in general, its only verbal elements are short, fragmentary samples.(16) Neither does it replace solo voices with instrumental ones: unlike a great deal of classical (and other) instrumental music, it does not as a general rule employ melody-and-accompaniment textures.
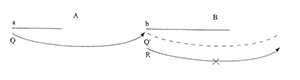
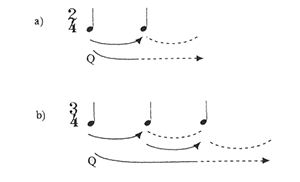
[14] Layering is also absolutely essential to the way electronic dance music is recorded and performed. In the studio, EDM is produced in a multi-channel environment, which allows all of its sound sources to be controlled independently, so that layers of motion can be combined in a variety of interesting ways. Of course, this technology is not limited to EDM; in fact, it is commonplace in contemporary popular music. In most pop traditions, however, audiences expect performers to be able to produce reasonable facsimiles of their recordings in live performance, a factor that may limit the complexity of metrical dissonance. This is not the case in EDM, though. In this repertoire, a completely different tradition of live performance exists, one in which DJs, rather than studio artists, take center stage.(17) For the most part, records are treated not as finished products but as raw material for manipulation by the DJ. While the music that one hears at a nightclub or a rave originates in the studio, records are rarely heard in their original studio-produced forms. Instead, they are manipulated and combined with other records in a real-time process that produces substantially different compositions. The DJ uses turntables to play two or more records at once and a mixing board to control the balance between the records (one record is usually more prominent). The mixing board also allows the DJ to control the high, middle, and low range of each record, which makes it possible to manipulate layers within as well as between records. This capability facilitates the real-time creation of displacement dissonances like those seen in Examples 1a/1b and 2 (which are taken from studio-produced recordings). For instance, reinterpretations (cf. Example 2b) can be created by playing a pattern such as that found in Example 2a on one record, then bringing in the bass drum of another record on the offbeats. The lower, more resonant bass drum sound “turns the beat around,” but the first pattern persists, thereby producing a displacement dissonance. Conversely, given a situation like that of Example 2c, the DJ might use the high- and low-range controls to remove the bass drum and high synth pattern, thus calling a seemingly clear metrical interpretation into question.
[15] Thus, while a layered conception of musical meter can be applied to many different repertoires, it is particularly well suited to electronic dance music, in which a layered approach is fundamental to musical construction. As we have seen, this approach manifests itself in a variety of ways: in techniques of performance and production, in the connection between metrical and textural layers, and in the relative equality of textural layers. In fact, this last feature promotes another distinctive characteristic of this repertoire: in many cases, especially near the beginning of a track, there is no definitive accentual interpretation of a passage. Examples 1 and 2 demonstrate this phenomenon quite clearly. In Example 1a, as previously discussed, it is unclear which layer is metrical and which is antimetrical; in Example 2, a layer that is suggested as metrical eventually turns out to be antimetrical.(18) The absence of a definite interpretation in such situations encourages the listener to experiment with different interpretations. In repetitive music such as EDM, this ambiguity often plays a crucial role in the creation of musical interest. In fact, Steve Reich has noted a similar phenomenon in minimalist music. Of his own music, he says: “If I compose music that is to use repeating patterns and is also to remain interesting I must build in rhythmic ambiguity to make it possible for the ear to hear a given pattern beginning and ending in different places depending on slight differences of accent and on how one listens.”(19)
[16] In the previous examples, ambiguity was created by the interaction of two or more patterns. As Reich’s statement suggests, however, individual patterns can also be inherently ambiguous. In fact, extreme simplicity often promotes such ambiguity. For example, consider the TICK-tock-TICK-tock-TICK-tock pattern of a clock. By focusing on the “tock,” one can easily hear the opposite accentual pattern: tick-TOCK-tick-TOCK-tick-TOCK.(20)
[17] This type of ambiguity also figures prominently in electronic dance music. As an example, let us consider another track by Underworld. This song, entitled “Moaner,” begins with a drumbeat articulating a steady quarter-note pulse; between these beats, a synthesizer plays three sixteenth notes, as shown in Example 3a. It seems probable that the drumbeat, being louder and longer in duration, would play the primary role in determining the accentual pattern. The synthesizer sound also attracts attention, however, by changing timbrally and dynamically, while the sound of the drumbeat does not vary. As one focuses on the synthesizer sound, one can hear an accent on the second sixteenth note of the pattern, as shown in Example 3b. It is also possible to hear an accent on the third sixteenth, as seen in Example 3c. This last hearing begins to be especially noticeable after about fourteen seconds of the song. At this point, the timbre of the sound begins to change, as a process called a filter sweep, which gradually begins to emphasize the upper partials, is applied to it. The sound crescendos at the same time. Underworld also draws attention to the sound changes by altering the drum pattern very slightly just before the changes begin.
[18] In a sense, the interpretations shown in Examples 3b and 3c create displacement dissonances with the drumbeat. These dissonances differ from the one heard in Example 2c, however, since they are created by the reinterpretation of an already-sounding pattern, rather than by the entrance of a new pattern. As such, they are inherently more fragile: if one focuses too much on the drumbeat, the new interpretations of the synthesizer pattern seem to fade away.
[19] In addition to highlighting the ambiguity found in these examples, I have tried to emphasize the way that accentual and/or metrical interpretations evolve or emerge while one listens to them. In this respect, I am inspired by the work of Christopher Hasty and Gretchen Horlacher, who have captured this quality of musical experience very effectively in their approaches to meter. For instance, Hasty writes that “a piece of music, while it is going on, is incomplete and not fully determinate—while it is going on, it is open, indeterminate, and in the process of becoming a piece of music.”(21) The processual quality that Hasty describes is particularly noticeable in electronic dance music. As in minimalist and other types of repetitive music, processes unfold very gradually in EDM. Patterns are repeated for long periods of time. For example, in “Moaner,” the patterns heard in Example 3 repeat almost constantly throughout the length of the song—approximately 7½ minutes. Such repetition is an asset in minimal music,(22) since it gives the listener time to rehearse different rhythmic interpretations. Although other sounds enter throughout the course of the song, masking the original, accentually indeterminate pattern, it continues to be heard beneath the surface, giving the entire song an aura of instability.
[20] We have now heard several examples of the rhythmic and metrical phenomena that occur in electronic dance music, including displacement dissonances and various types of ambiguity. In the next portion of this paper, I will focus on another feature—namely, the use of asymmetrical patterns. Although I will begin by looking at two musical examples, the majority of my discussion will focus on certain broader questions of rhythmic and metrical theory. I will highlight the issues raised by EDM’s asymmetrical patterns and will suggest some approaches that are particularly useful for dealing with them.
[21] All of the examples considered thus far have contained layers of steady quarter-note or half-note motion (even though the metrical context of these layers was not always clear). However, while electronic dance music often features even rhythms very prominently, this is not always the case. For instance, in the track “Compression” by Everything But the Girl, a prominent drumbeat repeats the pattern quarter-eighth/quarter-eighth/quarter throughout. Timbral changes within the pattern suggest divisions after each of the eighth notes, and almost all of the rhythmic patterns in the track reinforce this 3+3+2 division; the only exception is the triplet pattern played by Synthesizer 1, which occurs at a low dynamic level. (See Example 4, a–e.) Thus there is very little to suggest a quarter-note pulse in this track. A 3+3+2 pattern (again divided into quarter-eighth/quarter-eighth/quarter) also underlies much of Underworld’s “Pearls Girl” (though the variable fourth measure departs from this organization).
[22] Patterns that divide a measure asymmetrically occur in a number of different repertories, including folk music of the Balkans and drum ensemble music of sub-Saharan Africa. In some cases, especially in the former repertory, the number of pulses in the measure is a prime number, which means that the beat patterns comprising the meter must be irregularly spaced. In electronic dance music, however—as in much African percussion music—the measure contains a nonprime number of pulses.(23) This makes it considerably more difficult to determine the meter when asymmetrical patterns are prevalent, since the measure can also be divided evenly. Should the recurring asymmetrical patterns be considered metrical, resulting in meters such as 3+3+2/8 or 3+3+3+3+4/16, or should they be treated as syncopations against a regular background?
[23] In addressing this question, it is useful to see what scholars of African
music have to say, as some of them have given considerable attention to the issue.(24)
Thus in the next few paragraphs I will focus primarily on their arguments, though
I will also relate their observations to electronic dance music. In general, Africanists’
opinions on meter and asymmetrical patterns seem to fall into two different schools
of thought. On the one hand, scholars such as Robert Kaufmann argue that regularly
recurring asymmetrical patterns can become metrical, so that they do not seem syncopated.(25)
In such cases, notes that would be accented in a
[24] On the other hand, quite a few ethnomusicologists have rejected this sort of interpretation, arguing instead that listeners infer a background of evenly spaced beats behind groupings such as 3+3+2.(26) The view of meter as a grid—a regular background against which irregularity can occur—is also central to many music-theoretical models of meter. One of its most influential expressions occurs in A Generative Theory of Tonal Music. In this work, Lerdahl and Jackendoff posit the regular alternation of strong and weak beats as a precondition for meter. In their well-formedness rules for meter, they stipulate that “at each metrical level, strong beats are spaced either two or three beats apart” and that “each metrical level must consist of equally spaced beats.”(27) And while they focus specifically on Western tonal music, another music theorist, David Temperley, has recently applied their approach to both African traditional music and Western rock music.(28)
[25] Scholars of African music have objected to the grid approach for a number
of reasons. Some, like Kaufmann and Stone, feel that it represents a “Western” approach
to meter rather than an African one.(29)
Others, while not denying that the grid can be applied to African music, question
whether it really suits the music. Thus the question becomes not so much “is the
meter 3+3+2/8 or
[26] Furthermore, even if one accepts the separation between rhythm and meter that is fundamental to most grid approaches, there is much to suggest that the whole relationship between the two is different in EDM and African music. In much common-practice-era Western music, departures from the metrical structure end up reinforcing it; they pull against it just enough to call attention to it. Scholars have suggested that this phenomenon occurs with syncopation in rock as well; for instance, Temperley, arguing that rock syncopations are best understood as displacements from specific metrical beats, writes that “syncopated rhythms often seem to reinforce the metre of a song rather than conflicting with it.”(31) In African percussion music, on the other hand, the rhythms of the surface tend to set up expectations of their own through persistent repetition, in spite of their irregular spacing within the measure. Thus Jay Rahn writes:
[Asymmetrical] ostinatos
. . . are not mere outgrowths of the referential meters of the pieces in which they occur. In each case, they represent persistent deviations from the divisive patterns that accompany them. . . Ethnomusicologists have observed that African musicians say these sorts of asymmetrical time lines represent an audible point of reference for the ensemble as a whole. That is, in some instances, African performers apparently find their point of rhythmic orientation within a dense texture not with respect to a pulsating pattern or a divisive, unsyncopated pattern, but rather in relation to a seemingly syncopated pattern that appears to deviate constantly from the meter of the piece.(32)
In comparison, meter seems to be more purely referential, a simple yardstick rather than the focus of compositional attention—in the words of Arthur M. Jones, “a kind of metronome which exists behind the music.”(33)
[27] I contend that many of the same conditions apply to electronic dance music
in which asymmetrical patterns are prominent. Although almost all EDM can be transcribed
in
[28] These observations suggest a shift in emphasis, a change in the way rhythm is viewed with respect to meter in electronic dance music. Rhythm begins to seem not so much like a foreground phenomenon embellishing some deep background structure, but rather as a structurally significant element in its own right. Writers studying other repertoires have suggested similar changes in focus. For instance, Dave Headlam, in a discussion of rhythm and meter in the country blues, writes:
Is it more useful to regard, for instance, Robert Johnson’s songs as beginning from a regular metrical basis, as many writers do, with the surface described as “irregular”? Or is an irregular (or, better, not necessarily regular) rhythmic approach more appropriate, with any regular surface meter regarded as a compositional and performance by-product of the grouping structures?(35)
[29] Likewise, Jay Rahn argues with respect to African music that “one might like to determine how such syncopated patterns can be considered ‘rhythms of reference’ and whether there is any sense in which they can be viewed as regular. Rather than describing these patterns negatively (e.g., as deviations from a divisive organization), perhaps one can discern positive features in their structures.”(36) To this end, he has explored the special properties of these rhythms. In fact, Rahn is one of a number of writers whose work suggests alternatives to grid-based views of asymmetrical patterns. In the rest of this section (paragraphs 30–36), I will explore three of these alternatives. It is not my goal in discussing this research to suggest an all-encompassing model of asymmetry (or, more generally, of rhythm and meter) in electronic dance music, for much additional research would needed before such a model could be proposed. I believe, however, that the approaches of these authors will suggest some ways in which the construction of a broader model might proceed.
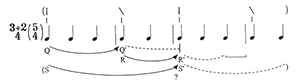
Example 5
[30] Much of Rahn’s work in this area builds upon diatonic set theory, drawing
parallels between pitch collections such as 7–35—a set that has long been treated
as “structurally privileged”—and asymmetrical rhythm patterns.(37)
For instance, following Clough and Douthett,(38)
Rahn notes that these “diatonic rhythms” are maximally even: in informal terms,
this means that the number of attacks within each pattern is distributed as evenly
as possible among the pulses in the cycle. This property can also be seen in EDM,
which contains many of the diatonic rhythms that Rahn discusses. For example, the
quarter-eighth/quarter-eighth/quarter (2+1+2+1+2) pattern of
Example 4 and Example 5
is a maximally even distribution of five attacks among eight pulses—in contrast,
for example, to the foursquare rhythm eighth-eighth-eighth-eighth-half.(39)
Furthermore, while certain foursquare patterns (e.g., four quarter notes in
[31] The properties cited by Rahn suggest possible reasons for the special presence of the asymmetrical patterns that occur in electronic dance music—the way in which they seem to stand on their own apart from any metrical grid. For instance, attacks within maximally even asymmetrical patterns are almost as regular as metrical beats. Because of the slight irregularities of these patterns, however, each attack has a unique relationship to every other attack, which is not the case in completely even rhythms. These structural features distinguish this type of organization from that of meter, even though the rhythms produced by diatonic organization can coexist with a variety of metrical structures.
[32] A quite different, though not unrelated, approach to the “presence” of asymmetrical patterns is suggested by some of Stephen Handel’s recent work. In a 1998 article, Handel considers how metrical structure interacts with a special type of grouping known as figural organization.(41) When figural organization is in effect, tones are heard as discrete groups. The listener attends to the number of tones constituting each group, but not to the exact timing between the groups. This means that different rhythms can have the same figural organization. For instance, in a 16-pulse pattern, the rhythms X.X..X....X.X... and X.X....X..X.X... (where Xs stand for attacks, dots stand for unarticulated beats, and tones separated by only one beat are considered part of the same group) have an identical figural organization, which Handel defines as two tones, silence, one tone, silence, two tones, silence (or 2-1-2-).(42) Cognitive psychologists have claimed that meter is necessary to compensate for the imprecision of figural hearing—that listeners use it to measure the differences between otherwise similar rhythms. The three experiments that form the basis of Handel’s article suggest, however, that figural organization may be just as important as meter in rhythmic perception. Handel found that listeners tend to have a hard time discriminating between rhythms with the same figural structure;(43) furthermore, the effect of meter (and of various strategies aimed at highlighting metrical organization) is particularly limited in “weakly metric” patterns (those in which the majority of attacks do not coincide with tactus-level beats). Handel’s focus on the relationship between meter and “weakly metric” rhythms makes his work promising for scholars of electronic dance music, since asymmetrical patterns frequently intermingle with even rhythms in this repertory. (A classic example is 808 State’s track “Cubik,” in which a prominent 3+3+3+3+4 synthesizer pattern sounds against even quarter-note drumbeats.) Handel’s findings, like those of Rahn, discourage us from viewing asymmetrical rhythms as embellishments of a metrical background and provide another way of accounting for their distinctive perceptual qualities.(44)
Example 6. Projected Potential (Hasty, Example 7.2, p. 85)
(click to enlarge)
Example 7. Continuation in Duple and Triple Meter (Hasty, Example 9.17, p. 131)
(click to enlarge)
Example 8. Deferral (from Hasty, Example 9.18f, p. 132)
(click to enlarge)
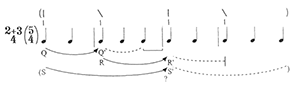
Example 9. Denial of Q′ in 3+2/4 (Hasty, Example 9.28d, p. 146)
(click to enlarge)
Example 10. Denial of R′ in 2+3/4 (Hasty, Example 9.28c, p. 146)
(click to enlarge)
[33] All of the grid alternatives discussed thus far emphasize rhythmic organization over metrical structure. Nonetheless, they still preserve some sort of separation between rhythm and meter. Another possibility is to reject this division altogether. This is the approach Christopher Hasty takes in his recent book Meter as Rhythm. Instead of seeing metrical accents as a series of timepoints, Hasty characterizes meter in terms of events. He claims that meter arises when the duration of an event is replicated through a process called projection. See Example 6, a reproduction of his Example 7.2. In this diagram, capital letters A and B represent two events. At first, we do not know how long A will last. When B begins, however, the duration of A becomes definite; it now has the potential to be replicated by B. This projective potential is shown by the solid arrow Q; the dotted line Q' shows the projected duration.(45)
[34] Hasty also classifies events as beginnings, continuations, or anacruses. He then uses these concepts to discuss different types of meter, claiming that certain types involve more complex perceptions than others. Duple, or equal meter, is the simplest type because it involves the perception of a second event as a continuation of an initial event (see Example 7, part a, in which continuation is shown by the arrow Q). Triple meter involves a more prolonged sense of continuation, as shown in Example 7, part b; it is also more complex than duple because it denies a potential two-beat duration, as indicated by the crossed-out arrow Q in Example 8. Hasty describes this special type of denial as deferral.(46)
[35] In Hasty’s system, meters consisting of irregularly spaced beats engender
considerably more complicated perceptual processes. In duple and triple, all suggested
projections are realized (although in the case of triple, the last projection is
deferred); in an asymmetrical meter, however, some projections will never be realized.
For example, in
[36] As the foregoing discussion has shown, the approaches of Rahn, Handel, and Hasty each provide a distinctive contribution to our understanding of the asymmetrical patterns that occur in electronic dance music. Rahn provides a structural account of the special characteristics of these rhythms, while Handel and Hasty focus more on issues of perception. Handel suggests an alternate mode of hearing that may play a role in the cognition of such patterns; Hasty, on the other hand, applies the same perceptual principle (projection) to all meters, while also showing the unique ways it plays out in irregularly spaced meters. While there are obvious differences between these approaches, they should not be considered mutually exclusive. For instance, although Rahn and Handel, unlike Hasty, preserve a separation between rhythm and meter, their respective emphases (structural properties and figural hearing) could still be situated within Hasty’s method.(49) Likewise, Hasty’s discussion of projection could be applied to asymmetrical patterns even if those patterns are not considered strictly metrical. In fact, I would ultimately conclude that such patterns are not generally metrical in electronic dance music (given that they usually occur in conjunction with regularly spaced patterns that can be heard as metrical more easily).(50) Nonetheless, I would argue that they should not be treated as transient foreground phenomena superimposed onto an underlying regular structure. Rather, as these three methods show us, these rhythms have a distinctive presence of their own and should be considered structurally significant in their own right.
[37] Our exploration has shown a variety of ways in which rhythm and meter are used to create musical interest in electronic dance music. Displacement dissonances subvert metrical stability; inherently ambiguous patterns encourage multiple interpretations; and asymmetrical patterns counteract the regularity of persistent even rhythms. The common link between all these phenomena is an emphasis on interpretive multiplicity. In other words, electronic dance music encourages us to hear it in a variety of ways. As we have seen, this multiplicity functions on many different levels. Individual patterns are often intrinsically ambiguous. Furthermore, they frequently remain so even when used in combination: when there is no definitive metrical layer, the distinction between metrical and antimetrical layers may not be apparent. Even when all the elements of a meter are in place, reinterpretations can turn the beat around, showing the listener that the metrical structure was not quite what it seemed to be. And finally, the persistent repetition of both asymmetrical and even patterns encourages multiple perspectives on rhythmic and metrical structure, thereby undermining any sense that there is a singular structure underlying the music.
[38] In spite of these conclusions, a number of questions remain. First, how might the instabilities and ambiguities that I have discussed be played out on a larger scale? In what ways do EDM musicians create subtlety in a work as a whole? What sorts of processes occur during the course of complete tracks, albums, and DJ sets? Second, how widespread are the phenomena considered here, and how broadly applicable are the approaches put forth to the various genres of electronic dance music?(51) Third, since EDM is first and foremost dance music, what is the relationship of dance to these rhythmic and metrical phenomena?
[39] Each of these questions is a potentially vast topic unto itself, and further research is needed before definitive answers can be given. Instead of trying to answer these questions at this time, I will leave them for future studies of electronic dance music to address.(52) Nonetheless, I believe that these issues, in combination with the phenomena already discussed, suggest something of the range and complexity that electronic dance music offers to listeners and scholars, both within music theory and without.
An earlier version of this paper was read at the Eleventh Biennial Symposium of Research in Music Theory, Bloomington, Indiana, February 25, 2000. I would like to thank all those who have read and commented on the paper, including the two anonymous reviewers, Gretchen Horlacher, Harald Krebs, Eric McKee, Jeffrey Magee, Felicia Miyakawa, and Tanner Menard.
Discography
Juan Atkins. WaxTrax! MasterMix Volume 1. Chicago: WaxTrax! Records, 1998. CD.
808 State. Cubik. New York: Tommy Boy Records, 1990. CD single.
The Chemical Brothers. Dig Your Own Hole. New York: Astralwerks, 1996. CD.
Everything But the Girl. Temperamental. New York: Atlantic, 1998. CD.
Underworld. Beaucoup Fish. New York: V2 Records, 1998. CD.
________. Second Toughest in the Infants. Chicago: WaxTrax! Records, 1996. CD.
Mark J. Butler
Department of Music
University of Pennsylvania
3700 Market St., Suite 300
Philadelphia, PA 19104
mabutler@sas.upenn.edu
Footnotes
1. Because of the profusion of terms describing the various subcategories of contemporary dance music, I prefer to use the umbrella term “electronic dance music” when speaking of the repertoire as a whole. Dance music fans in the general public—who are highly sensitive to issues of style and genre in this repertoire—also employ this term. Other catch-all terms, such as “techno” and “electronica,” are problematic in various ways: to dance music fans, “techno” frequently connotes something more specific (a particular style of electronic dance music), and “electronica” is often viewed suspiciously as a marketing term devised by the music industry. For descriptions of the various genres and subgenres of electronic dance music, see “Talking Music: Sounds from the Dance,” in The New York Times Online, http://www.nytimes.com/library/music/031300dj-techno.html; links to sound files, interviews, and other features are included. Please note that “electronic dance music” will occasionally be abbreviated in this article as “EDM.”
Return to text
2. These particular quotations are taken, respectively, from the following articles in the Detroit Free Press describing the 2001 Detroit Electronic Music Festival: David Lyman, “Detroit Dance Fever,” 28 May 2001, C6; Brian McCollum, Tim Pratt, and Tamara Warren, “Techno and Torrents in Hart Plaza,” 28 May 2001, C6; and Brian McCollum, “Unbeatable,” 29 May 2001, D3.
Return to text
3. Similar ambiguities have been explored by the psychologist Stephen Handel, who has studied the cognition of polyrhythms such as two against three, two against five, and so on. In a series of experiments, Handel and co-researcher James Oshinsky played selected polyrhythms for listeners and asked them to tap along with what they perceived to be the beat; their results suggest that certain combinations encourage a variety of beat placements. See Stephen Handel and James S. Oshinsky, “The Meter of Syncopated Auditory Polyrhythms,” Perception and Psychophysics 30.1 (1981), 1–9.
Return to text
4. Harald Krebs, Fantasy-Pieces: Metrical Dissonance in the Music of Robert Schumann (New York: Oxford University Press, 1999), 33. Krebs describes the type of polyrhythm discussed by Handel as a grouping dissonance. This type consists of layers whose cardinalities differ (for instance, a 3-layer against a 5-layer), whereas a displacement dissonance always involves two or more layers of the same cardinality (ibid., 31).
Return to text
5. Maury Yeston, The Stratification of Musical Rhythm (New Haven: Yale University Press, 1976).
Return to text
6. Krebs, Fantasy-Pieces, 2, 30.
Return to text
7. Krebs does refer very briefly to such a situation, noting that “where there is no metrical framework, the layer initiated earlier usually functions as the referential layer” (ibid., 261, n. 20). While this principle seems plausible, it remains hypothetical within the context of Krebs’s book, as none of his examples fall into this category. Even if we do accept it, it is difficult to apply in this case, as both layers begin almost simultaneously and at a low volume. Krebs has concurred with my assertion that selective attention can change which layer functions as referential in this example (personal communication, May 2000).
Return to text
8. Krebs believes that most displacement dissonances are heard as forward displacements; thus, he usually expresses them with positive numbers—for example, D4+3 rather than D4-1 (ibid., 35–36). In this example, since there is no definitive metrical layer, this distinction is not especially relevant.
Return to text
9. At the same time, the increase in metrical consonance is counterbalanced by the syncopation of the new pitch pattern. Interestingly, if any other note within this pattern were taken as the downbeat, it would be considerably less syncopated; one such rearrangement is shown in Example 1c. Such a move, however, would shift the percussion parts onto weak sixteenth-note beats. It would be quite unusual for the bass drum to be syncopated in this manner; when present, it tends to function as a source of metrical stability in EDM, most likely due to its status as the lowest and most resonant element in the texture. Research in music cognition supports this claim (for instance, Handel and Oshinsky found that when the frequency between metrically dissonant elements varies, listeners tend to choose the lower frequency as stable; see “Syncopated Auditory Polyrhythms,” 4), as does observation of EDM in performance (when played at a typical performance volume, the bass drum will be felt throughout the entire body).
Return to text
10. Here I employ a distinction between conservative and radical listeners first suggested by Andrew Imbrie. (See Andrew Imbrie, “‘Extra’ Measures and Metrical Ambiguity in Beethoven,” in Beethoven Studies, ed. Alan Tyson [New York: Norton, 1973], 45–66.) When presented with conflicting cues, conservative listeners tend to hold onto previously established metrical interpretations for as long as possible, whereas radicals move on to new interpretations more readily. In Example 2b, a conservative hearing is supported by the lack of a strong downbeat orientation in the drumbeat pattern and by the fact that the articulations of this pattern occur on weak beats of the previously established meter; a radical hearing is supported by the previously mentioned tendency of low drumbeats to function as metrically stable in EDM (in contrast to cymbals, which usually function as backbeats) and by the fact that the drum pattern begins one eighth note before the synth and cymbal patterns (if the drum were the backbeat, its pattern would more logically begin on the “and” of beat one).
Return to text
11. Dave Headlam, “Blues Transformations in the Music of Cream,” in Understanding Rock: Essays in Musical Analysis, ed. John Covach and Graeme M. Boone (New York: Oxford University Press, 1997), 73–79. Headlam does not use the term “displacement dissonance”; this application of Krebs’s terminology is my own.
Return to text
12. See John Covach, “Progressive Rock, ‘Close to the Edge,’ and the Boundaries of Style,” in Understanding Rock 11–14. It should be noted, however, that Covach’s examples differ from those previously cited, in that (in Krebsian terms) they would be considered grouping rather than displacement dissonances. (As before, the application of Krebs’s terminology is my own rather than the author’s, though Covach does use the term “metric dissonance.”) While displacement dissonances are quite common in electronic dance music, grouping dissonances are relatively rare.
Return to text
13. For instance, see Cynthia Folio, “An Analysis of Polyrhythm in Selected Improvised Jazz Solos,” in Concert Music, Rock, and Jazz since 1945: Essays and Analytical Studies, ed. Elizabeth West Marvin and Richard Hermann (Rochester, NY: University of Rochester Press, 1995), 103–34. Folio finds examples of both grouping and displacement dissonances (which she refers to as type A and type B dissonances, following an earlier usage of Krebs), as well as a third type (type C) involving out-of-phase tempos.
Return to text
14. Cf. Covach, “Progressive Rock,” 14.
Return to text
15. For the most part, however, Folio’s examples present a succession of distinct, short-lived dissonances, a feature that distinguishes them from Covach’s examples (in which considerable time intervals separate appearances of related dissonances) and from EDM (in which a single dissonance often repeats continuously for a long period of time).
Return to text
16. There are a few notable exceptions to this trend: certain styles of house music feature vocals quite prominently; drum-n-bass/jungle DJs sometimes perform in conjunction with rappers (MCs); and “crossover” artists such as Moby are also more likely to utilize vocals. Nevertheless, the above statement holds true for the majority of electronic dance music; it is quite common to hear several hours worth of music at an EDM performance without encountering a single vocal. Furthermore, the exceptions to this phenomenon tend to push toward or be classified as other genres; for instance, certain performers are classified as crossover acts because their vocally driven songs are seen as moving toward the style and structure of radio-friendly pop.
Return to text
17. DJs also play an important role in certain other genres, such as rap and turntablism. Rap in particular shares many aspects of EDM’s layered approach to musical construction, and layering has been emphasized in analytical approaches to rap as well. For instance, see Tricia Rose, Black Noise: Rap Music and Black Culture in Contemporary America (Hanover, NH: Wesleyan University Press, 1994); Robert Walser, “Rhythm, Rhyme, and Rhetoric in the Music of Public Enemy,” Ethnomusicology 39.2 (1995), 193–217; and Adam Krims, Rap Music and the Poetics of Identity (Cambridge: Cambridge University Press, 2000). Nonetheless, the absence of vocals, in combination with the more central role of the DJ, creates significant textural differences between EDM and rap.
It should also be noted that live performances (generally called “live p.a.’s”) are becoming increasingly common in electronic dance music, especially in its more experimental genres. These performances are usually quite different from those seen in other types of popular music, though. The artists do not play any sort of standard instrument; instead, they manipulate studio technology and software in a real-time environment. (An extreme example occurred at the 2001 Detroit Electronic Music Festival, when artist Nobukazu Takemura and another musician performed solely on laptop computers.) Another difference is that many EDM artists create new works when performing rather than attempting to recreate their recorded works.
Return to text
18. This contrasts with the example given by Headlam, in which a meter is definitively established before the introduction of an antimetrical layer. Covach also argues for a clear distinction between metrical and antimetrical layers in the first presentation of the dissonance he discusses (Covach, “Progressive Rock,” 11 and 13).
Return to text
19. Steve Reich, “Non-Western Music and the Western Composer,” Analyse musicale 11 (1988), 49.
Return to text
20. Cf. Simha Arom, “Time Structure in Music of Central Africa: Periodicity, Meter, Rhythm, and Polyrhythmics,” Leonardo 22 (1989), 91.
Return to text
21. Christopher Hasty, Meter as Rhythm (New York: Oxford University Press, 1998), 3.
Return to text
22. Cf. Gretchen Horlacher, “Multiple Meters and Metrical Processes in the Music of Steve Reich,” Intégral (forthcoming), 2, where this point is made with respect to minimalist (as opposed to more generally “minimal”) music.
Return to text
23. In EDM, measures usually consist of either eight eighth-note or sixteen sixteenth-note pulses; measure lengths of eight, nine, twelve, or sixteen pulses are common in African music. In both repertoires, however, the number of attacks articulating an asymmetrical pattern is usually an odd number, such as 3, 5, or 7. See Jay Rahn, “Asymmetrical Ostinatos in Sub-Saharan Music: Time, Pitch, and Cycles Reconsidered,” In Theory Only 9.7 (1987), 27–28, for a listing of some of the patterns that commonly occur in African music.
Return to text
24. In turning to this body of scholarship, I am not attempting to suggest a relationship of influence between West African percussion music and electronic dance music. Rather, I consider this literature because it addresses a musical characteristic shared by the two repertories. While I personally believe that EDM probably has been influenced by African music, either directly (e.g., through musicians’ experiences with African music) or indirectly (e.g., through African-American musical traditions), to consider this possibility in detail would take us well beyond the scope of this paper.
Return to text
25. Robert Kaufman, “African Rhythm: A Reassessment,” Ethnomusicology 24 (1980), 394. Other scholars who argue for the existence of irregularly spaced beats in African music include Ruth Stone and Rose Brandel. See Ruth M. Stone, “In Search of Time in African Music,” Music Theory Spectrum 7 (1985), 139–48; and Rose Brandel, The Music of Central Africa (The Hague: Martinus Nijhoff, 1961).
Return to text
26. For instance, see Richard Waterman, “African Influence on the Music of the Americas,” in Acculturation in the Americas (Proceedings of the 19th International Congress of Americanists), ed. Sol Tax (Chicago: University of Chicago Press, 1952), 207–18; J. H. Kwabena Nketia, The Music of Africa, (New York: W. W. Norton, 1974); and David Locke, “Principles of Offbeat Timing and Cross-Rhythm in Southern Eve Dance Drumming,” Ethnomusicology 26.2 (1982), 217–46.
Return to text
27. Fred Lerdahl and Ray Jackendoff, A Generative Theory of Tonal Music (Cambridge, MA: MIT Press, 1983), 69. Lerdahl and Jackendoff do posit these rules as idiom-specific, however, and acknowledge (97) that “certain other metrical idioms have more complex rules in place of MWFR4, permitting structured alternation of different-length metrical units.” (MWFR4, or Metrical Well-Formedness Rule 4, is the second of the rules given above.) Nonetheless, they address these idioms only briefly, and this exception is rarely mentioned in applications of their work.
Return to text
28. See David Temperley, “Meter and Grouping in African Music: A View from Music Theory,” Ethnomusicology 44.1 (2000), 65–96, and “Syncopation in Rock: A Perceptual Perspective,” Popular Music 18.1 (1999), 19–40. Although there are similarities between the GTTM approach and some of the views of meter expressed by ethnomusicologists, I would disagree with Temperley’s assertion that “there is almost unanimous agreement” among ethnomusicologists that African music has meter as defined by Lerdahl and Jackendoff (Temperley, “Meter and Grouping in African Music,” 68; see also 76). In fact, scholars present very diverse opinions on meter and rhythm in this music; even those who seem to share the same general view often differ markedly on various points. Furthermore, due to an unfortunate lack of intellectual exchange between music theory and ethnomusicology—a situation that has only begun to change quite recently—it is difficult to make claims that relate ethnomusicological views of meter to specific music-theoretical ones with any certainty.
In his 1999 paper, Temperley argues that syncopations in rock can be understood as displacements from specific positions in a metrical grid. While this is helpful in showing how Lerdahl and Jackendoff’s model might be extended to highly syncopated repertoires, it will not be discussed at length here, as it is not especially applicable to situations like the one presented above for several reasons: first, it is based on textual accentuation, which is rarely a factor in EDM; second, in all of the examples considered by Temperley, the accompanying instruments clearly convey an evenly spaced metrical structure; and third, none of Temperley’s examples contain regularly recurring asymmetrical patterns like the ones shown in Example 4e.
Return to text
29. Kaufmann, “African Rhythm,” 394; Stone, “In Search of Time,” 140.
Return to text
30. Temperley notes a similar problem with respect to Lerdahl and Jackendoff’s theory. In their approach, patterns that dissonate with the meter are simply described as syncopated; the ways in which syncopation functions remain relatively untheorized. Temperley, “Syncopation in Rock,” 25–26.
Return to text
31. Ibid.
Return to text
32. Rahn, “Asymmetrical Ostinatos,” 25.
Return to text
33. Arthur M. Jones, Studies in African Music, (London: Oxford University Press, 1959), 20–21.
Return to text
34. This general observation may be less applicable to subgenres that feature vocals or instrumental solos. In such cases, the voice or solo instrument may function as a rhythmic and textural “figure” against an accompanimental metrical “ground,” and Temperley’s rock-based model of syncopation may be more applicable.
Return to text
35. Headlam, “Blues Transformations,” 87. Headlam ultimately concludes that either approach may be relevant for different songs and even within the same song.
Return to text
36. Rahn, “Asymmetrical Ostinatos,” 25–26.
Return to text
37. See Rahn, “Asymmetrical Ostinatos,” and “Turning the Analysis Around: African-Derived Rhythms and Europe-Derived Music Theory,” Black Music Research Journal 16.1 (1996), 71–89. Another important article adopting a similar approach is Jeff Pressing, “Cognitive Isomorphisms between Pitch and Rhythm in World Musics: West Africa, the Balkans and Western Tonality,” Studies in Music 17 (1983), 38–61.
Return to text
38. John Clough and Jack Douthett, “Maximally Even Sets,” Journal of Music Theory 35.1 (1991), 93–173.
Return to text
39. In this paragraph I use Rahn’s term “diatonic rhythms” in place of “asymmetrical patterns”; describing the rhythm provided as an example (2+1+2+1+2) as “asymmetrical” is problematic, since its durations form a palindrome. In both “Compression” and “Pearls Girl,” however, this pattern is treated as a variant of 3+3+2, which clearly divides the measure asymmetrically. In fact, all of the diatonic rhythms I have observed in EDM are either literally asymmetrical or are grouped asymmetrically. Rahn himself includes 2+1+2+1+2 in a list of “asymmetrical ostinatos” in his 1987 paper (see pages 27–28), though he replaces this term with “diatonic rhythms” in his 1996 article. Since my paper as a whole is not about the “diatonic” aspects of these rhythms, I will continue to use the term “asymmetrical patterns” throughout the article.
Return to text
40. Rahn, “Turning the Analysis Around,” 79–80.
Return to text
41. Stephen Handel, “The Interplay between Metric and Figural Rhythmic Organization,” Journal of Experimental Psychology: Human Perception and Performance 24.5 (1998), 1546–61.
Return to text
42. Ibid., 1546–47.
Return to text
43. Handel first demonstrated this point in “The Differentiation of Rhythmic Structure,” Perception and Psychophysics 52 (1992), 492–507.
Return to text
44. Although Handel presents a wide variety of weakly metric rhythms, he does not focus specifically on the figural properties of asymmetrical patterns. This is certainly a promising topic for future research, however. He does in fact single out the rhythm found in “Cubik”, 3+3+3+3+4 (or X..X..X..X..X...), for special comment, noting that it differs from the other rhythms in his study in that it is comprised entirely of single-tone figures (its figural organization is 1-1-1-1-1-; Handel, “Metric and Figural Rhythms,” 1559). This attribute suggests an interesting relationship to the maximal evenness discussed by Rahn.
Return to text
45. Hasty, Meter as Rhythm, 84–86.
Return to text
46. Ibid., 131, 133–34.
Return to text
47. Ibid., 146.
Return to text
48. Another work that should be mentioned in this regard is Gretchen Horlacher’s article “Bartok’s ‘Change of Time’: Coming Unfixed,” Music Theory Online 7.1 (2001). Horlacher claims that the processive approach suggested by Hasty is “especially relevant for music that is vitally ‘irregular,’ for it values such irregularities as capable of shaping the essential nature of time within the context of a given piece” (paragraph 4.1).
Return to text
49. While figural hearing might seem incompatible with Hasty’s emphasis on the projection of specific durations, I would argue that it could still be posited as an additional mode complementary to projective hearing. Furthermore, Handel’s characterization of meter as “emergent” (“Metric and Figural Rhythms,” 1560) also resonates with Hasty’s approach. Hasty does in fact discuss research by Handel (see Meter as Rhythm, 124–25 and 173), though the passages cited do not address figural organization in particular.
Return to text
50. In other words, situations in which they occupy every layer of the texture without opposition for the course of an entire track (as in “Compression”) are somewhat exceptional. It is not uncommon, however, for them to dominate entire sections of a track (as in Walt J’s track “Reborn,” as remixed by Juan Atkins on WaxTrax! MasterMix Volume 1); even more common are situations in which they compete for prominence with symmetrical patterns, as in “Cubik.”
Return to text
51. Though (as I will argue in the concluding paragraph) further research is necessary to answer these questions fully, I would like to comment briefly on the issues raised in this sentence. As discussed above (paragraphs 10-15), the phenomena addressed in this paper are not limited to EDM, though their manifestations within it are part of a distinctive constellation of features. Regarding the various genres of EDM itself, I believe that the research presented here can be applied to a broad cross-spectrum of the music, though as I have noted elsewhere, certain features may be more applicable to some genres than others. In selecting the musical examples presented here, I have chosen works from relatively well-known artists with the intent of making the paper more accessible. The artists represented incorporate a variety of genres into their work. The Chemical Brothers are most commonly classified as “big beat,” a term referring to dance music that incorporates some of the song structures and sonic elements of rock and hip-hop (though I believe this aspect of their work has been overemphasized). Everything But the Girl have a long history that has only recently (ca. 1995) begun to include EDM elements; since then, however, they have collaborated with many prominent dance musicians and have successfully incorporated a variety of EDM styles into their work. Underworld (who recently disbanded) are difficult to place within a particular genre, as their individualistic sound shows the influence of techno, deep house, breakbeat, and dub; however, their music has often been characterized broadly as techno (for instance, see Dom Phillips, “Underworld,” in The Rough Guide to Techno [London: The Rough Guides, 2000]). In spite of the commercial success of these artists and the fact that some of their work includes elements of other popular music genres, I have avoided work that might be considered “crossover” (such as The Chemical Brothers’ collaborations with Oasis and other pop musicians), and I believe that the music included here represents trends central to EDM.
Return to text
52. Many of these questions will in fact be addressed in my doctoral dissertation, “A Study of Rhythm and Meter in Electronic Dance Music, with a Consideration of the Enactment of These Features in Dance” (Indiana University, in progress).
Return to text
It should also be noted that live performances (generally called “live p.a.’s”) are becoming increasingly common in electronic dance music, especially in its more experimental genres. These performances are usually quite different from those seen in other types of popular music, though. The artists do not play any sort of standard instrument; instead, they manipulate studio technology and software in a real-time environment. (An extreme example occurred at the 2001 Detroit Electronic Music Festival, when artist Nobukazu Takemura and another musician performed solely on laptop computers.) Another difference is that many EDM artists create new works when performing rather than attempting to recreate their recorded works.
In his 1999 paper, Temperley argues that syncopations in rock can be understood as displacements from specific positions in a metrical grid. While this is helpful in showing how Lerdahl and Jackendoff’s model might be extended to highly syncopated repertoires, it will not be discussed at length here, as it is not especially applicable to situations like the one presented above for several reasons: first, it is based on textual accentuation, which is rarely a factor in EDM; second, in all of the examples considered by Temperley, the accompanying instruments clearly convey an evenly spaced metrical structure; and third, none of Temperley’s examples contain regularly recurring asymmetrical patterns like the ones shown in Example 4e.
Copyright Statement
Copyright © 2001 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason and Tahirih Motazedian, Editorial Assistants