Serial Intervention in Nono’s Il canto sospeso
Jeannie Ma. Guerrero
KEYWORDS: Nono, total serialism, integral serialism
ABSTRACT: The instrumental movements of Luigi Nono’s Il canto sospeso exhibit a variety of procedures that override determinations made by serial structures. The overrides, as I describe them, yield novel textures in multiple musical dimensions and seem to inspire Nono’s experimentation with electronic media later in his career. Further, multidimensional textures create formal musical and symbolic regions that underlie Nono’s projection of highly charged textual matter.
Copyright © 2006 Society for Music Theory
[1] Nono’s experimentation with total serialism during his association with the Darmstadt Summer Courses (roughly 1950 to 1960) produced works whose lineage to serialism becomes interwoven with other compositional strands. The mixture of ideas fosters competition between organizing forces in his compositions from that time, yielding an outward appearance of erratic or conflicted behavior especially with regard to serial principles of ordering.(1) For instance, Nono’s studies in Renaissance puzzle canons during the previous decade shaped his musical endeavors.(2) Not unlike his contemporaries, he occasionally used imitative procedures inspired by puzzle canons as organizing elements that operated beyond the reach of serial material.(3) Pitch-class palindromes, for example, subject their generative twelve-tone series to replicative symmetry, in complete independence from any inherent symmetry that the series possess. As another example of competing organizational forces, Nono developed musical textures in several non-pitch dimensions. Relationships between dimensions evolve and change throughout a composition, driving its form independently of regions delineated by transformations of serial content.(4)
[2] Recent scholarship has loosely grouped these complex inter-dimensional relationships together under an umbrella term, “multidimensionality.” Large-scale multidimensionality shapes a 1960 piece for eight mixed voices, Sarà dolce tacere, and creates formal regions in a 1958 work for thirty-two mixed voices, Cori di Didone.(5) Both compositions, whose material is derived serially, achieve motion in various dimensions through imitation. For instance, in Sarà dolce tacere a particular durational value can echo throughout a passage of music, as can a single pitch (as opposed to a pitch-class) or a dynamic marking. Imitation also occurs in proportion (2:1 durations, for instance), taking inspiration from prolation canons. The echoes build threads in several dimensions. If the threads involve distinct performers, the threads intertwine in contrapuntal relationships analogous to contrary motion. Conversely, if echoes between threads occur within the same performers, the threads combine in a manner analogous to parallel motion. Sarà dolce tacere begins with densely skewed counterpoint and progresses gradually toward unison movement at its conclusion so that multidimensional textures give it shape, rather than serial transformations.
[3] Multidimensional motion as achieved by his choral works seems to have evolved dramatically when Nono experimented with electronic media. Nono describes his experiments with electronic sources as broadening traditional ideas of canonic imitation and musical motion, but the language he uses is directly derived from procedures used in his analog choral music:
Non è il canone alla Frescobaldi, o il canone rinascimentale, si tratta piuttosto di alcuni elementi che si compongono in modo canonico
. . . che si mettono in circolo ma non necessariamente; non si tratta cioè dell’intervallo, della durata o del timbro. . . quello che faccio oggi a Friburgo con questo strumento che si chiama Halaphon è qualcosa di analogo. Tu dinamizzi nello spazio attraverso vari altoparlanti a velocità contrastanti un suono e questo suono poi si protrae girando in una direzione unica e in plurime direzioni. Lo stesso suono puoi farlo girare con altri quattro movimenti nello spazio: per esempio, con dinamiche differenti, con tempi differenti, acceleranti e ritardanti, oppure a salti. . . L’ascolto risulta estremamente complesso, ma la cosa piü straordinaria è che non hai bisogno di quattro segnali differenti, basta un unico segnale.[It’s not the canon of Frescobaldi, or the Renaissance canon. It deals above all with some elements that are composed in a canonic way
. . . that you place in a circle, but not necessarily. It’s not a matter of, shall we say, interval, duration, or timbre. . . what I do now at Freiburg with this instrument called the “Halaphon” is somewhat analogous. You dynamize a sound in space through various loudspeakers at contrasting velocity, and this sound then extends itself by spinning in a single direction as well as in several directions. You can make the same sound spin with four other motions in space: for example, with different dynamics, with different tempi, accelerating and decelerating, or else with jumps. . . Listening turns out to be extremely complex, but the most extraordinary thing is that you do not need four different signals; a single signal suffices.](6)
[4] Nono’s work with electronic media revolved around spatial considerations and their acoustical effects. For instance, a sound approaching a listener rises in dynamics and fades as it passes. Its pitch level also rises and falls. By imitating the acoustic effects produced when a sound moves in relation to the perceiver, electronic instruments could simulate spatial motion. Actual spatial motion could also be achieved by having a signal travel across several acoustic sources. More importantly, a single electronic source could project several simultaneous movements quite clearly; multidimensionality required a large number of performers in comparison and created motion in several simultaneous dimensions much less audibly. Nono would refer to the spatially rendered music yielded by his electronic experiments as “il suono mobile.”(7)
[5] The present paper arises from the hypothesis that Nono’s serial experiments provided inspiration for his electronic experiments, with multidimensional textures serving as prototypes for “il suono mobile.” The 1956 cantata Il canto sospeso exhibits a crucial stage of multidimensional development, making additional innovations in text-setting that provide a complementary façade for multidimensional textures.(8) As I shall discuss later, various re-ordering operations (as opposed to row transformations achieved through pitch-class transposition and inversion) create serial complexes whose elements are systematically consumed one by one to furnish attributes for a corresponding number of notes.(9) Thus, a typical twelve-element series plus its eleven order-position transformations would create an ordered complex of 144 elements, which would determine the pitch-classes, durations, or dynamics of exactly the same number of notes. I shall refer to the determinations made by such complexes generally and simply as “serial material.” By building its music note by note from such complexes, the composition illustrates serial origins of multidimensionality more visibly than Cori di Didone or Sarà dolce tacere, for instance. Pieces like these represent a stage at which Nono created multidimensional textures directly and do not use large serial complexes to supply content for every note in the composition.
[6] With Il canto sospeso (the “suspended” or “interrupted” song) Nono made a dramatic stylistic shift from earlier choral works and bolstered his international standing as a composer. Written for soprano, contralto, and tenor soloists, mixed choir, and orchestra, the piece quotes letters written by members of the European Résistance before their executions. A 1954 collection of these letters circulated in Italy, providing direct inspiration for the cantata.(10) Further inspiration undoubtedly came from Arnold Schoenberg’s A Survivor from Warsaw, whose influence can be heard in Nono’s earlier choral works.(11)
[7] The piece uses ten letters written by persons from six countries. The textual translations appearing below are numbered according to the movement in which they appear:(12)
No. 2: I am dying for a world which will shine with light of such strength and beauty that my own sacrifice is nothing. Millions of men have died for this on the barricades and in war. I am dying for justice. Our ideas will triumph.
— Anton Popov, Bulgaria, 26-year-old teacher and journalistNo. 3: They are taking me to Kessariani for execution together with seven others. I am dying for freedom and for my homeland.
— Andreas Likourinos, Greece, 14-year-old studentToday they will shoot us. We die as men for our homeland. Be worthy of us.
— Eleftherios Kossès, Greece, 19-year-old studentThey are hanging me in the square because I am a patriot. Your son is leaving, he will not hear the freedom bells.
— Konstantinos Sirbas, Greece, 22-year-old hairdresserNo. 5: If the sky were paper, and all the seas of the world were ink, I could not describe my suffering and all that I see around me. I say goodbye to all of you and weep.
— Chaim, Poland, 14-year-old boyNo. 6: The doors open. Here are our murderers. Dressed in black. They drive us out of the Synagogue. How hard it is to say goodbye forever to life which is so beautiful!
— Esther Srul, PolandNo. 7: Goodbye mother, your daughter, Liubka, is going into the moist earth.
— Ljuba Schevtzova, Soviet UnionNo. 9: I am not afraid of death.
— Irina Malozon, Soviet UnionI will be calm and at peace facing the execution squad. Are those who have condemned us equally at peace?
— Eusebio Giambone, Italy, 40-year-old typesetterI go in the belief of a better life for [all of] you.
— Elli Voigt, Germany, 32-year-old worker
[8] The opening textual selection in No. 2 sets the stage thematically for the ensuing selections. No. 9 recapitulates No. 2’s themes, evoking a transcendent quality. Both Nos. 2 and 9 are set for choir, offering complicated vocal textures in line with their transcendent tone.(13) In contrast, No. 3 quotes three Greek citizens who provide frank, journalistic descriptions of the fates awaiting them. The remaining texts (Nos. 5, 6, and 7) evoke a third atmosphere, one of lament and departure.
[9] Beyond its textual matter, the composition has notable yet enigmatic features. The piece departs dramatically from Nono’s declamatory style in earlier works even though its textual matter (which bears uncanny resemblance to Survivor) begs for comprehension. The muddled textual delivery led Stockhausen to remark that the sonic content of the texts itself became subject to serial re-ordering, thereby creating a rift between phonetics and semantics.(14) Nono refuted Stockhausen’s (well-intended) observations, asserting that his music intertwined the phonetic and semantic aspects of its texts at historically profound levels.(15) In the debate Nono sheds all doubt that Sospeso’s texted movements preserved the letters’ meaning, but nowhere does he mention how the three instrumental movements (Nos. 1, 4, and 8) engage the piece’s textual content.(16) The analytical work of the present paper will focus on the instrumental interludes, and as will be seen, they make essential contributions to the piece’s overall artistic mission.
[10] Sospeso has also received the bulk of scholarly attention devoted to Nono’s earlier works, especially since the Archivio Luigi Nono in Venice furnished sketch materials to the public in the 1990s. Massimo Mila provides an overview of Sospeso’s compositional process and an analysis of the tenor solo in No. 3.(17) Kathryn Bailey’s analysis continues to be the most extensive study in English.(18) Insights since gained by examining sketch materials can fill many of the “gaps” left open by her analysis; I shall do my best to update her work in this regard.(19) Ivanka Stoianova addresses textual “spatializations” created by Sospeso’s text setting, categorizing various levels of “delinearization” according to whether they rearrange a word’s internal components or weave several words together.(20) Wolfgang Motz furnishes a summary of sketch materials and writes on the entire composition; in addition, he has reported on Nono’s “liberal fantasies” at the beginning of No. 1 in matters of registral placement and orchestration.(21) Erika Schaller also includes a chapter on Sospeso in her study of works composed between 1955 and 1959.(22) Nicholas Huber has commented extensively on Nos. 6a and 6b, revealing an overall palindromic structure that enacts a Nazi raid on a synagogue.(23) Gianmario Borio includes a brief overview of No. 4’s re-ordered row complex and relates it to procedures in Boulez’s Structures 1a.(24)
[11] My work here examines the multidimensional aspect of Nono’s music in relationship to its serial procedures, unlike previous studies. As mentioned, multidimensionality acts as an increasingly influential organizing agent in Nono’s serial compositions. For this reason, complexes generated by serial re-ordering operations, which are neatly outlined in Sospeso’s sketches, appear to lose their immediate connection to the resulting music, undergoing a procedure that I shall call “intervention” on their way to multidimensional realization. Nono saw intervention as an integral component of serial composition, citing Schoenberg himself:
Tu parli di un uso delle serie con riserva, io parlo invece di un uso della serie con fantasia libera. Bruno [Maderna] e io eravamo perfettamente convinti di questa necessità. Da analisi delle opere di Schönberg, per esempio le Variazioni op. 31, risulta che l’uso delle serie non segue mai la numerica schematizzata da Leibowitz e da tanti geometri catastali delle musica. Lettere di interpreti, di Kolisch e di Steuermann, interrogano Schönberg su possibili error ‘seriali’ in sue partiture non consequenziali alla sopracitata numerica schematizzata. La risposta di Schönberg chiarisce la sua fantasia libera: piü o meno (non ricordo a memoria) dice: “è possibile che voi calcoliate in un momento un data suono della serie, ma in quel momento ho sentito altre fantasie compositive.”
[You are talking about using the series rigidly; I’m speaking instead of using the series with liberal fantasy. Bruno [Maderna] and I used to be perfectly convinced of this necessity. Analyses of Schoenberg’s works, for example the Variations Op. 31, show that using the series never follows the numerical schematization by Leibowitz or by such geometric heaps of music. Letters by interpreters, Kolisch and Steuermann, interrogate Schoenberg on possible “serial” errors in his scores that are not consequences of the above-mentioned numerical schematizations. Schoenberg’s response clarifies his liberal fantasy. More or less (I do not have this committed to memory) he says: “It is possible for you to calculate at a[ny] moment a note determined by the series, but at that moment I have heard other compositional fantasies.”](25)
[12] The level of decision-making that serial “schematizations” do not encompass would always take precedence:
Und auch mit dem Etikett seriell kann ich mich nur unter Vorbehalt einverstanden erklären. Ich schrieb schon damals nicht, was die Presse durchorganisierte Musik hieß. Ich arbeitete immer sozusagen in drei Stufen. Zuerst wählte ich das Material, das intervallische, das klangliche, das rhythmische. Dann experimentierte ich mit diesem Material, unterzog es vielleicht auch verschiedenen präedeterminierenden Prozessen, aber nur um zu sehen, im welcher Richtung es sich entwickeln könnte. Und dann komponierte ich, leitete also aus dem Material und den ihm einbeschriebenen Möglichkeiten eine ihm gemäße Form ab. Dabei war für mich das Komponieren nie bloß die Konkretisierung von vorgeformten Strukturen. Stets spielten improvisatorische Momente mit; ich hielt mir die Entscheidungen bis zum letzten Augenblick offen.
[As for serial etiquette, I can only explain going along with it reservedly. Even back then [in Darmstadt] I was not writing what the press called totally organized music. I always worked, so to speak, in three stages. First I chose the material, the intervallic, harmonic, rhythmic [aspect]. Then I experimented with this material, subjected it perhaps also to various predetermined processes, but only to see in which direction it could evolve. And then I composed, derived from the material and its inscribed possibilities a form in accordance with it. In that regard composing was never for me merely the concretization of preformed structures. Improvisatory moments always played a part; I left decisions open until the last instant.](26)
[13] Nono’s interventions arise in part to create multidimensional textures in Sospeso. Serial re-orderings, even when affecting several dimensions simultaneously, cannot produce multidimensional motion directly. Thus, Nono’s interventions, and lack thereof, will shape the discussion. I shall present two main, provisional types of intervention in the following pages. I shall also present various manifestations of these two categories that appear in Sospeso. I do not intend for the details offered here to be exhaustive, as other works contain further variants. In addition, I shall use the interactions among various musical dimensions as a framework to rework existing analyses and present new ones altogether of the three interludes.
Type I: Intervention by systemic override
[14] In this intervention type, a secondary system mediates the implementation of elements generated by a primary system, re-ordered row complexes in the case of Sospeso. The secondary system directly overrides determinations such as the ordering of pitch-classes or rhythmic values. The overrides are mechanized so that they affect large numbers of notes, much as primary systems generate material in large quantities. I refer to any intervention by secondary system as a “systemic override” to reflect the competition between systems, as well as the automated nature of the overrides.
[15] A near-ubiquitous systemic override in Nono’s music intervenes with the implementation of duration material. To illustrate how this is done, I shall use a system for notating rhythmic durations as fractional values. In this scheme, denominators (bottom values) represent the number of parts that divide a quarter note; for this reason they are called “beat-divisions.”(27) For instance, an eighth-note divides a quarter note into two parts; it would be assigned a denominator of 2. Similarly, an eighth-note triplet receives a denominator of 3, and so on. Numerators in this system represent factors given by serial systems, which beat-divisions then distort. For example, the duration factor 12 strongly bears the influence of the beat-division applied to it. Applied to a beat-division of 3, the resulting duration (12/3) has a length equal to four quarter-notes. Applied to a smaller beat-division such as 4, the resulting duration (12/4) results in a shorter length, three quarter-notes as opposed to four. Beat-divisions can also invert size-relationships between duration factors. A large factor can be applied to a small beat-division (12/6, equivalent to two quarter notes) and result in a shorter duration than a small factor applied to a large beat-division (5/2, equivalent to two-and-a-half quarter notes). In all, beat-divisions maximize the rhythmic variety afforded by a given base duration series.
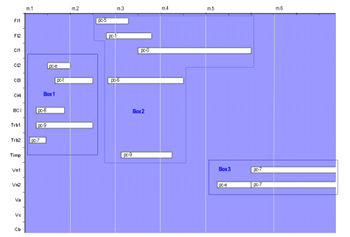
[16] The opening measures of No. 1 illustrate the wide range of durations that beat-divisions produce. Example 1 shows the first few measures of No. 1. Boxed areas in the example may be clicked on to show their contents. Box 1 in the figure contains five notes that bear duration factor 5.(28) Also, rhythmic values for pc-t and pc-7 in Box 1 are notated using beat-divisions that have been doubled, effectively dividing an eighth note rather than a quarter note, as before. Duration-factors have also been doubled, so that pc-t has the duration 10/6 and pc-7 the duration 10/14. The doubling of duration-factors and beat-divisions occurs rather late in the compositional process, as Motz discusses in “Konstruktive Strenge.” That is, Nono decided to double the values of some but not all notes after he had determined their durations. The rhythmic notation of the two notes here indicates that Nono doubled their values. However, the conversion does nothing to displace the original notes or to alter their overall length, and they could still have been notated using the original durations, which are shown in the boxes. Other doubled durations cannot be reduced back; they will be discussed shortly. Pitch-classes follow the ordering of Sospeso’s twelve-tone series (9 t 8 e 7 0 6 1 5 2 4 3), which shows that duration factors receive increasingly smaller beat-divisions (1/2, 1/3, 1/4, 1/5, and 1/7). The repeated pc-9 of Box 2 occurs not as an isolated incident but as a byproduct of a technique that I shall discuss later. Although all five notes in Box 1 share the same duration factor, they acquire distinct durations when applied to various beat-divisions. The beat-division process continues in Box 2, whose pitch-classes share a single duration factor (10) and course through the five successively smaller beat-divisions of Box 1.(29)
[17] Serial order can compete with a second systemic override that uses rests to displace notes within chords. Rests of varying length create staggered entries rather than a unison, chordal attack. Values of rests preceding notes can be viewed in Box 1 and Box 2. Those rests have duration factors determined by the integer succession from 1 to 5. The succession maps onto pitch-class order through permutation, and Box 2 rotates the factors from Box 1. The placement of notes has a twofold effect. First, originally successive members of a pitch-class series become a single vertical configuration, obscuring serial order on one level. That verticality undergoes distortion by having its members displaced. Altering the arrangement of offsets between chords obscures serial order even more pervasively and unpredictably.
[18] A third systemic override multiplies serially-determined values by a proportional factor. For instance, Table 1 contains the content for notes in measure 7 and measures 22–23 (not shown). In measure 7 the beat-division 5 is multiplied by 2 to create the proportionally smaller division 1/10. With a numerator of 11, the note cannot be reduced back to the original denominator. Likewise, measures 22–23 contain serial factors of double length (22 and 14) and doubly smaller beat-divisions.(30) While the values of these notes reduce mathematically to the original duration-factors and beat-divisions, the notes cannot be converted back to the original notation due to their metric placement. A rest of duration 5/6 precedes pc-t; the 5/6 rest cannot be converted to beat-division 3. Similarly, a rest of 1/6 duration precedes pc-2, and it also cannot be converted to beat-division 3. I have thus left the doubled values intact in Table 1. The multiplication reminisces of imitative procedures in augmentation and diminution canons, which reproduce material in proportional durations. Its use in Sospeso is not as pervasive as override by beat-division or rest-displacement, but it is worth mentioning in light of Nono’s fascination with puzzle canons.
Type II: Intervention by manual override
[19] The second type of override has a more destructive effect on serial determinations, and not surprisingly, multidimensional textures find their most efficient realization through it. Override results from direct intervention, such as the outright alteration of a serial value. Box 2, for instance, contains an anomalous duration-factor of 9 in a region governed by duration-factor 10. The truncation appears to be inadvertent, but the alteration does serve a justifiable purpose.(31) By having the timpanist play the note as part of a decrescendo to the quietest dynamic value, Nono may have intentionally shortened the note to accommodate aftershocks from the percussionist’s cut-off. To reflect Nono’s direct manipulation of serial determinations, I shall refer to any intervention of this type as a “manual override.” Manual overrides defy neat categorization, appearing in numerous guises to befit the varied purposes they serve.
[20] The dimension of dynamics affords one consistent realm for manual override. For instance, No. 4’s dynamics make a global hairpin shape, in which large groups of notes share one marking before a successive marking takes effect. Similarly, the first thirteen notes of No. 8 bear a single indication (fff) before another usurps it. The dynamics dimension contradicts pitch material in both movements, which changes with each note. In terms of multidimensional counterpoint, the pitch dimension employs serial material at a more rapid rate than the dimension of dynamics to create oblique motion between dimensions. Kathryn Bailey’s investigation of dynamics also suggests that Nono applied material in this dimension manually and designed his overrides to mimic the equalized distribution of elements in other dimensions.(32)
[21] In general, manual overrides intervene with the implementation of serial material, not its generation. For instance, Nono occasionally leaves out elements within a complex altogether or repeats them arbitrarily. At other times, he may interpret the same complex in multiple ways, or cease consuming it prematurely. More importantly, he may deliberately counteract an identifiable feature of a complex, and even override other overrides. In the end, Nono generally adheres to the possibilities presented by serial material, but he rarely refrains from intervening with it.
No. 4
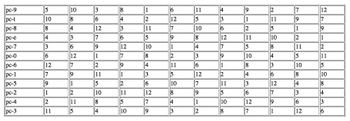
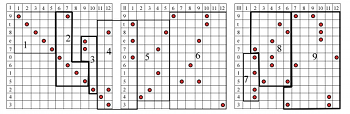
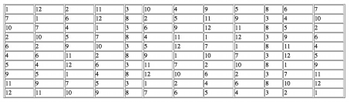
[22] Of the three interludes, No. 4 undergoes minimal intervention, thereby projecting its underlying serial complex clearly. Nono plots out the placement of notes in the score using a technique studied by Gianmario Borio and Veniero Rizzardi, and more recently, Christoph Neidhöfer.(33) First, the series 5x mod 12 (5 10 3 8 1 6 11 4 9 2 7 12; 12 stands in for 0 in this case) is permuted through order-number multiplication by 7 mod 13, with the result that even-numbered ordinal positions (i.e., 2, 4, 6, 8, 10, and 12) move to the front of the succession, followed by odd-numbered ordinal positions.(34) Systematic rearrangement produces the twelve collections shown by Table 2, each of which corresponds to a pitch-class in Sospeso’s all-interval, wedge-shaped series (9 t 8 e 7 0 6 1 5 2 4 3); I refer to this twelve-tone series as an “All-Interval Wedge,” AIW for short. Columns in the figure feature a distinct integer succession (5 10 8 4 3 6 12 7 9 1 2 11) in various rotations.(35)
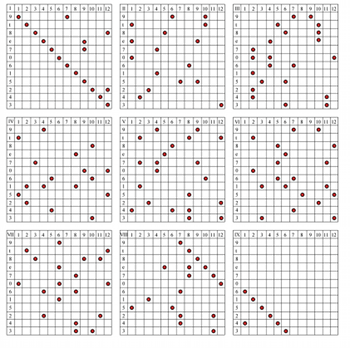
[23] The twelve collections form the basis for a network of nine 12 x 12 grids. Example 2 shows the mapping out of time-points in these grids.(36) Each rank in the grids corresponds to a pitch-class in the series, and each column corresponds to a distinct time-point in musical space. In the system, pc-9 initially assumes time-point 1, pc-t assumes time-point 2, and so on. The twelve numerical collections control the timing of subsequent pitch-class entries. The second entry of pc-9, for instance, occurs after five empty time-points, then ten time-points, and so on. Following its own scheme, pc-t enters after ten empty time-points have passed, then eight, and so on.
[24] I shall refer to the configurations in Example 2 as “Position-Grids.”(37) Serial pitch-classes begin at Position-Grid I and end at Position-Grid IX in immediate succession because of the technique, which creates a constant value of 90 time-points for each pitch-class (empty spaces equal the sum of the integers 1 through 12, plus 12 for each pitch-class’s occurrence). The scheme also controls when pitch-classes have coincident attacks with others. For example, time-point 7 of Position-Grid I contains pc-9 and pc-6 together, while time-point 9 contains pcs-5, -7, and -e together. The position-grid system serves as a proto-score for No. 4, with pitch-classes rendered as pitches (i.e., without octave replications) whose registral placement projects the AIW’s signature shape.
[25] Through order-number multiplication No. 4 offers a novel, serial type of canon, in concept and realization. The self-replication inherent in the position-grids has an ancestry in types of imitation used by traditional canons. The connection is poignant because Nono and Bruno Maderna studied Flemish polyphony extensively. Several times Nono cites his studies at Venice’s Biblioteca Marciana and of his “games” solving puzzle canons in particular. In addition, Dallapiccola’s own canon-based music influenced him greatly. The grids activate all twelve pitches simultaneously to produce a twelve-voice canon, and the permutations ensure that each pitch has its own, distinct pattern of acceleration and deceleration between entries. The single rearrangement scheme creates continuity from one voice to the next, thereby providing the same type of cohesiveness afforded by strictly imitative repetition. In line with their canonic heritage, I propose the provisional term “permutation canon” for the position-grids’ inherently imitative structure.
[26] The position-grids map out two orchestral layers in No. 4, one for the strings and the other for the remainder of the instruments (Example 3). Durations in the non-strings follow values in Table 2 by columns—not by ranks—proceeding from bottom to top. Values are applied to time-points left to right so that the first twelve time-points possess duration-factors of 11, 2, 1, etc. The second column in the rearrangement scheme, read bottom to top (5 11 2 1 9 7 etc.) determines the durations of the next twelve time-points in the score, and so on.
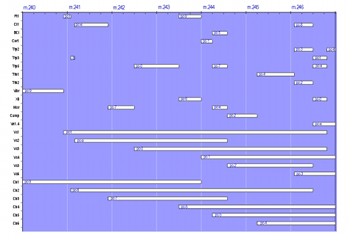
[27] The strings generally play long, sustained notes against short notes in the winds, brass, and percussion that are determined by the grid system. For instance, pc-9 occurs in the vibraphone at measure 240 and in the flute at measure 243. Bass 1 ties the two notes together and coincides with the vibraphone’s entrance and the flute’s exit. Cello 2 performs the same function for Clarinet 1 at measure 241 and Marimba at measure 244. Each pitch appears thirteen times in the system, an odd number, with only the first three and final three pairs of time-points being joined by the strings. The seventh occurrence of each pitch lacks doubling.(38)
[28] Material for two musical dimensions, pitch and duration, is thus plotted out for No. 4 in one sweeping, serial gesture. The unity of design accounts for the movement’s dynamics, which create a large-scale hairpin. The non-strings essentially follow a dynamics series (ppp, p, mp, mf, f, fff, fff, fff, f, mf, mp, p, ppp) that determines dynamics for each successive time-point within each pitch level in the position-grid system. Each pitch’s first appearance sounds at ppp, its second at p, and so on, with its three central appearances having the marking fff. At this point the dynamics reverse themselves in a gradual decrescendo. Shadowing notes in the strings echo the dynamics of the notes they connect; if the notes possess two different indications, the shadowing instrument makes a transition from the first to the second. While dynamic elements might appear to create multidimensionally oblique motion with durations and pitches, they actually form another serial component within the position-grids, thereby traveling in unison with pitch and durations.
[29] In contrast to their usual disruptive effect, beat-divisions articulate multidimensional unity even further by also forming a serial component of the position-grid system. The movement employs a single beat-division series (3, 4, 5, 7, 7, 5, 4, 3), which determines beat-divisions for each grid in the position-grid system, with Position-Grid IX appended to Position-Grid VIII. Beat-divisions gradually decrease in size for Grids I through IV. At the mid-point of the movement, beat-divisions increase in size so that all notes governed by Grids I and VIII/IX receive the beat-division 3, Grids II and VII receive beat-division 4, and so on. In a symmetric pattern, durations accelerate and decelerate proportionally (3:4:5:7), underscoring the movement’s hairpin dynamics.
[30] All told, No. 4 of Sospeso follows its serial material with minimal intervention, with only the precise instrumentation of the non-strings left open to Nono’s “liberal fantasy.” Instrumentation in the strings, in contrast, supports the canonic scheme. The outermost position-grids feature cello and bass soli in harmonics, and grids work their way inward with solo upper strings and then tutti. Non-string instruments seem to be chosen for their ability to play in the AIW’s range and, in the case of percussion, for their muted timbres.(39) While brass instruments inevitably diversify the timbral palette, coloristic effects are lessened by all non-string instruments playing tremolo rather than sustained notes. Beyond the inescapable variations in instrumental timbres, the music displays exceptional multidimensional unity. Moments of unity such as this would prove to be exceedingly rare in Nono’s compositional output.(40)
No. 1
[31] While No. 1 uses the same position-grid system as No. 4, it achieves contrast not only in its sound but also in the types of intervention it exhibits. The position-grid system governs pitch content, except that pitches now occupy various octaves. Wolfgang Motz traces the evolution of the first movement from serial genesis to final form, giving a preliminary discussion about the use of No. 4’s content in regard to instrumentation and registral placement.(41) I shall devote some time here to examining the movement in greater length and detail than Motz does in his brief study. As I shall show, both primary and secondary systems undergo manual overrides in No. 1, producing a multidimensional density that No. 4 lacks. Further, the movement breaks off before its serially determined conclusion, true to the idea behind the word “sospeso,” which translates as “interrupted” or “suspended.”
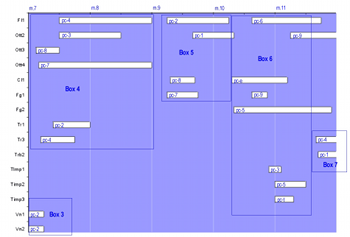
Example 4. Il canto sospeso No. 1, mm. 7–17
(click to enlarge and see the rest)
Example 5
(click to enlarge)
Table 3. Serial content for mm. 100–107 of Il canto sospeso No. 1
(click to enlarge)
Table 4. Duration-factors in Il canto sospeso No. 8
(click to enlarge)
Table 5. Duration content for Il canto sospeso No. 8
(click to enlarge)
Example 6
(click to enlarge)
Table 6. Rest-displacements for Il canto sospeso No. 8
(click to enlarge)
Example 7
(click to enlarge)
Example 8
(click to enlarge)
Example 9
(click to enlarge)
Example 10
(click to enlarge)
[32] Extensive systemic overrides by rest-displacement and beat-division distort the serial order of pitch-classes without actually transforming the position-grids themselves. Example 4 shows measures 7–17 of No. 1 (measures 1–6 are shown by Example 1). Boxed areas may be clicked to summarize pitch-class, beat-division, rest-displacement, and dynamics content. Example 5 shows the content of the nine boxes as they correspond to the position-grid system. Nono appears to start the movement in strict observation of systemic beat-divisions and rest-displacements. Both systems undergo manual override by the end of the movement, whose content Table 3 shows. Pitch content from Position-Grid VII (see Example 2) is applied to only two beat-divisions at most within chords, with two beat-divisions undergoing diminution (6 and 8). Rest-displacement values are limited to the range 0 to 3 rather than 1 to 5, and their usage does not suggest a systematic permutation of their order. Nono thus assumes a substantial degree of freedom, as if to let the music evolve, quasi una fantasia, to this point.
[33] Manual override produces contrapuntal complexity between dimensions and creates fluctuations of speed within dimensions. For instance, Box 1 contains the first duration factor in the series (5) exclusively. The content depicted by Box 2 follows in similar fashion as Box 1, with a single duration factor unifying the group.(42) Subsequent boxes are devoted to further members of the duration-factor series, with the pace speeding up (as in Boxes 3, 4, 6, and 9) and slowing down in turns (as in Boxes 5, 7, and 8).(43) In contrast, pitch-class material holds steadfast to changing with each successive time-point.
[34] Dynamics contribute added multidimensional density. In all, dynamics do not show the influence of any system analogous to those used for pitch-class placement and duration allotment. However, dynamic markings do occasionally mirror each other, such as mf-ppp and ppp-mf in Box 8 (measure 13). The content distribution also divides the movement into two large parts, coinciding with the juncture between the second and third traversals of the position-grid system. For the final two position-grid traversals, dynamics content is limited to single elements: ppp, p, mp, mf, f, fff.(44) The first two position-grid traversals use single elements except for fff, and pairs of elements arise in every conceivable combination (such as ppp-p or mp-mf). Because of the delayed entrance of fff until the third grid traversal, the second half of the movement achieves a generally louder dynamic than the first. The dynamics distribution also creates smaller formal regions, such as at Box 9 (measure 16), where all markings fall at the lowest levels (ppp and p). The rate of change for dynamics thus occurs at its own pace, sometimes unifying groups of notes (Boxes 3 and 9) or diversifying them (Boxes 1, 2, and 7).
[35] The movement implements the position-grid system roughly four times. Midway through the second implementation of Position-Grid V, duration material traverses values by columns in Table 2 rather than ranks. Duration material essentially remains fixed at this point, since the columns produce rotated versions of a single integer succession. During the final course of the position-grid system, many pitch-classes fail to appear, thereby accelerating the consumption of pitch material. Lastly, the final measures of the movement only reach what seems to be the end of Position-Grid VII (see Table 3), with pc-e and pc-9 appended at the conclusion. In this light, No. 1 concludes abruptly.
No. 8
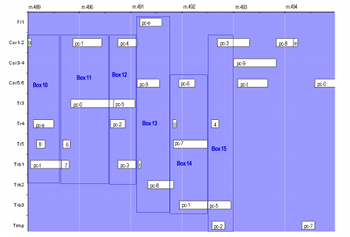
[36] No. 8 exhibits as extensive a level of override as No. 1, also yielding great multidimensional complexity. Like No. 1, it too has an underlying canonic structure that systemic and manual overrides distort and obscure. The movement’s duration factors undergo a procedure that produces the ten duration-factor collections shown by Table 4.(45) A recursively-applied rearrangement scheme reorders the collection from its outermost ordinal positions (working from right to left) to its center.(46) Complete duration material (notated as fractional values with duration-factors as numerators and beat-divisions as denominators) for No. 8 is shown by Table 5.(47) The resulting music uses only nine collections; a tenth collection, the integer succession 12 to 1, never makes its way into the music. Pitch-class material (i.e., the AIW) fuses itself to duration material to unify the two dimensions completely. At the tenth collection (after the first blank rank in the figure), individual ranks from Table 4 are applied in retrograde order from top to bottom. The final nineteen collections (after the second blank rank) form an exact retrograde of the preceding eighteen so that the thirty-six collections produce an overall palindrome.
[37] The music for No. 8, however, does not retain the symmetry of its serial material. First, Nono manually overrides serial values. Several individual durations (thirteen to be exact) do not match the rearrangement scheme. Of these, eight are very close (within one factor) to the scheme. The movement also omits two consecutive notes in the scheme from the second collection beginning at measure 535. Manual overrides exhibited here do not appear to contribute to multidimensional density, but their occurrence resonates with a spirit of extreme distortion in other realms.
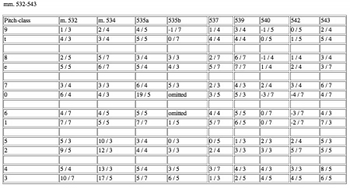
[38] Rest-displacement systemically overrides the ordering of durations. Box 10 of Example 6 contains the first four members of the AIW (pcs-9, t, 8, and e). The rest-displacement system, shown by Boxes 10-15, causes the pc-e (3/7 rest) to appear before the pc-8 (2/3 rest) rather than after. By the end of the movement, the rest-displacement system becomes manually overridden. Table 6 shows rest-displacement values for the final nine statements of serial material (i.e., the final quarter of the movement). The system generally governs pitches in pairs rather than individually. Beginning at measure 532, for example, the first note in each pair shows incremented rest-displacements. The second note in each pair arrives 3 duration factors after the first (for pcs-9 through 1), then 4 (pcs-5 and 2), and then 5 (pcs-4 and 3). The final four pitch-classes in each series generally follow the preceding eight at some distance, I have calculated their displacement from a distinct point of reference. The mode of displacement changes for each subsequent twelve-tone collection, as well as within each collection between the first four pairs and the final two.(48)
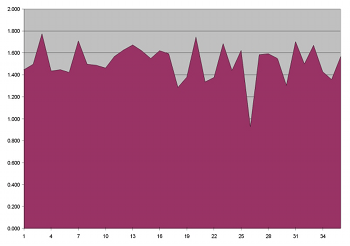
[39] Beat-divisions distort the inherent symmetry of serial material even further. Example 7 shows the progress of duration material throughout the movement. Peaks and valleys depict the average duration for each of the thirty-six collections; the vertical axis depicts notated durational values in terms of quarter-note lengths. Collection 26 (beginning within measure 528) features a dramatic dip in average duration because the smallest beat-division (1/7) remains active for the entire collection. The dip in Collection 26 does not find itself reflected in the movement, and thus the contour of the graph exhibits a noticeable asymmetric shape.
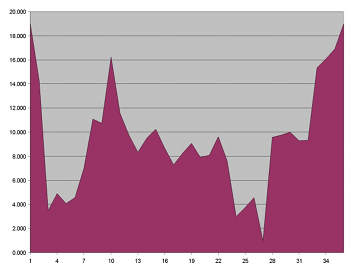
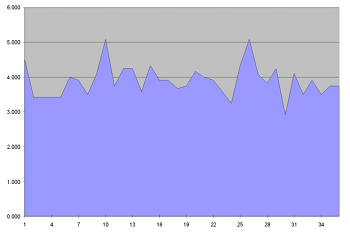
[40] Other dimensions enhance the through-composed nature of the movement. Example 8 shows the average dynamic range for each collection throughout the movement. The vertical axis depicts a linear scale of nineteen implemented dynamic indications, where 1=ppp and 19=fff. Intermediate values are ranked according to the loudest dynamic marking that is used; for example, the indication p-f is ranked below p-fff. As can be seen, several large-scale crescendi and decrescendi carve out an asymmetric pattern, although Collections 10 and 27 appear to invert each other. Octave placement also resists symmetry. Example 9 shows the average octave range for each collection (octave ranges correspond to ASA pitch designations; i.e., middle C begins Octave 4), again revealing an asymmetric pattern. For instance, the dip in Collection 30 seems at odds with the peaks in Collections 10 and 26. Finally, instrumentation even seems to contribute to the global defiance of symmetry. In an effort to convey instrumentation as an average value, I have assigned the values 1 through 28 to each instrument in the orchestra, grouping them by family (i.e., winds, brass, and percussion; strings do not play in this movement). Example 10, whose vertical axis only ranges from 1 to 25, shows the average timbral value per serial collection. Wind instruments (flutes, oboes, clarinets, bassoons) hold the lowest values (1 through 11), horns occupy medium values (12 through 17), trumpets and trombones assume high values (18 through 26), and timpani possess the top values (27 and 28). A prevalence of one instrumental family will affect the average value. For instance, the deepest valleys in the figure mark sections devoid of or sparsely populated by brass instruments (Collections 6, 17, and 26). Similarly, a high average value signals the presence of many brass instruments (Collections 8, 11, 14, and 30). All told, the orchestration does not establish a symmetric, or even a recurrent, pattern. Further, individual dimensions do not synchronize with each other.
[41] The high degree of intervention forms a multidimensional texture based on fundamental, inner conflict. In their initial state, pitch and duration values exhibit inter-dimensional unity and symmetry. As in No. 1, secondary systems override primary material, and both primary and secondary systems become overridden during the course of the music. The movement also shows what effect Nono’s control over beat-divisions, dynamics, registral placement, and instrumentation have on distorting the serial palindrome in an environment of extreme manual override where even serial values themselves undergo alteration. The conflict, which a simple hearing of the piece does not reveal, plays a significant role for the piece as a whole.
Wordless Music
[42] As mentioned previously, Nono did not discuss the instrumental interludes directly. However, works preceding and following Sospeso provide a meaningful context for its instrumental interludes. The second movement of Nono’s first published choral work, Epitaffio auf Federico García Lorca No. 1 (1952) is composed for flute and small orchestra, thereby not setting any words to music. Rather, textual verses appear at formal dividing points in the score so that only the performers know of their presence. The absorption prefigures the string quartet, Fragmente-Stille, an Diotima (1979–1980), whose Hölderlin fragments are printed in the score but not delivered. The stage work Prometeo, tragedia dell’ascolto (1984/1985) is based on Massimo Cacciari’s mixture of texts by Hölderlin, Aeschylus, Rilke, and others, many of which are never enunciated in performance. Boulez creates a similar effect during the “Commentaires” of Marteau sans Maître (1957), in which the texts are also not enunciated. All of these compositions have ample precedent in previous centuries, such as Beethoven’s String Quartet Op. 135 or the symphonic poem repertoire, to name only a few examples. Sospeso’s instrumental interludes, as I hope to show, belong to the current of wordless music that projects textual content.
[43] The multidimensional textures of the interludes carry the brunt of their textual gesture. Implemented without substantive intervention, serial material would have generated three canonic interludes. However, pervasive systemic and manual overrides ensure that only No. 4 attains realization as an unimpeded permutation canon. The canon provides a crucial moment of silence at this position, a silence not only achieved by the absence of text and singers, but also by the complete unity of motion among the pitch, duration, and dynamics dimensions. That is, the lack of multidimensional counterpoint creates its own type of silence. (49) In terms of Sospeso’s large-scale multidimensional organization, the distorted textures and multidimensional complexity in Nos. 1 and 8 create somewhat noisy regions that frame an expanse of silence. Space does not permit me to explore the meaning of this gesture fully, but suffice it to say, No. 4’s canonic silence has significant bearing on the flow of textual ideas throughout the composition.
[44] No. 4 falls strategically between the matter-of-fact statements of No. 3’s textual matter and the departing laments initiated by the letters in No. 5. At first glance, No. 4’s silence might appear merely to exhort contemplation on the texts in Nos. 2 and 3 as a type of commentary reminiscent of a sacred cantata, but in light of its position at the work’s center, its meaning for the movements ahead should also be considered. Further, Nos. 1 and 8 serve parallel functions as preludes to the choral movements in Nos. 2 and 9, with the latter movement recapitulating the former’s textual ideas of transcendence. The formal layout of textual themes thus follows a five-part symmetrical scheme: prelude-chorus (Nos. 1–2), exposition (No. 3), silence (No. 4), lament (Nos. 5–7), prelude-chorus (Nos. 8–9). The music fills the scheme at varying speeds, much as the dynamics and duration material of No. 1 slowed and hastened during its course. For instance, the “lament” region of the scheme fills the space of three musical movements, while the “exposition” condenses its ideas into a single movement. In the end, the canonic implications of the scheme do not attain realization; Nono manually overrides its symmetry, which makes the pristine canon of No. 4 even more remarkable.
[45] By immediately following No. 3’s exposition of imminent demise, the multidimensional silence achieved by No. 4 might be considered as an analog to death, or submission to death, so that the music appears to re-enact what actually transpired for “tutti di loro” [all of them].(50) Poignantly reinforcing this gesture, Nono quoted No. 4 in the operatic work Intolleranza 1960 at a moment that describes the outcries of victims during interrogation proceedings. In contrast, Nos. 1 and 8 begin a process of transcendence by resisting the symmetrical pull of their serial material. As parallel gestures, Nos. 2 and 9 conclude with codas whose duration material possesses palindromic symmetry, but whose implementation conspicuously avoids it. The transcendence finds resonance in No. 9’s main text-setting innovation, which apportions components of individual words to several performers so that the words attain new life on a collective plane of existence. The transcendence thereby affirms the themes presented by Thomas Mann’s forward to the edition of letters that inspired Sospeso, which Nono included as an integral part of the composition’s textual matter:
[46] [
[47] [
[48] In the end, Sospeso’s multidimensional considerations shape serial material to such a considerable degree that a strict serial analysis of the piece not only becomes frustrated, but also obscures the contribution that the interludes make to the composition’s textual content. The activation of systemic and manual overrides produces novel textures in multiple musical dimensions, which paved the way for Nono’s electronic experiments later in his career. Thus, what had originally served as overrides in his serial music became a technique for multidimensionality in later pieces, and ultimately, the poetics of “il suono mobile.”
Jeannie Ma. Guerrero
Eastman School of Music
Music Theory
26 Gibbs Street
Rochester, NY 14604
jguerrero@esm.rochester.edu
Works Cited
Babbitt, Milton. 1961. “Set Structure as a Compositional Determinant,” Journal of Music Theory 5 (1961): 72–94.
—————. 1962. “Twelve-Tone Rhythmic Structure and the Electronic Medium,” Perspectives of New Music 1.1 (1962): 49–79.
—————. 1973. “Since Schoenberg,” Perspectives of New Music 12.1 (Fall-WInter 1973): 3–28.
Bailey, Kathryn. 1992. “‘Work in Progress:’ Analysing Nono’s Il canto sospeso.” Music Analysis 11.2–3 (July-October 1992): 279–334.
Batstone, Philip N. 1972. “Multiple Order Functions in Twelve-Tone Music,” Parts 1, 2, Perspectives of New Music 10.2 (Spring-Summer 1972): 60–71 and 11.1 (Fall-Winter 1972): 92–111.
Borio, Gianmario. 1999. “Sull’interazione fra lo studio degli schizzi e l’analisi dell’opera.” In Gianmario Borio, Giovanni Morelli, and Veniero Rizzardi, eds., La nuova ricerca sull’opera di Luigi Nono (Florence: Leo Olschki), 1–21.
Clough, John. 1980. “Diatonic Interval Sets and Transformational Structures,” Perspectives of New Music 18.1–2 (Autumn 1979-Summer 1980): 461–82.
Flamm, Christoph. 1995. Preface to Luigi Nono’s Il canto sospeso (London: Eulenberg), iii–xviii.
Guerrero, Jeannie Ma. 2003a. “Text-Setting Techniques in Luigi Nono’s Choral Works (1956–1960).” Harvard University: Ph.D. dissertation.
—————. 2003b. “Multidimensional Counterpoint and Social Subversion in Luigi Nono’s Choral Works,” Theory & Practice 28 (2003): 1–26.
—————. 2005. “Tintoretto, Nono, and Expanses of Silence.” Paper presented at the Dublin International Conference on Music Analysis (University College Dublin, Ireland).
Headlam, Dave. 1985. “The Derivation of Rows in Lulu,” Perspectives of New Music 24.1 (Autumn-Winter 1985): 198–233.
—————. 1996. The Music of Alban Berg. New Haven: Yale University Press.
Huber, Nicolaus A. 1981. “Luigi Nono: Il canto sospeso VIa, b,” Musik Konzept 20: 58–79.
Kowalski, David. 1987. “The Construction and Use of Self-Deriving Arrays,” Perspectives of New Music 25.1–2 (1987): 286–361.
Lettere di condonnati a morte della resistenza europea. Turin: Giulio Einaudi, 1954.
Lewin, David. 1966. “On Certain Techniques of Re-Ordering in Serial Music,” Journal of Music Theory
—————. 1976. “On Partial Ordering,” Perspectives of New Musicc 14.2 and 15.1 (Spring-Summer/Fall-Winter 1976): 252–59.
Marvin, Elizabeth West. 1991. “The Perception of Rhythm in Non-Tonal Music: Rhythmic Contours in the Music of Edgard Varèse.” Music Theory Spectrum 13.1 (Spring 1991): 61–78.
Mead, Andrew. 1988. “Some Implications of the Pitch Class/Order Number Isomorphism Inherent in the Twelve-Tone System: Part One,” Perspectives of New Music 26/2: 96–163.
—————. 1989. “Some Implications of the Pitch-Class/Order-Number Isomorphism Inherent in the Twelve-Tone System Part Two: The Mallalieu Complex: Its Extensions and Related Rows,” Perspectives of New Music 27/1: 180–233.
Mila, Massimo. 1975. “Nonos Weg-Zum ‘Canto Sospeso’.” In Jürg Stenzl, ed., Luigi Nono: Texte, Studien über seine Musik (Zürich: Atlantis Musikbuch-Verlag), 380–393.
Morris, Robert. 1977. “On the Generation of Multiple-Order-Function Twelve-Tone Rows,” Journal of Music Theory 21/2 (Autumn): 238–62.
—————. 1982. “Review: John Rahn, Basic Atonal Theory,” Music Theory Spectrum 4: 138–54.
Motz, Wolfgang. 1996. Konstruktion und Ausdruck: Analytische Betrachtungen zu ‘Il canto sospeso’ (1955/56) von Luigi Nono. Saarbrücken: PFAU-Verlag, 1996.
—————. 1999. “Konstruktive Strenge und kompositorische Freiheit im ersten Satz des Canto Sospeso.” In Gianmario Borio, Giovanni Morelli, and Veniero Rizzardi, eds., La nuova ricerca sull’opera di Luigi Nono. (Florence: Olschki), 53–66.
Neidhöfer, Christoph. 2004. “Bruno Maderna’s Serial Arrays.” Paper presented at the annual meetings of the Music Theory Society of New York State (Rochester, NY) and the Society for Music Theory (Seattle, WA).
Nono, Luigi. 1960. “Text-Musik-Gesang.” In Jürg Stenzl, ed., Luigi Nono: Texte, Studien über seine Musik (Zürich: Atlantis Musikbuch-Verlag, 1975), 41–60.
—————. 1969. Interview by Hansjörg Pauli. In Jürg Stenzl, ed., Luigi Nono: Texte, Studien über seine Musik (Zürich: Atlantis Musikbuch-Verlag, 1975), 198–209.
—————. 1983. Handwritten notes for Guai ai gelidi mostri. In Angela Ida De Benedictis and Veniero Rizzardi, eds., Luigi Nono: Scritti e colloqui I.
—————. 1984. “Verso Prometeo. Frammenti di diari.” In Angela Ida De Benedictis and Veniero Rizzardi, eds., Luigi Nono: Scritti e colloqui I: 385–96.
—————. 1987. “Un autobiografica dell’autore raccontata da Enzo Restagno.” In Angela Ida De Benedictis and Veniero Rizzardi, eds., Luigi Nono: Scritti e colloqui II (Lucca: Casa Ricordi, 2001), 477–568.
Schaller, Erika. 1996. Klang und Zahl: Luigi Nono—Serielles Komponieren zwischen 1955 und 1959. Bochum: Ruhr-U.
Schönberg, Arnold. 1969. Letture, ed. E. Stein and L. Rognoni, transl. L. M. Rubino. Florence: La Nuova Italia.
Starr, Daniel. 1978. “Sets, Invariance, and Partitions,” Journal of Music Theory
—————. 1984. “Derivation and Polyphony,” Perspectives of New Music 23.1 (Fall-Winter 1984): 180-257.
Starr, Daniel and Robert Morris. 1974. “The Structure of All-Interval Series,” Journal of Music Theory 18.2 (Autumn 1974): 364-389.
Stockhausen, Karlheinz. 1958. “Sprache und Musik II,” Darmstädter Beiträge zur Neuen Musik 1 (1958). Reprinted in Texte zu eigenen Werken, zur Kunst Anderer, Aktuelles II (1952-1962) (Köln: DuMont Schauberg, 1964), 157-166.
Stoianova, Ivanka. 1987. “Testo-musica-senso. ‘Il canto sospeso.’” In Restagno, Enzo, ed., Nono (Turin: Edizioni di Torino), 126-142.
Westergaard, Peter. 1966. “Toward a Twelve-Tone Polyphony,” Perspectives of New Music 4.2 (Spring-Summer 1966): 90-112.
Footnotes
1. A useful comparison may be made between Nono’s
re-ordering procedures, which I shall discuss here, and order-relations as
explored by other composers: Milton Babbitt, “Set Structure as a Compositional
Determinant,” Journal of Music Theory 5 (1961): 72–94, “Twelve-Tone
Rhythmic Structure and the Electronic Medium,” Perspectives of New Music
1.1 (1962): 49–79, and “Since Schoenberg,” Perspectives of New Music 12.1
(Fall-Winter 1973): 3–28; Philip N. Batstone, “Multiple Order Functions in
Twelve-Tone Music,” Parts 1, 2, Perspectives of New Music 10.2
(Spring-Summer 1972): 60–71 and Perspectives of New Music 11.1
(Fall-Winter 1972): 92–111; Dave Headlam, “The Derivation of Rows in Lulu,”
Perspectives of New Music 24.1 (Autumn-Winter 1985): 198–233; David
Kowalski, “The Construction and Use of Self-Deriving Arrays,” Perspectives of
New Music 25.1–2 (1987): 286–361; David Lewin, “On Certain Techniques of
Re-Ordering in Serial Music,” Journal of Music Theory 10.2 (Winter 1966):
276–287 and “On Partial Ordering,” Perspectives of New Music 14.2 and
15.1 (Spring-Summer/Fall-Winter 1976): 252–59; Andrew Mead, “Some Implications
of the Pitch Class/Order Number Isomorphism Inherent in the Twelve-Tone System:
Part One,” Perspectives of New Music 26.2 (Summer 1988): 96–163; Robert
Morris, “On the Generation of Multiple-Order-Function Twelve-Tone Rows,”
Journal of Music Theory 21.2 (Autumn 1977): 238–62 and “Review: John Rahn,
Basic Atonal Theory,” Music Theory Spectrum 4 (1982): 135–54; Daniel
Starr, “Sets, Invariance, and Partitions,” Journal of Music Theory 22
(1978): 1–42 and “Derivation and Polyphony,” Perspectives of New Music
23.1 (Fall-Winter 1984): 180–257; Peter Westergaard, “Toward a Twelve-Tone
Polyphony,” Perspectives of New Music 4.2 (Spring-Summer 1966): 90–112.
Return to text
2. Under Bruno Maderna’s guidance, Nono and Maderna
transcribed many polyphonic works and studied historical treatises. A list of
intended transcriptions can be found among the holdings in the Archivio Luigi
Nono in Venice, ALN M02.01.06/8–35. Notes on treatises can be found in ALN
M02.01.03/1–49.
Return to text
3. Nono’s preoccupation with canonic symmetry is discussed
in Erika Schaller, Klang und Zahl: Luigi Nono—Serielles Komponieren zwischen
1955 und 1959 (Ruhr-U. Bochum: Ph.D. dissertation, 1996). Canons and canonic
devices populate Nono’s choral works, as discussed in Jeannie Ma. Guerrero,
“Tintoretto, Nono, and Expanses of Silence,” paper presented at the Dublin
International Conference on Music Analysis (University College Dublin, Ireland),
2005.
Return to text
4. An extended discussion of multidimensional evolution in
Nono’s choral music may be found in Jeannie Ma. Guerrero, “Text-Setting
Techniques in Luigi Nono’s Choral Works (1956–1960)” (Harvard University: Ph.D.
dissertation, 2003).
Return to text
5. Jeannie Ma. Guerrero, “Multidimensional Counterpoint and
Social Subversion in Luigi Nono’s Choral Works,” Theory & Practice 28
(2003), 1–26.
Return to text
6. Luigi Nono, “Un autobiografica dell’autore raccontata da
Enzo Restagno (1987),” in Angela Ida De Benedictis and Veniero Rizzardi, eds.,
Luigi Nono: Scritti e colloqui II (Lucca: Casa Ricordi, 2001), 489. All
translations are the author’s unless otherwise noted.
Return to text
7. Luigi Nono introduces the term in his handwritten notes
for Guai ai gelidi mostri (1983), in Angela Ida De Benedictis and Veniero
Rizzardi, eds., Luigi Nono: Scritti e colloqui I (Lucca: Casa Ricordi,
2001), 491–492. The term appears a year later in “Verso Prometeo.
Frammenti di diari,” in Angela Ida De Benedictis and Veniero Rizzardi, eds.,
Luigi Nono: Scritti e colloqui I (Lucca: Casa Ricordi, 2001), 385–396.
Return to text
8. Remarks about Sospeso’s novel textures can be
found in Luigi Nono, Interview by Hansjörg Pauli, in Jürg Stenzl, ed., Luigi
Nono: Texte, Studien über seine Musik (Zürich: Atlantis Musikbuch-Verlag,
1975), 200: “Ich wollte eine horizontale melodische Konstruktion, die sämtliche
Register ergreift; ein Schweben von Laut zu Laut, von Silbe zu Silbe: eine Linie,
die manchmal aus der Abfolge von Einzel-Tönen oder Einzel-Tonhölen entsteht und
manchmal sich verdickt zu Klängen.” An English translation by Angela Davies
appears in Christoph Flamm, Preface to Luigi Nono’s Il canto sospeso
(London: Eulenberg, 1995), ix: “I wanted an horizontal melodic construction
encompassing all registers; floating from sound to sound, from syllable to
syllable: a line which sometimes consists of a succession of individual tones or
pitches, and sometimes thickens into chords.”
Return to text
9. For an examination of the various generative complexes
used throughout Sospeso, see Kathryn Bailey, “‘Work in Progress’:
Analysing Nono’s Il canto sospeso.” Music Analysis 11.2–3
(July-October 1992): 279–334.
Return to text
10. Lettere di condonnati a morte della resistenza
europea (Turin: Giulio Einaudi, 1954) was also reprinted in German as Und
die Flamme soll euch nicht versengen (Zürich: Steinberg-Verlag, 1955).
Return to text
11. Another socially engaged composition by Schoenberg,
the Ode to Napolean, provided the musical basis for Nono’s first
published work, Variazioni canoniche sulla serie dell’op. 41 di Arnold
Schoenberg (1950). His first published choral work, the first of the three
Epitaffios auf Federico García Lorca (1952–1954), sets poems by Federico
García Lorca and Pablo Neruda that pertain to the Spanish Civil War (1936–1939).
Like Survivor, the choir, soprano, and baritone soloists deliver texts as
Sprechstimmen against a sparse texture in the orchestra. A traditional
Spanish melody sung in unison concludes the third movement, also calling
Survivor to mind. La Victoire de Guernica (1954) for mixed choir and
orchestra also takes the Spanish Civil War as its subject, setting Paul Éluard’s
verses and Picasso’s painting of the same title. While short textual phrases
undergo polyphonic treatment that somewhat confuses their apprehension, longer
textual phrases are delivered as Sprechstimmen, thus continuing the link
to Schoenberg’s sound-world. Like the first Epitaffio, as well as
Survivor, the piece ends with the choir singing in unison.
Return to text
12. Luigi Nono, Il canto sospeso (Edition: Ernst
Eulenberg, 1995), 90–91.
Return to text
13. The innovative choral textures of No. 9, in
particular, persist in Nono’s choral writing for the remainder of his career.
Their precise production through serial mechanisms receives more extensive
discussion in Guerrero, “Text-Setting Techniques.”
Return to text
14. Karlheinz Stockhausen, “Sprache und Musik II,”
Darmstädter Beiträge zur Neuen Musik 1 (1958). Reprinted in Texte zu
eigenen Werken, zur Kunst Anderer, Aktuelles II (1952–1962) (Köln: DuMont
Schauberg, 1964), 157–166.
Return to text
15. Luigi Nono, “Text-Musik-Gesang (1960),” in Jürg Stenzl,
ed., Luigi Nono: Texte, Studien über seine Musik (Zürich: Atlantis
Musikbuch-Verlag, 1975), 41–60.
Return to text
16. Nono’s commentary focuses predominantly on the work’s
textual innovations, as in “Text-Musik-Gesang,” and letters between Nono and
Eigel Kruttge revolve around the performance implications for the choir.
Excerpts from these letters may be found in Flamm, v–vii.
Return to text
17. Massimo Mila, “Nonos Weg-Zum ‘Canto Sospeso’,” in Jürg
Stenzl, ed., Luigi Nono: Texte, Studien über seine Musik (Zürich:
Atlantis Musikbuch-Verlag, 1975), 380–393.
Return to text
18. Bailey, “Work in Progress.”
Return to text
19. I diverge from Bailey and others in matters of
terminology. The twelve-tone series that generates Sospeso belongs to the
class of “All-Interval Series,” as discussed by Daniel Starr and Robert Morris
in “The Structure of All-Interval Series,” Journal of Music Theory 18.2
(Autumn 1974): 364–389. I shall refer to this series in my discussion by a more
specific name, “All-Interval Wedge,” to distinguish it from other all-interval
series. Nono uses an AIW beginning on pc-0 in the choral works La terra e la
compagna (1957) and Cori di Didone (1958), as well as two
instrumental works, Incontri (1955) and Canti per 13 (1955). The
AIW appears throughout Sospeso, beginning on pc-9 instead.
Return to text
20. Ivanka Stoianova, “Testo-musica-senso. ‘Il canto
sospeso,’” in Restagno, Enzo, ed. Nono (Turin: Edizioni di Torino, 1987),
126–142. Stoianova argues that Nono’s processes are akin to the ‘exploration of
intertextual space’ discussed in works of literary criticism, notably by Mikhail
Bakhtin, Ferdinand de Saussure, and Claude Levi-Strauss.
Return to text
21. Wolfgang Motz, Konstruktion und Ausdruck:
Analytische Betrachtungen zu “Il Canto sospeso” (1955/56) von Luigi Nono,
Saarbrücken: PFAU-Verlag, 1996; and “Konstruktive Strenge und kompositorische
Freiheit im ersten Satz des Canto Sospeso,” in Gianmario Borio, Giovanni Morelli,
and Veniero Rizzardi, eds., La nuova ricerca sull’opera di Luigi Nono
(Florence: Olschki, 1999), 53–66.
Return to text
22. Schaller, Klang und Zahl.
Return to text
23. Nicolaus A. Huber, “Luigi Nono: Il canto sospeso VIa,
b,” Musik Konzept 20 (1981): 58–79.
Return to text
24. Gianmario Borio, “Sull’interazione fra lo studio degli
schizzi e l’analisi dell’opera,” in Gianmario Borio, Giovanni Morelli, and
Veniero Rizzardi, eds., La nuova ricerca sull’opera di Luigi Nono
(Florence: Leo Olschki, 1999), 1–21.
Return to text
25. Nono, “Un autobiografia,” 507. The Schoenberg
reference cites a letter dated 27 July 1932 regarding String Quartet No. 3, Op.
30, and printed in Italian in Arnold Schönberg, Letture, ed. E. Stein and
L. Rognoni, transl. L. M. Rubino (Florence: La Nuova Italia, 1969), 179–180.
Return to text
26. Nono, Interview by Hansjörg Pauli, 23–24.
Return to text
27. Elizabeth West Marvin employs the term and concept of
“beat-division” in her examination of duration contours in “The Perception of
Rhythm in Non-Tonal Music: Rhythmic Contours in the Music of Edgard Varèse.”
Music Theory Spectrum 13.1 (Spring 1991): 61–78.
Return to text
28. The duration-factor 5 leads a particular series based
on the integer succession 1 to 12, as I shall show later.
Return to text
29. The timpani’s pc-9 at measure 3 has a notated
duration-factor of 9 rather than 10. I shall discuss this note more extensively
later.
Return to text
30. Again, duration factors are limited to the integers 1
through 12, so numbers larger than 12 arise secondarily.
Return to text
31. The note appears in an earlier draft (ALN 14.13) and
does not undergo further alteration in the published version. A similar
truncation occurs in the bass clarinet at measure 497 (No. 8), where a serial
duration-factor of 6 is truncated to 5 (a difference of 1/8 a quarter note)
within a decrescendo. Another timpani note is truncated at measure 498 from
duration-factor 7 to 6 (a difference of 1/10 a quarter note), this time serving
a crescendo—here, concern for the timpani’s resonance still seems to motivate
the shortening. There are in total thirteen alterations throughout No. 8 of
which I am currently aware, without ruling out others that may be in the
remaining movements.
Return to text
32. “Cosmetic” permutation tables in dynamics, as she
calls them, are not created by any self-replicating process that generates
tables in other dimensions. As a smoking gun, the dynamics table for No. 9
appears to have been filled in one column at a time (thus without regard for the
base series), whereas other tables are filled one rank at a time through the
recursive re-ordering of the base series.
Return to text
33. According to unpublished work by Borio and Veniero
Rizzardi, cited by Borio in “Sull’interazione,” Nono and Bruno Maderna developed
the technique in or around 1951. Nono first used it in his Composizione per
orchestra and Maderna in his Improvvisazione No. 1. Borio also
illustrates the technique’s implementation for the fourth movement of Il
canto sospeso, but without the level of detail I provide here. Christoph
Neidhöfer also provides a high level of detail concerning the technique’s use in
several of Maderna’s compositions from the 1950s in “Bruno Maderna’s Serial
Arrays,” paper presented at the 2004 meetings of the Music Theory Society of New
York State (Rochester, NY) and the Society for Music Theory (Seattle, WA).
Return to text
34. I shall use italicized numbers to denote ordinal
positions in the hope of minimizing confusion between ordinal positions and
values contained by these positions. I enumerate ordinal positions beginning
with 1, as opposed to 0, to ease comparison with Bailey’s “permutation tables,”
which employ the numbering from 1 to 12. More importantly, the enumeration at 1
matches that used by David Lewin in his explication of the multiplicative
operation Mn in “On Certain Techniques of Re-Ordering in Serial
Music,” Journal of Music Theory 10.2 (Winter 1966), 279. The
rearrangement described here corresponds to Lewin’s M7. Dave Headlam
shows Berg’s use of essentially the same rearrangement to derive the Acrobat’s
row in “The Derivation of Rows in Lulu,” 214; and The Music of Alban
Berg (New Haven: Yale University Press, 1996), 306. Headlam categorizes the
rearrangement as an “extended rop-cycle,” where a “rop” is a “referential order
position/pc pair” (“Derivation of Rows,” 203).
Return to text
35. The particular permutations shown by Table 2 correspond to the Mallalieu complex described by Andrew Mead in “Some Implications of the Pitch-Class/Order-Number Isomorphism Inherent in the Twelve-Tone System Part Two: The Mallalieu Complex: Its Extensions and Related Rows,” Perspectives of New Music 27.1 (Winter 1989): 180–233. The shuffled ordinal positions are shown below:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2 | 4 | 6 | 8 | 10 | 12 | 1 | 3 | 5 | 7 | 9 | 11 |
| 4 | 8 | 12 | 3 | 7 | 11 | 2 | 6 | 10 | 1 | 5 | 9 |
| 8 | 3 | 11 | 6 | 1 | 9 | 4 | 12 | 7 | 2 | 10 | 5 |
| 3 | 6 | 9 | 12 | 2 | 5 | 8 | 11 | 1 | 4 | 7 | 10 |
| 6 | 12 | 5 | 11 | 4 | 10 | 3 | 9 | 2 | 8 | 1 | 7 |
| 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| 11 | 9 | 7 | 5 | 3 | 1 | 12 | 10 | 8 | 6 | 4 | 2 |
| 9 | 5 | 1 | 10 | 6 | 2 | 11 | 7 | 3 | 12 | 8 | 4 |
| 5 | 10 | 2 | 7 | 12 | 4 | 9 | 1 | 6 | 11 | 3 | 8 |
| 10 | 7 | 4 | 1 | 11 | 8 | 5 | 2 | 12 | 9 | 6 | 3 |
| 7 | 1 | 8 | 2 | 9 | 3 | 10 | 4 | 11 | 5 | 12 | 6 |
The reordered ordinal positions in the Mallalieu Complex arise by applying the twelve Mn ordinal-position operations (where n runs from 1 to 12) to the Mallalieu Row (0 1 4 2 9 5 e 3 8 t 7 6) and then ordering the resulting pitch-class transpositions by ascending index number (a unique property of the Row is that each M operation produces its own pitch-class transposition of the Row). The Mallalieu Row itself has received attention from Lewin, “Certain Techniques of Re-Ordering,” as well as Starr and Morris, “The Structure of All-Interval Series.” Interestingly, the same results can be achieved by recursively applying M7 to each successively transformed row, which seems to describe Nono’s procedures more precisely. Without recourse to a proper mathematics arsenal, I shall attempt to explain the presence of the invariant columns as follows:
Within the Mallalieu complex, columns contain rotations of an invariant numeric string, 2x mod 13, where x=0 to 11; horizontal ranks produce the strings 2xy mod 13, where y=1 to 12. That is, there is a 2-cycle in the second rank, a 4-cycle in the third, and so on until the last rank, which features a 2048-cycle. The vertical invariance arises because of the particular, and unique, way in which 2x and its multiples map out in mod 13, a prime-number modulus. While the prime-number modulus ensures that each of the twelve arithmetic series (i.e., the number cycles 1 to 12) yield all twelve factors without replication (incidentally, the prime-number modulus 7 assures the same for diatonic sets; John Clough makes this observation in “Diatonic Interval Sets and Transformational Structures,” Perspectives of New Music 18.1–2 (Autumn 1979-Summer 1980), 473.), it does not guarantee the same results for all exponential series. In fact, only four exponential series (2x, 6x, 7x, and 11x) produce a twelve-member invariant string mod 13; it is the twelve-member string that guarantees the presence of invariant columns throughout the complex. The remaining exponential series produce shorter invariant strings, and thus when multiplied generate two or more distinct, invariant strings that are doled out into separate columns. The mappings change, as might be expected, with different prime-number moduli. I offer one last notable observation: 7x (which is generated by recursive M2) yields the retrograde of the vertical string produced by 2x (which is generated by recursive M7).
While the complex shown above stems from M7, there are rearrangement schemes used elsewhere in Sospeso that cannot be produced through a simple multiplicative operation, as happens for No. 8 (to be discussed later). Bailey’s Figure 1b (“Work in Progress,” 282) reflects the order-position transformations for No. 8:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 12 | 1 | 11 | 2 | 10 | 3 | 9 | 4 | 8 | 5 | 7 | 6 |
| 6 | 12 | 7 | 1 | 5 | 11 | 8 | 2 | 4 | 10 | 9 | 3 |
| 3 | 6 | 9 | 12 | 10 | 7 | 4 | 1 | 2 | 5 | 8 | 11 |
| 11 | 3 | 8 | 6 | 5 | 9 | 2 | 12 | 1 | 10 | 4 | 7 |
| 7 | 11 | 4 | 3 | 10 | 8 | 1 | 6 | 12 | 5 | 2 | 9 |
| 9 | 7 | 2 | 11 | 5 | 4 | 12 | 3 | 6 | 10 | 1 | 8 |
| 8 | 9 | 1 | 7 | 10 | 2 | 6 | 11 | 3 | 5 | 12 | 4 |
| 4 | 8 | 12 | 9 | 5 | 1 | 3 | 7 | 11 | 10 | 6 | 2 |
| 2 | 4 | 6 | 8 | 10 | 12 | 11 | 9 | 7 | 5 | 3 | 1 |
Two distinct operations recursively produce the collections above. Lewin’s M2
operates on ordinal positions 1–6, and (order-inversion) I12(M2)
operates on ordinal positions 7–12. The resulting invariant columns resemble
those of the Mallalieu Complex except for two columns that bear the values 5 and
10 exclusively. Also, the 2x series reverses direction and breaks
into fragments, as do the cycles in the horizontal ranks. A
heterogeneously-derived complex such as this is not remarked upon in the
Mallalieu literature and, admittedly, merits further investigation and
formalization.
Return to text
36. The diagram replicates information from Figura 1 in
Borio, “Sull’interazione,” 16.
Return to text
37. While Borio calls ranks in the arrangements by the
term “Tondistanzreihen,” I prefer Motz’s more generic term “Positionreihe”
and call the arrangements “Position-Grids” to reflect the interlocking between
ranks and columns.
Return to text
38. These time-points fall at Column 12 of Position-Grid
IV and throughout Position-Grid V (measures 260–263).
Return to text
39. The orchestration omits the piccolo, oboe, bassoon,
timpani, Glockenspiel, celesta, and harp.
Return to text
40. The placement of canonic devices within the choral
works exhibits symbolic consistency, as discussed in Guerrero, “Tintoretto,
Nono,”
Return to text
41. Motz, “Konstruktive Strenge.”
Return to text
42. Again, noting the one exception in the timpani, whose
duration-factor is 9 rather than 10.
Return to text
43. The boxes correspond to the first three grids of the
system. Further, Box 8 represents an overlap between the end of the first duration-factor series and the beginning of the second (i.e., 10 8 6, etc.).
Return to text
44. The elements form the basis for the content of the
entire cantata, so their presence might have some affinity with a direct
statement of the AIW or an unimpeded application of duration factors.
Return to text
45. The table coincides with the upper-left block of
Figure 27 in Bailey, “Work in Progress,” 318. Bailey does not include the tenth
collection. The permutation of ordinal positions is discussed above in Note 35.
Return to text
46. As discussed in Note 35, two distinct order-number
multiplications shuffle ordinal positions in No. 8. M2 operates on
ordinal-positions 1 through 6, while I12(M2) operates on
ordinal-positions 7 through 12.
Return to text
47. The table adds beat-division information to Motz’s
Beispiel 49 (“Konstrucktion und Ausdruck,” 126) and Bailey’s Figure 27 (“Work in
Progress,” 318), which show only duration factors.
Return to text
48. The overrides account for the high degree of
distortion in Bailey’s Figure 27 towards the end of No. 8.
Return to text
49. A similar multidimensional silence, in the guise of a
retrograde canon, concludes Nono’s 1960 choral piece Sarà dolce tacere
which is discussed extensively in Guerrero, “Multidimensional counterpoint.”
Return to text
50. In Guerrero, “Tintoretto, Nono,” canons are shown to
be consistently associated with silence and death in the choral works. It would
appear that No. 4, and perhaps earlier canonic structures, belonged to a larger
current in Nono’s compositional output.
Return to text
51. Nono, Il canto sospeso, 89.
Return to text
Copyright Statement
Copyright © 2006 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason, Managing Editor and Tahirih Motazedian, Editorial Assistant