Moving Through Triadic Space: An Examination of Bryars’s Seemingly Haphazard Chord Progressions

[1] Transformational theory enables listeners to conceive of specific musical elements, such as pitches or chords, within a structured “space” of possibilities, such that the transformation of one element into another of the same type may be imagined as motion along a pathway within that space. To a certain extent, the type of object suggests the nature of the space and its pathways. For example, it is comfortable to think of pitch-class space as a twelve-node network whose pathways correspond to transposition or inversion, or of triadic space in which the transformations represent the discharge of harmonic functions. However, much creative work has been done to define less familiar transformations for which we do not have such intuitions. Examples include Lewin on Babbitt’s lists, Gollin on Bartók, Callendar on Ligeti; many others could be cited (Lewin 1995; Gollin 1998; Callender 2007). In these cases the special transformational family is suggested by processes specific to a particular composition—that is, the recurrence of certain changes may suggest that they are structurally integral to a musical space.

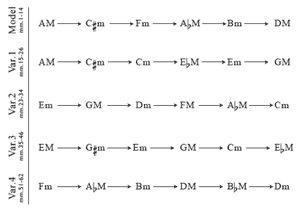
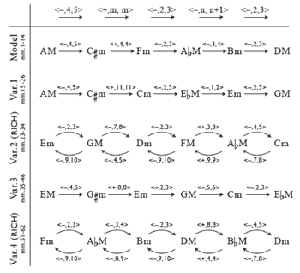
[2] For example, consider the work “A Man in a Room, Gambling” (1992) by the contemporary British composer Gavin Bryars.⁽¹⁾ Its final section (or “programme”) is composed for pre-recorded voice, clarinet, and a string quartet that mostly plays a series of arpeggiating triads. The chord progression of measures 1–14 is isolated from the rest of the work by a break in texture that ends it, suggesting that it is of some formal significance. Indeed, we shall see that it serves as a harmonic “model” for four other progressions that follow, listed in Example 1. I will therefore refer to these later progressions as “variants” of this model.

[3] Inspecting these progressions, we may notice certain recurring changes of root and quality. Both the model and Variant 1 begin by changing A major into C minor, transposing the root by four semitones and reversing the mode, and the same change transforms the first triad in Variant 3 (E major) to the second (G minor). A different transformation changes the third to the fourth triad in each of these same progressions: transpose the root by three semitones and reverse the mode. These two changes thus seem characteristic of the piece. However, the progressions are not otherwise transpositions of each other, raising the question of how these characteristic transformations befit the progressions as a whole. Since many of the triadic successions do not conform to harmonic-functional intuitions, it would seem necessary to approach this question with a broad and flexible theoretical framework.

[4] Just such a framework is the simple algebraic structure that Julian Hook proposed to model the entire range of triadic progressions (Hook 2007). He defines a “uniform triadic transformation” (henceforth UTT) as an operation that acts on the collection of major and minor triads. Each UTT affects all major triads the same way and all minor triads the same way (but possibly in a different way than major triads). They are expressed in the form <+, m, n> or <−, m, n>: the + or − indicates that the operation preserves or reverses the mode of the triad, respectively, and the integers m and n indicate how the root is transposed depending on whether the triad is major or minor, respectively. For example, the UTT <−, 3, 4> transforms E major to G minor and G minor to B major; <+, 7, 7> transforms C major to G major and C minor to G minor, that is, it simply transposes a triad by seven semitones.

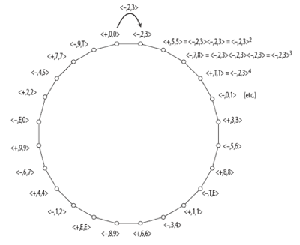
[5] The UTT from any given triad to another is not uniquely determined. For example, the transformation from C major to E minor could be <−, 4, 8> (the same transformation as the neo-Riemannian Leittonwechsel), but it could also be <−, 4, n>, where n is any pc-interval. Hook addresses this profligacy by drawing attention to those subgroups of UTTs that are simply transitive, and which he calls K(a, b).⁽²⁾ Example 2 focuses on the K(1,1) subgroup, listing the UTTs it contains. (In this and subsequent examples, I will use T and E to denote 10 and 11, respectively.) The mode-preserving members are simply the twelve transpositions, while each of the mode-reversing members transposes the roots of all major triads by n and the roots of all minor triads by n + 1. For instance, <−, T, E> transforms D major to C minor, and C minor to B major.

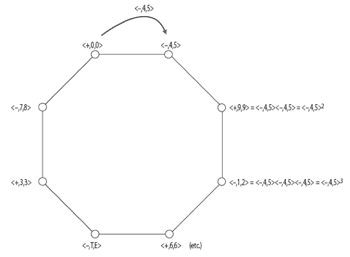
[6] Some formal features of the K(1,1) subgroup make it especially practical and intuitive for analysis. Its members, like transpositions, commute. Also, it can be generated (that is, every member can be derived) via the repeated application of at least one of its mode-reversing members. More specifically, any UTT of the form <−, m, m+1> where 2m + 1 is equal to 1, 5, 7, or E, can generate all the members of K(1,1).⁽³⁾ Example 3a shows how the K(1,1) subgroup is completely generated by its mode-reversing member <−, 2, 3> (for which 2m + 1 = 5) while Example 3b shows how another mode-reversing member, <−, 4, 5> (for which 2m + 1 = 9), generates a cycle that does not include all of the members of the subgroup. Such properties make it possible to consider the UTTs of K(1,1) as members of a generalized interval system (henceforth GIS) that can be used to measure and compare “distances” between triads.⁽⁴⁾ Restricting transformations to K(1,1) solves the problem of profligacy: there is only one possible way to analyze the succession of any two triads. For example, the chord progression from C major to B minor can be described within K(1,1) only as <−, T, E>. Indeed, under this restriction <−, T, E> describes every succession from a major triad to a minor triad whose root is a major second lower, and so we may conceive of this transformation as the generalized-intervallic distance between the two triads.

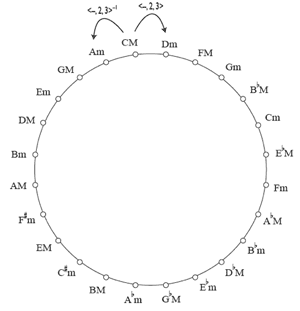
[7] This sense of “distance” that one may ascribe theoretically to simply transitive subgroups of UTTs is more apparent when one considers that certain mode-reversing members of the K(1,1) subgroup can generate all the members of that group. Example 4 fixes the cyclic graph of Example 3a to specific major and minor triads, showing how all 24 are generated via the repeated application of <−, 2, 3>.⁽⁵⁾ By comparing these two examples, we can see how powers of <−, 2, 3> act as intervals within the space of the 24 major and minor triads. For example, E major resides six clockwise-steps from C major on Example 4. Therefore, the transformation <+, 3, 3> can be expressed, in consideration of our established GIS, as <−, 2, 3>⁶. Similarly, there are nine counterclockwise steps from G major to A minor. This transformation is achieved by the UTT <−, E, 0>, or <−, 2, 3>⁻⁹. The cycle in Example 4 may be regarded as a single-path network, in the sense that there is only one arrow entering and one arrow leaving (via its inverse) each node. Also, it has a single generator in the sense that each of these arrows is labeled with the UTT <−, 2, 3>ⁿ or its inverse, <−, 2, 3>⁻ⁿ, depending on the direction of the transformational path. Thus it seems sensible to refer to the distance from some triad x to another triad y in Example 4 as the number of steps by <−, 2, 3>ⁿ or <−, 2, 3>⁻ⁿ from x to y.⁽⁶⁾

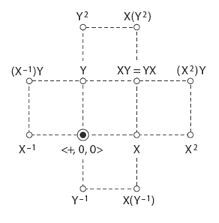
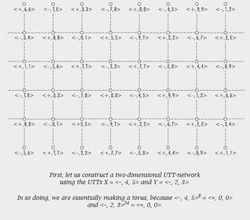
[8] Accepting this notion of distance opens the door to further analogies with well-known musical spaces: two-dimensional networks of pitch classes, in which each dimension is generated by a different interval.⁽⁷⁾ It is possible to similarly structure the major and minor triads as a multi-path space, where each dimension is generated by a different UTT. Example 5 shows a generic model for creating such a graph. As a reference, the central point is labeled <+, 0, 0>. Nodes to its right and left are generated by the reiteration of a UTT, X and its inverse X⁻¹, and nodes in the vertical dimension are generated by the reiteration of another UTT, Y and its inverse Y⁻¹. Thus every node is labeled with some product of these four UTTs. For the graph to be well formed, X and Y must commute, that is, XY = YX,⁽⁸⁾ and to make sure the graph is comprehensive, X or Y must generate all 24 triads. If X and Y belong to K(1,1), these two conditions are easily satisfied.

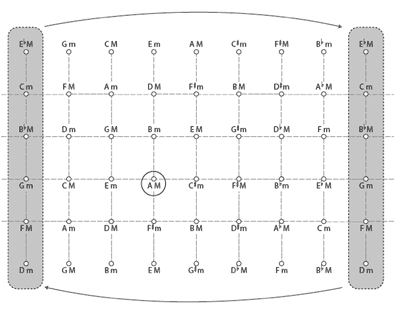
[9] Animation 1 illustrates the process of constructing this graph using the K(1,1) UTTs X = <−, 4, 5> and Y = <−, 2, 3> (the same that were used in Examples 3a and b). The resulting space is copied over onto Example 6. Each node is labeled with the UTT that is the product of the horizontal (X) and vertical (Y) moves that it takes to get there from the node labeled <+, 0, 0>. Any triad may be associated with the <+, 0, 0> position to produce a network including all 24 triads. Consider, for instance, Example 7, which places A major into the <+, 0, 0> position. The nodes in the rightmost column correspond to the nodes in the leftmost column, because, as shown in Example 3b, <−, 4, 5> applied eight times is the same as <+, 0, 0>. In the other dimension, there is a similar identity of rows (which are not shown in the example) because <−, 2, 3>²⁴ = <+, 0, 0>. Thus both dimensions curve back on themselves, making the whole network a torus.

[10] Within this space, any triadic relationship can be represented as a path made up of a series of horizontal and/or vertical steps. I will represent such a path as the ordered pair (a, b), where a and b respectively represent the number of horizontal and vertical steps that constitute it. Because <−, 2, 3> alone generates all 24 major and minor triads, this path could always be completely vertical. For example, the transformation of A major to D minor can be expressed as <−, 2, 3>¹⁷ (recall Example 3a), totaling seventeen upward steps within the space; that is (0, +17). Similarly, a path of seven downward steps can be taken; that is, (0, −7), via <−, 2, 3>⁻⁷. However, because every triad appears as a node in every vertical column, there are multiple paths from one triad to another. Therefore, Animation 2 shows how, by combining dimensions, this same transformation can follow a path of two steps to the right and one step down, (+2, −1), reducing the total number of steps to three. This path expresses the UTT identity <−, 6, 7> = <−, 4, 5>²<−, 2, 3>⁻¹. The same series of moves also transforms G major to C minor and C major to F minor, as well as E minor to B major and D minor to A major. Therefore, we can see that (+2, −1) will always result in the same triadic transformation: when starting from any major triad, reverse the mode and transpose the root by T₆; when starting from any minor triad, reverse the mode and transpose the root by T₇. We can also see how an odd number of moves through our space results in a reversal of mode and, thus, corresponds with traditional inversion; an even number of moves results in a preservation of mode and, thus, corresponds with traditional transposition. In general, we may now conceptualize triadic distances in Example 7 in terms of the total number of vertical and horizontal steps from one point to another. In general, since each triad has multiple representations on the graph, there are many possible pathways between any two given triads. Sometimes the path involving the least number of steps may be of the greatest analytical interest, but not necessarily, for instance if a different path with more steps is reproduced between other triad pairs in the piece. We shall see that the latter situation obtains in this passage.

[11] Although any two commuting UTTs would serve equally well in creating such spaces, I have three specific reasons for choosing <−, 4, 5> and <−, 2, 3>. First, the consecutive application of these two UTTs results in a direct transposition by perfect fifth, a familiar functional progression. (In this regard, the resulting network also resembles the Tonnetz constructed from the intervals X = 3 and Y = 4, whose combination is also a perfect fifth.) Second, I have shown that the K(1,1) subgroup to which these UTTs belong can be used to analyze characteristic triadic transformations in two other works by Bryars, both of which were composed in the same year (Roeder and Cook 2006; Cook 2006).⁽⁹⁾ My final reason is that <−, 4, 5> and <−, 2, 3> are the K(1,1) members that describe the two transformations that I identified above as characteristic in the final programme of “A Man in a Room, Gambling.” Indeed, while this programme exhibits a greater diversity of triadic transformations than the other passages I have analyzed, analyzing it in terms of pathways in a two-dimensional K(1,1) space reveals a surprising consistency to its progressions.

[12] Example 8 copies over the model and four variants of Example 1, and identifies the progression from each chord to the next with a K(1,1) UTT. Every one of these chord progressions can be represented by a UTT-chain of the form: <−, 4, 5>, <+, m, m>, <−, 2, 3>, <−, n, n + 1>, <−, 2, 3> (as shown in the topmost part of the example). The unchanging UTTs involved in the chain are those characteristic ones that were used to generate the UTT-space of Example 6; that is, they are each a single step in one direction or the other. The UTTs in the second and fourth positions vary throughout the piece, but they can all be understood as members of K(1,1), and they always retain their respective mode-preserving or mode-reversing characteristics. Note that the second and fourth variant progressions present the fixed UTTs of the chain in retrograde. That is, the <<−, 4, 5>, X, <−, 2, 3>, Y, <−, 2, 3>> series is retrograded to <<−, 2, 3>, W, <−, 2, 3>, Z, <−, 4, 5>>. Loosely speaking, the triad-chains of Variants 2 and 4 are RI-chains of that found in the model (they are labeled RICH on the example, and the transformational chain is shown in the top of the respective progressions). Although the repetitions of the characteristic <−, 4, 5> and <−, 2, 3> UTTs within each progression are striking, especially since variants begin with either major or minor triads, this analysis leaves open the question of how the changing UTTs—the second and fourth in each variant progression—function.

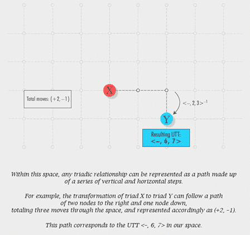
[13] To begin answering this question, Animation 3 traces a transformational path for the model progression (PROG. 01, measures 1–14) through the two-dimensional UTT-network constructed from <−, 4, 5> and <−, 2, 3>. Each chord in the progression appears as a colored node when it begins on the soundtrack. The five UTTs in the series are animated as five changes of location from one node to another, and each is identified (at the arrival of each new chord) in the box labeled “Resulting UTT.” Each change comprises motion along one or both directions, and is summarized at the bottom of the animation as an ordered pair that lists the number of unit steps in each dimension. As in previous examples, each <−, 4, 5>, or its inverse, corresponds to one step to the right or left on the horizontal axis, and each <−, 2, 3>, or its inverse, corresponds to one step up or down on the vertical axis. So the transformation <−, 4, 5> of A major to C minor is represented as (+1, 0), signifying one horizontal step to the right and no vertical steps. Similarly, the transformation <+, 4, 4> of C minor to F minor is analyzed as (+3, +1), signifying three horizontal steps to the right and one vertical step up. (As is evident on Example 7, C minor to F minor could also be analyzed as (+2, −2), but that would also involve four steps in total.) The entire progression involves eight horizontal steps and four vertical steps, totaling twelve steps in all.

[14] Animation 4 similarly analyzes the remainder of the programme, starting from where Animation 3 left off (measure 15). It traces paths for Variants 1 to 4 in the same space, tallying the total number of X- and Y-moves. The only difference between the UTT-network in Animation 3 and that of Animation 4 is the particular triad used to initiate the space (that which is input into the <+, 0, 0> node). In this analysis, the remark above ([9]) about alternative paths becomes pertinent. It is not the shortest distance between chords that interests us. Rather, we are interested in discovering to what extent each variant progression can be heard to repeat the structure of the model progression. By studying the variants in this way we are strengthening their ties to the model by limiting the number of possible paths between chords. In each case, the totals of the individual moves are 1 + n + 1 + m + 1. Of course, this structure reflects the structure of the UTT-chain that defines our harmonic model and variants, where the transformations in the first, third, and final positions are fixed and unchanging, and the transformation in the first position differs from those in the third and final, which are identical. However, it is very striking that, even though X- and Y-moves are not the same UTTs at all, the model and every variant can be analyzed into twelve total X- or Y-moves. In other words, even though the second and fourth UTTs in each variant differ from those in the other, and so the six-triad series varies considerably from variant to variant, the variants exhibit perfect consistency in this way. An even more striking consistency is that the second and fourth UTTs in each variant always involve four and five X- and Y-moves respectively, or vice versa, so that the twelve moves are always expressed as 1 + 4 + 1 + 5 + 1 or its retrograde.

[15] This analysis has shown that Hook’s suggestion to treat a simply transitive UTT subgroup as a generalized interval system is indeed productive. Adhering to Lewin’s conditions for constructing a transformational space, I first generated a single-path UTT-network in which various triadic relationships may be explored. By then incorporating a second dimension to this space, while still restricting the UTTs to the simply transitive group, I offered a way of measuring a kind of “distance” between any two triads. My representation of the seemingly unrelated chord progressions in “A Man in a Room, Gambling” within this UTT-network revealed repetitions of the opening progression that could have otherwise gone unnoticed. Perhaps UTT-networks, similarly constructed from characteristic transformations, may be able to account for various other types of contemporary, unorthodox progressions in other musical genres that make extensive use of triads, including popular music and jazz.

Scott Alexander Cook
University of British Columbia
School of Music
6361 Memorial Road
Vancouver, BC
V6T 1Z2 Canada
salexcook@yahoo.ca

Works Cited

Bernas, Richard. 1987. “Three Works by Gavin Bryars.” New Music 87: 34–42.

Callendar, Clifton. 2007. “Interactions of the Lamento Motif and Jazz Harmonies in György Ligeti’s Arc en ciel.” Intégral 21: 41–77.

Cohn, Richard L. 1997. “Neo-Riemannian Operations, Parsimonious Trichords, and Their ‘Tonnetz’ Representations.” Journal of Music Theory 41/1: 1–66.

Cook, Scott Alexander. 2006. “Triadic Transformation and Harmonic Coherence in the Music of Gavin Bryars.” M.A. thesis, University of British Columbia.

Gollin, Edward. 1998. “Some Unusual Transformations in Bartók’s Minor Seconds, Major Sevenths.” Intégral 12: 25–51.

Hook, Julian. 2002. “Uniform Triadic Transformations.” Journal of Music Theory 46: 57–126.

—————. 2007. “Cross-Type Transformations and the Path Consistency Condition.” Music Theory Spectrum 29: 15.

Lewin, David. 1987. Generalized Musical Intervals and Transformations. New Haven and London: Yale University Press.

—————. 1995. “Generalized Interval Systems for Babbitt’s Lists, and for Schoenberg’s String Trio.” Music Theory Spectrum 17/1: 81–118.

Roeder, John and Scott Alexander Cook. 2006. “Triadic Transformation and Parsimonious Voice Leading in Some Interesting Passages by Gavin Bryars,” Intégral 20: 43–67.

Siciliano, Michael. 2002. “Neo-Riemannian Transformations and the Music of Franz Schubert.” Ph.D. dissertation, University of Chicago.

Footnotes

1. An introduction to Bryars’s music can be found in Bernas 1987.
Return to text

2. A group of operations (STRANS) is simply transitive on a given family of elements (S) when the following condition is satisfied: “Given any elements s and t of S, then there exists a unique member OP of STRANS such that OP(s) = t” (Lewin 1987, 157).
Return to text

3. More generally, Hook shows that if a = 1, then the members of K(a, b) commute, and if a = 1 and b is odd, then K(a, b) can be generated by the repeated application of at least one of its mode-reversing members. That is, any UTT of the form <−, m, n> where m + n is equal to 1, 5, 7, or E, can generate all the members of the subgroup (Hook 2002, 88).
Return to text

4. David Lewin’s formulation of a Generalized Interval System consists of a family of elements, a group of intervals, and a function that maps pairs of those elements to the intervals, which are subject to the conditions that: (A) the interval from one element to a second element, followed by the interval from the second to a third element, is equal to the interval from the first to the third; and (B) for any given interval from any given element there is a unique element. This second condition means that a GIS can be defined on a given space when the set of transformations that function within that space constitute a simply transitive group: that is, when only one transformation in the set will map a given element of the space to another (Lewin 1987, 26).
Return to text

5. This space orders triads as does the Musical Circle in Johann David Heinichen’s Neu erfundene und gründliche Anweisung zu vollkommener Erlesung des General-Basses (Hamburg, 1711), 261.
Return to text

6. Various networks of the standard neo-Riemannian operations LPR, and some intuitions about distances in them, are developed in Siciliano 2002.
Return to text

7. For a general exposition of the Tonnetz, see Cohn 1997.
Return to text

8. This is stipulation 9.2.1D of Lewin’s definition of transformational graphs in Lewin 1987, 195. The importance of commutativity is clearly expressed in Example 7 of Hook 2007, 15.
Return to text

9. Some of the present discussion is taken from Cook 2006.
Return to text

Copyright Statement

Copyright © 2009 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.

Prepared by William Guerin, Cara Stroud, and Tahirih Motazedian, Editorial Assistants
Number of visits: