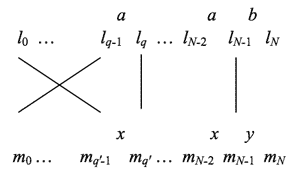Modes, the Height-Width Duality, and Handschin’s Tone Character *
David Clampitt and Thomas Noll
KEYWORDS: mode, diatonic scale, well-formed scale, regions, tone character, Jacques Handschin, Carl Dahlhaus, Glarean, Dodecachordon, hexachord, divider incidence, algebraic combinatorics on words, Christoffel word, Sturmian morphisms, Christoffel duality
ABSTRACT: The theory of well-formed modes is a modal refinement of the theory of well-formed scales. The mathematical approach is based on various results from the subdiscipline of algebraic combinatorics on words. Section 1 provides anchors and motivations for this investigation both in music theory and in mathematics and traces some earlier cross-connections. An overview of the theory is presented in terms of a dichotomy between generic and specific levels of description. Section 2 presents a first group of basic theoretical results. Height-width duality mediates between scale step patterns and fifth-fourth folding patterns. Both are encoded through divided words, on two-letter alphabets, such as aaba|aab and yx|yxyxy. The letters a and b denote ascending whole and half steps, and the letters x and y denote ascending perfect fifths and descending perfect fourths, respectively. These words are well-formed words; i.e., in the language of word theory, they are conjugate to Christoffel words and inherit a duality that is akin to Christoffel duality. Qualitative differences between the modal varieties of the same underlying scale can be detected and formalized through word-theoretical arguments. For example, a property we refer to as divider incidence characterizes modes corresponding to standard words. Positive standard words generalize the ascending authentic Ionian mode. Sturmian morphisms provide a transformational meta-language for the study of well-formed modes. Section 3 revisits Jacques Handschin’s concept of tone character and defends it on the basis of the mathematical results against two criticisms that had been raised by Carl Dahlhaus. Section 4 explores distinctions among the modes based upon considerations of word theory, especially divider incidence and concomitant properties that support major-minor tonality. A concluding section connects these arguments with other lines of investigation.
Copyright © 2011 Society for Music Theory
Table of Contents
- 1. Introduction
- 2. Scale Step Patterns and Scale Foldings
- 3. Thoughts on Jacques Handschin’s Tone Character
- 4. Further Distinctions Among the Modes, via Algebraic Combinatorics on Words
- 5. Conclusions
- Acknowledgments
- References
Where actual musical practice is concerned, the relevant historical fact is that people have evidently internalized the diatonic pitch set—carried it around in their heads as a means of organizing, receiving, and reproducing meaningful sound patterns—as far back as what is as of now the very beginning of recorded musical history, some three and a half millennia ago.
[1] Thus says Richard Taruskin, in the first chapter (“The Curtain Goes Up”) of The Oxford History of Western Music, concerning what he calls “our most fundamental musical possession” (Taruskin 2005, 30, 29). Scale theory studies have addressed the robust nature of the usual diatonic in terms of properties such as non-degenerate well-formedness, Myhill’s Property, Cardinality Equals Variety for lines, and self-similarity, to mention only some equivalent characterizations (Clough and Myerson 1985, Carey and Clampitt 1989, Carey and Clampitt 1996a). Other concepts may be productively studied in relation to the aforementioned equivalences, such as maximal evenness and coherence (Clough and Douthett 1991, Agmon 1989, Agmon 1996, Carey 2002, Carey 2007). These properties, however, are attributable to the general diatonic scale or set (and to analogues of the diatonic, notably the usual pentatonic) under octave equivalence; they do not easily distinguish among the modal varieties. Moreover, the studies above have not generally engaged with tonality, surely the seat of some of the deepest questions in music theory.
[2] We argue that mathematical word theory provides a way to extend musical scale theory, to begin to approach issues of modality and tonality. We hasten to acknowledge that, given the abstraction of the word-theoretical level of description, we can hope to do no more than to open a new perspective on these perennial topics. The present article is a contribution to a mathematical theory of music that aims to complement philological methods of accessing knowledge about the diatonic modes and related music-theoretical concepts. The methodology can be characterized as an “experimental philology” that is concerned to study the interdependence of concepts irrespective of their emergence in historical discourse. Those music-theoretical ideas with historical philological anchors that participate in a multiplicity of mathematical interdependencies are those that deserve to be the focal point of our attention. For example, Myhill’s Property for the diatonic is the property that every non-zero generic interval comes in two specific varieties, e.g., generic diatonic thirds are either major or minor. This is known to every music theorist, as is the fact that the diatonic set is non-degenerate well-formed, i.e., is generated by an interval of a given size, all instances of which span the same number of step intervals.(1) That these properties are equivalent, however, is a different type of knowledge from the mere conjunction of the two facts, and therefore deserves additional music-theoretical interest. In the concluding summary we draw a balance of our results with respect to this methodological orientation.
1.1 Scale Theory and Word Theory
[3] Combinatorial word theory studies strings of symbols, usually drawn from a finite alphabet, and enjoys rich interconnections with several subfields of mathematics, such as number theory, geometry, and symbolic dynamics (Lothaire 2002, Berstel et al. 2008). This is a mathematical subfield that has roots in the eighteenth and nineteenth centuries, but is usually considered to have begun with the work of Morse and Hedlund (1938, 1940). As a field, however, it has had most of its growth in the last twenty-five years, i.e., contemporaneously with the developments in musical scale theory cited above, with which there is considerable intersection of methods and results. Word theory and mathematical music theory have proceeded in almost total ignorance of each other during this time. Notable exceptions include the rhythmic studies of Chemillier and Truchet 2003 and Chemillier 2004. The authors would like to acknowledge a remark by Franck Jedrzejewski pointing to a talk by Christian Kassel (2004), joint work published in Kassel and Reutenauer 2007, which directed their attention to word theory.
[4] This paper begins to explore transdisciplinary mappings between word theory and scale theory. It is not merely a matter of translation of existing music-theoretical conceptions into a new terminology (although that in itself is non-trivial), but of mapping word-theoretical constructions into music theory to create new music-theoretical understandings.
[5] Word theory studies strings of letters over an alphabet. The set of all finite words in alphabet A, A* = {a1...
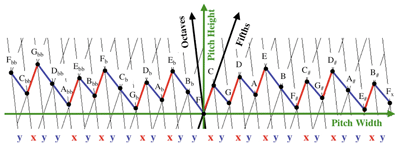
[6] Let A = {a, b}. One can define mappings f: A* → A*—so-called uniform rewriting rules—by simply specifying two words f(a) and f(b) which uniformly replace all occurrences of the letters a and b, respectively. For example, if a is replaced by f(a) = aaba and b by f(b) = aab, we induce a rewriting of the word w = ab as f(w) = aabaaab. The uniformity means that by construction the map f is a monoid endomorphism of A*, i.e., f(uv) = f(u)f(v) ∈ A*, whenever u and v are words in A*. We are interested in a particular subfamily of monoid endomorphisms, which are called Sturmian in the literature, denoted St. The elements of St are compositions of the following five morphisms, G, G~, D, D~, and E:(2)
D(a) = ba, D(b) = b, D~(a) = ab, D~(b) = b
E(a) = b, E(b) = a
Figure 1. The authentic tetractys modes as images of w = ab under D and D~
(click to enlarge)
Figure 2. The four authentic pentatonic modes, as images of w = ab under compositions
(click to enlarge)
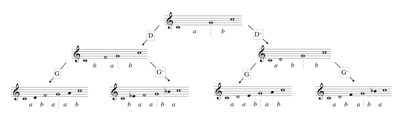
[7] Words over the alphabet {a, b} are interpreted as decompositions of musical intervals in terms of sequences of two basis intervals. If, for example, a and b denote ascending perfect fifth and ascending perfect fourth, respectively, as basis intervals, we interpret the word w = ab as an ascending octave, which is decomposed into fifth followed by fourth. In our interpretation of the effects of Sturmian morphisms f we treat them like coordinate transforms, i.e., we assume that the image f(w) of a word w denotes a new decomposition of the same interval, which was previously denoted by w. What actually changes under the transformation is the interpretation of the letters a and b as basis intervals. To be more precise: under the application of the morphism D or D~, the interpretation of the letter a changes, while the interpretation that a held previously is inherited by its image, D(a) = ba or D~(a) = ab. The interpretation of the letter b does not change, as D(b) = b and D~(b) = b. Thus, if a and b denote ascending perfect fifth (P5) and ascending perfect fourth (P4), respectively, before the transformations D or D~ are applied to a word w, we may conclude that after the transformation they denote ascending major second (M2) and ascending perfect fourth (P4), respectively. Under D and D~ the decomposition of the octave (P8) as an authentic division mode w = ab is transformed into the two authentic tetractys modes, D(w) = bab and D~(w) = abb. (See Figure 1.)
[8] The decompositions G(w) = aab and G~(w) = aba of the octave (P8) necessarily involve the descending major second (−M2) as a basis interval. These are not useful in the context of our present investigation. The transformations G and G~ become important, however, as transformations of the two tetractys decompositions D(w) = bab and D~(w) = abb into four authentic pentatonic modes. (See Figure 2.) Following word theory practice (which dovetails nicely with our music-theoretical application), we track the images of the initial a and b via the divider symbol “|”.
[9] Now consider further compositions of these morphisms applied to the initial word w = ab. If in the resulting words we understand final a’s as ascending major step intervals and b’s as ascending minor step intervals, then we have the six authentic modes of Glarean’s Dodecachordon (Glarean 1969) (albeit reordered):
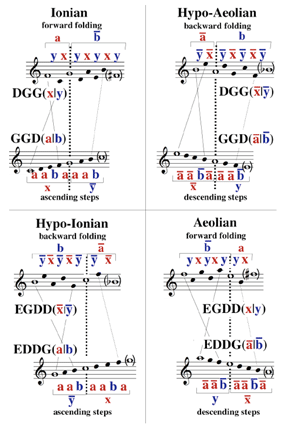
| GGD(a|b) = GG(ba|b) = G(aba|ab) = aaba|aab | Ionian |
| GG~D(a|b) = GG~(ba|b) = G(baa|ba) = abaa|aba | Dorian |
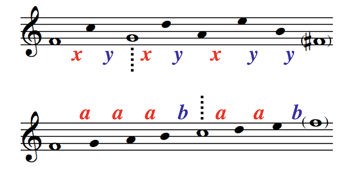
| G~G~D(a|b) = G~G~(ba|b) = G~(baa|ba) = baaa|baa | Phrygian |
| GGD~(a|b) = GG(ab|b) = G(aab|ab) = aaab|aab | Lydian |
| GG~D~(a|b) = GG~(ab|b) = G(aba|ba) = aaba|aba | Mixolydian |
| G~G~D~(a|b) = G~G~(ab|b) = G~(aba|ba) = abaa|baa | Aeolian |
If we interchange G’s and D’s and interchange G~’s and D~’s, and follow with the exchange morphism E, this yields Glarean’s six plagal modes:(3)
| EDDG(a|b) = EDD(a|ab) = ED(ba|bab) = E(bba|bbab) = aab|aaba | hypo-Ionian |
| EDD~G(a|b) = EDD~(a|ab) = ED(ab|abb) = E(bab|babb) = aba|abaa | hypo-Dorian |
| ED~D~G(a|b) = ED~D~(a|ab) = ED~(ab|abb) = E(abb|abbb) = baa|baaa | hypo-Phrygian |
| EDDG~(a|b) = EDD(a|ba) = ED(ba|bba) = E(bba|bbba) = aab|aaab | hypo-Lydian |
| EDD~G~(a|b) = EDD~(a|ba) = ED(ab|bab) = E(bab|bbab) = aba|aaba | hypo-Mixolydian |
| ED~D~G~(a|b) = ED~D~(a|ba) = ED~(ab|bab) = E(abb|babb) = baa|abaa | hypo-Aeolian |
[10] There are certain distinguished subfamilies of Sturmian morphisms. Those composed only of G’s, D’s, G~’s, D~’s (or, what amounts to the same thing, that include an even number of E’s), form the submonoid St0 of special Sturmian morphisms. Those that are composed purely of G’s, D’s, and E’s are called standard morphisms; those that are composed purely of G~’s, D~’s, and E’s are called anti-standard morphisms. In all cases, we may apply the attribute special, whenever the number of E-occurrences is even, and non-special otherwise. For example, we say that GGD is a special standard Sturmian morphism. We will use the terms standard and anti-standard to refer to words that are the images of the root word a|b under standard and anti-standard Sturmian morphisms, but we will apply the terms positive and negative for those that result from special and non-special morphisms, respectively. Thus, Ionian (aaba|aab) is positive standard, hypo-Ionian (aab|aaba) is negative standard; Aeolian (abaa|baa) is positive anti-standard, and hypo-Aeolian (baa|abaa) is negative anti-standard.(4) Moreover, as we add tildes (~) in a regular fashion, from standard to anti-standard, the resulting modes follow Zarlino’s ordering, with starting notes moving up the natural and hard hexachords, for the authentic and plagal modes, respectively.
[11] Glarean’s rejected modes, hyper-aeolius reiectus I and hyper-phrygius reiectus II, the Locrian varieties, do not appear: Locrian corresponds to what word theorists call “the bad conjugate” (Berthé et al. 2008). We call them amorphic, because they are not generated through Sturmian morphisms. This paper explores the meaning of these abstract derivations, and in particular the special status of the standard and anti-standard modes, which in some accounts correspond to the ancestors of modern major and minor.
[12] To reach these results, the exposition will treat a duality that we assert is essential to musical meaning in modal/tonal contexts. This concept of height-width duality is quite different in constitution and scope from the concept of major-minor dualism in the tradition of Arthur von Öttingen and Hugo Riemann. (Nonetheless, aspects of traditional dualism are accommodated and embraced later in the paper, but entirely separately from the notion of duality at issue in this moment.) We hope that this concept contributes to a sharpening of the concepts of modality and tonality as well as to a revealing of hidden diachronic connections between early and common practice periods in European music with respect to the constitution of tone relations. We regard a better understanding of the special status of the Ionian and Aeolian modes among the other diatonic modes as an important pre-condition for the investigation of their diachronic connections with modern major and minor in common practice tonality. This is not to minimize the complexities of the historical development, nor to downplay the significance of many other musical factors. Since even acoustics are pushed to the background in this account, the story is necessarily a partial one.
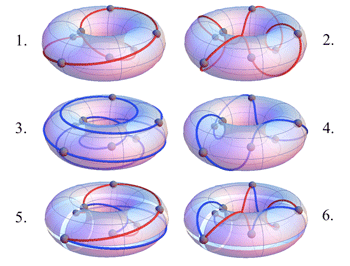
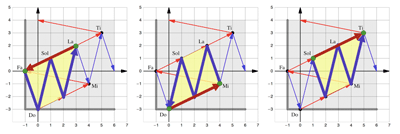
[13] To briefly illustrate the duality, we take the Lydian mode as an example. Although we will focus much attention on the Ionian mode, corresponding to the standard word in the conjugacy class of words representing the diatonic modes, it is the Lydian mode that corresponds to what is called the Christoffel word of the class, also distinguished in word theory (compositions of G’s and D~’s applied to ab). For each word affiliated with a given mode, there is a unique word given by what we refer to as the scale folding. Consider the notes of the Lydian mode (as in Figure 3), expressed as the sequence of upward perfect fifths and downward perfect fourths, from initial tone F to the (excluded) boundary tone
[14] Fundamentally, this relation is a common dichotomy of musical discourse, although rarely has it been treated as a mathematical duality. Louis and Thuille, for example, speak of a complementarity between Nachbarschaftsbeziehung and Verwandtschaftsbeziehung (Louis and Thuille 1907), which we might understand as “neighborhood relation” and “kinship relation,” respectively, approximately “melodic” vs. “harmonic”:
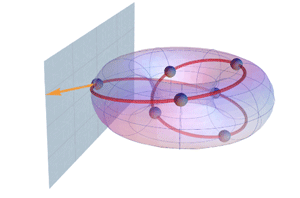
There is a neighborhood relation between [two tones] and a kinship relation. These relations are mutually contrasting, insofar as a close neighborhood relation between distinct tones excludes a close kinship relation and vice versa.(5)
[15] This dichotomy was taken up by Jacques Handschin, who elevates to axiomatic status “tone height” (Tonhöhe) and “tone character” (Toncharakter), the latter now explicitly defined as the position of a pitch class along a line of perfect fifths. He writes as follows of the “mutual intersection of tone height and tone character”:
If I consider these “characters” as embodying the truly musical property of a tone, I nevertheless do not intend to downplay the role of pitch height and pitch-height differences. The richness of music as melody is based on the play of both of these categories, which crisscross each other throughout, and a “musical person” in the full sense is somebody who is adapted to the inner tone relations and who perceives degrees of pitch height in connection to those relations...
One might characterize the contrast between the two mutually intersecting elements in the sense that one of them (pitch height) is the outer, sensorily perceivable one, while the other (tone character) is the inner, truly musical one.(6)
[16] If this sounds metaphysical, simply consider two enharmonically equivalent but distinct diminished 7th chords, or a dominant 7th and an enharmonically equivalent augmented 6th: musicians in the culture recognize these pairs as identical or at least minimally distinct acoustically but, in the context of their resolutions, very different in their musical meanings. This is fairly non-controversial, and one typically takes it for granted. Nonetheless, Handschin’s Der Toncharakter was very poorly received, at least in part because he framed his argument in the terms of his subtitle: Einführung in die Tonpsychologie. As Green and Butler have pointed out, the term “tone psychology” was by then anachronistic, and Handschin’s speculative approach was and is out of step with scientific studies in psychology of music (Green and Butler 2002). Handschin was later criticized by Dahlhaus, who (reasonably enough) asked how the character of E, as scale degree 2 of mode 1 and as scale degree 1 of mode 3, could remain the same. In section 3 of the paper we will reconsider Handschin’s project in the light of our formalization, and revisit Dahlhaus’s arguments against Handschin. In our formalization, the notions “tone height” and “tone character,” or “neighborhood relation” and “kinship relation,” are reconceived as the height and width dimensions.(7)
1.3 Height-Width Duality and the Generic/Specific Dichotomy
[17] In order to anchor the present approach against a background of established concepts it is useful to explore the dimensions of height and width with respect to two different levels of description in scale theory, generic and specific, coarser and finer intervallic measures, respectively, defined in paragraph 19 below. Important insights have been drawn in investigations into the interplay of these levels, in particular in Clough and Myerson 1985. Any refinement in scale theory should therefore be sensitive with respect to this dichotomy. The plan for this subsection is to expand both levels of description, in each case from a one-dimensional height-based model into a two-dimensional height-width-based model. Although the rest of this paper is dedicated most intensively to an exploration of the expanded generic level, here we provide the reader with a brief sketch of the whole picture.(8)
[18] In the choice of the notion of dimension we act with caution. On the mathematical side we stick to the concept of the dimension of the vector space ![]() n over the real numbers
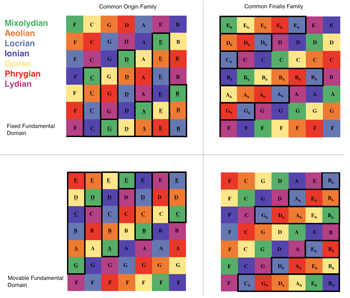
n over the real numbers ![]() , which is further inherited by the concept of the dimension of a manifold, such as the torus. With regard to the music-theoretical interpretation of this mathematical concept, we will present the reasons for our particular choice of a two-dimensional width-height space. At a deeper level of the music-theoretical interpretation of this concept of dimension we are concerned with the question of redundancy in a two-dimensional width-height space. We will see in section 2 that height and width are interdependent. Does an interdependency between the height and width coordinates of a mode provide music-theoretical insights, or does it constitute a theoretical “air bubble” without substance in it?
, which is further inherited by the concept of the dimension of a manifold, such as the torus. With regard to the music-theoretical interpretation of this mathematical concept, we will present the reasons for our particular choice of a two-dimensional width-height space. At a deeper level of the music-theoretical interpretation of this concept of dimension we are concerned with the question of redundancy in a two-dimensional width-height space. We will see in section 2 that height and width are interdependent. Does an interdependency between the height and width coordinates of a mode provide music-theoretical insights, or does it constitute a theoretical “air bubble” without substance in it?
[19] Whenever the elements of a countable set H are assembled into a sequential order (h0, h1, ... ), one may study them on the one hand as elements of the set H, and on the other hand as possessors of positions in the sequence. In scale theory one studies a scale as a finite set of real numbers representing different pitch heights and assembles them in ascending order ![]() N = {0, 1, ..., N−1}
N = {0, 1, ..., N−1}![]() /
/![]()
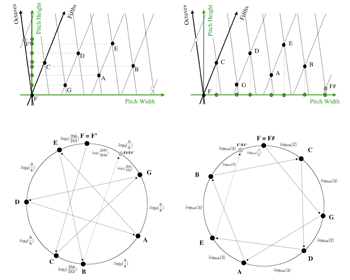
[20] The width dimension comes into play for generated scales and associated modes and—as in the case of pitch height—it involves a specific and generic level of description. Generic width has been investigated in the theory of well-formed scales in its interaction with generic height. Although the term perfect fifth is typically associated with the frequency ratio 3:2 or the specific pitch-height interval log23/2 (or some approximation thereto), it must not go unrecognized that the ordinal number “fifth” refers to the generic span of this interval by diatonic step intervals, which is the natural (cardinal) number 4. For concreteness, let us reconsider the derivation of the word associated with the fifth-fourth folding of the Lydian mode. The scale yields the sequence of pitch heights, h0 = F, h1 = G, ..., h6 = E (for the sake of simplicity, we use here the note names as place holders for the pitch-height values). Irrespective of the structure of the scale, simply considering the sequence of indices 0, 4, 1, 5, 2, 6, 3, (0) that folding upward fifths and downward fourths yields, and taking differences between consecutive values, one has the sequence 4, −3, 4, −3, 4, −3, −3, which we may encode as the word xyxyxyy. Thus, the word on two letters is a purely generic construction. The additional information at the specific level that the seven pitch heights may be connected in a chain of octave-equivalent ascending perfect fifths and descending perfect fourths characterizes a generated scale.
[21] In the case of generated scales another ordering of the same set H of pitch heights (more precisely: pitch-height classes modulo the octave represented by pitch heights within a fixed octave register) comes into play. Every element of H can be written as ![]() /
/![]()
![]() N,
N,
[22] What is the music-theoretical status of this symmetry? Let us inspect the map π: I → I in the particular case of the degenerate well-formed chromatic 12-tone scale. This is productive of insights because in the degenerate case the specific and the generic levels yield isomorphic structures, and so we can “pull” the symmetry in question from the generic level up to the surface of the specific level. If we interpret the 12 pitch classes from atonal set theory as a specific fifth-generated scale, we get
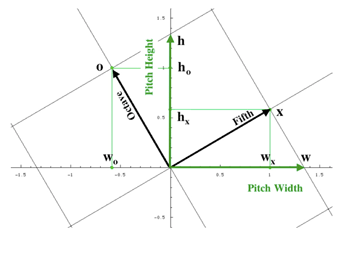
[23] The considerations of the preceding paragraph begin to motivate the introduction of a generic width parameter as an autonomous, but not independent, musical quantity. But this motivation remains nevertheless unsatisfactory, as long as the generic height and width parameters refer to the same set H of specific height values. It is desirable, then, to have also an associated set W of specific width values which can be assembled in ascending order w0 < w1 < ... < wN-1, such that its index set is—from a music-theoretical point of view—truly identical with the indices of (g0, g1, ..., gN-1). But how to define a (potentially continuous) pitch-width dimension? Recall that Handschin was in search of a unified theory, embracing traditional concepts of tone kinship with concepts from Stumpf’s tone psychology. How could such a unified theory be formulated in a mathematical language? The present two-dimensional approach seeks a music-theoretically productive mediation between the rather unconstrained accumulation of dimensions in speculative overtone theories of tone kinship on the one hand, and the rather modest perceptual investigation of tone kinship within a single pitch-height dimension on the other. In technical terms, it combines a free integer lattice of rank 2 in the role of the Pythagorean Tonnetz, generated by perfect fifth and octave, with a one-dimensional real vector space in the role of a single dimension of pitch height. However, it departs from the topologically dense embedding of the fifth-octave lattice into the one-dimensional pitch-height continuum, in favor of a discrete embedding of this lattice into a real vector space of dimension 2.
[24] Let the symbols x and o denote the musical intervals of ascending perfect fifth and ascending perfect octave, respectively. As an auxiliary assumption behind this construction—and in accordance with the traditional study of tone kinship in terms of the Pythagorean tone lattice—we simply regard the concatenation of fifths and octaves to be commutative. For example, the expressions ![]() -linear
-linear![]() ×
× ![]() .
.![]() x ×
x × ![]() o →
o → ![]()
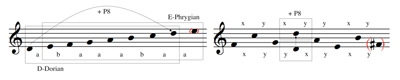
![]() permits its extension to the two-dimensional real vector space
permits its extension to the two-dimensional real vector space ![]() x ×
x × ![]() o →
o → ![]() .(10)
.(10)![]() x ×
x × ![]() o,
o,
[25] The construction is accomplished by another one-dimensional linear subspace of ![]() x ×
x × ![]() o,
o,![]() x ×
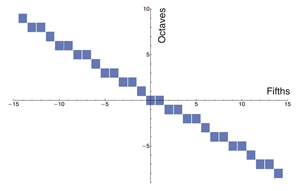
x × ![]() o.
o.![]()
![]() h,
h,![]() x ×
x × ![]() o →
o → ![]() h
h![]() x ×
x × ![]() o →
o → ![]() w,
w,
[26] A detailed example illustrates the two-dimensional construction of a well-formed scale: the perfect-fifth-generated diatonic scale with specific height coordinates in 12-tone equal temperament (12-TET). The pitch-height function for 12-TET is
For example, the width-height coordinates for G would be calculated as
![]()
[27] We obtain specific width-height coordinates:
[28] Observe that the projection of these points onto the height axis yields the traditional description of the diatonic scale as a well-formed scale in 12-TET:
[29] Slightly different specific coordinates are obtained by applying the matrix
(derived as in note 12, but with the slope y/x = −7/12 replaced by −log23/2) to the same seven essential tones and auxiliary boundary tones. This 2×2 matrix represents the transformation of the fifth-octave coordinates into Pythagorean specific width-height coordinates.(12) Figure 5 displays the height and width projections of these tones as well as circle diagrams for the associated well-formed height- and width-scales. These two specific scales exemplify and refine the duality that was defined in Carey and Clampitt 1996a on the generic level.
[30] These examples complete our overview of the theory of height-width duality, at both the generic and specific levels of description. In subsequent sections, we provide a refinement of well-formed scale theory that extends it to the study of modes.
2. Scale Step Patterns and Scale Foldings
[31] This section is dedicated to a thorough mathematical investigation of scale step patterns and their associated foldings. In particular, it treats a general situation that is manifest in the concrete anatomy of the Ionian mode. The first subsection, therefore, provides a detailed description of this concrete example, while the subsequent subsections investigate these observations in a more general context of word theory.
2.1 A Portrait of the Authentic Ionian Mode
Figure 6. Portrait of the Ionian mode as a duality between two hierarchical characterizations: scale folding and scale step pattern
(click to enlarge)
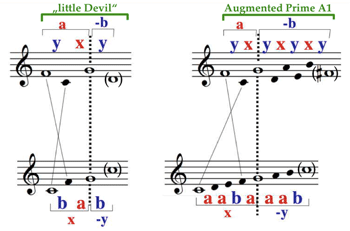
[32] Figure 6 provides a portrait of the Ionian authentic mode in terms of a duality between two characterizations, which we call the scale folding (or folding pattern) and the scale step pattern, respectively. As shown in the lower part of Figure 6, the scale step pattern a a b a | a a b fills the ambitus of an octave from a lower C to a higher
[33] In order to emphasize a hierarchical aspect that will enter into the discussion, the whole and half steps may be called surface intervals, in contrast to the background intervals perfect fifth and perfect fourth. Here again we consider the fifth as being primary and the fourth as secondary. Perfect fifth and perfect fourth are denoted by the letter x and the expression –y, respectively. The minus sign in this compound expression may appear irritating at first sight, but the duality between scale step pattern and scale folding receives a clearer expression thereby.
[34] The dual characterization is given in the upper part of Figure 6. The roles between the surface intervals and background intervals are now exchanged. More precisely, the primary intervals are mutually exchanged and likewise the secondary ones. In the scale folding the fifth is the primary surface interval and the whole step is the primary background interval. The direction of the secondary intervals is inverted. The secondary surface interval is now the fourth down and the secondary background interval is the half step down. Note that under this duality the generic height ambitus of the octave corresponds to the generic width ambitus of an augmented prime.
[35] An analogous duality applies to all other diatonic modes, and—from a theoretical perspective which we develop and explore in the subsequent subsections—to a much more general class of modes, which we term well-formed modes. Different scale step patterns are necessarily paired with different scale foldings; recall the folding for Lydian, xy|xyxyy, discussed in paragraph 13 above.
[36] Figure 6 also exposes some facts that apply only to the Ionian mode and not to the other diatonic modes, as we explore later in detail. To express these observations clearly it is useful first to declare some more or less self-explanatory notions.
[37] Whenever we wish to refer to the tone sequences (C, D, E, F, G, A, B,
[38] A significant observation about the Ionian mode is that the divider of the folding coincides with the divider of the scale.(13) The vertical dotted line in Figure 6 connects the divider G in the folding with the divider G in the scale. G divides the octave from C to
[39] The other connecting lines in Figure 6 show that the initial tones and the divider predecessors are mutually exchanged. The finalis C of the authentic Ionian mode is the initial tone of the scale and the predecessor of the divider G in the folding. Likewise, the initial tone F of the folding is the predecessor of the divider G of the scale. Finally, one may observe that the terminal predecessor of the scale—the leading tone B—coincides with the terminal predecessor of the folding. (In the generalized environment of well-formed modes to be proposed in subsection 4.1, the Ionian situation of divider incidence—that is, not only divider incidence, but also the coincidence of the initial tone of the scale with divider predecessor of the folding, coincidence of initial tone of the folding with divider predecessor of the scale, coincidence of the terminal predecessors of scale and folding—carries over to all modes corresponding to standard words.)
Figure 7. The two periods of the hexachord as divider prefix and suffix of the scale step pattern and the folding pattern of the authentic Ionian mode
(click to enlarge)
[40] These properties are tightly connected to the inner constitution of Guido’s hexachord and its location within the authentic Ionian mode (see Figure 7). The scale step pattern
[41] Note that for both scale step and folding patterns, it is the primary periods q and
[42] In Figure 6 we use musical notation and annotations with letters a, b, x, and y in order to refer to tones and intervals. The concepts of height and width—as used in the above portrait—have so far been defined by example. In this subsection we present an elementary mathematical procedure to turn two-letter words into sequences of integers. It will be well, however, to preface this otherwise mathematical section with a remark about the music-theoretical meaning of these constructed integer sequences. As discussed above in subsection 1.3, John Clough and Gerald Myerson formally introduced the distinction between generic and specific levels of description into the study of musical intervals, chords, tone sequences (lines), etc. (Clough and Myerson 1985, Clough and Myerson 1986). A brief glance at the diatonic scale will make this distinction explicit. The generic level of the diatonic scale comprises what is usually captured by the traditional interval names prime, second, third, fourth, fifth, sixth, seventh, octave. The specific level of description then distinguishes between major and minor seconds, major and minor thirds, perfect and augmented fourths and so forth, once these intervals are specified with concrete sizes in pitch height. Octave equivalence at the generic level is captured via the model of modulo 7 arithmetic. That is—and this is crucial in the face of our interest in the diatonic modes—the generic level of the theory of Clough and Myerson does not fundamentally distinguish between prime (unison) and octave. The same is true for the continuation of this approach in the theory of well-formed scales of Carey and Clampitt 1989 and Carey and Clampitt 1996a.
[43] The scale step pattern aaabaab of the Lydian mode is a representation of the distribution of major and minor step intervals. The opposition between the attributes “major” and “minor” is reminiscent of the specific pitch-height difference between the two step intervals. Thus, as a first approximation to the meaning of the word aaabaab, it is correct to say that the pattern reflects properties that are observable on the specific level of description of this mode. It is possible, though, to attribute another meaning to this pattern, which is undoubtedly located at the generic level of description (recall the discussion of the generic folding for Lydian in paragraph 20). In order to clarify this argument, we depart from the familiar attributes “major” and “minor” and replace them by the less misleading attributes primary and secondary instead. Insofar as we attribute primacy to the ascending perfect fifth (P5) with respect to the subordinate descending fourth (−P4), we may transfer this distinction to the step intervals. The primary ascending step interval is composed of a positive number of ascending fifths and a positive number of descending fourths. The secondary ascending step interval is composed of a negative number of ascending fifths and a negative number of descending fourths. Recall that the primary “major” step is the positive sum P5 + (−P4), while the secondary “minor” step is the negative sum −(2 P5 + 3 (−P4)).
[44] A closer examination of the degenerate fifth-generated seven-tone scale shows that the step-interval pattern aaabaab emerges even in the case when the primary and secondary step intervals have the same specific pitch-height value. The generator of this scale is 4/7. The specific height values constitute the seven-tone equal temperament, with
[45] A peculiarity of the degenerate specific scale is the fact that its origin g0 = 0 of the generation sequence is not uniquely determined. Any other entry may serve this role. But for each choice of an origin the modal interdependence between origin and finalis is clearly determined. If h0 = 0 is maintained while the role of the origin is changed, another of the seven modes results. The set {h0, h1, ..., h6} is invariant under transposition (i.e., addition) by 1/7 mod 1 and hence all modes with the same finalis share the same specific pitch heights modulo the octave. This does not affect the unique step-interval patterns for each mode. On the generic level of description the five primary and two secondary step intervals are clearly identified in each case. The degenerate status thus results in a modal ambiguity due to the coincidence of the seven transpositions on the specific level of description. It does not result, however, in a conceptual dilemma on the generic level. Another sensitive point of this argumentation is the distinction between ascending fifths and descending fourths. Recall that the difference between these intervals is the octave. A subsequent paragraph provides a geometric motivation for the preservation of the octave as a generic interval apart from the prime. The distinction between octave and prime may even be maintained for the standpoint where the two tones at the octave distance are identified. The underlying geometric concept and its algebraic counterpart are homonymously called torsion.
[46] A geometric digression will illustrate this position. We should bear in mind, though, that the usage of a continuous torus-model with continuous curves in the role of height and width trajectories serves first of all an illustrative function, auxiliary in terms of the music theory. A cautious balance of the music-theoretical meaning of the winding numbers(14) of these curves is given below. The trajectories in subfigures 1–6 of Figure 8a are known as torus knots. From a topological point of view they are characterized by the number p of windings around a horizontal circle inside the torus, and by the number q of windings around a vertical line through the hole in the torus. In accordance with our music-theoretical interpretation we may call p the number of height windings and q the number of width windings. A trajectory with exactly one height winding (p = 1) shall be called a height trajectory. This applies to the three trajectories 1, 3 and 5 on the left side of Figure 8a. They differ in the number of width windings as follows: The primary height trajectory (1) does two width windings, while the secondary height trajectory (2) does five width windings. Closer inspection shows that the seven generic tones are connected in the same order, but in opposite orientation with respect to the width parameter. This is reminiscent of the distinction between primary and secondary steps in paragraph 43. One could therefore further presume that the width winding number of the secondary height trajectory is −5 rather than +5. The width-bounced height trajectory in subfigure 5 has width winding number 0 and exemplifies geometrically the scale step pattern aaabaab. It is composed piecewise of step-segments from the primary and secondary height trajectories. Analogously, a trajectory with exactly one width winding (q = 1) shall be called a width trajectory. Subfigures 2, 4 and 6 show the primary, secondary and height-bounced width trajectories of the Lydian mode. Note that it is the generic tone in the front, being situated at the meeting point of the horizontal and vertical cuts in subfigures 5 and 6, which serves both as finalis and origin of the Lydian mode. The primary width trajectory consists of ascending and forward oriented fifth-segments and makes four height windings (p = 4). The secondary width trajectory consists of descending and forward oriented fourth-segments and makes three height windings in the opposite direction (p = −3). In Figure 11 (discussed in paragraph 55), we assemble all the height trajectories of the seven modes as a “mechanical flow” on the torus, and likewise we assemble a “mechanical width flow” on the torus of all the width trajectories of the seven modes.
[47] The torus knots are evocative of Shepard’s Figure 4, displaying a “double helix wrapped around a torus in four dimensions” (Shepard 1982). It consists of two disjoint torus knots with one height winding and one width winding each. The knots represent whole tone scales in a chromatic ambient space that are embedded into a continuous auxiliary ambient space. We are uneasy, however, with Shepard’s count of the number of dimensions in his geometrical models. Shepard refers to ambient real vector spaces of dimensions 4 and 5, rather than to the 2-dimensional inner geometry of the torus and the helical tube as manifolds.(15)
Figure 8b. Geometric interpretation of the primary step interval as a tangent vector (2,1) to the torus at some base point
(click to enlarge)
[48] How does our geometric digression illustrate the ambivalent role of the generic octave interval? It is clear that the height winding number counts octaves. But what represents the octave as such? This question is all the more urgent, as the representation of the generic intervals by arcs on the torus is not justifiable from a music-theoretical point of view. Literally speaking the arcs would represent generic width/height “glissandi” of various slopes. Even on the specific level of description such an interpretation would be more than dubious, not to mention on the generic level. If the two possible arcs between two generic tones have no proper music-theoretical meaning, what then is the advantage of the illustrations in Figure 8a? How does it illustrate the music-theoretical difference between primary and secondary step intervals? The answer arises from a geometrical interpretation of the concept of a musical interval as a tangent vector. The primary and secondary height and width trajectories can be described as integral curves, resulting from a smooth tangent vector field on the torus. Tangent vector fields reside in the tangent bundle consisting of flat tangent planes at each point of the torus. To define a tangent vector field one chooses one single vector in every single tangent space. (See Figure 8b.)
[49] This geometrical interpretation is somewhat reminiscent of David Lewin’s GIS model. Lewin postulates a map
[50] After a tentative understanding of these illustrative comments we may leave the continuous spaces and curves behind and finish our clarification of the concept of a generic interval. Inasmuch as the tone lattice ![]() 7 ×
7 × ![]() 7 is embedded into the continuous two-dimensional torus, there is a discrete “tangent-bundle” (
7 is embedded into the continuous two-dimensional torus, there is a discrete “tangent-bundle” (![]() 7 ×
7 × ![]() 7) × (
7) × (![]() ×
× ![]() ) embedded into the four-dimensional tangent bundle of the torus. Each generic discrete interval space is a copy of the free lattice
) embedded into the four-dimensional tangent bundle of the torus. Each generic discrete interval space is a copy of the free lattice ![]() ×
× ![]() . The target tones of octaves (0, 7) and augmented primes (7, 0) coincide with their base tones, while both generic intervals remain distinct from the generic prime (0, 0).
. The target tones of octaves (0, 7) and augmented primes (7, 0) coincide with their base tones, while both generic intervals remain distinct from the generic prime (0, 0).
Figure 9. Two ways of localizing the tones of the Ionian mode relative to the Lydian mode
(click to enlarge)
[51] The exposition that follows yields a modal refinement of the generic level of description. It takes into account the distinction (in height) between prime and octave and it characterizes the augmented prime as being generically different (in width) from the perfect prime. Every single mode consists of seven tones, which can be denoted by seven points on the discrete torus ![]() 7 ×
7 × ![]() 7. As soon as one point is given, we may construct the other six as well as the folding and step-interval trajectories. But from the anatomy of single modes it is not clear how the tones from two different modes should be chosen simultaneously. Figure 9 displays two alternative choices for the tones of an ascending Ionian mode. The usage of identical tone names {C, D, E, F, G, A, B} is a simplification which is going to be replaced further on (see Figure 12).
7. As soon as one point is given, we may construct the other six as well as the folding and step-interval trajectories. But from the anatomy of single modes it is not clear how the tones from two different modes should be chosen simultaneously. Figure 9 displays two alternative choices for the tones of an ascending Ionian mode. The usage of identical tone names {C, D, E, F, G, A, B} is a simplification which is going to be replaced further on (see Figure 12).
[52] What both choices have in common is that the Ionian finales and origins share exactly one coordinate with those of the Lydian mode. The two choices differ, though, in the roles of width and height coordinates. In the case of a fixed fundamental domain the Lydian and Ionian origins
[53] The following procedure shows how to calculate the width and height coordinates with respect to the movable fundamental domain directly from the words yxyxyxy and aabaaab. The coordinates are displayed in the table below for reference.
| Tone | F | C | G | D | A | E | B |
| Width | −1 | 0 | 1 | 2 | 3 | 4 | 5 |
| Tone | C | D | E | F | G | A | B |
| Height | −3 | −2 | −1 | 0 | 1 | 2 | 3 |
In the height table the values increase stepwise from −3 to 3. How can we know them directly from the folding yxyxyxy? If we knew in advance that each ‘x’ represents a fifth up and each ‘y’ represents a fourth down—that is, each ‘x’ is four steps up, and each ‘y’ is three steps down—we could simply replace every occurrence of the letter ‘x’ by the number 4 and every occurrence of ‘y’ by −3 to obtain the integer sequence (−3, 4, −3, 4, −3, 4, −3) as an evaluation of the abstract word yxyxyxy. From this sequence we may incrementally calculate generic heights as partial sums, starting from the value 0 for the tone F. This yields the height values as given in the height table, but sorted in the order of tones as given in the width table:
A strictly analogous calculation can be made with the word aabaaab. If we knew that every ‘a’ represents a whole step up with generic width 2 and that every ‘b’ represents a half step up with generic width −5, we could evaluate the word aabaaab in terms of the integer sequence (2, 2, −5, 2, 2, 2, −5). Calculating partial sums we would obtain the width values in step order: (0, 2, 4, −1, 1, 3, 5, 0). In subsection 2.3, which is dedicated to investigating the interdependence between folding patterns and step interval patterns, we will come across this calculation again, in a situation of greater generality.
Figure 10. Folding trajectories (left) and step-interval trajectories (right) of the seven diatonic modes within a fixed fundamental domain
(click to enlarge)
Figure 11. Folding trajectories (left) and step-interval trajectories (right) for the seven diatonic modes with a movable fundamental domain
(click to enlarge)
Figure 12. Two concrete manifestations of the family of seven modes: the common origin family (left) and the common finalis family (right)
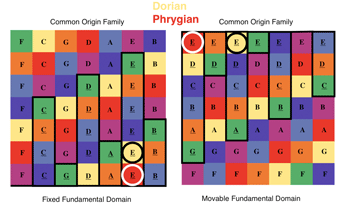
(click to enlarge)
[54] Both ways of localizing the Ionian mode relative to the Lydian mode can be extended to all seven diatonic modes. In either case we obtain a tiling of ![]() 7 ×
7 × ![]() 7 into seven tiles. The construction in the fixed fundamental domain {0, 1, ..., 6} × {0, 1, ..., 6} is easier to figure out. All folding trajectories start at width value 0 and all step-interval trajectories start at height value 0 (see Figure 10).
7 into seven tiles. The construction in the fixed fundamental domain {0, 1, ..., 6} × {0, 1, ..., 6} is easier to figure out. All folding trajectories start at width value 0 and all step-interval trajectories start at height value 0 (see Figure 10).
[55] In the case of the movable fundamental domain we assume that for every mode its origin has height 0 and that its finalis has width 0. Figure 11 illustrates this in terms of seven square-shaped fundamental domains. Every folding trajectory starts from the width axis (i.e., height 0) and returns to it. Every step-interval trajectory starts from the height axis (width 0) and returns to it. The scattered trajectories can be aligned very nicely modulo 7, i.e., in a fundamental domain for the discrete torus ![]() 7 ×
7 × ![]() 7. Unlike the labyrinthine arrangement of the trajectories in Figure 10, the collected trajectories in Figure 11 are reminiscent of a flow of a vector field.
7. Unlike the labyrinthine arrangement of the trajectories in Figure 10, the collected trajectories in Figure 11 are reminiscent of a flow of a vector field.
[56] The generic family of the seven modes can have several concrete manifestations. Most prominently there are two such families, which are defined by a common origin or by a common finalis. The origin F is shared by the seven “white-note” modes: C-Ionian, D-Dorian, E-Phygian, F-Lydian, G-Mixolydian, A-Aeolian, B-Locrian. The constitution of this family involves octave displacements of individual tones. The finalis F is shared by the seven “F-modes”: F-Ionian, F-Dorian, F-Phygian, F-Lydian, F-Mixolydian, F-Aeolian, F-Locrian. The constitution of this family involves alterations of individual tones. Figure 12 displays both families, the common origin family and the common finalis family in both views, namely fixed fundamental domain vs. movable fundamental domain. The underscored notes lie in the octave register below their unmarked counterparts. The configuration of registral displacements in the common origin family is strictly analogous to the configuration of flats in the common finalis family. The arrangement of alteration signs (flats) represents key signatures of modes with F as finalis; there is no accepted term, but we may, analogously, speak of registral signatures for the modes with F as common origin. For example, in Figure 12, yellow squares are occupied by Dorian mode elements. The key signature of F-Dorian is three flats, representing the number of displacements in the width direction between the shared finalis, F, and the new origin,
[57] Group extensions of the generic width-height space are investigated in Noll 2011. These include chromatic alteration as well as registral shift by octaves. The extensions are refinements within the generic level of description. No specific pitch height or width is involved. Different conjugacy classes of well-formed modes correspond to different addition laws of the group extensions. This approach is reminiscent of Eric Regener’s mathematical approach to musical notation (Regener 1973), whose model can be identified with a subgroup of index 7 (i.e., having 7 cosets) within a full extension of the diatonic width-height space. What our approach adds to Regener’s is the idea of moving this subgroup around within the diatonic width-height space, and of interpreting the cosets as modes. In conclusion, the considerations of generic height and width dimensions presented in this subsection also motivate a formalization of the Toncharakter in terms of generic width coordinates. In subsection 3.1 we take advantage of these proposals in defense of Handschin’s concept against criticism by Dahlhaus.
2.3 Plain Adjoints of Well-Formed Words
[58] When calculating the generic height values from the abstract word yxyxyxy, we first substitute the two letters x and y with the integers 4 and –3, respectively. How can we know these values? The number 4 is the step size of the fifth. But it is also the number of occurrences of the letter ‘y’ in the word yxyxyxy. It is easy to see that this is not an accidental coincidence. The primary surface interval of the scale folding is also the primary background interval of the scale step pattern. This implies that all tones below the divider of the scale must be reached by a downward interval of the scale folding. Each tone below the divider is the starting point for exactly one of the step intervals that contribute to the step size of the interval represented by x. An analogous argument applies to the step size of the downward interval of the scale folding, represented by y. The step size –3 of the downward-folded fourth coincides—up to minus sign—with the number of tones from G to B, i.e., of all tones above and including the divider, but excluding the terminal tone of the step scale. These tones are exactly the ones that are reached by an upward-folded interval. In other words, by multiplying the number of occurrences of the letter ‘x’ by –1 we obtain the step-interval size of the downwards-oriented folding interval y.
[59] This observation turns out to be very useful, as we can evaluate any given word on two letters directly, that is, we can construct a function from the word to the set of integers, ![]() :
:
Definition 1: Let w denote a word of length n over the ordered two-letter alphabet A = {x, y | x < y} (the ordering simply recognizes the lexicographic precedence of x before y; it says nothing about the “size” of x or y). Let |w|x and |w|y denote the numbers of occurrences of the letters x in w and y in w, respectively, and for any index k = 1, ... n let wk denote the letter in w which is at index k. Consider the following evaluationevw: {x, y} → of the alphabet, given by evw(x) = |w|y and evw(y) = −|w|x.
- The balanced evaluation of the word w is the sequence of evaluations of its letters (evw(w1), ..., evw(wn)).
- The balanced accumulation of w is the sequence (s0(w), s1(w), ..., sn-1(w)) of the partial sums of the balanced evaluation, where
s0(w) = 0,
s1(w) = evw(w1),
s2(w) = evw(w1) + evw(w2),
...
sn-1 = evw(w1) + ... + evw(wn-1).
[60] The total sum sn = evw(w1) + ... + evw(wn) is always zero: the number of occurrences of the positive value evw(wj) = |w|y among the n summands in sn is exactly |w|x. Likewise, there are exactly |w|y negative summands of the type evw(wj) = −|w|x. Thus the total sum sn can be expressed as sn = |w|x|w|y − |w|y|w|x = 0. This property legitimates the term balanced evaluation.
[61] We transfer the same definition to the ordered alphabet {a < b} and use the same notation as above. At this level of abstraction there is no reason to distinguish qualitatively between height and width, but it is useful to keep the two-letter words for foldings and for scale step patterns distinguishable.
[62] Our next goal is to formulate the duality directly on words. To that end we need to characterize the appropriate class of two-letter words for which the duality works. If we choose a two-letter word at random—say, yyxxy—we may be disappointed by the distribution of the values in the accumulation. In this example we obtain the sequence of partial sums (0, –2, –4, –1, 2) from the balanced evaluation (–2, –2, 3, 3, –2). Unlike the generic height and width sequences of the Ionian mode this sequence has gaps in the re-ordered list of values: between –4 and –2, and between 0 and 2. Words shall be called well-formed if their balanced accumulations have n consecutive different values, that is, n distinct values without gaps between them:
Definition 2: Let w denote a word of length n over the two-letter alphabet {x < y} and let m denote the minimal value of its balanced accumulation. The word w is called well-formed, if the set of all values of its accumulation equals {m, m+1, ..., m+n−1}, i.e., a complete set of consecutive residues modulo n.
[63] The choice of the term “well-formed word” deserves a comment. Under close inspection the above definition turns out to be equivalent to a well-established concept in the mathematical subfield combinatorics on words. Such words are either Christoffel words or conjugates of them, i.e., Christoffel words up to cyclic letter permutations. (Christoffel words are the images of a|b under compositions of G, D~, and E, i.e., generalizations of Lydian modes.) Notwithstanding our great respect for the classical work of Elwin Bruno Christoffel, we feel that the nominal phrase “conjugate of a Christoffel word” would be a cumbersome term for frequent use in music theory.(17) The choice of the attribute “well-formed” is motivated by the very close connection to the theory of well-formed scales. This becomes apparent in the light of the following mathematical fact:
Linearity Lemma: Let w denote a well-formed word of length n and consider the function f:n →
n which maps each residue class k mod n to f(k) = sk(w) mod n, i.e., to the reduction mod n of the corresponding coefficient of the balanced accumulation. The map f is a linear automorphism of the additive group
n and satisfies f(k) = k s1(w) mod n.
Proof: For the reduction mod n of the accumulated evaluation it makes no difference if in the balanced evaluation the letter y is substituted for |w|y or for −|w|x as both numbers represent the same residue class mod n. Thus:
(s0(w), s1(w), ..., sn-1(w)) = (0, |w|y, 2|w|y, ... (n−1)|w|y).
[64] The linear automorphism f: ![]() n →
n → ![]() n is the core of the generic side of well-formed scale theory (see Carey and Clampitt 1989).(18) Recall that in the diatonic scale every instance of a fifth (perfect or diminished) has the same generic step size, namely 4. As an illustrative example for the linearity lemma, we reduce the accumulated evaluations for the Ionian scale folding and the Ionian step pattern mod 7:
n is the core of the generic side of well-formed scale theory (see Carey and Clampitt 1989).(18) Recall that in the diatonic scale every instance of a fifth (perfect or diminished) has the same generic step size, namely 4. As an illustrative example for the linearity lemma, we reduce the accumulated evaluations for the Ionian scale folding and the Ionian step pattern mod 7:
(0, 2, 4, −1, 1, 3, 5) mod 7 ≡ (0, 2, 4, 6, 8, 10, 12) mod 7 ≡ (0, 2, 4, 6, 1, 3, 5).
[65] As a consequence of the linearity lemma there is a straightforward method to associate with each well-formed word w a plain adjoint well-formed word w* as shown in Figure 13 below. (NB: We include the divider to connect to the discussions above and below, but it is not part of the present construction.) Figure 13 provides a mnemonic for the calculation of the adjoint word. The steps of the calculation are graphically displayed from top to bottom. On the left side we have in detail:
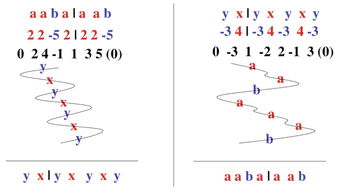
1st step: In the top row write down the original word: a a b a a a b.
2nd step: Beneath every a write the number of b’s in the original word and beneath every b write minus the number of a’s. This results in the second row: 2 2 −5 2 2 2 −5.
3rd step: Calculate the partial sums of this number sequence starting from 0 and write the results in the third row between the entries of the second row: 0, 0+2 = 2, 2+2 = 4, 4−5 = −1, −1+2 = 1, 1+2 = 3, 3+2 = 5, 5−5 = 0 which yields: 0 2 4 −1 1 3 5 (0).
4th step: The theory guarantees that the partial sums constitute a contiguous set of integers. The zigzag trajectory beneath the third row traces their ascending order against their positions within the third row. Starting from the position of the minimum −1 the trajectory takes the following route:zag (pass 3 positions to the left, from the position of −1 to the position of 0)
zig (pass 4 positions to the right, from the position of 0 to the position of 1)
zag (pass 3 positions to the left, from the position of 1 to the position of 2)
etc.Once the maximum value 5 is reached the trajectory returns with a final zag to the position of the minimum −1. The position of the ultimate partial sum (0) is not taken into account; therefore, it is written in parentheses.
5th step: The shape of the zigzag trajectory yields a two-letter word: Every “zig”-swing (to the right) is encoded in terms of a letter “x” and every “zag”-swing (to the left) encoded by an instance of “y.” The resulting word is written down in the bottom row: yxyxyxy.
The right part of Figure 13 shows how the same procedure converts the word y x y x y x y into its plain adjoint a a b a a a b. In this case x plays the role of the primary letter and is substituted for the number 4 of the occurrences of the secondary letter y. The secondary letter is replaced by −3 (i.e., minus the number of occurrences of the primary letter x).
[66] The basic idea of this method is to reinterpret the actual order of the numbers m, m+1, ..., m+n−1 in the balanced accumulation (s0(w), s1(w), ..., sn-1(w)) as a folding pattern. For each number k we find its successor either to the right or to the left. While successively moving through all values—from m to m+1, from m+1 to m+2, and finally from m+n−2 to m+n−1 and from m+n−1 back to m we make n binary decisions between a = “to the right” or b = “to the left” and thus construct a two-letter word. To be more precise, let 0 < p, q < n denote the standard representatives mod n of the multiplicative inverses |w|y−1 mod n and |w|x−1 mod n. It is necessarily the case that the two numbers p and −q are the possible position distances between any two successive numbers k and k+1 in the balanced accumulation. From the linearity lemma we infer that the residue mod n of any of these position distances is the multiplicative inverse mod n of the residue class mod n shared by the two numbers |w|y and −|w|x. We also know that the whole sequence (s0(w), s1(w), ..., sn-1(w)) occupies the range of exactly n successive integers. Thus, the actual position distances need to be either: p and −q, or −p and q. Closer observation shows that the first possibility is the right one.
[67] A clear link between well-formed scale theory and well-formed mode theory is given by virtue of the linear automorphism f: ![]() n →
n → ![]() n with f(k) = ks1(w) mod n. This map can be refined into a mode-sensitive affine automorphism fw of
n with f(k) = ks1(w) mod n. This map can be refined into a mode-sensitive affine automorphism fw of ![]() n which translates the minimum of the values sk(w) to the origin 0 ∈
n which translates the minimum of the values sk(w) to the origin 0 ∈ ![]() n. It maps generic height coordinates into associated generic width coordinates mod n (cf. Figure 9, movable fundamental domain). The adjoint word w* of a well-formed word w is uniquely characterized by the fact that fw* = fw−1. (For a detailed discussion of the (plain) adjoint and a twisted variant see Domínguez et al. 2009.) We may, then, in the appropriate contexts, identify modes of well-formed scales and well-formed words. The scale step patterns of modes of a well-formed scale and their associated folding patterns are captured by well-formed words and their plain adjoints.
n. It maps generic height coordinates into associated generic width coordinates mod n (cf. Figure 9, movable fundamental domain). The adjoint word w* of a well-formed word w is uniquely characterized by the fact that fw* = fw−1. (For a detailed discussion of the (plain) adjoint and a twisted variant see Domínguez et al. 2009.) We may, then, in the appropriate contexts, identify modes of well-formed scales and well-formed words. The scale step patterns of modes of a well-formed scale and their associated folding patterns are captured by well-formed words and their plain adjoints.
3. Thoughts on Jacques Handschin’s Tone Character
[68] The present article argues in favor of a concept of tone relation, where two dimensions, tone height and tone width, are tightly interconnected. In addition to the mathematical facts about the underlying duality of these dimensions and their music-theoretical interpretation as given in section 2, we wish to revisit a historical thread from discourse about closely related ideas.
[69] Jacques Handschin provides us with a highly ramified argumentation—re-reading medieval music theory against the concerns of nineteenth- and early twentieth-century music theory and tone psychology (see Maier 1991)—in favor of a central thesis: The perfect fifth is an elementary component in the constitution of musical tone relations (Handschin 1948). Handschin emphasizes the fact that different diatonic scale degrees have different musical qualities and explains the emergence of these qualities on the basis of their ordering in the chain of fifths. The position of a tone in the chain F–C–G–D–A–E–B determines its tone character. Tone height and tone character are conceived as two mutually intersecting dimensions in the constitution of musical tone relations, and Handschin tends to give even more weight to the tone character dimension, referring to it as “the inner, truly musical one,” as cited in the Introduction.
[70] Carl Dahlhaus, in his classification of justifications of music-theoretical systems, characterizes Handschin as a music-theoretical “ontologist,” who starts with the declaration of a tone system prior to the aesthetic study of a musical work. In his concrete arguments about Handschin’s proposals Dahlhaus is open-minded enough not to discard explanatory ambitions on the level of tone systems from the outset. On the contrary, in his Untersuchungen über die Entstehung der harmonischen Tonalität he is astutely engaged in many ramified arguments. For example, the reason he gives to disregard the hexachord as a tone system anticipates the modern concept of coherence in scale theory (Dahlhaus 1990, 172).
[71] Two critical and substantial arguments in connection with the tone character are particularly attractive for reconsideration in light of the word-theoretic approach. We discuss them in the subsequent subsections 3.1 and 3.2.
3.1 First Objection by Dahlhaus
[72] In one passage Dahlhaus points to the incapability of the tone character to distinguish between different modal meanings of the same tone within the same underlying diatonic system:
It could hardly be denied that e changes its meaning when it is introduced as the first degree of an e-mode and then continued as the second degree of a d-mode. And the thesis that the character of e is still primarily marked by its position in the circle of fifths can only be salvaged by adding that a tone’s character is concealed and modified by the mode, but not invalidated by it (Dahlhaus 1990, 153–54; 167–68 [1990]).
[73] Dahlhaus correctly paraphrases Handschin’s position with respect to the modal distinctions (e.g., see Handschin 1948, 55–56). Therefore—not without reason—he adds a small attack against the significance of tone character: “Yet it must be objected that in a music theory that seeks to describe phenomena, a modification that conceals a tone’s character is indistinguishable from an actual change of character.” This evocation of a pretended methodological problem can be regarded as a mere rhetorical maneuver. But Dahlhaus does detect a sore spot in Handschin’s theory. Firstly, tone character pretends to grasp the differences between musical tones, even if they sound the same. Secondly, tone character is especially sensitive toward the diatonic scale, as it can be arranged as a chain of fifths. Thirdly, the diatonic modes are relevant musical exemplifications of the diatonic system; and yet, tone character does not distinguish the different modal meanings of tones, which sound the same. This is indeed unsatisfying. In the following paragraphs we explore two possibilities to counter Dahlhaus’s criticism.
Figure 14. Minimal rotation of the scale step pattern corresponds to a minimal letter transposition
(click to enlarge)
[74] The subtlety of the word-theoretic level of description provides an immediate argument. Figure 14 shows the ascending scale step patterns and forward folding patterns for the D-Dorian and E-Phrygian modes. Instead of merely measuring the distance of the tone E from the origin F in the chain of fifths, we may characterize the tone E with respect to the complete folding patterns xyyxyxy and xyxyyxy in terms of the two prefixes of length five: xyyxy and xyxyy. As the prefixes do not coincide they can be said to represent different tone characters. With respect to the scale step patterns the story is less subtle. In the D-Dorian mode the tone E corresponds to the prefix a of length 1 of the word abaaaba, while it corresponds to the empty prefix of the word baaabaa. Figure 14 also illustrates how the octave shift +P8 of the lower note D into the higher
[75] These two kinds of derivations differ from each other from a phenomenological point of view. The rotation affects the pattern as a whole and moves it around. The letter transposition affects the pattern only locally. But the two phenomenological perspectives are not mutually exclusive. The minimal rotation abaaaba → baaabaa can be decomposed into two minimal letter transpositions, abaaaba → abaabaa → baaabaa, and the minimal letter transposition xyyxyxy → xyxyyxy can be decomposed into two minimal rotations, xyyxyxy → yxyyxyx → xyxyyxy. Yet, from a phenomenological point of view it is the minimal interpretation in each case that deserves to be acknowledged.
[76] This may have a consequence for the choice of generic coordinates. Recall from subsection 2.2 (paragraphs 51–55) that we distinguish two alternative encodings of the seven modes in terms of generic coordinates: fixed vs. movable fundamental domain. In the case of a global rotation it is more plausible to shift the generic coordinates altogether by the amount of the rotation. In the case of a local transposition it is more plausible to maintain the generic coordinates against which the transposition takes place. The latter argument therefore entails a preference for the fixed fundamental domain (see Figure 9). In application to the width coordinates of the tone E this choice seems to literally support Dahlhaus’s objection, because the common width coordinate alone does not distinguish the modal meanings of the tone E. But instead it is precisely the width parameter that maintains the generic contiguity of the two modes. We will look at this more closely.
[77] An implicit detail in Dahlhaus’s objection is that the argument includes a second part that—at first glance—is a matter of course. The tone denoted by “E” has the same pitch height, no matter whether it has the meaning of the second degree of a D-mode or of the first degree of an E-mode. The complete argument could be stated by also including the following: It could hardly be denied that the tone denoted by “E,” while maintaining its specific pitch height, changes its meaning when it is introduced as the first degree of an E-mode and then continued as the second degree of a D-mode. What we cannot take for granted, though, is that the generic height is maintained. We can verify on the basis of Figure 12 that for common-origin modes within the fixed fundamental domain representation, the height coordinates of the tone E in D-Dorian and E-Phrygian are different. We focus on the encircled small tone squares in the left checkerboard in Figure 15 (which reproduces the upper-left checkerboard in Figure 12). In this representation the problem is not to distinguish the two meanings of the “same” tone E. The problem is rather to trace the “sameness” of the two instances of E. Obviously, it is the identical width parameter that bails us out.
[78] With respect to the movable fundamental domain representation of the seven modes, the rebuttal of Dahlhaus’s objection would be more direct. To the disadvantage of the phenomenological argument about the minimal letter rotations (paragraph 75) one could simply postulate that an identity in specific pitch height must imply an identity in generic pitch height. For the common origin family this postulate is matched by the movable fundamental domain representation. See the encircled tone squares in the right checkerboard in Figure 15. The width coordinates 0 and 2 disambiguate the two modal meanings of E in this interpretation.
[79] We can only speculate whether Handschin himself would have been in favor of one or the other line of argument. His own notation of tone character in terms of integer powers of a generator x, such as in the D-centered encoding x−3, x−2, x1, x0, x1, x2, x3, provides a loophole toward the second possibility, which he does not exploit. In this particular choice of the neutral (or central) character x0, Handschin is attracted by D as a center of symmetry (Handschin 1948, 5–6). But he does not identify this encoding with the Dorian mode, and, for example, identify x−1, x0, x1, x2, x3, x4, x5 with the Ionian mode. In Handschin’s deliberations on the interpretation of the symbol x0, he speaks of the simplicity of this tone. This property is associated with the origin of the diatonic scale (or set), rather than with a particular finalis.
[80] In the common finalis family under both interpretations, the roles between what is moved and what remains fixed are exchanged. Figure 16 opposes the connection between C-Ionian and D-Dorian to the connection between C-Lydian and C-Ionian. The opposition includes the roles of the octave shift (+P8) versus the augmented prime shift (−A1), as well as the phenomenological involvement of the height and width parameters. C-Ionian is transformed into D-Dorian with a rotation of the scale step pattern and a local transposition in the scale folding. In contrast, C-Lydian is transformed into C-Ionian with a local transposition in the scale step pattern and a rotation of the folding pattern.
[81] Our ramified argument against Dahlhaus’s criticism refers to two different levels of description. On the word-theoretic level, the Toncharaktere of E in E-Dorian and E-Phrygian correspond to different prefixes of the associated folding patterns, respectively. On the level of generic width- and height-coordinates, we claim that the 49 tone meanings of the seven degrees in the seven modes are in one-to-one correspondence with the 49 elements in ![]() 7 ×
7 × ![]() 7. Thereby we distinguish between the fixed and movable fundamental domain representations (cf. Figures 10 and 11). In the latter case the Toncharaktere of E in E-Dorian and E-Phrygian are different (Figure 15, right side). In the former case, though, they coincide and thus seem to support Dahlhaus’s objection. But in this case we argue that, in turn, the generic height values are different (Figure 15, left side) and that therefore precisely the incidence of the generic width values is needed in order to trace a commonality between the two tone meanings.
7. Thereby we distinguish between the fixed and movable fundamental domain representations (cf. Figures 10 and 11). In the latter case the Toncharaktere of E in E-Dorian and E-Phrygian are different (Figure 15, right side). In the former case, though, they coincide and thus seem to support Dahlhaus’s objection. But in this case we argue that, in turn, the generic height values are different (Figure 15, left side) and that therefore precisely the incidence of the generic width values is needed in order to trace a commonality between the two tone meanings.
3.2 Second Objection by Dahlhaus
[82] The second target in Dahlhaus’s critique is the characterization of the semitone (“intensiver Schritt,” in Handschin’s terminology) in terms of the large inner character difference of five fifths: “The fact that the whole tone is defined as the difference between a fourth and a fifth, the major third as a combination of two whole tones, and the semitone as the difference between a major third and a fourth, does not imply that the fifth-relation on which the system is based is actually present in the ramifications of a derivation of intervals as three, four, or five fifths” (Dahlhaus 1990, 167–68 [1990]). And:
One can mentally reconstruct the intervening stages at the end of which stands the semitone. Musical perception, however, is limited. For it, the premises vanish in the actual outcome. Upon hearing an interval, one can make oneself aware of the last stage in its derivation, but not the earlier stages. Thus one can think at the same time of the fourth and fifth in reference to the whole tone, or of the doubling of the whole tone in reference to the major third, but not of four fifths in reference to the major third” (168).
[83] A psychological aspect shall only be mentioned in passing here. Dahlhaus misses a statement of Handschin’s that in fact addresses his argument about the difficulty of consciously comprehending the compound fifth-kinship for each single interval: “We must also say that tone characters are connected, to a greater extent, with unconscious tone perception and evaluation; tone heights, on the other hand, with the ‘conscious.’”(19)
[84] Moreover, in using the phrase “fifth-relation on which the system is based,” Dahlhaus seems to concede the premise of Handschin’s argument, but is not willing to explore some of its implications. First of all, the line-of-fifths measure is an invariant for specific intervals: it is fundamental that this measure is consistent. For example, any augmented sixth, modulo the octave, is a displacement of 10 moves along the line of perfect fifths. When the well-formedness condition is added, that is, within the context of a proper scale system, specific intervals have consistent generic descriptions as well. They consistently span the same number of scale step intervals; conversely, generic step intervals are, modulo the octave, compounds of a consistent number of generic fifths. Furthermore, within a given generated scale system, the multiplicity of an interval varies inversely with its measure in perfect fifths: in a fifth-generated scale system with N elements, if k is the fifth-measure of an interval, 0 < k < N, N−k is the multiplicity of that interval. This is equivalent to the common-tone hierarchy of diatonic sets, attributable to the circle of fifths, to which Babbitt drew significant attention. In turn, this distance between diatonic sets or triadic roots is what is referred to as harmonic distance.
[85] But Handschin’s tone character does not depend on the flowering of triadic tonality: he considers that it obtains already in the purely melodic environment of plainchant. The intensity, to use Handschin’s term, of a diatonic interval is correlated with its rarity: by the remark above, rarity in turn is correlated with the additive inverse modulo 7 of the interval’s associated displacement in perfect fifths. The uniqueness of the tritone, with its intense identity, is associated with a displacement of 6 fifths; and the semitone, Handschin’s intense step, of multiplicity 2, with 5 fifths. This is merely a correlation, which would hold in the case of any system generated by N fifths. The sign of a proper well-formed scale system is that the multiplicative inverses modulo N also express a musical generality, an inverse relation between multiplicities of step intervals and spans of generating intervals (Carey and Clampitt 1996a). For example, in the diatonic system, the semitone multiplicity 2 is the multiplicative inverse of the span in step intervals of the perfect fifth, 4: 2−1≡4 mod 7. This is the basis for the duality between scale step patterns and folding patterns explored in this paper.
[86] Dahlhaus’s alternative proposal for a model of the diatonic is modally cast:
The simple, “perfect” consonances are given directly: octave, fifth, and fourth. They form the framework of an octave scale(d–g–a–d ′ ore–a–b–e ′). On the other hand, the basic melodic interval is the whole tone—as the difference between the fifth and the fourth, it is a derived interval of the first rank, but one consolidated to an independent significance and comprehensibility . . .
In consequence, the principle which one must take as the basis for the concrete nature of the diatonic scale is the filling out by whole tones of a fourth-fifth-octave framework. Yet the result of this filling out is a mode. Or formulated another way, the diatonic scale, if one constructs it by filling out a fourth-fifth-octave framework, appears in modal form. In the fourths of this framework, the whole tones are inserted at the bottom (c–d–e–f), at the top (e–f–g–a), or the one whole tone at the bottom and the other at the top (d–e–f–g) (Dahlhaus 1990, 168 [1990]).
[87] Dahlhaus at first seems to overlook the fact that his proposal implies a combinatorial freedom for 32 = 9 possible modes instead of 7: two of them are ill-formed, namely baaaaab and aababaa. He addresses this objection by conceding the correspondence between the fifth-relationship and the whole step: “Since a whole tone implies two intervals of a fifth, the result of the filling out of a fourth-fifth-octave framework with whole tones is always a diatonic scale which in the abstract can be attributed to the chain of fifths from f to b” (Dahlhaus 1990, 168 [1990]). He goes on to say that, therefore, positing one of the ill-formed tetrachord-fillings would implicitly necessitate a contradictory chromatic element in the other tetrachord: “The whole tones
The construction of the older, modal diatonic scale from tetrachords is historically the earliest and objectively the most firmly established method. In the first place, it takes into account the fact that the conception of remote fifth-relations is in need of support. The semitone, whose definition as the fifth fifth is a flimsy abstraction, becomes intelligible if one understands it within the terms of a tetrachord as the intervallic remainder between a fourth and two whole tones (Dahlhaus 1990).
[88] Dahlhaus plays two derivations of the diatonic modes off against each other, tacitly conceding that they are not true alternatives, but then proceeding as if they are. He rejects the idea of iterated fifth-kinship in favor of concatenations of filled-in tetrachords. But in fact there are mathematical dependencies between the two derivations, which render the alternatives merely apparent. The following are two (related, but here separated) lines of argument.
[89] One interesting point is that, if Dahlhaus had—for example—included the Guidonian affinities as an additional criterion for the connection between the two tetrachord-fillings, he would have implicitly included the well-formedness condition that—as we have seen—implies the well-formed foldings. The three concatenations of disjunct tetrachords of the same species
[90] The second point to be made is to observe that the transformational reconstruction of the twelve Glarean modes in paragraph 9 formalizes the tetrachord fillings in terms of substitutions. For the authentic Ionian, Dorian, and Phrygian modes we find the tetractys mode
[91] Height-width duality can be partially reformulated in transformational terms. This works most elegantly for positive standard and Christoffel words, i.e., for the generalizations of the ascending authentic Ionian and Lydian modes. We demonstrate this for the Ionian case and refer to Domínguez et al. 2009 for further details. On word pairs u|v one may define the following concatenative transformations: Γ(u|v) = u|uv, Γ~(u|v) = u|vu, Δ(u|v) = vu|u, Δ~(u|v) = uv|v. The folding pattern yx|yxyxy of the authentic Ionian mode aaba|aab = GGD(a|b) can be generated through an associated concatenative transformation: ΓΓΔ(x|y) = ΓΓ(yx|y) = Γ(yx|yxy) = yx|yxyxy. The transformations Δ, Γ, and Γ are applied in the same order as their substitutive counterparts D, G, and G. At each stage of the generation we obtain a pair of dual (mutually adjoint) patterns: x|y and a|b for the authentic division, yx|y and ba|b for the first tetractys mode, yx|yxy and aba|ab for the first pentatonic mode, and yx|yxyxy and aaba|aab for the authentic Ionian mode. Thus, each step in the generation of the substitutive tetractys filling is paralleled by a dual generation of iterated fifth kinship. The latter follows the former like a shadow. This observation forces us to relativize Dahlhaus’s argumentation: the perfect fifth kinship relation is intrinsic to any consideration of diatonic modes as the concatenation of filled-in tetrachords.
[92] Note that in the presentation above, the substantive musical difference between words representing scale step patterns on the one hand and fourth-fifth folding patterns on the other is embodied in the application of differentiated types of transformations: substitutive for the scale step patterns and concatenative for the scale folding patterns. If we confine ourselves to substitutive morphisms (as we did, for convenience, previously in paragraph 13, when the duality was first introduced for Lydian), we may not be able to understand intermediate computations of the folding pattern as having any relationship to the comparable stages of generation of the scale step pattern. For example, the substitutive generation of the folding pattern, DGG(x|y) = DG(x|xy) = D(x|xxy) = yx|yxyxy, takes a different route, where the intermediate stages are not fifth/fourth foldings. In particular, the pentatonic positive standard scale step pattern GD(a|b) = aba|ab fails to match up with the comparable stage, the partial computation of the reversal, applied to a different alphabet, GG(x|y) = x|xxy. It stands to reason that partial reversals will not capture the structure at every stage, unless the initial morphism is a palindrome. A corollary in Noll 2009 permits us to confine ourselves to one type of transformation, and to assert that for standard and Christoffel words, mutually adjoint words arise by reversing the substitutive morphism. Similarly, plain adjoints are obtained by replacing in the same order G’s and D’s with Γ’s and Δ’s (or G’s and D~’s, in the case of Christoffel words, with Γ’s and Δ~’s). But these observations suggest that the asymmetric picture, with two different kinds of transformations for scale step patterns on the one hand and for foldings on the other, matches the music-theoretical situation better than the purely symmetric one. We return again to this refinement, an asymmetry within the duality, in our concluding remarks in subsection 5.3.
[93] A corollary fact is that the circle-of-fifths ordering of the modes is also a lexicographic order: represented as words in an ordered alphabet A = {a,b|a<b}, the undivided diatonic modes from Lydian to Locrian are placed in dictionary order (see Berthé et al. 2008). Since the size of the step interval represented by a is greater than the size of that represented by b, it follows that the Lydian intervals, upwards from the modal center, are large (larger of the two intervals for the given generic category). Thus, for example, as the finalis moves sharpwards along the circle of fifths, Aeolian mode is the first case where the interval of a sixth above the finalis becomes minor.
[94] The ramifications of the diatonic circle of fifths broached in the discussion above, taken together, suggest the unconscious knowledge Handschin’s tone character is meant to capture. These arguments serve as initial examples for a more thorough integration of mathematical and philological knowledge in this domain of music theory.
4. Further Distinctions Among the Modes, via Algebraic Combinatorics on Words
[95] In this section, we explore special properties of standard and anti-standard modes, as opposed to the others (generalized Guidonian modes, to be defined below). In subsection 4.1, we look more intensively at the property of divider incidence, introduced in section 2 as a property of authentic Ionian, which is in fact a property of all modes associated with standard words.
[96] In subsection 4.2, we show that well-formed modes that correspond to standard and anti-standard words are unique in having differentiated ways in which divider and initial/terminal scale elements are surrounded. This property of double-neighbor polarity characterizes Ionian and Aeolian modes among Glarean modes, and generalizes to all mode families associated with conjugacy classes of well-formed words.
[97] In subsection 4.3, we show that positive and negative standard words and positive and negative anti-standard words have the forms uab and uba, abu and bau, respectively, where u is a central word. That is, u is a palindrome, and has periods of the lengths of the divider prefix and divider suffix. The central word u is a generalization of Guido’s hexachord, as introduced in subsection 2.1, paragraphs 40 and 41. Double-neighbor polarity sets up a dichotomy of morphic modes, by characterizing the edge modes—that is, modes whose initial tone coincides with initial or final tone of u, which possess the property—and the interior or Guidonian modes, whose initial tone coincides with an interior tone of u, which do not possess the property. The Guidonian modes generalize the eight medieval modes, those whose finales form the tetrachord of the finals, D–E–F–G, in the interior of Guido’s natural hexachord, C–D–E–F–G–A.
[98] In subsection 4.1, we show that divider incidence implies the existence of a special interval at three locations in (almost) all modes corresponding to positive standard words (all those whose divider prefix contains the letter b). In ascending authentic Ionian, these are the three rising diatonic major thirds G–B, C–E, F–A. The interval in question extends from the divider to the leading tone (la note sensible) in both the scale and in the folding; we call it the sensitive interval. Of course, the leading tone enters powerfully into musical theorizing, associated with the notion of dominant. The major third that is associated with dominant (harmony or function) is privileged in the theory of the sensitive interval, and the three locations of the sensitive interval in the usual diatonic are sites of the trichotomy of functional harmony, dominant, tonic, subdominant.
[99] The plain adjoint of a positive standard word uab is a positive standard word
[100] As already mentioned in subsection 2.1, there is a peculiarity of the authentic Ionian mode with scale step pattern aaba|aab and scale folding yx|yxyxy. The dividing tone is in both cases the same: G divides the octave C –
[101] The step pattern aabaaab of the authentic Ionian mode as well as its associated folding yxyxyxy are instances of positive standard words, i.e., they are images ![]() (xy)
(xy)![]() the associated morphism, where the same sequence of D’s and G’s is concatenated in the reverse order. For example, given
the associated morphism, where the same sequence of D’s and G’s is concatenated in the reverse order. For example, given ![]() = DGG.
= DGG.
Figure 17. Different interpretations of standard words as step patterns (ascending major vs. descending minor) and foldings (forward authentic vs. backward plagal)
(click to enlarge)
[102] The concept of authentic division has a clear generalization as well. The word ![]() (xy)
(xy)![]() (x)
(x)![]() (y).
(y).![]() (xy),
(xy),![]() (x)|
(x)|![]() (y).(21)
(y).(21)
[103] We should point out, however, that all results discussed so far are based upon an a priori interpretation of authentic scales as being ascending in pitch height and of their foldings as being forward (sharpwards) in the positive width direction. There are two strategies to extend the theory so as to include descending scales and/or backward foldings. The easier way is to consider these as analogous, but separate, cases. This allows us to remain in the combinatorics of words on two letters. Nevertheless, the situation is not straightforward with regard to the treatment of the adjoints (see Domínguez et al. 2009). The twisted adjoint is defined on rising authentic scales and backward foldings, and under these assumptions divider incidence (but not the exchange of initial tones and divider predecessors) holds for the Dorian mode. We consider that the musically appropriate postulate associates authentic modes regardless of direction with forward foldings and plagal modes regardless of direction with backward foldings, but the ethos of mathematics requires the investigation of all possibilities. Still more demanding, and a subject for future work, is the integration of all these cases into one picture by means of the transformational investigation of the free group F2: forthcoming work places standard words and morphisms on letters representing ascending steps and forward foldings on an equal footing with anti-standard words and morphisms on inverse letters representing descending steps and backward foldings. We close this section, however, with a brief illustration of the first strategy.
[104] By inverting the music-theoretical interpretation of the generic height and width axes we obtain another instance of the same situation: descending hypo-Aeolian mode with backwards folding.
See the upper-right part of Figure 17. This operation mimics the traditional dualist perspective wherein major and minor (triads, scales, scale degrees, etc.) are related to each other by inversion. In this case a positive standard word, first understood as an authentically divided ascending and forward-folded Ionian mode, becomes understood as a plagally divided descending and backward-folded Aeolian mode. (The ascending authentic Aeolian mode behaves differently. Its scale step pattern is a positive anti-standard word and the generating morphism is a special anti-standard morphism. This mode has no divider incidence.) This rigid inversion of the interpretation of the entire Ionian mode is not the only possibility for bringing plagal division into play. In section 1 we already described the (ascending) hypo-Ionian step pattern aab|aaba = EDDG(a|b) as an image under the non-special standard morphism EDDG. We obtain divider incidence under the association of plagal with backwards folding from B to ![]()
![]()
![]()
![]()
![]() |
|![]()
![]() is the image of
is the image of ![]()
![]() under the non-special standard morphism EGDD(
under the non-special standard morphism EGDD(![]() |
|![]() ). Here, and in Figure 17, the bars indicate negatives:
). Here, and in Figure 17, the bars indicate negatives: ![]() represents a descending perfect fifth,
represents a descending perfect fifth, ![]() represents an ascending perfect fourth. The folding direction for authentic vs. plagal is associated with the reverse of the respective cadential motion: falling fifth or rising fourth for authentic, rising fifth and falling fourth for plagal.
represents an ascending perfect fourth. The folding direction for authentic vs. plagal is associated with the reverse of the respective cadential motion: falling fifth or rising fourth for authentic, rising fifth and falling fourth for plagal.
[105] We will show that well-formed modes that correspond to standard and anti-standard words are unique in that only in these modes are divider and initial/(terminal) scale elements marked with respect to each other by being surrounded by distinct double-neighbor figures. For example, all modes corresponding to positive standard words over alphabet
Figure 18. Double-neighbor polarity for words of length at least 3
(click to enlarge)
Figure 19. Diatonic and chromatic edge modes and Guidonian (interior) modes
(click to enlarge)
[106] This polarity distinguishes the Guidonian modes of the four maneriae from Glarean’s later additions. In the traditional eight modes of plainchant, on the one hand, the same step intervals surround the poles of initial scale tone and divider. This is the point of departure for the medieval doctrine of the affinities. In Ionian and Aeolian, on the other hand, one pole is marked with respect to the other, by virtue of the differentiated semitone-tone (ba) or tone-semitone (ab) interval succession at one pole in comparison with the undifferentiated tone-tone (aa) interval succession at the other. This property has implications for musical syntax, and is already suggestive of major-minor tonality, even before the introduction of the harmonic triad as a music-theoretical object. Note, however, that of the harmonic triads within the white-note collection, the C-major and A-minor triads have distinct double-neighbor configurations about each of their triadic constituents: ba, ab, and aa, in some order. That this property fails for the other four diatonic harmonic triads is entirely attributable to the lack, in these cases, of double-neighbor polarity between root and fifth. Figure 19 displays double-neigbor polarity for the edge modes, and affinity at finalis and confinalis for the interior Guidonian modes in the diatonic, and an example of the properties in the generalized edge and Guidonian modes in the well-formed chromatic scale.
[107] We may collate the double-neighbor polarity property with the divider incidence property. As exemplified in Figure 17 for the diatonic modes, modes corresponding to standard and anti-standard words exchange places, along with authentic/plagal divisions, if the directions of letters are reversed. That is, if the default assumption is that letters a and b represent ascending step intervals, then the positive standard word corresponds to an ascending, authentically divided mode. If the meaning of letters a and b is reversed to represent descending step intervals (alternatively, if the letters ![]() and
and ![]() are used with those meanings, as in Figure 17) then the positive standard word represents a descending, plagally divided mode; mutatis mutandis for the negative standard word; that is, it corresponds to an ascending, plagally divided mode or a descending, authentically divided mode.
are used with those meanings, as in Figure 17) then the positive standard word represents a descending, plagally divided mode; mutatis mutandis for the negative standard word; that is, it corresponds to an ascending, plagally divided mode or a descending, authentically divided mode.
[108] Directionality has musical force: in the context of the leading tone, the sense is that of a rising semitone (Handschin’s intensiver Schritt ) toward the Ionian finalis. The leading tone is correlated with the major mode, and with one of the extremes of the diatonic circle of fifths. The analogous correlation in the case of the minor mode, and the other extreme of the diatonic circle of fifths, is with a descending semitone, toward the terminal tone of the plagally divided Aeolian scale, thus toward the divider of the authentically divided scale. This is in accord with traditional dualism, and with Harrison’s “renewed dualism” (1994). It is furthermore in accord with Renaissance and Baroque presentations of mode, such as Bononcini’s, in which ascending motion is affiliated with authentic division, while descending motion is affiliated with plagal division (Bononcini 2009, 122–23). Similarly, authentic cadence is by falling fifth or rising fourth, while plagal cadence is by rising fifth and falling fourth; the folding patterns conventionally associated with authentic and plagal are anti-cadential in direction.
[109] But double-neighbor polarity for Ionian and Aeolian is independent of any invocation of traditional dualism. If we forego the collation of this property with divider incidence, the property remains attributable to the opposition of standard and anti-standard words. As mentioned in section 1, height-width duality is different from traditional dualism. The latter is based on an inversion of musical intervals and interval configurations, while the former is based on an interaction of two entirely distinct encodings of musical intervals. There is a formal opposition between major and minor, corresponding to that obtaining between standard and anti-standard in word-theoretical terms. This is not, however, to argue for a symmetrical binarism, because ascending and descending are not musically symmetrical; plagal is marked with respect to authentic. Since there is a musical asymmetry between ascending and descending, there is thus an asymmetry between the musical interpretations of standard vs. anti-standard words. Recall that the finalis is the marked pole in Ionian, by virtue of the differentiated neighboring step intervals, one of which is the rare half step, whereas the finalis is the unmarked pole in Aeolian. This again breaks the symmetry, reflecting the marked status of minor with respect to major.
Proposition: The structures of standard and anti-standard words of length at least 3 are
(1) Positive standard: rha|rkb (2) Positive anti-standard: ahr|bkr (3) Negative standard: rhb|rka (4) Negative anti-standard: bhr|akr
where r ∈ {a,b}, and h, k ∈ {a,b}*.
[110] The word-theoretical basis for the foregoing derives fairly immediately from the definitions and proof by mathematical induction. We begin with (1), all positive standard words of length at least 3 are of the form rha|rkb, where r is a letter, h and k are factors (possibly empty). Recall that G(a|b) = a|ab, and D(a|b) = ba|b. That is, special standard morphisms of length 1 yield positive standard words whose divider predecessor and terminal predecessor letters are a and b, respectively. In both cases, the character of the initial letter of the standard word matches that of the divider successor letter, and these are the only possible special standard morphisms of length 1, yielding positive standard words of length 3. We proceed by induction on the length of the special standard morphism. Assume that f is a special standard morphism of length n≥1 and that the proposition holds, i.e., f(a|b) = rha|rkb, r ∈ {a,b}, and h, k ∈ {a,b}*. Then, since G is by definition a morphism, Gf(a|b) = G(rha|rkb) = G(r)G(h)a|G(r)G(k)ab, and both divider prefix and suffix begin with a, since G(r) = a or ab. By the same argument, but applying D to f(a|b), the result is D(r)D(h)ba|D(r)D(k)b, and both divider prefix and suffix begin with b, since D(r) = b or ba. Thus, the conditions hold for all possible special standard morphisms of length n+1, and (1) is proven by induction on the length of the morphism.
[111] Next, we demonstrate (2): all positive anti-standard words of length at least 3 are of the form ahr|bkr, where r is a letter, h and k are factors (possibly empty). G~(a|b) = a|ba, and D~(a|b) = ab|b. That is, special anti-standard morphisms of length 1 yield positive anti-standard words whose initial letters and divider suffix initial letters are a and b, respectively. In both cases, the character of the divider prefix final letter matches that of the divider suffix final letter, and these are the only possible special anti-standard morphisms of length 1, yielding positive anti-standard words of length 3. Assume that f is a special anti-standard morphism of length n≥1 and that the proposition holds, i.e., f(a|b) = ahr|bkr, r ∈ {a, b}, and h, k ∈ {a, b}*. Then, since D~ is a morphism, D~f(a|b) = D~(ahr|bkr) = abD~(h)D~(r)|bD~(k)D~(r), and both divider prefix and suffix end with b, since D~(r) = b or ab. By the same argument, but applying G~ to f(a|b), the result is aG~(h)G~(r)|baG~(k)G~(r), and both divider prefix and suffix end with a, since G~(r) = a or ba. Thus, the conditions hold for all possible special anti-standard morphisms of length n+1, and assertion (2) is proven by induction on the length of the morphism.
[112] Furthermore, note that applying the exchange morphism E an odd number of times simply exchanges the letters a and b. The relative sameness or difference with respect to divider prefix and suffix initial and terminal letters is unaffected, for negative standard and anti-standard words. Thus, (3) and (4) hold, and double-neighbor polarity holds for all modes corresponding to standard and anti-standard words, positive or negative.
[113] Double-neighbor polarity holds only for morphic well-formed modes corresponding to standard and anti-standard words. (For amorphic modes, the question does not arise, because the divider is not defined.) That is, if f is neither a standard nor an anti-standard morphism, then it is asserted that f(a|b) = rhs|rks where r, s ∈ {a, b}, h, k ∈ {a, b}*. We note that G~D(a|b) = G~(ba|b) = baa|ba; that DG~(a|b) = D(a|ba) = ba|bba; that GD~(a|b) = G(ab|b) = aab|ab; that D~G(a|b) = D~(a|ab) = ab|abb; and that GG~(a|b) = a|aba = G~G(a|b) and DD~(a|b) = bab|b = D~D(a|b). These are the only possible mixed special morphisms (i.e., neither standard nor anti-standard) of length two. In each case, by inspection it is clear that the words support the assertion: baa|ba, ba|bba, aab|ab, ab|abb, a|aba, and bab|b. Now, let f be a morphism of length n>1. If f is special standard, then we know that f(a|b) = rha|rkb. If one applies either G~ or D~ to this positive standard word, then the proposition holds: G~f(a|b) = G~(rha|rkb) = G~(r)G~(h)a|G~(r)G~(k)ba, with G~(r) = a or ab; D~f(a|b) = D~(rha|rkb) = D~(r)D~(h)ab|D~(r)D~(k)b, with D~(r) = b or ba. Similarly, if f is special anti-standard, f(a|b) = ahr|bkr, and if one applies either G or D to this positive anti-standard word, by similar calculations, the proposition holds. Finally, under the induction assumption let us take f to be a mixed morphism (neither standard nor anti-standard) of length n>1 and f(a|b) = rhs|rks, with r, s ∈ {a, b}. Then if X is any of the morphisms G, G~, D, D~, Xf(a|b) = X(rhs|rks) = X(r)X(h)X(s)|X(r)X(k)X(s), and X preserves the equalities for initial and final divider prefix and suffix letters. Altogether this shows that the proposition holds for all special morphisms of length n+1 that are neither standard nor anti-standard. An odd number of exchange morphisms E exchanges the letters a and b, which has no effect on the equalities asserted, so the proposition holds for non-special morphisms as well, and therefore for both positive and negative words. The final result is that double-neighbor polarity characterizes modes corresponding to standard and anti-standard words.
[114] The positive way of expressing the lack of double-neighbor polarity for morphic modes of length N = p+q > 2 that are neither standard nor anti-standard is to say that in their corresponding well-formed words w = w1...wq|wq+1...wN it is the case that w1 = wq+1 and wq = wq+p. This is suggestive of the notion of periodicity, for periods q and p, respectively. That is, since letters separated by the lengths of the divider prefix and divider suffix are equal except at two locations where inequality of letters has been demonstrated, the possibility arises of double periodicity for factors of well-formed words. To identify the largest such factor, we need to understand the location of standard and anti-standard modes relative to each other.
4.3 Central Words as Factors in Standard and Anti-Standard Words
[115] We wish to show (in the interest of having a largely self-contained presentation; see also Lothaire 2002, chapter 2) the word-theoretical result that positive standard words are of the form uab where u is a central word: a palindrome of length p+q−2 where q is the length of the divider prefix and p is the length of the divider suffix, such that p and q are periods of u. The same holds true for negative standard words, except that they are of the form uba. Positive and negative anti-standard words will be shown to be of the form abu and bau, respectively, where u is a palindrome. It is then immediate that uab and abu are conjugates of each other: u(ab) and (ab)u are conjugate by definition. We obtain the mode corresponding to anti-standard abu from that corresponding to standard uab by starting two notes below the standard mode finalis (in the diatonic case, anti-standard relative minor in relation to standard relative major). Similarly, uba and bau are conjugates of each other, corresponding to plagal modes that begin two notes apart (in the diatonic context, separated by the interval “minor third”: here, ba).
[116] The proposition that gives a second structural description of positive standard/anti-standard words as uab, abu, respectively, and negative standard/anti-standard words as uba, bau, respectively, requires the following lemma.
Lemma: Let u be a palindrome in letters a and b, i.e., a member ofP = {u ∈ {a, b}* | u = u1...uN, u1 = uN, u2 = wN-1, ...}. ThenbD~(u) = D(u)b ∈ P, andaG~(u) = G(u)a ∈ P.
Proof by induction on the length of u.
If u is empty, then the lemma holds, and if u is a single letter: bD~(a) = b(ab) = (ba)b = D(a)b, and bab ∈ P; aG~(b) = a(ba) = (ab)a = G(b)a, and aba ∈ P. Assume the lemma holds for all u, 1 < |u| < n. Let u = u1...un, and since u ∈ P, u1 = un.
Let u1 = un = a. Then
bD~(u) = bD~(u1...un) = babD~(u2...un-1)ab = ba(bD~(u2...un-1)ab;
D(u)b = D(u1...un)b = baD(u2...un-1)bab = ba(D(u2...un-1)b)ab.
But the length ofu ′ = u2...un-1 < n andu ′ ∈ P, so by the induction hypothesis,bD~(u ′) = D(u ′)b ∈ P. Therefore,bD~(u) = ba(bD~(u ′))ab = ba(D(u ′)b)ab = D(u)b ∈ P.
Let u1 = un = b. Then
bD~(u) = bD~(u1...un) = bbD~(u2...un-1)b =b(bD~(u ′))b;
D(u)b = D(u1...un)b = bD(u2...un-1)bb =b(D(u ′)b)b.
Again,|u ′| < n andu ′ ∈ P, so by the hypothesisbD~(u ′) = D(u ′)b ∈ P. It follows therefore:bD~(u) = b(bD~(u ′))b = b(D(u ′)b)b = D(u)b ∈ P.
The same sort of argument holds for the case aG~(u) = G(u)a ∈ P, completing the proof.
[117] The alternative structural description for standard and anti-standard words follows from the lemma. Note that
[118] We may collate the two descriptions of standard and anti-standard words provided by the mathematical work above to fully characterize u. Having computed the standard and anti-standard words of length 3, we may assume that u is longer than a single letter. If w is positive standard of length
[119] The properties collected thus far, with respect to the usual diatonic—the asymmetries of double-neighbor polarity, on the one hand, and the symmetries of the affinities, on the other, the latter attributable to the double periodicity of the Guidonian hexachord—are closely related to the uniqueness of the tritone within the diatonic set, and the obverse fact, the generation of the diatonic by the perfect fifth or fourth. The position-finding capacity of the tritone (Browne 1981) and its essential role for tonality has been theorized at least since Fétis. But to uncover the systematic entailments of the simple musical facts of tritone uniqueness and perfect fifth multiplicity requires the theoretical elaboration we have been at pains to make.
[120] The foregoing word-theoretical results have been offered within the context of interpretations of the words as modal scale step patterns, rather than as scale foldings. Whereas double-neighbor polarity is a feature that applies to both standard and anti-standard words, it applies to the plain adjoint of a standard word, but not to the plain adjoint of an anti-standard word. Similarly, whereas we can assert the position of the central word u as prefix to a standard word and suffix to an anti-standard word, it is only in the case of standard words that we may assert that the plain adjoint of w = uab or uba is of the form ![]() (xy) is its plain adjoint, where
(xy) is its plain adjoint, where ![]() is the reversal of f), whereas in general the plain adjoint of an anti-standard word is not anti-standard. From this point, our presentation relies on results from Noll’s Ionian Theorem (Noll 2009), which demonstrates the properties of divider incidence, discussed above.
is the reversal of f), whereas in general the plain adjoint of an anti-standard word is not anti-standard. From this point, our presentation relies on results from Noll’s Ionian Theorem (Noll 2009), which demonstrates the properties of divider incidence, discussed above.
Figure 20. Construction of the sensitive intervals in diatonic and chromatic modes with divider incidence
(click to enlarge)
[121] That divider and terminal predecessor tones coincide in the scale and folding associated with standard words suggests a structural significance for the musical interval from divider to terminal predecessor. For scale step patterns and adjoint folding patterns corresponding to positive standard words, these intervals generalize the diatonic major third. We call this the sensitive interval: for ascending authentic Ionian, the G–B rising major third; for descending plagal Aeolian, the A–F falling major third. It will be demonstrated that a consequence of divider incidence is that the sensitive interval is replicated at two other locations: at the initial tone of the scale and at the initial tone of the folding (which coincide with the divider predecessor tones of folding and scale, respectively). As an introduction to sensitive intervals we inspect two music-theoretical examples, in Figure 20.
[122] On the left side of Figure 20 we find the mutually dual central palindromes
[123] The generalized sensitive interval is the interval from the divider to the next-to-last note (leading tone), an identical interval (between identical notes) in both the scale and the folding; it is replicated by two distinct intervals of the same size, from the divider predecessors to the notes that terminate the generalized hexachords (the tone structures corresponding to the central words): i.e., in the scale, from the origin to the endpoint of the central word u; in the folding, from the finalis to the endpoint of the central word
Figure 21. General situation of divider incidence for scale (li) and folding (mi), with respect to 6 elements
(click to enlarge)
[124] In the purely word-theoretical approach to scales and modes, musical intervals have representations in terms of factors in words. These factors do not only specify a difference between two notes, they also encode a precise intervallic pathway (in terms of scale step intervals or in terms of folding intervals). In subsection 2.2 we identified the notes of the scales and foldings along trajectories within a fundamental domain, so we also have at our disposal a language for identifying intervals between notes as points of a two-dimensional lattice. Let the ordered n-tuples li and mi represent, respectively, the notes of adjoint standard scale and folding, for a positive standard word w in {a, b}* and its dual word
[125] To demonstrate the generality of the sensitive interval property for standard modes, we require one final proposition, motivated by the observation in the previous paragraph that the divider suffix of a standard word is also a prefix of the associated central word.
Proposition: If w = f(ab) is a positive standard word such that f contains at least one occurrence of D, then the divider suffix f(b) is also a prefix of w.
Note that in the standard word D(a|b) = ba|b, it is the case that divider suffix b is also a prefix. If f is a positive standard morphism of length n ≥ 1 that is a power of G, Gn(a|b) = a|anb, then the morphism of length n+1 DGn contains at least one occurrence of D, and DGn(a|b) = D(a|anb) = ba|(ba)nb = (ba)n+1b = (ba)nb(ab), which has divider suffix (ba)nb also as a prefix. We may therefore make the induction assumption that for morphisms f of length n containing at least one occurrence of D, f(b) is a prefix of f(ab): f(a|b) = f(b)h for some suffix h ∈ {a, b}*. Let X be any of the morphisms G, G~, D, D~, then Xf is of length n+1 and Xf(a|b) = X(f(b)h) = Xf(b)X(h) = Xf(a)|Xf(b), and Xf(b) is both divider suffix and a prefix to Xf(ab). That proves the result by induction on the length of the morphism. Since the presence of the morphism D creates the presence of at least one letter b in the divider prefix, we may restate the result to say that in any positive standard word w such that the divider prefix contains the letter b, the divider suffix is also a prefix of w.
[126] An obvious corollary of this is that if f is a special standard morphism that contains D, not only is f(b) a prefix of f(ab), any prefix of f(b) is a prefix of f(ab). We are particularly interested in the prefix s of length |f(b)|−1.
Corollary: Let w = f(a)|f(b) be the scale step pattern andw ′ = f ′(x)|f ′(y) be the adjoint folding pattern for w, where f is a special standard morphism that contains D, that is, f(a) contains the letter b (and equivalently,f ′(x) contains the letter y).
Then we conclude from the proposition that any prefix s of f(b) is also a prefix of w, and any prefix
Figure 22. Three sensitive interval pairs, for modes associated with positive standard adjoint words
(click to enlarge)
[127] We consider prefixes s and ![]() ′,
′,![]() . Thus, the sensitive interval departing from the origin is encoded by
. Thus, the sensitive interval departing from the origin is encoded by ![]() in the scale step pattern, and by
in the scale step pattern, and by
[128] On this basis, we define the following three sensitive interval pairs, at three locations in positive standard adjoint modes, as displayed in Figure 22.
Definition: For adjoint positive standard modes and their associated scale step and folding patterns f(ab) andf ′(xy), with prefixes s of f(b) ands ′ off ′(y) of lengths |s| = |f(b)|−1 and|s ′| = |f ′(y)|−1, respectively, we define the three pairs α = (s,s ′), β = (s, and γ = (′),
, s) to be the sensitive interval pairs of the mode. The paradigmatic sensitive interval is α, from common divider to leading tone. With β we associate the prefix s of f(ab), and the factor
in ′
f ′(xy) starting from one letter before the divider. With γ we associate the factorin f(ab) starting from one letter before the divider, and the prefix
s ′ inf ′(xy).
Figure 23. Localization of the three sensitive pairs of the authentic Ionian mode in the height and width trajectories
(click to enlarge)
[129] Note that reversing a factor leaves its letter content fixed. That is, |s|a = |![]() |a, |s|b = |
|a, |s|b = |![]() |b, and
|b, and ![]() ′|a =
′|a =![]() ′|a,
′|a,![]() ′|b.
′|b.
[130] Finally, we observe how the sensitive interval property comports with traditional major-minor dualism. As we saw in subsection 4.1, the interpretation of the positive standard word aaba|aab as authentic Ionian is dependent upon the convention of reading the letters as ascending step intervals. Reading the letters as descending step intervals (equivalently, introducing a new binary alphabet to represent descending step intervals) transforms the positive standard word into a representation of (descending) hypo-Aeolian. Because of the inversional symmetry of the diatonic set, this reinterpretation or change of alphabet simply exchanges the assignments of the Glarean modes to particular Sturmian morphisms, and exchanges authentic with plagal. For much of our work, either convention would work equally well, or we could keep all possibilities available. But note that standard and anti-standard exchange assignments under change of alphabet, between Ionian and Aeolian, and remember that divider incidence is equivalent to standardicity. (In future work, within the free group on two generators, we will see essentially the same picture, but obviating the need to reinterpret the music-theoretical meanings of letters in an alphabet. Special standard morphisms applied to ab and xy will share privileged status with special anti-standard morphisms applied to a-1b-1 and x-1y-1, in the context of free groups generated by {a, b} and {x, y}.) As we have asserted above, musically speaking, up and down, ascending and descending, are not symmetric. Therefore, not only for cultural reasons, since representing scales as ascending seems more natural to us, but also since standardicity is privileged by virtue of its special word-theoretical properties, we make a choice that assigns the musically privileged authentic Ionian mode to the positive standard word. Nonetheless, following the aforementioned mathematical ethos of looking at an object or a situation from all possible vantage points, we may explore the ramifications of the opposite choice of orientation. In this interpretation, the positive standard word represents the scale step pattern of (descending) plagal Aeolian. The adjoint word represents the folding, understood as the plagal folding of descending fifths and rising fourths. The paradigmatic sensitive interval (α) is the descending major third from the common divider, A, to F, the upper leading tone to (excluded) lower boundary tone
[131] Together with double-neighbor polarity, divider incidence and its concomitant properties establish a rich structure that demands further investigation. The sensitive interval property in particular is evidently implicated in the way the diatonic set supports the functional harmony trichotomy: dominant, tonic, and subdominant.
[132] We present concluding remarks on the two-dimensional framework and on the utility and interpretation of the specific level, on the implications of the word-theoretical modal approach for the understanding of harmonic tonality, and offer reflections on the music-theoretical meaning of mathematical facts.
5.1 Two Degrees of Freedom Bound in a Duality
[133] How can one justify the initial theoretical decision upon which the central results of this paper are based, namely to regard height and width as different dimensions in the constitution of musical tone relations? In a meditation on the notion of dimension, the mathematician Yuri Manin reminds us that “the mental effort needed to grasp the meaning of ‘three’ in this context [the dimensions of physical space] is qualitatively different from the one involved in making sense of a sentence like ‘There are three chairs in this room.’ Counting dimensions, we are definitely not counting ‘things’” (Manin 2006, 139). Manin then points out that his advice is not primarily meant as an ontological statement about things and abstract non-things: “Euclid (ca. 300 BC), as some great thinkers before and after him, taught us not to bother so much about what things ‘are’ but rather how to think about them orderly and creatively.” On the one hand, our decision is the result of careful deliberation. Some of the arguments will be summarized below. On the other hand, we are of the firm opinion that investigations into music-theoretical concepts are not automatically in need of an ontological justification. The results themselves have a voice in the evaluation of their theoretical anchors. Some comments on the methodological, epistemological, and ontological orientation of this research are given in subsection 5.3.
[134] In fact, we have seen that treating tone character as a mathematical dimension, separate from pitch height, does allow one to think about diatonic tonal space in an orderly and creative way. In the underlying generic and specific parameter spaces we regard height and width as independent degrees of freedom. It is a central result on the generic level, though, that in every individual well-formed mode the width coordinates are mapped to height coordinates under an affine automorphism of ![]() n (and height coordinates are mapped to width coordinates under its inverse). This automorphism is one expression of height-width duality, another being the plain adjointness for well-formed words. In the case of standard words (and in the case of Christoffel words) one finds a third manifestation of height-width duality on the meta-level of the generating Sturmian morphisms, where it can be expressed as an anti-automorphism of the monoid
n (and height coordinates are mapped to width coordinates under its inverse). This automorphism is one expression of height-width duality, another being the plain adjointness for well-formed words. In the case of standard words (and in the case of Christoffel words) one finds a third manifestation of height-width duality on the meta-level of the generating Sturmian morphisms, where it can be expressed as an anti-automorphism of the monoid
[135] In contrast with the extended investigation on the generic level, we did not make explicit use of the specific-level theoretical framework, presented in subsection 1.3 (paragraphs 17 to 30). The aim of including this material was to show that the established constructions in scale theory can be smoothly extended, from the generic level to the specific level. The music-theoretical benefits of the concrete specific-level constructions have still to be explored. On the one hand, the specific level provides a high quantitative precision without losing theoretical strength. On the other hand, it might not be of central interest to the working music theorist. The real-valued height and width coordinates could become relevant, though, in collaborations between theoretical and empirical approaches. They could be helpful, for example, to meet the cognitive psychologists half way. Apart from these perspectives, the embedding of the Pythagorean lattice into a continuous two-dimensional vector space receives the preliminary status of an auxiliary construction, as previously discussed. This status applies first of all to the pitch-height and pitch-width axes, as their slopes are irrational with respect to the indisputable fifth/octave axes. Recall that the specific pitch-width axis is defined as the kernel of the linear pitch-height form, and the specific pitch-height axis is spanned by its gradient vector v (see paragraphs 24 and 25 and Figure 4). It remains an open question whether the auxiliary construction can eventually be understood in terms of a proper music-theoretical concept. A promising attempt can be illustrated by a visual analogy. To attempt to understand the course of the sloped continuous width and height axes with respect to the discrete fifth-octave lattice reminds one of the difficulty of drawing a sloped line on a digital computer screen with pixels on a rectilinear grid, in particular if the slope in question is irrational. In computer graphics one applies results from algebraic combinatorics on words. A convincing visual illusion of a straight line is achieved when the pixel-zig-zag has the structure of a mechanical sequence: Suppose that the graph of the linear function f(t) = g ⋅t with slope 0 < g < 1 shall be drawn. Suppose that horizontal pixel positions are parametrized by integers k = ..., −2, −1, 0, 1, 2, ... and that the vertical pixel position for each k is chosen as the floor value ![]() g ⋅k
g ⋅k![]()
![]() x
x![]()
![]() g(k+1)
g(k+1)![]() −
−![]() (gk)
(gk)![]()
Figure 24. Rendering of the pitch-width axis with “pixels” in a rectilinear fifths-octaves grid
(click to enlarge)
Figure 25. The infinite Pythagorean mechanical sequence of slope g = –log2(3/2)
(click to enlarge)
[136] For negative slopes −1 < g < 0 one obtains analogously mechanical sequences with the two letters 0 and −1. Figure 24 shows such a drawing of the pitch-width axis with respect to a rectilinear fifths-octaves-grid and irrational slope g = −log2(3/2) = −0.584963...
[137] Figure 25 shows a music-theoretically motivated construction of the same mechanical sequence (up to letter substitution 0 → x, −1 → y). The folding of the infinite chain of fifths into the pitch–height ambitus of an octave is called the Pythagorean mechanical sequence (cf. Carey and Clampitt 1996a). The rectilinear grid of Figure 24 is in Figure 25 squeezed and rotated in order better to convey the information visually (cf. Figure 5). This affine transformation does not, however, affect the music-theoretical meaning. The astonishing difference between the two applications is rather to be found in the meaning of the discrete units. While in the computer graphical application the single pixels are intended to merge into the visual illusion of a straight line, it happens that in the music-theoretical application the “pixels” are rather well-separated audible quantities: ascending fifths and descending fourths. The infinite folding pattern of the mechanical sequence is reminiscent of what Deleuze, in his meditation on Leibniz (Le pli), calls “le pli qui va à l’infini” (Deleuze 1988), which in turn is an inspiration for our choices of terminology, folding and folding pattern.
[138] If one considers the diatonic modes as (mechanical) discrete lines in width direction, namely as factors of the infinite Pythagorean mechanical sequence, it turns out that the seemingly vacuous width dimension is the “truly musical” one, as Handschin puts it. The specific pitch heights would then be degraded to side effects of the discretization, i.e., to mere “disturbances” off the width direction. In view of the duality, however, one is well advised to give equal weight to both dimensions and to anticipate more insights from their interaction alongside the duality. The strongest inspiration that we receive from Handschin’s project is the idea of a tight connectivity between perceptual and non-perceptual components of musical tones.
[139] From his theoretical investigations Handschin seeks to obtain explanatory power for psychological phenomena. The present investigation is primarily conceived as a contribution to the knowledge of music theory. Nevertheless, we sympathize with Handschin’s intentions and would like to share a speculation in this direction as a codetta to this subsection. Extrapolating from findings in neuro-acoustics by Langner and Ochse (2005), we speculate that the mind/brain has a particular disposition to manage dynamic processes in terms of conjugated variables. Langner and Ochse gained very detailed knowledge about the processing of acoustic signals in the central auditory system: “As a result of cochlear analysis, frequency is mapped along a tonotopic axis in all auditory brain areas. Similarly, as a result of temporal analysis, periodicity is mapped from the midbrain to the auditory cortex. In each case, tonotopic and periodotopic axes are orthogonal to each other. One may say that spectral information, as an important aspect of timbre, is mapped along a first neural axis, periodicity (pitch) is mapped along the second neural axis of the auditory system.” From a mathematical point of view the height and width dimensions remind one of conjugated variables (such as period and frequency). One may relate Sturmian morphisms to the subgroup ![]() ) =
) =![]() )
)![]() )
)
5.2 Elements of Harmonic Tonality in a Modal Perspective
[140] This subsection aims at positioning some results of this paper within a context of research into harmonic tonality. We believe that a deeper understanding of tone relations in common practice music remains to be achieved. A customary concept regards triads, diatonic scales, and the chromatic scale as levels of a nested hierarchy. This view is persuasive, as long as tone relations are identified on the basis of pitch height and pitch-height classes. But as soon as fifth- and third-relations are brought into play it becomes evident that the triadic-diatonic-chromatic hierarchy is a hybrid construction. According to traditional understandings of diatonic tone relations, the diatonic scale that encompasses the triads underlies either a chain of thirds or a framework of perfect fifths and major thirds, while the diatonic scale that inhabits the chromatic scale is constituted as a cycle of fifths. Carl Dahlhaus takes up a position wherein a fifths-thirds framework in harmonic tonality succeeds the older chain-of-fifths constitution of the diatonic scale. It would seem, though, that it is desirable to understand the coexistence of these different constitutions of diatonic tone relations. Handschin’s distinction between Toncharakter and Beicharakter reflects his awareness of this desire. A recent contribution by Marek Žabka transfers the properties of well-formed scales to analogous constructs in the generalized Euler–Öttingen–Riemann Tonnetz (Žabka 2010). The modal perspective of the present investigation follows a different strategy toward a similar goal. It focuses upon elements of tonality from within the domain of well-formed modes and is abstinent with respect to the manifold concepts of the triad. This by no means implies their abandonment, but is rather a methodological move in preparation for an eventual integration.
[141] Two genuinely modal elements play a central role in the constitution of the modern major tonality, albeit in a configuration that transcends the modal anchors: the root and the third of the dominant triad coincide with the authentic divider and with the leading tone of the authentic Ionian mode. The interval between these modally crucial tones is a major third—the new autonomous constituent of the Euler–Öttingen–Riemann Tonnetz. Apart from this autonomy of the third it cannot be denied that it systematically interacts with its modal precurser, the ditone as a factor of the diatonic scale step patterns. Schenker’s Ursatz is a celebrated manifestation of this interaction. In the context of height-width duality one may extend this interaction to the foldings yxyx and xyxy of the ditone aa into two ascending fifths and two descending fourths.
[142] The definition of the sensitive interval is closely connected with the properties of Guido’s hexachord. The scale step pattern aabaa and the folding pattern yxyxy are both palindromes, with ditones aa and their foldings yxyx and xyxy as prefixes and suffixes. The invariance of each of the palindromes under reversal explains why the presence of one ditone implies the presence of a second one. This is an aspect that relates to Öttingen–Riemann dualism. But the height-width duality deals with the interdependence of the two palindromes aabaa and yxyxy. Height-width duality reveals that the four involved tones—say, C, A, and F, E—are the beginning and terminating tones of the hexachord and its folding, respectively. The “a-ha!” experience that motivated our interest in the sensitive interval property is the observation that generally in standard modes these intervals across the generalized hexachord form the same intervals as between divider and leading tone. The “a-ha!” therefore involves also an appraisal of divider incidence because of the double articulation of the sensitive interval between divider and leading tone. Recall that the intervals, between the divider and the last essential tone in the step pattern and between the divider and the last essential tone in the folding pattern, connect the same two tones. We suggest that the generality of these observations qualifies them as potentially significant paradigmatic modal preconditions for the rise of major-minor tonality, affiliating them with features that generations of musicians have observed.
[143] Consider what is entirely general in the sensitive interval property for the usual diatonic authentic Ionian, and what is special. Recall that, in general, whereas the sensitive intervals we called proper (α) and tonic (β) are invariably related by the primary interval of the folding, the sensitive interval we called improper (γ) extends in the scale from the note preceding the divider. In authentic Ionian, this is subdominant, but in the old sense of soudominante (e.g., Dandrieu): the note below the dominant.(23) But it is not true in general that the relation of this note to the finalis is the secondary interval of the folding. That is, we do not in the general case have something comparable to the perfect-fifth relationship F–C–G that obtains between the elements identified with endpoints of the three sensitive intervals (that provides the usual justification for the term “subdominant” or sous-dominante as the note lying a fifth below the tonic). For a counterexample to authentic Ionian, see the chromatic example in Figure 20. This special feature of the diatonic participates in another aspect of tonal hierarchy arising from the height-width duality that begins to connect to issues of progression.
Figure 26. The tetractys analogue of the augmented prime is a minor third: the difference m3 = P4 – M2 of the major and the minor tetractys steps P4 and M2
(click to enlarge)
[144] De Jong and Noll apply the theory of well-formed modes to unify elements of Rameau’s fundamental bass and Riemann’s tonal functions and put them on a modified theoretical basis (De Jong and Noll 2011). Their approach is a modal refinement of the proposal in Carey and Clampitt 1989 to interpret the roots of the tonic, subdominant, and dominant triads as an instance of the structural scale, a well-formed fifth-generated three-note scale. Recall from subsection 3.2 that this scale framework also plays a central role in Dahlhaus’s discussion of the constitution of the diatonic modes. Its standard mode is also known as the tetractys of ancient musical theory. A view of the fundamental bass progression as an autonomous (virtual) melody motivates a modal approach wherein the function symbols T, S, D are used to denote the three different scale degrees of functional modes, i.e., tetractys modes. De Jong and Noll argue that the folding patterns of the standard and anti-standard tetractys modes constitute the core syntax of tonal fundamental bass progressions. The boundary tones of the forward (i.e., sharpward) folding patterns are a minor third below the origin. This interval behaves with respect to the tetractys modes like the augmented prime with respect to
the diatonic modes. The minor third is the difference between the large tetractys step P4 and the small tetractys step M2 (see Figure 26). This observation leads to the new concept of functional chromaticism that deals with the study of fundamental bass alterations by minor thirds. Altered fundaments are connected to other music-theoretical concepts such as Rameau’s double emploi, Riemann’s Terzwechsel (relative relationship, in anglophone terminology), and Lendvai’s axis tonality. None of the three concepts treats the minor third as an alteration interval. In the first two cases—double emploi and Terzwechsel—we find the idea of a substituted fundamental bass tone, where the substitution is sanctioned by chordal and contrapuntal considerations. Double employment is based on the reinterpretation of tone roles with respect to fundamental bass tones, and the alteration by minor thirds appears only incidentally as a side effect of the stacked thirds structure of triads and seventh chords (although the minor third root relation IV–ii is the most familiar case). Riemann’s Terzwechsel is also based on the reinterpretation of tone roles. The roots of the related triads form a minor third. The dualistic Riemann-roots, however, form a major third. Lendvai’s axis tonality does involve a functional equivalence between minor-third related fundamental bass elements. Functional chromaticism can thus be seen as a modal refinement of Lendvai’s “amodal” approach. The prototypical 1st (standard) mode progression is T S (
[145] In the context of the present paper it is illuminating to see that the standard and anti-standard modes play a crucial role on different hierarchical levels: among the diatonic modes they correspond to the new Glarean modes. Among the tetractys modes the edge modes turn out to be the only morphic modes. In other words, there are no Guidonian modes on this level. It stands to reason that the distinguished properties of the standard and anti-standard modes continue to be illuminative on the chromatic level as well. First explorations of the twelve chromatic modes give the impression that the standard extensions D(aaba|aab) = bababba|babab of the (standard) Ionian modes as well as the anti-standard extensions D~(abaa|baa) = abbabab|babab of the (anti-standard) Aeolian modes provide a promising framework for the analysis of chromaticism in interaction with underlying diatonic structures.
5.3 Music-Theoretical Interpretation of Mathematical Facts
[146] Applied mathematics in the domain of music and music research is a heterogeneous field with a multitude of methods, results, attitudes, and cross-connections. The present paper investigates music-theoretical concepts through mathematization. The relocation of their investigation in a domain of mathematical knowledge allows us to gain valuable insights about their interdependence. In paragraph 2 we used the term “experimental philology” in order to characterize the type of work that we have in mind. It supplements the historical interest in the emergence of concepts and ideas by a heightened interest in their compatibility. The dialectical method can be considered as a prototype of experimental philology and Carl Dahlhaus was certainly a master of its application to music-theoretical discourse. Mathematical music theory—as we conceive it in this paper—adds new types of knowledge to this tradition. This includes the exploitation of diverse realms of genuine mathematical knowledge, but it also includes certain epistemological attitudes.
[147] Among these attitudes is a penchant for generalization, with a view toward the evaluation of implications or equivalences, i.e., assertions stating that one fact implies or is equivalent to another fact. The addiction mathematicians have to generalize known facts is connected with their desire to find the most adequate formulation of those facts. This epistemological desire interferes in applied mathematics with the desire to cover a certain scope of investigation most effectively without unnecessary theoretical overload. Even if musicians are keen to experiment with new scales, it is not a matter of course that a given true statement about an infinite family of counterfactual musical objects truly expands knowledge about music. It is therefore a matter of balance between the two desires mentioned above. In paragraph 100, we pointed out that a generalization imposes a dichotomy between essential and accidental properties. Pythagoreans might regard the rational number 3:2 and its arithmetic properties to be essential for understanding the role of fifth-kinship in music theory. Word-theoretically-inspired music theorists instead highlight the hierarchical anatomy of the approximations of the logarithm log2(3/2) through continued fractions 1/2, 2/3, 3/5, 4/7, 7/12, ..., and their refinements in terms of words on two-letter alphabets. We regard the underlying hierarchical organization of well-formed modes to be music-theoretically essential. This position entails the following consequence: If a concrete node in a hierarchy appears to be music-theoretically relevant, one should expect that all previous nodes turn out to be relevant as well. The theory of functional modes (see paragraph 144) is only a rather local application of the theory of well-formed modes. But in addition to that it is a candidate for a crucial piece of the puzzle in the overall theoretical picture: the tetractys modes occupy the first non-trivial hierarchical level below the authentic division.
[148] The most delicate part of the music-theoretical interpretation is the identification of its scope, including musical repertoires to which it may be successfully applied, if analysis of individual works is even within the appropriate scope of the theory. Our discussion has been highly incomplete, of course, in that it so heavily emphasizes the paradigmatic domain as opposed to the syntagmatic, in the sense of McCreless’s expanded use of Saussure’s terminology (McCreless 1991). That is, much is suggested concerning the constitution of tone relations (i.e., the internal structuring of a tonal inventory, as internalized by musicians), as opposed to the relations between tone occurrences in a musical piece (the temporal distribution of elements drawn from the inventory). In the present paper we refrain from a concrete allocation of scope, but the following thoughts may indicate a direction for future work. In the opening paragraphs of his book Handschin assumes that his readers are bored by the circle of fifths as a didactic vehicle of theory teachers and as a guiding tool for piano tuners (Handschin 1948, 2). Therefore he intends to give higher value to it in the sense of a true subject of music theory and spends most of his attention on its role as a scale of character differences (8). Theoretical developments in recent decades (especially, much of the literature of mathematical scale theory) mitigate Handschin’s worry about the degradation (Herabwürdigung) of the circle of fifths. In light of the rhetoric of Handschin’s argument it is worthwhile, though, to apply the theory of well-formed modes also to those explicit manifestations of the circle of fifths, such as in fundamental bass progressions and modulations. The price for this intention is a very broad scope.
[149] In particular, under the perspective of the height-width duality we tend toward the hypothesis that in historically situated tone relations there is a markedness between height and width dimensions. In other words, the symmetry between height and width dimensions is typically broken. Recall from the elaboration of the duality of adjoint words in paragraphs 91 and 92 that the mathematics of the word-theory application to music already differentiates between the types of transformations that generate the adjoint patterns. This suggests that one pole or the other is marked, without pointing toward one or the other. Nor is this asymmetry necessarily diachronically immutable. The relative strictness or freedom, under different historical conditions, in the height and width dimensions is a question for future study.
David Clampitt
School of Music
The Ohio State University
Columbus, OH 43210-1770
clampitt.4@osu.edu
Thomas Noll
Escola Superior de Musica de Catalunya
C. Padilla, 155–Edificio L’Auditori
08013 Barcelona
Spain
noll@cs.tu-berlin.de
Works Cited
Agmon, Eytan. 1989. “A Mathematical Model of the Diatonic System.” Journal of Music Theory 33, no. 1: 1–25.
—————. 1996. “Coherent Tone Systems: A Study in the Theory of Diatonicism.” Journal of Music Theory 40, no. 1: 39–59.
Berstel, Jean. 1990. “Tracé de droites, fractions continues et morphismes itérés.” In Mots, Langue, Raisonnement, Calcul, ed. M. Lothaire. Mélanges offerts à M.-P. Schützenberger. Paris: Hermès.
Berstel, Jean, Aaron Lauve, Christophe Reutenauer, and Francisco Saliola. 2008. Combinatorics on Words: Christoffel Words and Repetition in Words. CRM Monograph Series. Providence, RI: American Mathematical Society.
Berthé, Valérie, Aldo de Luca, and Christophe Reutenauer. 2008. “On an Involution of Christoffel Words and Sturmian Morphisms.” European Journal of Combinatorics 29, no. 2: 535–53.
Bononcini, Giovanni Maria. 2009 [1673]. Musico prattico che breuemente dimonstra il modo di giungere alla perfetta cognizione di tutte quelle cose. Bologna: Giacomo Monti. [Kessinger Publishing].
Browne, Richmond. 1981. “Tonal Implications of the Diatonic Set. ” In Theory Only 5, nos. 6–7: 3–21.
Cafagna, Vittorio, and Thomas Noll. 2003. “Algebraic Investigations into Enharmonic Identification and Temperament.” Proceedings, Third International Conference: Understanding and Creating Music. Caserta: Seconda Università di Napoli. Available at: http://user.cs.tu-berlin.de/~noll/CafagnaNoll.pdf.
Carey, Norman. 2002. “On Coherence and Sameness, and the Evaluation of Scale Candidacy Claims.” Journal of Music Theory 46: 1–56.
—————. 2007. “Coherence and Sameness in Well-Formed and Pairwise Well-Formed Scales.” Journal of Mathematics and Music 1, no. 2: 79–98.
Carey, Norman, and David Clampitt. 1989. “Aspects of Well-formed Scales.” Music Theory Spectrum 11, no. 2: 187–206.
—————. 1996a. “Self-Similar Pitch Structures, Their Duals, and Rhythmic Analogues.” Perspectives of New Music 34, no. 2: 62–87.
—————. 1996b. “Regions: A Theory of Tonal Spaces in Early Medieval Treatises.” Journal of Music Theory 40, no. 1: 113–47.
Chemillier, Marc. 2004. “Periodic Sequences and Lyndon Words.” In Formal Systems and Music, ed. G. Assayag, V. Cafagna, M. Chemillier, special issue of Soft Computing 8, no. 9: 611–16.
Chemillier, Marc, and Charlotte Truchet. 2003. “Computation of Words Satisfying the Rhythmic Oddity Property (after Simha Aron’s works).” Information Processing Letters 86, no. 5: 255–61.
Christensen, Thomas. 2004 [1993]. Rameau and Musical Thought in the Enlightenment. Cambridge: Cambridge University Press.
Christoffel, E. B. 1875. “Observatio arithmetica.” Annali di Mathematica 6: 145–52.
Clampitt, David, and Thomas Noll. 2009. “Regions and Standard Modes.” In Mathematics and Computation in Music. Proceedings of the MCM 2009 and the John Clough Memorial Conference, ed. E. Chew, A. Childs, C.-H. Chuan. Berlin: Springer.
Clough, John, and Jack Douthett. 1991. “Maximally Even Sets.” Journal of Music Theory 35: 93–173.
Clough, John, and Gerald Myerson. 1985. “Variety and Multiplicity in Diatonic Systems.” Journal of Music Theory 29, no. 2: 249–70.
—————. 1986. “Musical Scales and the Generalized Circle of Fifths.” American Mathematical Monthly 93, no. 9: 695–701.
Dahlhaus, Carl. 1990 [1968]. Untersuchungen über die Entstehung der harmonischen Tonalität. Kassel: Bärenreiter. [Studies on the Origin of Harmonic Tonality, trans. R. Gjerdingen. Princeton: Princeton University Press.]
De Jong, Karst, and Thomas Noll. 2011. “Fundamental Passacaglia: Harmonic Functions and the Modes of the Musical Tetractys.” In Mathematics and Computation in Music: Proceedings of the MCM 2011, ed. Carlos Agon et al. Berlin: Springer. Preview available at http://user.cs.tu-berlin.de/~noll/FundamentalPassacaglia.pdf.
Deleuze, Gilles. 1988. Le pli: Leibniz et le baroque. Paris: Les Éditions de Minuit.
Domínguez, Manuel, David Clampitt, and Thomas Noll. 2007. “Well-formed Scales, Maximally Even Sets and Christoffel Words.” In Mathematics and Computation in Music: First International Conference, Proceedings of the MCM 2007, ed. T. Klouche and T. Noll. Berlin: Springer.
—————. 2009. “Plain and Twisted Adjoints of Well-formed Words.” In Mathematics and Computation in Music. Proceedings of the MCM 2009 and the John Clough Memorial Conference, ed. E. Chew, A. Childs, C.-H. Chuan. Berlin: Springer.
Glarean, Heinrich. 1969 [1547]. Dodecachordon, Basel. Reprint Hildesheim: Olms.
Green, Burdette, and David Butler. 2002. “From Acoustics to Tonpsychologie.” In The Cambridge History of Western Music Theory, ed. Thomas Christensen. New York: Cambridge University Press.
Handschin, Jacques. 1948. Der Toncharakter: Eine Einführung in die Tonpsychologie. Zurich: Atlantis.
Harrison, Daniel. 1994. Harmonic Function in Chromatic Music: A Renewed Dualist Theory and an Account of Its Precedents. Chicago: The University of Chicago Press.
Kassel, Christian. 2004. “From Sturmian Morphisms to the Braid Group B4.” Presentation at the Workshop on Braid Groups and Applications, Banff International Research Station.
Kassel, Christian, and Christophe Reutenauer. 2007. “Sturmian Morphisms, the Braid Group B4, Christoffel Words and Bases of F2.” Annali di Matematica 186, no. 2: 317–39.
Langner, Gerald, and Michael Ochse. 2005. “The Neural Basis of Pitch and Harmony in the Auditory System.” Musicae Scientiae, special issue 2005–2006: 185–208.
Lothaire, M. 2002. Algebraic Combinatorics on Words. Cambridge: Cambridge University Press.
Louis, Rudolf, and Ludwig Thuille. 1907. Harmonielehre. Stuttgart: Ernst Klett.
Maier, Franz Michael. 1991. Jacques Handschins “Toncharakter.” Zu den Bedingungen seiner Entstehung (Beihefte zum Archiv für Musikwissenschaft 31). Stuttgart: Steiner.
Manin, Yuri I. 2006. “The Notion of Dimension in Geometry and Algebra.” Bulletin of the American Mathematical Society 43, no. 2: 139–61.
Mazzola, Guerino. 2002. The Topos of Music. Basel: Birkhäuser.
McCreless, Patrick. 1991. “Syntagmatics and Paradigmatics: Some Implications for the Analysis of Chromaticism in Tonal Music.” Music Theory Spectrum 13: 147–78.
Morris, Robert. 1982. “Review: Basic Atonal Theory by John Rahn.” Music Theory Spectrum 4: 138–54.
Morse, M., and G. A. Hedlund. 1938. “Symbolic Dynamics.” American Journal of Mathematics 60: 815–66.
—————. 1940. “Symbolic Dynamics II. Sturmian Trajectories.” American Journal of Mathematics 62: 1–42.
Noll, Thomas. 2003. “A Mathematical Model of Tone Apperception.” Manuscript. American Mathematical Association conference, Baton Rouge. Available at http://flp.cs.tu-berlin.de/~noll/BatonRougeDraft.pdf.
—————. 2007. “Musical Intervals and Special Linear Transfomations.” Journal of Mathematics and Music 1, no. 2: 121–37.
—————. 2009. “Ionian Theorem.” Journal of Mathematics and Music 3, no. 3: 137–51.
—————. 2011. “Well-Formed Scales and Alteration: An Arithmetic Investigation into Music Notation.” Presentation at the Joint Meetings in Mathematics, American Mathematical Society, Special Session on Mathematical Techniques in Musical Analysis, New Orleans.
Noll, Thomas, David Clampitt, and Manuel Domínguez. 2007. “What Sturmian Morphisms Reveal about Musical Scales and Tonality.” WORDS2007 Proceedings. Marseille: Centre International de Rencontres Mathématiques.
Regener, Eric. 1973. Pitch Notation and Equal Temperament: A Formal Study. Berkeley: University of California Press.
Shepard, Roger N. 1982. “Structural Representations of Musical Pitch.” In The Psychology of Music, ed. Diana Deutsch, New York: Academic Press.
Taruskin, Richard. 2005. Oxford History of Western Music, vol. 1. New York: Oxford University Press.
Tymoczko, Dmitri. 2009. “Generalizing Musical Intervals.” Journal of Music Theory 53: 227–54.
Žabka, Marek. 2010. “Well-Formedness in Two Dimensions: A Generalization of Carey and Clampitt’s Theorem.” Journal of Mathematics and Music 4, no. 1: 1–30.
Footnotes
* Acknowledgments: The authors are grateful to Emmanuel Amiot, Norman Carey, and Manuel Domínguez for numerous inspiring discussions about the content of this paper. They thank three anonymous referees for critical comments and suggestions. Thanks also to Michiel Schuijer for his helpful correspondence. The second author thanks Franz Michael Maier for enlightening conversations about the life and thought of Jacques Handschin, in particular about Handschin’s 1936 lecture in Barcelona from which the book Der Toncharakter eventually emerged.
Return to text
1. The non-degenerate qualifier refers to the stipulation that the resulting scale is not an equal division of the octave; that is, the remainder interval is of a different specific size from the generating interval. In the usual diatonic, the perfect fifth generates the scale modulo the octave, and the diminished fifth is the remainder interval. Equal divisions of the octave may be construed as degenerate well-formed, with respect to a given generating interval. See Carey and Clampitt 1989 and Carey and Clampitt 1996a.
Return to text
2. The mnemonic motivation for the letters G, D, and E is gauche, droite, and exchange.
Return to text
3. It is easy to see that G and G~ commute:
Return to text
4. The term “non-special” is not an established one in the mathematical literature. We use it in order to characterize Sturmian morphisms whose incidence matrix has determinant –1. Although “special” might sound like the marked pole of the general/special dichotomy, it is the non-special case that is marked here with respect to the special case (determinant 1). In our music-theoretical interpretation this parallels the marked status of the plagal modes with respect to unmarked authentic ones. Our positive/negative terminology is motivated by the proper unmarked/marked connotation as well as by the reference to the determinantal signs. We will not use the incidence matrices themselves in this paper. For more information on the incidence matrices, see Noll 2007.
Return to text
5. “Es besteht zwischen ihnen eine Nachbarschafts- und eine Verwandtschaftsbeziehung. Beide Beziehungen verhalten sich insofern gegensätzlich, als ein enges Nachbarschaftsverhältnis zwischen zwei (voneinander verschiedenen) Tönen ein enges Verwandtschaftsverhältnis ausschließt, und umgekehrt” (Louis and Thuille 1907, §57, 278).
Return to text
6. “Wenn ich diese «Charaktere» als die eigentlich musikalische Eigenschaft des Tons ansehe, möchte ich damit die Rolle der Tonhöhe und der Tonhöhenunterschiede nicht herabgesetzt haben. Die volle Mannigfaltigkeit der Musik als Melodie beruht auf dem Spiel dieser beiden Katagorien, die sich ständig durchkreuzen; und der im vollen Sinn «Musikalische» ist derjenige, der sowohl auf die inneren Tonbeziehungen eingestellt ist, als auch die Höhenabstufungen im Verhältnis zu jenen wahrnimmt...
Man könnte den Gegensatz den beiden einander durchkreuzenden Elementen in dem Sinn characterisieren, dass das eine von ihnen das äussere, sinnlich wahrnehmbare, das andere das innere, eigentlich «musikalische» ist” (Handschin 1948, §9, Durchkreuzung von Toncharakter und Tonhöhe, 25–26).
Return to text
7. Within the domain of cognitive psychology a related strand was initiated by the investigations of Roger N. Shepard, in collaboration with Carol Krumhansl, into multidimensional representations of musical pitch in connection with statistical analyses of empirical data (see, for example, Shepard 1982). One source represented the judgments of listeners concerning the amount of relatedness of the 12 chromatic pitches within the span of an octave to a pre-established tonic pitch. A four-dimensional INDSCAL solution to these 12-dimensional data points yields convincing confirmation of an ordering following the chromatic circle in a first instance and following the circle of fifths in a second instance.
Return to text
8. The generic-specific dichotomy necessarily involves the dichotomy between the discrete and the continuous, and therefore mathematical structures defined by integers, on the one hand, and real numbers, on the other. In subsection 1.3, therefore, reference to the specific level of description requires the invocation of mathematical structures such as the vector space ![]() n over the real numbers, that is, ordered n-tuples of real numbers (vectors) and the algebraic properties of addition of vectors and scalar multiplication of vectors by real numbers. Although this is assumed knowledge in the natural and social sciences, it is not in the tool kit of many music theorists. But our use of this armamentarium is more conceptual than technical, and we hope that the reader without a strong background will nonetheless glean an intuitive sense of the issues at hand. Alternatively, we suggest that the reader skip first to section 2, which proceeds from the generic (discrete) point of view and picks up the word-theoretical approach again.
n over the real numbers, that is, ordered n-tuples of real numbers (vectors) and the algebraic properties of addition of vectors and scalar multiplication of vectors by real numbers. Although this is assumed knowledge in the natural and social sciences, it is not in the tool kit of many music theorists. But our use of this armamentarium is more conceptual than technical, and we hope that the reader without a strong background will nonetheless glean an intuitive sense of the issues at hand. Alternatively, we suggest that the reader skip first to section 2, which proceeds from the generic (discrete) point of view and picks up the word-theoretical approach again.
Return to text
9. See Robert Morris’s review of John Rahn’s Basic Atonal Theory. Morris ascribes the view that sets related by M operators “don’t necessarily sound alike” to others, but acknowledges that it is widely held (Morris 1982, 152).
Return to text
10. Mazzola defines the linear pitch-height function on the Euler lattice (generated by octave, perfect fifth, and major third) and uses an expression for this linear function as a scalar product with a fixed pitch-height vector (Mazzola 2002, 1049–51). See paragraph 25 below for further consideration of this vector. NB: The sets ![]() x,
x, ![]() x, etc. are the sets of all integer (or real) multiples of x (or o)—e.g.,
x, etc. are the sets of all integer (or real) multiples of x (or o)—e.g., ![]() x = {zx|z∈
x = {zx|z∈![]() }.
}.
Return to text
11. For the reader who wishes to follow the linear algebra, the rows of the matrix effecting the change of coordinates may be derived as follows: The first row (x1, y1) of the matrix applied to a point in fifth-octave coordinates yields the specific width coordinate. Since the normalized specific width coordinate of
Return to text
12. The numerical approximations of the transformation matrices for equal temperament and Pythagorean tuning demonstrate their closeness:
 ,
, 
Return to text
13. For a purely mathematical formulation and proof of this fact without recourse to musical notation, see Noll 2009.
Return to text
14. Vittorio Cafagna favored the term winding number for the characterization of the multiplication factor in the automorphism of a well-formed scale (Cafagna and Noll 2003). We believe that the torus knots provide a suitable way to explicate the underlying idea.
Return to text
15. Although our approach is not deliberately dedicated to a psychological perspective, we allude to a historically illuminating connection of ideas. The mathematician Bernhard Riemann, who introduced the influential geometric concept of the manifold, was also motivated by ideas from Johann Friedrich Herbart’s psychology, who proposed generalized concepts of space for the study of perceptions and associations.
Return to text
16. See Noll 2003. For a recent and relevant discussion of musical intervals in a geometric setting, see Tymoczko 2009.
Return to text
17. As a matter of intellectual history, it is interesting to note that the term “well-formed scale” appeared in 1989, one year before the term “Christoffel word” was introduced in mathematics (in Berstel 1990, cited in Berstel et al. 2008). This is not to suggest any priority in the abstract concept, which goes back at least to the late nineteenth century (Christoffel 1875), but only to say that there was no standard mathematical terminology in the 1980s, in the earlier years of the mathematical theory of musical scales.
Return to text
18. The mathematical context and terminology is given briefly here. ![]() n
n![]() n
n![]() n
n![]() n,
n,![]() n
n![]() n.
n.
Return to text
19. “Wir müssen auch sagen, dass die Toncharaktere in höherem Maße mit der unbewußten Ton-Wahrnehmung und -Abschätzung zusammenhängen, die Tonhöhen dagegen mit der ‘bewußten’” (Handschin 1948, 28).
Return to text
20. Another motivation for generalization is its experimental potential, namely to access musically counterfactual structures and to explore them in musical experiments. It is good, though, to keep track of these motivations separately.
Return to text
21. This is sufficient for our purposes here, but clearly unless f as a composition of G’s and D’s is a palindrome, the different intermediate stages of computing f and the reversal of f are not themselves reversals of each other. The more refined view, distinguishing between substitutive (e.g., G and D) and concatenative (e.g., Γ and Δ) morphisms, allowing intermediate stages to be compared, was introduced in paragraphs 91 and 92. As mentioned previously, Noll 2009 permits us to confine ourselves to the (substitutive) Sturmian morphisms.
Return to text
22. In the word theory literature, central words are also characterized as independent structures using iterated palindromic closure (Lothaire 2002, Berstel et al. 2008). See also Clampitt and Noll 2009.
Return to text
23. See Christensen 2004, 180: “When designated at all by French theorists, the fourth scale degree was referred to as the soudominante (not to be confused with Rameau’s sous-dominante). It was the scale degree directly below the dominant, just as the leading tone was below the tonic and so sometimes referred to as the soutonique.” Christensen cites by way of example Jean-François Dandrieu, Principes de l’accompagnement du clavecin (Paris, 1719).
Return to text
Man könnte den Gegensatz den beiden einander durchkreuzenden Elementen in dem Sinn characterisieren, dass das eine von ihnen das äussere, sinnlich wahrnehmbare, das andere das innere, eigentlich «musikalische» ist” (Handschin 1948, §9, Durchkreuzung von Toncharakter und Tonhöhe, 25–26).
,
Copyright Statement
Copyright © 2011 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by John Reef, Editorial Assistant
Number of visits: