Rendering the Prosaic Persuasive: Gould and the Performance of Bach’s C-minor Prelude (WTC I)

[1] Portrayals of the pianist Glenn Gould are often contradictory. Some hear in Gould’s performances of Bach a deeply introspective, analytical, almost clinical rendering, whereas others celebrate the pianist’s passion, virtuosity, and hypnotic ecstasy.⁽¹⁾ Some listeners and viewers are so caught up with the strikingly unique qualities of Gould’s playing, his body, and his unconventional interpretations that they often claim that “the music” is lost in the haze. Yet many of these same critics also marvel at his ability to “X-ray” Bach’s compositions, to reveal the inner voices and clarify his complicated counterpoint.⁽²⁾

[2] These seemingly oppositional perspectives of Gould, the self-indulgent versus the analytical pianist, can be seen to reflect not only the different stages of his career but also the conflicting perceptions of the same performance. Consider his 1962 interpretation of Bach’s Prelude in C minor from Book One of the Well-Tempered Clavier (BWV 847), which is featured in both François Girard’s 1993 film, Thirty Two Short Films About Glenn Gould and The Triplets of Belleville (2003), directed by Sylvain Chomet. In the former we hear and see Gould’s recording as though from the inside of the piano, the hammers striking the strings and the dampers lifting in coordinated precision with the pianist’s unmistakable rendition (Example 1). This juxtaposition—the sight of the piano’s inner workings with the sound of Gould’s disembodied and detached, almost mechanistic interpretation—evokes an analytical perspective, an “X-ray” of the performance that reveals Gould’s calculated dissection of Bach’s Prelude.

[3] In The Triplets of Belleville, by contrast, we see a cartoon version of Gould playing Bach’s music on an old black-and-white television.⁽³⁾ This caricature of the pianist plays on a low chair with legs crossed and long tangled fingers. His eyes are shut and his body sways as though lost in the moment (Example 2). As the work progresses, Gould’s hands and elongated fingers cross over and under each other, visually twisting Bach’s multiple voices into a disjointed tangle as a metaphor for the piece’s impenetrable texture.

[4] One might excuse these conflicting interpretations of Bach’s Prelude and/or Gould’s interpretation of the work, by recognizing that neither film director is a professional pianist nor a music theorist. But they might be onto something. A closer look at Gould’s idiosyncratic performance both clarifies and obscures what traditional analytical techniques tell us about the C-minor Prelude. Gould’s unique articulation and voicing clarify the musical texture in a manner that illuminates less tractable issues in counterpoint, hypermeter, and harmonic tension. Yet, by comparing and contrasting Gould’s performative “X-ray” of the Prelude with that of other performers and editors, we will demonstrate how the pianist ultimately opens up new unresolved questions, while still generating what is, for many, an artistically compelling interpretation of this work.⁽⁴⁾

[5] The C-minor Prelude, described by Tovey as an “arpeggio prelude,” is harmonically driven (Tovey 1924, 26). With his characteristically detached articulation, however, Gould does more than merely outline the harmonic progression.⁽⁵⁾ Consider the opening four measures: like its C-major predecessor, the C-minor Prelude uses a standard progression to establish the tonic (here, i–iv–vii^o7–i). But as opposed to David Ledbetter’s claim that Bach intended this Prelude to help bring the “thumb and little finger into line with the middle three fingers” so that “all five fingers are equal,” Gould distinguishes the notes on the first and third beats with a sharp accent (Ledbetter 2002, 136 and 151; listen to Gould’s performance in Example 1). We hear the soprano melody prominently as it falls from its initial C to A♭ in measure 2 before returning to C in measure 4 by way of the leading tone.

[6] One further note on the opening of this performance; on the third beat of the first measure—and only on this beat—Gould slurs the lower neighbor figure, E♭4–D4–E♭4. This slight deviation from convention has two effects. First, it distinguishes Gould’s melody from its motoric accompaniment. Second, Gould demonstrates in his performance what many scholars have indicated in their analyses, namely that this figure, which is also brought out by Gould in the Prelude’s final measure (C5–B4–C5), anticipates the “mordent of the fugue subject” that follows (Keller 1976, 52). We will return to the potential significance of this figure for Gould below.

[7] With C minor established in measures 1–4, Bach commences a chain of suspensions in the outer voices that reaches E-flat major in measure 14; relatively stable harmonies in measures 5 and 7 (A♭ major and G minor) are followed by measures of harmonic instability (D and C). The path between these relative keys, however, allows for and even encourages a fascinating array of interpretive solutions from an equally varied group of performers. We will continue with Gould’s performance in order to frame the issues in these measures (Example 3a). In keeping with the style he introduced in the first four measures, Gould continues to articulate the first and third beats of each bar. But the expression of these notes varies in accordance with the inherent contrapuntal tension, thereby creating a two-bar hypermeter. Gould’s E♭5s, for instance, resonate much longer than their sixteenth-note duration would suggest. As the E♭5 falls to D5 in measure 6, however, the pianist changes his melodic articulation to sharp, short staccati. Gould repeats this strong-weak pattern again in measures 7–8.

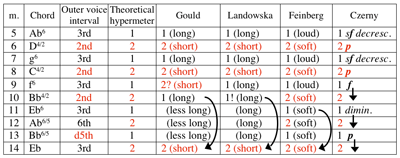
[8] Other pianists generate a similar two-bar hypermeter through different means. Samuel Feinberg, for instance, plays measures 5 and 7 loudly and with great gusto, retreating dramatically and dynamically in measures 6 and 8. (Example 3b) Other pianists such as Edwin Fischer, Sviatoslav Richter, Angela Hewitt, and András Schiff also create a subtle dynamic contrast that initiates a two-bar pattern starting in measure 5. Mostly strikingly Wanda Landowska, on her metal-framed Pleyel harpsichord, introduces a change of registration in measures 6 and 8 to distinguish them from the preceding measures. (Example 3c) Although each keyboardist leaves his or her own idiomatic mark on the Prelude, all of their interpretations respond to the harmonic and contrapuntal tension of the secondary dominants in measures 6 and 8 and the relative calm in the surrounding measures (5, 7, and 9).

[9] Nevertheless, given Gould’s reputation, it is tempting to assume that his distinctive articulation reflects an autonomous and fresh perspective. As we have just seen, his grouping of measure 5–8 resembles that of other musicians even if the manner in which he achieves that grouping stands apart. Additionally, many of his mannerisms correspond to the articulations given in an edition by Carl Czerny (first published by Peters in 1837) that he may have used or consulted (Example 4).⁽⁶⁾ In measures 1–2, for instance, Czerny’s accent on the first and third beats of each measure could very well have led to Gould’s introductory articulation. Similarly, the sforzandi at the beginning of measures 5 and 7 that diminish to piano in measures 6 and 8 suggest the hypermeter that Gould performs. The most significant link between Gould and the Czerny edition is the C in the left hand on the third beat of measure 18, an incorrect note (see Example 5) that the Czerny edition perpetuated (as did the 1866 Bach-Gesellschaft Ausgabe), and which Gould played. We would surmise that given his overall shaping of the Prelude (discussed more below), and his predilection for countrapuntal lines, Gould would have otherwise embraced the stepwise descent that a B♭ creates in measures 18–19 on the way to the dominant pedal in measure 21.⁽⁷⁾

[10] But where the harmonic and metric patterns of the first eight bars seem straightforward, this order is called into question after measure 9. Indeed, a closer look at the distribution of strong and weak measures in relationship with Bach’s harmony and counterpoint reveals an interesting problem. Looking ahead to measures 13–14, we find this pattern reversed harmonically. The diminished 5th from an unstable dominant harmony is prominent in between the outer voices of measure 13, while its resolution to a consonant 3rd, part of the newly established E♭ tonic, falls in measure 14 (See Figure 1a). How can we understand this reversal of consonance/dissonance within the two-bar hypermeter, or more to the point, to what understanding do Gould and other pianists lead us?

[11] Gould breaks away from the hypermeter in measure 9 where he maintains the short articulation of the downbeats (established in measures 6 and 8) and slightly increases the dynamic intensity. Once again, this dynamic contrast appears to resemble the editorial instructions in the Czerny edition. In measure 10, however, Gould makes a curious decision and returns to the ringing articulation first introduced in measure 5; the soprano B♭4 resonates over the entire measure. At first listen, one might understand measures 9–10 as a reversal of the hypermeter’s polarity, from the weaker (shorter) beat on the first measure of the pair, the stronger (longer) beat on the second.⁽⁸⁾ Indeed, these two bars could represent a transition in which the harmonic and contrapuntal pattern of the previous two measures is maintained while the metric emphasis switches in anticipation of the end of the phrase. But after measure 10, Gould continues to let the soprano note reverberate, ultimately suspending the hypermeter and eliminating the previously existing pattern as a plausible percept.

[12] There is no reason, however, why the hypermeter established in measures 5–8 cannot extend through the next three measures. The harmonic sequence and chain of suspensions continue through measure 11. Having reached his eventual tonal goal, Bach breaks the sequence in measure 12 and establishes E♭ major with a conventional cadential progression (IV–V–I). It is the introduction of the predominant here that forces a shift of some type. Although dominant-tonic pairs lay across “2–1” segments of the hypermeter during the sequence, it is not difficult to accept a reversal of the established harmonic/hypermetric linkage and instead privilege hypermetric continuation (see Figure 1b, first three columns).

[13] The performance by Feinberg presents an analysis that extends the sequence further than Gould in just this manner. Using dynamic contrast across the full bar rather than emphasis on individual notes, Feinberg establishes the two-bar hypermeter in measure 5 which he continues through measure 10 (see Figure 1b). In measure 11, Feinberg maintains the softer dynamic level of the previous measure, initiating a four-bar cadential phrase that resolves to E♭ (I⁶–IV–V–I). While he sets this cadential progression apart with a consistently soft dynamic level, he does nothing to disrupt the vestiges of the established hypermeter. Doing so he creates a phrase in measures 11–14 that mimics his own shaping of measures 1–4. In similar fashion, Czerny’s measure 9 moves away from the explicitly stressed pattern of the preceding measures, but his dynamic markings allow the established two-bar pairing to continue: forte in measures 9–10, diminuendo through measures 11–12, and piano in measures 13–14 (Figure 1b and Example 3).

[14] Although Gould muddies the hypermetric waters, his performance still carries within it a revealing logic. As the analysis in Figure 1 shows, Gould divides measures 5–14 into two groups of five bars that suggest rhetorically an antecedent-consequent phrase pair. As noted above, Gould’s oscillating articulations in measures 5–9 reinforce Bach’s harmonic sequence in its movement away from a stable key area. His gradual shortening of the soprano notes in measures 10–13 convey instead the sense of a single expansive teleological gesture leading into the more stable E♭ major in measure 14.

[15] Landowska’s interpretation represents something of a hybrid reading, one that combines features of both Gould’s and Feinberg’s. Like Feinberg, Landowska extends the two-bar hypermeter through measure 9. But like Gould, the harpsichordist marks measure 10 as the starting point for her own large-scale push towards the cadence in measure 14; this is her moment to disrupt the hypermeter, and it is more jarring than Gould’s disruption.⁽⁹⁾ Her instrument growls to a new level of intensity as the left-hand drops in register to more closely spaced and more dissonant patterns in measure 10, though she too uses consistently sustained soprano notes to weld these five bars together. Both Gould and Landowska in essence elide the sequence with the cadential progression, beginning a goal-oriented trajectory with the initial (and intra-sequential) occurrence of E♭’s dominant harmony, the B♭ in measure 10. A division at measure 10 brings a compelling balance to measures 5–14, the material between a typical key-establishing phrase (measures 1–4) and the tonic of the relative major (measure 14), while it creates interest by cutting across the audible boundary between sequence and cadential progression.

[16] Bach's score leaves open to interpretation the transition from sequence to cadential progression. Where Feinberg and Czerny follow the hypermetric structure and separate the cadence from the sequence in measure 11, Gould and Landowska disrupt the sequence, insisting on the inclusion of measure 10 as the moment that initiates the cadential drive. Indeed, it may be their intention to emphasize this cadence through the disruption of the hypermeter that also accounts for why they maintain intensity through measure 14, the opposite of Czerny and Feinberg, who pull away. Although all four musicians are unanimous in communicating a sense of arrival in m 14, each performer chooses a different path. Since each version uses a different moment of transition from sequence to cadence, to say nothing of their different means (dynamics, articulation, registration) and/or media (harpsichord, piano, score markings), comparing them is to compare apples and oranges (and pears and...). Nevertheless, Figure 1 attempts to demonstrate the diverse ways in which these musicians portray the organization and direction of Bach’s music.

[17] All three performers underscore their arrival in measure 14 by bringing out the soprano note on every quarter-note pulse (G4–E♭4–G4–E♭4), effectively changing the perceived meter from 2/2 to 4/4. In addition to the harmonic logic behind this shift of articulation, there is also a kinesthetic rationale behind it as well. This measure is the first time in the entire Prelude where the note on the second and fourth beats (E♭) sits above the offbeat mordent figures. One should be wary of suggesting that Bach changed his pattern specifically to emphasize this moment of arrival, since it was perhaps the closeness of both hands that forced Bach to write the E♭ in the elevated range. It is at the very least a happy coincidence that this change occurs at this cadential arrival and it should come as no surprise that all three musicians choose to subdivide the measure.

[18] Unlike most other musicians, however, who in measure 15 commence their push toward the dominant pedal, Gould transfers his articulation of the quarter-note pulse from the soprano of measure 14 to the bass line of measure 15, where he brings out the F3–E♭3–F3 on the second, third, and fourth beats; the F in the soprano still rings out on the downbeat (Example 3a). But he maintains this lower voice for a single measure before joining most other pianists and driving forward with a renewed feel of 2/2 in measure 16. How might this singular, idiosyncratic gesture that perhaps reinforces a self-indulgent image of Gould inversely shed light on Bach’s Prelude or, at the very least, on Gould’s conception of Bach?

[19] There are three explanations we can suggest. The first and most basic is that Gould’s voicing adds a degree of variety to the Prelude. Of this Prelude and the previous one, Gould writes: “Sometimes the preludes are just prosaically prefatory—the C-major and C-minor from volume 1 perhaps falling within that etudish category” (Gould 1984, 21). As a way to add interest to what might be taken for a finger exercise, the pianist gives voice to an impish gesture from within the left hand.

[20] But perhaps he is not so capricious. As mentioned above, Gould creates a transition from measures 14–15, using the suddenly subdivided half-note beat to elide the cadence in E-flat major with the harmonic departure that follows. The registral equality of all four beats that was noted in the right hand of measure 14 is replicated in the left hand of measure 15; the on-beat left hand pitches have never before been only a step apart. Gould makes the most of this link, using it to shift the emphasis from the soprano to the bass voice. With the ear now caught and directed to the lower range, it is easy for the listener to follow the subsequent descent of the bass line to G in measure 21, a descent that is emphasized by Gould.

[21] Is this stepwise bass motion interesting simply because it spans the better part of an octave? Our view is that Gould is doing something more. The analytical Gould is taking pains to show that this bass descent is simply a continuation of an overall stepwise descent beginning with the E♭5 of measure 5, the highest pitch in the first half of the Prelude as well as Schenker’s Kopfton. One can easily trace this descent in the upper voice to soprano G4 in measure 14, after which Schenker sees the line descending just two more steps to E♭4 in measure 18, completing a register transfer of the initial E♭5 (Schenker 1926, 48). Gould, focusing on line in general and not on voice-leading strata, takes measure 15 as the crux in a soprano-to-bass transition of the line; F4 arrives in the soprano and, with his peculiar dynamic encouragement, is itself transferred down an octave and heard as giving way to E♭3 in the bass.

[22] Gould’s overall achievement, then, is to divide the Prelude’s first 24 bars into two sections: the first a sequential departure from the tonic to the relative major (itself divided into two five-bar chunks, as discussed above), the second a return to the dominant harmony in C minor. Yet throughout, Gould maintains a larger sense of direction, tracing out for the listener the descending line that continues from the soprano’s E♭5 of measure 5 to the bass’s G2 of measure 21, from tonic to dominant.

[23] Finally, the three unique notes articulated by Gould in measure 15 resemble an augmented form of the three-note mordent figure originally noted in measure 1 of Gould’s performance, the same three notes that anticipate the subject of the Fugue. As Kevin Bazzana has argued, Gould’s interpretations were influenced by the idea of the developing variation of Brahms and Schoenberg (1997, 20–35). The pianist was known on more than one occasion to project innocuous or accompanimental lines, or to even change the notes in the score, in order to emphasize (or create) unifying motivic links (Bazzana 1997, 91–94). Indeed, as the Prelude continues after the texture change in measure 25, Gould alters the tempo regularly in order to frame this three-note figure.⁽¹⁰⁾ In the last measure, Gould allows the final C to continue ringing even as the concluding gesture continues, demarcating the end of the three-note figure (C5–B4–C5) heard at the top of the phrase.

[24] For those who believe in a clear distinction between the acts of composition and performance, of creation and interpretation, these final observations may beg the age-old question: how much of what we hear in Gould’s performance of this Prelude is imposed by the pianist or revealed within Bach’s score? In other words, is Gould X-raying the music in order to reveal its inner workings, or is he foisting his own whimsical and anachronistic aesthetic values onto the Prelude? The answer, it would seem, is both. More important, the observations in this article ultimately blur and undermine the distinction between these polar perspectives. Not only is Gould’s performance no less anachronistic than the analytical views of Schenker and other 20th-century theorists (even as they presume to speak for the composer’s intentions), but, as we have seen, the idiosyncrasies of his interpretation both reinforce and coincide with those qualities about which most analysts and performers appear to concur, e.g., the hypermeter in measures 5–8. In comparison with other editions and renditions, Gould’s performance draws our attention to complexities, tensions, and structures within Bach’s score that reveal the degree to which Bach’s Prelude is anything but prosaic.

Daniel Barolsky
700 College St.
Music Department
Beloit College
Beloit, WI 53511
barolskd@beloit.edu

Peter Martens
Texas Tech University
School of Music
Box 42033
Lubbock, TX 79409
peter.martens@ttu.edu 

Works Cited

Bazzana, Kevin. 1997. Glenn Gould: The Performer in the Work. Oxford: Clarendon Press.

—————. 2011. “FW: the Well Tempered Clavier.” E-mail to Daniel Barolsky. November 2, 2011 (sent via Mary Bond, Information and Research Services Division, Library and Archives Canada).

Gould, Glenn. 1984. “Art of the Fugue.” In The Glenn Gould Reader, ed. Tim Page, 15–22. New York: Alfred A. Knopf.

Keller, Hermann. 1976. The Well-Tempered Clavier by Johann Sebastian Bach. trans. Leigh Gerdine. New York: W. W. Norton, 1976.

Ledbetter, David. 2002. Bach’s Well-Tempered Clavier: The 48 Preludes and Fugues. New Haven: Yale University Press.

Martens, Peter. 2007. “Glenn Gould’s ‘Constant Rhythmic Reference Point’: Communicating Pulse in Bach’s Goldberg Variations, 1955 and 1981.” Music Theory Online 13, no. 4.
http://www.mtosmt.org/issues/mto.07.13.4/mto.07.13.4.martens.html

Ostwald, Peter F. 1997. Glenn Gould: The Ecstasy and Tragedy of Genius. New York: W. W. Norton.

Payzant, Geoffrey. 2005. Glenn Gould: Music and Mind. Toronto: Key Porter Books.

Said, Edward W. 2000. “Glenn Gould: The Virtuoso as Intellectual,” Raritan 20, no. 1: 1–16.

Schenker, Heinrich. 1926. “Das Organische der Fuge aufgezeigt an der I. C-moll-Fuge aus dem Woltemperierten Klavier von Joh. Seb. Bach,” in Das Meisterwerk in der Musik II, trans. Hedi Siegel as “The Organic Nature of Fugue as Demonstrated in the C minor Fugue from Bach’s Well-Tempered Clavier, Book I,” in The Masterwork in Music, edited by William Drabkin, Cambridge University Press, 1996, 31–54.

Temperley, David. 2008. “Hypermetrical Transitions.” Music Theory Spectrum 30, no. 2: 305–25.

Tovey, Donald Francis, ed. 1924. J.S. Bach: Forty-Eight Preludes and Fugues, Book I. London: The Associated Board of the Royal Schools of Music.

Discography

Gould, Glenn. 1962. The Well-Tempered Clavier I: Preludes and Fugues, Johann Sebastian Bach. Sony Classical SM2K 52600.

Feinberg, Samuel. 1959. Bach: The Well-Tempered Clavier (complete). Russian Disc 15013.

Fischer, Edwin. 1933. J.S. Bach: Well-Tempered Clavier, Book 1. Naxos Historical 8.110651-52.

Hewitt, Angela. 1998. Bach: The Well-Tempered Clavier, Book 1. Hyperion CDS44291/4.

Landowska, Wanda. 1949. Bach: The Landowska Recordings. RCA Red Seal 82876-67891.

Richter, Sviatoslav. 1969. Bach: Well-Tempered Clavier, Book I. RCA Red Seal 82876 62315.

Schiff, András. 1984. J.S. Bach: The Well-Tempered Clavier. Decca 4780391.

Filmography

The Triplets of Belleville. DVD. Directed by Sylvain Chomet. 2003; Sony Pictures Home Entertainment, 2004.

Thirty Two Short Films About Glenn Gould. DVD. Directed by François Girard. 1993; Sony Pictures, 2001.

Footnotes

1. Biographies by Peter F. Ostwald (1997) and Geoffrey Payzant (2005) explore Gould’s notion of ecstasy. By contrast, works by Kevin Bazzana (1997) and Edward W. Said (2000) examine Gould’s more critical and analytical side. In addition, Gould’s career is framed by two very different recordings of Bach’s Goldberg Variations, the first from 1955 and the second from 1981, and he comments on both during the 1981 recording sessions. These performances have come to represent the extremes of Gould’s interpretative development; see Martens 2007 for an analysis of Gould’s explicit manipulations of beat level in 1981 relative to 1955.
Return to text

2. Bazzana (1997, 90) notes that in his copy of Adorno’s Prisms, Gould “flagged a passage that reflected his own priorities as a performer: ‘True interpretation is an x-ray of the work; its task is to illuminate in the sensuous phenomenon the totality of all the characteristics and inter-relations which have been recognized through intensive study of the score.’”
Return to text

3. As of January 11, 2012, the Internet Movie Database lists Glenn Gould as the performer (http://www.imdb.com/title/tt0286244/soundtrack). A close listening reveals, however, that the recording is not Gould although it is clear to the authors that the pianist in the recording sought to emulate Gould’s idiosyncratic interpretation. Indeed, the pianist for the film captures Gould’s detached articulation but she or he fails to articulate the mordent in measure 1 and alter the articulation in measure 10 as Gould does in his 1962 recording as described below.
Return to text

4. See, for instance, Donald Satz’s review from 2001: http://www.bach-cantatas.com/NonVocal/Klavier-WTC1-Part1.htm (accessed January 11, 2012).
Return to text

5. For a discussion of Gould’s style and articulation and its broader context, see Bazzana 1997, 215–27.
Return to text

6. Bazzana 2011. Bazzana also states, however, “I don't think you can tell from his surviving scores which edition he used to learn a piece, only (in some cases) which one he used to record editing instructions, which is not necessarily significant.”
Return to text

7. For Gould’s interpretive construction of contrapuntal lines, see Bazzana 1997, 142–59.
Return to text

8. After Temperley (2008), this is a shift from odd-strong to even-strong hypermeter.
Return to text

9. Landowska’s interpretation is hybrid in another sense, relative to Temperley’s sudden and gradual hypermetric shifts. In measure 10, Landowska disrupts the 2-bar hypermeter suddenly, but its clear re-establishment is not evident until measure 14 or later. We might say, then, that the hypermeter of the intervening bars is more suspended than transitional.
Return to text

10. We would like to thank Mike Truesdell for this observation.
Return to text

Copyright Statement

Copyright © 2012 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.

Prepared by Michael McClimon, Editorial Assistant
Number of visits: