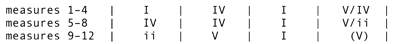“Possible Paths”: Schemata of Phrasing and Melody in Charlie Parker’s Blues

“I now understand improvisation as the real-time yet pre-heard—and even practiced—choice among possible paths that elaborate a pre-existing structure, using familiar patterns and their familiar combinations and embellishments.”—Steve Larson (2005, 272)

Introduction

[1.1] Charlie Parker was a master improviser. His extraordinary oeuvre carries an implicit question: how did he do it? How did he create such well-crafted melodies in the very act of performance? This is “the problem of improvisation”—a problem for both the improviser and the analyst.⁽¹⁾ Inspired by the epigraph from Steve Larson, this paper posits one kind of solution for Parker’s improvisations on the twelve-bar blues. I suggest that Parker developed two different sets of “possible paths” through the blues: phrase structures, to solve the problem of how to place phrases against a fixed meter; and melodic paths, to solve the problem of creating coherent melodies against a fixed harmonic structure. I call these paths schemata of phrasing and melody.

[1.2] The term “schemata” is most familiar from the work of Robert Gjerdingen on the galant style (2007). The galant composer confronted a similar “problem” to the bebop improviser: high-speed composition. Gjerdingen’s schemata are recurring patterns of scale-degrees. Through artful elaboration and combination of pre-learned schemata, galant musicians could compose efficiently and expressively. Without using this term, jazz scholars have similarly speculated that the improviser draws on a pre-learned repertory of (pitch-based) musical materials. An improviser imprints this repertory through practice, so that it spontaneously emerges in a solo. My schemata are based on this same view of improvisation. They are Parker’s raw improvisational materials, highly flexible in their details and application, and they facilitate efficient composition (to put it mildly). They inhabit two domains: melody, in the form of recurring sequences of scale-degrees (very similar to Gjerdingen’s); and phrasing, in the form of recurring relationships between phrasing and meter. The interaction of these domains further increases Parker’s economy of means: the same melodic schema sounds quite different when laid over two different phrasing schemata.

[1.3] The twelve-bar blues has been a basis for jazz improvisation perhaps longer than any other form. Example 1 gives a metrical-harmonic outline of a bebop blues.⁽²⁾ There are three four-bar hypermeasures, describing a single harmonic phrase. The first hypermeasure prolongs tonic, the second hypermeasure moves to the subdominant and then back to tonic, and the third hypermeasure presents a ii–V–I cadence.⁽³⁾ Harmonic substitution and interpolation are common; but alterations preserve the opening establishment of tonic, measure 5 motion to the subdominant, and cadence terminating in measure 11.⁽⁴⁾ Charlie Parker had a particularly intimate relationship with the blues: it represents around a quarter of Parker’s recorded output, and it likely constituted an equivalent portion of his practice time (Martin 1996, 3). It is only natural that he would develop shortcuts to improvising on this familiar form.

[1.4] To identify schemata, I sought recurring patterns in a sample of Parker’s blues. This sample included thirty-nine recorded performances totaling 156 improvised choruses, dating from between 1944 and 1953, after Parker’s style had reached maturity (Owens 1974, vol. 1, 5). These thirty-nine performances fit two criteria, one practical, the other theoretical: a recording and published transcription were readily available;⁽⁵⁾ and the tempo was at least 160 quarter-notes per minute.⁽⁶⁾ I speculate that the patterns in this sample would be found throughout Parker’s blues performances.

The Solo as Interpretation⁽⁷⁾

[2.1] The form of a bebop performance is often described as following a theme-and-variations model; this familiar analogy needs refining. The technique of “bebop variation” might be better understood if we distinguish how the theme’s three elements of meter, harmony, and melody are treated during the solos. The metrical structure of a solo, from the level of the quarter-note beat through the level of the chorus, is entirely based on that of the theme. During the performance, the musicians and experienced listeners maintain continual awareness of this structure, anticipating the downbeats of each measure, hypermeasure, and chorus. Any metrical dissonance is superimposed on this structure without threatening it. (Indeed, true disruption of the meter, in the form of added or subtracted beats or measures, is viewed as a mistake.) The ensemble or soloist can alter the harmonic structure, but they tend to preserve the harmonic middleground. In contrast with both of these elements—rigid meter, elastic harmony—the soloist’s melody is free.

[2.2] How is the soloist’s melody free? Though experts differ on this point, it is safe to claim that Parker usually avoids obvious thematic reference, and his practice is not unusual.⁽⁸⁾ Furthermore, the phrase structure of the melody need not follow the theme or the hypermeter. Example 2 illustrates this: through rests, Parker creates the phrase structure 2/8/2, with the last phrase spilling into the next chorus. I call such phrase structures “dissonant,” because the phrasing contradicts the theme’s 4/4/4 hypermeter (and the 4/4/4 phrase structure of the theme’s melody). (By extension, phrase structures in alignment with the meter are “consonant.”) Example 2 also demonstrates the soloist’s freedom to deviate even from the theme’s essential harmonic structure (though this is rarer): Parker follows the theme’s pre-dominant harmony in measure 9, but ignores the rest of the cadence. Instead, the final two measures of the chorus are filled with highly altered dominant harmony, as a long lead-in to the next chorus. Parker suppresses the theme’s final tonic resolution altogether.

[2.3] Because of the melody’s freedom, the solo is best understood not as a variation on the theme, but as an interpretation of it: a solo may follow the theme’s harmony, melody, or phrase structure, or it may not. To the extent a solo deviates from its theme, it presents a new, revised structure. As another example, soloists commonly transform a theme’s half-cadence and restart—“→V || I→”—into a full cadence by playing across the dominant and ending a phrase on the tonic: “→V→I||”. Such flexibility represents a major difference between bebop and common-practice strophic variation. Whereas the bebop soloist may reinforce, ignore, or revise the theme, in strophic variation, melody, harmony, and meter work in concert to elaborate the theme or an underlying common structure. The resemblance is much stronger between bebop and continuous (ostinato) variation. Consider the excerpt from “Dido’s Lament” shown in Example 3: in measures 32, 39, and 44, against an unwavering ostinato, the voice variously establishes a half-cadence, an elided cadence, and a full cadence. The ostinato is a foil to the vocalist, who may reinforce or revise its “natural” grouping and harmonic structure; the aggregate effect varies from cycle to cycle. Parker’s relationship to the theme is identical. The interpretive view of improvisation leads me to abandon the assumption of a consistent chorus-level structure. Instead, schemata describe the structures Parker actively creates.

Phrasing Schemata⁽⁹⁾

[3.1] Unlike thirty-two bar themes with eight-bar sections, the blues has no metrical or formal level between the four-bar hypermeasure and the complete chorus. The blues’ brevity increases the risk that a multi-chorus solo will become tedious. Furthermore, the blues’ three hypermeasures oppose the duple construction typical of eight- and sixteen-bar sections. These features heighten the improviser’s “meter problem”: how to organize phrases in a varied way over a repetitive metrical structure, without the need for continual invention.

[3.2] I propose that Parker solved the problem with phrasing schemata. Each is a “path” through the metrical structure of one blues chorus, an adaptable template for where phrases begin and end. For example, one common schema is 8/4: an eight-measure phrase followed by a four-measure phrase (the phrases may be further divided). By “phrase,” I do not mean a tonally defined phrase terminating in a cadence. Given a repetitive harmonic structure, the soloist has only limited control over those. Rather, I use the term in a deliberately colloquial sense: a phrase is a continuous musical gesture, surrounded by rests. These phrases are highly variable across choruses and performances. Soloists exert total control over their placement.

[3.3] Several authors mention phrasing as a broadly interesting aspect of jazz, though few explore it in detailed analysis.⁽¹⁰⁾ One exception to this is Steve Larson. In his analyses, he comments on the metrical lengths of phrases and describes the effect of “sentences” and “reverse sentences” (1993, 292–93; 1996, 154; 1999a, 298–99). He implicitly follows the colloquial definition for phrase given above. Contemplating an extended metrical dissonance in a Bill Evans solo, Larson even points to the concept of the metrical schema: “To make such a journey through the ‘metric space’ of this piece . . . Evans must have known that metric space intimately, must have internalized its possible basic rhythmic paths securely, and must have developed many ways of traveling those paths flexibly and fluently” (2005, 255). Though phrasing schemata are a more general kind of path, the core idea of “rhythmic paths” is common to both approaches.

[3.4] To refine the phrase’s colloquial definition, first I invoke three musical features that suggest a phrase division: inter-onset interval (IOI, or the time between subsequent attacks); melodic discontinuity; and proximity of a strong beat.⁽¹¹⁾ Taken together, these features establish the lowest-level phrase divisions in a chorus. Example 4 illustrates my approach. At the lowest level, we might identify six segments, separated in the example with dotted lines.⁽¹²⁾ The three features of IOI, discontinuity, and strong beat, in combination with other factors, especially melodic parallelism, further imply a hierarchy of phrases above this lowest level. In Example 4, the segments in measures 1–8 are united by their approximate parallelism and the closure suggested in measure 7 by the return of ♮$\hat{3}$ over tonic; melodic continuity unites the segments in measures 9–11 (up-down contour and Db–C connection); and these groups of segments are separated by the chorus’s longest IOI in measures 7–9. The lowest level might be modeled 2/2/2/2/2/2; the next level up is 8/4 (numbers correspond approximately with length in measures). Like many choruses, this chorus has a single deepest phrase division, shown with a double bracket, which I call the “primary division.”

[3.5] Phrasing schemata name the highest level of phrase structure within the chorus. In the case of Example 4, the schema is 8/4. This designation glosses over the chorus’s lower-level subtleties but permits comparison with other choruses that fit the same pattern. In total, I identify five phrasing schemata: 4/4/4, 8/4, 4/8, 6/6, and Through-Composed (TC). Example 5 depicts the group. The 8/4, 4/8, and 6/6 schemata have a primary division: they create a level of phrase structure between the 4/4/4 hypermeter and the twelve-measure chorus. 4/4/4 and TC do not exhibit any obvious phrase structure beyond the hypermetrical level. The schemata are defined exhaustively—in theory, every chorus can fit into one category or another, and most are easy to classify. However, when phrasing factors conflict, ambiguity can arise. Below, I discuss each schema in more depth and analyze two ambiguous choruses. Then I present data on schema frequency and syntax.

[3.6] In the 4/4/4 schema, there are two phrase divisions of comparable significance at or near the downbeats of measures 5 and 9. The phrase structure follows the hypermetrical structure, and can seem square or predictable: overly consonant. Example 6a is typical: the metrical rhyme between the three phrases highlights their equal status. Metrical rhyme (“rhyme” hereafter) is a form of parallelism among phrases arising when they begin or end at (or near) the same relative point in a measure or hypermeasure (Love 2012, 25). It would not make sense to group only two of the three rhyming phrases at a higher level. Example 6b also suggests 4/4/4, though it exhibits more complexity. The first two phrases are divided, but not the third. The second and third phrases begin at the same point in their hypermeasures (“beginning-rhyme”), and the tense ♯$\hat{5}$ in measure 8 blurs these phrases into a single gesture of tension-release. However, none of these factors decisively groups an adjacent pair of four-measure phrases together, as would suggest 8/4 or 4/8; 4/4/4 seems the best analysis.

[3.7] We have already seen one instance of the 8/4 schema in Example 4; two more appear as Examples 7a and 7b (below, Examples 21, 23, and 25 also follow 8/4). In this schema, the primary division falls in measure 7 or 8, roughly aligned with the division between the second and third hypermeasures. The effect is consonant: a seven-measure elaboration of tonic, separate from the more energetic cadence. In Example 4 above, the constituent phrases are further divided into two-measure segments; in Example 7a, the phrases are undivided, unfolding as continuous gestures and separated by a long rest. This pattern is common at fast tempos. In Example 7b, the eight-measure phrase is divided, but the stepwise connection from F to E♭ across measures 4–5 links its two subphrases together. The faster rhythm of the final four-measure phrase sets it apart. However, compared to Examples 4 and 7a, the eight-measure phrase is open-ended: Parker extends it past the tonic in measure 7, to V/ii. (Cf. Example 6b, measure 8, from the same performance, where other factors establish 4/4/4.)

[3.8] The 4/8 schema is the counterpart to 8/4, grouping the chorus’s second two hypermeasures together. The primary division falls before the arrival of IV in measure 5, roughly in line with the first hypermetrical division. Example 8a is typical. Measures 5–11 unfold as a single phrase, with a subphrase division in measure 9. (The A♭ in measure 12 is a pickup to the next chorus.) Note that Parker downplays the return to tonic in measure 7, so that the opening tonic prolongation seems only to occupy measures 1–4, with pre-dominant extending from measures 5–9.⁽¹³⁾ The 4/8 schema places the resulting “extended pre-dominant” (measure 5–9) in a single phrase with the final cadence. The listener might perceive an early increase in tension, as the drive to the cadence begins four measures earlier than in the 8/4 schema. Example 8b is another realization of 4/8. Though the long IOI (measures 3–4) firmly establishes the primary division, Parker presents a clear return to tonic in measure 7 (anticipated in measure 6), unlike in Example 8a. This can be interpreted as a passing chord (along with V/ii in measure 8) within a larger motion from IV to ii. The melody’s propulsive energy makes it unlikely that measure 7 would be heard as a stable return to the opening harmony. Example 8c deviates further from the prototypical form of 4/8: a long descent from $\hat{5}$ to $\hat{1}$ in measures 7–8 (a delayed variant of the “Descent to $\hat{1}$” schema, discussed below) emphasizes tonic and suppresses V/ii. Although the long phrase still spans the pre-dominant area, such a pronounced return to tonic is unusual. As a result, one might hear two distinct, overlapping phrases: IV–I | I–ii–V (measures 5–8 | 8–10).⁽¹⁴⁾

[3.9] In the 6/6 schema, the primary division falls between the IV chord in measure 5 and the return to tonic in measure 7. This causes two kinds of dissonance: between six-measure phrases and four-measure hypermeasures, and between phrasing and middleground harmonic structure. Whether one hears an extended tonic in measures 1–7 or an extended pre-dominant in measures 5–9, the primary division divides this area. Parker tends to present 6/6 with little ambiguity, using a long IOI at the primary division. This is evident in Examples 9a and 9b. (Other 6/6 choruses are Examples 15, 22, and 24, below.) Example 9b includes a sizable IOI in measures 8–9, a rival to the primary division, and an unusual feature for a 6/6 chorus. Parker’s subdivision of each six-measure phrase into 2/4 reinforces the chorus-level 6/6 structure: the subphrase in measures 1–2 has its counterpart in measures 7–8, and the subphrases in measures 3–5 and 9–11 nearly rhyme (compare their starting and ending beats). But the two-bar displacement with the hypermeter makes this parallelism hard to hear.

[3.10] TC choruses do not fit into any of the other categories. They may have phrase divisions in the “wrong” places, as in Example 10a, where Parker divides the first and last hypermeasures (cf. Example 2 above: another 2/8/2 structure). The long phrase from measures 2–9 is balanced by a brief final phrase that restores order: note the end-rhyme between measures 9 and 11, creating a sense of closure. (This has a remarkable counterpart in the beginning-rhyme between measures 0 and 2!) At faster tempos, TC choruses sometimes have no phrase divisions at all, as in Example 10b. TC and 6/6 choruses generally sound more dissonant than 8/4 and 4/8, whose primary divisions align with a hypermetrical division.

[3.11] Example 11a lends itself to multiple interpretations. Its phrase divisions in measures 4 and 6 point to 4/8 or 6/6. However, Parker blurs both of these, such that neither is likely to suggest the depth of a true primary division. The rhyme between the endings in measures 2, 4, and 6 cuts across the division in measure 4: all three subphrases end on beat 6.5 of a two-bar hypermeasure. The beginning-rhyme between measures 1, 3, 5, and 7—all four phrases begin just before a two-bar downbeat—cuts across both divisions, as does the unified up-down contour of measures 3–9—note especially the link between the high F in measure 5 and E in measure 6. It would be hard to hear a primary division anywhere in this chorus. Ultimately, I would classify this as TC by default, though the “square” placement of its divisions distinguishes it from most TC choruses.

[3.12] In Example 11b, Parker blurs the phrase divisions more subtly. Again, 4/8 and 6/6 are plausible interpretations. However, the first phrase ends on a note of tension at measure 4: B♭, the flat seventh, and a relative high point. The transparent voice leading from this B♭ to the A in measure 5 weakens the first division. The long IOI in measures 6–7 would initially indicate 6/6; but the parallelism between the phrase-beginnings in measures 5 and 7, arpeggiating through a dominant-seventh chord on IV and I, challenges this interpretation. One could decide between these possibilities by favoring one factor over another: an analyst emphasizing IOI would probably call this a 6/6 chorus; another, focusing on melodic continuity, would group the parallel beginnings in measures 5 and 7 together as part of a larger phrase, and call this a 4/8 chorus.

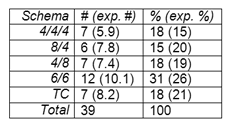
[3.13] For statistical purposes, I classified each of the 156 choruses as one schema or another—a problematic exercise, as Examples 11a and 11b illustrate. Thus, my findings should be taken with several grains of salt. Tables 1–3 present some of my results. In terms of overall schema frequency (table 1), no schema stands out in an obvious way, though 6/6 appears slightly more often than would be expected if the schemata were distributed at random. Tables 2 and 3 address the question of whether Parker prefers certain schemata for the first or last chorus of a solo. The tables compare Parker’s actual use of each schema in initial or final position with its expected use, given the overall schema frequencies in Table 1. None of the deviations from expectations are statistically significant. Another way to put this: knowing where a chorus fits in a larger solo makes it no easier to predict its phrasing schema.

[3.14] I also considered the question of whether Parker showed a preference for consistency or variety of phrasing between successive choruses. For example, if he uses the 6/6 schema in a particular chorus, is he more likely than expected to use it in the next chorus? That would suggest Parker prefers consistency from chorus to chorus. Or is it the case that, for example, if he uses the 6/6 schema in one chorus, he is less likely than expected to use it in the next chorus, disproportionately favoring other types? That would suggest he prefers variety from chorus to chorus. In fact, having considered 117 chorus-to-chorus successions, I could identify no such preferences: knowing what type of chorus Parker just played makes it no easier to predict what type of chorus he will play next.

[3.15] The absence of clear positional preferences or syntax may lead to doubts about the significance of phrasing to Parker himself. On this matter, possible points of view range from “Parker knew exactly what he was doing” to “The recurrence of these schemata is a coincidence arising from Parker’s consideration of other matters.” Surely, sometimes chorus-level phrase structures are a byproduct of other features—especially in the case of ambiguous choruses. But it is inconceivable to me that Parker did not have at least an intuitive sense of chorus-level phrase structure: for example, an awareness that all 6/6 choruses were alike in an important way, and that they embodied a certain metrical tension compared to, say, 4/4/4 choruses.⁽¹⁵⁾ I believe the schemata are an effective way of understanding recurring phrase structures—Parker’s solutions to the meter problem—and that they have some analog in Parker’s mind.⁽¹⁶⁾

Melodic Schemata

[4.1] Though Parker is free to deviate from the blues’ harmonic structure, he tends to work within it. This poses the harmony problem: how to improvise varied melodies roughly following the harmony, without the need to compose “from scratch” each time. I propose that Parker solved this problem with the melodic schemata: recurring stepwise paths, spanning around one to eight measures, which a melody seems to follow.⁽¹⁷⁾ Example 12 illustrates one schema commonly found in measures 4–7 of Parker’s blues, the “Descent to $\hat{1}$,” including $\hat{6}$–$\hat{5}$–$\hat{4}$–♭$\hat{3}$–$\hat{2}$–$\hat{1}$ in its complete form. (In this and subsequent examples, schematic notes are beamed together, and “Descent” is abbreviated to “D.”) Note that the path is interrupted several times by intervening notes.⁽¹⁸⁾ Schemata can also be interrupted by rests, or presented without interruption: one note after the other. (Since interrupted schemata tend to be more interesting, I focus on them here.)

[4.2] I identified schemata by observing salient stepwise paths throughout the corpus. Given the density of notes in a typical Parker solo and the stepwise voice leading built into the blues’ harmonic progression, it is possible to find many stepwise patterns, especially when interrupted schemata open the door for unsupported, “connect-the-dots” analysis. To counter this, I required that schemata contain at least three scale degrees. Furthermore, I preferred that the schematic notes on either side of an interruption be emphasized in some way. Emphases arise from duration, register, meter, dynamics, and placement within a phrase (proximity to the beginning or end). This is not a strict requirement, but it motivated me to reject many possible analyses. In the remainder of this section, I compare the schematic approach with similar approaches. Then I present four common melodic schemata.

[4.3] The schematic approach has two significant antecedents in jazz scholarship: formulaic analysis and Schenkerian analysis. In his seminal 1974 dissertation on Parker, Thomas Owens identifies approximately one hundred melodic formulas, ranging from four-note fragments to multi-measure phrases, that recur throughout Parker’s work.⁽¹⁹⁾ Though they often appear in verbatim repetition, Parker also subjects the formulas to “metric displacement, augmentation and diminution, addition and subtraction of notes, and altered phrasing and articulation” (vol. 1, ix). As the raw materials of improvisation, subject to local variation, each is thus a kind of schema.⁽²⁰⁾

[4.4] Compared to Owens’s formulas, the schemata consider more abstract melodic connections. Example 13 shows Owens’s examples of the “M.10” formula, $\hat{4}$–$\hat{1}$–$\hat{2}$–♭$\hat{3}$, which often occurs in measure 5 or 6 of the blues. Owens notes the variety of other formulas that can precede M.10, labeled in the example with “M.x”. However, I see common patterns here, shown with the dotted beams and stems: all of these excerpts realize a portion of the Descent to $\hat{1}$ (and the Descent from $\hat{1}$, described below). I view the “M.10” formula as a means by which Parker moves from $\hat{4}$ to ♭$\hat{3}$ within the Descent to $\hat{1}$. Thus, from my perspective, Parker can realize the melodic schemata through one or more formulas.⁽²¹⁾

[4.5] Another abstract feature of the schemata, relative to formulas (as typically understood), is that schemata are not key-specific: whereas formulas are commonly understood as embodied in muscle memory, thus, key-specific, Parker’s melodic schemata appear in all keys, including unusual keys like D♭.⁽²²⁾ Example 8c above illustrates this: Parker includes a late Descent to $\hat{1}$ from $\hat{5}$ (measures 7–8), as well as the delayed variant of “$\hat{1}$/ii” (measures 9–10; schema introduced below). The recurrence of these patterns even in an unusual key suggests that the schemata’s scale-degree identities have significance for Parker, instead of their tactile identities.

[4.6] Steve Larson, on the other hand, applies tools of orthodox Schenkerian analysis to jazz melody.⁽²³⁾ In this paper’s epigraph, Larson (2005) refers to two kinds of “pre-heard” materials. First, there are “possible paths,” which are stepwise middleground voice-leading paths through the pre-composed chord progression of a theme, typically involving one note per harmony. These are elaborated by a vocabulary of “familiar patterns”: Schenkerian diminutions, including octave transfers, motion to and from inner voices, linear progressions, and neighbor notes. Henry Martin refers to a similar vocabulary of middleground ideas in Parker’s work: “The same higher-level [voice-leading] structures may recur from piece to piece” (1996, 23). Though he does not say so explicitly, Martin implies that these structures form a part of Parker’s unconscious improvisational vocabulary (20–39). Austin Gross’s approach, in his work on Bill Evans (Gross 2011), is especially close to my own: he identifies recurring patterns (“paradigms”) across multiple performances of the same tune (110), situates his analyses between the surface and a theme’s deepest voice leading (4–5, 7), and argues that the paradigms were Evans’s solution to the improvisation problem (36–39). His approach is firmly aligned with Schenkerianism: he derives the paradigms from the tune’s harmonic structure and frequently invokes Schenkerian orthodoxy.

[4.7] I share the Schenkerians’ concern for melodic structures veiled by elaboration. However, there are two crucial differences between schematic and Schenkerian analysis. First, the schemata imply no structural levels. Consider Example 12 again: nothing in the example per se implies that the schematic notes constitute a deeper level; that would require an additional assumption. I argue that these notes’ significance comes only from their perceptual salience and their recurrence in analogous examples. The other main difference is that schemata are not tied to particular harmonic implications. Though they recur in specific harmonic “Zones” of the blues (roughly measures 1–7 and 8–11), their note-to-note harmonic meaning is contingent on other factors. Parker varies the placement of specific notes: in realizations of the Descent to $\hat{1}$, $\hat{6}$ sometimes enters in measure 4, as the thirteenth of V/IV (as in Example 12), sometimes in measure 5, as the third of IV. Neither form is the “true” form. Parker also varies the schema’s pacing: the same schema might last a single measure or five measures. Alterations in placement or timing should not be taken to change their identities, though it may have significant analytical consequences. The schematic notes simply are particular notes of the melody, not an abstract structure derived from or necessarily related to the harmony. Schematic notes do tend to relate to the harmony in tonally meaningful ways. But there is nothing in the schematic approach that presupposes this. Minimizing abstraction in this way comes at the expense of coherence: schematic voices seldom last more than a few measures before disintegrating. Overall, the schemata balance formulas’ perceptual immediacy with Schenkerians’ concern for medium-range stepwise connections.

[4.8] Example 14 shows, over a blues in C, the four schemata described in this paper: Descent from $\hat{1}$, Descent to $\hat{1}$, $\hat{1}$/ii, and $\hat{4}$/ii. This might be taken as Parker’s roadmap of the blues. Each schema falls in one of two “Zones” within the blues. Within their respective Zones, I have placed the schemata in an idealized fashion relative to the harmony; this is for convenience only, and does not represent a norm. The Zones divide the chorus roughly in half. Zone 1 spans the motion to and from the subdominant—roughly measures 1–7, with most activity taking place in measures 4–7. Zone 2 encompasses the chorus’s final ii–V–I cadence and the preparation for the ii chord—roughly measures 7–11, with 8–10 the most active area. (Though the Zone 2 schemata are named for the note that falls over the ii chord, they typically include a stepwise prefix or suffix, as shown.) The upward shift in register across measure 7 is not merely an artifact of this example, but also an element of many choruses. Given Parker’s preference for descending schemata in Zone 1, and the registral limitations of the saxophone, registral shifts in measures 6–8 are to be expected. This is analogous to the carriage return on a typewriter: it gives Parker a fresh octave to fill in.

[4.9] The two Zone 1 schemata recur with clockwork regularity: nearly every chorus I studied had significant portions of one or both. The first of these to be considered, the Descent to $\hat{1}$, was introduced in Example 12 in its prototypical, complete form: $\hat{6}$–$\hat{5}$–$\hat{4}$–♭$\hat{3}$–$\hat{2}$–$\hat{1}$. Before discussing the other schemata, let us consider the range of modifications each may undergo, taking the Descent to $\hat{1}$ as our model. These include truncation, extension, division, and inflection.

[4.10] Example 15 includes a truncated form of the Descent to $\hat{1}$: Parker descends only to ♭$\hat{3}$ before abandoning the schema. I identify this as a Descent to $\hat{1}$, though $\hat{1}$ is never reached, because of its similarity to complete forms found elsewhere. Notice how in this example, Parker resolves the dissonant $\hat{6}$ to $\hat{5}$ within measure 4, whereas in Example 12, he delayed resolution until measure 5—by which time $\hat{5}$ was no longer a consonance. $\hat{5}$–$\hat{4}$–♭$\hat{3}$ and ♭$\hat{3}$–$\hat{2}$–$\hat{1}$ are two other common truncated forms of the Descent to $\hat{1}$. The counterpart to truncation is extension. In Example 16, Parker extends the schema past $\hat{1}$ to $\hat{7}$.

[4.11] Division and inflection pull a schema further from its prototypical form. In Example 17 the schema is divided into $\hat{6}$–$\hat{5}$–$\hat{4}$–♭$\hat{3}$ / ♭$\hat{3}$–$\hat{2}$–$\hat{1}$. I unite this schema across the intervening phrase division and octave transfer because of Parker’s treatment of ♭$\hat{3}$: it first appears in measure 5 and reappears in measure 6. Notice that Parker delays $\hat{1}$ until measure 7, later than in previous examples. Example 18 illustrates the Descent to $\hat{1}$ as transformed by truncation, division, and chromatic inflection. Parker delays the descent of $\hat{4}$ and resolves it to $\hat{3}$, not ♭$\hat{3}$, in order to agree with the tonic harmony. Parker’s reiteration of $\hat{5}$–$\hat{4}$ at the end of measure 6 helps establish continuity across a long IOI.⁽²⁴⁾

[4.12] The other Zone 1 schema, “Descent from $\hat{1}$” ($\hat{1}$–♭$\hat{7}$–$\hat{6}$), seldom appears in isolation. Instead, it usually occurs with the Descent to $\hat{1}$, in one of two ways: as a lower-voice counterpoint, or combined into a single motion. Example 19 models both possibilities. As a lower-voice counterpoint (Example 19a), Descent from $\hat{1}$ typically enters before Descent to $\hat{1}$, and the latter begins from $\hat{5}$. As a result, $\hat{5}$ forms a dissonant seventh over the alto voice’s $\hat{6}$. Example 20 shows a realization of this.⁽²⁵⁾ More rarely, the Zone 1 schemata are combined into a single Descent from $\hat{1}$ to $\hat{1}$ through an octave (Example 19b). Above, Examples 2 and 10b present this combination across measures 4–6. In Example 21 the descent spans measures 3–9, and the schema falls quite dissonantly: ♭$\hat{6}$ is a thirteenth over V/IV, $\hat{5}$ is a ninth over IV, and $\hat{2}$ is a ninth over I.⁽²⁶⁾

[4.13] The Zone 2 schemata are named for the note Parker uses to define the ii chord, $\hat{1}$/ii or $\hat{4}$/ii. This note may appear anywhere within measures 9–10; when part of a schema, it adjoins a stepwise passage leading to or away from the note—a “prefix” or “suffix.” Example 22 illustrates $\hat{1}$/ii: in measures 8–9, the prefix of a chromatic descent from $\hat{2}$, with arpeggiations implying iii⁷–♭iii⁷–ii⁷, is standard for Parker (cf. Examples 2, 10a); the suffix in measures 9–10 recurs in near-verbatim repetition in many of Parker’s improvisations, making it a classic “formula” (cf. Examples 6b, 7b). In isolation, $\hat{2}$–$\hat{1}$–$\hat{7}$ or $\hat{1}$–$\hat{7}$–$\hat{6}$–$\hat{5}$ appear as alternate realizations of $\hat{1}$/ii.

[4.14] Often, Parker delays $\hat{2}$–$\hat{1}$–$\hat{7}$ so that $\hat{1}$ no longer signals the arrival of ii, but rather, the departure from ii to V: the seventh of ii⁷, descending to the third of V. Example 23 shows this, along with the (optional) subsequent resolution of $\hat{7}$ to $\hat{1}$.⁽²⁷⁾ It even includes a chromatic passing tone between $\hat{2}$ and $\hat{1}$, just as in Example 22, but two measures later. Such examples might be taken to realize a different schema altogether—perhaps “$\hat{2}$/ii”. I prefer to emphasize the similarities between these cases.

[4.15] In the schema $\hat{4}$/ii, $\hat{4}$ is usually approached by a descent from (♭)$\hat{7}$, the (flat) ninth of a V/ii chord. Example 24 is typical, including the subsequent resolution of $\hat{4}$ to $\hat{3}$.⁽²⁸⁾ In the next chorus of the same solo, Parker varies this schema in a remarkable way, as shown in Example 25. First, the descent begins from $\hat{7}$, not ♭$\hat{7}$; more significantly, it continues through an entire octave, terminating on $\hat{7}$ over the V chord in measure 10. Another view of this melody is as a combination of $\hat{4}$/ii and $\hat{1}$/ii. Stepwise motions define the arrival on and departure from ii: $\hat{5}$–$\hat{4}$ represents V/ii→ii, while $\hat{1}$–$\hat{7}$ represents ii→V. Also note the remarkable parallelism between C♭–B♭ in measure 5 and E–D in measure 7 (on the same relative beat): the first two notes of two schemata (Descent to $\hat{1}$ and the approach to $\hat{4}$/ii), interrupted by a subsequent phrase division, then continued. This example illustrates the flexibility with which Parker places schemata within subphrases.

[4.16] Though I specify four schemata, ubiquitous in this corpus, I do not believe that each was so circumscribed in Parker’s mind.⁽²⁹⁾ Rather, I attribute to Parker a strong (unconscious) preference for some paths over others. The schemata are a theoretical model of these preferences, not intended to represent Parker’s own understanding. A different theorist might arrive at slightly different but equally valid versions of the same four schemata. Furthermore, I omitted other possible schemata for the sake of brevity. Consider this an introduction to the schematic approach, rather than an authoritative list of “the” schemata.

Analysis: “Perhaps” (1948)

[5.1] Schematic analysis of Parker’s three-chorus solo on “Perhaps” (Example 26) will illustrate the variety possible even when using a small number of schemata. The same melodic schemata recur throughout the solo, with different phrasing.

[5.2] Chorus 1 (Example 26a) includes both Zone 1 schemata. The Descent from $\hat{1}$ is presented in two different ways: across measures 1–5, with an early descent to $\hat{6}$ in measure 3 followed by a recovery of ♭$\hat{7}$ in measure 4; and at the very end of measure 4 leading into measure 5.⁽³⁰⁾ These dovetail into a Descent to $\hat{1}$. Note how the phrase structure brings out this schema’s consonant placement: ♭$\hat{7}$ resolves to $\hat{6}$ on the downbeat of measure 5, an arrival highlighted by the preceding subphrase division; the subphrase division in measure 6 neatly divides the Descent to $\hat{1}$ by harmonic function, presenting $\hat{6}$–$\hat{5}$–$\hat{4}$ as an elaboration of IV ($\hat{5}$ is a clear passing tone) and ♭$\hat{3}$–$\hat{2}$–$\hat{1}$ as a return to I.

[5.3] No phrase division separates the Zones (in any chorus). In Zone 2, Parker employs $\hat{4}$/ii preceded by a descent from (♭)$\hat{7}$. At first, $\hat{3}$ arrives too early, as a suspended ninth over ii (measure 9). This note’s duration and the subsequent subphrase division highlight the dissonance. $\hat{3}$ descends to $\hat{2}$ in measure 11, again a dissonant ninth, now over tonic. Rather than resolving $\hat{2}$ to $\hat{1}$, as might be expected, Parker ultimately slides it back up to $\hat{3}$.⁽³¹⁾ I hear $\hat{3}$ as more salient than the earlier $\hat{1}$ because $\hat{3}$ falls on a stronger beat and receives further emphasis from the preceding scoop. The phrase structure of chorus 1 creates consonance in Zone 1 and dissonance in Zone 2—a motion from stability to tension appropriate for a solo’s beginning. At the chorus level, the Through-Composed phrasing schema emerges from all this, but it appears to be a consequence of other choices.

[5.4] The second and third choruses vary the structure of chorus 1 in different ways, through alteration of phrasing, timing, and the schemata themselves. In chorus 2 (Example 26b), measures 1–7, the melodic schemata play against the phrasing and metrical-harmonic structure. The Descent from $\hat{1}$ is a lower-voice counterpoint to the Descent to $\hat{1}$. Parker delays both schemata so that $\hat{6}$ does not arrive until halfway through measure 5—contrast this with its downbeat arrival in chorus 1. $\hat{5}$ in measure 5 now functions as an incomplete neighbor, rather than a passing tone as in chorus 1. Finally, $\hat{1}$ arrives earlier, in measure 6, failing to coincide with the measure 7 return to tonic. Parker proceeds directly to the $\hat{7}$ that will ultimately descend to $\hat{4}$/ii. No phrase divisions clarify the harmonic implications of these motions. Instead, the chorus’s primary division (measure 8) divides the approach to $\hat{4}$/ii. The placement of the primary division points to a chorus-level 8/4 phrasing schema. This division provides a necessary breath (literally and figuratively); its interruption of the drive towards $\hat{4}$/ii, however, creates anticipation for the line to continue. $\hat{4}$ arrives in alignment with the ii in measure 9. A subphrase division highlights this local consonance, balancing the analogous dissonance in chorus 1 ($\hat{3}$ in measure 9). Parker delays the arrival of $\hat{3}$ (measure 11) by embedding within the chorus’s final subphrase the other Zone 2 schema: the delayed variant of $\hat{1}$/ii. Only after this does $\hat{3}$ arrive.⁽³²⁾ Thus, both Zone 2 schemata appear in counterpoint, as in Zone 1.

[5.5] In chorus 3 (Example 26c), Parker truncates and interrupts both Zone 1 schemata. These alterations are especially effective because Parker has already presented the schemata twice: an attentive listener is likely to expect the full schemata again. The chorus’s primary division (measure 4) establishes the 4/8 chorus-level schema. It interrupts the Descent from $\hat{1}$, and $\hat{6}$ never arrives. (Contrast this with the interruption, in chorus 2, of the approach to $\hat{4}$/ii, which is ultimately completed.) Instead, Parker abandons this descent to present a blues-inflected, abbreviated Descent to $\hat{1}$ (measures 5–6)—interrupted by another phrase division. Parker downplays the arrival on $\hat{1}$, continuing directly to ♭$\hat{7}$ in measure 7 and giving a blue color to the tonic harmony as well. The high register, truncated schemata, and dissonance between phrasing and melody create tension suggestive of a climax. The blue ♭$\hat{7}$ (measure 7), originally sounding as a minor seventh above tonic, is converted to a flat ninth of V/ii in measure 8. There is a remarkable parallelism between measures 5–6 and 7–8: Parker introduces ♭$\hat{3}$ (measure 5) and ♭$\hat{7}$ (measure 7) on a two-bar downbeat; exactly six beats later in each case, he restates this note prior to a stepwise descent. This parallelism helps differentiate the melodic schemata, despite the lack of a rest between them. Parker’s treatment of $\hat{4}$/ii might be seen as a consonant revision of the analogous motion in chorus 1. Whereas in chorus 1, Parker highlights chordal ninths, in chorus 3, Parker emphasizes $\hat{4}$ and $\hat{2}$ over ii, aligns $\hat{3}$ with the arrival on tonic (measure 11), and reinforces the resulting consonances with a subphrase division. This mirrors the consonance of the solo’s opening measures, and reduces tension to prepare the next solo.⁽³³⁾

[5.6] Larson argues, “The real work of producing such improvisations happens not on stage or in the recording studio, but in the practice room,” where familiar paths are internalized (2005, 258). A stock of pre-learned schemata is necessary but not sufficient for skilled improvisation. With his mind freed from basic issues of melodic construction, Parker’s true mastery comes through in the coherence of this solo, with opening consonance, a dissonant climax, and consonant resolution.

Conclusion

[6.1] This study focused on the twelve-bar blues, a metrical-harmonic structure with which Parker was especially intimate. But if these speculations have a sound basis, then schemata are not confined to the twelve-bar blues or Charlie Parker. Any experienced improviser, playing bebop variations on a familiar and predictable metrical-harmonic structure, would come to employ schemata of these kinds: favored solutions to that structure’s problems. “Familiar metrical-harmonic structures” include not only specific themes, but also structures common across the thematic repertory: with respect to meter, the eight-bar sections of the thirty-two-bar song; with respect to harmony, any stereotypical progression, for example, I | V/ii | ii | V. Future research might seek phrasing and melodic schemata in these places.

[6.2] To make accurate generalizations, the schematic approach requires consideration of a large, coherent sample in order to distinguish the most common “possible paths” from mere local variation. In an oral tradition like jazz, this can be a demanding requirement. However, the techniques of identifying and comparing chorus-level phrase structures and melodic paths work equally well within a single solo. As seen in “Perhaps,” a schematic analysis of a single solo can bring out how each chorus varies or abandons the material of previous choruses, while making no assumptions about a chorus’s relationship to the theme. Grounding this analysis in the context of a musician’s or style’s most common schemata is valuable but not necessary.

[6.3] The schemata leave much about a solo unexplained. Fortunately, nothing about the schematic approach precludes its combination with other analytical techniques to view a solo from as many angles as possible. These techniques may shed light on Parker’s creative process; they may help guide our hearing. But theorists needn’t worry about “explaining” a solo completely: there will always remain a great deal of the ineffable about a brilliant Parker solo.

Stefan C. Love
University of Chicago
Department of Music
sclove@outlook.com

Works Cited

Aebersold, Jamey, et al. 1978. Charlie Parker Omnibook. Atlantic Music Corp.

Alper, Garth. 2005. “How the Flexibility of the Blues Has Helped Shaped the Jazz Language.” College Music Symposium 45: 1–12.

Downs, Clive. 2001. “Metric Displacement in the Improvisation of Charlie Christian.” Annual Review of Jazz Studies 11: 39–68.

Gjerdingen, Robert O. 2007. Music in the Galant Style. New York: Oxford University Press.

Gross, Austin Andrew. 2011. “Bill Evans and the Craft of Improvisation.” PhD diss., University of Rochester.

Hanninen, Dora. 2001. “Orientations, Criteria, Segments: A General Theory of Segmentation for Musical Analysis.” Journal of Music Theory 45, no. 2: 345–433.

Johnson-Laird, P.N. 2002. “How Jazz Musicians Improvise.” Music Perception 19, no. 3: 415–42.

Kenny, Barry. 1999. “Structure in Jazz Improvisation: A Formulaic Analysis of the Improvisations of Bill Evans.” Annual Review of Jazz Studies 10: 163–94.

Koch, Lawrence O. 1982. “Harmonic Approaches to the Twelve-Bar Blues Form.” Annual Review of Jazz Studies 1: 559–71.

Larson, Steve. 1993. “Dave McKenna’s Performance of ‘Have You Met Miss Jones?’” American Music 11, no. 3: 283–315.

—————. 1996. “The Art of Charlie Parker’s Rhetoric.” Annual Review of Jazz Studies 8: 141–66.

—————. 1997. “The Problem of Prolongation in Tonal Music: Terminology, Perception, and Expressive Meaning.” Journal of Music Theory 41, no. 1: 101–36.

—————. 1998. “Schenkerian Analysis of Modern Jazz: Questions About Method.” Music Theory Spectrum 20, no. 2: 209–41.

—————. 1999a. “Swing and Motive in Three Performances by Oscar Peterson.” Journal of Music Theory 43, no. 2: 283–314.

—————. 1999b. Review: The American Popular Ballad of the Golden Era, 1924–1950, by Allen Forte; The Music of George Gershwin, by Steven E. Gilbert; Charlie Parker and Thematic Improvisation, by Henry Martin. Music Theory Spectrum 21, no. 1: 110–21.

—————. 2005. “Composition Versus Improvisation?” Journal of Music Theory 49, no. 2: 241–75.

Love, Stefan. 2011. “On Phrase Rhythm in Jazz.” PhD diss., University of Rochester.

—————. 2012. “An Approach to Phrase Rhythm in Jazz.” Journal of Jazz Studies 8, no. 1: 4–32.

—————. Forthcoming. “Subliminal Dissonance or ‘Consonance’? Two Views of Jazz Meter.” Music Theory Spectrum.

Martin, Henry. 1988. “Jazz Harmony: A Syntactic Background.” Annual Review of Jazz Studies 4: 9–30.

—————. 1996. Charlie Parker and Thematic Improvisation. Lanham, MD: The Scarecrow Press.

Owens, Thomas. 1974. “Charlie Parker: Techniques of Improvisation.” PhD Thesis, UCLA.

Schachter, Carl. 1999. Unfoldings: Essays in Schenkerian Theory and Analysis. New York: Oxford University Press.

Smith, Gregory. 1983. “Homer, Gregory, and Bill Evans: The Theory of Formulaic Composition in the Context of Jazz Piano Improvisation.” PhD diss., Harvard University.

Strunk, Steven. 1979. “The Harmony of Early Bop: A Layered Approach.” Journal of Jazz Studies 6: 4–53.

Terefenko, Dariusz. 2009. “Jazz Transformations of the ii7–V7–I Progression.” Current Research in Jazz 1.

Waters, Keith. 1996. “Blurring the Barline: Metric Displacement in the Piano Solos of Herbie Hancock.” Annual Review of Jazz Studies 8: 19–37.

Footnotes

1. The characterization of improvisation as “problem-solving” was notably employed by pianist Bill Evans (Gross 2011, especially Chapter 1). It is employed here to capture the cognitive challenges of jazz performance.
Return to text

2. An important feature of bebop blues is the harmony of the final cadence, ii–V–I; traditional styles use V–IV–I.
Return to text

3. But see paragraph 3.8 and note 13, below.
Return to text

4. For a fuller treatment of jazz harmonic practice, see Martin 1988, Strunk 1979, or Terefenko 2009; for more on blues harmony, see Alper 2005 or Koch 1982.
Return to text

5. The transcriptions were drawn from two invaluable sources: Owens 1974 and Aebersold 1978, referenced as necessary. I edited transcriptions for accuracy and clarity.
Return to text

6. Most recordings I considered easily exceeded this tempo restriction. I imposed the restriction because at slower tempos Parker tends to play primarily sixteenth-notes rather than eighth-notes, altering his melodic construction. Martin similarly observes that Parker uses fewer melodic formulas at slower tempos (1996, 39).
Return to text

7. This section includes some material distilled from Love 2012 and forthcoming, especially on meter in jazz.
Return to text

8. Thomas Owens argues that the theme has no effect on Parker’s solos (1974, vol. 1, 178); Martin (1996) devotes an entire book to demonstrating the contrary, though the connections he describes are subtle.
Return to text

9. The theory of jazz phrasing outlined here is explored in greater depth in Love 2012. Paragraph 3.1 draws on Love 2011, 143–45.
Return to text

10. Discussions appear in Downs 2001, Martin 1996, 112, and Owens 1974, 14. Waters (1996, 23) touches on the closely related issue of hypermeter.
Return to text

11. Clive Downs defines the jazz phrase similarly, but in a far more rigid way (2001, 42). P.N. Johnson-Laird stops short of a clear-cut definition, but offers similar criteria (2002, 432). These criteria also relate to the general criteria of “segmentation” elaborated in Hanninen 2001.
Return to text

12. The precise placement of a phrase division within an IOI is determined by nearby strong beats. For example, in Example 4, the first division falls before the rest in measure 2 because the downbeat of measure 2 is the precise point of division; similarly, the division in measure 6 falls as near as possible to the downbeat of measure 6. See Love 2012, 11–14 for further clarification.
Return to text

13. Therefore, the blues’ harmonic structure is essentially ambiguous with respect to when pre-dominant function begins: measure 9, at ii, or measure 5, at IV (continuing through passing harmonies in measures 7–8 until ii in measure 9). The soloist may suggest either interpretation, or something in between. Carl Schachter (1999) perceives a parallel ambiguity in many common-practice examples.
Return to text

14. In Love 2012, 23–24, I further discuss the concept of phrase overlap in jazz.
Return to text

15. Unfortunately, Parker never addressed these issues directly in interviews; other jazz musicians, however, express conscious understanding of phrasing along the lines suggested here.
Return to text

16. Austin Gross speculates along similar lines about Bill Evans’s awareness of recurring melodic patterns in his solos (2011, 219).
Return to text

17. The idea that there is something special about stepwise paths gains support from Larson’s work on tonal prolongation (1997): a note that is a step away from a previous note seems to “displace” it, even if other, non-step-related notes intervene.
Return to text

18. “Interruption” refers only to the temporary disruption of a schema by an intervening note or phrase division; it is not intended to carry any of its Schenkerian connotations.
Return to text

19. Though Owens calls these “motives,” I use the term “formulas,” following Martin 1996, in order to distinguish them from motives subject to local development.
Return to text

20. Henry Martin’s article appearing in this issue discusses formulas further. Whether or not it adequately describes the bare facts of improvised melodies, Johnson-Laird challenges the formulaic approach as cognitively “impracticable” (2002, 430).
Return to text

21. Martin understands Parker’s formulas similarly: “What keeps Parker’s formulas . . . from sounding mechanical or stale is his ability to integrate them into a coherent whole characterized by voice-leading fluency” (1996, 118).
Return to text

22. Thanks to Henry Martin for pointing this out.
Return to text

23. Larson defends the orthodox approach to jazz in 1998 and 1999b.
Return to text

24. Larson might call this a “confirmation,” when “two versions of the same descending linear progression [at different levels] are completed at the same time” (2005, 253).
Return to text

25. Examples. 4, 7a, 9a, 9b, 10a, 11b, 23, and 25 also feature the two Zone 1 schemata in counterpoint. Examples. 9a and 11b have a truncated Descent to $\hat{1}$. In Example 6a, the Descent from $\hat{1}$ proceeds past $\hat{6}$ all the way to $\hat{4}$ (B♭, measure 5)— a “Descent to $\hat{1}$” in the key of IV! Then Parker makes the usual leap through a 7th, this time to ♭$\hat{3}$ (A♭, in measure 6), and descends to $\hat{1}$.
Return to text

26. Example 22 contains another remarkable combination of Zone 1 schemata, quite similar to that in Example 6a (discussed in note 25 above): in measures 4–5, the Descent from $\hat{1}$ proceeds all the way to $\hat{4}$ (measure 5: B♭); $\hat{4}$ is transferred up an octave (measure 6) and continues through ♭$\hat{3}$ in measure 6 and $\hat{2}$–$\hat{1}$ in measure 7.
Return to text

27. The delayed variant of $\hat{1}$/ii may also be seen in Examples 8a, 9a, 15, and 18.
Return to text

28. $\hat{4}$/ii may also be seen in Examples 6a and 11a, where Parker delays the arrival of $\hat{4}$. In Examples 9a and 9b, $\hat{4}$/ii is preceded only by $\hat{5}$. Examples. 9a and 15 include a striking chromatic approach to $\hat{4}$.
Return to text

29. This distinguishes them from Gjerdingen’s schemata, some of which were given names and definitions by composers of the time—most famously, Joseph Riepel’s Monte, Ponte, and Fonte.
Return to text

30. With respect to Example 26a, measures 1–5, the scrupulous reader might accuse me of contradicting my earlier dismissal of the melodic hierarchy: doesn’t the small Descent from $\hat{1}$ (measures 4–5) embedded within a larger Descent from $\hat{1}$ (measures 1–5) imply two different levels? This is simply a matter of perspective: I consider this to be two instances of the same schema that share a first note, traversing the same path at different speeds.
Return to text

31. The use of $\hat{3}$/I instead of $\hat{1}$ may be taken as a reference to the theme of “Perhaps”, which also features $\hat{3}$/I on the downbeat of measure 11. Parker’s use of ♭$\hat{7}$ in measure 8 is another possible thematic reference. Martin further discusses this solo along these lines (1996, 102–05).
Return to text

32. More locally, $\hat{3}$ concludes a stepwise descent from ♭$\hat{6}$ in measure 10. This is another example of a Larsonian “confirmation” (see note 24): both descents reach $\hat{3}$ at the same moment.
Return to text

33. The use of a phrase extension that continues into the next chorus, as seen here in measures 11–13, is a stylistic cliché with two roles: it creates a smooth transition to the next soloist, and, as a cliché, it alerts the ensemble and the listeners that the solo is over.
Return to text

Copyright Statement

Copyright © 2012 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.

Prepared by Michael McClimon, Editorial Assistant
Number of visits: