Species Counterpoint with a Moveable Tenor (SCAMET): Comparing Species Counterpoint and Polyphonic Music Without a Cantus Firmus

Efforts to discover laws of art can then, at best, produce results something like those of a good comparison: that is, they can influence the way in which the sense organ of the subject, the observer, orients itself to the attributes of the object observed.

Arnold Schoenberg.

Introduction

[1] This article applies a modified species-counterpoint model, entitled species counterpoint with a moveable tenor, or SCAMET, to compare species counterpoint and “real music” (as it is so often called in the classroom). The aim of the model is to show how species counterpoint exercises might be compared with works of polyphonic music without a species cantus firmus. To my knowledge, this has not been undertaken in a systematic manner suitable for the modern classroom (although near the end of the article, I shall discuss some noteworthy instances in which the question has been raised). While something like SCAMET appears in the work of other scholars (notably Henry Martin’s Counterpoint: A Species Approach Based on Schenker’s Counterpoint [2005] and Peter Schubert’s Modal Counterpoint, Renaissance Style [1999, 2008]) under the rubrics of “mixed values,” “mixed counterpoint,” or “free counterpoint,” nowhere is a comparison between species counterpoint and actual musical scores presented with the clarity of this model.

[2] Species counterpoint is normally used as a vehicle for teaching basic voice leading in the form of contrapuntal exercises. The principal limitation forbidding its application to actual music lies in the cantus firmus “tenor” part, a slow-moving melody against which counterpointed voice parts are placed in regulated measure (one counterpoint note against one cantus note, two counterpoint notes against one cantus note, etc.). While the slow moving “tenor” cantus is excellent for teaching basic species counterpoint, a slow cantus-like melody confined to one voice part is a rarity in real music. This complicates comparison between actual musical scores and species-contrapuntal exercises.

[3] The model described here remedies this problem. In lieu of a slow-moving “tenor” cantus firmus or “hard melody,” it proposes a succession of individual “hard notes” of varying durations. These “tenor” hard notes are not necessarily confined to one voice part, but instead can move between parts (for example, from the actual tenor voice for a whole note, to the altus for a half note, and then the bassus for a quarter, etc.). In essence, the hard note is the note of longest duration at any given moment, in any voice. Counterpointed voices are led against the hard note in corresponding duration (in the measure of the species as appropriate) and in any voice part. In applying SCAMET to real music, then, the student observes the voice-leading relationships of the moveable hard note to the notes in counterpointed voices as these might compare with a species-counterpoint exercise.

[4] The voice-leading rules observed in this article are taken largely from Salzer and Schachter’s esteemed Counterpoint in Composition (1969), and the rules therein for two-part species counterpoint: first species (pages 12–20), second species (39–46), third species (56–65), fourth species (78–86), and fifth species (101–106). I have drawn on this text in counterpoint classes, but any other clear articulation of species rules (such as Henry Martin’s, noted above) could take the place of Salzer and Schachter’s text. Regardless of text or particular rules, the SCAMET method is intended to complement an undergraduate course in species counterpoint. Advanced work along the lines of SCAMET but oriented toward analysis would require a more subtle and exhaustive framework of contrapuntal rules and guidelines along lines set forth, for example, by Peter Schubert (2008).

[5] The aim of this article—to show how species counterpoint might compare with instances of real music—is framed by the desire to bring musical scores into the species-counterpoint classroom. To this end, I draw upon modern performance editions readily available to students (and where necessary note editorial decisions or characteristics of the original score notation that might have an effect upon SCAMET decisions). I apply the SCAMET model to excerpts of works taken from Lasso, Isaac, Ockeghem, Purcell, Gesualdo, J.S. Bach, Corelli, Haydn, Mozart, Beethoven, and Shostakovich. I begin with simple comparisons intended merely to demonstrate the method. I conclude, however, by drawing comparisons of greater complexity to show something of the possibilities the method holds for describing sophisticated contrapuntal features.

The Model

[6] In species counterpoint instruction after Fux (e.g., Salzer and Schachter 1969, 12), the following three familiar rules are applied in classroom instruction.⁽¹⁾ Rule 1, which we shall call the proportion rule, stipulates that the counterpoint voice (“counterpoint” hereafter) must move against the cantus firmus voice (“cantus” hereafter) in a strictly regulated rhythmic proportion. The cantus comprises a series of long notes against which the counterpoint moves in equal or faster note values. The rhythmic relationship of counterpoint to cantus can be expressed as a ratio: 1:1 (one note of counterpoint to one of cantus), 2:1, and 4:1 (allowing for slight alterations and combinations of these in the fourth and fifth species). Rule 2, the constant cantus speed rule, stipulates that the duration of notes in the cantus must remain the same throughout the exercise in question (usually taking the duration of a whole note in a species exercise). Rule 3, the voice-identity rule, stipulates that the cantus must be confined to its own voice, often the “tenor,” and the counterpoint confined to its own voice or voices, throughout the exercise.

[7] The SCAMET model proposed here keeps largely to the first rule; it uses the conventional proportions of species counterpoint. As noted above, however, it applies these proportions to one note—a hard note—individually and in any voice part (but see paragraph 11, below). It treats the longest note at any one moment in a piece of counterpoint as if it were equivalent to a single note of a cantus. The first rule is modified thus:

1. Hard note. The hard note constitutes a long note in any given voice against which a counterpoint voice moves in shorter note values. The rhythmic relationship between the two voices can be expressed as a ratio indicating the note lengths of the counterpoint against the note lengths of the hard note: 1:1, 2:1, or 4:1, allowing for slight alterations and combinations of these in the fourth and fifth species.

[8] The model, however, markedly transforms rules 2 and 3. It allows for a hard note to be of any duration in a given instance. And it allows for successive hard notes to wander between voice parts beginning, for example, in the tenor for one note and then migrating to the superius for the next, much as a subject (or soggetto) in imitative counterpoint will migrate from voice to voice at a point of imitation.⁽²⁾ We shall call this proposition the moveable hard note. As a new rule 2, it stands in lieu of the former rules 2 (constant cantus speed) and 3 (voice identity):

2. Moveable hard note. A moveable hard note comprises at least two instances of a hard note in succession. One or both of the following conditions can apply:

2.1. The duration of the hard note changes from instance to instance.

2.2. The hard note passes between individual voice parts.

[9] The application of the SCAMET model will become more fruitful if one more clause is added to the new rule 2, allowing for a fictive hard note—a supplement—that shall be called a logical hard note:

2.3. A fictive “logical” hard note will be postulated where this aids in the understanding of a contrapuntal passage.

We call this fictional note “logical” because its choice should involve a voice-leading logic, wherever possible. In setting that logic, let us invoke customary rules of voice leading. For instance, the choice of logical hard note could observe one of the following familiar voice-leading constraints:

2.3.1. The logical hard note relates to a prior note in a real voice part as if it were a suspension thereof, or

2.3.2. The logical hard note relates to a prior note in a real voice part as if it were approached by stepwise motion from that note, or

2.3.3. The logical hard note relates to a prior note in a real voice part as if it were approached by consonant leap from that note.

The application of these logical constraints should allow for flexibility, as for example with the octave displacement of the logical hard note from its voice-leading predecessor.

[10] Without recourse to a logical hard note, many passages of polyphony will forbid comparison to species counterpoint. This is not to suggest that such passages are defective in any sense, for composers set their own compositional frameworks independent of constraints such as the species model. The use of logical hard notes merely opens more possibilities for comparison of scores to species counterpoint. In this regard, the student of counterpoint should have little trouble mastering the basic notion of logical hard note if a methodologically comparable notion—that of a postulated chordal root—is borne in mind. Like the chordal root, the logical hard note is merely a vehicle for making a comparison between assumed or attributed norms and specific musical passages.

[11] The principal difficulty with the concept of a hard note in general and a logical hard note in particular lies in its application. Often several possibilities will suggest themselves (where, for example, the longest duration appears in the score in several voices at the same time). Some of these can be winnowed away following the guidelines suggested above. Other possibilities might be eliminated for stylistic reasons—for example, to avoid the cross relation where uncharacteristic. The principal criterion for the choice of a logical hard note should be its utility in making comparisons with the score. Let the following guideline apply:

2.3.4. The choice of hard note should be determined by its utility in making comparisons between the score and species counterpoint. Two or more hard notes may be considered individually (in separate examples) if they yield independent and fruitful comparisons.

In some instances of multi-voiced counterpoint, however, two or more simultaneous hard notes will suggest themselves as equal in utility—and they may be considered together, in a single example. In such instances, simultaneous hard notes (normally whole notes) will be written in the species exercise and presumed to be of equal weight.

In the specific examples under consideration below, I shall refine the notions of both hard and logical hard notes.

[12] Finally, in a texture of three or more voices the model assumes the successive (rather than the simultaneous) composition of counterpointed voices. By this we mean that each counterpoint voice relates by the guidelines of species counterpoint to the hard-note voice, but not necessarily to another counterpoint voice. On this account, each counterpoint voice stands on its own in relationship to the hard note as if it were one layer, part of a process of enveloping the hard note with independent layers of counterpoint.⁽³⁾ Successive composition allows us to examine dissonance arising between counterpoint parts in a texture of three or more voices as the fortuitous byproduct of independent two-voice counterpoints. It allows us as well to delimit the application of the method: where dissonance is treated chordally—where there is an unresolved chordal seventh, for example—the SCAMET model as a vehicle of comparison might better yield to other forms of analysis.

Elementary SCAMET Analysis

[13] The following steps outline the procedure involved in this model.

[14] Step 1. Segment the score. In a given passage of music, find the successive notes of longest duration, or hard notes. Link the first hard note with the counterpointed part or parts above and below so as to make a contrapuntal segment the length of that hard note. Continue doing so with the hard notes that follow, so that the passage in question is accounted for as a succession of hard-note segments.

See, for example, Lasso’s two-part song “Scribantur,” from a modern performance edition of the Bicinias (Example 1a). The first three notes in the superius are, of course, not amenable to comparison with species counterpoint, since there is only one vocal line. In the superius in this modern edition, two half note Cs (the last beat of measure 2 and the first of measure 3) are joined by a tie, which we shall treat as a whole note. In the tenor voice, two successive half notes, F and A, sound against it. Thus the superius C and tenor F-A will be one hard-note segment.⁽⁴⁾

[15] We encounter a problem here, that of the modern performance edition, with the anachronism of the bar line and the tie between measures 2 and 3 imposed upon the notation of the original score. The best way to resolve this problem would be to rely upon either facsimiles or modern editions wherein bar lines are declared editorial. Unfortunately, recourse to scores of this sort is not always possible, and the counterpoint teacher is forced to adopt anachronistic performance editions such as Example 1. We shall take the following solution to this problem here: treat every hard note as if it were a species metric unit in its own right by transcribing it to fill a “species measure” of four beats. The “species measure” contrived thus is an abstract contrapuntal unit whose purpose is to regulate the species-contrapuntal relation of voice parts. (This procedure will be discussed further near the end of the article.)

[16] Step 2. Notate the pitches involved as if they were an instance of traditional species counterpoint, as in Example 1b, where every hard note has the length of a “species measure” as defined by dotted lines. Species measures are numbered continuously over the superius part in this instance. The student should:

Step 2.1. Convert the longest note of any given contrapuntal segment to a whole note.⁽⁵⁾ This becomes a hard note of a species measure. For the sake of clarity, the hard note can be preceded by an open bracket (as shown in Example 1b, measures 2 and 4). Otherwise, it shall be presumed that the whole note in the species measure is the hard note. Logical hard notes will usually be given on a separate staff above or below.

Step 2.2. Convert the counterpointed notes to half notes, quarter notes, or eighth notes corresponding to the correct note values of a species exercise.

In Example 1b, species measure 2, the tenor F and A become the two counterpointed half notes of a second-species bar.

[17] Step 3. At least initially, the student should indicate the species proportion—that is, the rhythmic proportion of the counterpoint notes to the hard note—as 1, 2, or 4 against 1. The ratio 1:1 will indicate comparison with first species, 2:1 with second and fourth species, and 4:1 with third and fifth species.

In the first moveable hard note instance in “Scribantur” (Example 1b, measure 2), the indication of the relationship would be comparable with 2:1, since two tenor notes—F and A—are heard beneath the superius C.

[18] Step 4. Note the intervals involved. Again, at least initially, the student should indicate the intervallic relationships between the note or notes of the counterpoint and the hard note. This can usually be expressed as an integer corresponding to a simple interval. Integers are written either above or below the hard note relative to the position above or below the counterpointed voice. In the first moveable hard note instance in “Scribantur,” the intervals are a fifth and third, indicated as 5 and 3 below the hard note C. In a three-voice passage where the hard note is in the middle voice, integers written above the hard note will normally indicate the relation to the upper counterpoint, while integers written below will indicate the relation to the lower voice. In a three-voice passage where, for example, the hard note is in the upper voice and a suspension (let us say a 2–3 suspension) is in the lowest, the integers corresponding to the dissonance and its resolution (2 and 3) will be written immediately beneath the hard note.

[19] Step 5. Treat counterpointed notes of equal duration as comparable to first species. On the last quarter note beat of score measure 4 in Example 1a, with B♭ in the higher voice and G in the lower, the note value is the same in both parts. We represent the rhythmic proportion in Example 1b, species measures 6, as 1:1, with whole notes B♭ and G in the superius and tenor. Neither note distinguishes itself intrinsically as a hard note, and so neither has a bracket.

[20] Step 6. In some instances, score notes can be combined or a score note suppressed so as to produce a new hard note that compares more favorably with species counterpoint. For example, a note and its immediate repetition might be joined into a single hard note, as in Example 1b, species measures 9 (superius G, compare score measure 5) and 13 (tenor B♭, compare score measure 7).

[21] Step 7. Convert monophonic passages to cantus-firmus-like melodies with equal whole note durations, each in a single species measure.⁽⁶⁾

[22] Step 8. In general, rests should be treated as equivalent to counterpointed notes, that is, governed by the species-proportion rules. Rests in a texture of three or more parts should be treated in a manner so as to clarify a counterpoint in the other voices. In such instances, rests can be altered where necessary so as to fit with a species model.

[23] Step 9. Add logical hard notes where necessary. Where the voice leading in the score does not accord easily with species-counterpoint guidelines, the student should consider the possibility of adding a logical hard note to accord with any or all of its counterpointed voices, thus enabling the comparison.

[24] Step 10. The student should take note of unusual voice leading, dissonant counterpoint, contrapuntal motives, exceptional vocal ranges, or other irregularities by means of asterisks and appended notes. In this article, we shall allow unusual dissonance treatment where we deem it idiomatic stylistically to the work in question. (The counterpoint instructor is free to choose an approach of greater severity.) Comparisons of these sorts will no doubt stimulate discussion in a classroom setting. We shall return to this in a section on advanced applications of the method below. I reiterate here, however, that the aim of SCAMET is to enliven the study of species counterpoint, not necessarily to assess style solely against a strict species-counterpoint model.

[25] The following examples apply the SCAMET method to short passages. The groundwork for more advanced analysis is laid in some of the commentary.

Lasso, “Esurientes”

[26] Another Lasso two-voice counterpoint will serve to solidify the procedure described above. In Example 2b (compare the performance score, Example 2a), from the duet “Esurientes,” the regular alteration of species proportions—principally 2:1 and 4:1—is readily observed.⁽⁷⁾ The one notable exception is in measures 8–9 of the performance score; a succession of parallel sixths leads to the 7–6 suspension at the cadence. Here Lasso chooses to end the phrase with a sweeping contrapuntal gesture of voices moving in equal duration. The passage is readily identified in the species example by the counterpointed whole notes, species measures 21–25 in Example 2b.

[27] I call this succession of parallel sixths a “contrapuntal” gesture. Even though it loses nothing of its force when heard as rapid notes in performance, in the context of comparison it is expressive as first-species counterpoint. The presence of five instances of note-against-note counterpoint in succession stands out as a contrapuntal event quite unprecedented in the duet. (Rapid homorhythmic motion sets up the cadence.) One of the advantages of SCAMET representation, then, is its ability to draw attention visually to such contrapuntal gestures, where they might be passed over otherwise.

[28] Worth noting as well in Example 2b are the two forms of consonant suspension in species measures 16 and 20. In the former instance, the superius leaps away from the consonant suspension; in the latter, it descends by step. I have notated the superius A in measures 6–7 as two tied whole notes so as to emphasize the fifth to sixth progression with the tenor on the downbeats of species measures 6 and 7. Alternatively the two species measures could be combined as one, with the superius A as the hard note and quarter notes D, A, C, and D in the tenor.

Ockeghem, “Fors Seulement”

[29] As soon as students feel comfortable with two-part application of SCAMET, they should be introduced to three-part works. Example 3a contains a passage from Ockeghem’s “Fors Seulement,” score measures 27–30. Note how the dissonant B in measure 29, beat 4, is left by step; this is the so-called “under third” cadence, an idiom perfectly at home in Ockeghem’s style (Reese 1959, 44, Example 5; Long 1987). The student should recognize this as exceptional, but SCAMET is not intended to “level out” counterpoint, as if species counterpoint were a standard by which all instances of counterpoint are assessed as correct or flawed. Where SCAMET’s goal is properly contrapuntal, idioms such as the under-third cadence are best viewed as exceptional or “reserved” practices, of which a long tradition exists in counterpoint. Put to the goal of describing style, SCAMET’s aim should be to serve as a horizon against which individual and particular contrapuntal configurations such as the under-third cadence might be set into relief. (We shall return to this below, with reference to an excerpt from Beethoven’s String Quartet in C♯ minor, op. 131.)

[30] Example 3b converts the measures in question into species measures. One particular feature of the example is worthy of attention: the altus C in species measure 4 is represented here as a consonant suspension. It is quit immediately, however, without resolution, so as to leave sufficient time (a species measure and a half) before what would be a cross related C♯ in species measure 6. An alternative would be to hold the altus C through the species measure, thus putting it in closer proximity to its cross relation, or convert it to a hard note and collapse species measures 3-4 into one.

Isaac, Missa Chargé de deul, Kyrie

[31] A longer, more complex passage is presented in score as Example 4a, taken from Isaac’s Missa Chargé de deul, a setting of the Christe eleison, from the Kyrie. The student will recognize both aurally and visually the stepwise descending patterns of thirds that begin in measure 48. This same pattern can be seen in Example 4b, species measures 14–22. The consonant suspensions are brought to the fore visually by the species bar lines. The dissonant third beats in the species measures can be placed readily in context as passing notes to the note of resolution, a third below the consonant suspension. In species measure 15, for example, B is a consonant suspension, G its resolution, and A is a dissonance passing between the two.

Advanced SCAMET Analysis

[32] The examples above are meant to illustrate the basic method of comparing score and species counterpoint. The following examples will illustrate advanced applications of the method. Central to most of them is the question of dissonance treatment, which is an important issue in the counterpoint classroom. It is important as well to encourage the student to find contrapuntal patterns—for example, patterns of dissonance treatment or sequences. And we shall consider the relationship between counterpoint and harmony by means of SCAMET in several examples.

[33] We begin with examples taken from Henry Purcell’s Second Fantasia, which use the logical hard note to illustrate dissonance treatment. An example taken from the C minor fugue of Bach’s Well-Tempered Clavier shows how voice-leading patterns can be extracted from a passage of highly compressed counterpoint. SCAMET is then applied to a Gesualdo madrigal and another Bach fugue, where chromaticism and voice leading are of a greater complexity. The following examples by Corelli, Haydn, Mozart, and Beethoven address the application of SCAMET in chordal harmonic contexts. Lastly, an example taken from a Shostakovich fugue illustrates the use of SCAMET to illustrate dissonance and voice leading in music of the twentieth-century.

Purcell, Second Fantasia: Chromatically Inflected Logical Hard Notes

[34] Let us refine our concept of logical hard note in the next example. The first thirteen measures of the Second Fantasia of Henry Purcell are reproduced in score form in Example 5a. The rewritten species score (Example 5b) contains five staves: the three middle staves—titled here “superius,” “tenor,” and “bassus”—correspond to the three parts of the original score; the highest and lowest staves are reserved for logical hard notes.

[35] On the downbeat of score measure 6 and species measure 10, three pitches—bassus E, tenor F, and superius G—sound together, the result being one of the many piquant dissonances in Purcell that endear him to modern listeners. The addition of the logical hard note C in the lowest part in species measure 10 offers an explanatory framework for the dissonance: there is a 4–3 suspension in the tenor, passing motion 3–4 in the bassus, and a leap from a fifth to a weak-beat octave in the superius. Again, this does not imply that we should emend or correct Purcell’s score; instead, it offers a species postulate accounting for the dissonance between bassus, tenor, and superius.

[36] In species measure 19 (compare score measure 10), the logical hard note D in the uppermost part offers a similar framework for the dissonance of a diminished fourth between the superius and the bassus: B♭ and F♯—dissonant with each other—are consonant with the logical hard note D.

[37] These two instances, species measures 10 and 19, necessitate a logical hard note, since their score harmonies will not conform with species counterpoint guidelines. By the nature of their component tones, no reasonable comparison to species counterpoint can be made without a logical hard note. The logical hard note should be reserved as a means of last resort, however, for its use can be both subtle and arcane.

[38] The third beat of score measure 8 and the downbeat of species measure 14 combine B♭, C, and F, the B♭ resolving to A. Rather than invoke a fourth tone as a logical hard note by which to elucidate the fourth between C and F, let us treat the bass A as a hard note embellished by a B♭ suspension. Accordingly, in Example 5b, species measure 14, the logical hard note is delayed by a suspended B♭. In other words, the dissonance can be framed easily, if we allow an embellishment of the hard note by the B♭ suspension. Accordingly, let us add the following clause to the definition of logical hard note:

2.3.5.. A hard note can be modified by customary species-contrapuntal idioms (such as a suspension or a passing tone) where this facilitates comparison between score and species counterpoint.

[39] Our definition of the hard note prescribed a single longest note, against which shorter notes in other voices moved in counterpoint. The conclusion of Purcell’s Second Fantasia (see the score, Example 6a) calls for us to modify ad hoc this rule: in these measures the hard note takes the form of two half notes, the latter being the chromatic inflection downward of the former. Two distinct half-note pitches, in other words, are joined as one hard note. Since the basic interval in question is retained but altered chromatically—a major sixth becomes a minor sixth, for example—we shall treat the two notes in question as one.⁽⁸⁾ Therefore, in Example 6b, species measures 7, 8, and 10–13, a virtual hard whole note encompasses two chromatically inflected half notes. These correspond to a chain of four descending semitones (score measures 59–60, repeated in measures 61–62) and a chain of fifth-related semitone pairs (score measures 62–65).⁽⁹⁾ The hard notes comprised of two half notes in score measures 59–60 produce 2–3 suspensions between the superius and tenor, while those in measures 62–65 produce 7–6 suspensions between tenor and bassus. The effect is one of a remarkable chromatic slippage intensified by the suspensions and made all the more extraordinary by the quasi-cadential arrival on F at the last measure, decorated by a simple 4–3 suspension.⁽¹⁰⁾ Accordingly let us add the following clause:

2.3.6. A hard note can be understood to comprise two component notes, one a chromatic inflection of the other, where this facilitates comparison of score and species counterpoint. One or both component notes shall be referred to as the hard note when applying species-contrapuntal rules.

Bach, Well-Tempered Clavier, Book 2, Fugue 2, C minor: Species Counterpoint Sequence Patterns

[40] Example 7a reproduces the score to a measure taken from Bach’s Fugue no. 2 in C minor from Book 2 of the Well-Tempered Clavier. The highly compressed counterpoint of the score is compared to a species counterpoint in Example 7b, so that the student might see aspects of the sequential motion with species clarity. The bass voice is, of course, a sequence pattern of four rising fourths and falling fifths in its own right, but this pattern divides itself into two sequential parts: species measures 1 to 4 and 5 to 8. Within these lies a sequential pattern of exchanging tenths and sixths between the outer voices on the downbeats of species measures, as represented in the table of Figure 1. Each column in Figure 1 represents one eighth-note beat of the score measure in Example 7a, and one whole species measure in Example 7b.

[41] The pattern contains a larger descending figure moving in tenths between outer voices (species measures 1, 3, 5, and 7, indicated with asterisks above the uppermost voice). A corresponding pattern of descending tenths appears between the middle and lower voices on alternating measures, as represented in Figure 2. (These tenths are indicated with asterisks above the middle voice in Example 7b.)

[42] Particularly noteworthy here is a tiny contrapuntal figure on beat 3 of the score (Example 7a), which is elucidated when compared to species measure 5 (Example 7b). Bach leaps away from the dissonant seventh suspension (reckoned against the lowest voice) to produce another dissonance, the augmented fifth A♭ to E♮. This tiny detail marks the division of these otherwise smooth progressions of tenths and sixths into two distinct segments.

Gesualdo, “Tu m’uccidi,” Madrigals for Five Voices, Book 5 (1613): Dissonance against a Consonant Backdrop

[43] The logical hard note can serve to frame obscure and difficult counterpoint, of which there are many instances in the music of Gesualdo. In the Gesualdo madrigal “Tu m’uccidi” (see Example 8a), dissonances arise on the last beat of score measure 1 (as a major second between superius and altus), and the first and third beats of score measure 2 (as a diminished fifth between altus 1 and altus 2 and a diminished fourth between superius and altus 1, respectively).

[44] In Example 8b, in the corresponding species measures 4 and the downbeat of measure 5, the superius and altus 1 are dissonant with each other but consonant with a logical B added above. Another possibility, however, presents itself as a logical hard note, a lower G♮ (noted in Example 8b with a double asterisk). While this works for the measures in question, the logical G would produce a cross relation to the altus 2 G♯ in species measure 5. The latter, however, is cross related to the superius G♮ in species measure 6. Implicitly or explicitly, Gesualdo is playing with potential cross relations in this passage, since D and D♯ as well as A and A♯ are brought into close proximity. Given this aspect of Gesualdo’s style, the low G♮ might be the preferred logical hard note in this instance, rather than the high B.

[45] Three instances of a logical hard note B, however, are invoked in species measures 4 to 6 in the uppermost part. Thereby the D♯ to G♮ diminished fourth of species measure 6 is regulated: both the G and the D♯ are consonant against the logical B, the D♯ now seen as chromatically raised resolution of the neighbor-note C♯ in species measure 5. The same is true of the first altus E in species measure 6 against the second altus B: as a dissonant perfect fourth against a lower B, the E cannot make a consonant preparation for the 2-3 suspension of measure 7; as a perfect fifth below the logical hard note, the E makes a suitable preparation, however.⁽¹¹⁾

[46] As a logical hard note, the B constitutes a point of reference governing a set of lines filling out melodic thirds, as shown in Example 8c. Example 8c reduces four species measures from Example 8b (measures 4–7) into two new species measures, with the logical B extended to cover them. From this species counterpoint perspective, the B serves as an overarching reference for an implied cross relation in the four lines: in the superius, which moves to a high G♮ in lieu of the G♯ in altus 2; in altus 1, which articulates a D to D♯ cross relation; and in altus 2, concerned in its turn with A and A♯. The B makes sense as a logical hard note because it frames this chromatic passage as species counterpoint.

[47] The concept of logical hard note, then, enables comparison of Gesualdo’s irregular counterpoints with a regular species standard. Without the logical hard note Bs, Gesualdo’s counterpoint looks chaotic or flawed, if not perverse. Seen in comparison with a species model, however, his counterpoint seems but a step removed from consonance, as if a guiding diatonic framework had been suppressed. Much the same is true of the downbeat of species measure 12 (Example 8b). On beat 1, the superius strikes a discord with the bassus as a tritone. Seen in light of a logical D in the lowest part, however, the superius creates a 7–6 suspension in species measure 12, and the bassus a consonant third, F♯. On beats 3 and 4, the first altus and tenor can be seen thus as passing-tone dissonances left by leap (indicated with large asterisks in the example). Again, this is not to suggest that Gesualdo was writing deliberately arcane counterpoint. Instead, it would seem as if he were writing a particularly advanced form of counterpoint for an audience that did not require an explicit regulatory frame of consonance for their understanding but might instead have been capable of adducing one, to their delight, from the nature of the dissonances.

Bach, Well-Tempered Clavier, Book 1, Fugue 22, B♭ minor: Species Counterpoint and Suspensions

[48] Of the many devices that lend Bach’s counterpoint its subtlety, the simultaneous occurrence of suspensions resolving against neighbor notes bears particular examination. Example 9a provides an excerpt from the B♭ minor fugue from Book 1 of the Well-Tempered Clavier. In score measure 4, the fugal subject lies in the uppermost part, the countersubject beneath. In species measure 3 of Example 9b, a hard note A♭ is ornamented by a G♮ lower neighbor and a passing B♭. The superius hard note G♮ of species measure 2 is tied over to become in measure 3 an ornamented 7–6 suspension against this embellished hard note A♭.

[49] In Bach’s counterpoint, the task of locating a hard note is not always an easy matter. In species measure 11, the hard note C, is delayed by an accented dissonant passing tone. In species measure 15, the hard note D♭ in the tenor on beat 1 is embellished on beat 2, and then transferred to the altus on beat 3 and back to the tenor on beat 4. Alternatively, the logical hard note in the lowest part of the example could be invoked.

[50] The counterpoint student will have encountered suspensions in fourth species and noted the proper use of suspensions in their coursework on harmony. Comparisons between Bach’s scores and species examples should build upon this foundation. In particular, Bach’s fugal counterpoint often includes suspension chains. In this regard, the counterpoint student will find in SCAMET a means by which to elucidate what might otherwise elude clear articulation.

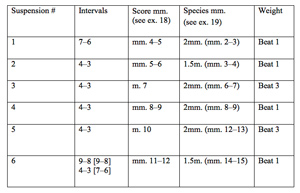
[51] Consider the six suspensions in Example 9c—derived from species measures 2–15 of Example 9b.⁽¹²⁾ For ease of reference, all six suspensions are numbered in Examples 18–20. The first of the six suspensions occupies species measures 2–3 in Example 9c—in the superius, preparation in measure 2, suspension and resolution in measure 3. The second suspension, however, occupies only one and one-half species measures, the second half of measure 3 and the whole of measure 4—preparation in species measure 3, beats 3 and 4, suspension and resolution in measure 4. Speaking in the abstract terms of species measures, let us say that suspensions 1 and 2 constitute two different suspension “durations”: long (2 measures) and short (1.5 measures). And the two suspensions present two suspension “interval types”: suspended seventh resolving to sixth, and suspended fourth resolving to third. Suspensions 1, 2, 4, and 6 occur on beat 1 in the actual score; suspensions 3 and 5 occur on beat 3. Let us call this a shift in “weight” and represent it in two forms: first, beat 3 dissonance with beat 1 resolution; and secondly, beat 1 dissonance with beat 3 resolution. To summarize, each suspension may be long (two measures) or short (one and a half measures), 7–6 or 4–3, and with dissonance on beat 1 or beat 3. Any combination of these three qualities is possible.

[52] The six suspensions addressed in Examples 9a–d are summarized in Figure 3. In addition to the three suspensions discussed above, suspensions 4 and 5 are both 4–3 suspensions, and both are two species measures in duration. Suspension 4, however, is struck on beat 1 (see species measure 9 in Example 9b; compare score measure 9, beat 1, in Example 9a), while suspension 5 appears on beat 3 (species measure 13; compare score measure 10, beat 3). Finally, I have treated suspension 6 (species measures 14 to 15; compare score measure 11 resolving in measure 12) in two ways. In Example 9b, 9–8 and 4–3 suspensions resolve above a logical B♭ hard note in species measure 15. In Example 9c, however, a different hard note is surmised, D♭, represented in the lowest part in species measure 15 (corresponding to the ornamented D♭ of score measure 12, in the middle staff).

[53] For ease of comparison with Example 9a, I have put the second to sixth suspensions of Figure 3 together in Example 9d, with score-measure numbering. We note a pattern of 4–3 suspensions rising sequentially by step from score measures 5–12. Each is separated by the interval of a sixth. Thus the whole pattern can be understood as a chain of rising sixths, alternating beat 3 to beat 1. Drawing a distinction in weight between suspension figures on beats 1 and beats 3—let us say the beat 1 suspensions in score measures 6, 9, and 12, and the beat 3 suspensions in measures 7 and 10—we note the possibility of a species-contrapuntal triple hypermeter comprised of beat 1 and beat 3 sixths embellished by 4–3 suspensions.

[54] In some instances, Bach’s dissonances cannot be explained in terms of strict counterpoint, score-measure 14 (see Example 9a) being a case in point. The E♭ quarter notes in the highest part on beat 1 and the middle part on beat 2 are dissonant sevenths above F quarter notes. But they do not resolve in the customary fashion of species counterpoint; their dissonance, in other words, is not framed as a suspended, passing, or neighboring note that resolves by step to consonance against a stationary tone. The E♭ dissonance on beat 1 rises upward to F. The E♭ on beat 2 falls downward by step, as it would normally resolve against a stationary F. But instead of remaining stationary, the counterpointed F rises to G♮, and thus any explicit resolution of the E♭ to F dissonance is eluded.

[55] These dissonant E♭ quarter notes and their counterpointed Fs move by a logic other than strict species counterpoint—the logic of Stufenharmonik or scale-degree harmony.⁽¹³⁾ Both the liberal exchange of E♭ and F between the superius and tenor, and the complementary transfer of A♮ between bass and alto, speak of a harmonic style in which the strict voice leading rules of species counterpoint are replaced by the guidance of an abstract Stufe—here the fifth scale degree, F, the dominant, which regulates the treatment of the E♭ as a chordal-harmonic seventh and thus excuses it from the need to resolve immediately to a consonance over a stationary note. A Stufenleiter F in this instance is not a SCAMET logical hard note, for the dissonances noted do not resolve against it following the guidelines of species counterpoint. Instead they follow the logic of chordal root.⁽¹⁴⁾

[56] In the tenor part in species measure 19 of Example 9b, a fictional suspended half-note F has been added so as to transform the contrapuntal function of the subsequent tenor E♭. (Compare score measure 14 of Example 9a, where the E♭ and F are struck simultaneously.) Thus the latter becomes a weak-beat passing dissonance. A similar alteration is made again in the superius in species measure 21, thus making a 4–3 suspension in the superius against the altus, and avoiding a percussed tritone with the A♮ in bassus 1. These fictions make the exercise conform to species rules. But they are not Bach.

SCAMET Analysis Adapted for Chordal Harmony

[57] The unresolved E♭s in Bach’s score hearken to a new, progressive Stufen texture.⁽¹⁵⁾ They fit into a scale-degree context as linear embellishments of scale degrees or as chordal sevenths. Consider Example 9e, where, in species measures 2 and 4, the dissonance between superius and altus could be understood to resolve over the barline (the altus resolving the dissonance against a stationary superius). But the passage makes better sense in terms of chordal harmony as a chain of descending-fifth chords (F, B♭, E♭, A♭, D♭). Therein the dissonance in the altus is a chordal seventh resolving over the barline to chordal third, which then prepares the next seventh. At a certain point, it makes sense to abandon SCAMET in favor of chordal harmony.

[58] With a certain liberty in species rules, in particular the rules governing the treatment of dissonance preparation and resolution, SCAMET can be applied to polyphonic and homophonic textures in Bach and afterward (especially where the influence of Stufen-Harmonik is acknowledged). Composers such as Haydn, Mozart, Schubert, Beethoven, and Bruckner were trained in Fuxian species counterpoint (Albrechtsberger, Seyfried, and Sechter being key Viennese figures in this regard), and the residual effect of such training is readily apparent. In the case of a homophonic texture, however, a species-contrapuntal structure will have to be extracted, and patently harmonic gestures (such as rapid arpeggios and scale passages) will have to be condensed into slower-moving voice parts. The examples that follow illustrate some of SCAMET’s potential for elucidating counterpoint in music of the later eighteenth and nineteenth centuries.

Corelli, Sonata op. 1, VIII, Grave. Stufen and Species-Contrapuntal Readings.

[59] The excerpt from a Corelli sonata, Example 10a, lends itself easily to a harmony classroom.⁽¹⁶⁾ Tonic, pre-dominant, and dominant harmonies are readily discerned. Particularly noteworthy is the expansion of the tonic from measures 1–3 to a pre-dominant to dominant progression in measures 3–4. The facility with which Corelli’s trio sonatas yield such observations makes them eminently suited to the instruction of harmony.

[60] Discerning species counterpoint in Corelli’s work, however, is a more difficult task. Example 10b sets forth a three-part counterpoint to be compared with the Corelli excerpt. The suspension figures are clearly set forth in light of species bar lines (species measures 1–2, 3–4, and 5–6). The enlargement of the bass line of measures 1–2 (C–A♭–G) in species measures 5–7 is perhaps clearer than in the score.

[61] Particularly noteworthy now, however, are melodic species of trichord, tetrachord, and pentachord that might be overlooked. The superius comprises two interlocking species of third, C–D–E♭ and E♭–F–G, labeled x and x’ in Example 10b. When combined they outline a species of fifth (reckoned by interval from bottom to top as tone-semitone-tone-tone [C–D, D–E♭, E♭–F, F–G]). The bassus, on the other hand, outlines the octave-complementary fourth, semitone-tone-tone [G–A♭, A♭–B♭, B♭–C] in measures 1–2 and 5–7, as indicated by the label z in the example. In measures 2–4, the bassus replicates as well the species of fifth heard in the superius. Thus the bassus outlines the important octave compass of these measures—C to C, divided into fifth and fourth. The role of the altus (although not indicated with a letter in the example) is that of sub-semitone emphasizing the C as a point of reference, a final. The suspension figures thus serve as contrapuntal motives establishing C as the final of the C–G–C frame.

[62] Corelli’s work lends itself easily, then, to harmonic analysis. With only a little more difficulty, however, it can be compared to a species counterpoint exercise. The two can be fruitfully examined together. A careful consideration of the difference between harmonic analysis and analysis using melodic species of intervals will encourage the student to consider the relation of harmony to counterpoint, a fruitful endeavor that should lead directly to more advanced analysis.

Haydn, String Quartet in G minor, op. 74, no. 3, I. Instrumental Textures and Species Vocal Style.

[63] If counterpoint might reasonably be overshadowed by harmony in classroom discussion of the Corelli passage above, the Haydn excerpt reproduced in Example 11a contains the chord of the German augmented sixth in measure 8, voiced in such a striking fashion as to eclipse discussion of counterpoint. (Particularly notable are the tritones between the two violins.) The passage, however, can be compared with the four-part species exercise in Example 11b, where Haydn’s augmented sixth chord (species measure 5) is tamed by smoother voice leading, while retaining the augmented sixth between outer voices. Chordal harmony accounts easily for the superius E in species measure 2 (marked with an asterisk)—as a chordal seventh. This reading, however, relegates the piquant tritone dissonance with the A♯ hard note (in the tenor) to the status of a chordal attribute rather than treating it as a voice-leading entity in its own right, albeit produced by an exceptional leap. In Example 11b, I have adduced a C♯ on the downbeat of species measure 2 so as to moderate the effect, if only slightly.

[64] The comparison of score to species exercise is useful in discussing the relationship between instrumental and vocal part writing. In species measure 6, the superius retains the outline of the F♯ to A♯ flourish in the first violin in score measure 9, but the flourish itself is sacrificed as not idiomatic to species counterpoint.⁽¹⁷⁾ In similar fashion, the arpeggio on the downbeats of score measures 5 to 8, B–E–G♯–B, is truncated at the G♯ in species measure 4, so that the E♯ of species measure 5 is approached by minor third rather than by tritone, as in the score.

[65] Example 11c subjects Haydn’s quartet writing to even greater compression. All the identifying features of the quartet score are reduced here; the string-quartet model could not reasonably be discerned from the species exercise alone. Notably, the ambitus of all three upper voices is no greater than the fourth. The result is a kind of ersatz or standard counterpoint, which we shall call here generic.⁽¹⁸⁾

Mozart, Requiem Mass, “Recordare.” Extracting Species Counterpoint

[66] Example 12a reproduces the opening measures of the “Recordare” movement to Mozart’s Requiem Mass. While the corni di bassetto parts lend themselves to comparison with species counterpoint (allowing for tritone leaps as exceptional), the cello part, by its rapid scales, leaps, and trills, does not. In the upper system of species exercise Example 12b, the bassus extracts a vocally idiomatic part from the cellos. Thus a useful comparison with Mozart’s score is produced, which shows contrapuntal features characteristic of Mozart’s writing.

[67] While the melodic tritones (altus in species measure 2, superius in measure 5) are not proper species writing, the 2–3 suspensions that precede and follow them are. The bassus line participates here by framing the suspensions from below (as 4–3 suspensions in species measures 2 and 3, and 9–8 suspensions in measures 4 and 5). In the lower three-voice system of Example 12b, the leaps of an ascending fifth (both tritone and perfect fifth) are eliminated so as to make the counterpoint even smoother, in first species. Doing so, however, reduces a salient feature of Mozart’s score, one of its identifying features.

Beethoven, String Quartet in C♯ minor, op. 131: Beethovenian and Generic Counterpoints

[68] Examples 13a–f are devoted to the opening measures of Beethoven’s op. 131 String Quartet, surely one of the most intransigent of his late works when it comes to analysis. Score measures 4–8 are reproduced as Example 13a, the two violin parts written on one staff for clarity. Example 13b presents a three-part species exercise for comparison. A third part, comprising logical hard notes, illuminates the part writing of the superius and altus, which is obscure both tonally and contrapuntally. The tritone between the upper voices in species measure 2 is notable: no doubt the B in the superius part could be analyzed harmonically as the seventh of the dominant chord in the key of F♯. The logical G♯, however, constitutes a kind of contrapuntal buffer between the B and E♯, relating by consonant minor third to both. Several expressive details make their way into Example 13b to provide a stronger link with the score. The E♯ quarter note of species measure 4 could have been eliminated (leaving A to F♯ in the superius), but it is retained here. The disjunct contrary motion into the octave A between the superius and the hard note in species measure 5 is perhaps too forceful for normative counterpoint. The force of this expanding disjunct motion is moderated, however, by contracting conjunct contrary motion in measure 6. The most striking feature of the species exercise is the 2–1 suspension of species measure 7, excessive in strict species style but a salient link to beat 2 of score measure 7.

[69] Example 13c compresses several scores measures into single species measures. It retains important pitches of the score while emphasizing the melodic intervals of ascending and descending thirds in the two parts. The diminished fifth in species measure 1 diverges notably from strict counterpoint, as does the perfect fourth resolving to an augmented second in species measure 3, beats 3 and 4. I keep them in the species exercise as a form of “license,” again so as to facilitate comparison with the score.

[70] Example 13d is a full four-part exercise with which to compare the violin duet. Fictional notes are added liberally so as to provide consonant support for dissonant intervals. Thus the identity of Beethoven’s model would be difficult to discern in the species example, if only because the particular dissonances of his score are not so much removed as framed in a generic species manner. We can thus compare Beethoven’s approach to the counterpoint in op. 131—perhaps as a contrapuntal reservata—with traditional species counterpoint.

[71] Lastly, Example 13e reproduces measures 8–12 of the score, the viola entry with the imitative subject on G♯ (instead of C♯ as in Example 13a). Example 13f adduces a new “logical hard note” voice. While its function here could be seen as entirely contrapuntal (with the occasional license), the addition of these hard notes makes the exercise sound like a four-part succession of triads and seventh chords. Some features link it back to the original score (notably the quarters in species measure 6, and the leap to violin 1’s F♯ in species measure 2, indicated with an asterisk), but the sound otherwise is that of plain generic counterpoint, a useful backdrop against which to measure Beethoven’s idiosyncratic part writing.

SCAMET and Dissonance Treatment in a Twentieth-Century Context

Shostakovich, Preludes and Fugues op. 87, Fugue 1

[72] Example 14a reproduces the opening measures of the first fugue in Dmitri Shostakovich’s op. 87 Preludes and Fugues. Comparison with the species exercise of Example 14b suggests that Shostakovich’s fugue, at least in these early measures, conforms in most regards with species rules, given the following exceptions. The right hand leaps excessively in fifths and fourths in the first ten measures (but its profile changes to seconds and thirds thereafter). Dissonances in species measures 8 and 12 are quit by leap over the barline. And the resolution of the suspension in measure 13 lasts a scant quarter note. These aside, it would seem as if Shostakovich were emulating species counterpoint in these measures. Were all such instances of twentieth-century counterpoint so conformant to species practice, the teaching of species counterpoint might prove easy, if not facile.

[73] Much the same conformity can be discerned in score measures 28–34, reproduced in Example 15a, to which species measures 1–7 of Example 15b compare. Thereafter, however, matters change. As species measures 8–11 of Example 15b suggest, a new style of counterpoint is at play, one based on the rhythms of the previous measures, but with strong-beat dissonances.

[74] The hard note indicated in species measure 8 is a bass G, embellished on beats 3 and 4 by passing motion through A and B. This G is presumed to be an abstract guiding reference point for the whole species measure, its force felt throughout the measure even though the bass voice itself moves onward from the G.⁽¹⁹⁾ The alto and tenor strike dissonant seconds (indicated as 2 and 9) on beat 1 but move to consonances on beat 2. As the actual bass moves on beats 3 and 4, so too the alto and tenor move, to A and F respectively, again forming dissonances with the abstract guiding bass G. Above the motion in the lower parts, the soprano holds a C, a dissonant fourth with the guiding G, on beats 1 through 3, and resolves (upward) to consonance finally on the fourth beat.

[75] Surely the customary rules governing species consonance have been left behind at this point. The downbeats of the two subsequent measures digress in striking fashion from the norm, the soprano notes in particular, these indicated by asterisks in the example. While the rhythms and the voice leading retain the character of the first measures, the dissonance treatment changes dramatically.

[76] Two ways of treating this state of affairs suggest themselves. The first would be to delimit the application of species counterpoint to passages that conform with species rules for dissonance treatment, and to ignore any measures that do not. This, however, would preclude the study of much twentieth-century music. The second possibility, touched on briefly here in conclusion, would necessitate deriving ad hoc fresh counterpoint rules appropriate to the passage under examination.

[77] By way of example, let us modify the customary rules for dissonance treatment for species measures 8–10 of Example 15b. The following new guidelines are reckoned in terms of SCAMET hard notes:

Rule 1: Consonances can be heard only on weak beats, and must be approached by step.

Rule 2: Consonances can be quit in one of four ways: by leap to a dissonance on a strong beat, by step to a dissonance on a strong beat, suspended to become a dissonance on a subsequent beat, or suspended to become a consonance on a subsequent beat (thus implicitly breaking rule 1).

Rule 3: Downbeats must be dissonant, except where a consonance has been suspended from a previous weak beat to form a consonance on the downbeat.

These three ad hoc rules constrain most of the voice leading in species measures 8–10. (Measure 11, however, returns to conformity with more traditional rules.)

[78] Obviously this ad hoc approach would invoke a considerable rethinking of species norms. The application of species counterpoint to recent music is made considerably more flexible, however, by the moveable hard note. Ad hoc SCAMET may be useful, then, in twentieth- and twenty-first century polyphony where contrapuntal rules are at times subject to radical modification and where additional notes invoked logically would clarify the voice leading.

SCAMET and the Style of Renaissance Polyphony

[79] SCAMET’s immediate purpose is to facilitate comparison between polyphonic scores and species exercises, and thereby bring “real music” into the classroom. It is not a reductive method suited to addressing tonal prolongation. (To this end, the Schenkerian analytic model and its derivatives are apposite.)

[80] Nor is SCAMET as set forth here intended to describe musical style, especially the period styles of the Renaissance. Perhaps the fons et origo of much thought on these matters is Richard Crocker’s elegant “Discant, Counterpoint and Harmony” of 1962. Therein, however, no mention is made of “species” counterpoint. The method as proposed here, then, is strictly delimited as a critical and a pedagogical tool.

[81] With considerable modification, however, SCAMET could render service to the stylistic analysis of polyphonic Renaissance music, since counterpoint is such an integral part of that music’s conception. Some of these modifications are considered below, expressed as problems and remedies.

[82] Problem 1: Species counterpoint needs a greater flexibility in application to Renaissance musical style. By their brevity the species rules as carried down to us from Fux and before are incapable of capturing polyphonic styles in their complexity, certainly with regard to dissonance treatment. This is not to suggest that the rules of the day were not simple in basis. As Margaret Bent (2002, 112) puts it: “The main and constant rules of counterpoint are few and simple. Perfect intervals are to be perfect, and they are to be approached correctly . . . . ” Bent suggests then that the “main and constant rules” are concise. This leaves open, however, the possibility of “secondary and inconstant” rules, subsidiary and malleable rules brought to bear upon individual instances. These soft rules may have eluded codification by theorists, being left instead to composers and performers to work out, aided by unwritten tradition. In redesigning SCAMET for the purposes of style analysis, its counterpoint rules might be put into categories—few and simple (after Bent), supplemented by manifold and complex rules required of individual musical works or repertoires (such as the works of Gesualdo).⁽²⁰⁾

[83] Solution 1.1: expand the rules and the framework of species counterpoint. This might be done with reference to theories of species counterpoint antecedent to and contemporary with Fux. In Adriano Banchieri’s Cartello Musicale (1968, 105–10), for example, a sixth species allows cantus motion against a fixed ostinato.

[84] While this author has never found the precepts of SCAMET articulated in toto in any treatise, the model is implied. For example, in Zarlino’s Istitutioni harmoniche, the third part, the theorist makes the transition from Chapter 28, “A Composition Must Begin with a Perfect Consonance,” to Chapter 43, “The Method of Writing Counterpoints upon a Part or Diminished Subject.” The former chapter would appear to describe species counterpoint. The latter chapter, however, shows a greater freedom in conception, much as its author confesses. Zarlino writes:

If he chooses to write his own subject, he may find that one part helps him compose the other so that the subject and the composition are completed more or less together. What I call the subject, as I said earlier, is either the first part to be written or the first to be imagined by the composer. The more he bears in mind the rules given in connection with counterpoint on a cantus firmus, the easier will be his task. The present method of composing, it is true, is much freer and spontaneous, because either the upper or the lower part may be diminished at will. Thus one part has somewhat longer note values than the other, or the values of the two parts correspond. These are all things not possible in the first mode of writing. (Zarlino 1976, 103)

[85] On Zarlino’s account, the composer must bear in mind the strictures of composing counterpoint to a cantus firmus. Neither part has priority, the two “completed more or less together.” And both parts can be ornamented, “diminished at will,” composed in other words in either first species (“the values of the two parts correspond”) or otherwise (“one part has somewhat longer note values than the other”).⁽²¹⁾ More work needs to be done with Zarlino’s treatise and others, as we apply species principles to free composition. In redefining SCAMET, then, species-like contrapuntal theories other than the traditional strict Fuxian need to be taken into account.

[86] Problem 2: The cantus firmus structure of species counterpoint needs rethinking in light of Renaissance imitative practices. SCAMET modifies liberally the cantus-in-whole-notes basic structure of the strict species exercise. In being further modified, however, it could take into account the idiomatic structures of Renaissance polyphony, especially the imitative structures with which phrases begin. No doubt, imitation is governed by counterpoint, and thus implicitly by hard notes and their counterpoints as these are passed between voices.

[87] Solution 2.1: Apply the notion of an embellished SCAMET species to describe Renaissance style. Drawing on treatises by Francesco de Montaños (the Arte de musica theorica y pratica of 1592) and Thomas Morley, James MacKay (2009) explores a species-based compositional framework for Renaissance music, Byrd’s in particular. He considers “how a composer, beginning with a note-against-note two-voice framework in semibreves, can rhythmicize long notes, add consonant skips, passing notes and suspensions in stages, thereby ultimately creating an imitative duo in florid rhythm” (Mackay 2009, 8). On this account, florid counterpoint is arrived at by successive elaboration of a basic first-species framework,⁽²²⁾ this including the elaboration of the cantus: “The cantus firmus itself is paraphrased so that it, too, can participate in the canon” (9).⁽²³⁾

[88] On first blush, this would seem to argue against application of the SCAMET model. In MacKay’s account after Morley, the basic structure of the cantus is confined to one voice, and the latter is simply elaborated. The cantus in other words remains implicit in the same voice and with a basic structure of a slow moving melody. SCAMET and Morley/MacKay can be seen as complementary, however. As the subject (or cantus voice) is “diminished” by embellishment, its diminutions could be measured against hard notes in a counterpoint voice; in other words, the hard note might pass from the cantus voice to the counterpoint as the former undergoes diminution, the cantus staying all the while in its proper voice. This would entail a division in function between cantus as subject and cantus as a counterpointing voice.

[89] Solution 2.2: Reconcile SCAMET with Renaissance polyphonic structures. Rather than leaving the hard note free to wander from voice to voice, constrain it to follow imitative structures such as “points of imitation.”

[90] In this regard, one of the most fruitful examinations of Renaissance polyphonic structure is Joseph Kerman’s (1975) “Old and New in William Byrd’s Cantiones Sacrae,” where he sets forth a concept of “cell.”⁽²⁴⁾ These cells are distinct features, separate in kind from the music around them (and from other types of structures in Byrd’s style). In essence, a cell is a short phrase ending with a cadence, typically in stretto imitation, passed around the voices imitatively. The cell is not a subject per se, but much shorter. The cell is subject to modification, but its repetition in various voices can be said to structure the piece. This notion resembles SCAMET on two accounts: first, the cell as point of reference—of focus—is moveable, migrating between voices. Second, it stands in lieu of a cantus in certain notable works of Byrd, and thus constitutes what Kerman (1975, 38) calls “a modern technique” (in comparison, for example, to ostinato). In SCAMET a point of reference is passed between voices to structure the counterpoint; in Kerman’s theory a melodic cell is passed between voices to structural ends.

[91] Kerman’s thought has borne fruit in the recent work of John Milsom (2005), where the author elaborates the notion of “cell” taken from Kerman: “Fugal cell: a repeatable block of polyphony made wholly out of interlocked statements of the subject” (2005, 298n4). The notion of “interlock” is a refinement of imitation: it means expressly structural imitation. Thus Milsom sets forth in remarkable detail the interlocking cells that structure a fuga.

[92] The principal element that distinguishes SCAMET from Kerman and Milsom is its reliance upon explicit counterpoint models by which to relate the structure of hard notes to counterpoints. Neither Kerman nor Milsom discusses at length the role of consonance and dissonance in regulating the contrapuntal combination of cells. Given the caveat expressed above (that Renaissance counterpoint is not as simple as species counterpoint) this omission is understandable. But the question arises, could a modified form of SCAMET be applied to the analysis of these interlocking cells, perhaps even as a determinant of cell combination? Julian Grimshaw (2007) points to the importance of counterpoint in Fuga, but only obliquely. SCAMET would aid in adapting species counterpoint to these cellular structures.

[93] Problem 3: The ontology of the Renaissance as work res facta. Perhaps the greatest obstacle to transposing SCAMET onto style analysis is the very notion of analytic abstraction. SCAMET implies an abstract conception of a polyphonic work—a pre-compositional framework of species counterpoint. Jessie Ann Owens suggests a form of reduction practiced by Palestrina, this implied in the following contemporary account:

Having passed recently through a serious illness and being thus unable to compose . . . Palestrina has begun to set the Kyrie and Gloria of the first mass on the lute . . . . As soon as his infirmity permits he will work out what he has done on the lute with all possible care.⁽²⁵⁾

She poses the question: “Was Palestrina playing the Mass as it would have sounded as a choral composition, or was he simply giving [his listener] a taste, perhaps playing the essential sonorities, the main motives, playing a kind of reduction for lute?” (Owens 1997, 295). Implied here is a conception of a work as bearing a structure abstracted from its surface, be it in the form of a reduction or perhaps along the lines of the “contrapuntal combination.”⁽²⁶⁾

[94] Solution 3.1: SCAMET as process-based. The very notion of a coherent all-encompassing systematic structure to polyphony has been set in relief against a “contextual and processed-based” conception by Sarah Fuller, her aim being “to understand how listeners and singers might become aware of tonal relationships in hearing or performing a song” (Fuller 1998, 62). Fuller invokes the notion of “directed progressions,” (69) these enlivened by “unsettled sonorities.” The concept of the lively directed progression standing in lieu of a determinate structure bears analogy with SCAMET. Presumably singers, knowing where a cantus melody moved by long and by short notes, could improvise counterpoint: where the cantus voice slowed, the counterpoint voice might flourish, and where the cantus voice moved rapidly, the counterpoint might slow down against it. The relation of the faster to the slower voice might have been regulated by species-like guidelines. SCAMET would serve in this regard to govern the relation of the quick-moving to the slow-moving voice.

[95] Problem 4: SCAMET and anachronism. Ultimately the principal charge against the application of SCAMET to the analysis of Renaissance music would be one of anachronism, that the very spirit of species counterpoint instruction, exemplified in Fux, belongs to an era of Liebhaber, rather than the era of the expert Renaissance singer or Kenner.⁽²⁷⁾ Implicit in Margaret Bent’s notion of “weakly-prescriptive notation” is a weakly-prescriptive counterpoint for the Liebhaber, a counterpoint described only minimally in the treatises. Presumably the complexities of Fuxian counterpoint would be beyond such a capacity. The expert understanding of the Kenner as performer, however, must have produced a musical capacity comparable to the Fuxian, if not exceeding. Hence the possibility of a Renaissance Fux (and a Renaissance SCAMET) is not beyond reason.

[96] Were SCAMET to work in a Renaissance context, its contrapuntal rules must be contextualized, compared for instance to the framework of musical notation, especially the framework of mensuration. As Bent (1998, 25) puts it: “Thus it is from the combination of notated music and learned counterpoint that the music can take shape; the two are complementary. We can understand it fully neither from the rules of counterpoint alone, nor from the notation read at ‘face value.’” In this regard, the most formidable problem of anachronism facing SCAMET is twofold—notational and contrapuntal. We ought to understand counterpoint in light of the notation of the day, to which the modern measure (and its rigid division into strong and weak beats) is counterintuitive. We ought to understand species counterpoint not as a set of rules complete in itself, but rather as an aural sketch of the contrapuntally possible—a mere sketch, not exhaustive.⁽²⁸⁾ (We could extend this here to condition counterpoint by tonality, the tonal framework—hexachord and solmization, species of fourth and fifth, mode—but the necessary relationship of counterpoint and tonality has been made explicit elsewhere, certainly in Schubert 2008.)

[97] Solution 4.1: Rethink the species measure as a species-contrapuntal “point.” The species measure presupposes accentuation only for the purposes of dissonance regulation: without a given point of reference, the species passing note or suspension cannot exist. The SCAMET system of notating species measures equal to the whole note length of the hard note, however, still suggests a sense of regular pulse organized around an accented downbeat and subsequent unaccented offbeats. To overcome the anachronism of a measure, some new stressed point of reference for the linking of consonant onset and subsequent dissonance needs to be developed.

[98] The rigid species-contrapuntal measure could be replaced with a species-contrapuntal time point—let us say the onset of a hard note—around which consonance and dissonance orient. Such a flexible framework requires the light of Renaissance mensuration, which far exceeds in complexity the simple duple metrics of Fuxian species.

[99] In summary, a dramatically modified notion of counterpoint is necessary were SCAMET to be applied to style analysis, certainly analysis of Renaissance music. This is the principal obstacle that confines it to, for the purposes of this article, a method of comparison aimed solely at enlivening the teaching of species counterpoint.

Conclusion:

[100] As noted in the introduction, some of SCAMET’s basic ideas have antecedents, but these are often expressed in terms of analysis or composition. Diether de la Motte’s fascinating Kontrapunkt: Ein Lese- und Arbeitsbuch (1981) applies species-like ideas to analysis, but not systematically. Fred Maus (1992, 93) suggests that the precision of Peter Westergaard’s rules “makes it easy to do without a cantus firmus,” but notes that Westergaard himself “does not take advantage of this possibility. . . .” (Both Maus and Westergaard, however, are concerned with composition, not analysis). Ernst Krenek (1959, [i]) omitted “traditional training in the ‘five species’” entirely, while attempting to “produce a style close enough to the compositional procedures of Palestrina . . . to achieve . . . something of the flavor of living great music.” But the resulting manual is really too succinct to be useful in this regard. Frederick Horwood (1958) addresses something like SCAMET, but informally, by introducing the notion of a cantus firmus itself in a florid style: “The melodic ideas already introduced consist of one, two, three or four notes to one beat, with some suspensions. It is possible to combine these rhythms in such a way that produces a flowing type of melody which combines well with a C.F. also in florid style” (27). Horwood’s treatment is so abbreviated as to do little but whet the appetite of the interested student. Almost any text that turns from strict species counterpoint to imitative counterpoint will involve “mixing” the species—not merely in the sense of fifth species, but more so by introducing notes of mixed durations in every imitative voice. Such is the case in Henry Martin’s Counterpoint: A Species Approach Based on Schenker’s Counterpoint (2005). Martin puts succinctly what I have laid out systematically here when he introduces two-part counterpoints “whose entrances are in imitation and unsupported by a C.F.” [my emphasis]. Where note values are the same in two parts, the passage “should follow the rules of the two-part first species. . . .” Where the note values differ, “then the slower note provides a momentary CF for the other voices. Accordingly, write the voice with the faster note values in the two-part mixed species relative to the slower note.” (Martin 2005, 91–92) In effect this is SCAMET, the method proposed in this article, albeit in highly condensed form and applied to composition.

[101] Something like SCAMET is found in Peter Schubert’s Modal Counterpoint, Renaissance Style (2008). Moveable hard notes are sprinkled throughout the text,⁽²⁹⁾ but the matter breaks out in force in chapter 11, “Two Parts in Mixed Values,” where he introduces canon. In this chapter, cantus firmus species in whole notes are more the exception than the rule. Schubert stipulates, “When half notes occur against half notes, or quarters against quarters, treat as first species . . . . When quarters occur against halves, treat as second species” (2008, 144).

[102] Schubert rethinks the suspension figure by allowing the cantus (the “agent,” as he calls it) to take different rhythmic values: “In previous chapters the agent was always a whole note, and always in the CF voice. In evaluating correct dissonance treatment in mixed values, you need to be able to spot the agent in either voice and in either a whole note or a half note value” (Schubert 1999, 138).⁽³⁰⁾ In Schubert, then, the spirit of the method described in this article is certainly present but not carried out in a systematic manner as it is here.⁽³¹⁾

[103] In his signal summation of the state of music theory and pedagogy, Michael Rogers notes the danger in teaching species counterpoint as “mechanical note manipulation.” As he puts it, “Although it seems difficult to question an approach that provided the musical foundation for most of the important eighteenth- and nineteenth-century composers, some maintain that species counterpoint is inherently unmusical, constricting creativity by rigid adherence to solving a time-consuming series of tedious exercises. Especially in a sixteenth-century style, where durational flow and flexibility are critical, the predictable metric regularity of the early species might stifle the elastic feel for nuances and gentle differences between rhythmic lifts and landings” (Rogers 2004, 66). It is precisely with such a danger in mind that this article is written. Without detracting from the basic exposure to the strict species exercise, the model proposed here would aim to lighten the study of counterpoint through comparison of species exercise to real music.

Murray Dineen
University of Ottawa
School of Music
Perez Hall, 50 University
Ottawa, CANADA K1N 6N5
pdineen@uottawa.ca

Works Cited

Banchieri, Adriano. 1968. Cartella musicale nel canto figurato, fermo & contrapunto. Bologna: Forni.

Bent, Margaret. 1998. “The Grammar of Early Music: Preconditions for Analysis.” In Tonal Structures in Early Music, edited by Cristle Collins Judd, 15–59. New York: Garland.

—————. 2002. Counterpoint, Composition, and Musica Ficta. New York: Routledge.

—————. 2003. “Ciconia, Prosdocimus, and the Workings of Musical Grammar as Exemplified in O felix templum and O Padua.” In Johannes Ciconia, musicien de la transition, edited by Philippe Vendrix., 65-106 Turnhout, Belgium: Brepols.

Crocker, Richard L. 1962. “Discant, Counterpoint, and Harmony.” Journal of the American Musicological Society 15, no. 1: 1–21.

Cumming, Julie. 2011. “Composing Imitative Counterpoint around a Cantus Firmus: Two Motets by Heinrich Isaac.” Journal of Musicology 28, no. 3: 231–88.

Dahlhaus, Carl. 1983. “In Namen Schenkers.” Die Musikforschung 36, no. 2: 82–87.

Dineen, P. Murray. 1994. “The Contrapuntal Combination: Schoenberg’s Old Hat.” In Music Theory and the Exploration of the Past, edited by Christopher Hatch and David Bernstein, 435–48. Chicago: University of Chicago Press.

Drabkin, William. 1989. Review of Heinrich Schenker Counterpoint, edited by John Rothgeb. Music Analysis 8, no. 1–2: 197–203.

Fuller, Sarah. 1998. “Exploring Tonal Structure in French Polyphonic Song of the Fourteenth Century.” In Tonal Structures in Early Music, edited by Cristle Collins Judd, 61–86. New York: Garland.

Fux, Johann Joseph. 1965a. From Gradus ad Parnassum, cited in Alfred Mann, The Study of Fugue. New York, Norton.

—————. 1965b. The Study of Counterpoint: From Johann Joseph Fux’s Gradus ad Parnassum. Revised edited by Translated and edited by Alfred Mann. New York, Norton.

Federhofer, Hellmut. 1982. “Fux’s ‘Gradus ad Parnassum’ as Viewed by Heinrich Schenker.” Translated by Alfred Mann. Music Theory Spectrum 4: 66–75.

Grimshaw, Julian. 2007. “Sixteenth-Century English Fuga: Sequential and Peak-Note Subjects.” Musical Times 148, no. 1900: 61–78.

Horwood, Frederick J. 1958. Elementary Counterpoint. New York: Robbins.

Jeppesen, Knut. 1970. The Style of Palestrina and the Dissonance, 2nd ed. Translated by M. Hamerick. New York: Dover.

Kerman, Joseph. 1975. “Old and New in William Byrd's Cantiones Sacrae.” In Essays on Opera and English Music in Honour of Sir Jack Westrup, edited by F.W. Stemfeld et al., 25–43. Oxford: Oxford University Press.

—————. 1981. The Masses and Motets of William Byrd. London: Faber and Faber.

Krenek, Ernst. 1959. Modal Counterpoint in the Style of the Sixteenth Century. London: Boosey and Hawkes.

Leach, Elizabeth Eva. 2000. “Counterpoint and Analysis in Fourteenth-Century Song.” Journal of Music Theory 44, no. 1: 45–79.

Long, Michael. 1987. “Landini's Musical Patrimony: A Reassessment of some Compositional Conventions in Trecento Polyphony.” Journal of the American Musicological Society 40: 31–52.

MacKay, James. 2009. “Into the Composer’s Workshop: Pre-Compositional Planning and Contrapuntal Design in William Byrd’s Imitative Points.” Theoria 16: 5–38.

Martin, Henry. 2005. Counterpoint: A Species Approach Based on Schenker’s Counterpoint. Oxford: Scarecrow Press.

Maus, Fred. 1992. “Teaching with Westergaard’s Counterpoint Rules.” Journal of Music Theory Pedagogy 6: 83–96.

Milsom, John. 2005. “Crequillon, Clemens, and Four-Voice ‘Fuga’.” In Beyond Contemporary Fame: Reassessing the Art of Clemens non Papa and Thomas Crecquillon, edited by Eric Jas, 293–345. Turnhout: Brepols.

Motte, Diether de la. 1981. Kontrapunkt: Ein Lese- und Arbeitsbuch. Muenchen: Deutscher Taschenbuch.

Owens, Jessie Ann. 1997. Composers at Work: The Craft of Musical Composition 1450–1600. New York: Oxford.

Reese, Gustave. 1959. Music in the Renaissance. New York: Norton.

Reynolds, Christopher. 1992. “The Counterpoint of Allusion in Fifteenth-Century Masses.” Journal of the American Musicological Society 45, no. 2: 228–60.

Riemann, Hugo. 1890. Analysis of J. S. Bach’s Wohltemperirtes Clavier. Part 1. Translated by J.S. Shedlock. London: Augener.

Rogers, Michael R. 2004. Teaching Approaches in Music Theory: An Overview of Pedagogical Philosophies. Carbondale: Southern Illinois University Press.

Salzer, Felix, and Carl Schachter. 1969. Counterpoint in Composition. New York: McGraw-Hill.

Schoenberg, Arnold. 1963. Preliminary Exercises in Counterpoint, edited by Leonard Stein. New York: St. Martin’s.

Schubert, Peter. 1995. “A Lesson from Lassus: Form in the Duos of 1577.” Music Theory Spectrum, 17 no. 1: 1–26.

—————. 1999. Modal Counterpoint, Renaissance Style. New York: Oxford.

—————. 2007. “Hidden Forms in Palestrina's First Book of Four-Voice Motets.” Journal of the American Musicological Society 60, no. 3: 483–556.

—————. 2008. Modal Counterpoint, Renaissance Style, 2nd ed. New York: Oxford.

Smith, Anne. 2011. The Performance of 16th-Century Music: Learning from the Theorists. New York: Oxford.

Strunk, Oliver. 1947. “Guglielmo Gonzaga and Palestrina's Missa Dominicalis.” The Musical Quarterly, 33: 228–39.

Walker, Paul Mark. 2000. Theories of Fugue from the Age of Josquin to the Age of Bach. Rochester, N.Y.: University of Rochester Press.

Zarlino, Gioseffo. 1976. The Art of Counterpoint: Part Three of L’Istitutio Harmoniche, 1558. Translated by G. Marco and C. Palisca. New York: Norton.

Musical Sources

Bach, Johann Sebastian. 1866. B♭ minor Fugue, Book I and C-minor Fugue, Book II. Das Wohltemperierte Clavier. Bach-Gesellschaft Ausgabe. Band 14. Clavierwerke. Band 3: 80–81, 98–99. Leipzig: Breitkopf & Härtel.

Beethoven, Ludwig van. 1970. String Quartet in C♯ minor, op. 131. In Ludwig van Beethoven: Complete String Quartets, 119–58. New York: Dover.

Corelli, Arcangelo. (1681) 1890. Sonate da chiesa, op. 1. In Les Oeuvres de Arcangelo Corelli. Livre 1, edited by J. Joachim and F. Chrysander, 46. London: Augener.

Gesualdo di Venosa. 1980. Madrigale für fünf Stimmen: Fünftes Buch. Edited by Wilhelm Weismann, after the edition of 1613, 60–63. Leipzig: VEB Deutscher Verlag für Musik.

Haydn, Joseph. 1979. String Quartet in G minor, op. 74, no. 3. In Eleven Late String Quartets: Opp. 74, 76, and 77, 59–82. New York: Dover.

Isaac, Henrici. 1984. Missa Chargé de deul. In Collected Works. Vol. 6, edited by Edward Lerner. American Institute of Musicology, 1–37. Neuhausen-Stuttgart: Hänssler-Verlag.

Lasso, Orlando di. 1971. “Scribantur” and “Esurientes.” Bicinium XIII and Bicinium VI of the Bicinia.http://javanese.imslp.info/files/imglnks/usimg/2/26/IMSLP151731-WIMA.3969-lass-bic-13.pdf and http://conquest.imslp.info/files/imglnks/usimg/f/f0/IMSLP151724-WIMA.6be5-lass-bic-06.pdf, accessed 23 July 2013. Taken from Novae aliquot, et ante hac non ita usitatae cantiones suavissimae, (Munich, 1577). The secundus is reproduced in facsimile at Bicinia Sacra, Ex Variis Autoribus In Usum Iuventutis Scholasticae Collecta, RISM B/I, 1591²⁷: http://purl.org/rism/BI/1591/27, accessed July 4, 2012. The collection is sometimes assigned the RISM number 1577c [1577d].

Mozart, Wolfgang Amadeus. 1991. “Recordare.” Requiem. Neue Ausgabe Sämtlicher Werke, Band 2: Geistliche Gesangswerke II, 18–27. Kassel: Bärenreiter.

Ockeghem, Johannes. 1992. “Fors Seulement.” From Collected Works, vol. 3, edited by Wexler and Plamenac. American Musicological Society. Reproduced in Allen W. Atlas, Anthology of Renaissance Music, 125–26. New York: Norton.

Purcell, Henry. 1959. Second Fantazia. Fantazias and Other Instrumental Music. Vol. 31 of The Works of Henry Purcell, edited by Thurston Dart, 3–4. London: Novello.

Shostakovich, Dmitri. 2006. Twenty-four Preludes and Fugues for Piano, op. 87. 5–7. Moscow, distributed by Hal Leonard.

Footnotes

1. See also Fux 1965b, 27.
Return to text

2. Addressing invertible counterpoint, Peter Schubert proposes the possibility of a migrating cantus: “a continuous two-voice piece in which the CF ‘migrates’ from one part to another” (2008, 339). His cantus, however, retains its traditional qualities—with long notes and melodic integrity in one voice part.
Return to text

3. The notion of envelopment is articulated in Schoenberg’s (1963) work on counterpoint. See also Dineen 1994.
Return to text

4. This notation restores something of the original notation in Lasso’s hand, with a semibreve in the superius.
Return to text

5. I am indebted to an anonymous reader’s suggestion that SCAMET illuminates the relationship between free composition and species counterpoint by renotating editorial notes as species notes doubled in value (i.e., renotating transcribed eighth notes as fourth-species quarters), thus remedying editorial error. I have chosen not to renotate my score examples, however, but relied instead on editions readily available to the counterpoint teacher.
Return to text

6. Alternatively, one might add a voice part and rework the monophonic passages in the form of species counterpoint. For example, the opening C, A, and B♭ of score measures 1–2 might be set as half note and two quarters (the B♭ as passing tone) against a logical hard note F (or a C, or A) in the tenor. The utility of this in preparation for writing points of imitation is patent. Unfortunately, the application of SCAMET to composition beyond the logical hard note must remain the subject of another essay.
Return to text

7. We might begin here with the species example, thus reversing the normal order in the classroom. Many “real” scores, however, can be adduced from a species example. Asking students to derive several “real” counterparts from one SCAMET model has proven useful. The practice encourages the ability to see many potential realizations for a given counterpoint. See my discussion of Schoenberg’s hat and Webern’s ashtray (Dineen 1994).
Return to text

8. One might read the bassus notes of score measures 59 and 60, A and D, as hard notes. On this account, the tenor in score measure 59 presents a 9–8 suspension, and the superius presents two successive thirds, the second of which is lowered chromatically. The A in the tenor on the second half of measure 59 would then become the preparation for a consonant suspension on the downbeat of measure 60. On the latter half of measure 60, however, this perspective breaks down: the consonant suspension A on the downbeat of measure 60 cannot resolve to a G, which is dissonant against the bassus D. In this case, then, reading the two chromatic superius tones of measure 60 as one virtual hard note is preferred.
Return to text

9. The semitones of measure 61 are not hard notes, however, for they are dissonant to the tenor.
Return to text

10. In species measure 4, the hard note D in the bassus is embellished by a passing tone E on the fourth beat. In species measure 5, the superius E (see the asterisks in the example) can be understood as a dissonant anticipation.
Return to text

11. See Schubert 2008, 78, on the “Fake Suspension,” and Jeppesen 1970, 236 and 239, on the “consonant fourth” in Palestrina.
Return to text

12. I am indebted to an anonymous reader, who notes in Riemann 1890, 146–47 an editorial reworking of the meter into ${}_2^3$ such that the G on beat 3 of score measure 7 appears on a downbeat (and thus as a suspension, much as I represent it in Example 9b, species measure 7). Riemann’s remarkable approach to Bach’s metrics bears comparison with SCAMET, but lies unfortunately beyond the scope of this article.
Return to text

13. I refer here to Stufen in the Viennese sense of scale-degrees after theorists such as Simon Sechter and Heinrich Schenker. At play here is a distinction between what Carl Dahlhaus might call voice-leading and harmony, Stimmführung and Harmonik, which he cautions us is not an absolute distinction but likely more a case of fluctuation and gradation between mutual sympathies (1983, 84).
Return to text

14. The relationship of logical hard note and chordal root is a topic for future research.
Return to text

15. Here Schenker’s prolongational method combining Stufenlehre with species counterpoint reveals its utility. As Hellmut Federhofer (1982, 68) puts it succinctly: around about 1900 a “new function of harmony and counterpoint” arose in Schenker’s thought: “The former was determined by the new significance attributed to the scale degree (Stufe) . . . [while] the latter was reduced to an exposition of the principles of part writing . . . . For according to Schenker the study of counterpoint “should not impart a particular style of composition so much as guide the ear of the music student into the infinite world of musical Urprobleme . . . . ” This, as William Drabkin (1989, 199 points out, is made readily apparent in both of Schenker’s treatises, Harmony and Counterpoint: “‘strict’ counterpoint differs from real music by the very absence of scale degrees other than the tonic. For Schenker, harmony and strict counterpoint were separate disciplines which had to be taught separately; once mastered, they could be used to produce ‘free,’ that is, original, composition.”
Return to text

16. The continuo figured bass is omitted in the example.
Return to text

17. Compressed here are details from the first violin part in beats 3 and 4 of score measure 8, details that might emerge as counterpoint in an intermediate SCAMET sketch: the passing motion between F♯ and C♯; the upper-neighbor motion F♯–G♯–F♯; and the subsequent E, which joins the second violin at the octave and resolves thereafter.
Return to text

18. There are similar-motion perfect intervals in measures 3 and 4 of Example 11c, albeit in inner parts.
Return to text

19. Other possibilities suggest themselves, for example breaking species measure 8 in two parts—with hard notes bass G for one whole measure (new measure 8) and tenor F for another (new measure 9). This approach, however, does not reconcile the soprano C to the bass G in the new species measure 8.
Return to text

20. But see Bent 2003, 71–73, where such a distinction is mooted. Peter Schubert (2008, xi) begins his text with a comparable distinction between hard and soft rules.
Return to text

21. Presumably, the use of the cantus firmus would differ according to the type of setting, for example the parody mass versus the chant-based mass as described by Christopher Reynolds 1992, 251–52.
Return to text

22. This compares with reductive theories of diminution. See Leach 2000, 49: “As simple counterpoint does not include dissonances, the next stage of analysis requires that the dissonances be treated as surface decoration and eliminated . . . ”
Return to text

23. MacKay (2009, 181) then compares two examples taken from Morley, “Thus Plain” and “Thus Divided.” In the first, the subject is given in semibreves; in the second the subject is embellished, although its original semibreve profile is readily discernable.
Return to text

24. The idea of a “cell” reappears in Kerman 1981; see for example pages 75 and 88.
Return to text

25. Owens 1997, 293–94, citing a translation by Oliver Strunk (1947, 99–100). The original letter is cited in Owens’s Appendix 4 (311).
Return to text

26. See Bent 2003, 87–103, on reduction and early music. Compare Schubert 2007 and Cumming 2011 on the notion of “module.” And see Dineen 1994 on the contrapuntal combination.
Return to text

27. Walker (2000, 292) aligns Fux with Kenner.
Return to text

28. Compare Smith 2011, Chapter 7, “Rhetoric of Counterpoint.”
Return to text

29. See Schubert’s (2008) example at the top of page 90. The passage, taken presumably from Cerone, places the cantus firmus whole note first in the lowest voice, then in the highest, returning to the lowest in the third bar. In all three instances, cantus firmus whole notes appear on the latter half of the measure but are missing entirely from the first half. In his commentary upon the example, Schubert acknowledges parenthetically the motion of the cantus from one part to another: “(in [Cerone’s] example, you can think of the whole notes as CF notes that move from one part to the other).” But he gives no accounting of the first half of the bar, apparently bereft of a cantus note. From the vantage point of this article, these measures are based on moveable hard notes, certainly the latter half of each measure. Similar intriguing passages appear elsewhere in Schubert’s text. We find one on page 11, Example 1-2, taken from Tigrini; this seems half in and half out of species counterpoint. We find another on page 22, from Zarlino, (Example 2-5), where the slow moving cantus firmus is broken in the second measure to make a cadence. And another on pages 118–19 (Example 9-2), from Morley, again to make the cadence.
Return to text

30. Curiously this passage is omitted in the 2008 edition.
Return to text

31. In Schubert’s defense, it should be noted that his text is devoted to composing species counterpoint in Renaissance style and not strictly to analysis (although he relies on analysis throughout).
Return to text

Copyright Statement

Copyright © 2013 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.

Prepared by Hoyt Andres, Editorial Assistant
Number of visits: