Convergence Points in Conlon Nancarrow’s Tempo Canons
Julie A. Nemire
In Memoriam Bruce B. Campbell (1948–2011)
KEYWORDS: Player piano, tempo ratio, duration ratio, arch canon, converging canon, acceleration canon, temporal dissonance
ABSTRACT: A major structural feature of Conlon Nancarrow’s tempo canons, in which canonic material moves at different speeds in different voices, is the places where the musical lines converge to a simultaneous attack. These convergence points can vary in importance and function, and, depending on the type of canon being used in the piece, there may be only one or two convergence points per piece, or many. This paper considers the work of Nancarrow scholars such as Kyle Gann, Margaret Thomas, and the current author, examines the features of convergence points in Nancarrow’s tempo canons, and illustrates the many ways they are used in his Studies for Player Piano. Attention is also paid to compositional choices made by Nancarrow regarding where opportunities for convergences would occur (i.e., points of simultaneity), and how these might be manipulated, emphasized, de-emphasized, or avoided. The discussion of convergence points leads to an analysis of Study No. 27, Nancarrow’s last acceleration canon.
Copyright © 2014 Society for Music Theory
[1] Conlon Nancarrow (1912–97) wrote approximately fifty Studies for Player Piano, many of which represent a new compositional genre: the tempo canon, in which canonic voices proceed at different speeds. The player piano proved to be the perfect vehicle for Nancarrow to realize a variety of textures (from two to twelve voices or strata) and tempo relationships among canonic voices. A primary and characteristic structural feature of Nancarrow’s tempo canons is the convergence point, or “the infinitesimal moment at which all lines have reached identical points in the material they are playing” (Gann 1995, 21). Convergence points (CPs) serve varying purposes in Nancarrow’s studies: sometimes they seem to be the raison d’être for an entire piece (particularly in his earlier brief tempo canons with just one CP, such as Nos. 14, 18, and 19); sometimes they vary considerably in significance within the same piece (such as the thirteen CPs in No. 24). They may also serve to mark the most structurally significant points in a piece (such as the three CPs in No. 27). As noted by Margaret Thomas, these “points of synchrony—whether at the beginning, ending, or middle of a piece or passage—operate as significant structural moments and thus help to articulate the design of the studies” (2000, 111). CPs are also important aids to the listener in following relationships between the voices or strata. Eric Drott observes: “Convergence points function as the seams that hold the layers together within a given study, marking the few moments when the listener can hear a direct and immediate connection between the otherwise uncoordinated layers” (2004, 541). Finally, convergence points in Nancarrow’s Studies represent the most temporally consonant areas in an otherwise temporally dissonant environment (Thomas 2000/01).
[2] The voices in Nancarrow’s tempo canons are often related temporally by ratios stated in the study’s title (e.g., 21/24/25).(1) Unlike conventional canons in which the voices proceed at the same tempo, tempo canons present the possibility for one or more CPs between the canonic voices because the voices are moving at different speeds and either converging or diverging. Thomas (1996) classified tempo canons into four basic types: (1) the converging canon, with one CP at the end; (2) the diverging canon, which begins with a CP; (3) the converging-diverging (arch) canon, in which a single CP is somewhere in the middle; and (4) the diverging-converging canon, which begins and ends with a CP. Nancarrow wrote examples of each type, although he did not write any canons that only diverge—there is, after all, not much perceptual interest in a piece that diverges immediately away from a beginning point of convergence, never to return.(2)
[3] In this paper I will examine the presence and placement of CPs in Nancarrow’s tempo canons and their significance to the overall structure. CPs will be examined in their more conventional uses in the canons, and other devices examined will include tempo switches and overlaps (which can be used to create additional CPs) and techniques for emphasizing and de-emphasizing CPs. Several of Nancarrow’s more complex works feature many CPs, and further complexity is possible through the addition of more voices to a canon, thereby providing opportunities for interior CPs among smaller groups of voices. A special sub-type of Nancarrow’s tempo canons is the “acceleration canon,” in which voices accelerate or decelerate. The discussion concludes with an analysis of Nancarrow’s final acceleration canon, Study No. 27 (“Canon 5%/6%/8%/11%”).
[4] The effect of convergence in Nancarrow’s tempo canons is perceptually heightened because it involves not only temporal convergence, but convergence of canonic material. The choice of canon as a means of portraying temporal proportions is quite natural. Thomas notes that in Nancarrow’s tempo canons “there is a palpable sense of the voices being in different places at the same time, of gradually moving closer together, of a brief moment of coordination, and then a departure” (Thomas 2000, 111–12). This “brief moment of coordination” is the CP, or Gann’s “infinitesimal moment” at which temporally divergent voices converge.
[5] A CP is an excellent example of what Jonathan Kramer (1988, 454) refers to as a “timepoint,” or “an instant, analogous to a geometrical point in space.” A time-point has no dimension, as explained by Kramer:
But what is a timepoint? Whereas a timespan is a specific duration (whether of a note, chord, silence, motive, or whatever), a timepoint really has no duration. We hear events that start or stop at timepoints, but we cannot hear the timepoints themselves [emphasis mine]. A timepoint is thus analogous to a point in geometric space. By definition, a point has no size: It is not a dot on the page, although a dot may be used to represent a point. Similarly, a staccato note or the attack of a longer note necessarily falls on and thus may represent a timepoint, but a timepoint in music is as inaudible as a geometric point is invisible. (Kramer 1988, 82–83)
[6] Like geometric lines in space, Nancarrow’s canonic lines converge at this dimensionless point in time, the timepoint, and the CP is an audible event that takes place at this point. Eytan Agmon, in his discussion of musical durations as mathematical intervals, notes that “every common musical duration is uniquely associated with a single moment in time, namely its attack” (Agmon 1997, 48). Indeed, most of Nancarrow’s CPs do occur on a coincident beat attack. In a number of cases, however, CPs occur on rests, and, in several cases (e.g., the end of Studies No. 32 and 37), a CP is at the end of a long held note. Whether articulated or not, a CP always represents a timepoint.
Tempo Canon Terminology and Features
Figure 1. Convergence point at middle of Study No. 14
(click to enlarge and listen)
[7] In addition to convergence point, Gann defines several terms relevant to tempo canons. An illustration directly from Nancarrow’s scores will be given here to show these features and introduce some additional concepts. Figure 1 shows a portion of Study No. 14 (“Canon 4/5”) at the point where the CP occurs: this example will illustrate the relationships among the terms convergence point, echo distance, convergence period, and potential points of simultaneity. Study No. 14 is a two-voice arch (converging-diverging) canon in which the CP occurs exactly in the middle of the piece. Echo distances—“the temporal gap between an event in one voice and its corresponding recurrence in another” (Gann 1995, 21)—are shown in Figure 1 by arrows. Gann points out that the echo distance “will grow shorter and shorter as the convergence point is approached, reach zero at the convergence point, then grow progressively longer as it moves away” (21), and this is clearly seen in this example. Thomas alludes to the aural effect of the echo distance when she discusses the relative degree of temporal dissonance near what she calls the “point of synchrony”:
The notable and increasingly proportionately significant changes in the gaps, and the attendant modifications in temporal dissonance, are responsible for the intense perceptual focus a point of synchrony achieves in a tempo canon, whether that synchrony occupies the beginning of a diverging canon, the ending of a converging canon, or the middle of a converging-diverging canon. Although it is clear that voices at different tempos are gradually and continuously drawing near to or away from one another, their degree of dissonance can seem nearly uniform for a good portion of a canon. Only near the point of synchrony does the fast approaching/departing [temporal] consonance claim perceptual prominence. (Thomas 1996, 138)
[8] Gann generalizes that as a CP is approached in a piece and the echo distance decreases, motives tend to splinter and become briefer; the opposite occurs as a CP recedes and the echo distance increases:
Typically, in the late canons, the following motion occurs: immediately following any convergence point, a quick echoing of brief figures creates excitement signalling the entrance to a new section of the piece. Usually voices lose their distinguishability in a bristling texture, then slowly separate. Short figures are gradually displaced by longer and longer motives which sound calmer (by virtue of their temporal stability) but also more complex, even developmental. As a new convergence point is approached, the echo-tempo picks up again, and figures splinter into ever briefer motives, creating a deliciously gradual feeling of cumulative climax. (Gann 1995, 173–74)
[9] Gann defines the convergence period as the distance between potential simultaneities, and points out that in canons involving superparticular ratios the echo distance “will approximate n beats at a point n convergence periods from a convergence point” (Gann 1995, 21).(3) In Figure 1, this is obscured somewhat by rests but can be most clearly seen at the points marked
![]() , where the echo distance is equal to the convergence period of five beats in the top voice and four beats in the bottom. At these points it is easiest to see that the respective lengths of the echo distance (in beats) in each voice are proportional to the operational tempo ratio at that point; for example, at a point in this 4:5 canon where the echo distance is 2 beats in the top voice, it will be 1.6 beats in the bottom voice.
, where the echo distance is equal to the convergence period of five beats in the top voice and four beats in the bottom. At these points it is easiest to see that the respective lengths of the echo distance (in beats) in each voice are proportional to the operational tempo ratio at that point; for example, at a point in this 4:5 canon where the echo distance is 2 beats in the top voice, it will be 1.6 beats in the bottom voice.
[10] In some of Nancarrow’s canons where the meter does not change, the location of some convergence periods is clearly marked by shared barlines. Also, for as long as the metric pulse does not change, the length of the convergence period remains the same. Shared barlines in Nancarrow’s scores are important markers of convergence, and they are sometimes the only way one can accurately measure the location of events elsewhere in the score (e.g., the number of beats elapsed to the entrance of a later voice).
[11] Two additional terms, timespan and point of simultaneity, are important in making determinations about the placement of CPs and the amount of delay that is needed in later-entering voices to make a CP occur at a certain point. Kramer defines the timespan as the “interval between two time-points” (Kramer 1988, 454). For determining the timespan of Nancarrow’s canonic subjects, the critical question becomes the location of the first and last timepoints. The first timepoint is clearly the first beat attack. There are generally two possibilities, however, for the location of the final timepoint: coinciding with either the attack of the final note, or the release of the final note (which can be said to coincide with the attack of the hypothetical beat that would follow the end of the final note). The most important criteria for making the determination of which should be the final timepoint are usually how the canon ends metrically and its prevailing metric pulse.
Figure 2. (a) Beginning and (b) ending (score, page 5) of Study No. 14
(click to enlarge)
Figure 3. Structural diagram of Study No. 14 (“Canon 4/5”), an arch canon
(click to enlarge)
Figure 4. Placement of interior CPs in relation to canonic midpoint, and the role of potential points of simultaneity
(click to enlarge)
[12] Study No. 14 will serve as an example of a canonic subject in which the final timepoint coincides with the final attack. There are 337 total eighth-note beats in the subject of Study No. 14 (see Figure 2). By measuring from the attack of beat 1 to the attack of beat 337, the distance between these two timepoints, the timespan, is 337 – 1 = 336 beats. From that measurement we can determine that the midpoint of the canon, where the CP occurs, is the attack of beat 169, with 168 beats occurring prior to this point and 168 beats after. Beat 169 is, indeed, the location of the CP (see Figure 3).
[13] Measuring the timespan is straightforward when the CP occurs at the end of the canon (i.e., converging and diverging-converging canons) because in these pieces the final CP defines the concluding timepoint. Most of the time (e.g., Studies No. 18, 19, and 24) the CP occurs on the final attack and the timespan would be measured from the first attack to the final attack. Occasionally, however, the CP occurs after the final attack (e.g., Study No. 32) and the timespan must be measured to a timepoint that follows the CP (usually a mentally supplied terminal beat). In other cases (e.g., Study No. 36), the final timepoint is the release of the final note.
[14] Potential points of simultaneity (i.e., the beginning of a convergence period) have tremendous importance in the structure of tempo canons. Obviously, a CP can occur only at a point of simultaneity in some or all sounding voices. A piece may have a large number of potential points of simultaneity if the tempo ratio involves fairly small numbers, or it may theoretically have only one point of simultaneity (especially in those tempo canons whose proportions involve irrational numbers). At the same time, many potential points of simultaneity are de-emphasized (or even avoided) through the use of rests, held notes, or other devices.(4) The importance of the location of potential points of simultaneity to the structure of tempo canons can be illustrated as shown in Figure 4. This example compares two Studies already mentioned, Nos. 14 and 36, both arch canons with a single CP in the middle. Nancarrow composed Study No. 14 so that its CP would fall exactly in the middle of its 337-beat theme—that is, on beat 169. In Study No. 36, the midpoint of the canon’s 843-beat timespan falls between beats 421 and 422, which is not an available spot for an audible CP.
[15] If it does not matter to the composer whether or not the entrances of later-entering voices coincide with beat attacks in voices that are already sounding (i.e., with the beginning of a convergence period)—and for Nancarrow it often did not—then the CP can essentially be placed wherever the composer chooses. Convergence periods will then proceed both backward and forward from the CP, depending on its location. In the two Studies shown in Figure 4, the entrance of the second voice in No. 14 is between beats 33 and 34 of the first voice, and none of the later voices in No. 36 enters on a beat attack in an earlier voice. In fact, in most of Nancarrow’s canons later entrances do not coincide with beat attacks.(5)
[16] Finally, two tempo change devices are used with some frequency in Nancarrow’s tempo canons: the tempo switch and the tempo overlap. The tempo switch is defined by Gann:
Another major, but less audible, event is the tempo switch, a device in which Nancarrow switches the fastest line to the slowest tempo and vice versa, so that the line that has been lagging catches up with the one that has been pulling ahead. By mathematical necessity, the tempo switch always occurs halfway between two convergence points. (Gann 1995, 21)
Tempo switches are useful in creating additional CPs. They are a significant part of Study No. 24 (“Canon 14/15/16”), where they are used to create thirteen CPs which delineate twelve sections (see Figure 29).
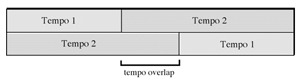
Figure 5. Diagram of a tempo overlap at a 3:2 ratio in a diverging-converging canon
(click to enlarge)
Figure 6. Structure of Study No. 17 (“Canon 12/15/20”) showing the relative duration of tempo overlap sections
(click to enlarge)
[17] Occasionally a tempo changes in only one voice to create a tempo overlap, where the same tempo occurs in more than one voice.
Figure 5 shows how two tempos can form a tempo overlap in a diverging-converging canon. This is exactly how Study No. 15 (“Canon 3/4”) is configured. The tempo overlap section in a two-voice canon will consist of a portion of the entire canon that is equal to
![]() , where m and n are the two elements of the tempo ratio. For instance, in Figure 5 the two tempos and the sectional durations are both related by the ratio 3:2, so the tempo overlap section occupies one-fifth of the entire canon.
, where m and n are the two elements of the tempo ratio. For instance, in Figure 5 the two tempos and the sectional durations are both related by the ratio 3:2, so the tempo overlap section occupies one-fifth of the entire canon.
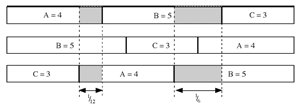
[18] Another Study with tempo overlaps is No. 17 (“Canon 12/15/20”). Tempo overlaps occur between section A in the top and bottom voices, and between section B in the top and bottom voices (see
Figure 6). Because of the inverse relationship between time and duration, the “duration ratio” of this 12:15:20 tempo canon is 3:4:5, which is how the durations of sections C, A, and B, respectively, relate to each other. In general, in a three-voice tempo canon where the elements of the duration ratio (not the tempo ratio) are x:y:z (with x being the smallest element and z the largest), the difference between the durations of x and y related to the length of the entire piece is
![]() ; between y and z it is
; between y and z it is
![]() ; and between x and z it is
; and between x and z it is
![]() . Thus, in No. 17 the sum of the duration ratio’s elements, x:y:z, is 12, and the durational relationship between contiguous elements in the ratio (3:4 and 4:5) is one-twelfth of the whole piece while between the outer elements (3:5) it is one-sixth. As shown in Figure 6, the tempo overlap involving section A occupies one-twelfth of the piece, and that involving section B occupies one-sixth of the piece. The section B overlap is long enough to be bisected by a tempo change in the middle voice between sections C and A.
. Thus, in No. 17 the sum of the duration ratio’s elements, x:y:z, is 12, and the durational relationship between contiguous elements in the ratio (3:4 and 4:5) is one-twelfth of the whole piece while between the outer elements (3:5) it is one-sixth. As shown in Figure 6, the tempo overlap involving section A occupies one-twelfth of the piece, and that involving section B occupies one-sixth of the piece. The section B overlap is long enough to be bisected by a tempo change in the middle voice between sections C and A.
Convergence Points in Nancarrow’s Tempo Canons
Tempo Canons With One (or Almost One) CP
Figure 7. Line diagrams describing Nancarrow’s tempo canons with only one CP (Gann 1995, 22, 23, 25, and 26)
(click to enlarge)
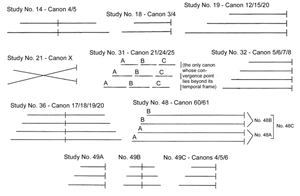
[19] Two of the basic types of tempo canon classified by Thomas have just one CP: the converging-diverging (arch) canon, and the converging canon.(6) In the arch canon the CP falls somewhere in the middle, and in the converging canon it falls at the end. Figure 7 shows line diagrams (from Gann 1995) of Nancarrow’s tempo canons with just one CP.
Arch Canons
[20] Nancarrow’s arch canons vary widely in ambition and scope. As already noted, Study No. 14 has its CP exactly at its canonic midpoint, and the realization of this structure appears to be the primary goal for the piece. Study No. 36 has one of the most spectacular CPs in all of Nancarrow’s oeuvre in terms of its preparation and realization. Study No. 21 has one true canonic CP in addition to an area of “crossing tempos,” and a loosely canonic CP on the last note. Study No. 49B returns to a simpler texture but also has a rather arresting CP.
[21] Study No. 14 (the first that Nancarrow subtitled “Canon”) exhibits the basic arch canon form with the CP exactly in the middle of its 337-beat theme (see Figure 3). With a tempo ratio of 4:5, the faster voice occupies 80% of the duration of the slower voice, with the remaining 20% of the timespan split so that 33.6 beats elapse prior to that voice’s entrance, and 33.6 beats after it concludes; thus, the second voice does not enter at the beginning of a convergence period with the lower voice, but rather it begins three-fifths of the way between the lower voice’s beats 33 and 34.
[22] Another important feature of arch canons, and any tempo canons with interior CPs, is the changing leader-follower relationship between the voices that takes place at interior CPs (see the CP in Figure 1(7)). For example, in Study No. 14 there is so little else calling attention to the CP that the changing leader-follower relationship is thrust into relief, and it is what most immediately captures the listener’s attention. Thomas (2000/01, 160) notes the importance at this point of the five consecutive measures of
Figure 8. Diagram of Study No. 36 (“Canon 17/18/19/20”), an arch canon with the CP slightly past the midpoint (top)
(click to enlarge)
[23] The formal sophistication of Study No. 36 (“Canon 17/18/19/20”) makes it a stark contrast to the more humble ambitions of Study No. 14. It is an arch canon in which the canonic midpoint falls between beats because the timespan is an odd number: 843 half-note beats, placing the canonic midpoint between beats 421 and 422. In this canon, then, it is not possible for the CP and midpoint to coincide on a beat attack as they did in Study No. 14 (Figure 4). Nancarrow instead delays the CP to beat 427, thus creating two sections consisting of 426 and 417 beats (see Figure 8). The final timepoint in this canon falls silently on the final release.
[24] Philip Carlsen notes that the placement of the CP on beat 427 creates a particular relationship of the elapsed time between statements of a recurring theme (which he calls a rondo theme) within the canon and the CP (see Figure 8, bottom diagram):
The rondo theme’s second appearance [at m. 107] is twice as fast as the first; it occurs at a point (system 36 in the bass voice)(8) exactly halfway between the beginning and the canonic midpoint, providing an obvious parallel with the well-known acoustical fact that the halves of a string vibrate twice as fast as the whole. (Carlsen 1998, 30)
The halfway point that Carlsen refers to is actually with the CP and not the canonic midpoint, as shown in Figure 8. Carlsen’s observation concerning the acoustical parallel can be carried further by noting that the first three statements of the theme occur on C2,
[25] The table of elapsed beats in Figure 8 describes the number of beats elapsed to the entrance and from the drop-out point of the top three voices, in relation to the first (or lowest) voice. The first column shows the beat elapse needed to place the CP exactly at the canonic midpoint; the second and third columns show the beat elapses that actually occur prior to and after, respectively, the statements in the top three voices.
Figure 9. Half-note beats associated with beginnings of convergence periods at the beginning of Study No. 36
(click to enlarge)
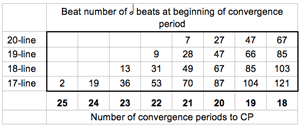
[26] None of the voices enters at the beginning of a convergence period, as shown in Figure 9. Even the first voice begins on the last beat of a convergence period, as half-note beat 2 marks the beginning of the first complete convergence period. The second voice’s 23.7-beat elapse places its entrance within the second convergence period. Figure 9 also shows how the echo distance decreases by one beat with the passing of each convergence period; at the beginning of each period, the number of beats between the voices is equal to the number of convergence periods remaining to the CP.
Figure 10. Section of Study No. 36 halfway between beginning of “mega-glissando” and the CP (score, page 21) where original pitch levels are restated in all four voices
(click to enlarge)
[27] The convergence point in Study No. 36 is preceded by what Gann identifies as a “mega-glissando” that begins 80 measures before the CP, creating a fine example of a “collective effect” that is an extraordinarily long preparation to the CP. Figure 10 shows a section in the middle of this passage. Exactly halfway between the beginning of the mega-glissando and the CP, the C1 half note in the lowest voice begins a restatement of the opening transposition levels, spelling out a widely spaced major-seventh chord. The last voice reaches its restatement at the beginning of the next convergence period; two measures prior to this, the lowest voice starts another restatement, this time an octave higher.
[28] This section of rising glissandos creates a tremendous build-up to the CP. The glissandos emphasize to the listener the leader-follower relationship of the four voices, and Nancarrow very cleverly manipulates the decreasing echo distance by using steadily decreasing gaps between the glissandos to eventually create long, continuous glissandos through the four voices. After the CP, the glissandos descend through the voices and the listener is once again acutely aware of how the leader-follower relationship has changed at the CP.
Figure 11. The CP in Study No. 36 (“Canon 17/18/19/20”)
(click to enlarge)
[29] The stunning CP provided in Figure 11 is one of Nancarrow’s finest moments. Even the composer was surprised to hear the effect of what Reynolds refers to as “low-register difference tones” (Reynolds 1984, 16) generated by the extremely rapid iteration of notes in all the voices. Carlsen describes the passage this way:
In this passage, the four voices sweep up to their point of convergence with rapid chromatic glissandos, arriving simultaneously on their highest notes—B♭ 3, D5, F6, and A7.(9) Each high note is then rapidly repeated at the speed of a quarter-note in its own voice’s particular tempo. . . . Even in the slowest voice, the reiterated high notes fly by at a rate of more than 340 per minute (5 per second). But that is not all: the spaces between high notes are filled in with ascending thirty-second-note glissandos. At such speeds, the perception of individual pitches is impossible. The thirty-second-notes (which, in the bass voice, move at over 3000 per minute or 50 per second) are fast enough to theoretically start generating additional low pitches with frequencies in the range of approximately 50–60 Hz. (Carlsen 1998, 25)
Figure 12. Area of tempo crossing in Study No. 21
(click to enlarge)
[30] An unusual and unique canon is Study No. 21 (“Canon X”), an acceleration canon whose subtitle is derived from the manner in which the tempos of the two voices “cross” in the course of the piece. Study No. 21 is unlike any of the other tempo canons: its gradually changing tempos (accelerating in one voice while the other voice decelerates) almost imperceptibly “cross” somewhere in the middle of the piece. In No. 21’s proportionally notated score there is no meter, and no shared down-beats are notated, but it appears that there are three significant convergences.(10) This Study thus fits somewhat uneasily into this section on arch canons with one interior CP; however, only one of the convergences is a true canonic CP, and it does appear in the interior of the piece. The first convergence, just over one-third of the way through the piece where the two voices cross tempos, is not a canonic convergence point but more of a convergence area (see Figure 12). Thomas (1996, 126, 281) identifies the bracketed area in the figure as a passage of “nearly simultaneous motion,” which occurs just before the tempos of the two lines coincide somewhere near the beginning of the next system (at a point where the note articulations are nearly evenly staggered between the voices). The crossing of the tempos is thus not marked by a convergence point.
Figure 13. Convergence point in Study No. 21
(click to enlarge)
[31] At just over two-thirds of the way through the piece, an actual canonic CP does occur (see Figure 13). Its significance is enhanced by several factors: the 54-note row (B–C–
Converging Canons
[32] The next group of canons to be examined is the converging canons shown in Figure 7, which include Nos. 18, 19, 31, 32, 34, 48, 49A, and 49C. One of the distinguishing characteristics of converging canons is that the leader-follower relationship of voices is maintained to the final CP. This is easily seen in a structural diagram for Study No. 18 (“Canon 3/4”), which was mentioned earlier as an example of a canon where the entrance of a later voice coincides with the beginning of a convergence period (see Figure 14). This is made possible because the canon’s timespan (1,680 eighth-note beats) is divisible by both 3 and 4 and the first voice begins at the beginning of a convergence period.
Figure 14. Structural diagram of Study No. 18 (“Canon 3/4”), a converging canon in which the entrance of the second voice coincides with the beginning of a convergence period (click to enlarge) | Figure 15. Structural diagram of Study No. 19 (“Canon 12/15/20”) (click to enlarge) |
Figure 16. Conclusion of Study No. 19 (“Canon 12/15/20”; score, page 7), showing the convergence point and alteration of final pitches to create V–I final cadence
(click to enlarge and listen)
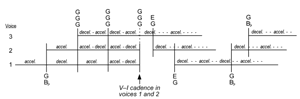
[33] In Study No. 19 (“Canon 12/15/20”), like most of Nancarrow’s tempo canons, later-entering voices do not enter at the beginning of a convergence period (Figure 15). The voices are related to each other by a duration ratio of 3:4:5,(11) and the bottom voice relates to the middle voice by the ratio 4:5 and to the top voice by the ratio 3:5. The timespan of 336 eighth-note beats is divisible by 3 and 4, but not by 5; thus, since both the middle and top voices relate to the bottom voice in ratios containing the factor 5, neither of these voices enters at the beginning of a convergence period with the bottom voice. The CP at the end of Study No. 19 is noteworthy because Nancarrow somewhat uncharacteristically alters the interval of imitation between the voices (from elevenths to double octaves) to create a unison V–I cadence (see Figure 16). It is likely that Nancarrow did this to convey an additional sense of finality because this canon concludes the six-canon set of Nos. 13–19, all of which are based on the rhythmic series {n – 1, n, n + 1, n}.
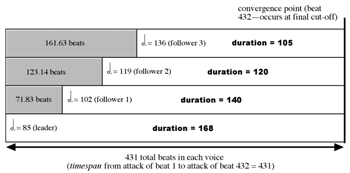
[34] Study No. 32 (“Canon 5/6/7/8”) is a straightforward four-voice converging canon whose structure is shown in Figure 17. No. 32’s final convergence point (see Figure 18) is unusual in that it occurs at the final cut-off—that is, at the hypothetical downbeat that follows the final beat. There are 431 dotted half-note beats in the canon, and the timespan is the same number because the CP actually occurs on hypothetical beat 432.
Figure 17. Structural diagram of Study No. 32 (“Canon 5/6/7/8”) (click to enlarge) | Figure 18. Convergence point of Study No. 32 (click to enlarge) |
Figure 19. Convergence point at end of Study No. 34
(click to enlarge)
Figure 20. (a) Convergence of arpeggio figures in Study No. 48A (page 43 of score); (b) diagram of proportions in Study No. 48
(click to enlarge)
[35] In Study No. 34 (“Canon
![]() ”), measuring entrances to later-entering voices is complicated by numerous factors: the almost complete lack of noted shared downbeats in the score; the multiple sections of the canon; and the unmetered rests that occur between many of the sections, thus making it impossible to establish a length for the canon’s timespan. The CP (Figure 19) occurs on the attack of the final beat (this is the only downbeat in the entire score shared by all three voices).
”), measuring entrances to later-entering voices is complicated by numerous factors: the almost complete lack of noted shared downbeats in the score; the multiple sections of the canon; and the unmetered rests that occur between many of the sections, thus making it impossible to establish a length for the canon’s timespan. The CP (Figure 19) occurs on the attack of the final beat (this is the only downbeat in the entire score shared by all three voices).
[36] Study No. 48 (“Canon 60/61”) is a remarkable achievement in convergence. It consists of three movements: movements A and B are each 60:61 canons, which are then played together to create movement C (with approximately a 60:61 ratio between A and B). The performance of C involves two carefully coordinated player pianos. Movement A has a major tenth level of imitation, with an echo distance that begins at about eight seconds dwindling to zero over the course of some 127 pages (the score is proportionally notated and includes additive acceleration in all four voices, thus measurements are inexact). The canon contains a minimal level of convergence between the two voices; the most pervasive is due to regularly recurring pairs of arpeggios in which the second of the pair in the bottom voice aligns with the first in the top voice (see Figure 20a).
[37] Movement B is slightly shorter than movement A, as—when both movements are performed together (in movement C)—movement B should enter after movement A’s faster voice (see Figure 20b). Movement B’s interval of imitation is the perfect fifth; this allows the final chord of movement C to spell out a
Figure 21. Structural diagram of Study No. 31 (“Canon 21/24/25”), a converging canon that ends before the CP is reached
(click to enlarge)
Figure 22. Conclusion of Study No. 31 (“Canon 21/24/25”; score, pages 8–9)
(click to enlarge)
[38] Study No. 31 (“Canon 21/24/25”) is an unusual case. It is a converging canon with no CP, as the canon is truncated before the CP is reached. As shown in Figure 21, the canon’s actual length is 669 eighth-note beats, which is 36 beats shy of the 705 needed to reach convergence (the timespan is 704 beats) at a ratio of 21:24:25. The lack of a temporal convergence is seemingly underscored by the three key areas a fifth apart to create what Thomas (1996, p. 67) refers to as an “unresolved asynchronicity” (see the canon’s conclusion in Figure 22). The canon is in three distinct sections, each separated by an eight-measure rest, and the third section is registrally enlarged (the level of imitation increases from a fifth between voices to an octave plus a fifth) and the canonic line is reinforced by octaves and full of melodic leaps. Based on these features, Thomas offers a very perceptive and plausible reason for the lack of convergence at the end:
It is in the final section of the study that the canon becomes most difficult to perceive, and in this lies what may have been a potential reason for ending the study before it can converge on a point of synchrony. Each single voice is difficult to follow in and of itself in this section because of its extreme registral leaps and because the articulation types are limited exclusively to staccato. . . . Since it is difficult to follow a single voice, it is nearly impossible to follow the canonic relationship among voices. The staggered ending thus reorients us to the canonic nature of the passage: as each voice drops from the texture in quick succession we are reminded retrospectively of them as linear entities, and we hear in their concluding gestures their shared material and imitative relationship. (Thomas 1996, 69–70)
Tempo Canons With More Than One CP
Figure 23. Line diagrams describing structures of Nancarrow’s tempo canons with more than one CP (Gann 1995, 22, 23, and 25)
(click to enlarge)
Figure 24. Structure of Study No. 15 (“Canon 3/4”), a diverging-converging canon in two voices with a tempo overlap
(click to enlarge)
[39] Canons with more than one CP are of the following types: diverging-converging canons (which begin and end with a CP), canons with interior tempo switches, and special cases such as acceleration canons. Figure 23 shows the simpler canonic structures that contain more than one CP. One of the basic types of tempo canon, the diverging-converging canon, has two CPs, one at the beginning and one at the end. Nancarrow wrote two examples of this type of canon: Studies No. 15 and 17. Canons of the diverging-converging type have at least one tempo overlap (the number of which depends on the number of voices and tempos in the canon). Study No. 15 contains a simple example of a tempo overlap. This two-voice Study has a tempo and duration ratio of 3:4 and a canonic subject of 336 eighth-note beats; the canon is stated twice in each voice, once at the slower tempo and once at the faster tempo. When the faster voice repeats the canon at the slower tempo, both voices state the slower tempo for a period of 84 eighth notes (one-fourth of the canon’s length), and this section comprises the middle one-seventh of the entire length of the piece (see Figure 24). An interesting by-product of this structure is that the top voice, which initially states the faster tempo, remains the leader in stating the canon throughout the piece.
[40] Another important structural feature of diverging-converging canons is that each voice successively states every tempo: each voice states the tempos in a different order and each tempo is uniquely associated with a canonic section that is the same length in each voice. This can be clearly seen in the structure of Study No. 17 (“Canon 12/15/20”), which was shown in Figure 6. The three sections are stated once in each voice: the A section is associated with the tempo of half-note = 172.5 and a duration of 4; the B section is associated with the tempo of half-note = 138 and a duration of 5; the C section is associated with the tempo of half-note = 230 and a duration of 3. As shown in Figure 6, there are no tempo overlaps involving C, the shortest section. The longest section, B, has the longest overlap, and the A section has an overlap half that length.
Figure 25. (a) Beginning and (b) ending (score, page 12) of Study No. 17 (“Canon 12/15/20”)
(click to enlarge)
[41] Study No. 17 does not exhibit as much harmonic convergence at section changes as No. 15 does, and, with almost continuous eighth-note motion in three different (and quite fast) tempos, it would be difficult to hear such coordination anyway. The CP at the beginning of No. 17 coordinates on a F-major triad while the final CP features a cadence on A (see Figure 25). Throughout the piece, the A section always begins on the note C, the B section on A, and the C section on F. Nancarrow keeps to a limited number of frequently changing key areas (mostly F, A minor, C, G, and D), which allows some brief and random areas of harmonic convergence to occur.
[42] Several Studies (Nos. 24, 33, and 43) use internal tempo switches to create additional CPs. The structures of Nos. 33 and 43 are shown in Figure 23; No. 24’s structure is shown in Figure 26. Study No. 43 (“Canon 24/25”), with its single tempo switch and two CPs, provides a simple structural framework for looking at the tempo switch; its two CPs and the tempo switch are shown in Figure 27. The two voices of Study No. 43 are not only very close in tempo ratio (24:25) but also in their interval of imitation, a major third. Gann describes the proportions of the Study in relation to the CPs as follows (219):
Figure 26. Structure of Study No. 24 (“Canon 14/15/16”; modified from Gann 1995, 23)
(click to enlarge)
Figure 27. Score sections from Study No. 43: (a) approach to first CP; (b) tempo switch; (c) final CP
(click to enlarge)
Table 1. Description of Canons and Convergence Points in Study No. 33
(click to enlarge)
Thus, the tempo switch occurs exactly halfway between the two CPs, after twelve convergence periods at a point where the echo distance is twelve quarter-note beats (this is shown by the arrow connecting the
[43] As in Study No. 36, Nancarrow precedes the first CP in No. 43 with ascending movement. The second CP, which is actually a rest, is followed by descending movement in sixteenth notes (the most rhythmically active section of the piece). The CPs are used to set off a middle section in the palindromic structure of the piece; Gann describes that structure in this way:
This 24/25 canon is more nearly palindromic than No. 36; no extravagant post-CP event appears to throw the symmetry off balance. Instead, the textures and motives of the first half of the piece return in almost exact reverse order in the second half, though varied, some of them more elaborately developed, others shortened. . . . No. 43 is palindromic in spirit, although there are no actual retrograde passages. (Gann 1995, 218)
The “palindromic spirit” and arch shape of the piece are also reinforced by increases and then decreases in note density and dynamics before and after the CP section. Gann’s generalization about the splintering of motives that become briefer as a CP approaches holds somewhat true here; some of the motives prior to the first CP are subjected to rhythmic compression, and in the section leading up to the CP there is a countdown extending from 12 quarter notes down to 1.
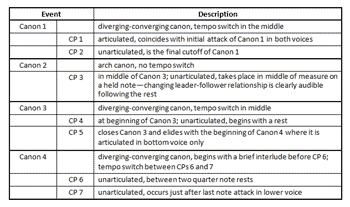
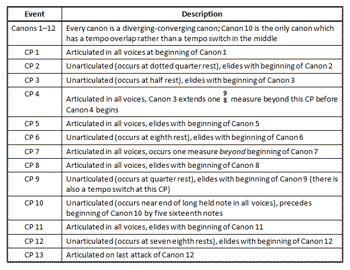
[44] Study No. 33’s irrational tempo ratio of \(\frac{\sqrt{2}}{2}\) presents special challenges in measuring and calculating distances and durations. The structure of the Study is shown in Figure 23. There are four distinct canons (which Gann labels A through D in the diagram, but refers to as Canons 1 through 4 in his narrative): Canon 1 is a diverging-converging canon with a tempo switch in the middle; Canon 2 is an arch canon with a CP in the middle; Canon 3 is another diverging-converging canon; and Canon 4 is also a diverging-converging canon, but it begins with a short interlude prior to the canon’s first CP. All told, there are seven CPs. Only the first one takes place on a note attack in both voices; most of the remainder occur either on held notes or rests. Even the final CP does not take place on a coincident beat attack. See Table 1 for a description of the canons and convergence points in Study No. 33.
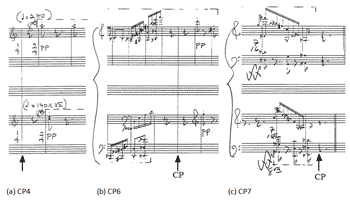
[45] Figure 28 shows three of the unarticulated CPs in Study No. 33. CP 4 marks the beginning of Canon 3, and begins on a rest. CP 6 is technically the beginning of the diverging-converging canon in Canon 4, but it also occurs at a rest. CP 7 is an enigma—the final beat attacks in both voices are almost coincident, but not quite, as indicated by the lack of a shared barline at the final measure. The effect, then, is that the top voice finishes slightly ahead of the bottom voice to create a sort of V–I cadence in Db. Unfortunately, it is impossible to calculate exactly where the final CP falls in the last measure. On the other hand, due to a shared barline, the exact location of CP 6 is discernible, but because the exact measurement from CP 6 to the tempo switch between CP 6 and CP 7 is not known or calculable, it is not possible to use the measurement of that half of Canon 4 to determine the full canon’s length and to project the exact ending point of the canon. If it were possible to calculate the exact measurement of the first half of the canon to the tempo switch, the exact location of CP 7 would be calculable. Thus its location can only be approximated.
Figure 28. Convergence points in Study No. 33 (“Canon \(\frac{\sqrt{2}}{2}\)”) (pages 12, 25, and 52, respectively, of the score) (click to enlarge) | Figure 29. Study No. 24 (portions of second and third systems of page 12), showing CPs 8 and 9 (click to enlarge) |
Table 2. Description of Canons and Convergence Points in Study No. 24
(click to enlarge)
Figure 30. Structure of rhythmic convergence area in middle of Canon 10, Study No. 24
(click to enlarge)
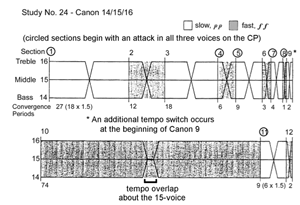
[46] Study No. 24 (“Canon 14/15/16”) has twelve canonic sections demarcated by thirteen CPs (see Figure 29). Each of the twelve canons is of the diverging-converging type, with a tempo switch between the outer voices (i.e., the fastest and slowest voices) in the middle of each canon; the middle voice stays at the middle tempo throughout the piece. Canon 10, however, has a tempo overlap section in the middle before the tempos switch. Also, in addition to the tempo switches in each of the other eleven canons, an additional tempo switch is inserted at the beginning of Canon 9. Thus, there are twelve tempo switches and one tempo overlap in this Study.
[47] Table 2 lists and describes the canons and CPs that occur in Study No. 24. As the table shows, the majority of the CPs elide the end of one canon with the beginning of another; the exceptions are CPs 4, 7, and 10. The table also shows that CPs 1, 4, 5, 7, 8, 11, and 13 are articulated in all voices while the others are unarticulated (i.e., take place on rests or held notes).
[48] CPs and tempo switches sometimes occur with startling rapidity in this Study, particularly in the area of Canons 6–9 where (as shown in Figure 26) CPs occur every 3, 4, 1, and 2 convergence periods, respectively. Figure 29 shows Canon 8 (the briefest canon, consisting of only one convergence period of 15 sixteenth notes) and the beginning of Canon 9. As mentioned earlier, an additional tempo switch is inserted at the beginning of Canon 9. Normally the leader-follower relationship between the top and bottom voices reverses at each CP; at Canon 9, however, the additional tempo switch allows the bottom voice to remain the leader for both canons.
[49] At Canon 10 (by far the longest canon, comprising 74 convergence periods), Nancarrow inserts a tempo overlap on the middle tempo (![]() . = 240) that lasts for 60 sixteenth notes (four convergence periods). The tempo overlap allows for a rare rhythmic convergence to be created in all three parts by repeating the same rhythmic pattern three times, as shown in Figure 30. After this rhythmic convergence, the top and bottom voices switch to the tempo opposite the one they had before the convergence.
. = 240) that lasts for 60 sixteenth notes (four convergence periods). The tempo overlap allows for a rare rhythmic convergence to be created in all three parts by repeating the same rhythmic pattern three times, as shown in Figure 30. After this rhythmic convergence, the top and bottom voices switch to the tempo opposite the one they had before the convergence.
Figure 31. Structural diagram of Study No. 37 (modified from Gann 1995, 26), showing the twelve canons and five convergence points
(click to enlarge)
Figure 32. CP4 from Study No. 37 (page 40 of score)
(click to enlarge and listen)
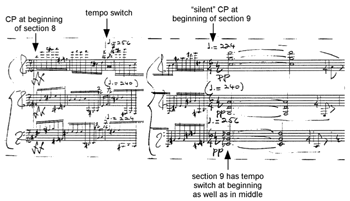
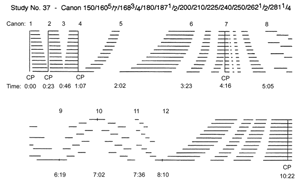
[50] Study No. 37, whose structure is shown in Figure 31, is another canon with multiple CPs. Its twelve voices state the tempo ratio of the justly-tuned scale, which seems imposing but allows Nancarrow the ability to create widely-ranging textures and to combine the tempos in different groupings (comparable to chordal structures) that are not rigidly bound by his usual practice of assigning the slowest tempo to the lowest voice, etc. Gann identifies twelve canons and five CPs in this Study, and although the structure in Figure 31 does not show this, different tempos are consistently applied to different voices. In Canon 1, the tempos are in Nancarrow’s usual order of fastest tempo in the top voice to slowest in the bottom voice, thereby expressing a rhythmic analogue of just intonation. In Canon 2, the order of tempos is reversed. In later sections of the Study, Nancarrow creates “chordal” groupings of tempos, such as in Canon 6 where the tempo order from bottom to top is 150 1871/2 240 1605/7 200 250 1683/4 210 2621/2 180 225 2811/4 (see Figure 32, left edge of score); as shown by the bold and italic type, the tempos are arranged into three interlocking “diminished-seventh chord” groupings.
[51] Convergences between voices are clearly important in this canon. In many places, Nancarrow has marked with vertical broken lines where entrances of new voices coincide with beats in other voices (something he could have marked in many other scores, but did not), even when the voices are widely separated in the score and the convergence is with an interior beat rather than a downbeat. These convergences between voices are more common than might be supposed from the unwieldy tempo ratios. In several of the later canon sections (e.g., canons 8, 9, and 10) where tempos are in “minor third” groupings, simpler tempo ratios such as 6:5 and 7:6 are common between voices. These middle and later canonic sections, then, are more temporally consonant, which is a virtual necessity for perceptual purposes because the melodic material here is much more active than in the earlier sections.
[52] Gann says about the convergence points in No. 37, “Convergence points are brilliantly de-emphasized in this study, for this is the work in which Nancarrow learned how to create beautiful effects with convergence points by omitting them” (1995, 195). The CPs are not omitted, but unarticulated, as not one of the five CPs occurs at a note attack. CPs 1 and 2 occur on a rest, the voices entering in a staggered fashion just after the CP. CP3 also takes place at a rest, just after the conclusion of canon 3. The most climactic CP is unquestionably CP4 at the beginning of canon 7 (Figure 32). This CP marks the most rhythmically active section of the piece and comes at a place where the texture thickens to all twelve voices after an extended section in canons 4, 5, and 6 where the voice saturation is considerably thinner. In comparison, the concluding CP5 is notably anti-climactic, occurring at a whole note in all twelve voices that is held over from twelve tied half notes and marked with a fermata.
[53] The processes of acceleration and deceleration create special challenges (and opportunities) for planning and placement of convergence points, and for this I will first discuss Studies Nos. 8 and 22, followed by an in-depth analysis of Study No. 27. Nancarrow used two varieties of acceleration: arithmetical and geometric. Arithmetical tempo changes involve adding or subtracting the same invariable rhythmic unit to the previous value, and geometric changes involve changing note values by an invariable percentage. Arithmetical acceleration creates a constantly increasing or decreasing rate of change, but can be notated in conventional notation due to a common background unit; geometric acceleration creates a smooth continuum of changing speed that must be notated in proportional notation.(12) Callender (2001) examines the difficulties with creating large-scale continuous acceleration through these techniques, particularly that of arithmetical acceleration, in which the rate of change is itself constantly changing rather than remaining constant as it does in geometrical acceleration. (Callender goes on to describe a model of acceleration that relates to an unchanging unit of time, allowing acceleration to be carried out on a larger scale than Nancarrow’s methods allowed.)
[54] Although it predates the first tempo canons, Study No. 8 (an early example of Nancarrow’s acceleration technique) makes considerable use of convergence points. Its first section, called by Carlsen the “trio” because it is in three voices, consists of canonic lines that alternately accelerate and decelerate within a series of nineteen durations, each of which consists of a pair of notes in a 2:1 rhythmic relationship (notated as an eighth note followed by a quarter note with a sustain line). The 2:1 rhythmic pattern creates a loping effect that particularly elucidates the processes of acceleration and deceleration. Although the notation is proportional, the process of tempo change is arithmetical as an invariable background unit is continually added or subtracted to determine the next note values.
Figure 33. First section of Study No. 8, showing convergence points (vertical connecting lines), whether durational series are accelerating or decelerating, and pitches at CPs
(click to enlarge)
[55] Nancarrow imposes strict order on the form of this section by bringing in each new voice at a convergence point, as shown in Figure 33. As Carlsen notes, the main pitch in this section is G, and all CPs take place on G octaves or triadic intervals involving G. No two voices ever state the same rate of change at the same time, even if they use the same tempo process. For instance, in the fourth phrase of this section, where both the first and second voices are in accelerating-decelerating patterns, the patterns begin and end, and also change speed direction, at different places in the nineteen-duration series. One of the interesting effects of this procedure is that the echo distance between voices is constantly different, and not steadily increasing or decreasing as would normally be the case. Despite this variety in the rate of change within voices, Nancarrow ensures convergences at regular time intervals by keeping the total number of background units the same in each voice within each phrase. Occasional near-convergences also pop out of the texture due to the use of the same limited number of durations within each voice; also, the short note in each durational pair casts such nearly aligned attacks, when they do occur, in stark relief.
[56] In contrast, Study No. 22 (“Canon 1%/1½%/2¼%”(13))—one of two studies to use geometric acceleration—has only three widely spaced convergence points (see Figure 23): the first concludes Canon A, a converging canon; the second is in the middle of Canon B, an arch canon; and the third begins Canon A’, a diverging canon. Study No. 22 is a strict palindrome in both rhythm and pitch; CP2, which takes place at a rest, is thus the rhythmic line of symmetry in the piece. In Canon A, the first note of each voice is the same length (75 millimeters in the score’s proportional notation), but by the CP the different rates of acceleration—the 2¼% line accelerates 125% as fast as the 1% line—have resulted in very different lengths for the last note before the CP: 7.5 measures in the fastest voice (a duration 10% as long as at the beginning); 17 measures in the middle voice (about 23% as long as at the beginning); and 30 measures in the slowest voice (about 40% as long as at the beginning). Thus, at the CP the fastest voice has sped up to four times the speed of the slowest voice. As a result, as the CP approaches one hears the exponential change in the echo distance between the voices.
Convergence Points in Study No. 27
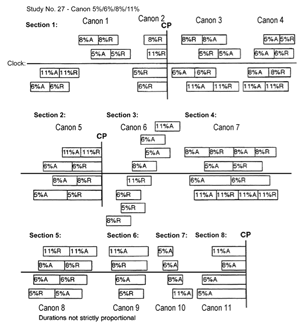
[57] Study No. 27 (“Canon 5%/6%/8%/11%”) is Nancarrow’s tour-de-force in the use of geometric acceleration and features four canonic voices (sometimes doubled) that use acceleration and deceleration at the four rates given in the title. Like Study No. 22, No. 27 has three widely spaced convergence points. However, whereas No. 22 consists of three of the basic canon types (converging, converging-diverging, and diverging), Thomas notes that No. 27 is unlike any of the four basic canon types and instead “incorporate[s] the technique of gradually changing speeds, so that the relationship between the voices is constantly changing” (Thomas 1996, 13). The use of four rates of acceleration/deceleration gave Nancarrow an unusual amount of freedom in arranging relationships among the four canonic voices and in placing convergence points in the piece.
General Observations
Figure 34. Reduction of the “clock line” of Study No. 27: ostinato line of four chromatically contiguous pitches and progression of its harmonic manipulations
(click to enlarge)
[58] Due to the geometric acceleration technique, Study No. 27 is notated entirely in proportional notation. The texture consists of staccato notes (notated as quarter notes) or sustained notes (quarter note with a solid line to the right to indicate the length of the note). In the middle of the canonic texture is a line of non-varying tempo that is commonly referred to as the “clock line” (reduction shown in Figure 34), representing what Nancarrow referred to as the ticking of an “ontological clock” (Reynolds 1984, 9), or a time-keeping device against which one can detect the constantly changing speeds of the other voices. According to Jan Jarvlepp (1983/84, 219), Nancarrow considered the clock line to be an ostinato even though it seems to have no recurring pattern of pitch or rhythm. Thomas’s description of the clock line emphasizes its function as an ostinato:
It is presented in staccato articulations at intervals equivalent to either quarter or eighth notes. . . . The basic rhythmic and pitch material of this layer is limited, to be sure, but it is subjected to perpetual, random reorderings. As a result, it has no recurring patterns nor metrical implications. Nonetheless, the layer functions contextually as an ostinato because of its constant presence and its relatively steady character: although its articulations are not regular, its tempo is unchanging, while all the other layers in the study are continually subjected to accelerandi and ritardandi. (Thomas 1996, 14)
Thomas further notes that when “two different time types
Figure 35. Formal diagram of Study No. 27 (modified from Gann 1995, 161)
(click to enlarge)
[59] Figure 35 shows Gann’s formal diagram of Study No. 27, modified to identify the convergence points and other features. It identifies the relative positions of the clock line and the four canonic voices; the percentage of acceleration or deceleration is indicated for each voice. It also identifies Gann’s eight sections; these eight sections correspond to the changing textures of the clock line shown in Figure 34. Section 1 contains four different canons (identified separately by Gann because the levels of imitation do not remain the same), and I have modified Figure 35 to identify these four canons; each of the other sections has one canon, for a total of eleven. CPs at the end of Canons 2, 5, and 11 are also identified, and the diagram is modified to more accurately reflect the relative relationships between canons and where voices enter and drop out. As shown, within each canon each percentage is uniquely affiliated with a specific voice that does not change within that canon; in some canons both acceleration and deceleration are used, and in some only one process is used.
Overall Structure
[60] The importance of convergence points in Study No. 27 is a matter for some disagreement. Gann asserts (1995, 163) that “convergence point is not an important issue in this study.” Thomas, on the other hand, points to the first CP as a place where “the process of convergence is very plainly the point of this particular canon” (Thomas 1996, 135). Indeed, it seems that given the kind of mathematical manipulations that were required to create this and the other CPs, it could hardly be otherwise. If convergence is not the main point of this Study, it certainly is at least a significant one. The first two CPs involve the canonic voices but not the clock line, whereas the CP that concludes the piece involves all the voices, increasing its emphasis.(14)
Table 3. Symmetrical Levels of Imitation in Selected Canons of Study No. 27
(click to enlarge)
Figure 36. The levels of imitation between adjacent canonic voices and order of entrances of the eleven canons of Study No. 27
(click to enlarge)
Figure 37. The first three lines of the clock line in Study No. 27, showing limited pitch content and proportional notation of the tempo)
(click to enlarge and listen)
[61] Carlsen points to this Study (along with Nos. 19 and 36) as one in which “It is significant that the exact midpoint on Nancarrow’s instruments is the note E4
[62] The first three lines of the ubiquitous clock line are shown in Figure 37. The clock line consists of two rhythmic values related 2:1, the longer value articulating the stated 220 tempo. Thomas points out that the clock line never approaches temporal consonance with the other voices (1996, 134), and since the rhythmic values in the canonic voices are always changing there are only random, non-consecutive cases where these values match the clock line’s. Short repeated pitches appear fairly frequently in the clock line, with the first set of three repeated notes articulating E4, the player piano’s central note. The longest series of short notes in the line is nine, and of long notes it is five.
[63] All references to the clock line in the main analytical sources comment on its apparent total randomness of both pitch and rhythm throughout the piece. Any rhythmic or melodic patterns or non-musical associations that Nancarrow may have incorporated into this line are so well hidden as to be indecipherable. Despite the overall appearance of randomness in both pitch and rhythm in this ever-present line, it still seems likely that some type of patterning must have been involved in its creation. For one thing, as Pickover (1995) has noted, it is quite difficult for humans to generate truly random sequences:
Sit down at a computer keyboard. . . and randomly press the 1 and 0 keys. Try to make the string of numbers as “patternless” as possible. In other words, try to generate random numbers. [Pickover then gives a 6-line example of 1’s and 0’s that he generated.]
. . . I have tested dozens of supposedly random sequences typed by colleagues, and found out that it is curiously difficult for humans to type patternless sequences. To start with, we would expect about a 50 percent occurrence of each digit, and I did amazingly well. The [example I typed] had 49.3 percent 1’s and 50.7 percent 0’s. Next, we would expect 25 percent occurrences of the following pairs: 00, 11, 01, 10. In fact, doing my best to make a random sequence, I produced 15 percent, 13 percent, 36 percent, and 36 percent occurrences, respectively. Apparently my fingers preferred to oscillate rather than producing doublets such as 00 and 11. Perhaps I was trying to avoid clumpiness of digits, when in fact strings of identical digits should exist in a truly random sequence. (Pickover 1995, 233)
In creating the clock line, then, Nancarrow would not only have been faced with this difficulty in creating randomness in rhythmic values, but also among the four pitches.
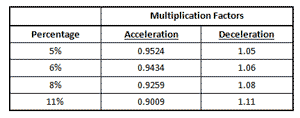
Table 4. Multiplication Factors for Acceleration and Deceleration in Study No. 27
(click to enlarge)
[64] The percentages in the Study’s subtitle are used to create both accelerating and decelerating series of rhythmic values. Table 4 shows the multiplication factors needed to derive successive values of the series. The factors can be applied over a series of accelerating or decelerating values by using successive multiplication; for example, an accelerating series of twenty values (i.e., a series of nineteen value changes) at 6% that begins with a rhythmic value of 100 millimeters will end with a value of 100 x 0.943419, or 33.1 millimeters. A decelerating series of twenty values at 6% that begins with a rhythmic value of 20 millimeters will end with a value of 20 x 1.0619, or 60.5 millimeters.
Sections of the Study
Canons 1 and 2[65] Study No. 27’s first CP concludes the section consisting of these two canons. Canon 1 is one of only a few canons in the piece in which more than one basic rhythmic value is used, and in this way it forms a rhythmic parallel to the clock line. Canon 2 forms a pitch parallel to the clock line in that each of the four canonic lines, like the clock line, consists of four contiguous chromatic pitches. Both Canons 1 and 2 (as well as 3 and 4—see Table 3 and Figure 36) have symmetrical patterns of levels of imitation between the voices. In Canon 1, the first two voices (A6%/R6% and A11%/R11%) finish stating the canon before the other two voices enter; in Canon 2, the four voices enter in succession so that the canon is eventually being stated in four voices at once.
Figure 38. Canon 1 in the lowest (A6%/R6%) voice, in rhythmic notation showing relative rhythmic values and pitch content
(click to enlarge)
Figure 39. Section from Canon 1 (page 3 of score), showing two unarticulated CPs and their leader-follower switches, pitch symmetry about these switches, and near-synchrony at second switch
(click to enlarge and listen)
Figure 40. Pitch content of Canon 2, also a decelerating passage
(click to enlarge)
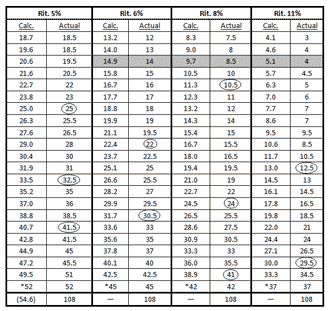
Table 5. Calculated and Actual Duration Measurements in Canon 2 of Study No. 27
(click to enlarge)
[66] The pitch content and relative rhythm of Canon 1’s lowest voice are shown in Figure 38. The first six notes—the first three in the equivalent of quarter notes and the next three in eighth notes—along with the first rest, serve to set up a pattern that divides the line primarily into trichords. This trichordal division is maintained throughout much of the canon through rests and changing note values. The most prevalent pitch-class set represented is 3-4 [015], while sets 3-2 [013] (Carlsen’s “par-titioned minor third”), 3-3 [014], and 3-9 [027] are presented three times each; melodic movement by half steps and P4/P5 prevails. The canon’s concluding pentachord, 5-Z18 [01457], is a subset of both the opening hexachord 6-Z10 [013457] and the hexachord that precedes it, 6-Z11 [012457].
[67] Figure 39 shows a section from Canon 1 where the canon is in two voices. This passage is a rare instance in Study No. 27 where the voices are close enough together in stating the canon that the echo distance is audible. There are two leader-follower switches on this page, and these are made more clearly audible because of the rests that accompany the switches. The passage is especially interesting because of the symmetry of the intervals between the voices at these points.
[68] Canon 2’s pitch content, like the clock line, is limited to four contiguous chromatic pitches (Figure 40). The canon concludes with a CP on the attack of the final pitch, which is the same as the first pitch of the canon’s pitch cluster (a minor seventh chord on E); these pitches, as shown in the figure, create a symmetrical pitch structure about the D? in the clock line. The CP is also a durational convergence, as all four voices reach the same duration on the final pitch. Table 5 reports the actual and calculated measurements in millimeters of the twenty-three decelerating pitches in Canon 2; the final note in the series represents the CP, which occurs at the attack of the final note in the canon. Within a certain amount of tolerance, there is generally good agreement between the actual and calculated measurements. The canon’s final pitch, the CP, is 108 millimeters long in all four voices, and this value happens to relate to only one of the voices: it is roughly double the value in the series at that point in the 5% voice.
[69] It is interesting to speculate how the CP at the end of Canon 2 might have represented a greater achievement in convergence had the opening values in each voice been such that 108 was double the value in the series at the CP. The bottom part of Table 5 shows the calculated values for opening durations that would have resulted in this “durational convergence” on the value 108 at the CP. The resulting values in the 6%, 8%, and 11% voices are closest to the values that occur in the third note of each series (shaded area in table). It would have been a simple matter for Nancarrow to begin the 6%, 8%, and 11% voices with these values in order to facilitate this durational convergence, if he had chosen to do so.
Canons 3 and 4
[70] These two canons conclude the first section, in which the clock line still iterates single pitches (Figure 34). In Canon 3, the voices above the clock line (8% and 5%) first decelerate and then accelerate, while the voices below the clock line (6% and 11%) do the opposite. In Canon 4, each voice first accelerates and then decelerates, with the fastest-changing voice (11%) at the bottom and the slowest (5%) at the top. Canon 3’s 23-note canon has a narrow pitch focus of a major sixth, tracing G to E — the primary pitch centers of the piece. The canon’s opening contour is similar to that of Canon 1, and there is a fairly strong implication of first E major and then B minor in the last half of the canon.
[71] The halfway point of the canon, the twelfth note, is where the A6%/R6% voice is notated to switch from acceleration to deceleration, but in the score the R5%/A5% and A11%/R11% voices are marked to switch on the note prior to this, and the R8%/A8% voice on the note following the halfway point. Besides the fact that this seems a violation of the spirit of the canonic process, there are other reasons to believe that all the voices should be marked in the score to switch at this halfway point. Based on measurements in the score, it appears that the tempo change process occurs as follows: ten duration changes take place in one direction (either accelerating or decelerating), the duration of the eleventh note is used again for the twelfth note, followed by ten duration changes in the opposite direction, and the final (23rd) note is a longer duration which is apparently unrelated to the prevailing duration series. If the switch takes place on the middle note, and the same number of duration changes takes place on both sides of this point, the opening value and the value preceding the long concluding note should be roughly the same. Indeed, this does seem to be the case with all four voices, leading to the reasonable conclusion that the switch in each voice should be marked at the twelfth note of the canon.
Figure 41. Canon 4, from lowest voice (A11%/R11%)
(click to enlarge)
Figure 42. Segment of Canon 4 (page 16, second system), at entrance of 5% voice
(click to enlarge)
[72] Canon 4 unites an organic principle of organization in both pitch and rhythmic duration, organizing both around five-note groupings separated by barlines. The melody’s five-note pattern is a sort of major/minor upper trill, including a total of 24 groupings and 16 iterations of the trill figure as shown in Figure 41; groupings of one to four of these “trills” are followed by a single short note. Fourths/fifths and triadic structures appear to dominate the melodic movement between the first notes of each “measure”; the trill in the fourth and fifth measures spells out the clock line’s tetrachord, and several other groupings include the chromatic tetrachord. The deceleration portion of the canon is two groupings longer than the acceleration portion.
[73] Like the pitch changes, the rhythmic durations of this canon change with each five-note grouping. Figure 42 shows a representative portion of the score and duration measurements from this section.
Canon 5
[74] Canon 5 introduces two related texture changes: the canon includes many half-step trills, and the ostinato line is reinforced by octaves and registrally divided between the bottom half-step pair (
[75] Canon 5 concludes with the Study’s second CP; the convergence takes place at the release of the final note. The convergence at the note release is made the more striking by the sudden change in dynamic from f to p and the change back to a single note texture in the clock line immediately following the CP. The final values in each voice at the CP are not equivalent and thus not a “durational convergence,” but in each voice the durations of the notes at the CP appear to be close to the next value in the deceleration series taking place at that point (although in some places, particularly in the 11% voice, the note lengths in the score do not match the series very well).
Canon 6
[76] At Canon 6, the ostinato line returns to its original single-note texture, and the dynamic level drops from f to p. As shown in Figure 35, each voice first decelerates in the bass register below the clock line, and then, in tempo, leaps five octaves plus a minor sixth to the treble register above the clock line for its accelerative portion. This registral separation is an extension of the texture used for the clock line in Canon 5.
Figure 43. Canon 6 in the lowest (R8%/A8%) voice
(click to enlarge)
[77] Canon 6’s melodic line is shown in Figure 43. Thanks to the registral separation within this canon, it covers the widest range in the Study—the lowest note of the lowest voice (8%) occurs at the last note of the ritardando portion and is the lowest note on the player piano keyboard (B0); the highest note of the highest voice (11%) is at the end of the acceleration and is the piano’s highest note, A7. Nancarrow has thus included a rough parallel between frequency and speed—the slowing pitches sink to the lowest register and the accelerating pitches climb to the top of the keyboard. Combined with the very close intervals of imitation (M2 – m2 – M2: another expression of the intervals in the clock line), this texture is an extreme contrast to any heard in the Study thus far. The tempo change scheme in Canon 6 is very straightforward, and each voice begins and ends with the same durational value.
[78] The canon opens with a chromatic descending line in which the intervals progressively widen (five m2’s, two M2’s, three m3’s, and a M3) in a manner reminiscent of the overtone series in retrograde. The first and last thirteen notes of the canon are the same melodic series in retrograde inversion; between these extremes, melodic movement again favors intervals of fourths and fifths. This canon’s use of retrograde inversion at the beginning and end of the melody, along with the use of the entire range of the keyboard, both highlight the significance of Canon 6 as the midpoint of the Study.
Canon 7
[79] Canon 7’s melody consists of sustained and staccato notes, all of which remain in tempo. The texture thickens dramatically in this canon. The clock line expands to harmonic major and minor thirds, and the canonic lines are doubled five octaves apart—Canon 7 thus represents a simultaneous (vertical) expression of the registral separation idea that was sequential (horizontal) in Canon 6. And, like Canon 6, which covered the entire range of the player piano keyboard, Canon 7 covers almost the entire range (minus the very top note). The extreme pitches—B0 in the lowest octave of the 11% voice and
[80] As shown in Figure 35, the tempo change pattern in the 8% and 11% voices is accel.–rit.–accel.–rit., while in the 5% and 6% voices it is just accel.–rit.; this is the only canon in this piece in which a different number of changes takes place in different voices. The 98 pitches of the canon are divided differently in each voice between acceleration and deceleration, as follows:
| 8% voice: | A = 36 | R = 34 | A = 17 | R = 11 | / = 98 total |
| 5% voice: | A = 46 | R = 52 | / = 98 total | ||
| 6% voice: | A = 49 | R = 49 | / = 98 total | ||
| 11% voice: | A = 24 | R = 27 | A = 25 | R = 22 | / = 98 total |
Canon 8
[81] From here to the end of the piece, the order of the percentages matches the order of the voices: first from slowest change (5%) in the bottom voice to fastest change (11%) in the top voice in Canons 8 and 9, then reversing in Canon 10, and reversing back once again in Canon 11. This canon’s main textural idea is the minor/major triad. The clock line here expands to major and minor triads:
Figure 44. Melody of Canon 8 from lowest voice, rewritten in rhythmic notation
(click to enlarge)
Figure 45. Melody of Canon 9 from lowest voice, rewritten in rhythmic notation
(click to enlarge)
[82] Figure 44 shows the canon melody from the bottom line (R5%/A5%). Canon 8 contains two rhythmic values in the ratio 2:1, a feature that was previously used only in Canon 1. The lowest note on the keyboard, B0, that was prominent in both Canons 6 and 7 is just as much so here: the lowest voice enters first, on a B major triad built on this note, which is then is repeated twice more. The melody in the lowest voice is tonally organized around B. The first section (to the point where the tempo direction changes) concludes on a supertonic triad. Near the middle of the second half of the melody, a minor/major triad alternates in function between the supertonic and the V/V, finally becoming (enharmonically) V/V moving to V at the very end. In the highest voice (11%), the keyboard’s highest note (A7) is stated four times.
Canon 9
[83] Canon 9 is rhythmically the most complex canon, encompassing note values related by the ratio 4:3:2:1. Figure 45 shows the canon melody as it would appear in rhythmic notation in the lowest voice; the treble and bass registers in each voice are rhythmically coordinated but there is never a simultaneous note attack between them. The trill in some triads in the treble register involving the chord third and the fourth degree is retained from the end of Canon 8. Like an arch canon, Canon 9’s voices are placed almost symmetrically about the durational center of the canon, but, unlike the arch canon in the middle of Study No. 22, the symmetrical placement of the voices here does not allow for a convergence in the middle because of the constantly changing tempos.
[84] The clock line in Canon 9 states various kinds of seventh chords, again with
Canons 10 and 11
[85] The final two canons are each very brief and both use only acceleration. Canon 10’s 21-note melody is an ascending chromatic scale extending an octave plus a minor sixth, against a clock line that has returned to its original form of four chromatic pitches. The intervals of imitation progressively increase by a minor second: the interval between the top two voices is a perfect fourth; between the second and third voices an augmented fourth; and between the third and fourth voices it is a perfect fifth (see Figure 36). The beginning pitches of the four voices—
[86] At the conclusion of Canon 10, both the clock line and the lowest voice of the canon conclude on
Figure 46. Conclusion of Study No. 27 (page 55)
(click to enlarge and listen)
[87] Canon 11 is the most tonally oriented canon in the Study; all the intervals of imitation are octaves, and the pitch content is entirely in G major. The major second expressed in the clock line is imitated in the canonic lines, where every note expresses a major second trill (thus, no trills involving the intervals B–C and
Final Observations for Study No. 27
[88] In Study No. 27, Nancarrow expresses the same ideas in several different contexts, sometimes sequentially and sometimes simultaneously. The clock line’s chromatic tetrachord, for instance, is manifested in the pitch content of individual voices in Canon 2, in the opening pitches of the canonic voices in Canon 6, and in the levels of imitation in Canon 9. As another example, the concept of registral expansion moves through three consecutive canons: first in the clock line in Canon 5, then in the canonic voices of Canon 6, and then a simultaneous (vertical) expression of this idea in Canon 7.
[89] Thomas finds Study No. 27 to be “decidedly non-tonal” (1996, p. 17), but several tonal areas do achieve some significance. The final tonal goal is clearly G, the note immediately above the chromatic tetrachord of the clock line; G major is stated unequivocally in all the voices of Canon 11, in contrast to the tonal aimlessness and ambiguity of the rest of the Study. G, the first pitch in the lowest voice, is established almost immediately in Canon 1, and the lowest voice in Canon 2 begins on this same pitch. By the conclusion of Canon 4, however, with its
[90] Study No. 27’s first two convergence points do little to support the establishment of these tonal centers. Each of the CPs is structured differently. The first two CPs involve only the canonic voices, take place at the end of a decelerating section, and end with sustained notes. The first CP has a durational convergence on a value related to only one of the voices, while the second CP’s final sustained note is of different durations and represents the next series value in each voice. The Study’s final CP, which concludes the piece, takes place in all the voices (including the clock line) at the end of an accelerating passage on the attack of the final staccato note; this CP also includes a pitch convergence on G. The final CP’s unification of the highly mechanical clock line via unison attack and pitch,(15) along with the constantly changing speeds of the canonic lines, resolves the dichotomy set up in the piece involving the co-existence of a constant background unit and constant change of unit in the canonic voices. It is a fitting achievement of what Drott (2004) terms the “technological sublime,” which in this case involves the simultaneous use of technology in its older mechanical form (the ratcheted punching mechanism) and its newer, less constricted form.
[91] It is somewhat surprising to note in Study No. 27 how little control Nancarrow seemed to exert in areas where he had typically done so in many of his other tempo canons: for instance, in the establishment of tonal centers, areas of harmonic convergence, and various kinds of symmetry. There is also very little in this Study that could be considered a “collective effect” other than the similar gestures in the canonic voices.(16) These gestures are generally quite disjointed and rarely achieve a level of interdependence except at the CPs.
[92] When considering both Studies Nos. 22 and 27 together, it is apparent that Nancarrow had far less success in creating collective effects, symmetry, and harmonic convergence in these two geometric acceleration canons than he did in a piece based on arithmetical acceleration, such as Study No. 8. The arithmetical acceleration technique allows for a common background unit, while geometric acceleration does not. Without the common background unit, it is nearly impossible to overcome the independence of the voices to create any sense of interdependence. Nancarrow must have felt this, and one is left to wonder how satisfied he was with the results of the acceleration canon technique when considering Gann’s observation that Nancarrow wrote no more acceleration canons after Study No. 27 (1995, 163).
Conclusion
[93] By exploring so many techniques through which he varied the tempo relationships between voices in his tempo canons, and through the implementation of various devices which created possibilities for additional convergence points, Nancarrow developed a variety of musical structures in which convergence points between voices play a primary role. Besides their structural importance, they are often the most arresting aural features of each piece. Sometimes they might be combined with traditional cadential structures, but often they stand alone as a musical phrase goal. One knows they are there, even if they are not articulated or are otherwise de-emphasized, and Nancarrow became a master at using CPs to create a palpable sense of anticipation for the listener. The great variety of effects and formal structures Nancarrow achieved with CPs remains a fascinating and fruitful area of further study for music analysts.
Julie A. Nemire
Western Michigan University
School of Music
Kalamazoo, MI 49008
allegretto226@hotmail.com
Works Cited
Agmon, Eytan. 1997. “Musical Durations as Mathematical Intervals: Some Implications for the Theory and Analysis of Rhythm.” Music Analysis 16, no. 1: 45–75.
Callender, Clifton. 2001. “Formalized Accelerando: An Extension of Rhythmic Techniques in Nancarrow’s Acceleration Canons.” Perspectives of New Music 39, no. 1: 188–210.
Carlsen, Philip. 1998. The Player Piano Music of Conlon Nancarrow: An Analysis of Selected Studies. I.S.A.M. Monographs, no. 26. Brooklyn, N.Y.: Institute for Studies in American Music.
Drott, Eric. 2004 (Winter). “Conlon Nancarrow and the Technological Sublime.”American Music 22, no. 4: 533–63.
Gann, Kyle. 1995. The Music of Conlon Nancarrow. Cambridge: Cambridge University Press.
Hocker, Jürgen. 2012. Encounters With Conlon Nancarrow. Translated by Steven Lindberg. Lanham, MD: Lexington Books.
Jarvlepp, Jan. 1983/84. “Conlon Nancarrow’s Study #27 for Player Piano Viewed Analytically.” Perspectives of New Music 22, no. 1–2: 218–22.
Kramer, Jonathan D. 1988. The Time of Music: New Meanings, New Temporalities, New Listening Strategies. New York: Schirmer Books.
Pickover, Clifford A. 1995. Keys to Infinity. New York: John Wiley and Sons.
Reynolds, Roger. 1984. “Conlon Nancarrow: Interviews in Mexico City and San Francisco.” American Music 2, no. 1: 1–24.
Scrivener, Julie A. [Julie A. Nemire]. 2002. Representations of Time and Space in the Player Piano Studies of Conlon Nancarrow. PhD diss., East Lansing, Mich.: Michigan State University.
Thomas, Margaret Elida. 1996. Conlon Nancarrow’s ‘Temporal Dissonance’: Rhythmic and Textural Stratification in the Studies for Player Piano. PhD diss., New Haven, Conn.: Yale University.
—————. 2000. “Nancarrow’s Canons: Projections of Temporal and Formal Structures.” Perspectives of New Music 38, no. 2: 106–33.
—————. 2000/01. “Nancarrow’s ‘Temporal Dissonance’: Issues of Tempo Proportions, Metric Synchrony, and Rhythmic Strategies.” Intégral 14/15: 137–80.
Footnotes
1. The use of ratios in Nancarrow’s Studies is discussed in Scrivener 2002, chapter 2.
Return to text
2. Perhaps a good real-life analogy to the perception of the diverging-converging process is airplane travel. A passenger on an airplane has a far more accurate perception of when the plane is going to meet the ground during the landing process (i.e., convergence) than of when the plane is going to reach cruising altitude after takeoff (i.e., divergence). Also, this perception becomes more acute as the plane approaches the point of “convergence,” and it is more acute than the perception of divergence (e.g., reaching cruising altitude).
Return to text
3. A superparticular ratio is one where the greater term is larger than the lesser by one.
Return to text
4. Drott discusses Study No. 33 (“Canon √2/2”) and the techniques Nancarrow uses to avoid points of simultaneity and thus convergence points (2004, 547–58). In a canon involving an irrational tempo ratio, one would expect potentially only one CP, but through the use of tempo switches and other devices, Nancarrow creates multiple opportunities for convergence and then subverts them—including falling an eighth note short of convergence at the end of the piece. See also Thomas (2000/01, 142–46) for a discussion on how the lack of simultaneous downbeats contributes to degree of temporal dissonance.
Return to text
5. One clear exception is Study No. 18 (“Canon 3/4”), a two-voice converging canon with the CP on the final attack. Since the 1,680 half-note beat timespan of this canon is divisible evenly by both factors in the canon’s ratio (3 and 4), the faster voice in this canon enters after 420 half-note beats have elapsed, coincident with the 421st beat attack of the slower voice. Thus, in this Study the second voice enters at the beginning of a convergence period, and this is confirmed in the score by a shared barline at the entrance of the second voice.
Return to text
6. The diverging canon type also has a single CP, but Nancarrow did not write any complete examples of these.
Return to text
7. It can be seen in Figure 1 that a feature of this and other early studies is a preference for staccato notes. Nancarrow’s early punching machine could punch only one hole at a time, and sustained notes require a series of closely spaced holes that require more time to punch. An excellent discussion of Nancarrow’s working process, including the working of his various punching mechanisms, can be found in Jürgen Hocker (2012, 130–37). Later Studies, beginning with No. 20, reflect Nancarrow’s enhanced ability to punch out sustained notes. A later section in Hocker (151–56) provides an illuminating description of the contents of Nancarrow’s studio, which reflect his wide interests and particularly his musical interests (and non-interests).
Return to text
8. Since there are no measure numbers in Nancarrow’s scores, analysts often number the systems and refer to these.
Return to text
9. The levels of imitation in Study No. 36 spell out a major-seventh chord.
Return to text
10. Note values in Nancarrow’s scores do not always have a relative time value; instead, the length of the note is approximated by the distance between notes on the page in proportional notation.
Return to text
11. The inverse relationship between tempo ratios and duration ratios is discussed in Scrivener 2002, chpt. 2.
Return to text
12. The technique of geometric acceleration became available to Nancarrow beginning with Study No. 21. Modifications made to his hole-punching device allowed punching the rolls at any interval along the continuum, rather than being restricted to a particular background unit. This had a profound effect on Nancarrow’s ability to control the placement of attacks in his music, making geometric acceleration possible.
Return to text
13. Each contiguous pair of percentages relates to the same ratio—3:2.
Return to text
14. Although Gann bases his structural diagram on the first four canons comprising the first section because of the non-changing texture of the clock line, one could also make a case that the first section ends at the convergence point at the end of the second canon, and that the piece as a whole is in three sections as demarcated by the CPs.
Return to text
15. I am reminded here of the sound of a telegraph machine, and briefly considered Morse code as a possible inspiration for the rhythms in the clock line, however the ratio between short and long impulses in Morse code is 3:1, not 2:1 as expressed in the clock line.
Return to text
16. Gann describes a “collective effect” in Nancarrow’s tempo canons where figures such as glissandi are first widely spaced and separated—then, as a CP approaches, they become closer and closer together until they fuse into a single gesture.
Return to text
Copyright Statement
Copyright © 2014 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Hoyt Andres, Editorial Assistant
Number of visits:
13312