Pitch Properties of the Pedal Harp, with an Interactive Guide *
Mark R. H. Gotham and Iain A. D. Gunn
KEYWORDS: harp, pitch, pitch-class set theory, composition, analysis
ABSTRACT: This article is aimed at two groups of readers. First, we present an interactive guide to pitch on the pedal harp for anyone wishing to teach or learn about harp pedaling and its associated pitch possibilities. We originally created this in response to a pedagogical need for such a resource in the teaching of composition and orchestration.
Secondly, for composers and theorists seeking a more comprehensive understanding of what can be done on this unique instrument, we present a range of empirical-theoretical observations about the properties and prevalence of pitch structures on the pedal harp and the routes among them. This is particularly relevant to those interested in extended-tonal and atonal repertoires. A concluding section discusses prospective theoretical developments and analytical applications.
Copyright © 2016 Society for Music Theory
I. Introduction
[1.1] Most instruments have a relatively clear pitch universe: some have easy access to continuous pitch (unfretted string instruments, voices, the trombone), others are constrained by the 12-tone chromatic scale (most keyboards), and still others are limited to notes of the diatonic or pentatonic scales (many non-Western-orchestral members of the xylophone family). The pedal harp, by contrast, falls somewhere between those last two categories: it is organized around a diatonic configuration, but can reach all 12 notes of the chromatic scale, and most (but not all) pitch-class sets. In short, while the diatonic state might be considered the “natural”—or perhaps “neutral”—one for this instrument, its pitch priorities and exclusions are much more subtle than this view suggests.(1)
[1.2] The uniqueness of the pedal harp’s pitch profile presents both a challenge to those wishing to learn to write for it, and also an intriguing case study for music theorists who wish to understand its range of possibilities. This article seeks to help with both goals, and does so by theorizing from a basis not in pre-existing compositional structures or patterns (which are well documented elsewhere), but in the very materiality of the instrument itself.
[1.3] The basic pedaling possibilities are illustrated by the interactive guide provided; click the ‘Enter’ link below to access the guide. The first part of this article explains how the harp and this guide work. In doing so, it also sets up some of the basic constraints on pitch organization which are developed further in the theoretical discussion that follows. No knowledge of the harp is required to use the guide, but rudimentary diatonic music theory is needed throughout the article, and basic pitch-class set theory is required for the more detailed information in the guide and the article’s later sections.
[Interactive guide: Click to Enter (opens in a new window)]
II. Introduction to the pedal harp and the interactive guide
[2.1] The guide presents three blocks of content: an adjustable “Pedal Configuration” at the top, a set of accompanying “Information” about the selected pitch collection in the middle, and a “Pitch-Class Set Chart” at the bottom. We begin with an explanation of the “Pedal Configuration” section, and of the harp pedaling mechanics that it sets out.
[2.2] On the pedal harp, there are seven strings per octave, and seven pedals (one for each set of octave-related strings) that can be set in three positions: flat, natural and sharp. Players depress pedals to shorten the corresponding strings and raise their pitch. The harp is in its “neutral” position when all of the strings are at full length (all of the pedals are up, and none of the mechanisms are engaged); this gives the
[2.3] In the “Pedal Configuration” section of the guide, users can make virtual pedal changes by clicking on the “sharpen” and “flatten” buttons above and below the relevant pedal. Click on the sharpen button above
[2.4] Also displayed in this “Pedal Configuration” section are the prime forms of the pitch-class sets corresponding to the pedal settings that can be reached by single pedal changes from the current state. This information is given by the button corresponding to the pedal change that would generate it. It should be stressed at the outset that this focus on single, semitonal pedal changes is for illustration only; composers commonly make two to four pedal changes at a time in the full flow of a piece, and any number in the breaks between sections and movements.
[2.5] The “Information” section of the guide describes some essential characteristics of the pitch content of the configuration in use. The following list explains the content of this central section, and illustrates each element with the information corresponding to one (rather complex) pedal configuration: D, C,
- Succession of notes used in the pedal setting, but presented in an alternative scalar order from C(
♭ /♯ ) to B(♭ /♯ ): for the above configuration, this would give C, D,E♯ ,F♭ ,G♯ , A,B♯ - Same succession of notes, but translated into pitch-class numbers where C = 0 (including any enharmonic duplications of pitch classes): [0 2 5 4 8 9 0]
- Pattern of intervals between the harp strings in ascending order: [2 3 -1 4 1 3 0]. This includes negative numbers where applicable, as in the progression demonstrated here from
E♯ toF♭ - Cardinality (the number of distinct pitch classes, in the available range between 4 and 7): here there are 6, as
B♯ = C - Accidentals, shown as the number of pedals that have been sharpened, flattened, and the combined total of altered pedals (
♯ ,♭ , total): here, (3,1,4) - List of pitch classes in numerical order, without duplication: [0,2,4,5,8,9]
- Normal form of the collection (included on the basis that inversion is not necessarily a meaningful equivalence for all users): here [0,1,4,6,8,9]
- Prime form as given by Forte 1972: [0,1,3,5,8,9]
- Pitch-class set identifier as given by Forte: 6-31
- Total number of different pedal settings which can generate this same set class: 78 (the range spans from 0 to 90)
- Interval vector: <223431>.
[2.6] The third and final section of the interactive guide is the “Pitch-Class Set Chart.” This chart shows the connections between adjacent pedal configurations indicated by the prime forms in the “Pedal Configuration” section. On the chart, all pitch-class sets of cardinalities 4 through 7 are organized into columns. The last four columns give those pitch-class sets that correspond directly to pedal configurations. The first four columns are discussed below. The chart is presented merely as a list; no Tonnetz-style layout of meaningful proximity has been attempted, though this prospect is discussed briefly in the conclusion. For the configuration selected, the corresponding set class is highlighted in red, those that can be reached from it by one pedal change are presented in bold, and the others are in regular text.
III. Observations for Composers and Theorists
[3.1] It is remarkable that the question of pitch-class set accessibility on the pedal harp has not been explored elsewhere. There are numerous monographs on the harp, of course, though they are primarily concerned with matters of history, culture, geography, and symbolism (see, for instance, Ellis 1991, Schaik 2005, Schechter 1992, and Marson 2005). There is also a literature on harp technique, which naturally includes pedalling. Some of those instruction manuals extend to an account of all 2,187 possible pedal settings (Marson 1966), but this is considered primarily from the perspective of practical limitations and of accessing standard tonal resources, rather than the compositional-theoretical perspective of comprehensively surveying the instrument’s pitch properties. Even iconic, explicitly modernist works (such as Salzedo 1921) pass over such matters in favour of a discussion of extended timbral effects.
[3.2] To summarize the theoretical observations touched upon in the introduction to the guide: there are 2,187 distinct pedal settings, which can reach many, but not all, of the pitch-class sets with cardinalities between 4 and 7. This section develops those observations.
Distinct pitch-class sets
[3.3] The number 2,187 arises from the fact that there are three pedal positions for each of the seven different pedals (37 = 2,187). Of the 208 distinct set classes, harp pedal settings can generate 93. This is a measure only of those sets generated by the full pitch content of a pedal setting; subsets are discussed below.
[3.4] The pitch-class set possibilities of the pedal harp are limited firstly by cardinality. The possible sets are all of cardinalities from 4 to 7. The maximum of seven is achieved when each pedal produces a distinct pitch class (such as the natural diatonic collection C, D, E, F, G, A, B); the minimum of four results when six of the seven pedals produce pairs of enharmonic equivalents, resulting in maximal duplication of pitch classes (such as
[3.5] The number of distinct pitch-class sets that can be reached is also limited by set-class equivalences among the pedal settings. For instance, when all the pedals are up, the collection is
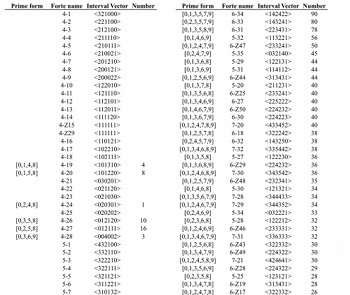
Table 1
(click to enlarge and see the rest)
[3.6] Table 1a, on the left, lists all set classes of cardinalities from 4 to 7. For those sets that correspond directly to one or more harp pedal settings, the prime forms are also included (leftmost column), along with the number of different pedal settings that generate them (rightmost column). Table 1b, on the right, presents the same list of available set classes with the number of pedal settings that generate them, but in order from the most preponderant (6-34, with 90 different pedal settings) to the least (those which occur only once), omitting those that do not occur at all.
Subsets of pedal settings
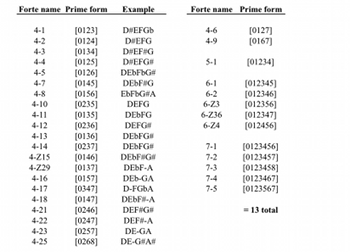
[3.7] Although the pedal settings on the harp necessarily include at least four distinct pitch-classes, pitch-class sets with cardinalities between 1 and 3 are available as subsets by using only some of the available notes (strings). In fact, all sets with cardinalities from 1 to 3 are available: note, for instance, that the “all-trichord hexachord” 6-Z17/6-Z43 is one of the possible pedal configurations. No supersets are possible, so a cardinality of 7 is a hard maximum for pitch-class sets within a pedal combination. Pedal changes are necessarily required to play in tonal spaces with higher cardinalities between 8 and 12.
[3.8] As well as sets of cardinalities 1 to 3, there are some sets of cardinalities 4 to 6 that are available as subsets of other sets, despite not corresponding directly to any pedal setting. Apart from these, there remain 13 set classes of cardinalities 4 to 7 which are unavailable, corresponding neither directly to any pedal setting nor to any subset thereof.
[3.9] Sets are unavailable if they have one or both of two excluding properties. First is the presence of excessive clustering. The maximum number of consecutive semitones in a pedal setting is four, which can be accomplished in one of two configurations:
Table 2
(click to enlarge and see the rest)
[3.10] The other, complementary, exclusion is of sets that are too gapped, having at least one interval between consecutive notes that is too large. The largest intervallic gap between consecutive harp strings is interval-class 4, reached by doubly augmented seconds (such as
Default collections, maximal evenness, and modes
[3.11] This exclusion of sets that are too clustered or gapped results from the neutral pitch arrangement of the harp, which is well described by the notion of maximal evenness: the most even distribution of elements in the available space (Clough and Douthett 1991). The interval pattern of the diatonic scale, 2212221, is a maximally even distribution of 7 elements in the 12-unit chromatic space. The construction of the pedal harp around this diatonic configuration is such that maximal evenness is the default position; pedal changes allow us to stray from maximal evenness into more clustered and gapped forms, but only so far (as we have seen). This orientation towards maximal evenness explains the greater availability and preponderance of the more evenly distributed sets of each cardinality. These more evenly distributed sets correspond to higher ordinal numbers on Forte’s list; notice, for instance, that set classes 7-1 through 7-5 are unavailable even as subsets, while all of the set classes from 7-6 to 7-38 are available.
[3.12] This bias towards (maximal) evenness connects the pedal harp with its diatonic roots and with a common structural property of scales and modes. The pattern 2212221 is common to all “white-note” modes,(3) and a relatively even distribution of pitches across the octave is a common and distinctive property of scales in general. Indeed, the term “gapped” has been adopted here from scale theory, in which it refers to scales containing intervals of a minor 3rd or larger, which seem “to be incomplete in comparison with heptatonic scales” (Drabkin 2016). At the other extreme of successive interval size, even those pitch progressions that imply a change of direction from the rest of the scale (such as
The most prevalent sets
Figure 1. Four plausible scales derived from the pitch-class set 6-34. Modifications are shown by “-” for missing scale degrees, and
(click to enlarge)
[3.13] That said, the most prevalent sets on the harp are not the best representatives of maximal evenness. 6-34 is realized by the greatest number of pedal configurations (90), but it is not maximally even, and it does not correspond to any scale in common usage. Figure 1 suggests four of the most plausible scale structures for this pitch-class set: two with the pitch-class set in prime form (“ascending”), and two for the inversion (“descending”). These four account for all possibilities involving a perfect interval between the final and fifth (a very common property among scales). Cumbersome nomenclature with numerous exceptions and modifications is required to relate these scales to any common practice.
[3.14] None of the most prevalent set classes for any cardinality are maximally even, though this property is often to be found nearby. The maximally even form of cardinality 5 (5-35, the pentatonic scale) comes second in the list of prevalent sets (after 5-32). Cardinalities 4 and 6 suggest a different kind of proximity, in that the most prevalent set differs by one semitone from the maximally even form: compare 4-27 (the half-diminished 7th, 0,2,5,8) with 4-28 (the diminished 7th, 0,3,6,9), and 6-34 (the near-whole-tone scale, 0,1,3,5,7,9) with 6-35 (the whole tone scale, 0,2,4,6,8,10).(4) For cardinality 7, however, neither form of proximity holds.
Cardinality
[3.15] Harp pitch configurations also fundamentally resemble scales in terms of cardinality constraints. Indeed, taken together, the two constraints on the harp pitch structure—that they must have between 4 and 7 distinct notes, and that these notes must be distributed relatively evenly within the space to yield a pattern with successive steps of near-equivalent size—go a long way towards a definition of scales.(5) At a more fundamental level, harp pedal configurations are also connected to scales in that both are periodic at the octave and both are used as referential background collections.
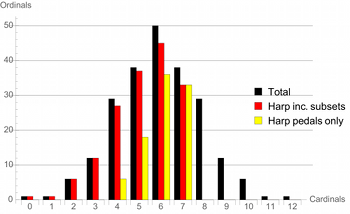
[3.16] The harp’s cardinality range of 4 to 7 is close to, though perhaps slightly lower than, what might be regarded as common practice in scales, which includes 8-note (octatonic) scales more readily than those with 4 notes (“tetratonic”).(6) Given the cross-cultural dominance of pentatonic and heptatonic scales, either a narrower (5 to 7) or broader (4 to 8) range of cardinalities would seem more fitting. That said, the harp’s range from 4 to 7 range belies the fact that its affordances of those cardinalities is strongly skewed towards the upper end, which has a closer relationship to the normative scale cardinalities. Cardinality 6 is the best represented among harp pedal settings: almost half (1,071 of 2,187 = 49%) have exactly 6 distinct pitch-classes.(7)
Table 3. Cardinality data: the total number of pitch-class sets of each cardinality; the number that can be realized on the harp, including subsets of pedal configurations; and the number that can be realized by the full pitch collection of a given pedal setting alone.
(click to enlarge)
Figure 2. A bar graph corresponding to the data in Table 3
(click to enlarge)
[3.17] There is a distinction to be drawn between the availability of pedal settings, which strongly emphasize cardinality 6, and that of set classes, for which cardinality 7 is proportionally better represented. Pedal settings can directly generate 33 of the 38 distinct set classes with cardinality 7 (87%), but only 36 of the 50 sets with cardinality 6 (72%).(8) Naturally, the emphasis changes back to cardinality 6 when subsets are included: subsets add 9 more of the cardinality-6 sets (45 total = 90%), but no more of those with cardinality 7, due to the unavailability of higher-cardinality (8+) sets of which the 7-cardinality sets could be subsets. Table 3 and Figure 2 summarize this data concerning the total number of pitch-class sets of each cardinality, and the corresponding number directly accounted for by harp pedal settings (with and without subsets).
The most prevalent pitches
[3.18] In addition to the question of relative prevalence among pitch-class sets and set cardinalities, there is also a two-tier division of prevalence among the pitches themselves. “White” notes with “black” notes on either side (D, G, A) can be reached by one string only; however, black, sharped notes (
[3.19] What is the proportion of pedal configurations involving a given pitch from the first, two-string type (C, B,
[3.20] As discussed, the total number of pedal configurations is 37 = 2,187. The number of configurations containing a C (specifically, with the C pedal on C natural) is 1/3 of 2,187 (36 = 729). The same number of configurations involve a
Routes among the pedal configurations and pitch-class sets
[3.21] So far, the discussion has centered on the properties of the pitch constellations themselves. We now turn to the connections or “routes” among these pedal settings and pitch collections, focusing primarily on individual semitone moves for illustration. These routes are restricted most obviously by the fact that each pedal has only three settings. This means that the maximum number of individual pedal changes that can be made from a given position is 14, from the “all natural” position (C major), where all the pedals are in the center. The lowest number of pedal changes can be made from the “all sharp” or “all flat” positions (
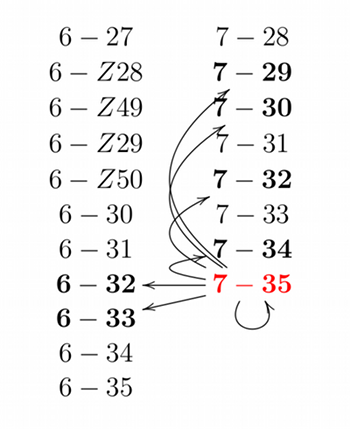
[3.22] The routes among pitch-class sets are further restricted by the duplication of set classes among the harp pedal positions (as discussed above). This duplication means that pedal changes do not always lead to distinct pitch-class sets. For instance, consider sets for which there is at least one ordering that is symmetrical under inversion. For these sets, there are pairs of pedal changes that lead to the same set class (subject to the availability of those changes from the starting pedal configuration). The diatonic collection has this symmetric property: reading C major from the pitch D (rotation 2, or the dorian mode) gives the symmetrical interval progression 2122212. This means that each pedal move from C major (7-35) is paired with another change that generates the same set class. For instance, raising F to
[3.23] Much has been written about the pitch properties of the diatonic collection, of course; the point here is simply to identify constraints on the number of distinct pitch-class sets that can be reached from a given pedal setting. Figures 3a and b set out the set classes reachable directly (by one semitonal pedal change) from
Figure 3a. Pedal changes from (click to enlarge) | Figure 3b. Pedal changes from C major: each pedal can move up or down, so 14 changes are possible, though they are paired, leading to the same 7 pitch-class sets (twice each). (click to enlarge) |
Harp pedal space
[3.24] Pedal settings can be considered as more or less closely related to one another according to the number of changes required to move between them. In this view, pairs of settings that differ by just one pedal position change are the most closely related, while the greatest distance is between the “all flat” and “all sharp” positions. This is in stark contrast to the pitch-class set view of relatedness, in which the most distantly related configurations in terms of pedal changes are instances of the same set class (
Table 4. A “pedal space” corresponding to harp pedal positions, with numbers of sharps plotted against numbers of flats and the number of pedal settings given for each grid square.
(click to enlarge)
[3.25] This view of pedal relatedness is suggestive of a “harp pedal space” where pedal changes are mapped onto moves between contiguous positions. A simple form of such a space can be realized on a two-dimensional grid, with the number of sharps plotted against the number of flats. This gives a grid of 28 squares (the seventh triangular number; i.e., the sum of the numbers from 1 to 7) with varying numbers of entries in each. Table 4 sets out that basic space, and gives the number of pedal positions in each block. Any single semitonal pedal change corresponds to a single horizontal or vertical step between neighboring blocks in the space. The number of flats and sharps in each pedal configuration (and thus the coordinates of the pedal configuration) is given in the interactive guide under “accidentals.”
Numbers of pedal positions per grid square (sharp/flat combination)
[3.26] Each grid square corresponds to a pedal configuration with a certain number of sharps and flats. The number of distinct pedal settings in any square is a combinatorial problem solved by the product of two binomial coefficients. Let n be the number of movable pedals (here, n =7), t be the combined number of pedals in sharp or flat positions (t ≤ 7), and f be the number of flats or sharps specifically, it doesn’t matter which (f ≤ t). The number of distinct pedal arrangements for a block, C, is given by the number of combinations of t from n (“n choose t”), multiplied by the combinations of f from t (“t choose f”’). Formally, \[ C = {n\choose{t}} \times {t\choose{f}}. \] For instance, for one flat and two sharps, \[ {7\choose{2+1}} \times {2+1\choose{1}} = {7!\choose{(7-3)!3!}} \times {3!\choose{(3-1)!1!}} = 35 \times 3 = 105. \]
[3.27] Both binomial coefficients are maximized by values of t and f in the center of their respective ranges; however, it does not follow that the product is greatest when those component parts are maximized separately. In fact, C is maximized by values of t closest to t = 2n/3, and values of f closest to f = t/2 (= n/3)—that is, by the integers that most nearly trisect the range 0 to n. This is because this product of binomial coefficients, C, is equivalent to the multinomial coefficient \(C = n!/((n-t)!(t-f)!f!)\); the greatest multinomial coefficients are the central multinomial coefficients, for which the terms in the denominator (here \(n-t\), \(t-f\), and \(f\,\)) are as nearly equal as possible given the constraint that they must be integers.(9) This is another example of maximal evenness, implying a maximally-even partitioning of the n = 7 strings into sharps, naturals, and flats. In the case of n = 7, the greatest number of distinct pedal settings is 210, given by t = 4 with f = 2; and by t = 5 with f = 2 or 3.
Minimum distance; distinct routes
[3.28] This space helps illustrate the number of distinct, direct routes between any pair of pedal settings related by individual semitonal steps. The minimum number of changes from one pedal setting to another is given by the sum of the chromatic distances each pedal has to move. This is intuitive: if you move each pedal directly from the old position into the new one, that ought to be the most direct way. However, if we consider the order in which multiple pedal changes are made, then we will have many different, equally direct routes.
[3.29] For instance, to move from G major (one sharp) to F major (one flat), one could cancel
[3.30] The number of distinct routes introduces another combinatorial calculation. Let n now be the number of chromatic changes to be made. For changes in which all pedals move by 1 or 0 semitones, the number of distinct routes is given by n! (that is, the number of possible orderings of those n changes). For changes which involve at least one string moving two positions (from flat to sharp or vice versa), there is an additional order constraint: the move from flat or sharp to natural has to come before the move from natural to sharp or flat (respectively). Let p be the number of strings that move by a whole tone (which is the number of order-constrained pairs: one pair for the two moves). The number of distinct routes, R, is given by \[ R = \frac{n!}{2^p}. \] This arises because, for every such pair, half of the (remaining) routes have the paired moves in the wrong order and have to be eliminated.
[3.31] These constraints can be relaxed to account for alternative views of distance among harp pedal positions. For instance, one could view a pedal change as a single operation, whether it is altered by a semitone or a whole tone. Here we return to the simpler combinatorial problem without order constraint: if n now stands for the number of pedals which change, rather than the chromatic distance they cover, then n! once again gives the number of distinct routes.
[3.32] Finally, it should be noted that these permutations of distinct routes are just as applicable when both the original and final pedal settings have the same number of sharps and flats (and so appear on the same square of Table 4). This might seem to be contrary to the structure of the grid, but such routes necessarily involve leaving the square in question before returning to it.
[3.33] Consider the 4! (= 24) direct routes between one pair of sharps and another (e.g.
IV. Conclusion and Outlook
[4.1] This paper presents an interactive guide for engaging with harp pedaling and how it relates to pitch content, as well as a range of associated empirical-theoretical observations. It was shown that the 2,187 pedal settings are necessarily limited to set classes of between 4 and 7 distinct pitch-classes, that these pedal settings can directly generate 93 of the 208 distinct set classes, and that some of the available set classes are more preponderant among the pedal settings than others. 6-34 was identified as the most available set class, with 90 different pedal settings yielding this collection. All but 13 set classes in the wider cardinality range from 0 to 7 either correspond directly to pedal settings or can be reached as subsets of others. Those remaining 13 set classes cannot be reached even as subsets because they are too clustered or gapped, and thus they diverge too drastically from the harp’s neutral arrangement of 2212221. This interval pattern was also discussed in relation to scale structure in general, and to the property of maximal evenness in particular. No sets of cardinalities from 8 to 12 can be reached within a single pedal setting because there are only 7 strings per octave, though the harp can still access those higher-cardinality collections through the use of pedal changes.
[4.2] Beyond set classes, certain cardinalities were also shown to be more prevalent than others. Cardinality 7 is proportionately the best represented among the pedal configurations, but cardinality 6 takes over when subsets are taken into account. Furthermore, there is also even a two-tier division of prevalence among individual pitch-classes, three of which (D, G, A) can be reached by one pedal only, while all others can be reached by two pedals. These 9 more available pitch classes occur more frequently in pedal settings by a ratio of 5:3.
[4.3] Finally, our observations turned from these properties to the question of routes among pedal settings and pitch-class sets. A rudimentary “pedal space” was proposed, organized on the basis of sharp versus flat pitch content, which models pedal changes by moves between contiguous blocks. The membership of each block, and the number of distinct, direct routes between any two pedal settings were solved as combinatorial problems.
Analysis
[4.4] The question of ‘routes’ among pitch/pedal collections is perhaps the most suggestive of musical works and their harmonic journeys unfolding in time. However, important caveats need to be raised regarding the prospects for applying these observations in analysis. Much of this article has focused on a theoretical account of the pitch properties of full pedal configurations. Although subsets have been discussed, the extent of their importance in real music has not been recognized as a central concern. Subsets, in the sense of using only some of the strings in a pedal configuration, are a mainstay of harp writing. In a musical work, pragmatism dictates that the pedals may well be changed only when they are needed, leaving pedal settings of which only the subset used is musically meaningful. The routes between pedal settings, in turn, focused on immediate connections between adjacent (fully represented) sets with multiple changes by extension. Again, this theoretical model accounts for all possibilities, but does not do justice to the fact that changing multiple pedals at once is a part of normal practice.
[4.5] Let us consider these issues briefly in the context of Paul Hindemith’s music, which seems well suited for exploiting the properties discussed here. Hindemith was essentially an extended tonal composer, who was prepared to use all pitch collections, but clearly prioritized triads and related tertian sonorities in their traditional roles as referential, consonant, and conclusive. Hindemith’s theoretical writings attest to this (Hindemith 1937), particularly in his notion of “harmonic fluctuation”: a measure of the relative harmonic intensity on the basis of interval content and vertical disposition. For Hindemith, this is a parameter to be controlled as part of the musical argument, usually following a trajectory from consonance to dissonance and back. While we might be circumspect about any composer’s testament, and especially about comments made in a primarily pedagogical rather than declarative context,(10) Hindemith does speak with passion about his desire to bring under control “the immense store of [harmonic] materials” which had “blinded” the Romantic composers in generations preceding him, and his comments accord well with his practice in general (1937, 3).
[4.6] Hindemith’s Sonata for Harp of 1939 is readily reflective of this style, and even dates from around the time of his writing the Craft of Musical Composition series. Being such an ideal candidate, it makes acutely clear this need for a distinction between the pitch content associated with a full pedal configuration, and those strings actually used (the subset).
Figure 4. Three illustrative excerpts from the first movement of Hindemith’s Sonata for Harp (1939)
(click to enlarge)
Figure 5. Pitch progressions in the three excerpts from Hindemith’s Sonata for Harp shown in Figure 4, making clear the important distinction between the pitches given by the pedal configuration (upper staff) and those actually used in the music (lower staff)
(click to enlarge)
Table 5. An internal sub-grid extending the pedal space. This 2-dimensional grid plots 1 sharp against 1 flat to occupy the relevant grid square { 1,1 } on the harp pedal space of Table 4.
(click to enlarge)
[4.7] Figure 4 sets out three illustrative extracts from the first movement, and Figure 5 sets out the relationship between pedal pitches (upper staff) and those actually used (lower staff) at these points in the piece. The lower stave of Figure 5 also suggests a tonal and scalar reading by rearranging the notes to place the final first, and defining the scale in relation to the most closely-comparable standard scale, noting deviations and omissions (as in Figure 1). Asterisks above the staff identify the changed notes on both systems (including one above a rest in the lower system of measure 16 where the new note is not used).
[4.8] The first extract corresponds to the very beginning (measure 1). Even here at the outset, the opening music, which is emphatically in
[4.9] As the movement progresses, the pragmatism described above duly dictates that pedals are only changed when they are needed, and at points where it is convenient to do so. The second extract of Figures 4 and 5 (measures 14–17) is a particularly clear illustration of this. E dorian is built up from a thoroughly different pitch collection, changing pedals gradually, when they are needed (measures 14, 15, 17), and when it is simply practical (measure 16).
[4.10] The final extract relates to the final pedal change of the movement, and is perhaps the clearest of all. The movement ends where it began on the tonic of
[4.11] In short, analytical commentary must distinguish between the full pedal pitch content and that actually used. To use the charts as a way of conveying the tonal trajectory of a work would require a modified or double use of those spaces. For instance, the pitch-class set chart would need to be taken in tandem with another array that connects each set with its many subsets.
Harp Spaces
[4.12] The point raised above speaks to the prospects for further developing these “harp spaces.” For instance, the arrangement sketched out in Table 4 gives a general sense of an overall pedal space and enabled a visualization of the routes taken, but it does not fully map out the space. Within each grid square we have only the number of configurations, with no shape to their organization. The problem is that pedal-position space is really suggestive of 7 dimensions: one per pedal, with each dimension having three states (sharp, natural, flat). Clearly, 7-D space is hard to visualize, so has little value as a heuristic.(11) Alternatively, a tree diagram would set out the possibilities in a logical way, though it is fundamentally hierarchical and thus ill-suited to the space based on the connections of pedal changes. Some hierarchy is needed to reduce the complexity, but the tree diagram would unduly emphasize certain pedals as being more important than others. As a compromise, one could develop Table 4 by constructing sub-grids for each square. For instance, the space for pitch collections with one sharp and one flat could be set out on its own 2-dimensional grid, as shown in Table 5.
[4.13] This compromise removes the need to choose sharps or flats as the primary element, a decision for which there is less of a rationale than in sharp- or flat-only cases, which can at least be listed according to the cycle of fifths (as on the borders of Table 5). The grid also provides an alternative top-down illustration of how the numbers of combinations are reached. In this table, for the possibilities of 1 flat and 1 sharp we have a grid of 7 sharps × 7 flats (= 49), minus the 7 impossible cases in which a single pedal would be both sharp and flat (49 – 7 = 42), which corresponds to the number for this square in Table 3. The equivalent to this grid for 2 sharps or 2 flats (and none of the other type) would correspond to one-half of Table 5 (21 elements), due to the duplicates when only flats or sharps are concerned for each of the 7 strings (e.g.
[4.14] This process could be extended by adding dimensions: for instance, adding a third dimension to Table 5 allows for combining each of its members with another flat (for 2 flats, 1 sharp) or sharp (for 2 sharps, 1 flat); however, that process quickly reintroduces the 7-dimensional space so far avoided. Alternatively, we can stick to two-dimensional space by reducing each previous block into a list.
[4.15] As the number of dimensions increases, the grids increase in size, but also in the number of redundancies. For the case of 2 sharps and 1 flat or vice versa, the number of distinct combinations is 105, given by a 7×21 grid (= 147) minus 2×21 (= 42) double uses of single pedals. For 3 sharps or flats, the reduction from 105 to 35 is due to three-fold duplications of the same sets.
[4.16] The tonal space used in the interactive guide’s “Pitch-Class Set Chart” is even less of a geometrical space, and could be developed or recast in different ways. Harp pedal changes are chromatic, stepwise transformations that connect readily with the chromatic tonal spaces based on semitonal motion developed in recent scholarship (Tymoczko 2011 and others), following the long tradition of models of parsimonious voice-leading in Riemannian and neo-Riemannian theory (see Gollin and Rehding 2011 or Cohn 1998). However, the space that is needed is essentially the same as a full pitch-class set space, which lacks an accessible visualization. Other recent developments may be useful in this regard. For instance, Hook’s (2007) concept of “cross-type transformations” addresses the need for pitch-class spaces (for harps or in general) to account for transformations between collections of differing cardinalities, and Hook’s (2008) “signature transformations” may provide a more direct point of departure through its basis in key-signature transformations of tonal and modal arrays.
Table 6. The start of a basic Hamiltonian path among all pedal settings.
(click to enlarge)
[4.17] Development of our proposed space could perhaps further illuminate paths among the sets, considering, for instance, whether and how many Hamiltonian paths there are among the sets, perhaps as a framework for a composition’s tonal trajectory.(12) There are certainly simple Hamiltonian paths among the pedal settings (such as that begun in Table 6), but the duplications of pitch-class sets within the possible pedal settings make Hamiltonian paths among sets a more interesting problem (and the shorter journey may make for a composition of more manageable length).
Parting words
[4.18] Whether or not the idea of Hamiltonian paths proves appealing or useful, we hope that composers will derive from this article a greater understanding of the harp’s pitch possibilities that provides at least technical guidance, and perhaps even material inspiration. For instance, some composers may find the effects of individual pedal changes to be a way of guiding successive pitch structures in a piece, or they may find that the relative preponderance of certain sets (and even pitches) make them attractive candidates as core pitch materials for a work.
[4.19] For music theorists and music analysts, we hope that this article’s overview of pitch properties will help provide a background against which to contextualize analyses of specific harp works or corpora. It would be interesting to conduct a corpus survey comparing the tonal materials used in the harp repertoire with their preponderance on the instrument. Are the more prevalent pitches and sets correspondingly more often used? Does this change when the time spent in a specific pedal configuration is taken into account? That is, are these preponderant sets treated as goals in themselves, or merely waypoints to other, less prevalent pitch collections that are attractive for other reasons? Indeed, does the harp repertoire depart from common practice in any such ways? This could form part of a wider analysis of idiomatic writing for harp that examines other aspects of the mechanics involved in performance, perhaps drawing from standard practitioner treatises, and also following the lead of Huron and Berec’s (2009) landmark work on idiomatic writing for the trumpet.
Mark R. H. Gotham
Faculty of Music
University of Cambridge
11 West Road, Cambridge CB3 9DP, UK
mrhg2@cam.ac.uk
Iain A. D. Gunn
School of Computer Science
Bangor University
Dean Street, Bangor, Gwynedd, LL57 1UT, UK
i.gunn@bangor.ac.uk
Works Cited
Adler, Samuel. 2002. The Study of Orchestration, 3rd ed. Norton.
Blatter, Alfred. 1997. Instrumentation and Orchestration, 2nd ed. Schirmer.
Carey, Norman, and David Clampitt. 1989. “Aspects of Well-Formed Scales.” Music Theory Spectrum 11 (2): 187–206.
Cohn, Richard. 2016. “A Platonic Model of Funky Rhythms.” Music Theory Online 22.2. http://mtosmt.org/issues/mto.16.22.2/mto.16.22.2.cohn.html
—————. 1998. “Introduction to Neo-Riemannian Theory: A Survey and a Historical Perspective.” Journal of Music Theory 42 (2): 167–180.
Clough, John and Jack Douthett. 1991. “Maximally Even Sets.” Journal of Music Theory 35 (1/2): 93–173.
Drabkin, William. 2016. “Scale” in Grove Music Online. Oxford University Press.
Ellis, Osian. 1991. The Story of the Harp in Wales. University of Wales Press.
Forte, Allen. 1973. The Structure of Atonal Music. Yale University Press.
Gawboy, Anna. 2009. “The Wheatstone Concertina and Symmetrical Arrangements of Tonal Space.” Journal of Music Theory 53 (2): 163–190.
Gollin, Edward, and Alexander Rehding. 2011. The Oxford Handbook of Neo-Riemannian Music Theories. Oxford University Press.
Hindemith, Paul. 1937. The Craft of Musical Composition, vols. 1 (Theory) and 2 (Exercises in two-part writing), translated by Arthur Mendel. Scott, 1942; originally published as Unterweisung im Tonsatz, vols. 1 and 2. Otto Ortmann, 1937 and 1940.
Hook, Julian. 2008. “Signature Transformations.” In Music Theory and Mathematics: Chords, Collections, and Transformations, edited by Jack Douthett, Martha M. Hyde, and Charles J. Smith: 137–160. University of Rochester Press.
—————. 2007. “Cross-Type Transformations and the Path Consistency Condition.” Music Theory Spectrum 29 (1): 1–39.
Huron, David and Jonathon Berec. 2009. “Characterizing Idiomatic Organization in Music: A Theory and Case Study of Musical Affordances.” Empirical Musicology Review 4 (3): 103–122.
Lendvai, Ernö. 1993. Symmetries Of Music. Kodaly Institute.
Marson, John. 2005. The Book of the Harp: the Techniques, History and Lore of a Unique Musical Instrument. Kevin Mayhew.
—————. 1966. The Complete Guide to the Harp Glissandi: Including a Comprehensive Table of All Possible Pedal Changes. Lyra.
Messiaen, Olivier. 1956. Technique de mon langage musical. Alphonse Leduc.
Piston, Walter. 1955. Orchestration. Norton.
Neumeyer, David. 1986. The Music of Paul Hindemith. Yale University Press.
Pressing, Jeff. 1983. “Cognitive Isomorphisms Between Pitch and Rhythm in World Musics: West Africa, the Balkans and Western Tonality.” Studies in Music 17: 38–61.
Salzedo, Carlos. 1921. Modern Study of the Harp. G. Schirmer.
Schaik, Martin van. 2005. The Harp in the Middle Ages: The Symbolism of a Musical Instrument, rev. ed. Editions Rodopi.
Schechter, John. 1992. The Indispensable Harp: Historical Development, Modern Roles, Configurations, and Performance Practices in Ecuador and Latin America. Kent State University Press.
Tymoczko, Dmitri. 2011. Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. Oxford University Press.
Whatley, Kirsty. 2007. “Rough Romance: Sequenza II for Harp as Study and Statement”’ In Berio’s Sequenzas: Essays on Performance, Composition and Analysis, edited by Janet K. Halfyard: 39–52. Ashgate.
Footnotes
* The authors wish to thank the editors and reviewers for Music Theory Online, as well as Anne Denholm, Official Harpist to HRH The Prince of Wales, for their helpful comments during the preparation of this manuscript.
Return to text
1. Accordions present another unique relationship between the diatonic and chromatic collections; see Anna Gawboy’s (2009) discussion of the Wheatstone Concertina, for instance.
Return to text
2. This is one of various standard notations used for the pedal harp; see orchestration textbooks such as Adler 2002, Blatter 1997, and Piston 1955 for alternatives.
Return to text
3. It is also a ubiquitous rhythmic pattern, as noted by Pressing (1983) and Cohn (2016), among others.
Return to text
4. For even-number cardinalities, maximal evenness divides the octave into equal units, an extent of evenness that is perhaps at odds with good scale structure, since the majority of scales in common use have two sizes of scale step (see Carey and Clampitt 1989 and Clough and Douthett 1991).
Return to text
5. For the most general definition of a musical scale, one need only add the notion of a tonic or final, though clearly additional criteria are often employed, particularly when defining scales or modes in relation to a specific repertoire. This can include an internal hierarchy, the assignment of subsidiary functions to certain notes (such as a dominant or a reciting tone) and the association of a scale or mode with particular melodic configurations.
Return to text
6. Four-note scales were preponderant in “primitive” musics; modern examples include the 1:5 distance model mode (Lendvai 1993) the construction of which connects to an octatonic scale popular among Western art-music composers similarly based on a distance model of 1:2, and therefore being of “limited transposition” (Messiaen 1956).
Return to text
7. Cardinality 4 = 42 (2%); 5 = 495 (23%); 6 = 1,071 (49%); 7 = 579 (26%).
Return to text
8. Cardinality 4 = 6/29 (21%); 5 = 18/38 (47%); 6 = 36/50 (72%); 7 = 33/38 (87%).
Return to text
9. The integer constraint can also be expressed by floor and ceiling functions. The product is maximized when each of (n – t), (t – f), and f is either floor(n/3) or ceiling(n/3).
Return to text
10. As David Neumeyer observes, “the most practical aspect of the craft—its compositional pedagogy—was Hindemith’s major concern from the start, not
Return to text
11. Although just such a 7-D space relating voice leadings between scales has been developed by Dmitri Tymoczko; see Tymoczko 2011 and related works.
Return to text
12. A Hamiltonian path visits each node of a graph exactly once.
Return to text
Copyright Statement
Copyright © 2016 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Rebecca Flore, Editorial Assistant
Number of visits:
11430