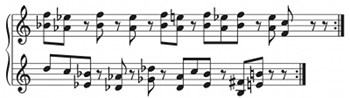Review of Emmanuel Amiot, Music through Fourier Space: Discrete Fourier Transform in Music Theory (Springer, 2016)
Jason Yust
KEYWORDS: discrete Fourier transform, maximal evenness, interval function, Ligeti, polyrhythm
Copyright © 2017 Society for Music Theory
[1] Emmanuel Amiot’s Music through Fourier Space (MFS) is an impressive and important milestone in mathematical music theory, presenting in a succinct volume the many discoveries made and theoretical ideas generated based on the discrete Fourier transform (DFT) over the past two decades—developments in which Amiot himself was a central player.
[2] Amiot’s book amply demonstrates that the DFT is relevant to a wide variety of musical questions—about rhythm, about pitch-class sets and interval content, and about tonality and non-tonality—so many theorists will find something in the book relevant to questions in their own research. Within each of these topics, Amiot’s discourse varies between questions of primarily mathematical interest and those of more direct musical interest. Yet for a book that generally proceeds in the manner of mathematical writing, from definition to proposition and lemma to theorem, it laudably never strays far from immediately appreciable musical relevance.
[3] Nonetheless, for theorists who do not have extensive mathematical background, the methods and notation may seem to be a barrier to entry. Part of the goal of this review, then, is to explain the notations and why Amiot uses them. The tutorial below does this, preceded by an overview of the book’s content and followed by a novel analytical example from Ligeti’s Etude no. 8 to illustrate some of Amiot’s results in the rhythmic domain.
[4] Musicians are likely to be most familiar with the Fourier transform as an operation performed on sound signals to translate raw amplitude-over-time information into frequency information. That application of the Fourier transform is one that Amiot’s book does not address. Instead, he applies the DFT to pitch-class sets and rhythms, which exist in completely different kinds of spaces. Rhythms are in a temporal space like waveforms, but exist on a different timescale and at a higher cognitive level. Pitch-class sets are harmonic objects, but exist in pitch-class space, something many degrees removed and abstracted from anything like a sound signal.
[5] Yet this must seem awfully suspicious: Why should this same mathematical technique apply to so many apparently unrelated aspects of music? The question is not answered directly by Amiot, so I will venture an explanation here. Wherever we look in music, we find cyclic spaces—or, more precisely, music seems to be intent upon imposing cyclic structure on whatever linear spaces it finds. Given the linear space of time, music wraps it into the cyclic space of meter. Given the linear space of pitch, music fashions a cyclic space through octave equivalence. Even such phenomena as formal rotations, which turn a linear narrative into a circular one, seem to point to this same basic musical impulse.
[6] Another aspect of cyclic spaces in music is that relative position is what matters, not absolute position. In pitch-class space, we readily recognize transpositions as essentially equivalent, and rhythms do not depend on the absolute time point where they begin. Only when considered in relation to some reference point, such as a tonic or downbeat, is the transposition of a pitch-class set or translation (displacement) of a rhythm meaningful. Even in such circumstances, the rhythm or pitch-class set retains some common internal character as it is shifted in relation to a reference point, just as, in psychoacoustics, one identifies a frequency with a pitch regardless of differences of phase. A musical rhythm is fully realized only when we imagine it on a loop. A scale or harmony is identified not by a single mode or voicing, but by all its possible temporal and registral arrangements. Even though a rhythm can only be realized over a finite amount of time, and a harmony can only be represented by a finite number of notes, such constraints are more like windows onto an object whose essence is eternal—without beginning or end.
[7] In sum, the identity of a musical object, regardless of what space it lives in, is defined by periodicity. Hence the Fourier transform: the basic mathematical procedure that allows us to view an object in a cyclic space as a collection of periodic elements.
Overview
[8] MFS may be divided roughly in half. The first half introduces the DFT and its most important mathematical properties (Chapter 1) and otherwise focuses largely on problems that were not formulated with the DFT in mind, but to which it gives elegant solutions (Chapters 2–3). The first part of Chapter 1, which defines the DFT, is essential. It ends with what may be the most deeply consequential result of the book, Theorem 1.11, which shows that the DFT is the unique transformation that converts the complex operation of convolution into simple multiplication. This is important because convolution is the essence of interval content, the fully relational way of thinking that is inherent to musical concepts. It produces Forte’s (1973) interval vector, Lewin’s (2001) interval function, and Boulez’s multiplications (i.e., Cohn’s (1988) transpositional combinations). The second part of Chapter 1 covers a number of useful and straightforward results concerning the DFT, and then (in 1.2.3–4) lays some other groundwork of mostly mathematical interest, mapping out three equivalent mathematical domains (distributions, circulating matrices, and polynomials) and showing how they interrelate and how the DFT is manifest in each.
[9] The first of the special pre-existing problems, treated in Chapter 2, is the Z-relation, which Amiot calls “homometry” (a better term, since it applies to the property of equivalent interval content as possessed by transpositions and inversions as well as the more exceptional cases). Though the classification problem for homometry cannot be said to be completely solved, the DFT gets us much closer to understanding the phenomenon. For anyone interested in Z-relations, this chapter is essential reading. For others, I would recommend sections 2.1.1, 2.1.2, 2.2.1, and 2.2.2 for a sense of how concepts and problems of classic pc-set theory have been begging for the DFT since Babbitt first proposed the hexachord theorem.
[10] The second set of preexisting problems solved using the DFT has to do with tilings, the topic of 3.2 and 3.3.4. In music, tilings are usually conceived in the domain of rhythm, as rhythmic canons, though equivalent constructions can be made in pitch-class domains, where they represent partitions of an aggregate. The literature on rhythmic canons and related tiling problems is large, and Amiot’s contributions have been crucial.(1) The overview in Chapter 3 demonstrates the centrality of Vuza canons—tilings built from nonperiodic elements—and offers an excellent introduction to the whole topic. The first part of Chapter 3 addresses Lewin’s (2001) application of the DFT to the “phase retrieval” problem (the existence of unique interval functions) and a seemingly unrelated problem formulated by Amiot and William Sethares (2011). They noted that, under certain conditions, any pitch-class set can be expressed as a linear combination of transpositions of some other set. These two problems, remarkably, turn out to be one and the same, equivalent to the presence of zeroes (nil coefficients) in the DFT.
[11] The organization of the book is logical, but not ideal in the sense that the less mathematically minded reader who inclines to a dogged cover-to-cover strategy will encounter some challenging deadfall on the trail early on. The mathematics in Chapters 2 and 3 gets into sophisticated territory in places; for the sort of reader who goes through all of the proofs, there is much delight in store. But those more interested in topics connected to traditional music theory and analysis will be better served by pressing ahead to Chapter 4 after getting the gist of Chapters 2 and 3.
[12] Chapter 4 addresses the question of what it means for a pitch-class set (or rhythm—but the discussion here is mostly centered on pitch-class sets) to have a particularly high value on one Fourier coefficient; Amiot calls this “saliency.” The first part of the chapter completely characterizes sets that maximize a given coefficient, and shows some intriguing connections to maximal evenness and generated collections more generally (which comes largely from Quinn 2006–7 and Amiot 2007). Section 4.3.2 will be especially valuable to those interested in music-analytical applications of the DFT. Here Amiot discusses the meaning of the six coefficients and gives examples of music that uses pitch-class sets with interesting Fourier profiles. Another example of a pre-existing musical problem clarified by the DFT appears in section 4.3.3, the matter of flat-interval distributions (a generalization of the “all-interval” property), which Jon Wild and Tom Johnson have shown to be of some compositional interest.
[13] Chapter 5 is the most heterogeneous, taking on sundry generalizations and variations on the use of the DFT and other related topics. Amito addresses Callender’s (2007) idea of chord spectra in [5.1], and [5.2–3] describes a different way of applying the DFT to scales (used in Amiot 2009a to analyze well-temperaments). The latter topic is potentially confusing, insofar as it applies the DFT to pitch collections differently from any other part of the book (and also unfortunately reuses the term “diatonicity” in a different sense), though Amiot does give ample warning of the switch. Section 5.4 improves upon a result of Tymoczko’s (2008) that relates the DFT to voice leading. Tymoczko showed that the size of a DFT coefficient correlates with the voice-leading distance from the nearest subset of a perfectly even collection (with possible duplications). Amiot shows analytically that the relationship is approximately quadratic rather than linear.
[14] Chapter 6 comes around to another topic of great interest to music analysis: phase spaces. Section 6.2 defines the toroidal phase spaces; shows how the space based on the third and fifth coefficient (a3 and a5), which I have called Ph3/5-space, embeds the familiar Tonnetz and its dual; and reproduces some of my analytical examples from Yust 2015b and 2016. Section 6.3 provides some mathematical results explaining why certain set classes (such as triads) line up along special flip-flop cycles (to use John Clough’s (2008) term) in the phase spaces—something I noted in Yust 2015a. (The term “Tonlinie,” though, is Amiot’s invention.) Amiot extends this observation to seventh-chord examples and shows that it can work for any pitch-class set in Z12 (though not necessarily in other universes).
Tutorial
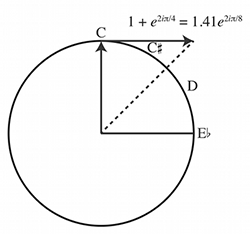
[15] To unlock this treasure chest, most readers will need to get comfortable with mathematical concepts and notations that Amiot largely takes for granted throughout the book. The book uses a system of notation that is ideal for mathematical reasoning about the DFT, but less so for accessibility to a wide range of music theorists. Nonetheless, the notations are not the barrier to entry that they may seem.
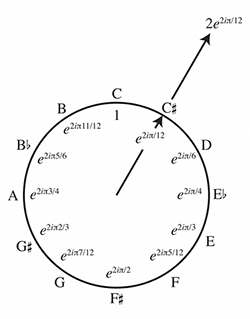
[16] Suppose that we have a potentially infinite dimension, pitch or time, represented with the real numbers, R, or—discretized in terms of semitones or sixteenth notes, for instance—with the integers, Z. To recognize a cyclic element of this space, such as an octave or beat cycle, we need another dimension within which to wrap the one-dimensional space into a circle. The complex numbers (C) fulfill this purpose. Mathematicians prefer to represent dimensions by sums (i.e., polynomials) with a position in each dimension given by a coefficient. A complex number has two coefficients, the real part a and imaginary part b, expressed as a + bi, and corresponds to a point (a, b) in the complex plane. We initially want to restrict this point to the unit circle, which can be done with trigonometry by specifying an angle, φ, and setting a = cos φ and b = sin φ. Because the circle is one-dimensional, we can now specify our point with one parameter: cos φ+ i sin φ. The parameter φ has the cycle 2π. To make a circle of, say, 12 semitones, we can take some pitch-class number x and let φ = 2π(x/12).
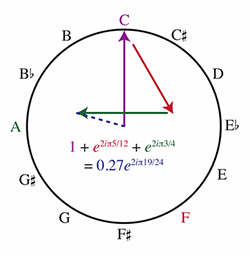
[17] Mathematicians have generally found it inconvenient to work with trigonometric functions like sines and cosines, however. At some point, these functions are needed for computation, but when doing mathematics at a more abstract level, they are excessively cumbersome, requiring complex trigonometric identities that clutter up proofs. Therefore, Amiot generally takes advantage of the Euler identity, the beautiful discovery of Leonard Euler, which is:
\[
e^{\phi{}i} = \cos \phi + i \sin \phi
\]
Example 1. 2e2iπ(1/12) (double-
(click to enlarge)
Example 2. Sums of C
(click to enlarge and see the rest)
Example 3. Sums of CG and FAC on the pitch class circle
(click to enlarge and see the rest)
[18] The number e is the natural number, but its value is not really important here, since we are raising it to an imaginary power. It is really just a way of specifying positions on the unit circle, with the constant φ in eφi ranging from 0 to 2π. Now we can express our familiar pitch-class circle with the expression e2iπ(x/12) for each pitch-class x. If, on the other hand, we want to express sixteenth-note positions in a
[19] So far, all we have done is manipulate symbols to translate familiar music-theoretic entities like the pitch-class circle or beat-class circle into a conventional mathematical form. The only real use of this is to have the whole complex space potentially at our disposal. By including a constant multiplier, we can indicate points not on the unit circle. For instance, to find the point 2e2iπ(1/12), go from the origin in the direction of 1/12 (the position of
[20] Now that we have translated our pitch-class circle or beat-class circle into complex space, we can formulate and take advantage of Fourier’s theorem. Suppose that we have a set of points on the unit circle, A = {a1, a2,
\[
1 + e^{2i\pi(3/12)} = (1.41)e^{2i\pi(1.5/12)} \\
\text{and} \\
e^{2i\pi(1/12)} + e^{2i\pi(2/12)} = (1.93)e^{2i\pi(1.5/12)}
\]
[21] The actual calculation of these coefficients requires trigonometry: converting the e2iπ(x/12) values into real and imaginary parts using sines and cosines, adding them, and then converting them back. But the important point can be seen by examining the drawing in Example 2: the sum points in a direction that essentially averages the positions of the pitch classes, and its distance depends upon how close together the pitch classes are. The fact that more tightly packed sets of points result in larger sums seems intuitively obvious, but Amiot proves it explicitly as his “huddling lemma” (Lemma 4.23).
[22] The point that results from a sum of pitch classes is not unique. Consider, for instance, the fifth C–G. As shown in Example 3, this sums to the same point as an F-major triad, FAC: (0.268)e2iπ(2.5/12).
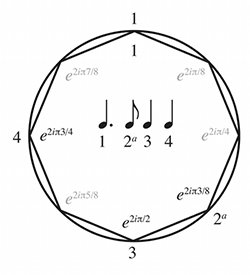
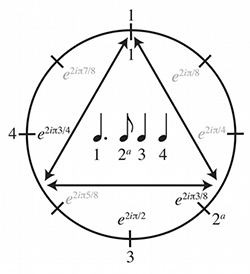
[23] Fourier’s theorem hinges on one other concept: multiplying the pitch-class or beat-class circle—that is, multiplying not the length of vectors in the space (the constant in front of e), but their positions on the unit circle (the exponent of e). Consider the tango rhythm (a favorite example of Amiot’s): Example 4 locates it on a beat-class cycle with eight positions, corresponding to  positions in a
positions in a
|
Example 4. The tango rhythm in a beat-class space, and the same in a 2-cycle of the beat-class space. The superscript a denotes “and of” (eighth note following the given beat) (click to enlarge and see the rest) |
Example 5. The tango rhythm in a 3-cycle (click to enlarge and see the rest) |
[24] We could also multiply by a value that does not evenly divide the eight beat classes. Example 5 divides the measure into three cycles by identifying the points indicated and superimposing the three resulting cycles. The eight points remain distinct because they fall in different places with respect to the tripartite division of the cycle. This is similar to producing the circle of fifths by multiplying the pitch-class circle by 5 or 7. Some elements of the tango rhythm are huddled on the 3-cycle, showing that it contains an underlying tresillo rhythm (see Amiot’s Section 1.2.1 and Fig. 1.6).
[25] The DFT sums the elements of a set (pitch classes or onsets), as I did in Examples 2 and 3, on each of the possible k-cycles, 0 ≤ k < n, where n is the universe (12 for pitch classes, 8 for the tango rhythm). This gives n complex numbers (one for each value of k):
\[
\sum_{\forall x \in A} e^{-2i\pi{}kx/n}
\]
(This is a slightly less general version of Amiot’s definition 1.4.) The magnitude of each complex number indicates the prominence of the given periodicity, while the phase positions that periodic element with respect to zero. The value for k is the same as for (n – k) with opposite phase, so about half of the coefficients are redundant. The basic Fourier theorem (Amiot’s theorem 1.5) tells us that this transform is an automorphism. In other words, we can recover the original set from its DFT; it contains the same information. It is as if we are looking at the same object, the pitch-class set or beat-class set, through a pair of glasses that reveals features that were there all along but not apparent to the naked eye: we see a collection of notes or onsets as a set of periodicities.
Example: Ligeti, “Fém”
Example 6. Rhythmic ostinati from Ligeti Etude 8, “Fém”
(click to enlarge)
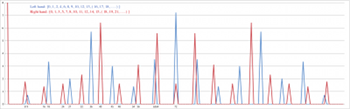
Example 7. DFT profiles of Ligeti’s ostinati: (a) left hand, and (b) right hand
(click to enlarge and see the rest)
[26] An analytical example might serve to bring some of Amiot’s results to life and show how one might use them. The all-embracing spirit of MFS stimulates me to look beyond the familiar universe of Z12—and away from pitch relations altogether—to an application of DFT to rhythmic cycles. György Ligeti’s later work plays on the possibilities of cyclic rhythms, filtering American minimalism and Central African rhythm through Ligeti’s unique musical sensibility. His Eighth Etude, “Fém,” is based on a counterpoint of rhythmic ostinati that cries out for DFT analysis. Example 6 gives the two ostinati, which repeat after 16  and 18
and 18  . In counterpoint, they produce a cycle that repeats after 144
. In counterpoint, they produce a cycle that repeats after 144  , or 12 measures of
, or 12 measures of
[27] The DFT magnitudes of these ostinati are shown in Example 7 using Amiot’s visualization method (a line graph). We notice that neither rhythm has nil coefficients. Amiot shows that this is an important property for a number of reasons related to the fact that their circulant matrices (Section 1.2.3) are invertible. It means that we can solve Lewin’s interval-function problem (from Lewin 1959 and 2001): the interval function is a list of how often a note of one rhythm occurs at a certain distance from a note of the other, for each possible distance. These rhythms have unique interval functions different from those of any other possible 16  or 18
or 18  rhythms. (Amiot calls this “phase retrieval,” meaning that one can recover one set from the other set plus an interval function.) It also means that we can express any other 16
rhythms. (Amiot calls this “phase retrieval,” meaning that one can recover one set from the other set plus an interval function.) It also means that we can express any other 16  or 18
or 18  rhythm as a linear combination of translations of these rhythms (Section 1.2.3). Finally, it means that these rhythms (or their complements) cannot produce tilings by translation (Section 3.2).
rhythm as a linear combination of translations of these rhythms (Section 1.2.3). Finally, it means that these rhythms (or their complements) cannot produce tilings by translation (Section 3.2).
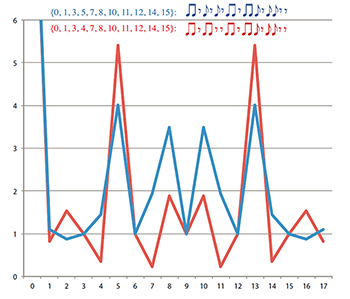
[28] Another notable feature of both rhythms is that their DFTs are rather uneven with some particularly large coefficients. The left-hand rhythm emphasizes a8 and a4, while the right-hand rhythm concentrates its energy in a5 and a8. A natural question is whether these rhythms actually maximize any of these coefficients. Section 4.3 shows how to maximize any coefficient. The numbers 5 and 18 are coprime, so a generated rhythm will maximize a5 for n = 18. The needed generator can be found by solving 1÷5 (mod 18), which is 11, or we can use the additive inverse of that, which is 7. Ligeti’s right-hand rhythm is actually very close to a 7-generated rhythm. Example 8 shows a rhythm that differs by moving one onset, and compares the DFT profiles of each.
|
Example 8. Comparison of the DFT of Ligeti’s right-hand ostinato (blue) and a similar generated rhythm that maximizes Fourier component 5 (red) (click to enlarge and see the rest) |
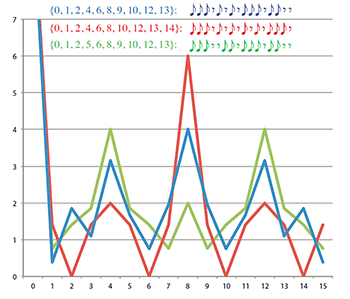
Example 9. Comparison of the DFTs of Ligeti’s left-hand ostinato (blue) to similar rhythms that maximize a8 (red) or a4 (green) (click to enlarge and see the rest) |
[29] A similar point may be made about the left-hand rhythm. We can maximize either the fourth or eighth coefficient by moving just one note; Example 9 gives the relevant rhythms and their DFT profiles. These are not generated rhythms, though, because 4 and 8 are not coprime to 16.(2)
Example 10. The DFT profiles of Ligeti’s rhythmic ostinati repeated over twelve measures
(click to enlarge)
Table 1. Values of some coefficients for Ligeti’s rhythms
(click to enlarge)
Example 11. A plot of 28.5 e2iπ(36t + 115)/144 (left hand, blue) and 32 e2iπ(40t + 133)/144 (right hand, red)
(click to enlarge)
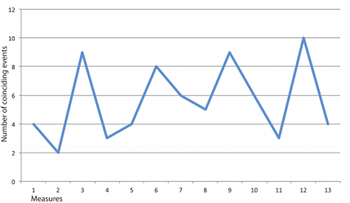
Example 12. The number of coinciding events (onsets or rests) between the hands per measure
(click to enlarge)
[30] Of course, because the left-hand and right-hand rhythms exist in different cyclic universes, they can be compared only by adapting them to a common cycle. Since Ligeti repeats them strictly over 24-plus measures, we can bring the rhythms into a common cycle by “oversampling”—repeating them nine and eight times over 144  s. Here, Amiot’s Theorem 1.21 tells us what we need to know: the DFT of a repeated “motif” is an upsampling of that motif’s DFT, as Example 10 shows. The most obvious feature of these is something predictable from the periods of the rhythms: because they share only one common factor, 2, one DFT always has a zero where the other has a positive value, except at 72. Coefficient a72 refers to the cycle of each quarter-note beat—that is, it compares on-beat to off-beat eighth-notes. Example 10 thus tells us something important about the convolution of the two rhythms. The convolution is the interval function, a catalog of all the durational intervals between one rhythm and the other. Amiot’s Theorem 1.10 (the convolution theorem) says that the DFT of the convolution is the product of the DFTs. Since the DFTs of Ligeti’s 144
s. Here, Amiot’s Theorem 1.21 tells us what we need to know: the DFT of a repeated “motif” is an upsampling of that motif’s DFT, as Example 10 shows. The most obvious feature of these is something predictable from the periods of the rhythms: because they share only one common factor, 2, one DFT always has a zero where the other has a positive value, except at 72. Coefficient a72 refers to the cycle of each quarter-note beat—that is, it compares on-beat to off-beat eighth-notes. Example 10 thus tells us something important about the convolution of the two rhythms. The convolution is the interval function, a catalog of all the durational intervals between one rhythm and the other. Amiot’s Theorem 1.10 (the convolution theorem) says that the DFT of the convolution is the product of the DFTs. Since the DFTs of Ligeti’s 144  cycles usually have a zero in one part or the other, the interval function is determined solely by coefficient 72, the number of on- or off-beat notes in each rhythm. It is large in the left-hand rhythm and small but not zero in the right-hand rhythm.
cycles usually have a zero in one part or the other, the interval function is determined solely by coefficient 72, the number of on- or off-beat notes in each rhythm. It is large in the left-hand rhythm and small but not zero in the right-hand rhythm.
[31] If a72 were zero in the right hand—that is, if the right hand had an equal number of on- and off-beat onsets—the interval vector would be completely flat; every interval would occur exactly an average number of times for the total number of onsets. But the non-zero a72 means that either the odd or the even intervals are uniformly more prevalent. Example 10 does not tell us which, though; for this, we need to know phases. These are given in Table 1 for a72 and other prominent coefficients. The a72 phases are opposite: the left hand has more on-beat notes (φ = 0) while the right hand has more off-beat notes (φ = π). Therefore, the interval vector will have more odd intervals. One of the even intervals is, of course, zero, meaning that there will be relatively fewer common onsets between the rhythms than one would expect by chance. In other words, because of the more off-beat character of the right-hand, it tends to fill in the gaps of the left-hand rhythm.
[32] Another thing that stands out in Example 10 is that the prominent components of each rhythm tend to be close together in periodicity. This is perhaps the crucial aesthetic feature of Ligeti’s ostinato pattern. Example 11 isolates the two largest noncoinciding “partials,” plotting the real parts of functions y = 28.5 e2iπ(36t + 115)/144 and y = 32 e2iπ(40t + 133)/144, which is to say y = 28.5 cos(2π(36t + 115)/144) and y = 32 cos(2π(40t + 133)/144). The phase difference of 4 means that the functions go in and out of phase in four cycles—what John Link (1994) calls coincidence cycles. Ligeti starts the two rhythms slightly out of phase, so the coincidence points occur in mm. 3, 6, 9, and 12. Example 12 plots the number of coinciding onsets and rests for each measure (where perfect equivalence is 12 and perfect complementation is 0). This clearly shows the four peaks. In other words, by constructing patterns with prominent components at similar periodicities, Ligeti builds a higher-order rhythm into his pattern: gradual fluctuations in coincidence and divergence that ebb and flow in three-measure cycles, rotated to mark the end of the larger cycle (in m. 12). Notice in Example 12 that this pattern varies a bit: in particular, the “low tide” in m. 8 is less pronounced. This reflects a single slow coincidence cycle created by the other prominent components, a63 in the left hand and a64 in the right, which come into phase in m. 8.
Errata
[33] The book, not surprisingly for such a complex project, does have occasional typos, including a few that might cause unfortunate confusion for the unwary:
• In Fig. 1.6 (p. 15) and Fig. 3.8 (p. 65), the DFT profiles are labeled starting from 1 instead of 0 on the x-axis, causing all the coefficient numbers to be off by 1.
• In Figs. 6.8–9 (pp. 168–9), the cycles are labeled incorrectly. The label C (indicating a C-major scale) is in the proper place, but the other labels should proceed in circle-of-fifths order (–G–D–A–
• In Fig. 6.11 (p. 173), the point labeled “3” should be labeled “9.”
Conclusion
[34] MFS looks at first like a culmination. It brings together research from the last decade on a wide variety of topics—research that Amiot has been helping to push forward using the DFT. The book has much to offer in new results and research, but the broad framework is set out by the existing literature, with each section summarizing and building on some existing body of articles. Nevertheless, I prefer to see it not as a goal but as a starting point. This amounts to an educated guess that the possible universe of DFT applications in music is quite large—a guess that is based upon observations and conjectures arising from my own brief experience with the method. These conjectures include:
• The DFT on pitch-class sets may be the route to a concise and operative definition of tonality.
• The DFT on pitch-class sets is a possibly universal tool that may help to organize, classify, and understand the diversity of harmonic styles in the twentieth century.
• Cyclic behavior and its accompanying mathematics, to which the Fourier transform is central, may be essential to the concept of music or musicality at a deeper level.
[35] These are undoubtedly bold and unproven assertions. I have argued the first two elsewhere (Yust 2016 and 2017), while the third has been inspired by Amiot and the range of DFT applications united in his book. Only time will prove their veracity or lack thereof.
Jason Yust
Boston University School of Music
855 Comm. Ave.
Boston, MA, 02215
jason.yust@gmail.com
Works Cited
Amiot, Emmanuel. 2007. “David Lewin and Maximally Even Sets.” Journal of Mathematics and Music 3 (2): 157–72.
—————. 2009a. “Discrete Fourier Transform and Bach’s Good Temperament.” Music Theory Online 15 (2).
—————. 2009b. “New Perspectives on Rhythmic Canons and the Spectral Conjecture.” Journal of Mathematics and Music 3 (2): 71–84.
—————. 2011. “Structures, Algorithms, and Algebraic Tools for Rhythmic Canons.” Perspectives of New Music 49 (2): 93–143.
Amiot, Emmanuel, and John Rahn, eds. 2011. “Tiling Rhythmic Canons.” Special half-issue, Perspectives of New Music 49 (2).
Amiot, Emmanuel, and William Sethares. 2011. “An Algebra for Periodic Rhythms and Scales.” Journal of Mathematics and Music 5 (3): 149–69.
Andreatta, Moreno, and Carlos Agon, eds. 2009. “Tiling Problems in Music.” Special issue, Journal of Mathematics and Music 3 (2).
Callender, Clifton. 2007. “Continuous Harmonic Spaces.” Journal of Music Theory 51 (2): 277–332.
Clough, John. 2008. “Flip-Flop Cycles and Their Groups.” In Music Theory and Mathematics: Chords Collections and Transformations, ed. Jack Douthett, Martha M. Hyde, and Charles J. Smith, 23–48. University of Rochester Press.
Cohn, Richard. 1988. “Inversional Symmetry and Transpositional Combination in Bartók.” Music Theory Spectrum 10 (1): 19–42.
Forte, Allen. 1973. The Structure of Atonal Music. Yale University Press.
Lewin, David. 1959. “Intervallic Relations between Two Collections of Notes.” Journal of Music Theory 3 (2): 296–301.
—————. 2001. “Special Cases of the Interval Function between Pitch-Class Sets X and Y.” Journal of Music Theory 45 (1): 1–29.
Link, John. 1994. “Long-Range Polyrhythms in Elliott Carter’s Recent Music.” PhD diss., City University of New York.
Quinn, Ian. 2006–7. “General Equal-Tempered Harmony.” Perspectives of New Music 44 (2): 114–58 and 45 (1): 4–63.
Tymoczko, Dmitri. 2008. “Set-Class Similarity, Voice Leading, and the Fourier Transform.” Journal of Music Theory 52 (2): 251–72.
Wild, Jonathan. 2007. “Flat Interval Distributions and other Generalisations of the ‘All-Interval’ Property.” Paper presented to the First International Conference for Mathematics and Computation in Music, Berlin, May 20, 2007.
Yust, Jason. 2015a. “Applications of DFT to the Theory of Twentieth-Century Harmony.” In Proceedings of the Fifth International Conference for Mathematics and Computation in Music, MCM2015, 207–18. Springer.
—————. 2015b. “Schubert’s Harmonic Language and Fourier Phase Space.” Journal of Music Theory 59 (1): 121–81.
—————. 2016. “Special Collections: Renewing Set Theory.” Journal of Music Theory 60 (2): 213–62.
—————. 2017. “Probing Questions about Keys: Tonal Distributions through the DFT.” In Proceedings of the Sixth International Conference for Mathematics and Computation in Music, MCM2017. Springer, forthcoming.
Footnotes
1. See Andreatta and Agon 2009 and Amiot and Rahn 2011 both of which feature contributions by Amiot (2009b, 2011).
Return to text
2. This is an example of the third, “somewhat messy” (109–10) case of Theorem 4.28, which gives three ways to maximize Fourier coefficients: with subsets of perfectly even collections, with generated collections, or with “huddled” collections of subsets of perfectly even collections. Unlike with generated rhythms, solutions in this third case are not generally unique up to translation.
Return to text
Copyright Statement
Copyright © 2017 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Samuel Reenan, Editorial Assistant
Number of visits:
6247