Spectral Meter: Dramatizing Entrainment and Communicating Form in Gérard Grisey’s Vortex Temporum I (1994–96) ^*

Introduction

[1.1] If anything unites the loose collection of composers commonly deemed “spectral,” it is their shared interest in exploring how perceptual and psychoacoustic research might inform musical composition.⁽¹⁾ Indeed, the term “Spectralism” itself alludes to spectral modeling, a method of electroacoustic synthesis that “simulate[s] how a sound is perceived by the listener” (Toiviainen 2007, 208). Spectral composers often begin composing by analyzing the psychologically relevant aspects of certain sounds. They base their compositional decisions on the sonic structures uncovered by this analysis, thus building musical processes that appeal to psychoacoustic norms and cognitive constraints. For instance, spectral composers generate their characteristic microtonal harmonies by performing Fourier analyses of sounds, then reproducing the effects of those sounds in a form of spectral modeling (Féron 2010, 2011). Similarly, they structure gradual formal processes with the aid of cognitive and psychoacoustic research on harmonic and timbral perception, precisely controlling their music’s perceived consonance, roughness, and predictability (Pressnitzer and McAdams 2000).⁽²⁾

[1.2] Past research into spectralism has largely focused on the harmonic and timbral precompositional methods outlined above, probably because spectral harmonies and timbres are the most immediately striking and radically different aspects of spectral music. Yet in their published writings, these composers make clear that perceptual and psychological research informs their thinking about all musical parameters, not just harmony and timbre. In fact, Tristan Murail and Gérard Grisey often discuss the rhythmic and temporal elements of their compositions as much if not more than their harmonic structures.⁽³⁾ Grisey has explicitly framed his music as the communication of temporal expectations and dynamic forms to his listeners, a communication facilitated by an understanding of rhythmic perception and cognition. For instance, in his article “Tempus ex machina: A Composer’s Reflections on Musical Time” (1987), Grisey explores how theories of rhythmic perception can help him more accurately convey specific expectations and perceptions by predicting listeners’ responses to certain rhythmic patterns and relationships.

[1.3] Grisey’s statements invite a psychologically grounded analytical approach to his music as a way to unpack his complex and frequently changing rhythms. Since Grisey was sensitive to rhythmic cognition when composing, analysis informed by recent theories of rhythmic cognition should help clarify Grisey’s compositional decisions and explain the resultant effects on listeners. Such an analysis would honor Grisey’s own emphasis on perception by adopting the perceiver’s perspective and locating rhythm and form in the cognitive responses prompted by his music.

[1.4] In this article, I propose a first step in this direction with an analysis of meter in Grisey’s Vortex Temporum I (Grisey 1994-96). I apply theories of metric cognition, especially Justin London’s (2012) theory of meter as entrainment behavior, to explain the processive form of the first section (Rehearsal numbers 1–37) in metric-cognitive terms. I show how the piece proceeds from the relatively simple and stable meter of the piece’s opening phrase (Example 1) to the complex and rapidly changing meters that characterize the end of the first section (Example 2). I further postulate why Grisey chose to structure this process around meter, concluding that Vortex Temporum I reveals a fundamentally spectral approach to meter—an instance of “spectral meter.”

[1.5] In the first part of the article, I consider how entrainment responses to Grisey’s meters describe the surface level structure of the first section and explain its motivation in psychological and experiential terms. Next, I briefly review Grisey’s temporal theory (1987), situating his ideas within the broader and more recent literature on metric cognition, metric conflict, and meter-driven forms. I enumerate the various ways in which Grisey complicates meter—and consequently, entrainment—as the first section progresses: introducing different meters, complicating metric evidence, and creating conflicts between the meters of successive phrases. Finally, I analyze two larger-scale, meter-driven forms, showing that as metric complexity increases over the course of the first section, listeners’ relationship to meter transforms from one of subconscious expectation to conscious audition. Therefore, I argue that the form of Vortex Temporum I is psychological as well as musical: our cognitive responses to the music undergo changes that parallel the structural changes of the stimulus itself. My paper thus proposes an expansion of spectral thought by showing how Grisey structures a piece around a metric cognitive principle much as he builds other pieces around cognitive principles in the domains of pitch and timbre.

Dramatizing Entrainment

[2.1] Each phrase in Vortex Temporum I dramatizes entrainment, the cognitive process by which listeners identify and coordinate with a meter. Entrainment is a response to the stimulus of rhythmic periodicity—equal durations and/or isochronous inter-onset intervals between events (London 2012, 9–23 and 50–52). Entrainment usually occurs quickly, in the first moments of listening to a piece (Thaut 2005, 175–177). In most cases, listeners entrain only once per piece, provided the piece remains in the same meter throughout.

[2.2] While it is possible to entrain to a single periodic pulse, entrainment usually describes coordination with a meter—a hierarchical, layered structure comprising several coordinated periodic pulses moving at different (but related) rates. Justin London (2012, 12) defines meter as “the anticipatory schema that is the result of our inherent abilities to entrain to periodic stimuli in our environment.” When we entrain we form a schema (a “metric image”) to fit the periodicities and relationships we perceive in the musical stimulus. Meter requires at least two, and preferably three, interlocking periodic layers. Entrainment entails coordinating with these periodic layers and relating the layers to each other. Typically, listeners use segmentation and grouping evidence to derive slower periodic layers from the composite rhythm of the musical surface and to hierarchically organize those layers into a meter.⁽⁴⁾ They identify the fastest layer, then note factors such as pitch contour, registral extremes, rate of harmonic rhythm, or motivic parallelism (Lerdahl and Jackendoff 1983, 68–104).⁽⁵⁾

[2.3] Not all metric layers are of equal importance. Rather, listeners tend to consider one layer in the middle of the metric hierarchy more salient and structurally significant than the others. This layer, the tactus, conceptually governs and constrains the faster and slower layers.⁽⁶⁾ The tactus can therefore serve as shorthand for a given meter, as it does in many of our metric notations.⁽⁷⁾ Listeners pay the most attention to the tactus layer, and consequently expect the most significant events to occur at this layer’s timepoints (London 2012, 31–33; Huron 2006, 175–85).

[2.4] Entrainment enables listeners to accurately measure durations and make several basic temporal predictions. Listeners expect events to occur “on the beat,” at the timepoints highlighted by the meter. Further, meter affords finer-grained predictions than does a simple periodic pulse stream because meter’s multiple periodicities allow listeners to “track rapid, moderate, and relatively slow event onsets” with a single coherent framework (London 2012, 17–19).⁽⁸⁾ Listeners attribute different levels of significance to expectations associated with each metric layer, generally judging expectations at the tactus layer and above (measure, hypermeasure) as more important than those associated below the tactus (subdivisions).⁽⁹⁾

Entrainment in Vortex Temporum I

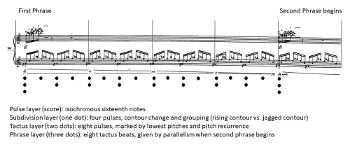
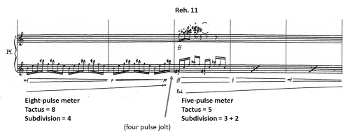
[2.5] The first phrase of Vortex Temporum I (Reh. 1) presents a straightforward meter that invites listeners to quickly and subconsciously entrain. Example 1 summarizes this meter with metric dot notation (Lerdahl and Jackendoff 1983). This meter projects at least four distinct layers that are strongly supported by contextual metric evidence, including pitch pattern, contour, and register. I will discuss the four layers in a “bottom-up” manner, beginning with the fastest phenomenal pulse stream and explaining the factors that support each slower periodic layer.

[2.6] The fastest layer is the pulse layer, which consists of the continuous swirling sixteenth notes (pulses) in the piano, flute, and clarinet parts. The pulse layer is periodic and consistent—it is a constant and uninterrupted presence throughout the first section—but it is too fast to act as a tactus (520 BPM). Instead, this layer serves as a ground for the other layers, providing fast consistent pulses that listeners can group into slower, more structurally significant metric layers (London 2012, 27–38).

[2.7] There is a subdivision layer with a periodicity of four pulses (notated quarter note). The subdivision layer is supported by two related contour factors. First, there are contour inflections (changes of direction) every four pulses. Second, the contour pattern changes every four pulses. For instance, in Example 1 the first subdivision unit ascends through four pulses, while the second subdivision unit displays a jagged, up-and-down contour. These two contour patterns alternate for the entire first phrase, supporting a subdivision layer when listeners notice the regular changes every four pulses.

[2.8] Next, there is a tactus layer with a periodicity equal to eight pulses (i.e. a notated half-note duration). The tactus is given by the lowest pitches of each part (the piano F♯) and by pitch recurrence (repetition of the pattern). The tactus provides an aurally salient, recurrent anchor point within the swirling “vortex” of the sixteenth notes. It moves at a more manageable rate (65 BPM) and organizes the faster pulse and subdivision layers into larger and more significant groups. In fact, the relationship of the tactus layer to the faster layers resembles the structure of familiar “simple” meters of Western art and popular music: the tactus layer is in a 2:1 ratio with the subdivision and an 8:1 ratio with the pulse layer.⁽¹⁰⁾ Most importantly, the tactus tracks several of the most significant events, especially the repetition of the basic pitch pattern.⁽¹¹⁾

[2.9] Finally, a longer periodic layer, the phrase layer, corresponds to the length of the entire first phrase. The phrase layer lasts exactly eight tactus beats (sixty-four pulses). This grouping is supported by motivic and dynamic parallelism. When the second phrase begins, like the first, with a loud articulation (Reh. 2) and the same motive, listeners form an expectation for phrases that last eight tactus beats.

[2.10] Successfully entraining to Example 1 generates several temporal expectations. Listeners assume that the constant sixteenth notes will continue for the foreseeable future (pulse layer), providing the basic information from which the other layers can be derived. They anticipate contour inflections and contrast every four pulses (subdivision layer) and expect the pitch pattern to repeat and to hear the salient lowest pitches every eight pulses or two subdivisions (tactus layer). They expect loud accented attacks and new phrase beginnings every eight tactus beats (phrase layer). Finally, they presume that this meter will persist uninterrupted into new phrases, as has just occurred between the first and second phrases.

[2.11] It is important to note here that these metric expectations are subconscious and reflexive.⁽¹²⁾ We are not normally aware of such fine-grained activity, and expectations this close to the musical surface rarely factor into musical analysis. Listeners can automatically entrain to this meter and adopt its attendant metric expectations without devoting conscious attention to the process because metric entrainment is cognitively grounded, and because they are acculturated to hearing metric music. Nevertheless, these expectations are crucial to the meter-driven formal processes I will discuss in my analysis. Grisey creates a meter-driven form by imparting, then carefully subverting, these reflexive and unnoticed expectations. In other words, in typical spectral fashion he creates an intriguing musical process by shaping listeners’ conception of, and relationship to, a cognitive phenomenon—in this case, meter. He transforms meter from a subconscious and reflexive cognitive process into a conscious and deliberate part of musical experience.

[2.12] Grisey enacts this spectral process by varying meters and thus altering the entrainment process from phrase to phrase. His metric manipulations influence entrainment in three main ways: they shape how frequently listeners must entrain, to what type of meter they must respond, and how relatively difficult it is to entrain to a given phrase. First, he arranges meters so that listeners must re-entrain at the start of every phrase after the second. Entrainment may be rote and unnoticed in the case of Example 1, but after entraining forty times in a three-minute span, listeners will become acutely aware of entrainment as a process—their relationship to meter will have changed. Second, Grisey presents nine distinct meters in this section, as summarized in Example 3. This variety keeps the focus on entrainment because listeners must navigate many different meters rather than following a single meter throughout the piece. In fact, after the first four phrases, meters change in every successive phrase. But as Example 4 shows, although these meters exhibit tactus durations ranging from eight to two pulses in length, Grisey’s meters present metric grouping evidence (contour accent, register, pitch repetition) that is strikingly like that of the initial meter shown in Example 1. The similarities between meters thus encourage listeners to entrain in the same way in each phrase, to compare their entrainments, and to reflect on the differences between meters. Third, Grisey complicates entrainment by progressively increasing metric ambiguity and conflict. For instance, Example 2 reproduces several phrases from the end of the first section, demonstrating how shorter phrases require more frequent cognitive adjustments; varied meters prompt different entrainment responses; and faster, more complicated meters inhibit quick entrainment.⁽¹³⁾ In these ways, Grisey crafts a meter-driven form that treats the cognitive process of entrainment as a spectral topic.

Grisey’s Communication and Meter Theory

[3.1] While Vortex Temporum I is perhaps an outlier case—most of Grisey’s compositions are not so straightforwardly metric—it nevertheless reflects Grisey’s aesthetic principles. In fact, Vortex Temporum I neatly expresses Grisey’s temporal theory in a limited context. Further, this piece’s prevalent meters invite comparisons of Grisey’s theory to music-theoretical studies of metric cognition, metric conflict, and meter-driven form, which share some of Grisey’s concerns and corroborate his assertions.

[3.2] In “Tempus Ex Machina: A Composer’s Reflections on Musical Time,” Grisey (1987) defines musical composition as the communication of specific temporal expectations and experiences to an audience.⁽¹⁴⁾ Building substantially on Abraham Moles’s Information Theory in Aesthetic Perception (1966), Grisey couches his discussion in a tripartite bodily metaphor: the skeleton, flesh, and skin of time. I will review the layers briefly here; see Hennessy (2009) for a more in-depth discussion. The skeleton of time refers to the composer’s time, to the absolute or “chronometric” durations notated in the score (Grisey 1987, 239). The flesh of time involves the qualitative, intuitive aspects of sound: here Grisey recognizes the dependence of temporal perception on rhythmic context, relationships, grouping, and predictability (Grisey 1987, 257–58; Exarchos 2018, 33–36). Finally, the skin of time is the subjective time of the listener, the subject of psychoacoustic and sociological study and dependent on culture, musical training, and memory (Grisey 1987, 272–73).

[3.3] Crucially, Grisey centers his discussion on perception—in the flesh and skin of time—concluding at one point that “structure, whatever its complexity, must stop at the perceptibility of the message” [emphasis original] (Grisey 1987, 257). He seeks to understand how he can impart specific expectations and surprises to his listeners, arriving at a method that builds on his explicit and intuitive knowledge of rhythmic perception and cognition. Grisey situates composition squarely in its perceptual outcomes, finding for instance that “the real material of the composer becomes the degree of predictability” (Grisey 1987, 258).⁽¹⁵⁾ Grisey attempts to control rhythmic and temporal predictability in his music in order to impart to his listeners certain expectations and to carefully subvert those expectations in service of dynamic developing forms.

[3.4] Grisey associates periodicity with maximal predictability and rhythmic “order.”⁽¹⁶⁾ According to Grisey, periodicity introduces an element of stability and repetition, thus creating a “pause in the music’s unfolding,” a break within Grisey’s dynamic, forward-looking forms. Consequently, periodicity “expands” the perceived present, objectifying the rhythmic “now,” promoting memory, and allowing listeners to attend both to details of the rhythmic surface and to form larger groups and predictions (Grisey 1987, 244–47 and 258–59). Because meter is a hierarchical outgrowth of multiple coordinated periodicities, these properties extend to meter, which consequently amplifies predictability beyond that of a single periodic pulse stream.⁽¹⁷⁾

[3.5] But Grisey considers periodicity too predictable for extended use in his music’s processive and dynamic forms. Instead, he argues that, “the whole art of the composer . . . consists of making this excessively redundant material [i.e., periodicity] more flexible” (Grisey 1987, 245). He avoids both what he calls the metric “obsession” of minimalism and the metric “repression” of Boulez’s serialism, instead balancing predictable periodicity with sufficient unpredictability.⁽¹⁸⁾ This context throws into relief Grisey’s metric choices in Vortex Temporum I: he balances the predictability afforded by his well-formed meters with frequent meter changes, growing metric ambiguity, abrupt interruptions, and stark contrasts between meters of different kinds.

[3.6] One way that Grisey communicates expectations is through periodic rhythmic patterns that elicit entrainment.⁽¹⁹⁾ His dynamic forms hinge on a balance between the fulfillment and subversion of temporal expectations. As a result, his forms appeal to cognitive processes (such as entrainment) and could be considered as much psychological as they are musical-structural. In Vortex Temporum I, Grisey’s temporal principles manifest in the meters he writes, the context of each meter, and the ways in which he subverts metric expectations at the subdivision, tactus, and phrase levels. While each phrase begins with straightforward metric evidence that encourages entrainment and promotes local metric expectations, changes from phrase to phrase upend these expectations and require frequent cognitive realignment. Listeners entrain at the beginning of each phrase and follow that meter until it no longer accurately predicts event onsets. The cycle then begins anew as listeners entrain to the new meter of the following phrase.

[3.7] Before turning to a fuller analysis of the first section and a discussion of Vortex Temporum I’s two higher-level formal processes, I will enumerate the various metric manipulations that support this phrase-level formal process. I review the first section’s different meters, explain how metric ambiguity increases as the form unfolds, and discuss the various conflicts between successive meters, which increase the difficulty of and draw attention to entrainment.

Meters

[3.8] The first section of Vortex Temporum I includes nine distinct meters, each with a different set of periodicities and relationships and requiring a different entrainment (refer to Example 3). Each meter has a different tactus duration; the first section includes every integer duration between eight and two pulses.⁽²⁰⁾ (In addition, there are two more meters with aperiodic tactus durations; I will discuss these meters in the section on metric conflicts below.) Yet despite this metric variety, the type of metric evidence is invariant. In every phrase, regardless of meter, sixteenth notes give the basic pulse, contour accents and changes support a subdivision layer, the pitch pattern and lowest pitches support a tactus layer, and parallelism suggests a phrase layer.⁽²¹⁾ While listeners must entrain to a variety of meters, that process is somewhat facilitated by these invariant elements of metric evidence.

[3.9] Crucially, each of these meters implies a different absolute phrase duration (number of seconds or sixteenth-note pulses) but the same relative duration (number of tactus beats). For example, an ideal eight-pulse tactus phrase would last sixty-four pulses, while a six-pulse tactus phrase would present only forty-eight pulses—but both phrases would contain eight complete tactus beats. Moreover, this durational variation does not preclude phrase-level expectations; rather, listeners can flexibly adjust to each meter by noticing the consistent relative phrase lengths despite differences in surface metric levels.

Metric Ambiguities

[3.10] Meters become more ambiguous in many phrases and ambiguity grows as the first section progresses. Metric evidence is loudest and clearest—and ambiguity lowest—at the beginning of each phrase. The initial metric clarity of each phrase enables listeners to entrain quickly and easily within the first bar or so. As each phrase unfolds, the metric evidence fades away, suggesting a sort of metric “decay” and forcing listeners to rely more on their internalized image of the meter.⁽²²⁾ The volume of the metrical parts (piano, flute, clarinet) falls gradually from fortissimo to piano, while the texture thins as the flute and clarinet no longer play constantly but instead stagger short snippets of sixteenth notes (see Example 1). Moreover, in some phrases the non-metrical string parts sustain tones and crescendo, occluding the moving, fading metrical parts. As shown in Example 5, the result is a sort of notated “cross-fade” that substantially augments metric ambiguity and makes metric hearing more difficult—and more conscious—by requiring more devoted attention.⁽²³⁾

Metric Conflicts

[3.11] Metric conflicts involve successive or simultaneous incongruities between an existing metric structure and a phenomenal pulse stream, resulting in a need for reinterpretation or realignment of a metric interpretation. For instance, a meter change is an example of a successive metric conflict: the new meter does not fit our existing metric image, so we must abandon it and entrain again in order to accurately predict events and timepoints. John Roeder (1994) has described this situation in post-tonal music as the “activation” of new pulse streams by successive periodic statements. The new pulse streams conflict with previous pulse streams, but because they structurally underpin the new section, they require a cognitive realignment—a new entrainment. In a sense, the notion of conflict reflects how a denial of expectations creates a disjunction in our predictive cognitive processes. We may experience the conflict in the psychological shift that occurs when our entrained meter fails and we initiate entrainment again.

[3.12] All metric conflicts in Vortex Temporum I are successive, arising from the contrast between adjacent meters. I identify three species of metric conflict. Each type of conflict has distinct effects on entrainment and metric expectations. Displacements occur when phrases end before or after their expected endpoints. I further divide displacements into jolts (phrase ends early) and deferrals (phrase ends late).⁽²⁴⁾ Meter changes juxtapose different periodicities and require new and different types of entrainments in each phrase. Most meter changes occur at the start of a new phrase, but a few phrases also include final bar meter shifts, changes of meter within (rather than between) phrases. Finally, some meters incorporate one or more aperiodic layers which add complexity and strongly contrast with other, more periodic layers like those of Example 1.

Displacements: Jolts and Deferrals

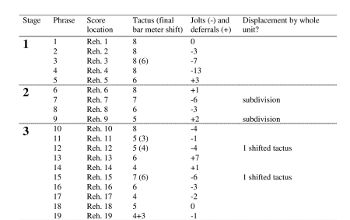
[3.13] As we can see with a cursory glance at Example 6, which summarizes the meters (third column) and conflicts (fourth and fifth columns) of each phrase, all but two phrases end in jolts or deferrals. These displacements undermine listeners’ “when” expectations for the strong articulation that marks a new phrase (Huron 2006). But although their cause is similar, jolts and deferrals elicit distinct listener responses. Jolts prompt sudden entrainment: listeners confront a new meter at a time when they expected to continue following the preceding meter (see Example 7). Deferrals present the opposite situation: when listeners expected to encounter a new phrase and meter, they hear only the continuation of the existing meter (see Example 8). They must delay entrainment to some later, unknown timepoint, now unable to predict the beginning of the next phrase since the phrase layer has exceeded its predictive duration. Deferrals therefore prompt imprecise metric expectations and amount to weaker metric surprises. This is probably why Grisey ends many more phrases with jolts than with deferrals: the sudden intrusion of a new meter into an existing phrase is more shocking and forward-oriented than the extension of an existing meter past its expected endpoint.⁽²⁵⁾ Referring to Example 6, we can verify that the first section includes thirty-four phrases that end with jolts (83%), compared with only five phrases ending with deferrals (12%).

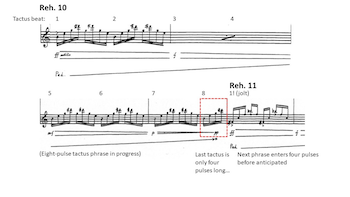
[3.14] The effect of a displacement depends on its duration and metric context. A short displacement may feel like a slight metric “hiccup,” something that listeners can ignore or correct without totally abandoning an existing metric framework (see Example 7).⁽²⁶⁾ Longer displacements feel more significant because they shift entrainment behavior much earlier or later than anticipated. Further, displacements by non-metric-unit durations feel more shocking than those by metric unit durations. This is because a unit displacement places the new phrase articulation at a relatively strong timepoint (on a beat or point of metric accent), whereas a non-unit displacement puts a strong articulation on a weaker offbeat, when listeners least expect it. Example 9 demonstrates the greater surprise generated by a non-unit jolt in contrast to the unit jolt shown in Example 7.

Meter Changes

[3.15] Meter changes create conflicts between successive phrases. Listeners confront multiple periodicities incompatible with the preceding meter. Meters change at the start of every phrase after the fourth phrase, prompting new entrainments. Further, Grisey avoids juxtaposing related meters, that is, those that share periodic layers of the same cardinality. To see this clearly, we can examine the ratios between the tactus durations of adjacent phrases. For example, the six- and three-pulse tactus meters are closely related because they share a periodic layer (three pulses as subdivision and as tactus), a fact illustrated by their 2:1 tactus ratio (refer to Example 3). If this succession occurred in Vortex Temporum I, listeners could maintain the three-pulse layer from the preceding phrase into the new phrase, getting a jump start on entrainment and experiencing a smoother transition between phrases and meters. But as Example 6 reveals, there are no such simple successions in the first section. Instead, adjacent meters share no layers in common (save the trivial pulse layer) and meter changes frequently yield complex tactus ratios such as 8:5, 7:4, and 3:2. See for instance Example 10, which depicts a change from an eight- to five-pulse tactus. In addition to disagreement between the tactus layers, the subdivisions of the former meter (four pulses) clash with the mixed three- and two-pulse subdivisions of the latter meter. As a result, listeners must entrain from scratch at the start of every phrase, building up a metric structure and forming new expectations every few seconds.⁽²⁷⁾

[3.16] Additionally, in four phrases the meter changes within, rather than between, phrases. I term this effect final bar meter shift because it always occurs in the last bar of the phrase. For instance, Example 11 shows a final bar meter shift from an eight- to a six-pulse tactus in the third phrase. Final bar meter shifts subvert local metric expectations. Listeners are entrained to one meter, but unexpectedly encounter a new meter early. Final bar meter shifts destabilize the current meter and break down current metric expectations, but listeners still anticipate a full meter change when the next phrase begins with a loud articulation.

Aperiodic Layers

[3.17] Some meters include one or more aperiodic layers, layers with multiple durational values. For instance, a single metrical layer might include alternating two- and three-pulse durations, as in the quarter and dotted quarter divisions of ${}_8^5$. Importantly, London (2012, 100–141) argues that partial aperiodicity does not preclude entrainment. Other layers remain periodic, particularly the pulse layer, so we can still hear metrically because most of the layers still facilitate entrainment and metric predictions. In Vortex Temporum I, aperiodic layers add an element of instability to some meters and mark them for contrast with the more periodic meters like those with eight- or six-pulse tacti.

[3.18] Grisey’s meters are aperiodic at three different timescales. First, there are aperiodic subdivisions of the tactus. Aperiodic subdivisions are characteristic of meters with seven- and five-pulse tacti: prime durations that cannot be divided periodically (see Example 12).⁽²⁹⁾ Aperiodic subdivision layers demonstrate the unevenness of prime tacti and conflict with nearby even meters (eight, six, and four pulses).

[3.19] Second, there are aperiodic bars, whose successive tacti are subdivided differently. For instance, in Example 12 we see that Grisey’s seven-pulse tactus divides into 4+3 and 3+4 subdivision units within the same bar.⁽³⁰⁾ The seven- and five-pulse meters are therefore aperiodic at two levels, the subdivision and the bar, adding to their contrast with the even meters. And in fact, these somewhat aperiodic meters are often juxtaposed with the highly periodic eight- and six-pulse meters, further foregrounding the conflicts between those types of meter.

[3.20] Third, two meters have aperiodic tactus layers. (These are shown in the bottom row of Example 3). London (2012, 100–141) calls such meters “non-isochronous” (NI) meters. In NI meters, the most salient metric layer is aperiodic, significantly increasing complexity. Listeners perceive conflict when they must shift between isochronous meters, such as the six-pulse tactus meter, and NI meters.

[3.21] Crucially, the first section’s invariant metric evidence ([2.12], Example 4) distinguishes the NI meters from the prime (seven- and five-pulse) meters. Example 13 compares the seven-pulse tactus meter with the NI 4+3 tactus meter. Note that the relevant tactus information (lowest pitches, pitch cycle) supports a seven-pulse span in the case of the former meter, while the same information clearly outlines a mixed 4+3 tactus in the latter. The subdivision layers of these meters further clarify matters. The seven-pulse tactus subdivides into alternate groups of four and three pulse durations via its contour changes and notated accents. By contrast, the written accents of the NI meter clearly divide its four-pulse unit into two-pulse subdivisions, while its three-pulse unit receives accents on its first and third pulses. In fact, these subdivisions demonstrate the hybrid nature of the 4+3 meter: the accents and contours are identical to those of the isochronous four-pulse and three-pulse tactus meters (see Example 3). Structurally, this NI meter is a literal joining of two different tacti into one meter, something that cannot be said of the seven-pulse meter.⁽³¹⁾

Communicating Form: Two Meter-Driven Forms in “Vortex Temporum I”

[4.1] Grisey’s meters, metric ambiguities, and metric conflicts support a dynamic form at the surface level (in each phrase) predicated on a balance between prediction and surprise. Each phrase follows a path from predictable meter to a state of unpredictability. The phrase-level process is also psychological: listeners entrain, find their expectations briefly fulfilled, then ultimately frustrated, requiring them to entrain all over again in the new phrase. In terms of Grisey’s theory, the phrase-level form reflects a balance between each phrase’s initial periodicity and predictability and its ultimate unpredictability.

[4.2] My metric analysis so far only supports a fragmentary, moment-to-moment reading of Vortex Temporum I, one where listeners perceive forty-one discrete segments in their immediate context, and entrain forty separate times, without making any larger formal connections or inferences. While theories of meter often focus on surface-level rhythms and brief cognitive processes like entrainment, there is also significant precedent for a meter-focused analysis of larger formal units. Authors generally concede that meters cannot create progressions as rich and varied as those generated by tonal harmony, but they nevertheless note similarities between forms suggested by metric changes and those based on tonal structures (Lewin 1981, 261–65; Leong 2007; Murphy 2009). Metric shifts between stability and conflict often outline familiar forms on local and global levels (Malin 2006, 2008). For instance, the Baroque hemiola is a metric means of designating the end of a formal unit (phrase) and a cadence. On local levels, metric conflicts resolve to metric stability, reflecting the “departure/return” and “tension/release” patterns of basic tonal harmonic progressions.⁽³²⁾ More globally, although most Classical and Romantic era pieces begin in a stable meter without conflict, composers often introduce metric conflicts and sometimes new meters in thematically looser or harmonically distant sections, such as transitions or developments. Composers thus metrically outline large-scale forms (Krebs 1999, 142–73). For instance, Richard Cohn analyzes the form of Brahms’s Von ewiger Liebe (op. 43, no. 1) in terms of motion through different metric states, noting the unique metric states of each stanza. Cohn relates these states to harmonic functions and analyzes a meter-driven formal path through the song that concludes with a return in the postlude of the first stanza’s “tonic” meter. Cohn finds that Brahms’s meters and metric conflicts reinforce not only the Lied's form but also its sense of tonal and thematic resolution (Cohn 2001, 312–21). John Roeder has come to a similar conclusion in a post-tonal context in his pulse stream analysis of Schoenberg’s “Mondestrunken”. Roeder notes a sense of “recapitulation” when the original pulse streams are restored and realigned with the opening motive at the end of the first stanza (1994, 238–42).⁽³³⁾ In sum, theorists have extensively shown that meters and metric relationships support large-scale forms in tandem with tonal and thematic factors; and significantly, this finding extends even to situations that lack tonal context.

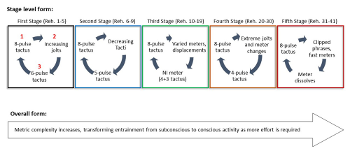
[4.3] In Vortex Temporum I, metric factors indeed support two higher-level formal interpretations that further reflect Grisey’s communicative principles and psychological focus. First, there is a stage-level form, unfolding over the course of five discrete stages (consecutive sets of phrases). Example 14 summarizes this form, noting the beginning meter (1), metric process of growing conflict (2), and closing meter (3) of each stage. Each stage begins with the same pitch collection, register, and meter—the eight-pulse tactus meter from Example 1. The stages become progressively more metrically complex as Grisey gradually introduces new types and degrees of conflict in successive phrases. Finally, each stage concludes with a phrase that pushes metric complexity to new heights, frequently including a new meter that conflicts with existing meters. This new meter then helps to mark the formal boundary between sections by contrasting with the eight-pulse tactus meter when it returns at the start of the next stage.

[4.4] Second, the first section exhibits an overall progression toward metric complexity and change. Or in cognitive terms, the first section passes from easy and rare entrainments to more difficult and frequent entrainments as metric variety increases and phrases are compressed. This form develops non-linearly because it embeds the stage-level form, which includes cyclical returns to the initial meter. Nevertheless, my analysis will show how the overall motion toward increased complexity and more difficult entrainment obtains despite this cyclicity. In fact, the stage-level form enhances the entrainment-based perspective on the overall form that I advance in the following analysis, a claim I will return to in my conclusion.

[4.5] In the following section, I flesh out this meter-driven formal analysis, discussing details of each stage, comparing the relative metric stability and conflict of phrases, and considering listeners’ entrainment responses to new metric situations. I provide text descriptions of the relevant metric developments in each stage. Readers may refer to Example 6 for details about the specific meters, displacement types, and displacement durations in each phrase. (Note that each phrase generally corresponds to a rehearsal number in the score, excepting stage 5, where multiple short phrases occur between rehearsal numbers.) For a broader perspective, refer to Example 14, which summarizes my prose description by noting the key aspects (beginning, process, ending) of each stage.

[4.6] I also invite readers to experience the process for themselves by listening to the provided audio clips (Ryan and Ensemble Recherche 1999) while following along with the proportional shorthand notation presented with each stage. Each shorthand example depicts an entire stage; each line within these examples corresponds to a single phrase. Tactus durations, corresponding to each labeled and uniquely colored box, represent the meter of each phrase. Shortened final boxes depict jolts, while elongated boxes show deferrals (and are labeled with “deferral”). A new color in the final box of a phrase designates a final bar meter shift. By following the proportional notation while listening, readers can get a sense of the dynamic psychological changes and meter-driven form arising from changes in our relationship with entrainment.

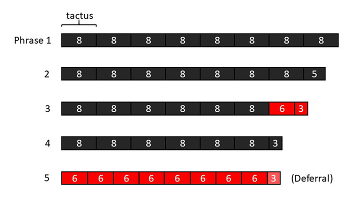
First Stage (Reh. 1–5)

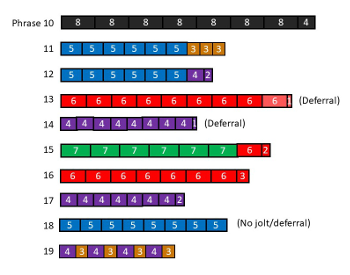
[4.7] The first stage elicits metric hearing and metric expectations and shows listeners what metric evidence is relevant to entrainment. See Example 15 for a proportional shorthand graph of this section. Unpredictability increases as phrases end in successively longer jolts. After the first phrase (refer to Example 1) fulfills its eight-tactus length—creating the phrase-level expectation—the second phrase ends three pulses too early, the third sheds seven pulses, and the fourth loses thirteen. At first a minor bump, by the fourth phrase these jolts elide more than an entire tactus duration.⁽³⁴⁾ Further, these are all non-unit jolts. The third phrase also incorporates a final bar meter shift, from an eight- to a six-pulse tactus. Together, these factors mean that listeners must entrain anew in each phrase even though the first four phrases share a meter. Finally, the fifth phrase begins in a new meter, with a six-pulse tactus. Unpredictability peaks as listeners encounter a phrase with a new meter thirteen pulses before they expected a new phrase to begin. The fifth phrase ends with a one-pulse deferral, another new metric conflict increases variety and sets up the advent of the second stage by slightly delaying the return to the stable eight-pulse tactus meter.

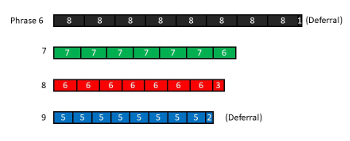
Second Stage (Reh. 6–9)

[4.8] In the second stage, short displacements cut short or extend phrases by a few pulses, but the primary type of new unpredictability comes from grouping conflicts. Whereas the phrases of the first stage remain largely within one meter (eight-pulse tactus), in the second stage every phrase has a different meter. See Example 16 for a summary of this section. Moreover, periodic and partially aperiodic meters are juxtaposed in successive phrases as tactus durations shrink from eight to five pulses. This juxtaposition throws into relief the differences between the periodic subdivisions of the meters with even tactus durations (eight and six pulses) and the aperiodic subdivisions of the prime tactus meters (seven and five).⁽³⁵⁾ Every phrase requires a more complete entrainment process because of these new meters and the stark conflicts between successive meters.

Third Stage (Reh. 10–19)

[4.9] In the third stage, metric conflicts become more extreme and diverse; see Example 17. Tactus durations and metric displacements no longer follow a logical ordering. Rather, meters flip from relatively fast to relatively slow tacti in successive phrases, and displacements vary widely in length from phrase to phrase. Listeners can no longer anticipate the type of meter in an upcoming phrase, nor can they predict what type or length of displacement will end the current phrase.

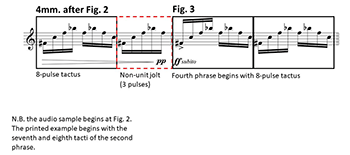
[4.10] A closer look at the first six phrases of the third stage (Reh. 10–15) will demonstrate the rapidly shifting metric situations of this stage. Example 18 reduces these phrases to their first and last bars. The first bar of each phrase shows the meter of that phrase, while the last bar demonstrates the displacement that ends each phrase. This reduction highlights the frequent shifts between even, periodic meters (Reh. 10 and 13–14) and prime, aperiodic meters (Reh. 11–12 and 15). Displacements vary in similar fashion: the first three phrases (Reh. 10–12) end with jolts, followed by two phrases ending in deferrals (Reh. 13–14), and finally another jolt (Reh. 15). Moreover, three of these phrases (Reh. 11–12 and 15) end with final bar meter shifts that introduce additional conflict within phrases.

[4.11] The third stage culminates in a new height of metric complexity when the first NI meter (4+3 tactus) is heard at Reh. 19. This NI meter contrasts with the preceding meters, which have all included a periodic tactus layer. Moreover, the NI meter points up how the temporal window for entrainment has decreased: its two tactus durations are half or less the duration of the initial meter’s tactus (eight). Listeners can now expect phrases half the length of the first phrase and must also entrain in half the time, and twice as often, as they did earlier.

Fourth Stage (Reh. 20–30)

[4.12] In the fourth stage, displacement conflicts grow to extreme proportions; see Example 19. Phrases consistently end early, with significantly longer jolts in some phrases. In fact, many phrases end nearer their midpoints than their expected endpoints, with the result that listeners can barely finish entraining to one meter before they encounter a new one. Entrainment occupies more of their experienced time and begins to draw their conscious attention. The initial phrase of this stage establishes this new status quo when it ends twenty-four pulses early (Reh. 20).⁽³⁶⁾ In other words, what should have been the most stable phrase of the section ends more than three full tactus durations early. The extreme jolt in this prominent position immediately signals to listeners the degree of conflict they can expect in this stage.

[4.13] The types of meter (periodic/aperiodic) again change from phrase to phrase. Meters appear in an even more unpredictable ordering now that there are eight meters in play, including two NI meters (4+3 and 3+2 tacti). Moreover, meters with vastly different tactus durations appear in succession, creating a sense of stratified motion between temporal levels. For instance, Example 20 shows the temporal stratification that results when the twenty-fifth phrase’s three-pulse tactus is followed by the twenty-sixth phrase’s seven-pulse tactus (Reh. 25–26). A meter change like this may seem more like a shift between metrical levels—between a subdivision and a tactus layer—because the shorter tacti (two and three pulses) share the durations of the slower meters subdivision units (seven, six, five, four pulse meters).⁽³⁷⁾

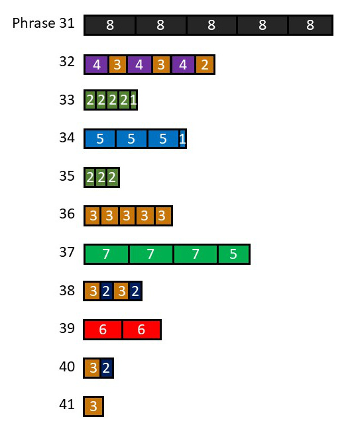
Fifth Stage (Reh. 31–37)

[4.14] In the fifth stage, metric complexity peaks while metric evidence becomes increasingly ambiguous; see Example 21. The non-metrical string parts more frequently and completely occlude the metrical information of the piano and wind parts.⁽³⁸⁾ As we saw in the fourth stage, an extreme jolt (twenty-five pulses) interrupts the stable opening meter (Reh. 31). In fact, the phrase length expectation is attenuated if not eliminated in this stage because almost every phrase ends shortly after it begins.⁽³⁹⁾ The shortened phrases diminish the dynamic differences between phrase endings and beginnings: phrases do not persist long enough to appreciably decay from their initial forte. The ninth and fastest meter arrives (two-pulse tactus) and stratified motion continues to be suggested by pairings of meters with short and long tacti. The increased metric complexity of this late stage is reflected in the prominence of meters with short (two- and three-pulses), prime (seven- and five-pulses), and aperiodic (NI) tacti.

[4.15] The section concludes as the metric evidence dissolves, ending a consistent texture that has persisted from the first sounds of the piece. The piano breaks from the sixteenth-note pulses, striking a low sustained E; then the winds, violin, and piano ascend a scale and arrive at a unison chord to mark the end of the first section on the downbeat of Reh. 38.

Conclusions: Psychological Form, Spectral Meter

[5.1] The scale of metrical ambiguity and conflict in the final stage may call my metric interpretation into question. Heard in isolation, the fifth stage would not seem to promote metric hearing, with its extreme conflicts and constantly changing meters. Listeners would probably not gravitate to an entrainment response if they heard this stage alone, perhaps instead focusing on the registral changes highlighted by Jean-Luc Hervé (2001, 25–27). How can listeners continue to entrain and attend to meter when phrases end abruptly, meters change every few seconds, sustained tones obscure the metric evidence, and most meters are rapid and at least partially aperiodic?

[5.2] But in the context of the overall metric process, a metric interpretation remains relevant, and in fact vital, to an understanding of Grisey’s communicated form here. Grisey points up metric hearing in the cyclic structure of the stages. By returning to the opening meter at the beginning of each stage, he reminds his listeners of their earlier metric experience and the easy entrainment they had at the start of the piece. When he opens even the fifth stage with this meter, he is prompting his listeners to engage with the following complicated meters via entrainment, to reflect on the challenges and relate their experiences to the way entrainment felt in the first phrase of the piece. If listeners respond to this aspect of the meter-driven form, they will gradually become more aware of entrainment. Entrainment occupies a greater significance in listeners’ experience as they devote more conscious control to interpreting meters and reconciling metric conflicts.

[5.3] From this perspective, the fifth stage culminates not just a musical process but also a psychological one. Musically, the first section progresses from simple, slow meters to complex, faster meters; rhythmic structure moves from simplicity to complexity; and tension generically increases as meters accelerate and conflict with their immediate context. Psychologically, the section begins with simple and subconscious experiences: easy, quick, unnoticed entrainment to a familiar meter. As the section unfolds, entrainment must happen more quickly, and requires active reasoning and attention to parse the increased variety of meters and possible changes. We could therefore think of the opening of Vortex Temporum I both as an intriguing meter-driven formal process and as a demonstration or enactment of a cognitive principle. In truly spectral fashion, Grisey communicates how (entrainment) and what (metric differences) to perceive in his formal processes, gradually revealing the psychological nature of a temporal experience to his audience.

Joseph R Jakubowski
Washington University in St. Louis
Department of Music
6500 Forsyth Blvd.
St. Louis, MO 63105
joseph.jakubowski@wustl.edu

Works Cited

Anderson, Julian. 2000. “A Provisional History of Spectral Music.” Contemporary Music Review 19 (2): 7–22.

Baillet, Jérôme. 2001. Gérard Grisey: Fondements d’une écriture. L'Harmattan.

Bourne, Janet. 2016. “Perceiving Irony in Music: The Problem in Beethoven'’ String Quartets.” Music Theory Online 22 (3). http://mtosmt.org/issues/mto.16.22.3/mto.16.22.3.bourne.html.

Cohen, Annabel J. 2005. “Music Cognition: Defining Constraints on Musical Communication.” In Musical Communication, ed. Dorothy Miell, Raymond MacDonald, and David J. Hargreaves, 61–84. Oxford University Press.

Cohn, Richard. 2001. “Complex Hemiolas, Ski-Hill Graphs and Metric Spaces.” Music Analysis 20 (3): 295–326.

—————. 2016. “A Platonic Model of Funky Rhythms.” Music Theory Online 22 (2). http://mtosmt.org/issues/mto.16.22.2/mto.16.22.2.cohn.html.

Cross, Jonathan. 2018. “Introduction: Spectral Thinking.” Twentieth-Century Music 15 (1): 3–9.

Exarchos, Dimitris. 2018. “The Skin of Spectral Time in Grisey’s Le Noir de l'Étoile.” Twentieth-Century Music 15 (1): 31–55.

Féron, François Xavier. 2010. “Sur les traces de la musique spectrale: Analyse génétique des modèles compositionnels dan ‘Périodes’ (1974) de Gérard Grisey.” Revue de Musicologie 96 (2): 411–443.

—————. 2011. “The Emergence of Spectra in Gérard Grisey’s Compositional Process: From Dérives (1973–74) to Les Espaces Acoustiques (1974–85).” Contemporary Music Review 30 (5): 343–75.

Fineberg, Joshua. 2000. “Spectral Music.” Contemporary Music Review 19 (2): 1–6.

Goldman, Jonathan. 2010. “Boulez and the Spectralists Between Descartes and Rameau: Who Said What about Whom?” 48 (2): 208–32.

Grisey, Gérard. 1987. “Tempus Ex Machina: A Composer’s Reflections on Musical Time.” Trans. S. Welbourn. Contemporary Music Review 2: 239–75.

—————. 1994–96. Vortex Temporum I, II, III pour piano et cinq instruments. Ricordi.

—————. 2008a. “La musique: le devenir du sons.” In Écrits, ou L'invention de la musique spectrale, ed. Guy Lelong and Anne-Marie Réby, 45–56. Éditions MF.

—————. 2008b. “Vortex Temporum,” in Écrits, ou l'invention de la musique spectrale, ed. Guy Lelong and Anne-Marie Réby, 158–60. L'Harmattan.

Haselböck, Lucas. 2009. Gérard Grisey: Unhörbares hörbar machen. Rombach Verlag KG.

Hasegawa, Robert. 2009. “Gérard Grisey and the ‘Nature’ of Harmony.” Music Analysis 28 (2–3): 349–71.

—————. 2015. “Rhythm and Repetition in Gérard Grisey’s Vortex Temporum.” Paper presented at the Annual Meeting of the Society for Music Theory, St. Louis, MO, November 2015.

Hasty, Christopher. 1997. Meter as Rhythm. Oxford University Press.

Hennessy, Jeffrey. 2009. “Beneath the Skin of Time: Alternative Temporalities in Grisey’s ‘Prologue for Solo Viola.’”Perspectives of New Music 47 (2): 26–58.

Hervé, Jean-Luc. 2001. Dans le vertige de la durée: Vortex Temporum de Gérard Grisey. L'Harmattan.

Horlacher, Gretchen. 2000/2001. “Multiple Meters and Metrical Processes in the Music of Steve Reich.” Intégral 14/15: 265–97.

Howland, Patricia. 2015. “Formal Structures in Post-Tonal Music.” Music Theory Spectrum 37 (1): 71–97.

Huron, David. 2006. Sweet Anticipation: Music and the Psychology of Expectation. MIT Press.

Imbrie, Andrew. 1973. “‘Extra’ Measures and Metrical Ambiguity in Beethoven.” In Beethoven Studies, ed. Alan Tyson, 45–66. Norton.

Iverson, Jennifer. 2014. “Statistical Form Amongst the Darmstadt School.” Music Analysis 33 (3): 341–87.

Krebs, Harald. 1999. Fantasy Pieces: Metrical Dissonance in the Music of Robert Schumann. Oxford University Press.

Leong, Daphne. 2007. “Humperdinck and Wagner: Metric States, Symmetries, and Systems.” Journal of Music Theory 51 (2): 211–43.

Lerdahl, Fred, and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. MIT Press.

Lewin, David. 1981. “On Harmony and Meter in Brahms’s Op. 76, No. 8.” 19th-Century Music 4 (3): 261–65.

London, Justin. 2009. “Temporal Complexity in Modern and Post-Modern Music: A Critique from Cognitive Aesthetics.” In Unfolding Time: Studies in Temporality in Twentieth-Century Music, ed. Darla Crispin, 45–68. Leuven University Press.

—————. 2012. Hearing in Time: Psychological Aspects of Musical Meter. Second edition. Oxford University Press.

Malin, Yonatan. 2006. “Metric Displacement Dissonance and Romantic Longing in the German Lied.” Music Analysis 25 (3): 251–88.

—————. 2008. “Metric Analysis and the Metaphor of Energy: A Way into Selected Songs by Wolf and Schoenberg.” Music Theory Spectrum 30 (1): 61–87.

Margulis, Elizabeth Hellmuth. 2007. “Surprise and Listening Ahead: Analytic Engagements with Musical Tendencies.” Music Theory Spectrum 29 (2): 197–217.

Miell, Dorothy, Raymond MacDonald, and David J. Hargreaves, eds. 2005. Musical Communication. Oxford University Press.

Mirka, Danuta. 2009. Metric Manipulations in Haydn and Mozart: Chamber Music for Strings, 1787–91. Oxford University Press.

Mirka, Danuta and Kofi Agawu, eds. 2008. Communication in Eighteenth-Century Music. Cambridge University Press.

Moles, Abraham. 1966. Information Theory and Aesthetic Perception. Trans. Joel E. Cohen. University of Illinois Press.

Moscovitch, Viviana. 1997. “French Spectral Music: An Introduction.” Tempo, New Series 200: 21–27.

Murphy, Scott. 2007. “On Metre in the Rondo of Brahms’s Op. 25.” Music Analysis 26 (3): 323–53.

—————. 2009. “Metric Cubes in Some Music of Brahms.” Journal of Music Theory 53 (1): 1–56.

Parncutt, Richard. 1994. “A Perceptual Model of Pulse Salience and Metrical Accent in Musical Rhythms.” Music Perception 11 (4): 409–64.

Pressnitzer, Daniel, and Stephen McAdams. 2000. “Acoustics, Psychoacoustics and Spectral Music.” Contemporary Music Review 19 (2): 33–60.

Radvansky, Gabriel A. and Jeffrey M. Zacks. 2014. Event Cognition. Oxford University Press.

Roeder, John. 1994. “Interacting Pulse Streams in Schoenberg’s Atonal Polyphony.” Music Theory Spectrum 16 (2): 231–49.

Rose, François. 1996. “Introduction to the Pitch Organization of French Spectral Music.” Perspectives of New Music 34 (2): 6–39.

Ryan, Kwamé, and Ensemble Recherche. 1999. Vortex Temporum/Talea. Westdeutscher Rundfunk B00004VLJ8, compact disk.

Thaut, Michael H. 2005. “Rhythm, human temporality, and brain function.” In Musical Communication, ed. Dorothy Miell, Raymond MacDonald, and David J. Hargreaves, 171–192. Oxford University Press.

Toiviainen, Petri. 2007. “The Psychology of Electronic Music.” In The Cambridge Companion to Electronic Music, ed. Nick Collins and Julio d'Escriván, 218–31. Cambridge University Press.

Yeston, Maury. 1976. The Stratification of Musical Rhythm. Yale University Press.

Footnotes

* This research began as a conference presentation given at the Spectralisms conference in Oxford, UK in March 2017. I am grateful to the attendees of that conference for feedback. Additionally, I wish to thank Paul Steinbeck, Robert Snarrenberg, Benjamin Duane, and the two anonymous reviewers at Music Theory Online for their helpful comments on earlier drafts of this article. Thanks are due to the Washington University in St. Louis Music Department for their help with licensing costs. Finally, all examples are copyright:

Vortex Temporum
Music by Gérard Grisey
Copyright 1996 by Casa Ricordi S.r.l., Milan—Italy
All Rights Reserved.
Reproduced by Kind Permission of Hal Leonard MGB S.R.L.

1. The most frequently discussed spectral composers are Gérard Grisey and Tristan Murail, but other core members (involved with the Ensemble L'Itinéraire) include Michaël Levinas, Roger Tessier, and Hugues Dufourt. Other composers that garner the spectral label include contemporaries Jean-Claude Risset, Claude Vivier, or Jonathan Harvey; and later composers (many students of Grisey and Murail) such as Phillipe Hurel, Phillipe Leroux, Kaija Saariaho, Joshua Fineberg, and Georg Friedrich Haas. See Moscovitch 1997 and Anderson 2000 for summaries of the history of Spectralism and the interactions of these composers as the movement developed. Cross 2018 discusses the thorny question of what music counts as spectral music.
Return to text

2. Hasegawa 2009 makes a similar argument regarding the importance of psychology and perception for understanding Grisey’s harmonic practice. Spectral compositional techniques are summarized in Toiviainen 2007, 208–11; Rose 1996; Moscovitch 1997; and Fineberg 2000.
Return to text

3. For this reason, Grisey and Murail often disavow the spectral label, preferring instead adjectives such as liminale or transitoire (Grisey 2008a).
Return to text

4. Grisey (1987, 239–43) discusses grouping and rhythmic notation.
Return to text

5. Roeder 1994 describes how timepoints accrue accents through these grouping factors, framing the perception of pulse streams (analogous to metric entrainment) in terms of comparisons of accent strength and recurrence. Christopher Hasty (1997, 84–91) posits that listeners first note periodicity at the surface and “project” expectations for regular durations. The fulfillment of expectations leads listeners to form higher-level expectations, corresponding to slower periodic layers, by grouping surface projections together. For a few alternative views of the derivation of meter from a surface, see (for instance) Yeston 1976; London 2012, 60–78; and Mirka 2009.
Return to text

6. David Huron (2006, 176) defines the tactus as “the basic beat that forms the most salient periodic pulse evident in a musical passage.” London (2012, 31–33) reviews the cognitive evidence for tactus perception and offers a brief history of music-theoretical discussions of the tactus as the primary metrical layer.
Return to text

7. For example, the ${}_4^4$ time signature describes that meter in terms of its tactus (quarter note) and its grouping into larger (bar) units (four tacti per bar). I will similarly summarize meters by their tactus values in my analysis below.
Return to text

8. See also Yeston 1976; and Lerdahl and Jackendoff 1983, 12–34.
Return to text

9. More generally, Radvansky and Zacks (2014, 51–52) discuss the differences of event salience and expectations at various timescales. Local events at faster timescales are less salient and engender weaker expectations than events at slower timescales. For example, expectations for tonal closure at the end of a phrase are stronger than expectations for tonal resolution within that phrase.
Return to text

10. In fact, Grisey notated this phrase in ${}_4^4$, probably the most common meter in Western art and pop music. But from the perspective of perceptual salience, it is the notated half note (eight pulses) and not the quarter note (four pulses) that corresponds to the tactus of this phrase.
Return to text

11. It is perhaps possible to hear my subdivision layer as a tactus, especially since its rate of motion fits better within the range of tempi judged ideal in tapping studies (e.g. Parncutt 1994; see also London 2012, ch. 2; and Huron 2006, ch. 10). I thank the anonymous reviewer for this observation. I call the next slowest layer the tactus because of the comparative salience of its metric evidence (pitch recurrence, lowest pitches) and the structural significance of that layer (as Grisey’s Gestalt for all of Vortex Temporum). The resemblance between this meter and familiar Western meters is not a coincidence: Grisey was inspired by and partially quoted a passage from Ravel’s Daphnis et Chloë when composing this piece. See Hervé 2001, 15–16.
Return to text

12. Huron 2006 unpacks the significance of prediction and anticipation at pre-conceptual levels. We do not need to be aware of an expectation for it to have a profound musical and cognitive effect.
Return to text

13. Importantly, this progressive increase in ambiguity and conflict obtains at multiple temporal levels. As my analysis (section 4) will show, Grisey enacts this process at the phrase, stage, and section levels.
Return to text

14. For background on musical communication, see Mirka and Agawu 2008 and Mielle, MacDonald, and Hargreaves 2005. Cohen (2005, 65–74) describes music-focused research into Gestalt psychology and information theory, while Thaut (2005, 171–174) specifically examines rhythmic-temporal communication.
Return to text

15. Grisey discusses predictability in terms of the flesh of time in Grisey 1987, 257–70. See also Hennessy 2009, 26–58.
Return to text

16. Grisey arranges different rhythmic structures on an information-theory-inspired “continuum.” See Grisey 1987, 244; Hennessy 2009; and Haselböck 2009, ch. 2–3. Not coincidentally, Grisey’s theory calls to mind Stockhausen’s “statistical form,” a discourse based on “rising and falling arches in pitch, loudness, and speed” and grounded in electroacoustic composition and information theory (Iverson 2014, 341).
Return to text

17. London asserts that meter facilitates greater rhythmic understanding because the predictability afforded by meter allows listeners to discern finer gradations of surface rhythm and project expectations over longer spans of time (London 2012, 48; London 2009).
Return to text

18. Goldman (2010) expounds the antagonistic relationship between Boulez and the spectralists. Much of the hyperbole in Grisey’s discourse can be attributed to his strident rejection of Boulez’s total serialist approach.
Return to text

19. The “origin” (Margulis 2007) of these expectations lies in psychological norms, in metric entrainment: our innate responses to periodicity, grouping, and metric structure. For an alternative, language-focused perspective on communication and expectation, see Bourne 2016, [8.1-8.4].
Return to text

20. The tempo is consistent at quarter note equals 130 BPM throughout the first section. Baillet 2001, 215–16 describes the different meters as transformations of the first meter via “progressive diminution of its periodicity” (from eight pulses down to two). Hervé (2001, 24), treats what I call the tactus unit as a Gestalt object and an “initial arpeggio,” noting that “over the course of the first part [of the movement], the duration of the sections is diminished and the meter changes, transforming the initial arpeggio formula, which becomes shorter and shorter. Its melodic profile is modified and the rhythmic accents are shifted” (my translation).
Return to text

21. In a more conservative reading (Imbrie 1973), the faster meters (four, three, two) could be interpreted as variations on the eight, six, and four pulse meters, in which case the later phrases would shift back to slower meters and metric variety would be somewhat reduced. While this hearing is certainly possible, several factors support designating the faster meters as full-fledged meters. First, the extremely salient lowest pitches and pitch cycles clearly differentiate four, three, and two from eight, six, and four. Moreover, these meters are structurally distinct: Grisey’s accent markings (which outline my subdivision layer) clearly differentiate six from three, as shown in Example 3; and because Grisey describes this piece in terms of temporal compression and expansion, it makes sense to take the faster meters as separate entities. Finally, all previous analyses (including one by Grisey’s student, Jean-Luc Hervé) describe these meters as distinct entities (Hervé 2001, Baillet 2001). However, choosing my reading or the conservative reading does not change my analysis of metric conflicts between successive meters: the even/periodic and prime/aperiodic differences obtain whether one takes the meters as five versus three or five against six. I thank the anonymous reviewer for suggesting the alternative reading.
Return to text

22. I thank Robert Snarrenberg for suggesting the term metric decay, which dovetails with the acoustic metaphors favored by Grisey in his writings.
Return to text

23. At the same time, the string crescendos reinforce the phrase layer when they culminate their crescendo in a loud, short burst at the downbeat of the new phrase.
Return to text

24. I borrow the term jolt from Grisey, who wrote of “unexpected acoustic jolts” that cause us “to skate over a portion of time” (Grisey 1987, 259). The notion of deferral comes from Christopher Hasty’s (1997, 133–135) theory of metric projection. Hasty defines deferrals as unexpected continuations or expansions of existing durations, where we instead expected a new duration to begin.
Return to text

25. Further, jolts affect the perceived past (we only recognize them after they have happened) while deferrals affect the perceived present (we recognize them when something should have happened but did not).
Return to text

26. This would reflect a more flexible hearing of the passage. And in fact, performers may take advantage of this flexibility for practical or aesthetic reasons. For instance, in the recordings accompanying my examples (Ryan and Ensemble Recherche 1999), the performers sometimes stretch time, breaking the flow (and breathing), in phrases with short (one- or two-pulse) deferrals.
Return to text

27. Meter changes could also be explained by Roeder’s (1994) pulse stream analysis. The new phrase initiates a different set of pulse streams that conflict with the preceding pulse streams, leading us to adjust our formal expectations and thus our rhythmic perceptions (of accent and beat strength). The difference here is that unlike Roeder’s original subject (Schoenberg’s atonal polyphony), the meters I am discussing are rhythmically homophonic: each set of layers is coordinated (i.e., is a meter in the cognitive hierarchical sense) and thus the changes resemble more familiar meter changes, or Krebs’s “indirect grouping conflicts” (Krebs 1999). Regardless, my analysis of meter changes still rests on entrainment theory because I emphasize the cognitive conflict listeners experience when hearing a change.
Return to text

28. Sometimes final bar meter shifts seem to set up the meter of the following phrase. However, these situations are always accompanied by non-unit displacements that prevent the shifted meter from continuing into the new phrase.
Return to text

29. In fact, Grisey’s notated time signatures hint at the audible subdivision layers of his prime-tactus meters. He often uses additive time signatures in place of simpler equivalent time signatures. For example, he notates the seven-pulse tactus meter in \(\substack{4+3\\16}\) time instead of the more common \(\substack{7\\16}\).
Return to text

30. Although the bar is aperiodic, it is symmetrical and palindromic. However, in a rebuttal of his teacher Messiaen’s rhythmic “anthropocentrism,” Grisey argues that rhythmic palindromes have “no perceptible value” (Grisey 1987, 240–43), so these symmetrical palindromes have no impact on entrainment or Grisey’s meter-driven communications.
Return to text

31. The seven-pulse meter does have an additional low note on its third pulse, but this note is unaccented and happens too soon after the first to constitute a tactus duration. If anything, this added note complicates the subdivision of the seven, immediately signaling its contrast with the preceding eight-pulse meter.
Return to text

32. See Krebs 1999, 31–45 on displacements and alignment; Horlacher 2000/2001 on metrical processes in Steve Reich’s phasing music; Malin 2006 on cyclical completion; Malin 2008, 61–87 on metric conflict and energy; Howland 2015, 71–97 on departure/return and tension/release parametric processes; and Cohn 2016 on local cycles of grouping dissonance and its resolution in music of the African diaspora.
Return to text

33. Roeder later generalizes this finding, noting that in Schoenberg’s rhythmic practice generally, “the transitions between the large musical sections setting complete stanzas typically involve the dissipation of conflicting or syncopated pulses, followed by the reorientation of voices and motives with their original pulse streams” (1994, 249).
Return to text

34. Although only the first phrase fulfills the expectation for a sixty-four pulse, eight tactus phrase duration, I argue that listeners maintain an expectation for phrases of that length throughout this sequence. The well-rounded length and simple durational ratios (8:1 pulse to tactus, tactus to phrase) presented in the first phrase activate basic metric expectations that we can conservatively maintain in the face of the relatively short jolts that follow in phrases 2–4. Further, the most relevant element of the expectation is the eight tactus beats per phrase, and each phrase except the fourth at least begins this beat. Therefore, the sensation is one of an eighth tactus beat begun but suddenly cut short; we can mentally fill in the missing durations and understand the jolts in the context of that unfulfilled final beat.
Return to text

35. Listeners might more likely use “template matching” to entrain to the even meters, which resemble ${}_4^4$ and ${}_8^6$, but are more likely to apply “period extraction” to the prime meters (London 2012, 50–53). The prime meters do resemble common templates in some non-Western and modern art music. Nevertheless, ${}_4^4$ and ${}_8^6$ are deeply culturally embedded through their prevalence in art and pop music and their templates will probably strongly influence entrainment to the even meters.
Return to text

36. Similarly extreme jolts cut short the twenty-sixth phrase (thirty-two pulses, Reh. 26) and the twenty-eighth phrase (twenty-four pulses, Reh. 28).
Return to text

37. This observation points up a possible alternate reading, in which some listeners might hear the three-pulse meter in Example 19 as a six-pulse tactus, and thus hear a change from six to seven instead of three to seven. I thank the anonymous reviewer for pointing out this possibility. This difference depends on the strictness with which listeners interpret metrical levels, i.e. if they identify the tactus exclusively with the low register pulsations in the piano left hand (my reading) or prefer to identify groupings at similar metrical levels (the alternative reading). Regardless, as noted previously the sense of contrast between aperiodic and periodic meters remains whether the ratio is 3:7 or 6:7.
Return to text

38. At the same time, the dynamic contrasts between phrases are attenuated. A suddenly louder dynamic (from the phrase ending’s piano to the phrase beginning’s forte) has usually marked the beginning of each phrase. But in this section, phrases are not long enough for the decrescendo to distinguish phrase endings and beginnings.
Return to text

39. Nevertheless, it is interesting to note that many phrases end with completed tactus units, as shown in Example 6.
Return to text

Copyright Statement

Copyright © 2018 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.