Feedback and Feedforward Models of Musical Key*
Christopher Wm. White
KEYWORDS: Corpus analysis, tonality, key, harmony, modeling, scale degrees
ABSTRACT: This study begins by drawing a distinction between two ways of framing the concept of musical key. Feedforward models understand key as arising from immediately apparent surface characteristics like the distribution of pitch classes or a melody’s intervallic content. Feedback models, on the other hand, understand key as being determined in tandem with other domains. Here, key arises from the surface being organized into other more complicated musical groupings or schemata—harmonic progressions, cadences, prolongations, meter, etc.—that themselves are informed by the music’s tonal center. While much music theory and theory pedagogy have acknowledged that feedback occurs in various approaches to tonality, formal modeling in the fields of music cognition and computation has focused primarily on feedforward systems. This article attempts to right this imbalance by presenting a corpus-based feedback computational model that can be tested against human behavior. My model will identify a passage’s key by organizing a surface into its constituent harmonies. Here, harmonic organization and key will be integrated into a feedback system with the ideal key being that which produces the ideal harmonic analysis, and vice versa. To validate the resulting model, its behavior is compared to that of other published tonal models, to the behaviors of undergraduate music students, and to the intuitions of professional music theorists.
Copyright © 2018 Society for Music Theory
Part I: Feedback and Feedforward Understandings of Musical Key
[1.1] David Temperley begins his 1999 article “What’s Key for Key?” by asking a crucial question underpinning listeners’ experience of tonal music: “By what method do people determine the key of a piece or changes of key within a piece?” (66) When we glance at a musical score or listen to a passage of music, how do we identify a tonal center and convert pitches into scale degrees? How do we know music’s “key”?
[1.2] Of course the topic of key finding and the establishment of tonal hierarchies has been theorized for centuries: any tonal theory formalizes how scale degrees or harmonies are expressed through pitches and rhythms. From Rameau to Schenker, Riemann to Krumhansl, any theory of tonal music converts musical surfaces into successions of scale degrees in some way.
[1.3] This article uses corpus analysis and computational modeling to identify an often-overlooked aspect of musical key, namely its interrelationship with other equally complex musical parameters. (Here, “tonal orientation” and “key” will simply mean the identification of some key center, although I will engage in more nuanced definitions later in this essay.) I argue that analyzing a tonal center in tandem with some other musical parameter (like harmony or meter) represents a fundamentally different strategy than treating key as a property that arises independently from other organizing musical structures. I call the former feedback models of musical key, and the latter feedforward models. In a feedback model, a passage’s key arises from parsing a musical surface into, say, harmonies while at the same time this harmonic analysis relies on the passage’s tonal orientation: here, harmony and key are intertwined in a feedback loop that produces an analysis or interpretation of both domains. In contrast, feedforward approaches find some immediate piece of evidence—say, the first lowest note or the repetition of a particular pitch—and uses that to determine the passage’s key. Here, key is determined separately from and prior to other musical domains: there is no feedback loop.(1) To put a fine point on the distinction: if knowing a passage’s key helps you know x, and knowing x helps you identify a passage’s key, your logic uses feedback; if you are simply using x to determine a passage’s key, your logic is feedforward.
[1.4] Having established this dichotomy, I argue that—while both approaches are represented in music theory, pedagogy, computational modeling, and psychology—feedback methods have received overall less attention, especially regarding formal models, empirical testing, and behavioral studies. I then present a proof-of-concept computational system that integrates key-finding with harmonic analysis into a feedback system, and show how such a model can be subjected to behavioral testing. My approaches will rely on insights from each of these domains—from computational, psychological, pedagogical and music theoretic research—but I will show that reaching across these discourses and disciplines can add to, complicate, and hone our understanding of musical key, and of tonality in general. This essay ends by discussing how such formalizations can add not only to our understanding of musical key and tonal orientation, but to how we present this concept in the classroom. Furthermore, while I frame this discussion formally/computationally throughout, I argue that this kind of thinking can contribute to how musicians and researchers think about and engage with the concept of musical key.
Part II: Defining Feedforward and Feedback Approaches
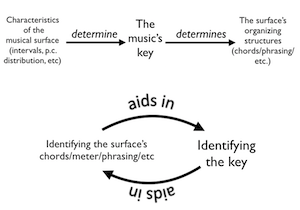
[2.1] Example 1a schematizes feedforward key finding. This kind of logic first identifies some property, schema, or template apparent on the musical surface and uses that parameter to identify the music’s key. There is a one-way mapping between the music’s “surface” and its “organizing structure”—namely key. This surface/structure dichotomy is drawn from Temperley (2007), but also tracks the musical perception/cognition dichotomy of Huron (2006): the former categories correspond to uninterpreted musical phenomena (think: pitches and rhythms), while the latter category involves interpreting those phenomena in some way (think: scale degrees and meters).(2) Consider Example 2: if a key-finding process tallied the pitch classes used in the first phrase (a surface phenomenon) and concluded that they corresponded to the key of D major (an organizing structure), that process would be using a feedforward approach. Similarly, if we identified the excerpt’s modulation by noting that the diminished fifth between
Example 1a and b. Feedforward and Feedback ways of schematizing how key interacts with other musical parameters (click to enlarge and see the rest) | Example 2. Mozart, Piano Sonata, K. 284, iii, mm. 1–8 (slurring from Breitkopf edition) (click to enlarge) |
[2.2] Alternately, we might identify the key of a passage using a feedback process, as outlined in Example 1b. This kind of process views a passage’s key as dependent upon larger organizational structures like chord progressions, metric hierarchies, or harmonic/melodic groupings. The organizing structure of “key” arises concomitantly with—not prior to—other musical interpretations: key is determined as part of a feedback loop with other musical organizations. Rather than being an immediate property of the musical surface, key emerges as a byproduct of organizing the surface into more complex structures, which themselves are dependent on the passage’s key.(4)
Example 3. Grieg, “The Mountain Maid,” op. 67, no. 2, mm. 4–7, along with tonal analyses provided by two computational models
(click to enlarge)
[2.3] Example 3 shows a tonally ambiguous excerpt that highlights the differences between feedforward and feedback methods, measures 5–7 of Grieg’s “The Mountain Maid” op. 67 no. 2. Below the example, I show how two computational systems parse this excerpt, one feedforward and one feedback. The first roughly follows the methods of Krumhansl (1990), determining musical key by the pitch classes present in some passage (a “key-profile analysis”),(5) while the second uses a chord-based approach drawn from my previous work in this area (White 2015). (I will discuss the specifics of these different algorithms below.) Both models return more than one possible key at each point, shown by the different rows allocated to each model.(6)
[2.4] The two models provide overlapping but different answers, with the collection-based method finding
[2.5] But most notably, being a feedback system, the harmonic analysis of the chord-based model changes within its different tonal interpretations: the different keys use and ignore different surface pitches to create the chordal analyses. The same is not true of the feedforward logic of the collectional approach: the key (or ambiguity of key) is simply a product of the notes as they exist in the score. Consider how both methods interpret the chord on the downbeat of measure 6. In the feedforward method, it is not obvious how to interpret the chord, given the tonal ambiguity. However, in the feedback method, the key is part and parcel of how the passage is parsed into chords. The key is ambiguous because the chords are as well, and the chords are ambiguous because so too is the key.
Part III: Feedforward and Feedback Logics in Music Research
[3.1] For our purposes, the discourse surrounding key can be usefully divided into four overlapping dimensions/components: theory, pedagogy, computation, and behavioral testing. Together, these approaches constitute a larger multifaceted conceptual symbiosis: while theories creatively engender a concept’s speculative formal structure, a computer rigorously implements and parameterizes all aspects of this formal structure. Behavioral experiments can then test if and how a formalization describes the cognition or experience of that concept.(8) Finally, pedagogy informs how we present and teach these ideas. Missing any corner of this disciplinary reciprocity means that the discourse surrounding a concept misses some important facet or approach. In this section, I argue that while scholarship in music perception and cognition has shown that feedforward methods are mutually supported by each of these domains, feedback systems have not received comparable attention.
[3.2] Feedforward models of key and tonal centers are manifested in all four of these domains. For instance, a theoretical approach might include Harrison’s (2016) “dronality” model, in which a key center is expressed by a constantly sounded pitch, while feedforward pedagogical approaches might include Clendinning and Marvin’s (2011) advice to identify modulations by focusing on a phrase’s opening notes and final chords. Feedforward computational systems would encompass implementations like Longuet-Higgins and Steedman (1971), which identify a passage’s key by matching its pitch classes to a diatonic set, as well as Quinn (2010) and White (2014), which match the interval structure of chord progressions to a scale-degree interpretation.(9) Similarly, key-profile analyses identify a passage’s tonal orientation by matching its pitch-class distribution to the ideal distribution of some key: this sort of modeling has been shown to output analyses that conform to human assessments (Temperley 2007, Temperley and Marvin 2008, Albrecht and Shanahan 2013) and has also been shown to predict human behavior in lab settings (Aarden 2003, Albrecht and Huron 2014).(10) Music-cognition work has also investigated the tonal implications of a passage’s interval content, focusing on how certain intervals (like the diminished fifth) draw listeners to particular key centers (Brown and Butler 1981, Brown, Butler, and Jones 1994, Matsunaga and Abe 2005 and 2012).(11)
[3.3] On the other hand, feedback systems are also represented in music research. Consider Lerdahl and Jackendoff’s (1983) intertwined metric and prolongational preference rules or Long’s (2018) argument that early tonal practices arose as a braid of interlocking metrical, poetic, and cadential expectations: these authors describe a feedback loop between metric emphases and tonal expectations, each domain informing and reinforcing the other.(12) Similarly, when Castile-Blaze (1810) or Agmon (1995) theorize tonal music as being traceable to the I, IV, and V chords, they are claiming that the presence of those chord prototypes express the corresponding key while concurrently claiming that a tonal orientation produces those chords. When Schoenberg (1978) locates a passage’s key using his relationships between chord roots,(13) when Riemann (1893), Louis and Thuille (1907), Straus (1987), Dahlhaus (1990), or Harrison (1994) describe key as something expressed through the progression of harmonic functions, or when Gjerdingen (2007) or Byros (2009, 2012) identify a passage’s key using a voice-leading schema, they are each engaging in harmonic-progression feedback systems.(14) In each of these theories, tonal orientation arises from a surface being organized into some series of structures with the key also informing how a passage organizes into chords and harmonic functions or which notes are chosen to participate in a voice-leading schema.(15) This kind of logic also enters into music pedagogy: for instance, students are often counseled to identify modulations using chord progressions (e.g., Piston 1941, Laitz 2008) or cadences (Clendinning and Marvin 2011).(16)
[3.4] Research in music informatics has relied on feedback mechanisms to determine key for some years. From a computational perspective, feedback systems would include models like Winograd (1968), Pardo and Birmingham (1999), Pachet (2000), Barthelemy and Bonardi (2001), Rohrmeier (2007), Illescas, Rizo, and Iñesta (2007), Quick (2014), and White (2015). Each of these authors relies on various organizational techniques—including metric emphasis, chord grammars, or chord progressions—to determine a passage’s key.(17) Of particular interest are Raphael and Stoddard (2004), who use harmonic functions to assist in key finding, and Stoddard, Raphael, and Utgoff (2004), as they convert MIDI integer notation to letter/accidental notation using key finding and modulation metrics: in both these instances, an organizing feature helps determine the key, while the key helps determine that organizing feature.(18) Similarly, Temperley (1997) ascertains a passage’s key using the chord-root patterns of a passage: he almost explicitly states the feedback nature of the task when he writes that his “analysis can be broken down into two problems: root finding and key finding,” (34) with both informing the other.(19) (Craig Sapp has summarized many of these key-finding topics in his 2011 dissertation, detailing various available approaches to key finding and how they interact with music theoretic concepts of modulation, circle-of-fifths distance, and harmonic analysis.)(20)
[3.5] These theoretical, pedagogical, and computational systems have been much less consistently connected to experimental testing in music cognition than have feedforward systems. A handful of studies address the interconnection of meter and key (Prince, Thompson, and Schmuckler 2009; Prince and Schmuckler 2014), and many studies address the role that harmony plays in tonal orientation (Thompson and Cuddy 1989, Thompson and Cuddy 1992, Trainor and Trehub 1994, Povel and Jansen 2002) as well as the role that tonal orientation plays in the stability of or distance between harmonies (Krumhansl, Bharucha, and Castellano 1982; Tillmann et al. 2003).(21) Some neural network modeling has even been done to account for these interlocking behavioral data (Tillmann, Bharucha, and Bigand 2001).
[3.6] These studies, however, generally focus on the role tonal orientation plays in how listeners interpret an already-assumed tertian harmonic structure, or how that harmonic structure affects the perception of key. What remains untested is how the actual organization of pitches into chords—the act of dividing the eighth notes of Example 1 or parsing the dissonances and consonances of Example 2—influences and is influenced by a passage’s tonal orientation.(22) In other words, while theoretical, computational, and pedagogical research has relied on feedback logics to relate harmonic organization and musical key, this relationship has been addressed implicitly, intermittently, and piecemeal in behavioral research.(23)
[3.7] In what follows, I implement a key-finding model based on some of my previous work—the method used to analyze Example 2 (White 2015)—that incorporates the key and harmony analysis tasks, adding a feedback system between those two domains. Having created this feedback system, I will show that such a model can be validated against human behavior by testing whether the model’s output conforms to theorists’ intuitions about tonal harmony and by comparing the model’s output both to human behaviors and to the outputs of representative feedforward tonal models.(24)
Part IV: A Model of Tonal Orientation Using Feedback Between Key and Chord Progressions
Example 4. A feedback loop between key and chord grouping
(click to enlarge)
[4.1] Example 4 schematizes a feedback loop between key finding and chord identification in terms of Example 1b, framing the chord identification task as grouping surface pcs into sets, and the key-finding task as identifying the optimal tonal orientation of those sets.
[4.2] Let us first assume “key” to be a particular transposition operation that maps some group of pitch classes onto what we will call mod-12 “scale degrees.” Let us assume a scale-degree (sd) set to be formed comparably to pc sets, but with 0 designating the tonic scale degree and with the integers mod-12 representing the chromatic distance from the tonic (such that 2 would be the supertonic degree, 7 would be the dominant degree, 11 the leading tone, and so on). (25) The key operation then transposes the tonic pc to zero, and transposes the remaining pcs by that same distance. Consider a D-major triad followed by a B-minor triad, or the normal-form pc sets <2, 6, 9> and <11, 2, 6>; interpreting the progression in D major (as a I–vi progression) would orient pc 2 with the tonic (mod-12) scale degree, or sd 0. Mapping the pc set <2, 6, 9> onto sd set <0, 4, 7> would involve subtracting the tonic degree from the pc set, a T−2 (or T10) operation. Equation 1 generalizes this assumption: observed pcs o at timepoint j in a succession of length n are transposed by some key k in modulo 12 space.
Equation 1: \[ \hat{k}_j = \text{argmax}_k(P ([o_{j-n} - k ]_{\bmod 12}, \ldots [o_j -k]_{\bmod 12}) ) \\ k \in |0 \ldots 11| \]
[4.3] The equation also states that the ideal key maximizes (argmax) the probability P of some series of solutions (again, see Temperley 2007 for more on musical probabilities). While these probabilities could in principle be defined in any number of ways, I use probabilistic Markov chains (also used in Pearce and Wiggins 2004, Quinn 2010, and White 2014; these are also called n-grams since an event’s probability is contingent on n preceding events). Equation 2 formalizes this, stating that the probability of a chord s at timepoint j is contingent upon n previous chords.
Equation 2: \[ P(s_j) = P(s_j) | P\big(s\,^{j-n}_{j-1}\big) \]
[4.4] We might intuitively connect Equation 1 to this Markov chain by treating a tonally oriented observation (\(o_{j-k}\)) as a member \(s_j\) in the chain, with the best key k at timepoint j being that which transposes Equation 1’s series of observations (\(o_{j-n} \ldots o_j\)) to the most probable series of chords (\(s_{j-n} \ldots s_j\)). (NB: the relationship between s and o will be more thoroughly formalized below). Example 5 shows a chordal syntax based on Kostka and Payne (2012) that we can treat as a toy 2-chord (or, 2-gram) probabilistic Markov chain. In the example’s toy system, we can imagine that any chord progression is possible, but the diagram’s arrows show only the most expected—the most probable—chord progressions.(26) Example 6 reproduces the music of Example 1 with pitch-class sets now grouped into beats (i.e., half-note durations) and using letter names for ease of reading.(27) We can apply Example 5’s toy syntax to Equations 1 and 2 to analyze the music of Example 3. The different scale-degree interpretations of the constituent sets would return varying levels of probability, and several such interpretations are shown below the example (using Roman numerals instead of scale-degree sets). While the first passage could be analyzed as I–vi–ii–V7, V–iii–vi–V7/V, or even IV–ii–v–I7 or
Example 5. A hypothetical toy chord-progression model, with arrows representing the most probable between-chord successions (click to enlarge) | Example 6. A probabilistic analysis of Mozart K. 284, iii, mm. 1–8, using the syntax of Example 5 (click to enlarge) |
[4.5] Note, however, that several of the “chords” identified ignore some subset of the observed pitches. Both dotted boxes include the pcs {
[4.6] What unites these theories is that there exists some set of harmonic prototypes into which surface pitches organize themselves, promoting those pitches that conform to the prototypes, excluding those pitches that do not conform (e.g., the act of excluding surfaces dissonances), and even changing or projecting notes not actually present on the surface (e.g., recognizing a chord without a fifth as representing a triad, or reading a ii chord as substituting for a IV chord). I adopt some of my previous work in White 2013b to formalize this relationship between surface and prototype, a relationship shown in Equation 3. The algorithm acts upon a series of scale-degree sets D with time points 1 to n such that \(D = (d_1, d_2, \ldots d_n)\), reducing them to other scale-degree sets s such that \(S = (s_1, s_2, \ldots s_n)\) and \(|s_i \cap o_i| > 1\) where the cardinality of the intersection between each d and its corresponding s is at least 1 (i.e., they share at least one scale-degree). The equation then produces a “translated” chord \(\hat{s}\) given the context \(\gamma\) and the proximity of the two sets \(\pi\). Here, \(P(s_i|\gamma(d_i))\) is the probability that a given s would occur in the context \(\gamma\) in which we observe the corresponding d. The maximized argument now optimally groups the observed scale degrees of series D. At each point j the set d includes all previous observed sets: the equation therefore determines how large a window results in the optimal vocabulary item.
Equation 3: Grouping a surface \[ \hat{s} = \text{argmax}_j\ P (s_j|\gamma(d_j))\ \pi (s_j, d_j ) \\ d_j = d_{j-1} \cup d_j \\ j \in |0 \ldots n | \]
[4.7] So defined, connecting key and chord into a Markov chain entails a feedback system. Knowing the ideal parsing of the musical surface (Equation 3) is contingent on knowing the ideal key (Equation 1); but, the reverse is also true: knowing the key is contingent upon knowing the ideal parsing of the musical surface. I show this interconnection in Equation 4, with the scale degree sets \(d_j\) now replaced with the tonally-oriented sets \([o_j-k]\), and the probabilistic relationship \(\gamma\) is now replaced with Equation 2’s Markov-chain probabilities (again, my implementation uses 2-grams, or n=1). Additionally, \(\pi\) will correspond to the amount of overlap (or intersection cardinality) between the two sets. Here, the best scale-degree set not only maximizes the key k but also maximizes the grouping at timepoint j. For the vocabulary of chords S, I adopt the machine-learned tertian (probabilistic) syntax developed in previous work (White 2013b): the constituent chords are I, i, V, V7, IV, iv, ii, ii7, ii°, iiø7, vi, vi7, iii,
Equation 4: An integration of two parameters \[ \hat{s} = \text{argmax}_{k,j}\ P \Big( P(s_j) | P \big( s^{j-n}_{j-n} \big) \Big) \ \pi(s_j, [o_j - k]) \\ o_j = o_{j-1} \cup o_j \\ j \in |0 \ldots n| \\ k \in |0 \ldots 11| \\ \pi( \hat{s},[o_j -k] )\ \propto\ |\hat{s} \cap [o_j - k ]| \]
[4.8] To maximize multiple parameters in tandem, I implement a feedback loop using the Maximum Product Algorithm (or Viterbi Algorithm). Considering all possible chord interpretations and key orientations at each timepoint would be intractable, as the possibilities exponentially increase at each timepoint. This integration therefore uses a process borrowed from language processing, the Viterbi algorithm (Viterbi 1967, Jurafsky and Martin 2000). In my adaptation of the algorithm, at each point the possible chord parsings and key solutions are arrayed within a table, and the algorithm navigates through the possible options to produce the ideal solution that maximizes all parameters. As formalized in Pseudocode 1, the algorithm divides the surface into scale-degree sets and returns at each timepoint t and for each key k the best vocabulary item—or “chord” s—to underlay that moment. The overall probability is calculated by combining the probability \(\pi\) of the vocabulary item \(s_t\) given the surface pitch classes \(o_t\), and the probability of the previous item \(s_{t-1}\) transitions into the current item \(s_t\) according to the transition matrix A. Instead of calculating the probability of each possible path through the interpretations, the algorithm only uses the probability of only the most probable pathway so far for each key at each increasing timepoint such that there are only K number of previous pathways at any point in time.(30) The analyses of Example 3, then, are the result of navigating the interrelationships of Equations 1–4 using the product maximization feedback system.
Pseudocode 1: The product maximization process
- Input
- A series of observed pc sets \(O = (o_1, o_2, \ldots o_n) \).
- A vocabulary of scale-degree sets \(S = \{s_1, s_2, \ldots s_L\}\).
- A transition matrix \(A\) of size \(L \cdot L\) defining the transition probabilities between each \(s\) in \(S\). (\(A_{s_{t-1}s_t}\) therefore defines the probability of transition between two scale-degree sets at adjacent timepoints.)
- A series of probabilistic relationships \(\Pi\) defining mappings between each \(o\) in \(O\) and each \(s\) in \(S\). (\(\Pi_{o_ts_t}\) therefore defines a probabilistic mapping between a pc set and a scale-degree set at timepoint \(t\).)
- A number of keys \(K\).
- Process
- Construct two 2-dimensional tables \(T_1\) and \(T_2\) of size \(T \times K\)
with coordinates of timepoints \(t\) and keys \(k\), such that:
- \(T_1[t,k]\) stores the probability of the most likely path so far at timepoint \(t\) in key \(k\)
- \(T_2[t,k]\) stores the scale-degree set \(x_{t-1}\) resulting from the most likely path so far at timepoint \(t\) in key \(k\)
- Table entries are filled in increasing order at each \(t\) in \(T\) such that:
- \(T_1[t,k] = \text{max}_s\ T_1[t,k] \times A_{x_{t-1}x_t} \times \Pi_{o_tx_t}\)
- \(T_2[t,k] = \text{argmax}_s\ T_1[t-1, k] \times A_{x_{t-1}s_t} \times \Pi_{o_ts_t}\)
- Construct two 2-dimensional tables \(T_1\) and \(T_2\) of size \(T \times K\)
with coordinates of timepoints \(t\) and keys \(k\), such that:
- Output
- A path \(X = (x_1, x_2, \ldots x_T)\) which is a sequence of scale-degree sets such that \(x_n \in S\) that traces the cells of \(T_2\) that correspond to the maximization sequence of \(T_1\).
Part V: Validating the Feedback Model
[5.1] Having computationally defined a feedback system of musical key, I now present studies that test its connections to established music theories, to the behavior and intuition of musicians, and even to the music theory classroom. These tests will begin to offer a richer picture of how such a feedback system behaves, how it compares to feedforward systems, and how the viewpoints of the various domains of music scholarship (theory, computation, cognition, and pedagogy) might interact with this model. In other words, I address the deficiency in the research surrounding feedback models of musical key by testing a “proof of concept” model, a model that shows that feedback logics can represent musical behavior, imitate pedagogical practice, and conform to the published theories of tonal practice.
[5.2] The next several sections therefore divide the feedback model’s processes into its constituent components: key finding, chord grouping, and its resulting analysis. Test 1 first observes whether this model assigns key to musical passages with accuracy comparable to other key-finding models, testing its computational validity. Test 2 then observes whether the model groups chords in ways comparable to existing models of tonal harmony, testing its relationship to music theory. Test 3 and Test 4 then determine whether the model analyzes music similarly to undergraduates, testing its ability to mimic and predict human behavior. Overall, these tests will give a multifaceted view on the characteristics, strengths, and weaknesses of this feedback model of key finding.(31) (All computation was implemented in the Python language using the music21 software package, as described in Cuthbert and Ariza 2011).
[5.3] Test 1: Comparing the performance of different key-finding models. In order to compare how well different key-finding models performed, I used the MIDI files of the Kostka-Payne corpus (Temperley 2009a), analyzed their openings with three different feedforward (key-profile) models as well as the current study’s feedback model, and compared their results with the keys identified in the textbook’s analyses. Forty-one of the corpus’s MIDI files were used, spanning the Baroque to the Romantic eras.(32)
[5.4] Three key profiles were used as the feedforward models, and were drawn from music21’s library of key-finding functions: the Krumhansl-Schmuckler (Krumhansl 1990), the Temperley-Kostka-Payne (Temperley 2007), and Bellman-Budge (Bellman 2005) weightings. Various window lengths were attempted for these analyses, and it was found that using the first 6 offsets of each piece produced the highest consistent results. (A similar test of only key-profile methods was run in Albrecht and Shanahan (2013); the test produced different rates of success than those reported here. While our different implementations do result in different values, the models’ relative performances basically track one another; however, it should be noted these authors’ reported higher success rates than those reported below and comparable to those values associated with my feedback approach.)
[5.5] For analysis using the feedback system, the first 20 salami slices (verticalities at which at least one pc is added or subtracted from the texture) of each file were analyzed, and the tonic associated with the most probable scale-degree interpretation was recorded. (33)
Example 7. The percentage of key assessments on the Kostka-Payne corpus that agreed with the instructor’s edition, divided by model
(click to enlarge)
[5.6] As shown in Example 7, of the 41 pieces analyzed, the chord-progression model assigned the same tonic triad as the textbook 87.8% of the time. Of the 5 that did not overlap, twice the model judged the key to be the passage’s relative major, twice the keys differed by fifth, and once the passage was too scalar for the model to recognize the correct underlying chords. Example 7 also shows how often each key-profile model produced correct answers. The profiles of Krumhansl-Schmuckler, Temperley-Kostka-Payne, and Bellman-Budge produced rates of 78.0%, 85.4%, and 73.2% correct, respectively.
[5.7] As implemented here (and with the caveats regarding Albrecht and Shanahan 2013), the feedback model performs similarly to, if not better than each of the other computational models. These results suggest that a feedback approach can find a passage’s key with accuracy comparable to established feedforward analyses. (And, given that the model is being tested against a textbook, this test begins to connect the computational side feedback systems to both the pedagogical and theoretical dimensions.) However, it remains to be seen whether the way in which the model understands chords and chord progressions resembles that of contemporary music-theory discourse and pedagogy. The following test, then, compares the feedback model to other published models of tonal harmony, essentially testing whether this feedback system uses a harmonic syntax comparable to those used by professional music theorists.
[5.8] Test 2: Comparing the model to the Kostka-Payne corpus (and to other models). Test 2 asks whether the feedback model’s syntax overlaps with published models of harmonic syntax, thereby testing this feedback system’s relationship to models proposed within and used by music theorists. In particular, I investigate this by a) implementing five models based on other authors’ work that capture some aspects of harmonic syntax, b) implementing the above-described feedback model, and then c) using these six models to assess the probability of a corpus of human-made chord-progression analyses drawn from the Kostka-Payne textbook. I will quantify and compare these probabilities using cross entropy, a measurement of how well a model overlaps with the series of chords it is observing, a procedure I will describe below.
[5.9] Test 2: The Models – The five models include three Western European common-practice models and two models drawn from a decidedly different repertoire, American 20th-century popular music. Each model uses 2-chord probabilistic Markov chains. I name each model after the author(s) and source behind its dataset: the three common-practice models are the Tymoczko-Bach, the Quinn-YCAC, and the Temperley-Kostka-Payne; the popular music models are the deClercq-Temperley and the McGill-Billboard. The Tymoczko-Bach corpus comprises the datasets reported in Tymoczko (2011): this source uses hand-analyzed Bach chorales and tallies how frequently each diatonic Roman numeral moves to each other. This model’s vocabulary includes triads on the standard major scale degrees with the addition of those on the minor third and minor sixth scale degrees as well, producing a total of nine chords.(34) (I use the word vocabulary here to mean the universe of possible chords within a system.) The 2-gram (i.e., Markov chains of 2-chord progressions) transitions of the Temperley-Kostka-Payne corpus are those reported in Temperley (2009a) and are drawn from the harmonic analyses within the instructor’s edition to the Kostka-Payne harmony textbook. This corpus involves only root information and the mode of the excerpt, totaling 919 annotations. (Here, V7, V, and v would all be represented as ^5, conflating chords that are distinguished in several of the other models.(35)) The Quinn-YCAC, the largest corpus used here, is comprised of transitions between each chord in the YCAC (White and Quinn 2016b). (The “chords” here consist of this corpus’s salami slices, those verticalities arising each time a pitch is added or subtracted from the texture.)(36) The deClercq-Temperley model uses the same annotations as the Kostka-Payne corpus (chord roots without modal or figure designations) but is drawn from a corpus of popular music (deClercq and Temperley 2011). Finally, the McGill-Billboard corpus uses key-centered leadsheet notations, thereby introducing seventh chords, incomplete chords, and dissonances into its vocabulary (Burgoyne, Wild, and Fujinaga 2011). Its vocabulary includes 638 distinct chords.(37) The same model was used as in the previous test: I will refer to it here as the “Feedback YCAC” model.
[5.10] Test 2: Cross entropy – As in the previous test, the Kostka-Payne harmony textbook was used as a ground truth; the Temperley-Kostka-Payne corpus was therefore used as a baseline from which to compare other models. To make these comparisons, I used several measurements involving the cross entropy resulting from each model assessing this corpus, a measurement that shows how different two models are (Temperley 2007): the higher the cross entropy, the more “surprised” a model is by what it is observing. In other words, models that returned lower cross entropies would better conform to this (literally) textbook model of harmony.(38)
[5.11] Equation 6 shows the formula for calculating average cross entropy. With a probabilistic model m assessing some set of events O, cross entropy H represents how well m predicts O, with m assessing the probability of each o in O, or \(m(o)\). In our tests, O is the series of chord progressions being analyzed, and m is one of the 2-gram chord-progression models. Conforming to the norms of information theory, the value’s base-2 logarithm is used.(39) These logarithms are averaged over the series of length n, and the negative sign transforms the negative logarithm into a positive value (Temperley 2010).
Equation 6: Cross Entropy \[ H_m(O) = -\frac{1}{n}\, \log_2\big(m (o_1, o_2, \ldots o_n ) \big) \]
[5.12] However, the varying sizes and components of each model’s harmonic vocabulary make a single cross entropy measurement insufficient—trying to compare apples to oranges requires multifaceted descriptors. Therefore, two differently-executed cross entropy measurements were taken, along with two additional supplemental values. These two approaches represent different ways of dealing with zero-probability events, or progressions that are in the Temperley-Kostka-Payne corpus (the progressions being observed, O) but not present in one of the models (or, m).(40) The first solution uses what informatics researchers call “smoothing”: the with-smoothing cross entropy measurement ascribes a very low probability (but not zero!) to all such zero-probability events.(41) These smoothed non-zero probabilities will penalize the model if it has less overlap with its observed chord progressions, yielding a higher cross entropy (or, more “surprise”). The second without smoothing cross entropy measurement ignores those 2-grams that the model has never seen before, passing over them as its probability assessments are made. This approach captures how well each model performs when its vocabulary and 2-grams overlap with those of the Kostka-Payne observations; however, if a model overlaps with the observed chord progressions only during high probability events, the cross entropy will be relatively low (i.e., low “surprise”) even though the process ignores most of the observed sequence. Therefore, to observe the amount of overlap between corpora, the percentage of the Kostka-Payne 2-grams excluded in the without-smoothing measurement was calculated as the exclusion rate. Finally, the size of each model’s chord vocabulary was also represented.(42)
[5.13] As a baseline, the Kostka-Payne model assessed itself as well. Using a corpus’s statistics to assess its own data is not strictly a cross-entropy measurement, but rather a measurement that captures the corpus’s overall complexity—a more complex system will have more trouble predicting itself than will a simple system. This self-assessment will then let us ask how much better or worse other models predict the Kostka-Payne corpus versus the corpus’s own predictions of itself.
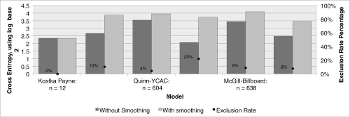
Example 8. Cross entropy results for each corpus-based model
(click to enlarge)
[5.14] Test 2: Comparing the Various Chord-Progressions Models. Example 8 shows cross-entropy quantities for the six models used to assess the Kostka-Payne 2-grams, allowing for one to see whether, in fact, the feedback model creates chord progressions that have a relationship to the Kostka-Payne textbook comparable to other tonal models. The first group of bars shows the Kostka-Payne corpus predicting itself, returning both cross entropies of 2.4. Since the model and the observations are identical, the observations would never present the model with “impossible” 2-grams: therefore, 100% of the corpus is used in the first cross-entropy value (yielding a 0% exclusion rate), and since no smoothing is necessary, the second value is identical.
[5.15] The Quinn-YCAC model provides the lowest percentage of exclusion: only 4% of the Kostka-Payne 2-grams are not present in its model. This low exclusion is not surprising, given that the model has such a large vocabulary of salami slices. The model’s size also can account for its relatively high unsmoothed and smoothed cross entropies, 3.4 and 4.0, respectively: with its probability mass divided among its large vocabulary of slices, the probabilities it assesses will be relatively low. In contrast, the Tymoczko-Bach model produces a high exclusion rate and considerably different smoothed and unsmoothed cross entropies due to the size of the model. Since it uses only diatonic triads, the model assesses diatonic progressions with high probabilities and excludes or smooths all chromatic progressions, yielding the low unsmoothed cross entropy (1.9) and high smoothed cross entropy (3.9).
[5.16] While using the same method of annotation as the observed corpus, the differences in pop/rock’s musical syntax caused the deClercq-Temperley model to perform somewhat poorly. Even though its unsmoothed cross entropy is relatively low, its smoothed cross entropy is relatively high due to the presence of root progressions in the Kostka-Payne corpus that never occur in the popular music corpus. For instance, chords with a root of
[5.17] These results show that cross-entropy values do benefit from using the same chord vocabulary (as in the deClercq-Temperley model) and from a small vocabulary (as in the Tymoczko-Bach model), and that exclusion rates benefit from a large vocabulary (as in the YCAC salami-slice and McGill-Billboard models). The Feedback-YCAC model produces results that somewhat balance these factors: even though it uses the same underlying dataset as does the salami-slice model, its cross-entropy rates approach the more-constrained Tymoczko model while sacrificing less exclusion.
[5.18] In sum, the feedback model seems to provide a sufficient method to organize a musical surface into chords that approximate the Kostka-Payne textbook with similar precision to other published models. Importantly these results do not argue that the feedback model ideally represents textbook models or even human intuition. However, there exists variation between how different theorists would define an ideal model (the difference between the Kostka-Payne and Tymoczko-Bach models evidence the potential variance between different human intuitions when creating hand-annotated corpora) and the feedback model seems to exist within this window and does so better than a simple surface model or models using a foreign syntax.
[5.19] The model therefore seems to use a harmonic system somewhat comparable to those used within this sample of music theory discourse, forging a stronger connection between the computational and the theoretical dimensions. To extend this theoretical connection and begin connecting the model to behavior, I now turn my attention to how well the model identifies chords, prolongations, and points of modulation. The following test therefore compares the output of the analytical model to Roman numeral analyses of the same excerpts produced by undergraduate music majors. In other words, I now test the model’s behavior against that of trained musicians in a pedagogical context.
[5.20] Test 3: Comparing against the performance of music majors. Of the Kostka-Payne excerpts whose key was successfully analyzed by the Feedback YCAC model in Test 1, 32 were chosen to be analyzed in depth by both humans and the feedback model. The examples were selected to control for the passages’ different characteristics, dividing into four groups with 8 examples in each group. Groups were labeled “Simple,” “Modulating,” “Chromatic,” and “Chromatic Modulating.” (I chose these categories in relation to their placement in the Kostka-Payne textbook and the type of analytical knowledge they seemed designed to teach or reinforce.)
[5.21] The model’s parameters were set as in Test 1, with several additions to allow for whole excerpts to be analyzed.(43) For the automated analysis, the algorithm was run using a moving window designed to provide the model with a consistent number of non-repeating chords. The window began with four chords, but if the feedback process reduced that span to fewer than 4 chords, the window was extended until the process produced a four-chord analysis.(44) The window then moved forward, progressing through the piece. I transcribed the results of this windowed analyses using a “voting” process. If three or more windows agreed on a scale-degree set at any given timepoint, the Roman numeral annotation of that set was placed in the score at the appropriate timepoint. Using this voting process allowed the model to read modulations: for instance, if three earlier timepoints read a C-major triad as I, and three later timepoints read it as IV, then both those Roman numerals were placed under that moment in the score. If there was no agreement, a question mark was placed in the score. Since the final windows in the piece would only produce one or two annotations, the automated annotations ended before the example’s final measure in several examples. If a series of chords was reduced to a single annotation, a line was used to indicate the prolongation of that single chord.
[5.22] The same 32 examples were analyzed by 32 undergraduates in their fourth and final semester of a music-theory sequence at the University of North Carolina at Greensboro’s School of Music, Theater and Dance. (Six subjects were drawn from my theory section, 26 were not.) Students were given 10 minutes to analyze their example and were asked to use Roman numerals without noting inversion. As in the algorithmic analyses, if the student could not make sense of a chord, they were instructed to place a question mark under that chord. In situations where the model’s moving window did not allow for the annotations to extend to the end of the excerpt, the unannotated music was covered in a grey box: just as in the automated analysis, the students could take the greyed music into consideration when making their analyses, but they were asked to not annotate this music. (The full instruction page, as well as all examples, can be found at http://chriswmwhite.com/mto-supplement.)
[5.23] Eight music-theory faculty (each from different institutions, all currently teaching a music theory or fundamentals class) were then asked to grade a randomly selected group of 8 analyses, not knowing which of the set was algorithmically or human generated. The theorists were asked to provide a grade from 0 to 10 for each example, indicating the level of expertise in Roman numeral analysis the annotations seem to convey (i.e., 0 = a student with no music theory experience, 10 = the expertise of a professional).
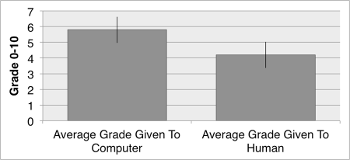
Example 9. Comparing graders’s assessments of both groups of analyses
(click to enlarge)
[5.24] Example 9 shows the average grades given to the computer model and to the human analyses.(45) The example includes error bars that indicate the window of statistical significance surrounding each result.(46) Note that these bars slightly overlap, indicating that while the averages are different, they are not quite significantly different(47)—while the computer was given consistently higher grades, the variation renders these grades statistically indistinguishable from those given to the human analyses.(48)
[5.25] These results indicate that the grades assigned by professional music theorists to the human and automated feedback-generated analyses were statistically similar, and that there was even a trend toward the computer performing slightly higher. Even though neither computer nor human perform with anywhere near an “expert” proficiency (in an ideal world, one would hope that both the computer and our undergraduates would perform somewhat better than these grades!), these results do suggest comparable behavior between humans and computer, as they perform within the same range on this task. (In terms of my earlier formulation, this test now connects the computational model not only to the theory and pedagogy of key, but also to behavioral evidence.) But this test does not quantify specific differences between the two groups of analyses: are the humans and computer making the same types of errors and achieving similar successes? To answer this, I ran a final test in which expert theorists were asked to distinguish between two analyses of the same example, one produced algorithmically and one produced by a human.
[5.26] Test 4: A musical Turing Test. In 1950, the “father of the computer” Alan Turing proposed a simple way to judge whether a machine’s behavior approximates that of a human. In what has become known as a “Turing Test,” humans engage in typed conversations in front of a screen, not knowing whether the other conversant was another human or a computer algorithm. If a critical mass of participants could not distinguish between the human and computer-generated conversations more than a certain percentage of the time, the computer program could be seen as approximating human behavior.(49)
[5.27] Musical Turing Tests have been a part of algorithmic musical creation for some time. Since much algorithmic composition is designed to “pass” for convincing musical utterances in the concert hall, work like Cope (1987, 2005) and Quick (2014) undertake implicit Turing Tests. However, explicit Turing Tests are frequently used by researchers and engineers whose aim is to create pleasing and human-like music, be it chord progressions (e.g., Burnett et al. 2012), folksong composition (Dahlig and Schaffrath 1998), vocal production (Georgaki and Kosteletos 2012) or even expressivity (Hiraga et al. 2004).(50) (For a thorough overview, see Ariza 2009.)
[5.28] In order to test how well this feedback model conformed to musical intuitions, I adapted this paradigm to involve the human and automated analyses of Test 3, now reordered into pairs. Each pair included the same excerpt analyzed twice, once by a human and once by the algorithm, with sequential and pairwise ordering randomized. Eight music theory faculty (again, each from different institutions, all currently teaching a music theory or fundamentals class, with two having participated in the earlier grading task) were presented with eight pairs of analyses. Each excerpt was assessed twice by different graders. The theorist’s task was to report which of the two they believed to be created by the computer and to provide a short, written explanation of their choice. If the sorts of analytical choices made by humans were different than the algorithm’s behaviors, the theorists would perform better than chance in their choices. (I have included the full packet of analysis pairs in the online supplement.)
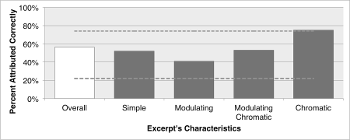
Example 10. Percent of participants who correctly distinguish the human/computer analysis
(click to enlarge)
[5.29] Example 10 shows the number of times the theorists correctly distinguished the feedback model’s analysis from the human’s analysis, first shown as an overall percentage (in white) and then grouped by the excerpt’s characteristic (in grey). The significance window now relies on a P(.5) binomial distribution, a method that tests whether the theorists performed better than a coin toss.(51) Overall, the theorists did not: of the 64 choices made by the graders, only 35 were correct. However, excerpts tagged with the “chromatic” characteristic were significantly distinguishable: of the 16 choices made by theorists, 75% (12) were correct, a sufficiently lopsided result to indicate the theorists were performing better than chance.(52)
Example 11. Human (left) and computer (right) analyses of mm. 29–37 of Brahms’ “Und gehst du über den Kirchhof” op. 44, no. 10
(click to enlarge)
[5.30] Recurrent observations within the attached comments suggest that the theorists used two strategies when producing a correct answer within the “chromatic” category: 1) noticing that the humans made “typically human” mistakes, and 2) noticing the computer model behaving in a distinctly mechanized way. Example 11 shows both behaviors in mm. 29–37 of Brahms’s “Und gehst du über den Kirchhof” op. 44 no. 10. The human analysis is on the left, and the computer model’s appears on the right. The theorist justifies their (correct) assessment by writing, “The (hypothesized) computer is a bit more systematic about which chords it chooses to analyze and which it chooses to omit. Also, the faulty analysis of the second half of m. 6 (implicitly identifying it with the first half of m. 7) seems like a more computer-style choice.” Another grader similarly writes about the human analyses, “the V7-of-vi is correct but it shows the vi in the wrong place, which looks like human error. In the [computer] one, the cadential \(\substack{6\\4}\) is misidentified as a iii chord, which looks like a mechanical error.” In these instances, the computer has misidentified the salient pitches (for instance, m. 6.2 shows a iii chord that extends into m. 7), while the human output contains more inconsistencies than one would expect in a mechanical algorithmic analysis.
[5.31] Overall, this test further refines the model’s connection to human behavior: while the algorithm often produced annotations that seemed very human-like, the feedback system’s mistakes involve identifying something a human would not while the humans misidentify something a computer would not. This is not surprising, given that “chromatic” exercises are designed to test a student’s ability to parse complicated music replete with applied chords and chromatic embellishments. This music, then, seems to provide more opportunities for these cases to happen: this music creates more occasions for humans to make “human-like” inconsistencies while presenting more possible chord choices for the computer, increasing its chances to choose an unintuitive pitch set from the texture.
Part VI: An Argument for a Feedback Approach to Tonal Modeling
[6.1] These tests indicate that a model that integrates chord formation and key finding into a feedback system seems, in many ways, to conform to music theories, pedagogical systems, and to human behavior and expectations and performs comparably to feedforward methods. This work formalizes a proof-of-concept model of key finding that integrates the tasks of harmonic and key analysis into a feedback loop. In sum, it potentially legitimizes the feedback systems used in music theory, computation, and pedagogy as cognitive and behavioral models.
[6.2] There are four important outcomes of this work: first, it shows that a feedback system can analyze music in ways that conform to human behavior; second, it adds a formal specificity to connections between harmony and key, theorizing the gears and sprockets that possibly underlie some fundamental aspects of feedback-based notions of key. Third, it proposes some pedagogical strategies to teaching key and harmony in the music theory classroom. Finally, it suggests some broader ideas about tonality and what it means to be “in a key.”
[6.3] To the first: these results constitute a proof of concept that organizing a surface into harmonies can be integrated into a feedback loop with key finding, and this feedback model can produce analyses that seem to align with human behavior and with other established tonal models. This is important, given that—to my knowledge—no such model has yet been tested against human behavior.
[6.4] To the second point: this work formalizes exactly how harmony and key might interact, and how a tonal center can arise from chordal analysis. Through its engineering, the model specifies 1) the structure of a chordal vocabulary and syntax that might underpin key finding, 2) the process by which a surface might conform to this vocabulary and syntax by editing the observed sets into subsets and supersets, and 3) the way these pc sets group together and transpose into the scale-degree sets that maximizes the conformance to the vocabulary and syntax.(53)
[6.5] Third, this feedback model suggests several specifics aspects of music pedagogy that might be informed by this work. While many of these insights are not unique to this work—indeed, many have been suggested in one way or another by several probabilistic/computational approaches to key finding (Temperley 2007 or Quinn 2010, for example), it is nevertheless worth making explicit the pedagogical payoffs of this type of work. I imagine these as four suggestions or tactics that might be helpful for students as they learn to identify key centers.
- There are potentially different ways keys can arise. This article has argued for a distinction between feedforward and feedback model, showing both to be potentially effective. Given the potential applicability of different models, a student may be well-served being open to more than one key-finding strategy.
- If key is not obvious, start analyzing some other parameter. In feedback systems, key arises alongside other organizational tactics. Therefore, analyzing various aspects of a passage—from the metric structure to the chord structure, from the melodic contour to the cadential articulations—can help clarify a passage’s tonal orientation
- Even if your first impression suggests one key, be open to revising this impression. As the model’s windowed analysis and “voting method” shows, various pieces of evidence can point to conflicting key centers in a passage. Just because there exists one piece of evidence for a key, does not mean further inspection might not reveal evidence for another key.
- Think in terms of probability, not rules. Regardless of the strategy used, determining a passage’s key is a matter of maximum probability, not of certainty. Much music can potentially be analyzed in more than one key, conforming in one domain or another to a suit of incompatible keys. The process of key finding does not determine which key is absolutely right to the complete exclusion of others, but which key describes events better than the others.
[6.6] Finally, the feedback process suggests a certain conception of what it means to be “in a key.” In these terms, “key” is then a relationship between scale-degree orientations and the ways in which we organize a musical surface—with harmony used here as the primary organization. “Key” is not a first principle, but rather a characteristic of the way a passage is organized. From this perspective, my model’s relationship to other tonal parameters is dramatically different from a feedforward one: a key-profile model, for instance, would require some additional post-hoc procedure to accomplish the harmony-identification tasks of Experiments 3 and 4 whereas my model integrates harmony and key as equal partners in a holistic process of tonal analysis. This idea is especially evident in the different ways feedforward and feedback methods approach tonal ambiguity. When a feedforward method finds contradictory or insufficient information to yield a single key with some degree of confidence, that has a unidirectional effect on other musical parameters: not knowing the key means that you might not know the passage’s harmonies, cadence points, etc. Feedback methods make ambiguity a more dynamic process. Consider again the Grieg excerpt of Example 2. In a feedforward analysis, you might not know which notes are dissonances and which are consonances because you don’t know what the tonal center is. In contrast, in a feedback analysis, the tonal ambiguity also results in ambiguous consonance/dissonance relationships, but not knowing which notes are consonant and which are dissonant is itself the cause of the tonal ambiguity. Allowing feedback systems into our understanding of key allows for this dynamism in tonally ambiguous passages.
[6.7] And while I initially professed to not be interested in notions of Tonality writ large, we might momentarily relax that caveat to reflect on how feedback tonal logics interact with such broader ideas. In particular, in a feedback model, a key’s transposition of pitch classes into scale degrees is part of the larger process of cognizing and interpreting a variety of musical domains. This type of feedback system, then, allows key to be an active participant in the complexities of a theory of tonality, be it a theory of harmonic function, tonal prolongation, voice-leading prototypes, etc. Unlike feedforward models, key is not a backdrop to support other musical processes, but rather is an actor integrated into a larger tonal system. Feedback modeling, then, allows for more complex notions of tonal organization—and broader definitions of Tonality—to incorporate key-finding into their logic.(54)
[6.8] Importantly, I am not advocating for the overthrow of feedforward modeling: different definitions of, and approaches to, key and tonality call for different models of those concepts.(55) Clearly, there are different ways of knowing a passage’s key, and these approaches become even more divergent when considering the chasm between visual analysis/aural experiences (and as an extension, immediate/reflective hearings of tonal centers). That is, a situation in which “key” means looking at key signature would be poorly described by a feedback model, while the tonal implications of hearing harmonic functions would be underserved by a feedforward system. Rather than taking an exclusive stance on definitions of key, I would advocate for an ecumenism, holding multiple definitions simultaneously with different models thriving and faltering in different situations. For instance, a chord-based feedback model loses its power in scalar passages and in monophonic music, while sparser polyphonic passages would be better explained by a feedback system that considers a passage’s harmonic syntax. Indeed, feedback models represent the same musical information as feedforward methods, but with the latter being a simpler representation of the former phenomenon; and, by simplifying its representation, feedforward models can be more flexible. While this study’s feedback model seems to identify the key of chordal passages with a relatively high accuracy, a feedforward method like that of key-profile analysis could judge the key of any texture, be it scalar, chordal, monophonic, or polyphonic. A richer cognitive model of key finding could therefore potentially modulate between different modes of analysis, given the situation, using more complicated models when possible and using simpler and more generalizable models when needed.
[6.9] Computationally, psychologically, and intuitively, the feedback method presented here has much room for improvement: taking into consideration texture, bass pitch classes, inversion, and phrase position would all likely add accuracy to such a model. Indeed, given the fact that integrating harmony potentially adds musical validity (and even perhaps accuracy) to a tonal model, it would stand to reason that integrating other domains would improve the model even more. Furthermore, modal distinctions have been ignored within this work: key-profile analyses—my frequent proxy for feedforward modeling—distinguish between mode, while my feedback model does not. There are larger issues behind this difference. Are there indeed two distinct modes that contain different vocabularies and syntaxes, or is there one “tonal syntax” that unites the two modes? These questions lie outside the bounds of this essay.
[6.10] However, even with these caveats and shortfalls, the method is surprisingly successful, especially given its departure from the fundamental mechanisms of other previously tested computational systems. Empirically based speculative models such as the one presented here suggest new hypotheses, plausible explanations, and directions for future experimental research.
[6.11] These observations are also preliminary and speculative. This model of tonal cognition seems to adhere to many behavioral aspects of the key-finding task, but the cognitive validity of much of its engineering remains to be tested. After all, the value of computational work to music research is not only to model what is already known about some cognitive or theoretical process, but to model what might be true given what we know about that process.
Christopher Wm. White
The University of Massachusetts, Amherst
Department of Music and Dance
273 Fine Arts Center East
151 Presidents Dr., Ofc. 1
Amherst, MA 01003-9330
cwmwhite@umass.edu
Works Cited
Aarden, Bret. J. 2003. “Dynamic Melodic Expectancy.” Ph.D. diss., Ohio State University. http://etd.ohiolink.edu/.
Agmon, Eytan. 1995. “Functional Harmony Revisited: A Prototype-Theoretic Approach.” Music Theory Spectrum 17 (2): 196–214.
Albrecht, Joshua, and David Huron. 2014. “A Statistical Approach to Tracing the Historical Development of Major and Minor Pitch Distributions, 1400-1750.” Music Perception 31 (3): 223-243.
Albrecht, Joshua, and Daniel Shanahan. 2013. “The Use of Large Corpora to Train a New Type of Key-Finding Algorithm: An Improved Treatment of the Minor Mode.” Music Perception 31 (1): 59-67.
d’Alembert, Jean le Rond. 1752. Elémens de musique théorique et pratique suivant les principes de M. Rameau. Durand.
Alphonce, Bo H. 1980. “Music Analysis by Computer: A Field for Theory Formation.” Computer Music Journal 4 (2): 26–35.
Ariza, Christopher. 2009. “The Interrogator as Critic: The Turing Test and the Evaluation of Generative Music Systems.” Computer Music Journal 33 (2): 48-70.
Barthelemy, Jérome, and Alain Bonardi. 2001. “Figured Bass and Tonality Recognition.” Proceedings of the Second International Conference on Music Information Retrieval. University of Indiana: 129–136.
Barral, Jérémie, and Pascal Martin. 2012. “Phantom Tones and Suppressive Masking by Active Nonlinear Oscillation of the Hair-Cell Bundle.” Proceedings of the National Academy of Sciences 109 (21): 1344-1351.
Bellman, Héctor. 2005. “About the Determination of the Key of a Musical Excerpt.” Proceedings of Computer Music Modeling and Retrieval. Springer: 187–203.
Bharucha, Jamshed. J. 1987. “Music Cognition and Perceptual Facilitation: A Connectionist Frame-Work.” Music Perception 5: 1–30.
—————. 1991. “Pitch, Harmony and Neural Nets: A Psychological Perspective.” In Music and Connectionism, ed. by P. M. Todd and D. G. Loy. MIT Press.
Boulanger-Lewandowski, Nicolas, Yoshua Bengio, and Pascal Vincent. 2013. “Audio Chord Recognition with Recurrent Neural Networks.” Proceedings of the International Society for Music Information Retrieval, Curitiba, Brazil: 335–340.
Brown, Helen, and David Butler. 1981. “Diatonic Trichords as Minimal Tonal Cue Cells,” In Theory Only 5 (6-7): 37–55.
Brown, Helen, David Butler, and Mari Riess Jones. 1994. “Musical and Temporal Influences on Key Discovery.” Music Perception 11: 371-407.
Burgoyne, John Ashley. 2012. “Stochastic Processes and Database-Driven Musicology.” Ph.D. diss., McGill University.
Burgoyne, John Ashley, Jonathan Wild, and Ichiro Fujinaga. 2011. “An Expert Ground-Truth Set for Audio Chord Recognition and Music Analysis.” Proceedings of the 12th International Society for Music Information Retrieval Conference, Miami: 633-638.
Burnett Adam, Evon Khor, Philippe Pasquier, and Arne Eigenfeldt. 2012. “Validation of Harmonic Progression Generator Using Classical Music,” Proceedings of the 2012 International Conference on Computational Creativity, Dublin: 126–133.
Byros, Vasili. 2009. “Foundations of Tonality as Situated Cognition, 1730–1830: An Enquiry into the Culture and Cognition of Eighteenth-Century Tonality, with Beethoven’s “Eroica” Symphony as a Case Study.” Ph.D. diss., Yale University.
—————. 2012. “Meyer’s Anvil: Revisiting the Schema Concept.” Music Analysis, 31 (3): 273-346.
Cancino-Chacon, Carlos, Maarten Grachten, and Kat Agres. 2017. “From Bach to Beatles: the Simulation of Tonal Expectation Using Ecologically-Trained Predictive Models.” Proceedings of the International Society for Music Information Retrieval, Suzhou, China: 494-501.
Castellano, Mary A., Jamshed J. Bharucha, and Carol Krumhansl. 1984. “Tonal Hierarchies in the Music of North India.” Journal of Experimental Psychology: General, 113 (3): 394-412.
Castil-Blaze, François-Henri-Joseph. 1810. Dictionnaire de Musique Moderne. Au magasin de musique de la Lyre modern.
Clendinning, Jane P., and Elizabeth. W. Marvin. 2011. The Musician's Guide to Theory and Analysis, (Second Edition). W.W. Norton.
Colombo, Florian, Samuel P. Muscinelli, Alexander Seeholzer, Johanni Brea, Wulfram Gerstner. 2016. “Algorithmic Composition of Melodies with Deep Recurrent Neural Networks.” In Proceedings of the First Conference on Computer Simulation of Musical Creativity. Huddersfield, UK. https://csmc2016.wordpress.com/proceedings/
Cope, David. 1987. “Experiments in Music Intelligence.” In Proceedings of the 1987 Computer Music Conference. San Francisco: Computer Music Association, 170–73.
—————. 2005. Computer Models of Musical Creativity. MIT Press.
Creel, Sarah C., and Elissa L. Newport. 2002. “Tonal Profiles of Artificial Scales: Implications for Music Learning.” In C. Stevens, D. Burnham, G. McPherson, E. Schubert, and J. Renwick (Eds.), Proceedings of the 7th International Conference on Music Perception and Cognition, Sydney: 281-284.
Creel, Sarah C., Elissa L. Newport, and Richard N. Aslin. 2004. “Distant Melodies: Statistical Learning of Nonadjacent Dependencies in Tone Sequences.” Journal of Experimental Psychology: Learning, Memory, and Cognition, 30: 1119 –1130.
Thompson, William F., and Lola L. Cuddy. 1992. “Perceived Key Movement in Four-Voice Harmony and Single Voices.” Music Perception 9: 427–438.
Cuthbert, Michael, and Christopher Ariza. 2011. “Music21: A Toolkit for Computer–Aided Musicology and Symbolic Music Data,” Proceedings of the International Symposium on Music Information Retrieval: 637–42.
Dahlhaus, Carl. 1990. Studies on the Origin of Harmonic Tonality. Trans. by Robert O. Gjerdingen. Princeton University Press.
Dahlig, Ewa, and Helmut Schaffrath. 1998 “Judgments of Human and Machine Authorship in Real and Artificial Folksongs,” Computing in Musicology 11 (1998): 211-218.
deClercq, Trevor. 2016. “Big Data, Big Questions: A Closer Look at the Yale– Classical Archives Corpus.” Empirical Musicology Review 11 (1): 59-67.
deClercq, Trevor, and David Temperley. 2011. “A Corpus Analysis of Rock Harmony.” Popular Music 30 (1): 47–70.
Dineen, Murray. 2005. “Schoenberg’s Modulatory Calculations: Wn Fonds 21 Berg 6/III/66 and Tonality.” Music Theory Spectrum 27 (1): 97-112.
Eyben, Florian, Sebastian Boeck, Björn Schuller, and Alex Graves. 2010. “Universal Onset Detection with Bidirectional Long Short-Term Memory Neural Networks.” In Proceedings of the International Society for Music Information Retrieval. Utrecht, Netherlands: 589–594.
Fétis, François-Joseph. 1844. Traité Complet de la Théorie et de la Pratique de L'harmonie. Eugen Duverger.
Feulner, Johannes. 1993. “Neural Networks that Learn and Reproduce Various Styles of Harmonization,” in Proceedings of the 1993 Computer Music Conference. San Francisco, Computer Music Association: 236–239.
Forte, Alan. 1973. The Structure of Atonal Music. Yale University Press.
Gang, Dan, Daniel Lehman, and Naftali Wagner, 1998. “Tuning a Neural Network for Harmonizing Melodies in Real-Time,” in Proceedings of the 1998 Computer Music Conference, San Francisco: Computer Music Association.
Gjerdingen, Robert. 2007. Music in the Galant Style. Oxford University Press.
Harrison, Daniel. 1994. Harmonic Function in Chromatic Music: A Renewed Dualist Theory and an Account of its Precedents. University of Chicago Press.
—————. 2016. Pieces of Tradition: An Analysis of Contemporary Tonality. Oxford University Press.
Hiraga, Rumi, Roberto Bresin, Keiji Hirata, and Haruhiro Katayose. 2004. “Rencon 2004: Turing Test for Musical Expression.” Proceedings of the 2004 Conference on New Interfaces for Musical Expression. Hamamatsu, Japan.
Huron, David. 2006. Sweet Anticipation: Music and the Psychology of Expectation. The MIT Press.
—————. 2016. Voice Leading: The Science behind a Musical Art. Cambridge. The MIT Press.
Hyer, Brian. 2002. “Tonality.” In The Cambridge History of Western Music Theory, ed by Thomas Christensen, 726-52. Cambridge University Press.
Illescas, Plácido R., David Rizo , and José M. Iñesta. 2007. “Harmonic, Melodic, and Functional Automatic Analysis.” Proceedings of the 2007 International Computer Music Conference. San Francisco, Computer Music Association: 165–168.
Jurafsky, Dan. and James H. Martin. 2000. Speech and Language Processing: an Introduction to Natural Language Processing, Computational Linguistics, and Speech Recognition, 1st Edition. Prentice-Hall.
Kopp, David. 2002. Chromatic Transformations in Nineteenth-Century Music. Cambridge University Press.
Georgaki, Anastasia and George Kosteletos. 2012. “A Turing Test for the Singing Voice as an Anthropological Tool: Epistemological and Technical Issues.” Proceedings of the 2012 Computer Music Conference. San Francisco: Computer Music Association, 46-51.
Kostka, Stefan, and Dorothy Payne. 2012. Tonal Harmony with an Introduction to Twentieth-Century Music, 4th edition. McGraw-Hill.
Krumhansl, Carol L. 1990. The Cognitive Foundations of Musical Pitch. Oxford University Press.
Krumhansl, Carol L, Jamshed J. Bharucha, and Mary A. Castellano. 1982. “Key Distance Effects on Perceived Harmonic Structure in Music.” Perception & Psychophysics 32: 96–108
Krumhansl, Carol L., and Roger N. Shepard. 1979. “Quantification of the Hierarchy of Tonal Functions Within a Diatonic Context.” Journal of Experimental Psychology: Human Perception and Performance, S (4): 579-594.
Kurth, Ernst. 1920. Romantische Harmonik und ihre Krise in Wagners ‘Tristan.’ Berne (partial Eng. trans. in Ernst Kurth: Selected Writings, ed. L.A. Rothfarb (Cambridge, 1991): 97–147).
Laitz, Steven. 2008. The Complete Musician: An Integrated Approach to Tonal Theory, Analysis, and Listening, 3rd Edition. Oxford University Press.
Lerdahl, Fred, and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. A Generative Theory of Tonal Music. MIT Press.
Lerdahl, Fred, and Carol L. Krumhansl. 2007. “Modeling Tonal Tension.” Music Perception 24, 329-66.
Lewin, David. 1987. Generalized Musical Intervals and Transformations. Yale University Press.
Liu, I-Ting, and Richard Randall. 2016. “Predicting Missing Music Components with Bidirectional Long Long Short-Term Memory Neural Networks. Proceedings of the International Conference for Music Perception and Cognition: 103-110.
Long, Megan Kaes. 2018. “Cadential Syntax and Tonal Expectation in Late Sixteenth-Century Homophony.” Music Theory Spectrum 40 (1).
Longuet-Higgins, H. Christpherz, and Mark Steedman. 1971. “On Interpreting Bach.” In Machine Intelligence, B. Meltzer and D. Michie, eds.. Edinburgh University Press.
Loui, Psyche. 2012. “Learning and Liking of Melody and Harmony: Further Studies in Artificial Grammar Learning.” Topics in Cognitive Science 4: 1-14
Loui, Psyche, David L. Wessel, and Carla L. Hudson Kam. 2010. “Humans Rapidly Learn Grammatical Structure in a New Musical Scale.” Music Perception 27 (5): 377-388.
Louis, Rudolf and Ludwig Thuille. 1907. Harmonielehre. Carl Grüninger.
Matsunaga, Rie, and Jun-Ichi Abe. 2005. “Cues for Key Perception of a Melody: Pitch Set Alone?” Music Perception 23: 153-164
—————. 2012. “Dynamic Cues in Key Perception.” International Journal of Psychological Studies 4: 3-21.
Matsunaga, Rie, Pitoyo Hartono, and Jun-Ichi Abe. 2015. “The Acquisition Process of Musical Tonal Schema: Implications from Connectionist Modeling.” Frontiers in Psychology (Cognitive Science) 6:1348: http://dx.doi.org/10.3389/fpsyg.2015.01348.
Moore, Brian C.J. 2012. An Introduction to the Psychology of Hearing. Bingley, Emerald.
Oram, Nicholas, and Lola L Cuddy. 1995. “Responsiveness of Western Adults to Pitch-Distributional Information in Melodic Sequences.” Psychological Research 57: 103-118.
Pachet, François. 2000. “Computer Analysis of Jazz Chord Sequences: Is Solar a Blues?” In Readings in Music and Artificial Intelligence, ed. by E. Miranda. Harwood Academic Publishers.
Pardo, Bryan, and William P. Birmingham. 1999. “Automated Partitioning of Tonal Music.” Technical report, Electrical Engineering and Computer Science Department. University of Michigan.
Pearce, Marcus T., and Geraint A. Wiggins. 2004. “Improved Methods for Statistical Modelling of Monophonic Music,” Journal of New Music Research. 33 (4): 367–385.
Pearce, Marcus T., Daniel Mullensiefen, and Geraint A. Wiggins. 2008. “Perceptual Segmentation of Melodies: Ambiguity, Rules and Statistical Learning.” The 10th International Conference on Music Perception and Cognition. Sapporo, Japan.
Pearce, Marcus T., María Herrojo Ruiz, Selina Kapasi, Geraint A.Wiggins, Joydeep Bhattacharyade. 2010. “Unsupervised Statistical Learning Underpins Computational, Behavioural, and Neural Manifestations of Musical Expectation.” NeuroImage 50 (1): 302–313.
Piston, Walter. 1941. Harmony. Norton.
Plomp, Reinier. 1964 “The Ear as a Frequency Analyzer.” Journal of the Acoustical Society of America 36 (9): 1628–1636.
Povel, Dirk-Jan, and Erik Jansen. 2002. “Harmonic Factors in the Perception of Tonal Melodies.” Music Perception 20 (1): 51-85.
Prince, Jon B., and Mark A. Schmuckler. 2014. “The Tonal-Metric Hierarchy.” Music Perception 31 (3), 254–270.
Prince, Jon B., William F. Thompson, and Mark. A. Schmuckler. 2009. “Pitch and Time, Tonality and Meter: How Do Musical Dimensions Combine?,” Journal of Experimental Psychology 35 (5), 1598–1617.
De Prisco, Roberto, Antonio Eletto, Antonio Torre, and Rocco Zaccagnino 2010. “A Neural Network for Bass Functional Harmonization.” In Applications of Evolutionary Computation, 351-360. Springer.
Quick, Donya. 2014. Kulitta: A Framework for Automated Music Composition. Ph.D. diss., Yale University.
Quinn, Ian. 2010. “What’s ‘Key for Key’: A Theoretically Naive Key–Finding Model for Bach Chorales.” Zeitschrift der Gesellschaft für Musiktheorie 7 (ii): 151–63.
Quinn, Ian, and Panayotis Mavromatis. 2011. “Voice Leading and Harmonic Function in Two Chorale Corpora.” In Mathematics and Computation in Music, ed. by Carlos Agon, 230-240. Springer.
Rahn, John. 1980. “On Some Computational Models of Music Theory.” Computer Music Journal 4 (2), Artifical Intelligence and Music Part 1: 66-72.
Raphael, Christopher, and Joshua Stoddard. 2003. “Harmonic Analysis with Probabilistic Graphical Models.” Retrieved from https://jscholarship.library.jhu.edu/handle/1774.2/25
—————. 2004. “Functional Analysis Using Probabilistic Models.” Computer Music Journal 28 (3): 45–52.
Rameau, Jean Phillipe. 1726. Nouveau Système de Musique Théorique. Ballard.
Reicha, Anton. 1818. Cours de cCmposition Musicale, ou Traité Complet et Raisonné d’harmonie Pratique. Gambaro.
Riemann, Hugo. 1893. Vereinfachte Harmonielehre, oder die Lehre von den Tonalen Funktionen der Akkorde. Augener.
Rohrmeier, Martin. 2007. “A Generative Grammar Approach to Diatonic Harmonic Structure.” Proceedings of the 4th Sound and Music Computing Conference, SMC, Lefkada, Greece: 97–100.
Rohrmeier, Martin, and Ian Cross. 2008. “Statistical Properties of Tonal Harmony in Bach’s Chorales.” in Proceedings of the 10th International Conference on Music Perception and Cognition. Sapporo: ICMPC: 619–627.
Saffran, Jenny R., Elizabeth K. Johnson, Richard N. Aslin, and Elissa L. Newport. 1999. “Statistical Learning of Tone Sequences by Human Infants and Adults.” Cognition 70: 27–52.
Saffran, Jenny R., Karelyn Reeck, Aimee Niebuhr, and Diana Wilson. 2005. “Changing the Tune: the Structure of the Input Affects Infants’ Use of Absolute and Relative Pitch.” Developmental Science 8 (1): 1–7.
Sapp, Craig S. 2011. “Computational Methods for the Analysis of Musical Structure.” Ph.D. diss., Stanford University.
Schoenberg, Arnold. 1978. Theory of Harmony. Translated by R. Carter. University of California Press. Translation of Harmonielehre, 3. ed. Universal Edition, 1922.
Sechter, Simon. 1853. Die Grundsätze der musikalischen Komposition. Breitkopf und Härtel.
Shanahan, Daniel, and Joshua Albrecht. 2013. “The Acquisition and Validation of Large Web-Based Corpora.” Presented at the Conference for the Society for Music Perception and Cognition, Toronto, Canada.
Smith, Nicholas A., and Mark A. Schmuckler. 2004. “The Perception of Tonal Structure through the Differentiation and Organization of Pitches.” Journal of Experimental Psychology: Human Perception and Performance 30: 268–286.
Stoddard, Joshua, Christopher Raphael, and Paul E. Utgoff. 2004. “Well-Tempered Spelling: A Key Invariant Pitch Spelling Algorithm.” In the Proceedings of the International Society for Music Information Retrieval.
Straus, Joseph N. 1987. “The Problem of Prolongation in Post-Tonal Music.” The Journal of Music Theory 31 (1): 1-21.
Stumpf, Carl. 1883. Tonpsychologie. Breitkopf und Härtel.
Temperley, David. 1997. “An Algorithm for Harmonic Analysis.” Music Perception 15 (1): 31–68.
—————. 1999. “What's Key for Key? The Krumhansl-Schmuckler Key-Finding Algorithm Reconsidered.” Music Perception: An Interdisciplinary Journal 17 (1): 65-100.
—————. 2007. Music and Probability. The MIT Press.
—————. 2009a. “A Statistical Analysis of Tonal Harmony.” http://www.theory.esm.rochester.edu/temperley/kp-stats/.
—————. 2009b. “Distributional Stress Regularity: A Corpus Study.” Journal of Psycholinguistic Research 38: 75-92.
—————. 2010. “Modeling Common-Practice Rhythm.” Music Perception 27 (5): 355–376.
—————. 2012. “Computational Models of Music Cognition.” In Diana Deutsch (Ed.), The Psychology of Music, (3rd edition), 327-368. Elsevier.
Temperley, David, and Elizabeth W. Marvin. 2008. “Pitch–Class Distribution and the Identification of Key.” Music Perception 25 (3): 193–212.
Temperley, David, and Daniel Sleator. 1999. “Modeling Meter and Harmony: A Preference-Rule Approach.” Computer Music Journal 23 (1): 10–27.
Thompson, William. F., and Lola L. Cuddy. 1989. “Sensitivity to Key Change in Chorale Sequences: A Comparison of Single Voices and Four-Voice Harmony.” Music Perception 7 (2): 151–168.
Tillmann, Barbara, Jamshed J. Bharucha, and Emmanuel Bigand. 2001. “Implicit Learning of Regularities in Western Tonal Music by Self-Organization.” In Connectionist Models of Learning, Development and Evolution (R.M. French and J.P. Sougné, eds), 175-184. Springer.
Tillmann, Barbara, Petr Janata, Jeffrey Birk, and Jamshed J. Bharucha. 2003. “The Costs and Benefits of Tonal Centers for Chord Processing.” Journal of Experimental Psychology: Human Perception and Performance 29 (2): 470-482.
Trainor, Laurel J., and Sandra E. Trehub. 1994. “Key Membership and Implied Harmony in Western Tonal Music: Developmental perspectives.” Perception & Psychophysics 56 (2): 125-132.
Turing, Alan. 1950. “Computing Machinery and Intelligence.” Mind 59 (236): 433-466.
Tymoczko, Dmitri. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. Oxford University Press.
Viterbi, Andrew J. 1967. “Error Bounds for Convolutional Codes and an Asymptotically Optimum Decoding Algorithm.” IEEE Transactions on Information Theory 13 (2): 260–269.
Vogler, Georg J. 1776. Tonwissenshcaft und Tonsetzkunst. der kuhrfürstlichen Hofbuchdruckerei.
Vos, Piet G. 2000. “Tonality Induction: Theoretical Problems and Dilemmas.” Music Perception 17 (4): 403-416.
Vos, Piet G., and Erwin W. Van Geenen. 1996. “A Parallel-Processing Key-Finding Model.” Music Perception 14 (2): 185–223.
Weber, Gottfried. 1817. Versuch einer geordneten Theorie der Tonsetzkunst. B. Schott's Söhne.
White, Christopher Wm. 2013a. “An Alphabet-Reduction Algorithm for Chordal n-grams.” In Proceedings of the 4th International Conference on Mathematics and Computation in Music. Heidelberg: Springer, 201–212.
—————. 2013b. Some Statistical Properties of Tonality, 1650-1900. Ph.D. diss., Yale University.
—————. 2014. “Changing styles, changing corpora, changing tonal models.” Music Perception 31 (2): 244–253.
—————. 2015. “A Corpus-Sensitive Algorithm for Automated Tonal Analysis.” In Mathematics and Computation in Music, LNAI, 9110, T. Collins, D. Meredith, A. Volk, eds., 115-121. Springer.
White, Christopher Wm., and Ian Quinn. 2016. “Deriving and Evaluating SPOKE, a Set-Based Probabilistic Key Finder.” Proceedings of the International Conference for Music Perception and Cognition. San Fransisco: 68–73.
—————. 2016. “The Yale-Classical Archives Corpus.” Empirical Musicology Review: 50-58.
—————. Forthcoming. “Chord Context and Harmonic Function in Tonal Music.” Music Theory Spectrum.
Wiggins, Geraint A. 2012. “The Future of (Mathematical) Music Theory.” Journal of Mathematics and Music 6 (2): 135-144.
Wiggins, Geraint A., Daniel Müllensiefen, and Marcus Pearce. 2010. “On the Non-Existence of Music: Why Music Theory is a Figment of the Imagination.” Musicae Scientiae 14 (1): 231–255.
Winograd, Terry. 1968. “Linguistics and the Computer Analysis of Tonal Harmony.” Journal of Music Theory 12 (1): 2–49.
Zikanov, Kirill. 2014. “Metric Properties of Mensural Music: An Autocorrelation Approach.” Presented at The National Meeting of the American Musicological Society, Milwaukee.
Footnotes
* I would like to thank Megan Kaes Long, Pat McCreless, Jessica Racco, Ian Quinn and MTO’s anonymous reviewers for their input on earlier drafts. All experiments were undertaken with clearance from the IRB at the University of North Carolina at Greensboro.
Return to text
1. In this article, I will adopt Temperley’s understanding of “key” as the perception, cognition, or identification of some tonal center. Of course, the terms “tonality” and “key” have many different subtle definitions, depending upon the repertoire being considered; and, even in contemporary work in music cognition, “tonality” can be defined in a wide variety of ways. Vos (2000), for instance, argues that “tonality” can mean so many different things—from the simple perception of some privileged pitch class to a complex hierarchy of tones and chords—that the word is at risk of losing any definitive meaning. It is outside the bounds of this article to parse out all the different meanings associated with that concept; however, every theory that makes some kind of claim about the mechanics behind tonal orientation does so using either a feedforward or feedback logic. I do, however, return to some definitional aspects of “key” at the end of this essay.
Return to text
2. Furthermore, surface or perceived musical events are actually observed within whatever musical medium is being used: a rhythm is seen in a score and a pitch is heard in a performance. On the other hand structures or cognized musical events are the result of some interpreted act: rhythms interpreted in some meter and pitches are interpreted in some key.
Return to text
3. This discussion conflates the sound signal with the score as well as the “in-the-moment” understanding of a key with a self-reflective/analytical understanding of key. I will discuss how visual and aural modes (and momentary and reflective processes) of music perception function in my argument below. However it should also be noted that the aural/visual domains and the listening/analytical acts are usefully and playfully intertwined in much music theory discourse (Lewin 1987), and using explicit and implicit tasks in key-finding behavioral experiments produces generally the same outcomes (Aarden 2003).
Return to text
4. Clearly, the feedforward/feedback dichotomy overlaps with other classic dichotomies, particularly bottom-up/top-down and connectionist/rule-based approaches; however, these mappings are by no means one-to-one. For instance, just as top-down and rule-based approaches use some pre-formed set of expectations or templates to make sense of some phenomena, so too do feedback systems use the organizations of broader structures to inform key finding. But a feedforward approach could also use some broader structure to identify a key if that structure was not, in turn, affected by the key center. In other words, these more classic dichotomies hinge upon the relationship between a complex phenomenon and the evidence used to support this phenomenon, while my dichotomy hinges upon whether there is a relationship between more than one type of high-level organization.
Return to text
5. For the computationally minded: I implemented this key-profile analysis with Bellmann-Budge weightings and a correlation procedure implemented in music 21 (Cuthbert and Ariza 2011). The procedure uses the number of quarter-note durations of each pitch-class as a 12-member vector and then calculates the correlation coefficient between that and the ideal vector of each of the 24 major and minor keys. The annotations for the first two measures use that two-measure window (mm. 5–6), and measure 7’s annotations use a three-measure window (mm. 5–7).
Return to text
6. These multiple solutions are possible because both models assign probabilities for each key: in this instance, the various probabilities of the different key assessments are comparable. Specifically, “probabilistic” understandings of musical keys allow for multiple key centers to vie for prominence within a passage (Temperley 2007). We might say, for instance, that when we hear or analyze a passage unambiguously in C major, we might be 95% sure of a C tonal center, with the remaining 5% allowing for an impending surprisingly modulation. Tonally ambiguous passages, then, might have the probability mass comparably divided amongst several keys.
Return to text
7. The chord-progression model ignores the
Return to text
8. Computational formalization often overlaps with behavioral testing, in that the former can be designed to model or mimic a cognitive process or predict human behavior. See Temperley (2012) for an overview of computational modeling of music cognition.
Return to text
9. For a full account of the rich history of computational implementations for music analysis, see Temperley 2007 or White 2013a.
Return to text
10. Generally, these profiles show tonic pcs occurring most frequently, followed by the other members of the tonic triad, other members of the diatonic set, and finally the chromatic pitches. Such a model can then match a passage’s pitch-class distribution to the ideal profile of one of the 24 major and minor keys, thereby assigning the best-fitting key interpretation to the vector that best correlates to the observed distribution of a musical surface. This sort of analysis arose from “probe-tone studies” in which participants were asked to rate how well various pitch classes fit into a tonal context. (See, for instance, Krumhansl and Shepard 1979, Castellano, Bharucha, and Krumhansl 1984, Oram and Cuddy 1995, Creel and Newport 2002, Smith and Schmuckler 2004, and Huron 2006). In her collaboration with Mark Schmuckler, Krumhansl (1990) noted that the relative distribution of scale-degrees within tonal music seemed to mostly conform to the goodness-of-fit ratings found in probe-tone studies, and that this correspondence could be used in automated key-finding models.
Return to text
11. We would imagine that identifying a tritone as a particular pitch-class spelling (i.e., a diminished fifth versus an augmented fourth) to be specifically a visual cue; however, this is not always the case. Tuning and surrounding pitch cues can assist in the aural interpretation; several of the above-cited studies also suggest that presenting a tritone in ascending versus descending patterns contributes to how it is interpreted.
Return to text
12. Metrical Preference Rule 9 states, “Prefer a metrical analysis that minimizes conflict with the [harmonic] time-span reduction” (90), and Time Span Reduction Preference Rule 1 states, “Of the possible choices for head of a timespan T, prefer a choice that is in a relatively strong metrical position.” (160).
Return to text
13. See Dineen 2005 for a review of Schoenberg’s tonal theories.
Return to text
14. It is worth reflecting on the omnipresence of schemata in theories of key and how they underpin feedforward and feedback models. Scales or key profiles, for instance, are learned ways to organize pitches in much the same way cadential gestures are. Energetic relationships between scale degrees are as much preformed schematic templates as Gjerdingen’s (2007) partimenti patterns. Even interpreting a pitch involves a (albeit subconscious) process of parsing and grouping variegated sound stimuli into a single apperception (Plomp 1964, Moore 2012). More sophisticatedly, recognizing that a
Return to text
15. While I will engage with this concept in more depth below, it is important to note that the differences between these models hinge upon the different definitions of tonality these authors propose.
Return to text
16. Laitz, for instance, recommends his readers identify modulations when chord-progression analyses “become more complex or are nonsense” in relation to the prior tonic (2008, 572). Clendinning and Marvin (2011) instruct their readers to use cadences to identify keys, yet their instructions on cadence identification assume a student has already identified the underlying key.
Return to text
17. It should be noted that a theorist’s tonal logics need not exclusively be either feedback or feedforward. Clendinning and Marvin (2011) first introduce key as connected to diatonic scales, then nuance their discussion later to include beginning and ending notes, and finally to include cadence identification. Piston (1941) distinguishes between tonality and modality by saying, “Tonality is the organized relationship of tones in music. . . . Modality refers to the choice of the tones between which these relationships exist. Tonality is synonymous with key, modality with scale. . . [Any of the] modes may be transposed into all tonalities, simply by changing the pitch of the tonic note and preserving the interval relationships” (30–31). When describing how tonal relationships are obtained, he writes, “The strongest tonal factor in music is the dominant effect. Standing alone, it determines the key much more decisively than the tonic chord itself. . .” (34) This passage suggests that identifying a dominant chord yields a tonal center, something that would place the theory on the distributional side (as one simply asks whether there is a dominant harmony in the distribution of chords), and would use a feedback logic (since knowing a key would help identify a “dominant effect”). Piston, however, goes on to write, “The greatest strength of tonality in harmonic progressions involving only triads lies in those progressions which combine dominant harmony with harmony from the subdominant side. . . The progressions IV-V and II-V cannot be interpreted in more than one tonality, without chromatic alteration.” (36) The theory is not a linear one, and therefore is structural. However, given that Piston’s logic seems to be that the pitch content of these successions immediately point to a single diatonic set, the logic is now feedforward: identifying two triads linearly related by T5 or T2 places you in a single key.
Return to text
18. Indeed, Raphael and Stoddard’s (2003, 2004) implementations of an Expectation Maximization procedure for their study heavily influenced my own implementation.
Return to text
19. Vos and Van Geenen’s (1996) algorithm also assigns key by aligning a melody to a scale collection and to chords membership in parallel in a way very reminiscent of the current article; however, their algorithm is designed specifically for monophonic contexts.
Return to text
20. The literature within music information retrieval and artificial musical intelligence is also replete with so-called “feedback” systems. In fact, the current emphasis within this literature on Deep Learning (especially Recurrent Neural Networks) is heavily reliant on this logic, be it for harmonization (e.g., Feulner 1993, Gang, Lehman, and Wagner 1998, De Prisco et al. 2010), pattern completion (Liu and Randall 2016), melodic composition (Colombo et al. 2016), or even the analysis of musical characteristics (Eyben et al. 2010, Boulanger-Lewandowski, Bengio, and Vincent 2013). In these models’ engineering, many different parameters are maximized concomitantly: key might be dependent upon meter, which is dependent on the harmonic structure, which is dependent on key, and so on. This literature is important because it is useful: this kind of modeling underpins technologies like Spotify, Google Music, algorithmic DJs, and the like. However, these models’ complexity and their emphasis on usefulness/production make it difficult to dissect and test their connection to music cognition and music theory. A notable exception is Cancino-Chacon, Grachten, and Agres (2017), which uses an RNN to simulate actual listeners’ expectations by training their model on audio recordings of tonal music.
Return to text
21. Even more generally, we could consider any cognitive study of tonal harmony to implicitly involve key information.
Return to text
22. In fact Vos and Van Geenen 1996 explicitly put their finger on this issue (see their discussion on pp. 207–8, for instance). Alternately, from a modeling perspective, Lerdahl and Jackendoff’s (1983) Generative Theory of Tonal Music attempts a rigorous formal theory of tonal music via a generative grammar accompanied by preference rules. Several empirical tests of certain aspects of this theory have been performed (for instance, Lerdahl and Krumhansl 2007) as well as attempts to computationally implement the theory (Temperley and Sleator 1999). While these studies remain provocative, the learning of these preference rules and the particulars of the integration of various domains remain to be accounted for.
Given that the experimental designs are traditionally feedforward in their logic, the lack of empirical tests on feedback models is not surprising. Experimental designs generally test a parameter’s effect on some outcome by varying that parameter and testing the resulting changes in outcome: different outcomes are generated (unidirectionally) by different parameters’ settings. Consider, for instance, the straightforward parallels between a key-profile model and an experiment that tests the effects of pitch-class distribution on key assessment. Changing the pitch-class distribution modifies the model’s output, and such changes correspond to the hypothesized behavior of the participant. This crisp mapping of a theoretical model onto an experimental design likely has some influence on the popularity of these sorts of tonal models in music cognition research.
Return to text
23. There are two main benefits of computational analysis that I rely upon in this article: formal rigor and cognitive mimicry. To the first: in the words of Bo Alphonce, “the computer unrelentingly demands theory” (1980, 26) and in the words of John Rahn, “to explicate something is, ultimately, to formalize it, that is, to make it into a machine at whose metaphorically whirring and clicking parts we are happy to stare, and be enlightened” (1980, 66). Formalizing key-finding into computational algorithms then, challenges us to a specificity and precision that allows us to inspect and test our assumptions about some topic. Second, a computational model can potentially mimic some aspect of a cognitive process. As described by Temperley (2012), if a program takes in the same data as a human, manipulates the data in the same way as a human, and produces the same output as a human, then claims of human/computer parallelism can be made. (This idea is provocatively framed by Wiggins, Müllensiefen, and Pearce’s (2010) and Wiggins’s (2012) understanding of traditional music theory as an informal system that provides fodder for empirical testing.) Additionally, certain programming techniques can not only claim to undertake a process that mimics human cognition, but can also imitate a human’s learning of that process. Such “machine-learning” techniques imitate aspects of humans’ “statistical learning,” or the idea that listeners can form expectations by being exposed to sequences (musical or otherwise) with certain statistical regularities. (For examples in music, see Saffran et al. 1999; Creel, Newport, and Aslin 2004; Saffran et al. 2005; Huron 2006; Pearce, Mullensiefen, and Wiggins 2008; Loui, Wessel, and Hudson Kam 2010; Loui 2012; Pearce et al. 2010.) Being based on the statistical regularities of some dataset by their very nature, corpus-based models (or models based on large datasets) can map the ways in which exposure to a repertoire might allow listeners to form expectations or create some cognitive model. The engineering of such models, then, can make claims not only about a cognitive process, but also about the properties of a corpus that might allow humans to learn to perform that process. (More in-depth discussions of connections between musical statistics and learning can be found in Bharucha 1987 and 1991, Temperley 2007, Rohrmeier and Cross 2008, and Byros 2009.)
Return to text
24. There are certain limits to this computational methodology. First, using computer-readable formats to represent aspects of “human perception” conflates visual (score-based) and aural (listener-oriented) experiences and perceptions. This conflation can exclude important distinctions: for instance, the information gleaned from hearing a tritone can be very different than that gleaned from visually identifying an interval as a diminished fifth. Relatedly, the current study conflates the concept of musical surface with the raw elements of a computer-readable score. While I discuss my data formatting in more depth below, this generally entails something like a “piano roll” representation, with each note’s pitch, duration, timepoint, loudness, and instrumentation as being the essential elements. The present study aims to honestly embrace these conflations; it will remain for future work to manipulate the computational formatting to highlight different aspects of the visual/aural dichotomy and the musical surface. Third, just because a computer does something that adheres to human behavior does not mean the computer is undertaking the same processes as the human. While the input and output of a computational process can be somewhat rigorously tested in an experimental setting, understanding the process is somewhat more obscure: pinpointing the specifics of a cognitive process is difficult at best and impossible at worst. Computational modeling of cognitive or theoretical systems therefore is undertaken with the caveat that their most important claims—the mechanics of how they produce their output—are usually orthogonally testable experimentally against human behavior rather than directly. This orthogonal relationship between computer and cognitive engineering is a primary reason to frame my model as a “proof of concept” rather than conclusive evidence. Finally, what computational analysis gains in specificity it also gains in complexity. Each minute step in an action creates a to-do list that becomes quite long. Consider the prototypical frustration a seasoned musician might encounter when describing “key” to a non-musician: this exemplifies the complexity and minutiae of the computational parameterization of such a process. Using computational modeling for music analysis, then, can often seem ungainly, but only insomuch as it reflects the complexities of some theoretic, analytical, or cognitive process.
Return to text
25. Functionally, converting pcs to these mod-12 scale degrees transposes all pcs to the key of C, since in all keys the tonic pcs will be transposed to 0, the supertonic will become 2, etc. Importantly, while the natural environment for diatonic scale degrees is modulo 7 space, using mod-12 space 1) allows for chromatically altered scale degrees (e.g., V/V would be <269>, 2) uses the same space for the major and minor mode (a I chord would be <047> while a i chord would be <037>, and 3) uses the same size universe for scale degrees and pcs. This follows White 2015.
Return to text
26. Note that these Roman numerals are stand-ins for scale-degree sets: the algorithm under consideration neither interprets nor outputs a “I” chord per se, but rather the set <0, 4, 7>. This is the same for letter names used in the text and examples, as the program only ever deals in numerical pitch classes. Also note that since the algorithm uses unordered sets, the Roman numerals are always represented here without inversion. The implications of this are discussed below. I am also imagining this toy as treating sevenths and triads identically (i.e., V7 has the same 2-gram properties as V), and for simplicity I have removed the iii chord from the original formulation in the Kostka-Payne textbook.
Return to text
27. Using informatics “n-gram” parlance in which n equals the number of chords in a sequence, these sequences would be 2-grams, since the arrows express the probability of two-chord successions. That is, the probability of a chord appearing within this syntax is contingent only on the chord that appears before it: this process therefore assigns probabilities using only successions of two chords.
Return to text
28. Following previous work in White (2013b), the prototypes used here were produced by applying Equation 3 to the raw data of the Yale Classical Archives corpus (White and Quinn 2016b). The corpus contains 14,051,144 salami slices, or sets of notes occurring each time a pitch is added or subtracted from the texture, from music across the Western-European common practice. The reduction process was allowed to iterate until no more changes were made, and any repeated chords that arose during the reduction process were conflated into a single chord event. Even though the corpus is noisy and error-laden (Shanahan and Albrecht 2013, deClercq 2016), the corpus is quite large, and as such is ideal for a machine-learning process.
White’s (2013b) process produces a distribution of chords that occurs most frequently in the YCAC corpus. Following Pardo and Birmingham (1999), Bellmann (2005), and Quinn and Mavromatis (2011), I exclude the long tail of the distribution, or those chords that make up the majority of chord types, but the minority of chord instances of the distribution. The top 22 chords account for 85.3% of all chord occurrences, with the remaining chords accounting for only 14.7%. These infrequent chords were removed from the series, and chord transitions were normalized. For the purposes of this paper, I exclude the non-tertian vocabulary members.
Return to text
29. Contrast this with the encircled pitch content ending the second window, {D,
Return to text
30. This computational analysis ignores certain musical parameters in order to focus on others. Readers will likely have punctuated the preceding discussion with such thoughts as, “surely the voicing of the Alberti bass encourages us to hear certain pitches as the salient chord tones!”, and “the metrical emphasis clearly favors some notes over others!” This study’s focus on certain organizational structures will necessarily exclude the inclusion of others. Musical characteristics such as the bass voice, and the presence of arpeggios, melodic gestures, and the like all help listeners and analysts distinguish chord tones from non-chord tones; however, these parameters are not considered in this study and will remain for future investigation.
Additionally, given the above-cited literature on the importance of meter to the key-finding task as well as the difficulties I encountered in early implementations of meter-blind implementations, I incorporated a metric parameter into this model. In particular, my early experimental models would often divide the pitch contents of a beat between the surrounding chords to create more probable – but unintuitive – chord sequences. Consider the Mozart example: by eliding the barline and considering the
Return to text
31. A more technical report on how I implement this engineering can be found in White 2015.
Return to text
32. The corpus contains 46 examples of Western European common-practice music; five pieces were removed due to difficulties converting them into digital representations usable by the methods described below. The removed pieces all used pulses that were problematic to quantize—I did not want the findings unduly influenced by meter, a musical parameter that this article does not address. The reason for the difficulties occurred when adding repeating decimals: a triplet converts to 0.33333 of a quarter note, three of which do not equal 1.0, but rather 0.999999. While this difficulty could certainly be overcome, it was decided to forgo those examples in the current analysis.
Return to text
33. The metric parameter here divided the music into eighth-note pulses. While the implementation is explained in more detail in the supplement, the essential problem is that of constraining all the possible ways one can divide a musical surface into chords. (Earlier implementations of the analysis model used no such segregation, and their precision suffered from this complication.) Dividing a musical surface into a metrical grid (instead of just salami slices, for instance) constrains the possible ways a surface can be segmented: in my implementation, pitches that appear on pulses that are more metrically emphasized are first considered in the reduction method, and the less emphasized pulses are reduced to the surrounding stronger pulses. For this, I use the meter-finding algorithm of Zikanov (2014), and the pulse closest to the eighth note was selected as the metric division. This level was chosen because it excludes pulses at which harmonies almost never change but places it conservatively below the levels at which harmonies tend to change: the corpus analysis of Temperley (2009b) found that harmonies change on the notated “beat” (the quarter note in
Return to text
34. Tymoczko separates his models by mode; since the current model operates by agglomerating both modes, I combine his two datasets into one. Again, more details can be found in the technical report.
Return to text
35. Two other peculiarities should be noted. The corpus also includes chords with no discernible root (often augmented 6th chords and passing chords) within the corpus: these are removed. The corpus designates chords by their root shown as chromatic scale degrees, such that chords on the minor mediant and on the raised supertonic would both be represented as having the same chromatic root.
Return to text
36. The 2-grams that occurred less than 3 times in the corpus were discarded to simplify the model (following Quinn and Mavromatis 2011).
Return to text
37. Given that they represent a vastly different musical style, selecting popular music corpora may seem unusual; however, their difference will provide a useful guidepost for assessing other models. That is, if a supposedly common-practice model acts similarly to a popular-music corpus, this would call that model into question.
Return to text
38. Since many corpora had somewhat different definitions of a “chord,” the most frequent chord in the assessing corpus was identified with each of the Kostka-Payne chord roots. For instance, when the Quinn-YCAC was used for the cross-entropy measurements, its most frequent chord with a dominant root, V7, was mapped onto each of the Kostka-Payne annotations; for the Tymoczko-Bach, V was used, and so on.
Return to text
39. Applying the logarithm here rescales the unworkably small numbers that would result from taking the product of so many successive probabilities.
Return to text
40. In other words, if m(on) = 0 at some point n in the sequence, the probability of the whole sequence would be zero.
Return to text
41. This was done using the Laplace smoothing method, with an additive factor of 1 (Jurafsky and Martin 2000).
Return to text
42. Note that these four values together provide a multifaceted depiction of a model’s similarity to the observed analyses. Two low cross-entropy values with a low exclusion percentage would indicate that the model successfully predicts the observed chord progressions using parameters that overlap with those of the observation stream, while a low without-smoothing cross entropy coupled with a high smoothed value indicates that the model predicts a fraction of the observed progressions very well but cannot account for a large portion of them. Finally, the number of vocabulary items will help capture each model’s relative complexity: a low smoothed cross entropy derived from a model with a large vocabulary is unsurprising, given that a complex model would be expected to account for any number of surface progressions. On the other hand, a low smoothed cross entropy from a smaller model would indicate an economy within its vocabulary, with its small vocabulary accounting for a large portion of the observed chord progressions.
Return to text
43. As before, the excerpt was metrically analyzed, and the pulse closest to the notated eighth note was chosen to be the broadest metric division.
Return to text
44. Given that the metric division chosen (the eighth note) is shorter than most harmonic rhythms, this extension happened at most timepoints: the process produced windows with an average of 11.4 metric slices.
Return to text
45. To be sure there were no unusual aberrations in data (e.g., graders performing vastly differently from one another), an Analysis of Variance (ANOVA) statistical test was run between the three primary factors in this model (the grader, the example’s characteristic, and whether the analysis had been produced by a human or computer) and the grades given to the examples, but the results were not significant (F(1, 25) = .123, MSE = .615, p = .729). There also was no interaction between the grade and the computer/human producer (F(1, 25) = .265, MSE = 1.324, p =.611).
Return to text
46. In particular, the bars show the standard error given the number of responses and variation in those responses, or how different the averages must be in order for those differences to be only 5% (or less) likely to have arisen by chance.
Return to text
47. Using a two-sided t-test, the results are nearly significant (p =. 07).
Return to text
48. The one significant effect was the interaction between grade and the example’s tagged characteristic (F(3, 25) = 3.053, MSE = 15.27, p = .047), due to the fact that “simple” grades were significantly higher than others.
Return to text
49. Turing (1950) proposes this percentage to be 70% of the time. He imagines this “imitation game” as a proxy to begin to ask whether computers can think in the same way a human can. Importantly, even though this was a motivating question to this test, it is not my own: here, I am simply interested in the computer’s ability to approximate a particular human behavior.
Return to text
50. Dartmouth Neukom Institute’s even hosts a musical Turing Test competition. http://bregman.dartmouth.edu/turingtests/
Return to text
51. Imagine that if you flipped a coin 20 times, it is most likely to come up heads 10 times and tails 10 times; however, if you flipped heads 11 or 12 times, you wouldn’t believe your coin is rigged. However, if it came up heads, say, 18 times, you would be almost certain the coin flip was not operating with a 50/50 probability of heads and tails. The binomial test works in exactly this way. If the computer and humans were indistinguishable, the probability of either being chosen would be 50/50; if they were distinguishable, the results would act like the rigged coin, and skew in one direction.
Return to text
52. p = .0384
Return to text
53. Another aspect of this idea is its connection to “statistical learning.” By deriving its vocabulary and syntax from a machine learning procedure, this work not only suggests the structure of a cognitive task, but how that task is learned via musical exposure.
Return to text
54. I want to highlight that the “process” aspect of this concept shifts the definitional location of “tonality” from a formal model to a human cognitive process. For instance, the analysis of Example 3 is “correct” insomuch as it is well-formed in terms of a formal model; however, it does not conform to some human process, and was therefore revised to incorporate meter into the model.
Return to text
55. The fact of the matter is that feedforward methods are very successful predictors of human key-finding behavior and underpin many compelling psychological and computational studies. Given that the above results do suggest the validity of a feedback-based approach, there are four logical explanations: 1) that feedforward theories are correct, and the current study’s results are aberrations and feedback-based theories are incorrect; 2) the success of feedforward approaches are statistical aberrations, arising by chance; 3) the success of feedforward theories captures their partial participation within an feedback approach – they model a cog within the greater feedback machine; or, 4) Both feedforward and feedback logics are used, but in different situations. Given the consistent success of key-profile-based psychological studies and the analytical usefulness of several feedforward theories, the second solution seems unlikely. And while the first option is a statistical possibility, given the dearth of quantifiable work associated with it, the third and fourth solutions seem to provide the most compelling and musically interesting option. Under the former, feedforward theories adequately model musical phenomena because they capture a subset of the concept of key. For instance, in terms of key profiles, tonic, mediant, and dominant scales degrees are the most frequent because tonic triads are the most frequent vocabulary item to which other vocabulary items progress. To the latter, the way people hear “key” may potentially modulate depending upon the particular situation: reading a key signature versus listening to a chord progression versus hearing an unaccompanied melody might all encourage different key-finding strategies.
Return to text
Given that the experimental designs are traditionally feedforward in their logic, the lack of empirical tests on feedback models is not surprising. Experimental designs generally test a parameter’s effect on some outcome by varying that parameter and testing the resulting changes in outcome: different outcomes are generated (unidirectionally) by different parameters’ settings. Consider, for instance, the straightforward parallels between a key-profile model and an experiment that tests the effects of pitch-class distribution on key assessment. Changing the pitch-class distribution modifies the model’s output, and such changes correspond to the hypothesized behavior of the participant. This crisp mapping of a theoretical model onto an experimental design likely has some influence on the popularity of these sorts of tonal models in music cognition research.
White’s (2013b) process produces a distribution of chords that occurs most frequently in the YCAC corpus. Following Pardo and Birmingham (1999), Bellmann (2005), and Quinn and Mavromatis (2011), I exclude the long tail of the distribution, or those chords that make up the majority of chord types, but the minority of chord instances of the distribution. The top 22 chords account for 85.3% of all chord occurrences, with the remaining chords accounting for only 14.7%. These infrequent chords were removed from the series, and chord transitions were normalized. For the purposes of this paper, I exclude the non-tertian vocabulary members.
Additionally, given the above-cited literature on the importance of meter to the key-finding task as well as the difficulties I encountered in early implementations of meter-blind implementations, I incorporated a metric parameter into this model. In particular, my early experimental models would often divide the pitch contents of a beat between the surrounding chords to create more probable – but unintuitive – chord sequences. Consider the Mozart example: by eliding the barline and considering the
Copyright Statement
Copyright © 2018 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
10124