Fundamental Bass and Real Bass in Dialogue: Tonal Aspects of the Structural Modes*
Karst de Jong and Thomas Noll
KEYWORDS: structural modes, fundamental bass, real bass, partimento, bass arpeggiation, tonal analysis, Scriabin
ABSTRACT: This article focuses on the interpretation of the fundamental bass in terms of structural modes. The aim is to develop an analytical interpretation that relates tonality and tonal form to the fundamental bass. The approach is anchored in the Ramellian tradition by considering the fundamental bass as an autonomous level of analysis. A contiguity principle is governed by the modes of the musical tetractys, or structural modes: P4–M2–P4 (first mode), M2–P4–P4 (second mode), and P4–P4–M2 (third mode). These modes consist of three-scale degrees, which are labeled tonic, subdominant, or dominant, respectively, thus creating a conceptual bridge between scale theory and functional harmony. The dialogue between fundamental bass and real bass reflects a broader dialogue between a structural approach to fundamental bass and elements from thoroughbass and partimento traditions.
DOI: 10.30535/mto.24.4.10
Copyright © 2018 Society for Music Theory
[1] This article presents a novel approach to the tonal interpretation of fundamental bass and real bass progressions. The theoretical foundation is set out first (Section 1), and is then elaborated on the basis of analytical work (Sections 2 and 4). The approach is anchored in, and motivated by several historical conceptual frameworks. Although reviewing the sources and disentangling the respective ideas and motivations from our own exceeds the scope of this paper, Section 3 briefly introduces some of these cross-links and outlines directions for further work.
[2] The impulse for the theoretical and analytical work here originated in our reading of William Caplin’s article “Schoenberg’s ‘Second Melody,’ or, ‘Meyer-ed’ in the Bass” (2008). We share Caplin’s intention to regard the bass as an autonomous object of theoretical and analytical interest, and we propose to develop independent principles to analyze the bass melody.
1. The Structural Modes
[3] In a previous article (De Jong and Noll 2011), we demonstrated the relevance of the concept of structural modes for a systematic analysis of harmonic progressions in common practice tonal music. The term refers to our elaboration of the concept of the structural scale, coined by Norman Carey and David Clampitt (1989) in the context of their theory of well-formed scales. Subsection 1.1 systematically introduces the structural modes, and in subsection 1.2 some conventions for structural bass analysis are illustrated.
1.1 The Structural Modes: Basic Properties and Observations
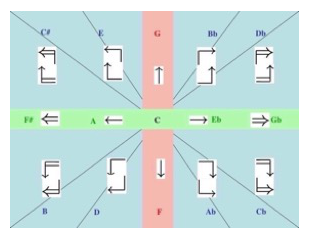
Example 1. Octave species of the structural scale. The first, second, and third modes share the same circular interval pattern, but each one traces a different circular permutation
(click to enlarge)
[4] Structural modes are instances of well-formed modes (Clampitt and Noll 2011). The governing idea behind well-formed modes is a double articulation of tone relations in terms of step-interval patterns, on the one hand, and fifth/fourth foldings, on the other. Before explaining these concepts, we will discuss the concept of double articulation on the simpler, abstract level of the structural scale. The starting point is a three-note scale, generated by a fifth, respecting octave identification. In consideration of the scale being generated we have two obvious orderings: by fifths and by steps. The pie chart on the right side of Example 1 displays the circular interval structure of this scale. The letter a designates the single major second and the two instances of the letter b designate the two instances of the perfect fourth. The numbers 0, 1, 2 as well as the growing radii represent the generation order of this scale as a chain of two fifths.
[5] The concept of well-formedness (Carey and Clampitt 1989) connects two ways of dealing with intervals: (1) the measurement of their specific sizes, and (2) the determination of their systematic behavior by measuring their generic spans. The name of the fifth, for example, refers to its systematic behavior within the fifth-generated diatonic scale: the six instances of the perfect fifth (P5) are not only equal in size, but they also consist of four scale steps each (that is, they have the same spans). This property also holds true for the structural scale. The two instances of the generating interval are not only equal in size, but they both consist of two structural scale steps. The gap interval between the last and the first generated tones is also filled by two steps. In other words, well-formedness stands for the compatibility of specific and generic interval measurement. The fifth-generated 4-note and 6-note scales are not well formed, for example.
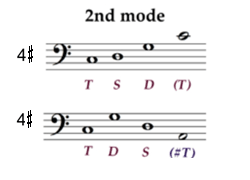
[6] To avoid a complicated mathematical explanation, which in any case is already available (Clampitt and Noll 2011), here we will use analogies in order to convey the main concepts. Although the diatonic scale is more complicated than the structural scale, its properties are more familiar. Therefore we may transfer the knowledge of the diatonic scale and its modes to the structural scale and its modes. For instance, we can distinguish seven diatonic species of the octave, in present-day practice called Ionian, Dorian, Phrygian, Lydian, Mixolydian, Aeolian, and Locrian. Likewise, in a 3-note scale one may form three species of the octave. We call them the first, second, and third modes, respectively. The particular choice of the numbers is driven by insights that will be explained in paragraph [8] below. The left side of Example 1 displays the three octave species, which are obtained by cutting the circle at either C = 1, F = 0, or G = 2.
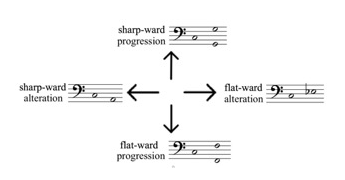
Example 2. The three structural modes over the same final (or tonic) C
(click to enlarge)
[7] By transposing these modes to the same final or tonic, one obtains the structural analogues of the tonoi, the family of modal varieties within a fixed range of an octave (see Example 2). Carey and Clampitt (1989) refer to the tonic–subdominant–dominant relationship as an instance of the structural scale. Employing this framework, we use the symbols T, S, D in this example simply as designators for the three scale degrees:
Example 3. The first and second structural modes can be interpreted as refinements of the authentic division of the octave (left side) and likewise of its plagal division, respectively (right side)
(click to enlarge)
[8] Another analogy between the diatonic and the structural modes is motivated by the concept of the so-called pseudo-classical modes. This term refers to the medieval and post-medieval concept of dividing the octave species authentically and plagally into species of the fifth and of the fourth. All the modes except for the Locrian entail such divisions. These sum to 12, the reason that Glarean in 1547 refers to the family of modes as the Dodekachordon (six authentic + six plagal modes). In the structural case, the combinatorics of the species of fifth and fourth is quite simple: we have two species of the fifth, namely ba (perfect fourth followed by a major second) and ab (major second followed by a perfect fourth). However, there is only one species of the fourth, namely b (the perfect fourth itself). Hence the structural analogue to Glarean’s Dodekachordon is, in fact, a “Tesserachordon” (two authentic + two plagal modes). Our numbering of the authentic modes of the scale {C, F, G} associates the first mode with the final on C and the second mode with the final on F (see Example 1). If we consider these two modes only as species of the octave (disregarding their authentic division), there is also a third mode of this scale: namely G–C–F–G. The third mode with its final on G is the structural analogue of the Locrian mode, the outsider among the diatonic modes. This mode possesses a species of the octave, but it is not inherited from an authentic division of the octave. Thus, our numbering is in strict analogy to the present-day practice in the ordering of the diatonic modes, which is in agreement with Zarlino’s (1571) emphasis on the hexachordal order of the six finals C, D, E, F, G, A. Example 3 displays the authentic and plagal divisions of the first and second modes on the same final C.
Example 4. Duality between step-interval patterns and the fifth/fourth foldings for the first structural mode (left) and the first diatonic mode (right)
(click to enlarge)
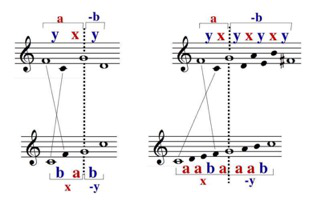
[9] We come now to the modal refinements of the concept of well-formedness. A detour into the diatonic case explains the concept of a duality, which refines the property of well-formedness for the Ionian mode on the basis of the right side of Example 4. The lower staff displays the Ionian mode within the range from C to C′, divided authentically at note G. The letters a and b designate major and minor seconds, respectively. The divided step-interval pattern reads as aaba|aab. The final C, divider G, and co-final C′ are highlighted with open note heads. The ascending fifth interval is designated by the letter x. Labeling the ascending fourth -y appears counterintuitive and in need of an explanation. To that end we turn our attention to the upper staff. It displays the notes from F to
[10] With these observations in mind we turn our attention to the first structural mode. Its step-interval pattern ba|b and fifth/fourth folding yx|y are displayed on the lower and upper staffs on the left side of Example 4. The role of the major second (a) and the perfect fourth (b) as step intervals of a structural mode within the range of an octave has already been explained in paragraph [9]. The intervals of the fifth (x) and the fourth (y) as folding intervals are the same as the diatonic case. The two folding patterns yx|y and yx|yxyxy differ only in their width. A particularity of the structural mode is the fact that the fourth in the step pattern is not further divided. While the perfect fifth, P5, is the dual counterpart of the major second, M2 (the smaller structural step), the fourth is its own dual counterpart. It is a folding interval and the larger step interval at the same time.
[11] The sharp-ward directed minor third from F to D is the framing interval of the folding yx|y and can thus be seen as the structural analogue of the augmented prime. Therefore we will call it the structural augmented prime. It is divided into a sharp-ward (ascending) major second and a sharp-ward (descending) perfect fourth. The interpretation of the minor third, m3, as the structural augmented prime is crucial for this article and involves two aspects: (1) structural alteration, that is, the alteration of a structural scale degree by a minor third does not affect the scale degree of the underlying mode as such; (2) it offers itself as a vehicle of modulation. In this case the altered scale degree of the mode of departure becomes a proper scale degree of the mode of destination.
Example 5. Step-interval patterns and sharp-ward fifth/fourth foldings for the three structural modes over the same tonic C. Not only is the step-interval pattern characteristic for each mode but so also is the position of the framing minor third of the folding pattern
(click to enlarge)
[12] Each structural mode has its dual, the unique sharp-ward folding of the structural augmented second (or minor third). Choosing a common tonic C for all three modes obtains three different locations for this interval: F–D for the first mode, C–A for the second mode, and
Example 6. Prototypical fundamental bass progressions for each of the three structural modes. The downward directed arrows designate flat-ward fifths (or fourths) while the leftward directed arrows designate sharp-ward directed structural augmented primes
(click to enlarge)
[13] In our proposed application of the structural modes to the study of the progressions of fundaments, we now reach a decisive point. The step-interval patterns and fifth/fourth foldings capture the anatomy of abstract modes in terms of tone relations. But fundament progressions need to be captured as trajectories possessing a temporal order. In the common practice repertoire, flat-ward progressions (authentic, based on falling fifths) significantly outweigh sharp-ward ones (plagal, based on rising fifths). This effect is linked to the downward resolution of dissonances. With less usage of dissonant sevenths, such as in seventeenth-century music or twentieth-century rock music, one often finds descending voice leadings between consonant triads that are connected with rising (that is, sharp-ward) fifths progressions of the fundaments. We restrict our attention here to the typical common practice progressions. Reading the fifth/fourth foldings from Example 5 backwards in a cyclic manner, we obtain the appropriate temporal trajectories. As shown in Example 6 each prototypical progression involves the characteristic framing interval for the mode in question. As fundamental bass progressions, these prototypical progressions can be elaborated in many different ways. A few examples of a first mode (classical, cadential) progressions are: I–IV–II–V–I, I–IV–V/V–V–I, I– IV–![]()
![]()
[14] The fundamental progression may also depart from the pure folding pattern and take its course along the step-interval pattern, that is, on the “other” side of the doubly articulated structural mode. In a T–S–D–T progression in the first structural mode we may interpret the T–S–D part as a progression along the step-interval pattern that is eventually completed within the folding pattern. In this case the analysis would interpret the major second S–D as a pure structural step.
1.2 Arrow Notation for Structural Intervals
[15] Neither musical staff notation nor conventional harmonic annotations are suitably adapted to notation of the structural bass. Musical intervals regarded as elementary from a structural viewpoint—namely fifths, major steps, and minor thirds—are not quite elementary in terms of diatonic staff notation, not to mention their awkward implicit representation in terms of relations between Roman numerals. When musicians speak of “falling fifths” they seem to associate a vertical axis with a gravitational connotation, which is then implicitly conflated with a vertical pitch height metaphor. As outlined above, there are good theoretical reasons to avoid this conflation, as—on the line of fifths—falling fifths are abstractly identified with raising fourths. This is why Nicolas Meeùs (2000), for example, reminds his readers about Rameau’s usage of the terms subdominant and dominant to specify harmonic directions (rather than to name harmonic loci or functions). Jacques Handschin (1948), who deliberately separates the line of fifths from the dimension of pitch height, distinguishes a masculine and a feminine side. Textbooks sometimes borrow the attributes authentic and plagal from the names of the cadences that exemplify the two harmonic directions, which in Section 1 we call flat-ward and sharp-ward.
Example 7. Arrow notation for elementary structural progressions and alterations
(click to enlarge)
Example 8. Arrow notation for compound structural progressions and alterations
(click to enlarge)
[16] We decided to adopt the gravitational up-down metaphor in our arrow notation, and to use the more neutral terms sharp-ward and flat-ward in order to emphasize our focus on the scale foldings. Flat-ward progressions are represented by a down-arrow, while sharp-ward progressions are represented by an up-arrow. The arrow notation simply ignores the registral information from the abstract modal folding patterns. However, another indicator is taken into account for the modal distinctions: the structural alteration. The decision to represent sharp-ward directed structural augmented primes (descending minor thirds) with leftward arrows has two motivations: (1) its side-ward direction is reminiscent of Schoenberg’s term, Seitenbewegung, for stationary or altered tones in chord progressions; (2) the choice of the left represents the direction of the descending minor third on a piano keyboard (see Example 7). Other intervals can be represented by concatenations of the four arrows (see Example 8). This entails information about the order, in which two elementary intervals are concatenated. The unmarked, or typical, order is that an alteration precedes a progression.(1) In addition to the arrow notation for intervals we identify structural modes through note names with subindices, such as C1, C2, C3 for the first, second, and third modes of C, or
2. Selected Structural Progressions
[17] The analytical potential of the structural modes within common practice tonality is broad, reaching from Baroque and Classical styles, through Romantic styles well into the study of jazz and pop harmony. With respect to the proposed dialogue between fundamental and real bass it is interesting to observe that the chord symbols in jazz practice exhibit closer affinity to the fundamental bass, while the thorough-bass tradition focuses on the real bass as its navigation system. Progressions should be approached from both sides. Fundament-based approaches to composition and teaching can be traced back to Rameau. The older partimento-based teaching still prevailed well into the nineteenth century and beyond. As Ludwig Holtmeier (2008) points out, Rameau was attracted by the contemporary discourse around the “rule of the octave,” and he sees the fundament-based approach as the result of Rameau’s attempts to theorize it. Holtmeier therefore deplores the loss of attention concerning this paradigmatic example of the strands of Rameau’s reception in Germany in the eighteenth century, and its influential continuations in the nineteenth century. With this background in mind, it is clearly useful to tie in with the recent reprocessing of the partimento tradition. Robert Gjerdingen’s (2007) detailed classification of Galant schemata serves as a useful starting point for the opening of our dialogic approach.
2.1 Structural Modes and Partimento Schemata
[18] In his recent discussion of the voice-leading scheme of the Prinner, Caplin (2015) demonstrates the decisive role of an associated harmonic progression for compliance of the scheme with a formal function. He differentiates between prolongational, sequential, and cadential Prinners. These distinctions encourage a further investigation into the combinations of voice-leading models and structural modes, apart from their formal functions.
Example 9. Structural Mode Annotations for typical instances of the Quiescenza, Monte, and Fonte schemata
(click to enlarge)
[19] In the introduction of the Quiescenza scheme, Gjerdingen cites a comment from Zingatelli’s early nineteenth-century collection of partimenti and regole, where an underlying fundamental bass is explicitly mentioned. We are speaking of a I–IV–V–I progression with the soprano (or any other upper voice) C–
[20] The term solidarity applies also to the dialogue between the fundamental and real bass of the prototypical Monte and Fonte schemata (see Example 9, middle and right systems). The annotations show that both of these can be seen in close relation to a structural mode. Depending upon context the Monte schemata can be interpreted as stationary or modulatory. The first of these may be analyzed as a structural chromatization of a first mode with an explicit minor third alteration (structural augmented prime) between S and
[21] A central aspect of the Monte and the Fonte schemata is their formal model/sequence structure. From this perspective the second half of a Monte (the sequence) is a transposition of the first half (the model) by a major second. Consequently, the direct fundament progression of a sharp-ward structural augmented prime (descending minor third) between the last chord of the model and the first chord of the sequence (see again, Example 9) competes with the relation of parallelism between model and sequence. Thereby the relevance of the structural alteration could be put into perspective by the consideration whether or not the formal hierarchy would dominate the harmonic progression. A modulating interpretation of the Monte is possible, but makes functional attributions less convincing and may not even be necessary. To cite Riemann (1918, 202): “As Fétis was the first to understand correctly, the harmonic progression, the cadential motion, remains at a standstill for the duration of the sequence.”(2)
Example 10. Johann Sebastian Bach, Suite in D major, BWV 1068, II (Air), mm. 13–15, two structural interpretations
(click to enlarge)
[22] To illustrate the considerations in the paragraph above, we can look at a particularly nice example from J. S. Bach’s “Air on the G String” (Example 10). Here, a Monte is followed by a sequence of falling fifths (Fonte). Two competing interpretations in terms of structural scale degrees are given in the example. The first is a stationary interpretation that recognizes only fundaments from the first mode of D major. It is incapable of explaining the first half of m. 14, except for some kind of structural alteration, or minor third shift. The second, modulating interpretation follows the underlying sequential structures. The meaning of the symbols here is less clearly tonal.
2.2 Structural versus Diatonic Levels of Description
Example 11. W. A. Mozart, Don Giovanni, Overture, mm. 5–11
(click to enlarge)
[23] Given the analogy between the structural and diatonic modes (see again, Example 8 in sub-section 1.2), it is important to understand their interaction as well. The structural modes are refinements of the essential (authentic and plagal) divisions of the octave, but in relation to the diatonic modes, they occupy a higher position in the hierarchy of well-formed fifth-generated modes. While it is insightful to observe each level of hierarchy separately, it is also necessary to investigate the levels in interaction. We claim that the interpretation of the structural modes as skeletons embedded in the diatonic modes offers interesting explanations for the interaction of the structural and real bass. (3) The diatonic scale can be interpreted as a structural skeleton filled with two tetrachords. In analysis, this becomes relevant in situations where tetrachordal bass lines diminute one of the two structural intervals of the perfect fourth. A prominent instance of this is the chaconne bass as a diminution of the I–V progression through a descending tetrachord in the real bass. The linear real bass is primarily supporting the passing motions between the structural chord progressions. This does not exclude the possibility that a structural bass can provide a secondary interpretation in solidarity with the primary linear one. Measures 5–11 in the opening of the overture to Mozart’s Don Giovanni provide an illuminating example (see Example 11). A chromatically descending “lamento” bass from D to A governs the chord progression, which at the same time can be coherently interpreted in terms of the first and second modes of D. Among the galant-style schemata, the prolongational Prinner with the tetrachordal bass line ––– supporting the harmonies IV–I6–![]()
Example 12. Beethoven, Symphony no. 3 in
(click to enlarge)
[24] The simplest instance of the chaconne bass is a linear filling with sixth chords on scale degrees and between root position chords on and . As an aside, we mention another type of interaction between fauxbourdon chords and a structural bass, because it nicely illustrates the hierarchical embedding of the first structural mode into the major scale. In Example 12, the second theme in the second movement of the Eroica Symphony by Beethoven realizes a situation where a complete sequence of sixth-chords is interpreted on the basis of real (or virtual) fundaments underneath. In this example the upper three voices form a complete fauxbourdon over the range of an octave and thereby provide coherent linear unity. Yet, from a structural point of view this line interacts with a first mode in
[25] The sixth-chords on real basses C and G at the downbeats of mm. 39 and 40 have no such support, yet it is meaningful to interpret them as first inversions with regard to the parallelism in the upper register. To be more precise, the sixth chord on C can be plausibly interpreted as an inverted
3. Intermezzo: Historical anchors and potential cross-links
[26] The structural scale and its modes have several manifestations in music theory. In this article, we wish to acknowledge some of them and to suggest further studies in order to explore potential theoretical relations between these manifestations.
[27] The first structural mode already had immense appeal to the Pythagoreans. In his famous fresco “The School of Athens,” Raphael depicts Pythagoras with a tablet where a diagrammatic representation of the musical tetractys (6 : 8 : 9 : 12) appears together with the triangular figure of the symbolic tetractys. The musical tetractys epitomizes the intervals of the diapason (octave), diapente (fifth), diatessaron (fourth), and epogdoon (major second). It plays a role as a skeleton in the ancient construction of the diatonic modes through disjunct tetrachords. This construction was later reconsidered in the context of tonality, for example, by Fétis. Furthermore, it is analytically exemplified by the interplay of tetrachordal models and structural modes, as mentioned in subsection 2.3.
[28] In late medieval theory the three-note scale C–F–G appears as the skeleton of the three-hexachord system. Therein, the intervals of the fourth and the fifth represent the two periodicities of the hexachord, both of which support the construction of two-hexachord regions within a diatonic ambient system. These periodicities, which had already been described as affinities by Guido of Arezzo, play an important role throughout the later Renaissance practice of imitative counterpoint, as hexachordal subjects can be transposed at the fifth and the fourth without leaving a unifying diatonic scale. To state it the other way around: hexachordal subjects can be diatonically transposed by a fifth or a fourth without changing their intervallic character.
[29] One early manifestation of the three-note scale C–F–G as a bass pattern is the “I–IV–V–I” ground of the bergamasca dance. A promising line for future investigation would be to look more systematically into the ground basses of sixteenth- and seventeenth-century dance music.
[30] Regarding common practice harmony, several variants of a three-triad-system resonate with Carey and Clampitt’s (1989) idea of an underlying structural scale. Rameau (1737) derives the major scale from a superposition of three contiguous triads. Johann Friedrich Daube (1756) promotes a three-triad-system as a mnemonic for thorough-bass practice.
[31] Moritz Hauptmann (1853) defines keys as hypertriads (triads of triads) and interprets tonal thinking as a kind of dialectical behavior. Hugo Riemann (1895; 1918) develops his theory of harmonic functions from a combination of Hauptmann’s ideas and elements of Arthur von Oettingen’s (1866) dualistic approach to triads. Carl Dahlhaus (1990) reformulates Riemann’s system of tonal functions by eliminating the dualistic component and by relating the dialectical principle to the principle of functional difference. His approach logically leads to the concept of embedded structural modes into the diatonic system (see Noll 2016a).
[32] Rameau’s concept of the double employment (for example, IV with an added sixth and II7) competes with the concept of structural alteration. While Rameau attempts to explain these fundament substitutions from the chords’ anatomy, the structural mode approach explains them as alterations in the step-interval patterns. To understand the solidarity between voice-leading properties and fundament progressions in greater depth, the authors are collaborating with Jason Yust (see De Jong, Noll, and Yust 2015).
[33] By ascribing functional indifference only to the minor third, Ernö Lendvai’s axial system neutralizes the structural difference between the major step and the perfect fourth as elementary intervals between fundaments. His system can therefore be interpreted in terms of a generic description of the structural modes to which the modal distinctions provide specific refinements. The minor third substitution, in particular, becomes a crucial dynamic element of this refinement.
[34] In a recent talk entitled “Rock Logic,” Dmitri Tymoczko (2016) presented his research into rock harmony on the basis of the voice leading behavior among consonant triads using a principle of diatonic proximity. Descending melodic motion corresponds to sharp-ward motion of the chord fundaments. The typical progressions that Tymoczko derives with his method correspond to different structural modes. Unlike the progressions in Example 6, they are directed sharp-wards, something that seems to be quite common in Pop and Rock styles.
[35] The interdependence of the voice-leading direction among triads and seventh chords, on the one hand, and the sharp-ward or flat-ward direction of the associated fundament progression, on the other hand, is also the subject of a combined historical and systematic study by Christophe Guillotel-Nothmann (2017). This work explores the behavior of the harmonic vector (flat-ward vs. sharp-ward progressions) and is based on Nicolas Meeùs’s (2000) article “Toward a Post-Schoenbergian Grammar of Tonal and Pre-tonal Harmonic Progressions.”
[36] The governing idea of a double articulation of tone relations can be anchored in Jacques Handschin’s (1948) treatise on the tone character. The scope of Handschin’s approach goes beyond the study of the bass in common practice tonality: he attaches importance to the fact that the line of fifths is of much deeper significance to music theory, rather than merely serving as a navigation tool in tonal modulation. Carey and Clampitt’s (1989) approach to well-formed scales as well as Clampitt and Noll’s (2011) approach to well-formed modes are consistent elaborations of Handschin’s theoretical ideas.(4)
[37] Early intimations of the conceptualization of the double articulation of tone relations through step interval patterns and fifth/fourth foldings can be found in the two senses of the term subdominant. Its two competing readings (scale degree under the dominant versus a dominant under the tonic) can already be found in Rameau (1737). Heinrich Schenker (1979) thematizes the ambivalent conceptualization of scale step 4 in connection with the derivation of middleground fillings of the bass arpeggiation. He also highlights the first and second structural modes (his Examples 14.2c/d, 14.5 and 14.6) in addition to the triadic filling (his Examples 14.1a and 14.2a).
[38] William Caplin (2008) takes some of the Ramellian and Schenkerian ideas as a point of departure and highlights the bass as an autonomous object of theoretical and analytical interest. Caplin identifies two different internal streams of the bass voice, which he calls the prolongational and the cadential streams. An attempt to integrate Caplin’s approach with our approach using the structural modes provokes two questions: (1) Can the two streams convincingly be related to the tonic and dominant scale degrees of structural modes at middleground levels?; (2) Can a foreground analysis integrate structural modes into either stream? The prominence of the authentically divided first and second modes supports an affirmative answer to the first question. Furthermore, it seems that second modes typically fulfill a prolongational function while first modes attain a cadential function. Caplin’s emphasis on scale degree as a switch between the streams, however, does not resonate with our approach. But scale degree is halfway between scale degrees and , and therefore the structural alteration is an alternative candidate for the switching function between the streams.
4. Analytical Considerations for Scriabin, Etude in C-sharp minor, op. 2, no. 1
[39] Scriabin’s Etude in C-sharp minor, op. 2, no. 1, is a particularly interesting example of the dialogue between elements of the bass and the structural modes in which they are embedded. The structural modes are active on both foreground and middleground levels. Actually, the entire piece can be segmented by structural modes. As we will see, the tonics
4.1 Analytical observations
Example 13. Scriabin, Etude in C-sharp minor, op. 2, no. 1, structural analysis of mm. 1–4
(click to enlarge)
[40] For the following analysis we advise the reader to look at the attached score. The analytical observations below are represented by a reduction of the score on three staves and one annotation layer (see Example 13). The upper system contains the main melody. In the middle system we extract notes from the score, which we regard to be constitutive for the real bass. In the lower system we display notes that we regard to be constitutive for the structural bass. These can be notes from the real bass and/or chord fundaments. Below we add an analytical annotation that provides the arrow-notation and the interpretation in terms of the structural modes:
[41] Scriabin’s compositional style is quite strict. The Satz-type structure of the opening sentence consists of a two-bar basic idea: a partly filled upward arpeggio (motive a), followed by a dotted appoggiatura figure resolving downward (motive b), with a characteristic repeating tone that is connected to the pulsating chords in the accompaniment. The varied repeat of this basic idea in m. 3 consists of a transposition to the subdominant. The harmony I–IV is not simply transposed but changed to a left-down pattern (IV–II–V), resulting in a first phrase that is supported by a complete first mode of
Example 14. Scriabin, Etude in C-sharp minor, op. 2, no. 1, structural analysis of mm. 5–8
(click to enlarge)
[42] The continuation modulates to the dominant key
[43] In the subsequent transitional passage the real and structural bass coincide for the most part (Example 15). The
Example 15. Scriabin, Etude in C-sharp minor, op. 2, no. 1, structural analysis of mm. 9–12 (click to enlarge) | Example 16. Scriabin, Etude in C-sharp minor, op. 2, no. 1, structural analysis of mm. 13–16 (click to enlarge) |
[44] A secondary thematic idea follows in m. 17 with its initial four measures standing on the dominant of
Example 17. Scriabin, Etude in C-sharp minor, op. 2, no. 1, structural analysis of mm. 17–20 (click to enlarge) | Example 18. Scriabin, Etude in C-sharp minor, op. 2, no. 1, structural analysis of mm. 21–25 (click to enlarge) |
Example 19. Scriabin, Etude in C-sharp minor, op. 2, no. 1, structural analysis of mm. 34–37
(click to enlarge)
[45] Arriving at the key of
Example 20. Scriabin, Etude in C-sharp minor, op. 2, no. 1, structural analysis of mm. 38–41 (click to enlarge) | Example 21. Scriabin, Etude in C-sharp minor, op. 2, no. 1, structural analysis of mm. 42–45 (click to enlarge) |
4.2 Real Bass and Structural Bass
[46] Looking at the relationship of real bass and structural bass, we observe that, wherever corresponding chords are in fundamental position, structural bass notes coincide with the real bass notes. As a result, certain segments of the complete real bass can be viewed as diminutions of the structural bass progressions, which delimit these segments. The tritone related positions of the real bass in mm. 23–24 mimic the highly chromatic melody preceding it. The descending melodic line of the bass in the closing section mirrors the ascending melody of motive a. The modulatory scheme of mm. 9–14 is a continuous sharp-ward movement constructed from a sequence of truncated second modes. Each instance contains a descending three-note bass line followed by a falling fifth. The implied lamento line is finally presented in the coda, as the fulfillment of an unspoken promise.
[47] One type of deviation between real and structural bass relates to ambiguities between dominant and subdominant functions. The ![]()
[48] Another noteworthy aspect is the continuation of the descending linear bass motion from B to E in the closing passage, which we already mentioned. The real bass turns upwards into a typical cadential motion 3–4–
4.3 Structural Modes and Large Form
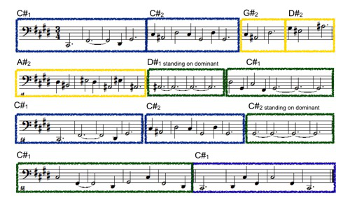
Example 22. Scriabin, Etude in C-sharp minor, op. 2 no. 1, structural analysis: overview
(click to enlarge)
[49] The analysis above concerns not only the relation of the structural modes to the middleground, but also to the larger musical form. A graphical overview of the form is given in Example 22. The large structure consists of 20 + 5 + 20 measures (45 measures, organized as 5x4, 1x5, 5x4). It resembles a simplified sonata form without development: a first thematic idea in the main key of
[50] Throughout the piece we find a limited number of harmonic patterns:
- Full structural modes to establish harmonic stability: used in the primary thematic idea, its recapitulation, and the coda
- A sequence of left-down-down patterns, modulating and raising the tension: used in the transition (truncated modes)
- A sequence of falling fifths for the retransition: used for the return to the recapitulation (truncated modes)
Example 23. Scriabin, Etude in C-sharp minor, op. 2 no. 1, structural analysis: The second mode in
(click to enlarge)
[51] When looking at the larger tonal plan, one notices a striking connection to the second structural mode of
[52] In other musical forms, such as the sonata form or the Baroque suite, we see similar “reversed” modal patterns in the large tonal structure. One future task could be to investigate this further. This could be part of further integration of the structural modes with various levels of analysis, including form, harmony, and voice-leading schemata.
Karst de Jong
Royal Conservatoire Den Haag and Escola Superior de Música de Catalunya
karstdj@gmail.com
Thomas Noll
Escola Superior de Música de Catalunya
thomas.mamuth@gmail.com
Works Cited
Biamonte, Nicole. 2008. “Augmented-Sixth Chords vs. Tritone Substitutes.” Music Theory Online 14 (2). http://www.mtosmt.org/issues/mto.08.14.2/mto.08.14.2.biamonte.html
Caplin, William. E. 2004. “The Classical Cadence: Conceptions and Misconceptions.” Journal of the American Musicological Society 57 (1): 51–117.
—————. 2008. “Schoenberg’s ‘second melody’, or, ‘Meyer-ed’ in the bass.” In Communication in Eighteenth Century Music, edited by Danuta Mirka and Kofi Agawu, 160–184. Cambridge University Press.
—————. 2015. “Harmony and Cadence in Gjerdingen’s ‘Prinner’.” In What Is a Cadence? Theoretical and Analytical Perspectives on Cadences in the Classical Repertoire, edited by Markus Neuwirth and Pieter Bergé, 17–58. Leuven University Press.
Carey, Norman, and David Clampitt. 1989. “Aspects of Well-formed Scales.” Music Theory Spectrum 11 (2): 187–206.
Clampitt, David, and Thomas Noll. 2011. “Modes, the Height-Width Duality, and Handschin’s Tone Character.” Music Theory Online 17 (1). http://www.mtosmt.org/issues/mto.11.17.1/mto.11.17.1.clampitt_and_noll.html.
Dahlhaus, Carl. (1968) 1990. Untersuchungen über die Entstehung der harmonischen Tonalität. Bärenreiter. Translated by R. Gjerdingen as Studies on the Origin of Harmonic Tonality. Princeton University Press.
Daube, Johann Friedrich. 1756. Generalbaß in drey Accorden, gegründet in den Regeln der alt und neuern Autoren. Johann Benjamin André.
De Jong, Karst and Thomas Noll. 2008. “Contiguous Fundamental Bass Progressions. ”In Dutch Journal of Music Theory, Volume 13 (1): 84–97.
—————. 2011. “Fundamental Passacaglia: Harmonic Functions and the Modes of the Musical Tetractys.” In Mathematics and Computation in Music: Proceedings of the MCM 2011, edited by Carlos Agon et al., 98–114. Springer.
De Jong, Karst, Thomas Noll, and Jason Yust. 2015. Handout for “Mathematical Approaches to Scale Degrees and Harmonic Function in Analytical Dialogue.” Paper read at the Annual Meeting of the Society for Music Theory, St. Louis, MO. https://societymusictheory.org/files/2015_handouts/noll.pdf
Fétis, François-Joseph. 1844. Traité complet de la théorie et de la pratique de l’harmonie. Schlesinger.
Gjerdingen, Robert. 2007. Music in the Galant Style. Oxford University Press.
Guillotel-Nothmann, Christophe. 2017. Asymétrie conditionnelle et asymétrie spontanée des progressions harmoniques. Le rôle des dissonances dans la cristallisation de la syntaxe harmonique tonale (c. 1530–1745). PubliQation – Academic Publishing.
Handschin, Jacques S. 1948. Der Toncharakter. Eine Einführung in die Tonpsychologie. Atlantis. Reprinted in 1995. Wissenschaftliche Buchgesellschaft.
Hauptmann, Moritz. 1853. Die Natur der Harmonik und der Metrik. Breitkopf und Härtel.
Holtmeier, Ludwig. 2008. “Zum Tonalitätsbegriff der Oktavregel.” In Systeme der Musiktheorie, edited by Clemens Kühn et al., 7–19. Hochschule für Musik “Carl Maria von Weber.”
Lendvai, Ernö. 1979. Béla Bartók: An Analysis of his Music. Kahn & Averill.
Meeùs, Nicolas. 2000. “Toward a Post-Schoenbergian Grammar of Tonal and Pre-tonal Harmonic Progressions.” Music Theory Online 6 (1). http://www.mtosmt.org/issues/mto.00.6.1/mto.00.6.1.meeus.html
Noll, Thomas. 2015a. “Die Vernunft in der Tradition: Neue mathematische Untersuchungen zu den alten Begriffen der Diatonizität.” In Carl Dahlhaus und die Musiktheorie, edited by Stefan Rohringer. Special Issue of Zeitschrift der Gesellschaft für Musiktheorie (2012). Olms. http://www.gmth.de/zeitschrift/artikel/864.aspx
—————. 2015b. “Triads as Modes within Scales as Modes.” In Mathematics and Computation in Music: 5th International Conference, MCM 2015, London, UK, edited by Tom Collins, David Meredith, and Anja Volk, 373–384. Springer.
—————. 2016a. “The Sense of Subdominant: A Fregean Perspective on Music-theoretical Conceptualization.” In Proceedings of the International Congress on Music and Mathematics, edited by Gabriel Pareyon, Silvia Pina-Romero, Octavio A. Agustín-Aquino, Emilio Lluis-Puebla, 207–15. Puerto Vallarta, Mexico, November 26–29, 2014. Springer.
—————. 2016b. “Handschins ‘Toncharakter’. Plädoyer für einen neuen Anlauf, ausgehend von neueren musiktheoretischen und kognitionspsychologischen Untersuchungen zu den tonalen ‘Qualia’.” ZGMTH 13/2, 237–95.
Oettingen, Arthur von. 1866. Harmoniesystem in dualer Entwicklung. Studien zur Theorie der Musik. Verlag W. Gläser. Dorpat and Leipzig.
Rameau, Jean-Philippe. 1726. Nouveau systême de musique théorique. Ballard.
—————. 1737. Génération harmonique, ou Traité de musique théorique et pratique. Prault.
Riemann, Hugo. (1893) 1895. Vereinfachte Harmonielehre oder die Lehre von den tonalen Funktionen der Akkorde. Translated (Anon.) as Harmony Simplified or The Theory of Tonal Functions of Chords. Augener Limited.
—————. 1918. Handbuch der Harmonie- und Modulationslehre. 8th edition. Max Hesses Verlag.
Schenker, Heinrich. (1935) 1979. Der freie Satz. Universal Edition. Translated and edited by Ernst Oster as Free Composition. Longman.
Tymoczko, Dmitri. 2016. “Rock Logic.” Lecture at the ESMUC (Barcelona), May 17, 2016.
Footnotes
* We wish to thank Christophe Guillotel-Nothmann for his tremendous work as the session organizer and editor of this special issue, and the anonymous reviewers for very helpful suggestions for the revision of this article.
Return to text
1. See De Jong and Noll 2008 for further discussion.
Return to text
2. “Wie zuerst Fétis richtig erkannte, steht aber die eigentliche Harmoniebewegung, die Kadenzierung, so lange still, als die Sequenz währt.”
Return to text
3. On this point, see also Noll 2015b.
Return to text
4. See also Noll 2015a; 2016b.
Return to text
Copyright Statement
Copyright © 2018 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Sam Reenan, Editorial Assistant
Number of visits:
8114