Conditional Asymmetry and Spontaneous Asymmetry of Harmonic Progressions: The Changing Status of the Directional Tendency of Root Progressions in Madrigal Cycles from Verdelot to Monteverdi (c. 1530–1638)*
Christophe Guillotel-Nothmann
KEYWORDS: root progression, theory of harmonic vectors (THV), tonality, dissonance, elaboration, privileged direction of chord progressions, Philippe Verdelot, Jacques Arcadelt, Cipriano de Rore, Orlando di Lasso, Giaches de Wert, Claudio Monteverdi, voice leading, clausula formalis, conditional and spontaneous asymmetry, statistical analysis
ABSTRACT: The theory of harmonic vectors (THV) postulates that, of the six possible root progressions in a given tonality, those up a fourth, down a third, and up a second (+4, -3, +2) are present in significantly greater numbers than the complementary root motions down a fourth, up a third, and down a second (-4, +3, -2) (Meeùs 1988; 1989; 2000). This imbalance sheds light on a specific aspect of the tonal system (Meeùs 2001, 63). The progressions +4, -3, +2 arise almost accidentally in pre-tonal polyphony through the constraints of contrapuntal rules, but in later repertoires they become a decisive syntactical feature that actively constrains tonality. A model combining voice leading and harmonic progression is tested against a body of madrigal cycles by Verdelot, Arcadelt, Lassus, Rore, Wert, and Monteverdi. These cycles, published between c. 1530 and 1638, contain about 50,000 chord progressions, permitting a close examination of the phenomena that reflect the changing status of the prevalent root progressions, the technical aspects that may have fostered it, and the compositional possibilities that result from the evolution outlined.
DOI: 10.30535/mto.24.4.8
Copyright © 2018 Society for Music Theory
[1] The theory of harmonic vectors (THV) postulates that of the six possible root progressions in a given tonality those up a fourth, down a third, and up a second (+4, -3, +2) are present in significantly greater numbers than the complementary root motions down a fourth, up a third, and down a second (-4, +3, -2) (Meeùs 1988; 1989; 2000). These will be referred to below as “dominant vectors” and “subdominant vectors,” respectively. The imbalance between root progression categories sheds light on a specific aspect of the tonal system (Meeùs 2001, 63).
[2] Previous studies have confirmed the tendency for the primary group—that is, the dominant vectors—to dominate in stylistic genres ranging from Renaissance polyphony to twentieth-century popular music (Desbordes 2003, Meyer 2009, O’Donnell 2011, Cathé 2012, Guillotel-Nothmann and Meyer 2013). Although root progressions of the primary group do become more prevalent with the development of tonality, the increase is not as dramatic as might have been expected (Tymoczko 2003, 43; Hedges and Rohrmeier 2011), a result suggesting that prevalence is less crucial for harmonic tonality than initially thought, and instead it is the nature of these progressions that needs to be considered.
[3] I will argue that it is less the change in frequency of these preferred progressions that is critical for harmonic tonality, than it is the change in their quality: the progressions +4, -3, +2 arise almost accidentally in pre-tonal polyphony through the constraints of contrapuntal rules, but in later repertoires they become a decisive syntactical feature that actively constrains tonality.
[4] To test this hypothesis, a model that combines voice leading and harmonic progressions will be tested against a body of madrigal cycles by Verdelot, Arcadelt, Lassus, Rore, Wert, and Monteverdi. These cycles, published between c. 1530 and 1638, contain about 50,000 chord progressions. The empirical results in conjunction with the model will allow a close examination of how and why the primary group dominates. They will show the phenomena that reflect the changing status of the prevalent root progressions and the technical aspects that may have fostered it. Finally, the results will help to identify the compositional possibilities that result from the evolution outlined.
1. Vectors, voice leading, and asymmetry of root progressions
1.1. The theory of harmonic vectors
Example 1. Classification of harmonic progressions in the THV
(click to enlarge)
[5] The theory of harmonic vectors, or THV, is based on a systematic classification of root progressions and provides rules of syntax that constitute the embryo of a tonal grammar (Meeùs 2003, 8). The theory categorizes harmonic progressions into two distinct groups of dominant and subdominant functions. Each group includes one main progression that moves by fourth and two substitute progressions that move by second or third (Example 1).
[6] The progression up a fourth (+4) and the substitutions down a third (-3) and up a second (+2) are classified as dominant vectors. The complementary chord progressions (-4, +3, -2) belong to a category of subdominant vectors. The main progressions are named with reference to the dominant and subdominant progressions in the perfect (V–I) and plagal cadence (IV–I), while the substitutions are inferred—in the theory’s initial formulation—from Rameau’s double emploi (Rameau 1737) and Riemannian functional equivalences (Riemann 1909).
Example 2. Paradigmatic cadence with harmonic vectors
(click to enlarge)
[7] Studies of corpora of sixteenth- and seventeenth-century music have shown that dominant vectors are always in the majority. This imbalance increases from the seventeenth century onwards and peaks around 1750 (Cathé 2012). The hegemony of dominant vectors can be deduced most effectively from the progression I–IV–V–I–IV–I (Example 2), where all changes, with the exception of the plagal closure IV–I, correspond to dominant vectors. Following Tymoczko (2003, 38), I term this imbalance the “asymmetry of root progressions.” This asymmetry corresponds to the difference in frequency between dominant vectors (DV) and subdominant vectors (SV):
Asymmetry = DV – SV
[8] In the THV, vector categories are assigned opposing directions. These are visualized with arrows to the right for dominant progressions, and arrows to the left for subdominant progressions (see Example 2). The predominance of the rightward arrows makes explicit the cadential teleology that plays a key role in tonality. This cadential direction will be referred to as the “privileged direction” of chord progressions. The THV does not claim that tonal harmony can be exclusively reduced to dominant progressions, but it does highlight the crucial role of these progressions in tonal syntax.(1)
1.2. Model
[9] As shall be demonstrated, the asymmetry of root progressions has its source in cadence patterns that go back to the late Middle Ages and the early Renaissance. The earliest madrigals considered in this study date from the early sixteenth century, a time when the cadence becomes a locus of theoretical thought. Through the concept of clausula formalis, and taking as point of departure the idiomatic melodic and harmonic formulae associated with the cantus and the tenor, theorists of that time describe the additional bassus and altus lines, the voice’s permutation, the intermingling of dissonances, and the exception of the mi-cadence.
Example 3. Cantus-tenor framework
(click to enlarge)
[10] The intervallic progression sixth-to-octave between the penultimate and the finalis of Example 3 has remarkable qualities. It combines a gradual transition from the relative imperfection (imperfect consonance) to the relative perfection (perfect consonance) with stepwise upward (cantus) and downward (tenor) motion. This characteristic progression (and its complementary progression third to unison) becomes established in the fourteenth century as the canonical cadential formula of the cantus-tenor framework (Eberlein and Fricke 1992, 34).(2) From the fifteenth century onwards, because triadic harmony weakens the distinction between imperfect and perfect consonances, this formula is regularly preceded by a dissonant suspension. This dissonance on the antepenultimate note (D4–C5 in Example 3) expands and reinforces the cadence by launching the teleological drive earlier (Dahlhaus 1990a).
Example 4a. Harmonic progressions implied by the cantus-tenor framework
(click to watch animation)
Example 4b. Harmonic progressions implied by the cantus-tenor framework with restricted final chord
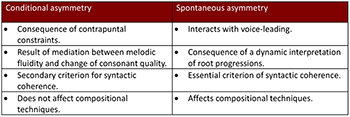
(click to watch animation)
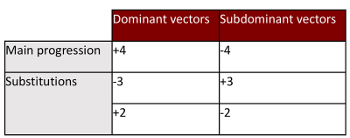
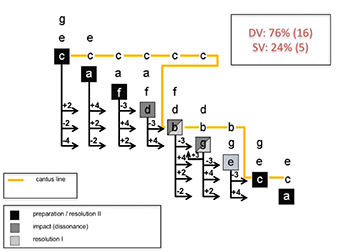
[11] Example 4a presents the triadic contexts that may follow from the cantus-tenor framework, the possible harmonizations and compatible roots through which the cantus and tenor lines may pass. The initial consonance E4–C5 that prepares the suspension may be harmonized by a triad on either C or A (in black). The dissonance D4–C5 that follows can be harmonized by triads on D, B, or G (in dark grey). The resolution onto the D4–B4 imperfect consonance that follows is harmonized by triads on B or G (in light grey). Finally, the resolution onto the perfect consonance C4–C5 is tied to the roots C, A, and F (in black).
[12] The cadence pattern as a whole implies a fall through a cycle of thirds between the different intervals of the cadential chain. The arrows in Example 4a represent the root progressions that may occur between the preparation, the impact, and the resolution of the dissonance. They indicate that in the harmonic progressions generated, dominant vectors (56%) occur more frequently than subdominant vectors (44%). This confirms that under specific conditions the cantus-tenor framework is a potential source of asymmetry, even if the imbalance between the vector categories is still notably low.
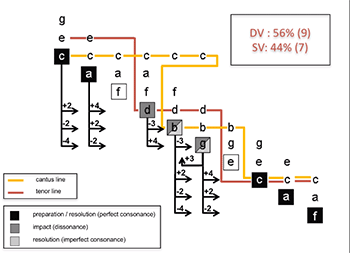
[13] Some roots are excluded from the cadence pattern. The harmonization of the final consonance C4–C5 using a triad with root F, although theoretically possible, was not included here. With the exception of the Phrygian cadence (the harmonization of a final E with a triad on A), composers tend to avoid the harmonization of the final by the lower fifth. If one excludes the chord on root F as final chord, the asymmetry between dominant (64%) and subdominant (36%) vectors significantly increases, as shown in the animation of Example 4b.
[14] Furthermore, in the previous examples, the third triad in the cycle (also on F) cannot be involved in the cadence pattern as the tenor line excludes its use. The same applies to the triad on E, the seventh triad in the cycle.
[15] The tenor line is not entirely stable yet, either in theory or in practice. It can be replaced by the movement –– or be absent (see Eberlein and Fricke 1992, 56–62). In the first case (––), harmonization with a triad on F becomes possible at the beginning and leads to three additional dominant progressions (F–D, F–B, and F–G) thus reinforcing the asymmetry between dominant (71%) and subdominant vectors (29%), as shown by the animation in Example 4c.
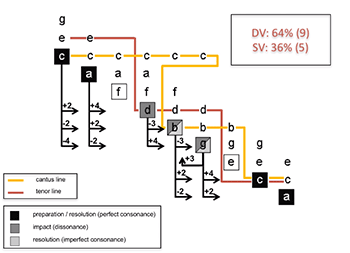
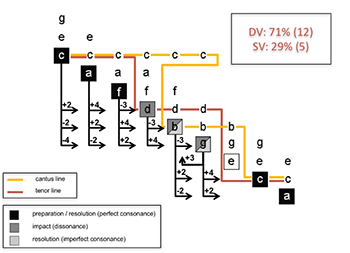
[16] In the second case (absence of the tenor line), the possibilities increase still further: a triad with root E becomes possible at the resolution on B. This leads again to intensifying the asymmetry between dominant vectors (76%) and subdominant vectors (24%) by allowing four additional dominant progressions (B–E, G–E, E–C, E–A), as shown by the animation of Example 4d.(3)
Example 4c. Harmonic progressions implied by the modified tenor line -- in the cantus-tenor framework (click to watch animation) | Example 4d. Harmonic progressions implied by the cantus line (click to watch animation) |
[17] The model described here has affinities with Tymoczko’s thirds-based grammar of tonal harmony (Tymoczko 2011, 226–30). Both favor the downward direction in the cycle of thirds with the upward motion limited to a restricted number of progressions. Both also restrict the use of the chord on (E in Example 4) but allow subdominant progressions, especially in a-b-a patterns like I–V–I, or I–VII–I (C–G–C, C–B–C in Example 4). The model does not claim, however, to be an accurate representation of tonal harmony. Its contrapuntal constraints do not equate to constraints that govern tonal organization. It nevertheless allows four important observations about asymmetry in Western polyphony and its links with other characteristics of harmonic tonality.
[18] First, the model supports the hypothesis that dominant progressions are not the result of tonality but, on the contrary, help to create some of its characteristics, both ontologically and historically. It suggests that rules of root motion that constrain tonality might have evolved at an earlier stage through contrapuntal constraints at the cadence. This indirectly corroborates an intuition of Lowinsky (1962, 4) when he designated the cadence as the “cradle of tonality.”
[19] Second, the model also sheds light on the concept of substitution. Theories of chord progression from Rameau (1721) to De Jong and Noll (2008) and theories of harmonic function such as Riemann’s Funktionstheorie assume—at least implicitly—a hierarchy between main representatives and substitutions.(4) The contrapuntal perspective presented in this model, however, conceives of the alternative harmonizations as equivalent. This equivalence results from the harmonic affinities between thirds in a distinctly diatonic context and the position of the harmonizations in the cadence. The concept of substitution then, both in its transformational and in its functional interpretation, is closely linked to the asymmetry of dominant versus subdominant root progressions. It also appears as a hierarchical reinterpretation of a more general principle in a specific tonal context.
[20] Third, the model shows that asymmetry, substitution, and tonicization are interrelated. The confirmation of the tonic through the cadential teleology both elicits dominant chord progressions and concludes them. Without this gravitational force, the harmony would move forward perpetually in an unlimited harmonic space (Meeùs 2003). Directional tendency thus cannot be the only criterion for an advanced theory of harmonic tonality because it is not restrictive enough (De Jong and Noll 2008, 87). It is nonetheless this criterion of directional tendency that facilitates the utterance of the tonic and constrains tonality, and not the converse.
[21] Fourth, the model does not allow us to infer a causal relationship between contrapuntal constraints and asymmetry. On the one hand, contrapuntal rules actively affect root progressions and encourage asymmetry. On the other hand, dominant vectors allow the preparation and downward resolution of dissonance and the upward motion of the leading tone. Therefore, I argue that contrapuntal constraints and the hegemony of dominant vectors influence each other mutually, but this link evolves and we see their causal relationship change through centuries of polyphony. This evolution is key to my argument and to the concepts of conditional and spontaneous asymmetry presented below.
1.3. Changing asymmetries
1.3.1. Spontaneous asymmetry
Example 5. J.S. Bach, Man singet mit freuden vom Sieg, BWV 149, “Herlicht lieb hab ich Dich, o Herr”
(click to enlarge)
[22] Nicolas Meeùs (1992a) argues that in tonality the chord’s mode and the characteristic dissonances—the subdominant ![]()
![]()
[23] The concept of spontaneous asymmetry supposes the assimilation by the listener of the prevalent dominant direction, which thus becomes a key syntactical element. Dahlhaus (1990b, 133) alludes to this when he argues that chordal dissonances are the result of a “reciprocal relationship between root progression and the resolution of dissonance.” This means that the chordal dissonance depends on a dynamic interpretation of chord progressions: one based on the expectation of specific chord progressions (dominant vectors +4 or +2) that coincide with the dissonance’s resolution. Spontaneous asymmetry thus interacts with voice leading: the upward direction of the leading tone or the downward resolution of the dissonances in Example 5 are the consequence of a specific kind of listening that hears root motion as an essential relationship between the chords. Or, to put it another way: “The ‘dynamic’ conceptions of root progression and the resolution of dissonance are two sides of the same coin” (Dahlhaus 2014, 134).
Example 6. Beethoven, Sonata op. 14, no. 1, III, mm. 131–4
(click to enlarge)
[24] This tonally oriented understanding of musical syntax also means that the grammatical consistency of the counterpoint can be preserved despite elaborations and irregularities in the foreground, as in Example 6. Here, the cadential effect is maintained despite the extensive elaboration of the tonic (measures 131–132), and the incomplete dominant and tonic chords, which are deprived of the upward motion of the leading-tone (measures 133–134) and reduced to the characteristic bass movement down a fifth. Accordingly, spontaneous asymmetry, based as it is on a chordal background that implies directional tendencies, also carries new compositional possibilities, such as register transfer, diminution, elision, elaboration, and irregular voice leading, any of which can be exploited in free composition.
[25] This organization around spontaneous asymmetry is the result of a specific, tonally oriented type of listening. But harmonic syntax and the status of asymmetry have changed during the history of Western polyphony, and to understand this one must take into account a possible shift between constitutive elements (i.e., elements that are critical for syntactic meaning) and characterizing elements (i.e., elements that reinforce this meaning without being decisive).
1.3.2. Conditional asymmetry
Example 7. Dufay, Missa Se la face ay pale, Kyrie, mm. 75–76
(click to enlarge)
[26] In Dufay’s Missa Se la face ay pale the progression from the penultimate to the final harmony at the end of the Kyrie (Example 7) cannot be distinguished from a tonal dominant-tonic progression, as in the model cadence in Example 2. In the middle of the fifteenth century, however, the +4 progression between penultimate and finalis is not the result of an emerging awareness of dominant-tonic relationships, as Besseler (1950) suggests, but the result of a strict observation of compositional rules in four-voice modal counterpoint (Eberlein and Fricke 1992, 39–41).
Example 8. Frottole libro Primo (1504), Frottola XXIX, “Tromboncino, Ah partiale e cruda morte”
(click to enlarge)
[27] The impact of writing constraints is also evident earlier in this cadence. In the usual configuration of the clausula formalis, the harmonic progression between the antepenultimate and penultimate note consists of a subdominant vector -4 (Example 7). The introduction of a dissonant seventh in the penultimate harmony, as seen in Example 8 with the dissonance C3–
[28] In these cases, the dominant direction is in fact conditioned by the contrapuntal rules of preparation and resolution. This specific type of asymmetry, where the dominant progression is induced by contrapuntal constraints, I call conditional asymmetry.
[29] In this type of writing, the syntactic consistency and cadential meaning result from melodic fluidity—parsimonious voice leading—and from the alternation between dissonance, imperfect consonance, and perfect consonance. These elements play a critical role for cadential teleology. The preference for the dominant direction in chord progressions arises almost accidentally from contrapuntal constraints and plays only a secondary role as a factor of syntactical coherence.
[30] Correspondingly, compositional techniques are not affected by this type of asymmetry. Although polyphony becomes inherently triadic from the beginning of the sixteenth century onwards (Lowinsky 1962, 3), the compositional possibilities that result from the triadic background—register transfers, harmonic elaborations, irregular voice leading (see 1.3.1 and 4 below)—are not fully developed. The preferred direction is not an element acting on voice leading but is a phenomenon that results from contrapuntal constraints.
Example 9. Conditional asymmetry vs. spontaneous asymmetry
(click to enlarge)
[31] These different features that characterize conditional and spontaneous asymmetry are summarized in the table of Example 9.
1.3.3. Empirical verification
Example 10. Fluctuation of total asymmetry and asymmetry associated with the dissonance
(click to enlarge)
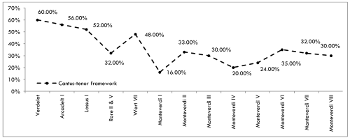
[32] How does the relationship between conditional and spontaneous asymmetry evolve in the corpus? To answer this question, the line AsyT in Example 10 illustrates variation in total asymmetry (AsyT) and asymmetry associated with the preparation and the resolution of the dissonances (AsyA) in the madrigal cycles. Total asymmetry (AsyT) corresponds to the difference between all dominant (DV) and subdominant (SV) vectors encountered in the madrigal cycles (DV – SV = AsyT). For example, the total asymmetry in Arcadelt I equates to 62.72% – 32.28% = 35.44%. The line AsyA, on the other hand, represents the difference between all dominant (DVA) and subdominant (SVA) vectors associated with the preparation and the resolution of the dissonance. Contrary to expectations, the privileged direction does not increase at the same rate from the beginning to the end of the corpus.(5) The asymmetry is significantly high in Arcadelt’s and Verdelot’s books. It is low in the cycles by Lassus and Rore and then increases with a remarkable regularity over fifty years until Monteverdi’s book V, peaking in his books VII and VIII.
[33] The constant imbalance in favor of the dominant vectors confirms that asymmetry is not specific to harmonic tonality. It is a general feature of Western polyphony, although this feature tends to intensify and change in quality. Furthermore, the way the asymmetry varies within the corpus implies that the phenomenon is superficial and does not belong to the deep structure of the harmonic language. It must depend instead on compositional techniques (homorhythmic textures, imitative counterpoint, thorough bass, and so on) and stylistic criteria (strict counterpoint, free counterpoint, stile recitativo).
[34] From this perspective, it is worth noting that the level of asymmetry found in Verdelot’s and Arcadelt’s cycles—which still share important characteristics with the earlier frottola—are almost identical with the level of asymmetry found more than a century later in Monteverdi’s books VII and VIII, in which tonality partly crystallizes. Einstein (1949, 865) had already observed “how closely the extremes approach one another—the beginning [of the madrigal], about 1500, and the end, about 1620.” These “strange bonds” were also indirectly grasped by Lowinsky (1962, 14), who claimed that some aspects of tonality—especially of the major mode—are anticipated in the lighter polyphonic genres of the early sixteenth century.
[35] The statistical results here confirm an affinity between the earlier and later repertoires of the corpus in asymmetry of their root progressions. They also show that the madrigal cycles more representative of modal polyphony—such as Lassus’s book I of 1555—stand out through their syntactic properties.
[36] At the same time, a closer examination of the nature of the asymmetry suggests that its conceptual background changed dramatically between the beginning and the end dates of this corpus. Example 10 shows how the variation in overall asymmetry in the composers’ works (line AsyT) relates to contrapuntal constraints. The line AsyA, on the other hand, shows the asymmetry that relates specifically to chord progressions that involve dissonances: suspensions and note against note dissonances.(6) A comparison of line AsyA with AsyT confirms that the total asymmetry and asymmetry associated with dissonance are strongly correlated from Verdelot to Monteverdi’s book III. This correlation weakens in Monteverdi’s books IV to VI and the significant increase in the asymmetry from books VI to VII occurs independently of the dissonance.
[37] It is not so much the accentuation of the asymmetry that seems critical here, but the fact that this increase is not conditioned by asymmetry associated with the dissonance, which decreases between VI and VII. Where previously the asymmetry was induced by contrapuntal constraints, it now occurs largely independently and spontaneously. Considering the theoretical implications of asymmetry (from [1.2]) and its possible repercussions on compositional techniques (from [4]), I argue that this emancipation is an important hint of the progressive crystallization of tonality.
Example 11. Evolution from conditional asymmetry to spontaneous asymmetry
(click to enlarge)
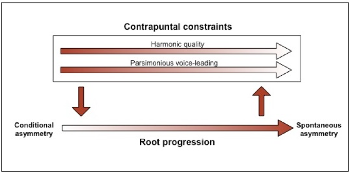
[38] The move from conditional to spontaneous asymmetry is modeled in Example 11. Contrapuntal constraints, represented by the arrows at the top, give rise to intervallic progressions that mediate between the change of harmonic quality (dissonance, imperfect consonance, and perfect consonance) and parsimonious voice leading. The rectangle that frames both arrows signifies that these parameters—harmonic quality and voice leading—are interrelated. Both are decisive for syntactic consistency at the beginning of the period considered. However, they lose in significance as times goes on. This is suggested by the gradient from red to white in the arrows.
[39] During the period considered harmonic quality and parsimonious voice leading interact with root progressions. However, the causal relationship between these criteria evolves. Initially, the contrapuntal constraints affect root progression, as is shown by the left-side vertical arrow pointing downwards from “contrapuntal constraints” to “root progression.” At the end of the period considered, it is the root progression and its constraints on tonality that become the main vector of harmonic meaning and actively determine the polyphonic stream, as suggested by the arrow pointing in the opposite direction on the right. This global evolution corresponds to the shift from conditional to spontaneous asymmetry of root progressions represented by the arrow at the bottom of the figure. Its gradient from white to red (opposite to the gradient of the arrows associated with contrapuntal constraints) implies that root progression, as a conceptual category, undergoes a conceptual change. While being the result of contrapuntal constraints at the beginning of the period, it becomes a decisive criterion for syntactic consistency at the end of the corpus. It has to be stressed however that this move is not continuous as might suggest the gradient. On the contrary, it is irregular and localized in time, occurring, at least in part, between Monteverdi’s madrigal books III (1592) and VII (1619) in the corpus.
[40] Tymoczko (2011, 232) has pointed out that the circle of thirds, as modeled in Example 4 above, might indirectly have “influenced the developing conventions of functional harmony.” The scenario of a shift from conditional to spontaneous asymmetry puts this hypothesis into a tangible historical context and helps to confirm it through empirical evidence.
[41] The move from conditional to spontaneous asymmetry continues beyond the end of the corpus. It must also be borne in mind that neither extreme—a completely conditioned asymmetry and a fully spontaneous one—ever appears in pre-tonal polyphony or in common practice harmony.
[42] This last point is corroborated by the empirical results. On the one hand, in all the madrigal cycles considered, there is a residual asymmetry, seen in the gap between both lines of the histogram in Example 10. This residual asymmetry, which by definition cannot be explained by contrapuntal constraints, shows that progressions of three note chords are never completely free as regards their direction: from all possible root motions the dominant ones are always favored and this preference tends to increase. On the other hand, even in the last two madrigal cycles, characterized by the highest residual asymmetry, the overall asymmetry remains partly correlated to the asymmetry tied to the dissonance: between book VII and VIII the increase of the total asymmetry (AsyT) goes hand in hand with the increase of the asymmetry associated with the dissonance (AsyA). Thus, the results and the model do not imply a radical reversal from conditional to spontaneous asymmetry but rather a gradual exchange in the hierarchy between the two kinds of asymmetries.
2. Signs of the evolution from conditional to spontaneous asymmetry
[43] The shift from conditional to spontaneous asymmetry is conceptual in nature. It is not inherent in the harmonic syntax itself but in how the syntax is interpreted. This shift can nevertheless be inferred from the evolution of compositional techniques. From the many criteria that might reflect this evolution, three will be examined in detail here: the realization of the cantus-tenor-framework, the use of major and minor triads, and the morphology of dissonant chords.
2.1. Cantus-tenor framework
[44] As has been stated in [10], the cantus-tenor progression of the clausula formalis has remarkable properties. As the tenor and cantus in Example 12 demonstrate, it combines parsimonious voice leading with a gradual change of harmonic quality, for example, in the move from measure 23.2 to measure 24.1 in the tenor and cantus parts: the change from the dissonance (C4–D4) to the imperfect consonance (B3–D4) and the perfect consonance (C4–C4). This framework is not always complete. The downward stepwise motion of the tenor line (D4–C4 in the cantus) is frequently replaced by an upward movement to the third of the final chord. This is the case in Example 13 where the tenor figure is sung by the altus (D4–E4) and the cantus figure by the tenor (B3–C4).
Example 12. Arcadelt (1539), Benedetti i martiri, mm. 25–26 (click to enlarge) | Example 13. Verdelot (1530), Amor quanto più lieto, mm. 6–7 (click to enlarge) |
Example 14. Percentage of cadences using the cantus-tenor framework in the madrigal cycles
(click to enlarge)
[45] How does the realization of the cantus-tenor framework evolve over time? To answer this question Example 14 represents the percentage of cadences implying the cantus-tenor framework in each madrigal cycle. While exhibiting high levels of local variations, the percentage of cadences realizing the cantus-tenor framework decreases gradually from Verdelot (where the cantus-tenor framework is realized in 60% of the cadences) to Monteverdi’s book VIII of madrigals (where the cantus-tenor framework corresponds to 30%. This evolution is linked to questions of voice leading and to the changing status of triadic harmony. In four-part writing, the regular cantus-tenor framework prevents a conclusion on a full triad and only permits an ending on a third or on an empty fifth, as in Example 12. The upward movement of the modified tenor line, however, allows a full triad as in Example 13 (if the G in the cantus is prolonged).
[46] What distinguishes a cadence by the middle of the sixteenth century is no longer an intervallic progression from imperfect to perfect consonance. This is because the change of the harmonic quality from the imperfect consonance to the perfect consonance is completely dissolved in the general imperfect sonority of the complete triads. In this harmonic context dominated by imperfect sonorities, two factors become decisive for the cadence: 1. the passage from dissonance to (imperfect) consonance and 2. the characteristic melodic movements of the cantus-bassus framework (Eberlein and Fricke 1992, 57). This leads on the one hand to an increased use of dissonant structures which, as has been shown, condition the asymmetry of root progressions. On the other hand, this change in what constitutes a cadence also brings increased attention to the outer voices. By this means the idiomatic bass movements become, in the long term, a prominent factor of syntactic coherence. The empirical results thus corroborate that the logic behind intervallic cadence patterns coexists with one based on the melodic movements of the lowest voice. During the period under consideration the latter logic tends to increase and to supersede the former one based on intervallic cadence patterns.
2.2. Major versus minor triads
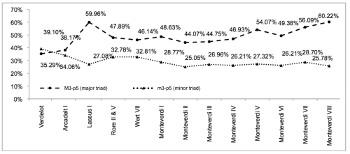
Example 15. Major and minor triads in the madrigal cycles examined
(click to enlarge)
[47] The diagram in Example 15 shows the proportions of triads with a major third and a perfect fifth (M3–P5) and triads with a minor third and a perfect fifth (m3–P5) in the corpus considered. It takes into account every verticality that corresponds to these morphologies without presuming that they are actually understood as a harmony, i.e. as an autonomous harmonic unit. As can be seen, the relationship between major and minor triads evolves in an interesting manner. While Verdelot and Arcadelt use both chord types in equal measure, the use of the major triad increases significantly in frequency with Lassus and then again at the end of the corpus from Monteverdi’s Book III onwards.
[48] The French musicologist Serge Gut noticed a similar evolution when, in his study of the harmonic third, he examined the final chord in cadences from large polyphonic corpora of the Middle Ages and the Renaissance. Gut (1969, 191) suggests two explanations for this phenomenon. The first implies a possible link between: (a) the predominance of the major mode, (b) the systematic use of the leading tone in the minor mode, and (c) the hegemony of the major triad as the final chord. The second argues that an awareness of harmonic overtones, together with an evolution from an intervallic understanding to a harmonic understanding, contributed to the increased use of major chords. Both explanations are problematic, however, in part because the hypothesis of a gradual integration of overtones remains debatable and in part because the two arguments fail to explain why increase in use of the major triad should happen at this particular period in the history of Western music.
[49] I would like to suggest instead that the prevalence of major triads may partly be linked to an increasingly tonally oriented type of listening. Once the triad is understood as a whole, once the bass is perceived as the triad’s root, and once root progression become salient from a cognitive point of view, then the use of the major triad reinforces the link between the syntactical units because of the harmonic quality of the triad and because of the upward melodic movement, by semitone, of the major third. In this explanation, which characterizes the chord’s mode as “rection” (see again section 1.2.), the increased use of the major triad is also linked to a more and more dynamic interpretation of chord progressions. Thus, the greater use of the major third indirectly reflects the increase of spontaneous asymmetry.
2.3. Morphology of seventh chords
Example 16. Arcadelt (1539), Fra più bei fiori, mm. 19–23
(click to enlarge)
[50] The possible shift from conditional to spontaneous asymmetry can ultimately be deduced by considering the make-up of dissonant chords, especially seventh chords. These appear, both with and without fifth from the beginning of the corpus, as in the madrigal Fra più bei fiori by Arcadelt (Example 16), where the descending chain of suspensions in measures 20–21 gives rise to three dissonant chords: two sevenths harmonized with only the third (A–C–G and G–B–F), and one seventh to which the third and the fifth have been added (F–A–C–E).
Example 17. Morphology of seventh chords in the madrigal cycles examined
(click to enlarge)
[51] The histogram in Example 17 represents the proportion of verticalities whose morphology correspond either to full “seventh chords” (7th + 5th + 3rd) or to incomplete “chords” without the fifth. Here again, every verticality that corresponds to these morphologies has been taken into account without presuming that they are actually understood as autonomous harmonic unit. The diagram shows that the use of both chord types is correlated in the early madrigal cycles and that both increase between Rore and Monteverdi’s book III. From the latter onward, however, the treatment of the two kinds of seventh chords diverges: the use of the full seventh chord increases and peaks in Monteverdi’s books V and VIII, while the seventh chord without the fifth appears less frequently. This tendency contradicts the Belgian theorist Fétis assertion that the presence of the fifth, along with the major third and minor seventh, distinguishes a seventh acting as a non-harmonic tone from a true dominant seventh chord. For Fétis, the latter appears from Monteverdi’s book III onwards, and marks the beginning of the “tonalité moderne” (Fétis 1840, 36).
[52] The evidence from the corpora suggests a definite change in the use of the chord both with and without its fifth at the beginning of the seventeenth century, but cannot on its own explain the dramatic changes polyphonic syntax undergoes at that time. As Dahlhaus has shown, the very concept of chordal dissonance depends on a dynamic interpretation of chord progression (Dahlhaus 1990b, 133–135). His deduction reflects the more general conviction that the distinction between essential and non-essential chords made by a listener is not a natural phenomenon but depends on harmonic schemata assimilated in tonally oriented listening. The traditional distinction between suspensions as non-harmonic events and “real” chordal dissonances, as implied by Fétis and still largely used in rudimentary music theory, is thus irrelevant in syntax that essentially relies on conditional asymmetry—that is, in syntax prior to harmonic tonality. The gradual rise of the complete seventh chord may be indicative of a transformation in the way harmonic syntax was implicitly understood, but it can neither explain the increase of spontaneous asymmetry nor be considered as a decisive feature that actively contributes to the origin of “tonalité moderne.”
3. Factors contributing to an intensification of spontaneous asymmetry
[53] Several factors may have fostered the evolution from conditional to spontaneous asymmetry. I already mentioned the hegemony of triadic harmony. The practice of basso continuo may also have contributed to this evolution. There is, however, another factor that appears crucial: irregular dissonances in music of the seventeenth century. The frequent use of contrapuntal license—i.e. the use of irregular dissonances justified by rhetorical and expressive purposes—undermined the relationship between the vertical and horizontal dimensions of polyphony and partly worked against syntactical coherence. Since this coherence was no longer derived exclusively from parsimony and the smooth change of harmonic quality characteristic of intervallic writing, movements of the real bass and thereafter abstract root progression became prominent determinants of harmonic meaning.
Example 18. Monteverdi (1605), Ch’io t’ami, e t’ami più della mia vita mm. 22–28
(click to enlarge)
[54] Signs of this shift can be seen in measures 22–26 of Monteverdi’s madrigal Ch’io t’ami (Example 18) where the eight note-against-note dissonances infringe radically on contrapuntal rules. Unquestionably the parsimonious voice leading and the contrary motion of the outer voices help to soften the harshness of these irregular structures, but it seems at least as significant from the point of view of syntactic consistency that, despite the contrapuntal irregularity and with only one exception, all harmonic units are arrived at and left by dominant vectors.
[55] These observations lead to the following hypothesis. Opposition to rules of regular counterpoint at the beginning of the seventeenth century provoked a search for new criteria of syntactic coherence, in the course of which root motion became the focal point—the main vector—of cadential meaning. The contrapuntal licenses compatible with dominant vectors were maintained, while the incompatible were gradually excluded. This process contributed to the strengthening of spontaneous asymmetry.
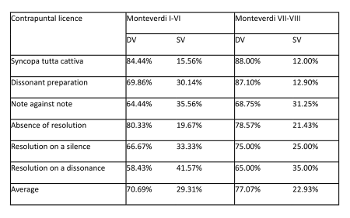
Example 19. Proportion of dominant and subdominant vectors associated with irregular dissonances in Monteverdi’s books I-VI and VII-VIII
(click to enlarge)
[56] The table in Example 19 supports this hypothesis.(7) It shows the proportions of dominant and subdominant vectors associated with irregular dissonances in books I–VI and VII–VIII by Monteverdi. More precisely, it measures the rate of dominant and subdominant vectors that occur when the dissonance is reached and left. Only actual root motion is taken into account. In the case the dissonance is approached or left over the same root, the repetition of the same root has not been considered. As the table shows, irregular dissonances mainly occur with dominant vectors in both sub-corpora (books I–VI and VII–VIII). On average, however, the percentage of irregular structures linked to dominant vectors increases by 6% in the last cycles, regardless of any contrapuntal constraint. These results suggest that irregular structures were gradually integrated in line with the dominant direction of harmonic vectors occurring spontaneously.
[57] Because these irregular dissonances are compatible with the dominant direction of chord progression (which always allows the preparation and downward stepwise resolution of dissonances), they can be reduced at a deeper level to strict counterpoint. This is not, however, to be understood as the result of a slavish obedience to the strict counterpoint of the past, but instead as the indirect consequence of the privileged direction of root progressions occurring spontaneously.
4. Spontaneous asymmetry and compositional techniques
[58] The bonds between asymmetry and the treatment of irregular dissonance demonstrate that the emancipation of the privileged direction from contrapuntal constraints grants new compositional possibilities. These will be discussed briefly here from the point of view of possible links between spontaneous asymmetry and elaboration techniques. In her study of the transition from modal to tonal organization in the works of Monteverdi, Susan McClary argues that the hierarchical shift between the structural line and the melodic foreground is decisive for the emergence of tonality (1977, 179). According to this view, in pre-tonal counterpoint the harmony-generating structural line corresponds, in a one-to-one relationship, to the foreground melody, that is, both the structural line and the foreground melody belong to the same hierarchical level. In tonality, on the other hand, each pitch of the structural line gives rise to further elaborations: the structural line corresponds to a higher hierarchical level, distinct from the subordinated melodic foreground, a shift that also affects harmony. Each structural pitch is able to generate what McClary calls “harmonic collections,” but at the same time harmony actively projects the structural line, articulates it, and becomes decisive for freer voice leading and for increased elaboration in the foreground.
[59] The increased elaboration and ornamentation of the foreground, which goes hand in hand with a decrease in the harmonic rhythm, assumes that chords have to be understood as immediate harmonic units, and their progression has to be interpreted from the dynamic point of view, as outlined above. These conditions can also be inferred from Schenker’s explanation of free composition:
In reality however, the tactics of voice leading become ever freer to the extent to which, in free composition, there erupts suddenly the force of the scale-step, under whose cover the individual parts may manoeuvre in a less inhibited way even than in strict composition. The scale-steps then resemble powerful projector lights: in their illuminated sphere the parts go through their evolution in a higher and freer contrapuntal sense, uniting in harmonic chords, which, however, never become end in themselves but always result from the free movement. (Schenker 1954, 155)
[60] The projector-lights metaphor reflects the importance of the harmonic degree as a conceptual unit that enhances freer voice leading. If we accept the scale degree’s meaning as depending on how it is arrived at and left, one can argue that at least some elaboration techniques are closely linked to the increase in spontaneous asymmetry. Two particular cases of elaboration, closely linked to the dynamic interpretation of chord progressions, will be discussed here: the elaboration of the dominant itself and of the predominant.
4.1. Elaboration of the dominant
Example 20. Monteverdi (1585), Se nel partir da voi, mm. 24–30
(click to enlarge)
[61] At measure 28 of the madrigal Se nel partir da voi from Monteverdi’s first book (Example 20), the syncopated seventh F–
[62] This extension has two consequences. On the one hand, it suspends the distinction between the antepenultimate and the penultimate harmony in the cadence. More precisely, this distinction is no longer established from a contrapuntal point of view, but through harmonic progression. As is shown by the reduction in Example 21, harmonically the antepenultimate event in the cadence is pulled backwards, corresponding to the chord on root C in measure 27.
Example 21. Monteverdi (1585), Se nel partir da voi, mm. 27–30, reduction
(click to enlarge)
[63] On the other hand, the extension prolongs the penultimate harmony on F by stretching it in time. In particular, the elaboration of the seventh
4.2. Elaboration of the predominant
Example 22. Monteverdi (1592), Poi ch’ella in sé tornò, mm. 36–40
(click to enlarge)
Example 23. Monteverdi (1592), Poi ch’ella in sé tornò, mm. 36–40, reduction
(click to enlarge)
[64] At measure 38 of the madrigal Poi ch’ella in sé tornò from Monteverdi’s book III, the predominant is reached by a note-against-note dissonance D–C (Example 22). At a local level, however, the dissonant pitch is implicitly prepared by the root C of the previous chord and could be explained by a register transfer. This is shown by the reduction (Example 23) and confirms that free composition can always be reduced to strict parsimony and regular counterpoint if a triadic background is presumed and if the triads move in a dominant direction. What is more, the predominant D is involved in relatively important elaborations from measure 36 onwards. Thus, from a broader perspective, C5 at measure 38 could be interpreted as a mere passing note that resolves onto B4, the fifth of the dominant. The fact that the subdominant involves a note-against-note dissonance and that it is elaborated intensively over three measures grants it relative autonomy. This suggests that it derives its legitimacy and meaning from how it is arrived at and left, harmonically.
[65] The elaboration techniques revealed in Examples 22 and 23 do not lead to a large distance between foreground and background, but they do show a real link between asymmetry and elaboration, a connection that allows us to make two observations. First, the elaborations happen in a tonal context: they focus specifically on the dominant and predominant to enhance tonal coherence. Second, spontaneous asymmetry is crucial to the integration of these superficial phenomena: it is the way the harmonic units are reached and moved from that allows for the integration of the contrapuntal licenses and grants them a particular syntactical meaning. From this perspective, the above elaborations result indirectly from the integration of spontaneous asymmetry.
[66] In his attempt to formalize a generative syntax of tonal harmony, Martin Rohrmeier (2011) tries to reconcile Riemannian tradition with recursive and prolongational approaches. His results tend to confirm that a comparatively simple set of rules suffices for the explanation of a large range of examples because “tonal harmony is fundamentally grounded in elaborations of cadential harmony” (2011, 48). The empirical results and theoretical reflection outlined here partly corroborate this hypothesis. At the same time, they suggest that both the crystallization of static tonal functions and the hierarchical articulation of tonal syntax may be historically linked to the changing status of the asymmetry of root progression. A systematic consideration of the asymmetry of root progressions could thus provide a better understanding of the hierarchical and functional characteristics of tonality, historically.(8) What is more, it could also help to integrate contrapuntal structures, those lying outside the tonal framework, into this same understanding of tonal harmony.
5. Conclusion
[67] The theory of harmonic vectors argues that the dominant direction of chord progressions is a characteristic feature of tonality. This paper in turn suggests that it is not so much the mere prevalent direction that is crucial but the fact that this directional tendency emancipates itself from contrapuntal constraints and acts on them. This evolution from a conditional to a spontaneous asymmetry can be deduced from several phenomena: the dissolution of the cantus-tenor framework, the increased use of major triads, the morphology of the seventh chord, and the fact that irregular dissonances are increasingly compatible with the preferred dominant direction.
[68] The recurrent use of cadential progressions helped assimilate this preferred direction over decades. The increase of spontaneous asymmetry may have been influenced decisively by irregular dissonances that temporarily suspend contrapuntal logic. This study has shown that the assimilation of spontaneous asymmetry provided new compositional possibilities and contributed to a greater distance between foreground and background.
[69] This evolution did not come to an end at the turn of the seventeenth century: it continued through the following centuries. However, the evolution outlined in the corpus suggests that the shift from conditional to spontaneous asymmetry, with all its theoretical implications, had already taken place, in large part, in the last madrigal cycles analyzed above.
[70] This paper does not claim that all aspects of tonality can be reduced to asymmetry. It does not even suggest that asymmetry is a characteristic feature of tonality, but, because asymmetry is tightly related to other important tonal features and because it interacts with these features, this analytical and theoretical criterion has a significant heuristic value for understanding tonality.
Christophe Guillotel-Nothmann
Institut de Recherche en Musicologie (IReMus – UMR 8223)
2 rue de Louvois
75002 Paris, France
christophe.guillotel-nothmann@cnrs.com
Works Cited
Besseler, Heinrich. 1950. Bourdon und Fauxbourdon. Studien zum Ursprung der niederländischen Musik. Breikopf und Härtel.
Cathé, Philippe. 2010a. “Harmonic Vectors and Stylistic Analysis: A Computer-aided Analysis of the First Movement of Brahms’ String Quartet Op. 51-1.” Journal of Mathematics and Music 4 (2): 107–119.
—————. 2010b. “Nouveaux concepts et nouveaux outils pour les vecteurs harmoniques.” Musurgia 17 (4): 57–79.
—————. 2012. “Synchronie et diachronie: musique française (1870–1950) et théorie des vecteurs harmoniques.” Thesis (Habilitation), Université Paris-Sorbonne.
Cohen. David E. 2003. “’The Imperfect Seeks Its Perfection’: Harmonic Progression, Directed Motion, and Aristotelian Physics.” Music Theory Spectrum 23 (2): 139–169.
Dahlhaus, Carl. 1966. “Über den Begriff der tonalen Funktion.” Beiträge zur Musiktheorie des 19. Jahrhunderts, ed. Martin Vogel, 93–102. Bosse.
—————. 1975. “Terminologisches zum Begriff der harmonischen Funktion.” Die Musikforschung 28 (2): 197–202.
—————. 1990a. “Die maskierte Kadenz, Zur Geschichte der Diskant-Tenor-Klausel” In Neue Musik und Tradition. Festschrift Rudolf Stephan zum 65. Geburtstag, ed. Josef Kuckertz et al., 89–98. Laaber.
—————. 1990b. Studies on the Origin of Harmonic Tonality. Trans. Robert O. Gjerdingen. Princeton University Press.
De Jong, Karst, and Thomas Noll. 2008. “Contiguous Fundamental Bass Progressions.” Dutch Journal of Music Theory 13 (1): 84–97.
Desbordes, Bertrand. 2003. “Le langage harmonique des récitatifs simples mozartiens: une approche par les vecteurs harmoniques.” Thesis (Habilitation), Université Paris-Sorbonne.
Eberlein, Roland, and Jobst Peter Fricke. 1992. Kadenzwahrnehmung und Kadenzgeschichte: ein Beitrag zu einer Grammatik der Musik. Lang.
Einstein, Albert. 1949. The Italian Madrigal. Princeton University Press.
Fétis, François-Joseph. 1840. Esquisse de l’histoire de l’harmonie considérée comme Art et comme science systématique. Bourgogne et Martinet.
Guillotel-Nothmann, Christophe. 2007. “Dissonances et progressions harmoniques: Le cas du Tractatus augmentatus compositionis (c.1655–1659) de Christoph Bernhard.” Master’s thesis, Université Paris-Sorbonne. https://hal-bnf.archives-ouvertes.fr/dumas-01447702.
—————. 2009. “Dissonance and Harmonic Progression: The Impact of Seconda Pratica on the Advent of Tonality.” 2nd International Conference for PhD Music Students, ed. Athanasia Kyriakidou, 34–42. Aristotle University of Thessaloniki. https://hal-bnf.archives-ouvertes.fr/halshs-01501241v1.
—————. 2010. “Traitement des dissonances et progressions harmoniques. L’impact de la seconda pratica sur l’origine de la tonalité.” Musurgia 17 (4): 33–55.
—————. 2017. Asymétrie conditionnelle et asymétrie spontanée des progressions harmoniques. Le rôle des dissonances dans la cristallisation de la syntaxe harmonique tonale (c. 1530–1745). PubliQation – Academic Publishing.
Guillotel-Nothmann, Christophe and Claire Meyer. 2013. “Polarisation et direction privilégiée des progressions. À la recherche du fonctionnement tonal et de ses fondements.” In Regards sur la Tonalité, ed., Henri Gonnard, 29–48. Delatour.
Gut, Serge. 1969. La tierce harmonique dans la musique occidentale. Heugel.
Hedges, Thomas, and Martin Rohrmeier. 2011. “Exploring Rameau and Beyond: A Corpus Study of Root Progression Theories.” Paper presented at the Mathematics and Computation in Music, Third International Conference, Paris, June 15–17. http://www.researchgate.net/publication/220846592_Exploring_Rameau_and_Beyond_A_Corpus_Study_of_Root_Progression_Theories.
Lowinsky, Edward. 1962. Tonality and Atonality in Sixteenth-century Music. University of California Press.
McClary, Susan. 1977. “The Transition from Modal to Tonal Organization in the Works of Monteverdi.” PhD diss., Harvard University.
Meeùs, Nicolas. 1988. “Vecteurs harmoniques. Essai d’une systématique des progressions harmoniques.” Fascicules d’Analyse Musicale 1: 87–106.
—————. 1989. “Systématique des progressions harmoniques.” Fascicules d’Analyse Musicale 2: 11–20.
—————. 1992a. “Transitivité, rection, fonctions tonales. Une approche cognitive de la tonalité.” Analyse musicale 26: 26–29. http://nicolas.meeus.free.fr/NMSemio/NMTransitivite.pdf.
—————. 1992b. “Vecteurs harmoniques. Essai d’une définition opératoire de la tonalité.” Thesis (Habilitation), Universitè Paris-Sorbonne.
—————. 2000. “Toward a Post-Schoenbergian Grammar of Tonal and Pre-tonal Harmonic Progressions.” Music Theory Online 6 (1).
—————. 2001. “Note sur les vecteurs harmoniques.” Musurgia 8 (3/4): 61–64.
—————. 2003. “Vecteurs harmoniques.” Musurgia 10 (3/4): 7–34.
Meyer, Claire. 2009. “Les Sacri concentus (1630–31) de Léonard Hodemont (c. 1580–1636).” Doctoral diss. Paris-Sorbonne.
O’Donnell, Aidan. 2011. “Le rôle de l’alfabeto dans le développement de la pensée harmonique en Italie, 1600–50.” Doctoral diss., Paris-Sorbonne.
Rameau, Jean-Philippe. 1737. Génération Harmonique, ou Traité de Musique Théorique et Pratique. Prault fils.
Riemann, Hugo. 1909. Hugo Riemanns Musik-Lexikon. Seventh edition. Hesse.
Rohrmeier, Martin. 2011. “Towards a Generative Syntax of Tonal Harmony.” Journal of Mathematics and Music 8 (1): 35–53.
Schenker, Heinrich. 1954. Harmony. Ed. by Oswald Jonas, trans. by Elisabeth Mann Borgese. University of Chicago Press.
Sechehaye, Albert. 1926. Essai sur la structure logique de la phrase. Champion.
Tymoczko, Dmitri. 2003. “Progressions fondamentales, fonctions, degrés: une grammaire de l’harmonie tonale.” Musurgia 10 (3/4): 35–64.
—————. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. Oxford University Press.
Footnotes
* I would like to thank Aidan O’Donnell for his endless patience and invaluable help in editing and proofreading this paper. Thank you also to the anonymous reviewers for the helpful suggestions during the revision of this article and to the editors of MTO.
Return to text
1. Tymoczko (2003, 46–47) draws attention to the particular status of subdominant progressions. Occurring on specific scale degrees, they can play a critical role in establishing tonality, as for example the subdominant progressions embedded in the a–b–a patterns I–V–I and I–IV–I.
Return to text
2. Theorists of the fourteenth century award a special status to two particular progressions: major sixth – octave and minor third – unison. They thus systematically apply the principle of voice-leading proximity to intervallic classes.
Return to text
3. The relationship between the evolution of cadential lines and harmonic progressions has been studied in detail in Guillotel-Nothmann and Meyer 2013 and Guillotel-Nothmann 2017, 461–471.
Return to text
4. These questions of the hierarchy between different representatives of the same tonal function and of a possible distinction between a main representative and substitutes are discussed in detail in Dahlhaus 1966; 1975.
Return to text
5. Compare these results with those reported in Cathé 2012, 25, 129, 159.
Return to text
6. In the case of the suspension dissonance, the chord progressions associated with the preparation, and the successive resolution of the dissonance onto the imperfect and perfect consonance have been taken into account (see the model in Example 4). In the case of the dissonance note against note, only the chord progressions associated with the dissonance’s impact and immediate resolution have been selected.
Return to text
7. The “Syncopa tutta cattiva” corresponds to a particular type of dissonant syncopation where the dissonance is reached and left by stepwise melodic movement up and down at the same voice (compare in Example 8 how the dissonance C4–F4 is reached and left at bar 24). In the case of the “dissonant preparation” the regular consonant preparation of the suspension is replaced by a dissonance. A dissonance “note against note” occurs when the dissonant interval is reached by simultaneous movements at both voices (see Example 18, bar 26, the way the dissonance D3–E5 is reached). An “absence of resolution” occurs when the dissonant note of a suspension remains in place and never resolves downwards. Finally, the categories “resolution on a silence” and “resolution on a dissonance” self-evidently correspond either to the resolution of a dissonance (suspension, passing note, neighbor note or anticipation) on a silence or on another dissonance (see Example 18, bars 22–23, the resolution of the dissonance
Return to text
8. Tymoczko (2003, 42) has argued that if the historian could confirm that functional tonality appeared when composers gradually began to favor dominant progressions over subdominant progressions, it would constitute a decisive step towards an explanation of tonal harmony. The results obtained here suggest that it is not so much the accentuation of asymmetry that seems decisive from a historical point of view for the crystallization of functional harmony but the changing status of asymmetry.
Return to text
Copyright Statement
Copyright © 2018 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Rebecca Flore, Editorial Assistant
Number of visits:
5364