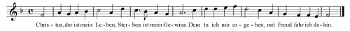Harmonic Vectors
and the Constraints of Tonality

1. The Theory of Harmonic Vectors

[1] The Théorie des vecteurs harmoniques (“Theory of harmonic vectors,” or THV) deserves a few words of introduction, even though an English-language presentation has already appeared in Music Theory Online, following the SMT meeting in Atlanta in 1999 (Meeùs 2000; see also Meeùs 1988 and 1989).⁽¹⁾ The THV has been described as close to “a pure root-motion theory” (Tymoczko 2003, 3), in that it asserts the syntactic value of harmonic progressions solely in terms of root motions. The THV is based on the conviction that harmonic functions are not inherent in the chords themselves, but arise from the relation between chords and, more specifically, from the progression from one to the next.

[2] The use of the term “vector” to describe root progressions does not refer so much to its mathematical meaning as to the somewhat metaphorical usage of process philosophy, where the word denotes a flux, a carrier, a transmitter, the dynamic process by which an input is transformed into an output. The conception of harmonic functions as residing in the chord progressions rather than in the chords themselves is a recognition of the fact that, in our traditional view, “the ‘scalar’ form overwhelms the original ‘vector’ form. . . . The vector form is not lost but is submerged as the foundation of the scalar superstructure” (Whitehead 1978, 212). As in Newtonian physics, “the dominance of the scalar physical quantity . . . obscured the recognition of the truth that all fundamental quantities are vector and not scalar” (Whitehead 1978, 177). The THV is a transformational theory. A “vector,” in the sense considered here, is properly speaking a “function,” linking an output to an input.

[3] An isolated chord has no harmonic function. No chord can be recognized as a dominant or a subdominant unless by its relation to a tonic (or one of its substitutes). Schoenberg expressed a similar point of view when he stated that “structural functions are exerted by root progressions” (1969, 6) and when he spoke of “a dominant with the function of V–I” (1969, 28): the dominant function, in this description, does not reside in the V chord, but in its relation to I. Even the tonic function arises from a retrospective relation to other chords. Harmonic functions, in other words, are transitive, both from a syntactic and from a semantic point of view, both with respect to their position in the tonal syntax and to their tonal meaning (Meeùs 1992).

[4] The THV identifies two types of harmonic vectors. The first type is the dominant vector (DV), the relation between two chords of which the first is a fifth above (or a fourth below) the second in terms of fundamental bass, e.g., V→I or I→IV. The second type is the subdominant vector (SV), between two chords of which the first is a fifth below (or a fourth above) the second, e.g., I←V or IV←I. The abstract “direction” of the vectors, conventionally denoted by arrows pointing to the right for dominant vectors and to the left for subdominant ones, can be equated neither with the succession of the roots in time—represented by their order from left to right—nor with the ascending or descending direction of the actual progressions, since the roots are understood as pitch classes. The vector’s “direction” may be considered a “semantic” direction, for which it would be difficult at this point to propose other translations than merely “dominant” and “subdominant”—or, more generally, “function.”

[5] The size of the vectors (the interval of the progression) can be a fourth, a third, a second, or their inversions (fifth, sixth, or seventh). The usual techniques of substitution (e.g., Rameau’s double emploi or Riemann’s “feigned consonances”) allow reducing all six to the two types described in paragraph [3] above. Substitutions consist in replacing a chord by the one a third above or below, that is, assuming an implied additional third progression. Reverting the substitutions reduces all progressions to those of a fifth or a fourth—see Example 1. Because the THV is based on root progressions, neither the mode of the chords nor the size of the second or third progressions is important at this stage (although they may have to be taken in account under some specific conditions). The only progression not covered is that of the tritone (diminished fifth or augmented fourth, ascending or descending), because its direction cannot be ascertained.

[6] One important premise of the THV is that the progressions are not constrained a priori by the tonality of a work or a passage. On the contrary, tonality itself may be constrained by the progressions. Roman numerals were used above for convenience, but the progressions are assumed to be independent of their position in the tonal scale. The items in Example 1 can be rewritten with symbols denoting by the figures 4, 3, or 2 the magnitude of the interval, and signs + or – for the ascending or descending direction of the progressions, without assigning them positions in a scale. See Example 2. From this it can be seen that the ambition of the THV is to be able to discuss tonality without presupposing it. It usually is not possible to assign a Roman numeral (or a tonal function) to a chord without having presupposed the tonality that it expresses and the key to which it belongs. Harmonic vectors can be assigned without such presuppositions.

[7] The common conception that tonal progressions are constrained by the tonality, to the point that they actually result from it, usually is subsumed under notions of tonal tension and resolution, which entail ideas of attraction, obligatory voice leading, etc. In such descriptions, the progression V–I results from the fact that the dominant chord is attracted by the tonic chord, that the leading note is attracted by the tonic note, possibly that the dissonance (the seventh) is attracted by its resolution, and that all these are cases of tonal tension resolving in relaxation. The THV, on the contrary, is based on the conviction that the truth is the other way around, that tension and attraction can only be retrospective. A dominant chord cannot be shown to be attracted by a tonic chord unless it resolves to it; indeed, it cannot be considered a dominant unless it resolves to the tonic—a so-called “dominant” chord that does not explicitly or implicitly resolve on a tonic or on one of its substitutes is not truly a dominant. And reciprocally, a “tonic” that is not included in a “dominant” relation, a Dominant Vector (DV), of the type V→I (or a subdominant relation, a SV, of the type IV←I) may not be really a tonic. Tonal functions result from root progressions, they are not their causes.

[8] This is not to say that the THV rejects the semantic value of tension, attraction, or relaxation in tonal music. But these too can only be retrospective: a supposed tension in a chord can too easily be negated by an unexpected resolution. If dominant chords appear in themselves loaded with tonal tension, it can only be by force of habit, that is, by force of the tonal usage and of typical progressions. The “dominant” meaning does not reside in the chord itself, but in the expected progression following it. Tension and attraction reside in the “vector character” (Whitehead) of the link between chords.

[9] The THV is dualist in the sense that it considers two possible “directions” for the harmonic vectors, either “dominant” or “subdominant.” This view is similar to Rameau’s when he wrote that “any fundamental note that is not tonic, and that descends a fifth, is therefore dominant. . . . Any fundamental note that ascends a fifth is always subdominant” (1760, 29). The THV, however, is not comparable to nineteenth-century German dualism, because that tradition took the tonic itself as its central point: the opposition is between the chord a fifth above and another a fifth below the tonic (which Riemann [1896, 7] associated with the tonic’s overtone and undertone series, respectively). The directions of the harmonic vectors should also not be confused with the ascending or descending direction of the progression itself: as we have seen, the main “dominant” progression, for instance, is either or , where the + and – signs indicate the ascending or descending direction, while → denotes the abstract “dominant direction.”

2. Constraints

[10] The THV does not consider all degrees entirely free to progress in any direction, but merely avoids discussion in terms of a presupposed tonal hierarchy: the case of tonality is methodologically left aside. De Jong and Noll (2008, 87) rightly stress that “the assumption of a free unlimited space for the progression of the fundamental bass is not realistic for an advanced theory of harmonic tonality. . . . Tonal harmony constrains the routes taken by the fundament. But little is known about the principles that govern these constraints.” They consider nevertheless that “although it is desirable to make tonally sensitive fundamental-bass analyses, it is a disembarrassment for the analyst to have a tonally free neutral level of description, where the path of fundaments may be traced without the constraints of bulky theories of harmonic tonality.” And they add that the THV “highlights aspects of harmony that are submerged in the traditions of scale degree theory and functional harmony. Both traditions pay much attention to the chords or functions in the sense of positions within systems of harmonic signifiers or signifieds, and suffer from a lack of attention for the harmonic process” (2008, 88). The THV indeed is a theory of harmonic processes—a transformational theory—but it will not provide a satisfactory explanation of tonality so long as it fails to justify tonal constraints and their relation to the harmonic progressions.

[11] Classifying root progressions in a pure root-motion theory opens questions that should be answered by any theory of tonality, but that are not often raised in this context. The point is not of discovering how “tonal harmony constrains the routes taken by the fundament,” as De Jong and Noll claim, but instead of describing the rules of root-motion that may constrain tonal harmony. The principal questions can be placed under the following headings:

[11.1] Asymmetry: The asymmetry of the root progressions, by which DV appear more frequent than SV, especially in common practice tonality. The asymmetry (or the directional orientation) itself is a well-known fact, but it is too often explained by tonal attractions, the effect being taken for the cause, as explained above. This problem has been the concern of some recent French research, which deals with, among other things, the statistics of progressions in large corpora (e.g., Cathé 2012 and Guillotel-Nothmann 2017).

[11.2] Diatonicity: The limited span covered by root progressions, often no more than four or five roots in any given key and usually confined within one or a few diatonic collections in a full composition. A constant succession of vectors would inexorably lead away from the starting point: the limitation of the span covered plays an important role in tonal centricity. Meeùs (2000) had already stated that a well-formed tonal phrase requires at least one substitution, but this needs further consideration.

[11.3]Tonicization: The assignment of the position of tonic within the span covered by the progressions probably is constrained mainly by cadences. In the major/minor system the possibilities reduce to just two: if the diatonic scale is presented in the order of six ascending fifths, say F C G D A E B, the major tonic is the second degree (C), the minor tonic is the fifth degree (A);⁽²⁾ while in modal polyphony of the sixteenth century, six of the seven degrees could serve as “tonic.”

[11.4] Asymmetry, diatonicity, and tonicization appear as the three main constraints of tonality. They are interdependent, however, and must at some point be considered together: this is what I will try to indicate in this article, without claiming to afford any definitive answer.

[12] Lerdahl (2001) does give some consideration to these questions, but too often takes tonality for granted. He does not really problematize the question of asymmetry: while his geometric representations allow a description of paths and journeys in the tonal space, they do not explain the mechanisms at work or the reasons why these paths usually choose one direction and not the other. His view of diatonicity is restrictive: any accidental seems considered to denote a modulation, or at least a change of diatonic collection. The problem of tonicization therefore seems to reduce for him to considering the diatonic collection concerned.

[13] Schoenberg did propose a classification of root progressions based on common notes between the two chords involved: in so doing, he took account not only of the interval, but also of the direction of the progression. Much earlier, Rameau (1737; 1750) had done the same, but based on common overtones rather than common notes; this, however, only raises additional problems (that will not be considered here). In Schoenberg’s case, he described the progressions as “ascending” or “descending,” depending on the relative position of the common tone in each chord, as shown in Example 3 (adapted from Schoenberg 1969, 6-7, examples 10a, 11a, 12a and 13a). His “ascending” and “descending” progressions correspond to what is called here the “dominant” and “subdominant” progressions—except for the important difference that he did not include progressions by a second, which he placed in a separate category of “superstrong” progressions.

[14] The case of progressions with two common notes (progressions by a third) tacitly involves the additional criterion of diatonicity. In the example from Schoenberg above, the descending third progression, I–VI, is a minor third from major to minor, because in a diatonic scale the chord a third below a major one always is minor and always distant by a minor third; the ascending one, I–III, is a major third, again from major to minor, for similar reasons. The mode of the chords cannot be changed unless the size of the intervals and the direction of the progression are modified at the same time. And any other third progression would not be diatonic: such progressions are possible in nineteenth-century harmony, where they form the essence of the romantische Terzverwandtschaft, but they cannot involve two common tones.

[15] Diatonicity also constrains progressions up or down a second between major or minor triads: the progression, in these cases, must involve a major second (a whole tone), or would result in a false (non-diatonic) relation between the fifth of the lower chord and the prime of the higher one. In order to remain diatonic, a progression of a semitone must include a diminished triad as its lower chord. Fourth progressions are less constrained: they may occur between major or minor triads; however, the progression of a fourth with a change of mode can occur only if the major chord is the higher, that is, ascending from minor to major or descending from major to minor.

[16] Because several of the diatonic constraints just described apparently concern voice leading more than progressions of the fundamental bass, a word must be said at this point concerning the relation between them. Primarily concerned with the parsimony of the voice leading, neo-Riemannian theory tends to reduce all root progressions to those involving only one movement in the voice leading—in the case of diatonic progressions between triads, progressions with two common notes, and progressions by a third. But this involves the problems briefly described in [14] above. It is necessary to take account of both the ascending or descending direction of the progression and the major or minor interval covered: the voice leading then appears to determine the root progression.

[17] Matthew Shirlaw discussed the double nature of Rameau’s basse fondamentale, on the one hand expressing the theory of chord inversion—in which case the fundamental note really is the root of the chord—and on the other hand trying “to discover the underlying principles that govern the progressions from one harmony to another” (1917, 98)—in which case the fundamental bass forms a more abstract view of the whole. The fundamental bass may be seen in first instance to represent the succession of the roots (see, for instance, Brower 2008, 69–70), but at a more speculative level it forms an abstract representation of the harmonic/polyphonic complex as a whole. As Rameau himself wrote, “with respect to the progression of the parts that include each one note of these chords, . . . it must be diatonic and this obligation arises from the consonant progression of the fundamental bass; therefore, if one knows the size of the intervals, one feels inclined as if involuntarily to give to the high parts this diatonic progression” (1722, 52; on his theories of voice leading, see also Book II, Chap. XIX). Rameau considers that the progression of the individual parts is ruled by that of the fundamental bass, but this could as easily be reversed, the voice leading ruling the fundamental bass. For our purpose, it will suffice to consider that they represent each other and that, especially in terms of pitch classes, the progression of the fundamental bass merely subsumes the progressions of the parts.

3. Analyses

[18] In all the examples below, the fundamental bass is notated on a separate staff under the score, with the following conventions: half notes denote major chords, quarter notes minor chords; DV (dominant vectors) are indicated by arrows pointing to the right, SV (subdominant vectors) by arrows pointing to the left; thick arrows mark progressions by a fourth, thin ones indicate a substitution (that is, progressions by a third or a second). Main cadences are underlined by a “swan slur” stressing the succession predominant–dominant—that is, a major chord preceded by another one a second or a fourth lower and followed by another one a fourth above or a fifth below.⁽³⁾ A statistical overview is given, showing the number of pitch classes, major triads, dissonances, roots, and DV. As the examples and statistics will show, the THV allows an approach to tonality different from that of our usual analytic usages.

[19] The first example is a fragment from Lassus’s Bonjour mon Coeur (1564), mm. 16–22—see Example 4. The fragment’s overall key may be D minor or D Aeolian, but if so with a very high tonal instability despite the extremely strong asymmetry (94% of DV).⁽⁴⁾ The bass covers one single diatonic collection, the seven notes of the cycle of fifths from B♭ to E. All triads are in root position: the bass part and the fundamental bass are identical. Cadences follow each other almost without interruption but in too many different keys to produce any sense of tonal stability (E is the only root not approached by a cadence). The fast succession of major triads—all seven roots support at least one major triad—obviously could not belong to one single diatonic collection, and it produces frequent chromatic relations: this is one of the stylistic features that make this fragment (and the piece itself) hardly tonal.

[20] Questions raised by this fragment concern both the very high asymmetry and the composer’s attitude concerning diatonicity. Even although it is not the purpose of this paper to discuss sixteenth-century harmonic usages, one may note that the chromatic inflections in the upper voices (B♮, F♯, C♯, and G♯) always concern the third of the triad, transforming minor chords into major ones (the only exception being the G minor triad in m. 21). As such, they must be considered of the order of musica ficta—they represent mere inflections of an essentially diatonic substrate, as evidenced by the diatonic bass part, and with relatively little concern for the affirmation of a unified key. This may be a general characteristic of sixteenth-century modal polyphony, even in less chromatic compositions.

[21] The passage above may be compared with the beginning of the same piece, mm. 1–6 (Example 5; mm. 6–12 are a repeat of the same). Here the music is more clearly diatonic (the few chromatic inflections are concentrated in m. 5), and it may give a more coherently tonal effect, despite the lack of asymmetry. The key of G (the main key of the piece as a whole) indicates a Mixolydian mode—that is, a “tonic” in third position in the cycle of ascending fifths. The major triads on F, C, and G are those dictated by the diatonic system of the piece (in systema regulare, that is, without key signature); the single triad on A and one of the two on D are rendered major by an inflection of their thirds in m. 5; this also is the sole full cadence in the fragment. The first measures of the fragment are occupied mainly by “pendular” progressions, C–G–C, G–C–G, or C–F–C.⁽⁵⁾

[22] Let us turn to a second example, the chorale Christus, der ist mein Leben, by Melchior Vulpius (1609; Example 6). There are five different roots, and these are not equally distributed: ten chords on F, five on C, three each on G and on B♭ (which are substitutions for each other), and just one on D. All pitch classes, in addition, belong to the diatonic collection in the cycle of fifths from B♭–E. Yet, the asymmetry remains rather low, with only 64% of DV. It is therefore the diatonicity of the pitch classes and the irregular distribution of the roots (almost one chord out of every two is an F triad) that marks the somewhat more tonal effect of this piece. The number of “pendular” progressions remains rather high and they always concern F (F–C–F, F–B♭–F or F–G–F). On the other hand, of the six cadence figures, four are on B♭, against two on F.

[23] J. S. Bach’s realization of the same chorale (BWV 281; see Example 7) at first appears less diatonic, with nine different pitch classes instead of seven. The additional pitch classes are the passing E♭ in m. 1 and two B♮s (mm. 5 and 6). The third phrase, framed in the example below, is written in a different diatonic collection, fifths from F to B instead of from B♭ to E; the shift in the diatonic collection is confirmed by the cadence on C at the end of phrase 3—compare the example by Vulpius above, where all four phrases end on an F triad. On the basis of this example, it would seem that modulation itself may have to be considered an additional constraint on tonality. The reason remains unclear, but it may correspond to a desire to stress the diatonic scale and to reserve chromatic inflections to wider spans, resulting in changes in diatonic collections, instead of a lack of concern for diatonicity, as in the first Lassus example above.

[24] The last example, Max Reger’s harmonization of the same melody, his op. 79b, no. 9 (Example 8),⁽⁶⁾ raises additional questions concerning the harmonic analysis itself. Because of the large amount of figuration (passing and neighbor notes), the identification of the chords is not as straightforward as in the previous examples.

[24.1] In some cases, although the voice leading produces vertical arrangements of notes that could be identified as chords, these would result in a questionable harmony, as in m. 3; these “chords” have not been included in the calculations. In other cases, chords that produce a coherent harmony nevertheless could also be explained as resulting from the voice leading: their roots are then inscribed as notes without stem. Pendular progressions (upbeat to m. 1; mm. 5 and 8) are not included. In the other cases, the corresponding vectors have been inscribed above the main line of vectors, but they have not been taken in account for the statistics. One could easily verify that they would not significantly modify the statistics.

[24.2] The remaining chords evidence a harmonic rhythm similar to that of the previous examples. Some of them could also be explained as resulting from the voice leading and therefore may not qualify as Stufen in the Schenkerian meaning of the term. The question whether more elaborated Stufen could be taken in account in the THV, and how, will not retain us here, but it remains an open question for future research.

[25] Reger’s version of Christus, der ist mein Leben shares several features with the first Lassus fragment studied above: it is fully chromatic (12 pitch classes), with all 6 roots supporting at least one major chord. It would be pointless to try to single out any diatonic collection for any significant span of time. The asymmetry is extremely high, 93%. Cadences conclude on five of the six roots, F, G, B♭, C, and D. More specifically, the first phrase cadences on D in m. 2, the second phrase ends in D without a formal cadence; the third cadences in C; and the fourth in F.

[26] To some extent, such a piece closes the era of common practice tonality by returning to usages of the late sixteenth century. There are important differences, however. While several of the chromatic alterations do function to change the mode of the chords, the proportion of major chords (73%) nevertheless remains lower than in the preceding examples (the identification of the chords’ quality, however, is moot in more than one instance). Many chromatic degrees are passing notes, foreign to the harmony. The first half of the piece may be described as being in D minor, a tonality that was not even hinted at in the Vulpius and Bach examples. The importance given to the minor relative of F major may be put in relation with the rather high percentage of root progressions by third, more frequent here than those by second: this reflects the importance of Terzverwandschaften in nineteenth-century tonality.

* * *

[27] Identifying the tonality of a tonal work is a complex task, involving many interrelated characteristics. One point that the above discussion fails to take into account is that the melody Christus, der ist mein Leben, probably by Vulpius (1609), already is “tonal” in its monodic form: Example 9. It is not useful to discuss whether this is transposed Ionian, or Lydian, or F major. The melody covers one octave from F4 to F5, with a single lower neighbor note E4, clear ascending and descending arpeggiations F4–A4–C5–F5–C5–A4–F4, a conspicuous upper neighbor D5 above C5, and passing notes filling in this “tonal space.” Root progressions, or more generally the harmony, in such a piece may not be sufficient to describe its tonality.

[28] The THV proposes a novel way of approaching and analyzing harmony; more specifically, it proposes an alternative view of harmonic functions. It appears particularly convenient for the statistical study of corpora—that is, it may be a help for stylistic analysis. It does not say—no more than any other analytic method—whether a piece is tonal, modal, or anything. But it does give insight into the inner functioning of harmony, and it does open paths for further research.

Nicolas Meeùs
Institut de Recherche en Musicologie (IReMus – UMR 8223)
2 rue de Louvois
75002 Paris, France
nicolas.meeus@sorbonne-universite.fr

Works Cited

Brower, Candace. 2008. “Paradoxes of Pitch Space.” Music Analysis 27 (1): 51–106.

Cathé, Philippe. 2012. “Synchronie et diachronie: musique française (1870–1950) et théorie des vecteurs harmoniques.” Thesis (Habilitation), Université Paris-Sorbonne.

De Jong, Karst, and Thomas Noll. 2008. “Contiguous Fundamental Bass Progressions.” Dutch Journal of Music Theory 13 (1): 84–97.

Guillotel-Nothmann, Christophe. 2017. Asymétrie conditionnelle et asymétrie spontanée des progressions harmoniques. Le rôle des dissonances dans la cristallisation de la syntaxe harmonique tonale, c. 1530–1745. PubliQation – Academic Publishing

Hedges, Thomas, and Martin Rohrmeier. 2011. “Exploring Rameau and Beyond: A Corpus Study of Root Progression Theories.” Mathematics and Computation in Music, C. Agon e.a. ed., Berlin, Heidelberg: Springer, 334–7.
Online: https://www.academia.edu/18037648/Exploring_Rameau_and_Beyond_A_Corpus_ Study_of_Root_Progression_Theories

Lerdahl, Fred. 2001. Tonal Pitch Space. Oxford University Press.

Meeùs, Nicolas. 1988. “Vecteurs harmoniques : Essai d’une systématique des progressions harmoniques.” Fascicules d’Analyse Musicale I (3): 87–106.
Online: http://nicolas.meeus.free.fr/NMVecteurs/Vecteurs.pdf

—————. 1989. “Systématique des progressions harmoniques.” Fascicules d’Analyse Musicale II (1): 11–20.
Online: http://nicolas.meeus.free.fr/NMVecteurs/Systematique.pdf

—————. 1992. “Transitivité, rection, fonctions tonales. Une approche cognitive de la tonalité.” Analyse musicale 26: 26–29.
Online: http://nicolas.meeus.free.fr/NMSemio/NMTransitivite.pdf

—————. 2000. “Toward a Post-Schœnbergian Grammar of Tonal and Pre-tonal Harmonic Progressions.” Paper read at the annual meeting of the Society for Music Theory, Atlanta, November 13, 1999. Music Theory Online 6.1: http://www.mtosmt.org/issues/mto.00.6.1/mto.00.6.1.meeus.html

Rameau, Jean-Philippe. 1722. Traité de l’harmonie: réduite à ses principes naturels. Imprimerie royale. Online: http://gallica.bnf.fr/ark:/12148/btv1b550084575?rk=21459;2

—————. 1737. Génération harmonique ou Traité de musique théorique et pratique. Prault fils.
Online: http://gallica.bnf.fr/ark:/12148/btv1b8623285t

—————. 1750. Démonstration du principe de l’harmonie. Durand, Pissot.
Online: http://gallica.bnf.fr/ark:/12148/bpt6k1082246

—————. 1760. Code de musique pratique. Imprimerie royale.
Online: http://gallica.bnf.fr/ark:/12148/bpt6k1080202

Riemann, Hugo. 1896. Harmony Simplified or the Theory of the Tonal Functions of Chords. Third printing. Augener.

Schoenberg, Arnold. 1969. Structural Functions of Harmony. Revised edition. L. Stein ed. Faber & Faber. First edition 1954.

Shirlaw, Matthew. 1917. The Theory of Harmony. Novello.

Tymoczko, Dmitri. 2003. “Root Motion, Function, Scale-degree.” English version, http://dmitri.mycpanel.princeton.edu/files/publications/tonaltheories.pdf. Original in French: Musurgia X (3–4): 35–64.

Whitehead, Alfred North. 1978. Process and Reality. An Essay in Cosmology. Corrected edition, D. R. Griffin and D.W. Sherburne, eds. The Free Press.

Footnotes

1. Several publications about the THV may be found at, or obtained through, http://nicolas.meeus.free.fr/NMVecteurs.html.
Return to text

2. Although this description of the minor is not entirely accurate—since it presupposes that the “normal” version is diatonic (the Aeolian scale), some degrees of this scale possibly being accidentally altered—the point will not be further explored in this article.
Return to text

3. This is a quite restrictive definition of “cadence,” resulting from the fact that no consideration is taken of position in the tonal scale. Cadences in this sense do not need to end on I or V, nor do they need to contain V as penultimate chord. Even the condition that the penultimate chord be major would in fact be unnecessary: as Christophe Guillotel-Nothmann explains in his article, the leading tone and its resolution are not considered essential for a dominant progression. Leading tones belong to the realm of rection (see also Meeùs 1992). It is only for the sake of my argument that the narrower definition of cadence has been chosen here, that is, the one that presupposes a major chord as penultimate.
Return to text

4. Tymoczko (2003, 4) writes that the THV takes asymmetries “to characterize the difference between modal and tonal styles,” and Hedges & Rohrmeier (Hedges and Rohrmeier 2011, 336) claim that the THV “suggest[s] the strength of dominant/subdominant symmetry to be a useful distinction between tonal and pre-tonal music.” These are misconceptions, or at least overstatements: the asymmetry, at best, is one indication among several, and certainly cannot serve as a measure of the level at which a piece is tonal.
Return to text

5. The case of pendular progressions will not be pursued further here. It may be noted that they often consist in progressions of a fourth or fifth and that they do not occur on all degrees of the diatonic scale. As such, they could represent interesting case studies for the link between progressions and tonality.
Return to text

6. The original is in E♭ major, a tone lower. It has been transposed here for the sake of comparison.
Return to text

Copyright Statement

Copyright © 2018 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.