Polarization, Modal Orientation, and Voice Leading: Interaction between Hierarchical Levels of Tonal Structure in Dohnányi’s op. 26
Hugues Seress
KEYWORDS: neo-Riemannian theory, post-triadic tonality, harmonic transformation, tonal function, Dohnányi Ernö
ABSTRACT: This article seeks to define tonality as an interaction between different levels of structure in terms of a conjunction of intervallic distance, polarization, modal direction, and voice leading of the harmonic progressions. Intervallic distances depend on the modal direction of transformations as well as on polarization on the circle of fifths in any hierarchy level. Voice leading creates pitch spaces that both embody and outweigh the abstract concept of tonal event according to transformational theories. This model of tonality is particularly relevant to music of the later nineteenth and earlier twentieth centuries, where works are based on complex, developed structures composed of non-symmetrical recurring units. The potential for analysis is demonstrated with several passages from Dohnányi’s Piano Quintet, op. 26, first movement.
DOI: 10.30535/mto.24.4.13
Copyright © 2018 Society for Music Theory
1. Introduction
[1] Transformational theories regard the tonal system as a set of operations acting upon a chord (or a tonality) such that a second chord (or tonality) results independently of a context based on a single point of reference. Among such models, neo-Riemannian theory is based on the concept of transformation of simple harmonic collections: major and minor triads and seventh chords. Chord succession follows the law of the shortest path, which favors common tones and parsimonious voice leading. The theory defines these transformations within a dualist system based on the chromatic scale and enharmonic equivalence. Inasmuch as tonal syntax is inferred, not taken for granted, the theory seems particularly well suited for analysis of discursive units of a tonal system where hierarchy and function are no longer those of traditional (or “common practice”) tonality, that is, a kind of tonality based on a triadic system for which the centripetal force of the tonic and polarity through falling fifths are no longer the principal compositional controls.
[2] For Riemann himself, the PLR transformational model was meant primarily to study a structure still grounded in the diatonic, governed by a tonality unified by the principles of dynamic function and the progression of chord roots. It is in a completely different context that some neo-Riemannian theorists take up nineteenth-century descriptions, removing them from the concepts of unified tonality and fundamental bass and introducing into their theories a chromatic logic that did not exist in the original formulation.
[3] When focusing on the functioning of the system, transformational theories do not make the identification of tonality a priority. In a way, the transformational approach is linked to a universal monotonality, that is, to the very absence of tonality as a category that lends itself to segmentation. The description of successive events often does not allow one to go beyond the framework of microstructure because the criteria underlying them are not directly transferable to higher levels. This observation is particularly relevant for the music of the transition from the nineteenth to the twentieth century, whose works rely on complex and often long forms made up of non-symmetrical recurring units.
[4] If tonality can be successfully grasped as a global system and should we also be able to reveal how local tonal systems work, then the missing link would be this “middle plane,” not only through the inner ties between tonalities themselves but also in the way they articulate each other. Nevertheless, whereas we can recognize the double nature of the system—classically tonal from a general point of view but chromatic when considered from local modulations (Cohn 2012)—transformational theories offer us no options to study the articulation between a general syntactic structure and local organization of tonal regions. In this sense, they may not be able to grasp in their entirety the seemingly contradictory forces that ensure the cohesion of the tonal system.
2. About the repeated characters of the levels
[5] The recursion of levels in tonal structure constitutes a much-debated topic in the theory of tonality. As early as the nineteenth century, confusion between harmonic progression and tonality stemmed from a belief in the possibility of a direct transfer from the one to the other, even though at the same time theorists held at best an imprecise definition of each of these levels.
[6] By describing harmonic progressions in terms of melodic fluidity, theories of voice leading consider the paradigm of the law of the shortest path to be the basis of all tonal phenomena. Admittedly the implications are much more far reaching than might at first seem to be the case: a strictly event-based vision of the system gives way to an organicist conception that spreads to every element of the language and applies at whatever scale this component is expressed. This extension of the process beyond the boundaries of merely successive events induces an area of ambiguity between chord and tonality. Thus, Arthur von Öttingen (1866) observed and classified progressions as combinations of thirds and mode change that, by definition, cannot be considered as belonging to the same tonality. Otto Tiersch (1868) maintained the confusion between tonal categories of different levels but developed an original theory of kinship according to a gradation of sounds either common or reciprocally connected, from which the signification of the chordal relation is evaluated in terms of dynamism.
[7] Theories of voice leading are not the only ones to cross the border between chord and tonality: models that consider the function of harmonic relationships as a starting point for their classification and their meaning also expand the concept of attraction from the functional cycle of chords to the tonal path. The functional equivalencies discovered by Hugo Riemann (1880) are the end result of combinations of steps of fifth (Schritt) and third relations (Wechsel): all the triads are attainable from an initial triad without specifying how many among them can be considered as pertaining to a single tonality. By default, then, Riemannian theory is ambiguous with respect to the relative size of tonal units. This is also the case with the theory of Rudolf Louis and Ludwig Thuille (1907), which effects the intervallic relations of functional qualities (dominant or subdominant) through the substitution of secondary intervals (thirds) for primary intervals (fifths).
[8] This long-standing tendency to confusion of the different levels of tonal structure is probably maintained by the idea that levels cannot be reduced to separate observation of chords and tonalities. Tonalities seem to be subordinated and not hyperordinated to harmonies, and thus articulation is thought to stem from the elaboration at a higher level of an element of a lower level. But even if the vertically orientated observation of the transformation of components is one of the most enlightening analytical attitudes concerning the relations between triads and tonalities, examining components from a horizontal segmentation can turn out to be significant. The latter is what I aim at in this paper. Whereas the topic as observed by neo-Riemannians essentially consists in the successive character of these progressions, I propose to shift the analysis of the microstructure to the articulation between the different levels of tonal organization.
3. Features of the transformational model: distance, modal orientation, and polarity
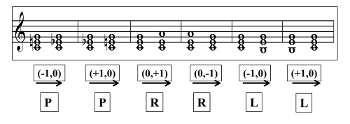
Example 1. Basic transformations
(click to enlarge)
3.1. Distance of transformations
[9] If we consider the three basic transformations—the ones that maintain two out of the three pitches of a triad—we observe that the third voice moves by one or two semitones in the same or opposite directions (Example 1). The figures within brackets (x,y) indicate the number of semitones (x) or whole tones (y) this voice moves through. They are indexed with the + sign (leading upwards) or – sign (leading downwards).
3.2. Modal orientation of transformations
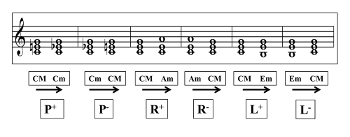
Example 2. Modally orientated basic transformations
(click to enlarge)
[10] The distance in semitones between the chord roots is a trait that characterizes transformations in a unique way (P = 0, R = 3, L = 4) and therefore is assumed in the label itself. The labels, however, say nothing about the modalities of the original and goal chords. We will call this distinctive character “modal orientation” (Example 2). The label proposed by the model is marked by a negative exponent when the transformation effects a change from the minor triad to the major triad, and by a positive exponent in the opposite direction.(1) The modal orientation represents a distinctive character that is particularly significant, in that reaching a major chord from a minor chord by an intervallic distance equivalent to P, R, or L cannot be considered equal to the same relation going in the opposite direction, from major to minor. To illustrate this, consider the transformations R- and R+. The R- progression Am–CM can underlie the tonal structure between the primary material and the secondary thematic material of the minor-key movements in a classical sonata, whereas the retrograde progression of R+, or CM–Am, can never have that function in this discursive pattern.
[11] Thus, within this model, a similar basic relationship—one for which the interval distance is equal—may very well not take the same role within the musical form and thus will not have the same harmonic meaning.
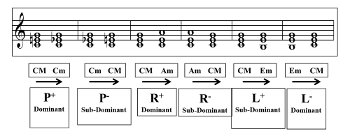
3.3. Polarity of transformations
[12] Polarity is the most meaningful property of triadic relationships, even if these relations are not strictly considered from a transformational point of view. It is, however, not so much the modal orientation but the polarity that seems to be involved in the familiar processes of harmonic progression and tonal hierarchy. Indeed, if we compare two transformations with the same modal orientation—L+R- and R+L-—and then realize them as CM–GM and CM–FM, respectively, we can easily recognize that the harmonic meaning, understood in terms of tension and resolution, is based on the axis of thirds and fifths, so: FM–Am–CM–Em–GM. Directionality, however, is essential: the meaning differs if the progression ascends or descends along this axis. The same is true, though perhaps less obviously, for the transformations CM–Am and Am–CM. The key distance on this axis is equal to 0, and thus these transformations are restricted to potential substitutions for a fifth relationship: R+L-: (CM–FM) for R+ and L+R-: (CM–GM) for R-.
Example 3. Modally orientated and polarized basic transformations
(click to enlarge)
[13] Because of the functional equivalence created by these substitutions, in the elaboration of the transformational model below, the polarity—that is, the direction on the circle of fifths—will not be included in the label as + or -, but will be indicated by means of a subsidiary label: Dom. or Sub. The progression is dominant (Dom.) if it goes down the circle of fifths (downwards or dominant direction), subdominant (Sub.) if it goes up (upwards or subdominant direction). For the third-transformations, | R | and | L|,(2) the polarity is similar to that of the fifth relationship for which they substitute (see Example 3). The distinction between dominant and subdominant progressions gives birth to a diatonic interpretation, when evaluating a chromatic system likely to self-govern itself away from the strict tonal framework. This distinction is necessary if we want to understand how the different levels of the structure articulate themselves, keeping in mind that some of them probably maintain a narrow link with the traditional functioning of the tonality.
3.4. Elaboration of the transformational model
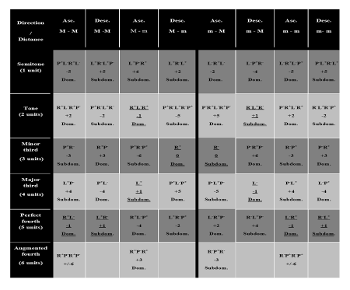
Example 4. The chains of transformations with distance and direction
(click to enlarge)
[14] The operations linking two harmonic entities can be sorted in three dimensions, as described above: intervallic distance, modal orientation, and polarity on the circle of fifths. The model can then be expanded by adding elementary transformations, thus creating a set of 44 chains or compounded progressions, all of them being equally characterized by a distance in semitones (from 1 to 6), a modal orientation (from major to major, major to minor, minor to major, minor to minor), and a polarity expressing itself by a number of steps on the circle of fifths (from -6 to +6). See the table in Example 4.
[15] The attribution of polarity to these compounded progressions is not self-evident, nor is the preferred label for each progression. We can consider these determinations, on the one hand, as completely independent, but, on the other hand, as strictly theoretical, not related to the discursive context of a musical piece. The first difficulty that we meet is with the best choice of a label. This is due to redundant chains; in other words, we observe that one cannot name a progression beyond three transformations uniquely. In the double or even triple designations of some chains, we either choose arbitrarily a particular label, or we regard some among them as complex variations of a main chain that is logically or chronologically pre-existent. For this article, the second option will be chosen. Thus, for example, the progression L+R- P+: CM–Gm, from CM–Em–GM–Gm, will be regarded as a variation of the progression L+R-, or CM–GM to which a chromatic transformation P+ is added. Note that each main chain (or in row 5 each pair) governs its half row.
[16] This conception, which interprets these tonal categories as potential and historically implemented substitutions—Gm for GM in the present instance—has as a direct consequence the attribution of a polarity that is not strictly theoretical, but that takes into account the discursive function of the harmonic or tonal progression. Here, L+R-P+ (CM–Gm) does not appear as a chain of a dominant polarity (0–2
[17] Example 4 organizes the set of labels (designations of the harmonic progressions) in relation to their arithmetic polarity: see, in the vertical axis, the six intervallic distances (from semitone to augmented fourth). In the horizontal axis, the eight modal orientations appear, beginning with the ascending major to major (MM) and ending with the descending minor-to-minor (mm). For the major second, minor third, major third, and perfect fourth, the main chain (as described above) has been underlined. It is according to this relation that this contextual polarity of the complex chain has been established. The coincidence between arithmetic polarity and contextual polarity is maximal for chromatic progressions. At a distance of a semitone, there is no main chain, strictly speaking (thus there is no underlining in row 1 of the table). To reach the minor by one semitone from the major and vice-versa, the shortest way follows the thirds path: higher from major to minor as L+P-R- or R+P-L+, lower from minor to major as L-P+R- or R-P+L-. For perfect fourth chains, the coincidence is equal to 75%,(3) which means that the main chains of these progressions (|LR|, |RL|) are only partially significant in the phenomenon of substitutions. It is not at all the same for the major second and minor third chains that the coincidence of which, only amounts to 25%. The chromaticism clearly comes from a substitution of the original diatonic relations |RLR| or |R|.
[18] Finally, major third relations are unique: all of the eight chains of the group show a coincidence of arithmetic and contextual polarities.
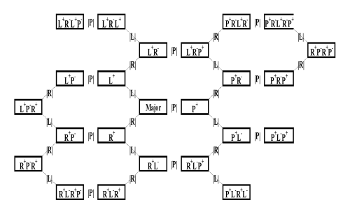
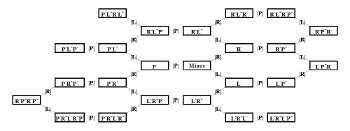
Example 5. The 23 chains of transformations oriented from a major chord or tonality
(click to enlarge)
Example 6. The 23 chains of transformations oriented from a minor chord or tonality
(click to enlarge)
[19] Examples 5 and 6 present a comprehensive view of all these transformations on a representation of tonal categories according to the proximity induced by the model. Example 5 shows the twenty-three chains of transformations oriented from a major chord or tonality. The chain labels result from an accumulation of the successive transformations that make up the chains. For example, from CM to
[20] Because the model distinguishes modal orientation, the map of categories and progressions from a minor category (see Example 6) is the mirror inverse of the previous one (compare the upper left of Example 5 to the lower right of Example 6).
[21] Each chain or generator of chains has three derivative forms, that is, chains expressing relations closely linked to the original, as retrograde, inversion, or retrograde inversion. The first of these produces a return to the initial chord or tonality: for instance, R+L- for L+R-. Inversion recreates the same relation with opposite modalities: for instance, R-L+ for L+R-. And retrograde inversion recreates the same relation from the opposite modality by retrograding: L-R+ to L+R-.
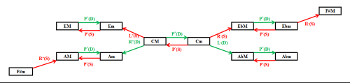
Example 7. Tonnetz and third relationships
(click to enlarge)
[22] Example 7 provides a partial realization of the model, where the transformations are oriented from a pair of C-major and C-minor triads. Here we can notice that the chain of minor thirds (combination of relative relations) unfolds from northeast to southwest, whereas the chain of major thirds (combination of leading-tone relations) is oriented from northwest to southeast.
4. The transformational model and voice leading
Example 8. Direction of the polarity and the voice leading
(click to enlarge)
[23] Intervallic distance is partly linked to the direction and modal orientation of the transformation. These orientated and polarized distances assume a discursive and formal function and hence play a role in the structure. Adding the observation of voice leading to the chains of transformations distributes the latter into three groups: those for which the voice leading can be rising, falling, or both simultaneously. This parsimony in voice leading between two tonal categories—which expresses itself in the form (x,y), where x is a number of semitones and y a number of whole tones—shows a direction that can coincide with, contradict, or be partially similar to the polarity. In Example 8, the polarity is indicated by the abbreviations “Dom” for dominant (towards the descending fifths), and “Sub” for subdominant (towards the ascending fifths). Thus, in the first row, the first progression, CM–Em, shows “Sub” polarity. Voice leading moves in the opposite direction, descending rather an ascending: (-1, 0). For each half row, the main chain is written in italic text. In row 1, first half (cells 1–4), the main chain is L+: each of the progressions in cells 2–4 can be understood as prepending or appending a P- (see again paragraphs [15] and [16]); the polarity is referred back to the main chain, so that cells 2–4 are all “Sub.” The situation is slightly different in the first half of row 4, where there are two main chains, R+L- and its retrograde L-R+, both of which are “Dom” because of the overall chord-root progression C–F. Here again, voice leading moves in the opposite direction, rising by a half step and a whole step.
[24] The confrontation between direction of polarity and voice leading shows that the progressions by distances of a major third behave in a particular manner; they constitute an isolated group (L+ [row 1, cell 1] and L- [row 1, cell 5]). For the relations of minor third, perfect fifth, minor or major second, with changes of mode—that is, for the great majority of relations—voice leading moves in the opposite direction from the polarity. Finally, concerning the minority group of relations of the major third and augmented fifth with changes of mode, that is, for the six chains L+P-, P-L+, L-P+, P+L-, P+L-P+, P-L+P- (cells 2–4, 6–8 in row 1), voice leading is partially accomplished in the same direction as polarity, with a balanced leading of voices.
[25] The coincidence between polarity and voice leading is identical for the relations of more than two transformations: from the ternary generators and beyond (more than three transformations), the fifth and major or minor seconds behave identically to the binary generators. On the other hand, and consecutively to the voice-leading principles, this relationship between polarity and voice leading is inverted if the relation is moved backwards, except for progressions featuring major thirds.
[26] Example 9 shows, for example, the cases of relations by distances of a perfect fourth. In cases where a chain of transformations appears in inversion or retrograde, the coincidence between polarity and voice leading remains in the same direction. This working principle is generalized because of the choice of the main chain‘s polarity, which does not concern the particular group of progressions by distances of major thirds (see Example 10).
Example 9. Inversion, retrogradation, and voice leading in fourth progressions (click to enlarge) | Example 10. Inversion, retrogradation, and voice leading in major third progressions (click to enlarge) |
5. Tonal path, orientated polarity, and voice leading: Ernő Dohnányi, Piano Quintet op. 26, I
Example 11. Dohnányi, Piano Quintet op. 26, I, tonal and thematic paths
(click to enlarge)
Example 12. Dohnányi, Piano Quintet op. 26, I, mm. 8–11, voice leading
(click to enlarge)
[27] In this section, we provide a case study of the transformational model described above. The chosen work is the first movement of the Piano Quintet, op. 26, by Ernő Dohnányi (1914). We will focus our interest on the possible correlation between polarity and voice leading as enhancing the hierarchy of tonalities. This method can perhaps be particularly suited to rhapsodic forms or to those based on juxtapositions where the border between the different degrees of tonal category (tonality and harmony) can be difficult to define.
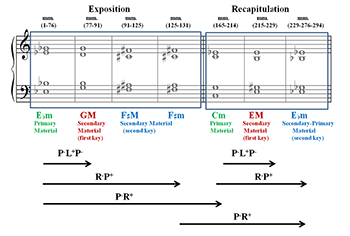
[28] Example 11 shows the sequence of tonalities throughout the movement. Three groups of thematic materials are presented (Th. 1, mm. 1 and 57; Th.2, m. 77; Th.3, m. 117), represented respectively in green, red and blue. The three groups are repeated in mm. 165, 215, and 263. The tonal relations between the successive or similar themes are expressed in the form of neo-Riemannian chains. The relations of the tonal path are mostly thirds, major between themes 1 and 2, minor between the exposition and the recapitulation. The design overall is a binary form without central development, as the different thematic elements are linked by means of sections functioning in harmonic sequences.
[29] Within the first thematic area (mm. 1–77) in E minor, a secondary tonality of G minor is inserted, in the context of which the theme‘s first sentence is repeated by the second violin and viola. This “in-between” color of G minor is based on the repetition of the characteristic motif of the rising melodic fifth as well as the chord of the tonic degree. The voice leading enabling the sequence of the two triads is mapped in Example 12.
[30] Voice leading between the triads of E minor and G minor features a double contrary motion of semitones (
Example 13. Dohnányi, Piano Quintet op. 26, I, mm. 28–35, harmonic progression
(click to enlarge)
[31] In the transition between the two repetitions (strings, then piano) of the first thematic element (mm. 28–35), two chords of
Example 14. Dohnányi, Piano Quintet op. 26, I, mm. 64–71, harmonic progression
(click to enlarge)
[32] The G triad reappears in its major version as the tonality of resolution for the first thematic element (mm. 71ff), and as a starting point for the second theme area (mm. 77ff). In mm. 64–71, the harmonic sequence
[33] The second theme area, the starting tonality of which is G major, eventually—like the first theme—settles on a triad of another tonality (m. 131). It is the moment when
Example 15. Dohnányi, Piano Quintet op. 26, I, mm. 82–93, tonal branching of G major to
(click to enlarge)
[34] Example 15 shows, by means of two thematic units played successively (note the bar line in the center of the example), how the branching is done from G major to
[35] The tonal progressions are connected with each other, be they paradigmatic (G and
Example 16. Dohnányi, Piano Quintet op. 26, I, mm. 94–108, system of harmonic sequences
(click to enlarge)
[36] Moreover, a system of sequences using combinations of major third and P transformations features the articulation of the second and third thematic elements (Example 16, mm. 94–108). Voice leading between the intermediate chords A–
[37] At m. 134, the first part of the movement ends with a perfect fifth downwards cadence in
5. Conclusion
[38] The observation of a progression of tonalities by means of a pattern of description, utilizing the distinction of intervallic distance, modal orientation, and polarity in confrontation with orientated voice leading, shows that the principles ruling a tonal progression are very different according to the scale at which they are examined. If a relationship is clearly polarized or orientated by itself in the framework of broad formal strategies for which the tonal hierarchy still constitutes the predominating syntax, the same features are not necessarily present in the lower categories; that is, what takes place at the level of successive chords cannot be assumed to be duplicated at the higher level. The composition discussed above is based on a binary form, in effect a sonata form without development; the tension corresponds to a rise on the major relative tonality, the resolution to a falling on the minor relative tonality, even if it is majorized (secondary theme). The built-in and parallel treatment of the two tonal categories of G and
[39] But that is not all: voice leading also offers clues that clearly distinguish the relationships of major third and minor third. This movement, like other classical designs, is based on clearcut tonal directions, that existing for example between primary and secondary areas. These directions are ensured by relations of the minor third, second, or perfect fifth, for which voice leading is unidirectional, coinciding either with the polarity or against the polarity. In this quintet movement, however, there are also less clearcut tonal progressions, those leading from the main area to the transition and those located inside the tonal areas, which are made up of relations of a major third. For them, the directional ambiguity is much more significant: balanced and multidirectional voice leading, partially coinciding with the polarity. Owing to their ambiguity, be it directional or modal, implying a chromaticism distinct from the functional qualities of the other intervals, the relations of a major third take a privileged part in the leading of microstructural tonal paths. These often coexist with more traditional paths of fifths or even minor thirds. Consequently, the observation of different criteria of intervallic relations between tonal categories can help illuminate the border between tonalities or more less stable harmonic relations, defined by the choice of voice leading and polarity.
[40] Richard Cohn (1996) observed that the three contextual inversions, R, L, and P, are accompanied by parsimonious voice leading. Thus, even if it demonstrates an obvious interest in harmonic progressions, neo-Riemannian studies, at least since the development of the concept of parsimony, positions its starting point essentially in voice leading. It is safe to say that harmonic entities constitute secondary data in the neo-Riemannian conception. Reducing one of these entities to its harmonic root is often only a way to sum up the polyphonic voices. The observation of the voice leading probably forms a specificity of the Anglo-American transformational theory.
[41] On the other hand, in reference to the relationship between chromaticism and diatonicism, Cohn contends that the very idea that a musical work is necessarily based on a unique system was the starting point of a unitary conception of tonality, a requirement that could constitute an obstacle to the use of Riemannian tools for analysis of music of the later nineteenth and early twentieth centuries. European and Anglo-Saxon transformational theories started taking different paths after 1987,(4) in the aftermath of David Lewin‘s Generalized Musical Intervals and Transformations, which created the conceptual framework needed for the interpretation of the transformations REL (R), LT (L), and PAR (P) as contextual inversions. Insofar as the components are not linked to a diatonic organization of the system, that framework allows one to consider the transformations as independent and the harmonic network as a set of operations on a chord x generating a chord y (Lewin 1987). Through this, the diatonic collections, such as major and minor triads, were understood as the result of the self-contained and modeled transformations selected and classified according to their symmetric properties (Hyer 1995).
[42] If the description of voice leading can offer a possible answer to the problems posed by post-tonal music, it does not seem to oppose an observation according to the movement of the roots. Indeed, Nicolas Meeùs (2005, 3) contends that “a description of movements of the chord roots is nothing but a summarized description of the upper voice leading.” Consequently, taking in consideration harmonic phenomena in their vertical dimension does not seem to contradict the traditional procedures of neo-Riemannian analysis: insofar as intervallic distance, modal orientation, and polarity do not presuppose the tonality, they constitute valuable tools for its analysis.
Hugues Seress
Institut de Recherche en Musicologie (IReMus – UMR 8223)
2 rue de Louvois
75002 Paris, France
contact@seress-hugues.hu
Works Cited
Cohn, Richard. 1996. “Maximally Smooth Cycles, Hexatonic Systems and the Analysis of Late Romantic Triadic Progressions.” Music Analysis 15 (1): 9–40.
—————. 2012. Audacious Euphony: Chromaticism and the Triad’s Second Nature. Oxford University Press.
Hyer, Brian. 1995. ”Reimag(in)ing Riemann.” Journal of Music Theory 39 (1): 101–38.
Lewin, David. 1980. “On Generalized Intervals and Transformations.” Journal of Music Theory 24 (1): 143–51.
—————. 1987. Generalized Musical Intervals and Transformations. Yale University Press.
Louis, Rudolf, and Ludwig Thuille. 1907. Harmonielehre. Grüninger.
Meeùs, Nicolas. 2005. “Théorie des vecteurs harmoniques et théorie néo-riemannienne”. Paper given at the Dublin Conference on Music Analysis (June 23, 2005). http://nicolas.meeus.free.fr/NMVecteurs/VHDublin.pdf.
Öttingen, Arthur von. 1866. Harmoniesystem in dualer Entwickelung. Glaser.
Riemann, Hugo. 1880. Skizze einer neuen Methode der Harmonielehre. Breitkopf und Härtel.
Tiersch, Otto. 1868. System und Methode der Harmonielehre. Breitkopf und Härtel.
Footnotes
1. For the labeling of the model, I considered that the positivity or the negativity of the sign depends on the nature, major or minor, of the first triad.
Return to text
2. Here “| R |” stands for R+ or R-, and “| L |” for L+ or L-.
Return to text
3. See the coincidence between positive sign and subdominant polarity on the one hand, and between negative sign and dominant polarity, on the other hand, in rows 4–5 and columns 1, 2, 3, 6, 7, 8.
Return to text
4. This is quite a generalization that would need more precision.
Return to text
Copyright Statement
Copyright © 2018 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Rebecca Flore, Editorial Assistant
Number of visits:
5060