Theory and Practice of Long-form Non-isochronous Meters: The Case of the North Indian rūpak tāl*
Martin Clayton
KEYWORDS: Meter, Indian, Hindustani, tāla, rāga, khyāl, empirical, non-isochronous, corpus analysis
ABSTRACT: This paper addresses important issues in the theory of meter by means of a detailed study of a particular form of non-isochronous (NI) meter, the North Indian rūpak tāl. Rūpak tāl is described as comprising 7 equal mātrās (time units), organized into three groups (3+2+2 mātrās), and is therefore non-isochronous at the group rather than the beat or subdivision level. The term “long-form non-isochronous meter” is introduced to describe the phenomenon of metrical structures including a non-isochronous pulse level with IOIs >1000ms, of which this is an example. This phenomenon is explored with the aid of empirical analysis of a corpus of recordings of rūpak tāl performances, focusing particularly on vocal performances in khyāl style. This empirical data is considered in light of extant literature on Indian metrical organization, on ethnomusicological theories of aksak, on psychological theories of rhythm perception in NI-meters, and on metrical theory more broadly.
The implications for a general theory of musical meter are then considered, leading to an argument that (a) while theorization is not a necessary condition of metrical perception, a recognized metrical pattern must be treated not only as a form of perception based on the entrainment of attention (London 2012), but as a form of culturally-shared knowledge contributing to top-down processing of meter; and (b) the theorization and representation of aspects of metrical structure means that metrical cycles are not limited to the extent of the psychological present.
DOI: 10.30535/mto.26.1.2
Copyright © 2020 Society for Music Theory
Introduction
[1] This article discusses the implications for metrical theory of the practice of a temporal structure known as rūpak tāl,(1) used in North Indian (Hindustani) rāga music.(2) Rūpak tāl is commonly described as a rhythmic cycle of 7 mātrās (time units), which are organized into three groups: 3+2+2.(3) It therefore appears to be an example of what Justin London (2012) calls non-isochronous or NI-meter, or of what Curt Sachs (1953) had earlier referred to as additive rhythm, and is closely related to the phenomenon Constantin Brăiloiu (1951) dubbed aksak (“limping,” after the Turkish). However, rūpak tāl is unusual in that it comprises a regular and stable 3+2+2 pattern even at slow tempi. It therefore allows us to extend and adapt London’s theory of NI-meters to long-duration cycles.
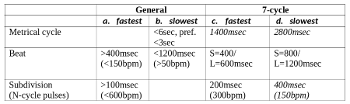
[2] The first aim of this article is to establish the existence of what I term “long-form non-isochronous meter,” distinguishing it from other forms of meter in which the beat or subdivision level is non-isochronous. Long-form non-isochronous meter is defined here as having at least four pulse levels, listed below from the fastest to the slowest:
- Subdivision (at least 2x the pulse rate of the beat)
- Beat (IOI > c. 400 ms)(4)
- Group (groups comprise a number of beats, normally 2 or 3; this group level is non-isochronous by virtue of the fact that it includes groups of different numbers of beats)
- Cycle (comprising at least one each of two different beat groups; the minimum cycle is therefore a 5-beat pattern comprising groups of 2 and 3 beats)
[3] Rūpak tāl is used here as an example of such metrical structures and is described in detail with the aid of empirical study of natural performances. This study focuses first on tempo ranges, patterns of tempo variation, tablā (drum pair) accompaniment patterns, and composition structures in a selection of forty-two audio recordings in various genres: khyāl vocal performances (and instrumental renderings in khyāl style), instrumental gats,(5) and tablā solos. Secondly, a smaller sample of ten multitrack recordings for which event onset data is available is explored in further detail to give a more complete picture of rūpak tāl as it is practiced in its most common (and slowest) genre, khyāl. This analysis includes variations from isochrony of the beat (mātrā) durations and variations in stroke density in the tablā accompaniment.
[4] The second aim of this paper is to explore the implications of the phenomenon of long-form NI-meter for metrical theory. Viewing rūpak tāl through the twin lenses of North Indian tāla theory and London’s (2012) approach to NI-meter reveals some tensions that are relevant to slow tempo tālas in general, not just those with non-isochronous temporal levels. Crucially, while London regards meter as a perceptual phenomenon and thus limits the extent of a metrical cycle to a few seconds, due to the extent of the psychological present (5–6 seconds) (27), many North Indian tālas have cycles extending well beyond this limit. This tension can be resolved in a number of ways. For example, we might view Indian tālas as a distinct phenomenon outside the scope of meter; although if we do so, we nonetheless need to explain how it relates to meter. Alternatively, while acknowledging the distinctive features of the tāla system, we might regard it as a form of meter, in which case we would need to explain why the theoretical limit on cycle length may be ignored.
[5] This article will argue that rūpak tāl should be regarded as instantiating a particular metrical structure, with the support of theory and explicit representation allowing otherwise plausible limits on metrical duration to be transcended. Although such a “long-form meter” is unlikely to be perceived in a purely bottom-up fashion, the combination of top-down knowledge and bottom-up perception allows for a robust metrical pattern to be maintained well beyond that durational limit. The most important argument made here, therefore, is that meter should be regarded as a perceptual phenomenon in which bottom-up processing may be supported by top-down priors informed by theoretical knowledge. Although made possible by innate cognitive processes, in practice most metrical perception relies on knowledge acquired through past listening and music-making. That meter cannot be a purely bottom-up phenomenon is of course recognized also by London (2012, 4); the specific challenge to London’s theory here is to propose that the learned nature of metrical patterns may allow the upper durational limit for metrical cycles to be overcome.
[6] London’s approach has come to represent an important nexus between music theory and music psychology, and between theoretical and empirical approaches to meter. Although his book has relatively little to say about non-Western musical traditions, his approach has inspired research beyond Western tonal music (see, for instance, Goldberg 2017; Polak and London 2014). If aspects of London’s theory offer important possibilities for the development of a general theory of musical meter—which I believe is attainable—it is also inevitable that aspects of the theory will need to be significantly amended and extended as part of such a programme. Rūpak tāl is presented here as an example of this.(6) To be clear, this article does not present a case against psychological approaches to meter, or against London’s theory, but it does ask critical questions about these approaches.
[7] In order to make this argument, I need to introduce the reader to the practice of rūpak tāl in some detail. The rationale here is to provide enough detail and sufficient examples to (a) illustrate some of the richness and variety of practice, particularly for readers unfamiliar with the musical tradition; and also (b) introduce some novel methods of empirical rhythmic corpus analysis that both strengthen my argument and offer tools for others to adapt; while not getting bogged down in very fine details of performance practice. Rūpak tāl exists not only as a simple theoretical formula but as a range of practical possibilities. I suggest here that aspects of practice, such as the variability of mātrā durations or the preference for subdividing certain mātrās more than others, give us indications of the form of knowledge that rūpak tāl represents. I contend that any such aspect of practice may contribute to an individual’s model of rūpak tāl, and thus in principle influence its top-down perception. Demonstrating the impact of specific features of performance practice on metrical perception, however, is beyond the scope of this study.
Non-isochronous meter, aksak, and 7-beat meters
[8] A distinct type of metrical pattern comprising groups of 2 and 3 time units was first recognized by literate European music culture in the late 19th century: the first transcriptions not to be “crammed. . . into the nearest commonly-available Western meter” date from 1886 (Rice 1980, 62). From the early decades of the 20th century, Bulgarian scholars began to theorize this type of meter in more appropriate terms. Stoyan Djoudjeff (1931), for example, outlined a categorization of Bulgarian meters in which he coined the term “heterogenous compound meter,” according to which the main beats were divided into either 2 or 3 parts. Some twenty years later, when Curt Sachs ([1936] 1952) coined the term “additive rhythm,” Constantin Brăiloiu (1951) proposed that the Turkish term aksak be adopted as a general term for this form of rhythmic organization and enumerated the various possible types at length.
[9] More recently, the general theory of aksak first discussed by Brăiloiu has resurfaced as a theoretical topic. Significantly for my purposes in this article, Jérôme Cler (1994) seems to have been the first to discuss slow tempo aksak-type patterns. In southwestern Turkey, he noted that aksak patterns, in which the ratio between short and long units is 2:3, are found in a wide range of tempi, the slowest given in his charts being 35 beats per minute (bpm). Cler argues that if we regard all fast and strictly co-metric patterns comprising unequal units as aksak, then the same patterns slowed down, retaining the co-metric character, should also be considered a variety of aksak.
Example 1. Groupings of seven subdivisions into 2, 3, and 4 beats
(click to enlarge)
[10] As for 7-cycles in particular, Simha Arom’s (2004) theory allows for the seven to be divided into units of 2, 2 and 3 in any permutation (i.e., 223, 232 or 322). His list of published examples includes all three possibilities, although 223 and 322 are much more widely documented than 232.(7) Nice Fracile (2003), on the basis of a study of 6,000 extant transcriptions, lists 322 and 223 varieties but not 232. In Alice Singer’s (1974) analysis of music and dance steps in Macedonian dances, two varieties of 7-beat patterns are listed, 322 and 223 (in her terms, SQQ and QQS, where S and Q refer to “slow” and “quick” steps respectively). Her consideration of the corresponding dance steps shows an interesting feature that had not been spotted by earlier musicologists: that the two short or quick units can be danced either as two short steps or one long step. In other words, from a dancer’s point of view the pattern is either 322 or 34 (“Sarakinskoto” dance) (395–96).(8) Rice (1980, 63) cites 223 and 322 varieties, as well as a four-unit pattern, 2212, in Bulgaria. The two most common patterns are therefore clearly 322 and 223.(9) Although noted only by Singer (1974), there is no reason to assume that the flexibility in dance to shift from 22 to 4 and back is limited to Macedonia. In fact, if we consider the two basic types as 34 and 43, with the 4 optionally decomposing into 2+2, then the relative lack of 232 patterns is not surprising. These different divisions of the 7-cycle are illustrated in Example 1.
[11] Daniel Goldberg’s recent work discusses the common Bulgarian dance rhythm rŭchenitsa (223) extensively,(10) defining it as a “class of dance done individually or in small groups without holding hands. In a simple form of the dance, dancers take small, sometimes shuffling steps on the three beats in the fast SSL sequence” (2017, 69–70). Goldberg’s study addresses many aspects of rŭchenitsa in performance, particularly its timing patterns; patterns are typically reckoned in two-cycle units (223223) lasting on average 1615 ms (fastest level IOI = 115 ms), and the relative frequency of onsets occur on different beats. While some of this work is relevant to the present study, tempo is a key difference between rūpak and rŭchenitsa. As we shall see, rūpak tāl’s 7-pulse level is played more than twice as slowly as this, and sometimes more than twenty times slower.
[12] In Western music theory, as distinct from comparative musicology or ethnomusicology, these aksak patterns were until recently little considered, despite the interest of Bela Bartók ([1938] 1981) (see discussion in Rice 2000), Sachs ([1936] 1952, 1953), and others. Fred Lerdahl and Ray Jackendoff (1983, 98) noted their existence, citing Singer as their source. Their metrical well-formedness rules explicitly exclude these structures, but they implicitly admit that for repertoires other than Western tonal music, these rules need not hold. Aksak patterns are considered in far greater detail by London, labelled at different times as “complex” and “non-isochronous,” rather than as “additive.” In a 1995 article on complex meter, London introduced some of the ideas foundational to Hearing in Time (2012). For London, complex meters rely on an isochronous pulse (SD for Subdivision); pulses at the beat (B) level may be categorised as either long (L) or short (S), comprising 3 and 2 subdivisions, respectively. Thus, these complex meters are non-isochronous at the B-level, while an isochronous subdivision (SD) level must be present, whether articulated or inferred by the listener (1995, 72). He proposed that “complex meters require explicit specification of their invariant features through the patterns of duration and organization on the musical surface, and once established, these patterns can be varied only within extremely narrow limits” (69). Or as Cler (1994) would have it, they are strictly co-metric. London (1995, 73) argued further that a peculiar feature of such patterns is that all levels of the meter “must come into being together and be maintained together, in order for the integrity of the meter to be preserved,” and that the sense of beat and tempo is in effect based on a non-isochronous pulse.(11)
Example 2. Representation of a (fast tempo) 3+2+2 metrical structure as a circle
(click to enlarge)
Example 3. Representation of a (fast tempo) 3+2+2 metrical structure according to Lerdahl and Jackendoff’s (1983) notation
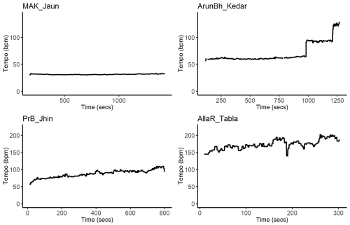
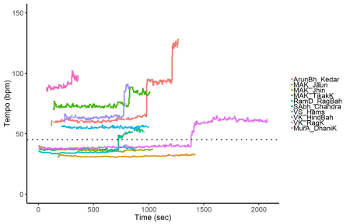
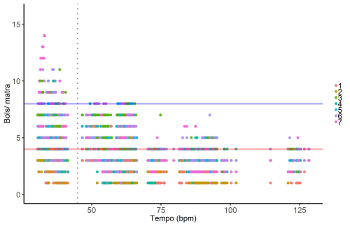
(click to enlarge)
[13] London’s theory is developed in more detail in Hearing in Time, but its basic features are retained. As for tempo, he notes that having two distinct beat classes (the L and S) means that NI-meters are more highly constrained in terms of tempo than I(sochronous) meters (2012, 136, 141). 7-cycles are not dealt with in detail in Hearing in Time; London simply notes that the subcycle must comprise one long and two shorts, or one 3 and two 2s, which can be arranged in any of three possible rotations (322, 223, 232). Indeed, according to the principle of maximal evenness developed in London’s book, a 7-cycle would need to be split into one of the possible rotations of 34 (two beat), 322 (three beat) or 2221 (four beat)—nine varieties in total.
[14] Based on London’s theoretical apparatus, then, we can describe a typical 7-cycle as comprising three non-isochronous time units forming an irregular beat (tactus) level, supported by seven isochronous pulses (SD). Example 2 is an illustration of a 7-cycle with a 3+2+2 non-isochronous subcycle, analogous to those presented by London. Example 3 illustrates the same structure in a linear meter diagram in the style of Lerdahl and Jackendoff (1983), with the levels marked up as subdivision, beat, and measure, as per London (1995).
Example 4. Proposed general constraints on the absolute durations of metrical cycles, beats, and subdivisions
(click to enlarge)
[15] Typical durations for each level in such a pattern would be subject to general constraints on metrical structures, as outlined in Example 4. Taking as the basis for these calculations London’s (2012, 121) suggestion that beat rates should fall between 400 and 1200 msec, the maximum range of subdivision rates is 150–300 bpm, and of cycle lengths, 1400–2800 msec.(12) Some published estimates of tempo ranges in aksak meters are higher: Bartók insisted that a fast tempo was one of the essential criteria for “Bulgarian rhythm” (Rice 2000, 206–7) and gave a range from 200–400 bpm, although he also describes what he names “hyperbulgarian” rhythms at up to 600 bpm (Bartók [1938] 1981). London’s interpretation of a 7-beat meter as non-isochronous at the beat level with the 7-cycle as a subdivision is compatible with the great majority of examples in the literature from Turkey and the Balkans. It does not, however, fit the Indian tāl well: the slowest example analyzed in this study has a beat rate of 22 bpm and a cycle of about 18,600 msec, an order of magnitude slower than a “typical” aksak or predictions based on London’s model of durational constraints.
[16] The aksak phenomenon has been the subject of empirical and cognitive studies in recent decades, including Goldberg’s (2015, 2017) work. Dirk Moelants (2006), for example, studied performance timing in Bulgarian traditional tunes as well as in Bartók piano compositions. Tempo was generally fast, with cycle lengths in the region of 1–2s. Erin Hannon and colleagues have explored the implications of these metrical types for rhythm processing. Bulgarian and Macedonian participants performed differently from their North American counterparts in rhythm-processing tasks between “simple” and “complex” meters—the North Americans being unable to detect structural violations of a 7-beat meter (fastest IOI = 250 ms) that Bulgarians and Macedonians could detect. But infants were equally able to process both types, indicating the effect of enculturation on rhythm processing ability (Hannon and Trehub 2005). Ullal-Gupta, Hannon, and Snyder (2014) tested a similar idea using a 7-beat meter (again, IOI = 250 ms), showing differences in performance between Indian and North American participants when the 7-beat meter is involved. A number of studies have explored the learning of such complex metrical patterns. For instance, Tillmann, Stevens, and Keller (2011) show an effect of learning an unfamiliar pattern of durations in a 223 relationship over short-term exposure (the pattern length of 1050 ms for a three-element pattern, equivalent to a 7-pulse IOI of 150 ms). Overall however, while fast aksak-type non-isochronous metrical patterns have been explored in recent years in music theory and cognition, slow-tempo versions of these patterns—such as those I term “long-form non-isochronous meters”—are rarely taken into account.
[17] As noted above, music psychologists have explored the implications of aksak-type rhythms for the role of learning and enculturation in rhythm processing. This raises questions in relation to metrical perception. Models based on the entrainment of endogenous rhythms produced by neural oscillators—consistent with London’s explanation—currently represent the dominant explanation for metrical perception. Neural resonance theory, as discussed for example by Large, Herrera, and Velasco (2015), could be described as a bottom-up theory of metrical perception: given an auditory stimulus with a periodic component, computational models of banks of neural oscillators become entrained and output a beat structure very close to the way a human listener extracts such a structure from the musical surface. While this provides an elegant description of many examples, results to date with aksak-type patterns are mixed (Goldberg 2017, 194). Long-form non-isochronous meters present a further challenge, in that existing models assume that the longest metrically-significant intervals are in the region of 2000ms (London 2012). Large et al.’s (2015) models of neuronal oscillation show output down to a frequency of 0.4Hz, with periodicities in this range linked to a slow “sub-delta” band of neural rhythms. It seems highly improbable that a physiologically plausible model of neural resonance can reproduce a rūpak tāl pattern of over 10 secs in duration.(13)
[18] A common challenge in modelling rhythm perception is to understand the place of learning, knowledge, and anticipation. As London recognizes, metrical structures are learned; papers on the perception of NI meter cited above illustrate short-term learning of aksak-type patterns. In many kinds of music, changes in tempo, meter, or rhythmic emphasis can also be anticipated based on prior knowledge, training, notation or cueing in performance. The role of prior knowledge in metrical perception is nonetheless given relatively little attention. London’s theory draws, like Neural resonance theory, on Dynamic attending theory (Jones 1976, 2019), which is a predominantly bottom-up theory in that perception of meter depends on the entrainment of endogenous rhythms to an auditory stimulus. This entrainment then allows for prediction of the timing of future events, since the established pattern is presumed to continue by default. Such a system might account for the fact that individuals learn musical meters, if the connections in the neural oscillator populations can be modified by the stimuli encountered. Although the idea of structural representation is alien to much thinking in dynamical systems theory, some recent approaches introduce top-down processes within a non-linear model of temporal perception under the rubric “active sensing” (Schroeder et al. 2010; Morillon and Schroeder 2015), which allows “any available source of top-down priors” (Rimmele et al. 2018, 876) to influence metrical perception.(14)
[19] The following sections address this issue from a music-theoretical angle, asking what rūpak tāl is and how it is represented, and thus conveying something of the “knowledge” that may be learned. I argue that the reason rūpak tāl (and other Indian tālas) can be perceived even with cycles extending well over 10 seconds is precisely that its perception is not a purely bottom-up process: perceptual mechanisms are able to draw on a robust body of learned knowledge and, by doing so, can overcome the proposed 5–6-second limit on metrically-salient periods. From the perspective of Western music theory, this may seem to be an extreme example, in that rūpak tāl is a very long, asymmetrically divided cycle and thus not the kind of structure many theorists would take into account. However, metrical knowledge may take many different forms, and I argue that perceptually-based metrical theory in general should give greater consideration to the ways in which top-down processes play a role in perception and the ways in which they interact with bottom-up processes.
[20] Theoretical knowledge and performance practice contribute to rich representations of the metrical pattern, which include embodied elements. This study demonstrates some of the richness and complexity of rūpak tāl. My contention is that rūpak tāl, particularly when performed at a slow tempo as in khyāl, exceeds accepted temporal limits for the perception of meter; the estimated limit of the perceptual present does not however present a barrier to its perception, and the reason that this is possible is that musicians and listeners have acquired rich representations of the structure that inform perception.
[21] The next two sections first describe rūpak tāl and then present the results of an analysis of a corpus of recorded performances. A summary of this material can be found in the Discussion section for readers who prefer to jump to the conclusions.
Rūpak tāl: An introduction
Example 5. Rūpak tāl’s ṭhekā (archetypal or basic drum pattern)
(click to enlarge)
Video Example 1. Rāg Dhānī Kauns performed by Murad Ali (sāraṅgī) and Gurdain Rayatt (tablā)
(click to watch video)
[22] Rūpak tāl is one of the core metrical cycles employed in the Hindustani classical music tradition.(15) It is described as a pattern of 7 mātrās, grouped 3+2+2 (the groups are called vibhāg). The first mātrā of the group of three is always regarded as sam (the “one”), around which composition and improvisation are oriented. It is described with reference to both a clapping pattern and an archetypal drum pattern known as a ṭhekā. The clap pattern comprises a gesture at the start of each group: the first is a wave (rūpak is the only tāl to feature a wave on sam), followed by two claps at the start of the other two groups. Ṭhekās vary according to context, as we will see, but Example 5 and Video Example 1 illustrate the simplest version of rūpak tāl’s ṭhekā. A noteworthy feature is the use of a light stroke tin, without a resonant bass sound, on sam and throughout the first group. This corresponds to the wave gesture, and the initial group of 3 mātrās is called a khālī vibhāg (“empty group”) (Naimpalli 2005, 119).
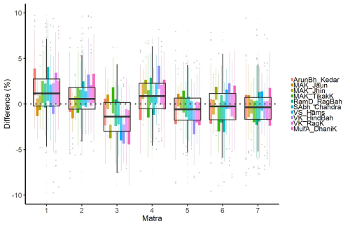
[23] Rūpak tāl is not the only 7-cycle used in Hindustani music. In the dhrupad vocal genre, a 7-cycle called tīvrā tāl (or tevra) is sometimes used, which features the same 3+2+2 division but not the initial khālī section or wave gesture. Similarly, when classical singers sing bhajans (devotional songs) they sometimes use a drum pattern called sātvā, which again divides the 7 into 3+2+2 but has a different drum pattern and does not have the first section khālī. Other 7-beat patterns that might be heard in classical or related contexts include paśto and mughlāī, both names suggesting an origin in regions now lying within Afghanistan or Pakistan. James Kippen (2006, 91) suggests that historically, rūpak may have developed as a fusion of paśto (ṭhekā: ti – tirakita / dhi – na na/), which is used in ghazal (sung poetry) accompaniment, and tīvrā tāl (ṭhekā: dha din ta/ tita kita/ gadi gana/). Elaborating on this view, rūpak tāl may represent a synthesis of a folk-derived 7-cycle with a light first beat (paśto), with aspects of Indian classical time theory embodied by tīvrā tāl, a synthesis that resulted in the anomalous sam-is-khālī (light beat one) phenomenon. Both paśto and tīvrā tāl are played relatively briskly. The slow tempo that has become typical of rūpak tāl is part of a wider process of deceleration that took place in the 20th century and affected many tāls, some even more dramatically than rūpak tāl (Clayton 2000, 50–52).
[24] In south Asian music traditions, groups of 7 are always divided 3+4, and groups of 5 2+3. The fact that 7-beat Indian tāls are described as 322 rather than 223 is consistent with this preference (Clayton 2000, 161). Although the description of rūpak as 322 is normative, however, earlier theoretical accounts and current oral tradition attest to a degree of ambiguity, with an alternative interpretation of the same structure as 223. In some recordings it is perhaps easier to hear rūpak’s cycle as 223 than 322. Listen, for example, to the conclusion of Alla Rakha’s tablā solo on the album Music of India: Ragas and Talas (1959) (Audio Example 4). In fact Gurudev Patwardhan, a prominent drummer and pedagogue of the early twentieth century, notated rūpak beginning on what is now considered the fourth mātrā (i.e., as 223; Kippen 2006, 104), asserting that rūpak “does not begin from sam” (Patwardhan 1903; translated in Kippen 2006, 277). Magriel notes that similarly, the singer Krishnarao Shankar Pandit’s book Rag Pravesh (1953–54) describes rūpak tāl’s sam as falling on the third group (i.e., the starting point is the fourth mātrā; Magriel and du Perron 2013, vol. 1, 64). This relates to a story of rūpak tāl’s origin attributed to the master tablā player Suresh Talwalkar by my interviewee (and Talwalkar’s student) Vishwanath Shirodkar. According to this account, an unidentified singer was performing an older version of rūpak tāl with the structure 2+2+3, but became confused and inadvertently started placing the sam of his composition on the fifth mātrā. Since the result sounded good, musicologists discussed the issue subsequently and agreed that this should be the new form of rūpak tāl (interview, May 5, 2014).(16)
[25] Relatively little has been written about rūpak in published works on tāl or in those on the tablā and its repertory. Many works contain brief descriptions of rūpak tāl similar to that at the beginning of this section. Some develop this with practical examples. Sadanand Naimpalli (2005, 178–84), for instance, includes elaborated ṭhekās that would actually be played in accompaniment, as well as a brief selection of compositions for tablā. In general though, the number of tablā compositions described is very limited. Tablā repertoire is dominated by tīntāl (4+4+(4)+4 = 16), and a lot of what is played in other tāls is, in practice, derived from tīntāl compositions (Vishwanath Shirodkar, interview, May 5, 2014).
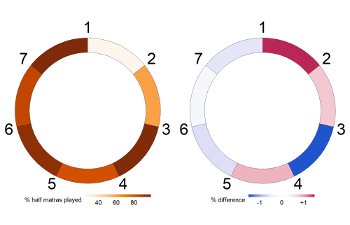
[26] Musicologist Subhadra Chaudhary describes rūpak in terms of a contrast with tīvrā tāl: “[tīvrā tāl] has a steady, firm gait whereas [rūpak tāl] has a liquid, unsteady, springy flow” (1997, 421). According to Chaudhary, this binary relationship is not restricted to 7-cycles but is common to several other pairs of tāls. My earlier description focuses instead on the effect of the alternation of groups of different lengths being “a continual alternation of speeding up and slowing down, tension and relaxation” (Clayton 2000, 67–68).(17) Although it is not unusual to hear musicians affirm that tāls each have their own character, it is much less common to hear verbal descriptions of these characters, and aside from one interview with Vishwanath Shirodkar exclusively on rūpak tāl, from which I have already quoted, my own enquiries in interview contexts have been only modestly productive. In an earlier conversation, however, Shirodkar drew attention to the different tāl used in different gharānās (teaching lines or schools), with rūpak played somewhat slower in Jaipur gharānā than in other schools (interview, May 19, 2005). A well-known Jaipur gharānā singer Manjiri Asanare-Kelkar, who is represented in the core corpus with three separate rūpak tāl performances, suggested that she would often use rūpak tāl for the second rāga in a concert: the usual convention—not only for Jaipur style singers—is that the longest, most serious and slowest piece comes first and the second rāg will both contrast in terms of pitch material and often be slightly faster and shorter (interview, Feb 12, 2010).(18) Manjiri also pointed out that due to the relatively short cycle (short, that is, in comparison to slow 12- and 14-cycles that can last up to a minute), she would normally plan a passage of improvisation to last not one cycle but two or three.
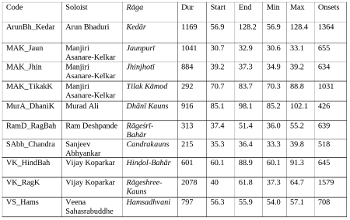
Example 6. Recordings in rūpak tāl consulted
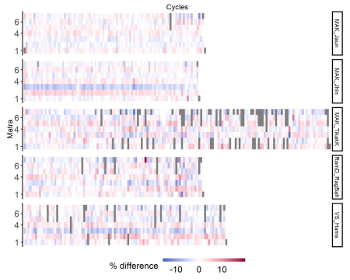
(click to enlarge)
[27] Patiala gharānā singer Sudokshina Chatterjee pointed out another consideration, which is that different tāls may be suited to the character of particular rāgs. In the case of rūpak tāl, she cited a composition in Rāg Kauśī Dhānī, which is the same one included in Nicolas Magriel and Lalita du Perron’s 2013 collection of khyāl songs (which will be discussed further below) as performed by the great Patiala singer Bade Ghulam Ali Khan. She suggested that since Kauśī Dhānī is difficult to sustain for a whole hour and would normally be sung for about twenty minutes at most, it is suited to a shorter cycle such as rūpak tāl (interview, June 8, 2006). Looking at the lists of rāgas represented in my corpus of rūpak tāl performances (Example 6), there is perhaps a preponderance of such “second rāgas.” Our corpus includes performances of well-known compositions also represented in Magriel and du Perron’s collection: Sūra saṅgat rāga vidya in Rāg Tilak Kāmod (Magriel and Perron use the version sung by the great Jaipur singer Kesarbai Kerkar; our recording is performed by Manjiri Asanare-Kelkar) and Mero pīyā rasiyā in Rāg Nāyakī Kānaḍā (sung by another great Jaipur singer Mogubai Kurdikar in Magriel and du Perron, and in ours by published recordings of Ashwini Bhide Deshpande and Basavi Mukherjee). It is striking that four out of fifteen gats are similar pieces in the important afternoon rāg, Bhīmpalāsī.
[28] Two important themes emerged from interviews with tablā players. First, it is important to distinguish the playing style of rūpak (a tablā tāl) from a tāl such as dhamār, which is associated with the barrel drum pakhāvaj and its heavy, booming strokes (the pakhāvaj is used to accompany dhrupad). In other words, there is more to a tāl than the number of beats in the cycle (Abhijeet Banerjee, interview, Feb 8 2007). The other theme is that their overriding concern in playing rūpak tāl is the necessity in solo passages of dividing the tāl cycle into equal halves of 3½ mātrās each. Tablā solos in rūpak tāl therefore tend to be inherently contrametric.(19) This reinforces the notion that tablā players adapt material originally developed in the context of the binary pattern of tīntāl—where the symmetry between the two halves of the pattern is crucial—to very different structures, such as rūpak.(20) Rūpak tāl, as noted above, does not have an extensive solo tablā repertory of its own.
Rūpak tāl: Empirical description, first stage
Corpus
[29] As noted above, rūpak tāl is used principally in accompaniment of idiomatic instrumental gat performance (for example, of sitār or sarod) and of khyāl vocal performance, as well as occasionally in tablā solo.(21) In order to establish the main features of rūpak tāl as performed in these genres, I present a characterisation of the tāl in practice based on empirical investigation of a corpus of forty-two audio recordings (mean duration = 886 secs). This study establishes tempo ranges and patterns of tempo variation, and also discusses other aspects such as the usage of accompanying drum patterns (ṭhekā) and the rhythmic setting of composition melodies. These recordings fall into two groups:
- Core (“C” in Example 6). A selection of multitrack recordings made by the author and colleagues. These are particularly valuable because (a) the source is known (and thus we can be sure what editing has taken place), (b) using multitrack recordings individual instruments and voices can be isolated, and (c) video recordings of the same performances are also available (see Clayton, Leante, and Tarsitani 2019 for details).(22)
- Additional (“+” in Example 6). Other recordings, some published and some from private collections. Although lacking the advantages of the above, it is necessary to use a wider sample in order to make robust claims about some of the issues discussed here, especially for instrumental gat performances.(23)
Tempo ranges
Example 7. Tempo curves for four representative performances in rūpak tāl
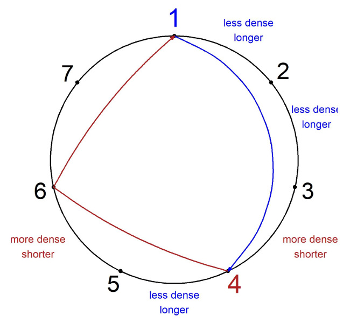
(click to enlarge and listen)
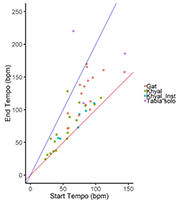
Example 8. Start vs. end tempo for 42 recordings in rūpak tāl
(click to enlarge)
[30] The tempo of the full corpus of forty-two recordings was established by manual tapping of the beats.(24) Example 7 and Audio Examples 1–4 illustrate a selection of four of these performances, chosen to show the range of tempo and the different patterns of variation: (1) a slow tempo khyāl, decelerating very slightly (MAK_Jaun); (2) a khyāl that accelerates in clear stages (ArunBh_Kedar); (3) a medium-fast gat, illustrating gradual acceleration (PrB_Jhin); (4) a fast tablā solo, which features an overall acceleration with a higher degree of tempo fluctuation (AllaR_Tabla). Example 8 plots the starting and ending tempi for each of the forty-two recordings, and is colored by genre. This illustrates that khyāl recordings generally cover a lower tempo range than instrumental gats and that instrumental khyāls tend to occupy the upper range of the vocal khyāls. Tablā solos include the fastest performances of all. While a few khyāl performances remain at a constant tempo, some even ending at a marginally slower tempo than that at which they begin, it is far more common for performances in all genres to accelerate, sometimes very considerably.
[31] Hindustani musicians do not generally concern themselves with quantifying tempo in terms of bpm. Terms used for tempi are quite simple: vilambit, madhya and drut, meaning slow, medium and fast, respectively, occasionally with the prefix ati-, meaning very, or hyphenated in terms such as madhya-drut (“medium-fast”). It is not clear how these terms should map onto absolute tempo measurements, however, as they are inconsistently used. It is also the case that typical bpm ranges are quite different for vocal and instrumental music, so what is “medium” for an instrumentalist may be “fast” for a vocalist (Clayton 2000, 86). In the case of rūpak tāl, the term vilambit (“slow”) is sometimes used. But such tempo modifiers are often conspicuously absent, suggesting that rūpak is regarded as the same entity simply played faster or slower. Vishwanath Shirodkar’s estimates of the minimum and maximum comfortable tempi, given in the form of ṭhekā recitation in interview, are c. 30–108 bpm.(25) Anything slower, he suggests, makes it difficult for the listener to follow, although he conceded that this might occasionally be justified (interview, May 5, 2014).
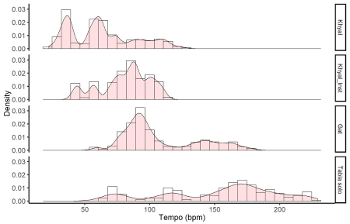
Example 9. Tempo histograms/ density plots by genre
(click to enlarge)
[32] Our corpus of recorded performances suggests a somewhat wider range in practice (see again, Example 8). The tempo density plots/ histograms in Example 9 show that the tablā solos include the fastest tempi, although they also extend down to about 60 bpm. The overall range is 61–229 bpm. Next fastest are the gats, played on instruments such as sitār, sarod, guitar and santūr, which range from about 57–182 bpm. The khyāl vocal performances range from about 22–129 bpm. The instrumental versions of khyāl on sāraṅgī, flute, violin, and harmonium occupy a somewhat narrower range of 41–113 bpm.
[33] It is difficult to confidently separate out regions of these plots to be labelled slow, medium, and fast, although a few areas stand out: below 45 bpm in the vocal khyāls, for example, and below 65 bpm in the instrumental khyāls, which perhaps could be called vilambit. A less clear-cut possibility would be to label the area over 120 bpm in the instrumental gats as drut.
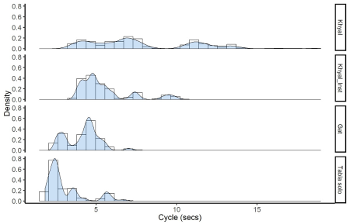
Example 10. Cycle length histograms/ density plots by genre
(click to enlarge)
[34] The same data is converted to show cycle lengths in Example 10. These distributions confirm that the cycle duration spreads well beyond 5–6 seconds. The range is from under 2 seconds (in tablā solos only) up to over 14 seconds (in vocal khyāl only).
[35] Since slow tempi and long cycles are of particular interest here, and since a general deceleration at the slower end of the spectrum over the twentieth century is widely acknowledged, it is worth asking whether there is any evidence that the slowest tempo band (22–45 bpm) developed over the course of the twentieth century. Only one of Magriel and du Perron’s examples goes below 45 bpm: Kesarbai Kerkar’s Rāg Tilak Kāmod, which starts at 42.4 bpm and probably dates from the 1950s or ’60s.(26) Recordings analyzed in this paper in the 22–45 bpm range date from later: Ashwini Bhide-Deshpande’s Nāyakī Kānaḍā dates from 1997; Basavi Mukherjee’s performance of the same composition, 2006; and our recordings of Manjiri Asanare-Kelkar, Ram Deshpande and Vijay Koparkar, the 2000s. Although not conclusive, this is consistent with the idea that tempi below 45 bpm may have come into common usage in the second half of the twentieth century, influenced by a wider trend of deceleration in Hindustani music.
Tablā accompaniment and mātrā subdivision
Example 11. Rūpak tāl ṭhekā versions
(click to enlarge)
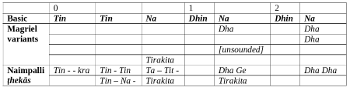
[36] As noted above, the simplest version of rūpak tāl’s ṭhekā is usually quoted as Tin tin na/ dhin na/ dhin na. Magriel notes some variations in early recordings: replacing the “na” stroke on 5 and 7 with “dha” (which adds bass resonance); replacing only the seventh mātrā “na” with “dha”; leaving mātrā 5 unsounded or weakly sounded; or replacing the “na” on mātrā 3 with Tirakita, a feature which he notes (after Kippen 2006) is derived from paśto (Magriel and du Perron 2013, vol. 1, 269). Naimpalli (2005, 180) prints two elaborated “Thekas for Solo and accompaniment,” which share some features with these. Example 11 summarizes these important variants.(27)
[37] A number of patterns emerge in the ṭhekās in our corpus. First, as noted by Magriel, there is a tendency to lose the khālī (bass-less) feel on mātrā 7, and more rarely mātrā 5. Only a few of the slowest performances (e.g., those of Basavi Mukherjee and Bhimsen Joshi) retain the khālī bol (bol, meaning “stroke”) on mātrā 7. The Tirakita pattern on mātrā 3 seems to have become an important reference point, although there are still some variations in use of this pattern: this can be rather different from slow khyāl tāls such as ektāl (12 mātrās), where this pattern tends to be played as a very clear and unelaborated sequence of four tablā strokes. In rūpak tāl, the Tirakita may be varied, either simplified (at fast tempi, Ti-kita) or decorated (at slow tempi, Ti-ra-Tirakita). In the majority of performances, there is at least a clear reference to this bol (and hence at least a 4:1 subdivision), with only a minority of performances avoiding it altogether.
[38] A selection of tablā audio extracts from our Core corpus illustrate some of these variants (described from slowest to fastest):
- Audio Example 5 (Tablā: Milind Pote, first cycle = 31 bpm): simple TinTin on mātrā 3 rather than Tirakita; khālī retained on 5 but not 7; elaboration relatively simple (gentle Kat or Tat on sub-beats)
- Audio Example 6 (Tablā: Milind Hingne, 39 bpm): clear articulation of Tirakita on 3;(28) khālī mostly retained on 5 but not 7
- Audio Example 7 (Tablā: Ajinkya Joshi, 40 bpm): clear articulation of Tirakita on 3; khālī bols not retained on 5 or 7
- Audio Example 8 (Tablā: Vishwanath Shirodkar, 56 bpm): mātrā 3 varies between Tirakita and Ta-Tit (3rd cycle); khālī retained on 5 but not 7
- Audio Example 9 (Tablā: Ajinkya Joshi, 60 bpm): taken from the same concert as VK_RagK, this faster piece uses Tirakita on 3 but not as consistently; khālī bol is retained on 5 but not 7; note the fills towards the end of mātrā 5, giving a greater sense of urgency
- Audio Example 10 (Tablā: Vishwanath Shirodkar, 71 bpm): clear articulation of Tirakita on 3; khālī mostly retained on 5 but not 7
- Audio Example 11 (Tablā: Gaurishankar Karmarkar, 74 bpm):(29) by way of contrast, in an instrumental example, the distinctive feature of the ṭhekā seems to be the two heavy strokes on mātrās 4 and 6, which give a very different feel to all of the vocal examples
Tablā track from: Rāg Jaunpurī performed by Manjiri Asanare-Kelkar (voice), Milind Pote (tablā) and Chinmay Kolhatka (harmonium). Pune, Maharashtra, 9/12/2006. Source: NIRP1_MAK_Jaun_Tabla.wav, 3'03"–3'46".
Tablā track from: Rāg Jhinjhotī performed by Manjiri Asanare–Kelkar (voice), Milind Hingne (tablā) and Shubhash Dasakkar (harmonium). Nashik, Maharashtra, 13/2/2011. Source: NIRP1_MAK_Jhin_Tabla.wav, 3'04"–3'46".
Tablā track from: Rāg Rāgeśrī–Kauns performed by Vijay Koparkar (voice), Ajinkya Joshi (tablā) and Rahul Gole (harmonium). Pune, Maharashtra, 25/2/2010. Source: NIRP1_VK_RagKauns_Tabla.wav, 5'31"–6'06".
Tablā track from: Rāg Hamsadhvani performed by Veena Sahasrabuddhe (voice), Viswanath Shirodkar (tablā) and Seema Shirodkar (harmonium). Pune, Maharashtra, 15/12/2006.Source: NIRP1_VS_Hams_Tabla.wav, 3'31"–4'03".
Tablā track from: Rag Hinḍol-Bahār performed by Vijay Koparkar (voice), Ajinkya Joshi (tablā) and Rahul Gole (harmonium). Pune, Maharashtra, 25/2/2010. Source: NIRP1_VK_HinBah_Tabla.wav, 3'54"–4'22".
Tablā track from: Rāg Tilak Kāmod performed by Manjiri Asanare-Kelkar (voice), Vishwanath Shirodkar (tablā) and Kaviraj Singh (harmonium). Durham, England, 30/4/14. Source: NIRP1_MAK_TilakK_Tabla.wav, 2'12.5"–2'44".
Tablā track from: Rāg Jhinjhotī performed by Prattyush Banerjee (sarod) and Gauri Shankar Karmakar (tablā). Kolkata, West Bengal, 28/1/2007. Source: NIR_PrB_Jhinjhoti_2Gats_Tabla.wav, 1'23.5"–1'53.5".
Audio Example 12
Tablā track from: Rag Tilak Kāmod performed by Manjiri Asanare-Kelkar (voice), Vishwanath Shirodkar (tablā) and Kaviraj Singh (harmonium). Durham, England, 30/4/14. Source: NIRP1_MAK_TilakK_Tabla.wav, 14'29.5"–15.05".[39] These examples show a tendency for the ṭhekā to be more elaborated at slow tempi, at least in the sense that the articulation of the ½ and ¼ mātrā subdivisions feels more consistent and less decorative in A5 and A6 than in the faster examples. However, tablā players are aware of the danger of over-elaboration: the more bols (strokes) are added, the more one risks losing the character of the tāl. So for some, at least, an important principle is that bols should be added only when it becomes impossible to sustain the sound of the ṭhekā’s main bol (Vishwanath Shirodkar, May 5, 2014). Nonetheless, at slower tempi the ṭhekā tends to be filled out more. At the slowest speed, as these examples show, at least two strokes are played per mātrā, with fills increasing the density to x4 or x8. At the fastest tempi, just one stroke per mātrā is frequently used (the bol on mātrā 2 is sometimes dropped altogether). In some performances, tablā players use a variety of fills towards the end of the cycle, including playing a 3:2 polyrhythm on the last 2 mātrās. In Audio Example 12, for example, we can hear 7 cycles in which tablā player Vishwanath Shirodkar uses a variety of elaborations in his accompaniment, including syncopations and cross-rhythmic patterns, particularly in the latter part of each cycle.
Compositional structures
[40] The only study of khyāl compositions in rūpak tāl of which I am aware is Magriel and du Perron’s The Songs of Khyāl (2013). This two-volume compendium transcribes, translates, and describes a corpus of 492 compositions as recorded in the first three-quarters of the 20th century. Of the 492 songs, only eight are in rūpak tāl, confirming that it is relatively uncommon in this genre.(30) Magriel and du Perron nonetheless describe these performances in some detail, concluding that “rūpak, being infrequently performed compared to the main khayāl tāls, has afforded less opportunity for the establishing of conventions or standardized modes of presentation” (2013, 271).
[41] In brief, Magriel and du Perron found no consistent pattern in terms of the structure of the vocal compositions. This contrasts with khyāls in medium tempo tīntāl (16 mātrās), many of which feature an anacrusis (mukhṛā) of 5 mātrās, and therefore begin on mātrā 12; or those in slow ektāl (12 mātrās), where a similar mukhṛā pattern, due to the slow tempo, extends over roughly 1¼–1½ mātrās (cf. Clayton 2000, 119).
[42] A selection of khyāl audio examples from our corpus again illustrate some of the possibilities:
- Audio Example 13 (Tablā: Vishwanath Shirodkar, first cycle = 37 bpm): this slow-tempo piece uses a mukhṛā of about 1½ mātrās
- Audio Example 14 (Tablā: Milind Hingne, 39 bpm): this example uses a mukhṛā extending over 2½ mātrās; the syllable falling on sam is extended, sometimes over more than 4 mātrās, giving a sense of repose after a cadence
- Audio Example 15 (Tablā: Vishwanath Shirodkar, 56 bpm): this composition in the light Rāg Hamsadhvani has an unusual structure with a long, melismatic opening from mātrā 2.5
- Audio Example 16 (Tablā: Ajinkya Joshi, 60 bpm): similar to RamD_RagBah (A13) in structure, this composition clearly divides into a single syllable first part (mātrās 1–3) and a second part (mātrās 4–7) from which a 1½ mātrā mukhṛā can be split off
- Audio Example 17 (Tablā: Vishwanath Shirodkar, 71 bpm): this composition is unusual in that it does not include a mukhṛā, but starts from sam (mātrā 1)
Rāg Rāgeśrī-Bahār performed by Ram Deshpande (voice), Viswanath Shirodkar (tablā) and Anant Lakhe (harmonium). Nashik, Maharashtra, 13/2/2010. Source: NIRP1_RamD_RagBah_StereoMix.wav, 5'49"–6'23".
Rāg Jhinjhotī performed by Manjiri Asanare-Kelkar (voice), Milind Hingne (tablā) and Shubhash Dasakkar (harmonium). Nashik, Maharashtra, 13/2/2011. Source: NIRP1_MAK_Jhin_StereoMix.wav, 3'02"–3'35.5".
Rāg Hamsadhvani performed by Veena Sahasrabuddhe (voice), Viswanath Shirodkar (tablā) and Seema Shirodkar (harmonium). Pune, Maharashtra, 15/12/2006. Source: NIRP1_VS_Hams_StereoMix.wav, 3'24"–4'05".
Rāg Hinḍol-Bahār performed by Vijay Koparkar (voice), Ajinkya Joshi (tablā) and Rahul Gole (harmonium). Pune, Maharashtra, 25/2/2010. Source: NIRP1_VK_HinBah_StereoMix.wav, 3'51"–4'24".
Rāg Tilak Kāmod performed by Manjiri Asanare-Kelkar (voice), Vishwanath Shirodkar (tablā) and Kaviraj Singh (harmonium). Durham, England, 30/4/14. Source: NIRP1_MAK_TilakK_StereoMix.wav, 2'12"–2'55".
Audio Example 18
Rāg Nāyakī Kānaḍā performed by Mogubai Kurdikar. Source: Magriel and du Perron 2013.Audio Example 19
Rāg Nāyakī Kānaḍā performed by Basavi Mukherjee (voice), Debashish Sarkar (tablā), Ramesh Mishra (sāraṅgī), and Prosenjit Sengupta (harmonium). Source: Eclectic Expression, P&M Records PMR048 (2006), 1'26.5"–1'55".Audio Example 20
Rāg Cārukeśī performed by Shahid Parvez Khan (sitār) and Hindol Majumdar (tablā). Source: Amazon.com Song ID: 243404211 (2013), 0'00"–0'30".Audio Example 21
Rāg Bhīmpalāsī performed by Debashish Bhattacharya (Guitar) and Samir Chatterjee (tablā). Source: ‘Hindustani Slide Guitar’, India Archive Music IAM 1026 (1997), 0'23.5"–0'56.5".[43] The ten khyāls show that a mukhṛā of 1½–2½ mātrās, followed by an extended articulation (syllable or stroke) on sam, is the most common pattern, but significant variations from this are not uncommon.(31) In the additional corpus examples, other structures are found. For instance, recordings of Rāg Nāyakī Kānaḍā by Basavi Mukherjee and Ashwini Bhide-Deshpande, the slowest performances in the corpus, manage to squeeze an eight-note melismatic mukhṛā (on the word “mero”) into the last half-mātrā of the cycle. The version of this composition transcribed by Magriel and du Perron (2013, vol. 1, 470) from Mogubai Kurdikar’s 1948 performance, for comparison, has this melisma on mero lasting for the full seventh mātrā (Audio Example 18). It seems clear in this case that in slowing the tempo from 60 bpm to less than 30 bpm, this gesture has been retained but now takes up only a half rather than a full mātrā (the phrase on mero begins the performance, and then recurs in its mukhṛā form, filling the last half mātrā at c. 20 secs) (Audio Example 19).
[44] The structure of the instrumental compositions is somewhat different, given three factors. First, instruments such as the sitār cannot sustain a single syllable for as long as the voice can. Secondly, improvisations are more likely to conclude with tihāīs (triple repetitions) than simply returning to the mukhṛā as in khyāl. Thirdly, the mukhṛā cannot be identified by the words. A variety of structures is therefore encountered, often introducing an element of rhythmic interest. In Prattyush Banerjee’s Rāg Jhinjhotī, for example (Audio Example 3), we can hear in the initial statement of the gat that the last 3 mātrās are split into 1½ + 1½, creating a simple cross-rhythm. Shahid Parvez Khan’s Rāg Carukeśī (Audio Example 20) is more radical, starting the melodic line from mātrā 1.5, just half a mātrā after sam. At faster tempi, compositions often take up two cycles per section (Clayton 2000, 129; cf. Goldberg 2017, 155, on rŭchenitsa). In Debashish Bhattacharya’s Rāg Bhīmpalāsī (Audio Example 21), the two lines can be disassociated and the first half of the sthāyī repeated alone.(32)
Rūpak tāl in Khyāl accompaniment: Further investigation
[45] Bearing in mind the theoretical questions set out in the introduction, the more detailed analysis in this section uses onset timing data and video recordings to explore the following issues in particular:
- Consistency of mātrā duration and patterns of variation. Are there any significant divergences from strictly equal mātrā lengths? Mātrās felt to be “stronger” or “heavier” might be expected to be slightly longer than the mean.
- Drum patterns in tablā accompaniment (ṭhekā). How is rūpak tāl actually played in accompaniment? How does practice relate to the theoretical ṭhekā patterns? Mātrās that serve as anacruses preparing for the stronger metrical positions may be expected to be more elaborated, and hence include more bols.
- Gesture and movement. What does the practice of tāla-marking gestures, especially the wave performed on the first beat, tell us about the nature of rūpak tāla? What is the significance of the normative “wave” on beat 1?
Example 12. Ten recordings comprising the core corpus used in the second stage analysis
(click to enlarge)
Through these analyses, we will build up a more detailed picture of rūpak tāl as it is used in practice in the khyāl genre.
Corpus
[46] The core corpus used for this section comprises ten khyāl recordings (nine vocal with tablā and harmonium accompaniment, and one sāraṅgī solo with tablā), recorded as multitrack audio and video between 2006 and 2014. Tablā onset data was extracted using a Matlab function created by Tuomas Eerola.(33) Original media files and onset annotations are freely shared for research purposes (see Clayton, Leante, and Tarsitani 2019), as are the data files and R scripts used to produce the figures. Each mātrā was annotated manually by tapping along with the audio file in Sonic Visualiser. Gross errors in these timings were corrected and then tablā onsets within specified intervals of those reference points were selected (the size of the window varying between examples). The resulting set of annotated tablā onsets was then manually checked. See Example 12 for details of the recordings.
Tempo in khyāl accompaniment
Example 13. Tempo curves for all ten core recordings, based on tablā onset data
(click to enlarge)
[47] Tempo ranges and acceleration have been discussed in detail in the previous section. Example 13 illustrates the tempo curves of all ten recordings used in this section. A reference line is added at 45 bpm to illustrate the division between slow/vilambit and other sections.
Consistency of mātrā duration and patterns of variation
Example 14. Difference in mātrā lengths from isochrony
(click to enlarge)
[48] In this subsection, data relating to the durations of individual mātrās is considered, based on IOIs between annotated tablā onsets. It is worth pointing out that the position of the onset of a tablā stroke should not be taken unquestioningly as the position of “the beat”: in a sense, the beat is constantly being negotiated between all of the musicians, and the drummer’s performance is subject to his own human limitations in precision. Nonetheless, tablā onset data are important here for two reasons: (1) because any timing errors are those of the musician, not the researcher; and (2) because if rūpak tāl is characterized by regular deviations from isochrony at the beat level, then we should expect to find this manifested in the tablā accompaniment part most of all. Example 14 shows that for these ten recordings, mātrās 1, 2, and 4 overall tend to be slightly longer and mātrās 3, 5, 6, and 7 slightly shorter, compared with the even subdivision of the cycle. The margins are small when we look at the mean deviations, however, the largest mean difference (mātrā 1) being about 1.5%.
Example 15. Plot of differences in mātrā length from isochrony in four khyāl performances
(click to enlarge)
[49] These patterns do vary somewhat between examples. To illustrate this in more detail, Example 15 visualizes differences from isochrony across five different pieces. An underlying pattern of mātrās can be discerned— mātrās 1, 2, and 4 tending to be longer, and 3 shorter. There are differences, however: MAK_Jhin, RamD_RagBah, and VS_Hams all have a consistently shorter mātrā 3 but this is not apparent in MAK_TilakK, while MAK_TilakK also tends to have a longer mātrā 5. These examples were chosen to allow comparison between three recordings with the same singer (the top three), as well as between three recordings with the same tablā player (the bottom three). The visual differences do not group in any obvious way according to either singer or tablā player, so the differences must be accounted for elsewhere (i.e., the rāga or tempo could have an influence).
Tablā accompaniment and mātrā subdivision
[50] Having explored variations in the basic ṭhekā pattern used to accompany rūpak tāl, we can now explore practice in more detail using the tablā onset data. A number of previous studies have used the distribution of note or stroke onsets as an index of metrical strength (Goldberg 2017, 143ff). In these studies, the hypothesis is generally that stronger metrical positions (beats at slower pulse levels) have a higher probability of coinciding with note onsets. Palmer and Krumhansl (1990, 732) also find a higher incidence of onsets falling on anacruses.(34) In the current study, virtually every mātrā position is marked by a tablā stroke, and thus tablā event distribution on the mātrās tells us very little about the metrical structure. The subdivision of the mātrā is a different question, however. Since the logic of improvisation in this music tends to be an increase in tension and excitement leading up to a metrical downbeat, followed by relaxation, our hypothesis is that strong metrical positions in North Indian tāla will be associated with lower rates of subdivision, and weaker positions—particularly anacruses—with higher rates of subdivision.
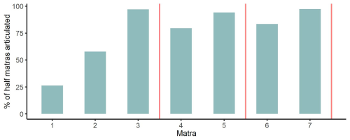
[51] Across the whole corpus, the proportion of mātrās subdivided 2:1 by the tablā part was estimated by searching for drum onsets within +-50ms of the midpoint between two mātrā onsets. The result is plotted in Example 16. The mātrās most consistently subdivided (more than 95% of the time) are those at the end of the vibhāgs, namely 3, 5, and 7. The mātrā least subdivided is 1 (28%). Note that this could not have been surmised from the published notations of ṭhekās used for rūpak tāl, and nor was attention drawn to this phenomenon by tablā players in interview.
Example 16. The proportion of beats in each mātrā position featuring a tablā stroke at the half-mātrā position (click to enlarge) | Example 17. The number of detected tablā onsets (bols) per beat by mātrā position (click to enlarge) |
Example 18. Strokes (bols) per mātrā across five performances
(click to enlarge)
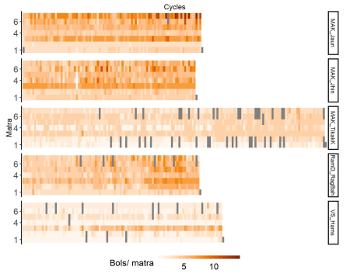
[52] The rate of subdivision by the tablā part was explored further by counting the number of extracted onsets in each pair of tablā onsets between successive mātrā. It is clear in Example 17 that mātrā 3 is the densest on average, surely related to the prevalence of the 4:1 subdivision in the common Tirakita stroke pattern. Breaking this down by performances, the variability of practice is clear: while mātrā 1 is sparsely played and 3 relatively densely across the board, we see, for example, that MAK_Jaun features particularly dense subdivision of mātrā 7, while VS_Hams and MurA_DhaniK are much sparser on the same mātrā.
[53] Another way of visualizing practice in tablā accompaniment is by representing more densely subdivided mātrās in a darker color, as in Example 18, which compares the same five recordings illustrated in Example 15, featuring three by singer Manjiri Asanare Kelkar and three with tablā player Viswanath Shirodkar. In a comparison between three performances of the same singer, we can see that in MAK_Jaun, mātrā 7 becomes denser as the performance proceeds and tablā player Milind Pote plays more fills at the end of the cycle. Mātrā 3 is quite dense throughout. In MAK_Jhin (tablā: Milind Hingne), this increase in density is less marked and more focused on mātrā 6. MAK_TilakK (tablā: Vishwanath Shirodkar) features less subdivision overall.
Audio Example 22
Tablā and vocal tracks from: Rāg Rāgeśrī-Bahār performed by Ram Deshpande (voice), Viswanath Shirodkar (tablā) and Anant Lakhe (harmonium). Nashik, Maharashtra, 13/2/2010. Source: NIRP1_RamD_RagBah_Tabla.wav (L) / NIRP1_RamD_RagBah_Vox.wav (R), 19'35"–20'47".[54] The different performances featuring the same tablā accompanist Vishwanath Shirodkar illustrate the fact that he varies his style according to circumstances (the rāga, tempo, and singer’s style could all play a part). His playing on VS_Hams features increasing subdivision of mātrā 3, while on RamD_RagBah, he increases density on both mātrā 3 and elsewhere in the cycle, especially 2, 5, and 7. The latter case evidences a more active accompaniment style and rhythmic interplay with the singer (Audio Example 22), which has tablā on the left channel and vocal on the right).
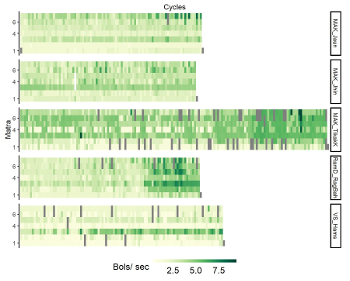
Example 19. Stroke density per second across five performances
(click to enlarge)
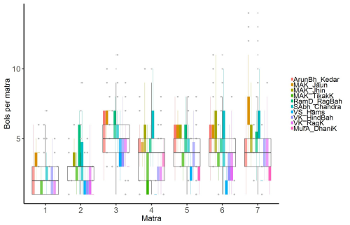
Example 20. Distribution of number of bols (detected tablā onsets) per mātrā by tempo
(click to enlarge)
[55] If we plot the density in strokes per second for the same five performances (Example 19), we can see that in MAK_TilakK the stroke density increases, thanks to an increase in tempo. VS_Hams maintains a low stroke density throughout, apart from mātrā 3, while in RamD_RagBah, the density increases substantially across the cycle.
[56] Another way of illustrating the interaction of mātrā subdivision and tempo is plotted in Example 20. If we explore the subdivision of mātrās by tempo range, unsurprisingly we find higher rates of subdivision at slower tempi: they only go above 8:1 in sections below 45 bpm (mātrā > 1333 ms), although they are still frequently around 4:1 even at 120–130 bpm (mātrā < 500 ms). Consistent with the result reported above, mātrās 1 and 2 show up as less densely subdivided. It is also striking that the fastest subdivisions (10:1–15:1) fall almost exclusively on mātrā 7 in the slowest example MAK_Jaun.
Movement
[57] Video recordings offer the opportunity to look at the way musicians and audiences move in the course of rūpak tāl performances. In particular, the use of tāl-related manual gestures provides additional clues as to the perceived structure and feel of the tāl. All musicians are taught the basic wave-clap-clap pattern, but it is rarely performed as such in live concerts. Rather, this is a pattern that can be referenced as and when needed. For example, if the singer feels that the tablā player is finding it difficult to grasp the structure of a composition, he or she might use a wave to indicate where sam falls. For most singers, the majority of hand gestures will relate to melodic flow or contour, or to dynamics, rather than to tempo or metrical structure (Clayton 2007). Gestures relating to the tāl tend to occur at the beginning of the performance, when they indicate the required tempo to the tablā accompanist, and in the course of improvisation, when a range of gestures are used to indicate that sam has been reached (especially on cadential downbeats).
[58] In starting the performance, the singer’s focus is on the correct tempo and feel. Therefore, at slow or medium tempi the singer will often start with a sequence of taps of the right hand on the knee, sometimes indicating not only the mātrā beats but also the ½ or ¼ mātrā level. Subsequently, some singers will use a gesture that clearly indicates the sam—most often at the end of a passage of improvisation while singing the mukhṛā (refrain), but sometimes also in the middle of their improvisatory flow, indicating that they remain conscious of the tāl. In many cases, this gesture will be related to a “wave”—for instance, a sharp movement of the hand will be made with the palm facing upwards. It can also be observed that sam gestures in this corpus often include an opening of the arms and/or a relaxation of one or both arms, and thus contribute to a sense that sam is a point of relaxation.
Video Example 2. Rāg Rāgeśrī-Bahār
(click to watch video)
Video Example 3. Rāg Jhinjhotī
(click to watch video)
Video Example 4. Rāg Jaunpurī
(click to watch video)
Video Example 5. Rāg Hamsadhvani
(click to watch video)
[59] Five video clips, featuring one male singer, two female singers, and one sāraṅgī solo, illustrate the variability in manual gestures. Brief descriptions are given below:
- In Ram Deshpande’s Rāgeśrī-Bahār, sam is indicated initially with a tap of the right hand on knee (0:08), then typically with a combination of flicks of right and left hand (0:19, 0:30, 1:16); but also with a pointing gesture with the left index finger (1:27), or as a rapid rotation of the fingers of the left hand (2:01) or of the left index finger (2:24) (Video Example 2)
- In Manjiri Asanare-Kelkar’s Rāg Jhinjhotī, she begins by indicating the sam to her accompanists with a pointing gesture of the right hand (0:07). This is replaced by a gentle wave of the left hand (0:18) and then by a downward movement of both hands (e.g., [1:12]), which appears to suggest the action of making an offering. This gesture is sometimes elaborated into four downward steps coinciding with the preceding half-mātrā points (1:53–1:57) (Video Example 3)
- In the same singer’s Rāg Jaunpurī, she indicates sam with a more perfunctory, gentle grasping gesture of the left hand (e.g., [0:28]) or an equally gentle release of the fingers of the left hand (1:46). This difference from her Jhinjhotī may be accounted for in at least one of two ways: (1) the Jhinjhotī was performed for a large, communicative audience, whereas the Jaunpurī was recorded privately with a much smaller group of listeners; (2) in the Jaunpurī she plays the tānpūrā with her right hand, whereas for the Jhinjhotī she is not playing the tānpūrā. It is not clear whether the difference is due to one or both of these factors, or to a difference in mood between Jaunpurī (a late morning rāg, contemplative in character) and Jhinjhotī (evening, more lively and romantic) (Video Example 4)
- Veena Sahasrabuddhe begins her rendition of Rāg Hamsadhvani with very tāl-focused gestures, striking both her knees on the first sam (0:08) and continuing to mark a basic version of the tablā’s rhythm with her own hands for several beats. At 0:23 she gives a subtle gesture with the left hand, which suggests “release” (cf. both hands at [1:00]). At (0:38), sam is marked with a more flowing left-hand gesture (Video Example 5)
- Murad Ali Khan’s scope is obviously highly constrained, in contrast, but it is worth observing the way he and tablā player Gurdain Rayatt mark sam with coordinated downwards nods of the head (e.g., [0:17] and [0:27]) (Video Example 1)
[60] As can be seen from this selection of video clips, manual gestures are by no means used in a standardized fashion. Soloists use them when they are salient—at the start of a performance when coordination with tablā accompanists needs to be secured, and then at cadential points when improvisatory episodes are concluded. Tāla gestures are part of a mixture of gesture types, with other referents including the shape of the melodic line often being more prominent. Where they do occur, the wave may be a useful referent, but the range of movements is quite varied, including a range of flicks, points, grasps and other gestures. It is difficult to say definitively which of these tāl-related gestures is rūpak-specific without carrying out a similar survey of other tāls. But the prominence of gentle movements with an open hand, often palm upwards, and relative rarity of forceful downward hand-strokes and claps does concur with theoretical descriptions of the tāl’s character. Most of the gestures here are consistent with a description of the sam as “light” or “gentle” and with a sense of relaxation or release, rather than of an energetic coming together. In any case, Manjiri Asanare-Kelkar’s downward-moving open-handed gestures in Rāg Jhinjhotī are not simply generic rūpak tāl gestures; rather they are specific to the singer and rāga, and perhaps even to the specific composition or concert performance.
Discussion
Rūpak tāl
[61] Rūpak tāl is an important metrical pattern in the Hindustani tradition. It seems to have developed through a combination of fast 7-beat patterns used in North-western India, Pakistan, and Afghanistan with principles from India’s very different historical tāla system, but is played more slowly than any of its progenitors. It has a distinctive drum pattern (ṭhekā) and clapping pattern, and its own distinctive “feel” characterised by a light first beat. In Hindustani classical music, it is used in three distinct genres: in khyāl vocal, in gat, and in tablā solo, as a means to create rhythmic variety.(35) Particularly in khyāl, rūpak tāl is often played rather slowly; the mātrā (basic time unit) can extend to well over 1500 msec in duration, creating a very long metrical cycle and necessitating subdivision of the mātrā, so that the tactus may shift from the mātrā to the half-mātrā level. Even at tempi less than 30 bpm, the 7-cycle is remarkably stable.(36)
Example 21. Rūpak tāl’s structure
(click to enlarge)
[62] In both vocal and instrumental music, rūpak tāl is favored by particular musical lineages or individuals. Most of those who perform rūpak tāl tend to regard it as in some sense “secondary,” suited to the second rāg of a concert or to a rāg of “limited scope.” Being performed much less often than some other tāls, its practice is less standardised, with a wide range of composition structures and a fair amount of quirkiness in evidence. As practice has developed over the 20th century, the adoption of the Tirakita bol elaborating mātrā 3 has also become all but standard, and the use of khālī bols (without bass) on mātrā 7, and to a lesser extent mātrā 5, almost entirely abandoned. This has implications for our interpretation of the structure. In practice, tablā players tend to fill out the last mātrā of each group significantly more than the others, especially mātrā 1, which is played the most sparsely. The length of mātrās 1, 2, and 4 tend to be very slightly extended, and 3, 5, and 7 slightly shortened compared to an isochronous division of the cycle. This finding about the variation in mātrā subdivision and the small variations from isochrony in mātrā lengths is summarized in Example 21.
[63] The structure is unusual in the Indian context, not because it is a 7-cycle, but because the sam is khālī (indicated with a wave or played with a light drum beat). This is remarkable enough to deserve an explanation. Although the heavier drum beats thus fall on mātrās 4 and 6, the cycle is nowadays universally described as 322 rather than its rotation 223. The significance of this is that the main point of emphasis and release in compositions falls at the start of the group of 3 mātrās, and improvisation is oriented with respect to this point in the cycle.
Example 22. A representation of rūpak tāl’s structure
(click to enlarge)
[64] This suggests a balance between two main points of emphasis, either of which can be perceived as the strongest. Mātrās 1 and 4 are therefore the two most important time points in the cycle. The Tirakita pattern that has now become all but standard (with variations) on mātrā 3 enhances a sense of driving to mātrā 4, which balances the emphasis on sam which is created or supported by the structure of vocal and instrumental compositions. This interpretation is supported by the variations to the bols on mātrā 3 and the slight shortening and increased stroke density of mātrās 3 and 7. On the other hand, the change of practice in tablā accompaniment of mātrās 4–7, where the standard ṭhekā’s alternation of heavy and light strokes is often abandoned in favor of four “heavy” strokes, means that the perceived structure may tend towards 34 rather than 322. Example 22 illustrates an interpretation of the structure as oriented around this alternation between the two main downbeats on mātrās 1 and 4. This division of the cycle into two unequal halves contrasts with the conception of tablā soloists, for whom it is necessary to divide any cycle equally into halves and quarters.
Metrical theory and long form NI meter
[65] The description of rūpak tāl’s structure in the previous section makes some reference to tempo-related differences—for example, in the maximum subdivision levels revealed by the empirical analysis. What is more striking, however, is the extent to which rūpak tāl is conceived as the same structure over a tempo range of about 30–130 bpm (a factor of more than 4:1), and up to a cycle length of over 15 secs. (For the additional corpus, the range across all genres is about 22–229 bpm, or >10:1.) This is not to say that the difference in tempo is not perceived, of course, but that the tāl is conceived and represented as invariant, and that, as a result, its identity is much more strongly perceived than one might expect over such a wide tempo range. I argue that the theoretical knowledge of rūpak tāl’s structure is activated regardless of tempo, that it influences perception in a top-down manner, and that this enables a cycle of >15 secs duration to function as a part of the metrical structure.
[66] I suggest that this is the case for most metrical cycles in most musical traditions. Listeners’ metrical perception is never a “raw” perception based simply on neurological entrainment to quasi-periodic events. In practice, metrical perception always involves reference to knowledge acquired over a lifetime’s listening. This can include a sense of how quasi-periodic patterns are produced and how one might typically participate in or respond to such patterns (for example, by dancing), as well as how one might match perceived patterns against learned models. I suggest that what happens in a case such as rūpak tāl is that a knowledge of the structure and its representation in clapping pattern and typical drum patterns becomes essential for the 7-cycle to be perceived as such, because the learned structure of the pattern, represented in practice by archetypal drum patterns and hand gestures, provides priors to support top-down perception of the pattern.
[67] In all aspects of the metrical structure of rūpak tāl, we can see an interaction between general principles of meter as underpinned by cognitive constraints, and more local factors such as the preference for certain kinds of structures, and the use of explicit knowledge to fix these structures and to try to maintain them as “the same” over a very wide tempo range. I have argued that this application of explicit knowledge means that it makes sense to regard structures lasting well over 15 seconds as being metrical units. For someone with access to this knowledge, it is just as much a pattern of 7 beats at 22 bpm as it is at 180 bpm. This interaction of bottom-up and top-down factors is by no means unique to rūpak tāl. What the particular features of rūpak tāl afford us, however, thanks to their accidental contrast with elements of metrical theory developed in a very different musical tradition, is the opportunity to expand our understanding of the kinds of structures and representations that may contribute to top-down metrical perception, and to acknowledge that the psychological present does not impose an absolute limit on metrically-significant timescales.
Conclusion
[68] The general points that I have discussed in this article regarding metrical theory can be summarised as follows: (1) certain metrical structures employ a level between the beat and the cycle with a distinct function, labeled here as the group level. I have termed such structure “long-form meter.” Just as beat and subdivision levels can be non-isochronous in other musical traditions, so too can the group level, as is the case with rūpak tāl—what I have termed an example of “long-form non-isochronous meter”; further, (2) metric cycles that extend well beyond any commonly-accepted limit for the psychological present are understood by musicians and listeners in the same way as analogous structures within this limit, and in these cases, metric theory should recognize that explicit knowledge structures make it possible for meter to extend well beyond 5–6 seconds.
[69] Beyond the specific argument made in these pages regarding metrical theory, the approach taken here introduces an approach to empirical analysis of tāl that could be further developed in the future. The idea of empirical analysis of rhythmic and metrical structures per se is not new. This article has pioneered the exploration of large openly-shared annotated corpora of natural music performances, combining statistics, data visualization, and musical analysis in order to build a picture of canonical tāl structures in performance. This characterization includes significantly more information about the tāl than is present in any written or oral theory, because it takes into account the variability of practice, with the tāl figuring not simply as an abstraction but as a range of possibilities accepted under the same label. Understanding why, for example, a drum pattern might be played differently according to the tempo, the melodic content, the relationships between performers, or other factors, amounts to a complex musicological issue, but the availability of empirical data can usefully feed into that analysis alongside historical, ethnographic and other sources. Expanding this approach to other tāls would add significantly to our understanding of the system as a whole, and this approach could be adapted to other musical traditions or to aspects of Indian music other than the tāl system.
Martin Clayton
Durham University
Department of Music
Palace Green
Durham, DH1 3RL
United Kingdom
martin.clayton@durham.ac.uk
Works Cited
Arom, Simha. 2004. “L’aksak: Principes et typologie.” Cahiers de musiques traditionnelles 17: 11–48.
Bartók, Béla. [1938] 1981. Musique de la Vie. Selected and translated by Philippe A. Autexier. Editions Stock.
Brăiloiu, Constantin. 1951. “Le rythme Aksak.” Revue de Musicologie 33 (99–100): 71–108.
Chaudhary, Subhadra. 1997. Time Measure and Compositional Types in Indian Music. Aditya Prakashan.
Clayton, Martin. 2000. Time in Indian Music: Rhythm, Meter and Form in North Indian Rāg Performance. Oxford University Press
—————. 2007. “Observing Entrainment in Music Performance: Video-based Observational Analysis of Indian Musicians’ Tanpura Playing and Beat Marking.” Musicae Scientiae 11 (1): 27–59. https://doi.org/10.1177/102986490701100102
Clayton, Martin, Kelly Jakubowski, and Tuomas Eerola. 2019. “Interpersonal Entrainment in Indian Instrumental Music Performance: Synchronization and Movement Coordination Relate to Tempo, Dynamics, Metrical and Cadential Structure.” Musicae Scientiae 23 (3): 304–31. https://doi.org/10.1177/1029864919844809
Clayton, Martin, Laura Leante, and Simone Tarsitani. 2018. IEMP North Indian Raga. https://doi.org/10.17605/OSF.IO/KS325
—————. 2019. NIRP1 Rupak Tal Khyals. https://doi.org/10.17605/OSF.IO/FQUB5
Cler, Jérôme. 1994. “Pour une théorie de l’aksak.” Revue de Musicologie 80 (2): 181–210.
Djoudjeff, Stoyan. 1931. Rythme et mesure dans la musique populare bulgare. Librairie Ancienne Champion.
Fracile, Nice. 2003. “The ‘Aksak’ Rhythm, a Distinctive Feature of the Balkan Folklore.” Studia Musicologica Academiae Scientiarum Hungaricae 44 (1–2): 197–210.
Gao, Lixia, Xiankai Meng, Changquan Ye, Haitian Zhang, Chunhua Liu, Yang Dan, Mu-ming Poo, Jufang He, and Xiaohui Zhang. 2009. “Entrainment of Slow Oscillations of Auditory Thalamic Neurons by Repetitive Sound Stimuli.” Journal of Neuroscience 29 (18): 6013–21. https://doi.org/10.1523/JNEUROSCI.5733-08.2009
Goldberg, Daniel. 2015. “Timing Variations in Two Balkan Percussion Performances.” Empirical Musicology Review 10 (4): 305–28. http://dx.doi.org/10.18061/emr.v10i4.4884
—————. 2017. Bulgarian Meter in Performance. PhD diss., Yale University.
Hannon, Erin E., and Sandra E. Trehub. 2005. “Metrical Categories in Infancy and Adulthood.” Psychological Science. 16: 48–55. https://doi.org/10.1111/j.0956-7976.2005.00779.x
Jones, Mari Riess. 1976. “Time, Our Lost Dimension: Toward a New Theory of Perception, Attention and Memory.” Psychological Review 83 (5): 323–55.
—————. 2019. Time Will Tell: A Theory of Dynamic Attending. Oxford University Press.
Kippen, James. 2006. Gurudev’s Drumming Legacy. Ashgate.
Kvifte, Tellef. 2007. “Categories and Timing: On the Perception of Meter.” Ethnomusicology 51 (1): 64–84.
Large, Edward W., Jorge A. Herrera, and Marc J. Velasco. 2015. “Neural Networks for Beat Perception in Musical Rhythm.” Frontiers in Systems Neuroscience 9: 1–14. https://doi.org/10.3389/fnsys.2015.00159
Lartillot, Olivier, Petri Toiviainen, and Tuomas Eerola. 2008. “A Matlab Toolbox for Music Information Retrieval.” In Data Analysis, Machine Learning and Applications. Studies in Classification, Data Analysis, and Knowledge Organization, ed. Christine Preisach, Hans Burkhardt, Lars Schmidt-Thieme, and Reinhold Decker. Springer.
Lerdahl, Fred, and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. MIT Press.
London, Justin. 1995. “Some Examples of Complex Meters and Their Implications for Models of Metric Perception.” Music Perception 13 (1): 59–77.
—————. 2012. Hearing in Time: Psychological Aspects of Musical Meter. 2nd ed. Oxford University Press.
Magriel, Nicolas, and Lalita du Perron. 2013. The Songs of Khayal. 2 vols. Manohar.
Moelants, Dirk. 2006. “Perception and Performance of Aksak Metres.” Musicae Scientiae 10 (2): 147–72.
Morillon, Benjamin, and Charles E. Schroeder. 2015. “Neuronal Oscillations as a Mechanistic Substrate of Auditory Temporal Prediction: Neuronal Oscillations and Temporal Predictions.” Annals of the New York Academy of Sciences. https://doi.org/10.1111/nyas.12629
Naimpalli, Sadanand. 2005. Theory and Practice of Tabla. Mumbai: Popular Prakashan.
Palmer, Caroline, and Carol L. Krumhansl. 1990. “Mental Representations for Musical Meter.” Journal of Experimental Psychology: Human Perception and Performance 16 (4): 728–41.
Patwardhan, Gurudev. 1903. Mṛdaṅg aur Tablā Vādanpaddhati. Lahore: Mufīd-e ‘Ām Press.
Polak, Rainer, and Justin London. 2014. “Timing and Meter in Mande Drumming from Mali.” Music Theory Online 20 (1). https://mtosmt.org/issues/mto.14.20.1/mto.14.20.1.polak-london.html
Rice, Timothy. 1980. “Aspects of Bulgarian Musical Thought.” Yearbook of the International Folk Music Council 12: 43–66
—————. 2000. “Béla Bartók and Bulgarian Rhythm.” In Bartók Perspectives: Man, Composer, and Ethnomusicologist, ed. Elliott Antokoletz, Victoria Fischer and Benjamin Suchoff, 196–210. Oxford University Press.
Rimmele, Johanna M., Benjamin Morillon, David Poeppel, and Luc H. Arnal. 2018. “Proactive Sensing of Periodic and Aperiodic Auditory Patterns.” Trends in Cognitive Sciences 22 (10): 870–82. https://doi.org/10.1016/j.tics.2018.08.003
Sachs, Curt. [1936] 1952. “Rhythm and Tempo: An Introduction.” The Musical Quarterly 38 (3): 384–98.
—————. 1953. Rhythm and Tempo: A Study in Music History. J. M. Dent.
Saxena, Sushil. 1979. The Winged Form: Aesthetical Essays on Hindustani Rhythm. Sangeet Natak Akademi.
Schroeder, Charles E., Donald A. Wilson, Thomas Radman, Helen Scharfman, and Peter Lakatos. 2010. “Dynamics of Active Sensing and Perceptual Selection.” Current Opinion in Neurobiology 20: 172–76. https://doi.org/10.1016/j.conb.2010.02.010
Singer, Alice. 1974. “The Metrical Structure of Macedonian Dance.” Ethnomusicology 18: 379–404.
Snyder, Joel S., Erin E. Hannon, Edward W. Large, and Morten H. Christiansen. 2006. “Synchronization and Continuation Tapping to Complex Meters.” Music Perception 24 (2): 135–45. https://doi.org/10.1525/mp.2006.24.2.135
Swets, Wouter. 1958. “Development of Unusual Metrical Types in the Folk Music of the Balkans and Asia Minor.” Antiquity and Survival II (4): 387–404.
Ullal-Gupta, Sangeeta, Erin E. Hannon, and Joel S. Snyder. 2014. “Tapping to a Slow Tempo in the Presence of Simple and Complex Meters Reveals Experience-Specific Biases for Processing Music.” PLoS ONE 9 (7). https://doi.org/10.1371/journal.pone.0102962
Thatte, Arawind D. 2010. Sangeet Vimarsha: A Bouquet of Thoughts about the North Indian Classical Music. Swanandi Prakashan.
Tillmann, Barbara, Catherine J. Stevens, and Peter E. Keller. 2011. “Learning of Timing Patterns and the Development of Temporal Expectations.” Psychological Research 75 (3): 243–58. https://doi.org/10.1007/s00426-010-0302-7
van der Steen, M.C. (Marieke), and Peter E. Keller. 2013. “The ADaptation and Anticipation Model (ADAM) of sensorimotor synchronization”. Frontiers in Human Neuroscience 7: 253. https://doi.org/10.3389/fnhum.2013.00253
Vuust, Peter, and Maria A. G. Witek. 2014. “Rhythmic Complexity and Predictive Coding: A Novel Approach to Modeling Rhythm and Meter Perception in Music.” Frontiers in Psychology 5: 1111. https://doi.org/10.3389/fpsyg.2014.01111
Wade, Bonnie. 1984. Khyal: Creativity within North India’s Classical Music Tradition. Cambridge University Press.
Footnotes
* Recordings made by the author and colleagues were assisted by grants from the AHRC (RGST/ 6186/ APN19244 and SG/ AN6186/ APN19110) and British Academy (SG-38692), and by Open University and Durham University. Colleagues who contributed to the recording and editing include Laura Leante, Simone Tarsitani, Mark Doffman, Andy McGuiness, Adrian Poole, Morgan Davies and Lara Pearson. I would like to thank in particular all of the artists whose recordings and interviews have contributed to this article, including Murad Ali, Dr. Arawind Thatte, and Sanjeev Abhyankar for kindly responding to queries and confirming permissions by email; and to thank colleagues for their comments on earlier versions of this paper. Grateful thanks to Tuomas Eerola for the onset detection script, to Tuomas, Laura Leante, and other colleagues for their valuable feedback, and to Simone Tarsitani for assistance with preparation of media examples.
Return to text
1. This article transliterates Hindi terms according to the Library of Congress romanization table (http://www.loc.gov/catdir/cpso/romanization/hindi.pdf). For those unfamiliar with the system, the most important elements are that the macron sign indicates a long vowel (ā, ī, ū), <h> indicates an aspirated consonant, <c> indicates an unaspirated <ch> sound and <ś> a <sh> sound.
Return to text
2. “North Indian” and “Hindustani” are both commonly-used labels for the same art music tradition, increasingly commonly abbreviated to HCM (Hindustani Classical Music) and NICM (North Indian Classical Music). “North Indian” is preferred in this article, as is the term rāga (the system of melodic modes that characterizes the tradition) over “classical.”
Return to text
3. This article will retain the term mātrā for the basic time unit in this paper, since translating it as “beat” would create problematic ambiguities: at slow tempi the perceived beat of the music may move to the half-mātrā level. Nonetheless, the default position of this article is that the mātrā maps onto the beat level.
Return to text
4. The abbreviation IOI stands for “inter-onset interval” (i.e., the time interval between the start of two events, such as beats or drum strokes).
Return to text
5. Gats are idiomatic compositions based on stroke patterns, as opposed to instrumental versions of vocal compositions.
Return to text
6. It would be instructive to explore tāla in light of the full range of extant metrical theories. Unfortunately, space does not allow such an extensive treatment.
Return to text
7. The 232 example is from Swets (1958, 394), who gives a Serbian example but also suggests that it “occurs very seldom.” One of Bartók’s ([1938] 1981, 143) examples is also a 232.
Return to text
8. Timothy Rice (1980) took a somewhat different approach in a paper discussing the emic categories used by Bulgarian musicians. In this account, musicians “did not traditionally discuss their songs, tunes, or dances in terms of the number of beats per measure” (62), but were more likely to conceive the patterns in terms of the number of units in a measure (“unit” here refers to a group of 2 or 3 short pulses or subdivisions); the only aspect of rhythm to be discussed explicitly by performers was tempo. Rice uses the term “beat” here to refer to the upper figure in a time signature (e.g., the 7 in 7/8), and he uses “unit” for the level London describes as a non-isochronous beat. Thus, according to Rice, 322 = 7/8 would be described by Bulgarian musicians as having three units.
Return to text
9. According to Swets 1958, the 322 pattern is most characteristic of Greece, where it is known as Kalamatianós. In Greece and Albania, it is “moderately fast,” and it is also found in Macedonia (cf. Singer 1974) and in Bulgaria, where it is exclusively played fast. In terms of the 223 pattern, Swets 1958 noted that it is common in the Turkish Black Sea region (cf. Singer 1974 on Macedonia, once again).
Return to text
10. Transliterated rŭchenitsa by Goldberg (2017) and rûchenitsa by Rice (1980), and elsewhere as račenitca.
Return to text
11. While subsequent research has demonstrated that metrical patterns in general need not be based on a fast isochronous referent (Kvifte 2007; Polak and London 2014), this need not concern us here if we circumscribe the present topic to cover only those patterns where long and short are subdivided into 3 and 2 pulses respectively.
Return to text
12. A more generous range of possible beat rates would be 250–2000 msec, that between tempos considered respectively too fast and too slow “to be useful” in music (London 2012, 28).
Return to text
13. Although evidence has been reported of entrainment of slow-tempo brain oscillations (periods in the order of seconds) by sound stimuli (Gao et al. 2009), much more research would be needed to demonstrate the significance of this mechanism for metrical perception.
Return to text
14. Alternative models of rhythm perception and synchronization face similar challenges in incorporating learning and representation. Linear models that assume that listeners keep track of a beat through a process of continuous error correction that maintains phase alignment do not have to face such a strong principled objection as dynamical systems approaches, and in some cases do include an element of anticipation (see, for instance, van der Steen and Keller 2013), although much remains to be explored in terms of what may be anticipated. Vuust and Witek (2014) take a somewhat different approach to the same problem, arguing for a mechanism of “predictive coding” by which the brain seeks to minimize the difference between sensory information and prediction based on statistical processes. According to these authors, such an approach needs to take account of the fact that “neural structures underlying musical expectation are influenced by culture, personal listening history, musical training, mood, listening situation, and biology” (5).
Return to text
15. The word rūpak comes from the Sanskrit rūp, meaning shape or form, face, or beauty (i.e., beautifully formed). It has a variety of other usages in the performing arts.
Return to text
16. Hindustani music also features several 14-beat meters, which can be regarded as 322 or 34 patterns doubled in various ways:
- dīpcandī and jhūmrā tāls: 3+2+2+(3)+2+2 or 3+4+(3)+4, where only the second 3-group is khālī; or
- ada cautāl: 2+2+(2)+2+(2)+2+(2), which can be regarded as an elaboration of 6+4+4, or 3+2+2 with each mātrā divided into two; or
- dhamār tāl: clapped 5+2+(3)+4, which can be regarded as an idiosyncratic way of indicating a 3+2+2+(3)+2+2 pattern, omitting two of the gestures
17. The description is of the 322 pattern and thus would also apply to tīvra tāl.
Return to text
18. In this respect, rūpak is often bracketed with jhaptāl (10 mātrās, 2+3+(2)+3). The difference between the two, apart from the number of mātrās, is that jhaptāl has a longer documented history and an association with the dhrupad vocal genre, so its performing style is usually somewhat different to rūpak’s.
Return to text
19. We have also observed the tablā master Suresh Talwalkar’s class when he was teaching advanced students to improvise in rūpak tāl, and his emphasis was precisely on the art of splitting the cycle into equal halves and then into equal quarters (interview, Nov. 15, 2013).
Return to text
20. According to Kippen (2006), Gurudev Patwardhan used the term vibhāg (lit. “section”) in a very different sense to its modern usage, to indicate a half cycle. Thus rūpak comprises 2 x 3½ beats. He shares this interpretation with the legendary singer, musicologist, and educator Vishnu Digambar Paluskar. This suggests that the principle in tablā composition and improvisation of dividing even asymmetrical cycles into equal halves was well established by the early 20th century at the very latest.
Return to text
21. See Example 6, items AllaR_Tabla, LatifAKh_Tabla and SS_Tabla.
Return to text
22. In one case, SAbh_Chandra, we have the singer’s permission to release only a portion of the recorded media.
Return to text
23. Private recordings include the author’s recording of sitarist Deepak Choudhury, taken on stage in the UK in 1991 using a portable cassette recorder (recordings DCh_Bhim & DCh_TilakK), and solo harmonium recordings kindly provided by Dr. Arawind Thatte (AraTh_Bihag & AraTh_NatBh; see also Thatte 2010).
Return to text
24. As indicated in Example 6, some performances are taped from beginning to end and others only for a couple of minutes each at the start and end.
Return to text
25. Shirodkar specialises in khyāl accompaniment, so it is not surprising that this is closer to the observed khyāl range than the instrumental gat range.
Return to text
26. Kesarbai died in 1977, and the recording was released posthumously in 1985. The sound of the recording suggests a date well before that, although the fact that a 28-minute piece was preserved suggests that it was most likely recorded onto magnetic tape in the 1950s or later. Magriel and du Perron also describe a 78 rpm performance of the same composition dating from 1954 (which begins at 110 bpm), commenting that this wide divergence indicates that “Kesarbai was exceedingly flexible, adjusting tempo to suit the situation or her mood of the moment” (2013, 270). This is surely true. It may also be the case that, faced with a recording medium that allowed only a short performance, artists tended to start their performances somewhat faster than they would have done in a live concert (the 42.4 bpm performance was a concert).
Return to text
27. Sushil Saxena (1979, 119–20) refers to the tirakita bol but is clear that it does not form part of rūpak’s ṭhekā.
Return to text
28. It may be noticed that references to Tirakita in the tablā parts of these performances are subject to variation, both between and within examples. The detail and significance of these variations is beyond the scope of this paper.
Return to text
29. The recording can be found in another published corpus. See Clayton, Leante, and Tarsitani 2018.
Return to text
30. Similarly, Bonnie Wade (1984) cites only one rūpak tāl composition in the whole of her study of the genre.
Return to text
31. In this section I refer only to the structure of the first section or sthāyī of each composition. Khyal and gat compositions usually comprise two main parts, called sthāyī and antarā. The sthāyī is sung at the start of the performance: it often comprises two lines of text, the first of which can be repeated on its own over one cycle or alternated with a second text line covering two or more cycles. The second part, the antarā, is often not sung until much later in the performance: it is therefore much less important in defining the artist’s approach to the tāl.
Return to text
32. For a discussion of gat structures, see Clayton 2000, 28–29. Shahid Parvez discusses and demonstrates in Rāg Yaman two-cycle rūpak tāl compositions from 44’12” in a published interview, stressing the importance of the two-cycle (and thus 14-beat) pattern to the conceptualization of the gats: https://www.youtube.com/watch?reload=9&v=gs6KeyzdGBw (in Hindi/Urdu).
Return to text
33. Onsets were extracted based on envelope characteristics using MIR Toolbox (Lartillot, Toiviainen, and Eerola 2008). First the audio signal is band-pass filtered, and the envelope of the filtered signal is then extracted and subjected to low-pass filtering and half-wave rectification before applying peak-picking algorithms with three parameters. This approach generates onset annotations for the tablā with a high degree of timing accuracy, catching >95% of drum strokes and creating few false positives. For more information and onset data, see Clayton, Leante, and Tarsitani 2019.
Return to text
34. Although Goldberg (2017, 244) notes regional variation, his analysis in Bulgarian rŭchenitsa recordings shows the highest probability of a drum stroke on sub-beats 1, 3, 5, and 7––the three main beats plus the upbeat.
Return to text
35. Rūpak tāl is also sometimes used in kathak dance performance. This is not discussed in this article.
Return to text
36. One might suppose that performing such a cycle is very challenging, and indeed it is. But our recordings show that it is a challenge many professional musicians who attempt it can meet with some comfort. Although rare, musicians occasionally make errors in performance, such as adding or dropping beats. In the ten core performances, there are a total of four such errors––three in one performance, and one in another. It is unusual to hear as many as three tāla errors in one piece. Otherwise, added or dropped beats happen extremely rarely, apparently due to momentary lapses of concentration.
Return to text
Copyright Statement
Copyright © 2020 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
11233