Consonance, Dissonance, and Formal Proportions in Two Works by Sofia
Gubaidulina*
Noah Kahrs
KEYWORDS: Gubaidulina, timbre, consonance, dissonance, perception, form, proportion, golden section, Fibonacci series, sketch study, Paul Sacher Stiftung
ABSTRACT: Consonance and dissonance are frequently invoked in discussions of Gubaidulina’s music, particularly in terms of the composer’s intentional contrasts between timbres and her golden section-oriented formal planning. In this paper, I use the notion of dissonance to mediate between several competing theories of Gubaidulina’s music and theories of timbre more broadly. Certain passages in her Meditation on the Bach Chorale “Vor deinen Thron tret’ ich hiermit” (1993) are identified as dissonant based on her compositional theories and on sketch material from the Paul Sacher Stiftung, and on further examples drawn from her Am Rande des Abgrunds (2002). Broadly speaking, “dissonant” sounds are closer to white noise than “consonant” sounds, aligning with empirical studies of dissonance perception as well as with spectralist compositional theories. However, Gubaidulina’s music uses this extended notion of dissonance particularly musically; dissonances have specific structural roles in a work and resolve to consonances.
DOI: 10.30535/mto.26.2.7
Copyright © 2020 Society for Music Theory
Introduction
[1.1] Sofia Gubaidulina’s music is often noted for its timbral inventiveness and dramatic approach to form, but these are seldom related to one another analytically. Most discussion of Gubaidulina’s music focuses on how some compositional technique might relate to her religious philosophies, rather than on how different aspects of her music influence each other or how a listener might perceive timbre and form. Although religious discussions of Gubaidulina’s music are historically meaningful—she worked in the same Composers’ Union as, and often shared concert billing with, composers such as Arvo Pärt and Alfred Schnittke(1)—her musical poetics are quite different from those of such composers, so such discussion is often detached from the details of her music. Gubaidulina’s spiritual and musical goals, however, are very clear in her treatment of consonance and dissonance, which she extends beyond harmony to include factors such as timbre and form. In this article, I use the notion of timbral dissonance to mediate between theories specific to Gubaidulina’s music, psychoacoustic studies, and other composers’ theories of timbre.
[1.2] In the context of Gubaidulina’s music specifically, I address the relation between timbre and form by connecting two notions of consonance and dissonance that have arisen for her music: Valentina Kholopova’s “parameter complex,” which focuses on the note-and-phrase level, and Gubaidulina’s own golden section-based theories, which she uses to organize larger form. Gubaidulina has discussed how her ratio-oriented formal planning relates to consonance and dissonance (Lukomsky 1999); by looking at her works in those terms as established by sketches in the Paul Sacher Stiftung, I identify specific timbres and motives as consonant and dissonant within certain sections of Meditation on the Bach Chorale “Vor deinen Thron tret’ ich hiermit” (1993; henceforth, Meditation) for string quintet and harpsichord. I then extend these distinctions to other parts of Meditation and to Am Rande des Abgrunds (2003; henceforth, Am Rande) for seven cellos and two waterphones, to demonstrate how the parameter complex at the phrase level and the golden section at the form level both contribute to understanding dissonance in Gubaidulina’s music. I also present several psychoacoustic theories of timbral dissonance, generally focused on spectral similarity to white noise, that align with examples from these two works, which suggests that timbre in Gubaidulina’s music can be heard as contributing to a listener’s experience of tension and resolution.
Example 1a. A parameter complex from Ewell 2013, Example 1
(click to enlarge)
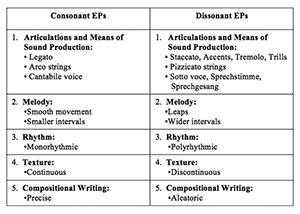
[1.3] The “parameter complex,” which demarcates consonance and dissonance in Gubaidulina’s earlier works, was devised by Russian musicologist Valentina Kholopova (2001) and presented to the English-speaking world by Philip Ewell (2013). Kholopova writes that in Gubaidulina’s music, “expression parameters (EPs)” such as articulation, timbre, interval, and rhythm are grouped into consonant and dissonant. Consonance and dissonance are not defined in this context so much as they are taken for granted as referential terms by which examples can be assigned labels, although in articulation they tend to align with legato and staccato, respectively. As shown in Example 1a (which reproduces Ewell 2013, Example 1), a “consonant” passage might consist of a legato stepwise melody with a steady continuous rhythm, whereas “dissonance” would entail a pizzicato leaping melody with aleatoric polyrhythms. Parameters such as rhythm, timbre, and articulation are presented in alignment with the traditional consonance-dissonance axis developed for pitch in tonal music. As presented in Ewell’s article, this system is designed for Gubaidulina’s early (pre-1980) works, and is justified by composer intent, with evidence drawn from Kholopova’s personal friendship with Gubaidulina; Ewell, paraphrasing Kholopova, writes that with Gubadiulina’s 1971 Concordanza, the parameter complex “became Gubaidulina’s favorite method for composing” (2013, [9]).
Example 1b. A list of numerical series of increasing dissonance, from Lukomsky and Gubaidulina 1999, p. 28, Ex. 1
(click to enlarge)
[1.4] As Gubaidulina continued to develop her compositional style in the 1980s and beyond, she extended the dichotomy of consonance and dissonance to include integer series, with a technique she calls “the rhythm of form.”(2) In her system, the most consonant series possible is the Fibonacci series, and as shown in Example 1b, integer series with the same rule are considered dissonant if they start with different integers than the Fibonacci series. In the example, sequences further down are more different from the Fibonacci series, as indicated by a larger number after 1; the further such a series deviates from the “consonant” Fibonacci series, the more dissonant it is. These integer series are then used to organize a work’s large-scale proportions: a piece might contain several competing proportions, each from a different integer series, which are audibly made to contrast with one another.(3) Through such techniques, consonance and dissonance have contributed to Gubaidulina’s music up to the present day.
[1.5] Gubaidulina discusses both the parameter complex and the golden section in religious terms, implying that they involve similar notions of consonance and dissonance. In the 1970s, when she composed her first parameter-based works, in which legato and staccato are respectively consonant and dissonant, she “often said that art has a religious function, that in the ‘staccato’ of life it must restore the ‘legato’” (Kurtz 2007, 96). In Concordanza, composed with the parameter complex, this plays out as follows:
Concordanza means “agreement,” “concord,” or “harmony” [all synonyms for “consonance”], and here [. . . ] is illustrated on the level of articulation types: in the legato, in the flow of the voices without punctuation or rests. [. . . ] The opposite, discordanza [synonymous with “dissonance”], is exhibited in the staccato of the winds, pizzicato of the strings, [and also] in trills and tremolos. (Redepenning 1994)
Likewise, Gubaidulina has said when discussing “the rhythm of form” that the golden section, derived from the Fibonacci series, is “the perfect ratio, representing the universal proportion of life” (Lukomsky 1999, 28–29). Gubaidulina associates both the “perfect [
Example 1c. An example of dissonance between conflicting proportions, from Lukomsky and Gubaidulina 1999, p. 28, Ex. 2
(click to enlarge)
[1.6] Parameters and ratios relate not just spiritually, but also musically in the context of Gubaidulina’s compositions. Describing Example 1b and Example 1c, Gubaidulina said in a 1999 interview:
For example, if we build a composition in such a way that in the first section there is one unit of time, and in the second section two equal units of time (that is, we take this ratio from the Fibonacci series), then the Golden Section is located between these two sections, and something important always happens in this point of the composition. Now, we'll take the ratio from the sixth series (1:7); it means that in the first section there is one time unit, whereas the second section contains seven units. Such a proportion will cause a terrible dissonance, which occurs between these two points (i.e., between the “almost perfect” and the “dissonant” Golden Sections).
The extreme tension between these two points calls for extraordinary musical events that should happen in this area. Let’s suppose that there are two different musical layers, and the tension arises between the two layers. And, in the point of their meeting, something should occur: a dialogue, or a conflict, or something else—whatever I can imagine. (Lukomsky 1999, 28–29)
Gubaidulina says that the events that occur between two proportions, one from the golden section and one from some divergent integer series, are governed by “extreme tension” and contain a “terrible dissonance.”(4) Thus Gubaidulina’s preplanned proportions are closely tied to her notions of consonance and dissonance at the phrase-level. Most works, however, offer few explicit clues as to where their exact proportional points are. To analyze such claims, then, it is helpful to consult Gubaidulina’s sketches to see what proportions and structural subdivisions are actually at play by her own standard.
[1.7] In particular, by consulting sketch material and locating precise proportional divisions within complete works, specific sections of pieces such as Meditation can be identified as composed-out dissonances. Although dissonance is not exclusive to regions between proportional divisions, we nonetheless know that all sounds in these regions will consistently be dissonant, as opposed to the more fleeting use of dissonance elsewhere. Limiting the scope of such demarcations, however, both the parameter complex and the golden section theory of dissonance are grounded in the composer’s intentional classifications of sounds in a specific piece, with little attention to the syntactic roles, inherent sonic or phonological qualities, or, more generally, a listener’s experience of dissonance. To contextualize the resulting classifications, I will compare the results to more theories of timbral dissonance grounded not only in Gubaidulina’s music, but also in psychoacoustical studies and in compositional theories of more scientifically minded composers. Supporting these notions of dissonance, Gubaidulina does not just classify sounds as dissonant in her pre-compositional process, but further follows pre-atonal norms of dissonance treatment. This article considers dissonance in Gubaidulina’s music through separate intentional, sonic, and syntactic lenses, then, to see how each of those theories might clarify a different aspect of her music’s dissonances.
What is Timbral Dissonance?
Example 2a. The first entrance of the waterphones in Am Rande, in which the sound is linked to high notes in the cello
(click to enlarge, see the rest, and listen)
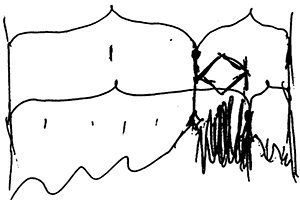
[2.1] As a preliminary example of how dissonance might function in Gubaidulina’s music, I will briefly discuss her treatment of the waterphone in Am Rande.(5) I argue that this sound is marked as dissonant not only by its place in a pre-compositional scheme of sonic classifications, but also by its treatment as a dissonance in the sense of a voice-leading event. The title translates to “On the Edge of the Abyss,” and although Gubaidulina claims that “the abyss” of the title strictly refers to the gap between the fingerboard and the bridge in the cello’s highest register, the title nonetheless invokes an aura of death and the beyond (Sikorski 2008). Example 2a shows the first entrance of the waterphones, approximately halfway through the piece. This moment is immediately followed by a high tremolo in the cello, linking the waterphones to the titular abyss and its extra-musical connotations.
Example 2b. Late re-entrance of waterphone in Am Rande, in conjunction with indeterminate cello slides and return of high-register “abyss”
(click to enlarge and listen)
Example 2c. Brief reappearance of waterphone in conjunction with sul ponticello and tremolo near the end of Am Rande, contextually presenting such sounds as dissonances to be resolved
(click to enlarge and listen)
[2.2] The waterphone and the sounds it is linked with are marked as dissonant by a cadential gesture at the work’s conclusion. After the initial alignment of Example 2a, the waterphones are presented exclusively in combination with specific sounds later in the piece, implying that those sounds will all be on the same side of a parameter complex, as shown in Example 1a. Example 2b shows a typical use: upon their final structurally sustained re-entrance, the waterphones are grouped with sounds that inhibit pitch perception, such as minimally pitched slides in cello 1. These sounds are made to imply dissonance, rather than consonance, by a gesture resembling a cadence at the end of Am Rande. Example 2c shows the end of the piece; an analytic overlay provides a functional context, in which waterphones and associated sounds can be considered dissonant, and contrasting sounds perhaps consonant. Having been silent for some time, at this moment the waterphones briefly reenter and are matched by brief motions in the cellos towards sul ponticello and tremolo, which resemble the high tremolo of the “abyss” sound that matched the waterphones’ entrance.
[2.3] Filling in the parameter complex, minimally articulated clean sounds with clear pitches are consonant. Because the cadential gesture of Example 2c leads to consonance, the waterphone, sul ponticello, and tremolo from the middle of the example are only temporary dissonances. Furthermore, after the waterphone exits, the strings do not just shift from sul ponticello to ordinario and simultaneously decrescendo, but they actually continue this gesture away from the waterphone sound with a decrescendo to niente and a bow position shift to sul tasto. The final gesture of the piece then consists of the following elements: a shift from sul ponticello to sul tasto, a decrescendo, an exit of the waterphone sound, and a shift from tremolo to standard articulation. In the context of the piece’s last two measures, all of these timbral changes can be interpreted as cadential gestures, analogous to a final V–I resolution at the conclusion of a tonal work. In this analogy, “tonic” is the timbre of least dissonance, in this case sul tasto and non-tremolo, both of which ensure a strong, clearly pitched fundamental and few high partials or noisy attack transients.
[2.4] Pitch clarity provides a new lens through which to consider the waterphones’ initial entrance. Leading up to R28 at the beginning of Example 2a, the cellos are all playing a full tone with rich vibrato, as would be the norm in tonal music, and the accompanying cellos (2–4) are even playing an unambiguously consonant major triad. The following gestures, then, both in waterphone and in cello 1’s high tremolo, are contrastingly dissonant specifically because their timbres obscure the clear pitch previously valued. Even though cello 1 is already at the potentially dissonant “abyss” before the waterphones enter, it is still timbrally consonant; the registral ascension increases musical tension that is extended by a similar shift to dissonance in the timbral domain.
[2.5] This reading of the conclusion of Am Rande clarifies both the purely sonic as well as contextual roles of dissonance in that work’s musical language. It shows that we can consider sounds such as waterphone, sul ponticello, and tremolo to be dissonant in the parameter complex, and therefore in the entire piece. The very sounds associated with the title, then, are simultaneously spiritual allusions (to the “abyss” of the beyond) and dissonances—if religion restores consonance, as Gubaidulina describes, then religion here provides solace in death, strengthening this analogy. Furthermore, this particular passage showcases dissonance at the work’s conclusion, where a work of tonal music might have a final statement of dissonance that leads into consonance in the framework of a cadence. Mimicking that syntax, the same gesture that might conclude a tonal work is still present, but with timbre instead of pitch as the defining parameter. Although Gubaidulina’s classification of sounds as dissonant is foreign to any pitch-oriented notions of tonality, her dissonance treatment nonetheless aligns with norms of tension and resolution.
[2.6] Although the specific definition of dissonant parameters varies from piece to piece, certain sounds and sonic characteristics are frequently considered dissonant. Furthermore, even if these notions of dissonances seem absolute in that they are in the “dissonant” column of a table such as Example 1a, they are actually defined relative to consonances; there are two columns in such a diagram. Contextual juxtapositions such as at the ending of Am Rande clarify which sounds are consonances and which are dissonances: without a resolution into consonance, a dissonance like the concluding sul ponticello tremolo above might be heard as just another sound, rather than as a dissonance. Then upon classification, not all sounds fit perfectly into one column—in the middle of the ponticello–tasto transition, for example, is a sound played ordinario, which would be in between consonance and dissonance in this scheme. Clusters are another frequently dissonant sound, as discussed below in the analysis of Meditation, but Gubaidulina often approaches clusters by successively adding adjacent pitches to a unison, which is a consonant starting point. A cluster spanning a small interval, then, is in between full consonance and full dissonance, whereas a large interval with a chromatically saturated interior is particularly dissonant. However, because Gubaidulina uses the terms consonance and dissonance as a firm binary opposition in descriptions of her compositional process, the dichotomy remains useful even as sounds traverse points in the middle.
[2.7] Despite the apparent context-specificity of a table such as Example 1a or the descriptions above of Am Rande, many of Gubaidulina’s dissonances can be considered to resemble noise, whereas consonances instead resemble pure tones, and this distinction is hardly unique in post-1945 music. Clusters obscure the pitch by concentrating equal energy in multiple nearby pitches, tremolo obscures pitch by constantly reintroducing attack noise, and sul ponticello obscures pitch through the plethora of inharmonic partials that become audible. Rebecca Leydon (2012) has noted Gubaidulina’s use of the pitch-noise axis in the context of large-scale “timbral trajectories,” in which one instrument moves from noise to quasi-sinusoidal pure tone, and another instrument vice versa, but she does not explicitly describe such events in terms of musical tension. The pitch-noise axis, however, has been associated with the consonance-dissonance axis in a number of other writings. Kaija Saariaho (1987, 94), for instance, has written that “in an abstract and atonal sense the sound/noise axis may be substituted for the notion of consonance/dissonance,” displaying the same fusion of timbral sensitivity and traditional musical concerns that is present in Gubaidulina’s music. Likewise, Fred Lerdahl (1987, 142) has theorized that “brighter” sounds, sharper attacks, and inharmonic spectra all constitute relative timbral dissonance, and these aspects all correlate with some notion of noisiness. Both Saariaho and Lerdahl present these timbral distinctions as aspects of their own compositional theories, in Saariaho’s case, to justify similar dissonance treatments to those in Am Rande discussed above.(6)
[2.8] If the consonance-dissonance axis is viewed as a classification of isolated sounds, Gubaidulina’s music can be seen to align with many other attempts to extend beyond pitch to timbre. But by realizing this notion of dissonance in the expressive context alluded to in interviews, she is placing these timbral functions into the sea of associations that the concept of “dissonance” entails. The inherent musicality and communicative potential of Gubaidulina’s timbres has been discussed in works where timbral development is explicitly foregrounded, but their role in an extended notion of dissonance is particularly crucial.(7) Distinguishing the notions of dissonance as an “event” versus as part of a “voice-leading rule,” Alexander Rehding writes:
Although many theorists and musicians have attempted over the centuries to discuss consonance and dissonance as isolated acoustic phenomena—that is, as “events”—as the previous section has shown, these attempts have always been complicated by the rules of counterpoint: dissonances need to resolve into consonances. The two approaches, while historically related to each other, are not fully congruent and can at times cut across one another. (2018, 447)
Gubaidulina’s music spans this divide by showcasing an event-level generalized notion of dissonance—the parameter complex, which generalizes to the pitch-noise axis—in a traditional musical context, so that marked changes in timbre become voice-leadings.
[2.9] Dissonance in Gubaidulina’s music can thus be considered through several different lenses, and a proper understanding might coordinate these approaches, as I attempt in the remainder of this article. I will first present an analysis of the sketches for Meditation available at the Paul Sacher Stiftung and their relation to Gubaidulina’s writings on her compositional techniques, to establish what dissonance sounds like in that work. I will then consider the work’s form and sketches more broadly, so that we can see how dissonance functions. Afterwards, I will step back and consider that work’s sounds through psychoacoustic notions, to see how her compositional theories of dissonance might align with phenomenological and perceptual theories. Finally, I will return to Am Rande in more detail to see how these competing notions of dissonance play out in a slightly different context and draw some general conclusions from the interplay between my analyses of the two works.
Proportions in “Meditation”
[3.1] So far I have addressed what dissonance might sound like as determined both pre-hoc by a parameter complex and contextually by a cadential gesture, but I have only informally considered its sonic, rather than purely contextual role in Gubaidulina’s self-described notions of form. The brief analysis above may seem too intuitive to naturally match the speculative approach to form described by Gubaidulina in her interviews; thus in order to substantiate classification of sounds in her music as intentionally dissonant (such as along the pitch-noise axis), it is necessary to return to her golden section-oriented compositional theories. Via proportion-oriented analysis, we can see how those theories relate to the sounds present in an actual composition. For this particular line of inquiry, Meditation provides a particularly clear testing ground on account of its high-quality sketch material, clear formal divisions, and variety of timbres.
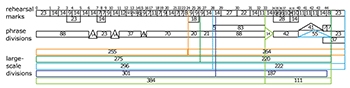
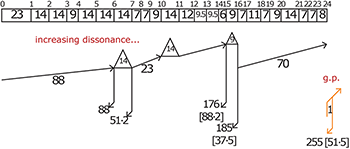
Example 3. The full form of Meditation, as compiled from sketches at the Paul Sacher Stiftung (used with permission)
(click to enlarge)
[3.2] The archival materials for Meditation show Gubaidulina working out different levels of proportions, from large divisions of the whole piece down to the lengths of individual phrases.(8) Example 3 summarizes the form of the piece as shown in the sketches. The rehearsal numbers running along the top and their lengths in quarter notes (at a constant 48bpm, despite various metric modulations) are my own calculations and annotations. All remaining numbers in the example are also 48bpm quarter notes, as noted by Gubaidulina in her sketches. The middle row, beginning with a large rectangle containing “88,” indicates the primary structural subdivisions indicated in the original planning. The triangles (other than at R33) all represent statements of the melody from the Bach chorale prelude on “Vor deinen Thron tret’ ich hiermit.” This setting was Bach’s final chorale prelude and has been subject to myth-making about its alleged completion on Bach’s deathbed, lending extra-musical death-focused associations to Gubaidulina’s choice of referent, analogous to her use of the “Dies irae” in Am Rande (Yearsley 2002, 2–5, 40–41).
[3.3] Most intriguing are the five structural divisions at the bottom of Example 3, the colors for which are presented as in the sketches.(9) These divisions are most clear in the work’s middle section, which will be discussed in detail here, with a focus on the dissonances created by their collisions. Each of these five structural divisions, if considered in isolation, splits the piece in two, but the overall form of the piece is nevertheless ternary—the opening lasts until the first of those divisions, at R24, and the conclusion of the piece begins at the final division, at R33. The opening contains three statements of the Bach chorale and surrounding meditations, as discussed above; both meditations and chorale statements become increasingly dissonant approaching R24, as discussed below. The conclusion of the work culminates in a full statement of the chorale melody in its original form, shown by the large triangle spanning from R40 to after R44. Crucially for our purposes, from R24 to R33 is the middle section in which the separate structural divisions are played off against each other, creating the “terrible dissonance” Gubaidulina describes (Lukomsky 1999, 28).
Example 4. An explanation of Gubaidulina’s use of the number alphabet, from Milne 2007, p.170, Table 4.1
(click to enlarge)
[3.4] As the diagram indicates, Meditation has five large-scale structural divisions simultaneously at play in the middle section, creating dissonances as discussed above. 275/220 is equal to 5/4, and 296/222 is equal to 4/3; as these proportions both clearly represent integer sequences strategically from the golden ratio, they create dissonance. 301/187 is approximately equal to 1.61, the golden section of the piece overall. The outermost ratios, 384/111 and 255/264, are significant not for their proportions, but for the actual lengths themselves; Jennifer Milne (2007) has explained that they are numerical allusions to Christ, Bach, and Gubaidulina herself, via the number alphabet, as summarized in Example 4 (reproducing Milne 2007, 170). The number 111, for instance, has its factorization [37·3] included in the score: 37 is the sum of the letters in “J. Chr.” Likewise 187, part of the golden section division, is derived from Bach’s name, and 255 of the orange division is [51·5], a Bach-Christ combination, as are two 88-length sections (R0–6 and R28–33). Not included in the table is 48, corresponding to “Sofia.” The number 384 is factored as [48·8], using Gubaidulina’s first name; the 384/111 proportion, then, references both Gubaidulina and Christ (Milne 2007, 158–67). Such proportions are unlikely to be explicitly noted by the listener, and their extra-musical references are inherently inaudible, but they both are integral to Gubaidulina’s conception of the piece—she claims that she “was guided especially by [her] own personal experience of the inner number relationships in the formal structure of Bach’s chorale prelude (BWV 668)” (Kremer et al. 1996).
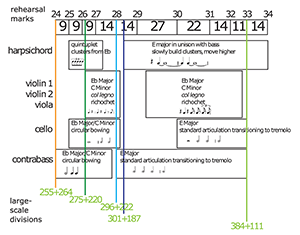
Example 5. The “dissonant” center of Meditation with divisions from the sketches and activity shown in each instrument
(click to enlarge)
Example 6. The incipit of the eponymous Bach Chorale (a) and its influence on the dissonant sounds of the middle section of Meditation (b–d)
(click to enlarge, see the rest, and listen)
[3.5] Although the different subdivisions present quite an array of hermeneutic possibilities, they all split the piece within a fairly narrow range of time, creating dissonance between those points. The first split, 255 beats in, occurs at R24, and the final split, 384 beats in, occurs at R33. According to Gubaidulina, we should find “a terrible dissonance” in the music filling the timespan between the golden ratio and other proportional divisions. Example 5 summarizes the passage between such divisions, from R24 to R33. All five string instruments continually quote the Bach chorale, the incipit for which is shown in Example 6a, but Gubaidulina nonetheless employs a number of techniques that make the pitch unclear, as created by indeterminate slide-based notation in the pitch or timbre domains. Before the golden section, as in Example 6b, the lower strings play with circular bowing and the harpsichord plays in shorts bursts that build from a unison to a cluster; after the golden section, as in Example 6c, lower strings play instead with a quasi-tremolo and the harpsichord slowly builds clusters from a unison. The upper strings, over the whole passage, consistently play with col legno and ricochet, as in Example 6d.
[3.6] All of the techniques in Example 6—circular bowing, clusters, tremolo, ricochet, and col legno—can be considered dissonant in Gubaidulina’s system, due to their structural placement between competing ratios, and are therefore dissonances in this piece’s parameter complex. In particular, as shown in Example 5, each dissonance either begins or ends at or close to a major proportional division, and no single dissonant block extends to both sides of the 5-beat space between the 296+222 division at R28 and the 301+187 golden section. Such alignments reinforce the role of such timbres as articulations of structural points. However, such dissonances are not exclusive to the middle section. Similar techniques are used—usually contrasted with more conventional (that is, found in the bulk of common-practice tonal music), and therefore “consonant,” techniques—in the introduction and conclusion of the work. The middle section, however, is distinguished by its sustained dissonances; rather than using dissonance fleetingly between consonances within a single section, the section consists of individual dissonant sounds composed-out between larger-scale consonant sections.
Beyond Proportions in “Meditation”: Consonance and Dissonance Outside the Middle
[4.1] Having established which sounds are considered dissonant in the parameter complex of Meditation, we can now look for shorter-duration instances of dissonance elsewhere in the piece and by comparison determine consonances. I will analyze dissonances and their treatments in the beginning and ending of the work in order to establish what consonances are in Meditation relative to dissonances and also to consider the syntax with which they are deployed.
Example 7. The opening of Meditation as shown in the sketches (used with permission)
(click to enlarge)
Example 8. Consonances and consonance-dissonance shifts in the three chorale statements in the opening of Meditation
(click to enlarge and listen)
[4.2] The opening of Meditation relies on repeated slow transitions from consonance to dissonance, with landmark points at chorale statements. For reference, Example 7 outlines the opening of Meditation as shown in the sketches. The end of the opening, just before the entrance of circular bowing at R24, is marked by a brief fermata, indicated in orange to represent the first structural division. Each of the three chorale statements, denoted by a triangle, is presented with some more conventional form of articulation and with determinate pitch, suggesting relative consonance. For example, Example 8a shows the first example of the initial statement, which is presented arco with ordinary bow position and accompanied only by a drone on the starting pitch. Conventional pitch-focused playing techniques with triadic harmonies, in contrast to the dissonant middle section, can therefore be considered consonant with respect to Kholopova’s parameter complex.
[4.3] Subsequent chorale statements are presented with increasing musical tension, articulated through both key area and dissonant parameters. Example 8a shows that the first statement, presented as a solo statement of the incipit in the double bass with clear pitch, is fully consonant—the only present timbre is arco and pitch materials are diatonic. Example 8b shows the second statement: the violins and viola present the chorale statement up a fourth (in D) with consonant parameters, but are joined by chromatic materials in the cello and harpsichord, along with a fully non-pitched dissonant scratch in double bass. Because the cello traces out the same chromatic ascent that the harpsichord presents as a full cluster, and because these chromatic gestures are presented as contextually synonymous, both cello and harpsichord are dissonant. In the third statement, shown in Example 8c, dissonance comes into even more direct contact with the chorale statement. Presented up yet another fourth (in G), the chorale statement moves from a unison to a large cluster, dissonant on account of its pitch masking, entirely within the harpsichord, so that the transition to dissonance is a transformation of a pre-existing layer rather than an addition of a new one.
[4.4] Each chorale statement is always a perfect fourth higher than the previous one in pc-space (not necessarily in p-space). The entrance of the dissonant middle section at R24, on C (as in Example 6b), is the final point of this trajectory, implying that the stream of ascending fourths leads the listener slowly from consonance to dissonance. Fourths are likely used to match the tuning of the opening double bass (in tonal music, upward fourths would often correspond to a motion from dominant to tonic, implying lessened tension); in Am Rande, scored largely for cello ensemble, fifths are used instead, drawn from the cello’s tuning. More importantly, in both Meditation and Am Rande, the intervals generally move from low to high—the lines from one chorale statement to the next in Example 7, reproducing the sketch material, consistently lead upwards.
[4.5] Dissonance increases through several timbral parameters over the course of the three chorale statements, and thus the opening of each statement is a relative consonance. Each chorale statement concludes with more noise than it begins with, and those noises become increasingly integrated into the statements over the course of the introduction. The opening three chorale statements thus provide a ramp to the sustained dissonance of the middle section, in which noise is an integral component of the melodic chorale statement from the beginning. We can then take each previous statement’s opening timbre—a single note played arco, or an unaccompanied harpsichord triad—as an example of consonance in Gubaidulina’s system.
Example 9. The opening of the second meditation, shifting from consonance to dissonance
(click to enlarge, see the rest, and listen)
[4.6] On either side of the chorale statements are the “meditations,” Gubaidulina’s musical reflections on the material. Each meditation contains a slow shift from consonance to dissonance, either followed by the consonant entrance of the chorale, implying at least partial resolution, or sustained in the chorale statement, to be resolved at a later point. Example 9 shows excerpts from R7–11, the full second meditation and subsequent chorale statement. At the left is the opening at R7, with quasi-tonal interval content, standard bow position, and usual arco playing method. At the right is the start of R8, which is transitional: the consonances of R7 slowly become more dissonant with the chromatic motives in the upper strings and rhythmic offsets in the harpsichord. The conclusion of the meditation, a bar from which is shown at R9, is entirely dissonant, featuring sul ponticello, tremolo, and glissando, all of which are used as dissonances in the middle section. This second meditation, however, is only one of several trajectories from consonance to dissonance. Each of the four “meditations” slowly increases tension; in sum, the full first section of the work, via these meditations, progresses from the consonance of the opening to the extended dissonance and tension of the middle section.
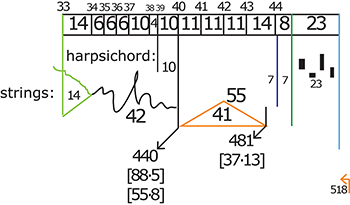
Example 10. Outline of form at the conclusion as shown in the sketches (used with permission)
(click to enlarge)
Example 11. Consonance and dissonance at the end of Meditation
(click to enlarge, see the rest, and listen)
[4.7] The final section of Meditation is likewise marked by large shifts from consonance to dissonance, which now span the full passage. Example 10 summarizes the sketches for the final section. The passage from R33 to R34 is marked with a triangle, which is used in the opening for the consonant chorale statement; however, the triangle is sideways. The strings play with their usual pitch-focused technique, hence the consonance implied by the triangle, but play different material than before, as shown in Example 11a. In the string instruments (the harpsichord has a slightly different pace), R34–40 consists again of non-pitched dissonant sounds, as in Example 11b, followed by a consonant statement of the full Bach chorale in its entirety at R40–44, the opening of which is shown in Example 11c. The dissonance-consonance transition, instead of being an element of local structure in a specific phrase as in the beginning, now governs the entire aftermath of the final proportional division.
Example 12a. Consonance and dissonance across the conclusion of Meditation
(click to enlarge)
Example 12b. Consonance and dissonance across all of Meditation
(click to enlarge)
[4.8] The harpsichord follows a similar trajectory from consonance to dissonance and back. The high squiggle in the sketches from R39 to just after R44 corresponds to the harpsichord part, which starts with a high trill on just two notes just before the strings’ chorale entrance—as in Example 11c—and moves downwards over the course of the chorale statement to large low clusters. Example 11d, which summarizes the progression of clusters from R39 to R44, shows the steady movement from unison to cluster. The harpsichord had similar, but shorter, gestures in the first part of the work; in the aftermath of the golden section and the dissonances on either side, these transitions are extended: whereas before, they had been contained within phrases, they now span the lengths of entire sections. Example 12a summarizes the trajectories at play in the work’s conclusion: the strings and harpsichord transition from dissonance to consonance at different times from one another, but both eventually end consonantly as the piece concludes.
[4.9] With respect to the broader formal design, Example 12b summarizes the consonance-dissonance trajectories across all of Meditation. As in Example 3, rehearsal numbers run along the top, with durations in 48bpm quarter-note pulses underneath. The five large-scale divisions are included with their respective colors underneath R24–33. Harpsichord and strings are graphed with separate lines, for which a higher position in the graph indicates increased tension. Before the first proportional division, from R0 to R24, each meditation and each chorale statement moves on its own from consonance to dissonance, although dissonance overall increases as R24 approaches. In this opening section, harpsichord and strings are either simultaneously consonant or simultaneously dissonant; they do not conflict with one another. From R24 to R33, between the proportional divisions, the strings sustain a constant level of dissonance to which the harpsichord contributes more and more over the course of the passage, particularly after the golden section (here delineated in blue as in the sketches).
[4.10] Meditation is consistently governed by the notion that dissonance should resolve to consonance. From R33 to the end, after the final proportional division, the consonance-dissonance trajectories are larger-scale, taking up entire sections rather than just subsections. However, these trajectories are separate in strings and harpsichord—the harpsichord increases dissonance over the course of R40–44, the last chorale statement, despite the strings’ unambiguous constant consonance. But characteristic of both the opening and closing sections is a consistent pattern of slow motion from consonance to dissonance, followed by immediate resolution from dissonance to consonance. Even though dissonances are not defined harmonically in this context, they are still tension-laden sounds expected to resolve. Returning to Rehding’s terminology, the nature of Gubaidulina’s classification of sonic “events” is supported by their formal treatment in terms of broadly conceived “voice-leading rules.”
Sonic Characteristics of “Meditation”’s Dissonances
[5.1] The previous section addressed how dissonance can be defined both intentionally by the composer in her pre-compositional process and contextually within the gestural syntax of a specific piece. Certain sounds are consistently more or less dissonant than other sounds in Gubaidulina’s work, however, and this section develops a characterization of those sounds. The composer’s notion of dissonance generally aligns with the pitch-noise axis as theorized by Saariaho, Lerdahl, and others, as discussed previously, and this will be borne out by a more quantitative assessment of the sounds in Meditation, as well as additional discussion of Am Rande.
[5.2] Judging purely by aural intuition, Gubaidulina’s dissonances are generally closer to noise than her consonances. Several instances of parameters, generally in pitch-space, are dissonant both in Gubaidulina’s system and in conventional common-practice usage. As in Examples 6b, 8c, and 11d, clusters are dissonant for Gubaidulina, whereas triadic harmonies are consonant; this distinction would hold in a tonal context.(10) Clusters additionally become more dissonant as they span larger intervals; that is, sounds with a wider band of equal-amplitude frequencies are both less recognizable in terms of pitch and more dissonant. It is not surprising that other techniques, such as tremolo and sul ponticello, are dissonant in this system, as these are conventionally associated with increased drama and tension (although they are not dissonant in the usual pitch-oriented sense). These dissonant sounds resemble white noise via stronger transients, high harmonics, and masking of pitch clarity. Consonant sounds, for comparison, have a certain resemblance to sine tones in addition to being the norm in common-practice music.
[5.3] The notion of noisiness, then, seems to suitably encompass both the timbral and pitch-focused aspects of Gubaidulina’s dissonances and corresponds with what music psychologists have found about listeners: that they perceive specific spectral characteristics of noisy timbres as corresponding to musical tension. In particular, spectral centroid, which measures “brightness” via average frequency, and spectral flatness, which measures how much a spectrum is not clearly harmonic, correlate both empirically with perceived musical tension and musically with timbral noisiness (Farbood and Price 2017; Kendall and Carterette 1993; Wallmark 2014, 26, 56–64; Wallmark et al. 2018). In other words, the more high frequencies a sound has, and the less its spectrum focuses around any specific frequencies, the tenser it is perceived to be by listeners; such tension corresponds here to dissonance.(11) These two metrics naturally correlate with features identified above—a sound like sul ponticello will have a higher spectral centroid because of its stronger high partials, as will a staccato sound, due to its attack transients; a cluster will have higher spectral flatness, because it has distinct frequencies interfering with one another in close proximity. Both spectral centroid and spectral flatness will be greater for white noise than for virtually any instrumental sounds, which will have both more harmonic spectra (lower spectral flatness) and overall lower-frequency pitch content within the human hearing range (lower spectral centroid), suggesting that these measures should align with a noise-based theory of dissonance.(12)
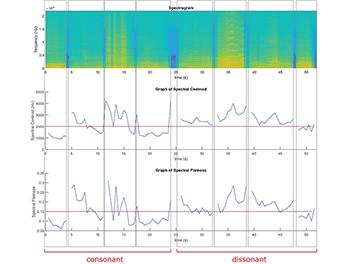
Example 13. Spectrograms and graphs of spectral parameters for clearly consonant and dissonant excerpts from Meditation
(click to enlarge, interact, and listen)
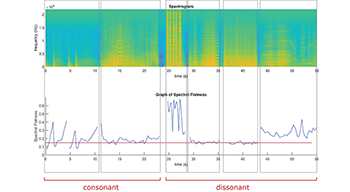
[5.4] These characterizations of dissonance do, in fact, align with characteristic examples from Meditation. Example 13 presents three pieces of quantitative data for a series of sounds marked as consonant and dissonant: a conventional spectrogram, a graph of spectral centroid, and a graph of spectral flatness.(13) Click on bracketed areas of these diagrams to see and hear the fragments the data correspond to: the consonances at left are generally articulated with conventional techniques that obtain a clear pitch and the dissonances at right each muddy the pitch via bow placement, auditory masking, and/or fingerboard slides. It is not difficult to intuit that spectrogram frames with stronger high frequencies have higher values in both centroid and flatness. The two graphs each have a red line, which is my attempt to draw a threshold separating most consonances from most dissonances. Although the segmentation is not perfect, many dissonances do have spectral centroids and flatnesses above this threshold. Likewise, consonances are mostly below the threshold, and the exceptions are easy to explain: many of the peaks, particularly as visible in the spectrogram around the 12-second mark, correspond to attack transients in the harpsichord, whose slow statement of the theme and low register come into conflict with the instrument’s inherent staccato nature and the high partials of those inevitable attack transients. Overall, however, both spectral flatness and spectral centroid serve as reasonably useful proxies for dissonance.
Example 14. Spectrogram and graphs of spectral parameters for the conclusion of the Meditation showing the distinct qualities of string and harpsichord sounds and the non-correlation of centroid and flatness
(click to enlarge)
[5.5] Although spectral centroid and spectral flatness tend to correlate closely, they can meaningfully differ, as is particularly apparent in the harpsichord’s clusters towards the end of Meditation. As shown in Example 11d, the harpsichord in this passage starts from a high unison and proceeds to large low clusters. Although the progression to low should mean reduced dissonance, via spectral centroid, the final clusters compensate in spectral flatness because of their increased registral saturation, and they are musically marked as dissonant by their resolution to a consonant triadic progression. To substantiate this assertion, Example 14 presents the same combination of spectrogram, centroid graph, and flatness graph applied to this passage. In addition to the continuous series of tremolos in harpsichord, this passage also contains a simultaneous consonant statement of the full chorale melody in the strings, in four distinct fragments. These four consonances are marked in the example by light blue bars under the relevant sections of the graphs; in these regions, the centroid and flatness are both visibly lower, implying that the string sound, on its own, would lie below the red boundary threshold. The gray lines show general trends in spectral centroid and flatness as the harpsichord clusters shift downwards—although they are always relatively high-frequency and above the dissonance threshold on account of their transients, they decrease in register, lowering spectral centroid, but increase in span, maintaining constant spectral flatness despite the registral shift. In this sense, spectral flatness better models Gubaidulina’s notion of dissonance in this particular passage.
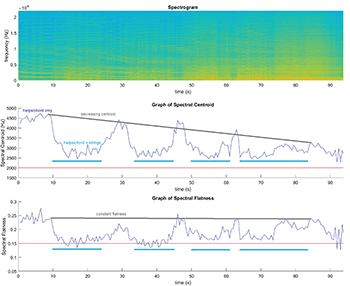
Example 15. Spectral centroid as a proxy for dissonance over all of Meditation with formal overlay from the sketches as represented in Examples 3, 7, and 10
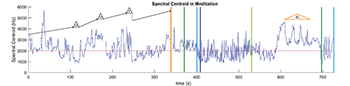
(click to enlarge)
[5.6] In the context of the entire piece, spectral centroid and flatness provide useful short-term trajectories, but they do not correlate with dissonance as closely as in the preceding examples. Example 15 presents a graph of spectral centroid over all of Meditation, with the sketch-based overlay from Examples 3, 7, and 10 superimposed. The horizontal red line is the dissonance threshold from Example 13b, and the triangles and vertical colored lines are the chorale-statements and large-scale proportions from Example 3. Between the piece’s primary proportions, the sounds are generally dissonant—they are clearly above the threshold just before the golden section, between orange and dark blue, but even between the dark blue and light green divisions there are frequent enough transients that the dissonance is quite clear. Although the chorale statements always start out consonant in a strictly pitch-based sense, they are not consistent in their positions with regards to other notions of dissonance. For example, the second chorale statement, shown above in Example 8b, is not only in a very high register, but is also superimposed with a scratch-tone circular bowing in the bass, a continuation of the dissonance from the preceding meditation; these features together make that statement relatively dissonant. What is clear is that the meditations following each chorale statement move unambiguously from consonance to dissonance, or from low to high spectral centroid, aligning with the upwards arrows in Gubaidulina’s sketch as summarized in Example 7.
[5.7] In a general sense, then, Gubaidulina’s dissonant timbres differ from her consonant timbres by having an overall higher frequency spectrum whose harmonics are less distinct, providing a more precise definition of their closer proximity to noise than to pitch. Although this description does not perfectly follow her musical practice, it fits well enough to be of immediate descriptive use, and it also aligns with empirical studies of listener perception. In line with composers and theorists such as Saariaho, McAdams, and Lerdahl, one could argue that this alignment allows for Gubaidulina’s system of dissonance to easily become aurally meaningful to listeners. Although Gubaidulina does not make such perceptual claims explicitly, her treatment of sounds resembling white noise is nonetheless similar to that of Saariaho or Lerdahl.
Extension to “Am Rande”
[6.1] This characterization of dissonance, although tied to the sketches of a specific work, is applicable more broadly to Gubaidulina’s output. I will demonstrate this through a brief outline and analysis of Am Rande, which formed the initial case study shown in Example 2.(14) This work dates from ten years after Meditation and is composed for a very different ensemble: seven cellos and two waterphones. Nevertheless, it is very similar in its large-scale treatment of consonance and dissonance, as I will discuss, and is also semiotically quite similar: as mentioned above, both pieces feature a quotation invoking death. In the following analysis, I will first introduce the piece’s form and apparent parameter complex, after which I will re-evaluate its sounds in terms of the parameter complex and spectral model for the dissonances of Meditation.
Example 16. Appearance of the “Dies Irae” in close contact with dissonant sounds as discussed in Example 2
(click to enlarge and listen)
Example 17. Consonance and dissonance in the opening of Am Rande in (a) score and (b) schematic summary; “Dies Irae” statements expand in length as consonant statements become registrally higher and introduce timbrally dissonant tremolo
(click to enlarge and listen)
Example 18a. Context for a “Dies Irae” entrance near the beginning of Am Rande
(click to enlarge and listen)
Example 18b. Context for a “Dies Irae” entrance near the end of Am Rande
(click to enlarge and listen)
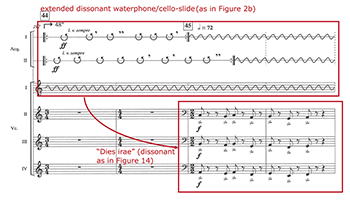
[6.2] Am Rande’s dissonances include the waterphone sound, high cello tremolos, and the “Dies irae” itself (particularly as articulated by Bartók pizzicato and by conventionally dissonant dyads). As I outlined in the opening discussion of Example 2a, the waterphone is marked as dissonant by the dramatic pause around its entrance, itself surprising because the preceding pitch-focused triadic harmony does not set up an expectation of a metallic sound with a wide variety of pitches. Based on a contextual “resolution” to consonance at the end of the piece as shown in Example 2c, I argued that both waterphone and high tremolo are dissonant. In the specific context of a special moment in the middle of the piece—which may or may not be an actual golden section, but is likely bounded by several distinct proportions—those sounds are dissonant in Gubaidulina’s formal sense. Furthermore, in this particular context of middle-section dissonance, these linked sounds are followed by the “Dies irae,” as shown in Example 16. The extra-musical connotations of the titular “abyss,” articulated as dissonances through structural placement, thus encompass not only the cello’s high tremolo as discussed earlier, but also the “Dies irae” itself.
[6.3] The opening of Am Rande, like that of Meditation, relies on continuous opposition of consonance and dissonance. Example 17a shows an excerpt from shortly after the beginning. Note that the “Dies irae” is presented in cellos 5 through 7, and that each attack is an eighth-note Bartók pizzicato chromatic cluster; this is dissonant in its staccato articulation in Kholopova’s parameter complex theory, as a cluster in the standard harmonic sense, and in its “Dies irae” quotation as from the middle section. The contrasting “consonance” is the surrounding texture: cellos 1–4 play harmonics in widely spaced traditionally consonant triads. Although cello 1 plays pizzicato, cellos 2–4 are arco, consonant in Kholopova’s sense, and the durations are consistently at least two eighth-notes, in contrast to the shorter durations associated with staccato articulation. As in the opening of Meditation, the piece alternates between these two textures until the sudden arrival of a new sound.
[6.4] Just as the opening section of Meditation slowly introduces dissonant materials, that of Am Rande likewise continuously increases the amount of dissonance present, culminating in a textural rupture. Example 17b summarizes the opening of Am Rande, until R11. Cellos 1–4 play widely spaced harmonics that are generally consonant; however, as the piece progresses, these harmonics get higher in pitch, to a maximum of
[6.5] The end of Meditation was characterized by two treatments of dissonance: a dissonant sound from the middle section was extended into the conclusion (the harpsichord moved towards clusters), and that dissonance was resolved to consonance at the very end (the harpsichord ends the piece in triads). Am Rande likewise demonstrates these dissonance treatments. Example 18b illustrates the composed-out dissonance near the conclusion of Am Rande: at R44 the waterphones, determined as dissonant earlier, are presented in isolation for the first time since their introduction. The waterphones are presented in conjunction with cello 1, which is dissonant because it consists entirely of slides in which no clear pitch can be heard. At R45, cellos 2–4 enter with the “Dies irae,” another dissonance from the middle section. All three elements of dissonance continue until R52: the waterphones and cello 1 are marked with constant squiggles, and the remaining cellos all play the “Dies irae” with increasing dynamics and constantly higher register. As with the final harpsichord gestures in Meditation, dissonance continually increases until a resolution to the final consonant “tonic.”
Example 19. Summary of consonances and dissonances in both Meditation and Am Rande
(click to enlarge)
[6.6] Dissonant sounds in Am Rande, like those in Meditation, are defined largely in opposition to the consonant ideal of a sustained clear pitch. In particular, dissonant sounds in Am Rande include sul ponticello, tremolo, and staccato, as well as waterphone and short durations. Consonant sounds include harmonics, long durations, triadic harmonies, and sul tasto. These parameters are summarized along with those of Meditation in Example 19. Most of the parameters specific to one work in the bottom rows can be considered a specific instance of a common parameter from the top row; short durations in Meditation, for instance, are almost synonymous with staccato and could be considered dissonant for the same reason. Furthermore, in both Meditation and Am Rande, sounds with slide-based notation of pitch or bow placement are dissonant, because the realization of such notation inherently hinders pitch clarity. Circular bowing in Meditation, for instance, is a dissonant parameter that, because of the extent of bow motion required, is sonically close to the sul ponticello dissonance in Am Rande. Likewise, the waterphone in Am Rande is notated the same way as the cello’s slides in the same piece, implying that waterphones can be considered dissonant because their inherent imprecision forbids the pitch clarity that would be normative in tonal music.
Example 20. Spectrograms and graphs of spectral parameters for clearly consonant and dissonant excerpts from Am Rande
(click to enlarge, interact, and listen)
[6.7] This familiar pitch-noise distinction recalls the quantitative discussion of the sounds in Meditation, in which Gubaidulina’s dissonant sounds were, broadly speaking, those considered dissonant by a typical listener. Those psychoacoustical methods yield similar results here in Am Rande, although the prevalence of staccato weakens the distinctions. Example 20, like Example 13, shows the spectra and spectral flatnesses for fragments from Am Rande identified as consonant and dissonant (click on the bracketed portions of the example to see and hear the selected fragments).(17) The 0.15 threshold for dissonance from Meditation is repeated in the spectral flatness graph of the example and is again shown with a red line. This line does not divide consonances from dissonances as cleanly as before—although the dissonant sounds’ profiles on the right side of the example are often clearly above the threshold, consonant sounds on the left side often exceed it as well. Again, much of this can be explained musically. The opening consonances, consisting of harmonics doubled with harmonic-pizzicato attacks, have high spectral flatness with the initial attack transients and again at the threshold of silence due to background noise, but low spectral flatness is visible in the primary sustain portion of the sound.
[6.8] Although consonant sounds can be somewhat ambiguous in their spread across spectral centroid values over time, several dissonant sounds are harsh enough to be unambiguous by the same measure. Despite the frequent correlation of centroid and flatness, several low-pitched dissonant sounds are unambiguously well above the flatness threshold. The Bartok pizz used for the “Dies Irae” quotation, for example, is actually well below middle C, and thus lower than many of the preceding consonant sounds, but resembles white noise fairly closely because its attack transients overwhelm its resonance. The next two dissonances are arco and of relatively low spectral flatness; although they are still contextually dissonant, they are not quite as sonically harsh, and perhaps take on an intermediary role. Finally, the high sul ponticello harmonics and waterphone at the end of the example are of high spectral flatness throughout. The most dissonant sounds here are not distinguished by merely having noisy elements, then, but by those aspects of noise being integral to the sounds’ full duration; the attack of a Bartok pizzicato, for example, endures long enough to cover the rest of the string’s resonance. The overall sonic notion of dissonance is similar to that of Meditation in that dissonances resemble noise, and as shown through the preceding analysis, are syntactically treated like dissonances in older music.
Conclusion
[7.1] The conclusion of Am Rande links Gubaidulina’s sonic and syntactic notions of dissonance. In both Meditation and Am Rande, sounds from the middle section were defined as dissonant sonic events on account of their placement in the piece relative to Gubaidulina’s writings on musical form, and that classification is supported by their resemblance to white noise. But in Example 2c, the consonance of the last few bars features a fleeting return of dissonant timbres—by subsequently being syntactically “resolved” into consonances, they are made dissonant not just as isolated sounds or as “events,” but as contextual counterparts to consonances, mediated by “voice-leading rules.”
[7.2] Certain sounds are implied to be dissonant by structural placement, but their specifically dissonant sonic qualities as “events” are clarified by their traditional treatment in terms of “tension and resolution.” Tremolo and sul ponticello, as in Example 2c, are dissonant on account of three intertwined factors: (1) as elements of Gubaidulina’s musical language, they are dissonant because she considers them so in her compositional process; (2) as sound stimuli perceived by a listener, even potentially in isolation, they are dissonant because they have strong high partials and attack transients, resembling white noise; (3) as part of a specific compositional context, they can be dissonant because they are resolved into consonances via a generalized notion of voice leading. Gubaidulina describes dissonance primarily in terms of pre-compositional formal planning, but her notion of dissonance aligns with listener perception and syntactic norms.
Noah Kahrs
Eastman School of Music
Department of Music Theory
26 Gibbs St
Rochester, NY 14604
nkahrs@u.rochester.edu
Works Cited
Birch, Alexandra. 2017. “Balancing Mathematics and Virtuosity: A Performer’s Guide to Sofia Gubaidulina’s Dancer on a Tightrope.” In ASU Electronic Theses and Dissertations. Arizona State University. http://hdl.handle.net/2286/R.I.45955.
Davies, Hugh, and Laurence Libin. 2011. “Waterphone.” In Oxford Music Online. Oxford University Press. https://doi.org/10.1093/gmo/9781561592630.article.L2215099.
Drott, Eric. 2017. “Saariaho, Timbre, and Tonality.” In Tonality Since 1950, eds. Felix Wörner, Ullrich Scheideler, and Philip Ernst Rupprecht, 259–81. Franz Steiner Verlag.
Ewell, Philip A. 2013. “The Parameter Complex in the Music of Sofia Gubaidulina.” Music Theory Online 20 (3). http://www.mtosmt.org/issues/mto.14.20.3/mto.14.20.3.ewell.html.
Farbood, Morwaread M., and Khen C. Price. 2017. “The Contribution of Timbre Attributes to Musical Tension.” The Journal of the Acoustical Society of America 141 (1): 419–27. https://doi.org/10.1121/1.4973568.
Kazazis, Savvas, Nicholas Esterer, Philippe Depalle, and Stephen McAdams. 2017. “A Performance Evaluation of the Timbre Toolbox and the MIRtoolbox on Calibrated Test Sounds.” In Proceedings of the International Symposium on Musical Acoustics (Montreal), 18–22. https://isma2017.cirmmt.mcgill.ca/proceedings/pdf/ISMA_2017_paper_65.pdf.
Kendall, Roger A., and Edward C. Carterette. 1993. “Identification and Blend of Timbres as a Basis for Orchestration.” Contemporary Music Review 9 (1–2): 51–67. https://doi.org/10.1080/07494469300640341.
Kholopova, Valentina N. 2001. Sofii͡a Gubaĭdulina: putevoditelʹ po proizvedenii͡am. Kompozitor.
Kremer, Gidon, Viktor Suslin, Sofia Gubaidulina, and Astraea. 1996. Gidon Kremer and Kremerata Musica: Live at Lockenhaus. BIS-CD-810, compact disc. Liner notes.
Kurtz, Michael. 2007. Sofia Gubaidulina: A Biography. Translated by Malcolm Hamrick Brown. Russian Music Studies. Indiana University Press.
Lartillot, Olivier, and Petri Toiviainen. 2007. “A Matlab Toolbox for Musical Feature Extraction from Audio.” In International Conference on Digital Audio Effects (Bordeaux), 237–44. https://dafx.labri.fr/main/papers/p237.pdf.
Lerdahl, Fred. 1987. “Timbral Hierarchies.” Contemporary Music Review 2 (1): 135–60. https://doi.org/10.1080/07494468708567056.
Leydon, Rebecca. 2012. “Clean as a Whistle: Timbral Trajectories and the Modern Musical Sublime.” Music Theory Online 18 (2). http://www.mtosmt.org/issues/mto.12.18.2/mto.12.18.2.leydon.php.
Lochhead, Judith Irene. 2016. Reconceiving Structure in Contemporary Music: New Tools in Music Theory and Analysis. Routledge Studies in Music Theory 2. Routledge.
Lukomsky, Vera. 1998. “Sofia Gubaidulina: ‘My Desire Is Always to Rebel, to Swim against the Stream!’” Perspectives of New Music 36 (1): 5–41. https://doi.org/10.2307/833574.
—————. 1999. “‘Hearing the Subconscious’: Interview with Sofia Gubaidulina.” Tempo, no. 209: 27–31. https://doi.org/10.1017/S0040298200014662
McAdams, Stephen, and Kaija Saariaho. 1985. “Qualities and Functions of Musical Timbre.” In 1985 International Computer Music Conference (Burnaby), 367–74. http://hdl.handle.net/2027/spo.bbp2372.1985.058
Milne, Jennifer Denise. 2007. “The Rhythm of Form: Compositional Processes in the Music of Sofia Gubaidulina.” PhD Diss., University of Washington.
Neary, Fay Damaris. 1999. “Symbolic Structure in the Music of Gubaidulina.” PhD diss., Ohio State University.
Peeters, Geoffroy, Bruno L. Giordano, Patrick Susini, Nicolas Misdariis, and Stephen McAdams. 2011. “The Timbre Toolbox: Extracting Audio Descriptors from Musical Signals.” The Journal of the Acoustical Society of America 130 (5): 2902–16. https://doi.org/10.1121/1.3642604.
Redepenning, Dorothea. 1994. Liner notes for Sofia Gubaidulina, Orchestral Music. Radio-Philharmonie Hannover des NDR, conducted by Johannes Kalitzke (tracks 1–4) and Bernhard Klee (track 5). cpo 999 164-2, compact disc.
Rehding, Alexander. 2018. “Consonance and Dissonance.” In The Oxford Handbook of Critical Concepts in Music Theory, eds. Alexander Rehding and Steven Rings, 437–66. Oxford University Press. https://doi.org/10.1093/oxfordhb/9780190454746.013.14.
Saariaho, Kaija. 1987. “Timbre and Harmony: Interpolations of Timbral Structures.” Contemporary Music Review 2 (1): 93–133. https://doi.org/10.1080/07494468708567055.
Schmelz, Peter J. 2009. Such Freedom, If Only Musical: Unofficial Soviet Music During the Thaw. Oxford University Press.
Sikorski Music Publishers. 2008. “A Composer Who Does Not Write Works, but Cultivates Them: Sofia Gubaidulina.” http://www.sikorski.de/1569/en/a_composer_who_does_not_write_works_but_cultivates_them_sofia_gubaidulina.html.
Sul, Sookyung. 2015. “Symmetries and Asymmetries in Sofia Gubaidulina’s Quasi Hoquetus.” PhD diss., University of Pittsburgh. http://d-scholarship.pitt.edu/24821/.
Tsenova, Valeria. 2001. “Number and Proportion in the Music of Sofia Gubaidulina.” Mitteilungen der Paul Sacher Stiftung, no. 14: 23–28. https://www.paul-sacher-stiftung.ch/en/research-publications/publications/official-bulletin/nr-14-april-2001.html
Wallmark, Zachary. 2014. “Appraising Timbre: Embodiment and Affect at the Threshold of Music and Noise.” PhD diss., UCLA. https://escholarship.org/uc/item/99t2t939.
Wallmark, Zachary, Marco Iacoboni, Choi Deblieck, and Roger A. Kendall. 2018. “Embodied Listening and Timbre: Perceptual, Acoustical, and Neural Correlates.” Music Perception 35 (3): 332–63. https://doi.org/10.1525/mp.2018.35.3.332.
Waters, Richard A. 1975. Tonal percussive musical instrument. US Patent 3,896,696, filed February 15, 1973, and issued July 29, 1975.
Yearsley, David. 2002. Bach and the Meanings of Counterpoint. Cambridge University Press.
Recordings cited
Recordings cited
Kremer, Gidon, Viktor Suslin, Sofia Gubaidulina, and Astraea. 1996. Gidon Kremer and Kremerata Musica: Live at Lockenhaus. BIS-CD-810, compact disc.
Gubaidulina, Sofia, Julius Berger, Stefan Hussong, Viktor Suslin, et al. 2006. Am Rande des Abgrunds / De profundis / Quaternion / In croce. Wergo 6684 2, compact disc.
Footnotes
* Preliminary versions of this article were presented at Music Theory Midwest (London, ON) and the conference “Timbre is a Many-Splendored Thing” (Montreal, QC), both in 2018. I would like to thank Zachary Bernstein, Robert Hasegawa, Orit Hilewicz, Robert Morris, Steven Rings, Anne Robertson, and two anonymous reviewers for helpful comments on many drafts of this document, and everyone at the Sacher Stiftung for facilitating my visit—particularly to Evelyne Diendorf for tracking down numerous materials in the collection and to Felix Meyer for allowing me to consult the original manuscripts (rather than exclusively microfilm) and for permission to reproduce examples based on sketch material. My travel to the Paul Sacher Stiftung was made possible by a grant from the Yovovich Family Fund for Research and Language Study in Europe, offered through the University of Chicago College’s Summer International Travel Grants program.
Return to text
1. Additionally, Gubaidulina overlapped in her studies at the Moscow Conservatory with Schnittke, as well as with Edison Denisov. Her connections to Pärt were not as direct, but she nonetheless knew his work, and all four composers attended the Warsaw Autumn festival in the same few years (Schmelz 2009, 29, 48–49, 184–85, 218–22, 232, 325).
Return to text
2. The canonical source for this term is Lukomsky 1998 (10, 36) in which she refers to it as “the rhythm of the form” (emphasis mine), but the term has been explicated in the most detail in Milne 2007 (25–35) and Tsenova 2001 (23–24).
Return to text
3. The precise mechanics involved here have been documented in many interviews, essays, and dissertations: see Lukomsky 1999; Tsenova 2001; Milne 2007; Sul 2015; Neary 1999.
Return to text
4. Gubaidulina is not entirely consistent about whether dissonance is an inherent property of a numerical series, or is a property of a relation between two distinct series. However, she consistently values the Fibonacci series (and golden section) as an inherent natural consonance. Other numerical series are considered dissonant, but are made so specifically by their deviation from the Fibonacci series. Consequently, the timespan between two series is dissonant because it articulates the relative dissonance of the non-Fibonacci series.
Return to text
5. The waterphone is a percussion instrument invented in 1967 and best known for its inclusion in film and television soundtracks on account of its “creepy” sound. It consists of a number of metal rods connected to a resonator partially filled with water, so that changes in water position alter the instrument’s resonance. For more information, see Davies and Libin 2011; Waters 1975.
Return to text
6. A more detailed discussion of Saariaho’s theories of dissonance can be found in Drott 2017. Drott’s article not only provides a discussion of how Saariaho’s notion of dissonance is grounded in the early history of spectralism, but also notes that she uses the ponticello-tasto axis in a role similar to tonal dissonance treatment, as does Gubaidulina in the example above. Saariaho also makes similar claims to Lerdahl’s in terms of the importance of hierarchy to dissonance, in McAdams and Saariaho 1985. Despite the similarity to Gubaidulina’s system in practice, however, she was not active at IRCAM in the 1980s, limiting the applicability of Drott’s historically situated analysis. Given the similarities, however, my discussion of Gubaidulina’s music should not necessarily be taken as claiming that her music is unique in all regards.
Return to text
7. For discussion of diverging articulations of a unison G4 in Gubaidulina’s Second String Quartet, see Lochhead 2016. For discussion of the extended usage of non-pitched techniques inside the piano in Der Seiltänzer, see Birch 2017. In a slightly more pitch-oriented context, several timbres and techniques of cello and bayan are discussed through a hermeneutic lens in Leydon 2012.
Return to text
8. The sketches are available at the Paul Sacher Stiftung in Basel, Switzerland. In addition to several sketches explicitly showing large-scale divisions abstractly, the archive also contains a preliminary draft of the work with markings showing where in the score each proportionally derived phrase begins and ends. The same sketches are also discussed in Milne 2007, which provided a useful reference as I prepared for sketch study, but all discussion and illustrations of the sketches in this paper are my own.
Return to text
9. The colors and large-scale divisions are presented exactly as in a single page in Gubaidulina’s sketches (in Sacher’s collection, Tape 487, Slide 515). Colors and numbers display the same correspondences in other pages of the sketches, such as when outlining the phrase structure shown in the middle level of my example.
Return to text
10. Some triads would be dissonant in tonal music; however, such dissonances are determined by context and voice-leading rules, rather than by inherent characteristics of the sounds themselves. My characterization here is in line with Rehding’s “consonance/dissonance as event.”
Return to text
11. In other contexts, dissonance and tension might not be synonymous, although they are here. Rehding (2018) provides a third model of dissonance—distinct from events or voice-leadings—called “consonance/dissonance as tension and relaxation,” and problematizes its relation to the sonic model through enharmonic reinterpretations in Haydn. In the psychoacoustic literature discussed above, dissonance may indeed be more sonic, as in Helmholtz’s or Plomp’s “sensory dissonance” or “psychoacoustic roughness,” whereas tension is musically emergent. However, the dissonances theorized in a musical context by Saariaho or Gubaidulina are inherently intended as tensions in the way the composers use them.
Return to text
12. Even comparing different noise sounds, it is not too difficult to imagine spectral centroid and flatness corresponding to dissonance. For a simple example, imagine the sounds of white noise and pink noise. White noise is distinguished here by its stronger high frequencies, corresponding to higher spectral centroid, and thus also by all of its component frequencies being more equal, corresponding to higher spectral flatness. White noise is also, compared to pink noise, generally considered much more aurally harsh.
Return to text
13. This example was generated with MIRToolbox in Matlab (Lartillot and Toiviainen 2007), with an unusually long one-second window size and half-second hop size, to obtain a less jagged curve. The recording used was Kremer et al. 1996. Discussion of similar tools and surveys of important quantitative characteristics of timbre can be found in Peeters et al. 2011; Kazazis et al. 2017.
Return to text
14. So that I can clearly develop a single example, yet argue that sketches are not necessary for this sort of analysis, I focus entirely on Am Rande in this section. However, a number of Gubaidulina’s works can be interpreted through this lens either with or without sketches. As discussed in Birch 2017, Der Seiltänzer displays Fibonacci proportions at sectional divisions that correspond to timbre changes; the pianist plays on the keys (as opposed to inside the piano) only in the work’s beginning and ending, again marking a technique from common-practice music as consonant. Among Gubaidulina’s more recent compositions, both So sei es and Die Pilger display middle-section dissonances with similarly non-pitch-oriented sounds to those discussed here, both involving multi-register piano tremolos, marimba glissandi, and violin and bass cadenzas.
Return to text
15. The highest pitches present in this passage are the fifth-partial harmonics of the cello’s open strings, and thus consistently move upwards by fifths; although this is a contrast to the fourths of Meditation, it is in both pieces a consistently upwards motion aligned with the instrument’s tuning.
Return to text
16. Tremolo is, of course, not a higher pitch, but it functions as if it were. Contextually, it is an additional level of progression “upwards” in Gubaidulina’s music. Spectrally, the constant reintroduction of attack transients raises its spectral centroid, just as the increase in pitch previously did. Progression upwards in pitch and towards noise are thus both dissonant in this context.
Return to text
17. These examples are generated in the same way as Examples 13–15 were for Meditation, except with halved window and hop sizes so that the sustain portion of pizzicato/arco harmonics can be more clearly seen in a consonant context, rather than being overwhelmed by the sharp attack. The overall magnitudes present are unchanged by this alteration. The recording used was Gubaidulina, Berger, Hussong, Suslin, et al. 2006.
Return to text
Copyright Statement
Copyright © 2020 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Lauren Irschick, Editorial Assistant and Brent Yorgason, Managing Editor
Number of visits:
10400