Review of Keith Waters, Postbop Jazz in the 1960s: The Compositions of Wayne Shorter, Herbie Hancock, and Chick Corea (Oxford University Press, 2019)
Ben Baker
KEYWORDS: jazz, postbop, harmonic function, harmonic substitution, axis progression, ic3/4 dual interval cycle
DOI: 10.30535/mto.26.3.14
Copyright © 2020 Society for Music Theory
[1] Keith Waters’s Postbop Jazz in the 1960s (2019) brings together more than two decades of work by one of the most prolific jazz scholars in music theory. Over the course of his academic career, Waters has focused consistently on the practices of a particular set of jazz musicians in the 1960s. During this period, the output of musicians like Miles Davis, Wayne Shorter, Herbie Hancock, and Chick Corea often blended elements of tonal jazz from earlier decades—including bebop, hard bop, and soul jazz—with features of emergent modal and free (or avant-garde) jazz practices. Waters and others use the term postbop to refer to the compositional and improvisational tendencies that emerged from this confluence, which are exemplified by a small but influential repertoire of jazz compositions and associated recordings.(1) His enduring engagement with this music has yielded a series of widely cited publications. While a few of these studies broadly address improvisational (2013) or harmonic (Waters and Williams 2010) strategies, most confront analytical or methodological issues through the lens of a specific musician’s output. These include examinations of form and metric displacement in improvisations by Hancock and Keith Jarrett (1996, 2001), nonfunctional harmony in compositions by Hancock (2005) and Corea (2016), the influence of the ic4 cycles in John Coltrane’s “Giant Steps” on postbop composers (2010), and improvisatory practices in Miles Davis’s celebrated second quintet (2003, 2011).(2)
[2] In contrast to the focus on postbop improvisation in Waters’s first monograph (2011), the primary aim of his second book is to characterize the compositional tendencies of postbop musicians.(3) Some of these tendencies overlap with tonal and modal jazz practices, while others evolve or problematize them. For example, both postbop and modal jazz tunes often weaken or abandon the monotonal frameworks and locally functional harmonic motions of tonal jazz; but postbop compositions, like their tonal jazz predecessors, usually maintain a faster harmonic rhythm than modal jazz tunes.(4) To elucidate these and other postbop trends, Waters draws widely on his previous scholarship to provide detailed analyses of compositions by some of the music’s most celebrated composers. For readers conversant with Waters’s earlier work, many of the analytical ideas presented in this book will be familiar, and Waters deploys them with slightly less formality than in his prior publications—a choice that makes the book more accessible to a broad readership. But the book’s occasional informality hardly detracts from the perspicacity of its ideas—readers looking for more technical treatment of a topic can usually consult a relevant earlier source—and the integration of these ideas into a single monograph offers a coherent and compelling angle on the larger analytical challenges posed by postbop. I imagine readers familiar with this music will find themselves nodding along appreciatively with Waters’s analyses, which are at once insightful and intuitive.
[3] The book divides into six chapters. The first chapter establishes a methodological foundation by defining a loose set of postbop compositional techniques and framing their points of overlap and contrast with tonal and modal jazz. Chapters 2–4 offer detailed analyses of tunes by three titans of postbop composition—Shorter, Hancock, and Corea—while Chapter 5 treats compositions by Booker Little, Joe Henderson, and Woody Shaw. The thorough examinations of harmony, melody, and form in these four central chapters represent the core of the book and contain its most trenchant insights. In a two-part final chapter, Waters suggests a few additional analytical techniques and briefly ruminates on the nature of syntactic evolution in jazz.
[4] Because the book is organized by composer, arranging its myriad analytical techniques into a systematic or broadly applicable methodology is not its primary focus. Nevertheless, both the specific techniques Waters uses and the deeper methodological posture they reflect are usefully versatile. This utility is bolstered by the fact that, as Waters notes in the final chapter, postbop has exerted significant influence on subsequent generations of jazz musicians, and many of its characteristics manifest in more recent music that has yet to receive significant scholarly attention. A short survey of some of these analytical techniques will provide insight into the potency and relevance of Waters’s work.
[5] Waters’s basic analytical method treats irregular musical phenomena as complications of patterns that are in some way more conventional, systematic, or coordinated. He characterizes these simpler patterns as examples of “first-order grammar,” whose subsequent deregulation yields various types of “second-order grammar” (101), and as schemata that have both shaped, and been shaped by, changes in jazz syntax (152–55).(5) This approach resonates with Waters’s assertion that postbop practices frequently represent evolutions of tonal jazz conventions, rather than complete abandonments of them. And indeed, Waters often treats conventions of tonal jazz as analytical foils for understanding postbop tunes.(6) This comparative approach packs the biggest punch in the harmonic and melodic domains, where Waters posits two kinds of generalized schemata as analytical exemplars. The first are familiar patterns of functional root motion from tonal jazz: chains of descending fifth or—in the case of tritone substitution—half-step motion that appear in turnaround progressions and often generate harmonic momentum toward cadences. The second are “axis progressions,” Waters’s term for cyclic patterns of root and/or melodic motion by a single interval, which often preserve a consistent chord quality. While axis progressions may use any interval and can structure both local progressions and larger formal spans, the concept is exemplified by the major third (M3rd) cycle of tonicized key centers in John Coltrane’s “Giant Steps,” which moves in parallel with a structural M3rd cycle in the melody in the tune’s second half.(7) Waters argues that these basic patterns serve as departure points for postbop composers. Their tunes often preserve vestiges of functional motion and use axis progressions as organizing melodic and/or harmonic schemes, but they also frequently obscure or deregulate these structures.
[6] To highlight these attenuated musical forces, Waters’s analyses make broad use of harmonic substitution—the assertion of affinities between chords that can reasonably stand in for one another in particular contexts. As Waters notes in his opening chapter, harmonic substitution in tonal jazz was given its most thorough and influential treatment in Strunk 1979. In the case of a familiar tritone dominant substitution,
[7] While Strunk’s substitution sets are confined to basic seventh chords, Waters embraces the malleability of taller-tertian jazz harmonies to expand the scope of common-tone substitution for postbop harmonic syntax. The ontology of upper-extension chord membership in jazz harmony is notoriously slippery. While most jazz scholars agree that seventh chords are primary harmonic objects, jazz musicians usually realize these chords with some combination of additional ninths, elevenths, and thirteenths, which can range from optional coloristic additions to integral parts of a chord’s identity.(9) Waters’s approach to substitution frequently occupies a middle ground between recent analytical approaches to this issue by adopting a notion of chordal “upper structure” that refers generally to idiomatic combinations of tertian chord members stretching from the chordal third (or suspended fourth) up to the thirteenth. This approach leverages the voice-leading potential of both guide tones and additional upper extensions without eliminating all semblance of chordal shape via the abstraction of chord-scale isography, which equates a given chord with a source scale from which it can be derived.(10) Waters invokes these substitutions for a multitude of reason: to illuminate latent local dominant and tonic functions, uncover remnants of axis designs, and examine contrapuntal relationships between root and melodic motions.
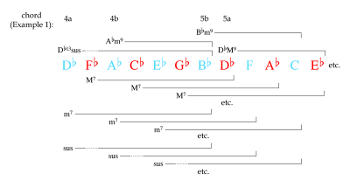
Example 1. Waters’s dominant substitutions (transposed to C)
(click to enlarge)
[8] With regard to functional harmony, Waters emphasizes postbop’s tendency to suppress dominant function by eliminating one or more tones that traditionally animate resolution to a subsequent tonic.(11) Example 1 summarizes some of the harmonies to which he attributes weakened dominant function using this approach and compares them with more standard dominant chords.(12) The prototypical dominants are numbered and appear first in each bar; one or two substitutions follow and are labeled with additional letters. All harmonies are transposed to reflect an ensuing local tonic with root C, and the conventional voicings are derived from Waters’s prose descriptions.(13) Chords 1a and 2a participate in what Waters calls “upper structure progressions,” retaining characteristic upper-voice shapes but eschewing standard bass pitches. While Waters explains chord 3a via chord-scale isography—the slash chord derives from the same octatonic collection as a standard dominant (in this case, OCT1,2)—it might also be understood as an upper-structure progression, albeit one that omits a local leading tone. Chords 4a and 5a preserve a tritone substitute root in the bass, instead enervating dominant function via a change in chord quality to a sus (V’7sus) or major-seventh (V’M7) chord. Upper-structure common-tone substitutions further transform this latter pair of harmonies: chord 4b is a dominant-function ii’7 chord that acts as the tertian upper structure of an implied (but rootless) V’7sus, while 5b acts as a relative minor substitute for V’M7.(14)
[9] In Waters’s analyses, most of these dominant substitutions occur within turnaround progressions or similar chains of otherwise functional root motion. But the kinds of upper-structure common-tone relationships that link chords 4a–b and 5a–b also selectively underpin substitute tonic functions. Near the end of Hancock’s “Dolphin Dance,” for example, Waters observes that the functional ii–V progression
Example 2. Common-tone relationships in a subset of the m3/M3 cycle
(click to enlarge)
[10] While he doesn’t invoke it explicitly in any of the substitutions discussed so far, the common-tone relationships instanced by chords 4a–b and 5a–b connect to Waters’s recurrent use of what he calls the “dual m3/M3 axis.” This dual axis also figures prominently in Waters 2016, where he refers to it as the “ic3/4 dual interval cycle.” To avoid confusion with axis progressions, I will refer to the structure with the term “m3/M3 cycle,” or simply “cycle” where appropriate. Example 2 displays a 12-element subset of this cycle, annotated with the common-tone relationships between chords 4a–b and 5a–b from Example 1.(16) The cycle comprises two interlocking circles of perfect fifths, shown in blue and red. Considered in total, the cycle’s 24 members contiguously encode all twelve diatonic collections, as well as one instance of each major-seventh, minor-seventh, and sus chord, each with its conventional upper extensions of ninth, (sharp) eleventh, and thirteenth. Sus chords are considered as gapped cycles (gaps are indicated with dotted lines), built on the same roots as minor-seventh chords; the chordal eleventh is equivalent to the suspended fourth.
[11] The cycle’s interlocking circles of fifths can be found in adjacent rows of a standard toroidal Tonnetz, and its structure has a rich music-theoretic history.(17) For Waters, the primary utility of the cycle is that it highlights networks of potential common tones shared between complexes of tall-tertian major-seventh, minor-seventh, and sus chords whose roots are cyclically proximate; examples of these networks are shown below the cycle in Example 2. The tertian structures that unite these cyclic complexes imbue their respective members with significant substitution potential. This potential extends beyond chords with adjacent roots—which can be related with tall-tertian versions of neo-Riemannian L and R transformations—to encompass chords whose roots are two or three positions apart.(18)
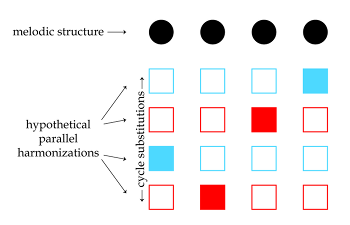
Example 3. Generalized schema for Waters’s m3/M3 cycle substitutions
(click to enlarge)
[12] In addition to implying the m3/M3 cycle’s structure in the specific functional substitutions outlined above, Waters relies on cycle-based substitutions to examine more broadly how postbop composers decouple root and melodic motions. Recall that in the second half of Coltrane’s “Giant Steps” the melody moves in sequential lockstep with the M3 cycle of tonicized keys, alighting on the chordal fifth of each tonicized major-seventh chord. One of Waters’s central arguments is that postbop composers often bypass similar parallel harmonizations, both of melodic axis progressions and other melodic structures, while preserving voice-leading remnants of such parallelism. In passages where a melodic structure is supported by a non-parallel series of major-seventh, minor-seventh, or sus chords, he highlights these remnants by outlining a range of m3/M3 cycle-based substitutions for each original harmony and arranging these substitutions into hypothetical parallel harmonizations of the melody. Example 3 schematizes his general approach. Pitches of a notable melodic structure in a tune—axis progression or otherwise—are represented by filled-in circles in the top row. Each row of squares below the melody represents a hypothetical parallel harmonization of that melody; the chords in each column are related by m3/M3 cycle substitution, and the filled-in squares represent the tune’s actual progression, whose roots avoid rote parallel motion with the melody.(19)
[13] When considered with their full range of diatonic upper extensions, major- and minor-seventh chords encompass entire diatonic collections, and sus chords fall only one pitch short. In some sense, the assertion of m3/M3 cycle-based relationships between chords thus skews toward chord-scale isography. But unlike pure scales, the cycle preserves a useful conceptual semblance of tertian chord shape. Even if this shape is not entirely preserved by actual chord voicings on the musical surface, the cyclic pathways traced by the m3/M3 cycle fall more readily under the hand as voicings at the keyboard than their pure scalar equivalents do. Waters’s use of the cycle thus straddles the divide between the tertian structure of chords and the flexibility of chord-scale isography. This productive contact between theory and (embodied) practice is a signature strength of Waters’s analytical method.(20) While the flexible spirit of his approach to substitution in both functional and cycle-based contexts allows the analyst a great deal of interpretive latitude, Waters’s substitutions are largely convincing because they resonate with concrete harmonic, melodic, or formal details of the music in question. From this perspective, the adaptability of his method is an analytical boon, one that capitalizes on the multivalent quality of tall-tertian harmonies. In appropriate musical contexts, one can imagine adapting Waters’s general techniques to identify latent dominant function in additional kinds of chords, to deploy other (cyclic) structures to undergird substitution relationships, or to refine transformational models for other common chord successions in postbop and its musical descendants.
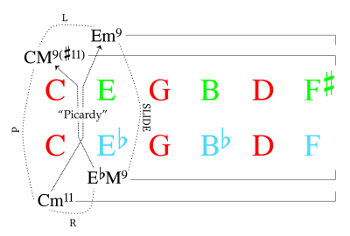
[14] A brief illustration of this transformational potential involves what Waters describes as the “Picardy effect” (36–39) that characterizes progressions between third-related tall-tertian chords of the same major or minor quality. The first chord of the incipient descending axis motion
Example 4. “Picardy” effects between common-tone-related pairs of m3/M3 cycle subsets
(click to enlarge)
[15] Although Waters does not cite the m3/M3 cycle in reference to either type of progression, it has obvious utility in both. Example 4 plots these successions on a pair of cycle subsets that preserve one of the cycle’s interlocking chains of perfect fifths as common tones (shown in red), while allowing the other to toggle up and down by half-step (shown in blue and green). The root motion of each progression requires two shifts: one shift along a subset, and one shift between them. Waters’s descriptions of the Picardy effect suggest a hearing of these progressions as resulting from paired applications of cyclic analogues to neo-Riemannian P and L or R transformations. In each modeling, L and R generate motion laterally along a single cycle subset, while P produces motion between the pair of subsets. As shown in the example, the latter motion can also be generated parsimoniously by invoking a SLIDE transformation in lieu of P. This is a potentially more meaningful transformation in a tall-tertian context, in that a cycle of perfect fifths quite literally slides up and down by half-step to produce the (enhanced) Picardy effect. But all four of these involutions are ultimately designed for triadic contexts. Perhaps as a testament to the pervasive influence of postbop harmony, tall-tertian progressions that move simultaneously along and between pairs of common-tone-related m3/M3 cycle subsets are increasingly prominent in modern jazz and jazz-adjacent genres like neo-soul and R&B. In light of this prominence, a dedicated transformational framework that captures these motions with a well-defined composite transformation could be useful.(21)
[16] Just as Waters’s m3/M3 cycle-based substitution techniques echo neo-Riemannian transformations, the larger correlation between the target repertoires of these approaches is a frequently cited trope—that is, in both Western art music and jazz, the gradual relaxing of functional harmonic norms gave way first to scalar tonality, then to relative freedom. Waters’s final chapter correctly warns against over-investment in this correlation and its attendant value judgements. But the analogy between the harmonic practices in 1960s postbop and nineteenth-century Western art music does productively spotlight how cyclic patterns of root motion can erode—and ultimately substitute for—functional monotonality on various levels of musical structure in both repertoires. Waters’s evolutionary argument on this topic in postbop recalls Perle’s (1990) notion of cyclic elements as “windows of order” that can both destabilize otherwise tonal environments and act as organizing forces in the absence of tonal hierarchy. Readers well versed in other areas of music-theoretic scholarship will find additional resonances in Waters’s work as well. His “double-axis progressions” (143–46), for example, are simply chromatic sequences.(22) And his flexible approach to dominant substitution invites comparisons with the scale degree-based notions of harmonic function in Western art music developed by Harrison (1994), and in rock music by Biamonte (2010) and Doll (2017).(23)
[17] The book has some minor drawbacks. Copyright issues compel Waters to omit lead sheets for several of the tunes he discusses; the “explanatory diagrams” that often substitute for these lead sheets, while useful and clever, are frustratingly incomplete. A broader underuse of musical notation necessitates detailed prose descriptions that sometimes become unwieldy, especially when they expound ideas that could be easily communicated with concise annotated score examples. The monograph would benefit from additional editorial fine-tuning—the text is occasionally redundant (e.g., pp. 90–91), and the prose and examples feature a number of typographic errors. A more robust bibliography would also lend useful context to Waters’s work—perhaps owing to its non-specialist orientation, the book features surprisingly few citations.(24)
[18] On the whole, though, these frustrations are negligible; they neither obscure the book’s many insights nor diminish the utility of its methodological stance. For both scholars and jazz enthusiasts, Waters’s monograph stands as a definitive account of an essential but still understudied body of music, full of ideas that can be fruitfully adapted to examine related repertoires. I hope and expect that numerous scholars—including Waters himself—will continue to leverage this potential in coming years.
Ben Baker
Eastman School of Music
26 Gibbs Street
Rochester, NY 14604
bbaker@esm.rochester.edu
Works Cited
Ake, David. 2002. Jazz Cultures. University of California Press.
Baker, Ben. Forthcoming. “A Cyclic Approach to Harmony in Robert Glasper’s Music.” Theory and Practice 44.
Biamonte, Nicole. 2010. “Triadic Modal and Pentatonic Patterns in Rock Music.” Music Theory Spectrum 32 (2): 95–110.
Callender, Clifton. 2007. “Interactions of the Lamento Motif and Jazz Harmonies in György Ligeti’s Arc-en-ciel.” Intégral 21: 41–77.
Carey, Norman, and David Clampitt. 1989. “Aspects of Well-Formed Scales.” Music Theory Spectrum 11 (2): 187–206.
Doll, Christopher. 2017. Hearing Harmony: Toward a Tonal Theory for the Rock Era. University of Michigan Press.
Givan, Benjamin. 2016. “Rethinking Interaction in Jazz Improvisation.” Music Theory Online 22 (3). https://mtosmt.org/issues/mto.16.22.3/mto.16.22.3.givan.html.
Gollin, Edward. 2007. “Multi-Aggregate Cycles and Multi-Aggregate Serial Techniques in the Music of Béla Bartók.” Music Theory Spectrum 29 (2): 143–76.
Hannaford, Marc. 2019. “One Line, Many Views: Perspectives on Music Theory, Composition, and Improvisation through the Work of Muhal Richard Abrams.” PhD diss., Columbia University.
Harrison, Daniel. 1994. Harmonic Function in Chromatic Music: A Renewed Dualist Theory and an Account of its Precedents. University of Chicago Press.
Hauptmann, Moritz. (1853) 1991. Die Natur der Harmonik und Metrik: Zur Theorie der Musik. Translated and edited by William Heathcote. Da Capo Press.
Julien, Patricia. 2003. “The Structural Function of Harmonic Relations in Wayne Shorter’s Early Compositions: 1959–1963.” PhD diss., University of Maryland, College Park.
Laitz, Steven. 2015. The Complete Musician: An Integrated Approach to Theory, Analysis, and Listening. 4th ed. Oxford University Press.
Lewin, David. 1982.“A Formal Theory of Generalized Tonal Functions.” Journal of Music Theory 26 (1): 23–60.
Love, Stefan Caris. 2017a. “An Ecological Description of Jazz Improvisation.” Psychomusicology: Music, Mind, and Brain 27 (1): 31–44.
—————. 2017b. “Ladders of Thirds and Tonal Jazz Melody.” Unpublished manuscript.
Martin, Henry. 2018. “Prolongation and Its Limits: The Compositions of Wayne Shorter.” Music Theory Spectrum 40 (1): 84–105.
Martin, Henry, and Keith Waters. 2016. Jazz: The First 100 Years. 3rd ed. Cengage Learning.
—————. 2017. “Hierarchy vs. Heterarchy in Two Compositions by Wayne Shorter.” Paper presented at the 2017 meeting of the Society for Music Theory, Arlington, VA.
Martins, José Olivera. 2007. “Affinity Spaces and Their Host Set Classes.” Conference proceedings, 2007 International Conference on Mathematics and Computation in Music.
—————. 2015. “Bartók’s Polymodality: The Dasian and Other Affinity Spaces.” Journal of Music Theory 59 (2): 273–320.
McClimon, Michael. 2017. “Transformations in Tonal Jazz: ii–V Space.” Music Theory Online 23 (1). https://mtosmt.org/issues/mto.17.23.1/mto.17.23.1.mcclimon.html.
Michaelsen, Garrett. 2016. “Rhythm Changes, Improvisation, and Chromaticism: Who Could Ask for Anything More?” Engaging Students Through Jazz. Vol. 4 of Engaging Students: Essays in Music Pedagogy. http://flipcamp.org/engagingstudents4/essays/michaelsen.html.
—————. 2018. “Chord-Scale Networks in the Music and Improvisations of Wayne Shorter.” Gamut 8 (1): 123–88.
—————. 2019. “Making ‘Anti-Music’: Divergent Interactional Strategies in the Miles Davis Quintet’s The Complete Live at the Plugged Nickel 1965.” Music Theory Online 25 (3). https://www.mtosmt.org/issues/mto.19.25.3/mto.19.25.3.michaelsen.html.
Mulholland, Joe, and Tom Hojnacki. 2013. The Berklee Book of Jazz Harmony. Berklee Press.
Perle, George. 1990. “Windows of Order.” In The Listening Composer, 55–92. University of California Press.
Pressing, Jeff. 1978. “Towards an Understanding of Scales in Jazz.” Jazzforschung 9: 25–35.
Rawlins, Robert. 2000. “Review of Mark Levine, The Jazz Theory Book.” Music Theory Online 6 (1). https://mtosmt.org/issues/mto.00.6.1/mto.00.6.1.rawlins.html.
Russell, George. 1959. The Lydian Chromatic Concept of Tonal Organization for Improvisation. 1st ed. Concept Publishing Co.
Salley, Keith. 2007. “Beyond Chord-Scale Theory: Realizing a Species Approach to Jazz Improvisation.” Journal of Music Theory Pedagogy 21: 101–22.
Smither, Sean. 2019. “Guide-Tone Space: Navigating Voice-Leading Syntax in Tonal Jazz.” Music Theory Online 25 (2). https://mtosmt.org/issues/mto.19.25.2/mto.19.25.2.smither.html.
Spicer, Mark. 2017. “Fragile, Emergent, and Absent Tonics in Pop and Rock Songs.” Music Theory Online 23 (2). https://mtosmt.org/issues/mto.17.23.2/mto.17.23.2.spicer.html.
Stover, Chris. 2014–15. “Jazz Harmony: A Progress Report.” Journal of Jazz Studies 10 (2): 157–97.
—————. 2016. “Strange Changes.” Engaging Students Through Jazz. Vol. 4 of Engaging Students: Essays in Music Pedagogy. http://flipcamp.org/engagingstudents4/essays/stover.html.
Strunk, Steven. 1979. “The Harmony of Early Bop: A Layered Approach.” Journal of Jazz Studies 6: 4–53.
—————. 2003. “Wayne Shorter’s ‘Yes and No’: An Analysis.” Tijdschrift voor Muziektheorie 8 (1): 40–56.
—————. 2005. “Notes on Harmony in Wayne Shorter’s Compositions.” Journal of Music Theory 49 (2): 301–32.
—————. 2016. “Tonal and Transformational Approaches to Chick Corea’s Compositions of the 1960s.” Music Theory Spectrum 38 (1): 16–36.
Sudnow, David, and Hubert L. Dreyfus. 2001. Ways of the Hand: A Rewritten Account. MIT Press.
Terefenko, Dariusz. 2016. “Fin de Siècle Harmony – A Jazz Perspective.” Engaging Students Through Jazz. Vol. 4 of Engaging Students: Essays in Music Pedagogy. http://flipcamp.org/engagingstudents4/essays/terefenko.html.
Tymoczko, Dmitri. 1997. “The Consecutive-Semmitone Constraint on Scalar Structure: A Link Between Impressionism and Jazz.” Intégral 11: 135–79.
—————. 2004. “Scale Networks in Debussy.” Journal of Music Theory 48 (2): 219–94.
—————. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. Oxford University Press.
Waters, Keith. 1996. “Blurring the Barline: Metric Displacement in the Piano Solos of Herbie Hancock.” Annual Review of Jazz Studies 8: 19–37.
—————. 2001. “Outside Forces: ‘Autumn Leaves’ in the 1960s.” Current Musicology 71–73: 276–302.
—————. 2003. “Motivic and Formal Improvisation in the Miles Davis Quintet 1965–1968.” Tijdschrift voor Muziektheorie 8 (1): 25–39
—————. 2005. “Modes, Scales, Functional Harmony, and Non-Functional Harmony in the Compositions of Herbie Hancock.” Journal of Music Theory 49 (2): 333–57.
—————. 2010. “‘Giant Steps’ and the ic4 Legacy.” Intégral 24: 135–62.
—————. 2011. The Studio Recordings of the Miles Davis Quintet 1965–68. Oxford University Press.
—————. 2013. “Postbop.” Entry in Grove Dictionary of American Music. 2nd ed. Edited by Hiroshi Garrett. Oxford University Press.
—————. 2016. “Chick Corea and Postbop Harmony.” Music Theory Spectrum 38 (1): 37–57.
Waters, Keith, and J. Kent Williams. 2010. “Modeling Diatonic, Acoustic, Hexatonic, and Octatonic Harmonies and Progressions in Two- and Three-Dimensional Pitch Spaces; or Jazz Harmony after 1960.” Music Theory Online 16 (3). https://mtosmt.org/issues/mto.10.16.3/mto.10.16.3.waters_williams.html.
Waters, Keith, Henry Martin, Steve Larson, and Steven Strunk. 2016. “Circular Thinking—A Roundtable on ‘Blue in Green’ and ‘Nefertiti’.” Journal of Jazz Studies 11 (1): 105–20.
Yudkin, Jeremy. 2007. Miles Davis, Miles Smiles, and the Invention of Post Bop. Indiana University Press.
Footnotes
1. Authors stylize this term in different ways: compare Waters’s consistent use of “postbop” (e.g., 2011, 2016, 2019) with “post bop” (Yudkin 2007) and “post-bop” (Michaelsen 2018).
Return to text
2. In addition to this scholarly output, Waters has coauthored a jazz history textbook with Henry Martin, currently in its third edition (2016).
Return to text
3. As a result of this focus, the monograph necessarily ignores topics related to improvisation that have garnered attention in recent music-theoretic jazz scholarship, including interaction (e.g., Givan 2016 and Michaelsen 2019) and affordance (e.g., Love 2017a and Hannaford 2019), as well as broader social, cultural, and political issues.
Return to text
4. Waters’s approach to postbop harmony has consistently deemphasized prolongation or global monotonality as analytical lodestars. For contrasting approaches that pursue these topics, see Martin 2018 and Strunk 2016; Waters 2016 functions in part as a response to the latter, while Martin and Waters 2017 directly addresses the coauthors’ contrasting views.
Return to text
5. These simpler patterns often function as hypothetical recompositions in Waters’s analyses, although he doesn’t characterize them as such.
Return to text
6. In the domain of form, for example, Waters contrasts typical tonal jazz tunes—with their sectional, 32-bar AABA or ABAC forms, balanced phrases, and regular cadences—with postbop tunes, which often feature single-section designs and irregular phrase lengths, avoid the standard cadences that create strong formal divisions, or exhibit circular elements that obscure the beginning of the form. For a discussion of circularity in jazz tunes, see Waters, Martin, Larson, and Strunk 2016.
Return to text
7. In mm. 9–16, the melody lands on the chordal fifth of every tonicized major-seventh chord. While mm. 1–4 and 5–8 also feature M3rd cycles of tonicized major-seventh chords, the accompanying melody in each span avoids a clear M3rd cycle, instead alternating between the chordal fifths and thirds of local tonics. See Waters 2019, 18–22, which summarizes observations from Waters 2010.
Return to text
8. For pedagogical perspectives on harmonic substitution in tonal jazz, see Stover 2016 and Michaelsen 2016.
Return to text
9. Terefenko (2016) provides a concise, pedagogically oriented chart that lists conventional extensions for all common jazz chord types, and notes that “[b]roadly speaking, the addition of diatonic extensions enhances the sound of individual chords, while the addition of chromatic extensions generally modifies the sound of chords and renders them harmonically less stable.”
Return to text
10. Some recent transformational approaches to tonal jazz syntax have privileged chordal thirds and sevenths either in conjunction with (McClimon 2017) or independent from (Smither 2019) chordal roots. These methodologies prioritize the central role of these guide tones in the voice-leading parsimony of tonal jazz syntax, while deemphasizing the similar voice-leading potential of upper extensions. Tonnetz-based approaches to postbop harmony have, by geometric necessity, also circumscribed chord membership to some degree—Strunk’s mappings focus on seventh chords (2016) or treat major- and minor-ninth chords as overlapping seventh chords (2003), while Waters and Williams (2010) construct a three-dimensional Tonnetz to model motions between ninth chords derived from diatonic, acoustic, hexatonic, and octatonic collections. Waters 2005 and Michaelsen 2018 apply an approach based on chord-scale isography to nonfunctional progressions in tunes by Hancock and Shorter, conceiving of harmonic motions as pitch-class voice leadings between source collections. These studies draw on earlier work by Pressing (1978) and Tymoczko (1997, 2004, 2011). In some sense, these chord-scale isographies efficiently model the complete voice-leading potential of tall-tertian chords. Like guide-tone-based analytical approaches, chord-scale isographies also have deep resonances with jazz pedagogy—although the origin of chord-scale isography in jazz is typically traced to Russell 1959, it achieved wider pedagogical influence at the Berklee College of Music in Boston, whose curricular approach is represented in a recent textbook by Mulholland and Hojnacki (2013). But as numerous commentators have noted (e.g., Rawlins [2000], Ake [2002], Salley [2007], and Stover [2014–15]), scales are insufficient pedagogical and theoretical stand-ins for chords in numerous respects—they ignore notions of root motion, chord voicing, and chord tone (including the distinction between, e.g., chordal elevenths and suspended fourths), and they collapse voice leading into the abstraction of pitch-class space. From this perspective, both chord-scale isographies and more restrictive approaches to chord membership omit potentially useful information about jazz harmonies.
Return to text
11. As Waters notes (27, n4), this tendency is also acknowledged by Julien (2003) and Strunk (2005, 2016).
Return to text
12. A similar chart appears as Example 21 in Waters 2016, 55, although this example only features substitutions in Corea’s music.
Return to text
13. There are, of course, multiple options for each hypothetical dominant—the examples could tolerate changes in upper-structure voicing, and the roots of chords 1–3 could swap with their tritone substitutes, all without sacrificing the chords’ explanatory relevance.
Return to text
14. Waters notes that the first of these substitutions reflects a larger “sus chord imperative” (42) in 1960s jazz. Compare Spicer’s notion of a “soul dominant” (2017, [3]).
Return to text
15. Waters also notes that the minor quality of this Bm9 upper structure departs from the expected B-major harmony implied by the
Return to text
16. These annotations follow Waters’s basic visual format; harmonies are read left to right.
Return to text
17. In addition to Strunk’s (2003) Tonnetz mappings of major- and minor-seventh and -ninth chords, scholars have deployed the cycle’s structure in jazz contexts to develop transformations between tall-tertian chords (Callender 2007), and to model the relative contextual stability of pitches in tonal jazz melodies (Love 2017b). The axis is a fixture of neo-Riemannian theorizing more generally, and its structure underpins both Hauptmann’s ([1853] 1991) famous conception of diatonic space and Lewin’s (1982) diatonic “Riemann System.” Outside of triadic harmony and jazz, the cycle is an example of both a “multi-aggregate cycle” (Gollin 2007) and an “affinity space” (Martins 2007, 2015), larger classes of spaces that have been used to analyze polymodality in music by Bartók and Stravinsky. In the realm of scale theory, Carey and Clampitt (1989) also identify the cycle’s ic3/4 structure as a critical third symmetry transformation of the diatonic set, in addition to its scalar and circle-of-fifths arrangements.
Return to text
18. In this book, Waters refers to substitutions between pairs of major- and minor-seventh chords whose roots are two cyclic positions apart as “P4 swaps.” Considering the left-to-right orientation of harmonies in the m3/M3 cycle, “P5 swap” seems a more fitting moniker. Waters 2016 develops a slightly different—and somewhat more complete—set of transformational labels for relationships between cyclically proximate chords, including sus chords whose representation as gapped cycles renders cyclic adjacency mildly problematic.
Return to text
19. The red-blue alternation between rows of squares echoes the m3/M3 cycle’s color-coding in Example 2. But while Waters uses a consistent chord quality for each parallel harmonization, one need not do so.
Return to text
20. This connection testifies to Waters’s engagement with this repertoire as both an analyst and accomplished pianist. Waters’s approach to functional substitution could also suggest an embodied approach—one can imagine dominant function stubbornly sticking to chord shapes that feel almost the same as conventional dominant voicings, for example. See Sudnow and Dreyfus 2001 for discussion of embodied keyboard pathways as a key component of improvisational fluency for jazz pianists.
Return to text
21. In forthcoming work on harmony in the music of jazz pianist Robert Glasper, I advance such a framework using commutative, m3/M3 cycle-based CURSOR and SLIDE transformations. Callender (2007) offers a similar approach in his analysis of Ligeti’s Arc-en-ciel, which applies commutative, invertible transformations that he calls Rotation (Rt) and Slide (Sl) to tall-tertian major- and minor-seventh chords.
Return to text
22. Waters’s labeling method for these progressions mirrors the sequence labeling technique used in Laitz 2015 (see especially Chapter 17).
Return to text
23. Waters’s bibliography includes both Biamonte 2010 and Harrison 1994.
Return to text
24. For example, Strunk 2003 and Callender 2007 both develop transformational approaches to tall-tertian major- and minor-seventh chords that have direct bearing on Waters’s m3/M3 cycle-based substitutions, and the former deals directly with non-functional progressions in Shorter’s music. Although it would also be gratifying to see Waters engage with Michaelsen 2018 and Martin 2018, which address Shorter’s music, both were likely published too recently to be incorporated into the monograph.
Return to text
Copyright Statement
Copyright © 2020 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Lauren Irschick, Editorial Assistant
Number of visits:
6898