Continuous Question-Answer Pairs
Yosef Goldenberg
KEYWORDS: period, sentence, phrase, cadence, form, tonal music
ABSTRACT: This article offers a generalized study of continuous question-answer pairs in common-practice tonal music. In all (and only in) question-answer pairs, the first ending is less conclusive than the second. The first ending need not, however, be a cadence. The category of question-answer pairs (QAPs) that are continuous cuts across various theme types in Caplin’s (1998) taxonomy. Examples of continuous QAPs include (1) continuous periods (with a dominant-version consequent or a consequent with a non-tonic beginning); (2) most, but not all cases of the hybrid theme type compound basic theme + consequent; and (3) many, but not all statement-response pairs in sentential presentations. Various aspects contribute to the evaluation of each specific case, including caesuras, motivic parallelism, symmetry, internal organization, unit length, independence of the hyper-unit, and melodic closure.
DOI: 10.30535/mto.26.3.2
Copyright © 2020 Society for Music Theory
1. Introduction
[1.1] This study aims to contribute to the understanding of the internal form of closed themes. It offers adjustments to the Formenlehre on the small scale, as has been most powerfully presented by William E. Caplin (1998). Beyond Caplin, the study of such issues, at least in the English-language literature, has taken place mainly in textbooks rather than in research publications. The intended audience of these textbooks varies, from upper-level undergraduates (notably Beach and McClelland 2012) to beginners (e.g., Laitz 2012). (Earlier pertinent treatises on form include textbooks by Wallace Berry (1966) and Douglas M. Green (1979). Most of these textbooks, however, are thoughtful studies by professional music theorists, and deserve attention.(1)
[1.2] “Question-answer pairs” (henceforth QAPs) is a new and deliberately general term that covers many manifestations that fall under different labels in existing musical taxonomy. All QAPs, and only QAPs, consist of two units where the first ends with a weaker ending, the second ends with a stronger ending, and it makes sense to group the two units together into a larger formal entity.(2) This definition is based on the definition of period by David Beach and Ryan McClelland (2012, 66), with the general terms “unit” and “ending” replacing “phrase” and “cadence,” respectively.(3)
[1.3] The main advantage of the term QAP is that it explicitly indicates its essential feature. QAPs might be regarded to be generalized periods, but the application of the term period is controversial in at least four ways: (1) Caplin (1998, 265, Chapter 4, fn. 1) limits its usage to parallel periods only, in opposition to the wider terminology that accepts contrasting periods; (2) Some texts (e.g., Green 1979, 64–65) accept periods of more than two units, which are by definition not question-answer pairs; (3) Historical usage of the term Period or Periode in German goes back to the late eighteenth century, but already in Koch’s and Vogler’s usages “the linkages between the terminological and conceptual planes do not conform” (Bent 1994, 132); and (4) Schoenberg (1967) includes among his examples of periods also cases that are not QAPs, in which both units end on an untonicized V,(4) or where the first ending is more stable than the second.(5) The latter option seems to be a normative kind of period according to Russian literature.(6) It has also appeared in a recent article in Music Theory Online, in which Mark Richards (2016, [25]) demonstrates an “open period,” where “the stronger of the two endings occurs in the antecedent.” Thus, while the definition of QAPs in [1.1] is worded as an expansion of a definition of period, other conceptions of periods include cases that are not at all QAPs.(7)
[1.4] The subject of this study is specifically continuous QAPs—that is, QAPs that exhibit continuity in their harmonic progression. Like QAPs in general, continuous QAPs fall under different categories in existing taxonomies: (1) Continuous parallel periods (a term used by Laitz [2012, 300 and 304] as well as Beach and McClelland [2012, 67]), especially with dominant-version consequents, as shown by Caplin (1998, 53; 2013, 82); (2) Continuous manifestations of contrasting periods, conceived by Caplin as hybrid themes of antecedent + continuation; (3) Most but not all cases of hybrid themes whose first unit is a compound basic idea (i.e., does not end with a cadence [Caplin 1998, 61]); and (4) One common type of statement and response in a presentation of a sentence (Caplin 1998, 39). On the one hand, then, this study combines generalizations that grasp the shared features of distinct theme types (and parts of theme types). On the other hand, it offers refinements that distinguish between dissimilar variants that count as belonging to the same label.
[1.5] The neutral term “unit” in the definition of QAPs could in principle serve for extremely long or short units, not at all compatible with phrases. Thus, the Schenkerian application of interruption to sonata form (even with development) understands sonata form as a huge enlargement of the tonal structure of a parallel period, with the exposition and recapitulation standing together for the antecedent, and the recapitulation standing for the consequent. Huge QAPs may also be continuous, as in Scarlatti sonatas. On a scale this large, QAPs cease to be theme types. However, some complete pieces of intermediate size (such as most Baroque binary dances) may indeed be perceived as direct enlargements of QAPs at the theme level.
[1.6] At the other edge end of the spectrum, miniature QAPs may consist of less than a phrase. For example, in the second movement of Beethoven’s Piano Sonata in G minor, op. 49, no. 2 (not shown), a single measure of question and a single measure of (continuous) answer form together the basic idea, half of the antecedent, a quarter of a period. This article is only concerned with QAPs that occur at or near the theme level, with unit length being one important factor in their evaluation.
[1.7] After presenting continuous QAPs in section 2, we will proceed in section 3 to a detailed examination of their relations to each of the theme types aforementioned in [1.4]. Section 4 of this study discusses the various elements of design that influence the evaluation of individual QAPs. Section 5 explores some special devices and section 6 concludes.
[1.8] The norm in parallel periods, the most common type of QAPs, is that the opening of what we might call the second hemistich (the consequent) “is supported by the same harmony as in the antecedent
2. Harmonic aspects of Question-Answer Pairs
2.1 Question-Answer Pairs with Clear Harmonic Continuity
Example 1. Beethoven, Minuet in E-flat major, WoO 82, mm. 1–8
(click to enlarge)
[2.1.1] Example 1 presents a paradigmatic continuous QAP, using Beethoven’s Minuet in E-flat major, WoO 82, as a case in point. Steven G. Laitz introduces this example in order to warn students not to consider it as a period since “although the excerpt divides into two musical units, they cannot be considered phrases because there is no cadence [at the end of the first unit], just a caesura on a dissonant ii6/5” (2012, 306). Evidently, the division into units is immediately noticeable, to the extent that it might obscure the lack of harmonic closure of the first unit. Laitz’s observation thus deliberately attempts to counter an intuitive component of hearing the passage.
[2.1.2] Rather than dismiss the divided design, I find that the features this representative example shares with a period are worthy of serious consideration: Example 1 is a QAP. In the specific example, the caesura is not the only factor that supports the division of the excerpt: (1) There is motivic parallelism between the two hemistiches, so that the division would have been preserved even without a general pause (for example, with renewed attacks of the ii6/5 at beats 2 and 3 of m. 4); (2) The units are equal in length; and (3) Each of the two units is subdivided into a basic idea and a contrasting idea (cf. [4.3.1]). None of these factors—parallelism, symmetry, and internal organization of basic and contrasting ideas—is a necessary condition for a QAP, but each of them reinforces the resemblance of the formal unit to a genuine period.
[2.1.3] Attention to non-harmonic factors notwithstanding, design alone is insufficient to create a sense of QAP. A mere repetition of a musical unit involves parallelism and symmetry, and may involve a caesura, but if the second ending is not stronger than the first, there is no QAP.
[2.1.4] Another element that makes the QAP in Example 1 resemble a period is that each unit occupies four real measures.(10) Thus, it is only due to the lack of a cadence that the first unit is not a genuine antecedent—not insufficient length.(11) On the other hand, two other related factors weaken the sense of a quasi-period: (1) The final ending is not very strong: it arrives at I, an apparent IAC, and even that cadence is undercut since the bass abandons the root of the V7 harmony, and resolves to the tonic by step; and (2) The hyper-unit (the QAP as a whole) is not an independent section or theme, and thus the entire passage may have initiation function. The two units may be conceived as a statement and response of a sentential presentation within a sixteen-measure sentence, or perhaps of a theme that is not exactly a sentence (mm. 9–12 [not shown] do create a certain sense of continuation, but without fragmentation or other devices typical of continuation in a sentence).(12) Indeed, a certain kind of statement and response within a sentence presentation (to be studied below) creates a QAP. As we will see ([4.4.1]), such pairs of statement and response often occupy four measures only, but they may at the same time constitute a complete period.
Example 2. Beethoven, Minuet in E-flat major, WoO 82, mm. 27–34
(click to enlarge)
[2.1.5] At the end of Beethoven’s minuet (Example 2), an abridged rounded binary return creates a stronger QAP, now leading to a PAC and making an independent hyper-unit. These features make the end of the minuet resemble a genuine period more than its opening.
Example 3. Mozart, Symphony no. 39 in E-flat major, K. 543, third movement, mm. 1–8
(click to enlarge)
[2.1.6] Some analyses that aim at pointing out the divided quality of a harmonically continuous QAP apply the term cadence in a broad manner, apparently in order to make the QAP fit into the definition of a period. A case in point is the I–IV, V–I QAP (an eight-measure presentation of a modulatory sixteen-measure sentence) that opens the minuet of Mozart’s Symphony no. 39 in E-flat major, K. 543 (Example 3). Daniel Harrison (1994, 29) demonstrates with this example a period whose antecedent has a “plagal HC.”(13) He detects the concept of a plagal HC back in the work of Moritz Hauptmann ([1883] 1888, 176), but Hauptmann refers in fact, in a more strictly dualistic approach, to the I–IV, IV–I pairing. Harrison also cites Yitzhak Sadai’s (1980, 142–43) discussion of the “subdominant HC.” Among Sadai’s examples, only one arguably ends the first unit of a QAP: Schumann, Album für die Jugend, op. 68, “Figurierter Chorale” (no. 42), mm. 17–20, which is based on “Ein Choral” (no. 4), mm. 25–28 (not shown). The complete QAP (no. 4, mm. 25–32) takes the form I–IV, I–I. Thus, the return of the tonic reinforces the point of division, and the QAP may be plagal but it is not continuous.(14)
Example 4. Haydn, The Seven Last Words of Christ, orchestral version, Hob. XX:1, second movement, final measures
(click to enlarge)
[2.1.7] Attempts to label every first-unit ending in a QAP as a cadence (see also note 49 below) are doomed to failure. Question units in QAPs (especially continuous QAPs) may end on various harmonies. Recall that “cadence creates musical closure, but not all closure in music is cadential” (Caplin 2004, 56). Consider Example 4. The final measures of Haydn’s The Seven Last Words of Christ, Hob. XX:1, second movement, constitute a QAP on two levels. On the larger level, it consists of an expanded cadential progression (as proposed in Caplin 1987) that occurs twice, the first of which does end with a cadence: a deceptive cadence, further weakened by the move to an open soprano position resembling an IAC.(15) It is on the surface level where the first unit of a QAP does not end with a cadence. The rhythmic pattern recurs four times in two pairs: I6–ii6/5, V–vi, repeated as I6–ii6/5, V–I. Rhythmic parallelism alone divides each two-measure phrase into two one-measure sub-units, each ending with longer notes. Since the first ending within each two-measure phrase is less stable than the second, each is a QAP, embedded within a larger period. The endings of the questions in the surface QAPs occur in the course of the expanded cadential progression, and cannot be cadential arrivals.
[2.1.8] In Example 5, Dvořák’s Piano Quintet in A major, op. 81, third movement, mm. 9–16, the question moves from I to iii
Example 5. Dvořák, Piano Quintet in A major, op. 81, third movement, mm. 9–16, piano part (click to enlarge) | Example 6. Dvořák, Piano Quintet in A major, op. 81, third movement, mm. 31–38, piano part (click to enlarge) |
2.2 Continuous QAPs whose Question Ends on a Weakened Dominant
[2.2.1] Ending a question unit on a weakened form of the dominant is close to an HC. Its status is subject to debate even with QAPs that restate the tonic at the beginning of unit 2 (see ahead [3.2.3]). Originally, Caplin stressed that in the instrumental works of Haydn, Mozart, and Beethoven, the V that is the goal of an HC must be a root-position triad (Caplin 2004, 70); but more recently, he accepted V7 as a “nineteenth-century HC” (Caplin 2018, 4, following Schmalfeldt 2011, 202–3). L. Poundie Burstein (2014, 211–15; 2015, 102) endorses an inverted V or V7 as a legitimate final harmony in an HC, even before the nineteenth century. Ultimately, Burstein (2014) finds the concept of HC “slippery.” In Janet Schmalfeldt’s and most of Burstein’s examples, the seventh lies in an inner voice.(18) When the first unit of a QAP ends with a V7 whose seventh is in the upper voice, the continuity is greater and challenges the experience of a cadence. A Schenkerian reading would probably conceive the upper-voice seventh at the end of unit 1 as an upper neighbor to that arrives in the second unit, not an offshoot to a pre-interruption . The neighbor configuration might work also in continuous QAPs with unit 1 ending on V.
Example 7. Haydn, String Quartet in B minor, op. 33, no. 1, third movement, mm. 41–44 (immediately after the double bar)
(click to enlarge)
[2.2.2] Consider Example 7, Haydn’s String Quartet in B minor, op. 33, no. 1, third movement, mm. 41–44. The final V of unit 1 is inverted, has a seventh in the upper voice, and, in addition, continues to the beginning of unit 2 (as in continuous periods), giving rise to a double neighbor in the bass. With all the continuity, the sense of a parallel and symmetrical QAP is strong.(19)
Example 8. Mozart, Piano Sonata in C minor, K. 457, first movement, mm. 1–8
(click to enlarge)
[2.2.3] A less common form of dominant function at the end of a question would be viio or viio7. In Example 8, from the first movement of Mozart’s Piano Sonata in C minor, K. 457, viio7 supports an upper neighbor to scale degree , not . Discussing this theme, Carl Schachter asks: “how is it that this phrase, with such strongly marked inner articulations, does not sound overly segmented?” and explains that “the patterns of tonal movement overlap the articulations and act as a counterforce to them” ([1976] 1999, 48).(20) This comment, like the one by Laitz that undervalues what is “just a caesura,” regards aspects of division in design as external factors that conceal the true essence of the music. One might, however, put Schachter’s question the other way around: how is it that this theme, despite its continuous tonal motion, is strongly divided by inner articulation? The reply is obvious, but must not be explained away: the division is created by a combination of rhythmic stop and motivic parallelism, with the additional supporting factors of symmetry and internal organization. The hierarchy between the endings of its units completes the conditions for a QAP.
3. Accepted Theme Types and Continuous Question-Answer Pairs
3.1. Continuous Periods Type 1: Periods with Dominant-Version Consequent
[3.1.1] The very concept of a continuous period challenges the essence of the period as a structure that is divided into two phrases: If it is continuous, in what sense is it not a single phrase?(21)
[3.1.2] The classification of periods is usually based on the ends of their constituent phrases:(22) the distinction between interrupted and sectional periods is based on the type of inconclusive cadence that ends their antecedents (the former ends with an HC, the latter with an IAC);(23) and modulatory (“progressive”) periods are determined by the end of their consequent in another key. By contrast, what distinguishes continuous periods from all other types of periods is the beginning of their consequents. We will focus on periods with consequents opening with the dominant, and discuss the endings of their antecedents, as well as additional parameters that influence their status as periods. Toward the end of this section ([3.5]), we will also explore continuous periods whose consequents start with a sequential statement of the antecedent in another harmony.(24)
[3.1.3] All periods (according to most definitions) are QAPs,(25) distinguished from other QAPs in that their first unit ends with a cadence. In most periods, and especially interrupted periods (I–HC, I–PAC), the harmonic progression itself is divided even when the realization is schematic. The design factors that enable the identification of QAPs with no cadence at the middle come to the fore in periods with dominant-version consequent—that is, when “the basic idea of the consequent is a dominant version, in relation to a tonic version of the antecedent” (Caplin 1998, 53; 2013, 82).(26) This is one type which Laitz (2012, 300 and 304) and Beach and McClelland (2012, 67) classify as continuous periods.(27)
[3.1.4] In some periods with dominant-version consequents, the V that ends the antecedent (as an HC or even as a local V:PAC) persists throughout the consequent until its final tonic. In such cases, the overall harmonic progression is an undivided I–V–I, and, as in QAPs that are not periods, design is necessary in order to perceive the division of the excerpt. The overall undivided harmonic progression downgrades the significance of the cadence at the end of the first unit—the very factor that is decisive for Caplin and others for distinguishing a period from a phrase group that is not a period.
Example 9. Beethoven, Piano Sonata in B-flat major, op. 22, third movement, mm. 1–8
(click to enlarge)
[3.1.5] Example 9 shows a case in point from Beethoven’s Piano Sonata in B-flat major, op. 22, third movement, mm. 1–8. Laitz (2012, 299) as well as Beach and McClelland (2012, 68) use this example to demonstrate a contrasting period. However, in this period, the motives are the same in both phrases, and only their arrangement differs; an ascending contour in the antecedent is answered by a descending contour for the first half of the consequent. This example is thus an intermediate case between a parallel continuous period and a contrasting continuous period.(28)
[3.1.6] The retention of the V throughout the consequent need not involve a straightforward pedal point, as in Example 9. Many examples give rise to analytical dilemmas between two options: (1) The dominant-version consequent continues the V that ended the antecedent up to the final tonic in an overall I–V–I single progression; (2) The consequent starts on the dominant, but later arrives at a structural tonic. The deeper structure of the period is interrupted (I–HC [or V:PAC], I–PAC), but the border between the thematic phrases is not aligned with the harmonic interruption. The potential discrepancy between thematic and harmonic borderlines between musical units should warn us against a straightforward reconciliation of tonal structure in the Schenkerian sense with form (as Schmalfeldt 1991 and especially C. Smith 1996 propose; see also [3.5.3] and [4.6.7] below).
Example 10a. Beethoven, Serenade for String Trio in D major, op. 8, fourth movement, mm. 1–8
(click to enlarge)
Example 10b. Two voice-leading graphs of the Serenade for String Trio in D major, op. 8, fourth movement, mm. 1–8
(click to enlarge and see the rest)
[3.1.7] We will demonstrate this dilemma with the excerpt that Caplin used as the paradigmatic demonstration of a period with a dominant-version consequent: the opening of Beethoven’s Serenade for String Trio in D major, op. 8, fourth movement, the first part of a small ternary section (Examples 10a and 10b). The short antecedent ends with an HC (or a PAC in the V, after a brief tonicization), but as the V continues into the consequent, the sense of an HC is weakened. The difference in harmonic content persists throughout the consequent. The arrival of I in the second measure of the consequent happens in a moment whose counterpart in the antecedent is already after the music left the tonic. The harmonic progression works better with a true tonic in the consequent. The strongest factor in favor of a single I–V–I reading is the omission of the lower register between the cadences that end the two phrases, as the cello is saved to end each of the QAP’s halves with open chords.(29)
3.2 Continuous Manifestations of Hybrid Themes Type 4: Compound Basic Idea + Consequent
[3.2.1] Caplin introduces the term “compound basic idea” (henceforth c.b.i.) for “a phrase consisting of a simple basic idea and a contrasting idea that does not close with a cadence” (1998, 61). The combination of a basic idea and a contrasting idea is for Caplin an essential feature of period antecedents. We will rethink this issue below in the discussion of the internal organization of each hemistich of a QAP ([4.3.1]). The central point is that a c.b.i., unlike an antecedent, lacks a cadence. Other theorists would not apply the term “phrase” to units that do not end with a cadence. For example, Beach and McClelland explicitly state: “phrases are defined by cadences. If there has been no tonal motion leading to a cadence, there has been no phrase” (2012, 65).(30) Even Caplin, who rejects the requirement that all phrases must end with cadences,(31) adheres to this requirement in relation to period antecedents: “If a cadence does not appear at the end of the phrase, then an essential component of antecedent function has been lost” (61). Specifically, the type of hybrid theme that consists of a c.b.i + consequent differs from periods “in only one respect: they lack the weak cadence in the fourth measure of the theme” (61).
[3.2.2] The examples with which Caplin (1998, 62) demonstrates the hybrid type c.b.i + consequent are continuous QAPs (i.e., with a non-tonic beginning of the consequent), constructed as I–V6/5, V7–PAC (his Example 5.7: Beethoven, String Quartet in G major, op. 18, no. 2, fourth movement, mm. 21–28) and I–ii, ii–V–I (Example 5.8: Haydn, Symphony no. 87 in A major, third movement, mm. 1–8). Caplin does not comment on this choice, but it seems no coincidence. A non-tonic beginning of the consequent contributes significantly to the continuity from question to answer, a continuity that Caplin presents to be solely the result of the lack of a cadence to the question unit. Again, establishing the distinction between theme types only on the existence of a cadence at the end of the question in the QAP turns out to be problematic.
[3.2.3] Caplin does apply the label “c.b.i. + consequent” also to QAPs whose consequent starts on the tonic (stressing the lack of a cadence at the ending of their question unit). These should count as non-continuous “c.b.i. + consequent” hybrid themes, but the classification obscures their strong resemblance to non-continuous types of genuine periods. Thus, in the form I–I6, I–PAC,(32) the ending on I6 is a corollary case for IACs, and thus the QAP as a whole is similar to sectional periods, with the difference being that it is the bass rather than the upper voice that prevents the authentic cadence from being perfect. Similarly, a first ending on a weak V is a weakened form of an HC, making the entire QAP similar to the interrupted period paradigm. This is true even in Caplin’s example,(33) where the V at the end of the question takes the form I–weak V over tonic pedal point, I–PAC, evidently a more extreme case of weakening the V than the “slippery” HCs studied above ([2.2.1]). In Caplin’s example, the upper voice supports a melodic –––, –––– interruption, and thus reinforces the relations to an interrupted period.
[3.2.4] Regarding non-continuous QAPs as modified sectional and interrupted periods (respectively) admittedly gives less weight to the lack of a genuine cadence at the end of their question unit. At the same time, it draws a distinction that Caplin’s taxonomy under-evaluates, as he combines continuous and non-continuous “c.b.i. + consequent” QAPs together.
[3.2.5] In principle, a variety of criteria for classification need not involve hierarchy between them. A red triangle has the same color as a red square and the same form as a yellow triangle. Sometimes, however, there is hierarchy between parameters. I and my pet are both parents, but I have more in common with human beings who are not parents. In our case, there is a point to asking “what is a continuous c.b.i. + consequent more like? A continuous genuine period or a non-continuous c.b.i. + consequent?” The kind of potential controversy is familiar from other disciplines, such as whether or not Pluto is a planet.
3.3 Continuous QAPs in Other Types of Hybrid Themes
[3.3.1] Caplin (1998, 59–61) presents three more types of hybrid themes. The first, antecedent + continuation, is identical to what other theorists call contrasting periods. When a pair of units does not share the same musical material, the feeling of question-and-answer might be less strict, yet QAPs without parallelism are possible. We have seen in Example 9 one continuous period whose consequent combined parallel motives with contrasting organization. Later (Example 15) we will meet a continuous and almost entirely contrasting QAP that is not a period.(34)
[3.3.2] Hybrid theme type 2, antecedent + cadential, may not be continuous, as the “cadential” function is based on the extended cadential progression (after Caplin 1987), starting on I6.
[3.3.3] Under hybrid theme type 3, c.b.i. + continuation: Caplin combines themes that are very different from each other, since a c.b.i. is defined by what it lacks (a cadence) rather than by positive features. Caplin gives two paradigmatic examples of c.b.i. + continuation, the opening eight measures of the first movement of Haydn’s Piano Sonata in C major, Hob. XVI:35 (62, Example 5.5), and of the third movement of Haydn’s Symphony no. 95 in C minor (62, Example 5.6). The former may be a corollary case of antecedent + continuation (contrasting period)—Caplin’s point is that the V at the end of unit 1 is “no HC,” but one might regard it as a “slippery” HC (see [2.2.1]). In the latter example, by contrast, the hybrid theme is not at all a QAP of any kind, as its first unit is closed in the tonic with soprano position (after no genuine harmonic motion has been performed).
3.4 Continuous Statement-Response Repetition in Sentential Presentations
[3.4.1] Statement-response repetition is one subtype of presentation phrases in sentences (Caplin 1998, 39). This is one more term that covers dissimilar themes. Some statement-response repetitions are not QAPs, as their statement is closed in the tonic and their response in supported by dominant harmony.(35) The kind of statement and response that forms a QAP is always continuous as it “involves motion away from tonic to dominant (I–V) in the statement and a return from the dominant to the tonic (V–I) in the response” (39). Schoenberg (1967, 21) strongly emphasizes this subtype in his original conception of sentences, calling it “the dominant form: the complementary repetition.” Caplin has noticed that the same overall harmonic design (I–V, V–I) also governs periods with dominant-version consequents (1998, 53). In our terms, both statement-response repetitions and periods with dominant-version consequents are continuous QAPs.
[3.4.2] The shared feature relates complete periods that have a dominant-version consequent to the first half only of certain instances of the sentence, the opposite prototype. We will refer to this non-congruence in [4.4] when discussing unit length as one parameter for the evaluation of continuous QAPs.
3.5 Continuous Periods Type 2: Periods with Sequential Beginning of the Consequent
Example 11. Mozart, Piano Sonata in D major, K. 576, first movement, mm. 1–8
(click to enlarge)
[3.5.1] The term “continuous period” also covers situations that do not fall under Caplin’s category of periods with a dominant-version consequent, but under a different category where “the consequent restates the basic idea of the antecedent sequentially, usually by being transposed up a step into the supertonic region” (1998, 53). This type usually exhibits at the beginning of the consequent a stronger sense of renewed beginning than in dominant-version consequents. The paradigmatic example of this procedure in a strict period (that is, after an HC) is the opening of Mozart’s Piano Sonata in D major, K. 576 (Example 11).(36) Yet, such a period with a sequential consequent may support an undivided skeletal melody. Notice the Schenkerian beam that continues across the division.
[3.5.2] The continuous descent is a counter-formal reading that connects the V at the HC with the V of the final cadence, and regards the opening harmony of the consequent as being subsidiary. The motivation for such a reading is the persistence of throughout the passage. Similarly, in QAPs that are “transpositional periods” in the form I–V, IV–I, where the consequent is a transposition of the antecedent (Morgan 1998, 28–33), the deep harmonic progression may retain the V until the final cadence and thus be more directional than the symmetrical framework might suggest (Cutler 2016).(37) Interpreting sequential consequents as variants of dominant-version consequents is compatible with cases where “as a variation on [the I–V, V–I statement-response] pattern, a pre-dominant harmony of some kind (II6, IV, V/V) precedes the dominant that appears at the beginning of the response” (Caplin 1998, 39). Caplin makes this observation in the context of sentence presentations, of the type that makes continuous QAPs.
Example 12. Three interpretations of periods of the I–V, ii–V–I type
(click to enlarge)
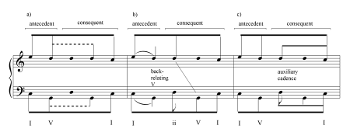
[3.5.3] Example 12 shows that additional interpretations are possible, however. Reading 12a shows the counter-formal interpretation, but 12b and 12c are more compatible with the motivic parallelism of the period, which in the case of Mozart’s Piano Sonata in D major, K. 576, is further supported by a clear division of each phrase into a basic idea and a contrasting idea.(38) In 12b, the HC is a back-relating dominant, after which the deep harmonic progression continues directly from the opening tonic (Laitz 2012, 292). Eric Wen (2008, Example 1) even suggests that the V is a corrective for a parallel fifth between I and ii. Reading a back-relating dominant also works when the transposed consequent is not to ii but rather to iii, as in the theme of Beethoven’s Piano Sonata in D major, op. 28, second movement (not shown). Example 12c reads the consequent as a subsidiary phrase that creates an auxiliary cadence in the Schenkerian sense.(39)
Example 13. Schubert, Piano Trio no. 1 in B-flat major, D. 898, first movement, mm. 1–12
(click to enlarge)
[3.5.4] When the V at the end of the question unit has a seventh in the upper voice, the QAP is not a period, and there is a stronger case for connecting the dominants in the I–V, ii–V–I progression. In such cases, the retained passing tone that connects both dominants is not but (Example 13).
[3.5.5] A different situation occurs if the answer unit indeed begins with a sequential restatement of the opening motive in ii, but the ii has already arrived at the end of the question unit. For that option, look ahead to Example 16. (Example 23 below, too, opens the answer unit on the supertonic, but there the harmonic change is not realized by means of melodic sequence.)
4. Elements of Design in Continuous QAPs
[4.1] The following discussion aims at a more nuanced evaluation of continuous QAPs. We will look separately into various parameters that influence the perception of continuous QAPs. First, we will discuss the two main factors that divide the hyper-unit despite the harmonic continuity: caesura and motivic parallelism. Then, we will discuss the internal motivic organization of each unit, the length of the units, independence of the hyper-unit, and melodic completion.(40)
4.1 Caesura
[4.1.1] The mere cessation of musical activity is not an essential component of a cadence (Caplin 2004, 97), and indeed a general pause in the midst of a tense moment (as in the second theme of Schubert’s Symphony no. 8 in B minor, D. 759 [“Unfinished”]) does not at all create a sense of a local ending. Nevertheless, caesuras (even “just a caesura” after a dissonance; recall Example 1) are probably the strongest component dividing phrases (or phrase-groups) that are harmonically continuous, especially if they occur at the middle of the phrase (or phrase-group). The significance of caesuras is strongest in those cases where the division is not supported by motivic parallelism, creating contrasting continuous QAPs. Two examples demonstrate.(41)
Example 14. Haydn, Symphony no. 21 in A major, third movement, mm. 1–8
(click to enlarge)
[4.1.2] Example 14, which shows the first eight measures from the third movement of Haydn’s Symphony no. 21 in A major, would count as a contrasting continuous period, since the question ends with an HC.(42) (The piece, from 1764, is reminiscent of the 1787 minuet of Mozart’s Eine kleine Nachtmusik.) The answer does share material with the question, but not the material from m. 1: the melody of mm. 2–3 returns in the first two measures of the answer. The deeper tonal structure of this example does include interruption. The tonic at m. 6, which is melodically analogous to that in m. 3, serves as the opening tonic of the post-interruption phrase, a counterpart of m. 1 in that respect.
Example 15. Schubert, Minuet in A major, D. 91, no. 2, mm. 1–8
(click to enlarge)
[4.1.3] Example 15, Schubert’s Minuet in A major, D. 91, no. 2, mm. 1–8, provides a contrasting continuous QAP that is not a period (I–IV, V–I). Not only is the melody of the answer different, but the texture as well. The contrast is so clear that it alone would divide the theme into two units. The upbeat in the answer, however, is a motive from the antecedent (hence, the beginnings are parallel). The caesura in the middle is decisive for the feeling of a division at the specific moment, which precedes the moment of motivic and textural change.
4.2 Motivic Parallelism
[4.2.1] Most QAPs are parallel. In non-continuous QAPs, the parallelism is by definition also harmonic, while in continuous QAPs it is thematic only. In QAPs that are not periods (i.e., their question unit does not end with a cadence), the parallelism reinforces their resemblance to genuine parallel periods.
Example 16. Schumann, Davidsbündlertänze, op. 6, no. 16, mm. 1–8
(click to enlarge)
[4.2.2] For a case of a parallel QAP with no rhythmic stop between its units, see Schumann’s Davidsbündlertänze, op. 6, no. 16, mm. 1–8 (Example 16). The I–ii answered by ii–tonicized V is a modulating variant of a continuous QAP (compare Example 22 below). The answer unit begins with a sequential restatement of the opening, but, unlike I–V, ii–V–I periods, here the second unit begins on the same harmony on which the first unit ended. Instead of a caesura, the gap between the units is filled by a harmonic progression that prolongs the ii. A dynamic contrast does provide a certain sense of caesura. One might rather have expected a piano caesura between thematic loud units, but Schumann reverses the dynamic contrast “in good humor.”(43)
4.3. Internal Organization
[4.3.1] Caplin (1998) contends that any antecedent and any compound basic idea consists of a basic idea and a contrasting idea. However, he admits that only “in the clearest cases” does the contrasting idea introduce “motives distinctly different from those of the basic idea” rather than merely a difference in the harmonic organization (49 and 61).(44) A truly motivic contrasting idea should not count as part of the definition of phrases that build a period, not only because it does not exist in all periods, but also because it is not unique to periods in Caplin’s strict sense, as it also exists in a c.b.i. Nevertheless, the existence of a motivically strong internal contrast within each unit in a QAP reinforces its resemblance to paradigmatic continuous periods.
Example 17. Mozart, Piano Concerto in B-flat major, K. 450, first movement, mm. 1–8
(click to enlarge)
[4.3.2] As one example, consider the first movement from Mozart’s Piano Concerto in B-flat major, mm. 1–8 (Example 17). The concerto opens with a sixteen-measure sentence, whose presentation consists of a I–V7, V7–I statement and response—a continuous QAP that supports the melodic segment –, – (see Example 13 above, and discussion of melodic completion below, [4.6]). Each of the two units is rich and includes a basic idea and a thematically highly contrasting idea. The basic idea features stepwise chromatic motion in the woodwinds while the contrasting idea consists of diatonic arpeggios in the violins, as if two different figures are interacting, one gentle and the other more resolute. Moreover, the answer unit repeats the contrasting idea rather than replacing it with a new contrasting idea, as is often the case. The sharp distinction between basic and contrasting ideas in the opening of K. 450 is a feature that makes the excerpt as a whole sound more like a typical period despite the lack of cadence at the end of its question unit.(45)
4.4 Unit Length
[4.4.1] As a norm, antecedent and consequent phrases in a period each occupy a complete phrase of four real measures, while statement and response in a sentence presentation each occupy two real measures only, adding up to a single phrase. However, themes can take larger proportions, so that (as in Example 17) the statement and response in a compound, sixteen-measure sentence have the same size as a non-compound antecedent and consequent. Thus, ideas concerning “a period in the first part of a sentence” (see note 49) make more sense with regard to compound sentences, whose first part has the size of a complete period.
[4.4.2] Unit length seems to influence the experience of QAPs. Very short passages sound less like periods even when their harmonic relations are similar to continuous periods. A case in point is Mozart’s Piano Sonata in E-flat major, K. 282, second movement, mm. 1–4, described by Wallace Berry as a “period relationship
Example 18. Dvořák, Piano Quintet in A major, op. 81, third movement, mm. 60–67
(click to enlarge)
[4.4.3] A related case—where period-like energies occur with very small units and even without any tonal motion whatsoever—takes place in Dvořák’s Piano Quintet in A major, op. 81, third movement, mm. 60–67 (Example 18). Even though the tempo remains the same throughout the entire movement (see again, Examples 5 and 6), now the activity is meager and the entire excerpt takes place within the tonic. Only does its melodic statement ascend (from lower or ) to the upper and its response descend from to . This example still obeys the basic requirements of a QAP: it is divided, with the first ending less stable. Motion from to and back would feel like a QAP also in the opposite contour, but the melodic ascent and descent certainly support the sense of opening and closing. Would the melodic direction create a sense of a QAP if the first unit ended on ? I would suspect not but interestingly, Adolf Bernhard Marx illustrated the concepts Vordersatz and Nachsatz with complete ascending and descending scale (quoted in Uribe 2011, 239, Example 10).
4.5 Independence of the QAP Hyper-unit
[4.5] Periods constitute independent hyper-units divided into two smaller units. Even when they are part of a larger whole, such as rounded binary themes, they are self-contained. Sentential presentations such as statement-response pairs, by contrast, require continuation. When a QAP stands by itself—for example, when it is immediately repeated (as in Example 9)—it gains independence, which alone reinforces its resemblance to genuine continuous periods. The existence of a sentential continuation after the QAP, on the other hand, makes the QAP function more like a sentence-response presentation, although it does not cancel out the statement-response resemblance to a continuous period (compare Example 2 versus Example 1 above).(47)
4.6 Melodic Completion
[4.6.1] The sense of open and closed endings of the units of a QAP is stronger when the answer unit completes a progression that had been left incomplete by the question unit—not just harmonically, but melodically as well.
Example 19. Chopin, Mazurka in C minor, op. 56, no. 3, mm. 81–88
(click to enlarge)
[4.6.2] Strongest of all are configurations that end on . Of these, the simplest is the melodic sequence –, –, which occurs in Chopin’s Mazurka in C minor, op. 56, no. 3, mm. 81–88 (Example 19). This is a continuous period, itself a consequent of a double period. The units are short and lack thematically contrasting ideas, but the melodic closure is strong.
Example 20. Haydn, String Quartet in B minor, op. 33, no. 1, third movement, mm. 1–8
(click to enlarge)
[4.6.3] The configuration –, – in general might seem too closed off to be followed by a continuation and thus unlikely to serve as a sentence presentation. See, however, the first eight measures from Haydn’s String Quartet in B minor, op. 33, no. 1, third movement (Example 20). An inner voice provides an ascending line –, – that works against the closure, and thus does call for continuation. Closure on might even belong to a literal outer (but conceptually inner) voice (see again Example 8).(48)
[4.6.4] Tonic closure with in the upper voice usually counts as an IAC, but this requires further classification according to the melodic direction from which it arrives. Thus, – answered by –—a divided, four-stage, version of the Sol–Fa–Mi galant schema,(49) as encountered in Mozart’s Piano Concerto in B-flat Major, K. 450, (Example 17)—gives a stronger experience of closure than ascents consisting of a – statement answered by –—a divided, four-stage version of the Do–Re–Mi scheme.(50) A somewhat weaker type of initial ascent is – answered by –. This happens in the main theme of Mozart’s String Quartet in C major, K. 465 (“Dissonance”), first movement (not shown), the paradigmatic example that Caplin (1998, 38, Example 3.8) gives for the continuous statement-response.
[4.6.5] In all four options mentioned so far (–, –; –, –; –, –; –, –), the final melodic tone of the question unit is a passing tone. At other times, it may serve as a neighbor tone to any tonic member, as in – answered by – (recall Berry’s example from Mozart’s Piano Sonata in E-flat Major, K. 282, mentioned in [4.4.2]) or –, – (Example 8, Mozart’s Piano Sonata in C minor, K. 457, with a final coming from an inner voice). More common are QAPs that have I and at both boundaries, with the tonal motion supporting neighbor tones.
Example 21. Mozart, Fantasy in D minor, K. 397, mm. 12–15
(click to enlarge)
[4.6.6] Consider Mozart’s Fantasy in D minor, K. 397, mm. 12–15 (Example 21). The passage is based on a –, – double neighbor, and on a more surface level, it is an ascending sequence (–––, –––), so that one could read it alternatively as ––.(51)
[4.6.7] Eugene Narmour (1977, 89–95) refers to this passage from Mozart’s Fantasy in D minor (Example 21) in his criticism of Schenkerian theory’s focus on harmony and voice leading. According to Narmour, this focus necessarily loses sight of the motivic parallelism in such passages. Actually, this lack of conformance takes place also according to theoretical perspectives that focus on the surface (consider the Meyer schema in Gjerdingen 2007, 111–28). The problem arises in any continuous parallel QAP, where the beginning of the question relates motivically to the beginning of the answer, but harmonically to the end of the answer. Rather than attempting a “conformant reading,” as Narmour did, it is better to confront the discrepancy between motivic relations and harmonic hierarchy in QAPs.
[4.7] The factors discussed—caesuras, motivic parallelism, internal organization, unit length, independence of hyper-unit, and melodic closure—all influence the degree to which specific QAPs resemble familiar theme types (or parts thereof): periods, hybrid themes, and statement-response presentations in a sentence. Since many factors are involved, it is impossible to achieve a scale for measuring the degree to which a specific case of QAP resembles a period, for example. Rather, it is advisable to map out the various examples, considering all the parameters (see Appendix).
5. Special devices
5.1 Modulatory Continuous QAPs
[5.1.1] The classification of periods into several categories (one of which is continuous) misleadingly implies that these categories are exclusive. Since the defining criteria of the categories are not the same, a period may be both continuous and modulatory.(52) Continuous QAPs that are not periods (i.e., their first unit does not end with a cadence) may similarly modulate.
Example 22. Mozart, Piano Concerto, K.453, third movement, mm. 1–8
(click to enlarge)
[5.1.2] The first eight measures from Mozart’s Piano Concerto in G major, K.453, third movement, mm. 1–8 (Example 22) are a genuine period that is not only continuous and modulatory but sectional as well. It is sectional, because its antecedent ends with an IAC (i.e., the antecedent might have served within a paradigmatic sectional [I–IAC, I–PAC] period); it is continuous, because its consequent begins on V; and it modulates to the key of V, ending with a PAC in that key. Such theme types seem rare, but, tellingly, the theme comes from the Classical repertoire and does not sound foreign to the style.(53) The only objection might be that since the entire consequent is within V, it might serve on the larger scale as an HC, less stable than the first ending, challenging its essence as a QAP.
[5.1.3] For another QAP that is both continuous and modulatory, see again Schumann’s, Davidsbündlertänze, op. 6, no. 16, mm. 1–8 (Example 16). In that excerpt, the question itself leaves the tonic, and thus the opportunity to perceive the first ending as stable is defied.
5.2 : Continuous QAPs with Invariant Melodic Beginnings
[5.2.1] It is generally understood that if the harmony at the beginning of the answer is different from its counterpart in the question, their melodic content is also different. They may of course share the same motives, but not the same notes. As an exceptional artistic device, however, it is possible for the beginning of the answer in a continuous QAP to reharmonize a melodically invariant content from the question.
Example 23. Bizet, Habanera from Carmen, mm. 1–9
(click to enlarge)
[5.2.2] As one example, the first nine measures from Bizet’s “Habanera” from Carmen (Example 23) are a single harmonic phrase, supported by the progression i–iiø4/2–V7–i over a tonic pedal point. Nevertheless, the melody alone could have taken place in an interrupted period from , going through all scale degrees to in the question, then to in the answer,(54) with an especially strong parallelism between the units and invariant pitches for two measures. It is as though the upper voice forms a clear interrupted period, but the harmony does not support it. The harmony remains iiø4/2 at the point of division, a seventh chord that includes both the that ends the question and the that opens the answer.
Example 24. Grieg, “Illusion,” from Lyric Pieces, op. 57, no. 3, mm. 1–8
(click to enlarge)
[5.2.3] Finally, Grieg’s “Illusion” from Lyric Pieces, op. 57, no. 3, mm. 1–8 (Example 24) is ultimately an interrupted period, but nevertheless there is a strong melodic continuity between the phrases, and re-harmonization does apply to the opening of the phrases. A most salient feature of this specific period is its continuous registral descent: in the antecedent, the melody is in the upper voice, while in the consequent, it is an octave lower. Registral difference between period phrases is ubiquitous, but the consequents are usually an octave above rather than below the antecedent.(55) Registral shifts usually mark a difference between the phrases, but when the melody has a clear direction and the shift of register moves in the same direction, melodic continuity arises even in periods where the structural borders are clear.(56) The Grieg passage is more complicated. Melodically, the antecedent descends a ninth that stands for a descending second –,(57) and the consequent expands the descent into a tenth. The harmony, however, changes. The antecedent begins with an augmented “III6,” a modified surface dominant that connects a preceding implicit tonic harmonization (of an unharmonized ) with the next VI.(58) In the consequent, is added to form an inverted V13/7, and it arrives directly from the HC that ends the antecedent. Dominant incursions into the consequent sometimes cancel out the interruption altogether (Jackson 1999; Suurpää 2005). In this case, however, the V does not continue all the way to the final cadence; rather, a true tonic that opens the consequent structurally arrives later. The most continuous aspect of this period lies in the lower voices. There is a direct scalar descent from E4, the lower sixth below the opening primary tone in the antecedent, to E2, the bass of V in the final PAC of the consequent. At the point of division between the phrases, an inner-voice chromatic tone serves as a modified form of interruption-fill. The opening of the consequent lies in a higher register than the bass of the preceding HC, and arrives from the preceding inner voice. The title of this lyric piece, “Illusion,” is apt in that the theme gives the illusion of a single, continuous progression while it is at the same time based on an interruption structure.
6. Conclusion and Areas of Further Research
[6.1] This study engages with tight-knit short phrases, a subject covered by all undergraduate textbooks on form. It is telling that current understanding of such basic tight-knit phrases is still very incomplete. This might be the result of the variety of parameters involved. Multiple possible relations exist between specific examples and configurations to genuine periods and other familiar theme types. Going beyond the identification of cadences or lack thereof, there is no single convenient condition to define similarity to true periods. The Appendix compares all of the examples shown (and a few that were only mentioned) and indicates that there is no single pattern that governs them all.
[6.2] The concept of QAP offers a framework that acknowledges aspects of design more than ordinary theory with its emphasis on cadences. This does not mean that we need to eliminate the roles of harmony and cadences. These should go without saying, and they are absorbed into the definition of QAPs, which sticks to the requirement that the first unit must end in a less stable manner than the second.
[6.3] There is still work to do. In my experience, the acknowledgment of continuous QAPs in their own right—rather than just as “not genuine periods” when their question units lack cadences—immediately draws attention to their ubiquity in the repertoire. Their actual frequency is still impossible to determine.
[6.4] Recognition of QAPs should also enable better inquiry of many passages of music, including non-Classical repertories. For example, in Balkan folk songs such as Jovano Jovanke, both paired phrases end on the dominant, but only the latter arrives at its root. A different relevant repertory is twentieth-century extended tonality, as in the opening of Shostakovich’s String Quartet no. 3 in F major, op. 73, where the power of cadences is weak, but the general principles of division into units and grouping of units are still in force. A detailed study of QAPs in such wider repertoires might in turn further illuminate their presence in common-practice tonal music.
Appendix: Comparison of all demonstrated examples and selected additional examples
U1: Unit 1; U2: Unit 2; u or i after V7 or its inversions: seventh in upper or inner voice; Y/N/I: yes, no, intermediate situation.
|
|
U1 end |
U2 start |
U2 end |
b.i. |
Length |
Ind. |
Melodic completion |
Caesura |
Parallelism |
Notes |
|
1 |
|
|
I |
I |
4+4 |
N |
N |
Y |
Y |
|
|
2 |
|
|
I |
I |
4+4 |
Y |
Y |
Y |
Y |
|
|
3 |
IV |
V |
I |
Y |
4+4 |
Y |
N |
Y |
Y |
|
|
4 (two levels) |
VI |
i6 |
i |
N |
2+2 |
Y |
N |
Y |
strong |
|
|
iiø |
V |
1. VI |
Y |
1+1 |
N |
N |
|
rhythm |
|
|
|
5 |
III (=iii |
ii |
I |
N |
2+2 |
Y |
N |
melody |
Y |
|
|
6 |
IV (=iv |
Gr |
i |
N |
2+2 |
Y |
N |
melody |
Y |
|
|
7 |
|
|
i/ |
Y |
2+2 |
Y |
N |
Y |
Y |
|
|
8 |
viio |
V |
i6 |
Y |
4+4 |
Y |
I |
Y |
Y |
|
|
9 |
V |
|
I |
I |
4+4 |
Y |
N |
Y |
complex |
some consider as contrasting |
|
10 |
V |
|
I |
N |
4+4 |
Y |
N |
Y |
I |
interrupted? |
|
11 |
V |
ii |
I |
Y |
4+4 |
Y |
, |
Y |
Y |
|
|
13 |
|
ii |
I |
Y |
4+4 |
Y |
,[] |
Y |
Y |
|
|
14 |
V |
|
N |
4+4 |
Y |
N |
Y |
weak |
dislocated motive |
|
|
15 |
IV |
V |
I |
N |
4+4 |
Y |
N |
Y |
N |
|
|
16 |
ii |
ii |
V:PAC |
N |
4+4 |
Y |
N |
(N) |
Y |
|
|
17 |
|
|
I |
Y |
4+4 |
N |
, |
I |
Y |
|
|
18 |
I |
I |
I |
N |
2+2 |
I |
N |
Y |
I |
no tonal motion |
|
19 |
v |
V (=V |
I |
N |
4+4 |
Y |
, |
N |
Y |
|
|
20 |
|
|
I |
Y |
4+4 |
N |
, |
Y |
Y |
|
|
21 |
|
|
i |
Y |
2+2 |
N |
, |
Y |
Y |
|
|
22 |
IAC |
V |
V:PAC |
I |
4+4 |
Y |
N |
Y |
Y |
|
|
23 |
iiø |
iiø |
i |
N |
4+4 |
Y |
N |
melody |
Y |
invariant; interrupted melody |
|
24 |
V |
Inver. |
i |
N |
4+4 |
Y |
N |
Y |
Y |
invariant, interrupted |
|
Haydn(note 29) |
V |
|
I |
I |
4+4 |
Y |
N |
Y |
Y |
invariant middle |
|
K. 550/I |
iiø |
V |
i |
I |
4+4 |
N |
, |
I |
Y |
|
|
K.465/I |
IV |
V6 |
I |
N |
2+2? |
N |
, |
Y |
Y |
|
|
Hauptmann |
IV |
IV |
I |
|
|
|
|
|
|
abstract |
|
Schumann |
IV |
I |
I |
N |
4+4 |
Y |
N |
Y |
Y |
non-continuous |
|
Beethoven |
V |
III |
v: |
N |
4+4 |
Y |
N |
Y |
Y |
|
Yosef Goldenberg
Jerusalem Academy of Music and Dance
Edmond J. Safra Campus
Giv’at Ram
Jerusalem 9190401
Israel
yosefg@jamd.ac.il
Works Cited
Beach, David. 2012. Advanced Schenkerian Analysis: Perspectives on Phrase Rhythm, Motive and Form. Routledge.
Beach, David, and Ryan McClelland. 2012. Analysis of 18th- and 19th- Century Musical Works in the Classical Tradition. Routledge.
Bent, Ian, ed. 1994. Music Analysis in the Nineteenth Century. Vol.1. Fugue, Form and Style. Cambridge University Press.
Berry, Wallace. 1966. Form in Music. Prentice-Hall.
Burstein, L. Poundie. 2005. “Unraveling Schenker’s Concept of the Auxiliary Cadence.” Music Theory Spectrum 27 (2): 159–86.
—————. 2014. “The Half Cadence and Other Such Slippery Events.” Music Theory Spectrum 36 (2): 203–27.
—————. 2015. “The Half Cadence and Related Analytic Fictions.” In What Is a Cadence: Theoretical and Analytical Perspectives on Cadences in the Classical Repertoire, eds. Markus Neuwirth and Pieter Bergé, 85–116. Leuven University Press.
Caplin, William E. 1987. “The ‘Expanded Cadential Progression’: A Category for the Analysis of Classical Form.” Journal of Musicological Research 7: 215–57.
—————. 1998. Classical Form: A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven. Oxford University Press.
—————. 2004. “The Classical Cadence: Conceptions and Misconceptions.” Journal of the American Musicological Society 57 (1): 51–118.
—————. 2009. “What Are Formal Functions?” In Musical Form, Forms, Formenlehre—Three Methodological Reflections, ed. Pieter Bergé, 21–40. Leuven University Press.
—————. 2013. Analyzing Classical Form: An Approach for the Classroom. Oxford University Press.
—————. 2018. “Beyond the Classical Cadence: Thematic Closure in Early Romantic Music.” Music Theory Spectrum 40 (1): 1–26.
Clendinning, Jane Piper, and Elizabeth West Marvin. 2005. The Musician’s Guide to Theory and Analysis. W. W. Norton & Company.
Cutler, Timothy. 2016. “‘Proper Boundaries’ and the ‘Incoherent’ Succession V(7)–IV.” Indiana Theory Review 32 (1–2): 41–84.
Darcy, Warren. 2000. Review of Classical Form: A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven by William Caplin. Music Theory Spectrum 22 (1): 122–25.
Doll, Christopher. 2017. Hearing Harmony: Toward a Tonal Theory for the Rock Era. University of Michigan Press.
Gauldin, Robert. 2004. Harmonic Practice in Tonal Music. 2nd ed. W.W. Norton & Company.
Gjerdingen, Robert O. 2007. Music in the Galant Style. Oxford University Press.
Goldenberg, Yosef. 2012. “The Interruption-Fill and Corollary Procedures.” Music Theory Online 18 (4). https://mtosmt.org/issues/mto.12.18.4/mto.12.18.4.goldenberg.html
—————. 2018. “When and How are Modulations Diatonic?” Intégral 32: 37–58.
Green, Douglass M. 1979. Form in Tonal Music: An Introduction to Analysis. 2nd ed. Holt, Rinehart and Winston.
Harrison, Daniel. 1994. Harmonic Function in Chromatic Music: A Renewed Dualist Theory and an Account of Its Precedents. The University of Chicago Press.
Hauptmann, Moritz. (1883) 1888. The Nature of Harmony and Metre. Translated by W. E. Heathcote. Swan Sonnenschein.
Hepokoski, James, and Warren Darcy. 2006. Elements of Sonata Theory: Norms, Types, and Deformations in the Late-Eighteenth-Century Sonata. Oxford University Press.
Jackson, Timothy. 1999. “Diachronic Transformation in a Schenkerian Context: Brahms’s Haydn Variations.” In Schenker Studies 2, eds. Carl Schachter and Hedi Siegel, 239–75. Cambridge University Press.
Kostka, Stefan, Dorothy Payne, and Byron Almén. 2013. Tonal Harmony. 7th ed. McGraw-Hill.
Laitz, Steven G. 2012. The Complete Musician: An Integrated Approach to Tonal Theory, Analysis, and Theory. 3rd ed. Oxford University Press.
Laskowski, Larry. 1980. “Symmetrical Design and its Relationship to Voice Leading.” Theory and Practice 5 (1): 57–65.
Marston, Nicholas. 2013. “The Development of Schenker’s Concept of Interruption.” Music Analysis 32 (3): 332–62.
Mazel’, Lev [Leo] Abramovich. (1960) 1986. Stroyeniye Muzïkal′nïkh Proizvedeniy (The Construction of Musical Compositions). 3rd ed. Muzyka.
Mazel’, Leo, and Viktor Zuckerman. 1967. Analiz Muzïkal′nïkh Proizvedeniy: Ėlementï Muzïki i Metodika Analiza Malïkh Form (Analysis of Musical Works: Elements of Music and Method of Analyzing Small Forms). Muzyka.
Morgan, Robert P. 1998. “Symmetrical Form and Common-Practice Tonality.” Music Theory Spectrum 20 (1): 1–47.
Narmour, Eugene. 1977. Beyond Schenkerism: The Need for Alternatives in Music Analysis. University of Chicago Press.
Ottman, Robert W. 1983. Elementary Harmony: Theory and Practice. 3rd ed. Prentice-Hall.
Parks, Richard S. 1976. “Voice Leading and Chromatic Harmony in the Music of Chopin.” Journal of Music Theory 20 (2): 189–213.
Rammos, Yannis. 2017. Review of Beach 2012. Music Theory and Analysis 4 (1): 131–44.
Richards, Mark. 2016. “Film Music Themes: Analysis and Corpus Study.” Music Theory Online 22 (1). https://mtosmt.org/issues/mto.16.22.1/mto.16.22.1.richards.html
Robins, Jeremy M., 2017. “Phrase Structure, Hypermeter and Closure in Popular Music.” PhD diss., Florida State University.
Roig-Francolí, Miguel A. 2005. Harmony in Context. 2nd ed. McGraw Hill.
Rothstein, William N. 1989. Phrase Rhythm in Tonal Music. Schirmer.
Sadai, Yitzhak. 1980. Harmony in its Systemic and Phenomenological Aspects. Yanetz.
Salzer, Felix. 1962. Structural Hearing: Tonal Coherence in Music. New corrected edition. Dover.
Santa, Matthew. 2010. Hearing Form: Musical Analysis With and Without the Score. Routledge.
Schachter, Carl. (1976) 1999. “Rhythm and Linear Analysis: A Preliminary Study.” Reprinted in Unfoldings: Essays in Schenkerian Theory and Analysis, ed. Joseph N. Straus, 17–53. Oxford University Press.
—————. 1994. “The Prelude in E minor Op. 28, No. 4: Autograph Sources and Interpretation.” In Chopin Studies 2, ed. John Rink and Jim Samson, 161–82. Cambridge University Press.
Schenker, Heinrich. (1935) 1979. Free Composition. Translated and edited by Ernst Oster. Longman.
Schmalfeldt, Janet. 1991. “Towards a Reconciliation of Schenkerian Concepts with Traditional and Recent Theories of Form.” Music Analysis 10 (3): 233–87.
—————. 1992. “Cadential Processes: The Evaded Cadence and the ‘One More Time’ Technique.” Journal of Musicological Research 12: 1–52.
—————. 2011. In the Process of Becoming: Analytic and Philosophical Perspectives on Form in Early Nineteenth-Century Music. Oxford University Press.
Schoenberg, Arnold. 1967 (posth.). Fundamentals of Musical Composition, eds. Gerald Strang and Leonard Stein. Faber & Faber.
Skoumal, Zdenek. 1994. “Liszt’s Androgynous Harmony.” Music Analysis 13 (1): 51–72.
Smith, Charles J. 1996. “Musical Form and Fundamental Structure: An Investigation of Schenker’s ‘Formenlehre.’” Music Analysis 15 (2–3): 191–297.
Smith, Peter E. 2013. “Hierarchy, Interruption, and Interpretation of ABA’ Forms.” Journal of Schenkerian Studies 7: 1–30.
Suurpää, Lauri. 2005. “The Undivided Ursatz and the Omission of the Tonic Stufe at the Beginning of the Recapitulation.” Journal of Schenkerian Studies 1: 66–91.
Tyulin, Yuri Nikolayevich, et al.. (1965) 1974. Muzïkal′naya Forma (Musical Form). 2nd ed. Muzyka.
Uribe, Patrick Wood. 2011. “A. B. Marx’s Sonatenform: Coming to Terms with Beethoven’s Rhetoric.” Journal of Music Theory 55 (2): 221–51.
Wen, Eric. 2008. “Commentary on Samuel Ng’s review of Peter H. Smith’s Expressive Forms in Brahms’s Instrumental Music: Structure and Meaning in His Werther Quartet.” Music Theory Online 14 (1). https://mtosmt.org/issues/mto.08.14.1/mto.08.14.1.wen.html
—————. 2017. Structurally Sound: Seven Musical Masterworks Deconstructed. Dover.
Footnotes
1. Also in the study of harmony, some areas covered by undergraduate curriculum are addressed mainly in textbooks. See Goldenberg 2018, 37.
Return to text
2. The flexibility of weighing endings offers an opportunity to encompass exceptional situations. For example, in Schubert’s Ländler in D-flat Major, D. 366, no. 14, the first ending (m. 4) on a PAC with a 9–8 suspension is weaker than the direct PAC of the second ending (m. 8).
Return to text
3. Additional definitions of period that lend themselves to the same word replacement include Green 1979, 56; Berry 1966, 18; and Roig-Francolí 2005, 277.
Return to text
4. Schoenberg 1967, 33, Example 43d (Bach, English Suite no. 4, Sarabande).
Return to text
5. Schoenberg 1967, 33 and 52, examples 43c (Bach, English Suite no. 4, Minuet no. 2) and 49c (Chopin, Nocturne op. 48, no. 1).
Return to text
6. I am indebted to Karel Volniansky for making this point, and to Bella Brover-Lubovsky for providing the following references: (1) Mazel’ and Zuckerman 1967, 521–22, Example 552, from Haydn’s Piano Sonata (or Partita) in E major, Hob. XVI:13, second movement, mm. 1–8. The first ending is on I but without tonal motion before it, the second ending is a HC, and the material is contrasting; (2) Tyulin et al. ([1965] 1974, 67 and 87, Example 24), from Beethoven’s Piano Sonata op. 31, no. 3 in E-flat major, third movement, mm. 1–8 (also provided in Mazel’ [1960] 1986, 174, Example 124). Both of these examples are independent phrases that end on a HC after they arrive at I in m. 4, the former without harmonic motion and the latter as a weakened IAC. Both examples lack internal parallelism, but the Russian literature also demonstrates parallel open periods. For example, the next example in Mazel’ ([1960] 1986, 174–75, Example 125) shows Beethoven’s Piano Sonata in G major, op. 49, no. 2, second movement, mm. 68–86: I:HC in the key of IV answered by a potential V:HC (=I:HC in the main key), but that latter potential cadence does not materialize.
Return to text
7. Nineteenth-century terms that might coincide with QAP are fore-phrase (Vordersatz) and after-phrase (Nachsatz). Rothstein (1989, 18) aims to distinguish these general terms from the stricter “antecedent” and “consequent.” While Rothstein wishes to reserve the latter pair of terms for interrupted periods alone, the original German usage was sometimes free indeed (see [4.4.3]). Notice that German terminology sometimes acknowledges also a middle-phrase (Mittelsatz). The issue requires further investigation.
Return to text
8. Caplin refers to “the basic idea of the consequent,” which for him occupies the consequent’s first half. See, however, note 26 below.
Return to text
9. The familiar abbreviations HC, IAC, and PAC stand for half cadence, imperfect authentic cadence, and perfect authentic cadence. The terms “interrupted” and “sectional” periods are in use in Beach and McClelland (2012, 67) and Laitz (2012, 304). In some antecedents that lead to an HC, the melodic aspect of interruption in the strict Schenkerian sense is questionable.
Return to text
10. In this case, the four real measures are also four notated measures. According to Caplin (1998, 35 and 256), real measures correspond to a listener’s perception of one full measure. An anonymous reader of this paper argues that even in a moderato tempo, one can reasonably read the passage as two real measures, especially given the harmonic rhythm (one chord every two measures). Such a listening strategy would weaken the resemblance of that QAP to a period.
Return to text
11. Beach and McClelland, among others, require that a phrase ends with a cadence; Caplin does not accept that requirement in relation to phrases in general, but does require that antecedents of periods end with a cadence. See [3.2.1].
Return to text
12. See Caplin (1998, 40–42) on typical continuation in a sentence.
Return to text
13. Laitz (2012) gives that example as an assignment shortly after the minuet discussed as Example 1. Most probably, he expects students to label it in the same manner, as “an eight-measure phrase, not a period” (307). Laitz does accept a predominant ending of an antecedent in a continuous period, as when it ends with a PAC in ii (300). In our Example 3, the first ending on a subdominant is not tonicized and does not arrive at an octave position, but, unlike those in Examples 1 and 2, it is not dissonant either.
Return to text
14. In popular music, there is a stronger case for subdominant cadences. See Doll 2017, 25, on subdominant pre-tonics, and Robins 2017, 144–45, on “subdominant HC” and “subtonic HC.”
Return to text
15. This might be a case of a “one-more-time technique” (Schmalfeldt 1992), albeit with no phrase expansion.
Return to text
16. The example shows the piano part alone in mm. 9–16. This is an adapted repeat of the theme that the strings play in mm. 1–8. A countermelody in the viola (not shown) runs against the symmetrical division of the theme. At the fifth measure, ii6 would create a smoother bass, as in the diatonic I–iii, ii6–V–I QAP in Schubert’s Waltz in A minor, D. 969, no. 9, mm. 1–8.
Return to text
17. A further example of design parallelism dividing continuous harmonic progressions (without a caesura) appears in mm. 1–4 of Tchaikovsky’s “The Hobby Horse” from Album for Children, op. 39 (no. 3): I–V4/2 of V, viio–I, all above a tonic pedal.
Return to text
18. An exception appears in Burstein’s Example 5b (2014, 101): a HC in the second movement of Haydn’s Symphony no. 104 in D major includes a V7 with the seventh in the upper voice.
A telling controversy concerns Chopin’s Prelude in E minor, op. 28, no. 4: the first unit ends with a V7 with the seventh in an inner voice. Parks (1976, 197) reads an interruption, whereas Schachter (1994, 173) does not.
Return to text
19. Gauldin suggests that the trio of Haydn’s String Quartet in E-flat major, op. 33, no. 2, second movement, similarly provides a “c.b.i. + consequent” with a V7 at the end of the first unit (2004, 157, Example 10.13). He later observes that “the weak cadence in m. 38 [V7]
Return to text
20. In K. 457, despite the upper-voice –– overall motion, the actual ending in an inner voice on does provide stronger closure.
Return to text
21. In terms of formal functions (after Caplin 1998, 2009), in any parallel period, the end of the beginning (the antecedent) is followed by the beginning of the end (the consequent), but in continuous periods the function of both as middle is intensified.
Return to text
22. See the classification of periods in Laitz 2012, 300 and 304, and Beach and McClelland 2012, 67.
Return to text
23. For the term “inconclusive cadence,” see Clendinning and Marvin 2005, 200.
Return to text
24. Laitz states that the consequent of continuous periods begins “on a dominant or pre-dominant function” (2012, 300). Beach and McClelland write that it begins “with a non-tonic harmony, almost always the dominant or the supertonic” (2012, 67).
Return to text
25. [1.3] discusses conceptions of period that include cases that are not QAPs.
Return to text
26. Later, I will discuss the thematic aspect of the “basic idea.” At least in later repertories, a consequent occasionally may begin on the tonic but leave the harmonic parallelism with the antecedent much earlier than mid-phrase. Green (1979, 89–90) demonstrates an especially early change in the consequent in the Romance from Berlioz’s La Damnation de Faust.
Return to text
27. The term “continuous periods” also covers periods whose consequent begins in a sequential statement of the antecedent (see [3.5]). Throughout [3.1] I focus on continuous parallel periods, following the position that contrasting periods are better considered as hybrid themes rather than as genuine periods (Caplin 1998, 265 n. 1; 2013, 76). In Laitz’s classification, parallel or contrasting design can be applied to any of the four tonal types of periods (interrupted, sectional, continuous, or progressive [modulatory]).
When the antecedent also does not begin in the tonic, the tonic is usually the first structural harmony of both phrases, as in the opening period of Chopin’s Mazurka in F minor, op. 63, no. 2. A beginning on V might create phrase overlap when the V from the end of the antecedent continues into the consequent. See the opening of Chopin’s Mazurka in F-sharp minor, op. 6, no. 1, as analyzed by Rothstein (1989, 46–48).
Return to text
28. Another continuous period whose phrases are motivically parallel but have a contrasting contour can be found in Mozart’s String Quartet in C major (“Dissonance”), K. 465, third movement, theme of the trio. A gradual approach that permits intermediate situations between repetition and contrast also has advantages on the smaller scale, as an alternative to the dichotomous division between a contrasting idea and a repetition of a basic idea ([4.3.1]).
Return to text
29. In his later, pedagogy-oriented, book on musical form, Caplin (2013, 82) replaced the example for a period with dominant-version consequent with Haydn’s Piano Trio in E major, Hob. XV:28, first movement, mm. 1–4. The dilemma applies to that example also. A specific device in the Haydn trio example is that the middle of the consequent (end of m. 3, beginning of m. 4) becomes invariant with its counterpart in the antecedent (end of m. 1, beginning of m. 2). Further examples in Caplin (1998) with a dominant-version consequent are the openings of Mozart’s Piano Concerto in F major K. 459, second movement (pp. 56–57, Example 4.12) and Haydn’s Symphony no. 101 in D major, fourth movement (p. 80, Example 6.8).
Return to text
30. This assertion is more rigid than Rothstein’s (1989, 5): “if there is no tonal motion, there is no phrase,” which allows for the option that a phrase has tonal motion, but the tonal motion does not end with a cadence. However, Rammos (2017, 136) notes that Beach’s (2012) practice applies the term “cadence” liberally.
Return to text
31. On Caplin’s acceptance of phrases that do not end with a cadence, see Darcy 2000, 123. Specifically, Caplin asserts that “a presentation [of a sentence]
Return to text
32. See, for instance, Caplin 1998, 78, Example 6.7: Mozart, String Quartet in E-flat major, K. 428, fourth movement, mm. 1–8.
Return to text
33. See, for instance, Caplin 1998, 80, Example 6.9: Beethoven, Symphony no. 7 in A major, op 92, first movement, first theme, mm. 67–74.
Return to text
34. Contrasting content seems to occur more often in continuous periods than in the harmonically more rigid types of period. See, however, the contrasting interrupted period that opens the quartet “Non ti fidar” from Mozart’s Don Giovanni. Salzer (1962, 146 and Example 267) uses this piece to “show that wide melodic differences between pre- and post-interruption periods [meaning here what we refer to as phrases within a period] may occur although the structure shows that the technique of interruption is adhered to.”
Return to text
35. See, for example, Caplin 1998, 36, Example 3.2: Beethoven, Symphony no. 5 in C minor, first movement, mm. 6-13.
Return to text
36. Caplin 1998, 52, Example 4.9; Morgan 1998, 25, Example 17.
Return to text
37. Laskowski (1980, 65) emphasized the validity of such transpositions in spite of their discrepancy with the structural voice leading.
Return to text
38. The new contrasting idea in Example 11 shares elements with the contrasting idea in the antecedent. It traces the same stepwise ascent plus a skip of a third at the end, but accelerated to provide the extra space needed to complete an authentic cadence. Once again, the dichotomy between contrast and repetition deserves refinement (see note 28 above).
Return to text
39. On auxiliary cadences, see Burstein 2005. Schenker endorsed a hierarchy between the two branches of interrupted periods as well. See also Marston 2013 and P. Smith 2013 2013.
Return to text
40. One parameter that will not be discussed is symmetry. All of the examples in this study are symmetrical. In parallel periods, deviations from symmetry are commonplace (Caplin 1998, 57), but such deviations seem to be rare in cases of QAPs that more strongly involve continuity. The issue of symmetry and its violation in continuous QAPs requires further research.
Return to text
41. Caesuras in general can occur with varying degrees of salience, and not all of them involve a general pause. See Hepokoski and Darcy’s (2006, 30) discussion of common characteristics of the medial caesura. For an example of a passing tone within the caesura of a clear continuous period, see Saint-Saens, Piano Concerto no. 4 in C minor, second movement, mm. 296–311 (starts nine measures after rehearsal number AD). This is a I–V, ii–V–I continuous period. The minorization of V within the caesura is carried by means of a chromatic descending passing tone, analogous to interruption fill (in the sense proposed by Goldenberg 2012).
Return to text
42. In Caplin’s terms, this is a hybrid theme that consists of an antecedent and a continuation.
Return to text
43. In Example 16, the question unit ends with a mild form of a PAC in ii. This is a marginal case of a cadence at the end of the first unit, and thus a marginal case for a genuine period.
Return to text
44. Caplin (1998, 49) contends that “different underlying harmonies” are sufficient to create a sense of contrasting idea when it has “shared motives” with the basic idea. This view, however, is inconsistent with the acceptance of repetition of a basic idea in another harmony within sentence presentations (Caplin 1998, 17–19).
Return to text
45. For a continuous QAP with a clear thematically contrasting idea, see Mozart’s Symphony no. 40 in G minor, K. 550, fourth movement, mm. 1–8. There, the question ends on V6, and the V in the consequent is preceded by viio4/3.
Return to text
46. Berry (1966) does not mention sentential themes in general and does not use the terms “statement” and “response.” For an example that might count as a very short but tonally genuine continuous period, see Mozart’s “Der Vogelfänger bin ich ja” from Die Zauberflöte, mm. 1–4.
Return to text
47. A sentence whose first half is built like a period is a complementary procedure to a sentence-like (or sentential) antecedent whose basic idea is built like a “small presentation” (Caplin 1998, 51).
Return to text
48. In other cases, the question unit arrives at a PAC but the voice leading that leads there is not straightforward. See Schubert’s Waltz in E major, D. 924, no. 2. Sometimes, a Schenkerian practice would use implied tones to create linear continuity, even if the literal voice leading includes leaps. For QAPs in I–V4/3, V6/5–I relations but with rather than as the actual upper voice of the generalized antecedent, see Kuhlau’s Sonatina in G major, op. 55, no. 2, second movement, mm. 1–8, and Rossini’s Il Barbiere di Siviglia, no. 3 (Vivace), mm. 1–16. In Meyerbeer’s Le Prophète, no. 15 (ballet), a linear path to might be an ascending tetrachord from .
Return to text
49. On the galant schema, see Gjerdingen 2007, 255–62. His final example of the four-stage Sol–Fa–Mi is the famous opening (mm. 2–9) of Mozart’s Symphony no. 40 in G minor, K. 550, first movement. That example is a presentation of a sentence (i–iiø4/2 statement and V6/5–i response), where a clearly continuous harmonic progression is subject to division purely due to aspects of design (caesura and sequential parallelism), with the iiø4/2 grouped backward. Wen (2017, 219 and 291) reads it at the same time also as an antecedent and consequent of a period, and Santa (2010, 28–29) regards it as “a period in the first part of a sentence,” labeling the caesura after iiø4/2 a “progressive cadence,” a non-technical term that can refer to any inconclusive cadence, but is usually demonstrated by the HC (Ottman 1983, 24; Kostka, Payne, and Almén 2013, 147). Santa’s divergent and problematic terminology of course reflects an attempt to reconcile the QAP with the rigid requirements of a period.
Return to text
50. Gjerdingen writes that “using a pair of musical events that could function as a call and response, or question and answer, may have encouraged a replaying of the re in the Do–Re–Mi” (2007, 85–88). This is a description of the QAP. Sol–Fa–Mi and Do–Re–Mi are schemas that (unlike the Prinner, for example) exactly match Schenkerian linear progressions.
Return to text
51. See also the reverse case of the double neighbor in the opening phrase of Schubert’s “Liebesbotschaft,” from Schwanengesang. In this example, a –, – double neighbor (with the upper neighbor first) represents a descending sequence –––, ––– that one might read as –– (after Salzer 1962, Example 476). The pre-caesura is harmonized as a tonicized II.
Return to text
52. According to the classification of periods in Beach and McClelland (2012, 67), the consequent phrase of a progressive (modulatory) period begins in the tonic; Laitz (2012, 304) tacitly leaves this issue open.
Return to text
53. For a continuous non-modulating period whose antecedent ends with an IAC like a sectional period, see the opening of Gershwin’s “I loves you Porgy” from Porgy and Bess (Kostka, Payne, and Almén 2013, 156).
Return to text
54. The normative prototype of the Habanera passage would be a descent from I to V in the antecedent answered by a full octave descent from I to I in the consequent. Schenker ([1935] 1979, 34 and 40) refutes that model, claiming that if the primary tone is , the interruption should take the form –, –. Another example of a reharmonized invariant melody in the answer of a QAP may be found in “Valse Noble” from Schumann’s Carnaval, op. 9, piece no. 4 (Caplin 2018, 15, Example 15).
Return to text
55. Another consequent an octave lower than the antecedent can be found in the main theme of Mozart’s Piano Sonata in C major, K. 279, third movement.
Return to text
56. See Beethoven’s Piano Sonata in E minor, op. 90, second movement, mm. 1–8.
Return to text
57. In Schenkerian terms, the descent of a ninth is an illusory linear progression (Schenker [1935] 1979, 74).
Return to text
58. The “III6” involves members of V and I together. Skoumal (1994) calls it “androgynous” harmony.
Return to text
Copyright Statement
Copyright © 2020 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Fred Hosken, Editorial Assistant
Number of visits:
12183