Instrumental Transformations in Heinrich Biber’s Mystery Sonatas*
Jonathan De Souza
KEYWORDS: violin scordatura, Heinrich Biber, Mystery Sonatas, performance and analysis, transformational theory, altered auditory feedback, musical instruments
ABSTRACT: Each of Heinrich Biber’s Mystery Sonatas features a distinct violin tuning. How do these scordatura relate to standard tuning? How might they affect the sonatas’ musical organization and players’ experience? Transformational voice-leading theory helps to reveal overlapping categories here. Quintal scordatura include adjacent-string fifths, creating zones where notated and sounding intervals match. Chordal scordatura, in which the strings realize a triad, involve more displacement. Psychological research on altered pitch feedback suggests that scordatura are most unsettling for players when they preserve aspects of standard tuning. Analyzing scordatura, then, shows how instruments function as spaces for musical action.
DOI: 10.30535/mto.26.4.1
Copyright © 2020 Society for Music Theory
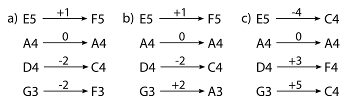
Example 1. Three ways to retune a violin’s open strings to an F-major chord
(click to enlarge)
[0.1] In “Some Ideas about Voice-Leading between PCSets,” David Lewin writes: “Suppose you want to retune your violin, so that all its open strings sound notes of the F major harmony. Maximally close voice leading indicates ways of doing so with (in some sense) as little overall strain as possible” (1998, 38). He demonstrates two possibilities (see Example 1a and b). With both, the E string rises one semitone, the A string remains unchanged, and the D string drops to middle C. The two choices differ only with the lowest string, which can go either up or down a whole tone. Both retunings involve an overall shift of five semitones, and Lewin shows that these are the two maximally close ways of retuning the violin to an F-major chord. The practical implications of Lewin’s “scordatura fantasy” are clear: if the strings are too loose, the tone will suffer; if they are too tight, they might break. Still, this is essentially a speculative exercise, a way to examine voice leading between set classes (in this case, from the open-string set to the major triad). It is a vivid theoretical illustration, but this section of Lewin’s article includes no analytical examples.
[0.2] Of course, Lewin is not the first musician to think about retuning a violin to an F-major chord. Heinrich Ignaz Franz von Biber (1644–1704) did this in the seventh of his fifteen Mystery Sonatas—a collection of pieces for violin and continuo, each of which features a distinct tuning. Biber, like Lewin, leaves the A string unchanged (see Example 1c). Meanwhile, the E string drops to C5. This moves to the nearest lower chord tone, avoiding extra tension on the string and recalling what Lewin (1998, 18) calls a “downshift voice leading.” But the lower strings are tuned up: the D string rises a minor third, and the G string, a perfect fourth. For a violinist, the E string feels floppy, and the G string feels dangerously tight. It is a remarkably inefficient solution, displacing twelve semitones overall.
Example 2. Biber, Mystery Sonata 7 (ca. 1678), Allemande, mm. 1–4
(click to enlarge and listen)
[0.3] The sonata’s notation can also be unsettling for the player. For example, the key signature includes a
Example 3. Excerpt from Biber’s manuscript for Mystery Sonata 7, featuring an illustration of “The Scourging at the Pillar”
(click to enlarge)
Example 4. Overview of Biber’s Mystery Sonatas
(click to enlarge)
[0.4] Biber’s F-major tuning offers some distinctive multiple stops. Yet scordatura, for Biber and his contemporaries, did not only expand the violin’s pitch affordances. It was also used “to tease the performer with another puzzle to decipher” (Barnett 2008, 118; see also Giles 2018, 72–73; Stowell 2001, 73). With the Mystery Sonatas, such puzzles have been interpreted in terms of the works’ religious associations. The collection’s common name derives from the “fifteen holy mysteries” mentioned in the dedication from Biber’s manuscript—that is, fifteen scenes from the life of Jesus and his mother, the Virgin Mary. The manuscript includes an illustration for each mystery (see Example 3), and these images match documents for the Salzburg Rosary Confraternity where Biber likely performed the pieces (Giles 2018, 78–80; Schmid 2008). As Example 4 indicates, these scenes are grouped into three affectively distinct sets of five—Joyful, Sorrowful, and Glorious Mysteries—which have formed the basis of Catholic rosary prayer since the middle ages. In several of the sonatas, the relevant scene corresponds to pictorial musical effects. For example, a trumpet topic in Sonata 12 heralds Jesus’s ascension to heaven. Theological significance arguably extends to physical aspects of the scordatura and players’ embodied experience as well. Sonata 7’s tense F-major tuning is associated with the Scourging at the Pillar, in which Jesus is publicly beaten. Lindsey Strand-Polyak argues that this tuning tortures the violin itself, with extreme tension differences potentially warping the bridge (2013, 132–33). For Strand-Polyak (2013, 121–23) and for Roseen Giles (2018, 89), performing theses sonatas is analogous to the practice of rosary prayer itself—a form of devotion that is essentially performative, repetitive, and corporeal.(1)
[0.5] Such perspectives advance a carnal musicology that centers the lived body and treats scores as scripts for performance (Le Guin 2006; Cook 2013). More specifically, they recall Suzanne Cusick’s analysis of a chorale prelude by J. S. Bach, in which the organist‘s physical balance or imbalance corresponds to the presence or absence of divine grace (1994, 18–19). Yet Lewinian transformational theory can also offer distinctive insights here. Joti Rockwell (2009) and James Bungert (2015) have used transformational thinking to explore spaces and actions of instrumental performance, analyzing players’ movements as well as the sounds they produce—and this approach has been central to some of my earlier work (De Souza 2017, 2018). With the Mystery Sonatas, Biber alters the instrumental space itself. How do his alternate tunings relate to standard tuning? How might these tunings affect the pieces’ organization and the players’ experience? This investigation mixes mathematical music theory with reflections on performance, connecting “Some Ideas about Voice-Leading between PCSets” with the poietic focus of “Music Theory, Phenomenology, and Modes of Perception” (Lewin 1986).(2) In a sense, it inverts Lewin’s scordatura fantasy. Where he used scordatura to investigate transformational voice leading, this study uses transformational voice-leading theory to investigate scordatura.
1. Instrumental Voice Leading
[1.1] Any scordatura can be modeled in terms of a voice leading from standard tuning to some other set. With this approach, each string is treated as a voice. Clearly, Lewin (1998) offers one way to evaluate such voice leadings. Joseph Straus (2003) extends Lewin’s approach, proposing three criteria: uniformity, smoothness, and balance. Straus’s article is concerned with atonal music, and for present purposes, some adjustments are required. First, where he focuses on pitch classes, sets of pitches seem more relevant with scordatura. Second, Straus considers many possible mappings between sets. Two tetrachords, for example, can be connected by twenty-four possible voice leadings (311–12). With strings, only a single mapping is needed—that is, the straightforward voice leading that Straus presents first, \(\{x_1–y_1, x_2–y_2, x_3–y_3, x_4–y_4\}\). In other words, the violin’s strings will be understood to form ordered pitch sets. This investigation, then, imagines standard tuning as <G3, D4, A4, E5>, not as a representative of the pitch-class set 4-23 [0257].(3) With these slight modifications, Straus’s voice-leading criteria readily apply to scordatura.
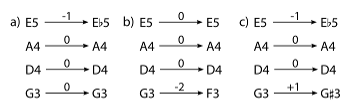
Example 5. Uniformity in violin scordatura
(click to enlarge)
[1.2] Uniform voice leadings are “transposition-like.” Here we ask, to what degree do voices move by the same interval? Uniformity can be measured in terms of offset (the number of semitones away from a crisp transposition) or consistency (the number of voices that move the same distance). Transpositional scordatura are relatively common. For Niccolò Paganini’s first violin concerto, the soloist tunes up a semitone (see Example 5a). The soloist then plays in “D major,” while the orchestra plays in
Example 6. Smoothness in violin scordatura
(click to enlarge)
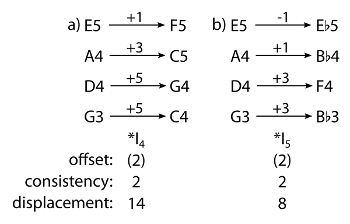
[1.3] With smooth voice leading, the voices’ movement is minimized. Smoothness is measured in terms of displacement—the total number of semitones shifted—as in Lewin’s scordatura fantasy. The scordatura featured in Camille Saint-Saëns’s Danse macabre, op. 40, involves minimal displacement. The E string is tuned to
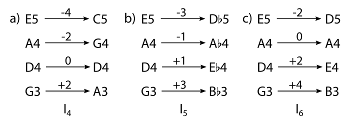
Example 7. Inversion in violin scordatura: Three maximally smooth ways to retune a violin in perfect fourths
(click to enlarge)
[1.4] Balanced voice leadings are inversion-like, and balance is measured in terms of offset from inversion. This might seem more abstract and less relevant to violin scordatura. Yet inversion-related retunings have been explored by guitarists who wish to retune violins in fourths instead of fifths. In one online guitar forum, a user asks, “How would one tune a violin in fourths like a guitar without putting too much tension on the strings or too little tension? I have always tuned my violin in standard fifths GDAE, so maybe trying something like ADGC would be in fourths” (Shawn 2007). The question again recalls Lewin’s scordatura fantasy. The guitarist is looking for inversional retunings that maximize smoothness. His suggestion <A3, D4, G4, C5> corresponds to the pitch-class inversion \(I_4\). With a displacement of 8 semitones, this does not seem especially smooth. But it is, in fact, one of three maximally smooth solutions (see Example 7).
Example 8. Balance in violin scordatura
(click to enlarge)
[1.5] Inversion-like retunings appear in Johann Pachelbel’s Musicalische Ergötzung (ca. 1695; see Example 8). Both are offset by two semitones from a crisp inversion. Again, these can be understood in terms of a trade-off among different voice-leading metrics. The G-string diverges from the inversional pattern, but it moves in parallel with the D string, increasing consistency and preserving the perfect fifth between the instrument’s lowest strings. As with Biber’s Sonata 7, these scordatura involve a voice leading that is not particularly smooth. This suggests that Biber’s and Pachelbel’s goals might differ substantially from those of Lewin’s hypothetical violinist.
Example 9. Bach, Prelude from Partita no. 3 in E major (ca. 1720), BWV 1006, mm. 20–28
(click to enlarge)
Video Example 1. Spatial-network animation for Bach’s BWV 1006 Prelude, mm. 20–28, showing smooth along-string voice leading
(click to watch video)
[1.6] While Straus’s voice-leading criteria can be applied to retuning, they can also illuminate moves in the instrumental space of the fingerboard. These voice leadings involve positions on the instrument, which represent pitches indirectly (see De Souza 2018, 5–6). Any position on the fingerboard can be represented via an ordered pair of integers. These ordered pairs take the form (f, s), where f refers to finger position and s to string. By convention, higher-pitched strings take lower numbers (i.e., for a violin in standard tuning, string 1 is the E string, string 2 is the A string, etc.). All of this recalls transformational models of the fretboard (De Souza 2018; Koozin 2011; Rockwell 2009), yet one adaptation is useful here. On a guitar, distances among frets correspond well to distances among fingers. But because the violin fingerboard is shorter and continuous, a finger typically covers both natural and inflected versions of a given note name. ”Second position” on the D string, for example, can be anchored on either F4 or
[1.7] In the two-dimensional space of the fingerboard, “voices” may move along or across the strings. For example, smooth motion along the strings appears in the prelude from J. S. Bach’s Partita in E major for Unaccompanied Violin (see Example 9, Video Example 1). From mm. 20–28, each change has a displacement of 1. Later in the prelude (mm. 70–78), this passage recurs one string lower: this involves minimal displacement in the cross-string dimension, via the transposition \(T_{(0, +1)}\). (With standard tuning, the cross-string move always sounds a perfect fifth. With scordatura, though, that instrumental move might correspond to various sounding intervals.) Clearly this transposition, unlike the along-string moves in mm. 20–28, is also completely uniform.
Example 10. (a) Excerpt from Krenek, Sonata no. 1 for Solo Violin, op. 33 (1925); (b) event network, emphasizing finger inversion
(click to enlarge)
Video Example 2. Spatial-network animation for excerpt from Krenek, Sonata, op. 33 (performed by the author)
(click to watch video)
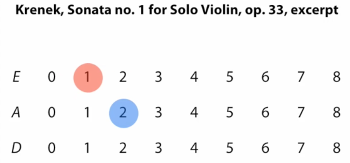
[1.8] As a final illustration, let us briefly consider a more complex example of instrumental voice leading from the solo violin repertoire. A gesture from Ernst Krenek’s Sonata for Solo Violin, op. 33, involves a series of double stops (see Example 10a). Though the sounding intervals vary, its instrumental shapes repeatedly feature the fingerboard intervals \((-1, -1)\) and \((+1, -1)\) (see Example 10b and Video Example 2). These diagonal shapes are related via along-string or finger-space inversion, fIn (see De Souza 2018, 25). (Similar to pitch-class inversion, finger numbers here sum to a relevant index number.) Until the final leap, most progressions are fairly smooth. The first three moves are relatively uniform, with an across-string transposition and two near-transpositions (with an offset of 1); the last two are completely balanced. This helps to clarify some performative aspects of the passage. First, the open-string dyad stands out. For the player, it can feel like an interpolation: the fingers “take a breath” as the bow changes strings, and then continue their inversional trading. Indeed, the finger positions that precede and follow the open-string dyad are related by inversion, just like those that close the gesture. The process of finger-switching, then, starts on a downbow at the notated crescendo, and the preceding sixteenth notes, with their transpositional relation to the following shape, function as a kind of upbeat (even in this non-metrical context). The leap that closes the gesture both continues and varies the sequence. It is completely balanced but much less smooth. This divergence between two of Straus’s voice-leading metrics sheds light on the leap’s performative and rhetorical effect. To summarize, uniformity, smoothness, and balance form a productive set of theoretical tools because they highlight different aspects of a given voice leading, which might converge or diverge.
2. Biber’s Scordatura
Example 11. Scordatura for Mystery Sonata 11, with crossed strings (Wikimedia Commons)
(click to enlarge)
[2.1] The religious illustrations in Biber’s manuscript have often been taken as a hermeneutic key to his unusual tunings. The tense, tortured scordatura for Sonata 7, mentioned earlier, is only one example. Sonata 6 represents another sorrowful mystery, the Agony in the Garden, through a relatively dissonant tuning <
Example 12. Tunings from Biber’s Mystery Sonatas, arranged according to their distance from standard tuning
(click to enlarge)
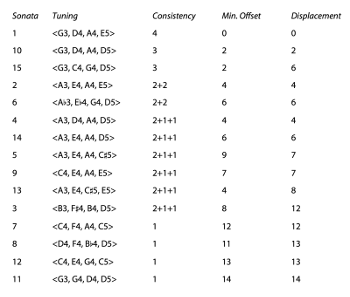
[2.2] Transformational interpretations, then, complement hermeneutic ones. They help to reveal characteristics of individual sonatas but also relations among them. In general, how uniform are Biber’s retunings? And how smooth? Example 12 presents the scordatura for all of the Mystery Sonatas and measures their distance from standard tuning. Uniformity here is measured in two ways: first, in terms of consistency, and second, in terms of minimum offset from a crisp transposition. (For several scordatura, the minimum offset is obtained at more than one transposition level.) Smoothness is simply measured via displacement. Displacement is equivalent to the offset from T0, so this value sometimes converges with minimum offset. For this collection of tunings, minimum offset and displacement are strongly and significantly correlated (\(r\ (13) = .91, p < .001\)). Mean minimum offset is 6.8 semitones (SD = 4.296), and mean displacement is 7.6 semitones (SD = 4.323). According to both metrics, the scordatura for Sonata 11 <G3, G4, D4, D5> is furthest from standard tuning—even though it leaves the pitch of the lowest string unaltered.
[2.3] Consistency also correlates with lower minimum offset and less displacement. Compared with minimum offset, consistency might seem to be an inferior measure of uniformity. Certainly, for Straus, “offset provides certain systematic advantages, particularly in its relationship to the notion of displacement” (2003, 316). Consistency produces a smaller range of values (for present purposes, from 1 to 4), because it maxes out at the total number of voices. Moreover, the counting becomes complicated with split transformations, when the voices move in pairs. A voice leading’s consistency, then, cannot fully be communicated by a single number because of an implicit remainder that might also exhibit consistency. As such, Example 12 distinguishes between consistency values of 2+2 and 2+1+1. (With four voices, 3 always implies 3+1, and 1 implies 1+1+1+1.) With scordatura, however, consistency has a practical benefit: this measure shows how many strings move together (i.e., how many inter-string relations are preserved).
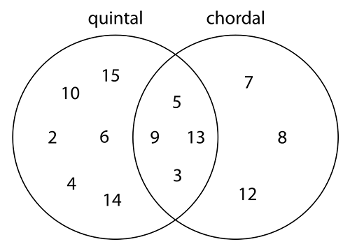
Example 13. Venn diagram categorizing scordatura from the Mystery Sonatas as quintal or chordal
(click to enlarge)
[2.4] When Biber’s tunings are ordered by consistency and then displacement (breaking ties), two main categories emerge: quintal scordatura and chordal scordatura. Quintal tunings involve at least one perfect fifth between adjacent strings. For example, the tuning for Sonata 15 <G3, C4, G4, D5> involves two adjacent fifths. With chordal tunings, all of the strings form a major or minor triad—as in the F-major tuning for Sonata 7. Sonata 5’s scordatura <A3, E4, A4,
[2.5] In a maximally quintal tuning, all three adjacent-string pairs are tuned to perfect fifths—and this, of course, simply describes standard violin tuning and transpositions thereof. Sonata 1 does use standard tuning, taking it as a point of departure for the collection. Biber’s manuscript explicitly indicates this tuning, just as it shows the scordatura for the sonatas that follow. His notation thus directs attention to an aspect of the instrument that is usually invariant and easily overlooked.
Example 14. Transposed passages with repeated fingering in sonatas whose scordatura include two adjacent perfect fifths
(click to enlarge)
[2.6] Biber’s other quintal tunings preserve familiar correspondences between notation, action, and sound, but only in certain zones. Four of the Mystery Sonatas include two adjacent-string perfect fifths: Sonata 2 <A3, E4, A4, E5>, Sonata 6 <
Example 15. Biber, Mystery Sonata 10, Variations, mm. 41–50. Fifths occur between strings 2 and 3, and strings 3 and 4
(click to enlarge and see the rest)
Video Example 3. String zones and tonal areas in Biber, Mystery Sonata 10, Variations, mm. 41–50
(click to watch video)
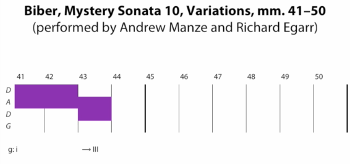
[2.7] By contrast, other sonatas with double-quintal scordatura highlight their non-normative cross-string interval. Sonata 10 closes with a set of variations on a binary-form aria in G minor, and its final variation features string crossing across this gap (see Example 15). In the first part, repeated thirty-second notes on the highest string, tuned to (D5), provide a background for the A string’s slower line. The pattern briefly steps down in cross-string space (m. 43), then reappears on the original string pair for the PAC in III that closes the first part (m. 44, see Video Example 3). The second part starts in new territory, with rapid three-string arpeggios that exclude the detuned top string. But Biber returns to the top string (end of m. 46), involving it in both of the variation’s string-crossing patterns. As the final cadence approaches, the three-string pattern is integrated with the starting position in cross-string space, in a passage with smooth along-string voice leading and fixed string crossing. (To maintain this cross-string pattern throughout, violinists might choose to play D4 in mm. 45–46 on the G string, not as an open string.) Except for the final close-position chord, all of the notes in this variation could be played in standard tuning—but its string crossing, which relies on the scordatura, would be lost. The variation journeys through cross-string space, much like its binary form departs from and returns to the home key. It involves tonal and instrumental excursions, which are not precisely aligned.
Example 16. Biber, Mystery Sonata 6, Lamento, mm. 28–45. Fifths occur between strings 1 and 2, and strings 3 and 4
(click to enlarge and listen)
[2.8] In longer sections, Biber seems to juxtapose contrasting instrumental zones. Consider a passage from Sonata 6’s C-minor Lamento, starting after a modulation to
Example 17. Biber, Mystery Sonata 2, final movement (complete)
(click to enlarge)
[2.9] Such interpretations can be highly suggestive, yet Biber’s juxtaposition of zones is not exclusive to the Sorrowful Mysteries. It is often involved in dramatic trajectories, though, as in the presto finale from Sonata 2 (see Example 17). This section begins with the continuo, which almost immediately modulates from A major to D major (IV). The violin enters with running sixteenth notes, a figure that uses one of the scordatura’s perfect fifths. After an echo, the figure repeats an octave higher, moved across two strings with the fingering unchanged (via the instrumental transposition T(0,-2)). As in Sonata 6, a new string-crossing idea appears with the home key’s dominant (m. 9). This initially exploits the gap between the scordatura’s fifths; then the idea appears on both fifth-related string pairs (again with repeated fingering). Finally, fifths and gap are combined in a climactic passage of triple stops (mm. 15–22). This movement, then, starts by juxtaposing separate quintal zones, then crosses and ultimately connects them. Again, a hermeneutic reading is possible: Sonata 2 corresponds to the Visitation, in which Mary visits her cousin Elizabeth, so instrumental dialogue between the string pairs might be understood in terms of a joyful meeting. Yet, though Biber was certainly interested in musical representation (and the specific religious context of Rosary devotion), such interpretations remain speculative. The central point, for present purposes, is that quintal scordatura partition the violin into distinct zones. These are salient for players, even if they are imperceptible for listeners, and they ground varied performative, tonal, and rhetorical processes.
Example 18. Open-string chords in sonatas with chordal scordatura
(click to enlarge)
[2.10] In chordal tunings, the open strings form a single major or minor triad. In the Mystery Sonatas, this is a tonic triad, except in Sonata 13 where the open strings sound the dominant. Though all of the Mystery Sonatas exploit open strings in melodic passages and multiple stops, Biber’s chordal scordatura afford triple and even quadruple stops that exclusively use adjacent open strings.(4) Only three such chords exist in fingerboard space: {(0, 1), (0, 2), (0, 3)}, {(0, 2), (0, 3), (0, 4)}, and {(0, 1), (0, 2), (0, 3), (0, 4)}. All but one of the sonatas with chordal tuning include these chords (see Example 18). They do not appear in Sonata 9, a quintal-chordal hybrid whose tuning leaves the A and E strings unaltered. (That said, Sonata 9 does feature the double stop {(0, 3), (0, 4)}.) It also bears mention that open-string triple stops appear in Sonata 4, where the quintal scordatura creates open fifths (D4, A4, D5). Nonetheless, open-string multiple stops are most characteristic of the sonatas with chordal scordatura.(5) In Sonatas 7, 8, and 12, the chordal tuning is particularly distinctive, affording close-position voicings that are impossible to play in standard violin tuning (see Example 2, m. 2.) These chords often appear in prominent moments, at the beginnings or ends of movements.
Example 19. Biber, Mystery Sonata 12, Intrada (complete)
(click to enlarge and listen)
[2.11] For Sonata 12, the open strings form a close-position C-major chord. Its Intrada starts by repeating the lowest string twenty-four times (see Example 19, Audio Example 3). The first seven measures—that is, more than half of the thirteen-measure movement—involve only open-string pitches, with the only stopped note doubling the highest string. As it moves through the triad, rocking back and forth across the strings, the fanfare topic becomes clear. This scordatura <C4, E4, G4, C5> recreates a sequence of harmonics from a valveless brass instrument (i.e., harmonics 4, 5, 6, and 8).(6) The trumpets have clear representational significance, heralding Jesus’s ascension to heaven. The bright, repeated open strings return in the Intrada’s final measures. Biber continues with an Aria Tubicinum, accompanied by solo violone, in which the violin imitates a pair of trumpets. In Sonata 12, then, the chordal scordatura aligns with the valveless trumpet’s idioms, evoking their distinctive tonal constraints and social functions. The piece references another instrument, even as it revels in the violin’s open strings.
Example 20. Biber, Mystery Sonata 8, Gigue (complete)
(click to enlarge and listen)
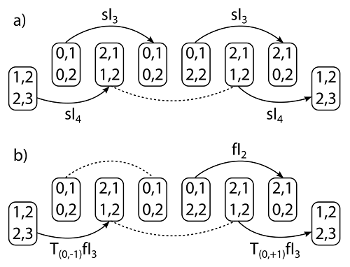
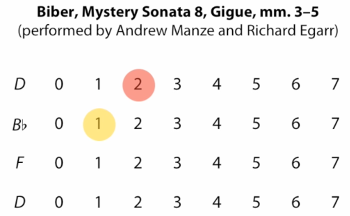
[2.12] In Sonata 8, the open strings might be less obvious for listeners—but for the violinist, they can feel like anchor points or centers of gravity. Its gigue builds finger patterns above the open strings and returns to them (see Example 20, Audio Example 4). These dancing double stops are engaged in instrumental inversion. With cross-string inversions (sIn), for example, finger positions remain unchanged, while string positions exchange (see De Souza 2018, 25–26). These inversionally related finger shapes are interspersed with open strings (see Example 21, Video Example 4). Note that the open strings sound tonic harmony in metrically strong positions and are supported by
Example 21. Event networks for Mystery Sonata 8, mm. 3–5 (with upbeat) (click to enlarge) | Video Example 4. Spatial-network animation for Biber, Mystery Sonata 8, Gigue, mm. 3–5 (click to watch video) |
Example 22. Biber, Mystery Sonata 11, mm. 6–10
(click to enlarge and listen)
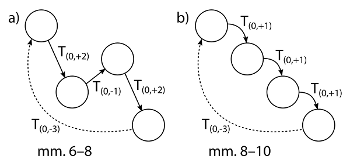
[2.13] Only one sonata has a scordatura that is neither quintal nor chordal: Sonata 11 <G3, G4, D4, D5>, with its crossed strings. Though this might be understood in terms of an incomplete G triad, the defining feature of this tuning is arguably its adjacent-string octaves. Near the beginning of the sonata, Biber repeats a simple 3–2–1–0 finger pattern on each string.(8) Though the string crossings interlock, this produces a descending scale (see Example 22, Audio Example 5). After an echo, Biber notates a descending scale. This written pattern nearly matches what has just been heard, but of course, the resulting melody does not simply descend (though it descends in cross-string space; see Example 23). The adjacent-string octaves are perhaps most prominent in Sonata 11’s central movement. Here the violin presents the Easter carol “Surrexit Christus hodie” in parallel octaves, notated as parallel fifths (see Example 24, Audio Example 6). Each fifth is played with a single finger, which simultaneously stops two strings. These adjacent-string octaves form a useful compositional and performative resource for Biber.
Example 23. Transformation graphs for the 3–2–1–0 finger pattern in Mystery Sonata 11, mm. 8–10 (click to enlarge) | Example 24. Biber, Mystery Sonata 11, mm. 112–21 (click to enlarge and listen) |
Video Example 5. Spatial-network animation for Biber, Mystery Sonata 10, Prelude, mm. 16–19
(click to watch video)
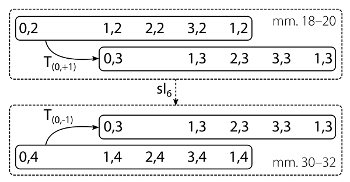
[2.14] Note, however, that nearly all of Biber’s scordatura feature octave-related strings. The only exception is the dissonant tuning for Sonata 6. Sonatas 2 and 4, like Sonata 11, have two octave-related pairs. In the Mystery Sonatas, octave-related strings appear at all possible distances in fingerboard space: one string apart (Sonata 11); two strings apart (Sonatas 2, 3, 4, 5, 9, 10, 13, 14, and 15); and between the outer strings (Sonatas 7, 8, 12). In the second situation, when a third string appears in the middle of the octave-related pair, Biber again explores cross-string inversions. This appears, for example, in the triple stops that end Sonata 10’s Prelude. These chords involve the highest three strings, which are tuned to D4, A4, and D5. As the pattern repeats, the fingering on the A string remains constant, while the high and low D strings trade fingering via sI4 (see Video Example 5). Again, this instrumental transformation is closely related to the tuning’s pitch affordances.
Example 25. Biber, Mystery Sonata 13, Prelude, mm. 12–21
(click to enlarge and listen)
Example 26. Biber, Mystery Sonata 2, first movement: (a) mm. 17–20; (b) mm. 31–34, with upbeat
(click to enlarge and listen)
Example 27. Network for points of imitation in Example 26, showing invertible counterpoint with cross-string inversion
(click to enlarge)
[2.15] Though cross-string inversions are clearest when three strings are involved, they also appear in passages with double and quadruple stops. The scordatura for Sonata 13 <A3, E4,
[2.16] Biber also uses cross-string inversions in contrapuntal settings. In the first movement of Sonata 2, a contrapuntal presto follows a lyrical prelude. The keyboard and then the violin introduce a short subject with an answer in stretto (see Example 26, Audio Example 8). On the violin, subject and answer have the same fingering, starting from the open second and third strings, respectively.(10) Fragments of the subject appear on the third and first strings in the following episode, which arrives at a HC at the presto’s midpoint (m. 30). The violin then returns to the subject/answer pair. This time, however, the passage has been recast via cross-string inversion (see Example 27). The subject and answer again have the same fingering, but the subject appears on the fourth string instead of the second, below the answer instead of above it. In such cases, Biber combines a kind of instrumental inversion with invertible counterpoint.
[2.17] Biber’s scordatura, then, are designed to afford particular sounding intervals—perfect fifths, triads, and octaves—at particular cross-string distances. These divide the violin into zones, some familiar and some strange, arranging the strings in pairs (2+2), a trio with a singleton (3+1), or a whole quartet. Metrics derived from transformational voice leading help to quantify each scordatura’s distance from standard tuning, to reveal broader categories, and to support analysis of interactions between scordatura and performative transformations. Such analysis, in the spirit of Lewin’s transformational attitude, takes up a position “within” the music (Lewin 1987, 159). It foregrounds a certain “occupational context” that grounds violinists’ embodied acts of perception (Lewin 1986, 359, 382). Yet theoretical distance from standard tuning, however illuminating, does not necessarily correspond to discomfort in players’ experience. And with this aspect of the Mystery Sonatas, transformational theory can be complemented by cognitive science.
3. Performance and Prediction
[3.1] Biber’s instrumental transformations afford particular experiences for the player, which can be historicized in terms of seventeenth-century Catholicism. For example, the sonatas can be understood as meditations that engage bodily senses, akin to the Spiritual Exercises of Ignatius of Loyola, the founder of the Jesuit order (Strand-Polyak 2013, 114–16).(11) Biber would have been aware of these exercises: his patron, Archbishop Maximilian Gandolph von Kuenburg, had received a Jesuit education, and the composer himself was associated with the Jesuit College in Opava, Moravia (Giles 2018, 78). Jesuit curricula also included theories about perception, influenced by the thirteenth-century scholastic Thomas Aquinas (Farrell 1970). For Aquinas, humans come to know the divine by “moving from what is familiar to what is unknown and unfamiliar” (Summa Theologiae III, q. 60, a. 2, quoted in Giles 2018, 68). He developed an influential pre-Cartesian psychology in which body and mind are unified and perception is essentially active. Arguably, this account is consonant with twenty-first-century perspectives on embodiment and action (Freeman 2008; cf. Cummins 2019), which can offer insights about what it feels like to play in Biber’s various tunings.
Example 28. Basic predictive processing schema
(click to enlarge)
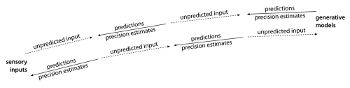
[3.2] One relevant cognitive-scientific paradigm is presented in Andy Clark’s Surfing Uncertainty: Prediction, Action, and the Embodied Mind (2016). The predictive processing paradigm integrates body, mind, and world. Though the brain involves complex, multilinear connections, it can be understood, very schematically, in terms of two main flows: a “top-down” flow involves predictions about the environment and one’s own actions, based on context and prior experience; meanwhile, a “bottom-up” flow transmits error signals that reflect unpredicted (and thereby, informative or newsworthy) sensory inputs (59; see Example 28). These flows intertwine in a kind of circular causality. The key thing is the dynamic balancing of top-down predictions and bottom-up errors, which Clark describes as a “delicate dance” (57). Sensory input can be adjusted through self-movement or the use of external technologies, in keeping with Clark’s earlier work on cognitive extension (e.g., Clark 2008). But the top-down/bottom-up balance is also modulated via “precision estimates,” which are probabilistic estimates of certainty or uncertainty.(12) In uncertain situations, sensory inputs are more heavily weighted. And when predictions are confident, unpredicted error is more surprising. To take a familiar music-theoretical example, harmonic predictions following a dominant chord are likely more precise than those following a major tonic. A subsequent
[3.3] Predictive processing, of course, largely takes place at an unconscious level. “The [predictive processing] suggestion is not that we experience our own prediction error signals (or their associated precisions) as such,” Clark explains. “Instead, those signals act within us to recruit the apt flows of prediction that reveal a world of distal objects and causes. Persistent unresolved prediction error signals may, however, yield amorphous feelings of ‘salient strangeness’” (207). It is important, then, to distinguish between neurocomputational prediction and conscious expectation, between “surprisal” (neural-surprise) and agent surprise (25, 78). But these are also related in various ways, and a kind of phenomenological description is part of Clark’s argumentative toolkit.
[3.4] Surfing Uncertainty uses predictive processing to interpret diverse psychological phenomena, including attention, imagination and dreaming, self-tickling, mental time travel, schizophrenia, autism, and various perceptual illusions. This paradigm can also help make sense of research on altered auditory feedback. Such research—like Biber’s scordatura—involves instrumental modifications that manipulate the relation between sound and action (see De Souza 2017, Ch. 4; Pfordresher 2019). In one experiment, keyboardists played two-part inventions by J. S. Bach (Finney 1997). Performance was impaired when auditory feedback was delayed by 250 milliseconds. But when participants played a silent keyboard—or a keyboard that produced random pitches without any delay—performance did not significantly differ from the normal-feedback condition. A later study again manipulated pitch feedback but not timing: pressing a key would sometimes produce a pitch from earlier or later in the melody that participants were attempting to play (Pfordresher and Palmer 2006). And this pitch alteration did compromise fluent performance.
[3.5] The predictive processing model suggests nuanced explanations for these effects. Under normal conditions, instrumental performance combines auditory, motor, and visual channels, in a network of top-down, bottom-up, and lateral connections. Predictions often work as self-fulfilling prophecies here: that is, expert performers predict a certain outcome, and then act to realize it. Their predictions, moreover, tend to be highly precise or confident, because of overlearned multisensory connections that respond to an instrument’s stable affordances (see De Souza 2017, Ch. 1). When these predictions are successful, error is low and bottom-up feedback is uninformative, so attention can turn to higher-level goals. This would support the experience that Martin Heidegger calls “withdrawal,” in which a player can focus not on body–instrument interaction per se but on “the music” (De Souza 2017, 20–22).
[3.6] Delayed feedback violates the temporal binding of action and effect. This creates an ongoing series of predictive errors that are difficult to tune out, partially because they violate a systematic “hyperprior” involving causal relations, learned in infancy or possibly innate (Clark 2016, 174–75; see also, Pfordresher 2019, Ch. 3). With a silent keyboard, by contrast, the flow of auditory feedback is simply shut off. If that flow mainly transmits error signals (which, for experts, are relatively uninformative), then it is not surprising that performance can proceed, with compensation from successful top-down predictions.(15) The random-pitch keyboard fills this same channel with noise. In response, the brain loses confidence and reduces the channel’s weight, effectively turning down the volume for that stream. When altered pitch feedback includes early or late notes, however, expected notes appear in unexpected places. This is harder to ignore, because those notes have high-level salience. The bottom-up feedback relates to top-down predictions and is mostly accurate, which maintains a certainty that makes the experimentally induced error signals all the more important. This kind of pitch alteration, then, resembles a scammer who embeds a key piece of disinformation within an otherwise trustworthy source. Its mechanism for disrupting performance differs substantially from delayed or random feedback.
Example 29. Hypothetical inverted-U function relating surprisal to distance from standard tuning
(click to enlarge)
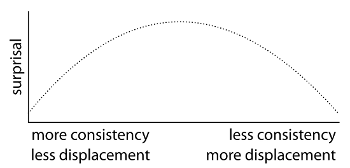
[3.7] To some degree, these results are keyboard specific. With string playing (relative to piano playing), error signals are more important for ongoing pitch control. For example, expert cellists’ fingers drift when they finger a melody without bowing (Chen et al. 2013). Still, it is possible to extrapolate, somewhat speculatively, to Biber’s scordatura. The theory of predictive processing and results from auditory-feedback experiments suggest, perhaps counterintuitively, that Biber’s scordatura are most unsettling or stimulating when they preserve elements of standard violin tuning. In this context, metrics from transformational voice-leading theory represent not only the distance from standard tuning but also the mismatch between a violinist’s established priors and sensory results. As retunings become less consistent and involve greater displacement, error signals for cross-string intervals will increase—but precision-weighting also decreases. At some point, this lack of certainty should attenuate surprisal, weakening the scordatura’s effects (as it did with the random keyboard). Levels of surprisal with Biber’s scordatura might correspond to an inverted-U function, which also characterizes affective responses to syncopation and expressive microtiming (Example 29; see also Schaefer, Overy, and Nelson 2013). Chordal scordatura, then, might be objectively “further” from standard tuning. But quintal scordatura would maintain higher levels of surprisal, more directly engaging and destabilizing players’ habits. Quintal scordatura, that is, would give rise to a kind of prediction error that is harder to ignore. In phenomenological terms, they would block withdrawal and set up moments of breakdown or “presence-to-hand” (De Souza 2017, 83), in which players become aware of their own bodily performance.
[3.8] Of course, individual players’ predictions and precisions will vary, being dynamic and highly mediated by context and culture. With practice, a violinist might become familiar with a particular scordatura. Normalization of a new tuning, however, might be hindered by the overwhelming emphasis on standard tuning in prior training, the juxtaposition of different scordatura, and the one-to-one association of a tuning with a single sonata. This last point seems crucial, in light of research with artificial musical grammars: when listeners repeatedly hear a small number of melodies, they do not develop generalized expectations for the new tonal system; generalization emerges, however, when they hear hundreds of these melodies (Loui, Wessel, and Hudson Kam 2010). Similar empirical tests might be conducted to probe these admittedly speculative arguments about scordatura and prediction.
Example 30. Biber, Mystery Sonata 5, Sarabande-Double, mm. 1–10
(click to enlarge)
[3.9] In the meantime, these suggestions from predictive processing align with my own lived experience as a performer of Biber’s sonatas. Consider the first section of the Sarabande-Double from Sonata 5 (see Example 30). The scordatura here is both quintal and chordal, and its mapping from standard tuning combines moderate consistency and near-average displacement. The movement begins on the bottom strings, which retain a perfect fifth from standard tuning, so I feel comfortable in “G” major. This makes it all the more striking when I finger a G arpeggio that turns into a stepwise figure (m. 5)—or a B–G sixth that gives a half cadence, not an authentic cadence (m. 10). These are moments when I am more likely to make a mistake. They jump out at me in performance, even though I know the piece well. Though I can sing the melody, the notation remains important. If I become overconfident and look away from my part, my fingers do not know what to do. They want to realize the melody in standard tuning, and I find myself off-balance, disoriented, reawakened to my instrument, my body, my spirit.
Conclusions
[4.1] The Mystery Sonatas can be understood as a treatise on scordatura, a research project akin to Lewin’s theoretical fantasy. They reveal several kinds of instrumental transformation. First, Biber transforms the violin itself, adjusting the instrument’s organization and affordances. Second, he composes distinctive performative patterns, instrumental transformations that the violinist enacts. While the music reflects a late seventeenth-century tonal idiom, its instrumental features are not reducible to it. Instrument and idiom co-evolve, in an example of “circular causality.” Biber both responds to the instrument and redefines it.
[4.2] Similar transformations emerge, more or less independently, in other violin traditions. Many jazz violinists improvise passages with cross-string parallel fifths, as in Sonatas 11 and 13. And several of Biber’s tunings (or their equivalents) are used by fiddlers in Ireland, Scotland, Norway, Canada, and the United States (Haigh n.d.; Perlman 1996, 26; Thede 1967, 17–18). For example, the tuning for Sonata 5, mentioned in the preceding section, is known in Appalachian circles as “Calico” or “Black Mountain” tuning, and in Norway as “Nackastamning.” According to fiddle expert Chris Haigh (n.d.), Norwegian fiddlers view it as “the devil’s own tuning.” “Such is the hypnotic nature of this tuning,” Haigh reports, “that players can go into a trance and may have to have the fiddle dragged from their hands after hours of playing; alternatively, the devil himself may show up at the dance, grab the fiddle and play until the guests are dead from exhaustion.” Though the context differs significantly from the devotions of the Salzburg Rosary Confraternity, this legend again gives scordatura a certain supernatural power and associates it with altered states of consciousness.
[4.3] The Mystery Sonatas, similarly, transform the violinist, in a process that can be understood via Thomist theology, phenomenology, or recent cognitive science. They recall a paradoxical relation between sound, embodiment, and spirituality that Braxton Shelley observes in African-American gospel performance, where “intensified physicality actually loosens the believer’s relation to the material world, enhancing his or her connection to what is often called ‘the spiritual realm’” (2019, 186). While the religious scenes in Biber’s manuscript can guide musical interpretation, they are also brought to life in performance—a kind of performance that, for Biber and his contemporaries, was both musical and devotional. The retuned violin thus opens up new ways of knowing, feeling, and experiencing the world. To change one’s instrument, ultimately, is to change oneself.
Jonathan De Souza
Western University
Don Wright Faculty of Music
Talbot College
London, ON N6A 3K7
Canada
jdesou22@uwo.ca
Works Cited
Barnett, Gregory Richard. 2008. Bolognese Instrumental Music, 1660–1710: Spiritual Comfort, Courtly Delight, and Commercial Triumph. Ashgate.
Bungert, James. 2015. “Bach and the Patterns of Transformation.” Music Theory Spectrum 37 (1): 98–119. https://doi.org/10.1093/mts/mtv003.
Chafe, Eric. 1987. The Church Music of Heinrich Biber. UMI Research Press.
Chen, Jessie, Marjorie Woollacott, Steve Pologe, and George P. Moore. 2013. “Stochastic Aspects of Motor Behavior and Their Dependence on Auditory Feedback in Experienced Cellists.” Frontiers in Human Neuroscience 7: 419. https://doi.org/10.3389/fnhum.2013.00419.
Cheung, Vincent K. M., Peter M. C. Harrison, Lars Meyer, Marcus T. Pearce, John-Dylan Haynes, and Stefan Koelsch. 2019. “Uncertainty and Surprise Jointly Predict Musical Pleasure and Amygdala, Hippocampus, and Auditory Cortex Activity.” Current Biology 29 (23): 4084–92. https://doi.org/10.1016/j.cub.2019.09.067.
Clark, Andy. 2008. Supersizing the Mind: Embodiment, Action, and Cognitive Extension. Oxford University Press. http://dx.doi.org/10.1093/acprof:oso/9780195333213.001.0001.
—————. 2013. “Whatever next? Predictive Brains, Situated Agents, and the Future of Cognitive Science.” Behavioral and Brain Sciences 36 (3): 1–73. https://doi.org/10.1017/S0140525X12000477.
—————. 2016. Surfing Uncertainty: Prediction, Action, and the Embodied Mind. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780190217013.001.0001
Colombo, Matteo, Elizabeth Irvine, and Mog Stapleton, eds. 2019. Andy Clark and His Critics. Oxford University Press. https://doi.org/10.1093/oso/9780190662813.001.0001.
Cook, Nicholas. 1998. Analysing Musical Multimedia. Clarendon Press.
—————. 2013. Beyond the Score: Music as Performance. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199357406.001.0001.
Cummins, Fred. 2019. “Audition as Sense-Making, and its Contribution to the Shared Human Lifeworld.” Keynote presented at the Conference on Interdisciplinary Musicology, Graz.
Cusick, Suzanne G. 1994. “Feminist Theory, Music Theory, and the Mind/Body Problem.” Perspectives of New Music 32 (1): 8–27. https://doi.org/10.2307/833149.
De Souza, Jonathan. 2017. Music at Hand: Instruments, Bodies, and Cognition. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780190271114.001.0001.
—————. 2018. “Fretboard Transformations.” Journal of Music Theory 62 (1): 1–39. https://doi.org/10.1215/00222909-4450624.
Finney, Steven A. 1997. “Auditory Feedback and Musical Keyboard Performance.” Music Perception 15 (2): 153–74. https://doi.org/10.2307/40285747.
Farrell, Allan P., trans. 1970. The Jesuit Ratio Studiorum of 1599. Conference of Major Superiors of Jesuits. https://www.bc.edu/sites/libraries/ratio/ratio1599.pdf.
Freeman, Walter. 2008. “Nonlinear Brain Dynamics and Intention According to Aquinas.” Mind and Matter 6 (2): 207–34.
Giles, Roseen. 2018. “Physicality and Devotion in Heinrich Ignaz Franz Biber’s Rosary Sonatas.” Yale Journal of Music & Religion 4 (2): 68–104. https://doi.org/10.17132/2377-231X.1105.
Haigh, Chris. n.d. “Cross-Tuning/Scordatura on the Fiddle.” Fiddling Around the World (website). Accessed November 1, 2019. http://fiddlingaround.co.uk/cross%20tuning.html.
Harrison, Daniel. 2016. Pieces of Tradition: An Analysis of Contemporary Tonal Music. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780190244460.001.0001.
Hatten, Robert S. 1994. Musical Meaning in Beethoven: Markedness, Correlation, and Interpretation. Indiana University Press.
Holman, Peter. 1994. “Mystery Man: Peter Holman Celebrates the 350th Anniversary of the Birth of Heinrich Biber.” The Musical Times 135 (1817): 437–41. https://doi.org/10.2307/1003253.
Huron, David, and Caitlyn Trevor. 2016. “Are Stopped Strings Preferred in Sad Music?” Empirical Musicology Review 11 (2): 261–69. https://doi.org/10.18061/emr.v11i2.4968.
Koelsch, Stefan, Peter Vuust, and Karl Friston. 2019. “Predictive Processes and the Peculiar Case of Music.” Trends in Cognitive Sciences 23 (1): 63–77. https://doi.org/10.1016/j.tics.2018.10.006.
Koozin, Timothy. 2011. “Guitar Voicing in Pop-Rock Music: A Performance-Based Analytical Approach.” Music Theory Online 17 (3). https://doi.org/10.30535/mto.17.3.5.
Le Guin, Elisabeth. 2006. Boccherini’s Body: An Essay in Carnal Musicology. University of California Press. https://doi.org/10.1525/9780520930629.
Lewin, David. 1986. “Music Theory, Phenomenology, and Modes of Perception.” Music Perception 3 (4): 327–92. https://doi.org/10.2307/40285344.
—————. 1987. Generalized Musical Intervals and Transformations. Yale University Press.
—————. 1998. “Some Ideas about Voice-Leading between PCSets.” Journal of Music Theory 42 (1): 15–72. https://doi.org/10.2307/843852.
Loui, Psyche, David L. Wessel, and Carla L. Hudson Kam. 2010. “Humans Rapidly Learn Grammatical Structure in a New Musical Scale” Music Perception 27 (5): 377–88. https://doi.org/10.1525/mp.2010.27.5.377.
Perlman, Ken. 1996. The Fiddle Music of Prince Edward Island: Celtic and Acadian Tunes in Living Tradition. Mel Bay.
Pfordresher, Peter Q. 2019. Sound and Action in Music Performance. Academic Press.
Pfordresher, Peter Q., and Caroline Palmer. 2006. “Effects of Hearing the Past, Present, or Future During Music Performance.” Perception & Psychophysics 68: 362–76. https://doi.org/10.3758/BF03193683.
Quinn, Ian. 1996. “Fuzzy Transposition of Pitch Sets.” Paper presented at the Annual Meeting of the Society for Music Theory, Baton Rouge.
Rockwell, Joti. 2009. “Banjo Transformations and Bluegrass Rhythm.” Journal of Music Theory 53 (1): 137–62. https://doi.org/10.1215/00222909-2009-023.
Schaefer, Rebecca S., Katie Overy, and Peter Nelson. 2013. “Affect and Non-Uniform Characteristics of Predictive Processing in Musical Behaviour.” Behavioral and Brain Sciences 36 (3): 226–27. https://doi.org/10.1017/S0140525X12002373.
Schmid, Manfred Hermann. 2008. “Die ‘Rosenkranz-Sonaten’ von Heinrich Ignaz Franz Biber.” In Rosenkranz-Sonaten: Bayerische Staatsbibliothek München: Mus. Mss. 4123, ed. Manfred Hermann Schmid, 90–107. Strube.
Shawn. 2007. “Tuning in Fourths.” Django Books (website). http://www.djangobooks.com/forum/discussion/2933/tuning-in-fourths.
Shelley, Braxton D. 2019. “Analyzing Gospel.” Journal of the American Musicological Society 72 (1): 181–243. https://doi.org/10.1525/jams.2019.72.1.181.
Stowell. 2001. The Early Violin and Viola: A Practical Guide. New York and Cambridge: Cambridge University Press.
Strand-Polyak, Lindsey. 2013. “The Virtuoso’s Idiom: Spectacularity and the Seventeenth-Century Violin Sonata.” PhD diss., University of California Los Angeles.
Straus, Joseph N. 2003. “Uniformity, Balance, and Smoothness in Atonal Voice Leading.” Music Theory Spectrum 25 (2): 305–52. https://doi.org/10.1525/mts.2003.25.2.305.
Temperley, David. 2007. Music and Probability. MIT Press. https://doi.org/10.7551/mitpress/4807.001.0001.
Thede, Marion. 1967. The Fiddle Book. Oak Publications.
Footnotes
* An earlier version of this article was presented at the 2017 Meeting of the Society for Music Theory in Arlington, Virginia. I would like to thank Lawrence Zbikowski, Steven Rings, the journal’s anonymous reviewer, and my former violin teacher May Ing (who introduced Biber’s music to me in the 1990s).
Return to text
1. Rosary devotion involves the repetition of a sequence of short prayers, such as the Hail Mary. With this in mind, Strand-Polyak (2013, 123) notes the prevalence of repetitive forms in Biber’s sonatas: variation sets, dance movements with doubles, the ciaccona, and the passacaglia.
Return to text
2. In “Music Theory, Phenomenology, and Modes of Perception,” Lewin argues that theorists should not take listening as a “paradigmatic musical activity” (1986, 327). If “‘music’ is something you do, and not just something you perceive (or understand)” (377), then a theory of musical behavior must also encompass performance and production. Singing, playing, composing, improvising, dancing, and even analyzing are productive or “poietic” ways of engaging with music.
Return to text
3. While the present study focuses on pitch, pitch-class relations can be useful in modeling instrumental pitch mapping, particularly with tunings that involve octave displacement (see De Souza 2017, 62n20).
Return to text
4. Arguably, open strings are generally privileged in violin repertoire, even though violin players often avoid them (by choosing to play stopped notes). One corpus study of string quartet movements by Haydn, Mozart, and Beethoven suggests that these composers matched keys and musical material to make more open strings available for players (Huron and Trevor 2016).
Return to text
5. Readers with an interest in corpus studies will note that this claim can be checked via a chi-square test. The results are statistically significant, assuming an α level of .05. That is, sonatas with chordal scordatura are more likely to include open-string chords, X2(1, N = 15) = 8.04, p < .01.
Return to text
6. The distinctive affordances of valveless brass instruments, such as natural trumpets and hunting horns, gives rise to a kind of tonality that Daniel Harrison (2016, 21–23) calls “bugleity.” Their idioms, of course, are often imitated by other instruments (see De Souza 2017, Ch. 6).
Return to text
7. This upbeat gigue might seem inappropriate for Sonata 8’s sorrowful mystery, in which soldiers place a crown of thorns on Jesus’s head and mockingly call him “King of the Jews” (Matthew 27:27–30). Hermeneutic possibilities for this movement, then, are unavoidably speculative, given what Nicholas Cook (1998) would call the “contest” between the piece’s musical and narrative layers. As a celebratory dance, the gigue might already anticipate the triumph of Jesus’s resurrection. It would overcome the painful scene by framing Jesus as a true king, uncovering a theological truth in the soldiers’ abuse. Alternatively, the gigue itself might be ironic, like the soldiers’ jeering. The latter interpretation stays within the biblical scene and suggests more aggressive performance strategies. Either way, the gigue’s meaning is less secure, relative to the fanfares of Sonata 12.
Return to text
8. Giles (2018, 93) comments on notation and visual incongruence in this passage, without discussing its repeated performative actions.
Return to text
9. Given these tonal affordances (and the stable bass), it is puzzling that Strand-Polyak (2013, 130) hears “ambiguous harmonies” in this passage.
Return to text
10. Points of imitation with repeated fingering also appear in Sonata 4 (mm. 33–34, 37–38) and Sonata 15 (first movement, m. 7). Like Sonata 2, these pieces involve quintal scordatura.
Return to text
11. Giles (2018, 80–86) further links Biber’s sonatas to contemporaneous visual art related to the Rosary devotion.
Return to text
12. For Clark (2016, 301–3) and others, probabilistic aspects of predictive processing can be modeled in terms of Bayesian inference—an approach to probability that weighs both current evidence and prior beliefs. For a Bayesian approach to music cognition, see Temperley 2007.
Return to text
13. A recent empirical study of harmonic expectancy in popular music, informed by predictive processing theory, considers interactions between uncertainty and surprise: “Uncertainty is the lack of a clear expectation when anticipating an event before it is heard, while surprise occurs when what is actually heard deviates from expectations” (Cheung et al. 2019, 2). The results of this study suggest that musical pleasure is evoked by chord progressions with low uncertainty and high surprise, or high uncertainty and low surprise. For a discussion of predictive processing and groove, see Koelsch, Vuust, and Friston 2019.
Return to text
14. While the predictive processing model is founded on a wide range of empirical findings, Clark emphasizes that it is still provisional. For critiques of predictive processing, see the responses in Clark 2013, and Colombo, Irvine, and Stapleton 2019.
Return to text
15. As Pfordresher (2019, Ch. 2) notes, auditory feedback is essential for learning, though less important for expert performance.
Return to text
Copyright Statement
Copyright © 2020 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
11402