A Transformational Approach to Gesture in Shō Performance*
Toru Momii
KEYWORDS: gagaku, tōgaku, shō, aitake, te-utsuri, transformational theory, gesture, performance, fingerings, tonal function, parsimony
ABSTRACT: Through an analysis of contemporary shō performance practice, this article explores the relationship between instrumental gesture and modal theory in contemporary gagaku. I demonstrate that the idiosyncratic arrangement of the pipes on the shō is closely related to the pitch structure and tonal function of the aitake pitch clusters.
My analysis synthesizes two approaches. First, I adopt David Lewin’s (1987) transformational attitude to conceptualize the aitake not as static musical objects but as processes of motion enacted by the te-utsuri—standardized fingering movements for shifting between two aitake. Second, I treat the aitake as sonic byproducts of a performer's instrumental gestures to examine how the aitake are related to one another kinesthetically, and whether these relationships correlate with the pitch structures of the aitake.
I argue that relatedness between aitake is determined by the parsimony of te-utsuri. The most parsimonious movements can be enacted between four aitake: bō, kotsu, ichi and otsu. These aitake are identical to the clusters that accompany the fundamental tones of five of the six modes: Ichikotsu-chō, Hyōjō, Taishiki-chō, Oshiki-chō and Banshiki-chō. These findings demonstrate that the pipes of the shō, while seemingly arranged in no discernable order, prioritize parsimonious te-utsuri between each of the aitake accompanying the fundamental modal degrees. An analysis of the pitch structure of aitake through the lens of te-utsuri reveals a striking correlation between gestural parsimony and tonal function.
DOI: 10.30535/mto.26.4.4
Copyright © 2020 Society for Music Theory
[1.1] Post-war scholars have challenged the conceptualization of gagaku (雅楽) as a musical practice that has been largely unchanged since its importation into Japan in the eighth century, engaging in comparative analyses of historical and contemporary melodies in tōgaku (唐楽)—a genre of gagaku (雅楽) court music that originated in Tang China.(1) Through studies of historical notation, initial research undertaken by Hayashi Kenzō and Laurence Picken’s Tang Music Project in the mid-twentieth century has identified a disjuncture between modern tōgaku and its predecessors (Hayashi 1969; Picken et al. 1981, 1985, 1986, 1987, 1990, 1997, 2000).(2) Building upon their work, more recent studies have sought to reconstruct and decipher scores from the Heian period (794–1185) (Endō 2005; Nelson 1986, 1988; Ng 2017; Terauchi 1996), trace the historical modification of tōgaku melodies (Endō 2004; Marett 1985, 1986; Ng 2011; Terauchi 1993; Tsukahara 2009), and examine similarities and inconsistencies between contemporary Japanese practice and Chinese theories of mode (Gamō 1970; Hayashi 1954; Masumoto 1968; Ng 2007; Ono 2016; Terauchi 2011).
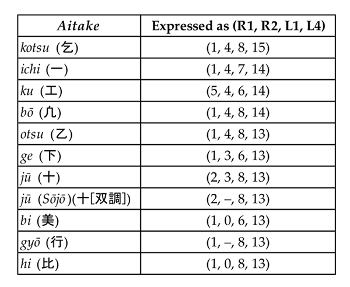
[1.2] While this monumental body of research has been invaluable for tracing the historical development of tōgaku and dismantling the characterization of gagaku as a timeless tradition carefully preserved over centuries, few existing studies have examined the relationship between modal theory and performance practice in contemporary tōgaku, a concern that has been raised by Robert Garfias (1975) and Terauchi Naoko (2007). In particular, Garfias has suggested that the aitake (合竹)—five- and six-note pitch clusters played by the shō (笙) in tōgaku repertoire—can illuminate our understanding of how performance practice and theory interact with one another. Aitake is produced by covering five or six of the shō’s seventeen pipes, and sound can be generated by either inhaling or exhaling into the mouthpiece. For Garfias, the aitake is essential for understanding the principles of modality in gagaku:
Ordinarily, discussions of theory in the traditional sources in Chinese and Japanese limit themselves to the consideration of scale and modal structures. These subjects have provided fodder for the theorists for hundreds of years and have enabled them to ensconce themselves in the complexities of theory while comfortably avoiding the problems of defining practice. One of these neglected aspects of practice, the harmonic structure executed by the mouth organ, shō, provides a convenient link between theory and practice. (1975, 63)
Using Garfias’s hypothesis as a starting point, this article explores the relationship between the performer’s instrumental gestures—physical movements necessary for generating sound from an instrument (Montague 2012)—and modal theories of tōgaku. Through an analysis of te-utsuri (手移り), the standardized ordering of fingerings to move from one aitake to another, I demonstrate that the idiosyncratic arrangement of the pipes on the shō is closely related to the pitch structure and function of the aitake.
[1.3] This article, inspired in part by my experience as a member of the Columbia University Gagaku Ensemble, synthesizes two approaches.(3) First, I adopt David Lewin’s (1987) transformational attitude to conceptualize the aitake not as static musical objects but as processes of motion enacted by the te-utsuri. Transformational theory offers a particularly fruitful framework for theorizing the role of te-utsuri in connecting each of the aitake. I draw upon Lewin’s oft-cited question “I am at s; what characteristic transformation do I perform in order to arrive at t?” (xxxi) to conceptualize te-utsuri as an operator of musical transformation, focusing on the process of change between the aitake rather than the distance between them. A transformational perspective therefore situates performers “inside the music,” in the words of Lewin (159). Rather than observing the distance between two static musical objects, a performer experiences the motion from one hand position to another when acting out the te-utsuri movements to arrive at the new aitake. As such, transformational theory offers an ideal methodology for demonstrating how pitch structures and bodily gestures are intertwined in contemporary shō performance.
Example 1. Parts of the shō
(click to enlarge)
Video Example 1. The shō
(click to watch video)
[1.4] Second, by treating the aitake as sonic byproducts of a performer’s instrumental gestures, my analysis examines how each of the aitake is related to the others kinesthetically, and the ways in which these physical relationships correlate with the pitch structures of aitake. A transformational analysis of te-utsuri quantifies the motion between aitake in two ways: 1) the number of finger holes a performer must traverse to get from one aitake to another; and 2) the number of fingers that are in motion. The first part of the article argues that relatedness between different aitake is determined by the gestural proximity of te-utsuri—as opposed to that of voice leading in pitch space.(4) This framework is consistent with gagaku performance practice: shō players refer to each tone of the aitake by the name of its pipe, rather than by the name of its sounding pitch.(5) In the second part of the article, I demonstrate that patterns of te-utsuri can help illuminate Garfias’s (1975) criteria for “consonance” and “dissonance” in gagaku. By analyzing kinesthetic relationships between aitake, I draw attention to the correlation between gestural proximity of te-utsuri and underlying tonal functions of aitake.
The Shō: An Overview
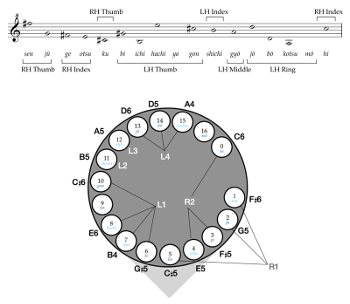
[2.1] Descending from the Chinese sheng (also written as 笙) and introduced to Japan from Tang China between the seventh and eighth centuries, the shō is a free-reed mouth organ comprised of seventeen bamboo pipes, each made from tubes of equal thickness but with different lengths (Miki 2008, 64).(6) As shown in Example 1, the seventeen pipes are attached to a wind chamber at the bottom and laid out in a circular fashion. Sound is produced by covering the finger holes above the reed and inhaling or exhaling into the mouthpiece, a mechanism similar to that of a Western harmonica (Video Example 1).(7)
Example 2a. Pipe holes and fingerings of the shō
(click to enlarge)
[2.2] Each pipe of the shō is assigned a different pitch with the exception of two muted pipes, ya (也) and mō (毛), as shown in Examples 2a and 2b.(8) There are specific ergonomically designed rules for fingerings, and the performer must be aware of which fingers should cover which holes. The kotsu (乞) pipe, for example, should only be covered by the left-hand ring finger. There are ten aitake in total, with eight six-pitch aitake and two five-pitch aitake (Example 3). Each aitake contains a fundamental tone, as indicated by the black noteheads in Example 3. Usually the lowest note of the aitake, the fundamental tone determines the name of each aitake and functions as a melodic cue for the hichiriki (篳篥; double-reed flute) and ryūteki (龍笛; transverse flute) during the shō’s process of te-utsuri.
Example 2b. Pitches of each shō pipe shown in Western notation (click to enlarge) | Example 3. List of aitake (click to enlarge) |
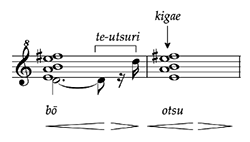
Example 4. Te-utsuri and kigae in Western notation
(click to enlarge)
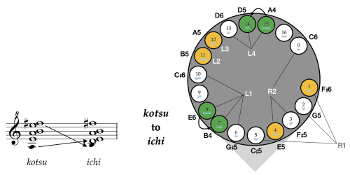
Video Example 2. Te-utsuri from aitake kotsu to aitake ichi
(click to watch video)
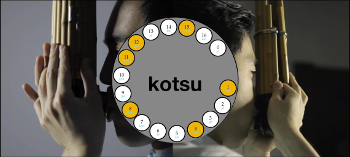
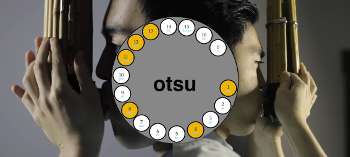
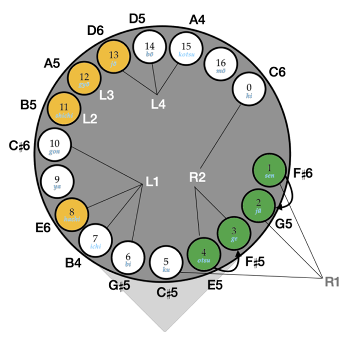
[2.3] In order to perform the shō at a high level, the performer must perfect the timing of the te-utsuri—the ordering and timing in which the fingers shift between holes to move from one aitake to another—and kigae (気替)—the changing of breath. As replicated in Western notation in Example 4, te-utsuri and kigae work in tandem to execute controlled dynamics, smooth out the melody, and create continuity between aitake (Masumoto 1968, 22). Each aitake, which typically lasts four beats, begins quietly and gradually crescendos into the fourth beat, followed by the te-utsuri motions that transition the fingerings into those of the new aitake. In Video Example 2, I demonstrate te-utsuri from aitake kotsu to aitake ichi. The left side of the screen captures movements in the left hand, whereas the right side of the screen displays the right hand. The diagram in the center of the video gives a bird’s-eye view of the wind chamber, showing all seventeen pipes. The yellow circles indicate the covered finger holes. As I execute the te-utsuri to move from one aitake to another, the yellow circles also shift to track the fingering movements involved in the process.
Example 5. The ato-uchi technique in Western notation
(click to enlarge)
[2.4] Whereas te-utsuri is completed between the fourth and first beats, kigae occurs on the arrival of the first beat.(9) In some cases, the te-utsuri occurs over two phases (Example 5): the first step immediately before the changing of the aitake (i.e., between the fourth and first beats) and the second step one or two beats after the new aitake has taken over, a technique called ato-uchi (後打ち; literally meaning “hitting after”). Ato-uchi usually occurs when the te-utsuri involves the shifting of three or more fingers. The te-utsuri not only functions as a systematized performance technique, but also as an aesthetic process that dictates the timbre and dynamics for playing the shō.
Analyzing Instrumental Gesture in Shō Performance
[3.1] Given the diverse contexts in which the term “gesture” has been used by music theorists, I will first specify the type of gesture to which I refer in my analysis. Jane Davidson (2005, 218), along with Manfred Nusseck and Marcelo Wanderley (2009, 335), classify gestures into 1) biomechanical movements that are necessary for producing sound from an instrument; and 2) movements used for expressive effect.(10) My analysis focuses primarily on gestures that function as a form of physical movement necessary for performance, referred to by Claude Cadoz as “instrumental gestures” (1988).(11) I analyze contemporary shō performance practice through the lens of instrumental gesture for two reasons. First, gagaku musicians are discouraged from drawing attention to themselves in performance, a hallmark of aesthetics in a variety of traditional Japanese performing arts. Gagaku performances, according to Alison McQueen Tokita and David W. Hughes (2008, 25), are characterized by a “lack of strong expressiveness” and an “excessively severe or solemn attitude,” which diminishes the possibility of overtly expressive gestures on the part of the performer.(12) Second, instrumental gestures for shō performance are tightly controlled through the rules of te-utsuri: unlike fingerings on the piano or violin, te-utsuri does not allow for any flexibility or individual discretion; a performer must follow the exact fingering procedures dictated by the te-utsuri when moving between aitake.
[3.2] My aim is to model the instrumental gestures of shō performance as transformational operations and explore the ways in which the kinesthetic relationships between aitake correspond with pitch relationships. My primary objective in drawing upon Lewinian transformational theory is to theorize the principles of te-utsuri—a core technique of shō performance in tōgaku—through the perspective of a contemporary shō player. By providing a theoretical grounding for investigating a performer’s musical actions, the transformational attitude effectively foregrounds the performer’s experience in navigating te-utsuri gestures in instrumental space. When learning te-utsuri, shō players must first memorize the required fingering movements (i.e., the number of finger holes traversed by each finger) and then build embodied knowledge of the physical distance between holes, since the performer is unable to see the finger holes for themselves when performing. In my own experience of learning te-utsuri, I often found myself thinking ahead to the upcoming aitake and asking the following questions: Which fingers do I need to move and where do they need to go? How far do the fingers need to move in order to reach the finger hole of the next aitake? Transformational theory provides a method for quantifying degrees of kinesthetic labor needed to move from one aitake to another. By situating the analyst as an active performer and thinking through te-utsuri as the performer’s motion through an instrumental space, transformational theory presents an amenable mechanism for addressing such inquiries. While issues of historical organology are certainly essential in examining the relationship between the arrangement of the pipes, gestural proximity of te-utsuri, and tonal construction of aitake, my analysis is conducted from the perspective of a contemporary performer. My aim is to model the experience of a twenty-first century shō player through a transformational model, rather than to speculate whether the construction of aitake was informed by the arrangement of the pipes.(13) By focusing on contemporary performance practice, I seek to challenge the narrative of gagaku as a “preserved fossilized remnant of the Heian period” and instead elucidate “how gagaku exists at present” (Harrison 2017, 22–24).
[3.3] In this article, I deliberately use Western pitch names to make the concepts of gagaku theory more accessible to a general readership. Because I do not assume any background in the Japanese language or knowledge of gagaku notation, pitches and aitake will be transcribed into Western notation as necessary. While the gagaku tone system is not entirely commensurate with that of Western music—the pitch A4 is tuned to 430hz on the shō, and pitches in the gagaku system are generated by stacking successive fifths—Western notation nevertheless offers an acceptable approximation for my purposes.(14) Language commonly associated with Western art music has been used frequently in discourse on gagaku, ranging from assigning “beats” and “measures” to the hyōshi rhythmic pattern as well as transcribing melodies into Western notation (Masumoto 1968; Shiba 1969, 1971).
[3.4] The potential controversy of analyzing non-Western music through an apparatus originally designed for Western art music has been addressed by a number of scholars. Challenging the limiting and essentialist framework of ethnotheory, Kofi Agawu (2017, 51) calls for analysts of African music to use the “sharpest tools irrespective of origin,” arguing that the cultural lineage of an analytical methodology should not disqualify its use in cross-cultural contexts. For Agawu, the central issue is “not who invented [theory] or for what initial purpose but whether it can be put to intelligent use in areas not initially envisioned by its first users” (2003, 195). Marc Perlman (2004, 3) observes two contrasting perspectives regarding the study of non-Western music adopted by scholars working within Western cultural and institutional contexts. On the one hand, Perlman notes that Western scholars studying non-Western musical forms have emphasized the importance of adopting an insider point of view. On the other hand, he observes that scholars have concurrently adopted a view of analysis as an act inevitably mediated by the culture within which the analyst is grounded (4). Taking a position which synthesizes these two viewpoints, Michael Tenzer has suggested that non-Western music should be studied using a “mixture of local and the researcher’s own terminology and techniques” (2006, 11). By analyzing my own embodied experience of te-utsuri through the lens of transformational theory—an analytical apparatus devised and developed within Western music theoretical discourse—my methodology follows Tenzer’s approach. By adopting transformational theory, I propose that Euro-American music theoretical techniques can be tailored to theorize contemporary shō performance in a way that highlights—rather than overwrites—perspectives and practices of gagaku musicians.
Transformational Perspectives of Shō Performance
Example 6. Distribution of finger holes across the left hand (LH) and right hand (RH)
(click to enlarge)
[4.1] Readers accustomed to Western instruments may find it peculiar that the pitches of the shō (Example 2b) seem to be arranged in no particular order. Commenting on the idiosyncratic design of the instrument, William Malm (2000, 111) notes that the pipes of the shō cannot be “arranged like piano keys, in a scalewise order,” due to physical restrictions posed by the fingerings. Unlike on a piano, moving from one pipe to its adjacent hole on the shō does not necessarily present us with a “nearby” pitch in pitch space, as shown in Example 6. For instance, moving the left-hand ring finger from kotsu to its adjacent hole bō takes us from A4 to D5, whereas moving the right-hand thumb from jū three finger holes away to ku shifts the pitch within a much smaller range, from G5 to
[4.2] Hayashi (1954), Masumoto Kikuko (1968), and Garfias (1975) have all suggested that the alignment of the pipes on the instrument is closely related to the fingering techniques of the aitake. Can we discern a relationship between the physical arrangement of the pipes and the pitch structure of the aitake? How can we determine whether, for example, if the aitake otsu is more closely related to jū or to ichi? Because of the way in which the pipes are arranged on the instrument, relationships between aitake are best revealed through an examination of te-utsuri rather than through pitch-class relationships. Instead of analyzing the pitch content of the aitake and attempting to explain its connection with the te-utsuri rules, I reverse the methodology: I will first establish how relatedness between different aitake is determined by degrees of gestural proximity in te-utsuri, and then explore the possible ways in which these kinesthetic relationships correlate with the pitch content of the aitake.
Example 7. Diagram of fingers used in shō performance
(click to enlarge)
Example 8. Te-utsuri from aitake kotsu to aitake ichi
(click to enlarge)
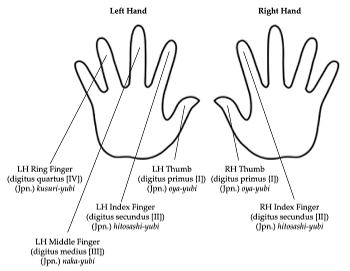
[4.3] First, I will demonstrate how the rules of te-utsuri facilitate a parsimonious movement of the fingers to get from one aitake to another. For clarity, Example 7 summarizes each of the finger types used in shō performance. Recall that each of the pipes is assigned to a specific finger. As summarized in Example 6, the left-hand thumb covers four pipes—gon (言;
Example 9. List of aitake expressed in the form of (R1, R2, L1, L4)
(click to enlarge)
[4.4] Lewin’s transformational attitude is particularly useful for theorizing shō performance, given that the performer experiences the music as movement between aitake rather than as static intervallic distances in pitch space.(17) Put another way, a performer who follows the rules of te-utsuri experiences a embodied process of shifting their fingers towards the finger holes of the new aitake. The analyst therefore experiences musical relationships from within the music, rather than as external neutral observer of musical objects (Lewin 1987, 158–59; Rings 2011, 10). As shown in Example 2a, each finger hole is numbered clockwise from 0 to 16.(18) We are now able to express each of the aitake in the form of (R1, R2, L1, L4)—kotsu, for instance, can be stated as (1, 4, 8, 15). The entire list of six-finger aitake in (a, b, c, d) form is provided in Example 9. To quantify the performer’s te-utsuri motions, I calculate the number of finger holes that each finger must traverse to get from one aitake to another. The process for playing aitake can be expressed as a permutation of four fingers pressing down on the pipes:(19)
$$ A= \big\{ (R1,R2,L1,L4) : R1 \in \{1,2,5\}, R2 \in \{0,3,4\}, L1 \in \{6,7,8,10\}, L4 \in \{13,14,15\} \big\} $$A in the formula above represents the aitake as a set (R1, R2, L1, L4), in which R1 is the right thumb, R2 is the right index finger, L1 is the left thumb, and L4 is the left ring finger.(20) While the index and middle fingers on the left hand are also necessary for forming aitake, as shown in Example 2a, the expression above excludes these two fingers as they are present in every aitake and thus are never taken off the gyō and shichi pipes during performance. In the interest of modeling the process of motion between clusters, each aitake is expressed as a combination of four finger holes rather than six. Applying this expression to Lewin’s STRANS function OP(s) = t, I reformulate te-utsuri as a transformational operation involving the movements of four fingers: (R1, R2, L1, L4): the s on the left-hand side expresses the first aitake, the t on the right-hand side represents the aitake to which the performer is moving, and the OP represents the te-utsuri expressed as operation \(TU_{(a, b, c, d)}\), in which the a, b, c, and d values quantify the motions each finger must enact to reach the next aitake \((a = R1^t–R1^s, b = R2^t–R2^s, c = L1^t–L1^s, d = L4^t–L4^s)\). Based on the formalization of A-set, we can now identify space S as the set of pipes \(\{0, 1, 2, \ldots 16\}\) and the group STRANS as the te-utsuri, expressed in the form \(TU_{(a,b,c,d)}\).
[4.5] Despite the abstract shō space being theoretically infinite, actual performance practice limits the number of transformational operations that are allowed in this space. First, strict systematization of the fingerings restricts motion between certain pipes. For example, since fingering rules are non-negotiable in tōgaku performance, there is no way to move from jū to ge since the two finger holes are not only held down by different fingers but also located on different sides of the pipe.(21) Moreover, since the gyō and shichi pipes are present in every aitake, motion from gyō to jō is similarly ruled out in practice. Second, the shō space S is non-modular, meaning that it cannot be wrapped around the face of a clock as per twelve-tone pitch-class space. Although the pipes sen and hi are theoretically adjacent to each other in shō space, for example, motion between them is not possible since the two are held down by different fingers. The only instance in which fingers can wrap around the clockface is the motion from hi to ge and otsu, since all three pipes use the right-hand index finger. As such, not all intervallic motions in shō space are conceivable in tōgaku given the restrictions of the systematized fingerings. A clockwise movement by four holes from sen to ku, both of which are played by the right thumb, cannot be replicated from jū to bi, since the former is played by the right thumb and the latter by the left thumb. The physical constraints of the systematized fingerings therefore limit the extent to which a formal transformational approach can be applied to shō space, since all intervallic motions must be theoretically conceivable when working within a GIS. Rather, the instrumental shō space closely resembles Lewin’s (1987, 37–46) direct-product GIS, which models aitake as a composite of multiple networks that operate independently from one another. There are four networks that each represent an individual finger—R1, R2, L1, and L4—which taken together form a single aitake. While the fingering rules of tōgaku performance impose limitations on modeling shō space as a GIS, Lewin’s transformational attitude nevertheless remains valuable for modeling te-utsuri from the performer’s perspective.
[4.6] To derive the te-utsuri operation that takes the performer from one aitake to another, I first reformulate each aitake as a set (R1, R2, L1, L4) and calculate the fingering motions necessary to reach the next aitake. To do this, we must subtract the a, b, c, and d values of the second aitake from those of the first. In these calculations, a positive value represents a movement of the finger in clockwise motion whereas a negative value corresponds to a movement in counterclockwise motion.(22) To present one example, moving from the aitake kotsu (1, 4, 8, 15) to ichi (1, 4, 7, 14) results in the following calculation:
$$ \begin{align} \textit{kotsu} &\quad (R1, R2, L1, L4) &= &\ (1, 4, 8, 15) \\ \textit{ichi} &\quad (R1, R2, L1, L4) &= &\ (1, 4, 7, 14) \\ \text{Difference} &&=&\ (0, 0, -1, -1) \\ \end{align} \\ TU_{(0,0,-1,-1)}[\textit{kotsu}] = \textit{ichi} $$Based on this calculation, moving from kotsu to ichi requires the performer to shift their left-hand ring finger counterclockwise by one hole and left-hand thumb one counterclockwise by one hole. Similarly, the motion required between ichi (1, 4, 7, 14) and ku (5, 4, 6, 14) can be calculated as follows:
$$ \begin{align} \textit{ichi} &\quad (R1, R2, L1, L4) &= &\ (1, 4, 7, 14) \\ \textit{ku} &\quad (R1, R2, L1, L4) &= &\ (5, 4, 6, 14) \\ \text{Difference} &&=&\ (+4, 0, -1, 0) \\ \end{align} \\ TU_{(+4,0,-1,0)}[\textit{ichi}] = \textit{ku} $$The motion from ichi to ku requires the performer to shift two fingers: right-hand index finger (moving clockwise by four holes) and left-hand thumb (moving counterclockwise by one hole). Combining these two operations yields a new operation, as shown below:
$$ \begin{align} \textit{kotsu} &\quad (R1, R2, L1, L4) &= &\ (1, 4, 8, 15) \\ \textit{ku} &\quad (R1, R2, L1, L4) &= &\ (5, 4, 6, 14) \\ \text{Difference} &&=&\ (+4, 0, -2, -1) \\ \end{align} \\ TU_{(+4, 0, -1, 0)}\{TU_{(0, 0, -1, -1)}[\textit{kotsu}]\} = TU_{(+4, 0, -2, -1)}[\textit{kotsu}] = \textit{ku} $$Example 10. Summary of te-utsuri between six-note aitake
(click to enlarge)
[4.7] Combining the te-utsuri between kotsu and ichi [\(TU_{(0, 0, -1, -1)}\)] and between ichi and ku [\(TU_{(+4, 0, -1, 0)}\)] generates the te-utsuri operation required to move directly from kotsu to ku [\(TU_{(+4, 0, -2, -1)}\)]. This process of binary combination applies to any of the te-utsuri operations between six-note aitake, as shown in Example 10. I have noted earlier in the article that there is only one possible way to move between any two aitake, since the technique of te-utsuri only allows for parsimonious finger movements. Put another way, there exists only one aitake t, which is operation \(TU_{(a,b,c,d)}\) away from aitake s. Moreover, combining the te-utsuri operation required to move from kotsu to ku [\(TU_{(+4, 0, -2, -1)}\)] and from ku to kotsu [\(TU_{(-4, 0, +2, +1)}\)] results in the identity operation \(TU_{(0,0,0,0)}\), which indicates no movement in any of the fingers.
Aitake, Te-utsuri, and Theories of Mode
Example 11. Comparing gestural proximity between two te-utsuri operations
(click to enlarge)
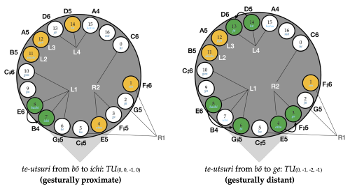
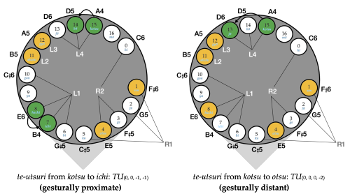
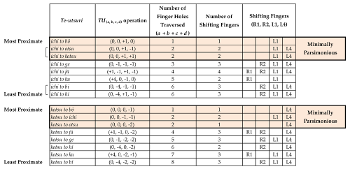
[5.1] Having outlined the methodology for calculating the size of te-utsuri, I will now generalize a set of rules for comparing the size of te-utsuri operations. Modeling kinesthetic relationships between different aitake through calculations of te-utsuri reveals that some aitake are farther apart than others. I suggest that the relative gestural proximity of the te-utsuri is one way to measure the relatedness between aitake from a performer’s perspective. In order to do so, we must take into consideration two aspects of te-utsuri: the number of fingers involved in the te-utsuri and the number of finger holes traversed by each of the fingers. I will begin with an examination of the former. While some te-utsuri require the performer to move just one finger, others require the movement of all four fingers. The shift from aitake bō (凢) to aitake ichi (一), for example, requires an operation of \(TU_{(0, 0, -1, 0)}\) with the performer shifting their left thumb from hachi (八) to its adjacent hole ichi, as shown in Example 11 and in Video Example 3. This shift is gesturally more proximate than that between bō and ge (下), which requires an operation of \(TU_{(0, -1, -2, -1)}\) and therefore a shifting of three fingers: the left ring finger must move from bō to its adjacent hole jō (上), the left thumb two holes from hachi to bi (美), and the right index finger one hole from otsu (乙) to ge (Video Example 4). From a kinesthetic standpoint, we can conclude that aitake ichi is related more closely to aitake bō than to aitake ge for two reasons: the motion from bō to ichi involves fewer fingers in the te-utsuri and requires only one finger hole shift, whereas the motion from bō to ge requires a movement of three fingers in total.
Video Example 3. Te-utsuri from aitake bō to aitake ichi (click to watch video) | Video Example 4. Te-utsuri from aitake bō to aitake ge (click to watch video) |
Example 12. Comparing gestural proximity between two te-utsuri operations with the same number of finger hole traversals
(click to enlarge)
Example 13. Rules for comparing the gestural proximity of multiple te-utsuri operations
(click to enlarge)
[5.2] So far, I have presented examples in which one te-utsuri operation unequivicolly requires more fingering motions than the other. Some relationships between aitake, as shown in Example 12, present an ambiguous case of whether a shift by two finger holes in one finger (e.g., \(TU_{(0, 0, 0, -2)}\) from kotsu to otsu) is larger or smaller than a shift by one finger hole each in two fingers (e.g., \(TU_{(0, 0, -1, -1)}\) from kotsu to ichi).(23) I suggest that two fingers each moving by one finger hole is more gesturally proximate than one finger moving by two finger holes. As such, the te-utsuri from kotsu to ichi [\(TU_{(0, 0, -1, -1)}\)] (Video Example 5a) is more gesturally proximate than the te-utsuri from kotsu to otsu [\(TU_{(0, 0, 0, -2)}\)] (Video Example 5b). This theory is consistent with the performer’s experience of playing the shō, since shifting by two finger holes demands a greater finger extension or contraction compared to moving by a single finger hole. Given the difficulty of visually locating finger holes while performing, the gesture of moving a single finger by two holes is more difficult to master than the gesture of moving the same finger by one hole. I have summarized the rules for determining the gestural proximity of te-utsuri in Example 13. In sum, determining the relative gestural proximity of te-utsuri requires us to take into consideration both the number of finger holes that are traversed and the number of fingers involved in the motion.
Video Example 5a. Te-utsuri from aitake kotsu to aitake ichi (click to watch video) | Video Example 5b. Te-utsuri from aitake kotsu to aitake otsu (click to watch video) |
Example 14. Te-utsuri operations from aitake jū to aitake ichi, kotsu, and hi, listed in order of gestural proximity
(click to enlarge)
[5.3] To further illustrate the rules in Example 13, I assess the gestural proximity of te-utsuri between aitake jū (2, 3, 8, 13) and aitake ichi (1, 4, 7, 14), kotsu (1, 4, 8, 15), and hi (1, 0, 8, 13), as shown in Example 14. STEP 1 alone cannot distinguish between the motion from jū to ichi, kotsu, and hi since all three operations require a traversal of four total finger holes. Following STEP 2 shows that the te-utsuri from jū to ichi is the most gesturally proximate operation since the operation distributes the four finger hole shifts evenly among the four fingers, each moving by one finger hole [\(TU_{(-1, +1, -1, +1)}\)]. Next in line is the te-utsuri from jū to kotsu, which involves the motion of three fingers, two shifting by one finger hole each and one shifting by two finger holes [\(TU_{(-1, +1, 0, +2)}\)]. The least gesturally proximate of the three is the the te-utsuri from jū to hi, which requires the shifting of two fingers: the right thumb shifts by one finger hole and the right index finger traverses three finger holes [\(TU_{(-1, -3, 0, 0)}\)].
Example 15. Te-utsuri operations from aitake ichi, listed in order of gestural proximity
(click to enlarge)
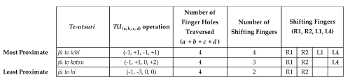
[5.4] With a methodology for quantifying te-utsuri firmly in place, I will now assess the size of each te-utsuri to determine the degree of relatedness between aitake. Taking ichi (1, 4, 7, 14) as an example, Example 15 shows the te-utsuri between ichi and each of the other aitake, ordered according to their degree of gestural proximity. Te-utsuri with equal degrees of proximity are indicated by brackets to the left of the table. The first step is to identify the te-utsuri operations that require the fewest number of finger hole movements in total. The te-utsuri from ichi to bō requires the fewest number of finger hole traversals (one finger hole), followed by the te-utsuri to kotsu and otsu (two finger holes). The te-utsuri from ichi to ge (three finger holes), jū (four finger holes), ku (five finger holes), bi, and hi (six finger holes each) are therefore less gesturally proximate than the te-utsuri between ichi and bō, kotsu, and otsu. The te-utsuri from aitake ichi to aitake bō, kotsu, and otsu is minimally parsimonious, spanning just one or two finger holes in total.
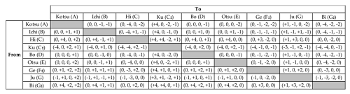
[5.5] By modeling te-utsuri as kinesthetic motion in instrumental space, it becomes evident that some pairs of aitake require more fingering shifts than others. The table in the Appendix displays all of the te-utsuri options between six-note aitake used in tōgaku performance, each expressed in the form of \(TU_{(a,b,c,d)}\). From the information in the table, we can make a number of observations on gestural proximity in te-utsuri. First, the most gesturally proximate relationships can be found in the te-utsuri from aitake bō to aitake kotsu, ichi, and otsu. Moving from bō to each of the three aitake only requires a shift by one finger hole in total. This relationship suggests that aitake kotsu, ichi, and otsu are in close kinesthetic proximity to bō. Second, the cluster ku (工) is relatively distant from many of the aitake; the closest aitake is ichi, which requires a total of five finger hole traversals: four in the right thumb and one in the left thumb. Moving to other aitake from ku requires a traversal across six (bō, ge), seven (kotsu, otsu), nine (bi) and eleven (hi) finger holes in total. A similar case can be made for bi, which requires a traversal of at least three finger holes in order to reach seven of the eight other aitake, and for hi, which involves a motion across four or more finger holes to seven of the eight other aitake. From these observations, I conclude that while some aitake cannot be reached through gesturally proximate te-utsuri from any of the other aitake, others are easily reached by proximate motion—and in a few instances, minimally parsimonious motion of one or two finger holes—from multiple aitake.
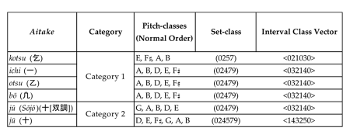
Categorization of Aitake
<Category 1>
Example 16. Categorization of aitake
(click to enlarge)
[6.1] Based on the gestural proximity of te-utsuri, I categorize aitake into three categories, as summarized in Example 16. I posit that the most proximate te-utsuri can be enacted between members of what I call the Category 1 aitake: bō, kotsu, ichi, and otsu. Whereas aitake in Category 1 are related to one another through the most proximate te-utsuri available to the shō player, aitake in Categories 2 and 3 require more fingering shifts when moving to other aitake.(24) As previously discussed, bō is just one finger hole shift away from kotsu, ichi, and otsu, and bō is the only aitake from which another cluster can be reached by shifting one finger hole. The other three members of Category 1—kotsu, ichi, and otsu—are each related to one another through two finger hole traversals, all in the left hand. The four aitake are connected through minimally parsimonious te-utsuri and are therefore closely related to one another from a gestural standpoint. Moreover, the four Category 1 aitake exhibit similarities in pitch content: each Category 1 aitake is a six-note subset of the same two-octave pentatonic pitch collection: A4-B4-D5-E5-A5-B5-D6-E6-
Example 17. Te-utsuri from aitake ichi to aitake gyō
(click to enlarge)
Video Example 6. Te-utsuri from aitake ichi to aitake gyō
(click to watch video)
[6.2] The four manifestations of the two-octave pentatonic pitch collection—aitake kotsu, ichi, bō, and otsu—are connected to one another through minimally parsimonious te-utsuri. Although two aitake in Category 2 are similarly subsets of pentatonic collections—gyō (A5-B5-D6-E6-
<Category 2>
Example 18. List of all minimally parsimonious te-utsuri
(click to enlarge)
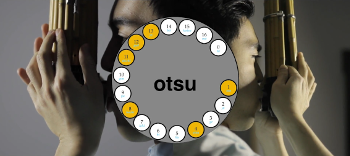
Video Example 7. Te-utsuri from aitake otsu to aitake jū
(click to watch video)
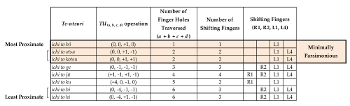
[6.3] Category 2 includes two six-note aitake: jū and ge. Members of Category 2 exhibit three characteristics. First, unlike the members of Category 1, the Category 2 aitake are not connected by minimally parsimonious te-utsuri to most of the other aitake. For Category 2, gestural proximity of te-utsuri is more the exception than the rule. The only exception is jū, which can be reached by minimally parsimonious motion from otsu through a \(TU_{(+1, -1, 0, 0)}\) operation.(27)
[6.4] Second, despite having similar degrees of gestural proximity, the motion from otsu to jū differs from te-utsuri between members of Category 1 in a crucial way (Example 18). While minimally parsimonious te-utsuri between members of Category 1 requires only the motion of the left hand (kotsu [pitch A4; pipe 15 as per Example 2a], bō [D6; pipe 14], jō [D5; pipe 13], hachi [E6; pipe 8], and ichi [B4; pipe 7]), te-utsuri between otsu and jū requires the movement of the right hand (sen [
[6.5] Third, with the exception of gyō and jū (Sōjō), Category 2 aitake contain a semitone within their intervallic structure, which creates a “richly dissonant texture against which the ryūteki and hichiriki perform their melodies” (Marett 2001a). This results in a sonority that contrasts significantly from the pentatonicism of the (02479) pitch-class collection that pervades the Category 1 aitake.(28) I will discuss in more detail the omission of gyō and jū (Sōjō) from the current discussion of Category 2 aitake in [9.6].
<Category 3>
[6.6] Finally, Category 3 contains aitake that are further apart from those of Categories 1 and 2: bi, hi and ku. Te-utsuri from bi to ichi and otsu, for example, each requires a shifting of six finger holes, and te-utsuri from bi to kotsu and bō requires a shifting of seven finger holes, indicating a low degree of relatedness with the Category 1 aitake. Similarly, hi requires non-proximate te-utsuri operations to reach any of the Category 1 aitake: a traversal of four finger holes for otsu, five for bō, and six for kotsu and ichi. Out of the Category 3 aitake, ku is the farthest from Category 1, requiring a shifting of five finger holes from ichi, six from bō, and seven from both kotsu and otsu. Ku requires similar degrees of transformations to reach other aitake in Categories 2 and 3: a shift of six finger holes to ge, seven to hi, and nine to bi. As such, motion to and from a Category 3 aitake is experienced by the performer as one of the most difficult and effortful te-utsuri used in tōgaku repertoire.
Pedagogical Connections
[7.1] My categorization of aitake based on the gestural proximity of te-utsuri is consistent with how aitake are taught to beginning shō students.(29) In 2017, I had the opportunity to participate in Miyata Mayumi’s courses at the Kunitachi College of Music in Tachikawa, Japan, a suburb of Tokyo. Miyata, one of the most distinguished performers of the shō today, teaches introductory-, intermediate-, and advanced-level classes on shō performance to undergraduate students specializing in Western art music performance. In the introductory course, students first learn the aitake otsu, followed by the three Category 1 aitake that are connected through minimally parsimonious te-utsuri: bō, kotsu, and ichi. One of Miyata-sensei’s exercises involves practicing te-utsuri between aitake that require a traversal of one finger hole: first from otsu to bō, then from bō to kotsu, before retracing the steps back to otsu (Video Example 8a). Another exercise requires the student to repeat the motion between bō and ichi, also one finger hole apart from one another, and between otsu and ichi, which are two finger holes apart (Video Example 8b). These exercises, which focus on developing the movement of the left hand, situate Category 1 as the most fundamental aitake from the perspective of te-utsuri.
Video Example 8a. Miyata Mayumi’s te-utsuri exercise (aitake otsu, bō, and kotsu) (click to watch video) | Video Example 8b. Miyata Mayumi’s te-utsuri exercise (aitake bō and ichi) (click to watch video) |
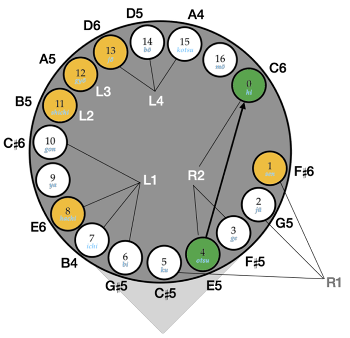
[7.2] Once the student has learned the basic te-utsuri for shifting between the Category 1 aitake, the fingerings for aitake in Categories 2 and 3 are then taught in relation to those in Category 1. Jū in Category 2, for example, is presented as a variant of otsu: the left hand placement for jū is identical to that of otsu, and the right hand requires each of its fingers to shift by one finger hole (Example 19a and Video Example 9a). The aitake hi in Category 3 is also introduced as a variant of otsu, with no change in the left hand and the right index finger placed on hi rather than on otsu (Example 19b and Video Example 9b).
Example 19a. Te-utsuri from aitake otsu to aitake jū (click to enlarge) | Example 19b. Te-utsuri from aitake otsu to aitake hi (click to enlarge) |
Video Example 9a. Te-utsuri from aitake otsu to aitake jū (click to watch video) | Video Example 9b. Te-utsuri from aitake otsu to aitake hi (click to watch video) |
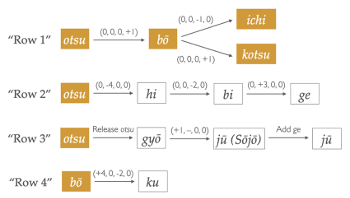
Example 20. Method of organizing aitake as proposed by Yamanoi Motokiyo’s “Te-utsuri Kudensho”
(click to enlarge)
[7.3] Miyata’s pedagogy finds a parallel in Gagaku Sankan no Shōkahō (「雅楽三管の唱歌法」) [Ōno 1996], a two-volume treatise on shōga authored by former Imperial Household Agency musician Ōno Tadao (多忠雄; 1911–2005). Although the treatise focuses primarily on the musical intricacies of shōga, Ōno’s discussion of mnemonics for shō outlines a method of organizing aitake based on their te-utsuri relationships.(30) I have reorganized the information presented in Ōno’s treatise in Example 20. Ōno presents a systematic way of learning each of the aitake by categorizing them into four groups. As shown in Example 20, Ōno situates otsu as the most fundamental aitake from which the rest of the aitake are derived. Ōno’s first group (“Row 1”) contains otsu, bō, kotsu, and ichi, all of which belong to Category 1. Bō is presented as a variant of otsu, and kotsu and ichi as modifications of bō. The order in which the aitake are presented is based on the gestural proximity of te-utsuri: bō is one finger hole away from otsu, and kotsu and ichi are each one finger hole away from bō. In other words, the shō player first starts with otsu, then learns bō, kotsu, and ichi, in that order. Only after learning the four basic aitake of Category 1 can the performer move on to learning the others. Out of the aitake in Categories 2 and 3, six (hi, bi, ge, gyō, and the two variations of jū) are derived from otsu and one (ku) is derived from bō. Miyata’s pedagogical method and Ōno’s categorization of aitake demonstrate that gestural proximity of te-utsuri plays a central role in the process of learning the shō.
Transformational Analysis of Te-utsuri in Goshōraku-no-kyū (五常楽急)
Example 21. Summary of te-utsuri and aitake in Goshōraku-no-kyū
(click to enlarge and see the rest)
Example 22. Notation of aitake for the piece Senshūraku in Banshiki-chō mode (notation is read from top to bottom and right to left. Each of the characters represents an aitake)
(click to enlarge)
Video Example 10. Excerpt from Goshōraku-no-kyū
(click to watch video)
[8.1] I now present an analysis of a tōgaku piece to demonstrate how a performer might experience a performance through te-utsuri, and how te-utsuri between different categories of aitake exhibit an ebb and flow between tension and release. To illustrate how the aitake in each of the three categories appears in the tōgaku repertoire, I analyze an excerpt from Goshōraku-no-kyū (五常楽急), a frequently performed piece in the Hyōjō (平調) mode.(31) The aitake and their accompanying te-utsuri operations in the piece are shown in Example 21a and a Western transcription of mm. 9–26 is provided in Example 21b. Although many contemporary gagaku musicians refer to column numbers (e.g., “first column,” “second column”; see Example 22 for an example of how columns are laid out in shō notation) rather than measure numbers when rehearsing a piece, I will refer to measure numbers in my discussion for purposes of clarity.(32) A video of the entire excerpt is also provided in Video Example 10. The aitake in mm. 17–22 all belong to Category 1, and their te-utsuri transformations are in their most parsimonious form: each motion only involves a shift by one or two finger holes. The string of minimally parsimonious te-utsuri transformations is momentarily broken up by the aitake jū in m. 23, but the Category 1 aitake return again in m. 24, lasting until the end of m. 26. This excerpt projects a sense of aural and kinesthetic stability. As previously discussed, each aitake in Category 1 is comprised of pitches from the two-octave pentatonic pitch collection A4-B4-D5-E5-A5-B5-D6-E6-
[8.2] So far, I have argued that motion between members of the Category 1 aitake yields minimally parsimonious (and as a result, most gesturally proximate) te-utsuri. As shown in the Appendix, some of the most laborious (and least gesturally proximate) te-utsuri takes place between members of Categories 2 and 3. Goshōraku-no-kyū presents a mixture of Category 1 (otsu, bō, ichi, kotsu), Category 2 (jū, ge), and Category 3 (ku) aitake (Example 21a). Examining the order and frequency in which the aitake of the three categories appear in Goshōraku-no-kyū reveals an alternation between proximate and distant te-utsuri transformations. Measures 10–12 proceed as follows: gesturally distant te-utsuri from a Category 1 to Category 3 aitake is counterbalanced by an immediate return to a Category 1 aitake. These events are then followed by a long sequence of minimally parsimonious te-utsuri operations between members of Category 1. In this passage, otsu moves to ku through a \(TU_{(+4, 0, -2, +1)}\) operation, a motion that stands out because it requires more fingers and finger hole traversals than any other te-utsuri up until this point in the piece. Rather than cycling through other aitake in Categories 2 and 3, we are immediately shifted back into bō at the end of m. 11, a motion that requires another gesturally distant transformation, \(TU_{(-4, 0, +2, 0)}\). Ku, which lasts for just one measure, is followed immediately by a chain of Category 1 aitake that continues until m. 22. The gesturally distant te-utsuri transformations that accompany the otsu—ku—bō motion in mm. 10–12 therefore contrast with the minimally parsimonious te-utsuri transformations afforded between members of the Category 1 aitake in mm. 12–22.
[8.3] If the gesturally distant te-utsuri for the otsu—ku—bō motion establishes a sense of tension in the performer’s fingers, then the minimally parsimonious te-utsuri between Category 1 aitake could be interpreted as a release of tension, given that mm. 12–22 require the movement of just one finger at a time throughout.(33) Category 3 aitake are treated similarly in Sandaien-no-kyū (三䑓塩急), Etenraku (越天楽), and Keitoku (雞徳) in Hyōjō mode: in all three pieces, every appearance of ku lasts for just two beats (i.e., half a measure) and is always preceded and followed by a Category 1 aitake. The proximity of te-utsuri between aitake is correlated with similarities in the aitake’s pitch content. Motion between aitake that are subsets of the two-octave pentatonic pitch collection A4-B4-D5-E5-A5-B5-D6-E6-
Example 23. Frequency of te-utsuri and duration of aitake in Goshōraku-no-kyū
(click to enlarge)
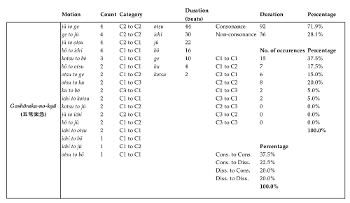
[8.4] Calculating the frequencies of te-utsuri in Goshōraku-no-kyū shows that the most common type of motion is that between Category 1 aitake, which constitutes 37.5% (15 out of 40) of all te-utsuri in the piece (Example 23). Including all motion to and from Category 1 aitake reveals that the overwhelming majority of te-utsuri (80%; 32 out of 40) either depart from or arrive at a Category 1 aitake. Other types of motion, such as that from Category 1 to Category 2 and between Category 2 aitake, occur less frequently. Moreover, Category 1 aitake are held for longer periods of time compared to aitake in other categories. Indeed, summing the duration (in beats) of each aitake type in the piece reveals that Category 1 aitake are played for longer durations than members of Category 2 or Category 3: the four Category 1 aitake occupy 71.9% (92 out of 128 beats) of the duration of the piece, the most out of any category (Example 23). These findings can be used to make the following generalizations for Goshōraku-no-kyū: first, the piece projects a predilection for minimally parsimonious te-utsuri motion, as evidenced by the higher frequency of motion between Category 1 aitake compared to that between aitake of different categories or between Category 2 aitake; and second, given that minimally parsimonious te-utsuri between Category 1 aitake is normalized as the most common type of motion in the piece, gesturally distant te-utsuri between members of different categories and within members of Category 2 present contrast and variety in the performer’s gestural experience.
Tonal Relationships between Aitake
Example 24. Pitch-class and intervallic structures of Category 1 aitake
(click to enlarge)
[9.1] My analysis of te-utsuri has shown how the arrangement of the pipes on the shō facilitates a high degree of relatedness between some aitake over others. In this final section, I demonstrate how expressing the te-utsuri as transformational operations reveals various pitch-based relationships between aitake. Why, for example, do movements between Category 1 aitake facilitate the most gesturally proximate te-utsuri? To address this question, I consider the tonal function of aitake within the context of gagaku modes. I suggest that Garfias’s (1975) theories of “consonance” and “dissonance” in gagaku can offer a possible explanation. According to Garfias, gagaku assumes a fixed notion of consonance and dissonance that is not “dictated by patterns of contrast, tension and release” as in Western art music (66). Rather, consonance and dissonance are “totally subservient to the fixed structure of each aitake and in turn are governed by the tones of the basic series in which the chōshi is found” (66).(34) Garfias categorizes the following four aitake as consonances, regardless of mode: kotsu (fundamental note: A4), ichi (fundamental note: B4), bō (fundamental note: D5), and otsu (fundamental note: E5). These four aitake are analogous to the members of Category 1. By contrast, Garfias categorizes the other aitake—which are analogous to the members of Categories 2 and 3—as dissonances (66–67). The aitake in Category 1 have two characteristics in common: first, all four Category 1 aitake are subsets of the two-octave pentatonic pitch collection A4-B4-D5-E5-A5-B5-D6-E6-
Example 25. Aitake organized into stacked consecutive fifths
(click to enlarge)
[9.2] What can the intervallic properties of consonant aitake tell us about the relationship between the Category 1 aitake and the te-utsuri transformations required to move between them? The answer is deeply intertwined with the structure of the tone system in gagaku. The method used for generating the tone system in gagaku offers an explanation for the correlation between the intervallic structures of each of the Category 1 aitake and the minimally parsimonious te-utsuri necessary to move between them. As Hayashi has observed, the pitch classes of each of the aitake can be rearranged into a chain of consecutive fifths, as shown in Example 25.(35) Hayashi admits that this conceptualization of the tone system is hardly new, as previous theorists such as Ogyū Sorai (荻生徂徠; 1666–1728) and Tayasu Munetake (田安宗武; 1716–71) have already taken note of this property in their respective treatises.(36) As Hayashi and others have shown, pitches of the gagaku tone system are calculated through the Chinese Sanbun son’eki (三分損益) method, which draws parallels with the Pythagorean tuning system of stacking successive fifths.(37) While the tone system consists of twelve pitches generated through this method, musicians use fewer tones in practice.(38)
Example 26. Six modes of gagaku
(click to enlarge)
[9.3] As shown in Example 26, the six seven-note modes used in contemporary gagaku are categorized into two groups according to their intervallic structure: the ryo (呂) modes Ichikotsu-chō (壱越調; fundamental tone: D), Taishiki-chō (太食調; fundamental tone: E), and Sōjō (双調; fundamental tone: G) and the ritsu (律) modes Hyōjō (平調; fundamental tone: E), Ōshiki-chō (黄鐘調; fundamental tone: A), and Banshiki-chō (盤渉調; fundamental tone: B).(39) The first degree of each mode plays a significant melodic and tonal function, and each seven-note collection can be divided into five main tones and two pien tones. These features are a legacy of the tonal system from Tang China on which gagaku theory is founded, which melodically emphasizes the “first five tones of the generating series” and treats the other two tones as “additional” pien tones used for “weaker roles” (Garfias 1975, 58).(40) The fundamental tone of a gagaku mode is analogous to the tonic degree of a Western scale, functioning as a “point of arrival and/or rest for most melodic lines” and are sustained for longer durations compared to non-fundamental tones (Kapuscinski and Rose 2013b). The intricacies of the gagaku tone system unfortunately cannot be presented in full here. For the purposes of this article, I will limit my discussion to the process through which tones are generated and their connection to the fundamental tones of the six modes.
[9.4] Having contextualized the intervallic structure of aitake within the gagaku tone system, I will now discuss the relationship between each of the Category 1 aitake and their accompanying te-utsuri operations. Recall that all aitake possess their own fundamental tone, as indicated by the black noteheads in Example 3. If we compare the fundamental tones of the Category 1 aitake with each of the fundamental tones of the six gagaku modes, we find that for Ichikotsu-chō (fundamental tone: D), Hyōjō (E), Taishiki-chō (E), Ōshiki-chō (A), and Banshiki-chō (B), the aitake representing their respective fundamental tones correspond to all four of the Category 1 aitake: bō (fundamental tone: D), otsu (E), kotsu (A), and ichi (B). In other words, the aitake accompanying the fundamental tones of five out of the six modes are connected to each other through a gesturally proximate relationship, requiring at most a shifting of two finger holes in the left hand. In sum, Category 1 aitake are similar to one another in two ways: first, they are related kinesthetically through minimally parsimonious te-utsuri; second, the four Category 1 aitake are analogous to the aitake accompanying the fundamental tone of all but one of the six modes, suggesting that members of Category 1 share similar tonal functions.
[9.5] There are two implications for this correlation between the Pythagorean construction of the gagaku tone system and gestural proximity of te-utsuri. First, each tone of the aitake can be generated by stacking successive fifths, which draws parallels with the Sanbun son’eki method.(41) The Sanbun son’eki method is consistent with the process for tuning the shō, which is similarly tuned in successive fifths starting on the pitch ichikotsu (analogous to D in the Western system).(42) Second, the pitches of each consonant aitake correspond to the five main tones of the mode for which the aitake functions as the fundamental tone. Although Garfias echoes this observation, his work does not explore the relationship between the gestural proximity of te-utsuri and the tone structure of the aitake representing the fundamental degrees of each mode. Recall that each mode is comprised of seven pitches, which can be further divided into five main tones and two pien tones. Out of the six-note aitake, only the Category 1 aitake can be generated by stacking the five main tones of the modes, while aitake in Categories 2 and 3 require the use of pien tones. Otsu, ichi, and bō, for example, are all comprised of generating tone D and the first four tones produced from it: A, B, E, and
Example 27. Two forms of the aitake jū
(click to enlarge)
Example 28. Two types of the aitake jū in Butokuraku (武徳楽) (Sōjō mode)
(click to enlarge)
Example 29. Pitch-class and intervallic structures of Category 1 aitake and jū
(click to enlarge)
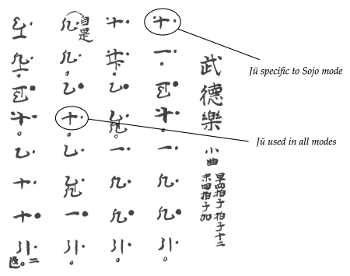
[9.6] The reader may notice that the Sōjō mode has been left out of the current discussion on the correlation between aitake pitch structures and the gestural proximity of te-utsuri. The reason for this omission is that jū, which is built on the fundamental tone of Sōjō mode (G), has two versions: a six-note aitake used in all modes (Example 27a) and a five-note aitake used exclusively in the Sōjō mode (Example 27b). In this article, I refer to the six-note version of jū as “jū” and the five-note version as “jū (Sōjō),” to reflect the latter’s specific usage. Both types appear in Sōjō mode, and the two versions are differentiated in the notation with a dot on the side of the jū character, as shown in Example 28. Based on the theoretical framework I have developed in this article, the five-note jū (Sōjō) meets the criteria for a consonant aitake: its pitches are limited to those of the five main tones of Sōjō mode (G, A, B, D, E), as shown in Example 25.(43) Jū, however, includes one pien tone (
[9.7] In sum, I have identified three shared features of Category 1 aitake that illustrate the close relationship between gestural proximity and tonal function. First, the Category 1 aitake correspond to the clusters on the fundamental degrees of five of the six modes—Ichikotsu-chō (D), Hyōjō (E), Ōshiki-chō (A) and Banshiki- chō (B). Despite sharing a similar pentatonic pitch structure, the aitake built on the fundamental degree of Sōjō (G)—jū (Sōjō)—cannot be considered a Category 1 aitake due to differences in cardinality and in the pentatonic scale from which it draws its pitches. Second, the aitake accompanying the fundamental modal degrees are comprised exclusively of the five main tones of the gagaku modal system. As such, all Category 1 aitake meet Garfias’s criteria for consonance in gagaku. Third, the aitake requiring the fewest total number of finger hole traversals are also the aitake that accompany the fundamental tones of each mode. We now understand that the pipes of the shō, while at first glance arranged in random order, are constructed in a way that allows for and prioritizes the most gesturally proximate te-utsuri between each of the consonant aitake on the fundamental modal degrees, a striking instance in which the physical structure of an instrument is ergonomically tailored towards the needs of the performer.
Conclusion
[10.1] In this article, I have theorized the performance of the shō as a set of transformational operations that result from instrumental gestures enacted upon the instrument. A Lewinian transformational approach for modeling the technique of te-utsuri is compatible with how performers of the shō conceptualize the motion between aitake. Moreover, a transformational approach models aitake as an aesthetic byproduct of gradual fingering movements rather than as a fixed harmonic entity, a characterization which would certainly seem out of place in gagaku. Incorporating the motion of te-utsuri into an analysis of aitake enables us to understand the centrality of instrumental gesture in shō performance, an approach that resonates with how gagaku musicians study and internalize the music. By quantifying the motion between aitake according to the number of fingers in motion and the total number of finger holes traversed by the performer during the process of te-utsuri, I have demonstrated that some aitake are more closely related to one another from a gestural standpoint. Furthermore, aitake that are related to each another through gesturally proximate te-utsuri operations share a number of commonalities: first, each Category 1 aitake is a subset of the same two-octave pentatonic pitch collection; second, aitake that are related through minimally parsimonious te-utsuri simultaneously function as the aitake for the fundamental degrees of each mode, revealing a striking correlation between the gestural proximity and tonal function. Examining connections between the pitch structure of aitake, gestural proximity of te-utsuri, and notions of consonance and dissonance in gagaku sheds light on the relationship between musical syntax and the physical arrangement of the pipes of the shō..
[10.2] By highlighting the intersections between te-utsuri and tonal relations in shō performance, this article has foregrounded the rich possibilities of incorporating instrumental gestures into music analysis. An embodied approach to musical analysis builds upon the work of Suzanne G. Cusick (1994), who has demonstrated how an analysis of a performer’s physical actions can productively enhance a structural reading of a piece. Critiquing music theory’s obsession with the “texts of composers” and neglect of the “presence of the body in music,” Cusick advocates for an embodied music theory that centers the performer’s role in the production of music (15).(44) As Joti Rockwell (2009a, 161) has suggested, the “seemingly pedestrian details of practice” that are essential to learning an instrument can be fruitful for understanding music from a performer’s perspective. Moreover, recent work by Timothy Koozin (2011) and De Souza (2017, 2018) has modeled musical performance through instrumental space to reveal insights that cannot easily be accessed through discussions of pitch-based parameters alone. While my use of transformational theory is indebted to their work, my analysis of te-utsuri has also exposed the limitations of adopting a formal transformational approach for modeling shō space. The systematized fingerings, non-modular construction of the instrument, and considerations of aitake cardinality raise provocative questions about the extent to which Lewin’s transformational apparatus—a methodology originally developed for analyzing Western art music—can be flexibly applied to analyses of instrumental gesture and topography in non-Western music.
[10.3] This project has suggested a number of avenues for further research. First, the potentiality of the te-utsuri transformational system could be explored further through an empirical analysis of the core gagaku repertoire in the Hōshōfu (鳳笙譜)—a compilation of tablatures for the shō, published by both the Ono Gagaku-kai and the Gagaku Department of Tenrikyō Church. A systematic analysis of the repertoire across all six modes will offer valuable data for exploring issues of syntax in tōgaku. An empirical methodology would help confirm whether the Category 1 aitake are used most frequently across all modes, how gesturally proximate relationships between aitake are consistent across all six modes, and how the syntax of the aitake relates to the melodic lines played by the ryūteki and hichiriki. Lastly, an in-depth examination of the interaction between modal and rhythmic theories of gagaku may reveal how the pitches of the aitake interact with those played by the other instruments of the ensemble.
Toru Momii
621 Dodge Hall
Columbia University
2960 Broadway
New York, NY 10027
tm2781@columbia.edu
Appendix
Appendix. List of all te-utsuri between six-note aitake used in tōgaku performance
(click to enlarge)
Glossary
Works Cited
Abrahams, Rosa. 2019. “Mimicry as Movement Analysis.” Analytical Approaches to World Music 7 (2): 41–68. http://www.aawmjournal.com/articles/2019b/Abrahams_AAWM_Vol_7_2.html.
Agawu, V. Kofi. 2003. Representing African Music: Postcolonial Notes, Queries, Positions. Routledge.
—————. 2017. “Against Ethnotheory.” In The Dawn of Music Semiology: Essays in Honor of Jean-Jacques Nattiez, ed. Jonathan Dunsby and Jonathan Goldman, 38–55. University of Rochester Press.
Akedo, Shinya. 2011. “Kihonteki na tōkei shuhō no katsuyō ni yoru nihon no jūniritsu no sentei.” Nihon Tōkei Gakkaishi 41 (1): 23–50.
Baily, John. 1977. “Movement Patterns in Playing the Herati Dutâr.” In The Anthropology of the Body, ed. John Blacking, 275–330. Academic Press.
—————. 2006. “John Blacking and the ‘Human/Musical Instrument Interface’: Two Plucked Lutes from Afghanistan.” In The Musical Human: Rethinking John Blacking’s Ethnomusicology in the Twenty-first Century, ed. Suzel Ana Reily, 107–23. Ashgate.
Baily, John, and Peter Driver. 1992. “Spatio-Motor Thinking in Playing Folk Blues Guitar.” The World of Music 34 (3): 57–71.
Berry, Michael. 2009. “The Importance of Bodily Gesture in Sofia Gubaidulina’s Music for Low Strings.” Music Theory Online 15 (5). https://mtosmt.org/issues/mto.09.15.5/mto.09.15.5.berry.html.
Cadoz, Claude. 1988. “Instrumental Gesture and Music Composition.” In Proceedings of the 1988 International Computer Music Conference, Cologne, Germany, 1–12. ICMA.
Cheung, Hon Ki. 2018. “A Study of Inter-Cardinality Voice Leading Using Voice-Leading Zones and the Extended 4-Cube Trio.” GAMUT 8 (1): 189–223.
Childs, Adrian. 1998. “Moving Beyond Neo-Riemannian Triads: Exploring a Transformational Model for Seventh Chords.” Journal of Music Theory 42 (2): 181–94. https://doi.org/10.2307/843872.
Cohn, Richard. 2012. Audacious Euphony: Chromaticism and the Consonant Triad’s Second Nature. Oxford University Press.
Cox, Arnie. 2011. “Embodying Music: Principles of the Mimetic Hypothesis.” Music Theory Online 17 (2). https://doi.org/10.30535/mto.17.2.1.
Cusick, Suzanne G. 1994. “Feminist Theory, Music Theory, and the Mind/Body Problem.” Perspectives of New Music 32 (1): 8–27. https://doi.org/10.2307/833149.
Davidson, Jane. 2005. “Bodily Communication in Musical Performance.” In Musical Communication, ed. Dorothy Miell, Raymond MacDonald, and David J. Hargreaves, 215–37. Oxford University Press.
De Souza, Jonathan. 2017. Music at Hand: Instruments, Bodies, and Cognition. Oxford University Press.
—————. 2018. “Fretboard Transformations.” Journal of Music Theory 62 (1): 1–39. https://doi.org/10.1215/00222909-4450624.
Doğantan-Dack, Mine. 2011. “In the Beginning was Gesture: Piano Touch and the Phenomenology of the Performing Body.” In New Perspectives on Music and Gesture, ed. Anthony Gritten and Elaine King, 243–65. Ashgate.
Easley, David B. 2015. “Riff Schemes, Form, and the Genre of Early American Hardcore Punk (1978–83).” Music Theory Online 21 (1). https://doi.org/10.30535/mto.21.1.3.
Endō, Tōru. 2004. “Tōgaku shōchoshi no kiso kōzō: ‘Sango Yoroku’ no bunseki ni yoru.” Tōyō Ongaku Kenkyū 69: 1–17.
—————. 2005. Heianchō no Gagaku: Kogakufu ni yoru Tōgakukyoku no Gakuriteki Kenkyū. Tōkyōdō Shuppan.
—————. 2013. Gagaku wo Shiru Jiten. Tōkyōdō Shuppan.
Gamō, Mitsuko. 1970. “Gakuri.” In Nihon no Koten Geinō, vol. 2, ed. Geinōshi Kenkyūkai, 137–67. Heibonsha.
Garfias, Robert. 1975. Music of a Thousand Autumns: The Tōgaku Style of Japanese Court Music. University of California Press.
Gibson, James J. 1986. The Ecological Approach to Visual Perception. Lawrence Erlbaum Associates.
Harrison, LeRon James. 2017. “Gagaku in Place and Practice: A Philosophical Inquiry into the Place of Japanese Imperial Court Music in Contemporary Culture.” Asian Music 48 (1): 4–27. https://doi.org/10.1353/amu.2017.0001.
Hayashi, Kenzō. 1954. “Shōritsu nikō: Jūshichikan shō no keitō to wasei ni tsuite.” Nara Gakugei Daigaku Kiyō 3 (3): 1–32.
—————. 1969. Gagaku: Kogakufu no Kaidoku. Ongaku no Tomosha.
Huron, David, and Jonathon Berec. 2009. “Characterizing Idiomatic Organization in Music: A Theory and Case Study of Musical Affordances.” Empirical Musicology Review 4 (3): 103–22. https://doi.org/10.18061/1811/44531.
Jensenius, Alexander Refsum, Marcelo M. Wanderley, Rolf Inge Godøy, and Marc Leman. 2010. “Musical Gestures: Concepts and Methods in Research.” In Musical Gestures: Sound, Movement, and Meaning, ed. Rolf Inge Godøy and Marc Leman, 12–35. Routledge.
Kapuscinski, Jaroslaw, and François Rose. 2013a. “Rhythmic Cycles in Kangen Music.” Center for Computer Research in Music and Acoustics, Stanford University. Accessed July 12, 2019. https://ccrma.stanford.edu/groups/gagaku/theory/rhythm-en.html.
—————. 2013b. “The Modal System in Kangen Music.” Center for Computer Research in Music and Acoustics, Stanford University. Accessed July 12, 2019. https://ccrma.stanford.edu/groups/gagaku/theory/pitch-en.html.
Kárpáti, János. 1983. “Tonality in Japanese Court Music.” Studia Musicologica Academiae Scientiarum Hungaricae T. 25, Fasc. 1 (4): 171–82. https://doi.org/10.2307/901970.
Kishibe, Shigeo, and Leo Mario Traynor. 1952. “Shō no fumei naru yonkan to sono nihon toden ni tsuite.” Tōyō Gakuhō 35 (1): 50–72.
Koozin, Timothy. 2011. “Guitar Voicing in Pop-Rock Music: A Performance-Based Analytical Approach.” Music Theory Online 17 (3). https://doi.org/10.30535/mto.17.3.5.
Kozak, Mariusz. 2019. Enacting Musical Time: The Bodily Experience of New Music. Oxford University Press.
Lewin, David. 1987. Generalized Musical Intervals and Transformations. Yale University Press.
Malm, William P. 2000. Traditional Japanese Music and Musical Instruments. Kōdansha International.
Marett, Allan. 1985. “Tōgaku: Where Have the Tang Melodies Gone, and Where Have the New Melodies Come from?” Ethnomusicology 29 (3): 409–31. https://doi.org/10.2307/851797.
—————. 1986. “In Search of the Lost Melodies of Tang China: An Account of Recent Research and Its Implications for the History and Analysis of Tōgaku.” Musicology Australia 9: 29–38. https://doi.org/10.1080/08145857.1986.10415163.
—————. 2001a. “Japan, V. Court Music.” Grove Music Online. Oxford University Press. https://doi.org/10.1093/gmo/9781561592630.article.43335.
—————. 2001b. “Mode, V. Middle East and Asia, 5. East Asia: diao and chōshi, (ii) Japan: chōshi. ”Grove Music Online. Oxford University Press. https://www.oxfordmusiconline.com/grovemusic/view/10.1093/gmo/9781561592630.001.0001/omo-9781561592630-e-0000043718.
Masumoto, Kikuko. 1968. Gagaku: Dentō Ongaku e no Atarashii Apurōchi. Ongaku no Tomosha.
—————. 2010. Shinpan: Gagaku Nyūmon. Ongaku no Tomosha.
Mead, Andrew. 1999. “Bodily Hearing: Physiological Metaphors and Musical Understanding.” Journal of Music Theory 43 (1): 1–19. https://doi.org/10.2307/3090688.
Miki, Minoru. 2008. Composing for Japanese Instruments. Edited by Philip Flavin. Translated by Marty Regan. University of Rochester Press.
Montague, Eugene. 2012. “Instrumental Gesture in Chopin’s Étude in A-Flat Major, Op. 25, No. 1.” Music Theory Online 18 (4). https://doi.org/10.30535/mto.18.4.4.
Nelson, Steven G. 1986. “Gogenfu shinkō–omo ni gogen biwa no jusei oyobi chōgen ni tsuite.” Tōyō Ongaku Kenkyū 50: 13–76.
—————. (1988). “Gagaku kofu to sono kaidoku ni okeru shomondai: shutoshite biwa ni tsuite.” In Iwanami Kōza Nihon no Ongaku Ajia no Ongaku 4, ed. Satoaki Gamō et al., 16–42. Iwanami Shoten.
Ng, Kwok-Wai. 2007. “The Modes of Tōgaku from Tang-period China to Modern Japan: Focusing on the Ōshikichō, Banshikichō, and Hyōjō Modal Categories.” PhD diss., The University of Sydney. https://doi.org/10.1080/17411912.2017.1350112.
—————. 2011. “In Search of the Historical Development of Double-Reed Pipe Melodies in Japanese Tōgaku: Early Hypotheses and New Perspectives.” Asian Music 42 (2): 88–111.
—————. 2017. “The Emergence of Chordal Accretions in the Lute Melodies of Tōgaku and Its Implications for the Historical Development of the Repertory.” Ethnomusicology Forum 26 (2): 215-46.
Nusseck, Manfred, and Marcelo M. Wanderley. 2009. “Music and Motion—How Music-Related Ancillary Body Movements Contribute to the Experience of Music.” Music Perception: An Interdisciplinary Journal 26 (4): 335–53. https://doi.org/10.1525/mp.2009.26.4.335.
Ōno, Tadao. 1996. Gagaku Sankan no Shōkahō: Dentō no Shōkahō to sono Gendai Gakuriteki Kenkyū. Vol. 2. Hakubunkan Shinsha.
Ono, Makoto. 2016. “Kindaika ni yoru gagakukai no henyō.” Kindaika to Gakumon: 175–87.
Perlman, Marc. 2004. Unplayed Melodies: Javanese Gamelan and the Genesis of Music Theory. University of California Press.
Picken, Laurence E.R., with Rembrandt Wolpert, Allan J. Marett, Jonathan Condit, Elizabeth Markham, and Yoko Mitani. 1981. Music from the Tang Court. Vol. 1. Oxford University Press.
—————. 1985. Music from the Tang Court. Vol. 2. Cambridge University Press.
—————. 1986. Music from the Tang Court. Vol. 3. Cambridge University Press.
—————. 1987. Music from the Tang Court. Vol. 4. Cambridge University Press.
—————. 1990. Music from the Tang Court. Vol. 5. Cambridge University Press.
—————. 1997. Music from the Tang Court. Vol. 6. Cambridge University Press.
—————. 2000. Music from the Tang Court. Vol. 7. Cambridge University Press.
Rings, Steven. 2011. Tonality and Transformation. Oxford University Press.
Rockwell, Joti. 2009a. “Banjo Transformations and Bluegrass Rhythm.” Journal of Music Theory 53 (1): 137–62. https://doi.org/10.1215/00222909-2009-023.
—————. 2009b. “Birdcage Flights: A Perspective on Inter-Cardinality Voice Leading.” Music Theory Online 15 (5). https://doi.org/10.30535/mto.15.5.4.
Satyendra, Ramon. 2004. “An Informal Introduction to Some Formal Concepts from Lewin's Transformational Theory.” Journal of Music Theory 48 (1): 99–141. https://doi.org/10.1215/00222909-48-1-99.
Service, Jonathan. 2012. “Orchestrating Modernity, Singing the Self: Theories of Music in Meiji and Taisho Japan.” PhD diss., Harvard University.
Shiba, Sukehiro. 1969. Kangenkyoku: Sōgaku-hen. Vol. 2 of Gosenfu ni yoru gagaku sōfu. Kawai Gakufu.
—————. 1971. Kangenkyoku: Engaku, Taikyoku-hen. Vol. 3 of Gosenfu ni yoru gagaku sōfu. Kawai Gakufu.
Shono, Susumu. 1987. “The Role of Listening in Gagaku.” Contemporary Music Review 1: 19–43.
Sterbenz, Maeve. 2017. “Movement, Music, Feminism: An Analysis of Movement-Music Interactions and the Articulation of Masculinity in Tyler, the Creator’s ‘Yonkers’ Music Video.” Music Theory Online 23 (2). https://doi.org/10.30535/mto.23.2.6.
Straus, Joseph N. 2003. “Uniformity, Balance, and Smoothness in Atonal Voice Leading.” Music Theory Spectrum 25 (2): 305–52. https://doi.org/10.1525/mts.2003.25.2.305.
Tenzer, Michael. 2006. “Introduction.” In Analytical Studies in World Music, ed. Michael Tenzer, 1–38. Oxford University Press.
Terauchi, Naoko. 1993. “Gagaku tōgakukyoku no hensō ni kansuru ichi kōsatsu: ‘Jinchi Yōroku’ ni okeru ‘dōkyoku’ wo megutte.” Tōyō Ongaku Kenkyū 56: 1–28.
—————. 1996. Gagaku no rizumu kōzō: Heian jidaimatsu ni okeru Tōgakukyoku ni tsuite. Daiichi Shobō.
—————. 2007. “Kokuritsu gekijō no gagaku ‘fukugen’ project ni okeru ‘dentō’ he no chōsen.” Kokusai Bunkagaku Kenkyū: Kōbe Daigaku Kokusai Bunka Gakubu Kiyō 27: 51–80.
—————. 2011. “Surface and Deep Structure in the Tōgaku Ensemble of Japanese Court Music (Gagaku).” In Analytical and Cross-Cultural Studies in World Music, ed. Michael Tenzer and John Roeder, 19–55. Oxford University Press.
Tōgi, Shintarō. 1989. Gagaku Jiten. Ongaku no Tomosha.
Tokita, Alison McQueen, and David W. Hughes. 2008. “Context and Change in Japanese Music.” In The Ashgate Research Companion to Japanese Music, ed. Alison McQueen Tokita and David W. Hughes, 1–33. Ashgate.
Tsukahara, Yasuko. 2009. Meiji kokka to gagaku: dentōno kindaika/kokugaku no sōsei. Yūshisha.
Tymoczko, Dmitri. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. Oxford University Press.
Watanabe, Shinichirō. 2009. “Gagaku no kita michi: kentōshi to ongaku.” Senshū Daigaku Higashi Asia Sekaishi Kenkyū Center Nenpō 2: 5–20
Windsor, W. Luke, and Christophe de Bézenac. 2012. “Music and Affordances.” Musicae Scientiae 16 (1): 102–20.
Yung, Bell. 1984. “Choreographic and Kinesthetic Elements in Performance on the Chinese Seven-String Zither.” Ethnomusicology 28 (3): 505–17. https://doi.org/10.2307/851237.
Footnotes
* I am grateful to Ellie M. Hisama, John Roeder, Mariusz Kozak, Nathan Pell, and Michèle Duguay for their insightful comments and suggestions on earlier versions of this article. This work would not have been possible without mentorship from my teachers, Miyata Mayumi and Miura Remi. Special thanks goes to Lan A. Li for her assistance with video production and to the reviewers at Music Theory Online for their time and feedback.
Return to text
1. A complete list of Japanese terminology appears in the glossary.
Return to text
2. Although tōgaku originates from Tang China, the style as we understand it today was reorganized between 833–50 by Emperor Saga (嵯峨天皇), who was responsible for standardizing the gagaku ensemble (Malm 2000, 99–100).
Return to text
3. A tōgaku ensemble is comprised of shō, hichiriki (篳篥; double-reed flute), ryūteki (龍笛; transverse flute), biwa (琵琶; lute), gakusō (楽箏; zither), and three percussion instruments: taiko (太鼓; big drum), shōko (小鼓; small gong) and kakko (鞨鼓; barrel-shaped drum). The primary melody is always played by the hichiriki and embellished by a similar yet not entirely identical melody on the ryūteki (see Terauchi 2011). The shō, gakusō, and biwa provide accompaniment.
Return to text
4. Timothy Koozin (2011) follows a similar approach, integrating transformational theory into an analysis of guitar performance to examine how harmonic patterns in pop-rock music are correlated with the layout of the guitar fretboard.
Return to text
5. The pitch
Return to text
6. The shō is currently used in four genres of gagaku: the instrumental (kangen; 管絃) and dance (samai; 左舞) genres of tōgaku and in the vocal genres of rōei (朗詠) and saibara (催馬楽).
Return to text
7. Crucially, performers must keep their instruments heated to prevent the reeds from trapping moisture. Using a charcoal or electric heater, shō players heat their instruments not only before and after performances, but also during any pauses or breaks between individual pieces.
Return to text
8. According to Shigeo Kishibe and Leo Mario Traynor (1952) and Hayashi (1954), the pipes ya and mō were assigned the pitches G and
Return to text
9. While an overview of the rhythmic and metrical principles of gagaku lies beyond the scope of this article, interested readers should consult Endō 2013, 147–52; Garfias 1975, 81–113; Kapuscinski and Rose 2013a; Masumoto 2010, 218–33; and Terauchi 1996.
Return to text
10. Alexander R. Jensenius et al. (2010, 23–24) propose four frequently used categories of gesture in music: sound-producing, communicative, sound-facilitating, and sound-accompanying.
Return to text
11. See also Berry (2009, [2]), who proposes the term “practical bodily gesture” to refer to “movements of the body that are concerned with producing sound from one’s instrument.”
Return to text
12. The minimization of the individual in gagaku is also reflected in the fact that names of composers for many classical pieces are seldom known or recorded.
Return to text
13. I thank Steven G. Nelson for bringing this point to my attention. Drawing upon James Gibson’s (1986) theory of affordances, previous work in music perception and empirical musicology has explored the correlation between instrument design and musical idiomaticity (Huron and Berec 2009; Windsor and de Bézenac 2012).
Return to text
14. The practice of translating gagaku into Western notation is also common outside the realm of scholarly discourse. For example, Shiba Sukehiro (1969, 1971), former head of the Music Department of the Imperial Household Agency, transcribed a number of Gagaku works into Western notation. For a brief introduction to the theory of the gagaku tone system, see Garfias 1975, 57–71.
Return to text
15. Andrew Mead also suggests the possibility of “different patterns of nearness for production versus perception” (1999, 8).
Return to text
16. The finger holes for the otsu, ge, and hi pipes are located on the inside rather than on the outside. Moreover, given its physical location on the instrument, the hi pipe is pressed using the backside of the ring finger.
Return to text
17. Whereas Lewin’s Generalized Interval System (GIS) is based on a Cartesian perspective, which positions the listener as an external observer to model distances between two musical objects, the STRANS system adopts a transformational perspective, which encapsulates both the idea of the interval as distance and as motion (Satyendra 2004, 100). The STRANS perspective rephrases the logic of measuring the “intervallic distance from s to t” into the following statement: “Ti is the unique transposition operation on this space that maps s into t” (Lewin 1987, 157).
Return to text
18. The reader will notice that the pipes ya and mō, respectively numbered 9 and 16 in Example 2a, are left out of the formula, as neither is used in playing aitake.
Return to text
19. The following formula is modeled after Joti Rockwell’s Definition 1 (2009a, 140).
Return to text
20. The alignment of the fingers on the shō from right to left correlates with the order of the letter designations in the formula.
Return to text
21. Whereas the finger hole for jū is located on the side of the pipe facing the performer, the hole for ge is located on the side of the pipe facing away from the performer.
Return to text
22. The performer’s experience of a movement in clockwise or counterclockwise motion, however, depends on which finger they are moving. While a movement in clockwise motion requires extending the right-hand thumb or left-hand ring finger, a movement in the same direction requires the performer to contract their right-hand index finger or left-hand thumb.
Return to text
23. Dmitri Tymoczko asks a somewhat similar question in the context of voice-leading size in Western common-practice music theory: “is the smaller voice leading the one that minimizes the total amount of motion or the largest distance moved by any voice?” (2011, 49). For Tymoczko, having more voices moving by smaller distances constitutes a “smaller” voice leading as compared to fewer voices that move by larger distances.
Return to text
24. The approach of categorizing aitake based on the gestural proximity of te-utsuri is similar to that of Richard Cohn’s voice-leading zones, which categorize major and minor triads based on the distance (in voice-leading units) from the C augmented triad (2012, 102–6).
Return to text
25. The only exception is aitake kotsu, which shares four out of the five pitches (A5, B5, E6, F
Return to text
26. The aitake gyō as well as jū in Sōjō mode pose interesting questions about issues of cardinality and present a promising direction for future research. The issue of cardinality has been a recurring theoretical issue in considering parsimonious voice leading: see Cheung 2018, Childs 1998, Rockwell 2009b, Straus 2003, and Tymoczko 2011.
Return to text
27. Otsu, in fact, is the only member of Category 1 that can be reached via minimally parsimonious te-utsuri from jū: moving from jū to ge and bō each requires a total of three finger hole traversals, and motion from jū to ichi and kotsu requires a total of four finger holes (Appendix). Moving from jū to aitake in Categories 2 and 3 requires more laborious te-utsuri. Similarly, the closest aitake to ge are ichi and otsu in Category 1, jū in Category 2, and bi in Category 3, each requiring a traversal of three finger holes in total, with bō and kotsu (both Category 1) requiring transformations of four and five finger holes, respectively.
Return to text
28. According to the rules established in Example 13, the te-utsuri from jū (Category 2) to otsu (Category 1) [TU(-1, +1, 0, 0)] is more proximate than that from kotsu to otsu [TU(0, 0, 0, -2)], both of which are in Category 1. This exception does not suggest that jū should also be considered a Category 1 aitake. Category 1 constitutes a network of aitake that are connected to one another through minimally parsimonious te-utsuri. Since there is only one aitake from which jū can be reached by minimally parsimonious te-utsuri, jū cannot belong in Category 1. While the reason for this will be explored in further detail later in the article, for now it is sufficient to note that jū cannot be categorized as a Category 1 aitake due to a lack of consistency in the te-utsuri proximity between jū and the other Category 1 aitake.
Return to text
29. In principle, shō players must first memorize shōga (唱歌), a system of mnemonics used for learning repertoire, before learning te-utsuri. To this day, all musical knowledge is transmitted orally from teacher to student through the recitation of shōga (Shono 1987, 25). In the Music Department of the Imperial Household Agency, for example, students are only permitted to lay their hands on an actual instrument after demonstrating mastery of shōga. In university courses and amateur ensembles, however, te-utsuri is taught in tandem with shōga.
Return to text
30. Ōno’s discussion of shōga for shō follows the format of “Te-utsuri Kudensho” (「手移口伝書」), a set of notes on te-utsuri compiled by his colleague Yamanoi Motokiyo (山井基清; 1885–1970). Yamanoi’s notes are considered by many to be the authoritative source on te-utsuri. The notes (published in Ōno 1996, 369–88) were originally passed down to Yamanoi from Imperial Household Agency musician Ōno Tadayori (多忠保; 1873–1941).
Return to text
31. Goshōraku-no-kyū, the third section of a three-part work, represents five moral principles: benevolence, social responsibility, respect, wisdom, and trustworthiness.
Return to text
32. Each hyōshi—which loosely translates to ”metrical phrase”—in Goshōraku-no-kyū is comprised of four “measures” consisting of eight beats for a total of 32 beats. Each measure contains either one or two aitake. If a single measure contains two aitake, their durations are equal and thus each aitake lasts for two beats.
Return to text
33. In his analysis of Sofia Gubaidulina’s Pantomime, Berry makes a similar case from the perspective of the audience, noting that audience members are able to “experience the piece through their bodies as it unfolds, recognizing periods of tension and relaxation as a kind of musical form” (2009, [14]).
Return to text
34. The definition of chōshi has no equivalent in Western music and thus requires an unpacking of Japanese aesthetics and the tone system of gagaku to fully appreciate its inner workings, which is beyond the scope of this study. Broadly speaking, the concept is construed as a pattern of melodic movement according to the mode in which the piece is set. For a more detailed discussion of chōshi, see Endō 2013, 137–45 and 153–62, Marett 2001b, and Masumoto 2010, 203–7.
Return to text
35. Hayashi has also noted that the pitch-class content for any given aitake falls within the range of seven consecutive fifths (Hayashi 1954, 22).
Return to text
36. Ogyū Sorai, Kingaku Dai-ishō (琴学大意抄)(1722); Tayasu Munetake, Gakkyokukō Furoku (楽曲考付録)(1768) (Hayashi 1954, 18).
Return to text
37. The procedures for tuning gagaku instruments—especially the shō and the gakusō—and the problems caused by these tuning systems are outlined in Tōgi 1989, Akedo 2011, and Service 2012.
Return to text
38. The shō is only capable of playing nine of the twelve pitch classes in the tone system. János Kárpáti has echoed this claim, noting that “there is no mention in the sources of actual musical material being transposed into all twelve degrees” (1983, 175).
Return to text
39. For a detailed theoretical discussion of the ryo and ritsu modes, see Garfias 1975 (59–63), Service 2012 (187–94), and Endō 2013 (134–46).
Return to text
40. More detailed comparisons of the Japanese and Chinese tone systems are offered in Hayashi 1954 and Garfias 1975, whereas historical analyses of the differences between the Japanese and Chinese traditions can be found in Marett 1985, Watanabe 2009, and Ono 2016.
Return to text
41. Tuning techniques used in gagaku (e.g., Method of Subtracting and Adding Thirds, Method of Advancing Six and Retreating Eight, and Method of Advancing Eight and Retreating Six; terms translated into English in Service 2012, 187–91) are outlined in Akedo 2011 and Service 2012, 187–92.
Return to text
42. This finding is consistent with Malm’s observation which designates D as “the basic pitch of the Japanese tonal system” (2000, 114).
Return to text
43. As with the aitake gyō, jū (Sōjō) is categorized as a Category 2 aitake due to differences in cardinality.
Return to text
44. Cusick’s vision towards an embodied music theory has been pursued by a growing number of music theorists in recent years (Abrahams 2019; Cox 2011; De Souza 2017, 2018; Doğantan-Dack 2011; Easley 2015; Koozin 2011; Kozak 2019; Montague 2012; Rockwell 2009a; Sterbenz 2017). The relationship between instrumental gesture and musical sound has also been explored by ethnomusicologists (Baily 1977, 2006; Baily and Driver 1992; Yung 1984).
Return to text
Copyright Statement
Copyright © 2020 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
12625