A “Proto-Theme” in Some of J. S. Bach’s Fugal Works
John S. Reef
KEYWORDS: J. S. Bach, fugue, schema, Schenker, variation
ABSTRACT: This article focuses on a pattern of harmony and voice leading that appears, elaborated, in several fugue expositions (and generically related passages) by J. S. Bach. I contextualize this pattern in examples of “schematic” Baroque fugal writing and suggest that for Bach it functions as a sort of “proto-theme,” with respect to which certain expositions stand as “variations.” These expositions eschew normative I–V–I progressions of Stufen and thus offer a challenge to William Renwick’s exhaustive methodology for fugue analysis. Bach’s variations may respond motivically and energetically to a sense of retrogression implicit the proto-theme, as I demonstrate with an analysis of the Fugue in A minor from Book II of The Well-Tempered Clavier, BWV 889.
DOI: 10.30535/mto.26.4.7
Copyright © 2020 Society for Music Theory
Introduction
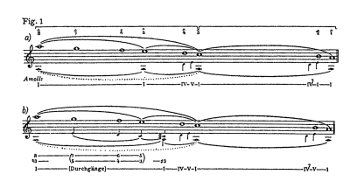
Example 1. Three fugue expositions by J. S. Bach
(click to enlarge and see the rest)
Example 2. A common pattern of harmony and voice leading, or “proto-theme,” in J. S. Bach’s fugal music
(click to enlarge)
[1.1] The three passages by J. S. Bach quoted in Example 1 noticeably resemble one another in a way that goes beyond their identity as two- and three-part keyboard fugue expositions: each elaborates the same pattern of harmony and voice leading. Example 2 summarizes their common pattern as a series of six chords, in A minor, whose upper voice makes a descending ➑–➐–➏–➎ tetrachord, preceded optionally by ➎. Capital letters A–F refer the chords in Example 2 to the passages in Example 1, in which each chord is elaborated (or expanded) until the onset of the next. (Gjerdingen-style white-on-black scale-degree symbols indicate upper-voice placement in these examples; black-on-white symbols will indicate lower-voice strands in some subsequent examples, and traditional capped numerals will mark structural voice leading in others.)
[1.2] Chords A–F largely correspond with the formal functions labeled on Example 1 (and boldfaced here). A and B concur with presentations of imitative content: in each excerpt a leading subject entry, or dux, sounds within an expansion of tonic chord A; and its answer, or comes, associates with dominant chord B, either transpiring entirely within an expansion of B, as in the Fugue in A Minor, BWV 944 (Example 1a), or beginning inside A and concluding on B, as in the Duetto in A minor, BWV 805 (Example 1b) and the Fugue in A minor from Book II of The Well-Tempered Clavier, BWV 889 (Example 1c). In BWV 944, a short “particle” figure follows the dux within A;(1) in all three excerpts, chromatic inflections of A (marked with asterisks) prompt motion to B. By expanding or concluding on dominant harmony, each excerpt’s comes (along with its counterpoint) imparts a sense of departure or a degree of mobility to a presentational function, which I designate presentation (mobilization). Such mobilization instigates form-functional development beyond each excerpt’s opening presentations.
[1.3] Descending-fifths sequences follow each dux–comes pair and express a continuational function across chords B–F as motivic repetitions break away from closed imitative shapes. The sequence in BWV 889 forms a bridge to another dux statement—thus, to a consolidation of presentational discourse following sequential fragmentation.(2) The analogous sequences in the other two expositions are pre-cadential: in BWV 944, descending fifths “evolve” (symbolized by an arrow, ⇒) beyond a continuational function, into an authentic cadence (with a stepwise upper-voice descent to ➊); and in BWV 805, they prepare a second sequence that evolves into a deceptive cadence.(3)
[1.4] Although originally intended for functions within Classical “sentences,”(4) the terms presentation, continuation, and cadence map neatly onto the imitations, sequences that depart therefrom, and formulaic closes in Example 1, with the qualifying terms mobilization, consolidation, bridge, and pre-cadential making them more apposite to Baroque fugal processes.(5) Brackets above staves in that example associate functions with grouping structure: most significantly, continuations may group either to the left, as evolutions of the presentations that precede them (as in BWV 889), or to the right, as more independent units (as in BWV 944 and BWV 805).(6)
[1.5] The three passages in Example 1 differ markedly in character. The pervasive sequential construction and sweeping sixteenth-note figuration of BWV 944 suggest an Italianate concerto and emphasize “Vivaldian” virtuosity; a prominent diminished-seventh leap imparts a degree of sternness to BWV 889 (although David Ledbetter hears that exclamation as parody of a cliché [2002, 315]), and the pathos of BWV 805 may veil bourrée characteristics (Williams [1980] 2003, 534–35). Yet they are “of a piece”: their similar frameworks are conspicuous. In fact, several fugues and otherwise imitative pieces by Bach—mostly but not exclusively for solo keyboard—contain passages formally related to the chords in Example 2. These passages are the focus of the present article.
[1.6] In his influential treatise Analyzing Fugue: A Schenkerian Approach, William Renwick proposes several middleground “exposition patterns” to describe tonal organization in fugue expositions (1995a, Ch. 4). These common patterns of structure are useful for demonstrating the underlying similarities of stylistically diverse fugues and for relating individual works to structural norms. My interest in the pattern in Example 2 would seem to be in line with, and even overlap with Renwick’s work. Indeed, I proceed in sympathy with his closing words, that
A clear and systematic process of recognition of structural similarities within the genre of fugue
. . . provides the best basis upon which to identify and assess the unique qualities that individuate fugues and give each creative work its characteristic shape and expression. (209)
I will argue, however, that expositions like those in Example 1 make a poor fit with Renwick’s methodology and demand alternative approaches to structural similarity. Examination of these and other expositions discloses tonal structures that do not accord with the I–V–I progressions Renwick takes as universal grounding for successive imitations in fugue expositions. Furthermore, I suggest that the common basis of these expositions is a musical entity different in kind from Renwick’s exposition patterns: not an ideal result of the theoretical working-out of structural possibilities, but a real, operational musical idea, situated historically in the decades surrounding Bach’s career.
[1.7] On the one hand, the chords in Example 2 relate to a common Baroque contrapuntal schema, as I will discuss below; on the other, they suggest a fragment of actual music, something like a thoroughbass piece in A minor. Passages by Bach like those in Example 1 may accordingly be understood in part as schematic reference and in part as thoroughbass elaboration, or variation, and these understandings may sometimes blur together. A variation conception may be especially salient, however, when two or more expositions exhibit similar motivic or phrase-rhythmic strategies as they elaborate the chords in Example 2. As I will demonstrate, certain strategically similar excerpts imply related compositional evolutions from the same guiding idea.
[1.8] Yet as Renwick notes, considering certain works against a background of common patterns can set their extraordinary qualities in relief. In Bach’s music I often sense a striking “formal dynamism,” whereby energetic processes extend across successive presentational, continuational, and cadential functions, uniting and giving impetus to them, and belying the appearance of demarcation that their labeling implies.(7) In this connection, I will draw out some energetic interactions in the A-minor Fugue from Book II of WTC, BWV 889, at the end of this article.
Bach’s “❽–❼–❻–❺ Proto-Theme” and a Related Schema
Example 3. The “➑–➐–➏–➎ schema”: (a) basic voice leading (b) with 2–3 suspensions (c) with interpolated lower-voice descending fifths/ascending fourths (d) with interpolated lower-voice descending thirds/ascending steps
(click to enlarge)
[2.1] The chords in Example 2 envelop the more abstract voice leading manifoldly illustrated in Example 3, a contrapuntal schema that many Baroque composers (including Bach) actualized in their fugue expositions. Various embellishments link a basic “first-species” schematic model to those chords, which thus crystallize as a particular development of this voice leading.
[2.2] Example 3a represents the schema as a piece of two-voice counterpoint, in which ➑–➐–➏–➎ (with optional ➎ initiator) sounds above ➀–➄–➃–➂. Its voices proceed (more or less) note against note and produce the interval succession (5)–8–3–3–3 as they pass through the space of a tonic triad. (Tenths may replace thirds in some instances.) The schema appears here in C major, although it may occur in any major or minor key; Dorian versions are also possible. Example 3b shows how 2–3 suspensions may embellish the “➑–➐–➏–➎ schema” (as I will call it), while Examples 3c and 3d illustrate lower-voice interpolations between schematic parallel thirds. Proceeding either by descending fifth/ascending fourth or by descending third/ascending step, these contrapuntal interpolations (shown in major- and minor-key versions) may imply descending-fifth root motion. Passages that hew to the note-against-note model (Example 3a) seem to be uncommon; usually at least one suspension or interpolated leap appears as an embellishment.
Example 4. ➑–➐–➏–➎ schema settings in (a) J. S. Bach, Fugue in C Major, BWV 952; (b) Bach, Contrapunctus II, Art of the Fugue, BWV 1080; (c) Johann Ernst Eberlin, Toccata No. 1 in D Minor; (d) Dietrich Buxtehude, Toccata in G Major, BuxWV 164; (e) Johann Pachelbel, Fugue in B Minor, PWC 141
(click to enlarge and see the rest)
[2.3] Example 4 gives several representative passages. In its simplest formal dispositions, the ➑–➐–➏–➎ schema spans a fugue’s initial dux–comes pair. Comes usually appears above dux, making the schematic ➑–➐–➏–➎ tetrachord roughly congruent to a tonal answer. The opening measures of Bach’s Fugue in C Major, BWV 952 (Example 4a), are typical. An alto-part dux transpires over an implied ➀ pedal, ascending ➎–➑ and then descending through the lower fifth of the C4–C5 octave (labeled in parentheses). A soprano-part comes then replies to the fifth-descent of the dux with the descending tetrachord ➑–➐–➏–➎. In counterpoint with the comes, the alto elaborates the schema’s ➀–➄–➃–➂ strand with descending-third/ascending-step interpolations (see Example 3d). The beginning of Contrapunctus II from Bach’s Art of the Fugue, BWV 1080 (Example 4b), disposes the ➑–➐–➏–➎ schema similarly (although over bass and tenor entries), embellishing its voice leading with one interpolated fifth and one suspension.
[2.4] In Johann Ernst Eberlin’s Toccata No. 1 in D Minor (Example 4c), dux appears above comes. The soprano-part dux establishes ➑ and descends through a preliminary ➑–➐–➏–➎ tetrachord; a tonal answer in the alto follows with the schema’s lower voice while the soprano’s counterpoint recaptures ➑ and provides a true schematic descent to ➎. (The redundancy of two descending tetrachords might make this excerpt seem less satisfactory than the others). Eberlin overlaps a tenor-part dux with the end of the comes—apparently a common arrangement—so that ➀ appears below the final ➎/➂ third of the schema.
[2.5] More formally complex ➑–➐–➏–➎ schema settings may include a continuation (bridge) along with dux and comes. Continuations are usually sequential, based on interpolations like those in Examples 3c and 3d. In Buxtehude’s Toccata in G Major, BuxWV 164 (Example 4d), dux and comes project partial upper and lower strands of the schema, ➎–➑–➐ and ➀–➄ (mm. 1–3.1). The remainder of the schema is taken up by continuational material (mm. 3–4.1), which sequences a motivic third figure, derived from dux and comes, through the parallel thirds ➐/➄–➏/➃–➎/➂ and their interpolations. The exposition of Pachelbel’s Fugue in B Minor, PWC 141 (Example 4e), is comparable, but lacks such a secure motivic relationship between imitations (mm. 1–4) and continuation (mm. 5–6.1). A passing ➑–➐–
Example 5. ➑–➐–➏–➎ schema settings with some deviations from the basic forms in Example 3: (a) Buxtehude, Canzonetta in A Minor BuxWV 225; (b) Buxtehude, Praeludium in G Minor, BuxWV 163
(click to enlarge and see the rest)
[2.6] All of these passages relate straightforwardly to the voice-leading models in Example 3 and seem to justify the schematic status of these models. Certainly, coeval passages with a less exact relationship to those models are common, and some of them may be understood, with more or less certainty, as representatives of the same schematic knowledge. For instance, the opening measures of Buxtehude’s Canzonetta in A Minor, BuxWV 225, reproduced in Example 5a, lack a schematic ➃, but understanding that scale degree as an implied tone (as D5 or D4) makes it easy to assimilate this passage.(9) The fugal exposition from Buxtehude’s Praeludium in G Minor, BuxWV 163, in Example 5b is more problematic, with ➃ appearing in an inner voice and with an inverted ➐/➄ dyad. But in this passage, too, a schematic conception may be grasped, if less securely; I offer a hypothetical, schematically normative alternative for comparison.(10) It may be impossible to specify how much deviation the ➑–➐–➏–➎ schema can brook before losing its schematic identity, but the schema surely does admit some amount of dyadic inversion and scale-degree implication.
Example 6. The ➑–➐–➏–➎ schema and evaded cadences in (a) Angelo Predieri, Dixit, cited in Martini [1774–75] 1958; (b) Bach, Fugue in E Major, WTC II, BWV 878
(click to enlarge)
[2.7] Also resistant to precise measure is the degree to which the ➑–➐–➏–➎ schema overlaps and blends with other schematic categories. For instance, a total inversion of some of the forms in Example 3 is conceivable, but such a transformation (which would move ➑–➐–➏–➎ to the bass) might merge to an indeterminate degree with lament bass formulas.(11) Or more germane: the “fourth-species” model given as Example 3b can describe a common type of evaded cadence—not the “deceptive” V–VI, but a feint to the dominant that falls back to tonic—and the schematic conception of certain dux–comes pairs appears to be bound up with cadential evasion. At the beginning of the D-Dorian Dixit opening by Angelo Predieri, reproduced in Example 6a (from Giambattista Martini’s Esemplare [1774–75] 1958, 274 ff.), the countersubject’s descent to A3 (m. 3) and subsequent leap E4–A4 (m. 4), in counterpoint with the comes, imply culmination in a dominant discant clausula, ➄–
Example 7. Schematic ➑–➐–➏–➎/➀–➄–➃–➂ voice leading in a nonimitative generic context: François Couperin, Ordre 8ème de clavecin, Rondeau
(click to enlarge)
[2.8] Lest schematic voice leading be circumstantiated within too narrow a generic range, I give in Example 7 a passage from the Rondeau of François Couperin’s Ordre 8ème de clavecin (cited as well by David Beach as a counterexample in his article on octave lines [1988, 280–83]), which is schematically normative but not imitative. ➎–➑–➐–➏–➎ and ➀–➄–➃–➂ sound plainly in mm. 1–4, whereupon continued stepwise descent, ➍–➌ over ➁–➀, leads to a half cadence in the Rondeau’s eighth measure. (The four- and eight-measure periodicities delineated here are uncharacteristic of the imitative works excerpted above.) Indeed, elements of the ➑–➐–➏–➎ schema can easily be found outside of imitative genres; they are not unusual in tonal music in general. It might be supposed that the mundanity of this voice leading argues against its special consideration as a fugal schema; against this, I note that this voice leading readily supports imitation at the fifth and therefore pairs naturally with fugal procedures. Examples 4–6—along with a host of additional passages by composers such as Froberger, Fux, Handel, Johann Krieger, Kuhnau, and Vivaldi—make clear the status of this voice leading as a common—but by no means a default—organizer of fugal imitation in Baroque counterpoint.
[2.9] In light of the foregoing examples, the pattern in Example 2 may be understood as a chordal representation of the ➑–➐–➏–➎ schema with descending-fifth interpolations (Example 3c)—a transformation, as it were, of a contrapuntal framework into a piece of thoroughbass. In this way, the passages in Example 1—which acknowledge the more chordal conception of Example 2 with their arpeggio-based figuration—attest to the same shared schematic knowledge. That the pattern in Example 2 should default to a minor key is not remarkable, as minor keys more naturally situate the descending-fifth motion to the mediant with which the pattern ends (chords E and F). What is curious, however, is that when Bach disposes this pattern over dux, comes, and continuation together, he reveals a strong preference for the key of A minor. (In contrast, no particular key tendencies are evident in his references to the ➑–➐–➏–➎ schema outside of its chordal crystallization in Example 2.) This suggests that in addition to the contrapuntal schema forms in Example 3, Bach’s compositional (and improvisational?) imagination may have apprehended the more concrete A-minor thoroughbass fragment in Example 2 as a distinct, if overlapping, category—less a “theme” to be varied than a “proto-theme,” left formally open, with no closing formula, and unmetered.
Example 8. Pieces by J. S. Bach with passages related to the proto-theme in Example 2
(click to enlarge and see the rest)
[2.10] Passages by Bach may refer, then, to either formulation, or to both. Example 8 lists several fugues and fugue-like pieces with expositional passages that appear to be “➑–➐–➏–➎ proto-theme” variations, at least in part. The first eight items, with a common key of A minor and chordal figuration evident in their elaborations, are the most clearly related. The others may differ in key, or they may lie in their conception somewhere between the chordal proto-theme and the contrapuntal schema forms in Example 3, yet they bear—to my ears, at least—a family resemblance sufficient to warrant their inclusion.
Example 9. Schenker’s analysis ([1926] 2014, 32) of J. S. Bach, Fugue in C Minor, WTC I, BWV 847, mm. 1–9
(click to enlarge)
[2.11] Although the ➑–➐–➏–➎ proto-theme does not imply identical tonal structures in all of the passages it underlies, it does impinge on tonal structure, with its first and last chords usually delimiting a discernable unit of voice leading that overarches dux, comes, and sequential material. An essential similarity among proto-thematic passages concerns chord B (an E-minor triad in the key of A minor), which may induce a tonal polarity between I and V at more immediate levels but does not serve as a functional dominant Stufe within the middleground counterpoint of the proto-theme as a whole, or in the formal context of a complete exposition. This would seem to be atypical in light of Renwick’s work and of a number of published analyses of fugues, which invariably align the successive imitations of an exposition with complete progressions of I, V, and I Stufen. For instance, the second line of Roman numerals in Example 9, from Heinrich Schenker’s analysis of the C-minor Fugue from WTC I, BWV 847, shows such a progression beneath the exposition’s imitations, Führer–Gefährte–Führer (dux–comes–dux).
Tonal Structure and Bach’s ❽–❼–❻–❺ Proto-Theme
[3.1] From recognition of the proto-thematic similarity of the passages in Example 1 and others, stems an investigation into what kinds of tonal structures the passages express and how similar those structures are. Two published graphical analyses of a short exemplar, Bach’s “Little” Prelude in A Minor, BWV 942, make a good starting point. The first is by Schenker and appears (with commentary) in Das Meisterwerk in der Musik, volume 1 ([1925] 2014). The second, by Allen Forte and Stephen E. Gilbert, is given as an exercise solution in their Introduction to Schenkerian Analysis Instructor’s Manual (1982b, 96).
Example 10. J. S. Bach, Prelude in A Minor BWV 942, mm. 1–9
(click to enlarge and see the rest)
[3.2] Example 10 shows the first phrase of this two-part “mini-invention,”(13) which presents fifth-related dux and comes entries at its outset. An upper-part dux (with lower-part accompaniment) expands chord A (Am) of the ➑–➐–➏–➎ proto-theme, sounding ➑ immediately and reiterating it several times. A lower-part comes then enters below ➐ and expands chord B (Em). A sequential continuation overlaps the end of the comes and elaborates chords B–F, and at F (CM) another comes enters in the upper part and prepares an imperfect authentic cadence.
Example 11. Schenker’s analysis ([1925] 2014, 63) of J. S. Bach, Prelude in A Minor, BWV 942 (annotated)
(click to enlarge and see the rest)
[3.3] Examples 11 and 12 reproduce portions of Schenker’s and Forte and Gilbert’s illustrations. The Schenker extract (Example 11) shows four distinct structural levels, with level a lying closer to the background and level d closer to the foreground.(14) At level a, an octave Urlinie appears as a sixth from to , followed by a third from to . The sixth spans the nine-measure phrase under consideration here and is itself articulated as the fourth ––– plus the third ––. The fourth transpires as a Leerlauf above a tonic pedal, the third over the cadential degrees I–IV–V
[3.4] Subsequent levels reveal more development of the fourth than of the third. At level b, an inner voice makes parallel tenths with the fourth’s –– succession. This combination produces the basic shape of the ➑–➐–➏–➎ schema (see Example 3a), which Schenker interprets as
[3.5] At level c, schematic intervals from level b materialize as complete chords. A minor, E minor, D minor, and C major (with a suspended seventh) appear under scale degrees ➑, ➐, ➏, and ➎, respectively, and correspond to chords A, B, D, and F of the proto-theme.
[3.6] Level d reveals “a more abundant flow of diminution” (62). Expansions of chords A and B carry the active voice leading of dux and comes, and elaborations of the other chords develop the passage’s sequential construction.
[3.7] Schenker contends that there is no progression of Stufen beneath the ––– tetrachord: “The richness of all these sonorities [chords B–F] in no way contradicts their passing nature. . . . no matter how much independence they feign, they must never be mistaken for the harmonic degrees [Stufen] V
Example 12. Forte and Gilbert’s analysis (1982b, 96) of J. S. Bach, Prelude in A Minor, BWV 942 (annotated)
(click to enlarge)
[3.8] A different understanding is evident in Forte and Gilbert’s illustration (Example 12), which comprises two aligned systems: a durational reduction (from
[3.9] Forte and Gilbert associate this phrase’s Urlinie span with I–IV–I plagal motion (see their beamed open-headed bass notes), in which both tonics are composed out and chord D (Dm) represents IV. Chords A–C expand the initial tonic beneath –, with C inflecting tonic as
[3.10] Schenker’s reading is undoubtedly simpler than Forte and Gilbert’s, and I think that it comports better with the motional character of this music. The Prelude begins with a sense of falling through tonal space; the comes entering on chord F (m. 6) checks this falling and then initiates a more controlled descent through a cadence. This Gestalt of musical motion is implicit in Schenker’s fluid representation, but it is effaced by Forte and Gilbert, with their isolation of IV and their reading of an auxiliary cadence that detaches the cadential scale degrees of this phrase from its opening tonic.
[3.11] Questions arise in considering both of these analyses together: If Schenker’s is preferable for the Prelude BWV 942, then can it guide the analysis of other passages based on the same proto-theme? And if so, what kinds of contextual adjustments might be required? If Forte and Gilbert’s analysis is somewhat adverse to the aural experience of BWV 942, can aspects of their analysis nevertheless prove useful in addressing other pieces? The first of these questions can be answered affirmatively. As for the second, it should be noted that the middleground counterpoint of the ➑–➐–➏–➎ proto-theme may interact with earlier and later levels in ways that impinge on its analytical representation. With respect to later levels, different alignments of chords A and B to dux and comes may affect how those chords are expanded. And with respect to earlier levels, the final proto-thematic chord, F, may be variously situated in larger tonal contexts; furthermore, the proto-theme may coincide with any Urlinie form. An affirmative answer to the third question is implied in [3.18], below.
Example 13. Tonal structures in the expositions by J. S. Bach quoted in Example 1: (a) Fugue in A Minor, BWV 944; (b) Duetto in A Minor, Clavier-Übung III, BWV 805; (c) Fugue in A Minor, WTC II, BWV 889
(click to enlarge and see the rest)
[3.12] In Example 13, I give voice-leading graphs of the three passages in Example 1. Following Schenker, I interpret the proto-thematic basis of each passage as passing tenths through tonic harmony—that is, as I(
[3.13] Like the Prelude BWV 942, BWV 944 places its initial dux above the subsequent comes and features a real answer, so that the dux introduces and composes out chord A, and the comes composes out chord B below ; but the arrangement in BWV 805 and BWV 899 is more complex. These two fugues feature tonal answers, with dux below comes. As I illustrate, their comites begin within expansions of tonic chord A and themselves introduce , thence leading to and chord B. In BWV 889, a “cast-out” root B2 combines with ––
[3.14] Finally, I show how the three passages situate chord F in ways that differ from the Prelude BWV 942. Whereas a tonic root appears below chord F (CM) in BWV 942 (according to Schenker’s analysis), passing tenths continue beyond F in BWV 944 and BWV 805. They lead into an authentic cadential progression in the former; in the latter they flow into a deceptive cadence, which I represent as a pair of unfoldings within the plagal relationship I–IV–I.(16) In BWV 889, the dyad C3–E4 represents chord F, and although this dyad initially seems to imply a C-major triad (C–G–E), it is probably better understood as A minor (C–A–E), a simple proto-thematic modification. Either way, chord F is caught up in an ascending progression of Stufen, I–IV–V
[3.15] It bears reiterating that the essential meaning of proto-thematic chord B—here and in other similar expositions—is not harmonic but contrapuntal. Even if B is prepared on the foreground by a strong I–II
Example 14. Tonal structure in the exposition of J. S. Bach, Fugue in A Major, WTC II, BWV 888
(click to enlarge)
[3.16] Example 14 gives a rarer major-key proto-theme elaboration from the Fugue in A major from WTC II, BWV 888, in which the leading tone, after sounding atop chord B (EM), turns down to
Example 15. Tonal structure in J. S. Bach, Fughetta in E Minor, BWV 900
(click to enlarge)
[3.17] While both and are obvious Kopfton candidates for pieces that begin with ➑–➐–➏–➎ proto-theme elaborations, the possibility of should not be discounted. Yet I have only found one possible example, and it is not an unambiguous one. Example 15 presents a complete graph of the Fughetta in E Minor, BWV 900, proposing a polyphonic Ursatz in which an Urlinie from (beamed up) lies above one from (beamed down).(18) The proto-theme is clear at the outset of this fughetta, although chord F is elided, in a way, for in m. 23 a lower-part dux asserts a root-position tonic triad in its place.(19) In light of this change, I have represented the proto-theme’s lower voice somewhat differently than in earlier graphs, not with a passing third-progression across chords B–F (as in Examples 13 and 14), but with a pair of interpolated fifths, one upper and one lower (E3–B3, [A2]–E3).(20)
Example 16. Adaptations of the ➑–➐–➏–➎ proto-theme that progress from I to III: (a) basic form, with as Kopfton; (b) basic form, with as Kopfton; (c) interpolated chords e and f, with as Kopfton; (d) interpolated chords e and f, with as Kopfton
(click to enlarge)
[3.18] Just as Schenker finds no progression of Stufen within the proto-thematic portion of the Prelude BWV 942, so too have I represented the proto-thematic chords in the foregoing examples as tonic-prolonging contrapuntal harmonies. But in some pieces, the ➑–➐–➏–➎ proto-theme interacts with early middleground levels in a way that yokes its chords to a progression from I to III, by way of the descending fifths IV and VII (II and V in the key of the mediant). In Example 16 I give four models of a I–IV–VII–III progression, for which I borrow Forte and Gilbert’s reading of chords A–D as I–IV (see Example 12). For the first two models (Examples 16a and 16b), I simply attach IV, VII, and III to chords D–F and adapt upper-voice motion to either an -line or a -line; I note that E may break the sequential motion of the chords preceding it to stand on the dominant of III and “stage” the arrival of that Stufe. With the other two models (Examples 16c and 16d), I show how progression to III may be embellished with duplicates of chords E and F (labeled with lowercase letters) to maintain a longer sequence inside a voice-exchanging prolongation of D.
Example 17. Tonal structures in (a) J. S. Bach, Prelude in A Minor, WTC I, BWV 865; (b) J. S. Bach, Fugue in E Minor, WTC I, BWV 855
(click to enlarge)
[3.19] With reference to these models, Example 17 graphs the Prelude in A Minor and the Fugue in E Minor from WTC I, BWV 865 and BWV 855. Their proto-thematic beginnings are diagrammed in detail, and subsequent passages are summarized. In BWV 865 (Example 17a), dux and comes separately compose out chords A and B, with the ––– ascent of the dux suggesting as Kopfton.(21) Chords A–C bound an initial tonic prolongation, and chord D (IV) is related by descending fifth. Duplicates e and f prolong D sequentially, as in Example 16c; E (VII or V/III) breaks their sequencing to stage the C-major dux that follows on F—III within a middleground Stufengang.(22)
[3.20] Subject design also suggests a particular Kopfton in BWV 855 (Example 17b): the rapid descent from to through tonic harmony, leading to more active –
Example 18. Tonal structure in J. S. Bach, Partita No. 3 in A Minor BWV 827, Gigue, mm. 1–21
(click to enlarge)
[3.21] One further tonal possibility appears in Example 18, a graph of the first twenty-one measures of the Gigue from the Partita in A Minor, BWV 827. A first elaboration of the ➑–➐–➏–➎ proto-theme (mm. 1–8) omits chord F (CM), so that chord D, as IV, leads through chord E (stated as B3–D4–F5, a 5–6 alteration of IV) to a cadential V
Bach’s Proto-Theme and William Renwick’s Exposition Patterns
[4.1] Consideration of tonal structure in certain fugue expositions (or cognate passages) entails comparison with the work of William Renwick, whose Analyzing Fugue (1995a) offers the most comprehensive account of expositional structure in the modern theoretical literature. The scope of Renwick’s methodology is well known; here I summarize only those points that are relevant to the present discussion.(24)
[4.2] Renwick assembles an array of simple voice-leading structures—linear progressions, neighbor-tone figures, and triadic arpeggiations—to describe the underlying construction of fugue subjects. He refers to these structures as “subject paradigms” (1995a, Ch. 2): nearly every fugue subject relates to a subject paradigm, and each subject paradigm implies a corresponding answer paradigm.
[4.3] According to Renwick, alternating subject and answer paradigms in fugue expositions cohere within middleground I–V–I progressions. For support, he cites Schenker’s observation in Der freie Satz that “[t]he fifth relation between the first three entries (subject–answer–subject) provided the form with direction and stability” (Schenker [1935] 1979, 1:143);(25) Renwick understands “fifth relation” specifically to involve harmonic progression.(26) In his methodology, an “exposition pattern” is the combination of a subject paradigm (and corresponding answer paradigm) with an “exposition scheme”—that is, a particular order in which polyphonic parts enter—disposed over I–V–I (1995a, 113). In exposition patterns for nonmodulating subjects, three consecutive entries compose out a complete I–V–I progression: a first dux prolongs I; a comes modulates from I to V; and depending on an exposition’s subject paradigm, either a continuation (bridge) effects a resolution to I for a second tonic-prolonging dux, or the second dux enters directly on V and itself effects a resolution. Exposition patterns for subjects that end on V (either with a tonic half cadence or with a modulation to V) place four entries over two concatenated progressions.
Example 19. Two of William Renwick’s exposition patterns: (a) for ––, subject paradigms and low–middle–high exposition schemes; (b) for –––, subject paradigms and low–middle–high exposition schemes; (c) analysis of the exposition of J. S. Bach, Fugue in G Minor, WTC II, BWV 885, according to the pattern in Example 19a
(click to enlarge)
[4.4] Any exposition pattern can describe at a middleground level many different fugue expositions. Example 19 reproduces two of Renwick’s exposition patterns (both given in the “neutral” key of C major): one for expositions whose subject’s paradigmatic voice leading is –– (tonal answer: ––) and whose parts enter in the order low–middle–high (Example 19a), and another for expositions with the same low–middle–high exposition scheme but with subjects describing ––– voice leading (answer: –––) (Example 19b).(27) The latter pattern requires a continuation (bridge) to resolve the dominant harmony at the end of the comes to tonic so that the succeeding dux may enter with ; the former does not, because its duces begin with and can therefore enter on I or V.(28) The exposition of the Fugue in G minor from WTC II, BWV 885 (graphed in Example 19c), accords with the first of these patterns.
[4.5] Yet for two key reasons, Bach’s ➑–➐–➏–➎ proto-theme-based fugue expositions do not comport well with Renwick’s exposition patterns. The first is that they do not describe complete I–V–I progressions through their alternation of dux and comes (as discussed above in [3.15] and elsewhere), whereas I–V–I is an invariant component of Renwick’s patterns. A reconciliation on harmonic grounds might be attempted either by “forcing” a proto-theme-based exposition (graphically) into a pattern-conformant I–V–I progression, or by regarding that exposition’s structure, without such a progression, as a “deformational” or “atypical” example of one of Renwick’s patterns. Neither choice may prove satisfactory.
Example 20. J. S. Bach, Fugue in A Minor, WTC II, BWV 889, exposition analyzed according to William Renwick’s exposition pattern in Example 19a: (a) pattern-conformant graph of BWV 889, mm. 1–8; (b) William Renwick’s exposition pattern, transposed to A minor
(click to enlarge)
[4.6] Example 20 takes the first of these approaches with the exposition of the Fugue in A minor from WTC II, BWV 889, which I previously graphed in Example 13c. The alternative graph in Example 20a largely conforms to the A-minor transposition of Renwick’s ––/low–middle–high exposition pattern in Example 20b, aligning the music’s opening imitations to a complete I–V–I progression and replicating the pattern’s total voice leading. Although the graph does show some transformations of the pattern—the dominant harmony at the end of the comes is extended across a continuation (bridge), and the initiation of the second dux is somewhat displaced from the onset of that harmony—they are slight and do not obscure the essential conformance. This is not an implausible reading,(29) and it falls within the parameters of Renwick’s methodology, but I think that it misconstrues the E-minor harmony at the end of the comes: linking that harmony tonally (as V) to the tonic harmony at the end of the exposition loses what I think is a more palpable, and meaningful, musical idea—the descending tetrachord ––– as a coherent piece of voice leading that responds to, and enlarges, the descending third –– of the initial dux. This reading also lessens the sense in which the dux at the end of the exposition is cadential—a characteristic better captured in my original graph, which shows the exposition’s structural V
[4.7] Alternatively, it might be supposed that the structure shown in my original graph (Example 13c) maintains enough contact with Renwick’s exposition pattern (Example 20b) to count as an atypical example of that pattern. After all, the separate voice-leading strands of dux, comes, and dux from Renwick’s pattern (––, ––, ––), and their registral dispositions, are still evident, even if their harmonic context is different. But that difference is crucial: without its imitations collectively developing a complete I–V–I progression—the entire harmonic basis of Renwick’s approach—the exposition of BWV 889 cannot be likened to Renwick’s pattern in any meaningful way—that is, in any way that goes beyond simply noting that BWV 889 shares a subject paradigm and exposition scheme with certain other fugues (which is, at bottom, a tautology).
[4.8] In other words, regarding ➑–➐–➏–➎ proto-theme-based expositions as atypical representatives of Renwick’s exposition patterns reduces to simply classifying them by subject paradigm and exposition scheme. This points to the second reason that the proto-theme and Renwick’s patterns do not comport well: the proto-theme is a different kind of entity altogether from the exposition patterns and thus describes a different kind of “similarity relation.” Coordinating these expositions with Renwick’s patterns entails placing them into many different expositional categories according to their various paradigms and schemes; yet they more naturally form a single category by virtue of their common chordal basis.
[4.9] Indeed, a variety of paradigms and schemes is apparent in just the five expositions graphed in Examples 12–14, above. BWV 944 (Example 13a) reveals the same subject paradigm (––) as BWV 889 but with an inverted exposition scheme (high–middle–low). (It also features a real answer, a situation that does not figure into Renwick’s exposition patterns for –– subjects.) BWV 888 (Example 14) exhibits the same exposition scheme as BWV 889 (low–middle–high), but I think that the best understanding of its subject’s voice leading is as an ascending third-progression, ––. The exposition of BWV 900 (Example 15) is again categorially different, because it features a –––– subject paradigm and a middle–high–low scheme. (The same –––– paradigm appears in the fugue from the Violin Sonata in B Minor, BWV 1014—another proto-theme-based exposition, not shown—but with a high–middle–low scheme instead). Finally, BWV 805 (Example 13b), with its two-part low–high exposition scheme, has a subject whose voice leading might suggest either one of Renwick’s paradigms, –– or ––—or ––, my interpretation, which falls outside of Renwick’s tally.
[4.10] Interpreting ➑–➐–➏–➎ proto-theme-based expositions in terms of Renwick’s exposition patterns would imply, for instance, that the exposition of BWV 889 (Example 13c) has more in common with the G-minor exposition from WTC II (Example 19c, an exposition unrelated to the proto-theme) than with the expositions of BWV 944 (Example 13a) and BWV 805 (Example 13b). The very essence of its similarity with the latter two, the ➑–➐–➏–➎ proto-theme itself, would be effaced. The proto-theme is not a structural model that, like Renwick’s exposition patterns, results from the theoretical combination of paradigms and schemes; it could not, in fact, be derived in this way, for nothing in that method would generate the sequential descending fifths (across chords B–F) that characterize it. It must be understood to have an identity—as a chordal framework and as a version of a common schema—that precedes and is independent of these combinatorial elements. Whereas “bottom-up” constructions like Renwick’s exposition patterns demonstrate effectively how paradigmatic (i.e., schematic) elements closer to the foreground can influence middleground structures, certain proto-thematic or schematic elements that originate in middleground counterpoint ask for more of a top-down perspective on expositional organization.(30)
Proto-Theme and Variations
[5.1] In his study of variation principles in the composition and pedagogy of J. S. Bach and his school, David Schulenberg (1982, 58–59) refers foremost to Friedrich Erhard Niedt’s Handleitung (1706), which demonstrates variation through the application of diminutions to bass lines and arpeggio figures to the chordal upper voices of thoroughbass realizations, and which shows how successive suite movements may be composed from a common bass line. For Bach, likewise and additionally, variation could consist of multiple elaborations of a thoroughbass progression, of a two-voice contrapuntal framework, or of a “Satz,” defined by Schulenberg as “an abstract contrapuntal underpinning which usually, but not always, includes the essential bass tones and their ‘realization’ in the upper parts” (75). The result might be two or more “versions” of a composition—such as the Sonatas BWV 1021, 1022, and 1038, notwithstanding questions of authorship (65–73)—or a dance suite movement and its double.
[5.2] David Beach, too, refers to Niedt in connection with variation, in his monograph on Bach’s partitas and suites; but in his closing pages, he suggests that a more expansive conception of variation is appropriate to his chosen repertoire, one that requires not a common framework, but, less stringently, “common harmonic and voice-leading constructs,” in addition to “motivic associations” (2005, 86). Significantly, Beach believes that musical evidence, more than contemporary theory, should determine an analytical threshold for variation.
[5.3] If the ➑–➐–➏–➎ proto-theme in Example 2 secures the mutual resemblance of the expositions I have discussed above, then it may be understood, as well, as a chordal and contrapuntal structure that is “varied.” Some of its variation—particularly, the consistent figuration of its sequential chords—accords with Niedt’s demonstrations. The application of imitative content to chords A and B suggests variation of a more distant sort (such as a more expansive conception, although not necessarily Beach’s, might subsume). Temporal or rhythmic relationships among the chords of the proto-theme are, of course, flexible, in contrast to a stricter conception of variation that maintains the rhythmic proportions of a model.
[5.4] This is not to say that Bach conceived of his proto-theme expositions wholly as variations. More likely, their conception involved the rhetorical stages of invention, disposition, and elaboration in equal measure: the creation of imitative content; the recognition of that content’s “fit” with the ➑–➐–➏–➎ proto-theme and the choice to dispose it accordingly; and then the sequential elaboration (variation) of the proto-theme, which Bach characteristically integrates motivically with his imitations. In this way, it is in a retrospective sense that the application of imitative content becomes an aspect of variation.
Example 21. Tonal-rhythmic reductions of outer-voice counterpoint in two fugue expositions, showing similar “fermatas”: (a) Fugue in A Minor, BWV 944; (b) Violin Sonata in A Minor, BWV 1003, II
(click to enlarge and see the rest)
[5.5] But variation can be more specific—and more experientially real—when two or more expositions betray close formal, phrase-rhythmic, and motivic connections. The expositions of BWV 944 and of the Fugue from the Violin Sonata in A minor, BWV 1003, appear to be related in these ways. Example 21 represents these expositions in tonal-rhythmic reduction, so that the durations of their underlying outer-voice counterpoint are apparent.(31)
[5.6] With right-grouping continuations whose sequential chords B–F lead to cadences, these expositions somewhat resemble the Fortspinnungstypus constructions Wilhelm Fischer described in his “Entwicklungsgeschichte” (1915), and in this way they stand apart formally from most of the other proto-thematic expositions I have discussed above. They may promise a grander rhetorical scope in their later working-out—and even concerto-like qualities.
[5.7] Both expositions feature prominent phrase-rhythmic “fermatas,” or retardations of tonal rhythm, at the onset of their continuations. In BWV 944, dux and comes are themselves largely sequential, and their respective sequences, inside expansions of chords A and B, elapse in dotted-half (measure-length) tonal-rhythmic durations. Once the sequential continuation of chords B–F commences, durations double to dotted-wholes—a relaxation, as if in phrase-rhythmic acknowledgment of the retrogressive implication of these chords. Tonal rhythm accelerates upon the arrival of chord F, as if to build energy into the cadence in mm. 18–19.
[5.8] Imitative presentations in BWV 1003 transpire mostly in half- and quarter-note tonal-rhythmic durations. (Between the dux in mm. 1–3 and the comes in mm. 7–9 another comes is interpolated, along with duplicated, inverted copies of continuational chords B–E.) An analogous “fermata,” consisting of whole-note durations, marks the beginning of the continuation in m. 9. Although this continuation’s terminal cadence differs, and its acceleration is less pronounced, its relationship to the continuation in BWV 944 is clinched by a common elaboration motive: a descending-scale-with-upper-neighbor figure (marked with an asterisk on Examples 21a and 21b) appears in both continuations and induces a change in texture in anticipation of a cadence. The connections between the expositions of BWV 944 and BWV 1003 are unmistakable, and they argue strongly for their consideration as variations.
Example 22. Continuations as variations in (a) J. S. Bach, Suite in A Minor, BWV 818, Gigue; (b) J. S. Bach, Prelude in A Minor, WTC I, BWV 865
(click to enlarge)
[5.9] Close connections are also evident in the Prelude in A minor from WTC I, BWV 865, and the Gigue from the Suite in A Minor, BWV 818 (or 818a). Example 22 reproduces their compound-meter sequential continuations that modulate from A minor to C major, breaking on
Analysis: Fugue in A Minor, WTC II, BWV 889
[6.1] Variation may serve a developmental role, or may contribute to what Joel Lester (2001) calls “heightening levels of activity,” if a single piece elaborates the ➑–➐–➏–➎ proto-theme more than once, in more than one formal section. A case in point is the Fugue in A minor from WTC II, BWV 889. This fugue’s first proto-theme elaboration has already been introduced (see Examples 1c and 13c); a heightened, second elaboration shortly follows the first. Attention to the energetic shape of the fugue’s subject and its development within both elaborations of the proto-theme can enrich formal interpretation, especially with regard to Bach’s dynamic negotiations of formal functions.
Example 23. Tonal structure in J. S. Bach, Fugue in A Minor, WTC II, BWV 889; circumpuncts indicate the ends of periods
(click to enlarge)
[6.2] Example 23 graphs the tonal structure of the entire fugue. Circumpuncts (⊙) indicate a formal division into three periods, each of which concludes with a cadential formula.(32) The first period begins with the ➑–➐–➏–➎ proto-theme and then modulates to C major.(33) C major folds back into tonic at the beginning of the second period, but its traces in the tonic’s inner voices connect surreptitiously to chord B (Em) within the second statement of the proto-theme (m. 13; see the upward beam between the staves). Following a cadence in A minor, the third period provides tonal contrast to the tonic-heavy first two periods with an extensive prolongation of IV and then furnishes a final tonic cadence.
Example 24. J. S. Bach, Fugue in A Minor, WTC II, BWV 889, first period (excerpt): (a) mm. 1–3, (b) mm. 3–8
(click to enlarge)
[6.3] The first proto-theme elaboration, which makes up most of the fugue’s first period, is diagrammed again in Example 24. An initial dux statement, isolated in Example 24a, expands the tonic A minor (chord A) and concludes its essential –– voice leading on beat 1 of m. 3—a small “resting point” (see Kirnberger [1771–76] 1982, 114), or a “comma,” as marked. The dux propounds a basic relationship between tonal motion and motivic design: a quarter-note head motive induces tension with a grim diminished-seventh leap; resolution is accompanied by an accelerated, freely transformed restatement of the same motivic shape. I label the shapes of the head motive and its restatement z (for zigzag) and z′. The acceleration that accompanies the resolution of dissonance suggests an activity like drawing back and then releasing an arrow: like an object in motion, the eighth notes of z′ evince a tendency to continue, and so they shoot beyond the true end of the subject and into another z′ shape.(34) Example 24b begins at m. 3, with the comes answering and moving to a local key of E minor (chord B). The same energetic process is evident as the motivic eighth notes of z′ continue beyond the end of the comes itself and into a continuation (bridge). Now, however, the descending tetrachord ––– and its parallel tenths (across sequential chords B–F) guide further repetition of z′ as it falls steadily through retrogressing surface harmonies (“V”–“IV”–“III”) and loses energy with the release of E minor’s tonicizing hold. This left-grouping continuation enlarges the energetic shape of the original subject with a protracted “deintensification” (–– in mm. 1–3 ⇒ ––– in mm. 3–6) and causes the resting point of the comes to “migrate” from the downbeat of m. 5 to the downbeat of m. 6. Undulating thirty-second-note figures—ascending and descending stepwise fourths derived from the countersubject beneath the comes—sound in the bass part against this deintensification and provide a compensatory energizing influence. As falling z′ repetitions come to rest on chord F, the undulation conducts musical energy into the next dux statement through the ascending fourth C3–D3–E3–F3 in m. 6. (The C-major cadence that completes the first period does not appear on Example 24; the IAC at the end of this example is penultimate, not final, with respect to the form of this period.)
Example 25. J. S. Bach, Fugue in A Minor, WTC II, BWV 889, second period (excerpt), mm. 13–17
(click to enlarge)
[6.4] Example 25 shows varied treatment of the ➑–➐–➏–➎ proto-theme, with increased motivic complexity, in the second period of BWV 889. (The example does not include the events at the beginning of this period: a bass-part dux statement in C major [mm. 10–11], and a sequence that folds C major back into the global A-minor tonic [mm. 11–13].) The soprano-part comes statement at the beginning of the example repeats the tonal answer from mm. 3–5 an octave higher, now accompanied by an additional countersubject and with a subtle metrical adjustment: whereas the original dux–comes pair assumed an afterbeat metrical orientation, imitative entries in the second period shift to an upbeat orientation. (This fugue is in compound C, so that each notated measure represents two measures of
[6.5] The sequential continuation that follows the comes in Example 25 evolves into a cadence in A minor. Chords B (Em) and D (Dm) represent parallel tenths, as in the first period, but chord F (Am instead of CM) is inverted to a sixth. The inversion is motivically significant, for it motivates a more extensive “spinning-forth” of z′ through contrapuntal, registral, and formal space. In this “spinning forth,” z′ first splinters off of the comes in m. 15, then echoes through successively lower polyphonic parts in mm. 15–16 (heightening the first period’s analogous sequential measures), and finally ends up in the bass, where it supports cadential IV and V
[6.6] The third period of this fugue contains no proto-theme elaboration; further analysis would nevertheless reveal similar energetic processes. The course of the Urlinie is somewhat obscure at points within this period (see Example 23). corresponds to a prolongation of IV that extends from m. 23, through a type of evaded cadence in mm. 25–26, to
* * *
[7.1] The fugal expositions discussed above reveal a common conception in the series of chords shown in Example 2—itself a chordal development of a common voice-leading schema. Prolongation of tonic harmony through
[7.2] Variation principles seem to underlie Bach’s ➑–➐–➏–➎ proto-theme-based expositions. This does not mean, as I noted above, that Bach’s composition of these passages was a unidirectional process from proto-theme to finished fugue exposition. It may be more likely that he sometimes selected this proto-theme as a good continuation for his chosen subject matter (one might imagine, as he improvised in A minor), so that the end result became, as it were, a variation. Certain examples, as demonstrated above, make variation principles especially striking.
[7.3] A significant experiential feature of many of these expositions is their retrogressive implication of “V”–“IV”–“III” across descending parallel tenths (see Example 13a). Bach’s variations sometimes appear to respond to this implication by fashioning tonal-rhythmic “fermatas” or by connecting motivic processes to tonal shaping.
Example 26. The ➑–➐–➏–➎ schema as a guide to analysis (a) J. S. Bach, Fugue in
(click to enlarge and see the rest)
[7.4] If the schema in Example 3 does lie at the heart of the ➑–➐–➏–➎ proto-theme, then that schema, too, might be understood as a top-down organizer of expositional structure. The most natural tonal interpretation of the schema—as passing motion through tonic harmony—may again challenge assumptions that complete I–V–I progressions should map, Stufe by Stufe, onto successions of dux and comes. Example 26 graphs two passages from WTC accordingly. For the Fugue in D-sharp minor from WTC I, BWV 853 (Example 26a), I suggest that an apparent foreground motion to V
[7.5] When all is said and done, some may determine that recognizing certain schemata in Bach’s fugal writing eliminates the need for finely tuned Schenkerian readings, finding, perhaps, that the graphs I have presented throughout section 3, above, do more to obscure what is really a very simple idea—a series of chords and their variation—than they do to elucidate it; or that interpretation by schematic reference alone stays truer to Bach’s craft. I have not reached such a verdict, but I do believe that confrontations between schematic and Schenkerian assumptions can be productive for Baroque scholarship and may even be defining for the emergence of a post-Schenkerian standard.(36)
[7.6] Bach’s ability to forge ever-new content from his raw material was remarkable. His use of compositional patterns is well known, but by no means do these patterns guarantee compositional brilliance, as one quickly realizes upon attempting to work with them for oneself!
John S. Reef
Nazareth College
School of Music
4245 East Ave.
Rochester, NY 14618
jreef2@naz.edu
Works Cited
Baker, Michael. Forthcoming. “A Dorian Middleground Schema in Bach’s Minor-Key Fugue Expositions.” Conference Proceedings, Ninth European Music Analysis Conference.
Bartels, Ulrich, and Frieder Rempp, eds. 2008. “Vorwort.” In J. S. Bach. Werke zweifelhafter Echtheit für Tasteninstrumente, ed. Ulrich Bartels and Frieder Rempp, v–vii. Bärenreiter.
Beach, David W. 1988. “The Fundamental Line from Scale Degree 8: Criteria for Evaluation.” Journal of Music Theory 32 (2): 271–94. 2nd ed. https://doi.org/10.2307/843437.
—————. 2005. Aspects of Unity in J. S. Bach’s Partitas and Suites. Eastman Studies in Music. University of Rochester Press.
—————. 2019. Schenkerian Analysis: Perspectives on Phrase Rhythm, Motive, and Form. Routledge. https://doi.org/10.4324/9780429453793.
Braunschweig, Karl. 2015. “Expanding the Sentence: Intersections of Theory, History, and Aesthetics.” Music Theory and Analysis 2 (2): 156–93. https://doi.org/10.11116/MTA.2.2.2.
Brody, Christopher. Forthcoming. “Second-Reprise Opening Schemas in Bach’s Binary Movements.” Music Theory Spectrum.
Burkhart, Charles. 1997. Review of Analyzing Fugue: A Schenkerian Approach, by William Renwick. Music Analysis 16 (2): 270–81. https://doi.org/10.2307/854468.
Caplin, William E. 1986. “Funktionale Komponenten im achttaktigen Satz.” Musiktheorie 1 (3): 239–60.
—————. 1998. Classical Form: A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven. Oxford University Press.
Dahlhaus, Carl. 1978. “Satz und Periode: Zur Theorie der musikalischen Syntax.” Zeitschrift für Musiktheorie 9: 16–26.
Dreyfus, Laurence. 1996. Bach and the Patterns of Invention. Harvard University Press.
Fischer, Wilhelm. 1915. “Zur Entwicklungsgeschichte des Wiener klassischen Stils.” Studien der Musikwissenschaft 3: 24–84.
Forte, Allen, and Stephen Gilbert. 1982a. Introduction to Schenkerian Analysis. W. W. Norton.
—————. 1982b. Introduction to Schenkerian Analysis: Instructor’s Manual. W. W. Norton.
Grave, Floyd E. 1985. “Metrical Displacement and the Compound Measure in Eighteenth-Century Theory and Practice.” Theoria 1: 25–60.
Kirnberger, Johann Philipp. (1771–76) 1982. The Art of Strict Musical Composition (Die Kunst des reinen Satzes in der Musik). Excerpts translated by David Beach and Jurgen Thym. Yale University Press.
Kholodova, Elena. 1994. “Die Kraft der Metapher in der Musik: Bachs Figuralsprache und moderne Metapher-Forschung.” International Journal of Musicology 3: 115–32.
Kurth, Ernst. 1917. Grundlagen des linearen Kontrapunkts. Einführung in Stil und Technik von Bach’s melodischer Polyphonie. Max Drechsel.
—————. (1927) 1990. Foundations of Linear Counterpoint (Grundlangen des linearen Kontrapunkts). 3rd ed. Excerpts translated by Lee A. Rothfarb. In Ernst Kurth: Selected Writings, ed. and trans. Lee A Rothfarb, 37–95. Cambridge Studies in Music Theory and Analysis. Cambridge University Press. https://doi.org/10.1017/CBO9780511470288.
Ledbetter, David. 2002. Bach’s Well-Tempered Clavier: The 48 Preludes and Fugues. Yale University Press.
Lester, Joel. 2001. “Heightening Levels of Activity and J. S. Bach’s Parallel-Section Constructions.” Journal of the American Musicological Society 54 (1): 49–96. https://doi.org/10.1525/jams.2001.54.1.49.
Marlowe, Sarah. 2014. “Tonal Answers and Their Role within Fugue Expositions: Two Revised Paradigms.” Theory and Practice 39: 47–73. https://www.jstor.org/stable/26477726.
Martini, Giambattista. (1774–75) 1958. Esemplare o sia saggio fondamentale prattico di contrappunto fugato. Excerpts translated in The Study of Fugue, by Alfred Mann (Rutgers University Press, 1958), 263–314.
Maul, Michael, and Peter Wollny, eds. 2007. Weimarer Orgeltablatur. Die frühesten Notenhandschriften Johann Sebastian Bachs sowie Abschriften seines Schülers Johann Martin Schubart. Mit Werken von Dietrich Buxtehude, Johann Adam Reincken und Johann Pachelbel. Bärenreiter.
Mutch, Caleb. 2019. “The Formal Function of Fortspinnung.” Theory and Practice 43: 1–32.
Neumeyer, David. 1987a. “The Three-Part Ursatz.” In Theory Only 10 (1–2): 3–29.
—————. 1987b. “The Urlinie from as a Middleground Phenomenon.” In Theory Only 9 (5–6): 3–25.
Niedt, Friedrich Erhard. 1706. Handleitung zur Variation, wie man den General-Bass, und darüber gesetzte Zahlen variiren / artige Inventiones machen / und aus einen schlechten General-Bass Præludia, Ciaconen, Allemanden, Couranten, Sarabanden, Menueten, Giquen und dergleichen leichtlich verfertigen könne / samt andern nötigen Instructionen. Vol. 2 of Musicalische Handleitung. Benjamin Schillern.
Prout, Ebenezer. 1891. Fugue. London: Augener.
Rautio, Riita. 2004. “Fortspinnungstypus Revisited: Schemata and Prototypical Features in J. S. Bach’s Minor-Key Cantata Aria Introductions.” PhD diss., University of Jyväskylä.
Reef, John. 2019. “Subjects and Phrase Boundaries in Two Keyboard Fugues by J. S. Bach.” Music Theory Spectrum 41 (1): 48–73. https://doi.org/10.1093/mts/mty029.
Renwick, William John Michael. 1987. “Voice-Leading Patterns in the Fugal Expositions of J. S. Bach’s Well-Tempered Clavier.” PhD diss., City University of New York.
—————. 1995a. Analyzing Fugue: A Schenkerian Approach. Harmonologia Series 8. Pendragon Press.
—————. 1995b. “Hidden Fugal Paths: A Schenkerian View of Handel’s F Major Fugue (Suite II).” Music Analysis 14 (1): 49–67.
Renwick, William John Michael. 1995b. “Hidden Fugal Paths: A Schenkerian View of Handel’s F Major Fugue (Suite II).” Music Analysis 14 (1): 49–67.
Schachter, Carl. (1981) 1999. “A Commentary on Schenker’s Free Composition.” In Unfoldings: Essays in Schenkerian Theory and Analysis, ed. Joseph N. Strauss, 184–205. Oxford University Press.
Schenker, Heinrich. (1925) 2014. “Bach: Twelve Short Preludes, No. 12 [BWV 942].” Translated by Hedi Siegel. In The Masterwork in Music, vol. 1, ed. William Drabkin, 62–66. Dover Publications.
—————. (1926) 2014. “The Organic Nature of Fugue as Demonstrated in the C Minor Fugue from Bach’s Well-Tempered Clavier, Book I.” Translated by Hedi Siegel. In The Masterwork in Music, vol. 2, ed. William Drabkin, 31–54. Dover Publications.
—————. (1935) 1979. Free Composition (Der freie Satz). 2 vols. Vol. 3 of New Musical Theories and Fantasies. Translated and edited by Ernst Oster. Distinguished Reprints Series 2. Pendragon Press.
Schulenberg, David. 1982. “Composition as Variation: Inquiries into the Compositional Procedures of the Bach Circle of Composers.” Current Musicology 33: 57–87.
—————. 2006. The Keyboard Music of J. S. Bach. 2nd ed. Routledge.
Stapert, Calvin R. 2000. My Only Comfort: Death, Deliverance, and Discipleship in the Music of Bach. Grand Rapids, MI: Wm. B. Eerdmans Publishing.
Walker, Paul Mark. 2000. Theories of Fugue from the Age of Josquin to the Age of Bach. Eastman Studies in Music. University of Rochester Press.
Walther, Johann Gottfried. 1732. Musicalisches Lexicon. Leipzig: Wolffgang Deer.
Williams, Peter. (1980) 2003. The Organ Music of J. S. Bach. 2nd ed. Cambridge University Press. https://doi.org/10.1017/CBO9780511481871.
Willner, Channan. 2005. “Durational Pacing in Handel’s Instrumental Works: The Nature of Temporality in the Music of the High Baroque.” PhD diss., City University of New York.
Footnotes
1. On “particles,” melodic links between dux and comes, see Walker 2000, 256.
Return to text
2. On bridges see, for instance, Renwick 1995a, 110. I adopt the term “consolidation” from Lee A. Rothfarb’s translation of selected passages from Ernst Kurth’s Grundlagen des linearen Kontrapunkts ([1927] 1990, 59–63). In Grundlagen, Kurth describes how repetitions of a fugue’s dux and comes intermittently “consolidate” (verdichten) and “dissolve” (auflösen) within an essential, sustaining current. I find the idea of “consolidation” particularly apposite to situations in which an imitation follows upon, or flows out of, a sequence.
Return to text
3. To be sure, a single continuational sequence may both link to subsequent imitations (as a bridge) and prepare a cadence—for instance, if it culminates in a cadence that is overlapped by an imitation. This occurs in mm. 12–19 of BWV 944 (Example 1a). I have labeled the continuation in that excerpt “pre-cadential” to stress its large-scale formal role and to differentiate it from more typical bridges, which do not lead directly to cadences.
Return to text
4. See, for instance, Caplin 1998, Ch. 3.
Return to text
5. I might have used instead, in light of a Baroque focus, vocabulary related to Wilhelm Fischer’s Fortspinnungstypus construction: “Vordersatz,” “Fortspinnung,” and “Epilog.” Although these terms have been more characteristically applied to dance-suite movements and to ritornellos (Fischer 1915; Dreyfus 1996), they may be appropriate for fugues as well (Rautio 2004, 17). I do refer to Vordersatz and Fortspinnung in connection with a pair of fugues with concerto-like qualities in [5.6–5.9], although for the present research, in general, I have found sentential terminology to be more descriptive and adaptable. (Uncertainties about what constitutes an Epilog somewhat complicate the use of Fischer’s terms; see Caplin 1986, 256). On the definition and limits of the Fortspinnungstypus, see Mutch 2019; the historical connections between sentence and Fortspinnungstypus noted by Dahlhaus (1978), Braunschweig (2015), and others would seem to mitigate the apparent anachronism of my choice in lieu of a more typically Baroque construction.
Return to text
6. Particle figures may fall somewhat outside of a larger grouping structure (as in Example 1a) or they may group with the duces they follow (as in Example 10).
Return to text
7. Rothfarb discusses “formal dynamism” in connection with the work of August Halm (2009, Ch. 2), although (to the best of my recollection) I came to this locution independently.
Return to text
8. The subjects of BWV 889 and PWC 141 refer, in their four-note head motives, to a common Baroque figure that is characterized by an isolated down–up–down or up–down–up contour and, typically, a dissonant intervallic leap: in such a figure, lines drawn between notes 1 and 4 and between notes 2 and 3 would make a cross shape (see, for instance, Kholodova 1994, 119–20; Stapert 2000, 16). These two subjects resemble numerous others, including those of “And with His Stripes We Are Healed” from Handel’s Messiah, HWV 56; and of the fugal portion of Buxtehude’s Prelude in
Return to text
9. BuxWV 225 (Example 5a) is not dissimilar in its opening measures to Bach’s “Little” Prelude in A minor, BWV 942, which Example 10 quotes.
Return to text
10. My normalization of BuxWV 163 (Example 5b) refers to Bach’s Fugue in C-sharp minor from WTC II, BWV 873, which also features a schematically deviant exposition.
Return to text
11. For instance, Pachelbel’s Fugue in D minor, PWC 154, with a passus duriusculus subject, inverts the schematic voices of Example 3, albeit with the final ➎ omitted from the ➑–➐–➏–➎ tetrachord (and a
Return to text
12. The Fugue in E major from Johann Caspar Ferdinand Fischer’s Ariadne musica, to which Bach’s Fugue in E major from WTC II refers, also represents the ➑–➐–➏–➎ schema and suggests an evaded cadence, although without inganno voice leading. On inganno see, for example, Prout (1891, 74), Renwick (1995b, 50–52). J. S. Bach’s cousin Johann Gottfried Walther identifies this voice leading as a technique of cadential evasion in his Musicalisches Lexicon (1732, 125), but he does not use the term inganno.
Return to text
13. David Schulenberg writes that of the four Preludes BWV 939–942, the present one “comes closest to the Inventions, not only in its restriction to two voices but in its more tortuous melodic lines and more sophisticated, dissonant counterpoint” (2006, 171). On the authenticity of this Prelude, see Bartels and Rempp 2008, vi.
Return to text
14. A fifth level, e, appears below level d in Meisterwerk, but it pertains only to the second half of the Prelude BWV 942. What appears in level d may be rightly understood as foreground, although Schenker does provide a separate “Foreground Graph” to show a later stage of elaboration ([1925] 2014, 64).
Return to text
15. The first period of the Fugue in A minor, BWV 944 (mm. 1–33), if it were to stand alone, might project an Urlinie of ––, with C6 in measure 19 as Kopfton. With respect to the entire fugue’s Kopfton, C6 represents a superposed inner voice. Therefore, I refer to the perceptible arpeggiation E5–A5–C6 as a “simulated” initial arpeggiation.
Return to text
16. Measures 32–33 give the effect of V
Return to text
17. The descending tetrachord ➑–➐–➏–➎ may be more problematic in major keys because of the tendency of to ascend (see Neumeyer 1987b, 3), although major-key examples of the ➑–➐–➏–➎ schema forms in Example 3 are common.
Return to text
18. On polyphonic (three-part) Ursätze, see Neumeyer 1987a.
Return to text
19. In this way, the proto-theme elaboration in BWV 900 resembles the Eberlin Toccata excerpt in Example 4c, in which ➀ appears below the ➎/➂ dyad of the ➑–➐–➏–➎ schema, also because of a lower-part dux entry.
Return to text
20. Compare Schenker [1935] 1979, 1:115, 2: Fig. 134, 5.
Return to text
21. On this choice of Kopfton, see Schachter [1981] 1999, 195.
Return to text
22. David Beach’s (2005, 66–68) analysis of the fugal Gigue from the Suite in A Minor, BWV 818a, shows a structure similar to the model in Example 16c as well. Beach has also published two analyses of BWV 865, the first (with as Kopfton) in his “octave lines” article that appeared seventeen years earlier (1988, 283–88) than his analysis of BWV 818a, and the second (from ) in his recent textbook (2019, 141–45): these derive a less directed progression from I to III, with no intermediate Stufen apparent. Curiously, the proto-thematic passages from these two pieces appear to be more than tangentially related; at certain points they even seem like variations of each other (see Example 22). Readings in which their tonal structures are also similar (more in line with Beach’s analysis of BWV 818a) would be preferable.
Return to text
23. It is not unusual for Bach, in elaborating a prior idea, to relocate some upper-voice tones to the bass. A good example is BWV 819a, which reworks (or varies) the Allemande from the Suite in E-flat Major BWV 819. In both Allemandes, Urlinie degree progresses to (within an octave line) in m. 20: BWV 819 situates these degrees in the upper of two parts, as
Return to text
24. For recent work that engages with Renwick’s methodology, see, for example, Marlowe 2014 and Baker forthcoming.
Return to text
25. Renwick suggests: “we may infer from Schenker’s use of the past tense an implication of historical causality, that the transpositional interval of the fifth motivated to some extent the development of the standard tonal structure of the fugue exposition” (1995a, 109n).
Return to text
26. “We can understand Schenker to mean by direction that the three statements give an initial sense of harmonic and voice-leading progression away from and back to tonic, and by stability that they establish an initial tonic-prolonging section that is completed by the third statement. In this view, then, the subject–answer–subject plan encompasses a three-element harmonic structure, I–V–I, expressed in two motions, a departure from and a return to the tonic” (Renwick 1995a, 109).
Return to text
27. The beams in these exposition patterns do not necessarily demarcate complete structural units, serving instead to clarify the essential voice leading of dux and comes.
Return to text
28. Actual expositions that reflect this pattern (Example 19a: ––/low–middle–high) may nevertheless include bridge passages, despite bridges not being an essential feature of the pattern (Renwick 1995a, 116–17).
Return to text
29. A similar reading appears in Renwick 1987, 116.
Return to text
30. In Renwick’s analyses of complete fugues (rather than of expositions alone), a “from-the-surface” approach to structure cedes in importance to a more typically Schenkerian “from-the-background” perspective. Charles Burkhart summarizes: “Schenker’s point of view was always to conceive of the composition in terms of large tonal forces from whence motives and themes subsequently grow. These large forces constantly impinge on the themes and can modify both their meaning and shape. This is eminently true in the analysis of fugue, wherein subject statements can vary greatly in meaning from one to the other. Renwick is well aware of this (and points out many such cases), but he is purposely adopting, as far as is possible, a contrary point of view—focusing on the thematic element, to see how it influences the larger course of the composition. The reader needs to remember that the paradigms refer first of all to the structure of the subject (or answer) by itself, and that, within the structure of the entire composition, paradigm-notes can be superseded in rank by other notes” (1987, 176).
Return to text
31. The durations I trace in Example 21 correspond to what Channan Willner calls “basic pace” (2005, 6). I discuss the exposition of BWV 944 and its basic pace fluctuations more thoroughly in Reef (2019, 53–57).
Return to text
32. On period-level segmentation in this repertoire see, for instance, Reef (2019, 49–50).
Return to text
33. The C-major chord on which the first period concludes (m. 10) is inverted in the actual music, with E3 appearing in the bass and C6 in the soprano; Example 23 restores its notes to their obligatory placement. Despite appearing as a
Return to text
34. Kurth (1917, 205–6) remarks on the motivic transformation in the subject of the Fugue in A minor from WTC II. Descriptions throughout this text of energetic processes in fugues have influenced the present analysis.
Return to text
35. The initial dux statement in BWV 889 follows immediately upon an implied A-minor tonic harmony on the downbeat of m. 1 (what Channan Willner would term a “suppressed” “pedal call” [2005, 186]) and the comes follows suit, beginning directly after the A-minor downbeat harmony in m. 3. The dux at the beginning of the second period (not illustrated), however, overlaps the final cadence of the first period, so that it begins just before the C-major cadential downbeat of m. 10. As a result, the dux concludes not on a notated downbeat, but rather on the third beat of m. 11, and in doing so, it occasions a reinterpretation, with beat 3 of that measure assuming the status of a (hypermetrical) downbeat. The reinterpretation (weak beat 1, strong beat 3) endures into the comes at the beginning of Example 25.
Return to text
36. In this connection, see Brody forthcoming.
Return to text
Copyright Statement
Copyright © 2020 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Andrew Eason, Editorial Assistant
Number of visits:
8320